-
由于原子实对价电子较强的束缚, IIIA族金属单价离子的1S0—3P0跃迁对外界环境不敏感, 使得其在量子精密测量领域具有广泛的应用[1–9], 特别是, Al+离子和In+离子已成为重要的光钟体系[2–4,9]. Ga+离子作为IIIA族金属单价离子中重要的一员, 在物理和化学等领域也具有较大的应用潜力[5,6]. Ga+离子4s2 1S0—4s4p 3P0跃迁具有较高的品质因子(Q值), 较小的运动频移(原子质量较大)等优势, 适合作为光钟等精密测量实验的参考跃迁[5,6]. 准确的测量和计算Ga+离子的光谱和原子结构性质, 如跃迁概率、振子强度、朗德g因子、同位素位移、极化率等, 对发掘Ga+离子的在量子精密测量领域的潜在应用和检验原子分子结构理论具有重要意义[5,6].
在这些原子结构性质中, 电偶极(E1)动态极化率至关重要, 其反应原子(或离子)能级在电场中的移动, 是量子精密测量领域很关注的一个物理量[1,8–15]. 电偶极极化率的精密测量, 能为评估外界环境造成对原子(或离子)跃迁造成黑体辐射频移(blackbody radiation shift, BBR)以及激光造成的光频移(light shift)提供重要的参考[1,8–15]. 使原子或离子跃迁电偶极动态极化率为零的光的波长(或频率), 即“魔幻”波长 (‘magic’ wavelengths), 在离子的全光囚禁方面具有重要的应用[16,17]. 在“魔幻”波长下进行全光囚禁实验, 可以对囚禁的粒子产生足够强的囚禁势能的同时避免在相应跃迁上产生不必要的光频移, 从而保证实验的精度[16,17]. 对于离子光钟而言, 实现全光(“魔幻”波长)的囚禁多离子的体系可以提高囚禁离子光频标的稳定度[16,17]. 同时, 精确确定“魔幻”波长可以反推出对应跃迁的跃迁概率(或者振子强度), 有助于精确评估原子(或离子)跃迁的黑体辐射频移[18]. 使原子(或离子)能级移动为零的光的波长, 称之为“幻零”波长 (‘tune-out’ wavelengths)[7,19–21]. 在量子调控领域, 可以利用“幻零”波长在光学晶格中操控原子的量子态相位, 从而实现对光学器件性能的精确调控[7,19–21]. 一个能级的“幻零”波长通常出现在与该能级相关的较弱共振跃迁的激发能附近, 与“幻零”波长邻近的共振跃迁通常对该波长处的动态极化率具有主导贡献. 因此, 对“幻零”波长的精密测量可以高精度地确定相关跃迁的约化矩阵元(或者振子强度)之比[7,19–21]. 对原子的能级或跃迁的电偶极动态极化率以及“魔幻”波长和“幻零”波长的理论计算, 一方面可以为一些精确评估原子静态极化率精确测量方法例如, “极化率”天平方法[8], “反推法”[18]的误差分析提供必要的依据, 另一方面, 也为一些精密测量实验, 例如, “魔幻”波长和“幻零”波长的精密测量实验, 提供必要的理论指导. 值得注意的是, 已有很多关于Al+离子和In+离子极化率的研究[1,2,7,8,15,22–24 ], 但鲜有对Ga+离子的极化率, 特别是动态极化率的研究.
基于上述动机, 本文利用基于相对论的组态相互作用加多体微扰的方法(relativistic configuration interaction plus many-body perturbation theory, RCI+MBPT)[7,15,25–30] 计算了Ga+离子基态和低激发态的能级结构以及电偶极跃迁约化矩阵元(reduced matrix elements, RMEs), 进一步计算了4s2 1S0态和4s4p 3P0态的动态极化率, 并分别给出两个态的“幻零”波长以及跃迁4s2 1S0—4s4p 3P0的“魔幻”波长, 并结合“极化率天平”方法, 讨论静态极化率测量过程中的理论计算误差随波长的变化. 第2节将介绍所用理论方法和计算细节; 第3节给出Ga+能级、约化矩阵元、电偶极动态极化率、“魔幻”波长和“幻零”波长的计算结果以及相应的讨论.
如无特殊说明, 本文所用单位制一律为原子单位(a.u.).
-
原子极化现象涉及物理学中的多个领域和过程[11]. 电磁场会使处于其中的原子体系的电荷发生不均匀分布, 这种现象被称为原子极化现象[7,11]. 由于极化现象的发生, 会使得原子体系的能级发生移动[7,11] , 其中与电场相关的能级移动称为Stark移动[11]. 电偶极极化率是极化现象和Stark移动的重要表征[7,11]. 原子能级的Stark移动在忽略高阶效应的情况下可表示为[7,8,11,28–30]:
其中,
$ \alpha \left(\omega \right) $ 为原子能级的电偶极动态极化率,$ \omega $ 是电场的频率, F是电场强度. 量子态的电偶极动态极化率一般由标量、矢量和张量3个分量组成[7,8], 可由态求和方法(sum-over-states approach, SOS)获得. 本文所涉及的Ga+离子的基态4s2 1S0和第一激发态4s4p 3P0的总角动量量子数J都为0, 这使得其极化率的矢量部分和张量部分都为0, 因此, 我们只考虑标量极化率, 它可以方便地分为3个部分[1,7,8,11,28–30]:式中,
$ {\alpha }_{{\mathrm{v}}}\left(\omega \right) $ ,$ {\alpha }_{{\mathrm{c}}{\mathrm{o}}{\mathrm{r}}{\mathrm{e}}}\left(\omega \right) $ 和$ {\alpha }_{{\mathrm{cv}}}\left(\omega \right) $ 分别代表价电子、原子实以及价电子和原子实的相互作用对极化率的贡献部分.$ {\alpha }_{{\mathrm{c}}{\mathrm{v}}}\left(\omega \right) $ 部分相较于其他两部分通常较小, 甚至可以忽略不计[5,31], 而价电子的贡献部分往往占主导$ {\alpha }_{{\mathrm{v}}}\left(\omega \right) $ . 价电子部分$ {\alpha }_{{\mathrm{v}}}\left(\omega \right) $ 可以表示为[1,7,11,27–31]式中, 下标g代表要求极化率的态, i代表能与g态发生量子跃迁的态,
$ \left\langle{{\psi }_{{\mathrm{g}}}\|D\|{\psi }_{{\mathrm{i}}}}\right\rangle $ 为态g到态i的约化跃迁矩阵元,$ {E}_{{\mathrm{i}}} $ 为态i的能量值,$ {E}_{{\mathrm{g}}} $ 为态g的能量值,$ {J}_{{\mathrm{g}}} $ 代表g态的总角动量量子数.$ \omega $ 为电磁场的频率. 当$ \omega $ 的数值逐渐趋近于0时, 动态极化率$ \alpha \left(\omega \right) $ 逐渐过渡为静态极化率$ \alpha \left(0\right) $ .由于Ga3+最低电子态跃迁的共振能量远高于可见光范围, 故在此范围内, 可认为原子实贡献部分
$ {\alpha }_{{\mathrm{c}}{\mathrm{o}}{\mathrm{r}}{\mathrm{e}}}\left(\omega \right) $ 不随频率变化而变化. 静态极化率和动态极化率之间的关系, 可以表示为[2,8]其中, 振子强度表示为
由(2)式和(3)式可知, 存在某个频率
$ {\omega }_{{\mathrm{T}}} $ , 使得$ \alpha \left(\omega \right) $ 为0, 该频率对应的波长$ {\lambda }_{{\mathrm{T}}} $ 就是“幻零”波长[7,19–21], 也存在某个频率$ {\omega }_{{\mathrm{M}}} $ , 使得某个跃迁相关的两个态的动态极化率之差为0, 这个频率所对应的波长$ {\lambda }_{{\mathrm{M}}} $ 被称为“魔幻”波长[16–18]. -
假设存在一种基态和某个激发态之间静态极化率之差精度较高离子, 可以用这种离子的基态和激发态之间极化率之差作为极化率参考, 称之为参考离子(reference ion), 这个离子的极化率可以看作是“极化率天平”的一个标准砝码. 想了解基态和激发态之间极化率之差的离子, 称之为目标离子(target ion)[8]. 将参考离子和目标离子囚禁在同一个离子阱中, 用一束光功率足够大、斑半径为百微米量级、瑞利距离为cm量级的红外背景激光, 从离子阱的轴向同时照射参考离子和目标离子, 使其在两种离子对应跃迁上同时产生光频移, 在两种离子上产生的光频移分别记作
$ {{{\Delta }}\upsilon }_{{\mathrm{R}}{\mathrm{e}}{\mathrm{f}}} $ 和$ {{{\Delta }}\upsilon }_{{\mathrm{T}}{\mathrm{a}}{\mathrm{r}}} $ . 假设背景光的频率为$ \omega $ , 记在此背景光下, 两种离子基态和所涉及激发态之间动态极化率之差分别为$ {{{\Delta }}\alpha }_{{\mathrm{R}}{\mathrm{e}}{\mathrm{f}}}\left(\omega \right) $ 和$ {{{\Delta }}\alpha }_{{\mathrm{T}}{\mathrm{a}}{\mathrm{r}}}\left(\omega \right) $ . 在频率为$ \omega $ 的激光照射下, 原子跃迁产生的光频移可以简单表示为(1)式.在离子阱中, 两个离子沿轴向排列, 且离子间的距离通常在μm量级, 远小于背景光的瑞丽距离(cm量级), 故两种离子感受到的光功率密度(或电场强度)近似相等, 是一种原位的测量. 因此, 参考离子和目标离子在此频率下相应跃迁上产生的光频移比值可表示为[8]
由于两个离子感受到的光功率密度之比
$ {I}_{{\mathrm{R}}{\mathrm{e}}{\mathrm{f}}}/{I}_{{\mathrm{T}}{\mathrm{a}}{\mathrm{r}}} $ 近似相等, 故光频移的比值就近似等于两个离子基态和对应激发态动态极化率之差的比值. 通过两个离子对应跃迁相关态的极化率之差的比值的高精度的测量, 就能将参考离子动态极化率的精度无损失的传递到目标离子上. 再通过(4)式、(5)式, 就能精确求得目标离子的基态和相关激发态的静态极化率之差. -
RCI+MBPT是基于相对论的组态相互作用加多体微扰方法的简称, 是一种非常卓越的原子结构计算方法[7,15,25–30,32]. 我们使用的RCI+MBPT程序包是由Kozlov等[26]开发的开源版本. RCI+MBPT方法充分结合了RCI和MBPT两种方法的优点. RCI方法在“冻结”原子实的近似下, 考虑了价电子(VV)之间的关联效应, MBPT方法处理原子实电子之间和原子实与价电子间的关联效应. 相应计算从Hartree-Fock-Dirac (HFD)方程的数值解开始, 使用有限差分法得到单电子HFD能量以及原子实电子和价电子的波函数. 这一步考虑到了1s-5s, 2p-5p, 3d-4d, 4f-5f和5g轨道. 然后通过嵌入在程序包中的自动生成子程序自动生成虚轨道. 虚轨道的最大的主量子数Nmax和最大轨道量子数Lmax分别设置为30和5. HFD轨道和自动生成的虚轨道构成了后续的RCI和MBPT计算的组态空间(或轨道空间). Ga+离子的电子构型可以看作是一个紧密的原子实(1s2 2s2 2p6 3s2 3p6)和原子实外的两个价电子. RCI空间是由一系列的组态构成, 这些组态包含了在给定的组态空间里面所有可能的价电子单激发和双激发. 本计算中, Ga+选取的参考组态分别为{4s2, 4s5s, 4s4d}(偶宇称态)和{4s4p}(奇宇称态). 单、双激发到最高轨道为30s, 30p, 30d和30f. 本计算中, 单电子轨道包括1s-30s, 2p-30p, 3d-30d和4f-30f轨道. 选取径向积分范围Rmax = 300 a.u..
在RCI+MBPT中, 两价电子有效的哈密顿量可以写成[7,15,25–30,32]:
式中,
$ {h}_{1} $ 和$ {h}_{2} $ 分别是相对论哈密顿量的单电子和双电子相互作用项. 在RCI计算方法中,$ {h}_{1} $ 包含电子的动能, 与原子实的库仑相互作用以及原子实闭壳层的HFD势能.$ {h}_{2} $ 是价电子之间的相互作用. 在RCI+MBPT程序中,$ {h}_{1} $ 是一个表示特定价电子与原子实关联相互作用的单电子算符,$ {h}_{2} $ 是一个表示在被原子实电子屏蔽情况下的两个价电子之间相互作用的双电子算符. 这两个算符都是按MBPT的二阶微扰来计算. 至于粒子间短程相互作用的量子力学效应, 则用Breit相互作用描述, 很多研究表明, Breit相互作用对较小质量数的体系影响较小[7,15,33], 故这里暂不讨论Breit相互作用带来的影响. -
本文利用RCI+MBPT方法给出了Ga+离子最低的23个能级的能量值以及4s2 1S0态和4s4p 3P0态的相关电偶极跃迁的RMEs, 计算细节在第2节已经给出. 能级的能量值见表1, 给出了RCI, RCI+MBPT方法得到的23个能级的能量值. 结果显示, RCI+MBPT方法得到的能量值结果精度相对于纯RCI方法得到很大提高, 约有一个数量级, 这是因为RCI+MBPT方法包含了更多的电子关联效应. 我们将得到的推荐能量值(RCI+MBPT得到的值)和美国国家标准局(NIST)的推荐值[34]进行比较, 结果表明, 本文结果与NIST推荐值之间的差别小于或等于0.7%, 甚至4个能级(4s4p 3P0, 4s4p 3P1, 4s4p 1P1和 4p2 3P1)能量值与NIST推荐值之间的差别低于0.1%. 据我们了解, 有8个能级(例如, 4s6p 3P1, 4s6p 1P1)的能量值由本文首次给出, 这为Ga+离子能级结构的实验研究提供了参考. 得到的能级能量值也同其他的实验值和理论计算值[5,35,36]进行比较, 结果与其他的实验值和理论计算值一致, 相对差值在1.5%以内.
Ga+离子的4s2 1S0态和4s4p 3P0态涉及的E1跃迁的RMEs使用RCI+MBPT方法得到, 并在表2中给出. 我们给出了长度和速度两种规范的结果, 结果显示, 两种规范的结果符合得较好, 4s4p 3P0涉及的跃迁约化跃迁矩阵元两种规范的相对差别均小于8%, 4s2 1S0态涉及的跃迁矩阵元两种规范的一致性稍差, 相对差异从0.1%—50%以上, 这是由于4s2 1S0态所涉及的跃迁大部分较弱, 导致相对计算误差较大. 也将计算的最终推荐值和NIST推荐结果[34]以及其他的理论和实验结果[5,35,37–40]相比较, 结果符合较好, 除去几个较弱的跃迁(例如, 4s2 1S0—4s4p 3P1), 差别均在10%以内, 这说明RCI+MBPT模型能较好描述Ga+离子的结构, 同时也说明, 我们选择的计算参数是合适的. 为了给出具有说服力的误差评估结果, 我们也给出了纯RCI的计算结果. 结果显示, RCI+MBPT方法得到的数值与其他参考方法得到的值[5,35,37–40]更为接近. 许多研究表明, 对于E1跃迁的RMEs, 长度规范的计算值与实验值符合得更好, 同时, 长度规范和速度规范的差异也是给定计算不确定度的重要依据[7,41,42]. 以RCI+MBPT得到的长度规范值为推荐认可值, 以纯RCI和RCI+MBPT两种方法两种规范的4个值中的最大值与最小值的差为不确定度. 上述几种方式得到的数值, 推荐值以及其不确定度见表2.
-
根据(2)式和(3)式, 结合以上得到相关E1跃迁的RMEs和其不确定度, 使用SOS方法得到Ga+离子基态4s2 1S0和第一激发态4s4p 3P0的静态极化率以及其不确定度, 如表3所示. 计算中, 我们使用的能量值来自于NIST数据库的推荐值, NIST数据库未收入的能量值则使用RCI+MBPT方法得到的计算值. 结果显示, 对于4s2 1S0态, 仅有跃迁4s2 1S0—4s4p 1P1贡献比较大, 其余项贡献较小; 对于态4s4p 3P0来说, 有3个跃迁(4s4p 3P0—4s4d 3D1, 4s4p 3P0—4p2 3P1, 4s4p 3P0—4s5s 3S1)贡献较大, 其他项贡献较小. 原子实贡献
$ {\alpha }_{{\mathrm{c}}{\mathrm{o}}{\mathrm{r}}{\mathrm{e}}}\left(0\right) $ 使用文献[5]的计算值, 为1.24 (1), 相较于价电子的贡献较小. 这里忽略$ {\alpha }_{{\mathrm{cv}}}\left(0\right) $ 的贡献. 我们也得到了两个态的静态极化率的差值为1.43 (3.2), 与其他计算结果[5]相比较, 本文结果包含更多跃迁的贡献项(例如, 4s2 1S0—4snp 3P1等跃迁的贡献). 本文结果和其他方法得到结果[5]有较好的一致性, 差别都小于14%,$ \alpha \left(0\right)( $ 4s2 1S0$ ) $ 差别为0.17%,$ \alpha \left(0\right)( $ 4s4p 3P0$ ) $ 差别为0.88%, Δα(0)差别为14%. 误差的主要贡献来自4s2 1S0—4s4p 1P1, 4s4p 3P0—4s4d 3D1, 4s4p 3P0—4p2 3P1三项. -
由(2)式和(3)式, 利用以上得到相关E1跃迁的RMEs和其不确定度, 也能得到两个量子态的动态极化率曲线. 极化率的原子实贡献部分
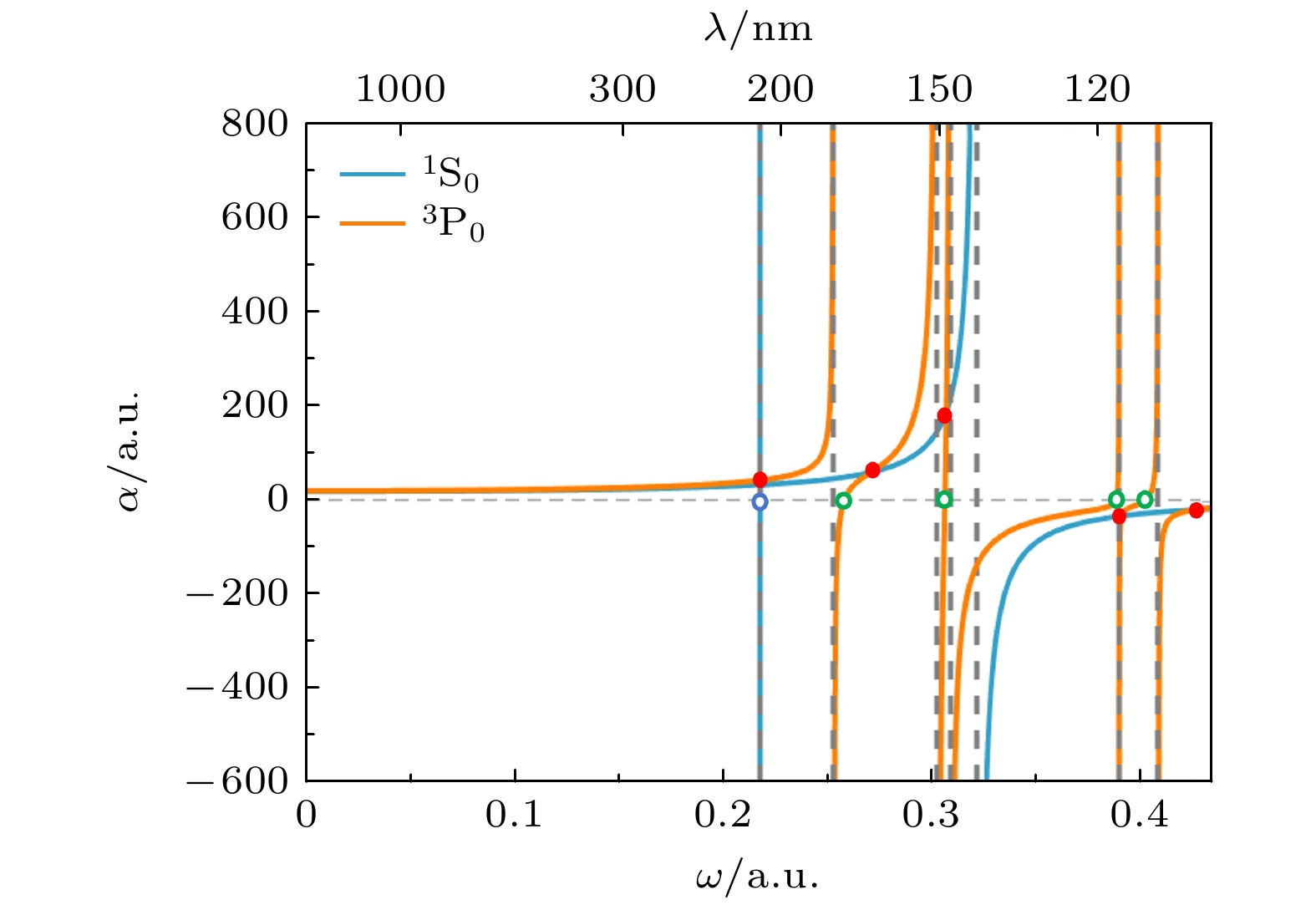
$ {\alpha }_{{\mathrm{c}}{\mathrm{o}}{\mathrm{r}}{\mathrm{e}}}\left(\omega \right) $ 为1.24 (1) a.u.[5], 且该值在我们计算的范围内(0—0.44 a.u.), 不随频率变化. Ga+离子4s2 1S0态和4s4p 3P0态的动态极化率曲线如图1所示. 从图1可以看出, 4s2 1S0态的动态极化率有2个发散点, 它们的横坐标对应着两个跃迁4s2 1S0—4s4p 3P1和4s2 1S0—4s4p 1P1的共振能量值. 在0—0.44 a.u.范围内, 4s2 1S0态的动态极化率有1个零点(图1中蓝色空心圆), 即存在1个“幻零”波长, 波长值为209.101 (26) nm (对应频率的中心值为0.217901 a.u.), 很接近4s2 1S0—4s4p 3P1的共振波长209.143 nm. 4s4p 3P0态动态极化率有5个发散点, 对应着相关5个较强跃迁. 4s4p 3P0态动态极化率曲线有4个零点(图1中绿色空心圆), 意味着4s4p 3P0态有4个“幻零”波长, 均处于紫外波段, 它们的数值分别是176.42 (34) nm (对应频率的中心值为0.25827 a.u.), 148.61(16) nm (对应频率的中心值为0.30660 a.u.), 117.197 (59)nm (对应频率的中心值为0.388775 a.u.)和113.09 (16) nm(对应频率的中心值为0.40290 a.u.). 这些“幻零”波长的不确定度全部来源于对应约化跃迁矩阵元的不确定度.同时可以看出, 两个态的动态极化率曲线有5个交点(图1中红色实心圆), 即跃迁4s2 1S0—4s4p 3P0存在5个“魔幻”波长, 它们也处于紫外波段, 它们的数值分别为209.286(11) nm (对应频率的中心值为0.217709 a.u.), 168.1(3.6) nm (对应频率的中心值为0.2710 a.u.), 148.27(17)(对应频率的中心值为0.30730 a.u.), 116.38(17) nm (0.391500 a.u.)和106.7(2.8) nm (对应频率的中心值为0.4272 a.u.). 这些“魔幻”波长的不确定度全部来源于对应约化跃迁矩阵元的不确定度.
表4为“幻零”波长和“魔幻”波长的不确定度评估. 这些不确定度均由相关约化跃迁矩阵元的不确定度通过求平方和的误差合成法则得到. 占主导贡献的部分在表中加重. 除去168.1 nm和106.7 nm处的两条“魔幻”波长不确定度为3.6 nm和2.8 nm外, 其余的“魔幻”波长和“幻零”波长的不确定度均小于1 nm, 这为Ga+离子全光囚禁实验的激光器选择提供了波长建议和指导. 对4s2 1S0 态的“幻零”波长的不确定度贡献最大的跃迁为4s2 1S0— 4s4p 3P1和4s2 1S0—4s4p 1P1, 对4s4p 3P0态的4条‘幻零’波长贡献较大跃迁为4s4p 3P0—4s4d 3D1和4s4p 3P0—4p2 3P1. 对5条“幻零”波长贡献较大的跃迁为4s2 1S0—4s4p 1P1, 4s4p 3P0—4s4d 3D1, 4s4p 3P0-4p2 3P1, 特别是4s2 1S0—4s4p 1P1占据主导地位. 进一步提升这3个跃迁约化矩阵元的精度(理论计算或精密测量), 能更加精确地获得这5条“魔幻”波长, 对Ga+离子全光囚禁实验激光波长的选择能给出更加精确的建议, 也能更准确地预言“幻零”波长的位置, 为相应的精密测量实验提供指导.
Holmgren等[19], Herold等[20,21], Yu等[30,43]以及Tang等[18]研究表明, 精密测量“幻零”波长和“魔幻”波长可以用于精确确定相关跃迁的振子强度或者约化跃迁矩阵元. “幻零”波长和“魔幻”波长处相关跃迁对两个光钟态4s2 1S0和4s4p 3P0的动力学极化率的贡献如表5所示. 表中占绝对贡献的部分已经着重标出. “幻零”波长和“魔幻”波长一般离相应的跃迁的共振频率较近, 在这些波长附近, 相应跃迁对动态极化率的贡献较大, 甚至处于主导地位, 精确测量这些波长以及这些波长附近的动态极化率的变化, 能精确获得相应跃迁的约化矩阵元. 例如, 在209.101 nm的“幻零”波长附近, 主导贡献跃迁4s2 1S0—4s4p 1P1(贡献90%以上)对4s2 1S0态动态极化率贡献随波长变化缓慢, 波长引起的动态极化率的变化可认为完全是由4s2 1S0—4s4p 3P1引起. 精确测量这个“幻零”波长以及此波长附近动态极化率的变化, 能精确测量出4s2 1S0—4s4p 3P1跃迁的跃迁矩阵元以及其与主导跃迁约化矩阵元的比值. 其他波长附近的情况与此类似. 精确测量Ga+离子基态和第一激发态的这5个“幻零”波长以及跃迁4s2 1S0—4s4p 3P0的5个“魔幻”波长, 有利于精确确定相关跃迁的振子强度或者约化跃迁矩阵元, 可以对精确测量Ga+离子4s2 1S0—4s4p 3P0跃迁的静态极化率提供理论指导.
-
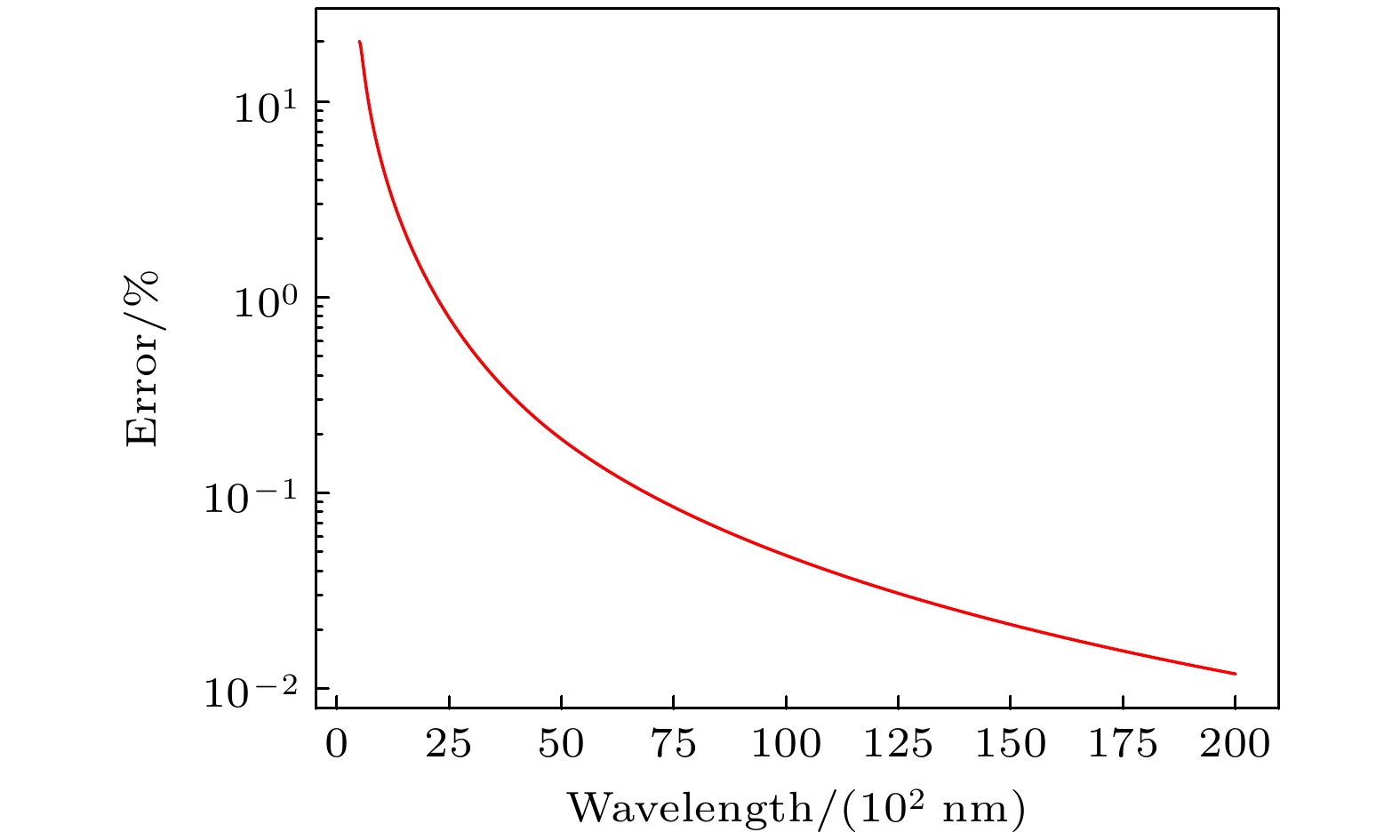
基于原位测量的“极化率天平”方法摆脱离子种类以及激光光斑性质和光功率的限制, 可以实现不同种类离子的极化率的相对误差无放大的测量, 提高了极化率的测量精度[8]. 基于“极化率天平”方法, 使用我们计算的RMEs, 由(4)式和(5)式对Ga+离子基态和第一激发态的静态极化率之差的理论计算误差进行计算, 理论计算误差与实验使用背景激光的波长的关系如图2所示. 可以看出理论计算误差随实验中使用的背景激光波长增大而减小, 使用长波激光, 特别是红外激光作为背景光, 有利于减小理论计算不确定度. 使用波长大于2 μm的背景激光, 可使理论计算误差低于1%; 使用波长大于6 μm的激光作为背景光, 可使得理论计 算误差低于0.1%. 计算中发现, 误差的主要来源是 4s2 1S0—4s4p 1P1, 4s4p 3P0—4s5s 3S1, 4s4p 3P0 —4s4d 3D1, 4s4p 3P0—4p2 3P1这4个跃迁的RMEs的误差, 因此, 更高精度的RMEs计算和测量, 有助于提高Ga+离子基态和第一激发态的静态极化率之差在“极化率天平”测量方法中的理论计算误差. 在实际测量过程中, 往往会引入一个参数
$ {\delta }_{0} $ 来调节误差分布, 从而减小理论计算误差[2,8], 但是$ {\delta }_{0} $ 对于不同误差的RMEs序列会有不同取值, 缺少一定的普适性, 本文仅作为普适规律性探讨, 故不做此演示. -
本文利用RCI+MBPT方法对Ga+离子的4s2 1S0态和4s4p 3P0态的动态极化率进行理论计算. 得到了4s2 1S0态和4s4p 3P0态的5个“幻零”波长和跃迁4s2 1S0—4s4p 3P0的5个“魔幻”波长, 均处于紫外波段. 精密测量这些“幻零”和“魔幻”波长, 有利于精确确定相关跃迁的振子强度或者约化跃迁矩阵元, 对研究Ga+离子的原子结构性质和发掘Ga+离子的潜在应用具有重要意义. 同时, 这些“魔幻”和“幻零”波长的精密测量, 对进一步研究Ga+离子的Ga+离子全光囚禁具有重要作用. 我们也基于“极化率天平”方法, 讨论Ga+离子基态和第一激发态静态极化率测量之差过程中的理论计算误差随波长的变化, 给出了相应背景激光波长的建议, 为进一步高精度确定4s2 1S0和态4s4p 3P0态的静态极化率提供理论指导.
感谢圣彼得堡核物理研究所 Kozlov M G 教授和中国科学院物理研究所于艳梅副研究员在RCI+MBPT程序方面的指导和讨论; 感谢中国科学院精密测量科学与技术创新研究院黄学人研究员和李承斌副研究员有帮助的指导和交流; 感谢山东师范大学物理与电子科学学院的孟庆田教授、孙平教授、刘劲松博士以及华东师范大学徐信业教授、唐志明博士有帮助的讨论.
Ga+ 离子4s2 1S0—4s4p 3P0跃迁动态极化率的理论计算
Theoretical calculation of dynamic polarizability of 4s2 1S0—4s4p 3P0 transition for Ga+ ion
-
摘要: 利用相对论的组态相互作用加多体微扰理论方法, 对Ga+离子的4s2 1S0—4s4p 3P0跃迁的动态极化率进行了理论计算. 并计算出了4s2 1S0态和4s4p 3P0态的“幻零”波长以及跃迁4s2 1S0—4s4p 3P0的“魔幻”波长, 对这些“幻零”波长和“魔幻”波长的精密测量提供了理论指导, 对研究Ga+离子的原子结构和4s2 1S0, 4s4p 3P0两量子态静态极化率之差的精确确定, 以及Ga+离子的全光囚禁具有重要意义. 同时, 基于“极化率天平”方法, 讨论了静态极化率测量过程中的理论计算误差随波长的变化, 为进一步高精度确定4s2 1S0态4s4p 3P0态的静态极化率提供了理论指导.Abstract: The transition of Ga+ ions from 4s2 1S0 to 4s4p 3P0 has advantages such as a high quality factor and a small motional frequency shift, making it suitable as a reference for precision measurement experiments like optical clocks. Calculating the dynamic polarizability of 4s2 1S0—4s4p 3P0 transition for Ga+ ion is of great significance for exploring the potential applications of the Ga+ ion in the field of quantum precision measurement and for testing atomic and molecular structure theories. In this paper, the dynamic polarizability of the Ga+ ion 4s2 1S0—4s4p 3P0 transition is theoretically calculated using the relativistic configuration interaction plus many-body perturbation (RCI+MBPT) method. The “tune-out” wavelengths for the 4s2 1S0 state and the 4s4p 3P0 state, as well as the “magic” wavelength of the 4s2 1S0—4s4p 3P0 transition, are also computed. It is observed that the resonant lines situated near a certain “turn-out” and “magic” wavelength can make dominant contributions to the polarizability, while the remaining resonant lines generally contribute the least. These “tune-out” and “magic” wavelengths provide theoretical guidance for precise measurements, which is important for studying the atomic structure of Ga+ ions. The accurate determination of the difference in static polarizability between the 4s2 1S0 and 4s4p 3P0 states is of significant importance. Additionally, based on the “polarizability scaling” method, this work also discusses how the theoretical calculation errors in static polarizability measurements vary with wavelength, which provides theoretical guidance for further determining the static polarizability of the 4s2 1S0 and 4s4p 3P0 states with high precision. This is crucial for minimizing the uncertainty of the blackbody radiation (BBR) frequency shift in Ga+ optical clock and suppressing the systematic uncertainty.
-
Key words:
- dynamic polarizability /
- Ga+ /
- atomic structure calculation /
- RCI+MBPT .
-

-
表 1 Ga+离子的最低的23个能级的能量值 (cm–1), 第1行数值为基态的绝对能量值, 其他行数值为激发态相对于基态的激发能
Table 1. Energies of 23 lowest energy levels of Ga+ ion (cm–1), the value in the first row represents the absolute energy of the ground state, while the values in the other rows represent the excitation energies of the excited states relative to the ground state.
State RCI RCI+MBPT NIST Diff./% Refs. 4s2 1S0 396252.81 412181.94 413285.38 –0.27 413285.41CICP [5] 4s4p 3P0 43174.90 47338.76 47367.55 –0.060 47367.57 CICP [5]; 47032 MCDHF [35]; 47368Expt [36] 4s4p 3P1 43584.84 47792.83 47814.114 –0.044 47469 MCDHF [35]; 47814 Expt [36] 4s4p 1P1 68389.17 70709.25 70701.427 0.011 70701.42 CICP [5]; 70455 MCDHF [35]; 70701 Expt [36] 4s5s 3S1 96653.91 102623.02 102944.595 –0.31 100749.90 CICP [5]; 102665 MCDHF [35]; 102945 Expt [36] 4s4d 3D1 106905.35 113471.29 113815.885 –0.30 113815.87 CICP [5]; 113305 MCDHF [35]; 113816 Expt [36] 4p2 3P1 109300.03 115272.94 115224.47 –0.042 115224.49 CICP [5]; 114590 MCDHF [35]; 115224 Expt [36] 4s5p 3P1 111880.88 118110.59 118518.461 –0.34 118236 MCDHF [35]; 118518 Expt [36] 4s5p 1P1 114324.78 120211.72 120550.431 –0.28 120715.81 CICP [5]; 120322 MCDHF [35]; 120550 Expt [36] 4s6s 1S0 126011.01 132559.65 133010.30 –0.34 130793.68 CICP [5]; 133517 MCDHF [35]; 133741 Expt [36] 4s5d 3D1 129989.22 136706.55 137157.524 –0.33 137155.79 CICP [5]; 136759 MCDHF [35]; 137157 Expt [36] 4s6p 3P1 132039.60 138646.98 — — — 4s6p 1P1 132671.60 139209.74 — — — 4s7s 1S0 138282.16 145005.12 145494.205 –0.34 145176 MCDHF [35]; 145494 Expt [36] 4s6d 3D1 140241.35 147033.96 147520.34 –0.33 — 4s8s 1S0 144640.75 151383.73 151923.93 –0.36 — 4s7d 3D1 145733.76 152563.77 153064.92 –0.33 — 4s7p 3P1 141291.01 148033.38 — — — 4s7p 1P1 141504.08 148239.62 — — — 4s8p 3P1 146349.69 153163.32 — — — 4s8p 1P1 146429.38 153251.11 — — — 4s9s 1S0 148859.67 154959.21 — — — 4s8d 3D1 149030.92 155885.88 156386.7 –0.32 — 表 2 使用RCI+MBPT方法得到的Ga+离子 4s2 1S0态和4s4p 3P0态的电偶极约化跃迁矩阵元 (a.u.)
Table 2. Reduced matrix elements of E1 transition for the 4s2 1S0 and 4s4p 3P0 of Ga+, obtained by using the RCI+MBPT methods (a.u.).
Method RCI RCI+MBPT Recommend Refs. Guage Length Velocity Length Velocity 4s2 1S0—4s4p 3P1 0.055752 0.059065 0.064832 0.072400 0.065 (17) 0.0744 [34]; 0.0895 MCDHF [35]; 0.0802 RRPA [38] 4s2 1S0—4s4p 1P1 3.0918 3.0507 2.8480 3.0361 2.84 (24) 2.69 CICP [5]; 2.87 [34]; 2.68 MCDHF [35]; 2.81 MP [37];
2.79 RRPA [38]; 2.71 MCHF [39]; 2.78 (11) Expt [40]4s2 1S0—4s5p 3P1 0.000595 0.000455 0.00594 0.000400 0.006 (6) — 4s2 1S0—4s5p 1P1 0.28458 0.27302 0.15426 0.23982 0.15 (13) 0.138 [34] 4s2 1S0—4s6p 3P1 0.00229 0.00237 0.00815 0.00272 0.0082 (59) — 4s2 1S0—4s6p 1P1 0.0741 0.0684 0.0868 0.0594 0.087 (27) — 4s2 1S0—4s7p 1P1 0.0264 0.0229 0.0143 0.0205 0.014 (12) — 4s2 1S0—4s7p 3P1 0.00232 0.00249 0.00803 0.00298 0.008 (6) — 4s2 1S0—4s8p 1P1 0.00986 0.00753 0.0183 0.00768 0.02 (1) — 4s2 1S0—4s8p 3P1 0.00202 0.00233 0.00787 0.003104 0.008 (6) — 4s4p 3P0—4s5s 3S1 0.93304 0.92359 0.92029 0.90827 0.920 (25) 0.974 CICP [5]; 1.00 MCDHF [35]; 0.982 MP [37] 4s4p 3P0—4s4d 3D1 2.1286 2.0871 2.0181 2.0670 2.02 (11) 2.00 CICP [5]; 2.08 [34]; 2.02 MCDHF [35]; 2.05 MP [37] 4s4p 3P0—4p2 3P1 1.8133 1.7818 1.6470 1.7695 1.65 (17) 1.64 CICP [5]; 1.64 MCDHF [35]; 1.72 MP [37] 4s4p 3P0—4s6s 3S1 0.26761 0.26392 0.26890 0.26353 0.269 (5) 0.214 CICP [5]; 0.205 MCDHF [35]; 0.217 MP [37] 4s4p 3P0—4s5d 3D1 0.66449 0.64536 0.62443 0.65590 0.62 (4) 0.461 CICP[5]; 0.442 MCDHF [35]; 0.479 MP [37] 4s4p 3P0—4s7s 3S1 0.14979 0.14750 0.15084 0.14798 0.151 (3) — 4s4p 3P0—4s6d 3D1 0.36574 0.35358 0.33986 0.36272 0.340 (26) — 4s4p 3P0—4s8s 3S1 0.10206 0.10042 0.10065 0.098613 0.1021 (34) — 4s4p 3P0—4s7d 3D1 0.24440 0.23567 0.22522 0.24281 0.225 (19) — 4s4p 3P0—4s9s 3S1 0.088839 0.087378 0.078599 0.078310 0.079 (11) — 4s4p 3P0—4s8d 3D1 0.18107 0.17433 0.16616 0.18060 0.181 (14) — 表 3 相关跃迁对态4s2 1S0和态4s4p 3P0的静态极化率α(0)的贡献
Table 3. Contributions of individual transitions to the static polarizabilities α(0) for 4s2 1S0 and 4s4p 3P0.
Transition Contributions Refs. $ \alpha \left(0\right)( $ 4s2 1S0$ ) $ — — 4s2 1S0—4s4p 3P1 0.013 (7) — 4s2 1S0—4s4p 1P1 16.69 (2.82) 16.601[5] 4s2 1S0—4s5p 3P1 4.4 (4.4)×10–5 — 4s2 1S0—4s5p 1P1 0.027 (27) 0.016[5] 4s2 1S0—4s6p 3P1 7.1 (7.1)×10–5 — 4s2 1S0-—4s6p 1P1 0.008 (5) — 4s2 1S0—4snp 3P1, n = 7—8 0.00012 (12) — 4s2 1S0—4snp 1P1, n = 7—9 0.0006 (4) — Core 1.24 (1)[5] 1.24 (1)[5] Total 17.98 (2.82) 17.95 (34)[5] $ \alpha \left(0\right)( $ 4s4p 3P0$ ) $ — — 4s4p 3P0—4s5s 3S1 2.23 (12) 2.257[5] 4s4p 3P0—4s4d 3D1 8.98 (98) 8.668 [5] 4s4p 3P0—4p2 3P1 5.87 (1.21) 5.945[5] 4s4p 3P0—4s6s 3S1 0.124 (5) — 4s4p 3P0—4s5d 3D1 0.62 (8) — 4s4p 3P0—4sns 3S1, n = 7—9 0.057 (13) — 4s4p 3P0—4snd 3D1, n = 6—8 0.283 (29) — Core 1.24 (1) [5] 1.24 (1)[5] Total 19.41 (1.56) 19.58 (38)[5] $ {{\Delta }}\alpha \left(0\right) $ 1.43 (3.2) 1.63 (72) [5] 表 4 “幻零”波长和“魔幻”波长的不确定度评估表, 占主导贡献的部分在表中加重
Table 4. The uncertainty evaluation table for the ‘Tune-out’ wavelength and the ‘Magic’ wavelength, the dominant contribution is emphasized in the table.
Transition ‘Tune-out’ wavelengths ‘Magic’ wavelengths 209.101 176.42 148.61 117.197 113.09 209.286 168.1 148.27 116.38 106.7 4s2 1S0—4s4p 3P1 0.025 0.085 <0.1 <0.001 <0.001 <0.1 4s2 1S0—4s4p 1P1 0.0076 0.049 2.7 0.049 0.16 2.5 4s2 1S0—4s5p 1P1 <0.001 <0.01 <0.1 <0.001 <0.01 0.11 4s2 1S0—4s6p 1P1 <0.001 <0.01 <0.1 <0.001 <0.01 <0.1 4s4p 3P0—4s5s 3S1 0.17 <0.001 0.0017 0.0073 <0.01 0.27 <0.001 <0.01 <0.1 4s4p 3P0—4s4d 3D1 0.19 0.077 0.034 0.0095 0.026 1.6 0.047 0.036 0.68 4s4p 3P0—4p2 3P1 0.22 0.15 0.048 0.13 0.030 1.7 0.16 0.047 0.96 4s4p 3P0—4s6s 3S1 <0.01 <0.001 <0.001 0.0065 <0.01 <0.1 <0.001 <0.01 <0.1 4s4p 3P0—4s5d 3D1 <0.01 <0.001 <0.001 <0.001 <0.01 <0.1 <0.001 <0.01 <0.1 Others <0.001 <0.01 <0.01 <0.001 <0.01 <0.01 <0.1 <0.01 <0.01 <0.1 Total 0.026 0.34 0.16 0.059 0.16 0.11 3.6 0.17 0.17 2.8 表 5 “幻零”波长和“魔幻”波长处相关跃迁对两个光钟态4s2 1S0和4s4p 3P0的动力学极化率的贡献, 占绝对贡献的部分在表中加重
Table 5. Breakdown of the contributions of individual transitions to the dynamic polarizabilities at the “tune-out” wavelengths and “Magic” wavelengths for the 4s2 1S0 and 4s4p 3P0 clock states of Ga+, the dominant contribution is emphasized in the table.
Transition ‘Tune-out’ wavelengths ‘Magic’ wavelengths 209.101 176.42 148.61 117.197 113.09 209.286 168.1 148.27 116.38 106.7 4s2 1S0—4s4p 3P1 –32.06 –0.03 –0.01 –0.01 –0.01 9.51 –0.02 –0.01 –0.01 0.00 4s2 1S0—4s4p 1P1 30.77 46.73 177.29 –36.57 –29.58 30.72 57.11 184.64 –34.99 –22.00 4s2 1S0—4s5p 1P1 0.03 0.03 0.04 0.05 0.06 0.03 0.04 0.04 0.06 0.06 4s2 1S0—4s6p 1P1 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 Others 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 0.01 Core 1.24 1.24 1.24 1.24 1.24 1.24 1.24 1.24 1.24 1.24 Total 0.00 47.99 178.58 –35.27 –28.27 41.52 58.39 185.93 –33.68 –20.68 4s4p 3P0—4s5s 3S1 8.59 –55.40 –4.78 –1.64 –1.46 8.54 –15.34 –4.71 –1.60 –1.21 4s4p 3P0—4s4d 3D1 18.64 33.00 –352.26 –13.85 –11.66 18.61 45.19 –297.43 –13.37 –9.07 4s4p 3P0—4p2 3P1 11.66 19.42 353.37 –10.10 –8.41 11.64 25.33 484.39 –9.73 –6.46 4s4p 3P0—4s6s 3S1 0.18 0.22 0.32 16.76 –1.87 0.18 0.24 0.33 –18.78 –0.62 4s4p 3P0—4s5d 3D1 0.87 1.0 1.43 6.46 20.77 0.87 1.12 1.44 7.43 –6.93 Others 0.44 0.52 0.68 1.13 1.39 0.44 0.61 0.68 1.13 2.37 Core 1.24 1.24 1.24 1.24 1.24 1.24 1.24 1.24 1.24 1.24 Total 41.62 0.00 0.00 0.00 0.00 41.52 58.39 185.93 –33.68 –20.68 Diff. 0.00 0.00 0.00 0.0 0.0 -
[1] Safronova M S, Kozlov M G, Clark C W 2011 Phys. Rev. Lett. 107 143006 doi: 10.1103/PhysRevLett.107.143006 [2] Brewer S M, Chen J S, Hankin A M, Clements E R, Chou C W, Wineland D J, Hume D B, Leibrandt D R 2019 Phys. Rev. Lett. 123 033201 doi: 10.1103/PhysRevLett.123.033201 [3] Cui K F, Chao S J, Sun C L, Wang S M, Zhang P, Wei Y F, Yuan J B, Cao J, Shu H L, Huang X R 2022 Eur. Phys. J. D 76 140 doi: 10.1140/epjd/s10053-022-00451-1 [4] Keller J, Burgermeister T, Kalincev D, Didier A, Kulosa A P, Nordmann T, Kiethe J, Mehlstäubler T E 2019 Phys. Rev. A 99 013405 doi: 10.1103/PhysRevA.99.013405 [5] Cheng Y J, Mitroy J 2013 J. Phys. B: At. Mol. Opt. Phys. 46 185004 doi: 10.1088/0953-4075/46/18/185004 [6] Tayal S S 1991 Phys. Scr. 43 270 doi: 10.1088/0031-8949/43/3/010 [7] 魏远飞, 唐志明, 李承斌, 黄学人 2024 物理学报 73 103103 doi: 10.7498/aps.73.20240177 Wei Y F, Tang Z M, Li C B, Huang X R 2024 Acta Phys. Sin. 73 103103 doi: 10.7498/aps.73.20240177 [8] Wei, Y F, Chao S J, Cui K F, Li C B, Yu S C, Zhang H, Shu H L, Cao J, Huang X R 2024 Phys. Rev. Lett. 133 033001 doi: 10.1103/PhysRevLett.133.033001 [9] Ma Z Y, Deng K, Wang Z Y, Wei W Z, Hao P, Zhang H X, Pang L R, Wang B, Wu F F, Liu H L, Yuan W H, Chang J L, Zhang J X, Wu Q Y, Zhang J, Lu Z H 2024 Phys. Rev. Appl. 21 044017 doi: 10.1103/PhysRevApplied.21.044017 [10] Huntemann N, Sanner C, Lipphardt B, Tamm C, Peik E 2016 Phys. Rev. Lett. 116 063001 doi: 10.1103/PhysRevLett.116.063001 [11] Mitroy J, Safronova M S, Clark C W 2010 J. Phys. B: At. Mol. Opt. Phys. 43 202001 doi: 10.1088/0953-4075/43/20/202001 [12] Porsev S G, Derevianko A 2006 Phys. Rev. A 74 020502(R doi: 10.1103/PhysRevA.74.020502 [13] Zhang P, Cao J, Yuan J B, Liu D X, Yuan Y, Wei Y F, Shu H L, Huang X R 2021 Metrologia 58 035001 doi: 10.1088/1681-7575/abe9c4 [14] Arora B, Nandy D K, Sahoo B K 2012 Phys. Rev. A 85 012506 doi: 10.1103/PhysRevA.85.012506 [15] Wei Y F, Tang Z M, Li C B, Yang Y, Zou Y M, Cui K F, Huang X R 2022 Chin. Phys. B 31 083102 doi: 10.1088/1674-1056/ac5880 [16] Liu P L, Huang Y, Bian W, Shao H, Guan H, Tang Y B, Li C B, Mitroy J, Gao K L 2015 Phys. Rev. Lett. 114 223001 doi: 10.1103/PhysRevLett.114.223001 [17] Huang Y, Wang M, Chen Z, Li C B, Zhang H Q, Zhang B L, Tang L Y, Shi T Y, Guan H, Gao K L 2024 New J. Phys. 26 043021 doi: 10.1088/1367-2630/ad3ea8 [18] Tang Y B, Qiao H X, Shi T Y, Mitroy J 2013 Phys. Rev. A 87 042517 doi: 10.1103/PhysRevA.87.042517 [19] Holmgren W F, Trubko R, Hromada I, Cronin A D 2012 Phys. Rev. Lett. 109 243004 doi: 10.1103/PhysRevLett.109.243004 [20] Herold C D, Vaidya V D, Li X, Rolston S L, Porto J V, Safronova M S 2012 Phys. Rev. Lett. 109 243003 doi: 10.1103/PhysRevLett.109.243003 [21] Safronova M S, Zuhrianda Z, Safronova U I, Clark C W 2015 Phys. Rev. A 92 040501(R doi: 10.1103/PhysRevA.92.040501 [22] Mitroy J, Zhang J Y, Bromley M W J, Rollin K G 2009 Eur. Phys. J. D 53 15 doi: 10.1140/epjd/e2009-00098-4 [23] Kallay M, Nataraj H S, Sahoo B K, Das B P, Visscher L 2011 Phys. Rev. A 83 030503 doi: 10.1103/PhysRevA.83.030503 [24] Yu Y M, Suo B B, Fan H 2013 Phys. Rev. A 88 052518 doi: 10.1103/PhysRevA.88.052518 [25] Dzuba V A, Flambaum V V, Kozlov M G 1996 Phys. Rev. A 54 3948 doi: 10.1103/PhysRevA.54.3948 [26] Kozlov M G, Porsev S G, Safronova M S, Tupitsyn I I 2015 Comput. Phys. Commun. 195 199 doi: 10.1016/j.cpc.2015.05.007 [27] Tang Z M, Yu Y M, Jiang J, Dong C Z 2018 J. Phys. B: At. Mol. Opt. Phys. 51 125002 doi: 10.1088/1361-6455/aac181 [28] Cheng Y J, Jiang J, Mitroy J 2013 Phys. Rev. A 88 022511 doi: 10.1103/PhysRevA.88.022511 [29] Jiang J, Tang L Y, Mitroy J 2013 Phys. Rev. A 87 032518 doi: 10.1103/PhysRevA.87.032518 [30] Yu W W, Yu R M, Cheng Y J 2015 Chin. Phys. Lett. 32 123102 doi: 10.1088/0256-307X/32/12/123102 [31] Wu L, Wang X, Wang T, Jiang J, Dong C Z 2023 New J. Phys. 25 043011 doi: 10.1088/1367-2630/acc81e [32] Tang Z M, Wei Y F, Sahoo B K, Li C B, Yang Y, Zou Y M, Huang X R 2024 Phys. Rev. A 110 043108 doi: 10.1103/PhysRevA.110.043108 [33] Hao L H, Liu J J 2018 J. Appl. Spectrosc 85 730 doi: 10.1007/s10812-018-0712-7 [34] Kramida A, Ralchenko Yu, Reader J, NIST ASD Team 2024 NIST Atomic Spectra Database (ver. 5.12) [Online]. Available: https://physics.nist.gov/asd. National Institute of Standards and Technology, Gaithersburg, MD [35] Jonsson P, Andersson M, Sabel H, Brage T 2006 J. Phys. B: At. Mol. Opt. Phys. 39 1813 doi: 10.1088/0953-4075/39/7/022 [36] Isberg B, Litzen U 1985 Phys. Scr. 31 533 doi: 10.1088/0031-8949/31/6/013 [37] Victor G A, Taylor W R 1983 At. Data Nucl. Data Tables 28 107 doi: 10.1016/0092-640X(83)90013-X [38] Chou H, Chi H, Huang K 1994 Phys. Rev. A 49 2394 doi: 10.1103/PhysRevA.49.2394 [39] Fischer C F, Hansen J E 1978 Phys. Rev. A 17 1956 doi: 10.1103/PhysRevA.17.1956 [40] Andersen T, Eriksen P, Poulsen O, Ramanujam P S 1979 Phys. Rev. A 20 2621 doi: 10.1103/PhysRevA.20.2621 [41] Fischer C F 2009 Phys. Scr. T134 014019 doi: 10.1088/0031-8949/2009/T134/014019 [42] Ekman J, Godefroid M R, Hartman H 2014 Atoms 2 215 doi: 10.3390/atoms2020215 [43] Yu W W, Yu R M, Cheng Y J, Zhou Y J 2016 Chin. Phys. B 25 023101 doi: 10.1088/1674-1056/25/2/023101 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: