高级搜索

基于卷积神经网络的非对称共光路相干色散光谱仪背景白光干扰去除

,  ,  ,  , 

downloadPDF

上一篇

下一篇

吴银花, 种喆, 朱鹏飞, 陈莎莎, 周顺. 基于卷积神经网络的非对称共光路相干色散光谱仪背景白光干扰去除[J]. 物理学报, 2025, 74(10): 104201-1. doi: 10.7498/aps.74.20250090
引用本文: 吴银花, 种喆, 朱鹏飞, 陈莎莎, 周顺. 基于卷积神经网络的非对称共光路相干色散光谱仪背景白光干扰去除[J]. 物理学报, 2025, 74(10): 104201-1. doi: 10.7498/aps.74.20250090
shu
Yinhua WU, Zhe CHONG, Pengfei ZHU, Shasha CHEN, Shun ZHOU. Removal of background white light in coherent-dispersion spectrometer based on convolutional neural network[J]. Acta Physica Sinica, 2025, 74(10): 104201-1. doi: 10.7498/aps.74.20250090
Citation: Yinhua WU, Zhe CHONG, Pengfei ZHU, Shasha CHEN, Shun ZHOU. Removal of background white light in coherent-dispersion spectrometer based on convolutional neural network[J]. Acta Physica Sinica, 2025, 74(10): 104201-1. doi: 10.7498/aps.74.20250090
shu

基于卷积神经网络的非对称共光路相干色散光谱仪背景白光干扰去除

  • 1.

    西安工业大学光电工程学院, 西安　710021

  • 2.

    火箭军工程大学, 西安　710025

    • 作者简介: 吴银花. E-mail: yinhuawoo@163.com .
    通讯作者: E-mail: zsemail@126.com.

  • 中图分类号: 42.25.Kb, 42.25.Hz, 42.30.Rx, 42.30.Va

Removal of background white light in coherent-dispersion spectrometer based on convolutional neural network

  • 1.

    School of Optoelectronic Engineering, Xi’an Technological University, Xi’an 710021, China

  • 2.

    Rocket Force University of Engineering, Xi’an 710025, China

    • Corresponding author: E-mail: zsemail@126.com.

  • MSC: 42.25.Kb, 42.25.Hz, 42.30.Rx, 42.30.Va

  • 摘要: 非对称共光路相干色散光谱仪(coherent-dispersion spectrometer, CODES)是一种基于视向速度法的系外行星探测仪器, 通过测量恒星吸收线干涉光谱的多普勒相移探测视向速度的变化. 然而恒星吸收谱线中背景白光对CODES相位解析产生干扰, 从而严重影响视向速度探测精度. 针对背景白光干扰问题, 本文利用CODES原理及其探测数据特点, 基于U-Net架构提出了背景白光预测网络模型(background white light prediction network, BWP-Net). 该模型先通过结合多通道卷积和深度可分离卷积, 从恒星吸收线干涉光谱逐步提取不同级别特征, 再通过多层注意力反卷积, 融合深层特征和浅层特征基础上逐步重建图像细节, 最终预测输出背景白光干涉光谱. 实验结果表明, 在不同吸收线、不同固定光程差、不同视向速度条件下, 利用BWP-Net模型输出消除背景白光干扰后, 视向速度探测误差均低于1 m/s, 误差范围主要集中在0—0.4 m/s. 该模型不仅能够准确预测背景白光, 且具有较强的稳定性和鲁棒性, 为CODES高精度稳定探测视向速度提供有力保障.
    Abstract: Coherent-dispersion spectrometer (CODES) is an exoplanet detection instrument based on the radial velocity (RV) method. It detects changes in RV by measuring the Doppler phase shift of the interference spectrum of stellar absorption line. However, the background white light in the stellar absorption spectrum disturbs the phase analysis of CODES, which leads to phase error and seriously affects the accuracy of RV inversion. The larger the cosine amplitude of the background white light, the greater the error is. In order to effectively remove background white light and correct Doppler phase shift, a background white light prediction network (BWP-Net) is proposed based on the U-Net architecture by utilizing the principle and data characteristics of CODES in this study. To accelerate the convergence of the BWP-Net model, the interference spectrum of absorption line from CODES and the ideal interference spectrum of background white light are used as inputs and labels for the model after image normalization, while the model output becomes the predicted interference spectrum of background white light after inverse normalization. The BWP-Net consists of symmetric 6-layer encoding path and decoding path. First, in the encoding path, different levels of features are extracted step by step from the interference spectrum of stellar absorption line through combination of multi-channel convolution and depthwise separable convolution, extracting features effectively while reducing computational costs reasonably. In each convolution layer, spatial downsampling is performed through convolution with a stride of 2 and the number of feature channels is increased until the fourth layer, thus various features, from simple to abstract, local to global, are extracted for the preparation of image reconstruction in the decoding path. Second, in the decoding path, the image details are gradually reconstructed from the features extracted through several layers of attention transposed-convolution. In each layer of attention transposed-convolution, spatial upsampling is performed based on the fusion of shallow features and deep features through matrix addition and the number of feature channels are reduced, at the same time attention of different levels is paid to the features through a learnable weight matrix, so as to suppress the absorption line information gradually during image reconstruction. At the last layer of the decoding path, the sigmoid activation function is used to control the model output in the 0-1 interval, making it easier to denormalize. Finally, a region weighted loss function that combines mean-square error and multi-scale structural similarity is used for training so as to consider pixel level differences and structural similarity between the model output and the labels, while enhancing the suppression of absorption lines in the central region of the interference spectrum through region weighting. And the output of BWP-Net is the prediction of the interference spectrum of background white light, which is subtracted from the interference spectrum of stellar absorption lines for phase analysis. The experimental results show that under different absorption lines, different fixed optical path differences, and different RVs, after removing background white light from the output of BWP-Net, the RV inversion error is less than 1 m/s, mainly concentrated in the region of 0–0.4 m/s, with an average error of 0.2353 m/s and a root mean square error of 0.3769 m/s. And the distribution of RV inversion error is relatively uniform under different parameter conditions, the median error is less than 0.25 m/s at different absorption line wavelengths, and less than 0.2 m/s at different fixed optical path differences. Thes indicate that BWP-Net not only predicts background white light accurately, but also has good stability and robustness, providing strong support for high-precision and stable RV inversion for CODES.
  • 加载中

  • 图 1  CODES　(a)工作原理; (b)实验装置

    Figure 1.  CODES: (a) Schematic diagram; (b) experimental setup.

    下载: 全尺寸图片 幻灯片

    图 2  S1int的余弦振幅

    Figure 2.  Cosine amplitude of S1int.

    下载: 全尺寸图片 幻灯片

    图 3  背景白光预测网络架构

    Figure 3.  Background white light prediction network (BWP-Net) architecture.

    下载: 全尺寸图片 幻灯片

    图 4  不同层数模型损失对比结果

    Figure 4.  Comparison result of loss between models with different layers.

    下载: 全尺寸图片 幻灯片

    图 5  吸收线干涉光谱

    Figure 5.  Interference spectrum of absorption line.

    下载: 全尺寸图片 幻灯片

    图 6  背景白光干涉光谱

    Figure 6.  Interference spectrum of background white light.

    下载: 全尺寸图片 幻灯片

    图 7  BWP-Net模型输出与标签对比

    Figure 7.  Comparison of BWP-Net output and label.

    下载: 全尺寸图片 幻灯片

    图 8  不同λa下视向速度误差分布

    Figure 8.  Distribution of radial velocity error with different λa.

    下载: 全尺寸图片 幻灯片

    图 11  不同t下视向速度均方根误差

    Figure 11.  RMSE of radial velocity error with different t.

    下载: 全尺寸图片 幻灯片

    图 9  不同λa下视向速度均方根误差

    Figure 9.  RMSE of radial velocity error with different λa.

    下载: 全尺寸图片 幻灯片

    图 10  不同t下视向速度误差分布

    Figure 10.  Distribution of radial velocity error with different t.

    下载: 全尺寸图片 幻灯片

    图 12  特征和参数可视化　(a)编码路径特征; (b)解码路径特征; (c)注意力权重

    Figure 12.  Visualization of features and parameters: (a) Encoder features; (b) decoder features; (c) attention weight.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  v1 = 0 m/s, v2 = 1000 m/s时, 不同光程差下相位差解析结果

    Table 1.  Phase shift with different optical path difference at v1 = 0 m/s and v2 = 1000 m/s.

    t/mmΔΦ/radΔΦabsorb/radΔvabsorb/(m·s–1)ΔΦemission/radΔvemission/(m·s–1)
    2.280.0195π1.9878π10200.420.0195π999.69
    3.370.0288π0.0292π1012.250.0288π999.68
    3.380.0289π0.0287π991.860.0289π999.68
    3.390.0290π0.0282π972.480.0290π999.69
    4.660.0398π0.0183π458.450.0398π999.69
    6.760.0578π0.0579π1001.500.0578π999.70
    7.800.0667π0.0880π1319.800.0666π999.71
    11.150.0953π0.0916π960.960.0953π999.75
    19.500.1667π0.1666π999.820.1666π999.87
    下载: 导出CSV

    表 2  测试集部分数据分析结果

    Table 2.  Analysis results of partial data in the test set.

    λa/nm Δλa/nm A t/mm v1/(m·s–1) v2/(m·s–1) Δvt/(m·s–1) Error/(m·s–1)
    710 0.02 0.9 11.98 1800 1900 99.9991 0.0009
    730 0.03 0.9 12.00 1300 1500 199.9988 0.0012
    740 0.02 0.9 12.01 1500 1700 200.0006 0.0006
    820 0.03 0.9 12.02 1600 1900 300.0036 0.0036
    750 0.02 0.8 12.02 1000 1400 400.0034 0.0034
    780 0.03 0.7 12.02 1200 1700 499.9901 0.0099
    860 0.02 0.9 12.00 1000 1600 599.9952 0.0048
    760 0.02 0.9 11.98 1300 2000 699.9988 0.0012
    770 0.02 0.7 11.99 0 800 799.7536 0.2464
    870 0.02 0.9 11.99 1100 2000 899.9507 0.0493
    830 0.03 0.7 12.01 100 1100 999.8383 0.1617
    690 0.02 0.8 12.01 0 1100 1099.8283 0.1717
    800 0.03 0.8 12.00 0 1700 1699.7822 0.2178
    850 0.03 0.9 11.98 0 1200 1200.0631 0.0631
    790 0.03 0.7 12.02 100 1400 1299.8981 0.1019
    720 0.02 0.8 12.01 100 1500 1400.0173 0.0173
    660 0.02 0.8 11.98 0 1500 1499.9827 0.0173
    670 0.03 0.8 12.02 100 1700 1600.3113 0.3113
    840 0.03 0.9 11.98 100 1800 1700.1090 0.1090
    700 0.02 0.9 12.01 100 1900 1800.1403 0.1403
    810 0.03 0.9 12.02 0 1900 1900.0923 0.0923
    680 0.02 0.7 12.01 0 2000 2000.4200 0.4200
    下载: 导出CSV
  • [1] Bailey I J, Mateo M, White J R, Shectman A S, Crane D J 2018 MNRAS 475 1609 doi: 10.1093/mnras/stx3266
    [2] Vanzi L, Zapata A, Flores M, Brahm R, Pinto T M, Rukdee S, Jones M, Ropert S, Shen T, Ramirez S, Suc V, Jordán A, Espinoza N 2018 MNRAS 477 5041 doi: 10.1093/mnras/sty936
    [3] Mamajek E E, Burgasser J A 2025 The Astronomical Journal 169 77 doi: 10.3847/1538-3881/ad991b
    [4] Laliotis K, Burt A J, Mamajek E E, Li Z, Perdelwitz V, Zhao J, Butler P R, Holden B, Rosenthal L, Fulton J B, Feng F, Kane R S, Bailey J, Carter B, Crane D J, Furlan E, Gnilka L C, Howell B S, Laughlin G, Shectman A S, Teske K J, Tinney G C, Vogt S S, Wang X S, Wittenmyer A R 2023 The Astronomical Journal 165 176 doi: 10.3847/1538-3881/acc067
    [5] The Extrasolar Planets Encyclopedia http://exoplanet.eu/ [2025-1-17]
    [6] Wang X, Chang L, Wang L, Ji H, Xian H, Tang Z, Xin Y, Wang C, He S, Zhang J, Lun B, Wei K, Li X, Jiang X, Wang H, Li H, Mao J 2020 Res. Astron. Astrophys. 20 032 doi: 10.1088/1674-4527/20/3/32
    [7] Xiao G, Teng H, Zhou J, Sato B, Liu Y, Bi S, Takarada T, Kuzuhara M, Hon M, Wang L, Omiya M, Harakawa H, Zhao F, Zhao G, Kambe E, Izumiura H, Ando H, Noguchi K, Wang W, Zhai M, Song N, Yang C, Li T, Brandt D T, Yoshida M, Yoichi Itoh, Kokubo E 2024 The Astronomical Journal 167 59 doi: 10.3847/1538-3881/ad11de
    [8] Luo X, Gu S, Xiang Y, Cameron A C, Kim K, Han I, Lee B 2022 The Astronomical Journal 163 287 doi: 10.3847/1538-3881/ac6954
    [9] Wang C, Bai J, Fan Y, Mao J, Chang L, Xin Y, Zhang J, Lun B, Wang J, Zhang X, Ying M, Lu K, Wang X, Ji K, Xiong D, Yu X, Ding X, Ye K, Xing L, Yi W, Xu L, Zheng X, Feng Y, He S, Wang X, Liu Z, Chen D, Xu J, Qin S, Zhang R, Tan H, Li Z, Lou K, Li J, Liu W 2019 Res. Astron. Astrophys. 19 149 doi: 10.1088/1674-4527/19/10/149
    [10] Grieves N, Ge J, Thomas N, Ma B, Sithajan S, Ghezzi L, Kimock B, Willis K, Lee D N, Brian Lee, Fleming W S, Agol E, Troup N, Paegert M, Schneider P D, Stassun K, Varosi F, Zhao B, Jian L, Li R, Mello P F G, Bizyaev D, Pan K, Dutra-Ferreira L, Lorenzo-Oliveira D, Santiago X B, Costa N L, Maia G A M, Ogando C L R, Peloso F E 2017 MNRAS 467 4264 doi: 10.1093/mnras/stx334
    [11] Grieves N, Ge J, Thomas N, Willis K, Ma B, Lorenzo-Oliveira D, Queiroz A B A, Ghezzi L, Chiappini C, Anders F, Dutra-Ferreira L, Mello P F G, Santiago X B, Costa N L, Ogando C L R, Peloso F E, Tan C J, Schneider P D, Pepper J, Stassun G K, Zhao B, Bizyaev D, Pan K 2018 MNRAS 481 3244 doi: 10.1093/mnras/sty2431
    [12] Wei R Y, Chen S S, Hu B L, Yan Q Q, Wu Y H, Wang P C 2020 Publ. Astron. Soc. Pac. 132 015003 doi: 10.1088/1538-3873/ab503a
    [13] Chen S, Wei R, Xie Z, Wu Y, Di L, Wang F, Zhai Y 2021 Appl. Opt. 60 4535 doi: 10.1364/AO.425491
    [14] Guan S, Liu B, Chen S, Wu Y, Wang F, Liu X, Wei R 2024 Sci. Rep. 14 17445 doi: 10.1038/s41598-024-66649-y
    [15] Wu Y, Chen S, Wang P, Zhou S, Feng Y, Zhang W, Wei R 2021 MNRAS 503 3032 doi: 10.1093/mnras/stab656
    [16] Guan S, Liu B, Chen S, Wu Y, Wang F, Wang S, Liu X, Wei R 2024 Opt. Commun. 561 130443 doi: 10.1016/j.optcom.2024.130443
    [17] 周静, 张晓芳, 赵延庚 2021 物理学报 70 054201 doi: 10.7498/aps.70.20201362 Zhou J, Zhang X F, Zhao Y G 2021 Acta Phys. Sin. 70 054201 doi: 10.7498/aps.70.20201362
    [18] 朱琦, 许多, 张元军, 李玉娟, 王文, 张海燕 2022 物理学报 71 244301 doi: 10.7498/aps.71.20221504 Zhu Q, Xu D, Zhang Y J, Li Y J, Wang W, Zhang H Y 2022 Acta Phys. Sin. 71 244301 doi: 10.7498/aps.71.20221504
    [19] Long J, Shelhamer E, Darrell T 2015 arXiv: 1411.4038v2 [cs. CV]
    [20] Roy S K, Krishna G, Dubey S R, Chaudhuri B B 2020 IEEE Geosci. Remote Sens. Lett. 17 277 doi: 10.1109/LGRS.2019.2918719
    [21] Ronneberger O, Fischer P, Brox T 2015 Medical Image Computing and Computer -Assisted Intervention Munich, Germany, October 5–9, 2015 p234
    [22] Nehaa F, Bhatia D, Shuklab K D, Dalvia M S, Mantzouc N, Shubbar S 2024 arXiv: 2412.02242v1 [eess. IV]
    [23] Siddique N, Sidike P, Elkin C, Devabhaktuni V 2020 arXiv: 2011.01118 [eess. IV]
    [24] Isola P, Zhu J, Zhou T, Efros A A 2018 arXiv: 1611.07004v3 [cs. CV]
    [25] Basu A, Mondal R, Bhowmik S, Sarkara R 2020 J. Electron. Imaging 29 063019 doi: 10.1117/1.JEI.29.6.063019
    [26] Hu Y, Tang Z, Hu J, Lu X, Zhang W, Xie Z, Zuo H, Li L, Huang Y 2023 Opt. Commun. 540 129488 doi: 10.1016/j.optcom.2023.129488
  • 加载中
图( 13) 表( 2)
计量
  • 文章访问数:  31
  • HTML全文浏览数:  31
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-01-20
  • 刊出日期:  2025-05-20

基于卷积神经网络的非对称共光路相干色散光谱仪背景白光干扰去除

    通讯作者: E-mail: zsemail@126.com.
    作者简介: 吴银花. E-mail: yinhuawoo@163.com
  • 1. 西安工业大学光电工程学院, 西安　710021
  • 2. 火箭军工程大学, 西安　710025
  • 收稿日期:  2025-01-20

摘要: 非对称共光路相干色散光谱仪(coherent-dispersion spectrometer, CODES)是一种基于视向速度法的系外行星探测仪器, 通过测量恒星吸收线干涉光谱的多普勒相移探测视向速度的变化. 然而恒星吸收谱线中背景白光对CODES相位解析产生干扰, 从而严重影响视向速度探测精度. 针对背景白光干扰问题, 本文利用CODES原理及其探测数据特点, 基于U-Net架构提出了背景白光预测网络模型(background white light prediction network, BWP-Net). 该模型先通过结合多通道卷积和深度可分离卷积, 从恒星吸收线干涉光谱逐步提取不同级别特征, 再通过多层注意力反卷积, 融合深层特征和浅层特征基础上逐步重建图像细节, 最终预测输出背景白光干涉光谱. 实验结果表明, 在不同吸收线、不同固定光程差、不同视向速度条件下, 利用BWP-Net模型输出消除背景白光干扰后, 视向速度探测误差均低于1 m/s, 误差范围主要集中在0—0.4 m/s. 该模型不仅能够准确预测背景白光, 且具有较强的稳定性和鲁棒性, 为CODES高精度稳定探测视向速度提供有力保障.

English Abstract

    全文HTML

    1.   引　言

    • 作为一种重要的系外行星探测方法, 视向速度法[1–4]利用恒星吸收谱线的多普勒周期性移动, 测量恒星视向速度的变化, 从而间接探测行星的存在, 该方法目前已探测确认了1200多颗[5]系外行星. 传统的视向速度法实现手段是利用高分辨率阶梯光栅直接测量因多普勒效应产生的恒星吸收谱线波长偏移[6–8], 进而获取恒星视向速度的变化, 显然这种实现方式高度依赖于光栅的色分辨本领, 容易使得系统透过率相对较低、环境敏感度相对较高. 另一种视向速度法实现方式是由迈克尔逊干涉模块和中低分辨率光栅组成的固定光程差干涉仪[9–11], 通过测量恒星吸收谱线的多普勒频移前后对应干涉条纹的相位差来间接获得恒星视向速度变化, 由于其在干涉模块中嵌入的固定光程差使得相位差相对波长偏移放大, 使用中低分辨率色散器件来实现与高精度阶梯光栅相比拟的探测精度, 是传统阶梯光栅光谱仪的有力补充. 非对称共光路相干色散光谱仪(coherent-dispersion spectrometer, CODES)[12–16]是在固定光程差干涉仪基础上进一步优化了环境敏感度和能量利用率, 利用共光路Sagnac干涉光路使两路光经过几乎相同的路径, 进而环境影响引起的光程差误差相互抵消, 同时利用非对称干涉仪结构使返回光源的一路干涉光产生平行移位再反射汇聚到后续光路中, 进而100%利用系统输入能量.

      然而, 由于恒星吸收谱线中不仅包含吸收线光谱, 还包含背景白光光谱, 同时考虑到探测器沿波长方向上的采样率, 导致CODES获取的干涉条纹相位是恒星吸收线和背景白光共同作用的结果, 进而严重影响视向速度的探测精度. 针对背景白光干扰, 目前主要有余弦振幅约束法和频域滤波法[15]: 其中余弦振幅约束法是通过选取背景白光振幅为零时的光程差来消除背景白光干扰, 但该方法对探测器沿波长方向的采样率和光程差的精度十分敏感, 导致视向速度探测精度很不稳定; 频域滤波法是利用沿波长方向上背景白光和吸收线的频率差异采用低通滤波器消除背景白光干扰, 但根据傅里叶变换性质, 该方法要求固定光程差为频域分辨率(由提取的波数范围决定)的整数倍, 以确保有效滤除背景白光干扰, 而为了满足整数倍要求往往需要提取较宽的波数范围进而带来其他相邻吸收线的干扰, 而当不满足整数倍要求时不能够有效滤除背景白光干扰, 导致视向速度的探测精度下降. 可见, 上述的背景白光干扰处理方法对固定光程差或目标光谱有较苛刻的要求, 这直接影响视向速度的探测精度.

      本文给出了CODES仪器模型, 并利用模型进行了背景白光对CODES相位的干扰分析, 在此基础上针对视向速度高精度探测稳定性问题, 基于深度学习理论给出了背景白光预测模型并进行了相关验证分析, 从不同固定光程差下不同恒星吸收线干涉光谱能够准确预测出背景白光, 进而有效去除背景白光对测量相位的影响, 且显著降低对固定光程差或目标光谱的敏感度, 进而确保视向速度探测精度的稳定性.

    2.   背景白光对CODES相位干扰分析

      2.1.   CODES仪器模型

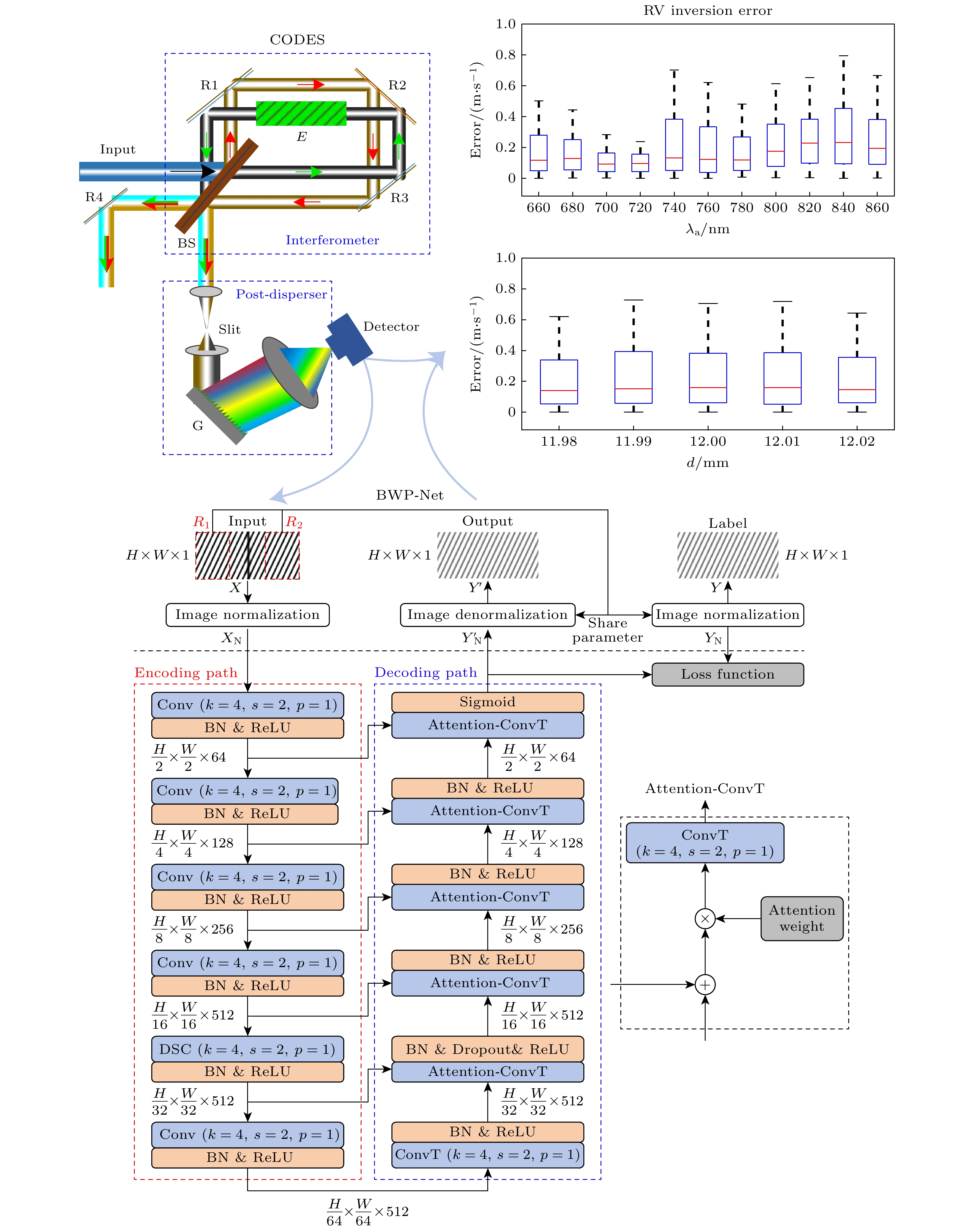
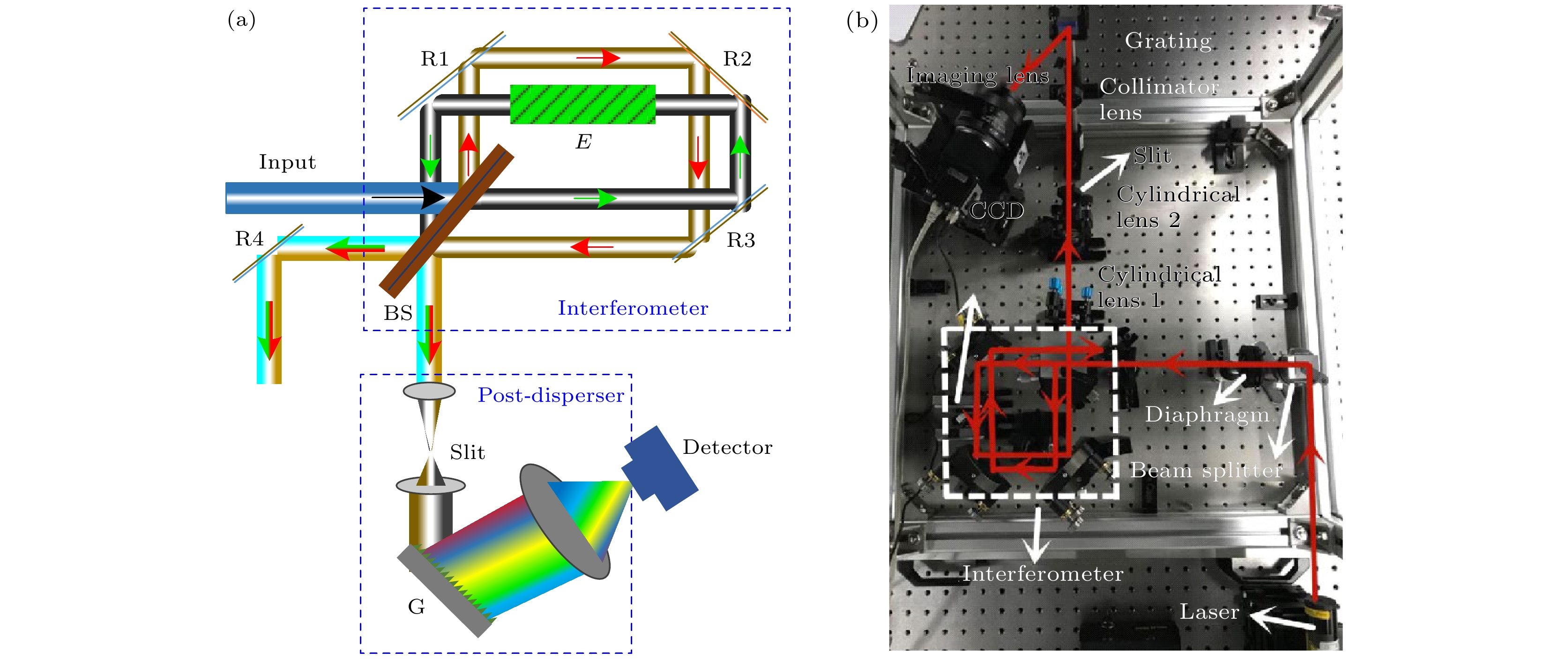
    • CODES工作原理[15]如图1(a)所示, 其中R1—R4是反射镜、BS是分束器、E是用于产生固定光程差的光学介质材料、G是光栅. 入射光进入非对称共光路Sagnac干涉模块后, 在狭缝处形成复色谱等倾干涉条纹. 再经过中低分辨率后色散模块分光, 由探测器获取二维干涉光谱. 经BS返回光源的光通过R4反射汇聚到与主光路相同的后续光路中, 因此图中省略. 图1(b)是搭建的CODES实验装置[14].

      根据CODES工作原理和恒星吸收谱线特征, 以吸收线中心波数λa (ka = 1/λa)、吸收线波长半高宽Δλa(Δka = Δλa/λ2)、吸收强度A、固定光程差t、光栅分辨率gr(Δk0 = k/gr)、探测器沿波长方向上的采样率λint (Δkint = Δλint/λ2)为输入, 以二维干涉光谱为输出, 建立了CODES仪器模型, 如(1)式—(3)式所示, 并利用图1(b)中实验装置进行了实验验证[15]. 其中, Nphoton表示光子散粒噪声, 由信号本身的泊松分布模拟, q1 = 1, q2 = –A时表示吸收线, q1 = 0, q2 = A时表示发射线(发射线主要用于模型验证), 即S1对应背景白光部分.

      • 2.2.   CODES相位分析

    • 由于色散模块中的光栅模糊效应, 吸收线沿波长方向上有一定的能量分布, 因此为了获取准确的相位信息, 应根据3σ准则提取以吸收线为中心、足够的波长带宽范围Δλc(Δkc = Δλc/λ2)内干涉条纹进行相位测量[15]. 此时, 背景白光的干涉光谱能量可表示为

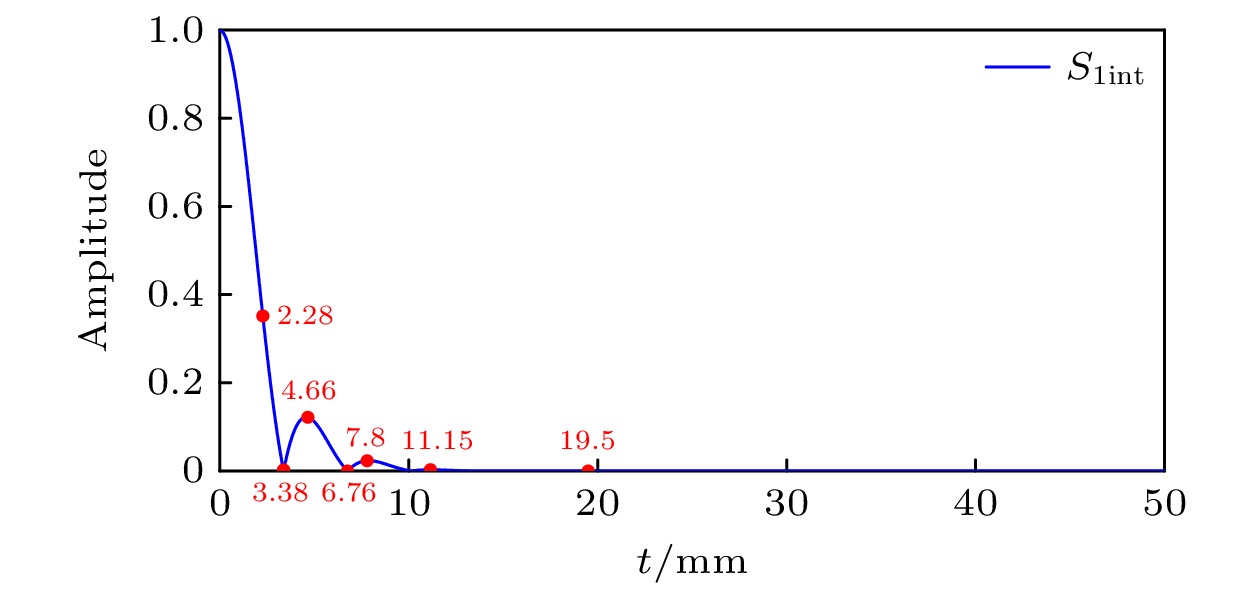
      显然, 背景白光对相位的干扰主要由S1int的余弦部分产生, 图2是λa = 780 nm, gr = 15000、Δλc = 0.18 nm时S1int的余弦振幅随光程差变化曲线. 为了进一步分析背景白光对相位的具体影响, 利用2.1节中建立的仪器模型以及基于傅里叶变换的相位解析方法[15], 在不同光程差(对应不同S1int余弦振幅)下对同一参数(λa = 780 nm, Δλa = 0.02 nm, A = 0.95)的吸收线和发射线进行了相位解析, 结果如表1中ΔΦabsorb和ΔΦemission所示, 并根据CODES工作原理计算得出了对应视向速度差Δvabsorb和Δvemission,

      其中c为光速. 表1中ΔΦ是由准确的视向速度差Δv = v1 – v2根据(5)式计算得出的准确相位差.

      结合图2和表1分析可以看出: 1)在不同参数下发射线相位误差均小于10–3π, 其视向速度误差均小于0.5 m/s, 而吸收线相位误差普遍较大, 导致其视向速度误差也很大; 2) t = 3.38 mm, t = 6.76 mm处吸收线相位误差较小, 这是因为此时与S1int余弦振幅零点基本接近, 但从视向速度可以看出仍有一定误差, 且t = 3.38 mm±0.01 mm处视向速度误差明显增大, 可见对光程差很敏感; 3) S1int余弦振幅越大吸收线相位误差也越大, 反之亦然, t = 19.50 mm处S1int余弦振幅几乎为零, 其视向速度误差也小于0.5 m/s, 但此时干涉条纹对比度太小, 不便于提取吸收线.

      上述分析结果再次验证了背景白光是相位干扰的主要因素, 如果能够有效去除背景白光, 即可大幅提高相位测量精度以及视向速度探测精度. 然而目前常用的余弦振幅约束法和频域滤波法[15]等背景白光干扰去除方法对仪器参数和观测目标光谱要求苛刻, 其视向速度探测精度随仪器参数或吸收线特征的变化而浮动, 即算法鲁棒性较低、视向速度探测精度不稳定. 深度学习通过“端到端”的学习方式直接从输入数据逐层学习并提取相关特征直到最终给出期望输出, 能够较好避免传统给定特征表示方式容易进入局部最优解的困境, 从而获得全局最优解. 因此, 本文拟基于深度学习训练有效的背景白光预测网络模型、消除背景白光干扰, 以提高视向速度高精度探测稳定性和鲁棒性.

    3.   背景白光预测网络模型

    • 卷积神经网络(convolution neural network, CNN)[17–20]作为深度学习的代表算法之一, 利用多层卷积运算, 将网络输入数据逐层抽象为自身任务所需的特征、再由特征映射到最终任务目标, 广泛应用于机器视觉、图像处理等领域. CODES获取的二维干涉光谱可视为仪器输入光谱经仪器函数卷积后的结果, 因此从干涉光谱中提取吸收线特征的过程属于反卷积范畴, 而反卷积的实质仍是卷积运算, 这意味着可利用CNN从吸收线干涉光谱提取出背景白光干涉光谱.

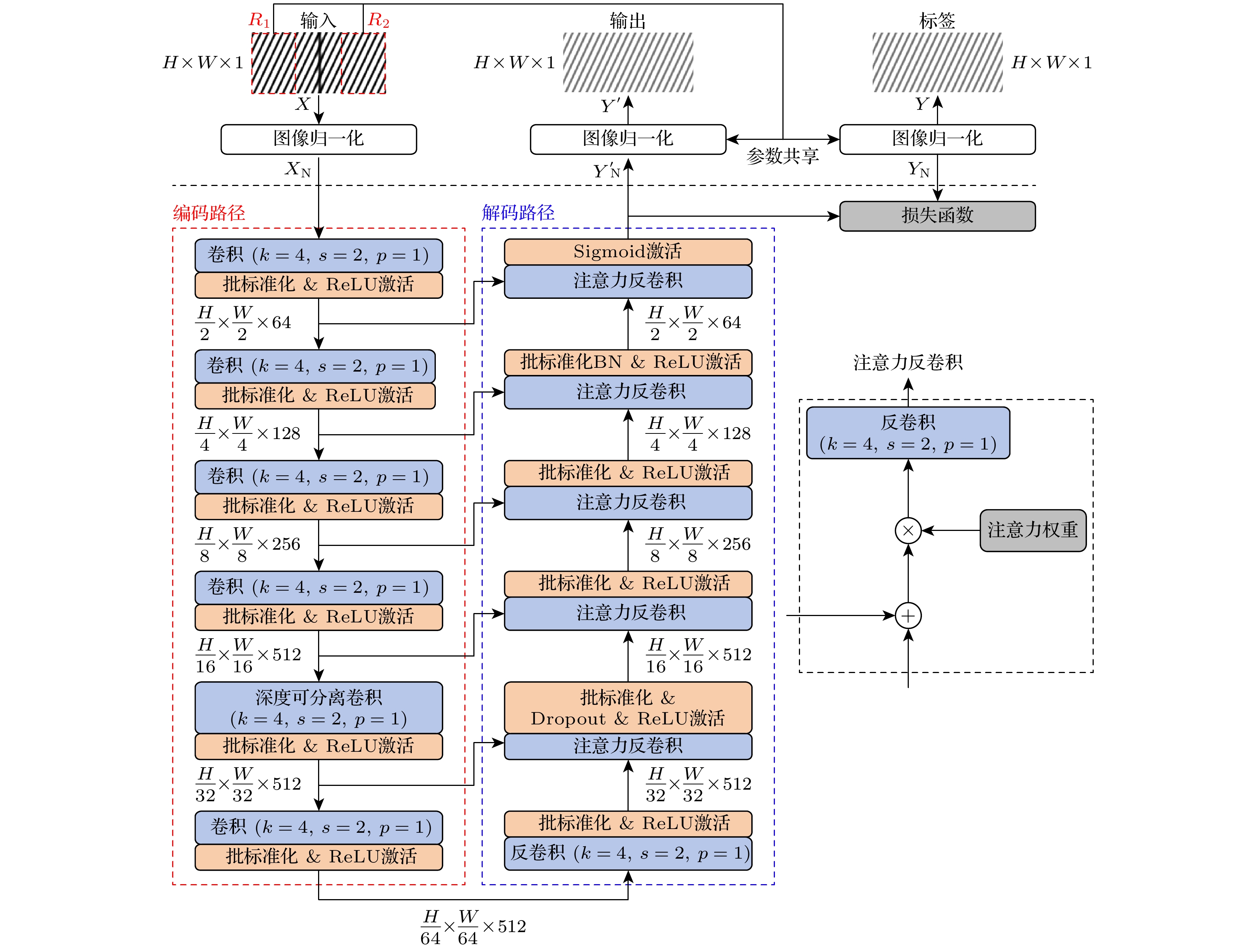
      U-Net[21–23]是建立在全卷积网络上的U型对称结构卷积神经网络, 主要由编码路径、解码路径和跳跃连接三部分组成, 其中编码路径通过一系列卷积和最大池化逐步提取输入图像的特征同时逐渐进行空间下采样, 解码路径通过一系列反卷积上采样和卷积逐步恢复特征分辨率并进行图像分割, 跳跃连接通过将编码器和解码器同样大小的特征按通道拼接在一起有效融合低级特征和高级特征, 进而实现高性能图像分割成为图像分析热门网络模型之一. Pix2Pix[24–26]是基于条件生成对抗网络的图像到图像翻译网络模型, 主要由生成器和判别器组成, 其中生成器采用U-Net架构的卷积网络将输入图像转换输出为目标图像, 判别器对生成器输出的图像和真实图像进行真假判断, 通过生成器和判别器的博弈对抗使生成器输出图像逐渐逼近真实图像, 该网络其以出色的图像转换性能广泛应用于多个领域. 鉴于U-Net和Pix2Pix在图像转换方面优异性能, 本文结合这两种网络基础上, 根据CODES干涉光谱数据特点, 构建了背景白光预测网络模型(background white light prediction network, BWP-Net), 由恒星吸收线干涉光谱预测对应背景白光干涉光谱, 如图3所示, 其中H和W分别表示输入图像的高和宽, k, s, h分别表示卷积核大小、步长和填充大小.

      为了使BWP-Net模型收敛加快, 本文分别将CODES生成的吸收线干涉光谱X和理想白光干涉光谱Y经过图像归一化为0—1区间的XN和YN作为模型的输入和标签. 其中吸收线干涉光谱X的归一化是利用X的所有区域计算归一化参数, 而理想白光干涉光谱Y的归一化是利用X的两端相对均匀白光区域R1和R2计算归一化参数, 即

      模型输出Y'N (由解码器最后一层sigmoid激活函数控制在0—1区间)利用与Y的归一化相同参数进行反归一化, 最终给出预测白光干涉光谱Y'.

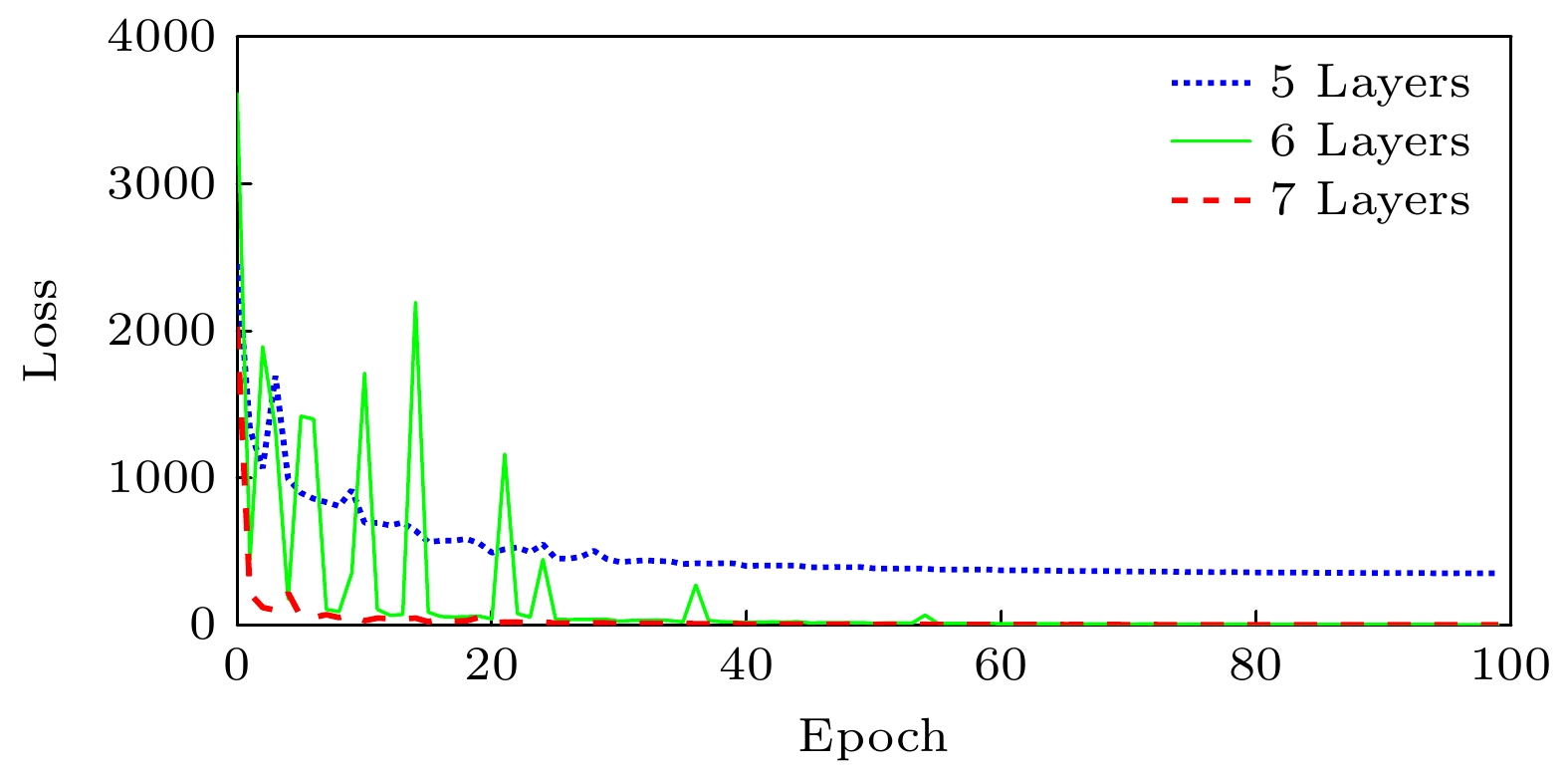
      BWP-Net模型整体架构是基于U-Net的6层编码-解码对称架构. 考虑到恒星吸收线干涉光谱图像复杂度并不高, 模型每一层采样了单卷积, 而非U-Net中的双卷积, 以减轻运算复杂度. 在此基础上参考U-Net的5层网络和Pix2Pix的7层网络, 本文将网络深度分别设置为5层、6层、7层进行了模型训练, 对应损失对比结果如图4所示. 随着层数的增多损失也逐渐降低, 5层网络的损失明显较大, 6层和7层网络损失差异随着训练轮次的增加而减小, 约第40轮之后二者损失基本接近. 因此本文选用6层网络架构, 确保损失足够低的同时减轻运算复杂度.

      BWP-Net模型左侧编码路径通过多层卷积逐步提取吸收线干涉光谱中由简单到抽象的不同级别特征, 其每一层是步长为2、填充为1的4×4多通道卷积, 随后是批标准化(batch normalization, BN)和修正线性单元(rectified linear unit, ReLU)激活函数, 通过其中步长为2的卷积进行特征空间下采样, 每层输出特征空间分辨率减半, 且前4层每层输出特征通道数加倍, 后2层输出特征通道数不变. 对于经过多层卷积和空间下采样得到的特征, 每个空间点对应原图像中的一块区域, 空间相邻点之间在不同通道上的相关性减弱. 因此本文在编码路径的第5层采用深度可分离卷积(depthwise separable convolution, DSC): 步长为2、填充为1的4×4逐通道卷积和步长为1、填充为0的1×1逐点卷积替代了常规卷积, 在能够有效提取特征的同时, 参数数量和计算量均减少为常规卷积的约1/15, 进而合理降低运算成本.

      BWP-Net模型右侧解码路径通过多层反卷积逐步由特征重建图像细节并预测输出与模型输入相对应的背景白光干涉光谱, 其每一层是步长为2、填充为1的4×4注意力反卷积, 随后是批标准化和ReLU激活函数, 通过其中注意力反卷积进行特征空间上采样, 每层输出特征空间分辨率加倍, 同时逐渐减少特征通道数, 模型最终的输出图像与输入图像尺寸相同, 并在最后一层采用sigmoid激活函数使模型输出控制在0—1区间进而与归一化后的标签图像相匹配. 注意力反卷积先将编码路径与解码路径中相同尺寸特征通过矩阵相加的方式进行了跳跃连接, 进而融合浅层和深层特征, 同时由于吸收线干涉光谱的中心区域(吸收线附近)相比两端对背景白光预测干扰较大, 利用与特征相同尺寸的可学习权重矩阵通过矩阵点乘的方式对特征不同区域添加不同程度的注意力进而抑制干扰, 并将有利于背景白光预测的特征通过反卷积恢复图像细节. 解码路径的第1层是直接由编码路径第6层特征经过反卷积进行上采样.

      BWP-Net模型作为图像到图像的深度学习任务, 一方面需要考虑模型输出图像与标签图像之间像素级别差异, 另一方面也需要考虑模型输出图像与标签图像之间结构相似性. 平均绝对误差(mean absolute error, MAE)和均方误差(mean-square error, MSE)常用于计算像素级别差异, 其中MAE对异常值相对不敏感. 恒星吸收线干涉光谱中吸收线与背景白光灰度差异较大, 使得模型输出的背景白光预测图像中吸收线干扰易表现为异常点, 而这些异常点会导致后续相位解析产生较大误差, 因此本文采用MSE计算像素级别差异, 以便更好抑制异常点. 结构相似度(structural similarity, SSIM)和多尺度结构相似度(multi-scale structural similarity, MS-SSIM)常用于计算结构相似性, 其中MS-SSIM在SSIM基础上引入多尺度分析能够更全面评估图像质量, 因此本文采用MS-SSIM计算结构相似性. 考虑到模型输出图像的中心区域易受吸收线干扰, 将模型输出图像分为左、中、右三个区域分别计算MS-SSIM并以2∶6∶2 (不同比例调试后选取的经验值)的比例加权给出模型输出图像的总结构相似性损失, 并将其与MSE以3∶7 (不同比例调试后选取的经验值)的比例加权作为整体损失. 同时由于模型输出与标签均控制在0—1区间会导致计算损失过小而不利于梯度优化, 对整体损失在进行10000倍的放大作为最终计算损失Loss,

    4.   实验与分析

      4.1.   实验数据及实验设置

    • 利用2.1节中建立的CODES仪器模型, 在不同吸收线、不同视向速度、不同固定光程差下生成吸收线干涉光谱和对应理想背景白光干涉光谱进而构建实验数据集. 其中, 对于吸收线干涉光谱, 将吸收线参数、仪器参数、视向速度等代入(1)式—(3)式, q1和q2分别设置为1和A; 对于理想背景白光干涉光谱, 将仪器参数和视向速度代入(1)式—(3)式, q1和q2分别设置为1和0. 具体参数值设置如下: 吸收线中心波长λa在660—870 nm范围内10 nm为间隔取值; 吸收线波长半高宽Δλa分别取值为0.02 nm和0.03 nm; 吸收线吸收强度A分别取值为0.7, 0.8, 0.9; 固定光程差t在11.98—12.02 mm范围内0.01 nm为间隔取值; 视向速度v在0—2000 m/s范围内100 m/s为间隔取值; 光栅分辨率gr设置为15000, 探测器沿波长方向上的采样率λint设置为0.02 nm; 吸收线干涉光谱和理想背景白光干涉光谱尺寸均为128×256×1, 分别如图5、图6所示.

      本文将构建的实验数据集按6∶2∶2的比例划分为训练集、验证集和测试集, 训练过程中采用Adam优化器(权重衰减为0.002)、学习率设置为0.04且每5轮调整为当前值的80%、Batch大小设置为16、解码器第2层采用dropout(系数为0.5). 每一轮利用训练集数据训练BWP-Net模型后, 计算验证集数据在当前模型参数下的损失, 并将验证集损失最小那一轮对应模型参数作为最终的模型参数.

      • 4.2.   实验结果分析

    • 本文将测试集数据输入到训练好的BWP-Net模型得到预测背景白光干涉光谱, 再将其从对应的吸收线干涉光谱减去后, 利用Wu等[15]报道中基于傅里叶变换的相位解析方法求解相位, 并将同参数(吸收线中心波长、吸收强度、吸收线波长半高宽、固定光程差)下不同视向速度数据配对计算相位差及视向速度差, 整体视向速度平均误差为0.2353 m/s、均方根误差为0.3769 m/s, 表2展示了部分测试集数据分析结果. 从表2可以看出, 在不同吸收线、不同固定光程差、不同视向速度下, 均准确反演了视向速度差, 视向速度误差小于1 m/s, 这说明BWP-Net模型在不同参数条件下均准确预测了背景白光干涉光谱, 进而背景白光干扰得到有效消除、相位解析准确.

      图7是吸收线中心波长λa为770 nm、吸收强度A为0.8、吸收线波长半高宽Δλa为0.02 nm、固定光程差t为12.02 mm、视向速度v1为0 m/s时BWP-Net模型输出图像与对应标签图像的第64行数据截取出来对比结果图, 可以看出二者几乎重叠, 曲线峰谷位置全部对齐, 再一次证明模型输出较好地预测出了对应背景白光干涉光谱.

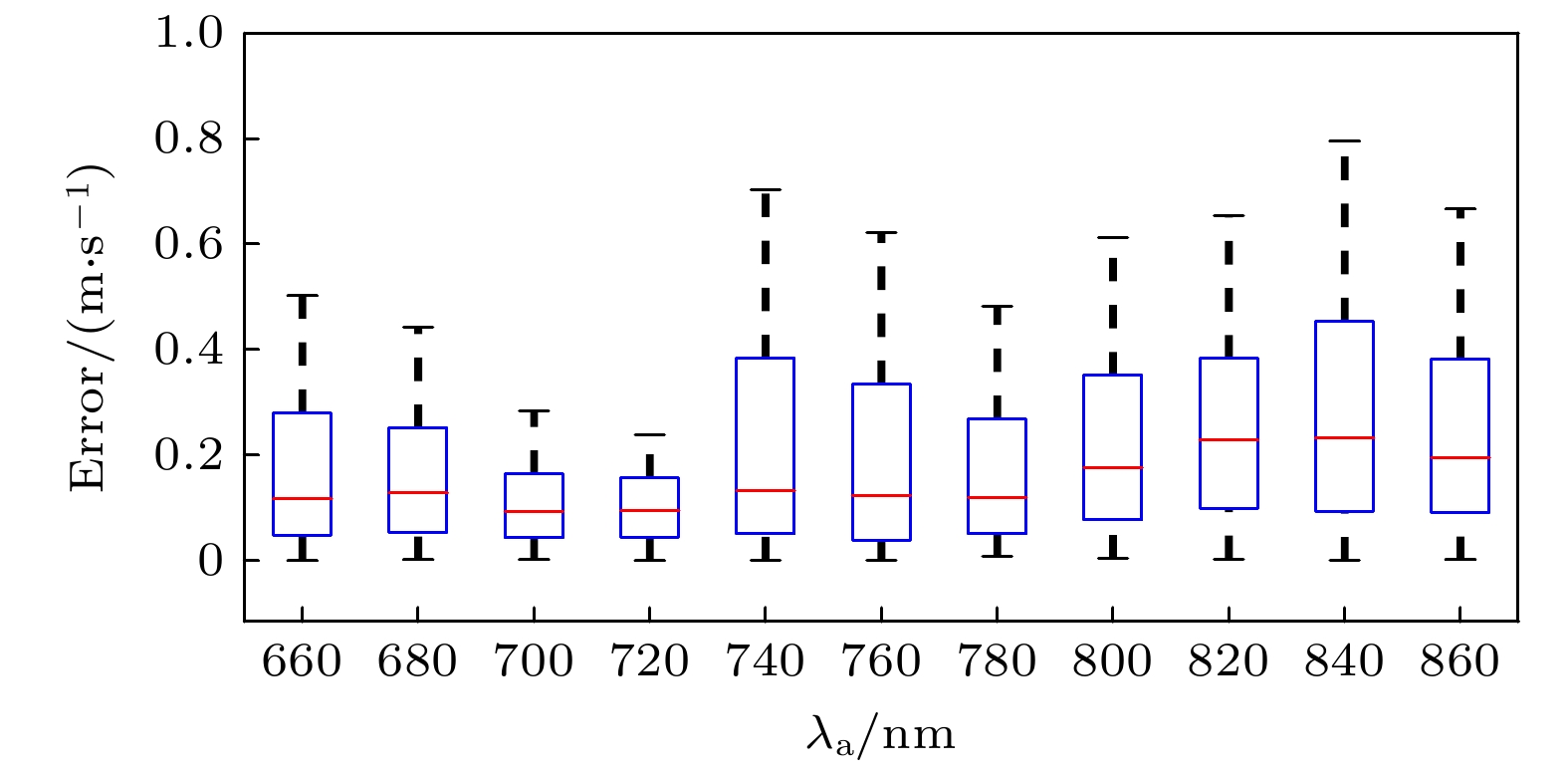
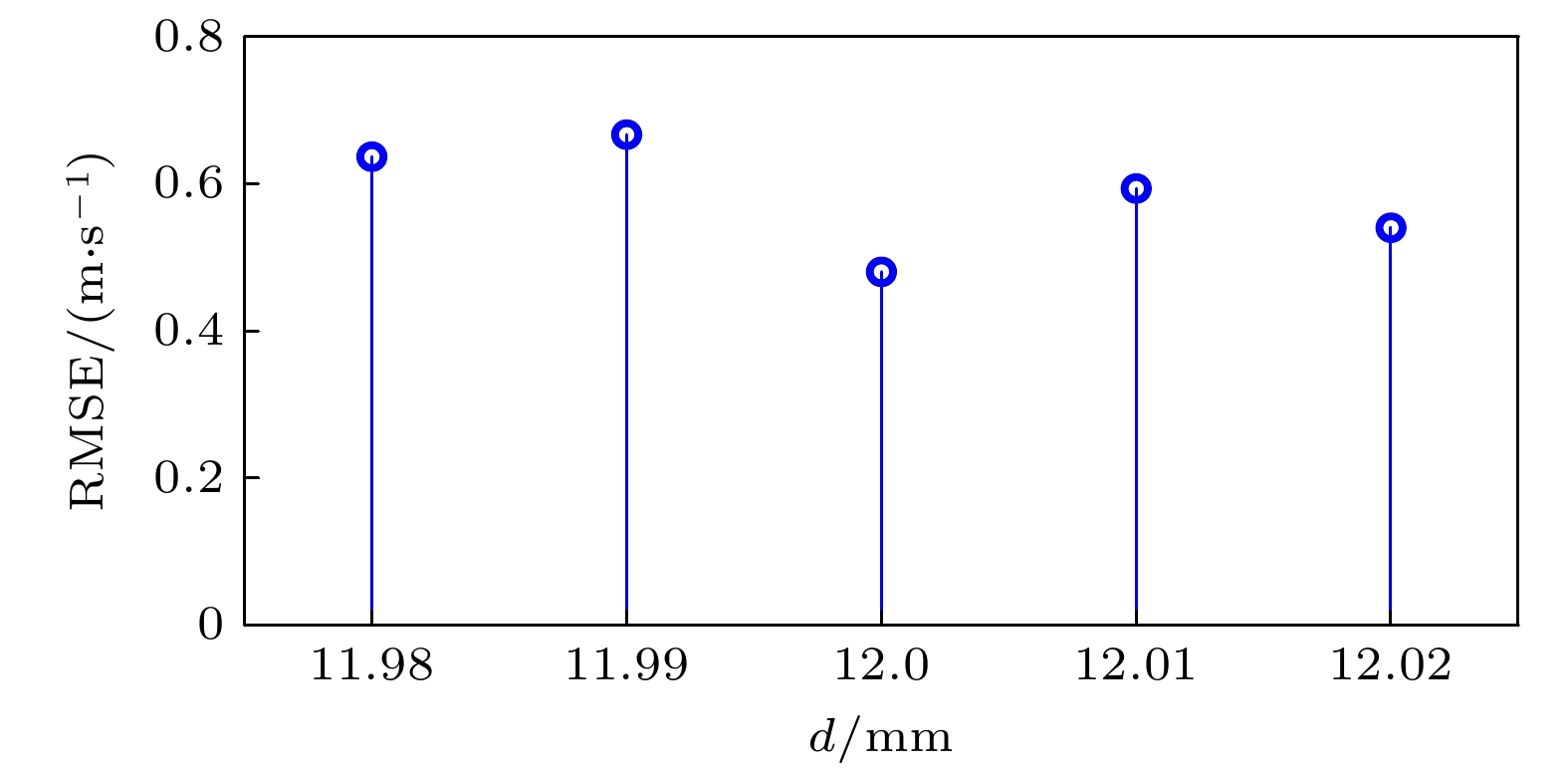
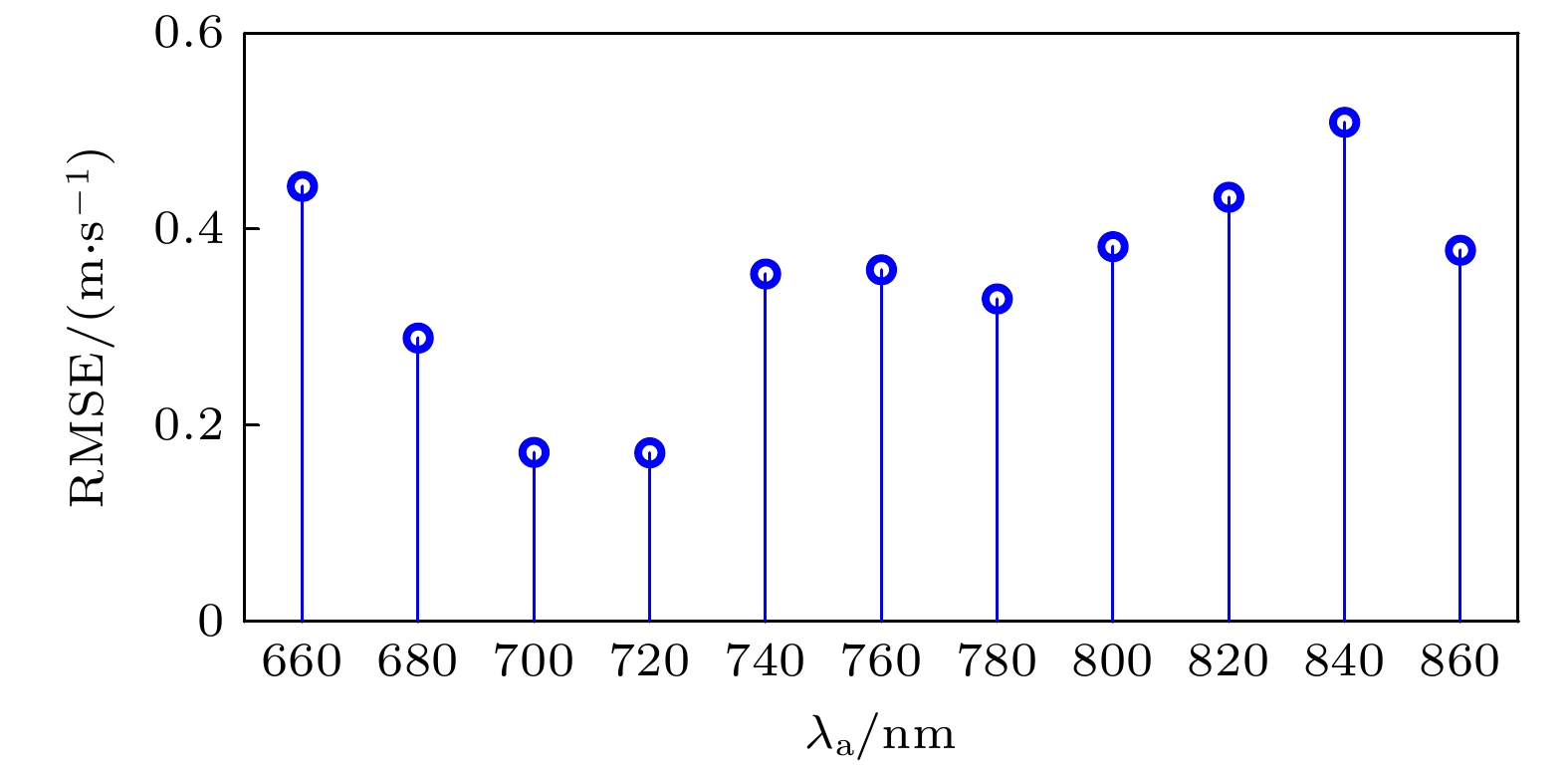
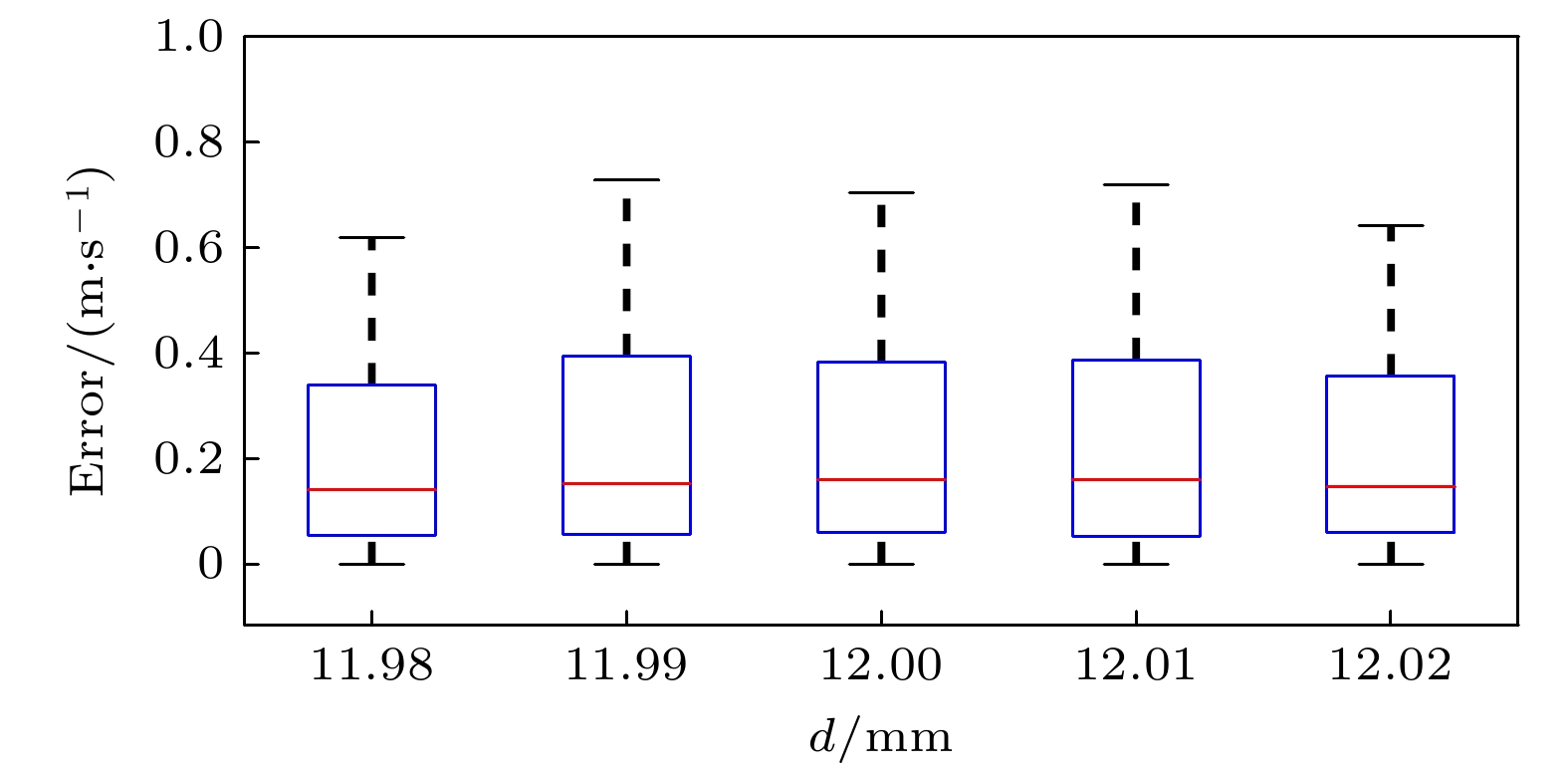
      为了验证BWP-Net模型的稳定性和鲁棒性, 分别统计了在不同吸收线中心波长λa下和不同固定光程差t下测试集数据视向速度误差分布和视向速度均方根误差, 结果如图8—图11所示. 从图8、图9可以看出, 在不同吸收线中心波长下视向速度误差分布略有差异, 其中700, 720 nm下视向速度误差相对较小、840 nm下误差相对较大, 但整体差异不大, 各波长下误差中位数均小于0.25 m/s、误差上四分位数均小于0.5 m/s、均方根误差均小于0.51 m/s. 从图10、图11可以看出, 在不同固定光程差下视向速度误差分布很相似, 各固定光程差下误差中位数均小于0.2 m/s、误差上四分位数均小于0.4 m/s、均方根误差均小于0.7 m/s. 可见, 不同参数条件下视向速度误差分布比较均匀, 说明BWP-Net模型在不同参数条件下背景白光干涉光谱预测水平比较稳定, 即BWP-Net模型稳定性较好、鲁棒性较高. 此外, 从图8—图11可以看出, 视向速度误差主要集中在0—0.4 m/s范围, 这与测试集整体视向速度均方根误差0.3769 m/s基本一致.

      图12是将BWP-Net模型编码路径第1层到第5层输出特征及与其尺寸相同的解码路径特征和注意力反卷积中可学习权重矩阵可视化的结果. 从图12可以看出: 1)编码路径特征第1层到第5层逐渐由简单特征变为抽象特征, 空间分辨率逐步下降, 且吸收线特征一直比较明显, 其中第1层特征在保留输入图像大部分细节基础上放大了吸收线边缘细节, 第2层特征主要放大了背景白光干涉条纹细节, 第3层特征展现了全局的水平和垂直等方向细节, 第4层和第5层特征是比较抽象的全局特征, 展示了吸收线与背景的差异, 第5层这种差异更加明显. 2)解码路径特征第5层到第1层逐渐由抽象特征恢复图像细节, 空间分辨率逐步上升, 且吸收线特征逐渐在弱化, 其中第5层是几乎全黑的全局特征, 第4层在第5层基础上恢复了一些细节, 但比较抽象, 第3层开始恢复图像样貌, 有了一些水平和垂直等方向细节, 能看到其中吸收线细节, 但与背景差异不明显, 第2层恢复了大量白光细节, 吸收线细节更加弱化, 第1层基本重建出背景白光干涉条纹细节. 3)注意力权重参数分布明显分为左、中、右三个区域且比较对称, 同时第5层到第1层中间区域逐渐变窄, 说明图像重建过程中三个区域作用程度不同, 越接近输出层中间区域作用越小, 这与解码路径中吸收线特征逐渐弱化相符合.

      显然解码路径和编码路径的同一层特征细节基本相对应, 编码路径逐渐放大吸收线细节, 为后续解码路径去除吸收线细节做准备, 解码路径利用跳跃连接和注意力权重逐渐弱化吸收线细节, 进而最终预测输出背景白光干扰. 特征与权重矩阵可视化再次验证了第3节中建立BWP-Net模型相关理论的可靠性和合理性.

    5.   结　论

    • 针对CODES工作原理和探测数据特性, 本文提出了基于卷积神经网络的背景白光预测网络模型BWP-Net, 以端到端的方式由仪器获取的恒星吸收线干涉光谱预测输出对应背景白光干涉光谱. 实验结果表明, 在不同吸收线、不同固定光程差、不同视向速度条件下, 利用BWP-Net模型输出消除背景白光干扰后, 吸收线反演视向速度平均误差为0.2353 m/s、均方根误差为0.3769 m/s, 即BWP-Net模型能够有效地预测输出背景白光干扰、且预测性能稳定. 本文下一步工作是基于恒星吸收线干涉光谱数据的频谱特性, 进一步优化背景白光预测模型.

    参考文献 (26)

目录

/

返回文章
返回