首页
登录
注册
-
高精度重力场的测绘对于自然资源勘探[1]、地球物理研究[2,3]、大地水准面模型建立[4–6]、地质灾害监测[7]等具有重要意义. 目前地面静态绝对重力测量精度已经达到微伽(1 μGal = 10–8 m/s2)量级[8–12], 然而这种测量方法的效率不高, 难以在较短的时间内迅速测量大区域的重力场数据. 此外, 它也无法在地形地貌复杂、人类活动稀少的区域进行有效的测量. 利用卫星重力测量技术可以得到地球重力场模型[13](例如EGM2008)虽然可以覆盖全球, 但其空间分辨率较低, 在小尺度区域存在一定失真、精度不够等问题. 而基于冷原子干涉仪的动态绝对重力测量利用轮船、飞机等载体进行测量[14–17], 具有效率高、覆盖范围广、分辨率高等特点, 其精度一般在毫伽(1 mGal = 10–5 m/s2)量级, 可有效提升地球重力场的测绘效率, 弥补目前的空间分辨率低、测量区域受限等问题.
动态绝对重力测量受到了国内外学术界的高度重视. Bidel等[16–18]自2017年起开展了多次机载动态绝对重力测量实验, 并将机载重力测量数据与海洋、陆地测量的重力数据进行了比较, 其标准偏差和平均值的差异约为2 mGal, 测线上的内符合精度在0.6—1.3 mGal. 国内也有多个团队开展了车载、船载的绝对重力测量实验[19–24]. Zhou等[21]在船载动态绝对重力测量中外符合精度达到0.42 mGal. 国内的机载绝对重力测量相关研究处于起步阶段. 赵远等[24]在机载冷原子干涉实验中测到了航空环境下的重力干涉条纹图样. 本文报道了动态绝对重力测量试验, 获得了机载绝对重力测量结果, 整段测线重力值变化标准偏差约为8.86 mGal, 评估了实测重力值与EGM2008模型残差的标准差, 经计算约为8.16 mGal. 本文的结果验证了机载动态绝对重力测量的可行性, 并提供了一套航空绝对重力测量的技术方案.
-
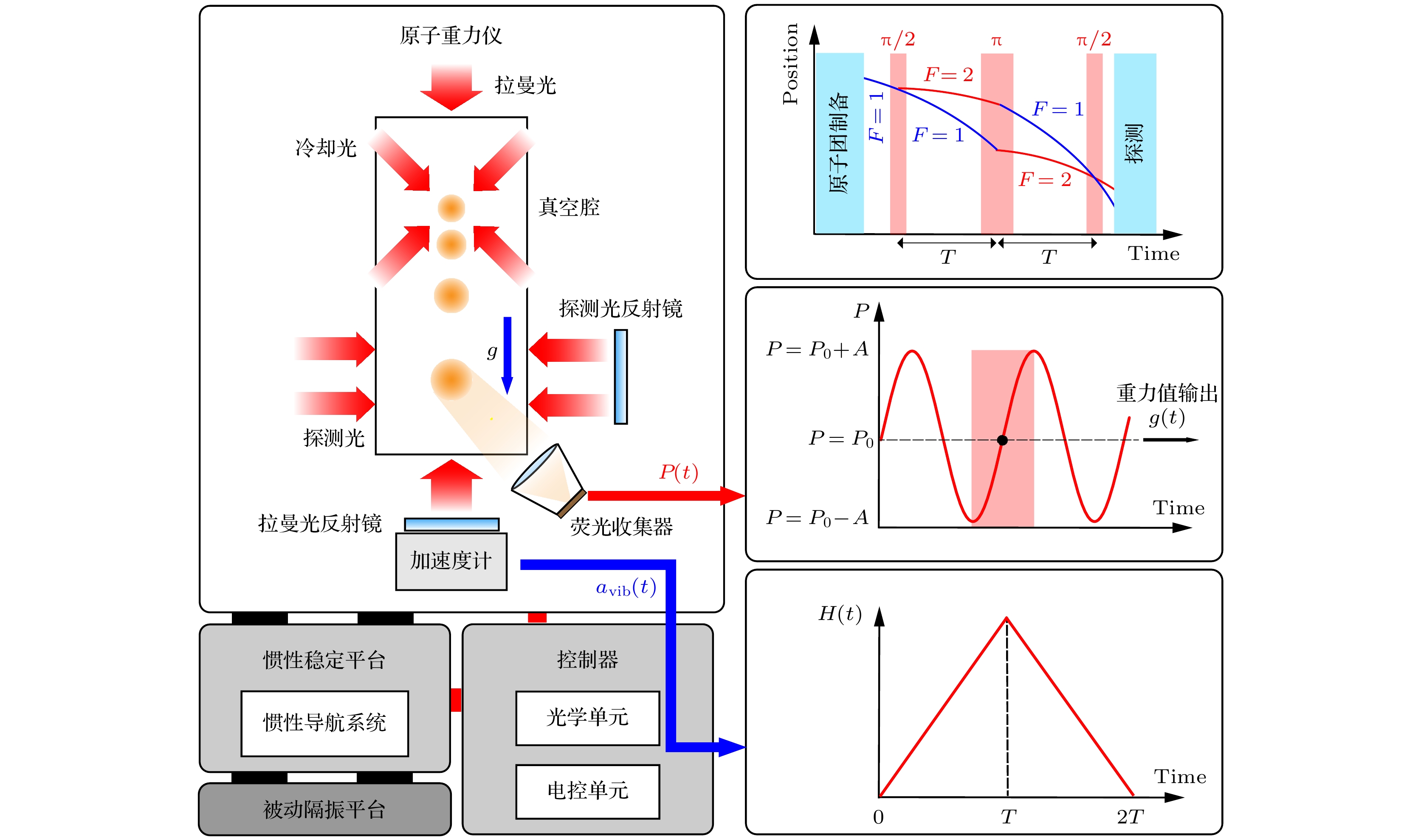
量子重力仪利用物质波构成的干涉仪来测量重力加速度, 通过拉曼激光实现原子物质波包的分束、反转、合束, 形成原子干涉图样, 通过提取原子干涉条纹的相位来精确测量重力加速度.
地面重力加速度g引起的原子干涉仪相移为
其中
${k_{{\text{eff}}}}$ 表示对射拉曼激光的有效波矢, T表示拉曼干涉脉冲之间的时间间隔.不同于静态情况, 动态环境下量子重力仪测量的加速度是重力加速度、载体运动导致的振动加速度
${a_{{\text{vib}}}}$ 以及由Eötvös效应导致的加速度$ {a_{{\text{E\"ot}}}} $ 的叠加, 因此在动态环境下需要使用高精度加速度计采集载体的加速度, 通过权重函数分离干扰加速度和重力加速度, 最终获取重力加速度信息. 实验中将拉曼激光以啁啾率α扫频, 原子干涉相移表示为振动引起的相移
$ \phi_{\text{vib}}\text{} $ 表示为其中,
$H(t)$ 为原子干涉仪的灵敏度函数,${a_{{\text{vib}}}}(t)$ 为实时测量的振动加速度.实验中通过高精度加速计采集振动加速度
${a_{{\text{vib}}}}(t)$ , 通过(3)式得到$ \phi_{\text{vib}} $ , 并基于此对原子干涉条纹进行还原, 最终得到原子干涉相移, 并提取重力加速度信息. -
我们的机载量子重力仪采用激光冷却技术捕获冷原子团并使其自由下落, 利用物质波干涉的方法测量落体的垂向加速度. 航空重力测量实验使用了新型动态量子重力仪(AG-1), 不同于本团队在静态绝对重力测量中所使用的量子重力仪ZAG或CAG[9,25], 为使量子重力仪体积更小、质量更轻、更适用于外场动态测量场景, AG-1摒弃了二维磁光阱结构, 跳过原子团预制备过程, 直接使用三维磁光阱和铷源释放器制备冷原子团, 如图1所示. 冷却激光频率相对87Rb原子
$| {5{\,}^2}{{\text{S}}_{1/2}}, F = 2 \to {5\,^2}{{\text{S}}_{3/2}}, F' = 3 \rangle $ 跃迁存在$ \varDelta = - {\text{12 MHz}} $ 的失谐. 捕获完成后调整冷却光失谐和功率进行偏振梯度冷却, 最终将原子团温度降至10 μK以下.完成冷原子团制备后关闭磁光阱, 原子团在重力场中做自由落体运动, 通过微波π脉冲将原子制备至对磁场不敏感的
$| {{5\,^2}{{\text{S}}_{1/2}}, F = 1, {m_{\text{F}}} = 0} \rangle $ 态. 再通过3束间隔时间为T的拉曼光脉冲$\left( {{\text{π/2 - \pi - \pi /2}}} \right)$ 对原子物质波进行分束、反转、合束, 形成类似于马赫-曾德尔干涉仪的物质波干涉仪. 利用时间飞行法探测原子布居数.如图1所示, 机载绝对重力测量系统主要由量子重力仪探头、重力仪控制柜、惯性稳定平台和隔振系统、惯性导航系统、卫星导航系统等构成. 惯性稳定平台与量子重力仪刚性连接, 保证在动态环境中量子重力仪始终保持在垂线方向; 隔振系统用于减轻机舱内高频振动对系统的影响, 在特定条件下可以避免共振; 卫星导航系统和惯性导航系统结合使用, 用以修正惯性导航系统的长漂, 提供高精度的导航数据, 包括载体的位置、速度、姿态等信息, 基于这些信息可以修正科里奥利力及经纬度变化引起的重力异常.
-
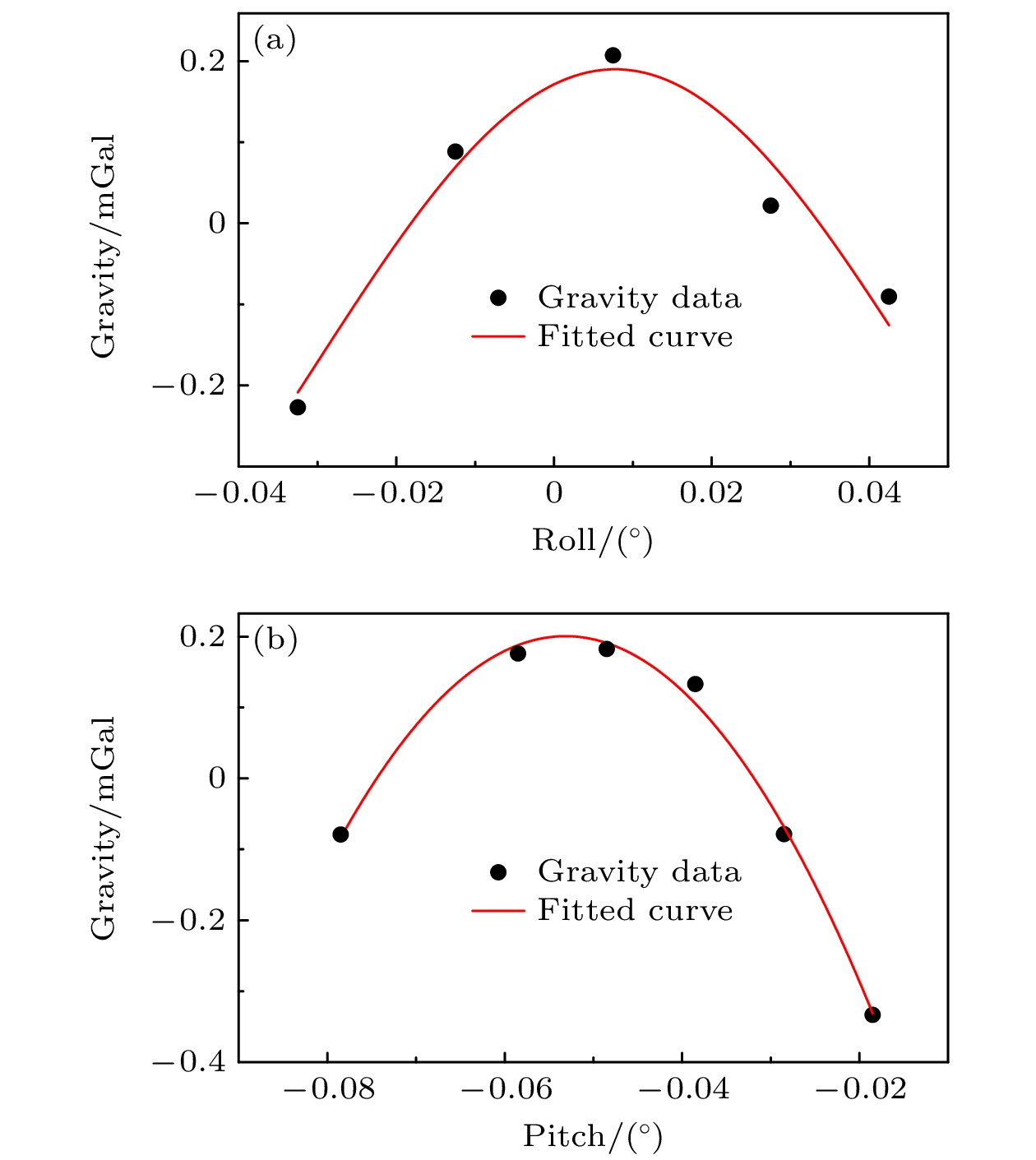
本次机载重力测量实验的飞机及绝对重力 测量系统现场照片如图2所示. 在进行航空动态 测量前, 首先在地面利用惯性稳定平台进行倾斜实验以寻找倾斜零点, 保证量子重力仪处于垂线方向, 如图3所示, 拟合曲线的顶点位置对应目标倾斜零点.
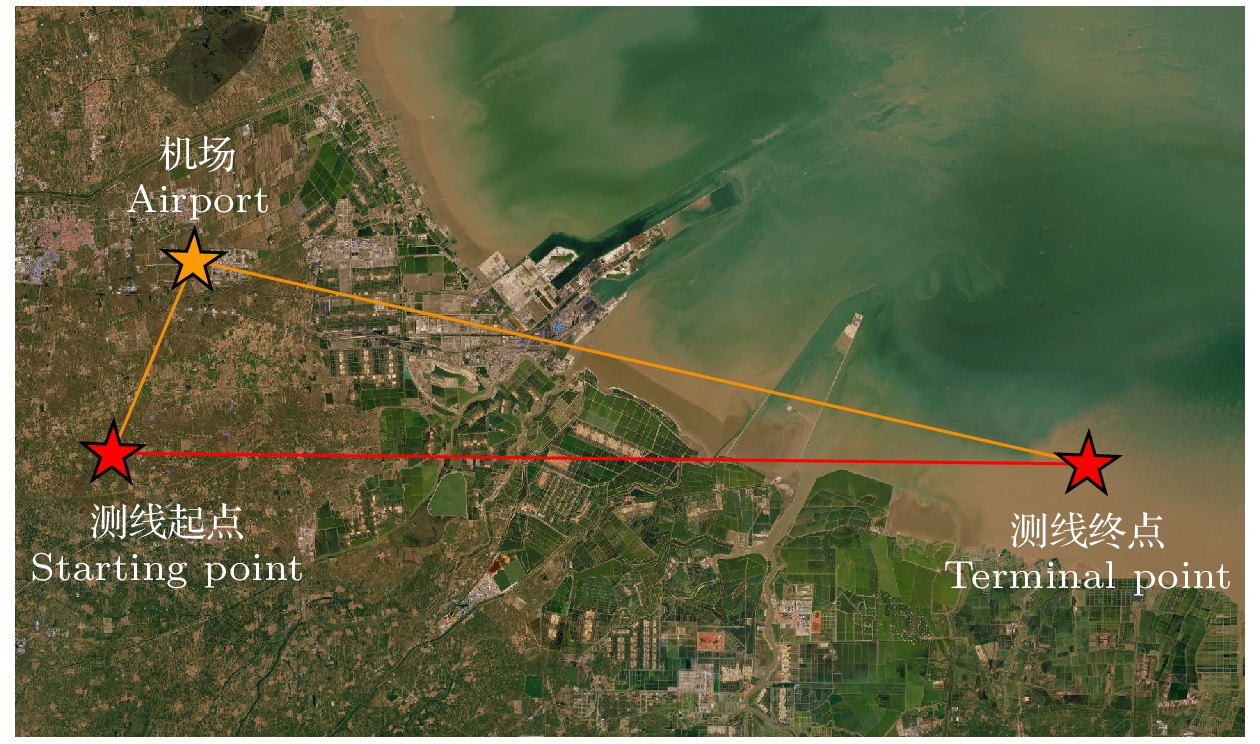
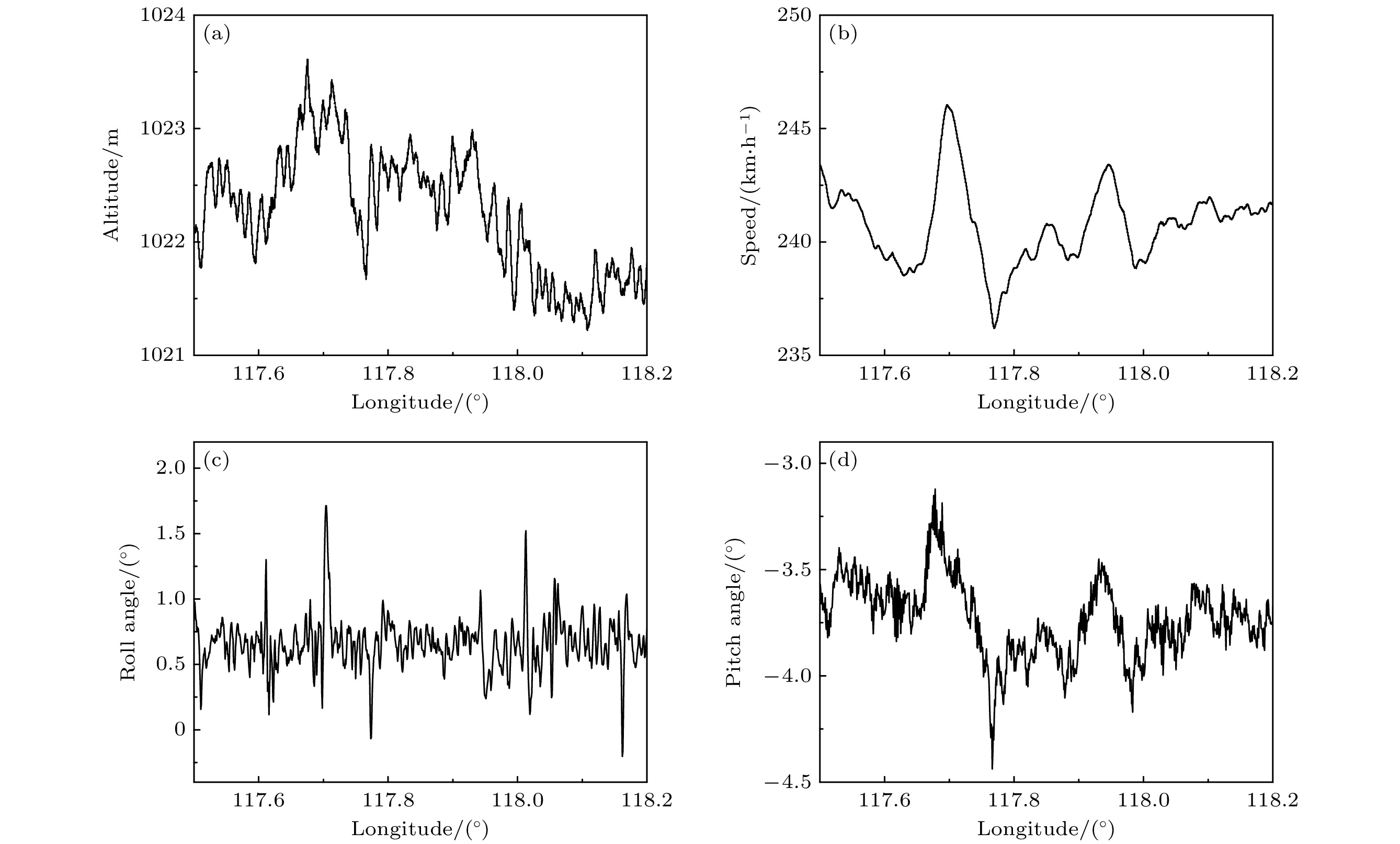
如图4(a)所示, 测量不同干涉时间T对应的原子干涉条纹, 找到实验地点对应的
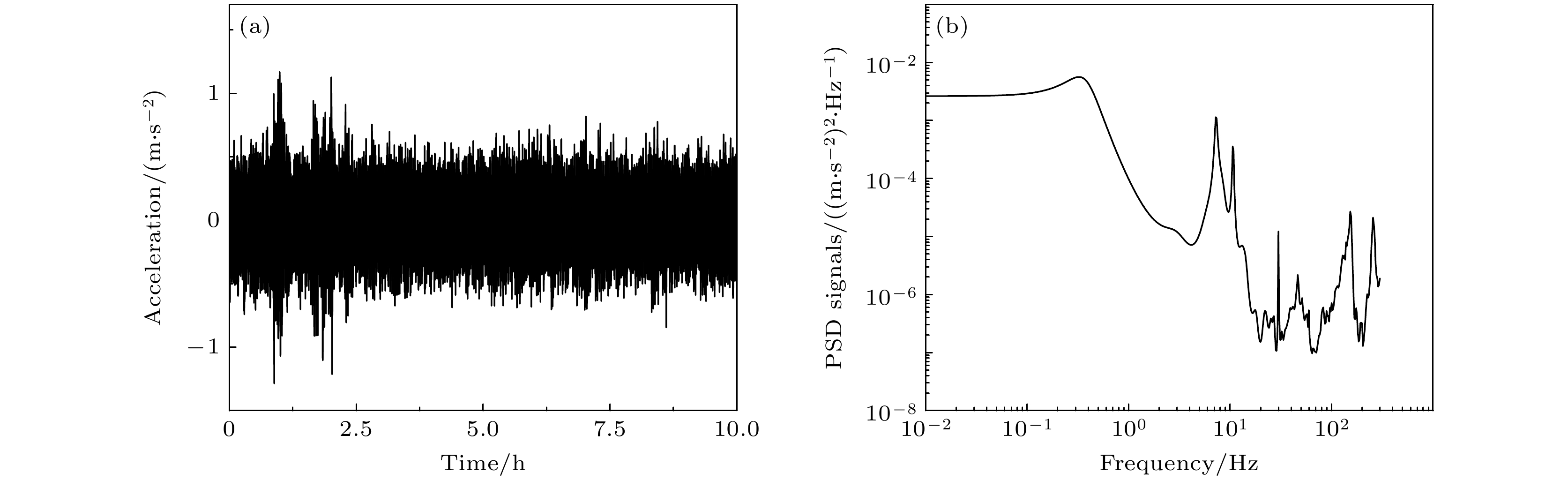
${\alpha _0} \approx - 25.12105\; {\rm {MHz/s}}$ . 在该点进行静态重力测量, 评估量子重力仪测量性能. 我们进行了约11.7 h的重力值长扫, 图4(b)为测量结果的Allan偏差, 评估的重力测量灵敏度约为${2.5}~{\text{mGal}}/\sqrt{{\text{Hz}}} $ , 在夜晚安静时段, 重力测量灵敏度约为${1.9}~{\rm mGal/\sqrt{ Hz}} $ , 测量精度约为0.04 mGal, 图4(c)为部分连续绝对重力测量数据.飞行测线如图5所示, 位于渤海沿岸, 整体为东西走向, 覆盖陆地、海陆交界地带、海洋等不同区域. 测线过程中飞机保持匀速平飞, 整体姿态平稳, 无明显、剧烈的颠簸和起伏. 通过海拔、航速、横滚角、俯仰角等数据的标准差评估飞行状态, 数据如图6(a)—(d)所示, 海拔整体保持在1022.2 m, 标准偏差为0.5 m, 峰峰值约为2.5 m, 引起的重力异常变化约为0.75 mGal; 航行地速整体在240.7 km/h, 标准偏差约为2.1 km/h, 根据Eötvös效应评估, 速度与经纬度变化共同引起的重力异常幅值约为37 mGal. 飞行过程中飞机横滚和俯仰角度变化小于2°, 测量系统使用惯性稳定平台进行姿态控制, 横滚角控制精度约为8'', 俯仰角控制精度约为20'', 对应重力误差仅有1 μGal左右, 整体而言测试过程中飞机姿态保持良好. 由于空气扰动、发动机振动等因素影响, 飞行过程中机舱振动环境较差, 如图7(a)所示, 振动的峰峰值达到1 m/s2, 其噪声功率谱密度如图7(b)所示, 高频部分噪声比较明显, 这在一定程度上限制了系统灵敏度.
受海拔变化影响, 机舱内环境参数会剧烈变化, 图8(a), (b)展示了飞行过程中舱内不同区域的温湿度变化情况. 由于控制柜中光电器件繁多、排布紧凑, 各个器件散发的热量在密闭机舱中难以排出, 热量积聚在系统中导致主光路温度变化, 温度的漂移导致光学元件的角度和形状发生形变, 从而改变输出激光的偏振、光功率, 引入额外的噪声和误差. 本文使用的控制柜具有温度主动控制系统, 在测试过程中光路温度保持在(25.004 ± 0.026) ℃. 整体温度变化处于可接受范围内, 捕获原子数、干涉条纹等现象处于正常情况, 未对实验结果造成明显影响.
当飞机进入测线且平飞后, 采集原子布居数信号, 使用高精度加速度计记录振动信号, 积分得到振动加速度引起的原子干涉条纹相位偏差, 用以修正恢复原子干涉条纹, 从中提取重力加速度.
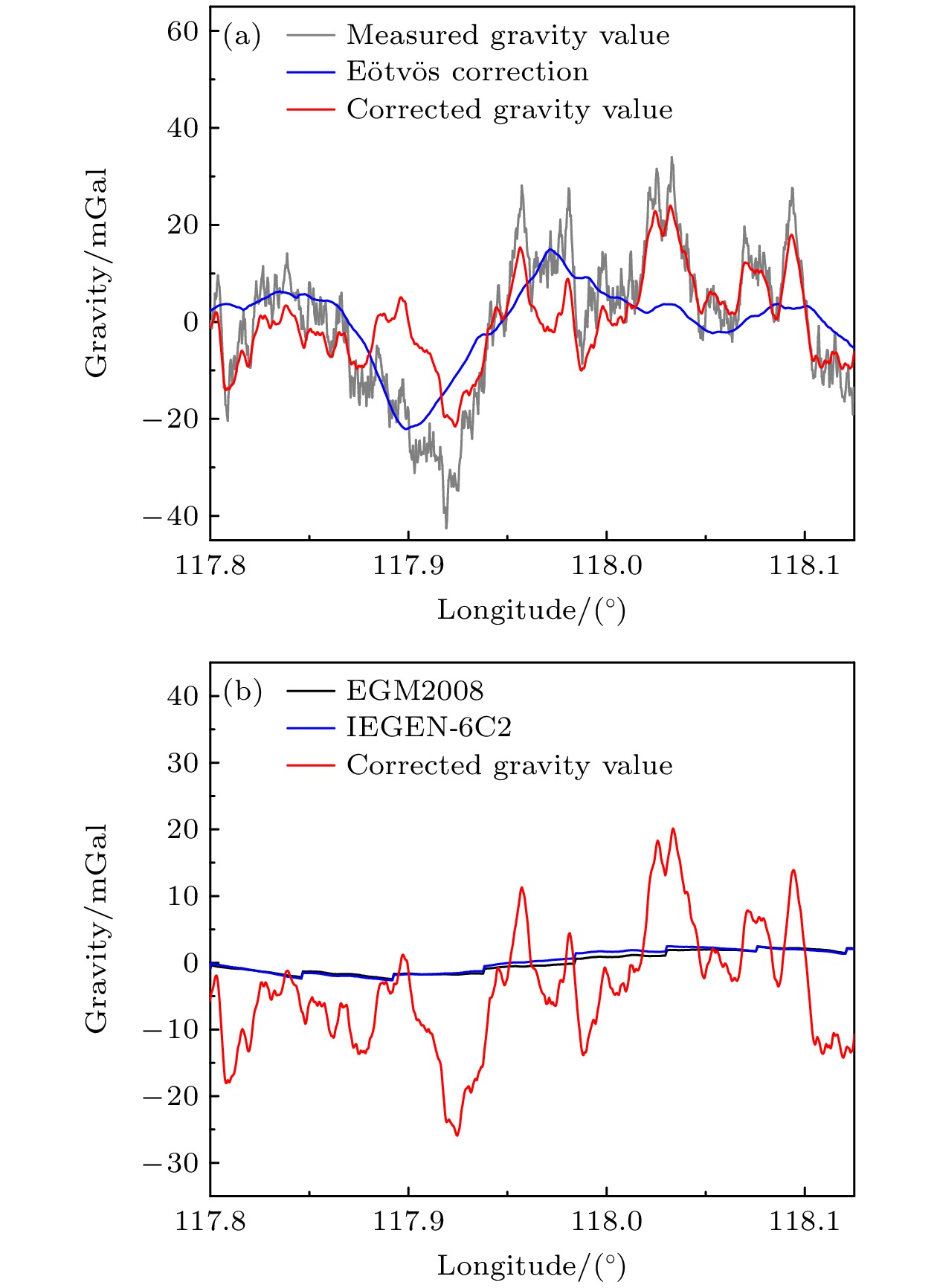
本次测试的飞行路线如图5所示, 受到空域限制, 去掉测量起点和终点附近的转弯区域后实际有效测线长度约为30 km. 图9(a)为本次飞行试验测得的重力加速度结果, 其中灰色实线为我们对布居数曲线进行振动补偿后获得的原始重力加速度数据, 原始数据的峰峰值约为70 mGal, 该数据的统计标准偏差为16 mGal. 飞行动态环境下测得的重力值会受到飞机航速、经纬度、高度等参数变化的影响, 利用同机的惯导记录这些参数的变化, 并根据Eötvös效应的理论模型计算各个参量导致的重力值变化情况, 如图9(a)蓝色实线所示, 飞行状态参数导致的重力值异常幅值是37 mGal. 将重力原始数据变化曲线减去由飞行状态引起的重力值变化曲线, 并进行长度为3 km的滤波后, 重力变化的峰峰值降至约45 mGal, 整段测线重力值变化的标准差约为8.86 mGal.
将实测重力数据与EIGEN-6C2、EGM2008模型进行了比对, 如图9(b)所示. 图中可以看出实际测量的航空绝对重力数据与基于EIGEN-6C2, EGM2008重力模型计算的重力值数据在整体趋势上基本一致. 选取EGM2008模型评估了测量重力值与计算值的残差的标准差, 约为8.16 mGal, 该性能受限于量子重力仪的数据提取算法. 航空测量环境下的振动情况十分复杂, 这对重力信号的处理和补偿技术提出了较大的挑战, 在后续的工作中会改进相位补偿、重力值计算与校正算法, 提高从复杂的融合加速度信号中分离出重力加速度信息的能力.
除了信号提取方法导致的噪声外, 航空测量过程中会引入额外的测量噪声, 比如姿态噪声、振动测量噪声、Eötvös噪声等, 表1给出了这些噪声在一般情况下能够引起的重力值误差范围. 飞行过程中, 载具姿态会发生较大变化, 测试中使用惯性稳定平台将重力仪探头始终维持在垂线方向[26,27], 角度变化在20'' 以下, 引起的重力值变化小于1 μGal. 动态测量条件下最主要的噪声来源是振动噪声, 其产生的噪声会导致无效的干涉条纹, 不做处理会导致几千毫伽的重力值偏差. 需要利用加速度计采集振动加速度噪声修正, 通过量子重力仪的响应函数与振动加速度在原子干涉时间内的卷积进行修正处理. 目前AG-1使用的加速度计存在温漂和装配误差, 这会导致采集到的振动信号与拉曼光反射镜实际感受到的振动并不完全一致, 会产生额外的噪声. 后续工作会进一步调整加速度计选型、优化装配方式及传递函数来减弱振动采集误差的影响. Eötvös效应在动态条件下导致的绝对重力测量误差非常显著, 载具的运动状态会导致几十毫伽甚至更高的重力异常, 该异常依赖于载具及重力仪上装配的惯性导航器件进行测量并建模矫正, 受到惯性导航器件和模型精度影响, 不可避免地会引入误差.
-
本文基于量子重力仪、惯性稳定平台、惯性 导航系统、隔振平台及控制单元等实现了一套机 载绝对重力测量系统, 并在此基础上开展了绝对重力静态和动态测量实验研究. 静止状态下重力测 量的灵敏度约为
$\rm 2.5~mGal/\sqrt{Hz} $ , 夜间振动条件 较好时的灵敏度约为$ \rm 1.9~mGal/\sqrt{Hz} $ , 测量精度约为0.04 mGal; 随后评估了飞行状态下的振动噪声、温度、湿度等环境参数; 最后, 通过航空飞行试验评估绝对重力动态测量性能, 测得30 km的测线上重力值变化的统计标准偏差为16 mGal, 进行Eötvös效应修正、滤波后整段测线重力值变化标准差约为8.86 mGal. 我们将实测航空重力数据与IEGEN-6C2、EGM2008等模型进行了比对, 实测结果与模型计算的重力值在整体趋势上基本一致, 实测航空重力值与模型计算值残差的标准差约为8.16 mGal. 本文的研究结果初步验证了基于原子干涉技术开展机载动态绝对重力测量的可行性, 为复杂地形的高精度、高分辨率重力场测绘提供了一种技术路径. 本次实验在验证了量子重力仪在航空绝对重力测量中具有高精度、高分辨率潜力的同时, 也揭示了振动噪声对测量精度和信号补偿的显著影响, 若要提升测量精度, 改进隔振措施和补偿算法是十分必要的. 此外, 考虑到航空环境的动态变化对仪器稳定性的影响, 建立环境保障系统以维持工作稳定性至关重要. 这些措施将有助于未来获取更精确的重力数据, 从而推动地质勘探、资源调查、环境监测、灾害预警及航空航天等领域的发展.
基于量子重力仪的航空绝对重力测量
Airborne absolute gravity measurements based on quantum gravimeter
-
摘要: 高精度重力场测绘对地质调查、资源勘探、大地水准面建模等领域具有重要意义. 地面静态绝对重力测绘效率低, 无法覆盖河流、湖泊、山脉等地形条件复杂的区域. 机载绝对重力测绘可以在复杂地形实现快速、连续重力测量, 满足实际应用需求. 本文报道了一种基于量子重力仪的航空绝对重力测量系统, 开展了机载动态绝对重力测量实验. 在飞行高度1022 m、航速240 km/h条件下, 得到3 km滤波后整段测线重力值变化的标准差约为8.86 mGal, 评估了实测重力值与EGM2008模型残差的标准差, 经计算约为8.16 mGal. 本文结果验证了量子重力仪在航空动态绝对重力测量方向的可行性, 为复杂地形条件下的高精度、高分辨率重力场测绘提供了一种新的技术手段.Abstract: High-precision gravity field mapping plays a critical role in geological survey, resource exploration, and geoid modeling. The traditional ground-based static absolute gravity measurements possess high accuracy, but they are fundamentally constrained by low operational efficiency and inability to survey complex terrains such as river networks, lakes, and mountainous regions. This study tries to address these limitations through the development of an airborne absolute gravity measurement system based on quantum gravimeters. At a flight altitude of 1022 m and a speed of 240 km/h of the airplane, after a filtering process of 3 km, the measured gravity value shows a standard deviation of approximately 8.86 mGal. Furthermore, a comparative analysis with the EGM2008 gravity model shows a residual standard deviation of 8.16 mGal, validating the consistency of the system with established geophysical references. The experimental results confirm the operational feasibility of quantum gravimeters in scenarios of airborne dynamic measurement, demonstrating the viability of this technological framework for high-resolution gravity field mapping.
-
Key words:
- quantum gravimeter /
- airborne absolute gravity measurement /
- cold atom /
- atom interference .
-
-
图 1 机载绝对重力测量系统组成及其测量原理图
Figure 1. System composition of the airborne absolute gravity measurement system and the basic measurement principle.
图 2 测试飞机及重力测量系统现场照片
Figure 2. Picture of aircraft and the absolute gravity measurement systems.
图 3 倾斜调制实验数据(图中黑点为实测重力值, 红色曲线为正弦函数拟合曲线) (a) 重力值随横摇角度变化; (b) 重力值随纵摇角度变化
Figure 3. Experimental data for tilt modulation, the black dots are the measured gravity values and the red curve is the fitted curve with the sine function: (a) Change of measured gravity values as the roll angle; (b) change of measured gravity values as the pitch angle.
图 4 (a) 不同T的拟合曲线, 其中实心红、蓝、黑点分别为T = 10 ms, T = 12 ms, T = 14 ms时的原子布居数, 实线为其对应拟合曲线; (b) 静态测量灵敏度; (c) 静态测量重力值
Figure 4. (a) The fitted curves for different T, where the red, blue, and black dots are the atomic population at T = 10 ms, T = 12 ms, and T = 14 ms, respectively, the solid lines are their corresponding fitted curves; (b) static measured sensitivity; (c) static measured gravity values.
图 5 飞行路线(红线为重力测线, 橙线为往返路线)
Figure 5. Trace of flight (The red line is the pratical measurement route, and the orange line is the take-off and landing route).
图 6 飞机的状态参数 (a) 高度; (b) 速度; (c) 横滚角; (d) 俯仰角
Figure 6. Detailed parameters of the airplane during the flight: (a) Flight altitude; (b) flight speed; (c) roll angle; (d) pitch angle.
图 7 飞行环境下的振动信号 (a) 时域振动信号; (b) 振动信号功率谱
Figure 7. Vibration signals in the case of flying: (a) Time-domain vibration signals; (b) power spectrum of vibration signals.
图 8 飞行环境下的温湿度变化 (a), (b) 温度和湿度变化曲线, 其中红线、蓝线、黑线分别为AG-1探头、机舱、AG-1控制器内部的温湿度变化; (c)光路模块的温湿度变化
Figure 8. Variations of temperature and humidity during the flight campaign: (a), (b) Temperature and humidity change curves, where the red, blue and black lines are the data measured in AG-1 sensor, cabin and AG-1 controller, respectively; (c) temperature and humidity variation in the optical module.
图 9 机载绝对重力测量结果 (a) 重力数据处理结果(灰色实线为原始重力数据, 蓝色实线为Eötvös修正量, 红色实线为经过Eötvös修正和滤波后的修正重力值); (b) 实测航空重力数据与模型计算数据的对比(黑色实线为基于EIGEN-6C2模型计算的重力数据, 蓝色实线为基于EGM2008模型计算的重力数据, 红色实线为实测的航空重力数据)
Figure 9. Measurement results of absolute gravity with airborne platform: (a) Gravity correction results. The gray line denotes the original gravity data, the blue line represents the gravity value dues to Eötvös correction, while the red line illustrates the gravity values after the Eötvös correction and filtering; (b) comparison of measured airborne gravity data with the data obtained with gravity models, black line is the gravity data calculated by the EIGEN-6C2 gravity model, blue line is the gravity data calculated by EGM2008 gravity model, and red line are the measured gravity airborne data.
表 1 噪声来源及其引起的重力值偏差
Table 1. Budget of noise sources and their resulted gravity deviations.
噪声来源 引起的重力值偏差/mGal 振动噪声 >103 Eötvös效应 0—37 惯性稳定平台姿态
控制残余噪声≈10–3 飞行高度变化 0—0.8 
下载: 导出CSV
-
[1] Zhang C G, Chen J G, Song M Y, Wang J K, Yuan B Q 2015 Pol. Marit. Res. 22 100 doi: 10.1515/pomr-2015-0040 [2] Nusbaum U, Rusnak I, Klein I 2019 Navigation-US 66 681 doi: 10.1002/navi.336 [3] 张倩文, 徐亚, 褚伟, 路书鹏 2024 中国科学: 地球科学 67 1836 doi: 10.1007/s11430-023-1288-1 Zhang Q W, Xu Y, Chu W, Lu S P 2024 Sci. China-Earth Sci. 67 1836 doi: 10.1007/s11430-023-1288-1 [4] Reager J T, Thomas B F, Famiglietti J S 2014 Nat. Geosci. 7 588 doi: 10.1038/ngeo2203 [5] Vidal-Vega A I, Trejo-Soto M E, Tocho C N, Romero-Andrade R, Nayak K 2024 J. South Am. Earth Sci. 148 105192 doi: 10.1016/j.jsames.2024.105192 [6] Elshewy M A, Thanh P T, Elsheshtawy A M, Refaat M, Freeshah M 2024 Egypt. J. Remote Sens. Space Sci. 27 656 doi: 10.1016/j.ejrs.2024.09.002 [7] Mcleod D P, King B T, Stedman G E, Schreiber K U, Vvrebb T H 2001 Fluct. Noise Lett. 1 R41 doi: 10.1142/S0219477501000068 [8] Zhu H R, Huang P W, Gao B, Tang B, Chen X, Hong J Q, Ang J, Zhong J Q 2024 Opt. Express 32 26157 doi: 10.1364/OE.528832 [9] Wu B, Li D R, Zhou Y, Zhu D, Zhao Y P, Qiao Z K, Cheng B, Niu J Y, Guo X C, Wang X L, Lin Q 2024 IEEE Sens. J. 24 9536 doi: 10.1109/JSEN.2024.3362371 [10] Ruan C J, Zhuang W, Yao J M, Zhao Y, Ma Z H, Yi C, Tian Q, Wu S Q, Fang F, Wen Y H 2024 Sensors 24 2395 doi: 10.3390/s24082395 [11] Li C Y, Long J B, Huang M Q, Chen B, Yang Y M, Jiang X, Xiang C F, Ma Z L, He D Q, Chen L K, Chen S 2023 Phys. Rev. A 108 032811 doi: 10.1103/PhysRevA.108.032811 [12] Ménoret V, Vermeulen P, Le Moigne N, Bonvalot S, Bouyer P, Landragin A, Desruelle B 2018 Sci. Rep. 8 12300 doi: 10.1038/s41598-018-30608-1 [13] Chen J L, Cazenave A, Dahle C, Llovel W, Panet I, Pfeffer J, Moreira L 2022 Surv. Geophys. 43 305 doi: 10.1007/s10712-021-09685-x [14] Huang C, Li A, Qin F, Gong W, Che H, Chen X, Fang J, Wang W, Zhou Y 2024 IEEE Sens. J. 24 32368 doi: 10.1109/JSEN.2024.3451434 [15] Huang C F, Li A, Qin F J, Fang J, Chen X 2023 Meas. Sci. Technol. 34 11 doi: 10.1088/1361-6501/ac8e8b [16] Bidel Y, Zahzam N, Bresson A, Blanchard C, Cadoret M, Olesen A V, Forsberg R 2020 J. Geodesy 94 20 doi: 10.1007/s00190-020-01350-2 [17] Bidel Y, Zahzam N, Blanchard C, Bonnin A, Cadoret M, Bresson A, Rouxel D, Lequentrec-Lalancette M F 2018 Nat. Commun. 9 627 doi: 10.1038/s41467-018-03040-2 [18] Bidel Y, Zahzam N, Bresson A, Blanchard C, Bonnin A, Bernard J, Cadoret M, Jensen T E, Forsberg R, Salaun C, Lucas S, Lequentrec-Lalancette M F, Rouxel D, Gabalda G, Seoane L, Vu D T, Bruinsma S, Bonvalot S 2023 J. Geophys. Res. Solid Earth 128 1 doi: DOI:10.1029/2022JB025921 [19] Wu B, Zhao Y P, Zhou Y, Yuan W W, Li D R, Bao S N, Zhu D, Cheng B, Wu L Y, Zhou J C, Qiao Z K, Wang X L, Lin Q 2024 IEEE Sens. J. 24 23527 doi: 10.1109/JSEN.2024.3408839 [20] Qiao Z K, Yuan P, Hu R, Zhou H, Wang Q Y, Zhang J J, Zhou H Q, Zhu L Y, Zhu D, Shi H Y, Zhou F, Wu B, Zhou Y, Lin Q 2024 IEEE Sens. J. 24 10620 doi: 10.1109/JSEN.2024.3362333 [21] Zhou Y, Wang W Z, Ge G G, Li J T, Zhang D F, He M, Tang B, Zhong J Q, Zhou L, Li R B, Mao N, Che H, Qian L Y, Li Y, Qin F J, Fang J, Chen X, Wang J, Zhan M S 2024 Sensors 24 1016 doi: 10.3390/s24031016 [22] Wu B, Zhang C, Wang K N, Cheng B, Zhu D, Li R, Wang X L, Lin Q, Qiao Z K, Zhou Y 2023 IEEE Sens. J. 23 24292 doi: 10.1109/JSEN.2023.3309499 [23] Zhou Y, Wu L Y, Wu B, Cheng B, Wang H L, Chen L W, Gao S T, Lin Q 2020 Geophysics 85 G115 doi: 10.1190/geo2020-0077.1 [24] 赵远, 郭梅影, 许云鹏, 胡栋, 王宇, 杨永军 2024 计测技术 44 115 doi: 10.11823/j.issn.1674-5795.2024.06.05 Zhao Y, Guo M Y, Xu Y P, Hu D, Wang Y, Yang Y J 2024 Metrol. Meas. Technol. 44 115 doi: 10.11823/j.issn.1674-5795.2024.06.05 [25] Zhu D, Liu N K, Cheng B, Cao P F, Wu B, Wang K N, Wu L M, Weng K X, Zhou Y, Bian J L, Wang X L, Lin Q 2024 Opt. Express 32 40554 doi: 10.1364/OE.535455 [26] Chen P J, Jiang M R, Lü X F, Zhou H, Yang D, Zhou Y, Jin Z F, Peng S P 2024 Heliyon 10 e23936 doi: 10.1016/j.heliyon.2023.e23936 [27] Chen P J, Zhou Y, Zhu D, Wang K N, Zhang C, Wang K, Peng S P, Cheng B, Wu B, Lin Q 2024 Appl. Phys. B 130 111 doi: 10.21203/rs.3.rs-3844349/v1 -
计量
- 文章访问数: 48
- HTML全文浏览数: 48
- PDF下载数: 2
- 施引文献: 0