-
轫致辐射(bremsstrahlung)也被称为刹车辐射, 指高速运动电子在与靶原子或离子碰撞时骤然减速而发出的电磁辐射. 此过程共有两种机制, 一种是普通轫致辐射(ordinary bremsstrahlung), 指因靶原子库仑场而减速的入射电子辐射出光子的过程, 这也是中高能电子入射原子及离子时主要发生的轫致辐射过程. 与普通轫致辐射相对应的是极化轫致辐射(polarizational bremsstrahlung), 也被称为原子轫致辐射(atomic bremsstrahlung), 此过程中辐射的光子不是由入射电子产生, 而是由靶原子电子受到入射电子库仑势场的影响发生极化而放出光子, 因此极化轫致辐射主要在低能电子入射时产生[1–3]. 轫致辐射作为电子-原子碰撞中的重要辐射过程, 一直都是原子分子物理、天体物理以及等离子体物理等领域中的研究热点[4–8]. 同时, 研究轫致辐射对于靶原子的电子结构和极化性质[9–11]、电子-原子碰撞动力学[12–14]、磁约束和惯性约束核聚变[15–19]、等离子体辐射及诊断[20–22]、X射线产生[23–25]、医学成像以及放射治疗[26–30]等方面都有重要应用.
由于轫致辐射过程的重要性, 国内外许多研究者已开展相关工作. 早期最为著名的理论方法是Bethe和Heitler[31]于1934年提出的基于非相对论量子力学的平面波玻恩近似(plan-wave Born approximation, PWBA), 该方法长期以来被广泛应用于中低能电子-原子的轫致辐射. 1971年, Tseng和Pratt[32]针对普通轫致辐射提出了基于相对论分波展开理论的计算方法, 通过求解相对论Dirac方程得到入射及出射电子的连续态波函数, 计算多极跃迁, 即可得到普通轫致辐射截面[33]. Poškus[34,35]基于相对论分波展开理论开发了用于计算电子入射能量从10 eV至30 MeV的BREMS程序包, 在程序中Poškus利用级数展开法精确求解连续态电子波函数, 并且使用外推法得到大角度下的轫致辐射微分截面以及高角动量分波时的积分截面从而保证计算结果的收敛性. 利用此程序Poškus对
$ Z=1 $ —100的中性原子的单重及双重微分截面进行了详细计算[36,37]. Wu等[38–41]近期也成功将PWBA方法以及相对论分波展开方法应用于研究等离子体环境下的原子轫致辐射过程. 对于极化轫致辐射, Avdonina和Pratt[42]以及Korol[43]基于Amusia等[44]的工作分别提出了两种不同的原子剥离近似(stripping approximation)用于计算包含极化轫致辐射的总轫致辐射截面, 这两种方法随后被Korol等[45]证明具有一致性. 需要特别注意的是, 当轫致辐射发生在电子-多电子原子碰撞时, 靶原子中的电子会削弱靶原子核对入射电子的库仑相互作用, 从而影响轫致辐射截面. 根据入射电子能量以及发射光子能量的不同, 电子屏蔽效应的影响也将不同. 电子屏蔽效应作为影响多电子原子轫致辐射过程的重要因素, 在许多研究工作中也被考虑[46–48].碳原子(C)及其各价态碳离子(C
$ ^{q+} $ )广泛存在于实验及天体等离子体中, 并且是各种无机、有机以及生物大分子的重要组成部分, 对其轫致辐射过程的研究具有重要的物理意义和实际应用价值. 当前文献中对C原子及其离子的轫致辐射研究较少, 例如, Yerokhin和Surzhykov[49]基于相对论分波展开法对C和Au原子的双重微分截面和轫致辐射的极化性质进行了计算, 并研究了高能电子入射时的电子屏蔽效应和与能量相关的辐射极化参数. Yerokhin等[50]还选取C和Au原子靶对电子-原子和正电子-原子碰撞的轫致辐射单重、双重微分截面以及斯托克斯参数进行了比较, 结果表明, 对于低Z靶的C原子, 电子和正电子的轫致辐射极化参数非常相似, 对于高Z靶的Au原子以及在高能量入射时, 正电子轫致辐射会被明显的抑制. García-Alvarez等[51]测量了C, Al, Te, Ta, Au原子在20—100 keV区域内的双重微分截面, 发现在此碰撞能量区间内绝大多数实验测量结果都与普通轫致辐射理论的预测值符合较好. Li等[52]给出了C和Al原子在光子发射能量为1—2 keV, 电子入射能量为5—25 keV时的轫致辐射双重微分截面, 并与普通轫致辐射理论以及原子剥离近似的预测结果进行了比较. 这些工作从不同角度对中性C原子和复杂原子体系的轫致辐射过程进行了研究, 但当前文献对等离子体环境中更广泛存在的多价态离子的轫致辐射研究较少. 本文将针对中高能相对论电子入射中性碳原子以及不同价态碳离子的普通轫致辐射进行研究, 着重探讨电子屏蔽效应对靶原子处于不同离化度时的轫致辐射单重、双重微分截面以及角分布函数的影响.本文基于相对论分波展开方法对C原子及离子的普通轫致辐射截面进行理论计算, 其中靶原子采用Dirac-Hartree-Fock理论描述, 并基于中心场近似构造电子-原子相互作用势, 电子碰撞能量区间为1—2000 keV, 光子发射能量占比区间为5%—95%, 在此碰撞能量范围内, 极化轫致辐射贡献较小可以忽略. 本文第2节介绍C原子及离子的电子结构计算以及普通轫致辐射截面的理论方法; 第3节给出不同靶离子的轫致辐射单重、双重微分截面以及角分布在不同电子入射和光子发射能量下的变化趋势, 并着重讨论电子屏蔽效应的影响; 第4节进行总结.
-
为了准确地描述靶原子的电子结构, 首先利用Gu[53]开发的FAC (flexible atomic code)程序包计算得到C原子及其不同价态离子处于基态时的各轨道能量及总能量, 数值在表1中列出. 表中同时列出了Rodrigues等[54]的Dirac-Hartree-Fock理论计算基态总能量以及NIST数据库[55]中的标准数据. 对比发现当前计算结果与Rodrigues等[54]的计算结果误差在1‰以内, 该细微差别来源于两者使用不同的原子核模型, 而与NIST数据库[55]中标准数据差别在0.5%以内.
基于FAC程序得到的靶原子电子波函数, 可以构造出电子-靶原子相互作用势. 由于本文只研究中高能相对论电子与靶原子的弹性碰撞, 因此采用中心场近似并忽略入射电子与靶原子电子的交换作用势, 此时得到的Hartree相互作用势表示为(这里采用相对论单位, 其中普朗克常量
$ \hbar $ 、光速$ c $ 与电荷$ e $ 均设为1):式中
$ r $ 为入射电子与靶原子的距离;$ Z $ 代表靶原子中的核电荷数;$ \alpha $ 为精细结构常数;$ \rho(r) $ 代表靶原子中的总电子密度, 表示为其中
$ q_a $ 为$ a $ 壳层中的电子个数,$ P(r) $ 和$ Q(r) $ 分别为Dirac-Hartree-Fock自洽场近似下靶原子电子径向波函数的大分量和小分量.为了更加清晰地描述靶原子电子对电子-靶核库仑相互作用的屏蔽效应, 定义屏蔽函数
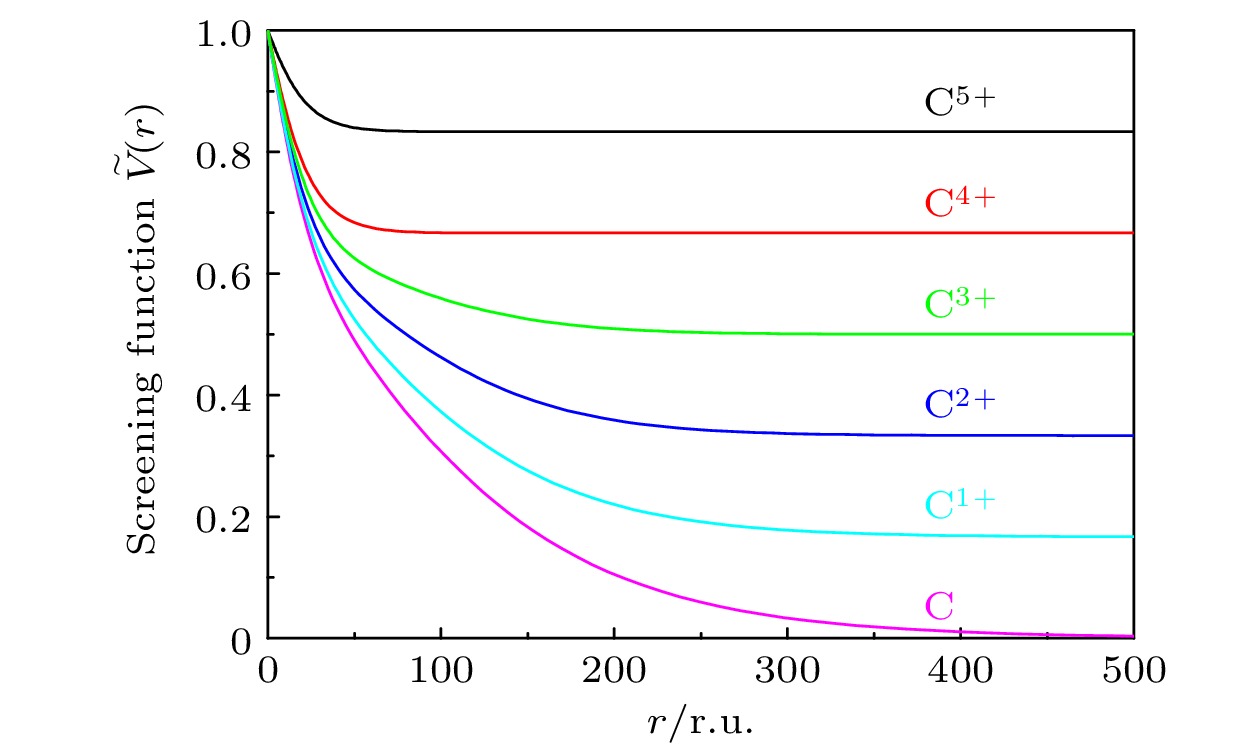
$ \widetilde{V}(r) $ 为电子-原子相互作用势与电子-靶核相互作用势之比:图1给出了计算得到的C原子及其各价态离子的屏蔽函数. 可以看出, 当
$ r \rightarrow 0 $ 时屏蔽函数总是趋近于1, 而当$ r \rightarrow \infty $ 时, 屏蔽函数等于靶原子离化度与原子核电荷数之比, 即$ {Z_{\mathrm{i}}}/{Z}=1-{N_{\mathrm{e}}}/{Z} $ (其中$ N_{\mathrm{e}} $ 为离子所带总电子数). 需要注意的是, 对于中性原子, 当$ r \rightarrow \infty $ 时, 屏蔽函数趋于0.在构建电子-靶原子相互作用势函数基础上, 通过分波展开求解Dirac方程可得到连续态电子分波波函数, 计算连续态电子的多极自由-自由跃迁, 即可对普通轫致辐射截面进行计算. 轫致辐射的双重微分截面(与发射光子的动量
$ k $ 和角度$ \theta $ 有关, 单位mb/sr, 应注意在相对论坐标下光子动量等于光子能量, 即$ k=E_{\mathrm{p}} $ )表示为[34,36,37]式中
其中
$ C_{\kappa, m} ^{\pm} $ 为Clebsch-Gordan系数,$ y_{l, m} $ 与球谐函数$ {\mathrm{Y}}_{lm}(\theta, \phi) $ 关系为$ {\mathrm{Y}}_{lm}(\theta , \phi) =y_{lm}(\theta){\mathrm{e}}^{{\mathrm{i}}m\phi} $ . 这里下标“1”和“2”分别表示入射电子和出射电子;$ E_1 $ 和$ E_2 $ 分别代表入射和出射电子的总相对论能量并满足能量守恒关系$ E_1=E_2+E_{\mathrm{p}} $ ;$ p_1 $ 和$ p_2 $ 分别代表入射和出射电子的动量大小; 求和式中$ m_2 $ 代表Dirac量子数$ \kappa_{2} $ 的磁量子数, 其取值范围为$ m_2= -|\kappa_2 |+1/2, -|\kappa_2 | + 3/2 $ ,$ \cdots, |\kappa_2 |-3/2, |\kappa_2 |- 1/2 $ .通过对双重微分截面立体角部分进行积分, 可得到轫致辐射单重微分截面(只与发射光子动量
$ k $ 有关, 单位mb), 其表达式为在计算双重及单重微分截面时, 引入了标度因子
$ k/Z^{2} $ 用于降低截面对核电荷数$ Z $ 的依赖, 因此$ \sigma(k, \theta) $ 和$ \sigma(k) $ 也被称为$ Z $ 标度缩放后的双重及单重微分截面[56]. 无论(6)式、(7)式, 还是(8)式中, 对$ R_{\kappa_{2} \kappa_{1}}^{\pm}(m) $ 项的计算最为关键, 其可分解为角度及径向部分:角度部分
$ Q_{1, 2}^{ \pm}(m) $ 和$ P_{1, 2}^{ \pm}(m) $ 由文献[34]给出, 径向部分$ S_{n} $ 表示连续态电子波函数大小分量的重叠积分:式中
$ {\mathrm{j}}_{l}(kr) $ 为$ l $ 阶第一类球贝塞尔函数;$ f_{\kappa}(r) $ 和$ g_{\kappa}(r) $ 分别为相对论电子连续态波函数的大分量与小分量, 满足径向Dirac方程:其中
$ V(r) $ 即为(1)式中求得的电子-靶原子相互作用势函数.为了描述轫致辐射中发射光子的角分布, 还可定义轫致辐射形状函数(shape function), 其定义为双重与单重微分截面的比值:
本文利用Poškus开发的BREMS程序包[34], 计算了C原子及其各价态离子的轫致辐射单重、双重微分截面以及角分布.
-
表2列出了中性C原子在不同入射电子动能
$ T_{1} $ 和不同发射光子能量$ E_{{\mathrm{p}}} $ 下的轫致辐射单重微分截面$ \sigma (k) $ . 表格中同时给出Pratt等[33]的相对论分波展开计算结果进行对比(Pratt等给出其数据不确定度在10%以内), 可以看出在$ T_1=1 $ keV时, 文献中结果比当前计算结果高10%左右, 这是因为在Pratt等[33]的计算中, 使用Kohn-Sham密度泛函理论描述靶原子并构造电子-原子相互作用势, 计算所得屏蔽因子在渐近区域远大于当前所使用的Dirac-Hartree-Fock波函数得到的屏蔽因子, 因此产生较大的轫致辐射截面. 从表2还可看出, 不同相互作用势得到的辐射截面差异随入射能量的增加而迅速减小, 当$ T_1>100 $ keV时, 两者相对误差在3%以内. 此外还发现, 在较高能量入射时, Pratt等[33]的结果略小于当前计算结果, 这可能是由于计算收敛不足或者跃迁矩阵元计算存在一定的误差.本文选择
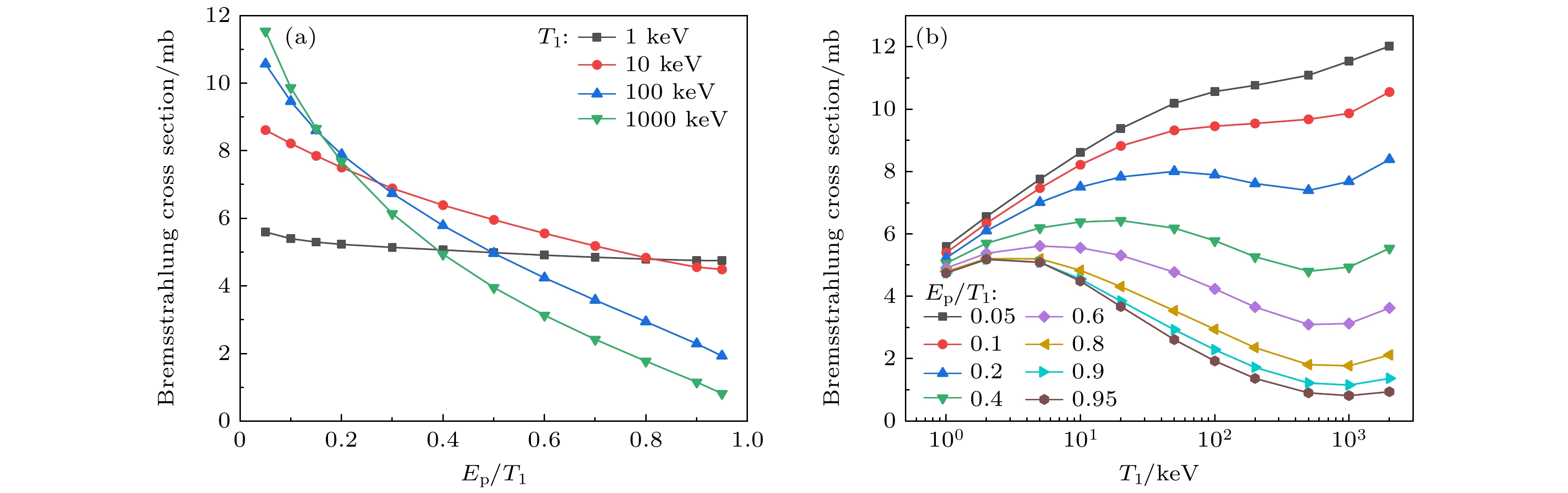
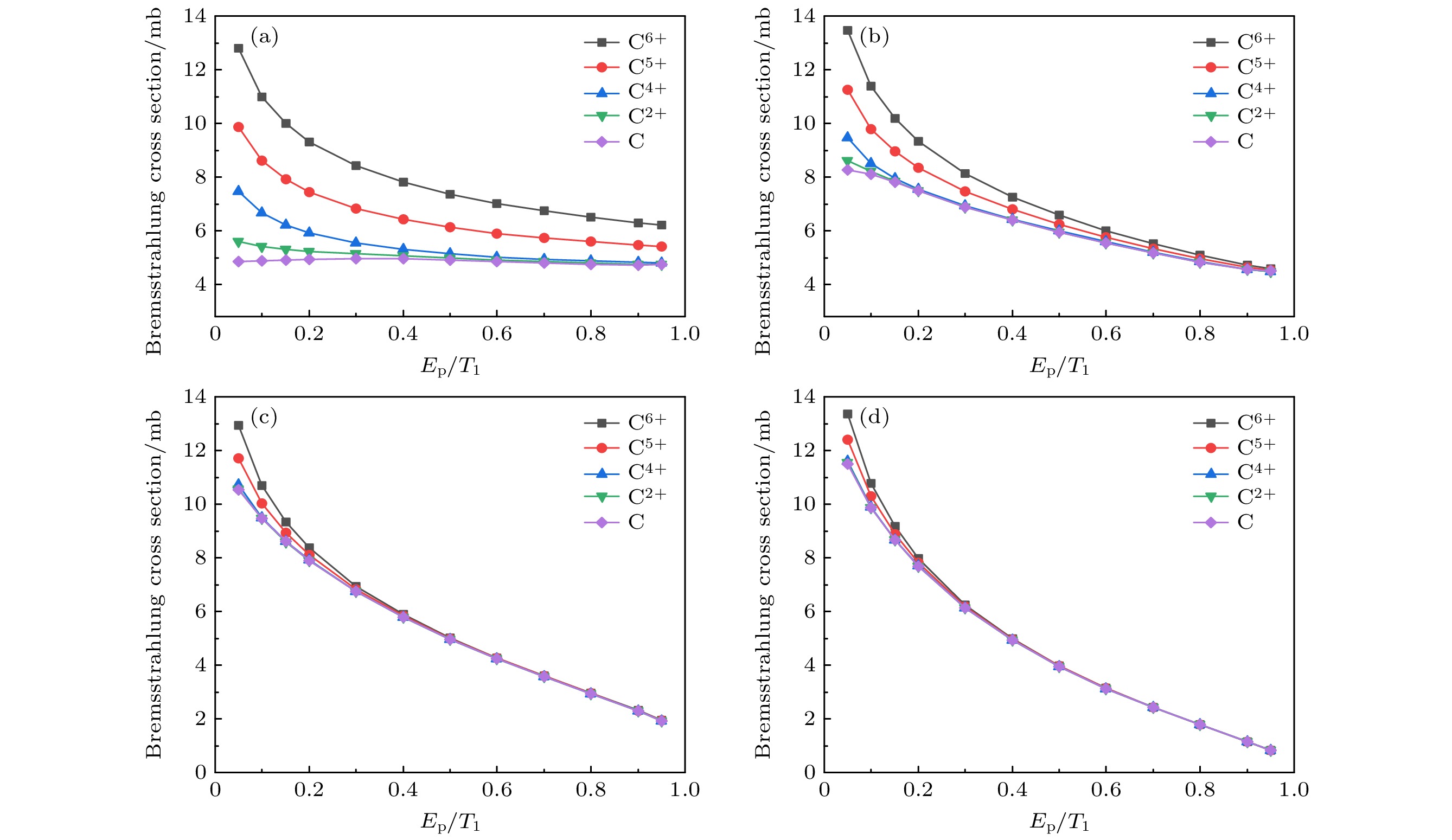
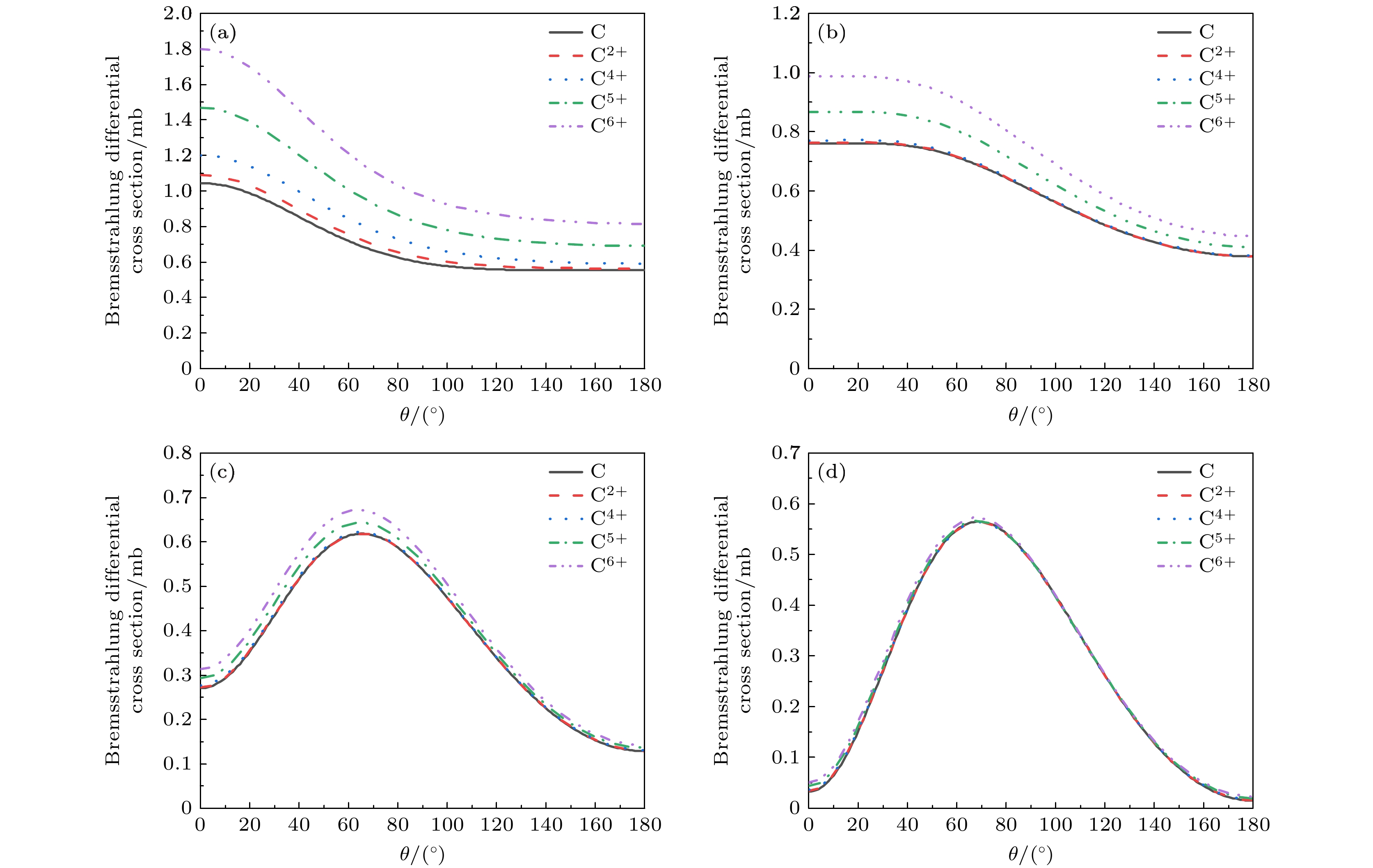
$ \rm C^{2+} $ 离子作为参考, 讨论轫致辐射截面随入射电子动能$ T_{1} $ 和发射光子能量$ E_{{\mathrm{p}}} $ 的变化规律, 结果在图2中展示. 在图2(a)中, 固定电子入射能量$ T_{1} $ 并改变发射光子能量占比$ E_{{\mathrm{p}}}/T_{1} $ 从0.05增至0.95, 其中$ E_{{\mathrm{p}}}/T_{1} $ 接近于0时被称为软光子区域(soft-photon region),$ E_{{\mathrm{p}}}/T_{1} $ 接近于1时称为硬光子区域(hard-photon region), 图2(b)固定发射光子能量占比而改变入射电子能量从1 keV至2000 keV. 可以看出, 单重微分截面在软光子极限达到极大值, 随着发射光子能量的增加而不断降低, 尤其在高能电子入射时, 截面下降速率较快. 图2(b)中展示不同$ E_{{\mathrm{p}}}/T_{1} $ 下单重微分截面随$ T_{1} $ 的变化趋势, 在$ E_{{\mathrm{p}}} $ 占比较小时, 截面单调递增, 而当$ E_{{\mathrm{p}}} $ 占比较高时, 截面随入射能量增加呈现先增后降趋势. 总体来说, 图2展示出轫致辐射的一般规律为: 低能光子发射概率要高于高能光子发射, 并且随着入射电子能量的增加, 这种差别逐渐增大.为了更加清晰地反映电子屏蔽效应对轫致辐射过程的影响, 图3将中性C原子及不同价态C离子的截面进行比较. 可以明显看出, 随着靶原子电子数量的增加, 电子屏蔽效应增强, 电子和靶之间的库仑相互作用整体减弱, 导致辐射截面降低. 通过改变入射电子能量, 发现电子屏蔽效应对低能电子入射时影响较大, 如图3(a)中,
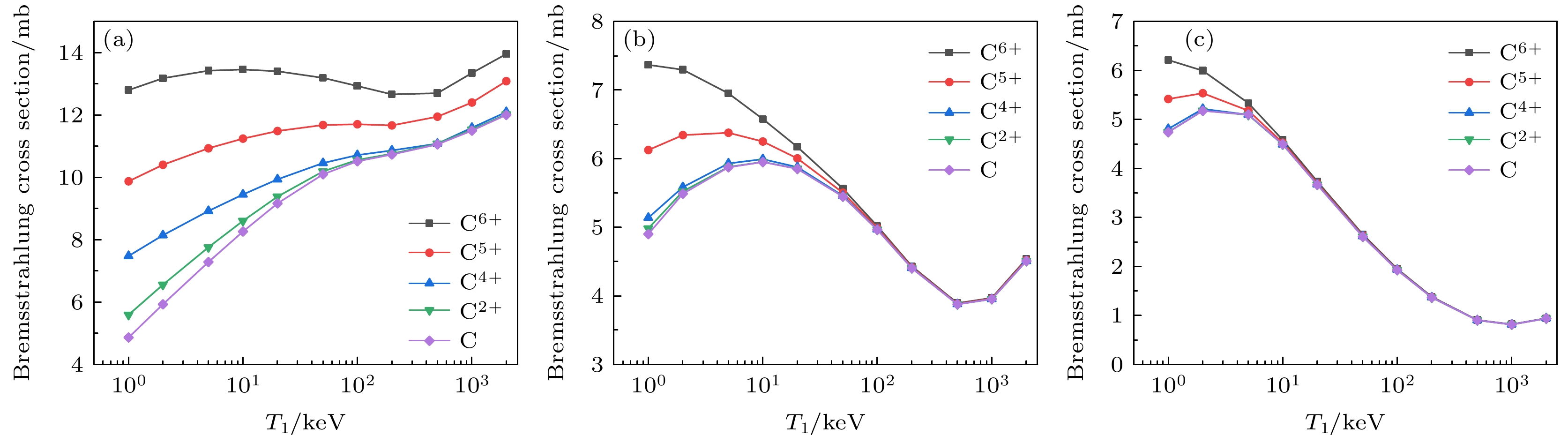
$ E_{{\mathrm{p}}} / T_{1}= 0.05 $ 时$ \rm C^{6+} $ 裸核轫致辐射截面约为中性C原子截面的2.6倍, 这种差距随着入射能量增加而迅速减弱. 这是因为当入射电子能量不断增加时, 电子穿透靶原子能力增强并且与靶原子相互作用时间较短, 因此核外电子屏蔽效应相应减弱. 当$ T_{1} $ 增加至100 keV和1000 keV时, 不同价态靶原子的单重微分截面在$ E_{{\mathrm{p}}}/T_{1} > 0.3 $ 区间已几乎不可区分. 此外, 从图3还可发现, 电子屏蔽效应对软光子区域影响较大, 而对硬光子区域则影响较小, 这一趋势在图4中显示更为明显. 图4(a)展示了不同价态靶原子在软光子区域$ E_{{\mathrm{p}}} / T_{1}=0.05 $ 的轫致辐射截面, 此时入射电子仅损失5%能量用于发射光子. 因此只需要在靶原子外部势场进行减速发射光子, 即入射电子受到靶原子的相互作用主要位于外部渐近区域, 根据图1所示, 此时不同价态靶原子的电子屏蔽效应差异显著. 反之, 在硬光子区域, 如图4(c)所示$ E_{{\mathrm{p}}} / T_{1} = 0.95 $ , 入射电子需要在原子势场中损失95%能量用于发射光子, 因而需要深入靶原子势场内部进行减速, 此时电子感受到的靶原子相互作用势接近于裸核时的库仑势场, 电子屏蔽效应几乎消失. 上述原因也与电子入射能量不断增加时屏蔽效应减弱相对应. -
相对于单重微分截面, 双重微分截面能够提供丰富的光子发射角度信息. 图5为中性C原子在不同电子入射能量
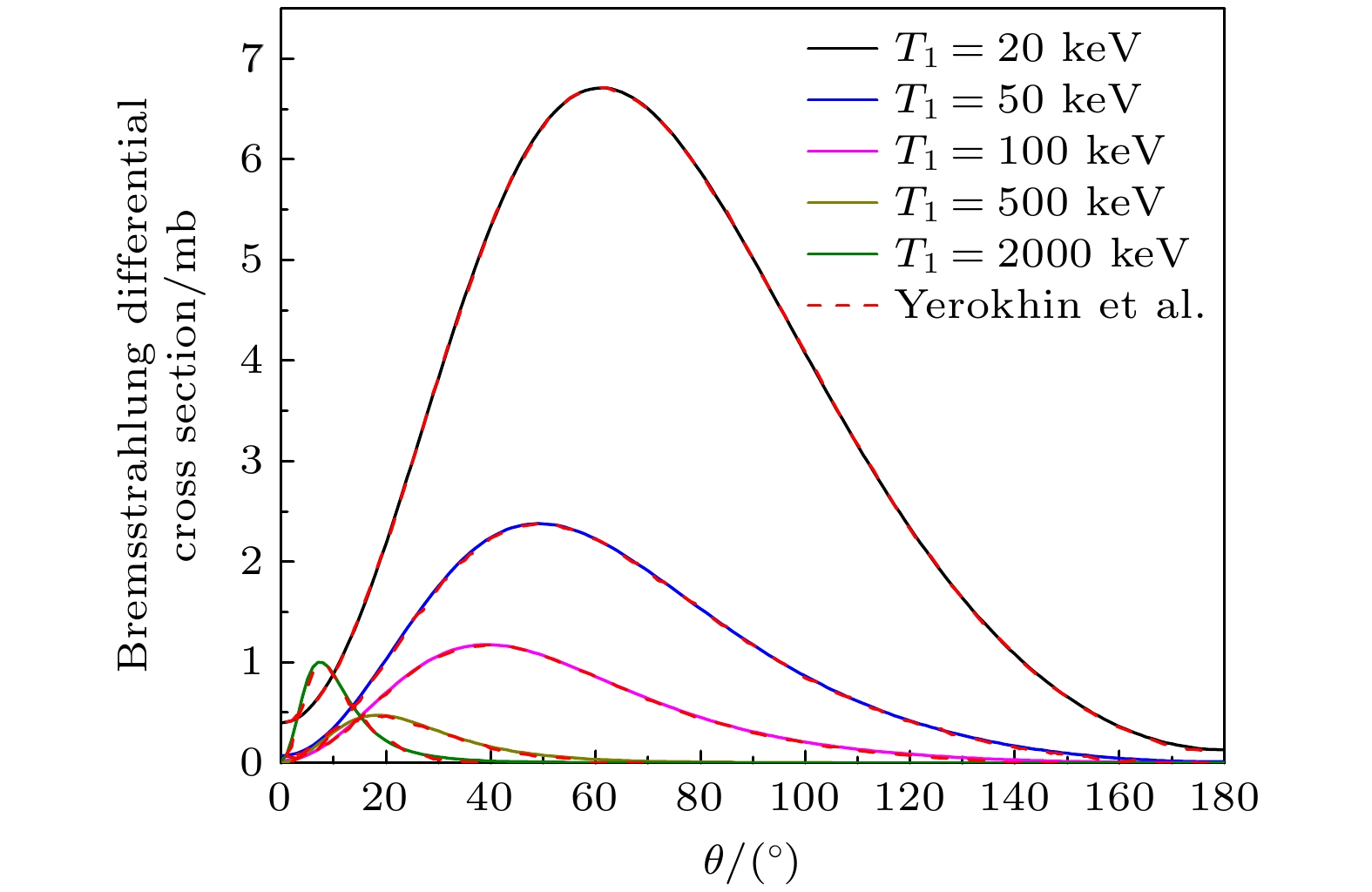
$ T_{1} $ 下, 出射电子能量$ T_{2} $ 为1 keV时的双重微分截面, 作为对比, 图中包含了近期Yerokhin和Surzhykov[49]的计算结果. 可以看出, 在$ T_{1}=20 $ —2000 keV的范围内, 当前计算结果与文献结果一致. 之前讨论中已知, 在固定出射电子能量条件下, 轫致辐射单重截面随着入射电子能量的增加而快速降低, 从图5还可发现, 双重微分截面呈现出典型的单峰结构, 并且光子发射主要集中于$ \theta < 90^{\circ} $ 的范围内, 即前向发射. 下面详细讨论不同价态靶原子下电子屏蔽效应对双重微分截面的影响.在图6中, 固定电子入射能量
$ T_1 $ 为10 keV, 给出不同光子发射能量$ E_{{\mathrm{p}}} $ 下的轫致辐射双重微分截面. 对比不同光子发射能量占比发现, 在软光子区域光子发射峰值位于$ 0^{\circ} $ , 随着光子发射能量的增加, 双重微分截面降低, 发射角分布更加集中, 并且峰位置向大角度方向偏移. 在硬光子区域, 光子发射峰约为$ 70^{\circ} $ . 与单重微分截面一样, 在$ E_{{\mathrm{p}}} $ 较小时, 靶原子电子屏蔽效应会使双重微分截面显著降低, 这种影响随着$ E_{{\mathrm{p}}} $ 的增加有减小趋势. 这主要是因为高能光子主要是由靶原子近核区域的轫辐射过程所产生, 入射电子感受到的电子屏蔽效应不明显, 如图6(d)所示, 当$ E_{{\mathrm{p}}}=0.95 T_1 $ 时, 不同价态靶原子对应的双重微分截面几乎不可区分.为了讨论不同电子入射能量对双重微分截面的影响, 图7固定光子发射能量占比
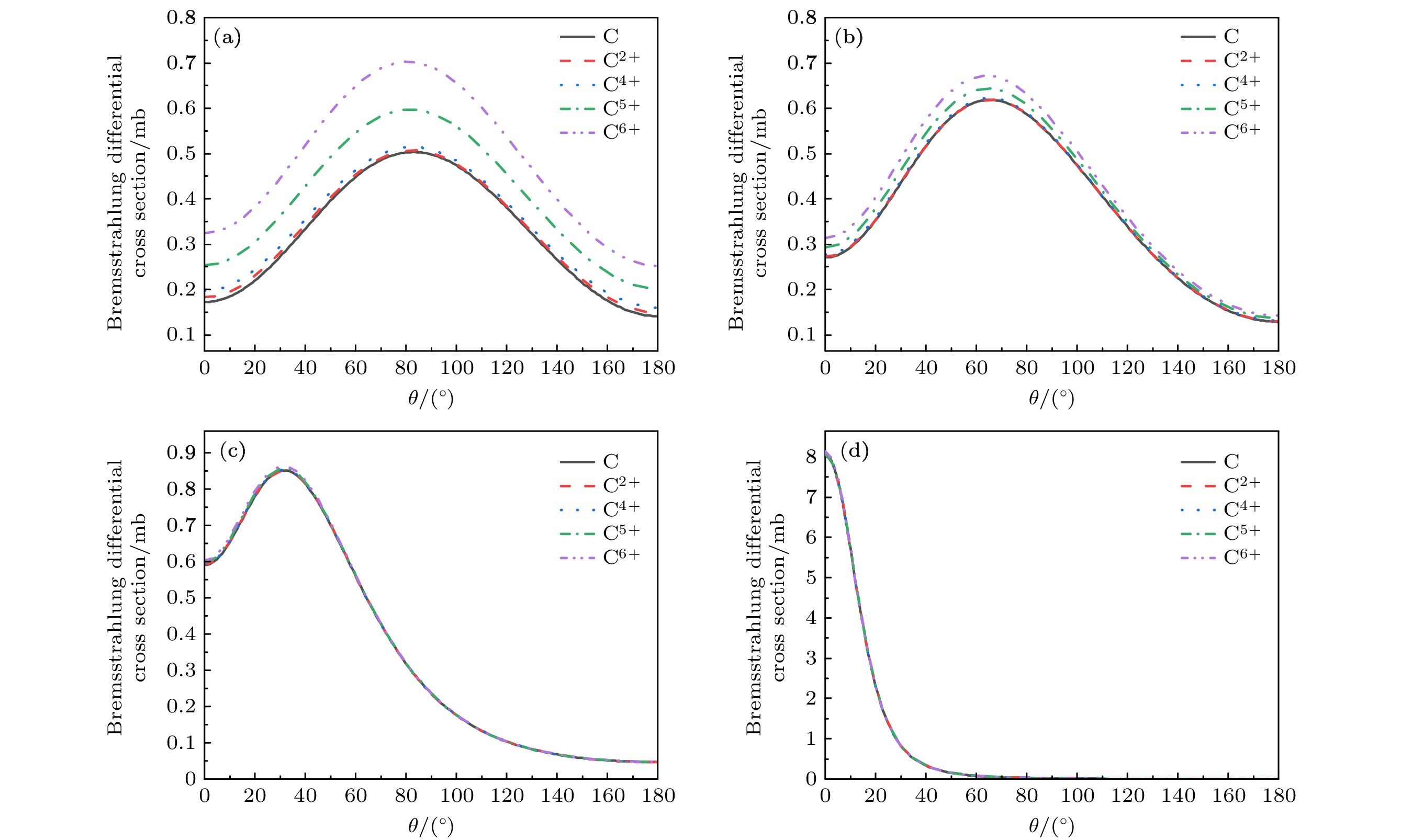
$ E_{{\mathrm{p}}}/T_{1} $ 为0.6, 电子入射能量$ T_{1} $ 从1, 10, 100 keV增加至1000 keV. 可以看到, 在低能电子入射时, 光子几乎沿着垂直于电子入射方向发射, 而随着$ T_1 $ 增加, 光子发射主要集中于前向, 即沿着入射电子运动方向. 这一规律也与电子弹性散射微分截面有相似之处, 低能电子往往能够发生大角度弹性散射, 而高能电子弹性散射则主要集中于前向方向. 与前面讨论单重微分截面一致, 电子屏蔽效应在低能电子入射时效果明显, 双重微分截面随着靶原子电子数的增加而迅速降低. 这是因为低能电子入射时, 轫致辐射主要发生在靶的远核区域, 核外电子的增加使得靶有效电荷减小, 从而降低辐射截面. -
轫致辐射形状函数由双重微分截面除以单 重微分截面得到, 因而更能反映光子在各角度发 射的相对占比. 表3列出了中性C原子轫致辐 射的形状函数在不同电子入射能量
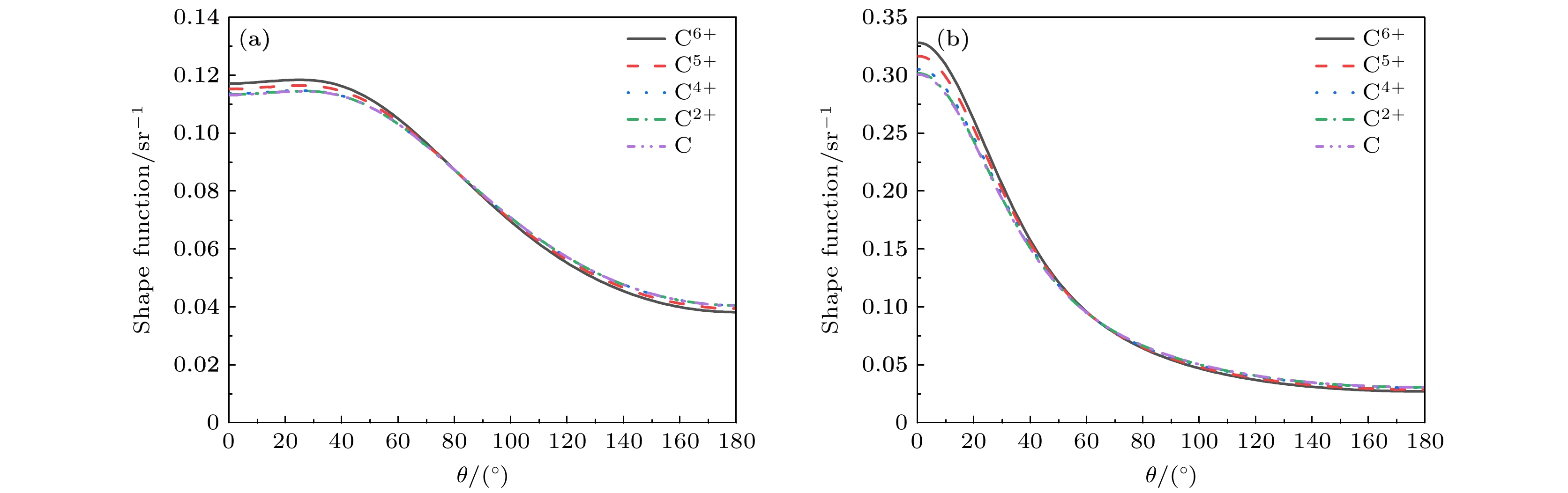
$ T_{1} $ 和光子发 射能量占比$ E_{\mathrm{p}} / T_1 $ 下的结果, 并与Kissel等[57]的结果进行对比. 表3列出$ E_{\mathrm{p}} / T_1=0.6 $ 时,$ T_{1}=10 $ , 50, 100 keV下的几个典型发射角的计算结果, 对比Kissel等[57]的数值结果发现, 相对误差均在4%以内.图8和图9分别展示了固定发射光子能量 改变入射电子动能, 以及固定入射电子动能改变光子发射能量的形状函数. 图8中光子发射能量 均为5 keV, 随着入射电子能量的增加, 光子小角度发射占比增加, 但随着入射能量持续增加, 光子将主要由平行于电子入射方向发射. 对比不同价 态靶原子下的形状函数, 可以看出电子屏蔽效应对形状函数影响较小, 这主要是因为电子屏蔽主要 影响单重及双重微分截面的绝对数值, 而几乎不 影响光子发射角分布, 这一规律也可从图7中发现. 通过细致对比图8, 可以发现电子屏蔽效应略微降低小角度光子发射占比, 并增加大角度占比, 并且在较高能电子入射时, 仅对前向光子发射有一定影响.
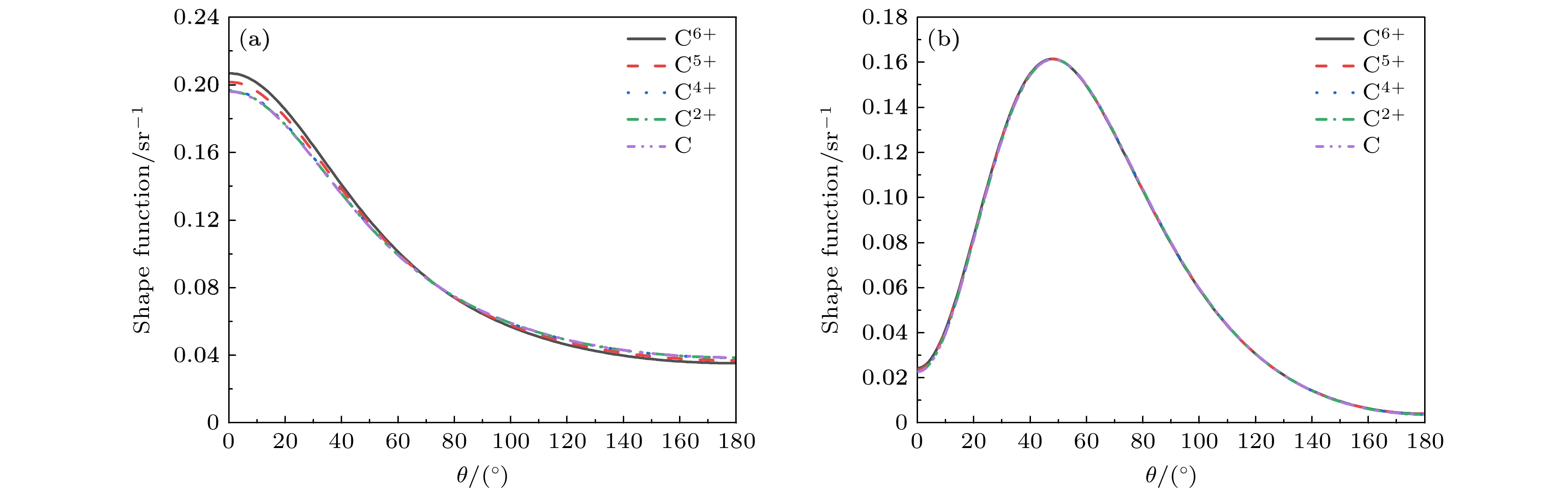
图8中主要针对软光子区域分析, 在图9(a)和图9(b)中, 固定入射电子动能为50 keV, 发射光子能量分别为5 keV和45 keV, 因此图9(b)位于硬光子区域. 对比不同价态靶原子发现, 即使电子入射能量较低, 电子屏蔽效应对硬光子区域角分布几乎无影响, 这也与图6中的分析一致.
-
利用相对论分波展开方法, 系统研究了中高能相对论电子碰撞中性C原子及其不同价态离子的轫致辐射过程, 并对轫致辐射单重、双重微分截面以及角分布进行了详细计算, 研究结果对现有C元素轫致辐射截面提供了重要补充. 本文利用中心场近似构造电子-靶原子相互作用势, 着重探讨靶原子中电子屏蔽效应对轫致辐射各物理量的影响. 研究发现, 屏蔽效应对低能电子入射以及软光子发射区域的单重及双重微分截面具有明显抑制作用. 这主要是因为低能电子入射时电子穿透靶原子能力较弱并且与靶原子相互作用时间较长, 因而电子屏蔽效应较强, 而软光子发射主要产生于入射电子在远核区域的减速过程, 此时电子主要受到渐近区域原子相互作用势的影响, 从而具有明显的屏蔽效应. 反之, 在高能电子入射以及硬光子发射区域, 单重及双重微分截面中无明显电子屏蔽效应. 此外, 对光子发射角分布也进行了详细研究. 分析表明, 在软光子区域光子主要在前向发射, 而在硬光子区域光子则倾向于垂直发射. 在固定发射光子能量占比的情况下, 角分布形状函数随着入射电子能量增加由垂直发射转变为前向发射. 无论在哪种条件下, 电子屏蔽效应对形状函数的影响都较小. 未来我们将研究更加复杂原子体系中的电子屏蔽效应对轫致辐射截面的影响.
感谢Andrius Poškus教授在BREMS程序使用中的悉心指导.
碳原子和离子轫致辐射过程中电子屏蔽效应研究
Electronic screening effects during bremsstrahlung of carbon atoms and ions
-
摘要: 轫致辐射作为原子物理中重要的辐射过程, 在天体物理、等离子体物理、磁约束和惯性约束核聚变等领域具有重要研究意义. 本文基于相对论分波展开方法研究了中高能电子碰撞中性碳原子以及各价态碳离子的轫致辐射过程, 并探讨电子屏蔽效应对轫致辐射截面及角分布的影响. 利用Dirac-Hartree-Fock理论构建靶原子波函数, 在中心场近似下建立电子-靶原子相互作用势, 基于相对论分波展开方法通过数值求解Dirac方程得到电子连续态波函数, 对不同价态碳离子的轫致辐射单重、双重微分截面以及角分布函数进行详细计算, 分析电子屏蔽效应在不同入射电子能量和出射光子能量下的作用. 结果表明, 电子屏蔽效应会使轫致辐射单重和双重微分截面降低, 在较低能电子入射时以及软光子区域抑制效果显著, 而随着入射电子能量和出射光子能量的增加, 电子屏蔽效应不断减弱. 电子屏蔽效应对轫致辐射角分布的影响则较不明显.Abstract: Bremsstrahlung, as an important radiation process in atomic physics, has significant applications in the fields of astrophysics, plasma physics, magnetic and inertial confinement fusion. In this work, the relativistic partial-wave expansion method is used to investigate the bremsstrahlung of neutral carbon atoms and different charged carbon ions scattered from intermediate- and high-energy relativistic electrons, with special attention paid to the electronic screening effect produced by the target electrons. The target wave function is obtained from the Dirac-Hartree-Fock self-consistent calculations, and the electron-atom scattering interaction potential is constructed in the central-field approximation. By solving the partial-wave Dirac equation, the continuum wave functions of the relativistic electron are obtained, from which the bremsstrahlung single and double differential cross sections can be calculated via the multipole free-free transitions between the incident and exit free electrons. The target electronic screening effects on the bremsstrahlung single and double differential cross sections are analyzed under a variety of conditions of incident electron energy and emitted photon energy. It is shown that the target electronic screening effect will significantly suppress the cross sections both at low incident energy and in the soft-photon region. Such a suppressing effect decreases with the incident electron energy and the emitted photon energy gradually increasing. Overall, the electronic screening effect has no significant influence on the shape function of bremsstrahlung.
-
Key words:
- bremsstrahlung /
- C atoms and ions /
- differential cross sections /
- shape function /
- electronic screening effect .
-

-
图 2
$ \rm C^{2+} $ 离子轫致辐射单重微分截面 (a)入射电子动能$ T_{1} $ 为1, 10, 100和1000 keV; (b)出射光子能量占比$ E_{{\mathrm{p}}} / T_{1} $ 为0.05—0.95Figure 2. Bremsstrahlung single differential cross section for the
$ \rm C^{2+} $ ion: (a) The kinetic energies of the incident electron$ T_{1} $ are 1, 10, 100 and 1000 keV; (b) the ratios of the emitted photon energy to the incident electron energy$ E_{{\mathrm{p}}}/T_{1} $ are in the range of 0.05–0.95.图 3 中性C原子及
$ \rm C^{6+} $ ,$ \rm C^{5+} $ ,$ \rm C^{4+} $ ,$ \rm C^{2+} $ 离子的轫致辐射单重微分截面随发射光子能量占比$ E_{{\mathrm{p}}}/T_{1} $ 的变化 (a)$ T_{1}=1 $ keV; (b)$ T_{1}=10 $ keV; (c)$ T_{1}=100 $ keV; (d)$ T_{1}=1000 $ keVFigure 3. Bremsstrahlung single differential cross sections of neutral C atom and
$ \rm C^{6+} $ ,$ \rm C^{5+} $ ,$ \rm C^{4+} $ ,$ \rm C^{2+} $ ions as a function of$ E_{{\mathrm{p}}}/T_{1} $ : (a)$ T_{1}=1 $ keV; (b)$ T_{1}=10 $ keV; (c)$ T_{1}=100 $ keV; (d)$ T_{1}=1000 $ keV.图 4 中性C原子及
$ \rm C^{6+} $ ,$ \rm C^{5+} $ ,$ \rm C^{4+} $ ,$ \rm C^{2+} $ 离子的轫致辐射单重微分截面随入射电子能量$ T_{1} $ 的变化 (a)$ E_{{\mathrm{p}}} / T_{1}=0.05 $ ; (b)$ E_{{\mathrm{p}}} / T_{1}=0.5 $ ; (c)$ E_{{\mathrm{p}}} / T_{1}=0.95 $ Figure 4. Bremsstrahlung single differential cross sections of neutral C atom and
$ \rm C^{6+} $ ,$ \rm C^{5+} $ ,$ \rm C^{4+} $ ,$ \rm C^{2+} $ ions as a function of$ T_1 $ : (a)$ E_{{\mathrm{p}}} / T_{1}=0.05 $ ; (b)$ E_{{\mathrm{p}}} / T_{1}=0.5 $ ; (c)$ E_{{\mathrm{p}}} / T_{1}=0.95 $ .图 5 中性C原子轫致辐射双重微分截面随光子发射角
$ \theta $ 的变化, 其中出射电子动能$ T_{2} $ 为1 keV, 入射电子动能$ T_{1} $ 分别20, 50, 100, 500和2000 keVFigure 5. Bremsstrahlung double differential cross sections of the neutral C atom as a function of the emission angle
$ \theta $ , where the kinetic energy of the emitted electron$ T_2 $ is 1 keV, and the kinetic energy of the incident electron$ T_1 $ is 20, 50, 100, 500, and 2000 keV.图 6 中性C原子和
$ \rm C^{2+} $ ,$ \rm C^{4+} $ ,$ \rm C^{5+} $ ,$ \rm C^{6+} $ 离子轫致辐射双重微分截面随光子发射角$ \theta $ 的变化, 其中入射电子动能$ T_1 $ 为10 keV, 发射光子能量占比$ E_{{\mathrm{p}}}/T_{1} $ 为(a) 0.05, (b) 0.2, (c) 0.6, (d) 0.95Figure 6. Bremsstrahlung double differential cross sections of neutral C atom and
$ \rm C^{2+} $ ,$ \rm C^{4+} $ ,$ \rm C^{5+} $ and$ \rm C^{6+} $ ions as a function of the photon emission angle$ \theta $ . The kinetic energy of the incident electron$ T_1 $ is 10 keV, and the ratios of the emitted photon energy$ E_{{\mathrm{p}}}/T_{1} $ are (a) 0.05, (b) 0.2, (c) 0.6 and (d) 0.95.图 7 中性C原子和
$ \rm C^{2+} $ ,$ \rm C^{4+} $ ,$ \rm C^{5+} $ ,$ \rm C^{6+} $ 离子轫致辐射双重微分截面随光子发射角$ \theta $ 的变化, 发射光子能量占比$ E_{{\mathrm{p}}}/T_{1} $ 为0.6, 入射电子动能$ T_1 $ 分别为(a) 1 keV, (b) 10 keV, (c) 100 keV, (d) 1000 keVFigure 7. Bremsstrahlung double differential cross sections of neutral C atom and
$ \rm C^{2+} $ ,$ \rm C^{4+} $ ,$ \rm C^{5+} $ and$ \rm C^{6+} $ ions as a function of the photon emission angle$ \theta $ . The ratio of the emitted photon energy$ E_{{\mathrm{p}}}/T_{1} $ is 0.6, and the kinetic energies of the incident electron$ T_1 $ are (a) 1 keV, (b) 10 keV, (c) 100 keV and (d) 1000 keV.图 8 中性C原子和
$ \rm C^{2+} $ ,$ \rm C^{4+} $ ,$ \rm C^{5+} $ ,$ \rm C^{6+} $ 离子的轫致辐射形状函数, 其中发射光子能量$ E_{\rm p}$ 均为5 keV, 入射电子动能$ T_1 $ 为(a) 20 keV, (b) 100 keV.Figure 8. Bremsstrahlung shape function of neutral C atom and
$ \rm C^{2+} $ ,$ \rm C^{4+} $ ,$ \rm C^{5+} $ and$ \rm C^{6+} $ ions. The emitted photon energy$ E_{\rm p} $ is 5 keV, and the incident electron kinetic energies$ T_1 $ are (a) 20 keV and (b) 100 keV.图 9 中性C原子和
$ \rm C^{2+} $ ,$ \rm C^{4+} $ ,$ \rm C^{5+} $ ,$ \rm C^{6+} $ 离子的轫致辐射形状函数, 其中入射电子动能$ T_1 $ 均为50 keV, 发射光子能量$ E_{\rm p} $ 为(a) 5 keV, (b) 45 keV.Figure 9. Bremsstrahlung shape function of neutral C atom and
$ \rm C^{2+} $ ,$ \rm C^{4+} $ ,$ \rm C^{5+} $ and$ \rm C^{6+} $ ions. The incident electron kinetic energy$ T_1 $ is 50 keV, and the emitted photon energies$ E_{\rm p} $ are (a) 5 keV and (b) 45 keV.表 1 中性C原子及其各价态离子(
$\rm C^{1+}$ ,$\rm C^{2+}$ ,$\rm C^{3+}$ ,$\rm C^{4+}$ ,$\rm C^{5+}$ )的基态轨道能量及总能量, 并与Rodrigues等 [54]的计算结果和NIST [55]的数据进行对比, 表中Diff表示当前计算结果和NIST数据相对误差Table 1. Orbital and total energies of the neutral C atom and different charged ions (
$\rm C^{1+}$ ,$\rm C^{2+}$ ,$\rm C^{3+}$ ,$\rm C^{4+}$ ,$\rm C^{5+}$ ) in their ground states and the comparison with results of Rodrigues et al. [54] and the NIST data [55]. “Diff” represents the relative errors between the present calculations of total energies and the NIST data[55].Target $ E/ {\rm eV }$ Diff/% $ 1 {\mathrm{s}}_{1/2} $ $ 2 {\mathrm{s}}_{1/2} $ $ 2 {\mathrm{p}}_{1/2} $ $ 2 {\mathrm{p}}_{3/2} $ Total Ref. [54] NIST [55] C –298.98 –16.86 –9.08 –9.07 –1025.12 –1026 –1030.11 0.48 $ \rm C^{1+} $ –314.60 –30.44 –22.65 –1014.57 –1015 –1018.85 0.42 $ \rm C^{2+} $ –336.99 –47.29 –990.72 –991 –994.47 0.38 $ \rm C^{3+} $ –362.47 –66.27 –945.03 –945 –946.58 0.16 $ \rm C^{4+} $ –392.48 –880.85 –882.08 0.14 $ \rm C^{5+} $ –490.04 –490.04 –489.99 0.01 表 2 中性C原子轫致辐射单重微分截面
$ \sigma(k) $ , 并与Pratt等[33]的结果进行对比Table 2. Comparison of present bremsstrahlung single differential cross section
$ \sigma(k) $ for the neutral C atom with the calculations of Pratt et al[33].$ T_1/{\rm{keV}} $ $ E_{\mathrm{p}}/T_1 $ $ \sigma(k) /\text{mb}$ Diff/% Present work Pratt et al.[33] 1 0.2 4.923 5.587 –11.88 0.5 4.902 5.525 –11.27 0.8 4.747 5.272 –9.96 0.95 4.741 5.162 –8.16 10 0.2 7.486 8.308 –9.90 0.5 5.953 6.405 –7.06 0.8 4.829 5.060 –4.56 0.95 4.495 4.573 –1.71 100 0.2 7.896 8.130 –2.88 0.5 4.964 5.018 –1.07 0.8 2.939 2.970 –1.05 0.95 1.925 1.963 –1.95 200 0.2 7.614 7.586 0.37 0.5 4.402 4.377 0.58 0.8 2.352 2.354 –0.08 0.95 1.366 1.380 –1.02 1000 0.2 7.687 7.515 2.29 0.5 3.953 3.879 1.91 0.8 1.773 1.762 0.65 0.95 0.815 0.818 –0.36 2000 0.2 8.387 8.303 1.01 0.5 4.507 4.451 1.26 0.8 2.118 2.112 0.31 0.95 0.941 0.947 –0.68 表 3 中性C原子轫致辐射形状函数, 并与Kissel等[57]的结果进行对比
Table 3. Comparison of the bremsstrahlung shape function for the neutral C atom with the results of Kissel et al[57].
$ T_1/ {\rm keV} $ $ E_{\mathrm{p}} / T_1 $ $ \theta/ (°)$ Shape function/sr–1 Diff/% Present work Kissel et al.[57] 10 0.6 0 0.0487 0.0498 –2.21 30 0.0783 0.0796 –1.68 90 0.0968 0.0962 0.60 120 0.0611 0.0602 1.44 180 0.0232 0.0232 –0.01 50 0.6 0 0.0877 0.0843 3.98 30 0.1386 0.1389 –0.23 90 0.0747 0.0746 0.19 120 0.0363 0.0360 0.83 180 0.0150 0.0149 0.61 100 0.6 0 0.1392 0.1380 0.87 30 0.2005 0.2019 –0.68 90 0.0558 0.0556 0.42 120 0.0244 0.0243 0.36 180 0.0111 0.0110 0.65 -
[1] Buǐmistrov V M, Trakhtenberg L I 1975 J. Exp. Theor. Phys. 42 54 [2] Amus'ya M Y, Baltenkov A S, Paiziev A A 1976 JETP Lett. 24 332 [3] Korol A V, Obolensky O I, Solov'yov A V, Solovjev I A 2001 J. Phys. B: At. Mol. Opt. Phys. 34 1589 doi: 10.1088/0953-4075/34/9/302 [4] Lea S M, Silk J, Kellogg E, Murray S 1973 Astrophys. J. 184 L105 doi: 10.1086/181300 [5] Cavaliere A, Fusco-Femiano R 1976 Astron. Astrophys. 49 137 [6] Hannestad S, Raffelt G 1998 Astrophys. J. 507 339 doi: 10.1086/306303 [7] Wang W Y, Lu J G, Tong H, Ge M Y, Li Z S, Men Y P, Xu R X 2017 Astrophys. J. 837 81 doi: 10.3847/1538-4357/aa5e52 [8] Steane A M 2024 Phys. Rev. D 109 063032 doi: 10.1103/PhysRevD.109.063032 [9] Maydanyuk S P, Zhang P M, Zou L P 2016 Phys. Rev. C 93 014617 doi: 10.1103/PhysRevC.93.014617 [10] Omar A, Andreo P, Poludniowski G 2018 Radiat. Phys. Chem. 148 73 doi: 10.1016/j.radphyschem.2018.02.009 [11] Jakubassa-Amundsen D H 2021 arXiv: 2103.06034 [physics. atom-ph] [12] Li L, An Z, Zhu J J, Tan W J, Sun Q, Liu M T 2019 Phys. Rev. A 99 052701 doi: 10.1103/PhysRevA.99.052701 [13] Kornev A S, Zon B A, Chernov V E, Amusia M Y, Kubelík P, Ferus M 2022 Atoms 10 86 doi: 10.3390/atoms10030086 [14] Milstein A I, Salnikov S G, Kozlov M G 2023 Nucl. Instrum. Methods Phys. Res., Sect. B 539 9 doi: 10.1016/j.nimb.2023.03.013 [15] Guazzotto L, Betti R 2019 Plasma Phys. Control. Fusion 61 085028 doi: 10.1088/1361-6587/ab2b22 [16] Bhaskar B S, Koivisto H, Tarvainen O, Thuillier T, Toivanen V, Kalvas T, Izotov I, Skalyga V, Kronholm R, Marttinen M 2021 Plasma Phys. Control. Fusion 63 095010 doi: 10.1088/1361-6587/ac156a [17] Bone T, Sedwick R 2024 Acta Astronaut. 220 356 doi: 10.1016/j.actaastro.2024.04.040 [18] Batani D, Antonelli L, Barbato F, et al. 2018 Nucl. Fusion 59 032012 doi: 10.1088/1741-4326/aaf0ed [19] Ren K, Wu J F, Dong J J, Li Y R, Huang T X, Zhao H, Liu Y Y, Cao Z R, Zhang J Y, Mu B Z, Yan J, Jiang W, Pu Y D, Li Y L, Peng X S, Xu T, Yang J M, Lan K, Ding Y K, Jiang S E, Wang F 2021 Sci. Rep. 11 14492 doi: 10.1038/s41598-021-93482-4 [20] Lindl J D, Amendt P, Berger R L, Glendinning S G, Glenzer S H, Haan S W, Kauffman R L, Landen O L, Suter L J 2004 Phys. Plasmas 11 339 doi: 10.1063/1.1578638 [21] Boozer A H 2005 Rev. Mod. Phys. 76 1071 doi: 10.1103/RevModPhys.76.1071 [22] Munirov V R, Fisch N J 2023 Phys. Rev. E 107 065205 doi: 10.1103/PhysRevE.107.065205 [23] Underwood C I D, Baird C D, Murphy C D, et al. 2020 Plasma Phys. Control. Fusion 62 124002 doi: 10.1088/1361-6587/abbebe [24] Singh S, Armstrong C D, Kang N, et al. 2021 Plasma Phys. Control. Fusion 63 035004 doi: 10.1088/1361-6587/abcf7e [25] Benitez J, Todd D, Xie D 2022 J. Phys.: Conf. Ser. 2244 012083 doi: 10.1088/1742-6596/2244/1/012083 [26] Rong X, Du Y, Ljungberg M, Rault E, Vandenberghe S, Frey E C 2012 Med. Phys. 39 2346 doi: 10.1118/1.3700174 [27] Roshan H R, Mahmoudian B, Gharepapagh E, Azarm A, Islamian J P 2016 Appl. Radiat. Isot. 108 124 doi: 10.1016/j.apradiso.2015.12.041 [28] Uribe C F, Esquinas P L, Gonzalez M, Celler A 2016 Phys. Med. 32 691 doi: 10.1016/j.ejmp.2016.04.014 [29] Porter C A, Bradley K M, Hippeläinen E T, Walker M D, McGowan D R 2018 EJNMMI Res. 8 1 doi: 10.1186/s13550-017-0352-6 [30] Tijani S A, Al-Hadeethi Y, Sambo I, Balogun F A 2018 J. Radiol. Prot. 38 N44 doi: 10.1088/1361-6498/aad2be [31] Bethe H, Heitler W 1934 Proc. R. Soc. London, Ser. A 146 83 doi: 10.1098/rspa.1934.0140 [32] Tseng H K, Pratt R H 1971 Phys. Rev. A 3 100 doi: 10.1103/PhysRevA.3.100 [33] Pratt R H, Tseng H K, Lee C M, Kissel L 1977 At. Data Nucl. Data Tables 20 175 doi: 10.1016/0092-640X(77)90045-6 [34] Poškus A 2018 Comput. Phys. Commun. 232 237 doi: 10.1016/j.cpc.2018.04.030 [35] Poškus A 2022 Comput. Phys. Commun. 278 108414 doi: 10.1016/j.cpc.2022.108414 [36] Poškus A 2019 At. Data Nucl. Data Tables 129-130 101277 doi: 10.1016/j.adt.2019.03.002 [37] Poškus A 2021 Nucl. Instrum. Methods Phys. Res., Sect. B 508 49 doi: 10.1016/j.nimb.2021.10.003 [38] Wu J Y, Wu Y, Qi Y Y, Wang J G, Janev R K, Zhang S B 2019 Phys. Rev. A 99 012705 doi: 10.1103/PhysRevA.99.012705 [39] Wu J Y, Wu Y, Qi Y Y, Wang J G, Janev R K, Zhang S B 2019 Mon. Not. R. Astron. Soc. 486 141 doi: 10.1093/mnras/stz859 [40] Wu J Y, Qi Y Y, Cheng Y J, Wu Y, Wang J G, Zhang S B 2020 Phys. Plasmas 27 043301 doi: 10.1063/1.5140830 [41] Wu J Y, Cheng Y J, Poškus A, Wu Y, Wang J G, Zhang S B 2021 Phys. Rev. A 103 062802 doi: 10.1103/PhysRevA.103.062802 [42] Avdonina N B, Pratt R H 1999 J. Phys. B: At. Mol. Opt. Phys. 32 4261 doi: 10.1088/0953-4075/32/17/310 [43] Korol A V 1992 J. Phys. B: At. Mol. Opt. Phys. 25 L341 doi: 10.1088/0953-4075/25/14/003 [44] Amusia M Y, Avdonina N B, Chernysheva L V, Kuchiev M Y 1985 J. Phys. B: Atom. Mol. Phys. 18 L791 doi: 10.1088/0022-3700/18/22/005 [45] Korol A V, Lyalin A G, Solovy'ov A V, Avdonina N B, Pratt R H 2002 J. Phys. B: At. Mol. Opt. Phys. 35 1197 doi: 10.1088/0953-4075/35/5/307 [46] Tseng H K, Pratt R H 1973 Phys. Rev. A 7 1502 doi: 10.1103/PhysRevA.7.1502 [47] Mangiarotti A, Lauth W, Jakubassa-Amundsen D H, Klag P, Malafronte A A, Martins M N, Nielsen C F, Uggerhøj U I 2021 Phys. Lett. B 815 136113 doi: 10.1016/j.physletb.2021.136113 [48] Groshev M E, Zaytsev V A, Yerokhin V A, Hillenbrand P M, Litvinov Y A, Shabaev V M 2022 Phys. Rev. A 105 052803 doi: 10.1103/PhysRevA.105.052803 [49] Yerokhin V A, Surzhykov A 2010 Phys. Rev. A 82 062702 doi: 10.1103/PhysRevA.82.062702 [50] Yerokhin V A, Surzhykov A, Märtin R, Tashenov S, Weber G 2012 Phys. Rev. A 86 032708 doi: 10.1103/PhysRevA.86.032708 [51] García-Alvarez J A, Fernández-Varea J M, Vanin V R, Maidana N L 2018 J. Phys. B: At. Mol. Opt. Phys. 51 225003 doi: 10.1088/1361-6455/aae6e8 [52] Li L, An Z, Zhu J J, Lin W P, Williams S 2021 Nucl. Instrum. Methods Phys. Res., Sect. B 506 15 doi: 10.1016/j.nimb.2021.09.001 [53] Gu M F 2008 Can. J. Phys. 86 675 doi: 10.1139/P07-197 [54] Rodrigues G C, Indelicato P, Santos J P, Patté P, Parente F 2004 At. Data Nucl. Data Tables 86 117 doi: 10.1016/j.adt.2003.11.005 [55] Kramida A, Yu Ralchenko, Reader J, and NIST ASD Team 2024 NIST Atomic Spectra Database (Ver. 5.12) https://physics.nist.gov/asd [2025-1-6] [56] Lee C M, Kissel L, Pratt R H, Tseng H K 1976 Phys. Rev. A 13 1714 doi: 10.1103/PhysRevA.13.1714 [57] Kissel L, Quarles C A, Pratt R H 1983 At. Data Nucl. Data Tables 28 381 doi: 10.1016/0092-640X(83)90001-3 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: