电子与原子(离子)碰撞激发(electron impact excitation)是最常见的微观粒子非弹性散射过程, 主要包括直接碰撞激发和间接碰撞激发^[1–8]. 直接碰撞激发是指原子直接吸收入射电子的能量从一个态激发到另一个高激发态的过程, 该过程中原子吸收的能量等于入射电子减少的能量^[4,5]. 间接碰撞激发又称为共振激发, 根据独立过程近似, 间接碰撞激发被视为一个两步过程: 靶原子中的电子首先吸收入射电子的能量跃迁至激发态, 同时入射电子被俘获至束缚态而形成中间双激发态, 中间双激发态再通过自电离跃迁到较低激发态^[6–8]. 值得注意的是, 间接碰撞激发与直接碰撞激发的初态和末态可以相同, 这两个过程会同时发生.

电子与原子(离子)的碰撞激发、电离和复合过程是天体、实验室和聚变等离子体中最为重要的碰撞动力学过程^[9–25]. 高精度的碰撞截面和速率系数在等离子体状态的诊断中具有重要的应用价值^[17–25]. 如在等离子体中, 电子温度和密度的测量主要由辐射光谱的强度确定, 而谱线的辐射强度主要由碰撞速率系数等参数确定. 在天体物理中, 研究者们通常通过分析电子与原子(离子)碰撞后产生的谱线强度比来确定等离子体中电子的温度和密度. 另外, 对这些过程的系统研究有助于深入理解微观粒子体系间的相互作用机制和探究各种微观物理效应^[9–25].

实验方面, 电子束离子阱(EBIT)可以在很小的体积中产生并约束高电荷态离子, 能提供近乎各种高电荷态离子的光谱, 并且有很窄的电荷态分布. EBIT可以对电子与离子和离子与离子碰撞的各种过程的截面进行绝对测量, 非常适合于研究电子与高电荷态离子的碰撞动力学过程^[26–31]. 除此之外, 实验方面还有用于研究电子与原子(离子)碰撞激发过程的交叉束或能损方法^[32–43]. 例如: 交叉束辐射方法被用于测量相对电子碰撞激发截面, 在高能情况下与玻恩近似的结果符合较好^[32]; 交叉电荷束方法是用可变能量的电子轰击靶离子, 被用于测量低离化态离子的绝对总截面, 优点是精确性好^[33,34]; 交叉束能损方法通常被用于测量不同角度的微分散射截面^[35–37]; 合并电子离子束能损方法可以探测非弹性散射出来的低能电子, 具有更高的检测灵敏度和更窄的电子能量分布^[38–43]. 近年来, 随着重离子加速器冷却储存环^[44–46]、电子能量损失谱仪^[47–49]、冷靶反冲离子动量谱仪^[50–52]、磁光阱^[53–55]、同步光子探测^[56,57]和辐射囚阱^[58,59]等实验技术的迅速发展, 已经可以对电子与离子或原子碰撞激发的绝对截面进行高精度测量.

理论方面, 目前常用的方法主要有平面波Born方法^[60,61]、紧耦合方法^[62–67]、R矩阵方法^[68–70]和扭曲波方法^[71–76]等. 其中, 平面波Born方法是最简单的理论方法^[60,61], 主要适用于处理高能散射问题. 其假设入射电子的波函数为平面波, 忽略了靶产生的势对连续电子波函数的影响以及连续电子与束缚电子的交换效应^[60,61]. 通过这种方法, 可以计算广义振子强度, 进而得到散射截面等关键物理量. 优点是方法简单, 计算低能散射或近阈值的散射时, 激发截面会远大于真实值. 紧耦合方法是将靶原子的最外层电子和连续电子作为活动电子, 并将原子核和其他电子的静电势用模型势代替^[62,63,67]. 它通过求解耦合微分方程, 得到系统从初态到某一末态之间的跃迁概率和相应的截面^[62,63,67], 该方法适用于处理中低能散射问题. R矩阵方法的主要思想是将空间区域分成内区和外区两个部分. 在内区中连续态与束缚态的计算类似, 主要计算(N + 1)体系的波函数. 然而, 在外区通过近似波函数来描述散射态的行为. R矩阵方法是一种处理低能散射问题非常有效的方法. 扭曲波方法是通过构造一个尽可能反映电子与靶之间相互作用的扭曲波来近似描述散射电子的波函数, 不仅改进了平面波方法, 而且可以很好地处理连续电子与束缚电子之间的关联和交换效应. 它具有非常好的适用性、简洁性和灵活性, 对研究中低能散射问题具有很好的优势, 目前被广泛地应用于电子与原子(离子)碰撞的研究中^[9,25,77,78].

碰撞动力学过程的研究中, 除了获得散射截面^[77]和速率系数^[78]外, 碰撞激发后辐射光子的Stokes参数也是实验和理论研究的热点. Stokes参数的获取可以用来揭示碰撞过程的各向异性特征以及确定碰撞激发所产生的电子云取向, 从而深入了解碰撞激发的物理机制. 理论方面: Macek和Jaecks^[79]给出了原子、光子与离子符合实验方法并提出了角关联参数理论, 得出了散射振幅与符合测量概率之间的关系; Barstschat等^[80,81]描述了自旋极化电子与原子碰撞激发过程中的微分和积分Stokes参数测量理论; Khalid和Kleinpoppen^[82]给出了极化电子与极化原子碰撞的角关联参数理论; Raeker等^[83]推导了电子云与态多极以及极化电子碰撞的散射振幅之间的关系. 实验方面: Kłosowski等^[84,85]将磁角转换方法引用在符合实验的测量中实现了全角度测量; Hussey等^[86,87]利用给定频率和极化的激光激发原子的同时在给定散射角上测量散射概率, 通过选择激光能量来分辨激发态的精细结构, 确定电子碰撞激发原子在完整散射几何上的微分截面.

本文基于全相对论性的多组态Dirac-Hartree-Fock (MCDHF)理论方法^[88–93]以及大规模计算原子结构和跃迁性质的程序包GRASP 92/2K/2018^[94–96]和RATIP^[97,98], 介绍了我们进一步发展的相对论扭曲波方法. 详细研究了电子与原子碰撞激发过程中的电子关联效应对总截面、微分截面、态多极、微分和积分Stokes参数(角关联参数)、取向参数的影响, 以及等离子体屏蔽效应对碰撞激发的影响.

相对论理论框架下, 连续态波函数的分波展开可写为^[99,100]

式中, $ \kappa $为连续电子的相对论量子数, 对于$ j=l- {1}/{2} $和$ j=l+{1}/{2} $ 态, $ \kappa =l $和$ \kappa =-(l+1) $; $ \varepsilon $为电子的动能; $ c $为光速; $ p $为动量; $ {\varepsilon }_{{\mathrm{c}}} $为电子的能量(包括静止质量); $ {c}_{{\mathrm{m}}} $表示归一化系数; $ {\delta }_{\kappa } $为库仑相移; $ C $为C-G系数; $ m $, $ {m}_{{{l}}} $和$ {m}_{{{s}}} $分别为连续电子总角动量、轨道角动量和自旋磁量子数在Z轴的分量; $ {{\mathrm{Y}}}_{l}^{{m}_{{{s}}}-m} $为球谐函数. 单个连续电子的Dirac自旋轨道波函数^[101–103]可以表示为

式中, $ {\chi }_{\kappa m}(\theta , \varphi ) $为自旋函数. $ {P}_{\varepsilon \kappa } $和$ {Q}_{\varepsilon \kappa } $分别为连续电子径向波函数的大、小分量^[9], 其满足耦合的Dirac方程^[25,77]:

式中, $ Y\left(r\right) $为直接势. 非齐次项 $ {\chi }^{\left(P\right)} $, $ {\chi }^{\left(Q\right)} $可以表示为

其中, $ {\varepsilon }_{ab} $为拉格朗日乘子, $ {X}^{\left(p\right)} $和$ {X}^{\left(Q\right)} $为交换势, 其详细的定义和求解参考文献[104,105].

扭曲波理论中, 对给定入射能量和自旋分量的电子$ \left|{\varepsilon }_{{\mathrm{i}}}{m}_{{s}_{{\mathrm{i}}}}\right.\rangle $和给定宇称总角动量以及角动量在Z轴分量的原子态$ \left|{P}_{{\mathrm{i}}}{J}_{{\mathrm{i}}}{M}_{{\mathrm{i}}}\right.\rangle $, 碰撞激发到末原子态$ \left|{P}_{{\mathrm{f}}}{J}_{{\mathrm{f}}}{M}_{{\mathrm{f}}}\right.\rangle $, 散射电子态为$ \left|{\varepsilon }_{{\mathrm{f}}}{m}_{{s}_{{\mathrm{f}}}}\right.\rangle $的散射振幅^[106–108]可写为

其中, 下标$ {\mathrm{i}} $和$ {\mathrm{f}} $分别表示碰撞电子和靶离子的初态和末态; $ {a}_{0} $为玻尔半径; $ {k}_{{\mathrm{i}}} $为入射电子的相对论波数; $ C({J}_{t}{j}_{t}{M}_{t}{m}_{t};JM) (t={\mathrm{i}}, {\mathrm{f}}) $是C-G系数; 1/2, $ {l}_{{\mathrm{t}}} $和$ {j}_{{\mathrm{t}}} $分别表示碰撞电子的自旋量子数、轨道量子数和总角动量量子数, 而量子数$ {m}_{{s}_{{\mathrm{t}}}} $, $ {m}_{{l}_{{\mathrm{t}}}} $和$ {m}_{{\mathrm{t}}} $是它们相对于量子化Z轴的分量; 在束状碰撞中$ {m}_{{l}_{{\mathrm{i}}}}=0 $, $ J $和$ M $分别为碰撞体系(电子+靶离子)的总角动量及其Z分量量子数^[78,109]. 入射电子的相对论波数$ {k}_{{\mathrm{i}}} $与动量$ p $或能量$ \varepsilon $的关系^[78,93]为

$ \varepsilon $的单位为Rydbergs, $ \alpha ={{{e}}}^{2}/\left(\hbar c\right) $为精细结构常数. 散射矩阵元T可以表示为

$ \left|{\gamma }_{{\mathrm{i}}}{J}_{{\mathrm{i}}}, {\varepsilon }_{{\mathrm{i}}}{\kappa }_{{\mathrm{i}}};J\right.\rangle $和$ \left.\langle {\gamma }_{{\mathrm{f}}}{J}_{{\mathrm{f}}}, {\varepsilon }_{{\mathrm{f}}}{\kappa }_{{\mathrm{f}}};J\right| $分别为碰撞体系初态和末态的波函数; $ r_{pq} $为两个电子之间的距离; $ {V}_{{\mathrm{B}}{\mathrm{r}}{\mathrm{e}}{\mathrm{i}}{\mathrm{t}}} $为Breit相互作用算符^[109–113], 当$ {\omega }_{qp}\to 0 $时表示为

其中, $ {\boldsymbol{\alpha }}_{q} $和$ {\boldsymbol{\alpha }}_{p} $是Dirac矩阵.

微分截面可写为

散射总截面表示为

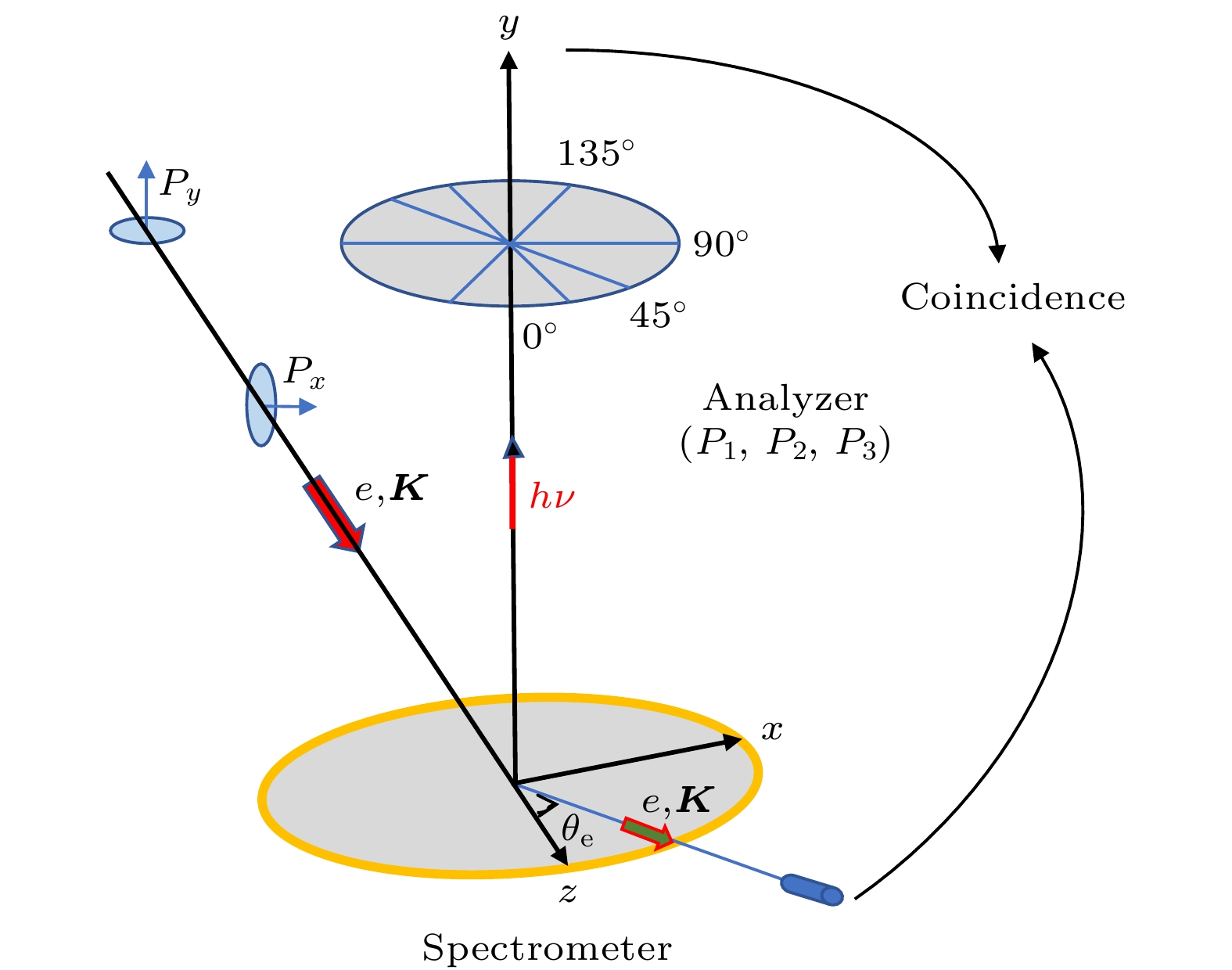
图1给出了极化电子与光子符合实验示意图, Stokes参数定义^[114]为

其中, $ {I}^{y}\left(\theta \right) $为所探测受激态退激偶极辐射光子偏振化方向与Z轴成$ \theta $夹角时的偏振光强, $ {I}^{y}\left({\mathrm{R}}{\mathrm{H}}{\mathrm{C}}\right) $和$ {I}^{y}\left({\mathrm{L}}{\mathrm{H}}{\mathrm{C}}\right) $分别为右旋和左旋极化光子的强度. 根据Bartschat等^[80,83]的理论可以得到Stokes参数与态多极的关系为

式中,

$ {G}_{k}\left(J\right) $为原子核自旋引起的修正系数,

这里, I为原子核的自旋量子数. 态多极$ \langle T({J}_{1}{)}_{KQ}^{+}\rangle $由密度矩阵理论引入, 散射后靶原子激发态(总角动量为J )的密度矩阵可用态多极展开^[25]. 态多极主要由散射振幅决定, 具体计算过程参考文献[80].

实验中如果只测量Stokes参数而不符合测量散射电子时, 所得到的参数称为积分Stokes参数. 理论上计算积分Stokes参数是将所有的态多极在散射角空间积分得到积分态多极, 将积分态多极代入(15)式—(20)式可得到积分Stokes参数:

从(21)式可以得出, 积分Stokes参数P₁正比于$ \langle T({J}_{1}{)}_{20}^{+}\rangle $, 而且与入射的极化度无关. 对于非极化电子, P₂和P₃为0; 对于极化电子, P₂和P₃正比于电子的极化矢量P_y.

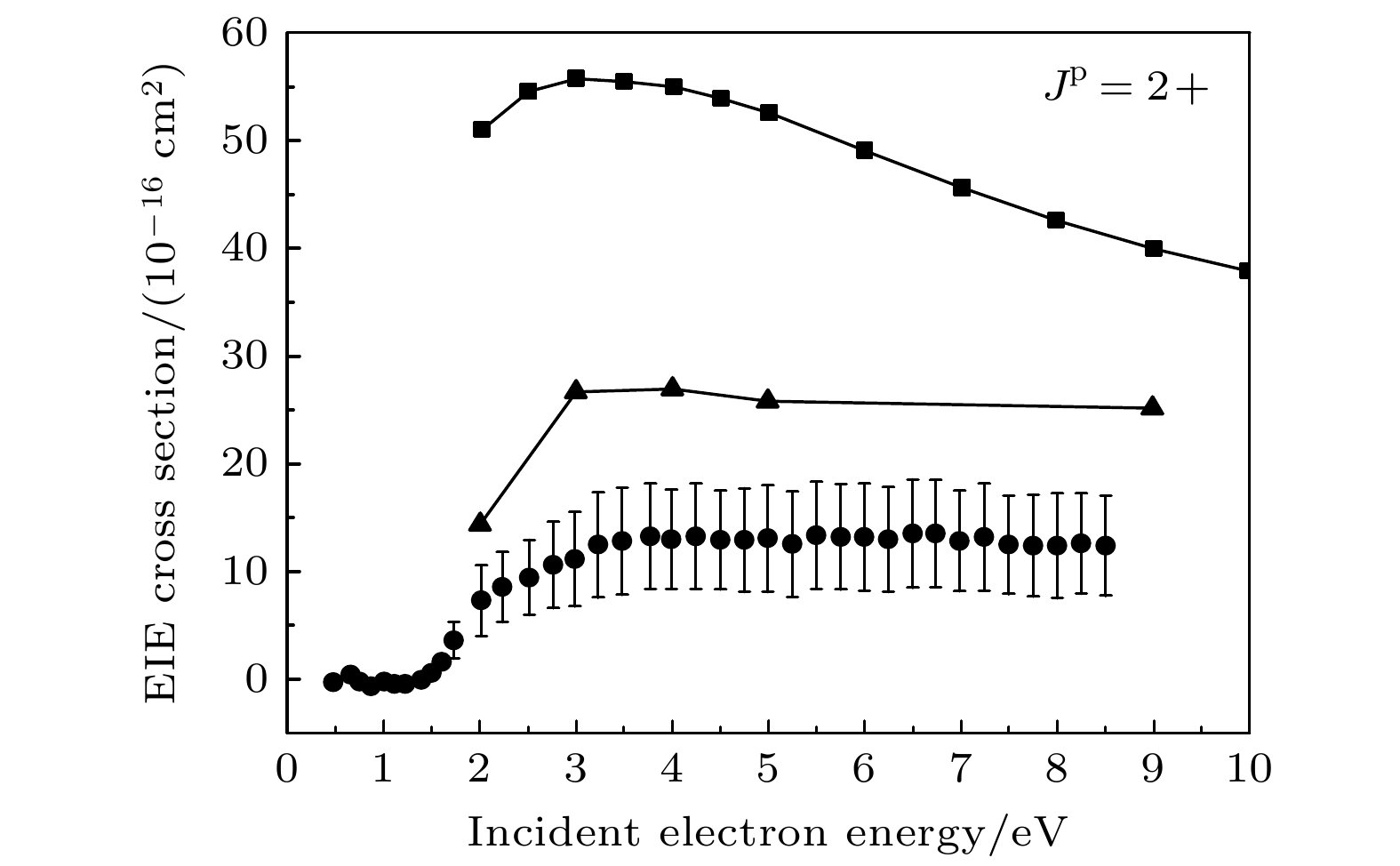
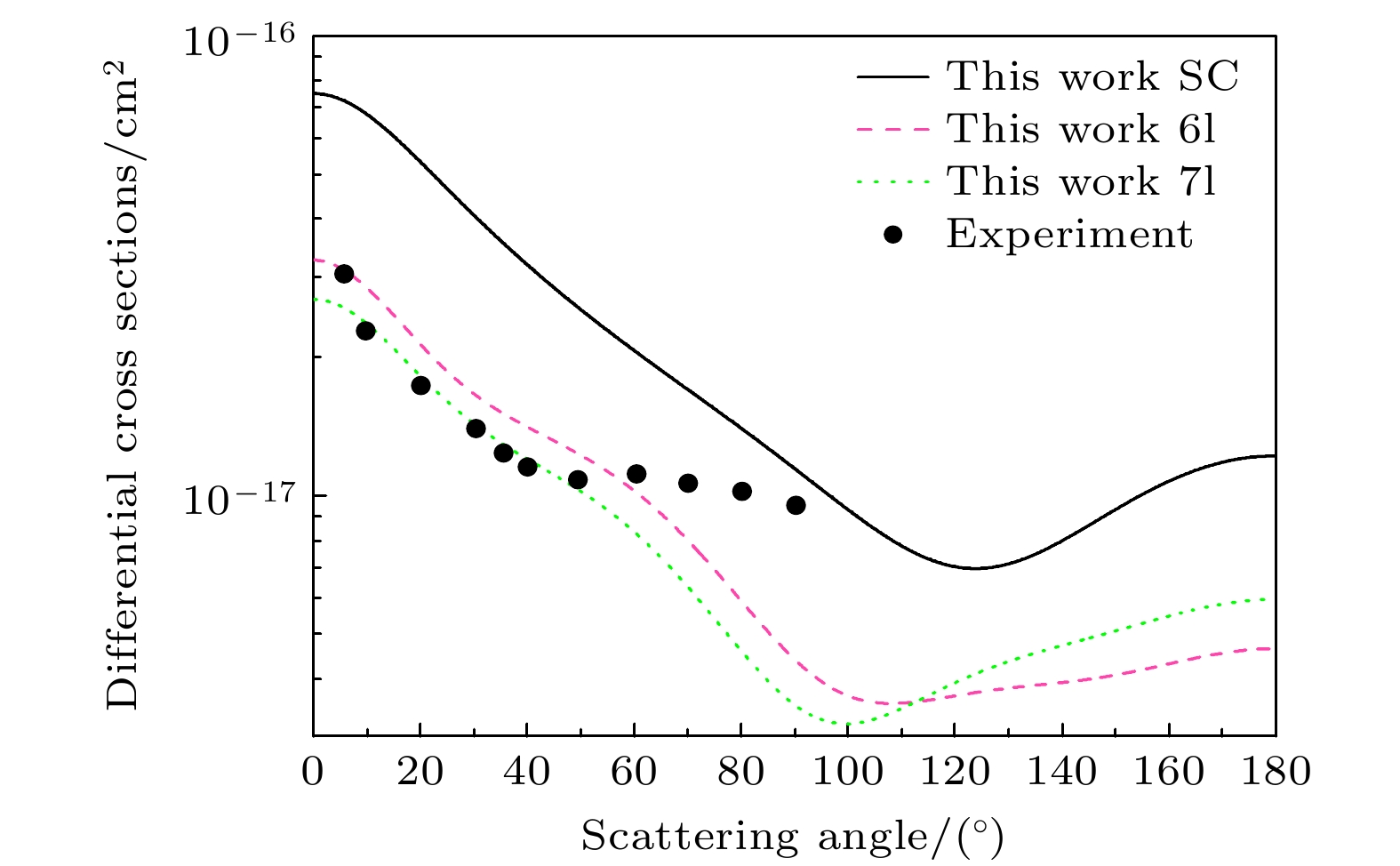
图2以中性Xe原子的亚稳态5p⁵6s J = 2能级到$ 5{{\mathrm{p}}}_{3/2}^{5}6{{\mathrm{p}}}_{3/2} $(J ^p = 2+)能级的碰撞激发为例, 给出了电子关联效应对激发总截面的影响. 为了讨论电子关联效应的贡献, 我们使用了两种关联模型. 其中, 模型A为单组态近似, 包含了5s²5p⁶, 5s²5p⁵6s和5s²5p⁵6p组态, 共有15个组态波函数. 计算中n = 1—4的轨道为原子实轨道, 价轨道包括5s, 5p, 6s和6p. 模型B中加入了5p⁵5d作为参考组态, 并将5d_3/2和5d_5/2轨道作为价轨道. 同时, 我们利用活动空间方法, 还包含了占据轨道5s和5p电子单或双激发到所有关联轨道的组态. 其中, 亚稳态有963个组态波函数, J ^p = 2+的态共有778个组态波函数. 图2给出了利用这两种相关模型计算的激发截面, 并与Jung等^[115]的实验结果进行对比. 可以发现, 在低能区域, 单组态近似的结果远大于多组态模型B的计算结果. 随着入射电子能量的增大, 两种模型计算结果的差别逐渐减小, 而且模型B的结果变化趋势与实验符合得非常好. 这表明在低能碰撞中, 电子关联效应占据主导地位, 然而在高能碰撞中, 电子碰撞激发截面受靶态波函数的影响较小. 模型A和B的计算中, 除了组态相互作用不同外, 这两种模型所选择的势也不同. 在模型A中, 我们选择的势是占据轨道单电子产生的平均势; 模型B中, 则包含了Core-价和Core-Core关联势. 因此, 模型B计算的精度要比模型A的精度高. 尽管模型B计算结果的精度有所提高, 但是理论和实验结果明显还有一定的差距, 高阶Born近似的贡献还需要进一步考虑.

图3给出了电子关联效应对入射电子能量为8 eV时, Hg原子从基态激发到6s6p ³P₁的碰撞激发微分截面的影响, 并与Goeke等^[117]利用符合测量技术的实验结果比较. 对于高Z中性原子, 由于其具有较强的关联效应, 大规模电子组态的扩展非常必要^[77]. 为了详细讨论电子关联效应对激发截面的影响, 采用3种计算模型来描述靶态波函数. 模型I是单组态近似, 原子实轨道包含主量子数n = 1—5的轨道, 价轨道包括6s, 6p_1/2和6p_3/2. 这些单电子轨道波函数用扩展能级(EOL)方法^[77,93]优化, 电子组态只包含了6s²和6s6p J = 1, 共有3个能级; 模型II中, 将基态和激发态分成2组分别优化, 而且单电子轨道中进一步加入6d和6f作为关联轨道, 并包含一个或两个虚电子激发到关联轨道的电子组态; 模型III中, 进一步加入n = 7的单电子轨道作为关联轨道, 也包含一个或两个虚电子激发到7l关联轨道的电子组态.

由图3可以看出, 在整个散射角范围内激发截面减小了一个量级. 对于低能散射, 随着散射角的增大, 激发截面减小得比较缓慢. 单组态计算的结果在散射角为120^o时出现了极小点, 模型II和模型III的计算结果在100^o时出现了极小点. 这是因为散射振幅计算公式中的球谐函数$ {{\mathrm{Y}}}_{{l}_{{\mathrm{f}}}}^{{m}_{{l}_{{\mathrm{f}}}}} $是散射角$ \theta $的函数, 不同分波通道求和之后会在一定的角度出现极小值, 此现象在物理上可以理解为不同分波通道干涉最小值的点. 另外, 对不同模型的计算结果与实验结果相比较可以发现: 利用模型I的计算结果与实验结果相差非常大, 利用模型II的计算结果已经接近于实验结果. 当散射角小于50°时, 利用模型III的计算结果与实验结果符合得非常好. 但是当散射角大于50°时, 目前的理论和实验还有比较大的差别.

共振激发可以看成两步过程, 即俘获和自电离, 共振截面^[108]可写为

式中, $ {\sigma }^{{\mathrm{c}}{\mathrm{a}}{\mathrm{p}}} $为俘获截面. 自电离过程的分值比B为

其中, $ {A}^{\mathrm{{a}}}(k-m) $和$ {A}^{{\mathrm{r}}}(k-{m}') $是能级之间的自电离和辐射概率.

Ba⁴⁶⁺离子M2线的共振过程可以表示为

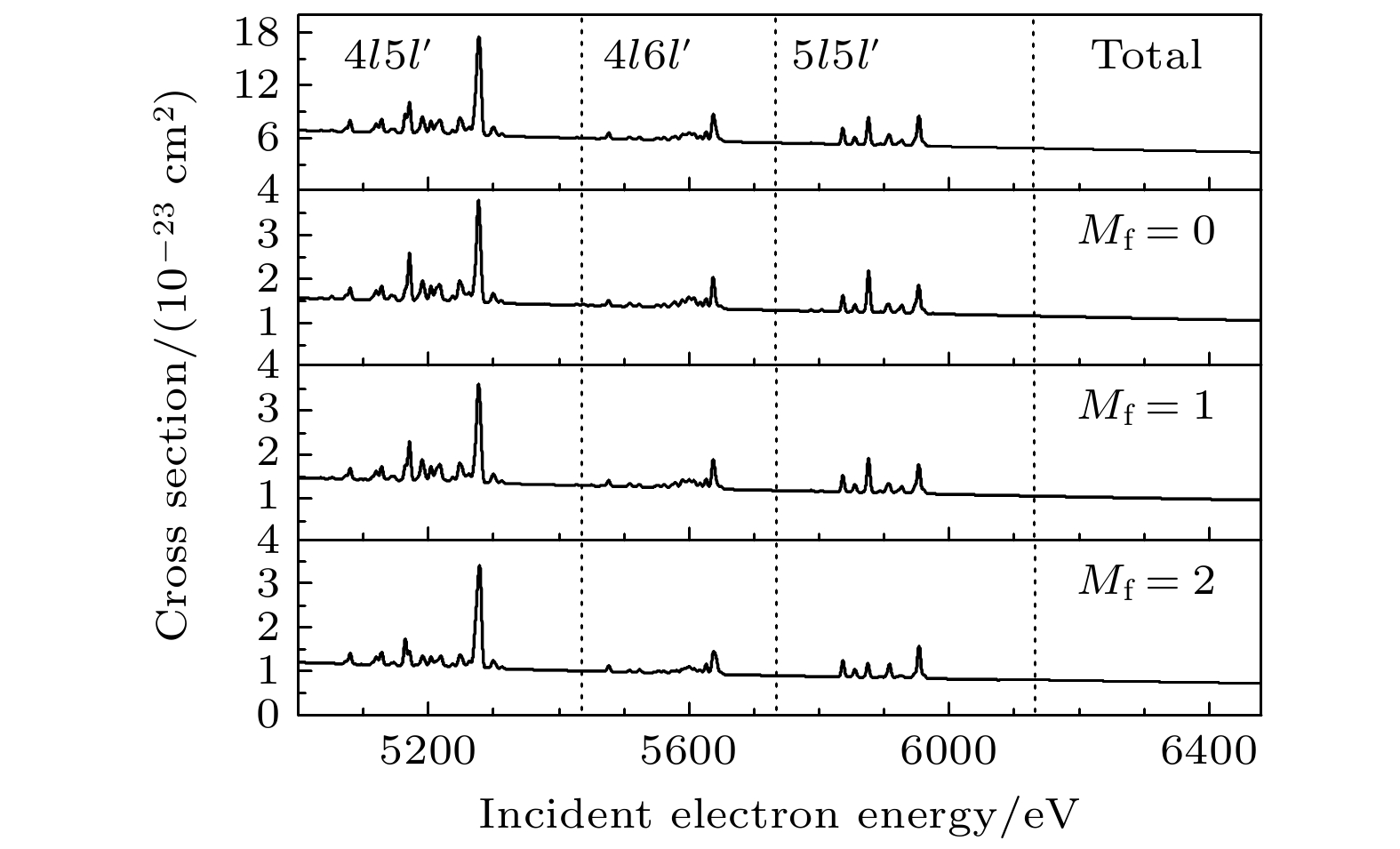
图4以类氢Ba⁴⁶⁺离子从基态2p⁶ J = 0到2p⁵3s J = 2的磁能级之间的激发截面为例, 讨论了共振激发对总截面的影响. 初态和末态波函数的计算中, 不仅包含了2s²2p⁶和2s²2p⁵3s参考组态, 而且包含了2s²2p⁵3p, 2s²2p⁵3d, 2s2p⁵3s, 2s2p⁵3p和2s2p⁵3d参考组态, 其中共包括37个能级. 对于低能量且高量子数的连续轨道波函数, 连续轨道不能很快达到正弦渐近行为, 并且在散射矩阵元的计算中, 大半径处连续轨道的贡献也非常大. 因此有必要计算非常大r的连续态波函数, 在该工作中选取最大的r = 190a₀.

图4的计算包括了从基态到4l 5l', 4l 6l' 和5l 5l' 共振激发的贡献, 可以看出共振结构在该能量范围内非常明显. 当入射电子能量在5—5.2 keV之间时, 4l 5l' 双激发共振占主导, 其中共振贡献的激发截面提高超过直接激发截面的2倍. EBIT装置实验^[118]中发现, 由于共振激发, 在该能量范围内M2辐射线强度增强了50％. 文献[119]中, 4l 6l'和5l 5l' 的贡献被认为非常小而无法在实验中观察. 但是在极化的实验测量中, 这两个共振过程是比较明显的. 从目前的工作可以看到, 5l 5l' 和4l 6l' 的贡献相对较小, 4l 6l' 比5l 5l' 共振过程的贡献更小.

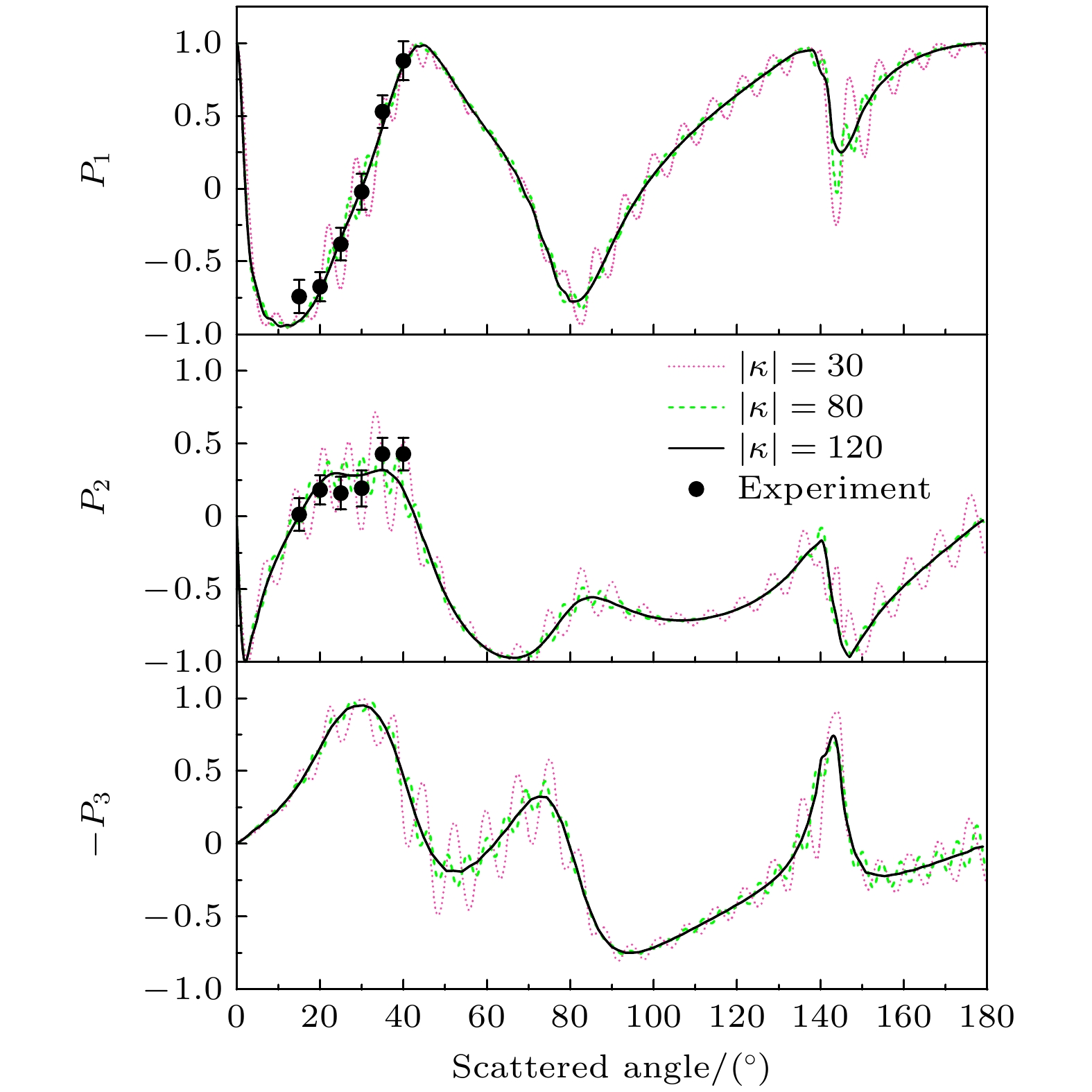
图5给出了入射电子能量为45 eV时, 包括不同分波情况下的电子与Ca原子从基态到4s4p ¹P₁的微分Stokes参数, 并与Dyl等^[120]利用电子与光子符合实验方法的测量结果比较. Ca原子4s^{2 1}S₀-4s4p ¹P₁的激发能为2.93 eV, 当入射电子能量大于40 eV时, 属于中能碰撞过程, 从理论的角度而言, 激发截面可以很快达到收敛. 计算Ca原子靶态波函数只包含了单组态的计算, 即参考组态只包含了4s²和4s4p J = 1. 比较包含不同分波的计算结果可以发现, 包含最大分波为30和80时, Stokes参数振荡非常大, 尤其是对于P₃. 只有分波达到120时, Stokes参数的变化才趋于光滑. 与实验相比较可以看出, 目前我们的计算结果与Dyl等^[120]的实验结果符合得非常好.

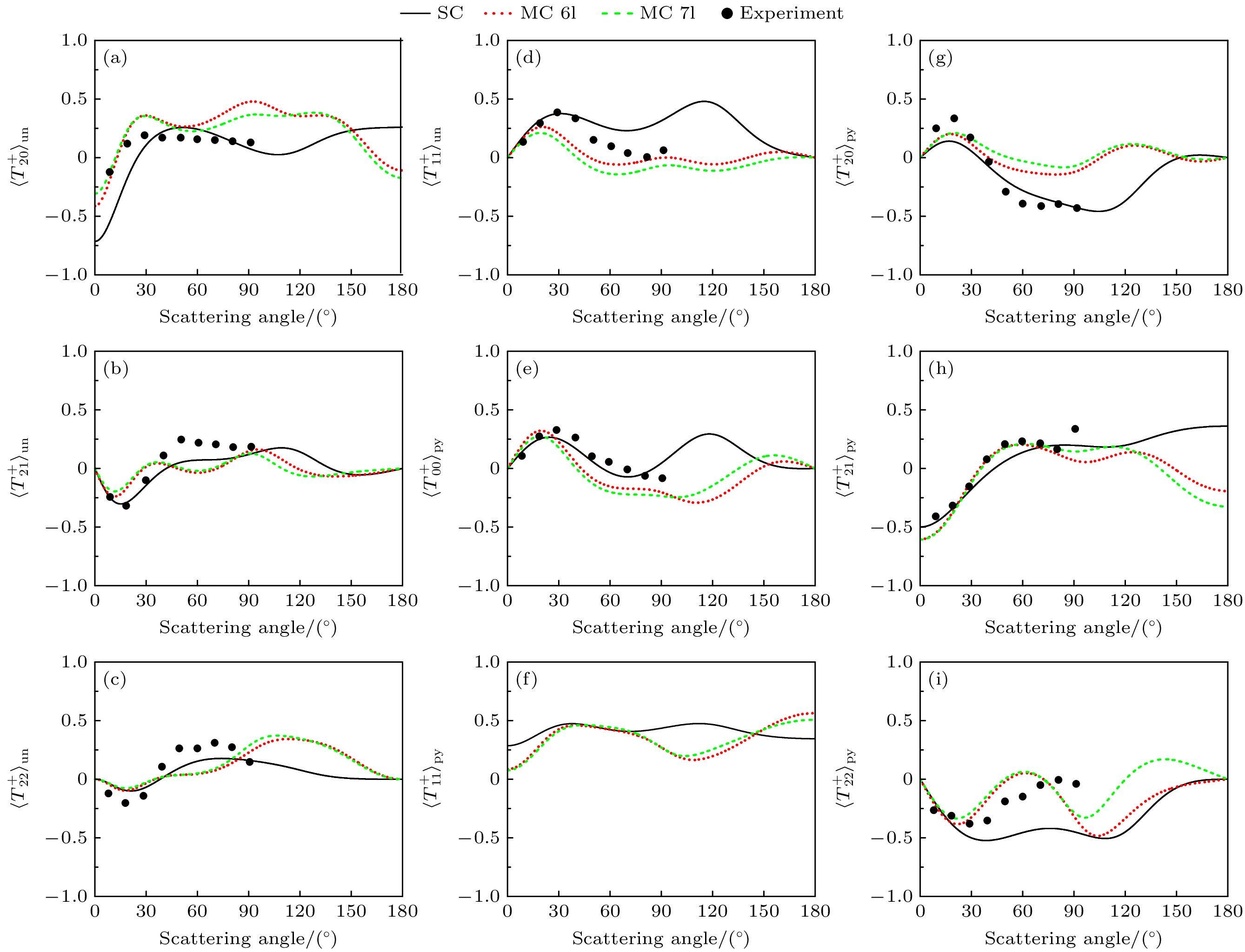
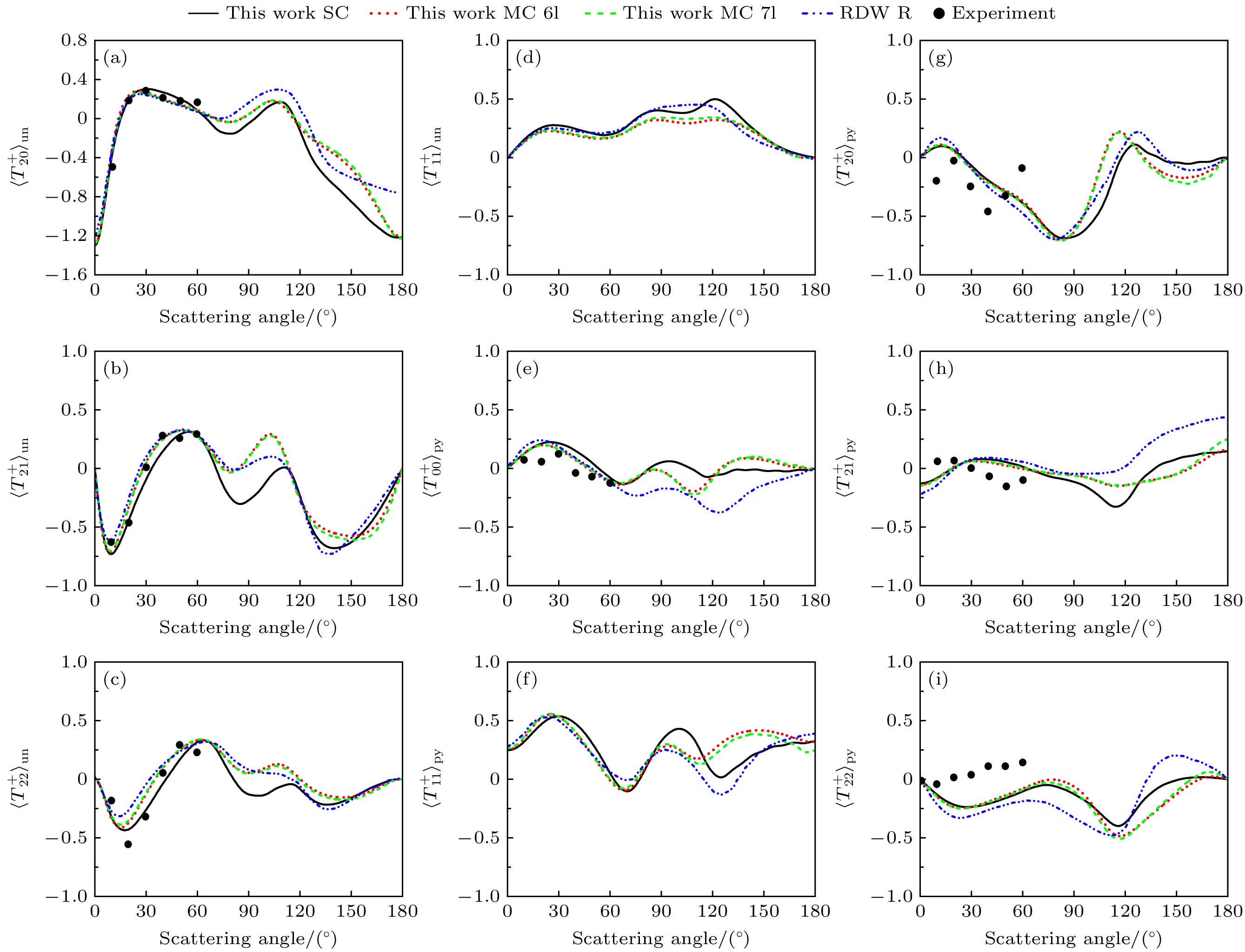
图6为入射电子能量为8 eV时, Hg原子从基态激发到³P₁的归一化的态多极, 并与Sohn等^[122]的实验结果进行比较. 可以看出, 由于入射电子能量比较低, 电子关联效应的影响非常显著. 比较不同模型的计算结果可以发现, 散射角小于30°时, 单组态和多组态计算的结果差异较小且与实验结果吻合较好. 图6(d)中的电子关联效应使得$ {\langle T(J{)}_{11}^{+}\rangle}_{{\mathrm{u}}{\mathrm{n}}} $的值减小, 当散射角大于50°时, 态多极逐渐接近于0, 而且随着散射角的增大, 实验结果逐渐靠近于多组态的计算结果. 对于$ {\langle T(J{)}_{20}^{+}\rangle}_{{\mathrm{u}}{\mathrm{n}}} $, $ {\langle T(J{)}_{21}^{+}\rangle}_{{\mathrm{u}}{\mathrm{n}}} $和$ {\langle T(J{)}_{22}^{+}\rangle}_{{\mathrm{u}}{\mathrm{n}}} $(图6(a)—(c)), 在实验测量的角度范围内, 理论计算和实验测量结果的变化趋势符合得比较好, 但是理论与实验之间还有一定的差别. 对比极化电子散射的态多极(图6(e)—(i))可以发现, 对于$ {\langle T(J{)}_{00}^{+}\rangle}_{{\mathrm{p}}{\mathrm{y}}} $和$ {\langle T(J{)}_{20}^{+}\rangle}_{{\mathrm{p}}{\mathrm{y}}} $单组态的计算结果与实验似乎符合得非常好, 但是对于其他(如$ {\langle T(J{)}_{21}^{+}\rangle}_{{\mathrm{p}}{\mathrm{y}}} $和$ {\langle T(J{)}_{22}^{+}\rangle}_{{\mathrm{p}}{\mathrm{y}}} $)多组态的计算结果与实验符合得比较好. 对于低能散射, 电子关联效应非常强, 实验上测量微分态多极参数也非常困难. 目前我们只能找到一组实验结果, 实验上也并未给出相应的误差分析, 我们建议高精度的实验是必要的.

态多极的计算结果依赖于入射电子的能量^[119], 图6中单组态和多组态的计算结果差异较大. 图7则给出了入射电子能量为15 eV时, Hg原子从基态激发到³P₁的归一化的态多极, 并与Srivastava等^[121]的理论结果和Sohn等^[122]的实验结果作比较. 图7(e)—(i)给出了横向极化电子碰撞激发的态多极, 通过比较不同模型的计算结果可以发现, 电子关联效应对态多极的影响与非极化电子碰撞对态多极的影响非常类似. 当散射角较小时, 电子关联效应的影响比较小. 随着散射角的增大, 电子关联效应逐渐显现, 但是其影响比电子关联效应对激发微分截面的影响小. 理论与实验结果相比可以发现, 部分结果符合较好, 而另一部分结果存在符合较差的情况. 例如, 图7(e)为值比较小的$ {\langle T(J{)}_{00}^{+}\rangle}_{{\mathrm{p}}{\mathrm{y}}} $, 并且理论与实验符合得相对较好. 但是, 对于$ K=2 $的态多极(图7(g)—(i)), 理论计算结果与实验测量值的差别非常大, 不仅理论值与实验值的变化趋势不一样, 而且理论值与实验值之间的符号都互不相同. 通过对实验结果以及不同模型的计算结果比较, 可以得到: 电子关联效应对小角散射的影响比较小, 随着散射角增大, 电子关联效应的影响逐渐变大, 但是相比电子关联效应对激发截面的影响较小. 对于非极化电子散射的态多极, 实验与理论结果符合得非常好, 对于极化电子散射的态多极, 理论与实验结果还有很大的差别, 还需要理论与实验做进一步的研究.

等离子体中, 热力学效应和库仑效应同时存在, 通常利用库仑参数Γ来判断哪种效应占主要地位^[123,124]. 目前, 理论上常用两种模型来描述等离子体静电屏蔽势, 即Debye-Hükel模型和离子球(IS)模型^[125]. Debye-Hükel模型由线性化的Poisson-Boltzmann方程得到, 主要应用于低密高温(Γ$ \ll $1, 弱耦合等离子体)等离子体^[123,124]. 我们知道等离子体屏蔽效应对原子动力学过程的影响非常大, 但是到目前为止, 理论方面没有关于等离子体屏蔽效应对谱线极化效应的研究.

在Debye屏蔽势模型中, N电子原子体系的哈密顿量^[126]可以写为

式中, $ \lambda $为Debye长度, 它与等离子体平均电子密度$ {n}_{{\mathrm{e}}} $及电子温度$ {T}_{{\mathrm{e}}} $之间的关系为

其中, k为Boltzmann常数. 根据(28)式, $ \lambda $与电子温度$ T_{\text{e}}^{{\text{1/2}}} $成正比, 与$ {n}_{{\mathrm{e}}}^{1/2} $成反比. 对于给定的$ \lambda $, $ \lambda $越小说明等离子体屏蔽越强, $ \lambda $越大说明屏蔽越弱. 本节中所涉及的是高离化态离子, 因此在计算等离子体屏蔽效应时, 采用了与Pindzola等^[127]相似的办法. 即等离子体的密度可以影响连续电子波函数以及连续电子与束缚电子之间的相互作用, 但不足以影响靶态中的束缚电子. 为了处理相对简单, 进一步采用了Whitten等^[124]的经典文章以及Pindzola等^[127]的屏蔽模型. 在这种情况下, 库仑径向矩阵元(所谓Slater积分)可以写为

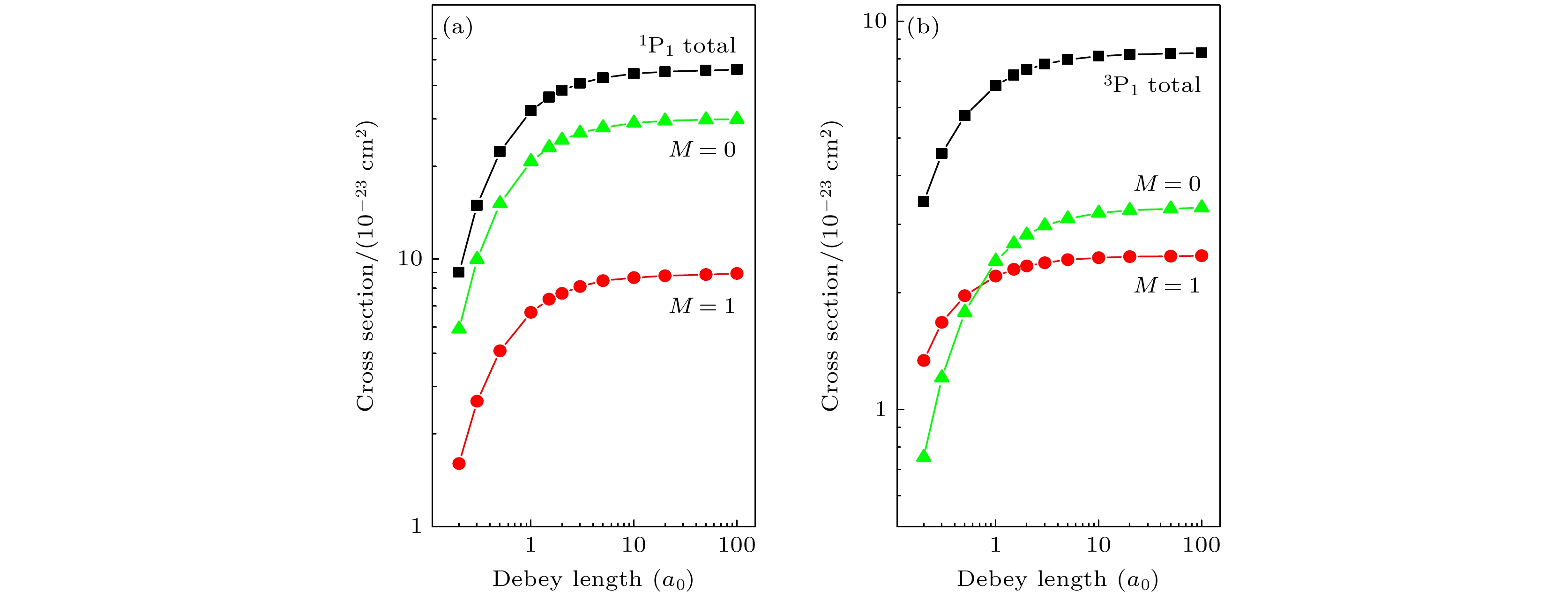
其中, $ P_i $和$ Q_i $(i = a,b,c,d)代表单电子轨道波函数. 连续态波函数方程可写为

为了更进一步说明等离子体屏蔽效应对激发截面的影响, 图8给出了入射电子能量为1.5倍的激发能时, 电子碰撞激发截面随Debye长度的变化. 从图8可以看出, 当Debye长度大于10a₀时, 所有的激发截面变化比较平缓, 说明等离子体屏蔽效应的影响不大. 但是当Debye长度小于10a₀时, 随着屏蔽效应的增大, 激发截面迅速减小. 而且, 对于到¹P₁以及相应的M = 0和M = 1磁量子能级, 激发的变化趋势相似, 3条曲线平行地变化. 但是对于到³P₁的激发, 到M = 0的激发截面比M = 1的激发截面减小得更快, 而且两条曲线出现了交叉.

本文基于全相对论多组态Dirac-Hartree-Fock (MCDHF)理论方法以及相应的程序包GRASP 92/2K/2018和RATIP, 发展并建立了一套全相对论理论框架下研究电子碰撞激发过程的扭曲波方法和程序. 该理论方法和程序系统有以下几个优点:

1)对连续电子波函数的求解中, 不仅考虑了靶原子产生的势场对连续态波函数的影响, 而且包含了束缚电子与连续电子的交换相互作用, 并采用连续电子与离子波函数的乘积构成的反对称化耦合波函数作为体系的波函数. 因此, 该方法可以很好地研究低能和中高能电子散射过程.

2)该方法中, 靶态波函数基于MCDHF理论方法得到. MCDHF的优势是能够很好地考虑电子关联效应、Breit相互作用和QED效应对靶态波函数的影响. 在碰撞激发矩阵元的计算中, 也包含了Breit相互作用的贡献. 因此, 该方法结合了MCDHF方法和扭曲波方法的优势, 可以研究高阶效应对碰撞动力学过程的影响, 得到高精度的理论数据.

3)该程序不仅可以研究电子与原子碰撞激发过程的散射截面和等离子体屏蔽效应对碰撞激发的影响, 而且可以很好地研究电子与复杂原子碰撞激发的态多极、微分/积分Stokes参数(角关联参数)和取向参数等, 为详细研究电子碰撞激发过程提供了很好的工具.