-
随着纳米技术的飞速发展, 材料的表面和内部纳米结构引起了广泛关注[1,2]. 在这一背景下, 人们对纳米孔隙或毛细管产生了浓厚兴趣. 通过化学蚀刻由高能粒子撞击绝缘体产生的离子轨迹, 可以将各种材料制作成具有各种横截面的纳米孔隙的微孔膜, 这种微孔膜在各大领域得到广泛应用[2]. 多年来人们进行了大量关于带电粒子通过纳米毛细管的研究[3–26]. 近年来, 带电粒子在纳米毛细管中传输表现出来的“导向效应[4]”和“成型效应[5]”成为研究热点. 使用锥形玻璃管可以将离子束准直、聚焦至微米量级, 形成微束. 微米量级的离子束已被用于生物细胞内部结构的辐照研究[6,7].
导向效应最早被发现是在3 keV的Ne7+离子穿透完全绝缘的聚对苯二甲酸乙二醇酯(PET)微孔膜的实验中[4]. 研究发现, 当毛细管倾斜角度大于离子束可以直接穿过的几何张角时, 离子仍能穿透微孔, 透射离子的角分布以毛细管轴向方向为中心, 且大多数透射离子保持初始电荷状态和动能, 这种现象被称为“导向效应”[4]. 导向效应的形成归因于离子在穿透微孔时与内壁发生碰撞, 导致电荷在壁面沉积形成的电荷斑, 这些电荷斑产生的电场对后续离子产生排斥作用, 迫使它们在远离内壁的地方发生偏转, 最终沿着轴向方向出射[4,8–10,12–19]. 而且由于后续进入的离子在电荷斑的作用下未与微孔壁发生碰撞, 因此出射离子的电荷态和能量保持不变. 电荷斑的形成是一个时间相关的过程, 随着入射离子数量增加, 通道壁上的电荷斑自组织排列, 离子穿透率逐渐增加, 直到达到稳态 (通道壁上的电荷沉积和放电过程达到平衡), 离子稳定传输穿透率最大[11]. 这种现象已经在聚对苯二甲酸乙二醇酯[4,8–11], SiO2[13–15], Al2O3[16–19] 和聚碳酸酯(PC)[11,20,21]等绝缘微孔膜上观察到. Schiessl等[22,23]提出了基于扩散模型的理论框架, 该模型解释了电荷斑的形成和离子的传输. 利用经典轨迹蒙特卡罗模拟, 成功复现了实验中的导向效应、角分布各向异性以及充放电行为. 但模拟结果在定量上与实验结果仍存在差距, 模拟得到的角分布半高宽明显小于实验值. 并且该模型无法解释电荷斑的动态变化和非线性效应. 2007年, Pokhil等[27]提出了基于电荷在电场中定向运动的电荷漂移模型, 很好地解释了毛细管充电和放电过程中电荷积累和泄漏的动态行为. 它能够描述实验中观察到的非指数充电和放电曲线, 并通过拟合实验数据确定电荷迁移率. 此外, 漂移模型还能够解释毛细管壁上电荷分布的非均匀性, 为理解离子束在毛细管中的引导现象提供了重要的理论支持. 2010年, Zhang等[15]通过考虑电荷斑的电势分布, 研究了电荷斑的形成、演化以及对离子传输的影响. 成功解释了传输角度分布的演化过程, 包括初始阶段的快速偏转、中间阶段的转向点以及稳态阶段的角度回归. 2013年, Stolterfoht[9,10]对电荷漂移模型进行了完善, 采用基于Frenkel理论的非线性电导率模型来描述电荷传输. 考虑了电荷传输的多维性, 包括沿毛细管轴向和垂直于轴向的传输. 更详细地描述了电荷传输的动态过程和离子引导的复杂行为, 如离子轨迹的聚焦、离子发射角度的振荡以及不同绝缘材料(如聚对苯二甲酸乙二醇酯和聚碳酸酯)之间的差异. 2020年, Eric. Giglio提出的电动力学模型能够准确描述绝缘直毛细管中电荷的动力学行为, 并通过多极展开方法解析地计算出电荷弛豫时间. 模型表明, 表面电导率对电荷弛豫过程有显著影响. 提供了如何利用实验数据提取毛细管的电学性质的方法, 为实验研究提供了理论支持和分析工具.
初期对导向效应的研究, 采用的都是具有圆形截面的纳米通道, 由于圆形通道具有高度的旋转对称性, 无法揭示离子和通道壁的其他相互作用机制. 2012年, 离子穿越绝缘微孔时的成型效应被报道, 揭示了微孔截面几何形状对透射离子束几何形状的影响[5]. 7 keV的Ne7+离子穿越具有菱形和矩形截面微孔的白云母膜, 结果显示, 穿越菱形微孔的离子成像为矩形, 而穿越矩形微孔则产生菱形成像[5]. 为进一步探究成型效应的成因, 通过在菱形微孔膜毛细管完全放电的情况下, 记录前期只有少量电荷入射, 不足以产生电荷斑的情况下的出射离子角分布, 图像仍然呈矩形, 具有成型效应[28]. 模拟计算也表明, 成型效应不是由通道内壁沉积的电荷斑引起的, 而这一现象归因于离子在穿越微孔时在绝缘体通道壁上产生的镜像电荷, 镜像电荷对离子施加的横向的镜像电荷力使其具有横向的动能, 与出口处毛细管对离子出射角度的限制作用一起将出射离子束裁剪成特定形状[5,28,29]. 成型效应的发现为控制离子束形状提供了一种新的技术手段.
本文通过理论推导, 对镜像电荷力表达式进行了完善, 并结合实验和理论模拟对低电荷态离子在纳米微孔中所受镜像电荷力进行了分析研究. 进行了1 keV
$ {\text{N}}_2^ + $ 离子穿越白云母微孔膜的实验, 测量得到了离子刚开始入射时, 穿透微孔膜出射离子的二维角分布. 在以往的模拟计算工作中, 为了简化计算过程, 都采用静态近似来计算镜像电荷力. 我们发现用这种方式计算得到的结果与实验结果仍存在差异, 因此尝试进一步完善这种计算方式, 以使模拟结果与实验结果更加吻合. 镜像力会极化表面电荷, 因此它依赖于离子速度和介电函数的频率响应, 这导致在较高速度下镜像力与速度为零时的静态极限相比强度降低. 结合依赖于离子速度和介电函数的频率响应的镜像电荷力表达式[30], 推导出与离子速度和离子与表面距离相关的极化因子, 给出了依赖于离子速度和离子与通道壁距离的镜像电荷力的表达式. 我们分别对实验结果进行了不同镜像电荷力作用下的模拟计算. 针对实验和模拟结果的差异, 我们在不同束流发散度和不同倾角下进行了模拟计算, 结果表明二者会对模拟结果产生一定影响, 但不足以消除模拟结果与实验结果之间的差距. -
本实验在兰州大学核科学与技术学院多功能加速器平台的低能离子束与微结构相互作用平台上进行(图1(a)). 实验所用的
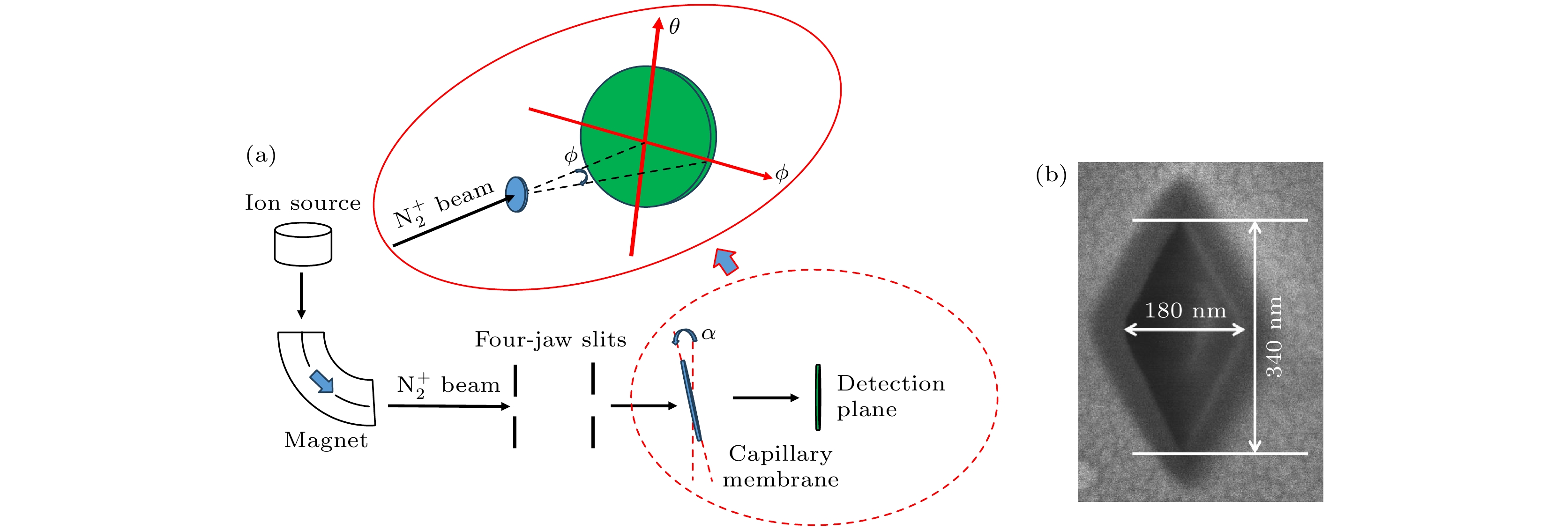
$ {\text{N}}_2^ + $ 离子是由自主研制的永磁潘宁离子源产生. 离子束经过初步聚焦后通过5 mm的限束孔进入一个90°的偏转磁铁, 这里可以通过调节磁场强度来筛选特定能量和种类的离子束. 得到的1 keV$ {\text{N}}_2^ + $ 离子束通过一对3 mm×3 mm的四颚狭缝, 在微孔膜上的电流范围为6—7 pA/mm2, 离子束发散度小于1.3°. 微孔膜被安装在测角仪上, 可以在三个空间方向以及两个旋转轴上独立调整. 微孔膜后方装有用于探测透射离子的探测系统, 探测系统是由微通道板(micro channel plate)、电阻膜阳极、模拟电子学系统以及基于FPGA的数字数据获取系统组成. 微通道板由数百万个独立的通道组成, 入射离子撞击通道壁产生次级电子, 电子再次撞击通道壁而倍增, 多次倍增后的电子最终从通道末端出射[31]. 采用两块微通道板叠加使用, 两块微通道板前中后施加电势逐级增加的电压, 以增加倍增效果同时抑制离子反馈限制. 从微通道板出射的电子云入射到电阻膜阳极形成的电荷被电阻膜的四个角收集, 电阻膜具有均匀的电阻率, 因此四个角收集的电荷量与其到入射点的距离成反比, 因此根据各个角探测到的电流强度关系可以判断出离子入射位置[32]. 基于FPGA的数字数据获取系统是由法国GANIL研究人员研发的FASTER系统, 是一种基于同步树模型的模块化数字采集系统, 能够进行脉冲信号的电荷和时间测量, 具有辐射测量能谱的数字整形-鉴别-峰值和保持功能, 能够解调回旋加速器的无线电频率, 能够对数据流做出复杂的决策[33].实验用的白云母微孔膜是由GSI亥姆霍兹中心的直线加速器UNILAC提供的快速重离子辐照白云母片, 辐照离子为11.4 MeV/u的Pb, 辐照密度5×107/cm2, 由于其质量大且能量高, 这些离子穿透白云母, 并产生直径为几纳米的轨迹通道[34]. 然后将辐照后的样品在20%的HF酸溶液中在室温(25 ℃)下蚀刻10 min. 每个离子轨迹比周围的未损伤基体材料更优先地被侵蚀, 且侵蚀速率更高, 从而形成了高度平行取向一致的纳米毛细管. 扫描电子显微镜(SEM)显示, 我们所使用的白云母膜上的毛细管呈菱形, 并且取向一致. 如图1(b)所示, 微孔的菱形截面短轴长180 nm, 长轴长340 nm, 孔密度为5×106 cm–2. 毛细管长度为20 μm, 沿短轴的几何张角为0.52°, 沿长轴的几何张角为0.97°. 结合孔密度和微孔的截面面积可以得到, 微孔膜的几何透明度(孔隙率)为0.306%, 由于这种低的孔隙率, 纳米通道可以被看作彼此是独立的、相互分离的. 为防止离子入射造成的电荷沉积使得微孔膜宏观带电, 在膜的入口和出口处都覆盖了厚度为10 nm的金层.
角度的定义如图1(a)所示, 通过调节微孔膜的倾角α可以改变入射离子束和纳米通道轴向的夹角. 以离子束入射方向为参考, 定义与离子束撞击位置相关的观察角ϕ和θ, ϕ和倾角α位于同一水平面内, θ垂直于该水平面. 通过扫描倾斜角和俯仰角, 使毛细管与入射光束平行排列, 即α = 0°, 从而获得最大离子透射量. 由于计数过大时探测器会饱和, 为了保护探测器, 在对初束进行测量时, 通过调节静电透镜, 改变离子束聚焦位置来降低束流强度. 初束的二维角分布在ϕ方向投影半高宽小于1.3°, θ方向的投影半高宽小于0.8°.
-
首先测量了1 keV
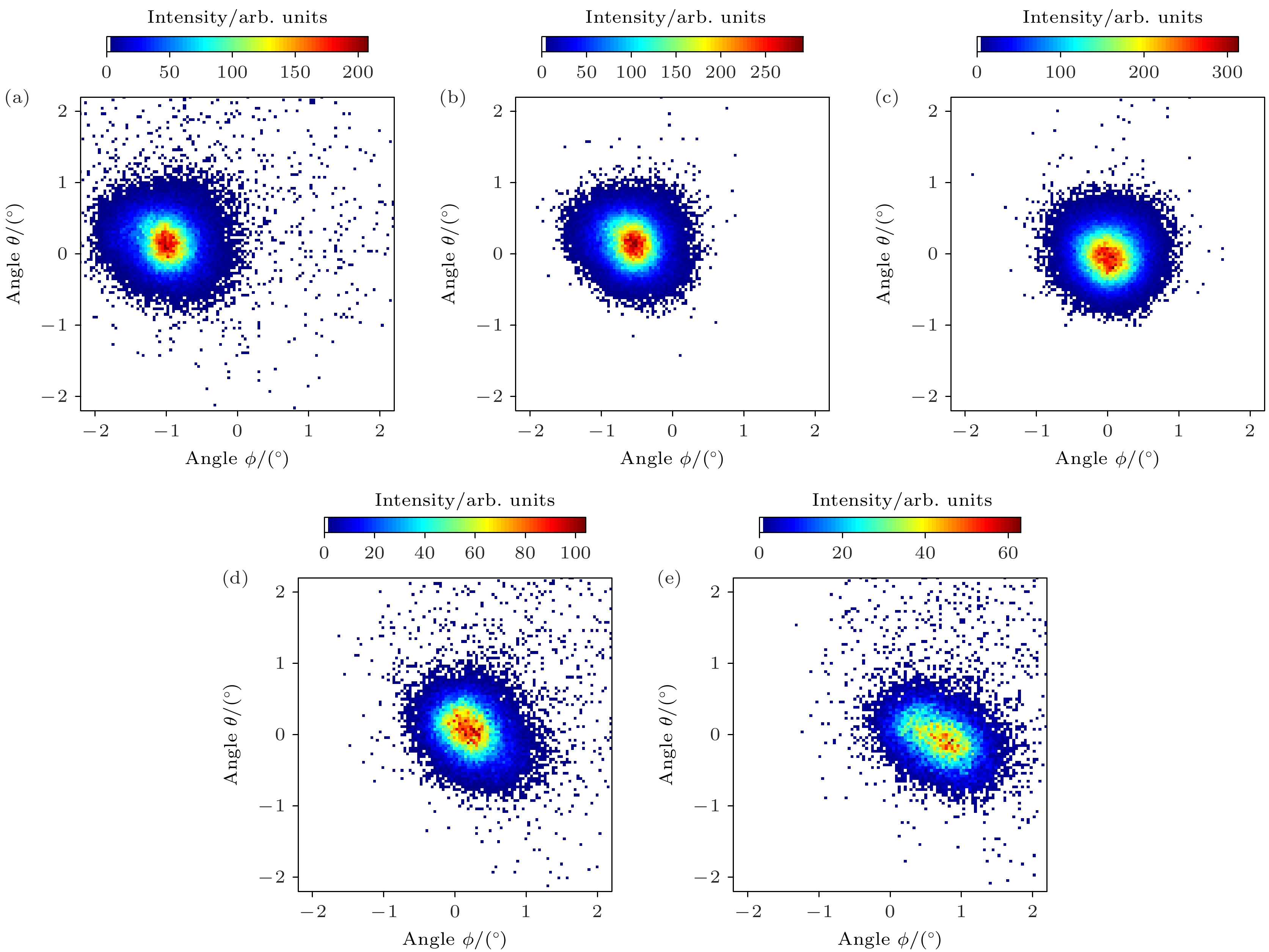
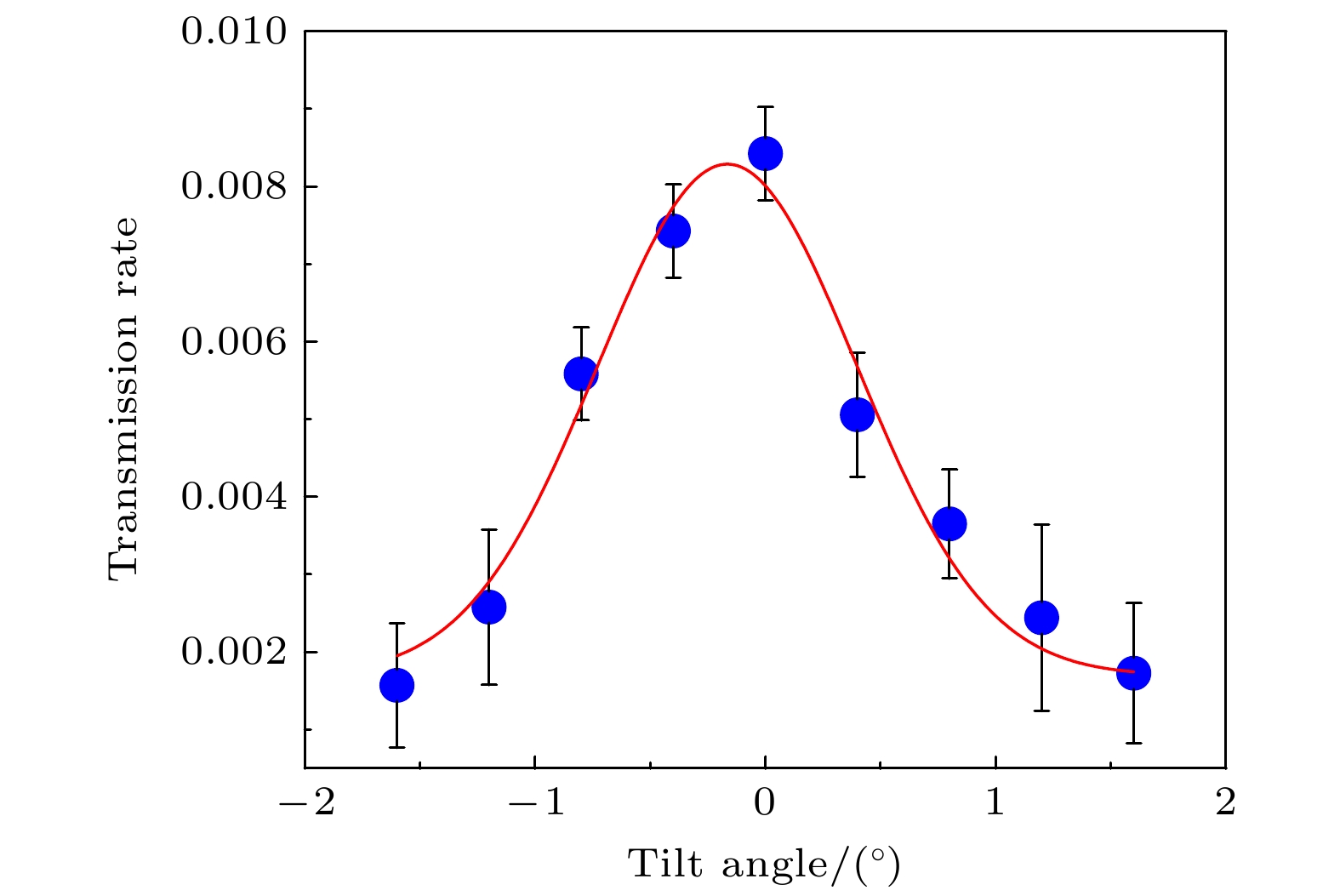
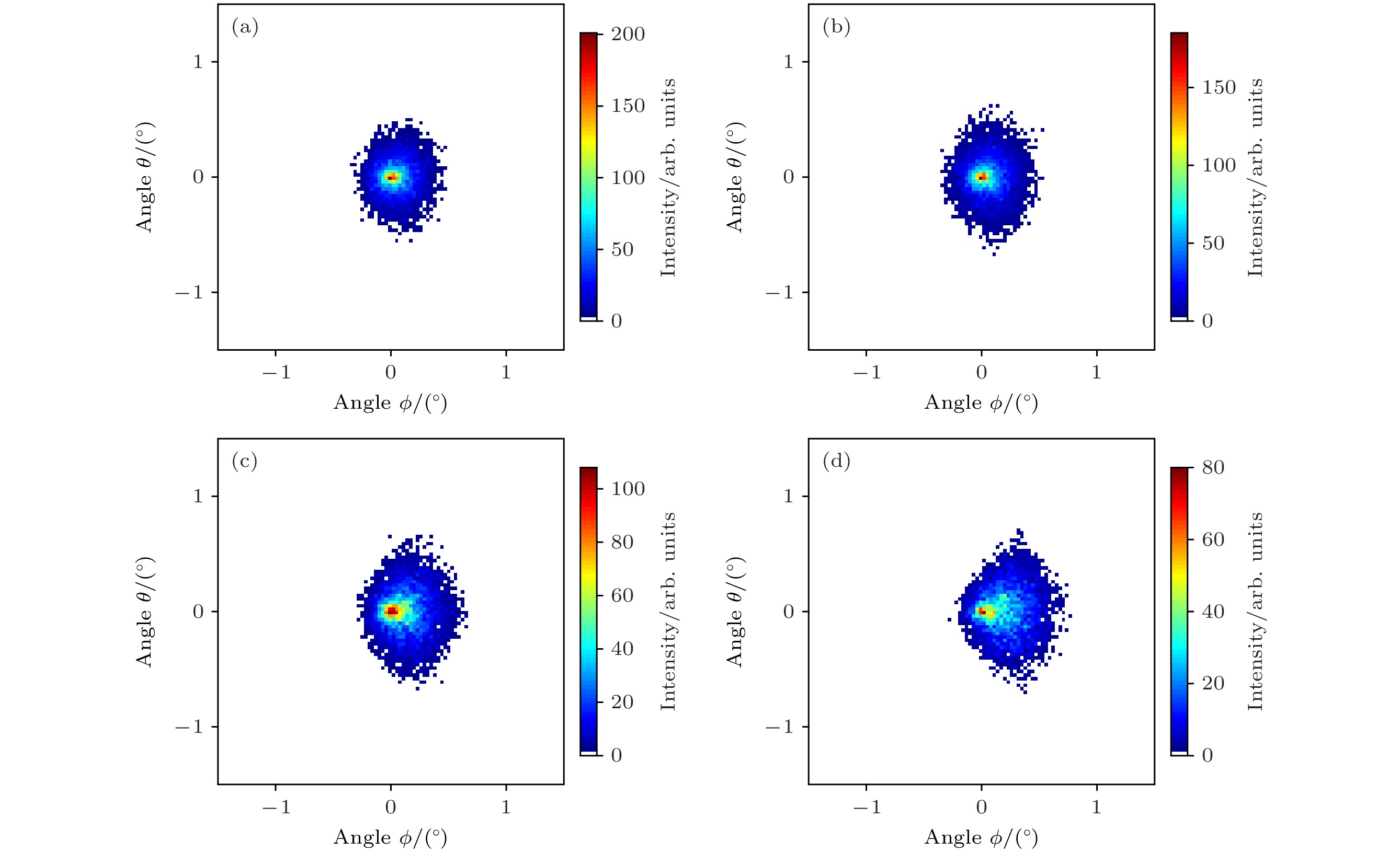
$ {\text{N}}_2^ + $ 离子在不同倾角下穿越白云母微孔膜达到稳态后的透射离子二维角分布和离子穿透率. 图2展示了部分不同倾角下透射离子的二维角分布, 分别提取自图3中相应倾角穿透率时的图像测量结果, 可以看出随着倾角的变化, 成像中心和透射离子强度随之改变. 离子穿透率定义为从微孔出射的离子数与进入微孔的离子数的比值, 图3中各点代表实验测量的全倾角下的离子穿透率. 由图3可以看出, 穿透率随倾角变化曲线呈正态分布, 倾角在靠近0°时穿透率逐渐上升, 最大值对应微孔轴向与离子束方向平行, 定义此时微孔膜的倾角为倾角零度, α = 0°.为了尽量消除沉积电荷导致的库仑力对透射离子角分布的影响而单独研究镜像电荷力的作用, 对微孔膜进行了几天的长时间放电. 在接近0°倾角下, 测量了离子束刚开始入射时的透射离子角分布, 如图4(a). 在离子刚开始入射的时候, 只有极少量的离子进入单个微孔, 这些离子不足以在微孔壁上沉积电荷形成电荷斑[28], 因此这个角分布反映出了镜像电荷力的影响.
-
在之前对镜像电荷力的研究中, 我们忽略了离子的速度对通道壁表面极化的影响, 本文对其进行了研究.
-
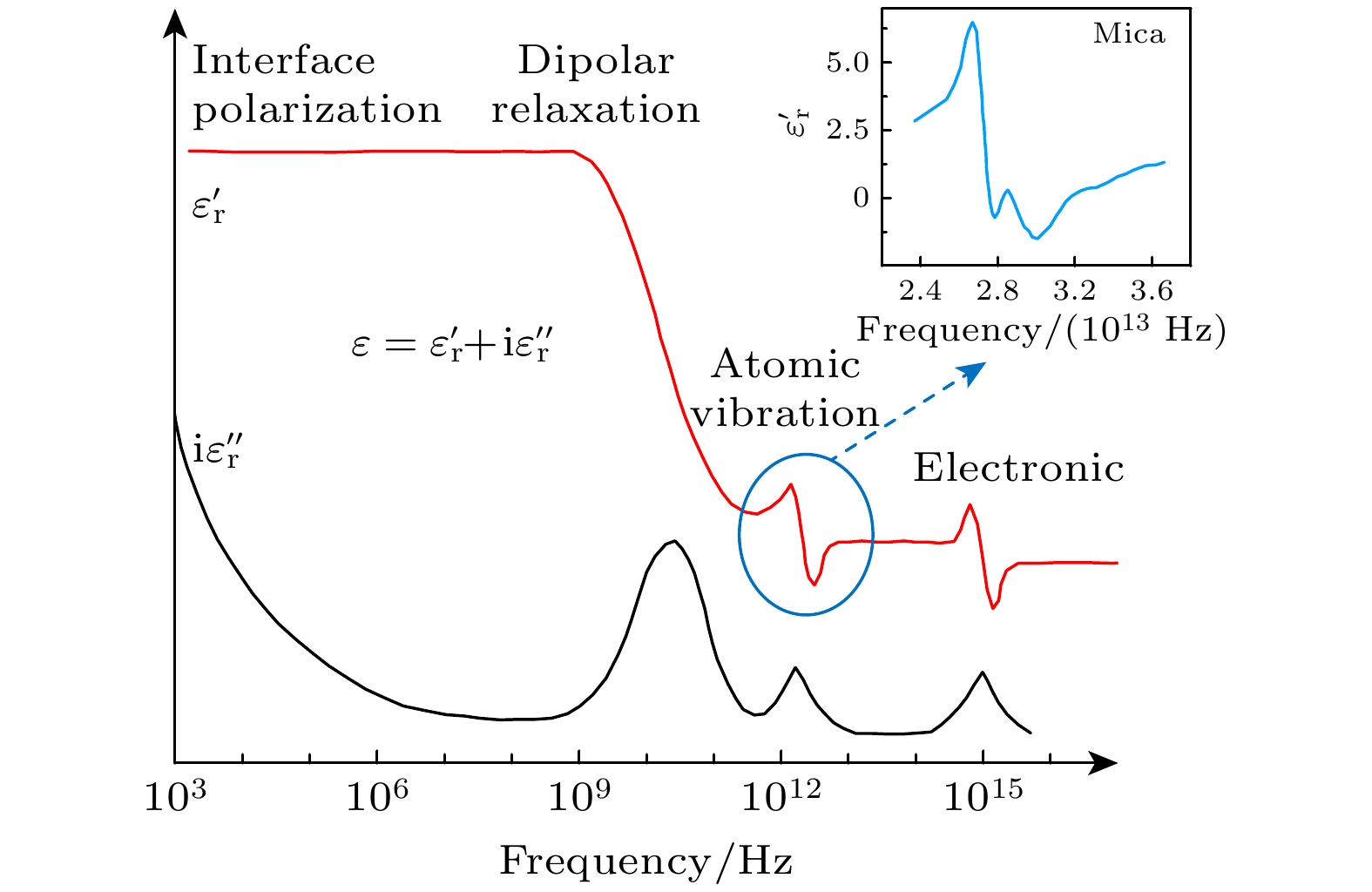
镜像电荷力源于离子靠近材料表面时, 其电场所引发的材料表面极化现象. 具体来说, 离子的电场会使材料表面的电荷分布发生改变, 从而产生极化电荷. 这些极化电荷会对离子产生吸引力, 这种由极化电荷所引起的对离子的吸引作用力, 即为镜像电荷力. 在电场作用下的极化能力取决于该材料的相对介电常数. 极化有几种不同来源: 电子云相对于原子核的位移、原子间相对位移、偶极子在电场中的排列以及界面处载流子的积累. 如图5为在很大频率范围内的任意介质介电谱[35], 图中这些极化的共振过程分别发生在电场角频率1015 , 1012, 109, 103 Hz量级. 不同的极化来源对电场的响应时间不同, 因此介电常数与外电场的角频率相关ε≡ε(ω)[36]. 假设在电磁场频率远低于光学频率, 且感应偶极矩的空间扩展远小于波长2π/k时, 介电函数εr对波矢k的依赖可以忽略[37]. 云母的原子间振动主要发生在红外频段, 在1012—1014 Hz之间[38]. 如图5中插图为从Fali等[39]研究中提取出来的云母的介电函数实部随频率变化的曲线, 可以看出在图中频段, 云母主要发生原子间振动.
-
对于无限大的平面, 其下方填满介电常数为εr的均匀电介质, 其上方为真空, 在距离表面d的位置有电量为q速度为v的离子, 作用在该离子上的镜像电荷力表达式为[36]
极化因子为
则镜像电荷力表达式可以写成:
在速度趋向于零时, 极化因子为常数:
静态镜像电荷力
其中εr为静态介电常数, q为电荷态, ω为角频率, d为带电粒距离表面的距离.
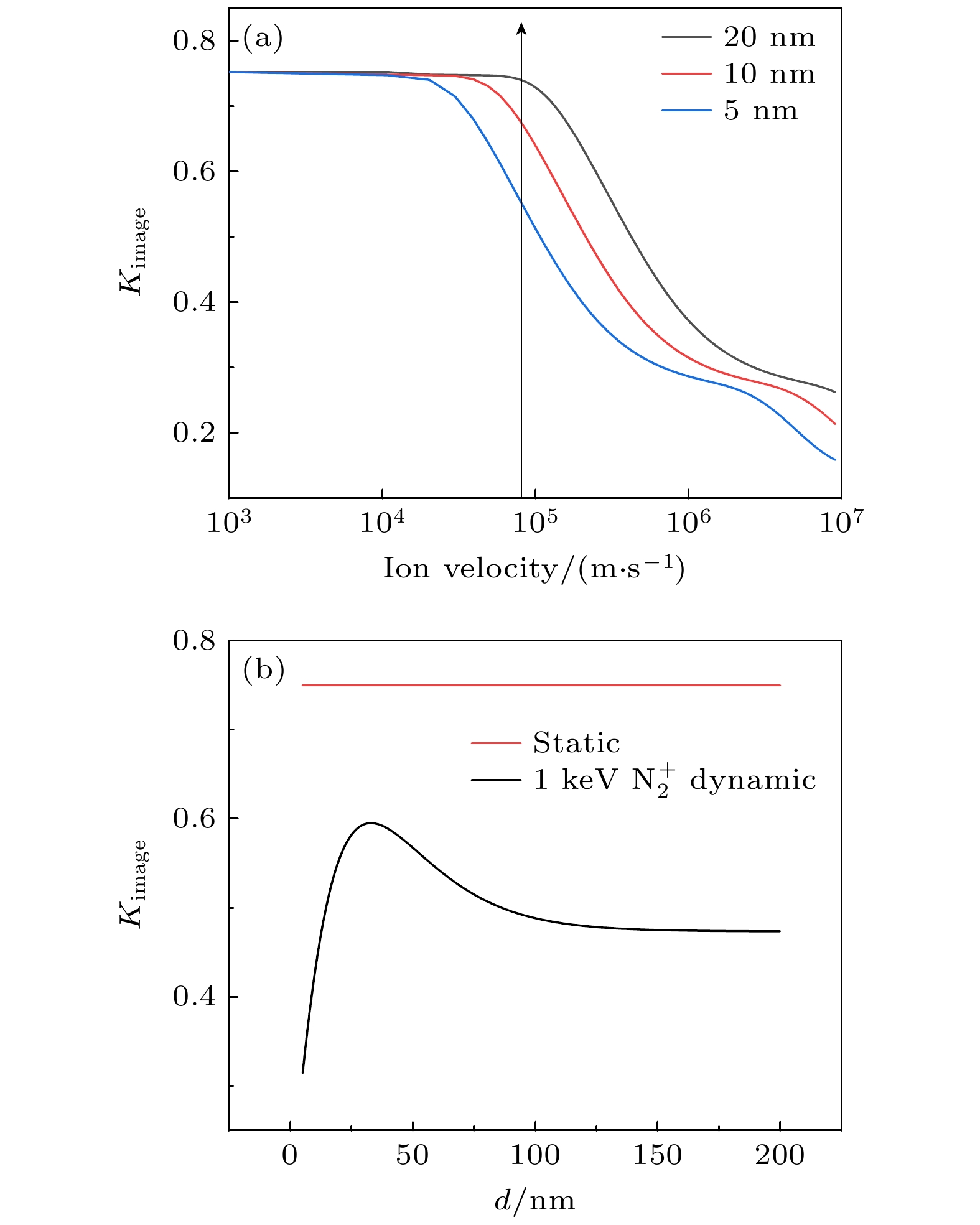
极化因子与离子速度的依赖关系如图6(a)所示, 展示了离子距离通道壁5, 10和20 nm时的极化因子的离子速度响应. 在这里使用了图5(b)所示云母的介电响应函数. 从图6(a)可以看出, 当速度大于106 m/s时, 各距离的极化因子都降低了40%, 原因是在速度大于106 m/s时, 位于THz范围内的原子和离子模式对时变电场响应不够快, 此时只有电子的响应足够快, 对表面极化有所贡献. 当速度大于107时, 电子响应也不够快了, 极化因子开始趋向于零.
1 keV
$ {\text{N}}_2^ + $ 离子与白云母相互作用的极化因子随离子与云母表面距离变化曲线如图6(b)所示, 速度不为零时, 极化因子随离子与云母距离增加而增加, 在25—50 nm的时候达到最大值, 随后逐渐下降, 在距离大于100 nm时逐渐趋于稳定. 且由图6(b)可以清晰地看出, 动态的极化因子始终明显小于速度为零的静态极化因子. 因此在镜像电荷力静态近似的模型中可能会高估镜像电荷力的作用.基于以上无限大的平面下的镜像电荷力的表达式, 可得到菱形微孔的镜像力表达式, 图7为菱形微孔的截面图, 展示了各阶镜像电荷的几何位置关系. 镜像电荷力的方向沿微孔壁(C1C2, C2C3, C3C4, C4C1)法相向内, 离子q与微孔壁内表面距离分别为d1, d2, d3, d4.
$q_1^{12}$ 是q关于C1C2边的一阶镜像电荷,$q_1^{23}$ 是q于C2C3边的一阶镜像电荷,$q_1^{34}$ 是q关于C3C4边的一阶镜像电荷,$q_1^{41}$ 是q关于C4C1边的一阶镜像电荷;$q_2^{12}$ 是$q_1^{41}$ 关于C1C2边的二阶镜像电荷,$q_2^{32}$ 是$q_1^{34}$ 关于C2C3边的二阶镜像电荷,$q_2^{34}$ 是$q_1^{23}$ 关于C3C4 边的二阶镜像电荷,$q_2^{41}$ 是$q_1^{12}$ 关于C4C1边的二阶镜像电荷;$q_3^3$ 是$q_2^{23}$ 关于C3C4边的三阶镜像电荷及$q_2^{34}$ 关于C2C3 边的三阶镜像电荷,$q_3^1$ 是$q_2^{12}$ 关于C4C1 边的三阶镜像电荷及$q_2^{41}$ 关于C1C2边的三阶镜像电荷.镜像电荷力表达式如下:
1)一阶镜像电荷力
2)二阶镜像电荷力
3)三阶镜像电荷力
-
毛细管内沉积电荷会影响绝缘体介电响应, 我们在实验中有意避免了沉积电荷产生, 所以本文不考虑沉积电荷对介电响应的影响. 通过叠加菱形纳米通道各壁的各阶镜像电荷力, 模拟了透射离子角分布. 利用龙格-库塔法(Runge-Kutta method)对离子在微孔中所受镜像电荷力的牛顿方程进行数值求解, 计算轨迹[40]. 为了提高计算效率, 缩短运行时间, 采用一根毛细管代替微孔膜上暴露在离子束下的数百万根毛细管的方法. 只用一根毛细管计算轨迹, 通过变换实验室坐标系、膜坐标系、毛细管坐标系, 将膜内许多毛细管的变化, 束流发散度以及毛细管轴向结合起来[41]. 离子能量和注入角度取自实验(图4(a)), 能量为1 keV, α = 0.1°.
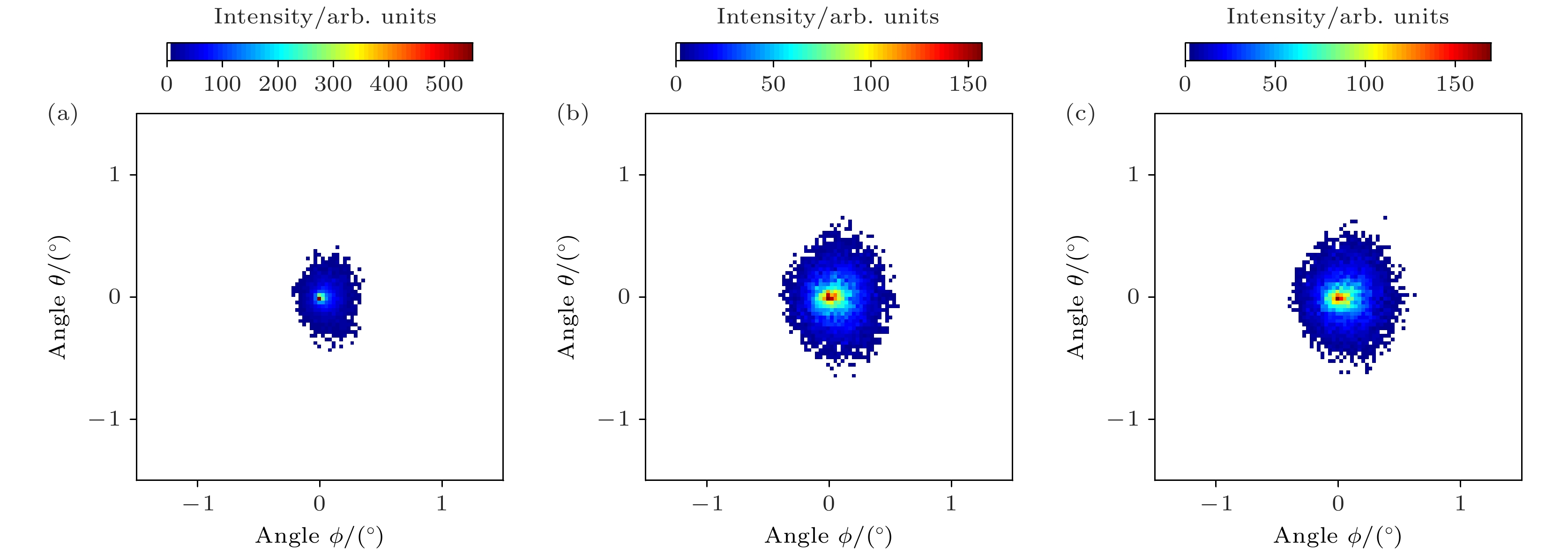
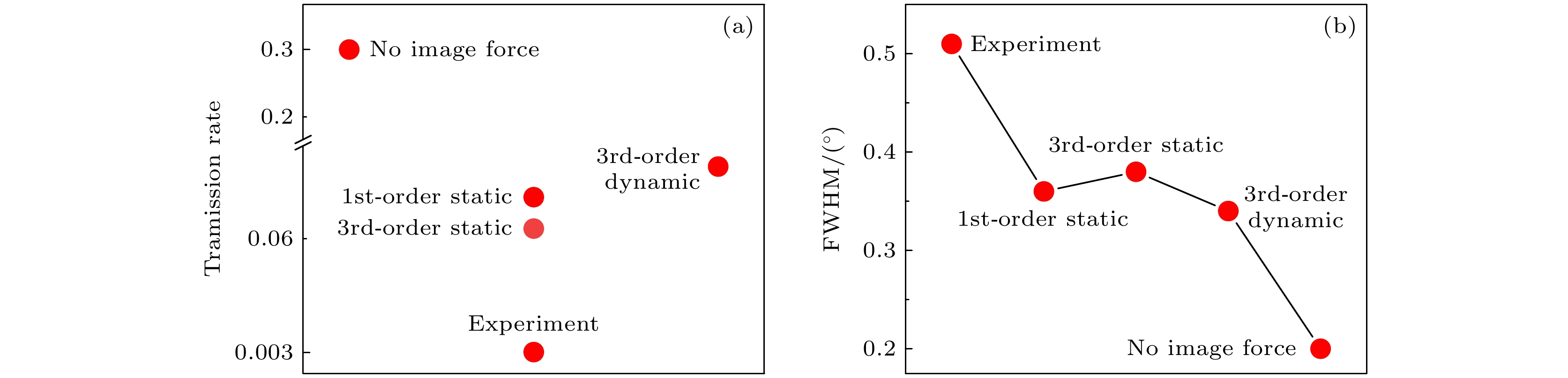
在不考虑镜像电荷力的情况下对实验结果进行了模拟(图8(a)), 对比发现, 考虑镜像电荷力时离子穿透率下降(图9(a)), 且图像半高宽(FWHM)明显变大(图9(b)). 这是因为镜像电荷力会对穿越毛细管中的离子产生横向能量增益, 所以角分布半高宽会变大, 穿透率变小[5]. 对比一阶静态和三阶静态近似结果, 完整考虑三阶镜像力的计算结果图像半高宽更大, 且穿透率更低, 见图9, 这表明采用一阶近似的方法会对镜像电荷力有所低估. 对比三阶动态和三阶静态镜像电荷力模拟结果可以发现, 动态角分布半高宽明显小于静态, 且穿透率也更高, 这是因为运动的离子产生的时变电场降低了云母的极化能力, 从而使产生的镜像电荷力低于静态近似. 相比于高电荷态离子, 低电荷态离子所受镜像电荷力对极化因子Kimage更加敏感, 因此低电荷态离子更适合用来研究离子与材料表面的介电响应机制.
在高电荷态离子(Ne7+)穿越菱形纳米微孔膜的实验中, 二维角分布成像呈现矩形, 研究表明这是镜像电荷力作用的结果[20]. 如图4为
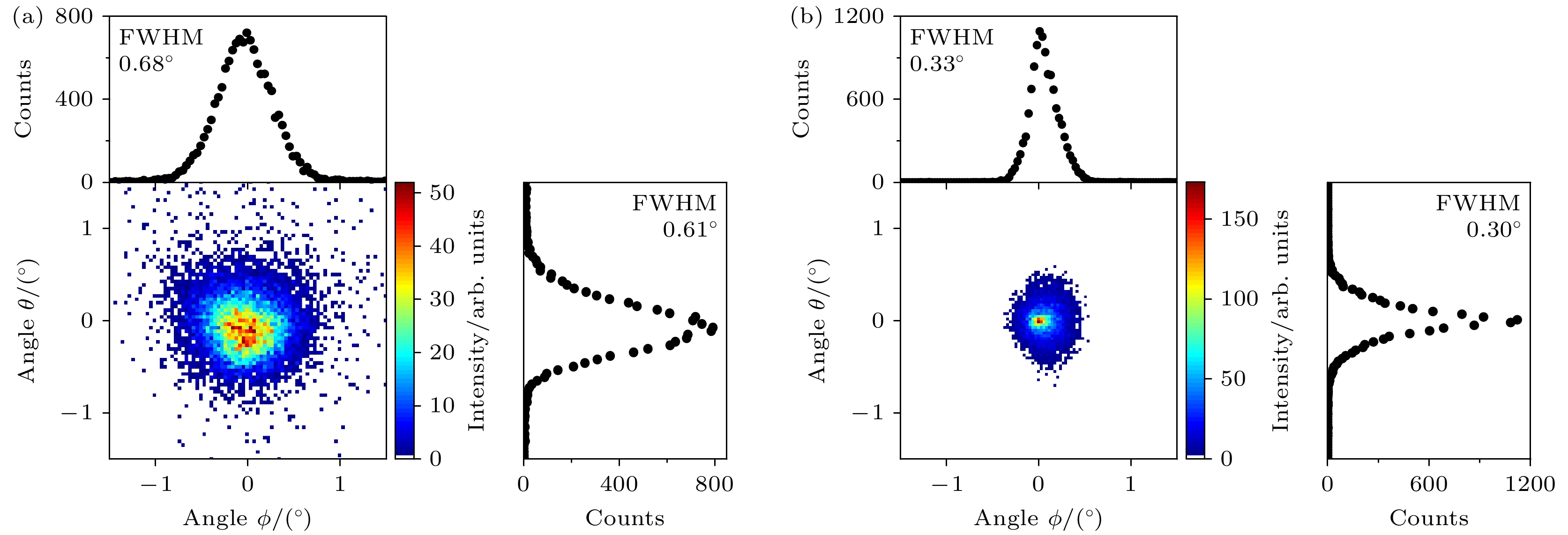
$ {\text{N}}_2^ + $ 离子穿越菱形白云母微孔膜的实验和完整考虑三阶动态镜像力的模拟结果, 二者角分布均未出现矩形成像, 这是因为镜像电荷力与离子电荷态的平方成正比. 相同速度下, 1价离子在穿越微孔的过程中所受的镜像电荷力远小于7价离子所受镜像力. 1 keV的$ {\text{N}}_2^ + $ 在穿越微孔时所受的镜像电荷力可能不足以使出射离子束表现出成型效应.对比实验(图4(a))和模拟结果(图4(b)), 可以看出模拟结果的穿透率(4.4%)和二维角分布半高宽(ϕ方向投影0.33°, θ方向投影0.3°)与实验穿透率(0.3%)和二维角分布半高宽(ϕ方向投影0.68°, θ方向投影0.61°)存在明显差距. 这种差异可能来源于在模型计算过程中对束流角发散度的描述与实验存在差异, 以及实验过程中对微孔膜与束流方向之间的倾角仰角的调节误差有关.
为了探究离子穿透率和出射离子二维角分布受束流发散度以及微孔轴向与束流夹角的影响, 考虑三阶动态镜像电荷力的情况下, 对1 keV
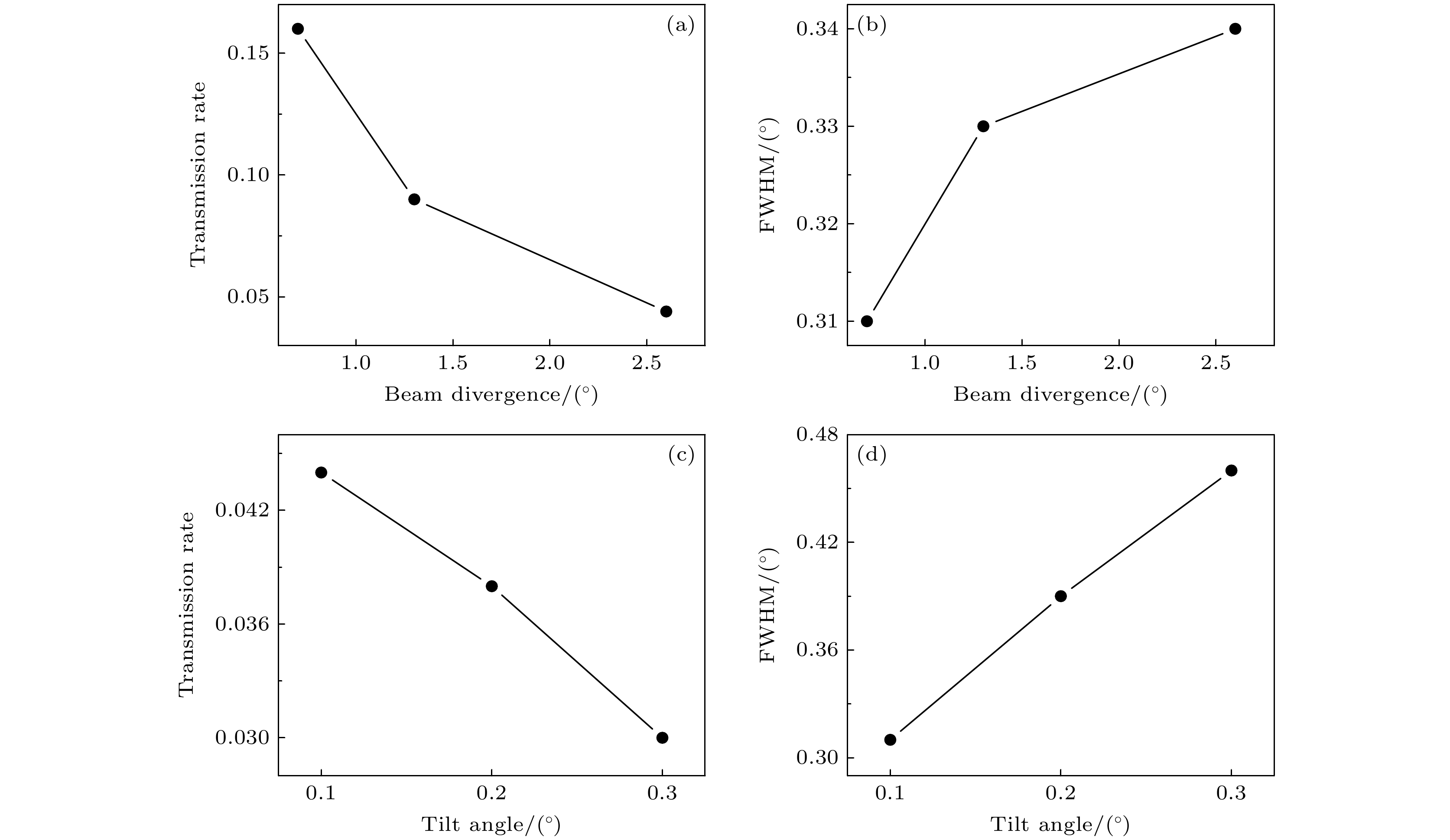
$ {\text{N}}_2^ + $ 不同束流条件进行了模拟计算. 倾角α = 0.1°, 束流发散度分别为0.7°, 1.3°和2.6°的模拟二维角分布如图10(a)、图4(b)和图10(b). 分析图11(a), (b)可得, 随着束流发散度从0.7°增加到3.6°, 离子穿透率下降了73%, 透射离子角分布半高宽增加了10%, 可以看出离子穿透率对束流发散度更敏感. 束流发散度为1.3°, 倾角α = 0.2°和0.3°的模拟二维角分布如图10(c)和图10(d)所示. 比较不同倾角下的离子穿透率和角分布半高宽如图11(c)和图11(d)所示, 倾角由0.1°到0.3°, 离子穿透率下降了32%, 角分布半高宽增加了26%. 通过改变束流发散度和倾角, 离子穿透率最多下降至3%, 角分布半高宽最大为0.46°, 与实验值(穿透率0.3%, 半高宽0.68°)仍存在一定差距. 根据以上模拟结果可以看出, 束流发散度会对离子穿透率产生巨大影响, 且离子束与微孔轴向夹角也会很大程度影响穿透率和透射离子角分布. 但是这些因素导致的模拟结果与实验出射离子角分布的差别还不够, 对于这种纳米尺度上离子诱发的材料表面的介电响应的理论更好的描述也许是最终解决模拟和实验之间的差异的途径. -
本文结合实验与理论模拟, 对离子在白云母微孔膜中的传输过程中所受到的镜像电荷力作用机制进行了系统分析. 在微孔膜完全放电的情况下, 测量了1 keV
$ {\text{N}}_2^ + $ 离子刚开始入射时的出射离子二维角分布及其穿透率. 基于离子在微孔中所受的镜像电荷力的表面介电响应理论, 给出依赖于离子速度和离子与通道壁距离的镜像电荷力表达式, 并对离子在菱形微孔中所受的镜像电荷力进行了三阶修正. 对实验结果进行了模拟计算, 对比是否考虑离子速度对材料表面介电响应的影响. 结果表明考虑离子速度对材料表面介电响应的影响, 会使离子所受的镜像电荷力低于静态近似. 对比了镜像电荷力修正前后的模拟结果, 三阶修正后的镜像电荷力的模拟结果更接近实验结果. 并且与高电荷态穿越菱形微孔膜出现的成型效应不同, 单电荷态离子没有发现出射离子角分布的成型效应, 验证了镜像电荷力强度与离子电荷量的平方成正比, 低电荷态离子所受镜像电荷力不足以产生成型效应. 对比实验和完整考虑镜像电荷力的模拟结果, 模拟结果的穿透率比实验结果高一个数量级, 角分布半高宽约是实验结果的一半. 为了探究束流发散度和微孔轴向与束流夹角对离子穿透率和出射离子二维角分布的影响, 对不同束流条件进行了模拟计算, 结果表明束流发散度和微孔轴向与束流夹角会对模拟结果产生影响, 但这些因素不足以消除模拟结果与实验的偏差. 这表明对于低电荷态离子在微孔结构中的传输特性, 镜像电荷力的作用机制仍需进一步深入探究.
镜像电荷对低能离子在菱形微孔中传输的影响
Influence of image charges on the transport of low-energy ions in rhombic micropores
-
摘要: 本文进行了1 keV $ {\text{N}}_2^ + $离子束穿越完全放电的白云母微孔膜实验, 测量了0°倾角下离子束入射初期的出射离子二维角分布图. 将离子速度对通道壁介电响应的影响引入镜像电荷力表达式, 对离子在菱形通道内所受镜像电荷力进行了多阶修正. 采用不同近似情况下的镜像电荷力对实验进行了模拟计算, 结果表明离子速度对通道壁介电响应的影响会使镜像电荷力降低. 对比对镜像电荷力进行多阶修正前后的模拟结果, 修正后的结果更接近实验值. 模拟计算出的穿透离子图像和实验测得的图像形状基本吻合, 均未出现体现成型效应的矩形. 但在穿透率和半高宽方面存在差距, 实验二维角分布半高宽比计算结果大, 且实验穿透率明显小于计算结果. 我们分析了模拟计算中的几个可能影响, 评估了束流的真实状态以及束流与微孔之间的夹角等因素对模拟和实验之间的差异的影响. 束流发散度和束流与微孔间的夹角会对模拟结果产生较大影响, 但是这些因素导致的模拟结果与实验出射离子角分布的差别还不够. 本工作提供了离子束作为探针进行微孔表面介电响应研究的可能性.Abstract:
The study of low-energy, high-charge-state ions traversing insulating nanochannels has focused on the guiding effects due to the deposition of charge, while experimental and theoretical research on the influence of image charge forces caused by the polarization of the channel walls during ion transmission is relatively scarce. In this work, the experiments on 1-keV $ {\text{N}}_2^ + $ ion beams passing through muscovite microporous membranes are conducted by combining the theoretical method. Under the condition of complete discharge of the microporous membrane, the two-dimensional angular distribution of ejected ions at the initial stage of ion beam incidence at a zero-degree inclination is measured. In previous simulation calculations, first-order image force approximation and static approximation are used to calculate the image charge forces so as to simplify the calculation process. It is found that the results obtained from these calculations are still different from the experimental results. Therefore, we refine the calculation formula for image charge forces by taking into account the full effect of these forces. In previous studies of image charge forces, the influence of ion velocity on the polarization of the channel walls was neglected. The surface dielectric response theory of the image force experienced by ions within the micropores, which depends on ion velocity and the distance between the ion and the channel wall, is used to simulate and compare with the experimental results. The influence of image charge forces caused by surface dielectric response due to ion velocity on the angular distribution of ejected ions is studied. The discrepancies between the simulated and experimental two-dimensional angular distributions are found, showing that the experimental results have a wider half-height width than the simulated results. To explore the effects of beam divergence and the angle between the micropore axis and the beam on ion penetration and the two-dimensional angular distribution of ejected ions, simulation calculations for 1 keV $ {\text{N}}_2^ + $ under different beam conditions are conducted, with the third-order dynamic image charge forces considered. The several potential influences in the simulation calculations are analyzed, and the influences of the true state of the beam and the angle between the beam and the micropore on the difference between simulation and experiment are assessed. This work provides the possibility for studying the surface dielectric response of micropores by using ion beams as probes. -
Key words:
- microporous membrane /
- image force /
- low charge state ion /
- dielectric response .
-

-
图 1 (a)实验装置的示意图. 倾角α代表毛细管轴线与入射束方向之间的夹角. 观察角ϕ是相对于入射束流方向和透射离子的方向的夹角来定义的. (b)通过化学蚀刻得到的云母膜微孔膜中单个微孔的SEM顶视图, 以及微孔的尺寸
Figure 1. (a) Schematic diagram of the experimental setup. The tilt angle α represents the angle between the axis of the capillaries and the direction of the incident beam. The observation angle ϕ is defined with respect to the direction of the incident beam and the transmitted ions as illustrated. (b) SEM top view of an individual pore in a muscovite mica membrane with rhombic capillaries obtained by chemical track etching, along with the dimensions of the capillaries.
图 2 不同倾角下, 1 keV
$ {\text{N}}_2^ + $ 离子穿越白云母微孔膜达到稳态时的实验透射离子二维角分布 (a) α = –0.8°; (b) α = –0.4°; (c) α = 0°; (d) α = 0.4°; (e) α = 0.8°Figure 2. Exprimental two-dimensional angular distributions for 1 keV
$ {\text{N}}_2^ + $ ions transmitted through phlogopite mica capillaries of rhombic cross-section during the steady state of transmission at various tilt angles: (a) α = –0.8°; (b) α = –0.4°; (c) α = 0°; (d) α = 0.4°; (e) α = 0.8°.图 4 (a)束流发散度为1.3°, 靶倾角α = 0.1°, 1 keV
$ {\text{N}}_2^ + $ 离子束刚开始入射时的透射离子角分布实验结果, 角分布上方为其在ϕ方向的投影, 投影半高宽为0.68°; 右边为角分布在θ方向的投影, 投影半高宽为0.61°. (b) 3阶动态镜像电荷力作用下对实验结果模拟计算的透射离子二维角分布, 角分布上方为其在ϕ方向的投影, 投影半高宽为0.33°; 右边为角分布在θ方向的投影, 投影半高宽为0.3°Figure 4. (a) The title angle α = 0.1°, the transmission ion with a beam divergence of 1.3° experimental angular distribution of 1 keV
$ {\text{N}}_2^ + $ ion beam just starting to strike, with the projection on the ϕ direction above the angular distribution, and the full width at half maximum of the projection is 0.68°; on the right is the projection of the angular distribution in the θ direction, with the full width at half maximum of the projection being 0.61°. (b) Simulated two-dimensional angular distribution of transmitted ions under the influence of third-order dynamic image charge force. The projection above the angular distribution is in the ϕ direction, with a full width at half maximum of 0.33°; the projection on the right is in the θ direction, with a full width at half maximum of 0.3°.图 5 在很大频率范围内的任意介质介电谱[35]. 介电函数的实部
$\varepsilon _{\text{r}}'$ (红线)和虚部${\mathrm{i}}\varepsilon _{\text{r}}''$ (黑线), 界面极化、偶极松弛、原子和电子在更高频率下的共振过程在图中标记; 右上角为24—36 THz下云母介电函数实部随电场角频率变化的曲线[38]Figure 5. Arbitrary dielectric permittivity spectrum over a wide range of frequencies[35]. The real
$\varepsilon _{\text{r}}'$ (red line) and imaginary${\mathrm{i}}\varepsilon _{\text{r}}''$ part (black line) of permittivity are shown. Various processes are labeled: Interface polarization, dipolar relaxation, atomic, and electronic resonances at higher frequencies. The upper right corner shows the curve of the real part of the dielectric function of mica as a function of the electric field angular frequency in the 24–36 THz range[38].图 6 (a)离子距离通道壁20, 10, 5 nm, 极化因子随离子速度v的变化曲线. 图中箭头处为1 keV
$ {\text{N}}_2^ + $ 对应的速度; (b) 1 keV$ {\text{N}}_2^ + $ 离子极化因子Kimage随离子与通道壁的距离d变化曲线, 速度趋向于零时的极化因子Figure 6. (a) Polarization coefficient (Kimage) is presented as a function of ion velocity v for three different distances from the channel walls: 20, 10, and 5 nm; (b) the polarization coefficient (Kimage) of 1 keV
$ {\text{N}}_2^ + $ ions in mica as a function of the distance d between the ions and the channel walls, with red line representing the static limit.图 8 束流发散度为1.3°, 1 keV
$ {\text{N}}_2^ + $ 离子穿越白云母微孔膜时在不同镜像电荷力作用下的模拟二维角分布 (a)不考虑镜像电荷力; (b)一阶静态镜像电荷力; (c)三阶静态镜像电荷力Figure 8. Simulated two-dimensional angular distributions of 1 keV
$ {\text{N}}_2^ + $ beam divergence at 1.3° under various image charge force conditions: (a) Without image charge force; (b) with first-order static image charge force; (c) with third-order static image charge force.图 9 (a)倾角α = 0.1°, 束流发散度为1.3°的1 keV
$ {\text{N}}_2^ + $ 离子穿越白云母微孔膜的实验穿透率以及不同镜像电荷力下模拟计算穿透率: 不考虑镜像电荷力、一阶静态镜像电荷力、三阶静态镜像电荷力、三阶动态镜像电荷力. (b)实验二维角分布半高宽以及模拟计算不同情况下的二维角分布半高宽: 不考虑镜像电荷力、一阶静态镜像电荷力、三阶静态镜像电荷力、三阶动态镜像电荷力Figure 9. (a) The experimental transmission rate of 1 keV
$ {\text{N}}_2^ + $ beam divergence at 1.3° and the simulated calculations for different scenarios, including no image charge force, first-order static image charge force, third-order static image charge force, and third-order dynamic image charge force. (b) Experimental two-dimensional angular distribution full width at half maximum (FWHM), as well as the simulated calculations for different conditions including no image charge force, first-order static image charge force, third-order static image charge force, and third-order dynamic image charge force, and the corresponding two-dimensional angular distribution FWHM under these conditions.图 10 模拟计算倾角α = 0.1°, 束流发散度为(a) 0.7°和(b) 2.6°时三阶动态镜像电荷力下1 keV
$ {\text{N}}_2^ + $ 离子穿越白云母微孔膜的出射离子二维角分布; 束流发散度为1.3°, 倾角为(c) 0.2°和(d) 0.3°时三阶动态镜像电荷力下1 keV$ {\text{N}}_2^ + $ 离子穿越白云母微孔膜的出射离子二维角分布Figure 10. Simulated two-dimensional angular distributions of 1 keV
$ {\text{N}}_2^ + $ ions emerging from muscovite microporous membranes under the influence of third-order dynamic image charge force: (a) Beam divergence is 0.7° with an incident angle α of 0.1°; (b) beam divergence is 2.6° with an incident angle α of 0.1°; (c) beam divergence is 1.3° with an incident angle α of 0.2°; (d) beam divergence is 1.3° with an incident angle α of 0.3°.图 11 模拟计算倾角α = 0.1°, 束流发散度为0.7°, 1.3°和2.6°时1 keV
$ {\text{N}}_2^ + $ 离子穿越纳米微孔在三阶动态镜像电荷力作用下的离子穿透率(a)和出射离子二维角分布的半高宽(b); 束流发散度为1.3°, 倾角α = 0.1°, 0.2°及0.3°时的离子穿透率(c)和角分布半高宽(d)Figure 11. Simulated calculations of the ion transmission rate (a) and the full width at half maximum (FWHM) of the two-dimensional angular distribution of emitted ions (b) for 1 keV
$ {\text{N}}_2^ + $ ions passing through nano-pores under the influence of third-order dynamic image charge force at incident angles α of 0.1° and beam divergences of 0.7°, 1.3°, and 2.6°. Ion transmission rate (c) and angular distribution FWHM (d) for beam divergence of 1.3° and incident angles α of 0.1°, 0.2°, and 0.3°. -
[1] Spohr R, Bethge K 1990 Ion Tracks and Microtechnology (Wiesbaden: Vieweg Verlag) p1 [2] Martin C R 1994 Science 266 1961 doi: 10.1126/science.266.5193.1961 [3] Stolterfoht N, Yamazaki Y 2016 Phys. Rep. 629 1 doi: 10.1016/j.physrep.2016.02.008 [4] Stolterfoht N, Bremer J H, Hoffmann V, Hellhammer R, Fink D, Petrov A, Sulik B 2002 Phys. Rev. Lett. 88 133201 doi: 10.1103/PhysRevLett.88.133201 [5] Zhang H Q, Akram N, Skog P, Soroka I L, Trautmann C, Schuch R 2012 Phys. Rev. Lett. 108 193202 doi: 10.1103/PhysRevLett.108.193202 [6] Iwai Y, Ikeda T, Kojima T M, Yamazaki Y, Maeshima K, Imamoto N, Kobayashi T, Nebiki T, Narusawa T, Pokhil G P 2008 Appl Phys. Lett. 92 023509 doi: 10.1063/1.2834695 [7] Lemell C, Burgdörfer J, Aumayr F P 2013 Surf. Sci. 88 237 doi: 10.1016/J.PROGSURF.2013.06.001 [8] Kanai Y, Hoshino M, Kambara T, Ikeda T, Hellhammer R, Stolterfoht N, Yamazaki Y 2009 Phys. Rev. A 79 012711 doi: 10.1103/PhysRevA.79.012711 [9] Stolterfoht N 2013 Phys. Rev. A 87 012902 doi: 10.1103/PhysRevA.87.012902 [10] Stolterfoht N 2013 Phys. Rev. A 87 032901 doi: 10.1103/PhysRevA.87.032901 [11] Stolterfoht N, Hellhammer R, Juhász Z, et al. 2009 Phys. Rev. A 79 042902 doi: 10.1103/PhysRevA.79.042902 [12] Rajendra-Kumar R T, Badel X, Vikor G, Linnros J, Schuch R 2005 Nanotechnology 16 1697 doi: 10.1088/0957-4484/16/9/048 [13] Sahana M B, Skog P, Vikor G, Rajendra-Kumar R T, Schuch R 2006 Phys. Rev. A 73 040901 doi: 10.1103/PhysRevA.73.040901 [14] Skog P, Zhang H Q, Schuch R 2008 Phys. Rev. Lett. 101 223202 doi: 10.1103/PhysRevLett.101.223202 [15] Zhang H Q, Skog P, Schuch R 2010 Phys. Rev. A 82 052901 doi: 10.1103/PhysRevA.82.052901 [16] Mátéfi-Tempfli S, Mátéfi-Tempfli M, Piraux L, et al. 2006 Nanotechnology 17 3915 doi: 10.1088/0957-4484/17/15/050 [17] Krause H F, Vane C R, Meyer F W 2007 Phys. Rev. A 75 042901 doi: 10.1103/PhysRevA.75.042901 [18] Skog P, Soroka I L, Johansson A, Schuch R 2007 Nucl. Instrum. Methods Phys. Res., Sect. B 258 145 doi: 10.1016/j.nimb.2006.12.127 [19] Juhász Z, Sulik B, Biri S, et al. 2009 Nucl. Instrum. Methods Phys. Res., Sect. B 267 321 doi: 10.1016/j.nimb.2008.10.017 [20] Li D, Wang Y, Zhao Y, Xiao G, Zhao D, Xu Z, Li F 2009 Nucl. Instrum. Methods Phys. Res., Sect. B 267 469 doi: 10.1016/j.nimb.2008.11.041 [21] Stolterfoht N, Hellhammer R, Sulik B, et al. 2011 Phys. Rev. A 83 062901 doi: 10.1103/PhysRevA.83.062901 [22] Schiessl K, Palfinger W, Tökési K, Nowotny H, Lemell C, Burgdörfer J 2005 Phys. Rev. A 72 062902 doi: 10.1103/PhysRevA.72.062902 [23] Schiessl K, Palfinger W, Tökési K, Nowotny H, Lemell C, Burgdörfer J 2007 Nucl. Instrum. Methods Phys. Res. , Sect. B 258 150 doi: 10.1016/j.nimb.2006.12.135 [24] 李鹏飞, 袁华, 程紫东, 钱立冰, 刘中林, 靳博, 哈帅, 张浩文, 万城亮, 崔莹, 马越, 杨治虎, 路迪, Reinhold Schuch, 黎明, 张红强, 陈熙萌 2022 物理学报 71 084104 doi: 10.7498/aps.71.20212335 Li P F, Yuan H, Cheng Z D, Qian L B, Liu Z L, Jin B, Ha S, Zhang H W, Wan C L, Cui Y, Ma Y, Yang Z H, Lu D, Schuch R, Li M, Zhang H Q, Chen X M 2022 Acta Phys. Sin. 71 084104 doi: 10.7498/aps.71.20212335 [25] 李鹏飞, 袁华, 程紫东, 钱立冰, 刘中林, 靳博, 哈帅, 万城亮, 崔莹, 马越, 杨治虎, 路迪, Reinhold Schuch, 黎明, 张红强, 陈熙萌 2022 物理学报 71 074101 doi: 10.7498/aps.71.20212036 Li P F, Yuan H, Cheng Z D, Qian L B, Liu Z L, Jin B, Ha S, Wan C L, Cui Y, Ma Y, Yang Z H, Lu D, Schuch R, Li M, Zhang H Q, Chen X M 2022 Acta Phys. Sin. 71 074101 doi: 10.7498/aps.71.20212036 [26] 万城亮, 潘俞舟, 朱丽萍, 李鹏飞, 张浩文, 赵卓彦, 袁华, 樊栩宏, 孙文胜, 杜战辉, 陈乾, 崔莹, 廖天发, 魏晓慧, 王天琦, 陈熙萌, 李公平, Reinhold Schuch, 张红强 2024 物理学报 73 104101 doi: 10.7498/aps.73.20240301 Wan C L, Pan Y Z, ZHU L P, Zhang H W, Zhao Z Y, Yuan H, Liu P F, Fan X H, Sun W S, DU Z H, Chen Q, Cui Y, Liao T F, Wei X H, Wang T Q, Chen X M, Li G P, Schuch R, Zhang H Q 2024 Acta Phys. Sin. 73 104101 doi: 10.7498/aps.73.20240301 [27] Pokhil G P, Vokhmyanina K A 2008 J. Surf. Invest. 2 p237 doi: 10.1134/S1027451008020146 [28] Zhang H Q, Akram N, Soroka I L, Trautmann C, Schuch R 2012 Phys. Rev. A 86 022901 doi: 10.1103/PhysRevA.86.022901 [29] Zhang H Q, Akram N, Schuch R 2016 Phys. Rev. A 94 032704 doi: 10.1103/PhysRevA.94.032704 [30] Harris J, Jones R O 1974 J. Phys. C: Solid State Phys. 7 3751 doi: 10.1088/0022-3719/7/20/012 [31] Wiza J L 1979 Nucl. Instrum. Methods. 162 587 doi: 10.1016/0029-554X(79)90734-1 [32] Lampton M, Carlson C W 1979 Rev. Sci. Instrum. 50 1093 doi: 10.1063/1.1135990 [33] FASTER http://faster.in2p3.fr/ [34] Ackermann J, Angert N, Neumann R, Trautmann C, Dischner M, Hagen T, Sedlacek M 1996 Nucl. Instrum. Methods Phys. Res. , Sect. B 107 181 doi: 10.1016/0168-583X(95)01037-8 [35] Ward A A 2016 ResearchGate 2 10 doi: 10.13140/RG.2.1.3481.5600 [36] Giglio E 2023 Phys. Rev. A. 107 012816 doi: 10.1103/PhysRevA.107.012816 [37] Petzelt J, Rychetský I 2005 Dielectric function, Encyclopedia of Condensed Matter Physics (Amsterdam: Elsevier) p426 [38] Beran A 2002 Rev. Mineral. Geochem. 46 351 doi: 10.2138/rmg.2002.46.07 [39] Fali A, Gamage S, Howard M, et al. 2021 ACS Photonics 8 175 doi: 10.1021/acsphotonics.0c00951 [40] Agostinelli S, Allison J R, Amako K, et al. 2003 Nucl. Instrum. Methods Phys. Res., Sect. A 506 250 doi: 10.1016/S0168-9002(03)01368-8 [41] Zhang Q, Liu Z L, Li P F, et al. 2018 Phys. Rev. A 97 042704 doi: 10.1103/PhysRevA.97.042704 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: