-
声的传输与局域调控能有效应对声信息处理的需求, 引起了广泛关注. 其中, 声场局域通过控制波的传播范围, 将声能束缚在特定区域, 使得声波在特定空间区域内能量或振幅显著增强. 在波动系统中, 波局域的实现涵盖几种典型的机制. 在周期结构中, 由于带隙频率位于延展态连续谱范围之外, 声波在带隙频率内激发会形成束缚态局域声场. 常规的缺陷类局域态是指在周期性结构中引入缺陷后, 由缺陷诱导的本征态出现在晶体带隙范围内, 其能量局域于晶格缺陷附近[1,2]. 不同于传统束缚态, 另外一种连续体束缚态在能谱上位于辐射连续谱内部, 可以和延展态共存, 但仍保持完美局域化. 例如, 人们在波导结构[3,4]和晶格阵列中[5]均构造出受对称性保护的连续体束缚态, 实现了高度局域化波场. 此外, 平带局域态, 由于零群速度特征, 在偏离平带本征频率时能够紧凑局域于特定激发位置, 实现精准的声/光场调控. 该类局域态依赖于特定激发条件和晶格耦合系数, 在准一维菱形晶格[6]、二维Lieb晶格[7,8]和三维简立方晶格[9]中均已被构造出来. 上述局域态的构造通常依赖于特定的能谱特征, 如带隙、平带或连续谱中的束缚态. 与此不同, 在无序介质中, 强无序引起持续散射, 多重散射波之间相消叠加, 可导致安德森局域化[10,11]. 例如, 相关学者通过研究超声波在无序介质中的传播特性, 发现当无序强度达到一定阈值时, 超声波的传播被显著抑制, 从而证实了安德森局域化[11].
最近学者们将研究兴趣转向了局域态与拓扑物理结合, 丰富了经典波的调控方案. 安德森局域化[12–14]和连续体束缚态[15–17]已在不同的声拓扑结构中证实. 值得一提的是, 声学高阶拓扑绝缘体具有拓扑非平庸的体带隙, 其中会存在不同维度的高阶拓扑态, 这些拓扑态局域在晶格的特定边界或角落区域[18–20]. 通常, 体极化类型高阶拓扑局域态与晶格对称性有很大关系, 因为晶格对称性可约束高阶角态出现在特定位置[21]. 此外, 基于两种不同的声学拓扑相, 研究者在拓扑界面处构造了多种类型的声学局域态[22], 包括声学平带局域态、拓扑界面态以及缺陷态. 其中, 缺陷态和平带束缚态的局域特性对局部参数的变化较为敏感. 因此, 对比拓扑界面处构造的局域态, 能否利用同一种声拓扑材料实现不同类型且不受激发位置限制的宽带声场局域, 是一个非常值得研究的问题.
得益于结构参数宏观易调, 人们通过引入负耦合在声学系统构造了等效
$ {Z_2} $ 规范场[23–30]. 这种规范场可以调控波函数在不同路径上的相位, 影响波的传播行为, 类似于Aharonov-Bohm (AB)效应[24]. 在规范场作用下, 时空反演对称性可以被投影表示[24,25,27], 从而在声学系统产生新的拓扑能带物理, 包括声学莫比乌斯绝缘体[25,29]、克莱因瓶绝缘体[28]及镜像陈类绝缘体[26]等. 在光学系统中, 相关学者基于间接耦合的微环谐振腔阵列引入等效规范场, 构造了光子Aharonov-Bohm (AB)笼晶格[31], 利用其平带特性在平带本征频率实现了硅基片上的光子局域. 通过上述研究可以发现, 等效规范场能够有效地调控声学能带结构, 这为在拓扑材料中实现声场局域提供了新的研究途径.本文通过在声学谐振腔阵列中构造等效规范场, 利用等效规范场设计多个声学平带, 实现宽带声波局域化操控. 具体而言, 通过在由声学耦合腔组成的菱形单元中同时引入正负实耦合来构造
$ \pi $ 通量, 设计等效规范场, 模拟类似于电磁场中磁矢势的效果. 这种设计能够改变声波在不同路径上的几何相位, 从而形成声学AB囚禁效应. 通过计算不同规范通量的晶格能带发现, 引入$ \pi $ 通量会使所有色散能带坍塌为无色散的平带. 基于不同声学平带的本征态激发, 可以调制出声学平带局域态. 进一步, 对比不同通量的声学菱形晶格, 探究等效规范场对声场局域的影响. 研究发现, 在引入$ \pi $ 通量后, 准一维菱形晶格体内和边界可分别获得局域态和拓扑边界局域态. 为揭示其结构依赖性, 在声学AB笼晶格中设置对称型和非对称型微扰, 发现AB囚禁效应诱导的局域态对称型微扰具有拓扑免疫性, 表明局域模式主要依赖于$ \pi $ 通量等效规范场的拓扑特征. 相比于以往的局域态研究, 本文基于等效规范场构造了具有多平带特征的声学拓扑结构. 研究发现, 在偏离平带频率时, 可激发声学平带局域态以及由AB囚禁效应诱导的局域态, 实现了宽带且不受激发位置限制的声学局域态. -
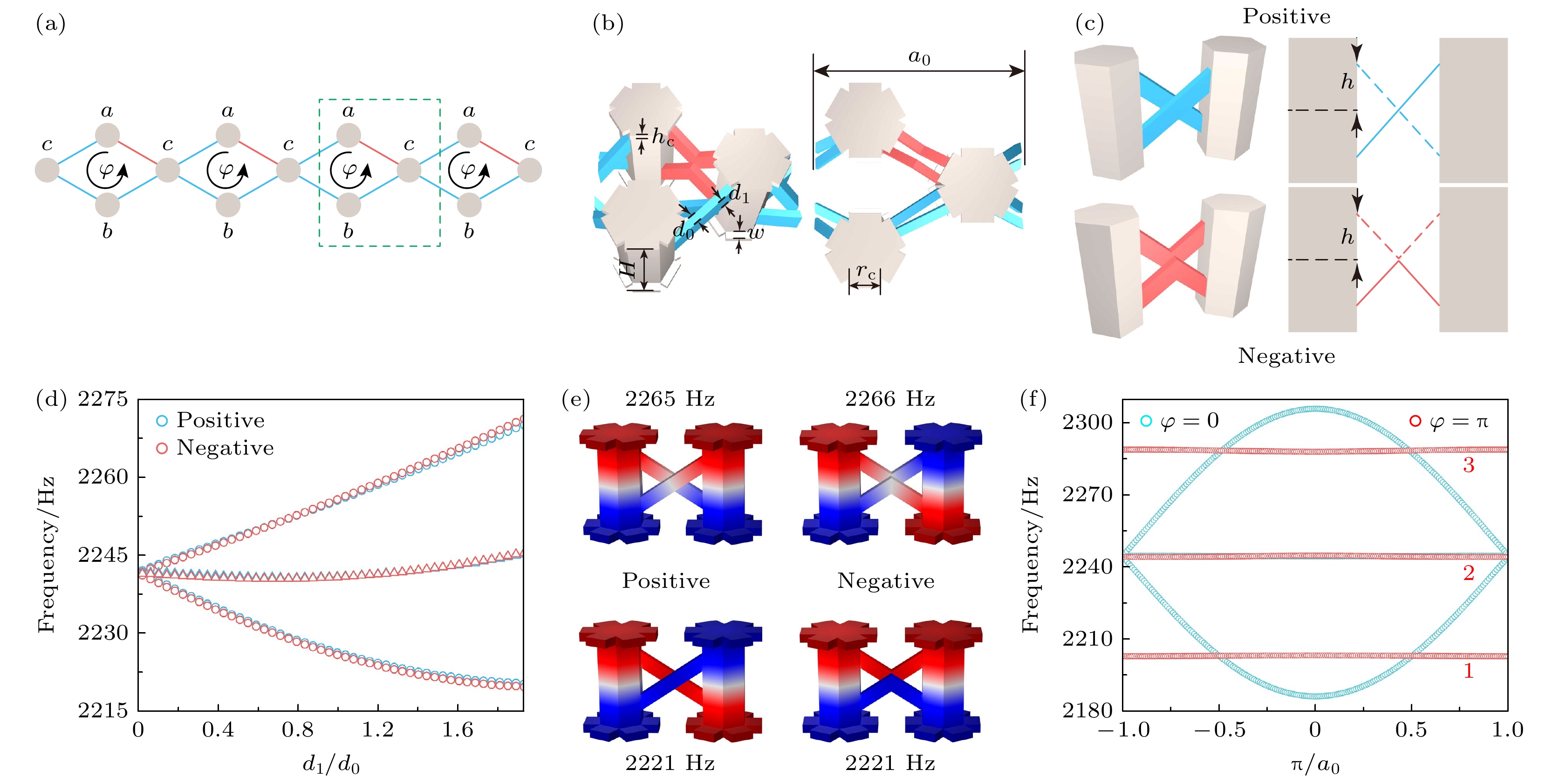
考虑图1(a)中的菱形晶格紧束缚模型, 每个原胞包含a, b, c 三个格点. 同时, 每个菱形单元含有三个正耦合(浅蓝色线)和一个负耦合(红色线), 其耦合强度为t和–t, 这种设计相当于在每个菱形环路中形成一个通量为
$ \varphi = \pi $ 的等效规范场, 该规范场可以模拟电磁场中磁矢势的效果. 对具有$ \varphi = \pi $ 通量的菱形晶格, 我们将其称为AB笼. 该晶格在动量空间的哈密顿量为其中
$ {\boldsymbol{k}} = \left( {{k_x}, 0} \right) $ 为布洛赫动量;$ t $ 代表耦合强度. 通过矩阵对角化, 求解得到三个本征值, 即$ - 2 t $ , 0,$ 2 t $ . 这些本征值与动量$ {\boldsymbol{k}} $ 无关, 表明引入通量$ \pi $ 会产生三个无色散平带. 对应不同本征值的本征矢分别为这些平带的产生源于波的干涉相消, 即波沿不同路径传播时积累的几何相位差异导致波的干涉相消. 这种干涉相消使得原本色散的能带变得平坦, 从而形成平带态. 值得关注的是, 上述哈密顿量((1)式)为块状对角矩阵, 具备手征对称性特征, 其性质类似平方根拓扑晶格[32–34], 因此会得到关于零本征值上下对称的能谱. 另一方面, 对于AB笼晶格拓扑性质, 可以通过Zak相位来表征[31]. 基于哈密顿量本征矢, 可得
其中三条平带的拓扑不变量分别为
$ - {\pi {/ } 2} $ ,$ - \pi $ ,$ {{ - \pi } {/ } 2} $ , 即上下体能带对应半整数体拓扑指数. 因此, 该类晶格具有上下两个拓扑非平庸的体带隙, 可以预测在有限晶格的带隙内存在拓扑边界态.相应的声学原胞模型如图1(b)所示, 原胞晶格常数为
$ {a_0} $ = 103.9 mm. 三个声学谐振腔(灰色部分)高度为$ H $ = 60 mm, 其上下部位附加的瓣状小立方体宽度、深度和高度尺寸分别为$ {r_{\text{c}}} $ = 13.8 mm,$ w $ = 10 mm和$ {h_{\text{c}}} $ = 5 mm. 如图1(c)所示, 耦合腔间的交叉连接(浅蓝色管)对应声学正耦合, V字形(红色管)连接对应声学负耦合. 两两连接的耦合腔体组合成菱形环路, 并在环路结构中同时引入正负耦合, 这种设计确保了每个声学菱形环路中具有等效的$ \pi $ 通量规范场. 从物理角度讲, 正耦合表示声波在传播过程中相位不变, 而负耦合则导致相位发生$ \pi $ 的反转, 因此正负耦合交替排列会导致波在回路单元中存在相位积累, 等效为引入了规范场. 此外, 在设计的通量结构中, 声波沿不同路径会积累不同的几何相位, 类似AB效应, 从而影响声波的行为. 与通量结构不同, 当每个菱形回路中的声腔耦合均为正耦合时, 等效规范场将消失, 相应结构称为0通量声学结构.对于负耦合, 采用V字形连接替代传统的水平连接方式, 可确保其与交叉连接结构(正耦合)具有相同的耦合强度. 耦合强度取决于连接杆的尺寸(
$ {d_0} $ 和$ {d_1} $ )和连接在腔体上的位置($ h $ ), 具体参数为$ {d_0} $ = 5 mm,$ {d_1} $ = 8 mm,$ h $ = 12 mm. 对于较大截面积的耦合管($ {d_0} $ 及$ {d_1} $ 决定), 由于其存在有限尺寸效应, 两腔之间的耦合会出现中心频率偏移, 而谐振腔两端附加的瓣状立方体可微调腔体等效高度, 使得在引入较大耦合强度的同时减小了声学一阶模式的中心频率移动[23].图1(d)给出了在耦合管参数
$ {d_1} $ 改变时两腔耦合的频率演化, 包括两个劈裂的本征频率$ {f_1} $ ,$ {f_2} $ (如圆形所示)和一个中心频率$ {f_0} $ (如上三角形所示). 浅蓝色曲线和红色曲线分别对应于耦合腔交叉连接和V形连接时的频率演化. 对于这两种情况, 不同参数时声学耦合强度为$ {{\left| {{f_2} - {f_1}} \right|} {/ } 2} $ , 而中心频率为$ {f_0} = {{\left( {{f_1} + {f_2}} \right)} {/ } 2} $ . 本文选取$ {{{d_1}} {/ } {{d_0}}} $ =1.6, 如图1(d)中黑色虚线所示. 相比声学单腔体, 该参数下两腔耦合的中心频率仅偏离了2 Hz. 通过分析两个劈裂频率的本征模式分布, 可以判定声学耦合符号的正负, 如图1(e)所示. 声腔在z方向驻波模式模拟原子轨道$ {P_z} $ 模式. 对于交叉连接的耦合, 同相(偶对称)耦合模比反相(奇对称)耦合模频率高, 对应声学正耦合[23]. 对于V字形连接的耦合, 同相耦合模转移到较低频率, 这表明实现了声学负耦合. 进一步, 利用COMSOL有限元软件的压力声学模块, 分别计算有通量结构和无通量结构体能带. 其中, 原胞$ x $ 方向采用Floquet周期性边界条件, 波矢扫描路径沿着$ {k_x} $ 方向的第一布里渊区. 对比两种参数的原胞色散能带, 如图1(f)所示, 发现无通量结构($ \varphi = 0 $ )含有两个色散能带和一个声学平带. 相比之下, 引入$ \pi $ 通量后, 由于波的相消干涉, 体带退化为三个色散极小的能带(频率范围约为1 Hz), 可称为声学平带, 其对应的中心频率分别为2203, 2244.5和2288.6 Hz. 值得一提的是, 上述中心频率$ {f_0} $ 的调节确保了声学原胞色散的第二条平带大致位于第一条和第三条平带之间的中间频率位置, 从而与紧束缚模型的结果相对应. 这些平带为构造丰富的声学局域态提供了契机. -
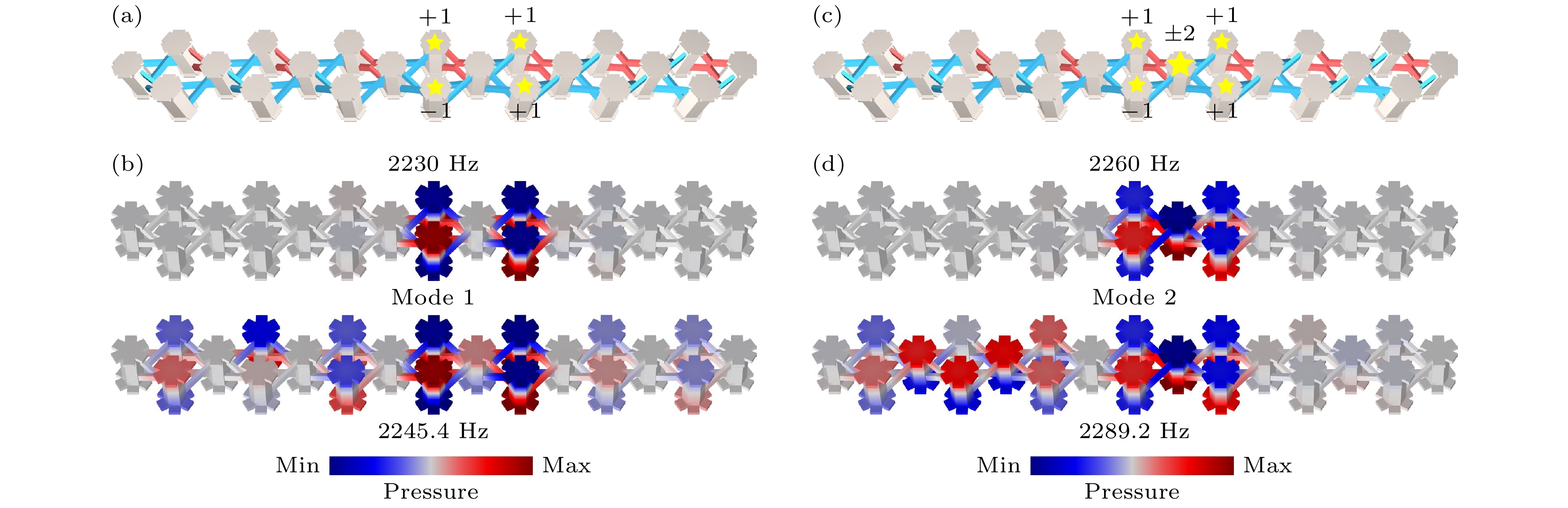
基于等效规范场引入的全平带, 首先探究声学平带本征态. 这类平带态是由于平带的零群速度和干涉相消效应导致, 表现为紧凑局域态. 平带态的产生依赖于激发条件, 具有频率无关性. 当激发条件符合平带本征矢特征[35,36]时, 会激发相关声学平带本征态. 利用七个平带色散特征的菱形环路单元, 构建准一维的声学有限晶格, 如图2(a)所示, 其中每个菱形环路具有
$ \pi $ 通量的等效规范场. 基于晶格格点间耦合强度关系, 设置对应第二条平带本征态的声源激发条件, 如图2(a)所示, 其中黄色星形标记声源位置, 数字正负表示声压的相位差为$ \pi $ . 图2(b)展示了不同激发频率下的平带本征态. 在数值模拟中, 通过COMSOL压力声学模块, 在腔体表面设置入射平面波为声源, 并在频域内求解声场的空间分布. 研究发现, 当激发频率2230 Hz偏离平带本征频率时, 由于平带群速度为零, 会形成平带局域态(模式M1), 声能仅分布在四个激发腔体内. 然而, 当激发频率靠近或处于平带本征频率时, 由于平带本征模式的简并特性, 会出现平带态之间的能量共振. 在此条件下, 平带态会扩展到整个晶格中, 形成一个扩展态[9].接下来, 改变声源激发条件, 如图2(c)所示, 使之与第一和第三条平带的本征矢相匹配, 激发对应的平带本征态. 此时, 激发源分布在五个腔, 其中1, 2数字大小表示对应位置声压幅值分别设置为1 Pa和2 Pa. 同样, 根据图2(d)可以看出, 当激发频率为2260 Hz (偏离平带本征频率)时, 出现平带局域态, 声波按照特定相位和幅值关系分布在5个激发腔内(模式M2). 然而, 当激发频率为2289.2 Hz (靠近平带本征频率)时, 同样由于简并平带态之间能量共振, 声场分布转变为平带扩展态. 因此, 平带本征态的分布取决于声源激发频率, 根据不同的激发频率, 可以实现平带态的局域调控.
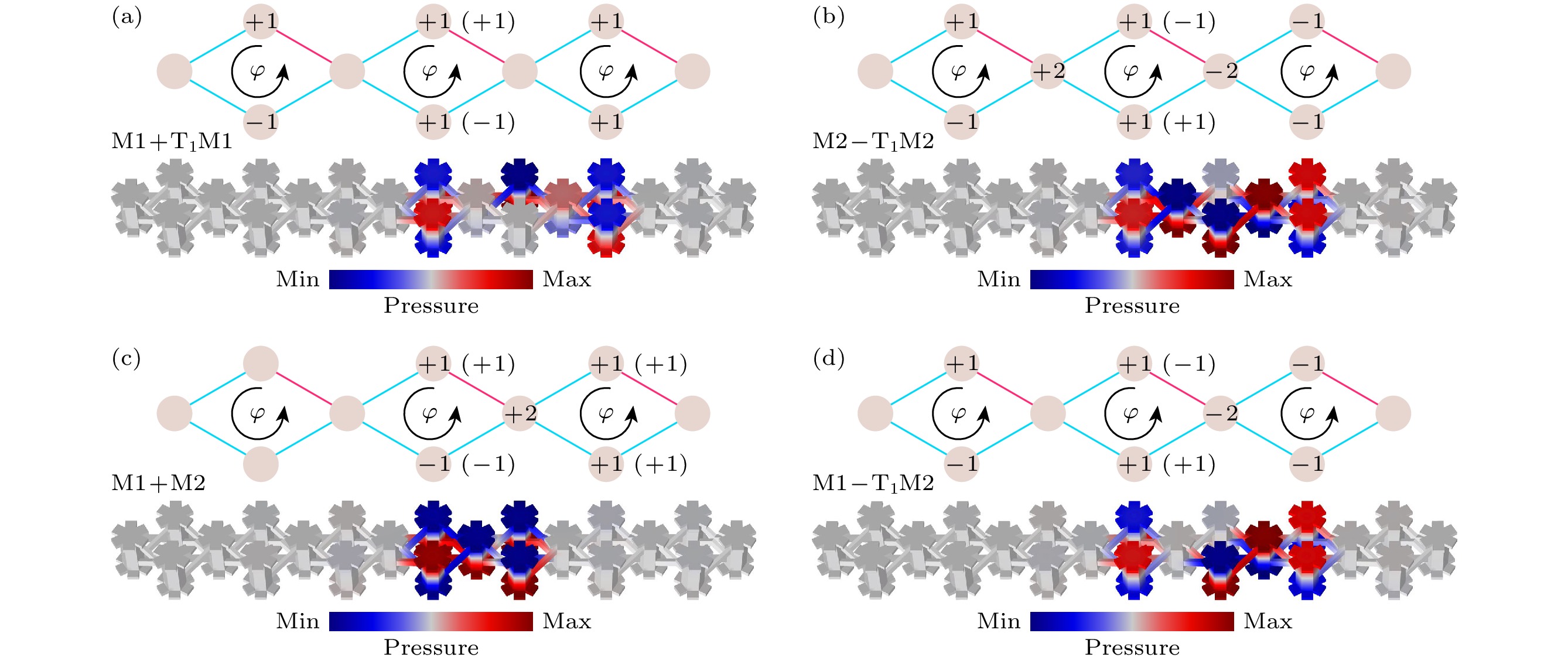
进一步, 利用上述平带局域态, 构造其线性叠加态. 如图3(a)所示, 通过将模式M1或M2向右平移一个晶胞, 并与其他局域模式叠加, 设计复合的平带局域态. 从图3(a)可以发现, 叠加态的声压分布特征(包括幅值与相位)与激发条件一致, 声波能量局域在指定位置. 同样地, 基于模式M2, 在图3(b)构造了不同的叠加态M2-T1M2, 发现声波紧凑局域在7个谐振腔内. 此外, 基于系统的多平带特征, 将M1和M2模式叠加, 设计了两种不同分布的叠加态, 如图3(c)和图3(d)所示. 在偏离平带本征频率时(2260 Hz), 声波同样能够按照一定的相位和幅值关系局域在特定区域, 从而实现了更为丰富的平带局域态.
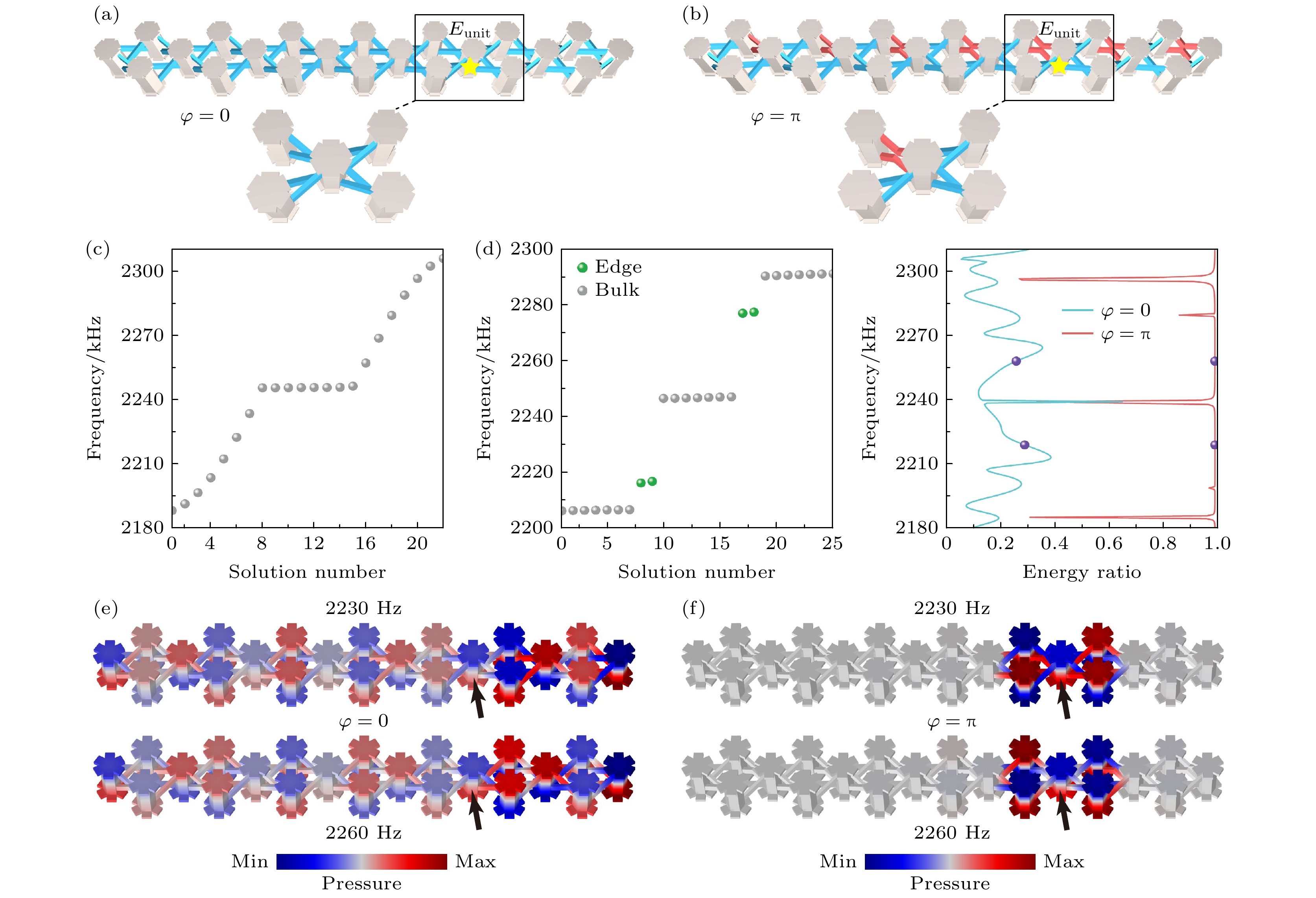
进一步, 利用有无等效规范场的两种有限菱形结构, 探究等效规范场对声场分布的影响. 图4(a)为普通无规范通量结构, 而图4(b)为每个环路引入
$ \pi $ 通量的拓扑结构. 对比两种有限结构对应的本征模式分布, 如图4(c)和图4(d)所示, 可以看出等效规范场的存在使得AB笼拓扑结构打开了带隙, 且两个带隙内均存在拓扑边界态, 其所在频率约为2216 Hz和2277 Hz. 为直观比较两种结构中声场分布, 引入能量比率$ {{{E_{{\text{unit}}}}} {/ } {{E_{{\text{sys}}}}}} $ , 其中$ {E_{{\text{unit}}}} $ 表示声场局域区域(图4(b)中黑框所示)的能量,$ {E_{{\text{sys}}}} $ 表示系统总能量. 通过能量比率分布曲线(见图4(d)右侧)可以发现, 除了边界态频率处由于边界腔能量共振会存在少许能量下降,$ \varphi = \pi $ 的拓扑结构在带隙范围内$ {E_{{\text{unit}}}} $ 值与$ {E_{{\text{sys}}}} $ 值接近, 即能量比率约为1, 表明声能具有强局域性, 在局域单元外的能量完全可以忽略. 与之相比, 在普通有限菱形晶格中, 结构单元(图4(a)中黑框所示)内的能量占比很低, 表明声波在$ \varphi = 0 $ 系统中为扩展态. 如图4(e)所示, 在$ \varphi = 0 $ 有限晶格中, 声场扩展到整个晶体, 对应为扩展态的场分布; 而在$ \varphi = \pi $ 声学AB笼晶格中, 在同样的激发频率下(2230和2260 Hz), 声场表现出较强的局域性(见图4(f)). 具体而言, 声压集中分布在激发腔体周围, 涵盖五个腔体. 因此, 当每个菱形回路引入$ \pi $ 通量后, 在整个带隙范围内能够有效地调控体内声场的局域化.同样, 将声源移动至有限结构边界位置, 激发边界局域态. 如图5(a)和图5(b)所示, 在通量
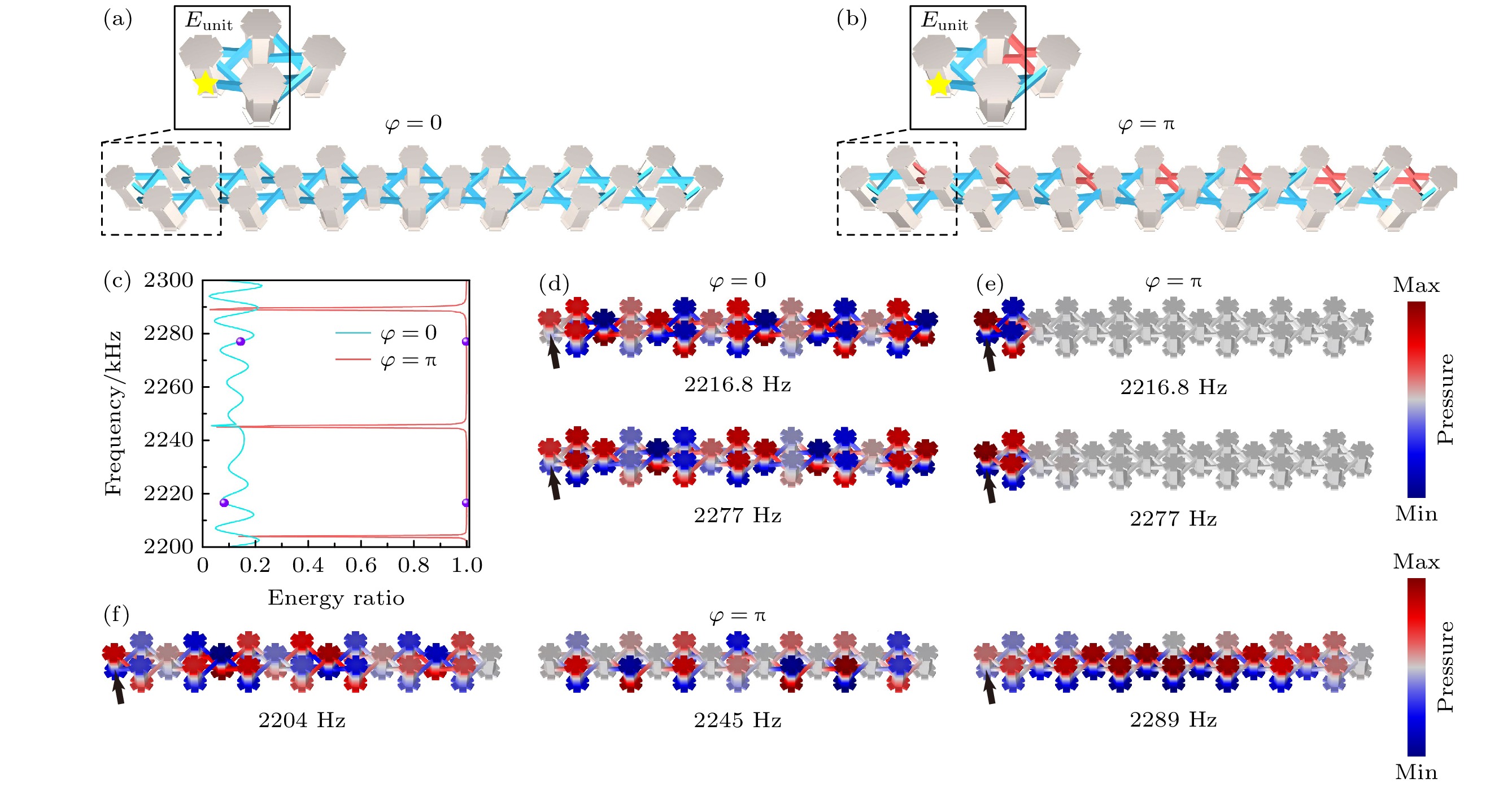
$ \varphi = 0 $ 和$ \varphi = \pi $ 两种有限晶格中, 黄色星形指示声源所 在位置, 黑框表示参照的局域单元. 类似于体激 发, 可以得到在边界激发情形下的能量比率曲线, 如图5(c)所示, 对于声学AB笼拓扑结构, 不同带隙范围内$ {E_{{\text{unit}}}} $ 能量几乎等于整个系统的能量$ {E_{{\text{sys}}}} $ , 如红色实线所示, 表明声波局域在$ {E_{{\text{unit}}}} $ 单元. 进一步, 在两个带隙内, 分别选取边界态的频率(2216.8 Hz和2277 Hz)作为激发频率(见图5(c)中紫色圆球标记), 并比较不同结构中的声场分布. 如图5(d)所示, 对于无平带色散的平庸晶格, 在不同激发频率, 声波均分布在整个晶体, 对应为扩展态分布. 当引入等效规范场后, 在同样边界态频率激发, 发现拓扑边界态声场局域在接近激发源的三个谐振腔内. 利用带隙内的其他频率激发, 会出现同样局域特征的声场分布. 因此, 基于菱形环路中引入的等效规范场, 在拓扑晶格不同体带隙范围均可实现边界声场局域, 其中拓扑边界态频率激发时形成拓扑边界局域态.对于
$ \varphi = \pi $ 通量的拓扑结构, 当激发频率处于三个平带频率时, 声波同样扩展到整个晶体, 体现出与声学平带扩展态类似的现象. 考虑上述体激发和边界激发的结果, 可知在声学AB笼晶格不同位置激发均可实现声场局域. 该类局域源于等效规范场诱导的平带色散. 得益于AB囚禁效应, 声波将被束缚在激发腔周围[6].最后, 在声学AB笼菱形晶格中引入结构微扰, 验证拓扑结构中局域态的鲁棒性. 在晶格的三排声学腔体中引入微扰, 构造结构缺陷. 该微扰由半径
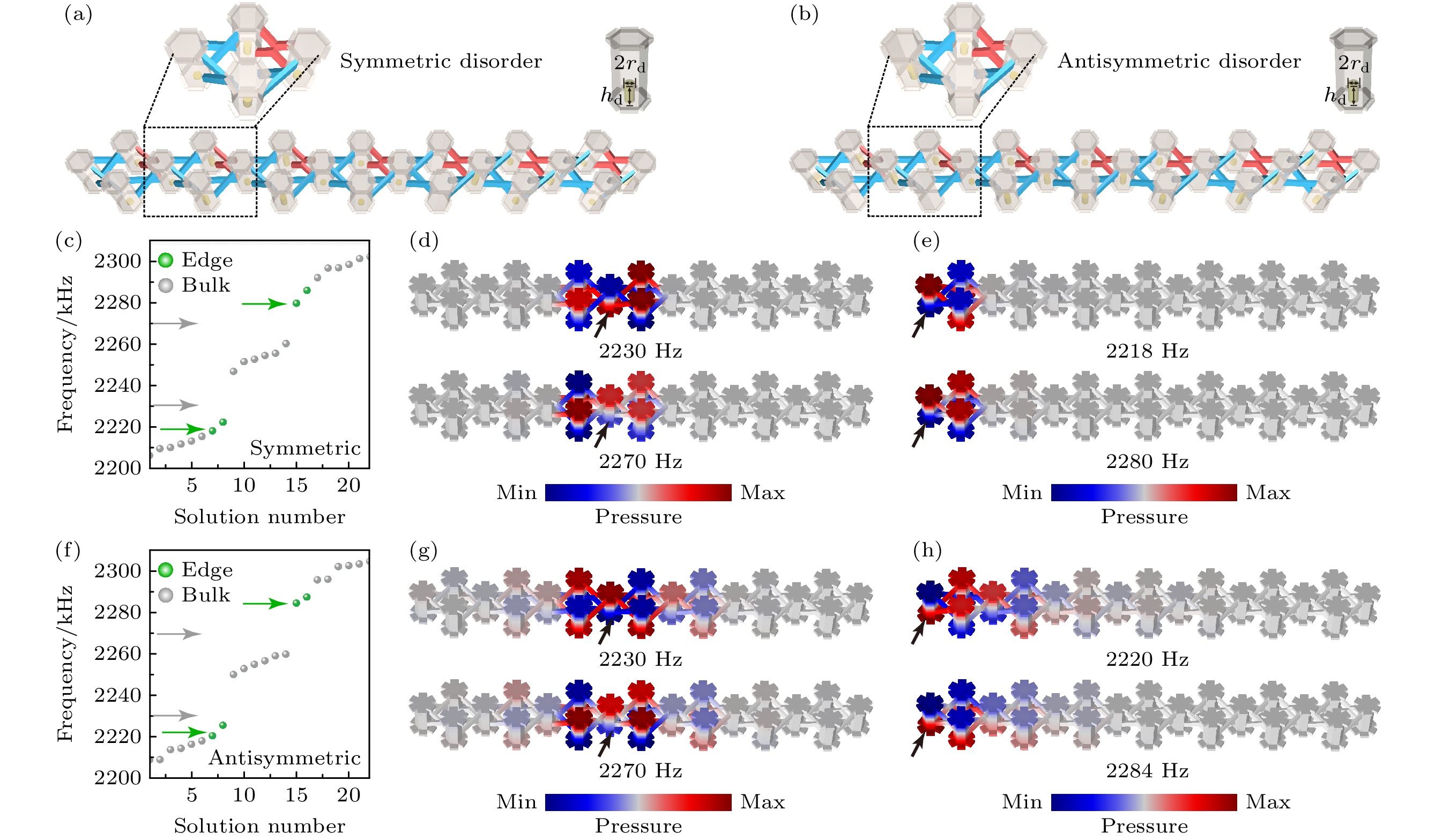
$ {r_{\text{d}}} $ = 5 mm、高度$ {h_{\text{d}}} \in $ 0—6 mm随机高度的圆柱组成, 其中随机参数由COMSOL Multiphysics连接Matlab软件生成. 具体来讲, 通过在外侧两排相对位置腔体内放入微扰高度相同和不同的小圆柱, 可分别构造对称和反对称两种类型的微扰, 如图6(a)和图6(b)中放大框所示. 这些随机高度小圆柱放置在空腔底部, 如图6(a), (b)右侧空腔内深绿色圆柱所示, 可以导致声学模式中心频率转移. 图6(c)展示了对称微扰结构(图6(a))的本征谱图, 可以看出体模式和边界模式均发生了频率扰动, 边界模式处于体带隙内. 基于本征谱分布, 分别选取两个带隙内频率(2230 Hz和2270 Hz)和两个边界态频率(2218 Hz和2280 Hz), 并分别用两种频率在晶格体位置和边界位置激发. 如图6(d)和图6(e)所示, 声场在对应频率分别局域在体内5个腔体和边界3个腔体, 没有多余的扩散, 表明对称微扰不会破坏声场局域性. 类似地, 图6(f)展示了反对称微扰(见图6(b))后晶格的本征谱图. 相比无微扰情况, 体和边界模式均存在频率扰动, 即原来简并的本征模式频率变得分散. 通过分析两个带隙内频率(2230 Hz和2270 Hz)和两个边界态频率(2220 Hz和2284 Hz)的场分布, 如图6(g)和图6(h)所示, 发现在对应频率下激发的声场在体和边界位置均出现了一定程度的能量扩散, 即使体激发频率位于带隙内, 这表明反对称微扰会破坏声场的局域特征. 这是由于反对称微扰改变了激发腔附近上下路径的几何构型, 使得每个菱形环路无法维持$ \pi $ 通量的等效规范场, 从而导致声场从局域态转变为扩散态. -
本文专注于准一维声学AB笼菱形晶格中声学局域态研究. 基于声学谐振腔一阶共振模式, 构造声学正负实耦合, 从而在菱形环路中成功引入等效规范场. 通过对比
$ \varphi = 0 $ 和$ \varphi = \pi $ 通量结构的原胞能带, 发现等效规范场可使色散能带退化为平坦能带. 相比其他色散带和平带共存的声学系统, 基于声学AB笼拓扑晶体可构造全平带系统, 有利于实现多种声学局域态. 通过构建0和$ \pi $ 通量的有限晶格结构, 并分析其本征模式分布, 研究了其在不同激发条件下声场分布的特征. 结果表明, 在满足平带本征态激发条件下, 声学AB笼结构能够实现与不同平带本征态相对应的声学平带局域态. 此外, 通过叠加不同的平带局域模式, 可以获得声场具有更丰富相位和幅值关系的平带局域态, 从而实现声波的精准调控. 进一步根据在平庸晶格和AB笼晶格中单源激发的情况, 发现等效规范场可以调控声场局域, 在AB笼晶格的体和边位置均出现较强的声局域态. 该种AB囚禁效应诱导的局域态对于对称类型随机微扰具有较强免疫性. 因此, 我们在一种拓扑结构中实现了不同类型的声局域态. 与以往缺陷态和高阶拓扑态相比, 这些局域态并不限定于某个特定频率, 能够在不同带隙频率范围束缚声波. 而且, 无论是平带局域态还是等效规范场诱导的局域态, 当激发频率为平带本征频率时, 声场从局域态分布转变为扩展态分布, 体现平带频率声滤波的功能特征, 表明带隙频率和平带频率的声场均具有应用价值. 需要指出的是, 通过选择适当的结构参数, 本文数值模拟结果可以在实验上实现. 具体方案如下: 采用3D打印技术制作环氧树脂材料的声学谐振腔样品(中空结构), 在腔体上下表面预留麦克风测量孔和声源孔. 实验过程分为两个步骤: 首先, 在AB笼拓扑结构中, 测量声响应谱, 确定平带频率对应的峰值频率. 其次, 在偏离平带频率时, 利用适当声源激发不同的声学局域态, 并测量相应的声场分布. 考虑到实验中声波在腔管结构内存在能量损耗, 在结构设计时需适当增大耦合管截面积. 在数值模拟中, 将声速设置为复数, 即$ c={c}_{{\mathrm{a}}{\mathrm{i}}{\mathrm{r}}}+{\mathrm{i}}{c}' $ , 其中$ {c}' $ = 8.0 m/s可等效实验损耗. 探究结果表明, 声损耗对声学局域态的分布影响较小, 但对声扩展态的影响较为显著. 因此, 实验的主要挑战在于如何在声损耗存在的条件下测量出扩展态声场, 从而确定其激发频率为平带频率. 总之, 本文研究结果丰富了声学局域态的构造方案, 有望在声波能量收集、振动控制、声学传感与滤波等方面获得潜在的应用.
基于Aharonov-Bohm囚禁的声学局域现象
Acoustic localization phenomenon based on Aharonov-Bohm cage
-
摘要: 声子晶体能带理论为声场调控提供了重要的理论基础. 基于声学平带特征, 可有效控制声波局域与扩散现象. 本文通过设计声学正负耦合结构, 在准一维声学菱形晶格中构建等效规范场, 并利用声学Aharonov-Bohm囚禁效应产生的全平带调控声场局域. 研究表明, 相比于零通量结构, 引入$ \pi $通量的等效规范场后, 在有限菱形晶格体内和边界位置均可有效控制声波局域. 这类Aharonov-Bohm囚禁效应诱导的局域态对对称结构微扰具有拓扑鲁棒性, 表明局域模式依赖于$ \pi $通量等效规范场的拓扑特征. 此外, 通过平带本征态激发, 可获得与不同本征态对应的声学平带局域态. 进一步将不同的平带局域态叠加, 调控特定位置的声波幅值和相位, 实现具有丰富声场特征的复合型平带局域态. 因此, 利用一种声学Aharonov-Bohm笼拓扑结构可实现不同类型的声学局域态. 这些局域态可在不同晶胞位置激发, 且在不同带隙频率均具有较强的束缚声波的能力, 实现了宽带的声场局域调控. 本文研究结果不仅为利用等效规范场调控声场局域提供理论指导, 而且在发展声波控制器件方面具有潜在的应用前景.Abstract:
The energy band theory of acoustic crystal provides an important theoretical foundation for controlling the features of sound fields. By utilizing the acoustic flat bands, the sound wave can be effectively modulated to realize the acoustic localization and diffusion. In this work, an artificial gauge field is used to design a system supporting multiple acoustic flat bands, leading to the emergence of diversified acoustic localizations. Initially, cavity resonators, linked with different connectivity based on the field profiles of acoustic resonators, are employed to emulate coupled pz-dipole modes of atomic orbitals. According to the band order of in-phase and out-of-phase modes in two coupled cavities, it can be confirmed that the cross-linked and V-shaped-linked tube structures can achieve the positive coupling and negative coupling, respectively. By introducing positive and negative coupling into a rhombic loop, a synthetic gauge field can be formed due to the $ \pi $ flux phase accumulation of acoustic wave in the loop. Correspondingly, the different geometric phases of acoustic wave in different paths are analogous to the Aharonov-Bohm caging effect. Due to the Aharonov-Bohm caging effect, the introduce of $ \pi $-flux into a rhombic loop causes the dispersion bands to collapse into dispersionless flat bands, providing the opportunity for controlling the localizations of sound fields. According to the finite structures of the cases with and without gauge fluxes, the eigenmodes and energy ratios are analyzed to investigate the sound field distributions. Compared with the zero-flux structure, the acoustic localization can be realized in the bulk and edge of a finite rhombic sonic crystal after introducing an artificial gauge field with a $ \pi $ flux in each plaquette. Here the localized states, induced by Aharonov-Bohm caging effect, are topologically immune to symmetrical structure disorder, indicating that the localized mode relies on the topological feature of the $ \pi $-flux artificial gauge field. Additionally, based on the excitation of flat band eigenstates, the acoustic flat band bound states corresponding to different eigenstates can be obtained. By superimposing acoustic flat band bound states, the amplitude and phase of sound wave can be manipulated at specific locations, realizing the composite flat band bound states with rich acoustic field patterns. Therefore, we achieve different types of acoustic localized states in an acoustic topological Aharonov-Bohm cage. These localized states can be excited in any primitive cell of the rhombic lattices, and possess the remarkable ability to trap sound waves at different bulk gap frequencies, which achieves the broadband sound localizations. At the eigenfrequencies of flat bands, the localized states will be transformed into the extended states, exhibiting acoustic filtering functionality. Therefore, the acoustic Aharonov-Bohm cage is promising for applications at bandgap and flat band frequencies. The findings in this work provide the theoretical guidance for exploring the acoustic localized states with artificial gauge field, and can realize potential applications in acoustic control devices. -

-
图 1 规范通量为
$ \pi $ 的菱形环路 (a)准一维AB笼菱形晶格示意图; (b)对应$ \pi $ 通量的声学原胞; (c)两腔耦合时的交叉连接及V形连接; (d)两腔正负耦合的劈裂频率及中心频率随耦合管参数$ {d_1} $ 的演化; (e)对应$ {{{d_1}} {/ } {{d_0}}} $ = 1.6时两种耦合结构的本征模式声压分布; (f)对应于菱形环路中$ 0 $ 和$ \pi $ 通量的声学原胞体能带Figure 1. Rhombic loop with gauge flux
$ \pi $ ; (a) Schematic of quasi-one-dimensional rhombic lattice. (b) acoustic unit cell with gauge flux$ \pi $ ; (c) cross and V-shaped connections in two coupled cavities; (d) the split eigenfrequencies and central frequency as a function of the tube parameter$ {d_1} $ for the two cavity structures with positive and negative couplings; (e) eigen-pressure patterns for the two structures, exemplified with$ {{{d_1}} {/ } {{d_0}}} $ = 1.6; (f) acoustic band structures for$ 0 $ and$ \pi $ fluxes in the rhombic loops.图 2 声学AB笼晶格中的平带态 (a)对应图1(f)第二条平带的本征激发; (b)在图(a)激发条件下的声学平带局域态和平带扩展态; (c)对应图1(f)第三条平带的本征激发; (d)在图(c)激发条件下的声学平带局域态和平带扩展态
Figure 2. Flat band states in acoustic AB cage: (a) Intrinsic excitation for the second flat band in Fig. 1(f); (b) acoustic flat band bound state and flat band diffusion state under the case in Fig. 2(a). (c) intrinsic excitation for the third flat band in Fig. 1(f); (d) acoustic flat band bound state and flat band diffusion state under the case in Fig. 2(c).
图 3 声学AB笼晶格中复合的平带局域态 (a)基于模式M1叠加的平带局域态, 其中T1表示将局域模式沿基矢方向平移一个晶胞; (b)基于模式M2叠加的平带局域态; (c), (d)模式M1和M2叠加的平带局域态
Figure 3. Composite flat band bound states in acoustic AB cage: (a) Composite flat band bound state based on the flat band bound state M1, and T1 represents the translation of the localized mode along the basis vector by one unit cell; (b) composite flat band bound state based on the flat band bound state M2; (c), (d) composite flat band bound states formed by the superposition of modes M1 and M2.
图 4
$ \varphi = 0 $ 和$ \varphi = \pi $ 两种有限晶格中的体激发声场分布 (a)通量为0的平庸晶格及体激发声源; (b)通量为$ \pi $ 的拓扑晶格及体激发声源, 其中黑框为选取的基准局域单元, 黄色星形标记声源激发位置; (c)对应$ \varphi = 0 $ 有限晶格的本征模式谱图; (d)对应$ \varphi = \pi $ 有限晶格的本征模式谱图, 其中绿球表示边界态. 右侧版面: 不同参数的$ {{{E_{{\text{unit}}}}} {/ } {{E_{{\text{sys}}}}}} $ 能量比率图, 紫球为选取的激发频率位置; (e)在2230和2260 Hz,$ \varphi = 0 $ 菱形晶格中扩展态的场分布; (f)在2230和2260 Hz,$ \varphi = \pi $ 菱形晶格中的局域声场Figure 4. Sound field distributions excited at the bulks of two finite lattices with
$ \varphi = 0 $ and$ \varphi = \pi $ : (a) Schematic of trivial lattice with gauge flux 0 and sound source for bulk excitation; (b) schematic of topological lattice with gauge flux$ \pi $ and sound source for bulk excitation. The black box represents for the selected standard area for sound localization, and the yellow star marks the excitation position of the sound source; (c) eigenfrequencies of the finite rhombic lattice with$ \varphi = 0 $ ; (d) eigenfrequencies of the finite rhombic lattice with$ \varphi = \pi $ , where the green spheres represent the edge states. Right panel: Comparison of the energy ratios$ {{{E_{{\text{unit}}}}} {/ } {{E_{{\text{sys}}}}}} $ for different structures, and the purple spheres indicate the positions of the selected excitation frequencies; (e) the field distributions of diffuse states at 2230 and 2260 Hz under the rhombic lattice with$ \varphi = 0 $ ; (f) the localized sound fields at 2230 and 2260 Hz under the rhombic lattice with$ \varphi = \pi $ .图 5
$ \varphi = 0 $ 和$ \varphi = \pi $ 两种有限晶格中的边界激发声场分布 (a) 0通量有限晶格中的边界激发示意图; (b)$ \pi $ 通量有限晶格中的边界激发示意图; (c)两种通量参数的能量比率曲线, 紫球为选取的激发频率位置; (d)在2216.8和2277 Hz,$ \varphi = 0 $ 有限晶格中的扩展态声场; (e)在2216.8和2277 Hz,$ \varphi = {\text{π}} $ 有限晶格中的边界局域声场; (f)在2204, 2245和2289 Hz,$ \varphi = \pi $ 有限晶格中的扩散声场Figure 5. Sound field distributions excited at the edges of two finite lattices with
$ \varphi = 0 $ and$ \varphi = \pi $ : (a) Schematic of the edge excitation for the finite lattice with flux$ \varphi = 0 $ ; (b) schematic of the edge excitation for the finite lattice with flux$ \varphi = \pi $ ; (c) the energy ratio versus the two types of gauge fluxes, and the purple spheres indicate the positions of the selected excitation frequencies; (d) the sound fields of diffuse states at 2216.8 and 2277 Hz under the finite lattice with$ \varphi = 0 $ ; (e) the edge localized sound fields at 2216.8 and 2277 Hz under the finite lattice with$ \varphi = \pi $ ; (f) the diffuse sound fields at 2204, 2245 and 2289 Hz under the finite lattice with$ \varphi = \pi $ .图 6 两种类型结构微扰对AB-笼效应诱导的局域声场的影响 (a)对称类型结构微扰示意图; (b)反对称类型结构微扰示意图; (c)对称微扰结构的本征频谱; (d)在2230和2270 Hz, 对称微扰结构中体激发的局域声场; (e)在2218和2280 Hz, 对称微扰结构中边界激发的拓扑边界局域态; (f)反对称微扰结构的本征频谱; (g)在2230和2270 Hz, 反对称微扰结构中体激发的非局域声场; (h)在2220和2284 Hz, 反对称微扰结构中边界激发的非局域声场
Figure 6. The influence of two types of structural perturbations on acoustic localizations induced by AB-cage effect: (a) Schematic of symmetric structure disorder; (b) schematic of antisymmetric structure disorder; (c) eigenfrequencies for the finite lattice with symmetric disorder; (d) the localized sound fields at 2230 and 2270 Hz excitated in the bulk of the finite lattice with symmetric disorder; (e) the topological edge localized states at 2218 and 2280 Hz excitated at the edge of the finite lattice with symmetric disorder; (f) eigenfrequencies for the finite lattice with antisymmetric disorder; (g) the non-localized sound fields at 2230 and 2270 Hz excitated in the bulk of the finite lattice with antisymmetric disorder; (h) the non-localized sound fields at 2220 and 2284 Hz excitated at the edge of the finite lattice with antisymmetric disorder.
-
[1] Wang X, Sun H, Chen T, Wang X 2019 Phys. Lett. A 383 125918 doi: 10.1016/j.physleta.2019.125918 [2] Jo S H, Yoon H, Shin Y C, Kim M, Youn B D 2020 J. Appl. Phys. 127 164901 doi: 10.1063/5.0003688 [3] Jia B, Huang L, Pilipchuk A S, Huang S, Shen C, Sadreev A F, Li Y, Miroshnichenko A E 2023 Phys. Rev. Appl. 19 054001 doi: 10.1103/PhysRevApplied.19.054001 [4] Yin Y, Duan Q, Zhu S, Li J, Xie Z, Qiu C W, Chen H 2024 Phys. Rev. B 110 054201 doi: 10.1103/PhysRevB.110.054201 [5] Vaidya S, Benalcazar W A, Cerjan A, Rechtsman M C 2021 Phys. Rev. Lett. 127 023605 doi: 10.1103/PhysRevLett.127.023605 [6] Mukherjee S, Thomson R R 2015 Opt. Lett. 40 5443 doi: 10.1364/OL.40.005443 [7] Mukherjee S, Spracklen A, Choudhury D, Goldman N, Öhberg P, Andersson E, Thomson R R 2015 Phys. Rev. Lett. 114 245504 doi: 10.1103/PhysRevLett.114.245504 [8] Vicencio R A, Cantillano C, Morales-Inostroza L, Real B, Mejía-Cortés C, Weimann S, Szameit A, Molina M I 2015 Phys. Rev. Lett. 114 245503 doi: 10.1103/PhysRevLett.114.245503 [9] Shen Y X, Peng Y G, Cao P C, Li J, Zhu X F 2022 Phys. Rev. B 105 104102 doi: 10.1103/PhysRevB.105.104102 [10] Weaver R L 1990 Wave Motion 12 129 doi: 10.1016/0165-2125(90)90034-2 [11] Dhillon J, Bozhko A, Walker E, Neogi A, Krokhin A 2021 J. Appl. Phys. 129 134701 doi: 10.1063/5.0041659 [12] Zhang W, Zou D, Pei Q, He W, Bao J, Sun H, Zhang X 2021 Phys. Rev. Lett. 126 146802 doi: 10.1103/PhysRevLett.126.146802 [13] Li S F, Zhou C Y Y, Lu J Y, Zou X Y, Cheng J C 2022 AIP Adv. 12 095111 doi: 10.1063/5.0114007 [14] Gu Z M, Gao H, Xue H R, Wang D, Guo J M, Su Z Q, Zhang B L, Zhu J 2023 Sci. Chin. Phys. , Mech. Astron. 66 294311 doi: 10.1007/s11433-023-2159-4 [15] Liu L, Li T, Zhang Q, Xiao M, Qiu C 2023 Phys. Rev. Lett. 130 106301 doi: 10.1103/PhysRevLett.130.106301 [16] Zhang H Y, Liu S, Guo Z W, Hu S Y, Chen Y G, Li Y H, Li Y, Chen H 2023 Sci. Chin. Phys. , Mech. Astron. 66 284311 doi: 10.1007/s11433-023-2136-y [17] Guo J, Gu Z, Zhu J 2024 Phys. Rev. Lett. 133 236603 doi: 10.1103/PhysRevLett.133.236603 [18] Xue H, Yang Y, Gao F, Chong Y, Zhang B 2019 Nat. Mater. 18 108 doi: 10.1038/s41563-018-0251-x [19] Zhang X, Xie B Y, Wang H F, Xu X, Tian Y, Jiang J H, Lu M H, Chen Y F 2019 Nat. Commun. 10 5331 doi: 10.1038/s41467-019-13333-9 [20] Li J, Deng C, Huang Z, Huang J, Wang X, Yang H 2024 Phys. Rev. Appl. 22 054039 doi: 10.1103/PhysRevApplied.22.054039 [21] Benalcazar W A, Li T, Hughes T L 2019 Phys. Rev. B 99 245151 doi: 10.1103/PhysRevB.99.245151 [22] Ye C, Chen Z, Geng Z G, Shen Y X, Zhu X F 2024 Appl. Phys. Lett. 124 182202 doi: 10.1063/5.0204524 [23] Qi Y, Qiu C, Xiao M, He H, Ke M, Liu Z 2020 Phys. Rev. Lett. 124 206601 doi: 10.1103/PhysRevLett.124.206601 [24] Xue H, Wang Z, Huang Y X, Cheng Z, Yu L, Foo Y X, Zhao Y X, Yang S A, Zhang B 2022 Phys. Rev. Lett. 128 116802 doi: 10.1103/PhysRevLett.128.116802 [25] Li T, Du J, Zhang Q, Li Y, Fan X, Zhang F, Qiu C 2022 Phys. Rev. Lett. 128 116803 doi: 10.1103/PhysRevLett.128.116803 [26] Li T, Liu L, Zhang Q, Qiu C 2023 Commun. Phys. 6 268 doi: 10.1038/s42005-023-01393-9 [27] Meng Y, Lin S, Shi B J, Wei B, Yang L, Yan B, Zhu Z, Xi X, Wang Y, Ge Y, Yuan S Q, Chen J, Liu G G, Sun H X, Chen H, Yang Y, Gao Z 2023 Phys. Rev. Lett. 130 026101 doi: 10.1103/PhysRevLett.130.026101 [28] Pu Z, He H, Deng W, Huang X, Ye L, Lu J, Ke M, Liu Z 2023 Phys. Rev. B 108 L220101 doi: 10.1103/PhysRevB.108.L220101 [29] Xiang X, Gao F, Peng Y G, Wu P, Li Z L, Zhu X F 2024 Sci. Chin. Phys. , Mech. Astron. 68 214312 doi: 10.1007/s11433-024-2503-0 [30] Xiang X, Peng Y G, Gao F, Wu X, Wu P, Chen Z, Ni X, Zhu X F 2024 Phys. Rev. Lett. 132 197202 doi: 10.1103/PhysRevLett.132.197202 [31] Chen S, Ke S, Zhao D, Ye J, Wang Y, Liu W, Huang K, Wang B, Lu P 2024 Nano Lett. 24 4810 doi: 10.1021/acs.nanolett.3c05095 [32] Yan M, Huang X, Luo L, Lu J, Deng W, Liu Z 2020 Phys. Rev. B 102 180102 doi: 10.1103/PhysRevB.102.180102 [33] Geng Z G, Shen Y X, Duan L, Chen Z, Zhu X F 2023 J. Phys. Condens. Matter 35 405001 doi: 10.1088/1361-648X/ace1c2 [34] Wu S Q, Lin Z K, Xiong Z, Jiang B, Jiang J H 2023 Phys. Rev. Appl. 19 024023 doi: 10.1103/PhysRevApplied.19.024023 [35] Longhi S 2014 Opt. Lett. 39 5892 doi: 10.1364/OL.39.005892 [36] Kremer M, Petrides I, Meyer E, Heinrich M, Zilberberg O, Szameit A 2020 Nat. Commun. 11 907 doi: 10.1038/s41467-020-14692-4 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: