活性物质是一类由自驱动个体组成的非平衡系统, 涵盖了从宏观到微观尺度的多种物质, 例如鸟类^[1]、鱼群^[2]、细菌^[3]和各种人工合成粒子^[4]等. 活性颗粒或生物体能够通过内部物理化学机制, 将储存的化学能或环境能量转化为动能, 从而实现自我驱动^[5,6], 因而在药物运输、心血管疾病治疗以及环境可持续发展等领域具有巨大的应用潜力^[7–9]. 活性粒子的速度对齐是当前的研究热点之一. 该现象最初被认为是显式对齐作用或某种微观对称性破缺的结果, 例如典型的Vicsek模型^[10,11]和哑铃状、杆状及细长形状的活性粒子系统^[12–14]. 惯性效应^[15]、空间约束^[16]、粒子几何不对称^[17]或偏心粒子^[18]等都可能产生对齐效应. 此外, 粒子通过链连接也可能产生速度对齐^[19].

然而, 近年来的研究表明, 在缺乏明确的对齐作用或微观对称性破缺的情况下, 活性粒子可通过某些特定机制实现自发速度对齐^[20,21]. 例如, 在具有纯排斥性相互作用的活性布朗粒子模型(active Brownian particle model, ABP模型)中, 已观察到局部自发速度对齐现象^[22,23] . 通过将自推进作用定义为一个时滞反馈力, 可以实现自发全局速度对齐^[24], 且系统呈现出均匀相. 对于具有吸引性相互作用的ABP模型, 发现了全局速度对齐程度较高的单一团簇^[25]. 此外, 吸引性相互作用在集群 生长与老化^[26]、活性粒子的相分离与集群运动^[27]、被动与活性粒子的分离^[28]、手性活性粒子的集群行为^[29]等方面的作用也已受到广泛关注与研究. 吸引性相互作用作为一种基本的粒子间相互作用, 已被证明对活性粒子的集体行为具有重要影响. 然而, 吸引相互作用如何诱导和影响速度对齐仍需进一步探讨.

为了解决这个问题, 本文研究了具有吸引性相互作用的活性布朗粒子系统中的团簇行为和自发速度对齐. 团簇结构对自发速度对齐程度有重要影响, 而研究表明, 自推进作用与吸引性相互作用之间的竞争显著影响了团簇行为. 随着自推进作用在竞争中的主导作用逐渐增强, 中低填充分数下, 系统依次呈现网状团簇、块状团簇、离散分布或不稳定团簇, 速度对齐程度呈现增大-稳定-减小的趋势; 高填充分数下, 系统从块状团簇向不稳定团簇转变, 速度对齐程度先保持不变后减小. 其中, 自发全局速度对齐现象出现在系统形成单一稳定的块状团簇时.

考虑$N$个直径为$\sigma $的圆形活性布朗粒子在二维周期矩形空间中的运动, 该空间尺寸为$L \times L$. 粒子运动由质心位置${{\boldsymbol{r}}_i} \equiv \left( {{x_i}, {y_i}} \right)$和方向${{\boldsymbol{n}}_i} \equiv ( \cos ({\varphi _i}), \sin ({\varphi _i}) )$描述, 其中${\varphi _i}$是粒子的自推进方向和$x$轴正方向的夹角. 任意两个粒子之间的空间相互作用由截断的Lennard-Jones势来描述:

其中, ${r_{ij}}$表示第$i$个与第$j$个粒子之间的距离, $ \epsilon $表示相互作用势的势强度. 粒子$i$受到的空间相互作用力为${{\boldsymbol{F}}_i} = - {\nabla _i}{U_{{\text{tot}}}}$, 其中${U_{{\text{tot}}}} = \displaystyle \sum\nolimits_{i < j} U ({r_{ij}})$.

对于平移热波动可忽略^[15]的ABP模型, 描述粒子动力学性行为朗之万方程为

其中, ${v_0}$为自推进速度大小, $\gamma $为平移斯托克斯阻力系数, ${D_{\text{r}}}$为旋转扩散系数, ${\xi _i}$为具有单位方差和零平均值的高斯白噪声, 满足$\left\langle {{\xi _i}(t)} \right\rangle = 0$和$\langle {\xi _i}(t){\xi _i}(t')\rangle = \delta (t - t')$的关系.

为了定量描述系统中粒子速度的全局对齐程度, 引入全局速度对齐序参量:

其中, ${\theta _i}$为第$i$个粒子的速度方向与$x$轴正方向的夹角. 当$P = 1$时, 表示系统内粒子的速度方向完全对齐; $P = 0$则表示粒子的速度方向完全无序.

引入系统的极性平均参量, 说明粒子取向平均方面的信息:

当$Q = 1$时, 表示系统内粒子取向是一致的, 即其自推进速度方向完全相同; $Q = 0$则表明粒子取向是完全无序的.

为了研究系统的团簇行为, 引入了最大团簇分数${\lambda _{{\text{max}}}}$、局域面积分数${\varPhi _{\text{V}}}$及其概率分布函数$P({\varPhi _{\text{V}}})$. 当两个粒子之间的距离${r_{ij}} < 1.2\sigma $, 认为它们属于同一团簇. ${\lambda _{{\text{max}}}}$表示最大团簇的粒子数与总粒子数之比. ${\lambda _{{\text{max}}}} = 1$表示所有粒子在同一团簇中, 而${\lambda _{{\text{max}}}} \to 0$则表示粒子完全离散. 为了进一步探讨团簇的结构, 采用了Voronoi剖分^[30], 定义第$i$个粒子的局域面积分数$\varPhi _{\text{V}}^i$为

其中${S_i}$为粒子$i$所在的泰森多边形的面积. $\varPhi _{\text{V}}^i$越大, 说明粒子$i$与其他粒子越紧密. $P({\varPhi _{\text{V}}}){\text{d}}{\varPhi _{\text{V}}}$表示粒子的局域面积分数在${\varPhi _{\text{V}}}$到${\varPhi _{\text{V}}} + {\text{d}}{\varPhi _{\text{V}}}$之间的概率, 并满足归一化条件$\displaystyle\int_0^1 {P({\varPhi _{\text{V}}}){\text{d}}{\varPhi _{\text{V}}} = 1} $.

本文分别以$\sigma $, $\varepsilon = {k_{\text{B}}}T$和${\tau _{\text{B}}} = \gamma {\sigma ^2}/({k_{\text{B}}}T)$作为长度、能量和时间单位. 约化吸引性相互作用势强度为$ \tilde{\epsilon}=\epsilon\tau^2/(m\sigma^2) $, 为了方便表示, 下文将$ \tilde{\epsilon} $写作$ \epsilon $. 采用随机欧拉算法对方程(2)和方程(3)进行数值积分, 积分步长${\text{d}}t = {10^{ - 4}}$, 积分总时长${T_{{\text{all}}}} = 5 \times {1}{{0}^3}$, 以${\text{d}}t$为间隔时间记录粒子的速度, 并设置粒子的初始位置和速度方向随机. 序参量$P$和$Q$的计算结果进行了200次平均. 考虑$m \ll 1$以研究过阻尼系统. 由于惯性效应只影响系统的暂态, 而${T_{{\text{all}}}} \gg {\tau _{\text{I}}} = {m {/ } \gamma }$, 因此粒子质量对于研究结果几乎没有影响. 无特殊说明时, 其他参数分别为$N = 500$, $m = 0.01$, $\gamma = 1$和${D_{\text{r}}} = 1$.

活性布朗粒子系统的自发速度对齐现象的出现被认为是粒子的自推进作用和空间相互作用耦合的结果^[22]. 在持续时间$\tau = 1/{D_{\text{r}}}$内, 自推进速度方向可视为恒定. 对于具有吸引性相互作用的活性粒子系统, 当团簇中的两个粒子相互靠近至${r_{ij}} < 1.12\sigma $时, 粒子间排斥力增大, 导致粒子的相对速度减小; 当两个粒子相互远离时, 由于彼此间的吸引作用和周围其他粒子的排斥作用的制约, 它们不能无限远离且相对速度和相对位置减小. 这样, 相对速度与其相对位置、相互作用力的反馈调节同时发生在所有粒子与其近邻粒子之间, 从而使粒子趋向于与周围粒子速度对齐, 且粒子间距趋近于平衡距离$ r_{ij0}=1.12\sigma $. 因此, $\tau $越大^[31]或粒子排布越紧密, 越有利于粒子通过反馈调节实现更大范围的自发速度对齐. 然而, 在团簇外的粒子或未形成稳定团簇的系统中, 粒子几乎无法实现自推进作用与粒子间相互作用的耦合, 此时粒子运动由自推进作用主导.

粒子间吸引性相互作用使粒子彼此靠近, 形成具有共同速度的局部微小团簇^[25]; 而粒子的自推进作用则为粒子提供了挣脱“牢笼”的动能, 从而使粒子倾向于脱离粒子对. 自推进作用和吸引性相互作用的竞争对粒子的运动产生了显著影响. 因此, 定义约化佩克莱特数$ Pe^*=Pe/\epsilon $, 即自推进作用强度与吸引性相互作用强度的比值, 用以量化这两者的竞争关系. 其中佩克莱特数$Pe = {v_0}\tau /\sigma $.

系统的填充分数$\phi = N{\text{π}}{\sigma ^2}/(4{L^2})$对粒子的集体行为有重要影响. 随着$\phi $的增大, 系统有可能出现运动诱导相分离甚至结晶. 以这两种特殊的集体行为能否实现为划分依据, 将系统划分为低填充分数系统($0 < \phi < 0.4$)、中填充分数系统($0.4 \leqslant \phi < 0.7$)以及高填充分数系统($\phi \geqslant 0.7$), 并分别以$\phi = 0.1$, $\phi = 0.4$和$\phi = 0.7$的系统作为代表.

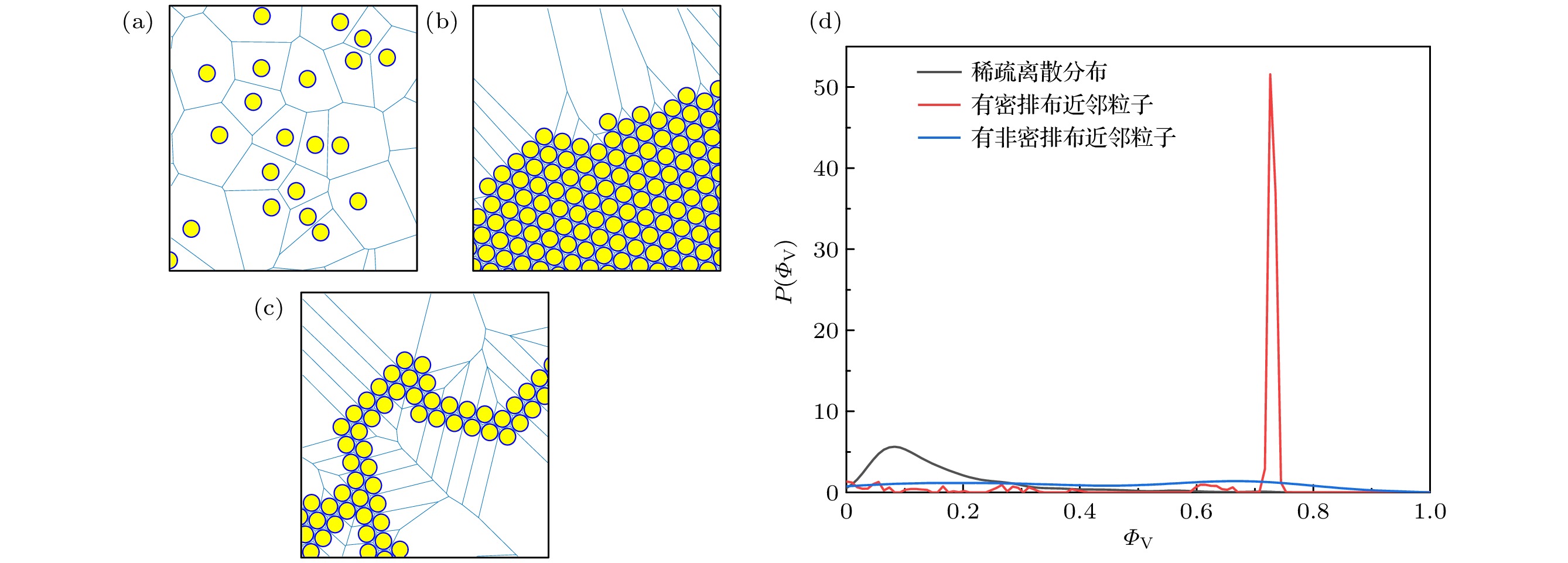
图1(a)—(c)分别展示了系统中几种典型的粒子分布, 图1(d)展示了相应的$P({\varPhi _{\text{V}}})$图像. 图1(a)中稀疏离散分布的粒子几乎没有近邻粒子, 因此${\varPhi _{\text{V}}}$较小, 相应的$P({\varPhi _{\text{V}}})$曲线出现${\varPhi _{\text{V}}} \in \left( {0, 0.2} \right)$的宽峰(低${\varPhi _{\text{V}}}$峰). 图1(b)展示了有密排布近邻粒子的粒子, 其近邻粒子形成了正六边形结构. 此时粒子在平衡位置附近有微小振动, ${r_{ij}} \approx 1.12\sigma $, 因此其${\varPhi _{\text{V}}} \approx 0.72$, 相应的$P({\varPhi _{\text{V}}})$曲线出现${\varPhi _{\text{V}}} \in \left( {0.7, 0.75} \right)$的高且窄的峰(高${\varPhi _{\text{V}}}$峰). 图1(c)展示了有非密排布近邻粒子的粒子, 其${\varPhi _{\text{V}}}$值主要取决于由粒子在带状结构中的位置: 拐角内侧粒子${\varPhi _{\text{V}}} \to 0.72$; 拐角外侧粒子${\varPhi _{\text{V}}} \to 0$; 其余粒子的${\varPhi _{\text{V}}}$值则在中间值附近分布. 因此, 由粒子带连接而形成的网状结构的$P({\varPhi _{\text{V}}})$曲线呈现为在${\varPhi _{\text{V}}} \in (0, 1)$的分布较均匀的曲线.

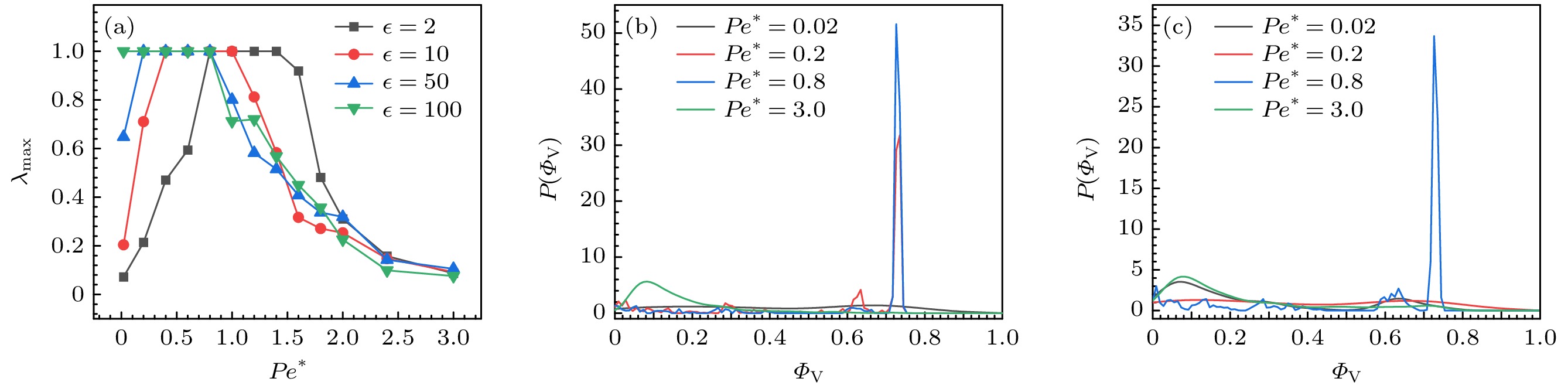
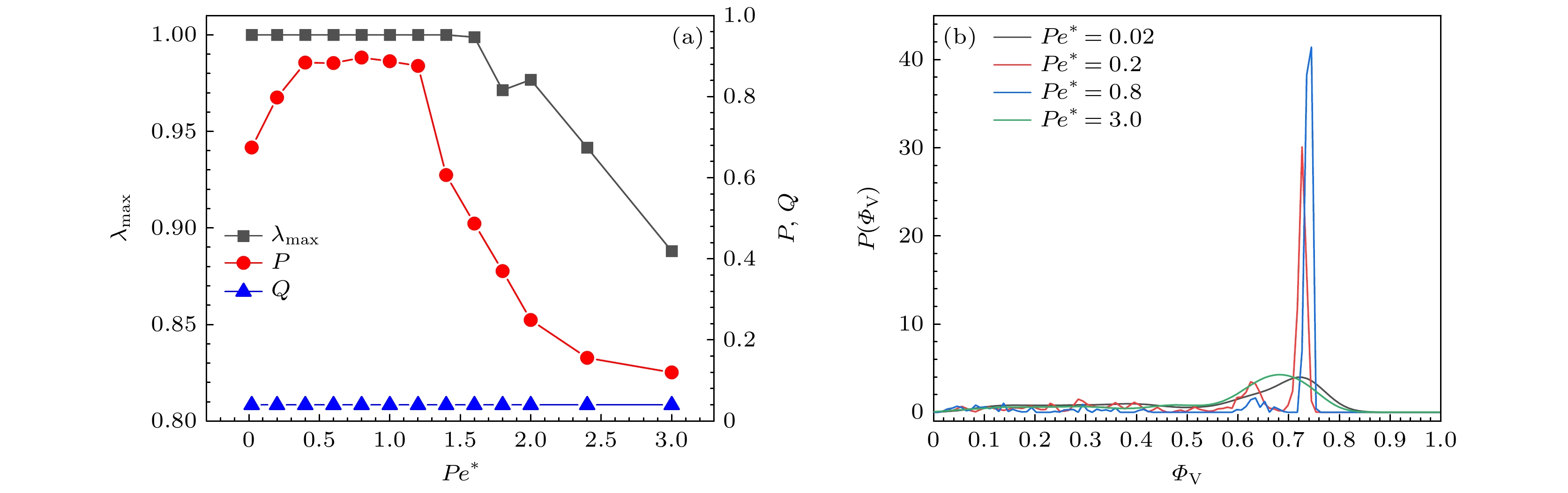
图2(a)描述了低填充分数($\phi = 0.1$)的系统在不同$ \epsilon $下, 最大团簇分数${\lambda _{{\text{max}}}}$随$P{e^*}$的变化. 对于$ \epsilon=100 $的系统, 随着$P{e^*}$的增大, ${\lambda _{{\text{max}}}}$先保持为1, 然后减小并趋近于0; 对于其他3个系统, ${\lambda _{{\text{max}}}}$随着$P{e^*}$的增大而由${\lambda _{{\text{max}}}} < 1$增至${\lambda _{{\text{max}}}} = 1$并保持不变, 然后减小并趋近于0, 且$ \epsilon $越小, ${\lambda _{{\text{max}}}}(P{e^*} \to 0)$越小. 图2(b)描述了当$ \epsilon=100 $时, 不同$P{e^*}$下的概率分布函数$P({\varPhi _{\text{V}}})$图像. 对于$ \epsilon=100 $的系统, 当$P{e^*} \to 0$时, ${\lambda _{{\text{max}}}} = 1$且$P({\varPhi _{\text{V}}})$在${\varPhi _{\text{V}}} \in (0, 1)$分布均匀, 表明形成了单一的网状团簇, 如图3(a)所示; 当$P{e^*} = 0.2$或$P{e^*} = 0.8$时, ${\lambda _{{\text{max}}}} = 1$且$P({\varPhi _{\text{V}}})$曲线呈现单一的高${\varPhi _{\text{V}}}$峰, 表明形成了单一的块状团簇, 如图3(b)所示; 当$P{e^*}$很大时, ${\lambda _{{\text{max}}}} \to 0$且$P({\varPhi _{\text{V}}})$曲线呈现单一的低${\varPhi _{\text{V}}}$峰, 说明粒子稀疏离散分布, 如图3(c)所示. 图2(c)描述了$ \epsilon=2 $的系统中不同$P{e^*}$下的$P({\varPhi _{\text{V}}})$图像. $ \epsilon=2 $与$ \epsilon=100 $的系统的不同在于: $ \epsilon=2 $的系统中, 当$P{e^*} \to 0$时, ${\lambda _{{\text{max}}}} \to 0$且$P({\varPhi _{\text{V}}})$曲线分别在${\varPhi _{\text{V}}} \in (0, 0.2)$和${\varPhi _{\text{V}}} \in (0.5, 0.8)$存在宽峰, 其快照如图3(d); 当$P{e^*} = 0.2$时, ${\lambda _{{\text{max}}}} \approx 0.2$且$P({\varPhi _{\text{V}}})$曲线在${\varPhi _{\text{V}}} \in (0, 1)$分布均匀, 其快照如图3(e). 图4对这种差异进行了讨论.

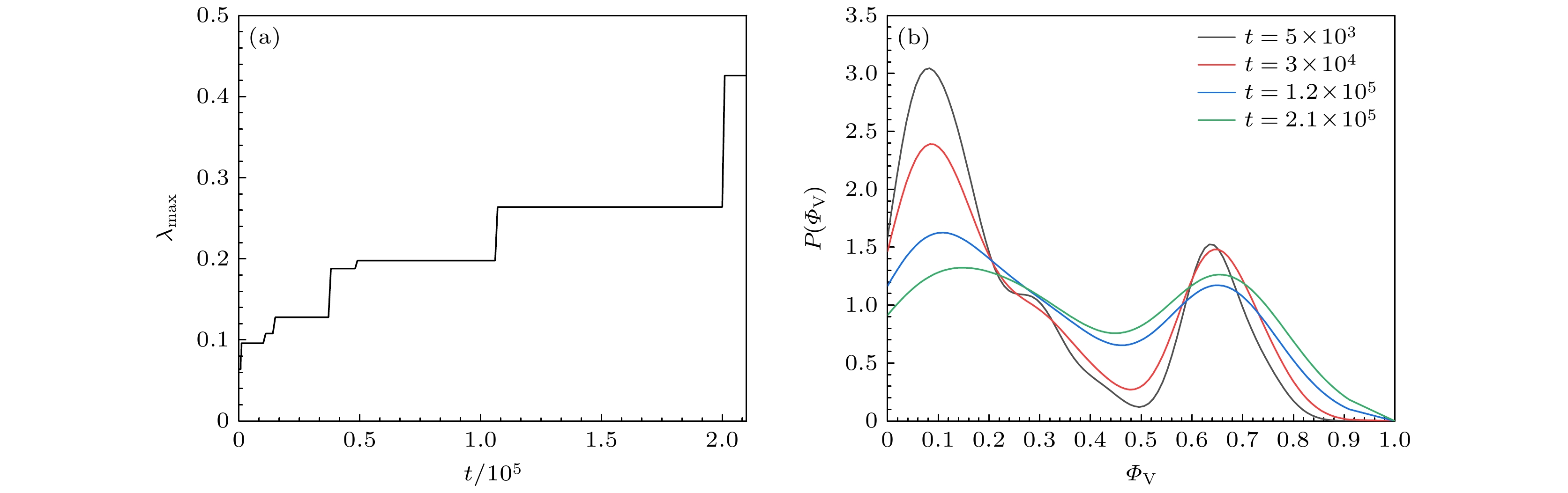
图4展示了当$ \epsilon=2 $且$P{e^*} = 0.02$时, 最大团簇分数${\lambda _{{\text{max}}}}$和概率分布函数$P({\varPhi _{\text{V}}})$随时间变化的情况. 随着时间的增加, ${\lambda _{{\text{max}}}}$呈阶梯状增大且$P({\varPhi _{\text{V}}})$曲线中的两个峰间的峰谷逐渐变浅. 这表明经过足够的长时间后, 将趋向于实现${\lambda _{{\text{max}}}}$=1且$P({\varPhi _{\text{V}}})$在${\varPhi _{\text{V}}} \in \left( {0, 1} \right)$均匀分布, 即系统将形成网状团簇结构. 这是因为当$ \epsilon=2 $且$P{e^*} = 0.02$时, 自推进速度${v_0} = 0.04$, 系统内粒子运动缓慢且方向随机, 需要很长的时间才能够相遇并形成大团簇. 因此, 当时间足够长时, 图2(b)将趋向于与图2(c)一致, 即不同$ \epsilon $的系统都将随着$P{e^*}$的增大而呈现由网状团簇到块状团簇的转变, 并最终趋向于形成离散态.

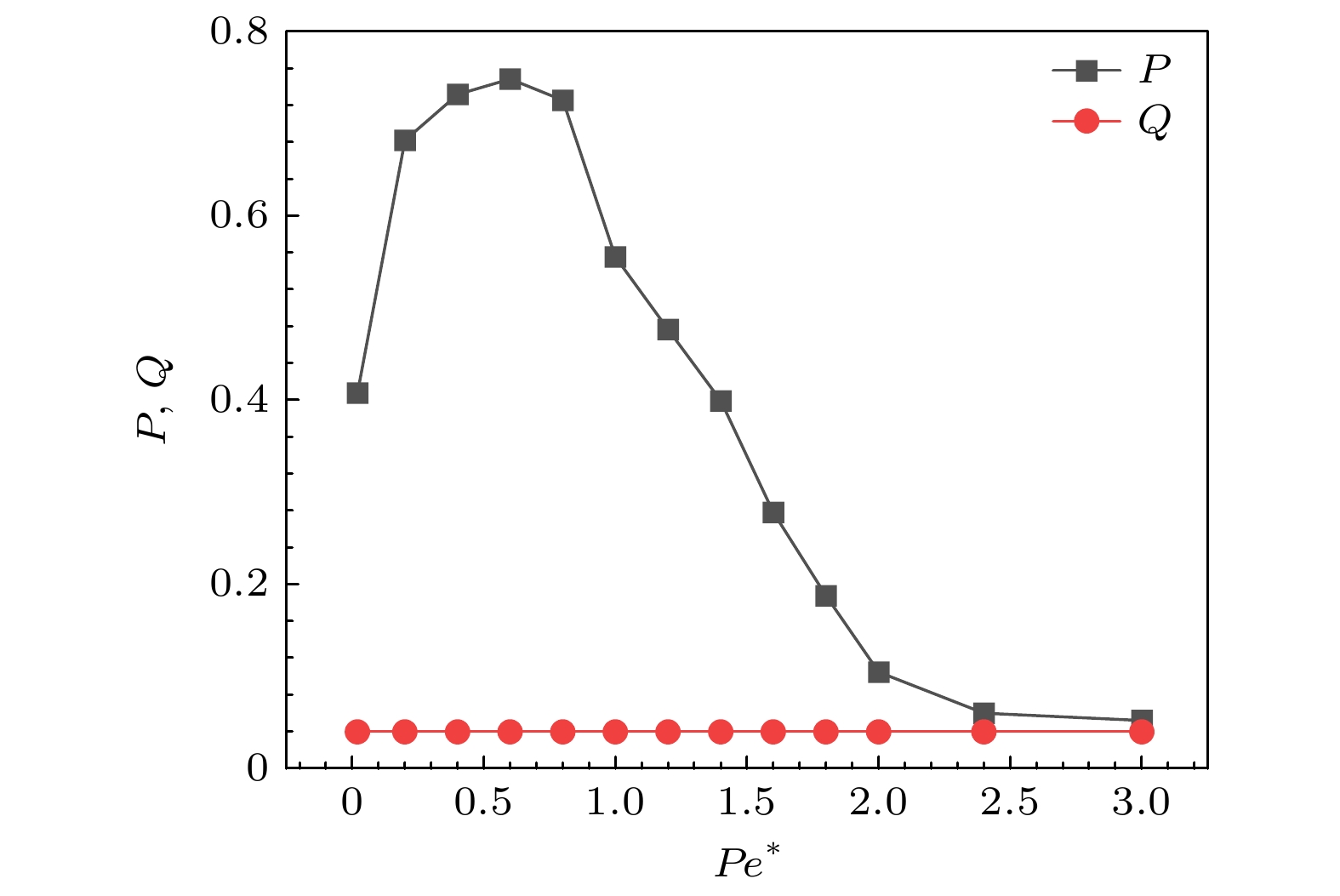
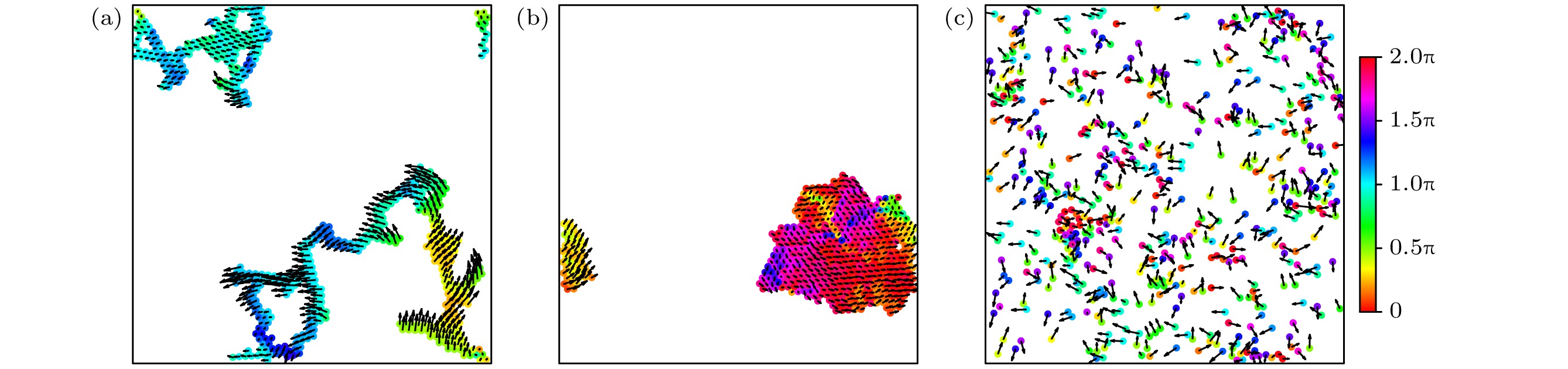
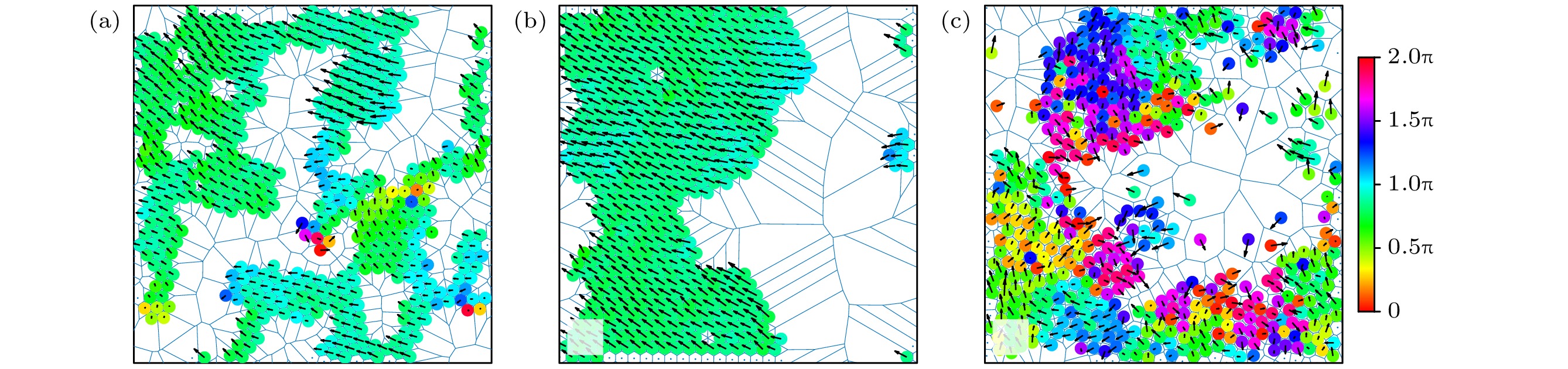
图5描述了全局速度对齐序参量$P$和极性平均参量$Q$随约化佩克莱特数$P{e^*}$的变化. 随着$P{e^*}$值的增大, $Q$值始终保持$Q \to 0$, 表明其粒子取向是无序的; $P$值则呈现出增大-几乎不变-减小的趋势. 当$P{e^*} \to 0$时, 系统形成了网状团簇, 粒子与相邻粒子的速度的微小偏差由于带状结构而被放大, 从而使$P < 0.5$, 如图6(a)所示. 随着$P{e^*}$的增大, 系统由网状团簇结构向块状团簇结构转变, 粒子排布更紧密, 更容易通过反馈调节机制实现速度对齐, 因此$P$值随之增大至$ P\to0.8 $, 出现了较高程度的全局速度对齐, 如图6(b)所示. $P{e^*} = 3.0$时, 粒子分布稀疏离散, 其运动由自推进作用主导, 因此$P \to 0$, 如图6(c)所示.

图7(a)描述了中填充分数($\phi = 0.4$)的系统的最大团簇分数${\lambda _{{\text{max}}}}$随约化佩克莱特数$P{e^*}$的变化. 随着$P{e^*}$的增大, ${\lambda _{{\text{max}}}}$先保持为1, 然后减小且${\lambda _{{\text{max}}}} > 0.8$. 图7(a)还描述了序参量$P$和极性平均参量$Q$随$P{e^*}$的变化. 随着$P{e^*}$值的增大, $Q$值始终保持$Q \to 0$, $P$值则呈现出增大-几乎不变-减小的趋势. 图7(b)展示了在不同$P{e^*}$值下的$P({\varPhi _{\text{V}}})$图像. 当$P{e^*} \to 0$时, ${\lambda _{{\text{max}}}} = 1$, $P({\varPhi _{\text{V}}})$曲线中出现一个${\varPhi _{\text{V}}} \in (0.6, 0.8)$的宽峰且峰值横坐标${\varPhi _{\text{V}}} > 0.72$, 表明出现了网状结构且有较多粒子密排布, 即形成了粗网状结构. 因此, $0.5 < P < 0.8$, 呈现局部速度对齐, 如图8(a). 当$P{e^*} = 0.8$时, ${\lambda _{{\text{max}}}} = 1$且$P({\varPhi _{\text{V}}})$曲线呈现单一的高${\varPhi _{\text{V}}}$峰, 表明形成了单一块状团簇. 因此$P \to 0.9$, 出现了全局速度对齐, 如图8(b). 当$P{e^*} = 3.0$时, 即使$0.8 < {\lambda _{{\text{max}}}} < 1$表明了系统中存在大团簇, 但$P({\varPhi _{\text{V}}})$曲线出现一个${\varPhi _{\text{V}}} \in (0.6, 0.8)$的宽峰且峰值横坐标${\varPhi _{\text{V}}} < 0.72$, 表明所形成的团簇中粒子并没有位于平衡位置, 而是更疏松的. 这揭示了系统内由于运动诱导相分离形成了不稳定团簇, 自发速度对齐被团簇的不稳定性破坏, 因此$P \to 0$, 如图8(c).

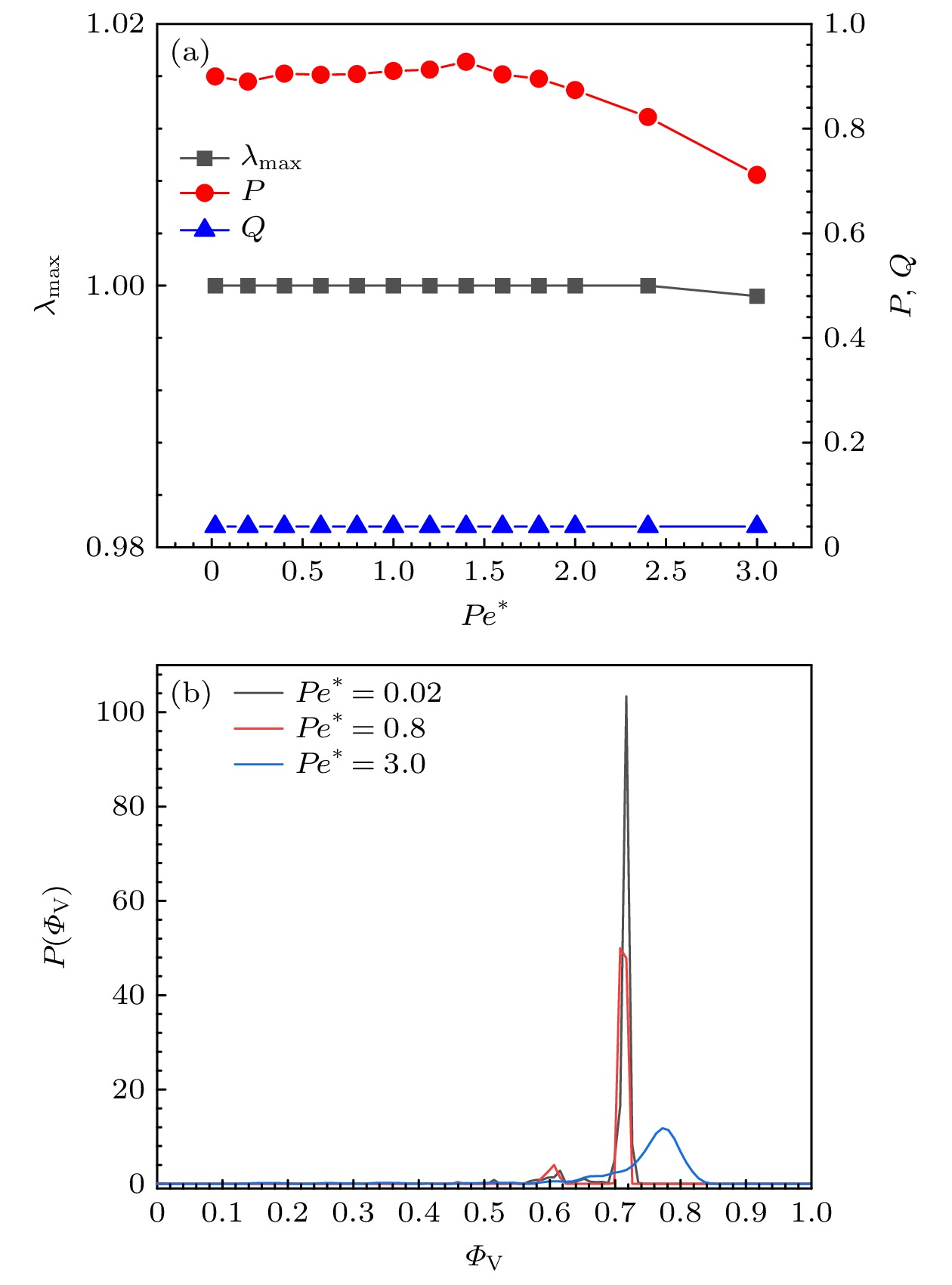
图9(a)描述了高填充分数($\phi = 0.7$)的系统的最大团簇分数${\lambda _{{\text{max}}}}$、序参量$P$和极性平均参量$Q$随$P{e^*}$的变化. 随着$P{e^*}$的增大, 从${\lambda _{{\text{max}}}} = 1$变为${\lambda _{{\text{max}}}} \to 1$, $Q$值始终保持$Q \to 0$, $P$值则先在$P = 0.9$附近几乎不变, 然后减小但保持$P > 0.7$. 图9(b)展示了在不同$P{e^*}$值下的$P({\varPhi _{\text{V}}})$图像. 当$P{e^*} \to 0$或$P{e^*} = 0.8$时, ${\lambda _{{\text{max}}}} = 1$且$P({\varPhi _{\text{V}}})$曲线呈现单一的高${\varPhi _{\text{V}}}$峰, 表明形成了块状团簇. 因此, 当$P{e^*} \leqslant 1.6$时, $P$值几乎不变且$ P \gtrsim 0.9 $, 出现了全局速度对齐. 当$P{e^*} = 3.0$时, ${\lambda _{{\text{max}}}} \to 1$, $P({\varPhi _{\text{V}}})$曲线呈现${\varPhi _V} \in (0.6, 0.8)$的宽峰且峰值横坐标${\varPhi _{\text{V}}} > 0.72$, 表明系统中形成不稳定团簇, 但大部分粒子由于高$\phi $值而能够维持在平衡位置附近, 形成不稳定的块状团簇. 因此, 即使团簇的不稳定性阻碍了粒子的自发速度对齐, 但粒子之间的距离始终较小, 仍能保持自推进与空间相互作用的较强的耦合, 所以$P$值的下降幅度较小.

值得注意的是, 本文结果存在有限尺寸效应, 可以用持续长度${l_{\text{p}}} = {v_0}\tau $和系统尺寸$L$来衡量. 当${l_{\text{p}}} \gg L$时, 系统内趋向于形成全局速度对齐; 当${l_{\text{p}}} \sim L$时, 形成局域速度对齐, 且全局速度对齐程度较高; 当${l_{\text{p}}} \ll L$时, 则呈现无序态. 然而, 在实验和应用中, 通常研究较小尺寸的系统, 因此有望通过调整参数来实现全局速度对齐. 此外, 本研究还忽略了平动热噪声的影响, 因为平动热噪声增加了粒子运动的随机性, 会扰乱粒子的自发速度对齐. 当平动热噪声很大以至于在粒子运动中占据主导地位时, 系统将呈现速度无序态.

实际上, 自推进作用与吸引作用在速度对齐效应上同时存在竞争和协同效应. 粒子排布越密集越有利于速度对齐效应的实现. 当吸引性作用趋近于无限大以至于自推进作用可以忽略时, 粒子分布由系统初始状态决定: 当初始粒子分布离散且稀疏时, 由于吸引性作用很强且作用范围有限, 粒子就近相互吸引形成离散的小团簇, 并经过足够长时间后就近连接形成网状结构, 因此全局速度对齐程度趋向于0; 当粒子分布密集时, 离散的小团簇能够结合形成大团簇甚至形成单一块状团簇, 因此全局速度对齐程度相对较高. 当吸引性作用很弱以至于可以忽略时, 粒子的运动由自推进作用主导, 因此全局速度对齐程度也趋向于0. 但当两者的强度相当时, 网状结构由于自推进作用而松动, 导致粒子带断裂并重新连接, 或粒子带转向, 直至形成更稳定的块状团簇结构. 此时大部分粒子有密排布的近邻粒子, 有利于全局速度对齐的实现.

本文探讨了具有吸引性相互作用的活性布朗粒子系统的团簇行为和自发速度对齐. 粒子排布越紧密, 越有利于粒子与周围粒子实现自推进作用和空间相互作用的耦合, 从而促进大范围的自发速度对齐. 这两种作用的竞争决定了系统的团簇形成及其结构, 进而影响了全局速度对齐程度. 在中低填充分数下, 当吸引性相互作用占主导、自推进作用可忽略时, 由于粒子初始位置随机, 系统形成了网状团簇结构, 粒子速度的微小差异被带状结构放大, 阻碍了速度对齐. 其中, 低填充分数系统形成细网状团簇, 中填充分数系统形成粗网状团簇, 因此前者的速度对齐程度更低. 随着自推进作用逐渐占优, 系统由网状团簇转变为块状团簇, 粒子密排布, 导致全局速度对齐. 当自推进作用占主导、吸引作用可忽略时, 粒子稀疏分布或形成不稳定团簇, 导致系统速度无序. 在高填充分数下, 粒子初始分布密集, 即使吸引性作用占主导、自推进作用可忽略, 系统也能够形成块状团簇而导致全局速度对齐. 当自推进作用占主导时, 尽管团簇的不稳定性在一定程度上阻碍了自发速度对齐, 但粒子依然呈密排布, 导致了局部速度对齐. 因此, 通过调节$P{e^*}$值, 可以促使系统形成单一稳定的块状团簇, 导致自发全局速度对齐的实现.

与以往的研究不同, 由吸引性相互作用和自推进作用的耦合而导致的粒子速度对齐机制是一种隐式的对齐效应, 即没有对齐作用力的各向同性的粒子也能够实现自发速度对齐. 并且对比与其他新颖的隐式对齐效应, 具有吸引力的ABP系统中形成的团簇更加单一稳定. 因此, 该工作能够促进人们理解具有吸引性相互作用的活性布朗粒子系统的自发速度对齐现象, 并为研究动物群体运动^[32]、细胞迁移^[33]等缺乏显式速度对齐相互作用的集群行为提供了新视角. 研究结果还可为活性胶体的设计提供参考, 推动对活性粒子定向运动的深入研究.