高级搜索

基于智能算法对脉冲在光纤中传输动力学的研究

,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

李君, 苏进, 韩小祥, 朱伟杰, 杨瑞霞, 张海洋, 严祥安, 张云婕, 王斐然. 基于智能算法对脉冲在光纤中传输动力学的研究[J]. 物理学报, 2025, 74(6): 060201-1. doi: 10.7498/aps.74.20241473
引用本文: 李君, 苏进, 韩小祥, 朱伟杰, 杨瑞霞, 张海洋, 严祥安, 张云婕, 王斐然. 基于智能算法对脉冲在光纤中传输动力学的研究[J]. 物理学报, 2025, 74(6): 060201-1. doi: 10.7498/aps.74.20241473
shu
Jun LI, Jin SU, Xiaoxiang HAN, Weijie ZHU, Ruixia YANG, Haiyang ZHANG, Xiang’an YAN, Yunjie ZHANG, Feiran WANG. Research on pulse transmission dynamics in optical fiber based on intelligent algorithms[J]. Acta Physica Sinica, 2025, 74(6): 060201-1. doi: 10.7498/aps.74.20241473
Citation: Jun LI, Jin SU, Xiaoxiang HAN, Weijie ZHU, Ruixia YANG, Haiyang ZHANG, Xiang’an YAN, Yunjie ZHANG, Feiran WANG. Research on pulse transmission dynamics in optical fiber based on intelligent algorithms[J]. Acta Physica Sinica, 2025, 74(6): 060201-1. doi: 10.7498/aps.74.20241473
shu

基于智能算法对脉冲在光纤中传输动力学的研究

  • 1.

    西安工程大学理学院, 西安　710048

  • 2.

    射线柔性防护技术陕西省高校工程研究中心, 西安　710048

  • 3.

    西安市核防护纺织装备技术重点实验室, 西安　710048

    • 作者简介: 李君: 3480275814@qq.com .
    通讯作者: E-mail: hanxiaoxiang@xpu.edu.cn.; 

  • 中图分类号: 02.30.Jr, 02.60.-x, 42.65.-k, 42.81.-i

Research on pulse transmission dynamics in optical fiber based on intelligent algorithms

  • 1.

    School of Science, Xi’an Polytechnic University, Xi’an 710048, China

  • 2.

    Engineering Research Center of Flexible Radiation Protection Technology, Universities of Shaanxi Province, Xi’an 710048, China

  • 3.

    Xi’an Key Laboratory of Nuclear Protection Textile Equipment Technology, Xi’an 710048, China

    • Corresponding author: E-mail: hanxiaoxiang@xpu.edu.cn.; 

  • MSC: 02.30.Jr, 02.60.-x, 42.65.-k, 42.81.-i

  • 摘要:

    非线性薛定谔方程(NLSE)在量子力学、非线性光学、等离子体物理、凝聚态物理、光纤通信和激光系统设计等多个领域中都具有重要的应用, 其精确求解对于理解复杂物理现象至关重要. 本文深入研究了传统的有限差分法(FDM)、分步傅里叶法(SSF)与智能算法中的物理信息神经网络(PINN)方法, 旨在高效且准确地求解光纤中的复杂NLSE. 首先介绍了PINN方法对NLSE的求解方法、步骤和结果, 并对比了FDM, SSF, PINN方法对复杂NLSE求解与脉冲远距离脉冲传输的误差. 然后, 讨论了PINN不同网络结构和网络参数对NLSE求解精度的影响, 还验证了集成学习策略的有效性, 即通过结合传统数值方法与PINN的优势, 提高NLSE求解的准确度. 最后, 采用上述算法研究了不同啁啾的艾里脉冲在光纤中的演化过程与保偏光纤对应的矢量非线性薛定谔方程(VNLSE)求解过程及结果误差. 本研究通过对比FDM, SSF, PINN在求解NLSE时的特点, 提出的集成学习方案在脉冲传输动力学研究和数据驱动仿真方面具有重要的应用.

    Abstract:

    Nonlinear Schrödinger equation (NLSE) has important applications in quantum mechanics, nonlinear optics, plasma physics, condensed matter physics, optical fiber communication and laser system design, and its accurate solution is very important for understanding complex physical phenomena. Here, the traditional finite difference method (FDM), the split-step Fourier (SSF) method and the physics-informed neural network (PINN) method are studied, aiming to analyze in depth the solving mechanisms of various algorithms, and then realize the efficient and accurate solution of complex NLSE in optical fiber. Initially, the steps, process and results of PINN in solving the NLSE for pulse under the condition of short-distance transmission are described, and the errors of these methods are quantitatively evaluated by comparing them with the errors of PINN, FDM and SSF. On this basis, the key factors affecting the accuracy of NLSE solution for pulse under long-distance transmission are further discussed. Then, the effects of different networks, activation functions, hidden layers and the number of neurons in PINN on the accuracy of NLSE solution are discussed. It is found that selecting a suitable combination of activation functions and network types can significantly reduce the error, and the combination of FNN and tanh activation functions is particularly good. The effectiveness of ensemble learning strategy is also verified, that is, by combining the advantages of traditional numerical methods and PINN, the accuracy of NLSE solution is improved. Finally, the evolution characteristics of Airy pulse with different chirps in fiber and the solution of vector NLSE corresponding to polarization-maintaining fiber are studied by using the above algorithm. This study explores the solving mechanisms of FDM, SSF and PINN in complex NLSE, compares and analyzes the error characteristics of those methods in various transmission scenarios, proposes and verifies the ensemble learning strategy, thus providing a solid theoretical basis for studying pulse transmission dynamics and data-driven simulation.

  • 加载中

  • 图 1  基于NLSE的脉冲在光纤中传输方程的FDM, SSF, PINN三种方法求解示意图

    Figure 1.  Schematic diagram of FDM, SSF, PINN methods for solving the propagation equation of pulses in optical fibers based on NLSE.

    下载: 全尺寸图片 幻灯片

    图 2  基于PINN的NLSE求解示意图, 其中NN为神经网络, AD为自动微分技术, PDE为NLSE实虚部分离对应的物理信息, Loss为优化物理信息损失函数

    Figure 2.  Schematic diagram of NLSE solution based on PINN. NN is the neural network, AD is the automatic differentiation technology, PDE is the physical information corresponding to the real and imaginary part of the NLSE, Loss is the optimized physical information loss function.

    下载: 全尺寸图片 幻灯片

    图 3  基于PINN的NLSE求解结果　(a) 脉冲在光纤中的传播演化图; (b) 损失函数曲线

    Figure 3.  Results of NLSE solving by PINN: (a) Evolution diagram of pulse propagation in fiber; (b) loss function curves.

    下载: 全尺寸图片 幻灯片

    图 4  多种算法对复杂NLSE求解的脉冲演化过程和对比图　(a) FDM求解的脉冲在光纤中的传播演化图; (b) SSF求解的脉冲在光纤中的传播演化图; (c) PINN求解对应的脉冲在光纤中的传播演化图; (d) FDM与SSF之间的交叉对比图; (e) PINN与SSF之间的交叉对比图; (f) PINN与FDM之间的交叉对比图

    Figure 4.  Pulse evolution process and comparison diagram of FDM, SSF and PINN: (a) Pulse evolution process based on FDM; (b) pulse evolution process based on SSF; (c) pulse evolution process based on PINN; (d) comparison diagram between FDM and SSF; (e) comparison diagram between PINN and SSF; (f) comparison diagram between PINN and FDM.

    下载: 全尺寸图片 幻灯片

    图 5  PINN, SSF, FDM求解基阶孤子在200 m光纤中传输的结果　(a) PINN在不同采样点数下的输入与输出对比图; (b) FDM, SSF, PINN求解的输入与输出对比图; (c) FDM, SSF, PINN求解的基阶孤子传输演化图

    Figure 5.  Results of PINN, SSF, and FDM solving the fundamental order soliton transmission in a 200 m fiber: (a) Results of PINN at different sampling number (SN); (b) results of FDM, SSF, PINN and input; (c) evolution of fundamental soliton transmission solved by FDM, SSF and PINN.

    下载: 全尺寸图片 幻灯片

    图 6  不同激活函数与神经网络设置下PINN的训练误差图　(a) 神经网络为FNN, 激活函数为Tanh的训练误差图; (b) 神经网络为FNN, 激活函数为Sigmoid的训练误差图; (c) 神经网络为FNN, 激活函数为Swish的训练误差图; (d) 神经网络为PFNN, 激活函数为Tanh的训练误差图; (e) 神经网络为PFNN, 激活函数为Sigmoid的训练误差图; (f) 神经网络为PFNN, 激活函数为Swish的训练误差图

    Figure 6.  Training error of PINN under different activation function and NN: (a) Training error with Tanh and FNN; (b) training error with Sigmoid and FNN; (c) training error with Swish and FNN; (d) training error with Tanh and PFNN; (e) training error with Sigmoid and PFNN; (f) training error with Swish and PFNN.

    下载: 全尺寸图片 幻灯片

    图 7  不同隐藏层和神经元设置下PINN训练误差图　(a) 隐藏层为3, 神经元为10的训练误差图; (b) 隐藏层为3, 神经元为15的训练误差图; (c) 隐藏层为3, 神经元为20的训练误差图; (d)隐藏层为4, 神经元为10的训练误差图; (e) 隐藏层为4, 神经元为15的训练误差图; (f) 隐藏层为4, 神经元为20的训练误差图; (g) 隐藏层为5, 神经元为10的训练误差图; (h) 隐藏层为5, 神经元为15的训练误差图; (i) 隐藏层为5, 神经元为20的训练误差图

    Figure 7.  Training error of PINN under different number of hidden layers and neurons: (a) Training error with 3 and 10; (b) training error with 3 and 15; (c) training error with 3 and 20; (d) training error with 4 and 10; (e) training error with 4 and 15; (f) training error with 4 and 20; (g) training error with 5 and 10; (h) training error with 5 and 15; (i) training error with 5 and 20.

    下载: 全尺寸图片 幻灯片

    图 8  不同集成方式对所得结果误差的影响　(a)—(c)分别为SSF, FDM, PINN求解的脉冲传输与解析解误差; (d)—(f)分别为SSF+FDM, PINN+FDM, PINN+SSF+FDM集成求解的脉冲传输与解析解误差

    Figure 8.  Influence of different integration methods on the results’ error: (a)–(c) The pulse transmission and errors of SSF, FDM and PINN solutions; (d)–(f) the pulse transmission and errors of SSF+FDM, PINN+FDM and PINN+SSF+FDM solutions.

    下载: 全尺寸图片 幻灯片

    图 9  多种NLSE求解方法对比不同啁啾艾里脉冲在光纤传输中演化　(a)—(c)分别为对应于FDM, 在C = 0.4, 0, –0.4时的脉冲演化; (d)—(f)分别为对应于SSF, 在C = 0.4, 0, –0.4时的脉冲演化; (g)—(i)分别为对应于PINN, 在C = 0.4, 0, –0.4时的脉冲演化

    Figure 9.  Comparison of Airy pulses’ evolution with different chirps by various NLSE solving methods in fiber transmission: (a)–(c) The pulse evolution corresponding to FDM with C values of 0.4, 0, –0.4; (d)–(f) the pulse evolution corresponding to SSF with C values of 0.4, 0, –0.4; (g)–(i) the pulse evolution corresponding to PINN with C values of 0.4, 0, –0.4.

    下载: 全尺寸图片 幻灯片

    图 10  SSF, FDM和PINN求解VNLSE对应的脉冲演化过程的交叉对比图　(a) SSF与FDM关于$u_x^2$ 的交叉对比图; (b) SSF与FDM关于$u_y^2$的交叉对比图; (c) SSF与FDM关于$ u_x^2{+}u_y^2 $的交叉对比图; (d) PINN与FDM关于$u_x^2$的交叉对比图; (e) PINN与FDM关于$u_y^2$的交叉对比图; (f) PINN与FDM关于$ u_x^2{+}u_y^2 $的交叉对比图

    Figure 10.  Comparison of the pulse evolution process corresponding to VNLSE solved by SSF, FDM and PINN: (a) SSF and FDM with respect to $u_x^2$; (b) SSF and FDM with respect to $u_y^2$; (c) SSF and FDM with respect to $ u_x^2{+}u_y^2 $; (d) PINN and FDM with respect to $u_x^2$; (e) PINN and FDM with respect to $u_y^2$; (f) PINN and FDM with respect to $ u_x^2{+}u_y^2 $.

    下载: 全尺寸图片 幻灯片

    表 1  集成学习和单一方法的误差表

    Table 1.  Error table of Ensemble Learning and single method.

    MAE MSE RMSE MAPE/%
    FDM 4.014×10–4 4.877×10–7 6.983×10–4 13.159
    SSF 3.396×10–4 3.112×10–7 5.579×10–4 8.979
    PINN 4.173×10–4 4.744×10–7 6.887×10–4 11.540
    SSF+FDM 2.625×10–4 1.466×10–7 3.829×10–4 10.933
    PINN+FDM 2.865×10–4 2.316×10–7 4.652×10–4 10.048
    PINN+SSF 2.793×10–4 1.753×10–7 4.188×10–4 12.237
    PINN+FDM+SSF 2.190×10–4 0.978×10–7 3.127×10–4 11.004
    下载: 导出CSV
  • [1] 阿戈沃 G P著 (贾东方, 余震虹 译) 2010 非线性光纤光学原理及应用 (北京: 电子工业出版社) 第18—109页 Agrawal G P (translated by Jia D F, Yu Z H) 2010 Principles and Applications of Nonlinear Fibre Optics (Beijing: Electronic Industry Press) pp18–109
    [2] Ngo N Q 2018 Ultra-fast Fiber Lasers: Principles and Applications with MATLAB® Models (Boca Raton: CRC Press) pp139–157
    [3] Chang Q S, Jia E H, Sun W 1999 J. Comput. Phys. 148 397 doi: 10.1006/jcph.1998.6120
    [4] Wang H Q 2005 Appl. Math. Comput. 170 17 doi: 10.1016/j.amc.2004.10.066
    [5] 赵磊, 隋展, 朱启华, 张颖, 左言磊 2009 物理学报 58 3977 doi: 10.7498/aps.58.3977 Zhao L, Sui Z, Zhu Q H, Zhang Y, Zuo Y L 2009 Acta Phys. Sin. 58 3977 doi: 10.7498/aps.58.3977
    [6] Xie S S, Li G X, Yi S 2009 Comput. Meth. Appl. Mech. Eng. 198 1052 doi: 10.1016/j.cma.2008.11.011
    [7] Wu L 2012 Numer. Meth. Partial Differ. Eq. 28 63 doi: 10.1002/num.20607
    [8] Caplan R M 2013 Appl. Numer. Math. 71 24 doi: 10.1016/j.apnum.2013.04.002
    [9] 崔少燕, 吕欣欣, 辛杰 2016 物理学报 65 040201 doi: 10.7498/aps.65.040201 Cui S Y, Lv X X, Xin J 2016 Acta Phys. Sin. 65 040201 doi: 10.7498/aps.65.040201
    [10] Feng X B, Li B Y, Ma S 2021 SIAM J. Numer. Anal. 59 1566 doi: 10.1137/20M1344998
    [11] Ibarra-Villalón H E, Pottiez O, Gómez-Vieyra A, Lauterio-Cruz J P, Bracamontes- Rodriguez Y E 2023 Phys. Scr. 98 065514 doi: 10.1088/1402-4896/acd22c
    [12] Zhang L F, Liu K, Zhong H Z, Zhang J G, Li Y, Fan D Y 2015 Opt. Express 23 2566 doi: 10.1364/OE.23.002566
    [13] Yu Y, Zhang Y T, Song X X, Zhang H T, Cao M X, Che Y L, Zhang H, Yao J Q 2017 IEEE Photonics J. 9 7904107 doi: 10.1109/JPHOT.2017.2701841
    [14] Xin W, Wang Y, Xin Z G, Li L 2021 Opt. Commun. 489 126889 doi: 10.1016/j.optcom.2021.126889
    [15] 罗民, 张泽贤, 陈乃妙, 刘萌, 罗爱平, 徐文成, 罗智超 2023 物理学报 72 204203 doi: 10.7498/aps.72.20230868 Luo M, Zhang Y Z, Chen N M, Liu M, Luo A P, Xu W C, Luo Z C 2023 Acta Phys. Sin. 72 204203 doi: 10.7498/aps.72.20230868
    [16] Lawal Z K, Yassin H, Lai D T, Che-Idris A 2022 Big Data Cogn. Comput. 6 140 doi: 10.3390/bdcc6040140
    [17] Karniadakis G E, Kevrekidis I G, Lu L, Perdikaris P, Wang S, Yang L 2021 Nat. Rev. Phys. 3 422 doi: 10.1038/s42254-021-00314-5
    [18] 李野, 陈松灿 2022 计算机科学 49 254 doi: 10.11896/jsjkx.210600184 Li Y, Chen S C 2022 Comput. Sci. 49 254 doi: 10.11896/jsjkx.210600184
    [19] Raissi M, Perdikaris P, Karniadakis G E 2019 J. Comput. Phys. 378 686 doi: 10.1016/j.jcp.2018.10.045
    [20] Pu J C, Peng W Q, Chen Y 2021 Wave Motion. 107 102823 doi: 10.1016/j.wavemoti.2021.102823
    [21] Pu J C, Li J, Chen Y 2021 Nonlinear Dyn. 105 1723 doi: 10.1007/s11071-021-06554-5
    [22] Wang L, Yan Z Y 2021 Phys. Lett. A 404 127408 doi: 10.1016/j.physleta.2021.127408
    [23] Zang Y B, Yu Z M, Xu K, Chen M H, Yang S G, Chen H W 2021 J. Lightwave Technol. 40 404 doi: 10.1109/JLT.2021.3139377
    [24] Jiang X T, Wang D S, Chen X, Zhang M 2022 J. Lightwave Technol. 40 21 doi: 10.1109/JLT.2022.3199782
    [25] Jiang X T, Wang D S, Fan Q R, Zhang M, Lu C, Lau A P 2022 Laser Photonics Rev. 16 2100483 doi: 10.1002/lpor.202100483
    [26] Fang Y, Bo W B, Wang R R, Wang W W, Chao Q D 2022 Chaos Soliton. Fract. 165 112908 doi: 10.1016/j.chaos.2022.112908
    [27] 田十方, 李彪 2023 物理学报 72 100202 doi: 10.7498/aps.72.20222381 Tian S F, Li B 2023 Acta Phys. Sin. 72 100202 doi: 10.7498/aps.72.20222381
    [28] 罗霄, 张民, 蒋啸天, 宋裕琛, 张希萌, 王丹石 2023 红外与激光工程 52 12 doi: 10.3788/IRLA20230188 Luo X, Zhang M, Jiang X T, Song X M, Zhang X M, Wang D S 2023 Infrared Laser Eng. 52 12 doi: 10.3788/IRLA20230188
    [29] Thulasidharan K, Sinthuja N, Priya N V, Senthilvelan M 2024 Commun. Theor. Phys. 76 115801 doi: 10.1088/1572-9494/ad6854
    [30] Psaros A F, Kawaguchi K, Karniadakis G E 2022 J. Comput. Phys. 458 111121 doi: 10.1016/j.jcp.2022.111121
    [31] Uduagbomen J, Leeson M S, Liu Z, Lakshminarayana S, Xu T H 2024 Appl. Opt. 63 3794 doi: 10.1364/AO.524426
    [32] Cuomo S, Di Cola V S, Giampaolo F, Rozza G, Raissi M, Piccialli F 2022 J. Sci. Comput. 92 88 doi: 10.1007/s10915-022-01939-z
    [33] Lu L, Meng X H, Mao Z P, Karniadakis G E 2019 SIAM Rev. 63 208 doi: 10.1137/19M1274067
    [34] Yu J, Lu L, Meng X H, Karniadakis G E 2022 Comput. Methods Appl. Mech. Eng. 393 114823 doi: 10.1016/j.cma.2022.114823
    [35] Wang T M, Cai L J, Xia C J, Song H, Li L B, Bai G X, Fu N Q, Xian L D, Yang R, Mu H R, Zhang G Y, Lin S H 2024 Adv. Sci. 11 2406476 doi: 10.1002/advs.202406476
    [36] Gong K W, Li L B, Yu W Z 2023 Mater. Des. 228 111848 doi: 10.1016/j.matdes.2023.111848
    [37] Ding B B, Li L B, Gong K W 2023 Appl. Surf. Sci. 22 156944 doi: 10.1016/j.apsusc.2023.156944
    [38] Mao D, He Z W, Zhang Y S, Du Y Q, Zeng C, Yun L, Luo Z C, Li T J, Sun Z P, Zhao J L 2022 Light Sci. Appl. 11 25 doi: 10.1038/s41377-022-00713-y
    [39] Mao D, Wang H, Zhang H, Zeng C, Du Y Q, He Z W, Sun Z P, Zhao J L 2021 Nat. Commun. 12 6712 doi: 10.1038/s41467-021-26872-x
    [40] Mao D, Gao Q, Li J Y, He Z W, Du Y Q, Zeng C, Sun Z P, Zhao J L 2022 Phys. Rev. Appl. 18 044044 doi: 10.1103/PhysRevApplied.18.044044
    [41] Rao C P, Ren P, Wang Q, Buyukozturk O, Sun H, Liu Y 2023 Nat. Mach. Intell. 5 765 doi: 10.1038/s42256-023-00685-7
    [42] Cao R H, Su J, Feng J Q, Guo Q 2024 Electron. Res. Arch. 32 6641 doi: 10.3934/era.2024310
    [43] Ismail M S, Alamri S Z 2004 Int. J. Comput. Math. 81 333 doi: 10.1080/00207160410001661339
    [44] Wang T 2011 J. Comput. Appl. Math. 235 4237 doi: 10.1016/j.cam.2011.03.019
    [45] Wu G Z, Fang Y, Wang Y Y, Wu G C, Dai C Q 2021 Chaos Solitons Fractals 152 111393 doi: 10.1016/j.chaos.2021.111393
  • 加载中
图( 10) 表( 1)
计量
  • 文章访问数:  134
  • HTML全文浏览数:  134
  • PDF下载数:  13
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-10-21
  • 刊出日期:  2025-03-26

基于智能算法对脉冲在光纤中传输动力学的研究

    通讯作者: E-mail: hanxiaoxiang@xpu.edu.cn.; 
    作者简介: 李君: 3480275814@qq.com
  • 1. 西安工程大学理学院, 西安　710048
  • 2. 射线柔性防护技术陕西省高校工程研究中心, 西安　710048
  • 3. 西安市核防护纺织装备技术重点实验室, 西安　710048
  • 收稿日期:  2024-10-21

摘要: 

非线性薛定谔方程(NLSE)在量子力学、非线性光学、等离子体物理、凝聚态物理、光纤通信和激光系统设计等多个领域中都具有重要的应用, 其精确求解对于理解复杂物理现象至关重要. 本文深入研究了传统的有限差分法(FDM)、分步傅里叶法(SSF)与智能算法中的物理信息神经网络(PINN)方法, 旨在高效且准确地求解光纤中的复杂NLSE. 首先介绍了PINN方法对NLSE的求解方法、步骤和结果, 并对比了FDM, SSF, PINN方法对复杂NLSE求解与脉冲远距离脉冲传输的误差. 然后, 讨论了PINN不同网络结构和网络参数对NLSE求解精度的影响, 还验证了集成学习策略的有效性, 即通过结合传统数值方法与PINN的优势, 提高NLSE求解的准确度. 最后, 采用上述算法研究了不同啁啾的艾里脉冲在光纤中的演化过程与保偏光纤对应的矢量非线性薛定谔方程(VNLSE)求解过程及结果误差. 本研究通过对比FDM, SSF, PINN在求解NLSE时的特点, 提出的集成学习方案在脉冲传输动力学研究和数据驱动仿真方面具有重要的应用.

English Abstract

    全文HTML

    1.   引　言

    • 超短脉冲在光纤中的非线性动力学研究是光纤光学、超快光学和信息光学的重要组成部分, 极大地推动了光纤激光器、光纤通信和光纤放大器的快速发展. 在光纤中, 激光脉冲的非线性传输过程可以通过非线性薛定谔方程(nonlinear Schrödinger equation, NLSE)来精确描述. 这一过程中蕴含着丰富而复杂的物理现象, 包括衰减、群速度色散(group velocity dispersion, GVD)、自相位调制(self-phase modulation, SPM)、交叉相位调制(cross-phase modulation, XPM)、四波混频(four-wave mixing, FWM)、受激拉曼散射(stimulated Raman scattering, SRS)以及受激布里渊散射(stimulated Brillouin scattering, SBS)等[1,2]. 鉴于NLSE在考虑多种效应时的高度复杂性, 直接求解其解析解显得尤为困难. 因此, 研究人员开发了多种数值方法来模拟这一过程, 如分步傅里叶法(split-step Fourier method, SSF)、有限差分法(finite difference method, FDM)和伪谱法(pseudo spectral method, PSM)等. 这些方法利用计算机的迭代计算能力和连续物理过程的离散化处理, 能够精确地模拟光脉冲在光纤中的展宽、压缩、频谱变化以及产生新的频率成分等非线性动力学过程.

      研究人员通过多种数值方法成功求解了NLSE, 显著推动了光纤技术的飞速发展. 例如, Chang等[3]于1999年运用Crank-Nicolson型、Hopscotch型、SSF及伪谱法等对广义非线性薛定谔方程(GNLSE)进行了深入解析, 探讨了各方法的有效性与稳健性. Wang等[4]于2005年利用分步有限差分法对各种NLSE方程进行求解. 随着时间的推移, 赵磊等[5]于2009年利用SSF算法求解GNLSE并讨论了窗口选择合理性. Xie[6]同年给出了一维非线性薛定谔方程两种不同有限差分法求解格式. Wu[7] 于2012年引入了双网格混合有限元格式, 为稳态与非稳态NLSE方程的求解开辟了新路径. 近年来, Caplan[8]于2013年基于龙格-库塔(Runge-Kutta, RK)线性稳定性理论将NLSE的非线性视为常数并采用显式有限差分法进行数值求解. 崔少燕等[9]于2016年运用SSF对外部势场下的GNLSE进行了数值求解. Feng等[10]于2021年针对NLSE方程, 提出了一套任意高阶全离散时空有限元方法. Ibarra-Villalon等[11]于2023年评估了FDM方法和伪谱方法验证脉冲在光纤中传播问题的适用性, 通过有限差分方法的四种格式和伪谱方法的三种格式验证基本孤子的传播, 进一步丰富了NLSE数值求解的工具体系. Zhang 等[12]利用SSF算法对啁啾艾里脉冲在光纤中的动态传播进行了数值模拟与结果分析, 展示了SSF算法在处理复杂脉冲传播问题时的强大能力及其广泛的应用前景. 然而尽管这些方法在精度与效率上取得了显著进展, 其复杂的参数设定与迭代设计仍对新手研究者构成挑战, 特别是SSF与FDM等方法要获得高精度的近似解需在时域内生成大量的网格点, 计算耗时且资源消耗大, 因此探索更加简洁高效的数值求解方法是当前亟待解决的问题[13–15].

      在人工智能技术的推动下, 机器学习和数据分析技术在多个前沿领域取得了显著进展, 包括模式识别、自然语言处理、计算机视觉、认知科学和基因组学等. 近年来, 计算物理领域提出了一种创新方法——物理信息神经网络(physics-informed neural network, PINN)[16–18]. PINN巧妙地将神经网络与物理信息相结合, 为直接求解偏微分方程（partial differential equations, PDE）提供了新的途径. 通过训练PINN不仅能解决监督学习任务, 还能严格遵循由一般非线性偏微分方程描述的物理定律. 这种结构化信息的编码极大地丰富了算法所处理的数据内容, 使其能够迅速找到准确解, 并在训练样本有限的情况下实现良好的泛化能力[19]. 此外, PINN作为一种无网格方法, 避免了传统网格差分的局限性, 有效缓解了数值求解中的维数爆炸问题和传统神经网络对数据的过度依赖. 在超短激光脉冲传输的NLSE求解、参数估计及算法改进等方面, 研究人员已开展了大量工作. 例如, 2021年Pu等[20,21]研究了导数非线性薛定谔方程(DNLSE)并提出了基于神经元局部自适应激活函数的改进PINN方法. Wang和Yan[22]则采用多层PINN深度学习方法研究了不同初始条件和周期边界条件下DNLSE的数据驱动异常波解. Zang等[23]提出了一种基于PINN的原理驱动光纤传输模型. 2022年, Jiang等通过求解NLSE反问题提出了基于PINN的光纤参数估计方法[24], 并系统验证了光纤中的色散、自相位调制和高阶非线性效应等多种物理效应[25]; Fang等[26]则将复合导数嵌入信息加入到PINN的软约束中提出了SCPINN, 用于预测单模光纤中亮皮秒光孤子和暗皮秒光孤子以及飞秒孤子分子的非线性动力学和形成过程, 揭示了孤子传输过程中脉冲能量振幅频谱和相位等物理量的变化. 田十方和李彪等[27]为了增强PINN稳定性提出了梯度优化物理信息神经网络(GOPINNs), 该网络结构对梯度波动更具鲁棒性. 2023年, Luo等[28]着眼于光纤非线性的建模, 针对光纤中光信号传输时受损耗、色散以及非线性等多种物理效应影响而发生演化场景展开研究. Thulasidharan等[29]引入了强约束理论引导神经网络(SCTgNN), 以研究NLSE局部解的行为. Psaros等[30]提出一种引入元学习(meta-learning)技术的PINN损失函数. Uduagbomen等[31]采用支架技术(scaffolding technique)和渐进块(progressive block)学习技术来进行PINN建模, 从而规避基于物理的正则化项造成的限制, 实现NLSE的准确求解. Cuomo等[32]进行了关于PINN全面综述, 表征不同PINN网络架构及其相关的优势和劣势. Lu等[33,34]研究正、逆偏微分方程问题的梯度增强物理信息神经网络, 提供了一个DeepXDE Python库, 有助于PINN的更快发展. 以上的研究者都分别把相应的物理信息嵌套到神经网络中, 以实现一定的物理约束. PINN不仅能够高效地求解PDE, 还能在数据稀缺的情况下实现良好的泛化能力. 随着研究的深入, PINN在光纤传输、非线性动力学等领域的应用将更加广泛, 为科学研究和工程实践提供强有力的支持. 然而, 尽管PINN在多个方面取得了显著进展, 但其在与其他数值方法求解的对比和集成学习方面的研究仍需进一步加强, 以期在更广泛的领域中发挥其优势.

      本文深入探究了不同算法对多个非线性效应共同作用下的超短脉冲在光纤中动力学演化过程. 系统地运用了FDM, SSF, PINN三种算法求解NLSE, 对比了3种方法求解精度误差, 并对远距离脉冲传输进行模拟分析; 深入讨论了 PINN不同激活函数、网络类型、网络结构对该方程求解精度的影响, 验证将传统方法(FDM和SSF)与PINN相结合的可行性, 提出提高该方程求解精度的集成学习方法. 最后讨论了两个案例: 对不同啁啾特性的艾里脉冲在光纤中的动力学过程进行数值模拟和分析; 对矢量的非线性薛定谔方程(VNLSE)进行数值模拟. 本研究为超短脉冲在光纤中传输动力学的研究提供了新的视角和有力的工具, 对于推动光纤通信、超快光学的发展具有重要意义.

    2.   非线性薛定谔方程求解

      2.1.   理论模型

    • 飞秒脉冲在单模光纤中的传输可以用NLSE来描述, NLSE可以描述单模光纤中的各种物理效应, 如群速度色散(GVD)、自相位调制(SPM)和受激拉曼散射(SRS). 通过NLSE研究这些物理效应对超短脉冲传输的影响, 可以为实现高容量、远距离飞秒孤子通信提供理论指导. NLSE可表示如下[1,2]:

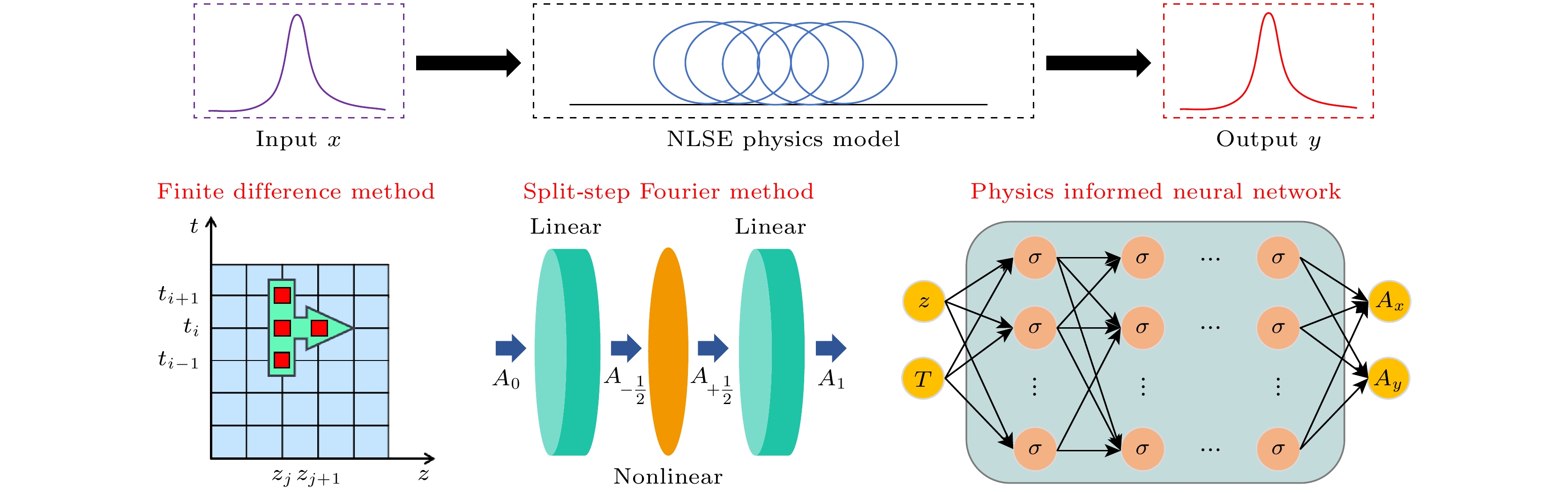
      其中, A是脉冲慢变振幅, z是传输距离, $\alpha $是光纤损耗系数, ${\beta _2}$是群速度色散, $\gamma $是非线性系数, $\omega $为脉冲的中心角频率, ${T_{\text{R}}}$为拉曼增益系数, T为随脉冲以群速度移动的参照系中的时间量度. 对于上述复杂的NLSE来说是没有解析解的, 本文利用PINN, FDM, SSF等方法对超短脉冲在光纤传播演化对应的NLSE进行数值求解并对比, 具体的求解方法示意图如图1所示.

      • 2.2.   有限差分方法

    • 有限差分方法作为分析脉冲在光纤中传输特性的重要工具, 被广泛应用于锁模激光器及其光纤传输过程的研究中. 这一方法以全时域的方式运作, 通过精确离散化NLSE, 有效地模拟了光脉冲在光纤中的复杂动态行为[4]. 在FDM框架下, 首先将NLSE中的时间和空间偏导数利用网格进行离散化: $z = j{\text{d}}z$, $T = i{\text{d}}t$, 其中${\text{d}}z$和${\text{d}}t$分别为空间域和时间域的步长, $ i $和$j$分别为整数. 把方程(1)进行离散具体如下:

      这一离散化过程将连续的偏微分方程转化为一系列可迭代离散公式(2), 采用迭代算法逐步计算, 从而模拟出脉冲在光纤中随时间演变的完整过程.

      • 2.3.   分步傅里叶法

    • 分步傅里叶法是一种常用于模拟光脉冲在光纤中传播的非线性效应的方法. 该方法结合了傅里叶变换的高效性和有限差分法的灵活性, 针对NLSE提供了强有力的求解手段. 在SSF的框架下, 光脉冲的初始形态与周期性边界条件的设定构成了模拟的基础物理约束, 其直接影响脉冲的演化特性. 在光纤传播过程中, 光脉冲会同时受到光纤中线性与非线性效应的双重影响[5,8]. 在SSF方法中, 当传播距离h极小时, 即NLSE是线性项和非线性项的组合, 可以把方程(1)改写成如下形式:

      其中, $\hat D$为线性微分算符, 描述光纤中的色散与损耗; $ \hat N $是非线性微分算符, 用于调控光纤非线性对脉冲传播的影响. SSF方法利用线性、非线性微分算符来对传输距离进行分段, 当光脉冲在光纤中传输了z时, 单独考虑线性效应推进到z + h/2处; 在区间中点z + h/2处集中处理非线性效应, 通过光场乘以非线性项来近似整个区间h内的非线性积累; 继续推进至z + h并剩余考虑线性效应, 从而得到该段距离的近似解. 然而, SSF方法依赖于快速傅里叶变换(fast Fourier transform, FFT), 这要求脉冲在时域与频域间转换时需进行加窗处理, 并限制窗口内的样本量. 尽管单次FFT计算高效, 但大规模数据下的频繁操作显著增加了计算负担. 特别地, 当脉冲能量快速扩散并接近窗口边界时, FFT的周期性假设导致能量从窗口一侧“泄漏”至另一侧, 引发数值失真. 通常应选择足够宽的时间窗口, 以保证脉冲能量一直限制在时间窗口内. 在实际计算中, 反复调整纵向传输步长、横向时间步长和脉冲取样点数来保证计算精度.

      • 2.4.   物理信息神经网络

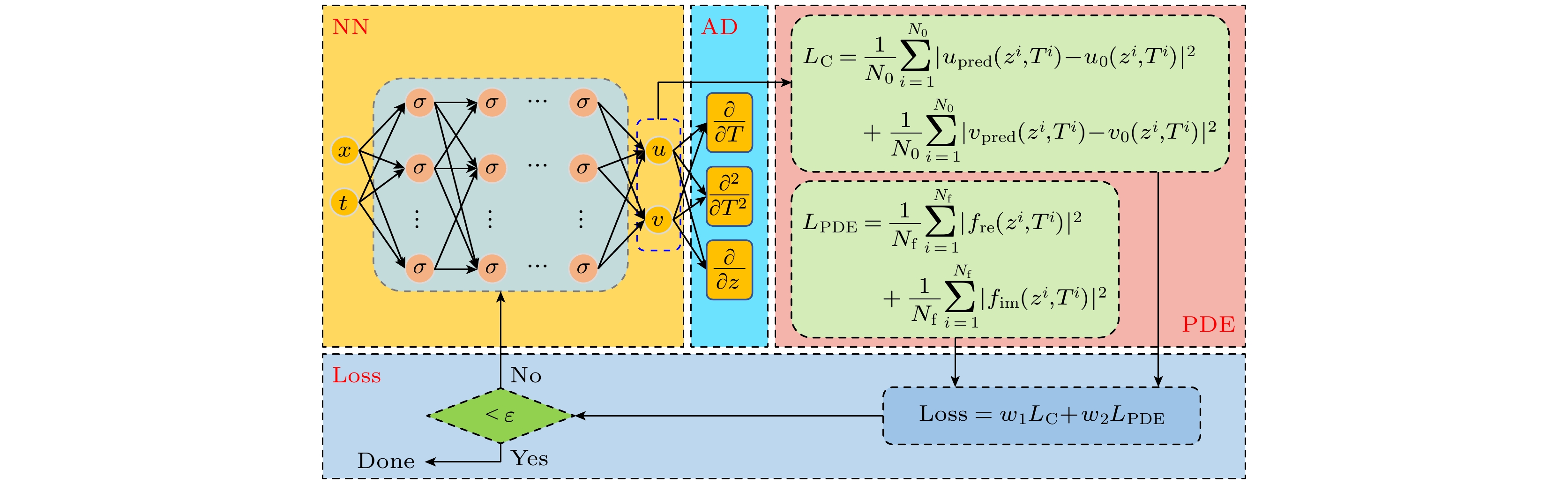
    • FDM, SSF都是基于网格差分进行数值求解, 但随着深度学习和数据驱动的发展, 出现了一个无网格的方法去求解传统的偏微分方程, 称为PINN. 该网络与数据驱动的神经网络不同, 数据驱动的神经网络只是简单去训练输入与输出之间的隐函数关系, 而PINN在数据驱动的基础上, 利用控制方程和物理约束构成的损失函数, 并作为正则化机制. 在计算中引入了自动微分的技术、梯度下降法等优化算法去优化损失函数, 将偏微分方程求解的问题转化为损失函数优化问题, 通过网络训练对应的参数已满足物理信息的先验条件. 采用上述方法对方程(1)进行数值求解[16,17]. 由于神经网络只能在实数域进行计算, NLSE是一个复数方程, 需要将该方程进行实部和虚部分离, 将A写成$A = {A_x} + {\text{i}}{A_y}$代入(1)式中进行化简可得NLSE的实部函数${f_{{\text{Re}}}}$和虚部函数$ {f_{{\text{Im}}}} $, 分别表示为

      为了求解方程NLSE, 建立一个由多层深度神经网络组成的PINN网络, 如图2所示. PINN网络采用时空辅助坐标$(z, T)$作为输入, 预测解(Ax, Ay)作为输出. 为了满足${f_{{\text{Re}}}}$与$ {f_{{\text{Im}}}} $的约束条件, 借助自动微分技术, 精确地计算空间导数、时间的一阶、二阶导数和非线性项对应的导数, 从而构造NLSE对应的实虚部损失函数. 此外, 自动微分作为一种无网格方法, 不会出现传统数值方法中截断误差和舍入误差等误差. 然后, 结合初始条件、边界条件与NLSE方程的均方误差(MSE)损失来学习网络参数, 其具有自适应权值的神经网络损失函数为[23,24]

      其中, ${w_1}$, ${w_2}$是引入PINN对应的自动更新权重变量. LC对应于初始脉冲与边界条件的实部和虚部约束, 而LPDE对不满足实部与虚部控制方程约束的训练结果进行惩罚. 此外, $ {u_0}({z^i}, {T^i}), {v_0}({z^i}, {T^i}) $分别表示初始脉冲与边界条件的实部和虚部输入, $ {u_{{\text{pred}}}}({z^i}, {T^i}), {v_{{\text{pred}}}}({z^i}, {T^i}) $分别表示初始脉冲与边界条件的实部和虚部预测输出. $ {f_{{\text{Re}}}}({z^i}, {T^i}), {f_{{\text{Im}}}}({z^i}, {T^i}) $分别表示NLSE对应实部和虚部约束方程. N0和Nf是计算初始条件、边界条件、控制方程的均方误差项所需的辅助坐标数. 采用优化算法不断的调节网络参数, 从而获得满足NLSE方程对应的数值解.

    3.   分　析

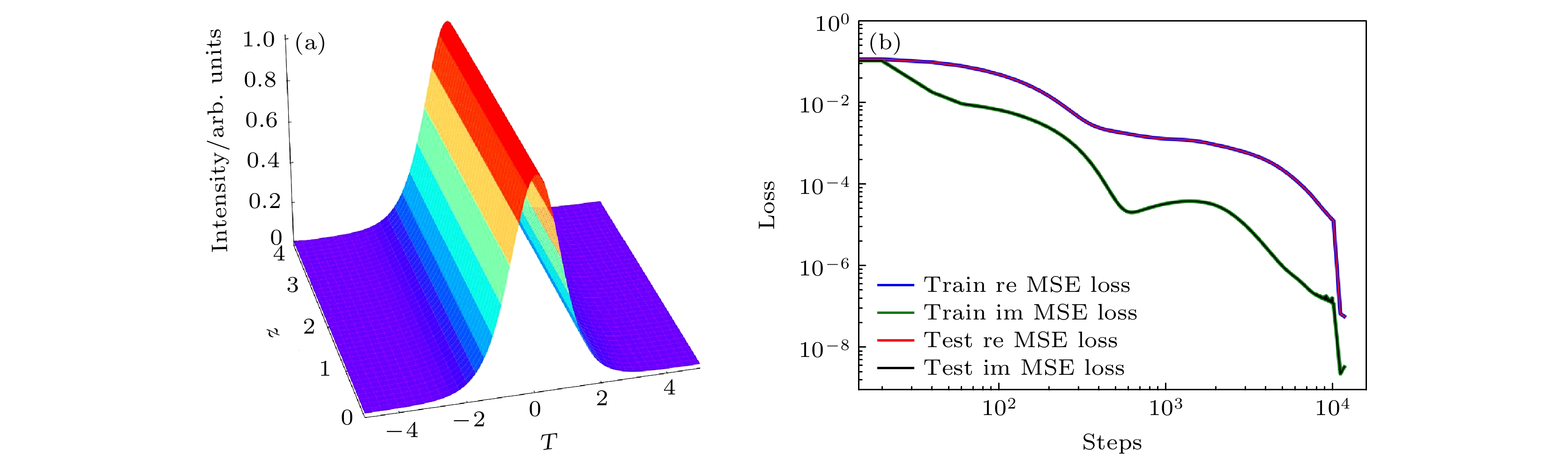
    • 本文对比了多种算法(FDM, SSF, PINN)求解超短脉冲在光纤中传播的NLSE结果. 鉴于FDM和SSF作为传统方法的求解方法已非常成熟, 其具体实现细节在此不再详述. 本文详细讨论了PINN求解该方程的具体步骤. 首先, PINN求解框架构建时, 需要定义NLSE方程对应的空间和时间域、PDE函数、边界条件和初始条件, 指定在域内、边界上、初始时间采样的训练点的数量分别为200, 20, 100, 使用伪谱法分布训练点. 随后, 鉴于输入特征为时间与位置, 输出为超短脉冲振幅的复数实部和虚部, 构造前反馈神经网络(FNN)输入层、隐藏层、输出层的神经元数量分别为2, 15, 2, 隐藏层的层数和激活函数分别为4和tanh, 权重初始化遵循Glorot normal原则, 学习率设定为1×10–3, 并采用Adam与L-BFGS双重优化算法对自定义的损失函数公式(6)进行迭代优化, 总迭代次数设置为10000次旨在最小化误差, 确保模型输出的精确性同时满足NLSE、边界和初始条件. 通过上述训练过程, PINN模型成功收敛, 每隔20次迭代显示一次训练结果, 并导出了损失函数性能评估图与最终模型. 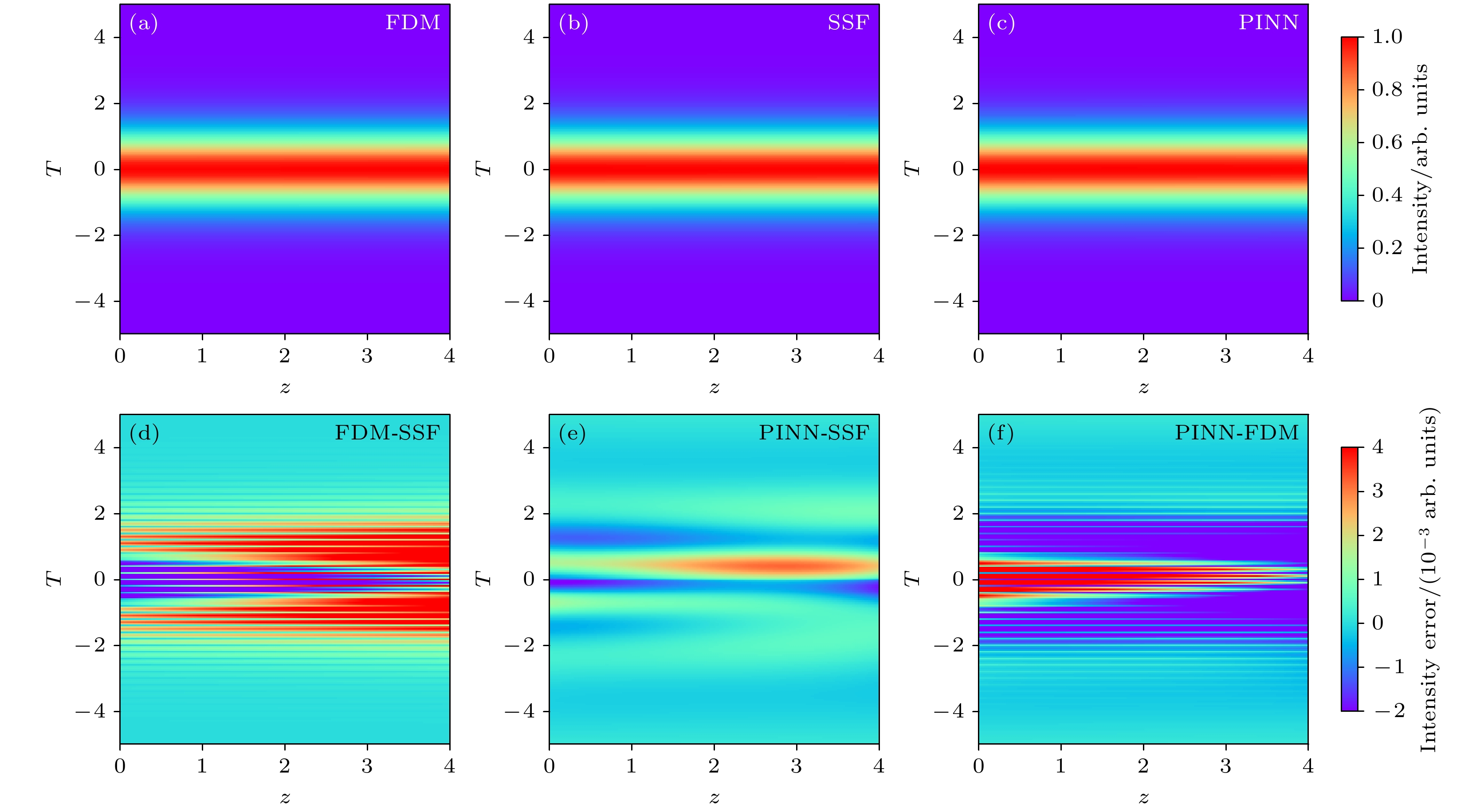其中PINN求解的参数设置为初始脉冲A0为sech(t); 传输距离z为4 m; 光纤损耗系数$\alpha $为0.001 dB/m; 群速度色散${\beta _2}$为5×10–27 (m·W)–1; 非线性系数$\gamma$为1×10–3 s2/m; 脉冲中心频率$\omega $为1.83×1015 Hz; 拉曼增益系数${T_{\text{R}}}$为0.4 (m·W)–1; 随脉冲时间范围T为–5—5 ps. 模拟可得脉冲在光纤中的传播演化图, 如图3所示. 从图3(a)可见, 随着传输距离的增大, 光强逐渐减弱, 脉冲宽度显著展宽. 从图3(b)可见, 损失函数的下降趋势, 其中针对NLSE方程实部与虚部的训练与测试均方误差, 显示训练与测试误差曲线几乎重合, 且随着训练迭代次数的增加, 误差持续减小, 最终稳定在较低误差水平, 充分证明了PINN模型在求解NLSE问题上的高精度与强大的泛 化能力. 为了保证实验的可重复性和结果的一致 性, 统一设置了随机数种子(tensorflow, random, deepxde, numpy均设定为42), 从而进一步提升研究结论的可信度与稳健性.

      为了深入剖析传统方法与PINN在处理NLSE上的性能差异, 在上述设定的PINN参数框架下, 分别采用SSF, FDM, PINN求解NLSE (1)式. 通过对比这3种方法的结果, 可以观察到脉冲在光纤中传输的时域演化及误差情况. 图4(a)—(c)分别展示了SSF, FDM和PINN方法模拟的脉冲在光纤中的时域传输演化过程. 尽管采用了不同的数值计算方法, 但三者的计算结果在整体上保持一致, 这验证了每种方法的有效性. 图4(d)—(f)则聚焦于误差分析, 分别展示了SSF与FDM、PINN与FDM以及PINN与SSF之间的误差对比. 结果表明, 这些误差的量级均维持在0.001 W/m²左右. 其中, SSF与FDM, PINN与FDM以及PINN与SSF的绝对误差总和分别为48.515, 50.068和21.201. 由此可见, PINN与SSF之间的误差最小, 显示出更为接近的数值解. PINN方法具有很好的可扩展性, 对于训练好的PINN模型被保存下来后, 面对类似的NLSE求解任务时, 可以直接调用该模型进行快速计算, 而无需重复耗时的训练过程. 这一特性使得PINN在复杂光纤激光器系统中大规模脉冲传输模拟中展现出巨大潜力, 能够显著缩短求解时间并提高计算效率.

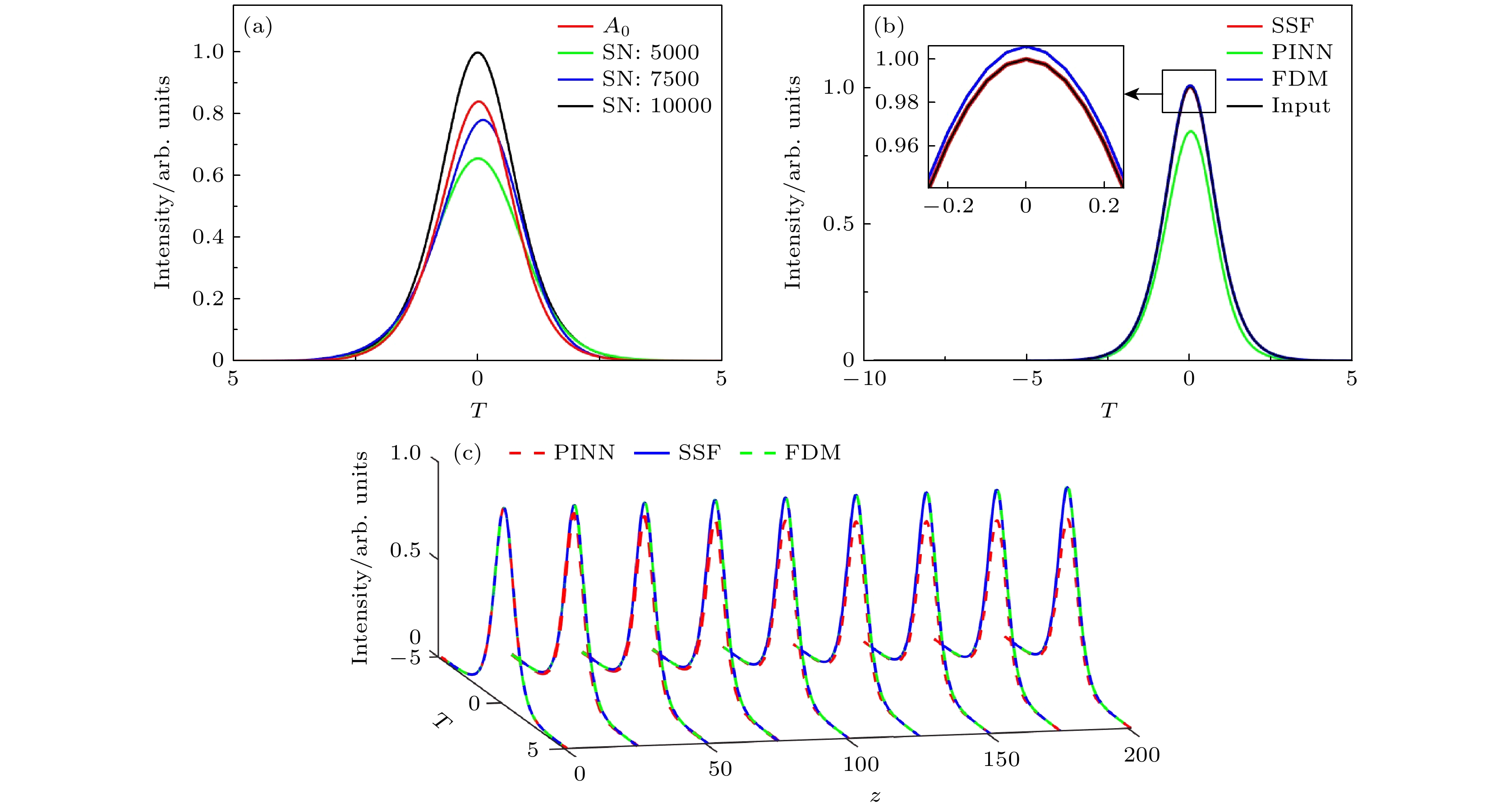
      进一步计算了基阶孤子在光纤中传输200 m的动力学演化过程. 设置光纤参数损耗系数$\alpha $、群速度色散${\beta _2}$、非线性系数$\gamma $分别为0 dB/m, 2× 10–27 (m·W)–1, 2.5×10–3 s2/m, 拉曼增益系数${T_{\text{R}}}$为0.4 (m·W)–1, 初始脉冲A0为sech(t), 传输距 离z为200 m. PINN, SSF, FDM的计算结果如图5所示. 在运用PINN进行求解时随着光纤传输距离的延长, 所需的采样点(sampling number, SN)的数量需要适当增加. 基于前反馈神经网络(FNN)的设置, 在边界上定义了80个采样点, 初始条件设置了300个采样点, 并在定义域内分别设置了5000, 7500, 10000个采样点来进行PINN的训练和求解. 图5(a)为PINN求解时不同采样点下, 基阶孤子在光纤中传输200 m后的输入与输出的对比图, 可见随着SN的增加, PINN训练求解的输出脉冲越接近输入结果, 求解越准确. 图5(b)为FDM, SSF, PINN求解基阶孤子传输的输入与输出的对比图, 其中SSF, FDM, PINN求解输出与输入对应的均方误差(MSE)分别为5.89×10–13, 2.52×10–6, 0.0037. SSF, FDM, PINN求解的输出与输入对应平均偏差误差(MBE)分别为4.25×10–9, –6.52×10–4, 0.036. 图5(c)为 FDM, SSF, PINN求解基阶孤子传输演化的过程图. 可见SSF在传输模拟中的误差最小, 而FDM由迭代过程中的误差累积效应, 其强度略有增大.

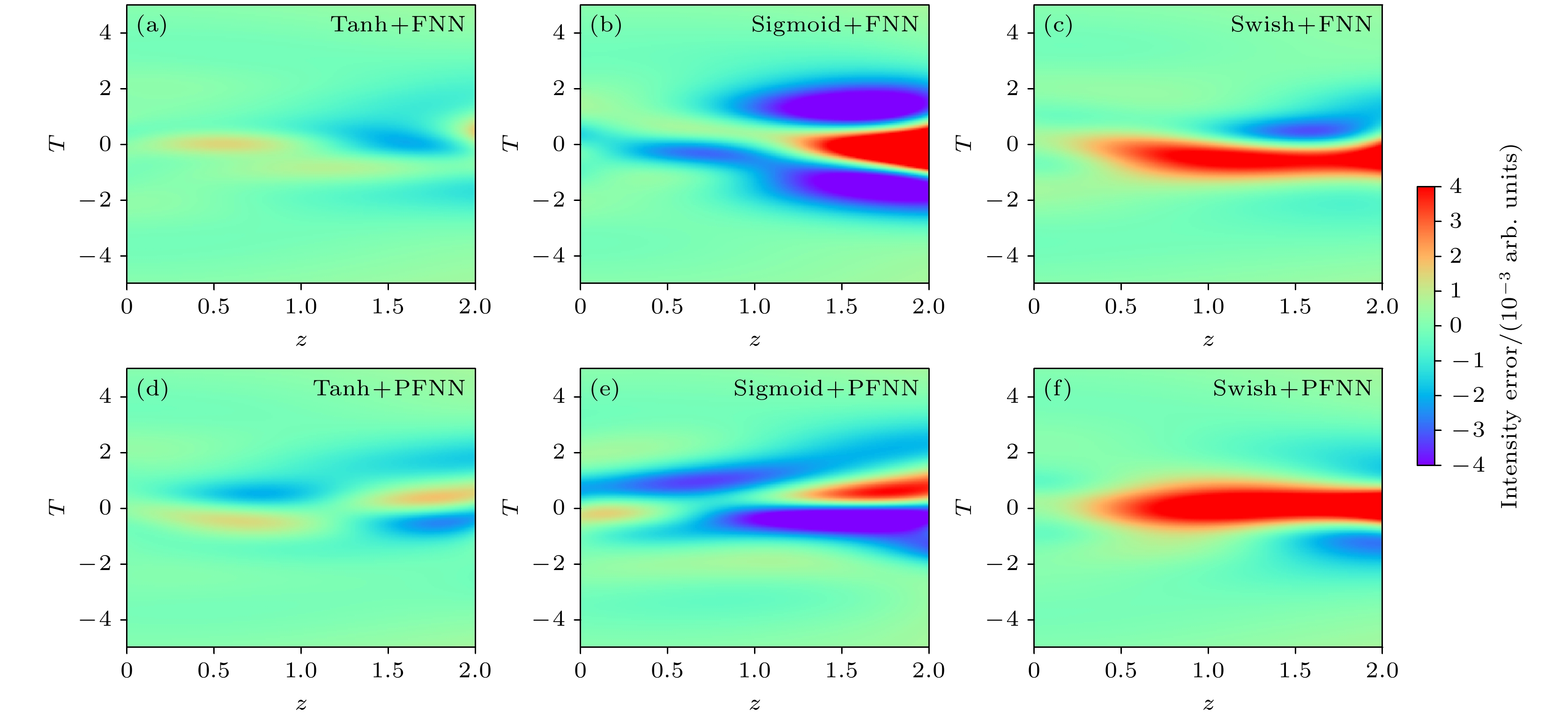
      为了研究PINN和传统方法的对比, 由于(1)式没有解析解, 无法验证所用方法的准确性, 因此在该方程的基础上, 忽略$\dfrac{{\text{i}}}{\omega }\dfrac{{\partial {{\left| A \right|}^2}A}}{{\partial T}}$, ${T_{\text{R}}}A\dfrac{{\partial {{\left| A \right|}^2}}}{{\partial T}}$, $\dfrac{\alpha }{2}A$项, 得到基础的非线性薛定谔方程$\dfrac{{\partial A}}{{\partial z}} = - \dfrac{{{\text{i}}{\beta _2}}}{2}\dfrac{{{\partial ^2}A}}{{\partial {T^2}}} + {\text{i}}\gamma {\left| A \right|^2}A$. 采用逆散射法可得到上述方程解析解为: $ A = \sqrt {\dfrac{|{{\beta _2}} |}{(\gamma {T_0}^2)}} {{\mathrm{sech}}} \bigg(\dfrac{T}{{{T_0}}}\bigg) \ \exp \bigg({\text{i}}\dfrac{{\left| {{\beta _2}} \right|}}{{2{T_0}^2}}z\bigg)$, 式中T0为脉冲轮廓的时间宽度, 设置初始脉冲 A0为sech(t); 传输距离z为2 m; 群速度色散${\beta _2}$为1 (m·W)–1; 非线性系数$\gamma $为0.5 s2/m. 通过上述方程的解析解来对比这3种方法的准确性[11].

      首先, 讨论不同神经网络类型与激活函数对PINN训练求解误差的影响. 神经网络类型分为部分全连接神经网络(partially-connected feedforward neural network, PFNN)和全连接神经网络(feedforward neural network, FNN)[21]. 在FNN中每一层的每个神经元都与下一层的每个神经元相连接, 这种连接方式确保了信息能够在网络中充分传播, 但增加了计算复杂度和参数数量; 在PFNN中每一层的神经元只与下一层的部分神经元相连接. 这种连接方式减少了网络中的参数数量和计算复杂度, 同时可能保留足够的表达能力. 在PINN的训练过程中, 采用3种不同的激活函数: tanh, sigmoid和swish. 其他超参数设置包括隐藏层数为4、每层神经元数为15、损失函数为均方误差, 并结合Adam和L-BFGS优化器进行训练. 通过设置不同的随机种子重复训练十次并取平均值, 得到了不同配置下脉冲在光纤中演化过程的误差图, 如图6所示. 图6(a)—(c)展示了在FNN网络中分别使用tanh, sigmoid和swish激活函数时的脉冲演化误差情况. 结果显示, 使用sigmoid激活函数的均方误差最大, 脉冲强度的变化也最为剧烈. 而在图6(d)—(f)中展示了PFNN网络中分别使用tanh, sigmoid和swish激活函数时的脉冲演化误差情况. 从图6可以看出, 当tanh激活函数与FNN组合时对应的误差最小; 相反地, sigmoid与FNN组合时的误差最大.

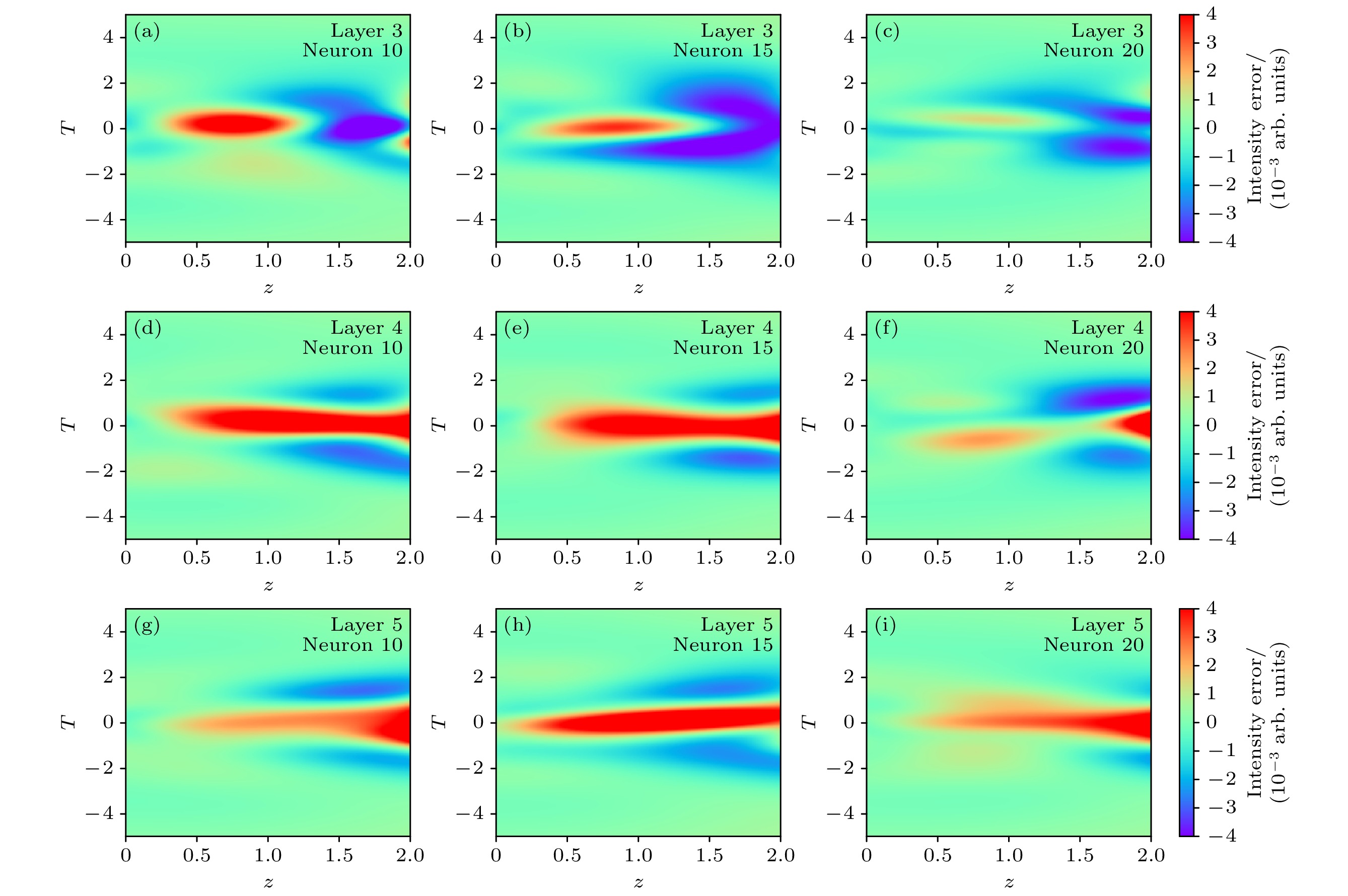
      在深入探讨PINN模型的网络架构时, 首先关注的是隐藏层的复杂度对模型泛化能力的影响. 隐藏层的复杂度主要通过神经元的数量和层数来体现, 这两者直接关系到模型的学习能力和预测精度. 采用tanh作为激活函数, 并指定了网络类型为FNN, 通过系统地调整隐藏层的层数与每层中的神经元个数来研究其对脉冲在光纤中演化过程模拟精度的影响. 为了更全面地评估这些参数变化的效果, 设置不同的随机种子并重复了十次训练过程, 可得误差图如图7所示. 在图7(a)—(c)中, 固定隐藏层为3层, 并逐步增加神经元个数. 结果显示, 随着神经元数量的增加, 模型的误差逐渐减小. 这表明增加神经元的复杂度能够有效地提高模型的预测精度. 当神经元个数从10增加到20时, 模型的误差显著降低, 这进一步验证了增加神经元数量对提升模型性能的重要性. 在图7(d)—(i)中, 进一步探讨了增加隐藏层数对模型性能的影响. 分别将隐藏层数增加到4层和5层, 并保持每层中的神经元个数不变. 结果显示, 神经元数量保持不变, 增加隐藏层数仍然能够进一步降低模型的误差. 这表明, 隐藏层数的增加对提升模型性能同样具有重要意义. 尽管增加神经元数量和隐藏层数能够显著降低模型的误差, 但随着网络复杂度的提升, 训练所需的时间和计算资源也会大幅增加. 这表明, 在实际应用中, 需要在模型精度和计算资源之间进行权衡, 以选择既经济又高效的网络参数配置.

      最后, 利用集成学习(ensemble learning)思想结合多个不同的模型来提高整体性能和泛化能力. 这里将传统方法(FDM, SSF)与数据驱动方法(PINN)相结合时, 可以充分利用各自的优势, 增强模型对复杂问题的适应能力. 为了全面评估集成学习的效果, 引入平均绝对误差(MAE)、均方误差(MSE)、均方根误差(RMS)、平均绝对百分比误差(MAPE)四个指标, 对FDM, SSF, PINN三种方法和集成学习的计算结果进行了评估. 4个指标的计算公式如下:

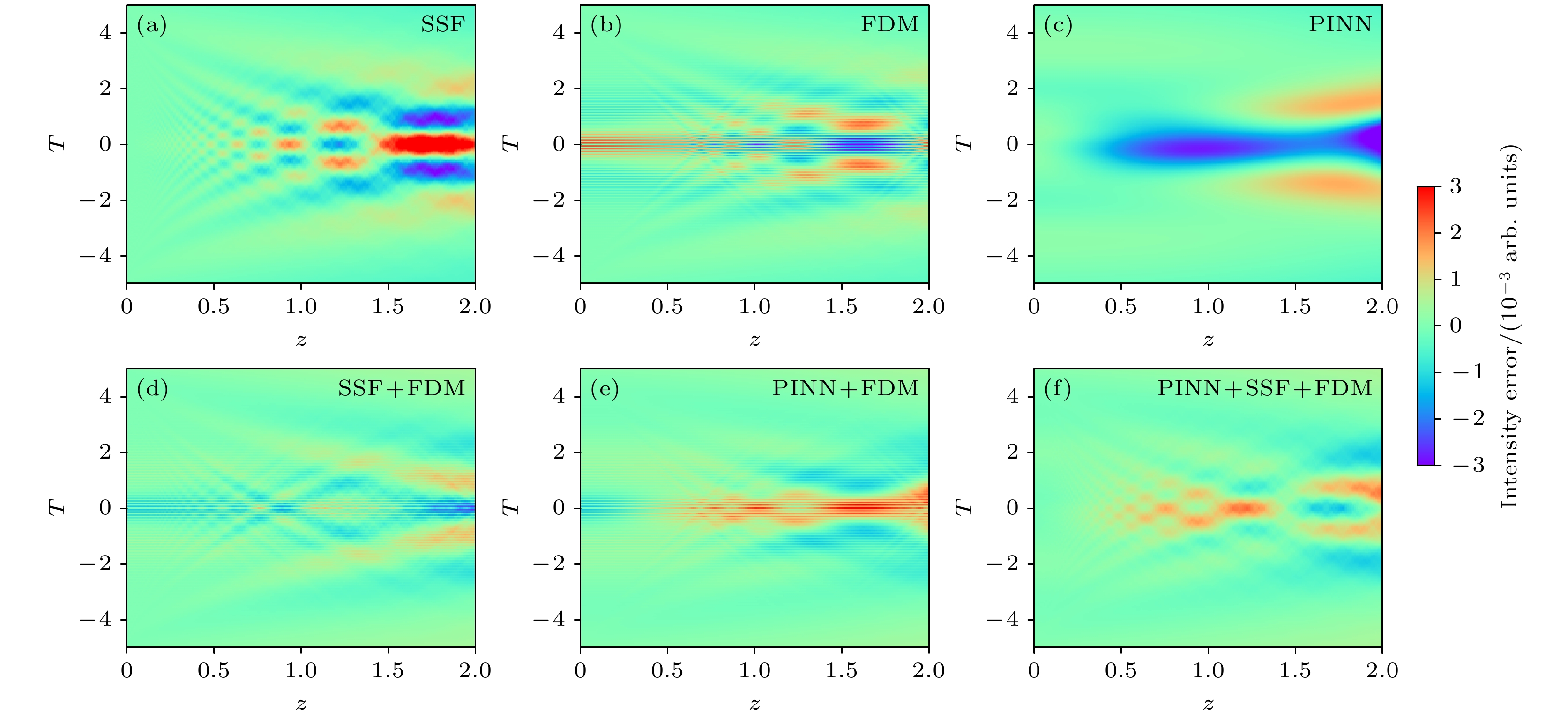
      其中, $ {A_i} $为模型的预测值, $ {\hat A_i} $为真实值. 具体的集成学习方法为采用累加FDM, SSF与PINN的预测结果, 并取平均$ {A_i} = ({A_{{\text{FDM}}}} + {A_{{\text{SSF}}}} + {A_{{\text{PINN}}}})/3 $, $ {A_i} $为集成学习后的数值解, $ {A_{{\text{FDM}}}} $, $ {A_{{\text{SSF}}}} $, $ {A_{{\text{PINN}}}} $分别为FDM, SSF, PINN三种方法的数值解. 根据上述方法得到的结果如图8所示. 图8(a)—(c)分别为独立使用FDM, SSF, PINN三种方法时的误差图, 可见每种方法因原理不同产生的误差不同. FDM与SSF随着迭代过程的进行, 误差逐渐累积, 这主要归因于数值方法中的误差传递效应. 图8(d)—(f)分别为SSF+FDM, PINN+FDM, PINN+SSF+FDM对应的集成学习误差图, 可见将3种方法集成结合可以大大减小与解析解的误差. 这一结果不仅验证了集成学习的有效性, 还凸显了将传统数值方法与数据驱动技术相结合的巨大潜力.

      为了深入剖析并精确评估3种方法(PINN, FDM, SSF)在不同集成策略下的性能优势, 计算了各集成方案下的关键误差指标: MAE, MSE, RMSE, MAPE. 表1的详尽数据清晰地展示了集成学习对数值求解精度的提升作用, 其中PINN+ FDM+ SSF的MAE, MSE, RMSE指标最好. 这证明了传统方法与数据驱动技术融合的集成学习方法在降低求解误差、提升预测精度方面的显著优势.

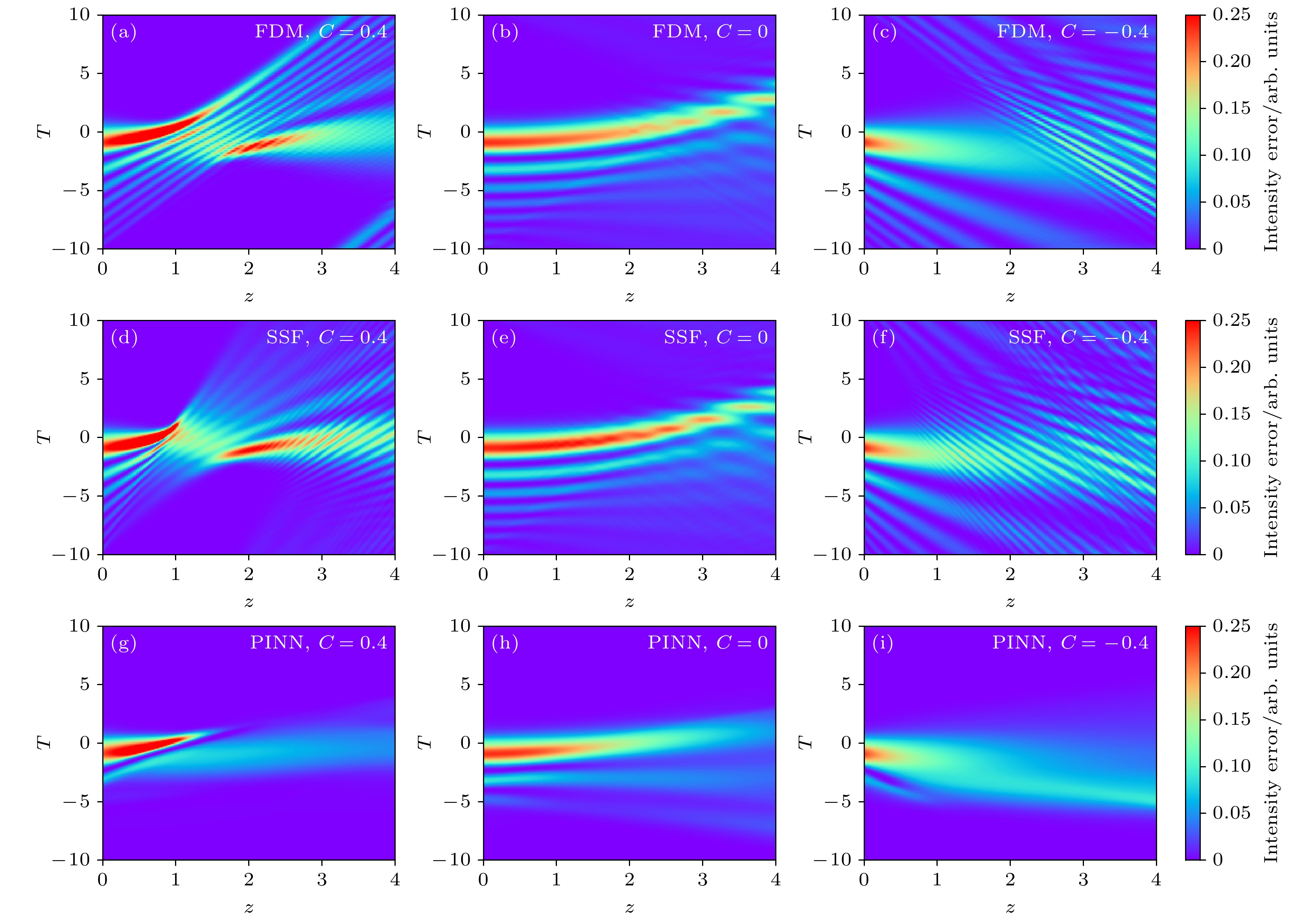
      为了更好地对比分析不同脉冲在(1)式的数值求解效果, 这里特别研究了啁啾艾里脉冲在光纤中的传播动力学演化过程. 引入的初始脉冲形式为$ U\left( {T, 0} \right) = {\text{Ai}}\left( T \right){\text{exp}}\left( {aT} \right){\text{exp}}\left( { - {\text{i}}C{T^2}} \right) $, 其中$\alpha $是截断因子, C为初始啁啾, Ai为Airy函数[29,30]. 通过3种不同的数值模拟方法, 详细探讨了这些脉冲在不同条件下的演化特性. 图9所示为不同算法和啁啾条件下艾里脉冲的演化过程. 从图9(a)—(c)可以清晰观察到, 无啁啾艾里脉冲在光纤中传播时, 起初能够保持其理想的自加速和无衍射特性; 然而随着传播距离的增大, 光纤色散逐渐占据主导地位, 导致无啁啾艾里脉冲的独特特性逐渐消失. 对于初始正啁啾艾里脉冲而言, 其在传播初期经历了一个减速压缩的过程, 能量向自加速方向聚集; 但随着传输距离进一步增大, 这种压缩达到一定程度后会进入一个崩塌区, 此时脉冲形状不再保持艾里形态. 而初始负啁啾艾里脉冲则在传输过程中表现出主瓣自加速现象减弱、旁瓣持续加速色散的特点, 同时主瓣和旁瓣的衍射及能量色散现象也显著加剧. 图9(d)—(f)展示了SSF与FDM二者遵循相同的变化趋势. 图9(g)—(i)中PINN显示出其独特的优势——无需迭代即可避免迭代误差问题、确保求解过程既连续又快速.

      为了更精确地模拟脉冲在介质中传输的动力学过程[35–37], 人们常会采用矢量的非线性薛定谔方程 (vector nonlinear Schrödinger equation, VNLSE)[38–40]. VNLSE包括双折射、非线性、色散、增益以及损耗等多种效应. 但由于增益项的存在使该方程含有积分项增加了求解的难度. 求解VNLSE通常采用SSF和RK方法, 将积分项转化为累加求和的形式, 利用迭代过程进行数值求解. 而传统的PINN在求解含有积分项VNLSE时有一定的困难. 近年来, 随着神经网络在求解偏微分方程领域的不断发展, 一种将时空分离处理的新思路被设计出来. 对时间维度采用时间序列或者循环神经网络等技术进行处理, 而空间维度则利用卷积或其他相关神经网络架构进行处理[41,42]. 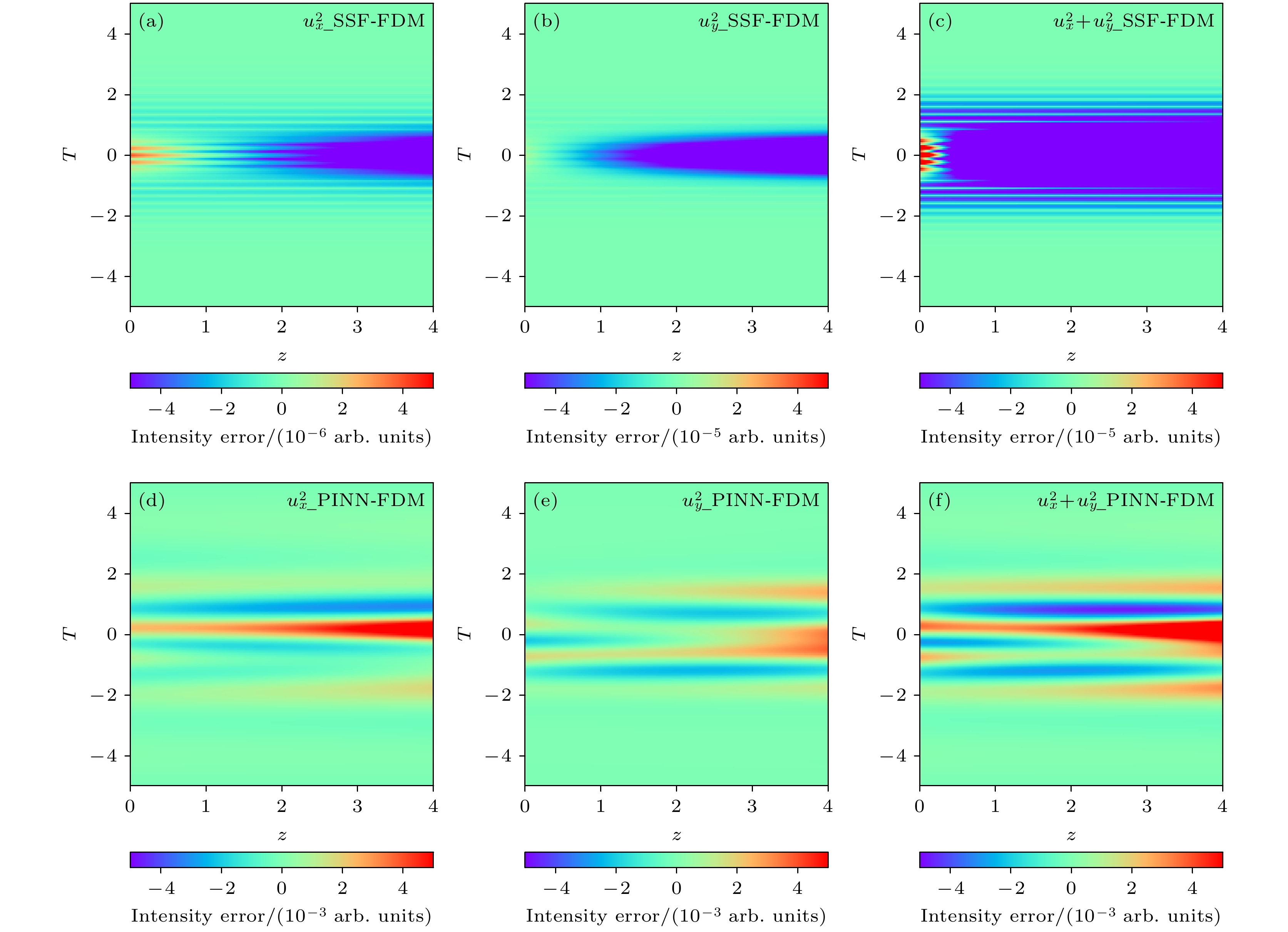在讨论中将含有多个效应的VNLSE忽略增益项、四波混频等进行求解公式为: $ \dfrac{{\partial {u_x}}}{{\partial z}} = - {\text{i}}\dfrac{{{\beta _2}}}{2}\dfrac{{{\partial ^2}{u_x}}}{{\partial {t^2}}} + {\text{i}}\gamma \Big({| {{u_x}} |^2} + \dfrac{2}{3}{| {{u_y}} |^2}\Big){u_x} $, $ \dfrac{{\partial {u_y}}}{{\partial z}} = - {\text{i}}\dfrac{{{\beta _2}}}{2}\dfrac{{{\partial ^2}{u_y}}}{{\partial {t^2}}} + {\text{i}}\gamma \Big({| {{u_y}} |^2} + \dfrac{2}{3}{| {{u_x}} |^2}\Big){u_y} $. 采用FDM, SSF, PINN三种方法模拟, 尽管不同算法求解过程有所差异, 但核心思想在于求解相互耦合项. FDM离散过程与一维相同, 利用离散公式代替一阶、二阶偏微分来构建耦合的离散的迭代公式[43,44]. SSF采用线性与非线性交替进行求解, 只是当有共轭项的存在时, 利用变量代换消除等式中共轭项进行SSF求解, 结束后变量逆代换即可[45]. PINN将物理系统的实部和虚部分离, 构造出更为精细的损失函数. 利用自动微分技术, 神经网络能够不断地调整其内部参数, 以使输出结果满足损失函数的约束条件. 与一维情况相比, 只是损失函数实虚部约束从2个变成4个, 约束变多、物理信息复杂计算量变大[23]. 设置群速度色散${\beta _2}$、非线性系数$\gamma $分别为2×10–27 (m×W)–1, 2.5×10–3 s2/m, 初始脉冲ux, uy为sech(t), $1.5{{\text{e}}^{( - 0.5{t^2})}}$, 传输距离z为4 m. 根据上述FDM, PINN, SSF算法、参数设置对化简后的VNLSE进行编程求解, 可得图10不同方向VNLSE对应的脉冲演化过程的交叉对比图. 图10(a)—(c)为SSF与FDM算法求解$u_x^2$, $u_y^2$, $ u_x^2{+}u_y^2 $的相互误差, 其中SSF与FDM求解的$u_x^2$, $u_y^2$, $ u_x^2{+}u_y^2 $结果相互误差量级在10–5左右, 说明SSF与FDM计算结果十分相似. 图10(d)—(f)为PINN与FDM算法求解$u_x^2$, $u_y^2$, $ u_x^2{+}u_y^2 $的相互误差, 其中PINN与FDM求解的$u_x^2$, $u_y^2$, $ u_x^2{+}u_y^2 $结果相互误差量级在10–3左右, 并且PINN与SSF对应的脉冲演化与图10(d)—(f)相似. 上述研究阐述了3种算法求解VNLSE过程, 并对这些方法的误差进行了对比分析, 深化了研究人员对相关求解方法的认识.

    4.   结　论

    • 本文深入探讨了利用多种算法模拟脉冲在光纤中NLSE传输的动力学过程. 详细阐述了PINN如何基于物理信息构建相应的损失函数, 并通过优化使其最小化, 从而实现对NLSE的数值求解. 在此基础上, 进一步讨论了PINN的训练步骤与结构, 并对FDM, SSF和PINN三种方法的求解结果进行了误差对比分析. 然后深入研究了PINN中不同网络类型、激活函数、隐藏层及神经元个数对求解结果的影响. 通过系统分析发现, 选择合适的激活函数与网络类型的组合能够显著降低误差, 其中FNN与tanh激活函数的组合表现尤为出色. 随后, 提出传统方法与数据驱动方法相结合的集成学习方案, 该方案在降低求解误差、提高精度方面的具有很好的效果. 最后, 运用FDM, SSF和PINN对具有不同啁啾参数的艾里脉冲演化、保偏光纤中VNLSE进行了模拟. 本文提出的基于FDM, SSF和PINN的集成学习方案为基于数据驱动的智能光纤激光器研究和开发奠定了坚实的基础.

    参考文献 (45)

目录

/

返回文章
返回