-
伽马单中子出射反应截面有助于理解核结构和核反应机制, 同时对屏蔽设计与放射性输运分析、核废料嬗变、医用同位素生产和天体物理应用等方面有着重要应用价值[1].
一直以来, 由于高品质光子源实验条件稀缺和光子能量校准等技术难题的限制, 光中子反应实验数据质量参差不齐, 实验数据分散性大, 给核数据评价带来很多困难[2]. 20世纪60年代, 美国的Dietrich和Berman[3]对准单能光源的光核反应实验数据开展系统分析与编撰, 为核数据评价做出了突出贡献. 为了进一步建立信息完整的光核数据库, 国际原子能机构(IAEA)分别在1996年和2016年组织国际协调合作, 给出了光中子核反应数据推荐值, 工作中部分分析了美国劳伦斯利弗莫尔实验室、法国萨克雷实验室以及俄罗斯国立大学等不同机构光中子测量的差异, 结合核反应理论方法, 先后建立了IAEA光核数据库IAEA-1999-PD[1]和IAEA-2019-PD[4]. 然而, 大量早期测量数据因年代久或者文献报道不完整难以追溯; 国际韧致辐射装置、准单能装置等测量之间分歧难以澄清; 同时众多核素尚缺少实测数据, 无法标定核数据可靠性. 上述问题在传统评价技术中尚无法得到处理, 需要发展新的核数据评价方法以提升光中子数据质量.
实验数据评价是核数据研究的核心任务之一, 其中评价测量数据中的异常数据点(即离群点)是提升核数据评价质量的重要环节. 近年来, 随着机器学习方法的快速发展, 相关技术已经被广泛应用于核物理的多个领域, 有效地促进了从理论模型到实验分析各方面的发展[5-10]. 例如, 在监督学习应用于核反应数据方面, 兰州大学白景虎等[8]利用多任务神经网络提高了光核反应中巨偶极共振参数的精度, 中国原子能科学研究院的邢康等[9]使用相移神经网络重现了
$^{235}\text{U}({\mathrm{n, f}})$ 反应共振能区的低频和高频振荡截面, 安徽大学的李伟峰等[10]采用贝叶斯神经网络方法改进了(n, 2n)反应截面的预测. 相较于监督学习, 非监督机器学习具有不用标签、适用于发现数据的隐藏结构和潜在模式等优势, 在数据聚类分析、离群点检测等工作中具有一定优势[5,11]. 目前, 非监督学习方法在核反应数据研究中已经有一些应用工作, 例如, 亚利桑那州立大学的Mitra等[12]使用非监督学习的变分自编码器(variational autoencoder, VAE)等神经网络, 学习和预测了2151个核素的截面关系, 预测准确性高; 美国阿贡国家实验室的Fox和Wendt[13]使用深度生成对抗网络开发了一个预测模型, 学习基于核反应程序TALYS建立的评价核数据库(TENDL)中偶-偶核的中子非弹性散射趋势, 为$ ^{12}\mathrm{C} $ ,$ ^{16}\mathrm{O} $ ,$ ^{20}\mathrm{Ne} $ ,$ ^{172}\mathrm{Yb} $ 和$ ^{174}\mathrm{Hf} $ 等多个核素的截面曲线提供了良好预测. 然而, 非监督学习尚未应用于开展核反应截面离群点分析.变分自编码器(VAE)是一种生成模型, 通过结合深度学习和贝叶斯推理的技术来学习输入数据的潜在表示[14]. 与传统的自编码器不同, VAE在编码器部分引入了概率分布, 使得生成的潜在空间具有良好的连续性和结构性, 在数据清理方面具有更好的应用前景. 为了有效查找光中子出射反应截面实验测量的离群点, 本文提出采用变分自编码器[14]的非监督机器学习方法开展研究, 从国际实验核反应数据库EXFOR中[15]获取实验光中子数据, 挖掘其潜在变量进而筛选实验离群点, 为核数据评价提供更为可靠的实验信息.
本文主要安排包括: 第2节介绍伽马单中子实验数据分析VAE网络模型原理与构建; 第3节介绍
$ ^{29}\text{Si} $ 到$ ^{207}\text{Pb} $ 光中子实验数据训练, 以及离群点识别结果与分析; 第4节对VAE方法在核数据离群点识别进行总结与展望. -
VAE网络由编码器和解码器两部分组成[14]. 假设x为原始训练数据, 其对应分布为
$p(x)$ , z为x通过编码器确定的潜在变量,$\tilde{x}$ 为解码器重建的x近似值. 整体来讲, 该网络首先建立编码器, 通过学习原始数据x提取其潜在变量z的后验分布$p(z|x)$ , 在$p(z|x)$ 基础上抽样以获取潜在变量z. 接着建立解码器, 使用编码器所得潜在变量z构建$\tilde{x}$ 的条件概率分布$p(\tilde{x}|z)$ , 再对$p(\tilde{x}|z)$ 抽样获得重建数据$\tilde{x}$ . 具体原理如下.根据贝叶斯定理, 编码器
$p(z|x)$ 可以表示为其中,
$ p(z) $ 为潜在变量 z 的先验分布, 一般选取$ p(z) $ 为标准正态分布$ \mathcal{N}(0, I) $ ; 由于$p(x)$ 和$p(x|z)$ 难以直接确定, 因此无法获得后验分布$p(z|x)$ . 在VAE网络中, 采用变分推断法, 使得编码器输出的变分后验分布$q_\phi(z|x)$ 逼近真实的后验分布$p(z|x)$ , 其中$q_\phi(z|x)$ 多采用高斯形式, ϕ为编码器参数.变分推断法的目标是最小化KL散度 (Kullback-Leibler divergence)[14]. 其中, 在VAE网络中定义KL散度
$ D_{{\mathrm{KL}}}(q_\phi(z|x) \| p(z|x)) $ 衡量$ q_\phi(z|x) $ 与$ p(z|x) $ 之间的距离, 如(2)式:通过最小化KL散度能够使编码器输出的分布逼近真实后验分布. 对
$ D_{{\mathrm{KL}}}$ 进行简单变换, 可转化为其中,
$\log p(x)$ 与积分变量z无关, 考虑到$\tilde{x}$ 是由z生成的x的近似值, 且联合概率分布$p(z, x)$ 可以表示为$p(z, \tilde{x}) = p_\theta(\tilde{x}|z) p(z)$ . 因此(3)式可以转换为其中, 左边第二项被称为证据下界(evidence lower bound, ELBO);
$p_\theta(\tilde{x}|z)$ 为解码器神经网络参数化后的潜在变量z的后验分布, θ是解码器神经网络参数. 考虑到原始训练数据x确定的条件下,$\log p(x)$ 为固定值, 为了最小化$ D_{{\mathrm{KL}}}$ , 需要最大化ELBO.ELBO经过简单变换可以转化为
一般将解码器的输出视为
$p_\theta(\tilde{x}|z)$ 的均值, 即重建数据$\tilde{x}$ , 无需再重复抽样. (5)式右边第一项被称为重建项, 为了最大化重建项, 需最小化原始数据x与重建数据$\tilde{x}$ 的差异; 右边第二项被称为正则化项, 由于$q_\phi(z|x) $ 与$p(z)$ 均取为高斯分布, 因此$D_{{\mathrm{KL}}}(q_\phi(z|x) \| p(z))$ 有解析解, 可以转换其中, 当潜在变量z数量大于1时, 通常采用参数化的均值
$\mu_k$ 和方差$\sigma_{k}^2$ 来表示第$z_k$ 个潜在变量的高斯分布$q_\phi(z_k|x) $ . 为了实现VAE网络中ELBO项最大化, 需要针对(5)式建立损失函数(LOSS). 其中, (5)式中的重建项通常通过计算均方误差(MSE)来实现, 同时通过在正则化项上乘以系数β共同建立VAE网络损失函数, 如(7)式所示[16]:基于上述公式体系, VAE网络的训练过程遵循如下步骤: 首先, 将原始数据x输入编码器获得潜在变量z的分布
$q_\phi(z|x)$ ; 其次, 从$q_\phi(z|x)$ 中获得潜在变量z的值, 将z输入到解码器中产生重建数据$\tilde{x}$ ; 最后, 通过计算损失函数LOSS获得损失, 并利用该损失进行反向传播以优化网络参数ϕ和θ. 训练过程涉及多次迭代, 直至网络达到设定的收敛条件, 训练结束. 其中需要注意, 在第二步计算中, 直接从$q_\phi(z|x)$ 中抽样得到z会导致VAE网络不可微分, 无法进行反向传播更新网络参数. 因此, 常常将z的值重建为一个关于随机噪声的可微函数, 如(8)式所示:即潜在变量
$z_k$ 被重构为均值$\mu_k$ 与方差$\sigma_{k}$ 的函数, 其中$\epsilon_{k}$ 为满足标准正态分布的随机值. -
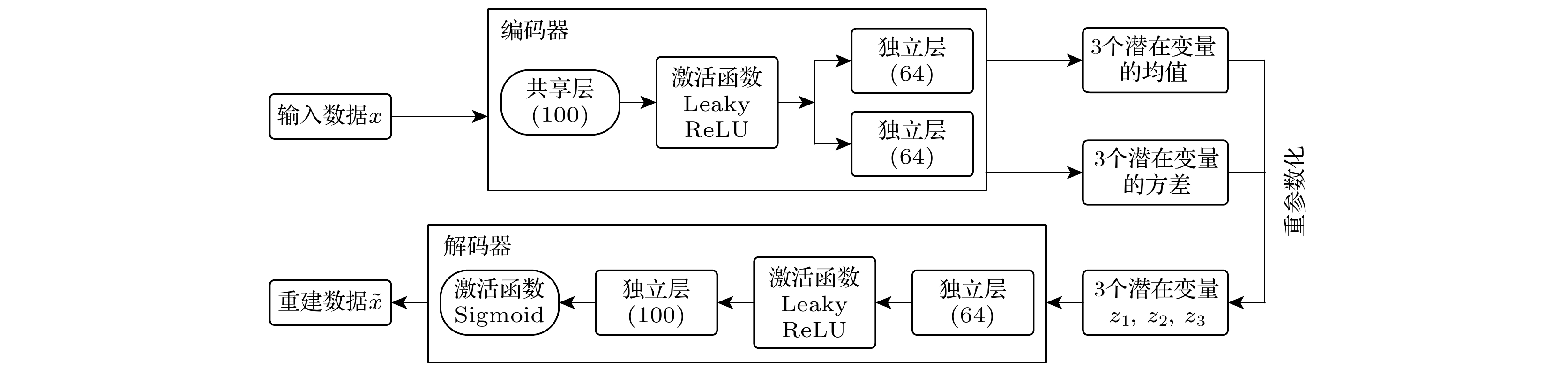
本研究基于光中子核反应截面的实验信息, 建立以VAE方法的离群点识别网络. 针对不同的原子核, 训练与质子数Z和质量数A相关的VAE网络参数ϕ和θ, 构建的VAE网络结构如图1所示, 其中每层均为全连接线性层, 图中括号内为神经元数量.
在图1的具体计算中, 首先将实验数据归一至0—1的范围内, 随后获取公共能量范围, 接着对公共能区使用核密度估计(kernel density estimation, KDE)[17]确定实验数据的能量分布概率密度
$\hat{f}(E)$ , 基于分布$\hat{f}(E)$ 随机获取100个能量点, 再将每家测量能量点对应的截面值组合为一批(batch)作为VAE网络的输入x. 将多家测量数据的能量E视为一维独立同分布的数据点, 则有如下KDE的表达式:其中, E为目标变量(能量),
$ E_i $ 为第i个实验测量点的能量,$ \hat{f}(E) $ 为E处的概率密度估计值, n为数据点数量, h为带宽参数(平滑宽度),$ K(\cdot) $ 为核函数. 本文选用高斯函数作为核函数$K(u)$ , 其定义为带宽h的选择对估计结果的平滑程度有显著影响. 为此, 本文采用了Scott规则(11)式自动计算带宽:
其中, σ为样本数据的标准差.
输入数据x通过一个共享层和两个独立层组成的编码器, 映射到三个潜在变量
$z_1$ ,$z_2$ 和$z_3$ 的均值和方差上, 随后利用均值和方差重参数化生成潜在变量z的值, 再通过由两个独立层组成的解码器输出重建数据$\tilde{x}$ . 为防止梯度消失, 编码器和解码器层间均采用Leaky ReLU激活函数[18]. 同时, 解码器尾部额外增加Sigmoid激活函数使输出数据重建在0—1之间. 网络采用何凯明初始化方法对网络参数进行初置[19], 偏置设置为0.01, 以防止偏置节点失效. 优化器使用Adam[20], 学习率为0.01. 损失函数LOSS中正则化项的β参数设为0.01.当VAE训练在最后100次迭代的线性回归斜率绝对值小于0.0005时, 可以认为损失函数趋于稳定, 同时潜在变量z的分布近似标准正态分布, 重建数据
$\tilde{x}$ 与原始数据x基本一致时, 可以认为网络训练完成, 所得VAE网络模型有效地捕捉到了数据的潜在结构特征. -
在VAE网络训练完成后, 将每家测量数据潜在变量的均值
$(\mu1, \mu2, \mu3)$ 进行聚类分析, 并选择具有最大成员数的簇作为判断标准. 处于簇之内的测量为正常数据, 簇之外的测量为离群数据. 聚类采用k-means算法[21], 簇数量k通过轮廓系数法确定[22], 令k的值至少为2. 每个样本的轮廓系数$s(i)$ 通过(12)式计算, 取值范围为–1—1,$s(i)$ 值越大表示聚类效果越好.其中,
$a(i)$ 是聚类的内聚度, 表示样本i 到其同一簇中所有其他样本的平均距离;$b(i)$ 是聚类的分离度, 表示样本i 到其他簇中所有样本的平均距离. -
本工作针对国际实验核反应数据库(EXFOR)中重核区光中子核反应实验测量进行整理, 目标聚焦包含三家及以上多能点测量的核素
$ ^{29}\text{Si} $ ,$ ^{54}\text{Fe} $ ,$ ^{63}\text{Cu} $ ,$ ^{141}\text{Pr} $ ,$ ^{181}\text{Ta} $ ,$ ^{206}\text{Pb} $ 和$ ^{207}\text{Pb} $ , 系统分析离群点, 实验数据的年份、第一作者、能量区间等信息如表1所列.以
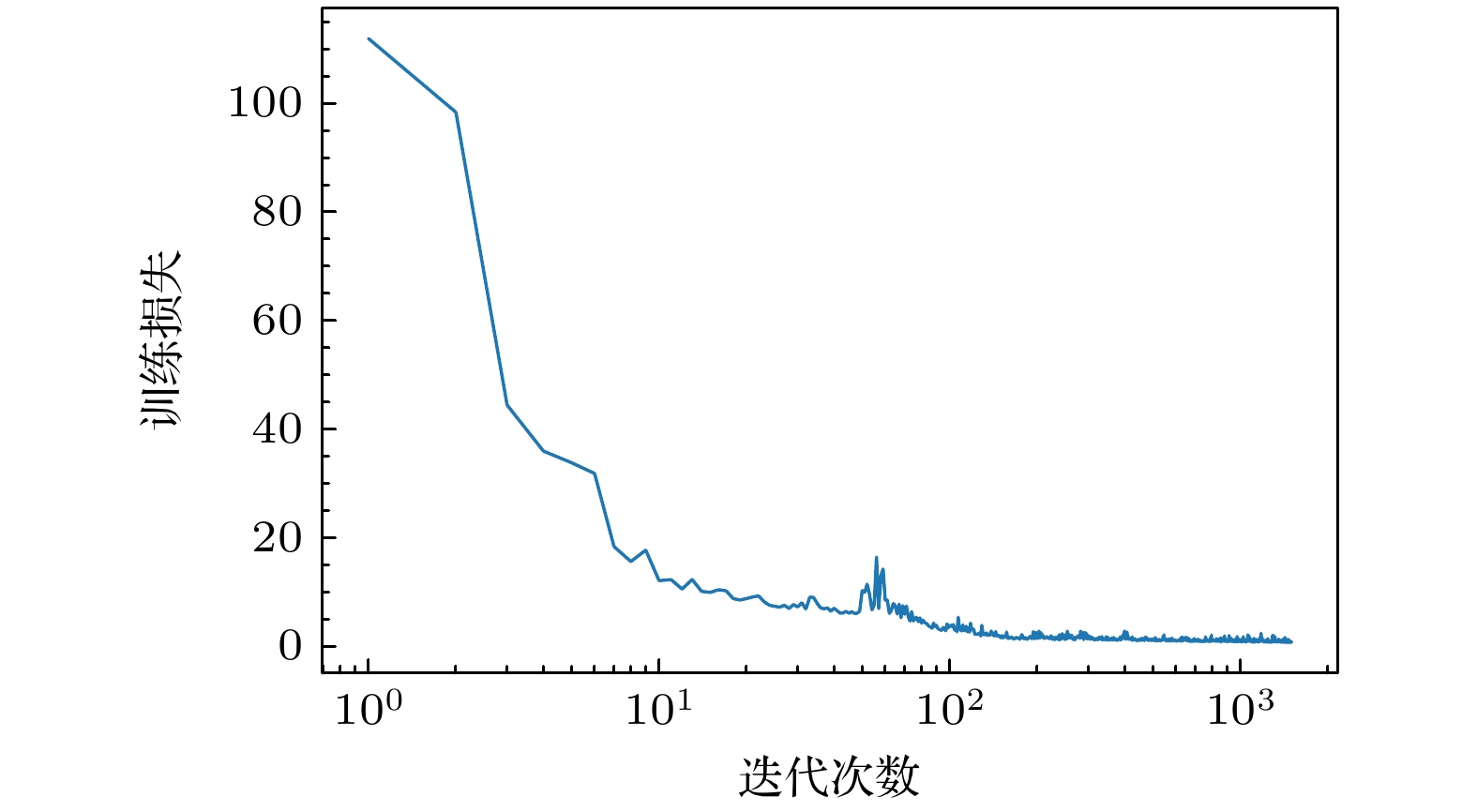
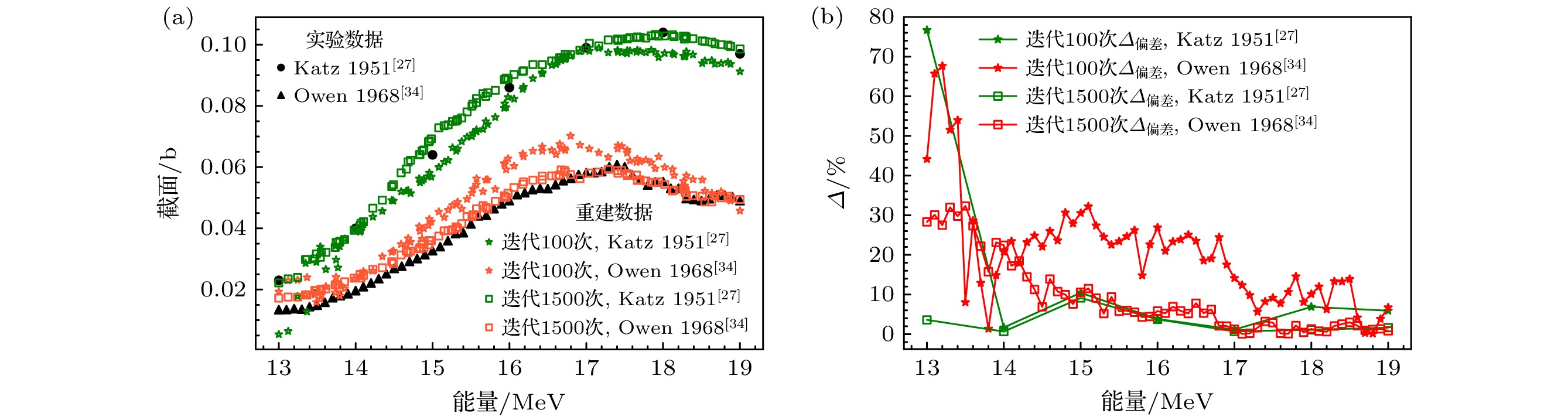
$ ^{63}\text{Cu} $ 为例, 图2给出训练过程中损失函数LOSS随迭代次数的变化, LOSS在前100次迭代中由112逐渐下降至5, 随后在至1500次迭代中缓慢下降并趋于收敛; 图3给出了Katz[27]和Owen等[34]的VAE重建数据$\tilde{x}$ 与输入的实验测量x比较图. 可以看出, 随着网络学习迭代次数的增加, 重建数据结果可以更好地再现实验测量, 两者截面之间的偏差也更接近零, 如图3(b)所示.
VAE网络收敛后, 对多家测量对应的潜在变量的均值μ1, μ2以及μ3进行聚类. 首先使用轮廓系数法获得k-means聚类算法的最佳簇数量k, 随后选取最大成员数簇内的实验数据作为正常数据, 该簇外的实验数据为离群数据, 完成实验离群点识别. 其中
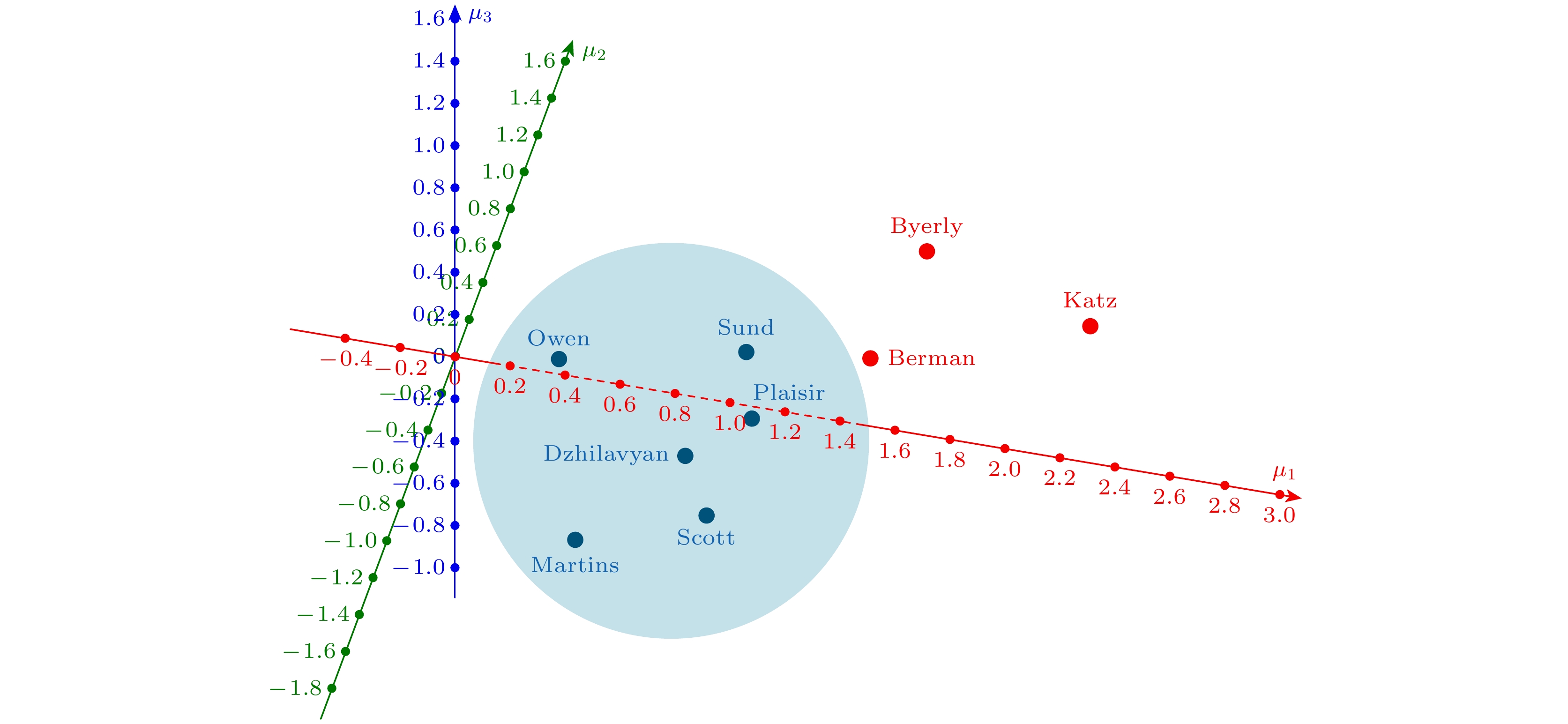
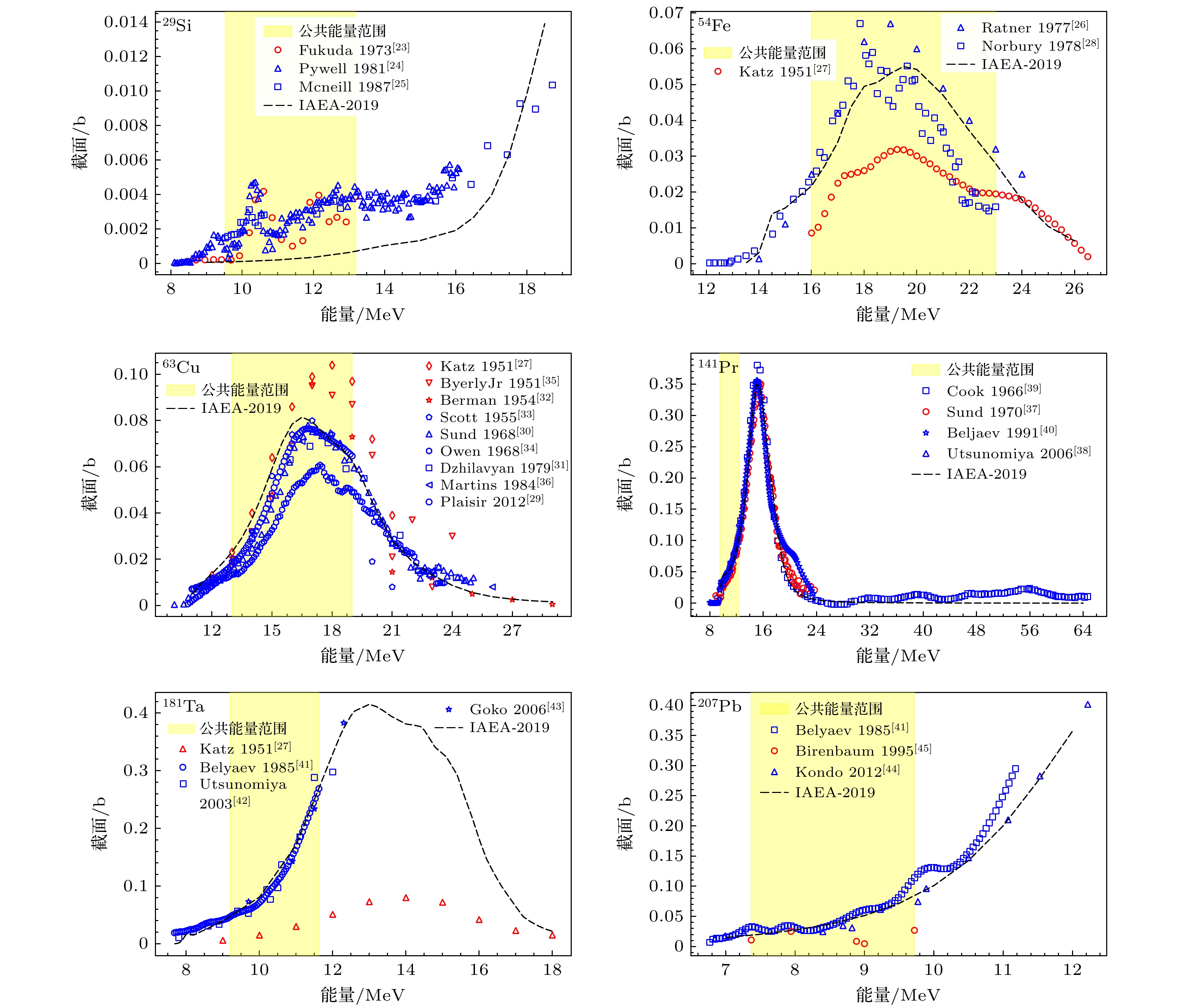
$ ^{63}\text{Cu} $ 的聚类结果如图4所示, Plaisir等[29]、Sund等[30]、Dzhilavyan和Plaisir[31]、 Scott等[33]、Owen等[34]和Martins等[36]的实验测量处于最大簇内, Berman和Brown[32]、Katz和Cameron[27]以及Byerly和Stephens[35]的实验测量处于最大簇外, 为本工作VAE网络识别所得离群点. 图5给出了本工作$ ^{29}\text{Si} $ ,$ ^{54}\text{Fe} $ ,$ ^{63}\text{Cu} $ ,$ ^{141}\text{Pr} $ ,$ ^{181}\text{Ta} $ 和$ ^{207}\text{Pb} $ 光中子核反应截面测量、VAE离群点和IAEA-2019评价库中的结果比较. 由图可知, 针对光中子核反应测量, 本文的VAE网络有效识别了目标核素中的实验离群信息, 排除离群点之后的实验数据与IAEA-2019评价数据一致性提升.为进一步评估变分自编码器在离群点识别中的效果, 在图5所示IAEA-2019数据与各家实验测量的公共区域, 定义排除离群点前后的实验室测量数据与IAEA-2019评价数据之间的偏差, 如(14)式和(15)式所示.
其中, n代表该核素的测量家数总数,
$\int_{\text{IAEA-2019}_i}$ 和$\int_{\text{实验}_i}$ 分别代表第i家测量IAEA-2019评价数据与实验数据公共能量范围内, 评价数据和实验数据的积分值. 积分过程首先对实验和评价数据进行线性插值, 随后采用梯形积分法进行积分.其中, n代表该核素的测量家数总数,
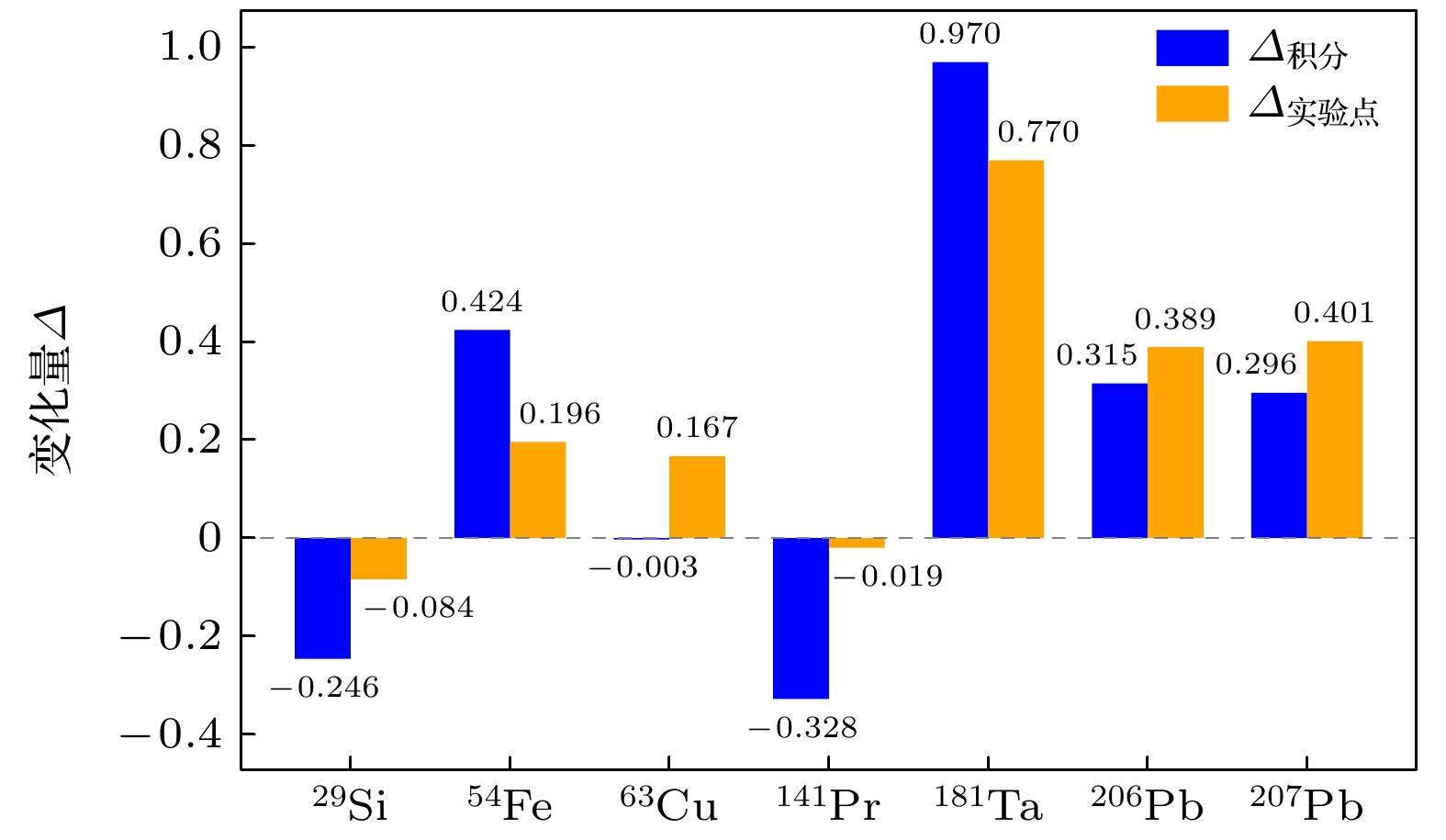
$m_j$ 代表第j家测量的测量总点数;$P_{\text{IAEA-2019}_{ji}}$ 和$P_{\text{实验}_{ji}}$ 分别表示第j家测量实验数据与IAEA-2019评价数据公共能量范围内, 第i个实验点能量对应的评价值和实验值.如图6所示,
$ ^{54}\text{Fe} $ ,$ ^{181}\text{Ta} $ ,$ ^{206}\text{Pb} $ 和$ ^{207}\text{Pb} $ 的$\varDelta_\text{积分}$ 和$\varDelta_{\text{实验点}}$ 均为正数, 表明在识别并排除离群点之前, 实验数据与IAEA-2019评价数据之间的偏差要大于排除离群点之后的偏差, 实验数据经过VAE排除离群点后与评价数据一致性更高;$ ^{63}\text{Cu} $ 的$\varDelta_\text{积分}$ 为负但$\varDelta_{\text{实验点}}$ 为正, 这表明实验数据点更接近评价数据, 但是整体较评价数据有偏移;$ ^{29}\text{Si} $ 的$\varDelta_\text{积分}$ 和$\varDelta_{\text{实验点}}$ 均为负数, 表明数据经过VAE排除离群点后与评价数据偏离, 结果仍待改进;$ ^{141}\text{Pr} $ 的$\varDelta_\text{积分}$ 和$\varDelta_{\text{实验点}}$ 同样为负, 这主要是因为实验数据的公共能量范围过小, 导致VAE无法有效地获取数据整体的潜在变量, 使得VAE方法评估不合理. -
本文研究了基于变分自编码器(VAE)的伽马单中子出射反应截面的离群点分析技术. 经过对EXFOR数据库中
$ ^{29}\text{Si} $ ,$ ^{54}\text{Fe} $ ,$ ^{63}\text{Cu} $ ,$ ^{141}\text{Pr} $ ,$ ^{181}\text{Ta} $ ,$ ^{206}\text{Pb} $ 和$ ^{207}\text{Pb} $ 等7个核素的29家数据训练, 并结合基于k-means方法的潜在变量聚类分析, 有效识别了实验数据离群点, 并且证明排除离群点前后数据与其对应的IAEA-2019评价数据的偏差有效降低, 验证了VAE网络在核数据实验信息离群点识别领域的应用潜力. 尽管VAE方法在处理数据中显示出一定的优势, 但在数据量较少、公共能区过窄等情况下, 模型训练可能不充分, 导致潜在空间聚类结果不准确, 从而误筛选出有效数据. 后期有望开展裂变核中子共振截面、裂变截面等测量数据丰富反应截面的VAE网络应用尝试.感谢中国原子能科学研究院张英逊研究员与北京大学赵鹏巍教授的热情讨论与帮助.
基于变分自编码器的伽马单中子出射反应截面实验数据离群点研究
Outliers identification of experimental (γ, n) reaction cross section via variational autoencoder
-
摘要: 伽马单中子出射反应截面是核工程输运计算中的重要参数, 部分核素(γ, n)的反应测量因来自不同实验室而分歧明显. 本文基于变分自编码器方法, 针对原子核质量数在29—207区域的伽马单中子出射反应截面实验测量数据进行分析, 有效识别多家测量之间的离群点. 首先, 研究变分自编码器方法, 建立伽马单中子光核测量数据离群点识别网络; 其次, 对$^{29}\text{Si}$, $^{54}\text{Fe}$, $^{63}\text{Cu}$, $^{141}\text{Pr}$, $^{181}\text{Ta}$, $^{206}\text{Pb}$和$^{207}\text{Pb}$的29家多能点测量数据进行离群点识别; 最后, 计算离群点识别前后的实验数据与国际原子能机构光核评价数据库(IAEA-2019-PD)评价值之间的偏差, 检测变分自编码器的分析效果. 研究表明, 变分自编码器方法可以有效识别(γ, n)反应实验测量离群点, 其中$^{54}\text{Fe}$,$^{63}\text{Cu}$, $^{181}\text{Ta}$, $^{206}\text{Pb}$和$^{207}\text{Pb}$的伽马单中子出射反应截面与IAEA-2019-PD评价结果一致性更高, 验证了该方法在核数据研究中的应用潜力.Abstract:
The (γ, n) cross-section is important in nuclear engineering transport calculations. The measurements of the (γ, n) reaction for some isotopes show significant discrepancies among different laboratories. Since the analysis of experimental data is the primary task in the evaluation of nuclear data, identifying the measured outlier data is crucial for improving the quality of nuclear data. Therefore, a variational autoencoder (VAE) method is used in this work to analyze experimental measurements of (γ, n) cross sections for nuclear mass ranging from 29 to 207, in order to provide more reliable experimental information for evaluating nuclear data. According to the proton number Z and nuclear mass A, we design a variational autoencoder network for outlier identification in the measurement of (γ, n). The silhouette coefficient method and K-means algorithm are used to cluster the latent variables of VAE. Subsequently, the experimental data with and without the outliers are compared with those from the IAEA-2019-PD to assess the VAE in its application to the evaluation of photoneutron measurements. The results demonstrate that the VAE can effectively identify outliers in the measurements of (γ, n). After excluding outliers, the (γ, n) cross-section for $^{54}\text{Fe}$, $^{63}\text{Cu}$, $^{181}\text{Ta}$, $^{206}\text{Pb}$, and $^{207}\text{Pb}$ showed higher consistency with the IAEA-2019-PD evaluation results. However, $^{29}\text{Si}$ and $^{141}\text{Pr}$ still deviate from the IAEA-2019-PD evaluation results, therefore requiring more analyses of the measurements themselves in future. The VAE method can effectively identify outliers and extract the latent structures in experimental data of (γ, n) reaction. It provides more reliable experimental information for evaluating nuclear data and validating the potential application of this method in nuclear data research. However, the generalizability of VAE method still needs further developing, especially in addressing the issues of uneven energy distribution for various measurements. -
Key words:
- variational autoencoder /
- (γ, n) reaction /
- cross section /
- outlier .
-

-
图 3
$ ^{63}\text{Cu} $ 光中子核反应截面VAE网络100次迭代和1500次迭代训练结果与Katz和Cameron[27]、Owen等[34]的实验测量比对 (a) VAE数据重建结果; (b)重建数据与实验数据的$\varDelta_\text{偏差}$ Figure 3. Comparison of the
$ ^{63}\text{Cu} $ photoneutron reaction cross section training results of the VAE network after 100 and 1500 epochs with experimental measurements by Katz and Cameron[27], and Owen et al.[34]: (a) The VAE data reconstruction results; (b) the$\varDelta_\text{偏差}$ between the reconstructed data and the experimental data.图 4 基于Plaisir等[29]、Sund等[30]、Dzhilavyan和Kucher[31]、Scott等[33]、Owen等[34]、Martins等[36]、Berman和Brown[32]、Katz和Cameron[27]以及Byerly Jr和Stephens等[35]的
$ ^{63}\text{Cu} $ 实验测量的潜在变量的聚类图. 其中, 三个潜在变量的均值μ1, μ2以及μ3作为坐标轴, 浅蓝色圆形阴影为最大成员簇的范围, 蓝色点为属于最大簇的实验测量, 红色为簇之外的实验测量Figure 4. Clustering plot of latent variables for experimental measurements
$ ^{63}\text{Cu} $ , based on the work of Plaisir et al.[29], Sund et al.[30], Dzhilavyan and Kucher[31], Scott et al.[33], Owen et al.[34], Martins et al.[36], Berman and Brown[32], Katz and Cameron[27], Byerly Jr and Stephens[35]. The plot uses three latent variables μ1, μ2 and μ3 as axes. The light blue circular shading represents the range of the largest cluster, with blue dots indicating experimental measurements belonging to the largest cluster, and red dots representing measurements outside the cluster.图 5
$ ^{29}\text{Si} $ ,$ ^{54}\text{Fe} $ ,$ ^{63}\text{Cu} $ ,$ ^{141}\text{Pr} $ ,$ ^{181}\text{Ta} $ 和$ ^{207}\text{Pb} $ 的光中子反应截面分布, 包括不同家实验数据(散点)和评价数据库IAEA-2019评估结果(黑色虚线). 黄色区域为所有实验测量的公共能量范围, 红色数据点属于最大成员簇之外的离群数据, 蓝色数据为最大成员簇之内的正常数据. 其中$ ^{141}\text{Pr} $ 给出了9—13 MeV的放大图Figure 5. Photoneutron reaction cross section distributions for
$ ^{29}\text{Si} $ ,$ ^{54}\text{Fe} $ ,$ ^{63}\text{Cu} $ ,$ ^{141}\text{Pr} $ ,$ ^{181}\text{Ta} $ , and$ ^{207}\text{Pb} $ , including experimental data from different groups (scatter points) and the evaluated database IAEA-2019 results (black dashed line). The yellow region represents the common energy range of all experimental measurements. Red data points correspond to outliers outside the largest cluster, while blue data points belong to normal data within the largest cluster. A zoomed-in plot for$ ^{141}\text{Pr} $ is provided for the 9 MeV to 13 MeV range.图 6 基于
$^{29}\text{Si}$ ,$^{54}\text{Fe}$ ,$^{63}\text{Cu}$ ,$^{141}\text{Pr}$ ,$^{181}\text{Ta}$ ,$^{206}\text{Pb}$ 和$^{207}\text{Pb}$ 的伽马单中子反应道$\varDelta_\text{积分}$ 和$\varDelta_{\text{实验点}}$ 变化量图Figure 6. Graph of the amount of change in (γ, n) reaction channel
$\varDelta_\text{积分}$ and$\varDelta_\text{实验点}$ based on$^{29}\text{Si}$ ,$^{54}\text{Fe}$ ,$^{63}\text{Cu}$ ,$^{141}\text{Pr}$ ,$^{181}\text{Ta}$ ,$^{206}\text{Pb}$ , and$^{207}\text{Pb}$ .表 1
$^{29}\text{Si}$ 到$^{207}\text{Pb}$ 共7个核素的实验测量信息汇总表Table 1. Summary table of experimental measurement information for 7 nuclides from
$^{29}\text{Si}$ to$^{207}\text{Pb}$ .核素 年份 第一作者 机构所属
国家机构 光源 能量区间 能点数 参考文献 $^{29}\text{Si}$ 1973 K.Fukuda 日本 Radiation Centre of Osaka Prefecture Bremsstrahlung 8.46—13.19 20 [23] 1981 R.E.Pywell 澳大利亚 University of Melbourne Bremsstrahlung 8.09—16.09 162 [24] 1987 K.G.Mcneill 加拿大 University of Toronto Annihilation radiation 9.52—18.71 29 [25] $^{54}\text{Fe}$ 1977 B.S.Ratner 俄罗斯 Institute for Nuclear Research of the Russian Academy of Sciences Bremsstrahlung 16.00—26.50 43 [26] 1951 L.Katz 加拿大 University of Saskatchewan Bremsstrahlung 14.00—24.00 11 [27] 1978 J.W.Norbury 澳大利亚 University of Melbourne Bremsstrahlung 12.13—23.00 57 [28] $^{63}\text{Cu}$ 2012 C.Plaisir 法国 Centre d’Etudes Nucleaires de Bordeaux-Gradignan Bremsstrahlung 11.00—19.00 81 [29] 1968 R.E.Sund 美国 Gulf General Atomic Annihilation radiation 10.12—25.06 66 [30] 1979 L.Z.Dzhilavyan 俄罗斯 Institute for Nuclear Research of the Russian Academy of Sciences Annihilation radiation 12.10—24.20 14 [31] 1954 A.I.Berman 美国 Stanford University Bremsstrahlung 13.00—29.00 9 [32] 1951 L.Katz 加拿大 University of Saskatchewan Bremsstrahlung 11.00—21.00 11 [27] 1955 M.B.Scott 美国 University of Illinois Bremsstrahlung 11.00—21.00 11 [33] 1968 D.G.Owen 澳大利亚 University of Melbourne Bremsstrahlung 10.80—23.60 129 [34] 1951 P.R.Byerly Jr 美国 University of Pennsylvania Bremsstrahlung 12.00—24.00 13 [35] 1984 M.N.Martins 美国 National Institute of Standards and Technology Virtual photons 11.00—30.00 5 [36] $^{141}\text{Pr}$ 1970 R.E.Sund 美国 Gulf General Atomic — 8.89—23.69 100 [37] 2006 H.Utsunomiya 日本 Konan University Compton scattering 9.50—12.40 9 [38] 1966 B.C.Cook 美国 Iowa State University Bremsstrahlung 9.19—64.68 113 [39] 1991 S.N.Belyaev 俄罗斯 Saratov Gosudarstvennyi University Bremsstrahlung 7.98—23.52 185 [40] $^{181}\text{Ta}$ 1985 S.N.Belyaev 俄罗斯 Saratov Gosudarstvennyi University Bremsstrahlung 7.68—11.63 80 [41] 1951 L.Katz 加拿大 University of Saskatchewan Bremsstrahlung 9.00—18.00 10 [27] 2003 H.Utsunomiya 日本 Konan University Compton scattering 7.80—12.00 13 [42] 2006 S.Goko 日本 Konan University Laser Compton
Scattered Photons9.20—12.30 6 [43] $^{206}\text{Pb}$ 2012 T.Kondo 日本 Konan University Laser Compton
Scattered Photons8.14—12.24 11 [44] 1985 S.N.Belyaev 俄罗斯 Saratov Gosudarstvennyi University Bremsstrahlung 8.10—12.35 88 [41] 1995 Y.Birenbaum 以色列 Ben Gurion University
of the NegevMonoenergetic photons 8.88—11.39 4 [45] $^{207}\text{Pb}$ 1995 Y.Birenbaum 以色列 Ben Gurion University
of the NegevMonoenergetic photons 7.37—9.72 5 [45] 2012 T.Kondo 日本 Konan University Laser Compton
Scattered Photons6.84—12.22 14 [44] 1985 S.N.Belyaev 俄罗斯 Saratov Gosudarstvennyi University Bremsstrahlung 6.77—11.18 95 [41] -
[1] International Atomic Energy Agency 2000 Handbook on Photonuclear Data for Applications: Cross-sections and Spectra (Vienna: IAEA) pp1–284 [2] Obložinskỳ P 2002 J. Nucl. Sci. Technol. 39 31 [3] Dietrich S S, Berman B L 1988 At. Data Nucl. Data Tables 38 199 doi: 10.1016/0092-640X(88)90033-2 [4] Kawano T, Cho Y, Dimitriou P, et al. 2020 Nucl. Data Sheets 163 109 doi: 10.1016/j.nds.2019.12.002 [5] Carleo G, Cirac I, Cranmer K, Daudet L, Schuld M, Tishby N, Vogt-Maranto L, Zdeborová L 2019 Rev. Mod. Phys. 91 045002 doi: 10.1103/RevModPhys.91.045002 [6] He W, Li Q, Ma Y, Niu Z, Pei J, Zhang Y 2023 Sci. China Phys. Mech. Astron. 66 282001 doi: 10.1007/s11433-023-2116-0 [7] He W B, Ma Y G, Pang L G, Song H C, Zhou K 2023 Nucl. Sci. Tech. 34 88 doi: 10.1007/s41365-023-01233-z [8] Bai J, Niu Z, Sun B, Niu Y 2021 Phys. Lett. B 815 136147 doi: 10.1016/j.physletb.2021.136147 [9] Xing K, Sun X J, Xu R R, Zou F L, Hu Z H, Wang J M, Tao X, Sun X D, Tian Y, Niu Z M 2024 Phys. Lett. B 855 138825 doi: 10.1016/j.physletb.2024.138825 [10] Li W, Liu L, Niu Z, Niu Y, Huang X 2024 Phys. Rev. C 109 044616 doi: 10.1103/PhysRevC.109.044616 [11] Bardhan J, Mandal T, Mitra S, Neeraj C, Patra M 2024 Eur. Phys. J. Spec. Top. 233 2559 doi: 10.1140/epjs/s11734-024-01235-x [12] Mitra S, Choi H, Liu S, Glatt R, Wendt K, Schunck N 2024 arXiv: 2404.02332 [nucl-th] [13] Fox J M, Wendt K A 2024 arXiv: 2403.16389 [nucl-th] [14] Kingma D P 2013 arXiv: 1312.6114 [stat.ML] [15] Otuka N, Dupont E, Semkova V, et al. 2014 Nucl. Data Sheets 120 272 [16] Higgins I, Matthey L, Pal A, Burgess C P, Glorot X, Botvinick M M, Mohamed S, Lerchner A 2017 ICLR (Poster) 3 [17] Parzen E 1962 Ann. Math. Stat. 33 1065 doi: 10.1214/aoms/1177704472 [18] Maas A L, Hannun A Y, Ng A Y, et al. 2013 Proc. ICML 30 3 [19] He K, Zhang X, Ren S, Sun J 2015 Proceedings of the IEEE International Conference on Computer Vision Santigago, Chile, December 13–16, 2015 p1026 [20] Kingma D P 2014 arXiv: 1412.6980 [cs.LG] [21] MacQueen J 1967 Proc. Fifth Berkeley Symp. Math. Stat. Prob. 1 281 [22] Rousseeuw P J 1987 J. Comput. Appl. Math. 20 53 doi: 10.1016/0377-0427(87)90125-7 [23] Fukuda K, Okabe S 1973 J. Phys. Soc. Jpn. 34 315 doi: 10.1143/JPSJ.34.315 [24] Pywell R, Berman B, Kean P, Thompson M 1981 Nucl. Phys. A 369 141 doi: 10.1016/0375-9474(81)90011-7 [25] McNeill K, Pywell R, Berman B, Woodworth J, Thompson M, Jury J 1987 Phys. Rev. C 36 1621 doi: 10.1103/PhysRevC.36.1621 [26] Ratner B, Sergiyevsky A, Verbitsky S 1977 Nucl. Phys. A 285 71 doi: 10.1016/0375-9474(77)90147-6 [27] Katz L, Cameron A 1951 Can. J. Phys. 29 518 doi: 10.1139/p51-056 [28] Norbury J, Thompson M, Shoda K, Tsubota H 1978 Aust. J. Phys. 31 471 doi: 10.1071/PH780471 [29] Plaisir C, Hannachi F, Gobet F, Tarisien M, Aléonard M, Méot V, Gosselin G, Morel P, Morillon B 2012 Eur. Phys. J. A 48 68 doi: 10.1140/epja/i2012-12068-7 [30] Sund R, Baker M, Kull L, Walton R 1968 Phys. Rev. 176 1366 doi: 10.1103/PhysRev.176.1366 [31] Dzhilavyan L, Kucher N 1979 Sov. J. Nucl. Phys. 30 151 [32] Berman A, Brown K 1954 Phys. Rev. 96 83 [33] Scott M, Hanson A, Kerst D 1955 Phys. Rev. 100 209 doi: 10.1103/PhysRev.100.209 [34] Owen D, Muirhead E, Spicer B 1968 Nucl. Phys. A 122 177 doi: 10.1016/0375-9474(68)90711-2 [35] Byerly Jr P R, Stephens W 1951 Phys. Rev. 83 54 doi: 10.1103/PhysRev.83.54 [36] Martins M, Hayward E, Lamaze G, Maruyama X, Schima F, Wolynec E 1984 Phys. Rev. C 30 1855 [37] Sund R, Verbinski V 1970 Phys. Rev. C 2 1129 [38] Utsunomiya H, Makinaga A, Goko S, et al. 2006 Phys. Rev. C 74 025806 doi: 10.1103/PhysRevC.74.025806 [39] Cook B, Hutchinson D, Waring R, Bradford J, Johnson R, Griffn J 1966 Phys. Rev. 143 730 doi: 10.1103/PhysRev.143.730 [40] Belyaev S, Semenov V 1991 Bull. Russ. Acad. Sci. Phys. 55 66 [41] Belyaev S, Kozin A, Nechkin A, Semenov S S, Semenko S 1985 Yad. Fiz. 42 1050 [42] Utsunomiya H, Akimune H, Goko S, et al 2003 Phys. Rev. C 67 015807 doi: 10.1103/PhysRevC.67.015807 [43] Goko S, Utsunomiya H, Goriely S, et al 2006 Phys. Rev. Lett. 96 192501 doi: 10.1103/PhysRevLett.96.192501 [44] Kondo T, Utsunomiya H, Goriely S, et al 2012 Phys. Rev. C 86 014316 doi: 10.1103/PhysRevC.86.014316 [45] Birenbaum Y, Berant Z, Kahane S, Wolf A, Moreh R 1995 Phys. Rev. C 51 3496 doi: 10.1103/PhysRevC.51.3496 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: