黑洞信息丢失问题, 即黑洞信息悖论, 是指基于弯曲时空量子场的半经典计算表明, 黑洞蒸发过程并非是幺正的, 但是全息原理和弦理论暗示这个过程应该是幺正的^[1,2]. 具体来说, 霍金辐射谱显示黑洞蒸发过程遵循一个平衡态的黑体谱, 这意味着信息在黑洞蒸发过程中似乎被永久丢失, 无法通过观测辐射恢复初始状态的信息. 这种非幺正性与量子力学的基本原理相冲突, 因为量子力学要求物理过程必须是幺正的, 即信息必须守恒. 然而, 弦理论, 特别是规范/引力对偶理论(如AdS/CFT对偶)的进展提供了另一种视角^[3–5]. 这些理论表明, 黑洞的形成和演化过程实际上是幺正的. 这是因为规范场理论中的物理过程总是满足幺正性, 即信息在演化过程中不会丢失. 通过规范/引力对偶, 可以将引力理论中的黑洞问题映射到一个边界上的规范场理论, 而在规范场理论中, 幺正演化是自然的. 因此, 黑洞信息悖论的核心在于半经典计算与量子引力理论之间的矛盾. 半经典计算预测的信息丢失与量子力学的幺正性要求不符, 而弦理论和规范/引力对偶理论则提供了一种解决这一悖论的框架, 表明在更完整的量子引力理论中, 黑洞辐射过程在微观上仍是幺正的. 然而, 现实中的黑洞(如史瓦西黑洞)存在于渐近平坦时空中, 其渐近结构与AdS时空存在本质差异, 导致AdS/CFT无法直接应用. 在平直时空中处理这个问题需要考虑几个方面: 岛屿机制通过量子极值面(quantum extremal surfaces)的涌现, 将黑洞内部信息与外部辐射关联, 确保熵的幺正演化. 近期研究表明, 在渐近平坦二维引力模型(如CGHS模型)中, 岛屿区域在Page时间后主导熵的计算, 其行为与AdS黑洞类似. 这一机制的关键要素可能独立于AdS边界条件^[6–12]. 本文作者早年关于黑洞信息丢失问题的工作, 详见文献[13–17].

近年来, 人们在解决黑洞信息丢失问题上取得了显著的进展^[18–34]. 通过发展基于二维引力的路径积分方法, 利用副本技巧(replica trick) 来计算Rényi熵 ¹, 发现在原来霍金计算的基础上, 存在另外一个鞍点解, 即副本虫洞鞍点(replica wormholes saddle). 然后, 通过取极限回到霍金辐射的冯·诺伊曼熵, 可以给出一条信息守恒的佩奇曲线, 即初态和末态的霍金辐射熵都为零. 该结果表明黑洞蒸发过程符合量子力学幺正性的要求, 因此在黑洞蒸发过程中并没有信息丢失的问题. 相关工作被认为朝着解决黑洞信息丢失问题迈出了关键的步骤, 特别是二维引力路径积分的发展及新的鞍点解的发现, 丰富了量子引力的研究, 成为近年来理论物理研究的热点^[35,36].

本文首先回顾另外一个古老的悖论——芝诺悖论, 通过分析芝诺悖论与黑洞信息丢失问题的相似性, 为黑洞信息丢失问题提供新的洞见. 即若把霍金辐射的冯·诺伊曼熵看作黑洞蒸发过程中的守恒量, 那么如何定义一个物理量来描述霍金辐射熵的“变化” ². 芝诺(约公元前490—公元前430年), 古希腊哲学家, 巴门尼德学派的坚决捍卫者, 以“飞矢不动”、“阿喀琉斯与乌龟”以及“二分法”等悖论闻名于世. 下文将主要关注“飞矢不动”这一命题, 其文字表述如下: 假设一支飞行的箭在某一时刻处于空间中的某一点. 在这个特定的时刻, 箭占据了一个确定的位置. 由于任何物体在任何一个瞬间都只能占据一个位置, 因此在这个瞬间, 箭是静止的. 进一步推论, 如果箭在每一个瞬间都是静止的, 那么在整个飞行过程中, 箭始终是静止的. 因此, 逻辑上可以认为箭实际上并没有移动, 而实际上观察者可以看到箭的确移动了, 故称“飞矢不动”悖论.

飞矢不动悖论的解决需要引入“极限”和“瞬时速度”等概念, 极限作为一个数学概念, 可以通过求极限从连续运动得到瞬时速度, 而瞬时速度这一概念定义在“速度空间”, 并不存在于飞矢所在的物理空间. 它存在于一个完全不同的、抽象的空间: 飞矢运动轨迹的切空间. 极限及其相关的微分的概念, 正是牛顿质点力学的内容. 除了瞬时速度的概念, 牛顿还引入了一个更加抽象的概念: “加速度”, 并认为“加速度”同速度是两个完全不同的概念. 正是在这些概念的基础上, 整个牛顿力学的框架由此建立起来了, 由此可见芝诺对于时间、空间和运动之间关系的思考有多深.

把芝诺悖论同黑洞信息丢失问题联系起来 需要以信息或者熵为载体. 前文提到规范/引力对偶, 这里给出一个严格表述: 规范引力对偶(anti-de sitter/conformal field theory correspondence, AdS/CFT对应)是指在一定条件下, 一个定义在d+1维anti-de sitter (AdS) 空间中的引力理论(通常是一个弦理论或超引力理论)与一个定义在d维边界上的共形场论之间存在一种精确的对偶关系. 根据规范/引力对偶, 可以把宇宙看作一个全息屏, 芝诺悖论指出为了看清宇宙的结构, 我们需要知道给定时刻全息屏上清晰的像素, 形成清晰的高质量的宇宙照片, 照片越清晰运动或者变化越不明显. 考虑初始态宇宙中只有一个有限大小的黑洞, 其外为真空. 这正是爱因斯坦方程的真空解. 黑洞信息丢失问题说, 因为有霍金辐射, 而且由于辐射的是黑体谱, 因此对于霍金辐射形成的物态也无从知晓, 导致最后宇宙的照片越来越模糊, 这对芝诺“飞矢不动”这一论断形成了严重的挑战. 按照飞矢不动的观点, 在任意时刻若客体不动, 则可对其进行成像, 不应出现照片变模糊的问题. 通过对$ {\Delta \boldsymbol{x}}/{\Delta t} $中取极限$ \Delta t \rightarrow 0 $, 得到了轨迹的切空间的矢量, 即“速度”这一概念. 同理, 冯·诺依曼熵通过对Rényi熵求极限得到, 即先把副本参数解析延拓至实数域, 可把Rényi熵看作连续的物理量, 而冯·诺依曼熵作为极限值是一个独立于Rényi熵的物理量. 在这个意义上, 芝诺悖论同黑洞信息悖论可建立直接的联系.

以芝诺悖论为对比, 黑洞霍金辐射的冯·诺依曼熵对应着其Rényi熵在$ n\rightarrow 1 $的极限, 说明冯·诺依曼熵可以被视为Rényi熵“切空间”中的 一个点. 而Rényi熵的计算需要计算物理量${\mathrm{ Tr}} \rho^n $. 引力路径积分中$ {\mathrm{Tr}} \rho^n $的计算, 主要涉及路径积分的“霍金鞍点”和“副本虫洞鞍点”. 即需要提前把量子态复制n份, 并在复制的量子态之间建立连接, 形成所谓的“副本虫洞”. 这种鞍点在计算$ {\mathrm{Tr }}{\boldsymbol{\rho}}^n $时起到了关键作用. 从这个角度看, 研究n依赖的物理量更有意义, 在计算中实施“副本技巧”对态密度复制n份, 这同量子不可克隆定理有冲突. 因此为了不违反量子不可克隆定理, 需要先验地准备或者提前知道量子态的n个备份. 当然, 不排除另外一种情况, 即量子引力理论允许在引力效应显著的情况下精确地复制量子态, 即当牛顿引力常数$ G_{{\mathrm{N}}} $对量子态的影响不可忽略时, 量子态的正交性有额外的修正. 总之, 有必要把这一问题进一步深化, 研究如何定义一个物理量来描述霍金辐射熵黑洞蒸发过程中的“变化”.

本文的结构和安排如下. 第2节通过对二维引力的路径积分进行回顾, 说明如何在黑洞蒸发的早期获得“霍金鞍点”, 以及如何在晚期获得“副本虫洞鞍点”. 这可以解释为什么在黑洞蒸发过程中量子力学的幺正性没有被违反. 第3节将深入探讨副本技巧与量子不可克隆定理之间的关系. 通过详细的分析, 揭示副本技巧如何看似挑战了量子不可克隆定理的基本原则. 具体来说, 存在一个可逆性的问题: 可以从一个已知的量子态的n个拷贝中重现这个量子态的全部信息. 然而, 对于一个未知的量子态, 由于量子不可克隆定理的限制, 无法对其进行复制, 因此也无法测量该量子态的其他信息. 第4节主要讨论模熵和纠缠容量. 通过类比热力学中的熵和力学中的加速度, 指出霍金鞍点和副本虫洞鞍点的相对熵可以作为描述系统不可逆性的关键物理量, 探讨了Rényi熵与热力学自由能之间的相似性. 第5节为了描述黑洞蒸发过程中状态的变化, 研究了相对熵和广义第二定律, 从而说明系统演化确实具有不可逆性. 总结与讨论在最后一节中给出.

通过对二维引力的路径积分做一次回顾, 说明如何在黑洞蒸发的早期得到“霍金鞍点”, 如何在晚期得到“副本虫洞鞍点”, 从而说明在黑洞蒸发过程中为什么量子力学的幺正性没有被违反. 在整个计算过程中, 考虑二维Jackiw-Teitelboim (JT)引力耦合到二维的共形场中, 这个共形场起到热浴的作用, 生长在没有引力的闵氏空间, 通过透明的边界同引力场连接. 详细讨论参见文献[35,36].

考虑二维引力中的作用量:

其中方程(1)的第二项描述了EOW膜(end of the world brane). 方程(2)中$ S_0 = 2\pi \phi_h $为常数, R为Ricci曲率标量, K为外曲率标量, ϕ为伸缩子场贡献了二维引力的自由度. 在EOW膜上生长了k个内部态可以用来描述早期霍金辐射的黑洞内部纠缠伙伴. 这k个态同一个辅助系统R相纠缠. 因此可以构造一个蒸发黑洞的早期辐射态. 把黑洞和辅助系统R作为一个整体, 可以写出系统的态函数:

这里$ \vert \psi_i \rangle_{\mathrm{B}} $描述了黑洞的量子态, 角标i表示EOW膜处于i态. $ \vert i \rangle_{\mathrm{R}} $表示辅助辐射系统R的量子态. 可以用二维引力路径积分来计算辅助系统R的熵. 可以写出密度矩阵$ {\boldsymbol{\rho}}_{\mathrm{R }}$

密度矩阵$ \rho_{\mathrm{R}} $的矩阵元为引力振幅$ \langle \psi_i\vert \psi_j\rangle $. 它满足以下边界条件:

这里箭头表示时间演化的方向, 从右矢量到左矢量. 考虑引力构型的领头阶, 满足边界条件的是如下的图形:

黑色带箭头的实线表示无穷远处的边界条件, 红色实线表示EOW膜. 在虚线和实线的交接处表示EOW膜同渐进边界交接. 黑色的渐近边界带有箭头代表引力构型(即涂色圆盘区域)的边界. 从方程(5)到方程(6), 用到了半经典极限即引力是经典的而物质场可以是量子的, 弱引力情况下方程(6)用约等于号. 一个重要的特点是, 同一条EOW膜同时连接到了i指标和j指标. 因为这里假设这些对应于EOW膜的正交内部状态, 所以结果将与$ \delta_{ij} $成比例. 这与标准量子力学的结果一致, 即在不考虑引力效应的情况下, 这里的计算与量子力学是一致的. 基于这个计算, ${\boldsymbol{ \rho}}_{\mathrm{R}} $似乎是最大程度混合的, 其熵为$ \log k $. 这同霍金的计算一致. 然而, 通过副本技巧, 可以通过考虑所谓的纯度$ {\rm{Tr}}({\boldsymbol{\rho}}^2_{\mathrm{R}}) $来计算熵, 这个纯度与$ n = 2 $的Rényi熵有关, 即

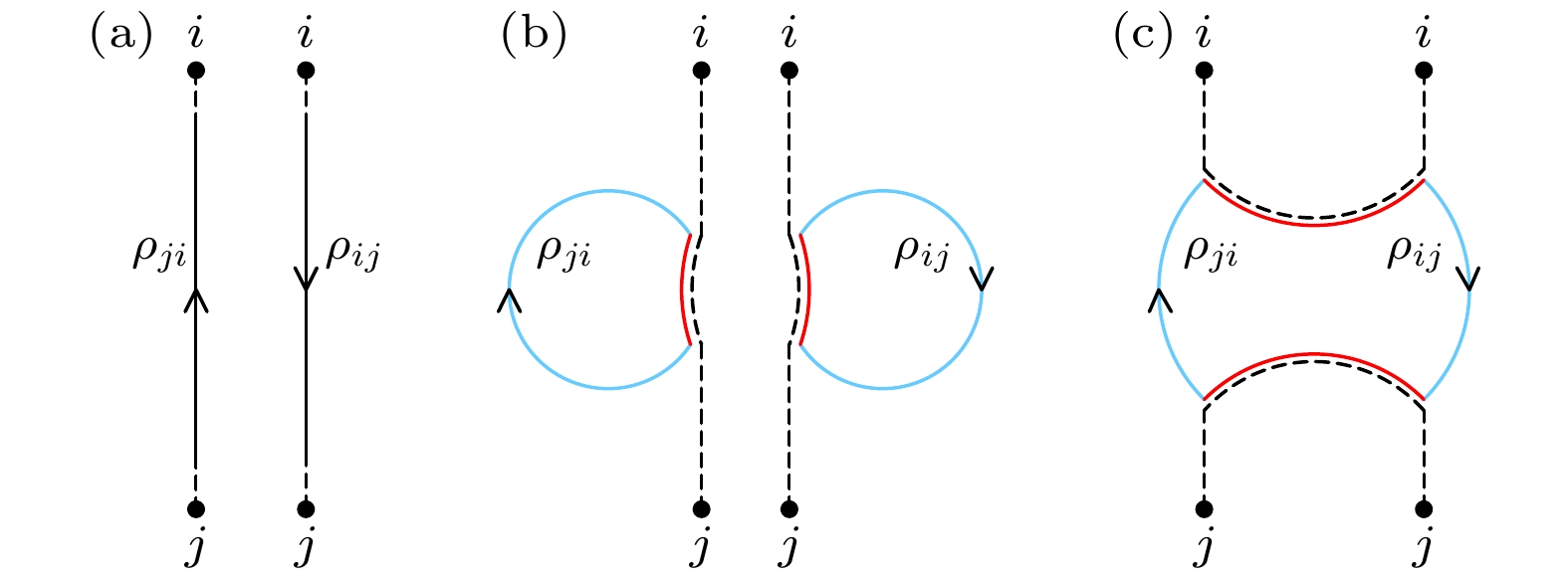
计算$ \vert \langle \psi_i\vert \psi_j \rangle \vert^2 $的边界条件如图1所示. 与冯·诺依曼熵的计算不同, 可以通过连接虚线以两种方式对$ i, j $进行求和. 可以有两种几何结构: 一种是具有两个圆盘拓扑的不连通几何结构, 另一种是具有单个圆盘拓扑的“欧几里得虫洞”连通几何结构. 对于连通几何结构, 对应的是将两个EOW膜几何体沿着EOW膜粘合在一起的情况. 那么, 在不连通的情况下, 拓扑将是两个圆盘; 而在连通的情况下, 拓扑将是一个圆柱体. 为了描述这些几何结构对$ {\mathrm{Tr}}({\boldsymbol{\rho}}^2_{\mathrm{R}}) $的贡献, 本文使用记号$ Z_n = Z_n(\beta) $表示在圆盘拓扑上的引力路径积分, 其边界由n段物理边界(每段的重整化长度为β)和n个EOW膜交替组成. 使用这种记号, 可以评估图中两种贡献的和:

在分子中有两种几何结构的贡献: 左边的不连通几何结构有一个k指标循环, 以及定义$ Z_1 $的几何结构的两份拷贝. 右边的连通几何结构有两个k指标循环, 以及定义$ Z_2 $的几何结构的一份拷贝. 分母除以了用于归一化密度矩阵的引力计算结果.

若要推广至更一般情况, 忽略高拓扑项的贡献后, 可以得到任意n的求迹运算表达式:

我们可以给出JT引力理论中配分函数$ Z_n $的近似形式, 即只考虑配分函数$ Z_n $对拓扑项$ S_0 $的依赖. 一般来说, 配分函数对拓扑项的依赖可表为$ {\mathrm{e}}^{\chi S_0} $, 其中χ为欧拉示性数. 因为对于一般的n, $ Z_n $对应的拓扑都是圆面, 其欧拉示性数为$ \chi = 1 $, 我们有$ Z_n \propto {\mathrm{e}}^{S_0} $, 方程(9)可以表示为

如果k相对较小, 不连通几何结构占主导地位, 会发现纯度为$ {1}/{k} $. 然而, 如果k非常大, 那么连通几何结构将占主导地位, 会发现纯度为$ {\mathrm{e}}^{-S_0} $, 且与k无关. 这两种鞍点主导地位的互换是防止辐射熵(这里指的是Rényi熵)无限增长的基本机制. 需要注意的是, 由于整个系统的状态是纯态, 这意味着即使当k非常大时, 黑洞中激发态(EOW膜状态)的熵仍然保持有限. 这一现象的基本机制是这些状态之间的微弱非正交性. 当k达到$ {\mathrm{e}}^{S_{{\mathrm{BH}}}} $的量级时, 这种非正交性的累积会产生显著的影响, 其中$ S_{{\mathrm{BH}}} $表示黑洞的贝肯斯坦-霍金熵.

通过副本技巧可以看到通过引力路径积分得到的$ {\mathrm{Tr}} {\boldsymbol{\rho}}^2 $受到了非微扰效应的影响. 这些非微扰效应来自引力路径积分中新的鞍点-副本虫洞. 该计算需要引入原始黑洞的n份副本, 在计算中把n解析延拓至非整数情况, 然后计算冯·诺伊曼熵. 推广到一般情况, 对于任意大的n, 可以考虑两种极端情况: 1)完全非连接几何的情况, 其拓扑由n个圆盘主导, 此时$ k\ll {\mathrm{e}}^{S_{{\mathrm{BH}}}} $, 此种情况仅k个独立的圆贡献, 可以写出配分函数

2)完全连接几何的情况, 其拓扑由一个单一的圆盘主导$ k\gg {\mathrm{e}}^{S_{{\mathrm{BH}}}} $, 此时配分函数的分子主要由$ Z_n $贡献:

式中k的贡献互相抵消, 因此密度矩阵的求迹运算主要由引力效应贡献. 为了计算冯·诺伊曼熵, 需要将$ Z_n $延拓到接近$ n = 1 $. 实现这一延拓的一个技巧是注意到与$ Z_n $相关的几何具有$ {\mathbb{Z}}_n $复制对称性. 当n趋近于1时, 将变成原来的未复制的几何, 冯·诺伊曼熵的计算简化为$ S_0+2\pi \phi_{\mathrm{h }}$, 其中$ \phi_{\mathrm{h}} $是伸缩子场在视界上的值.

在黑洞蒸发的早期, 时空几何包含原始黑洞的n个独立的复制样本, 这导致冯·诺伊曼熵的霍金鞍点, 霍金鞍点下冯·诺伊曼熵随时间线性增加, 这导致辐射熵的计算同量子力学的幺正性有冲突. 但是另外一个鞍点即副本虫洞鞍点, 通过把不同拷贝的黑洞连接起来, 形成了新的几何, 使得熵减少.

至此总结了二维引力中的引力路径积分, 并解释了在什么情况下出现霍金鞍点, 什么情况下出现副本虫洞鞍点, 从而说明黑洞的演化是幺正的, 因此没有信息丢失的问题. 需要说明的是, 目前虽然只有二维引力中的路径积分是可以严格计算的, 但是对说明物理问题已经非常难得了. 接下来的讨论将关注第二层面的问题, 即在模空间信息从霍金鞍点到副本虫洞鞍点的方向性问题, 或者说可逆性问题 ³. 之前的所有工作都表明从霍金鞍点到副本虫洞鞍点的演化在微观上是幺正的, 因此在微观上二者之间是可逆的. 根据之前的计算, 黑洞演化的早期阶段, 引力路径积分主要由霍金鞍点支配; 而在黑洞演化的晚期阶段, 则主要由虫洞鞍点支配, 二者的时间间隔约为佩奇时间. 整个黑洞蒸发过程是幺正的, 没有信息丢失. 然而, 为什么在黑洞演化的早期阶段, 主导的不是虫洞鞍点而是霍金鞍点？这显然产生了一个新的悖论.

在做副本计算时, 需要对密度矩阵复制n份, 但是量子不可克隆定理禁止对一个未知的量子态进行克隆. 因此若要对密度矩阵实现复制, 需要事先知道量子态$ \vert \varPsi\rangle $. 亦即要在实验中模拟黑洞的蒸发过程, 需要提前准备n份已知的量子态. 则取极限$ n\rightarrow 1 $可以得到有限的冯·诺伊曼熵. 因此, 从信息的角度来看, 也应该存在一个方向性的问题, 即只有先存在n份量子态$ \vert \varPsi\rangle $的信息, 才能有黑洞演化后的副本虫洞鞍点. 只有这样才可以满足量子不可克隆定理. 这暗示着对于黑洞蒸发来说, 多个副本的霍金辐射态应该先于单个霍金辐射态而存在.

副本技巧是一种处理无序系统和复杂相互作用的方法, 特别是在统计物理中, 其核心思想是通过对多个副本(replicas)的平均来提取系统的整体性质. 考虑一个量子系统, 其密度矩阵为ρ, 可以构造它的n个副本, 通过计算$ {\mathrm{Tr}}({\boldsymbol{\rho}}^n) $的平均值, 可以推出系统的自由能

在这个过程中, 我们并没有尝试直接复制未知的量子态$ \vert \psi\rangle $, 而是通过数学手段处理多个已知系统的副本, 从而提取系统的整体性质.

量子不可克隆定理指出, 不可能精确复制一个未知的量子态^[37]. 这里未知的量子态指的是形如

的量子态, 其中α和β为未确定的常数. 其精确表述如下: 对于任意未知的量子态$ \vert \psi\rangle $, 不存在一个量子操作U可以将单个量子态$ \vert \psi\rangle $复制为两个相同的量子态$ \vert \psi\rangle \otimes \vert \psi\rangle $. 可以用反证法证明该定理, 即假设存在一个量子操作U, 它可以将一个未知的量子态$ \vert \psi\rangle $和辅助量子态$ \vert 0\rangle $映射到$ \vert \psi\rangle \otimes \vert \psi\rangle $, 即$ {\boldsymbol{U}} \vert \psi\rangle \otimes \vert 0\rangle = \vert \psi\rangle \otimes \vert \psi\rangle $. 设存在两个未知的量子态$ \vert \psi\rangle $和$ \vert \phi\rangle $, 在复制操作U的作用下, 满足$ {\boldsymbol{U}}\vert \psi\rangle = \vert \psi\rangle \otimes \vert \psi\rangle $, $ {\boldsymbol{U}}\vert \phi\rangle = \vert \phi\rangle \otimes \vert \phi\rangle $. 考虑两个未知的量子态$ \vert \psi \rangle $和$ \vert\phi\rangle $的内积, 不失一般性, 可以写作$ \langle \psi \vert \phi\rangle = c $, 其中c为一个复数, 表示两个波函数的重叠. 可以计算量子态$ {\boldsymbol{U}}(\vert \psi\rangle\otimes \vert 0\rangle ) $和$ {\boldsymbol{U}}(\vert \phi\rangle\otimes \vert 0\rangle ) $的内积:

因为U是一个幺正矩阵, 所以有${\boldsymbol{ U}}^{\dagger}{\boldsymbol{U }}= {\boldsymbol{I }}$. 容易得到

注意左边的内积可以写为$ \langle \psi \otimes 0\vert \phi \otimes 0\rangle = \langle \psi \vert \phi\rangle \langle 0 \vert 0\rangle = \langle \psi \vert \phi\rangle $, 而右边的内积可以写为$ \langle \psi \otimes \psi\vert \phi \otimes \phi\rangle = \vert\langle \psi\vert \phi\rangle\vert^2 $. 于是可以得到$ c = c^2 $, 其平凡解为$ c = 0 $, 非平凡解为$ c = 1 $. 然而, 如果$ \vert \psi\rangle $和$ \vert \phi\rangle $是两个不同的量子态, c的取值应该介于0和1之间, 这导致了矛盾, 因此未知的量子态是不可克隆的.

下面从副本技巧的角度来理解量子不可克隆定理的适用范围. 考虑一个量子系统, 其状态由密度矩阵ρ描述. 假设存在多个副本$ \vert \psi_i\rangle $, 并且引入随机变量$ R_{ij} $来描述量子态之间的微小扰动:

其中$ S_0 $是黑洞的熵, 通常是一个非常大的数, 因此$ {\mathrm{e}}^{-S_0/2} $非常小, 随机变量$ R_{ij} $具有零均值和有限方差.

设$ \vert \psi_i\rangle $, $ \vert \psi_j\rangle $分别为两个不同的量子态, 存在一个幺正的量子操作U, 可将一个未知的量子态$ \vert \psi_i\rangle $和辅助态$ \vert 0 \rangle $映射到$ \vert \psi_i\rangle \otimes \vert \psi_i \rangle $. 类似于前面的讨论, 可计算量子态$ {\boldsymbol{U(}}\vert \psi_i\rangle \otimes \vert 0 \rangle) $和$ {\boldsymbol{U}}(\vert \phi_j\rangle \otimes \vert 0 \rangle) $, 和前面的内容不同的是还需要对随机量$ R_{ij} $做系综平均. 设$ c_{ij} $的平均值为c, 而$ \overline{R_{ij}} = 0 $, $ \overline{R^2_{ij}} = \sigma^2 $. 用上划线表示对随机变量取平均:

容易得到

此即

此时常数c显然具有介于0和1之间的非平凡解, 故量子不可克隆定理可被违反. 由此可见, 对于未知的量子态, 由于副本技巧允许不同量子态的关联, 因此实质上可以出现违反量子不可克隆定理的情况. 为了避免这种情况, 在副本操作进行前应该知道要被复制量子态的全部信息.

在副本技巧中, 我们考虑的是多个已知的系统副本, 而不是直接复制未知的量子态. 每个副本都是一个独立的系统, 它们之间可能存在相互作用, 但每个副本的状态是已知的. 在量子系统中, 即使不能直接复制未知的量子态, 仍然可以通过对多个已知系统的统计分析来提取有用的信息. 量子不可克隆定理限制了直接复制未知量子态的操作, 但副本技巧并不依赖于这种直接复制. 相反, 副本技巧通过数学手段处理多个副本的平均性质, 从而绕过了直接复制的问题. 副本技巧使用了数学工具, 如路径积分和鞍点近似, 来处理多个副本的平均性质. 这些数学工具允许我们在不直接复制量子态的情况下, 有效地处理和分析系统的复杂性质.

因此这里有一个可逆性的问题, 可以从一个已知的量子态的n个拷贝, 重现这个量子态的全部信息. 但是无法对一个未知的量子态进行副本复制, 从而测量该量子态的其他信息.

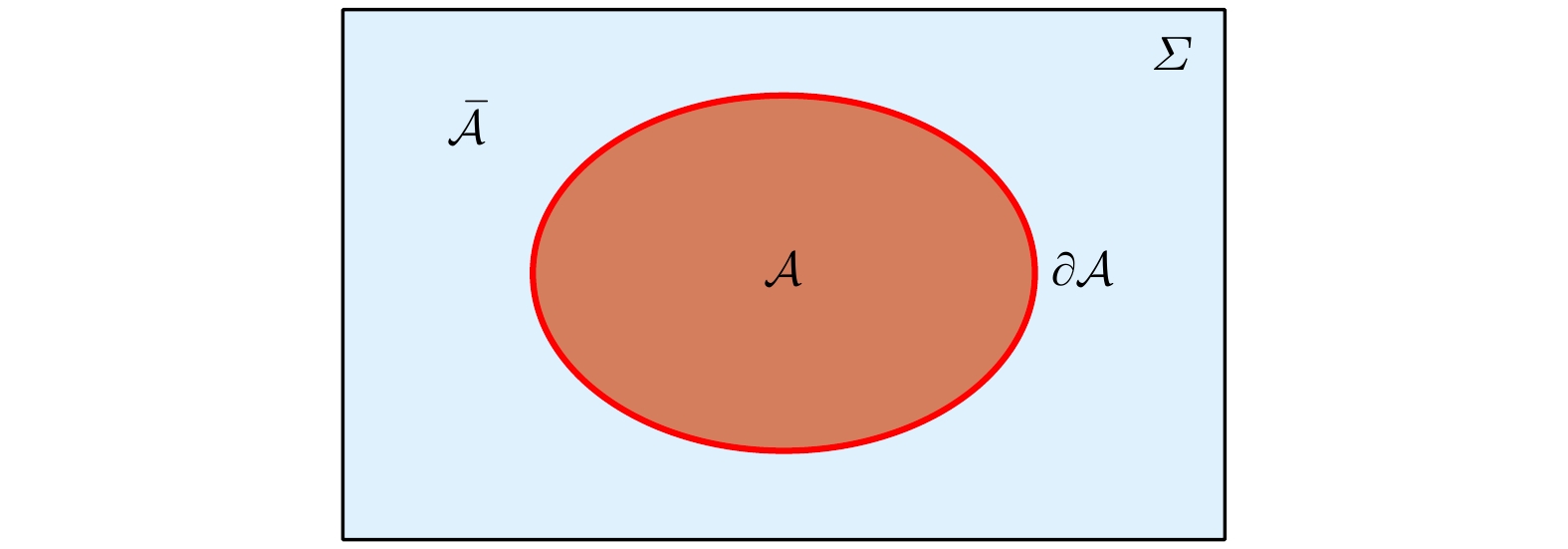
在上面的讨论中, 先把芝诺悖论同黑洞信息丢失问题做了类比. 可以看出对Rényi熵取极限类似于瞬时速度中位移的变化$ \Delta \boldsymbol{x} $对时间取极限$ \Delta t \rightarrow 0 $. 这样一来, 可以把冯·诺伊曼熵建立在数学上更加坚实的基础上, 因为可以像力学理论中一样把冯·诺伊曼熵同样看作某种守恒量, 在霍金辐射开始和结束的阶段, 黑洞霍金辐射的冯·诺伊曼熵保持不变. 近期关于黑洞霍金辐射的Page曲线计算证明了这一点. 而这显然是不够的, 因为一个自洽的理论, 除了描述物理过程中的不变量, 还需要其他的物理量描述变化. 在力学中描述变化的量是加速度, 在热力学中相应的物理量是熵. 加速度对应的物理量是力, 而熵描述的是系统过程进行的不可逆性. 需要注意的是热力学量, 不能简单地用分析力学中的数学框架来描述. 一般而言, 热力学具有更大的普适性. 下面可以看到, 纠缠熵的数学表述同热力学的理论框架具有更多的一致性.

为了给出模熵较为系统的描述并引入新的物理量, 一个直观的做法是做类比. 本文把纠缠熵同统计力学进行对比, 并解释为什么副本参数可以看作有效逆温度. 在量子场中, 如图2所示, 一个子区域$ H_{\cal{A}} $的冯·诺伊曼纠缠熵$ S_{{\cal{A}}} $定义为

其中$ {\boldsymbol{\rho}}_A $定义为

其中$ \bar{{\cal{A}}} $为$ \cal{A}$的补集. 这里考虑$ {\boldsymbol{\rho}}_{\rm{total}} $作为一个纯态, 即$ {\mathrm{Tr}} {\boldsymbol{\rho}}_{\rm{total}} = 1 $.

冯·诺伊曼熵是量子系统中用于量化混合状态纯度的一个指标, 它表征了系统最大纠缠对的数目, 并在完全纯态时取最小值零, 在最大混合态时达到峰值, 反映了量子态的不可区分性. 如果$ {\boldsymbol{\rho}}_{\rm{total}} $是一个混合态, 则有$ {\mathrm{Tr }}{\boldsymbol{\rho}}^n < 1 $. 纠缠熵满足可加性原理, 即

更一般地还可以定义Rényi熵^[38],

冯·诺伊曼纠缠熵可以作为一个极限从Rényi熵中导出,

稍后可以看到Rényi熵同热力学中的自由能具有相同的形式. Rényi熵具有以下性质^[39]:

我们可以进一步引入模哈密顿量(modular Hamiltonian) ⁴

此时Rényi熵可以写为

同热力学中的自由能定义相对比:

可以看出Rényi熵同自由能的微分形式非常类似, n起到β的作用. 接下来继续探讨n的作用及$ S_{m} $的物理意义 ⁵.

对比副本技巧与统计力学, 本文引入以下两个物理量:

1)模熵 (modular entropy) 是一个量子信息论中的概念, 其定义见表1. 相比较冯·诺伊曼熵, 模熵对参数n的依赖是导数形式. 它可以帮助我们量化系统内部的纠缠程度. 模熵的引入是因为在寻找Rényi 熵的全息对偶过程中, 人们意识到可以给出纠缠熵的另一种形式使之更像“热力学熵”, 而Rényi 熵在引力理论中对偶于宇宙膜(cosmic brane)的面积^[40].

2) 纠缠容量(entanglement capacity) 是另一个重要的物理量, 表示每增加或减少一个副本所对应的模熵的变化, 可以用来刻画在模空间中的相变.

接下来讨论Rényi熵与热力学量的类比. 引入模熵的形式为

观察可知, 若要把n看作逆温度, 模熵的定义相比Rényi熵定义更接近热力学熵. 可以把模熵写成如下形式:

同热力学的关系对比,

可以看出只要把n认同为β, 则模熵同热力学熵具有相同的表达式. 从表1可以看出, 模哈密顿量(modular Hamiltonian)对应于统计力学中的哈密顿量. 副本参数n对应于统计力学的逆温度β, 但是n并不是真正的逆温度, n表示希尔伯特空间被复制的次数. 由此可以看到, 在模空间可以定义配分函数、自由能、能量和模熵, 乃至纠缠容量, 具体的讨论参见即将完成的论文[41].

作为一个具体的例子, 考虑如下哈密顿量:

其中$ {\boldsymbol{\sigma}}_z = \begin{pmatrix} 1 & 0 \\ 0 & -1 \end{pmatrix} $为泡利矩阵. 它描述了由两个子系统A和B构成的贝尔态. 零温下该体系的密度矩阵可以写为

对子系统求迹, 可以得到子系统A的约化密度矩阵$ {\boldsymbol{\rho}}_A $为

在有限温度下, 假设子系统A和B各自处于热平衡状态, 相应的密度矩阵为

设子系统A和B的哈密顿量相同, 则可以得到子系统A的密度矩阵为

可以得到${\boldsymbol{ \rho}}^n_A $, 有

求迹可以得到

可以计算出模熵为

同样可以得到纠缠容量为

固定β, 当副本参数n变化时, 可以看出模熵和纠缠容量都会发生变化. 当$ n\rightarrow 1 $时, 模熵趋于一个有限值. 而当n增大时, 模熵减少, 可得$ S_{n\rightarrow \infty} < S_{n\rightarrow 1} $. 但是对于纠缠容量, 有

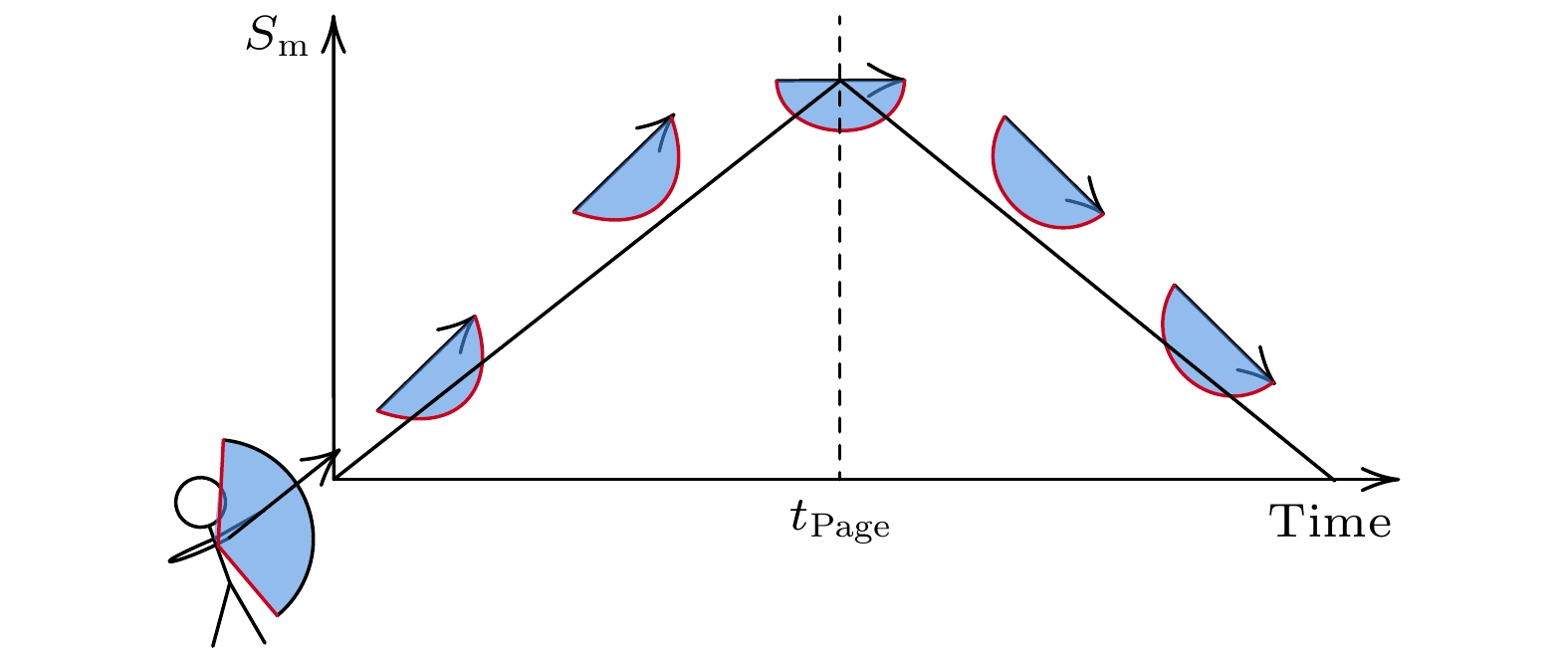
当$ n\rightarrow \infty $, $ C_{\infty}\rightarrow 0 $. 显然$ C_1 > C_{\infty} $. 当温度趋近于绝对零度时, $ \beta\rightarrow \infty $, $ \tanh{(n\beta \hbar \omega)}\rightarrow 1 $, 纠缠容量趋于零. 随着温度升高β减小, 纠缠容量增加, 反映了热效应对量子纠缠的影响. 当β固定而变化n时, 可以得到高副本参数下, 系统的模熵减弱, 且量子纠缠特性(由纠缠容量表示)减弱. 这反映了系统在高副本时逐渐趋向于“基态”行为的趋势. 在统计物理中德布罗意波长$ \lambda_{\mathrm{dB}}=\sqrt{\dfrac{\pi\hbar^2}{mk_{\mathrm{B}}T}} $是区分热效应与量子效应重要的物理量, 对于有限温度的量子系统, 当$ \beta \hbar \omega \ll 1 $时, 热效应将占主导; 而$ \beta\hbar \omega \gg 1 $时, 量子行为将变得非常显著. 为了清晰表征副本参数n的作用, 可以定义广义德布罗意波长, 即$ \lambda_{\rm{eff}}\equiv\lambda_{{\mathrm{dB}}}{\mathrm{e}}^{S_{{\mathrm{vN}}}-S_{m}} $, 当$ n\rightarrow \infty $时, 因为副本参数的作用, 广义德布罗意波长变大, 量子效应被放大, 而当$ n\rightarrow 1 $时$ S_{vN} = S_{m} $, 广义德布罗意波长回到统计力学中的情况.

黑洞辐射熵的变化过程可以分为两个阶段: 熵随时间线性增长; 熵随时间逐渐减少. 这两个阶段之间的转折点称为佩奇时间($ t_{{\mathrm{page}}} $), 这是一个非常长的时间. 一般而言, Page时间可以表示为^[19]

其中$ S_{{\mathrm{BH}}} $为黑洞的贝肯斯坦-霍金熵, κ为黑洞的表面重力, c为中心荷. 佩奇时间大约为黑洞寿命的$ {1}/{2} $. 对于天体质量的黑洞, 这个时间可能比宇宙的年龄还要长.

对于大质量黑洞, 由于黑洞蒸发过程非常缓慢, 可以将其类比于准静态过程. 准静态过程是指系统在每个时刻几乎都处于平衡状态, 因此可以近似认为黑洞蒸发过程是可逆的. 在这种假设下, 整个蒸发过程中辐射熵是守恒的, 从而可以得到佩奇曲线. 佩奇曲线描述了黑洞辐射熵随时间的变化, 具体表现为熵先增加后减少的过程. 这个曲线是基于理想化的假设, 即黑洞蒸发过程在微观上是幺正的. 然而, 实际的物理过程往往包含不可逆性, 因此需要引入额外的物理量来描述这些不可逆效应. 后面可以看到, n依赖的相对熵可以作为描述不可逆性的合适物理量.

根据Rényi熵与统计力学量的类比, 可知模熵的行为更加接近热力学熵. Casini在2008年提出了一种在量子场论中表达黑洞热力学第二定律(generalized second law, GSL)的新方法, 并论证了贝肯斯坦上限在这个框架下的自动满足性. Casini首先解决了在量子场论中定义局部区域内的熵和能量的问题. 为了克服传统上因量子场论的非局域性和紫外发散而导致的困难, Casini提出了减去真空涨落贡献的方法, 即计算状态相对于真空态的熵差, 即$ S_{{\mathrm{V}}} = S_{{\boldsymbol{\rho}}_{\mathrm{V}}}-S^{0}_{{\boldsymbol{\rho}}_{\mathrm{V}}} $以及相应的能量差$ K_{\mathrm{V}} = {\mathrm{Tr}}(K {\boldsymbol{\rho}}_{\mathrm{V}})-{\mathrm{Tr}}(K{\boldsymbol{\rho}}^{0}_{\mathrm{V}}) $, 其中K是由真空密度矩阵定义的局部哈密顿量. Casini建议使用相对熵$ S({\boldsymbol{\rho}}_{\mathrm{V}}\vert\vert {\boldsymbol{\rho}}^0_{\mathrm{V}}) $来重新表述贝肯斯坦上限. 相对熵是一个正定量, 表示两个状态之间的统计距离. 文中指出, 当一个物体被黑洞吞噬时, 最不具约束性的不等式就是$ S({\boldsymbol{\rho}}_1\vert\vert {\boldsymbol{\rho}}_{{\mathrm{HH}}})\geqslant 0 $, 这里${\boldsymbol{ \rho}}_1 $指的是在某个初始时间$ t_1 $黑洞外部区域的实际量子态, 而${\boldsymbol{ \rho}}_{{\mathrm{HH}}} $表示哈特尔-霍金热平衡态. 此不等式表明, 相对于热平衡态, 任何实际的量子态所携带的信息量(通过相对熵衡量)不会减少, 这支持了广义第二定律(GSL)的有效性. 这意味着, 即使物体掉入黑洞, 整个系统的总熵加上黑洞的贝肯斯坦-霍金熵仍然不会减少, 从而保证了广义第二定律的成立.

正如前面所提到的, 在黑洞蒸发过程中先出现了霍金鞍点, 此时最小量子极值面的面积接近于零, 副本虫洞鞍点的贡献可以忽略. 而在蒸发过程的晚期, 副本虫洞鞍点主导. 为了更有说服力, 这里尝试给出n依赖的相对熵广义第二定律, 从而说明n具有真实的物理意义. 一般而言, 对于密度矩阵ρ和σ, 可以定义相对熵$ S({\boldsymbol{\rho}}\vert\vert {\boldsymbol{\sigma}}) $,

它满足两个重要的性质: 正定性和单调性. 正定性是指相对熵对于任意两个密度矩阵是非负的. 若两个矩阵相等则相对熵为零. 相对熵的单调性则描述了在通过完全正定保迹(completely positive trace-preserving, CPT)映射作用后, 两个量子态之间的相对熵不会增加. 对于任意的两个量子态ρ和σ, 以及任意一个CPT映射Φ, 有

从物理的角度来看, 相对熵的单调性意味着任何有效的量子操作(如测量、演化等)都不会使我们比原来更精确地区分两个量子态.

将σ视为参考态, 并引入其模哈密顿量$ {\cal{H}}_{A} $. 可以以此定义模自由能$ F({\boldsymbol{\rho}}) = {\mathrm{Tr}}({\boldsymbol{\rho}} {\cal{H}}_{A})- S({\boldsymbol{\rho}})/n $, 其中$ S({\boldsymbol{\rho}}) $是密度矩阵的冯·诺伊曼熵. 利用这一点, 很容易得到

对于黑洞蒸发过程, 霍金鞍点的密度矩阵设为ρ, 而副本虫洞的密度矩阵为$ {\boldsymbol{\rho}}_n = {\mathrm{e}}^{-n H} $, 把它们皆同哈特尔-霍金态$ {\boldsymbol{\rho}}_{{\mathrm{HH}}} $相对比. 从方程(45)可以得到

表明随着时间的推移, 相对于热平衡态$ {\boldsymbol{\rho}}_{{\mathrm{HH}}} $, 实际态的信息损失不会增加. 由$ F({\boldsymbol{\rho}}_n)-F({\boldsymbol{\rho}})\leqslant 0 $, 可以得到

式中下脚标ρ代表霍金鞍点, 而n代表副本虫洞鞍点. 由此可得“相对熵第二定律”:

因此, 在模空间霍金鞍点和副本虫洞鞍点之间存在方向性, 该方向性由相对熵第二定律给出, 同时n确实起到逆温度的作用. 此论证过程同Casini在2008年通过相对熵的概念论证热力学广义第二定律相类似.

本文回顾了近年来人们在黑洞信息丢失问题上取得的最新进展. 通过把芝诺悖论同黑洞信息丢失问题做对比, 指出解决黑洞信息丢失问题应该考虑两个层面的问题. 第一个层面的问题是若信息没有丢失, 在黑洞辐射过程中除了霍金鞍点, 还需要“副本虫洞鞍点”, 从而使得黑洞霍金辐射熵满足纠缠熵演化的佩奇曲线. 通过对副本技巧和副本虫洞鞍点的讨论, 可以明确黑洞演化的早期, 霍金鞍点占主导, 而在演化的晚期, 副本虫洞鞍点占主导.

研究量子不可克隆定理与副本技巧之间的关系表明, 为了避免二者之间的矛盾, 在实施副本技巧过程中, 需提前考虑多个已知的量子态副本, 而不是复制未知的量子态的副本. 量子不可克隆定理禁止了直接复制未知量子态的操作, 但副本技巧并不依赖于这种直接复制. 相反, 它通过数学手段分析多个副本的统计性质, 从而绕过了直接复制的问题. 副本技巧利用了路径积分、鞍点近似等数学工具, 来处理多个副本的平均特性. 这些数学工具使我们能够有效地解析和评估系统的复杂行为, 提供了一种强大的分析方法.

这里提出了一个关键的问题, 在黑洞演化过程中, 霍金辐射态的多个复本应该先验地存在, 只不过在演化的早期不同副本之间的联系足够弱, 但在演化的晚期, 副本之间的连接(即副本虫洞)占主导, 从而使得信息恢复成为可能. 这似乎支持了量子力学的多世界假设.

对于蒸发黑洞, 冯·诺伊曼熵在黑洞演化的初末态保持不变说明霍金辐射熵可以作为一个守恒量来处理. 为了进一步刻画霍金辐射过程中物理量的变化, 以模哈密顿量作为切入点, 发现模熵同热力学熵具有类似的表达式, 从而可以建立模空间纠缠熵的“热力学”, 并可以发展纠缠容量的概念. 作为一个例子, 计算了最大纠缠贝尔态对应的模熵和纠缠容量, 发现随着n的增大, 模熵和纠缠容量都趋向于有限值或者零, 反映了副本参数n的确具有逆温度的效应.

为了更精确地描述这一过程的变化量, 并赋予副本参数n真实的物理意义, 本文引入了依赖于n的相对熵广义第二定律. 相对熵$ S ({\boldsymbol{\rho}}\vert\vert {\boldsymbol{\sigma}}) = {\mathrm{Tr}}({\boldsymbol{\rho}} \log {\boldsymbol{\rho}})-{\mathrm{Tr}}({\boldsymbol{\rho}} \log {\boldsymbol{\sigma}}) $是衡量两个量子态之间差异的重要工具, 它具有两个重要性质: 正定性和单调性. 正定性确保相对熵非负, 而单调性则指出任何有效的量子操作不会增加两个量子态之间的区分度. 对相对熵的研究揭示了从霍金鞍点到副本虫洞鞍点转变的方向性，这正是黑洞信息丢失问题的第二个层面. 该方向性由相对熵第二定律给出, 同时证实了n在此过程中确实起到了逆温度的作用.

作者对于黑洞信息丢失问题的研究可以追溯到2005年, 在中国科学技术大学交叉学科理论研究中心的讨论班上, 在卢建新、李淼等教授的指导下研读了S.Mathur的论文The quantum structure of black holes [arXiv: 0510180], 该篇论文提出了解决黑洞信息丢失问题的“模糊球理论”. 在论文讨论会上, 卢建新老师指出黑洞信息丢失问题的解决需要新的物理原理和数学语言. 转眼20年过去, 人们在黑洞信息丢失问题上取得了巨大的进展. 近年来, 作者注意到“副本虫洞”与“岛屿公式”作为新的数学语言丰富了这一课题. 在广义熵的岛屿公式中, 把黑洞内部态和黑洞外部态看作一个整体, 这在语言上仍有歧义. 从中可以看出, 黑洞信息丢失问题需要在数学语言上有新工具, 而且我们留意到仅仅有信息守恒是不够的, 需要新的物理量来描述变化. 感谢博士生余明辉为本文提供的作图.