随着激光技术的飞速发展, 对光学势阱中超冷量子气体的调控逐渐成为理论和实验物理学重要的研究方向^[1]. 超冷量子气体具有许多超越经典物理的新奇特征和常温物态无法比拟的调控优势. 一方面, 在极低温度下, 原子分子系综展示出奇特的量子统计性质, 这些性质本身超越了经典物理学范畴, 因而成为新物理学的生长点^[2]; 另一方面, 通过对光场参数的有效选择, 研究者们可以精确地操控原子间相互作用以及各种人造规范场^[3], 这不仅为模拟凝聚态体系中的量子多体现象提供了新的手段, 更催生了多种量子精密测量的新技术^[4–6].

特别是将玻色气体冷却至极低温度, 可以形成所谓玻色-爱因斯坦凝聚体^[7,8] (Bose-Einstein condensate, BEC). 光学势阱中的BEC兼具单原子内态丰富的能级结构和多原子体系独特的轨道动力学特性^[9–12]. 在实验上, BEC的内态(单个原子内部的超精细能级)和外态(原子体系的集体轨道状态)拥有各自独立的动力学特征, 因而往往需要不同的调控手段. 前者需要作用于原子超精细能级的有效塞曼场^[13,14], 后者需要作用于原子质心轨道运动的光子动量转移^[15]. 近年来实现的基于BEC的自旋-轨道耦合将原子的自旋态和轨道态进行有机组合, 提出了将原子内外态纳入统一描述框架的新命题^[16,17]. 截至目前, 基于BEC自旋-轨道耦合效应方面的研究已取得了大量进展. 例如, 研究发现原子间的短程碰撞会与自旋-轨道耦合诱导的非阿贝尔规范场相互竞争, 进而衍生出密度波条纹相和自旋极化相等一系列新奇的量子物态^[17–23]. 另外, 自旋-轨道耦合还会诱导出自旋依赖的质心偶极振荡等有趣的动力学效应^[24–32], 这些效应已部分地被应用于自旋纯化^[33,34]和自旋共振^[35,36]等领域.

在此背景下, 本文给出了一种自旋-轨道耦合BEC在内外态联合调控作用下的动力学响应效应. 此处的“内外态联合调控”指的是驱动场同时包含了作用于原子内态的塞曼场和作用于外态的轨道势场. 具体考虑BEC在某一时刻被快速晃动, 同时又感受到一外部施加的塞曼场. 通过适当简化模型, 得到了自旋在$ x $方向上动力学演化的解析表达式, 并从该表达式出发, 推导出自旋频谱对外场参数的响应关系. 对Gross-Pitaevskii (GP)方程的数值求解结果与解析表达式符合得很好. 进一步研究发现, 自旋频谱对外场驱动响应的物理本质是不同自旋-轨道态之间的量子干涉. 在此背景下, 本文给出了频谱响应的动力学调控图像和量子干涉仪图像. 由于BEC的内态和外态等特征参数可以直接反映于自旋频谱上, 本结果在量子控制和量子计量学等领域有潜在应用价值.

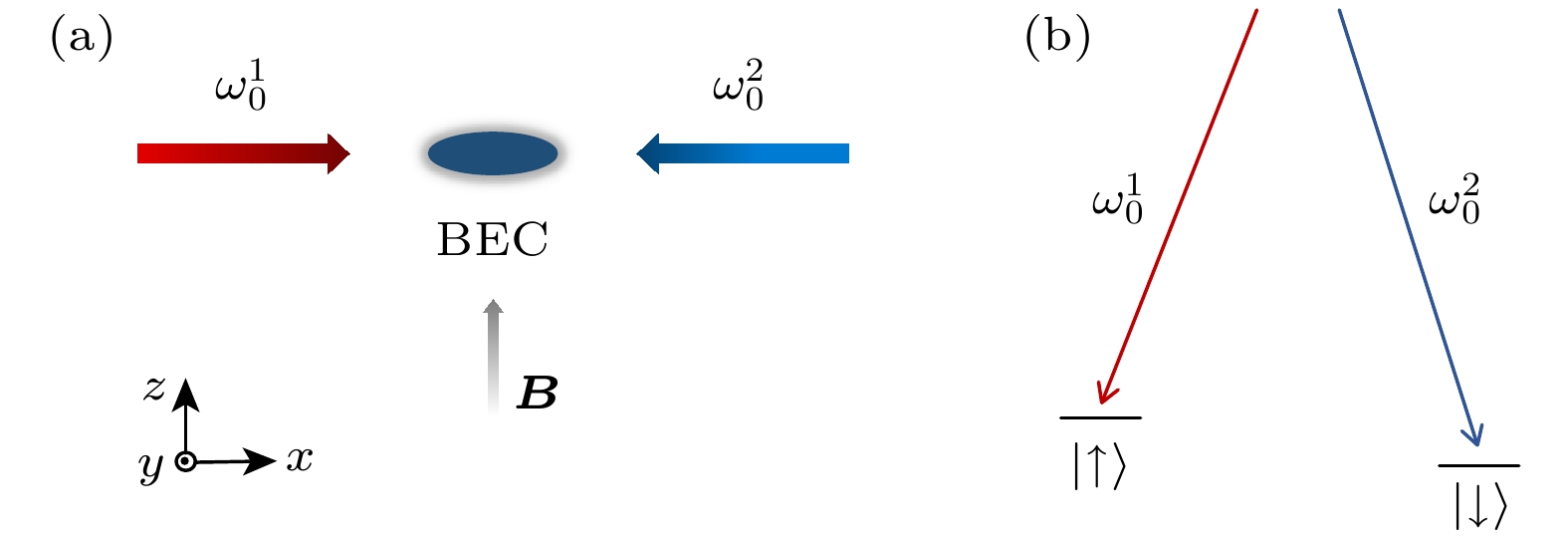
本模型的出发点是文献[16]所报道的超冷原子气体中的人工自旋-轨道耦合. 如图1(a)所示, 考虑一团$ ^{87}{\text{Rb}} $原子的BEC, 它的运动自由度被限制在x方向上. 凝聚体的两个赝自旋态$ \left| \uparrow \right\rangle $和$ \left| \downarrow \right\rangle $可分别选为$ ^{87}{\text{Rb}} $原子的两个基态超精细能级$ | F = 1, {m_{\text{F}}} = - 1 \rangle $和$ \left| {F = 1, {m_{\text{F}}} = 0} \right\rangle $, 这两个基态能级被来自x方向上的两束对向传播的拉曼激光(频率分别为$ \omega _0^1 $和$ \omega _0^2 $, 波长为$ \lambda $)所耦合(图1(b)). 沿z方向施加的磁场$ B $不仅确定了系统的量子化轴, 还同时使得两个赝自旋态产生大小为$ \hbar {\omega _z} $的能级劈裂. 在大失谐条件下, 通过绝热消除掉激发态能级, 系统的动力学被限制在由自旋态$ \left| \uparrow \right\rangle $和$ \left| \downarrow \right\rangle $张成的希尔伯特空间中, 其低能有效哈密顿量的矩阵形式为^[17]

其中, $ {p_x} $和$ m $分别是原子的动量和质量; $ {k_0} = 2{\text{π}}/\lambda $为单光子反冲动量; $ \varOmega $为双光子过程的有效拉比频率; 塞曼能量$ \eta $由拉曼光频移和磁场劈裂贡献, $ \eta = \omega _0^1 - \omega _0^2 - {\omega _z} $; $ V(x) = m{\omega ^2}{x^2}/2 $提供原子在x方向上的外场俘获势.

哈密顿量(1)在坠饰基$ \left| + \right\rangle = \exp ( - {\text{i}}{k_0}x)\left| \uparrow \right\rangle $和$ \left| - \right\rangle = \exp ({\text{i}}{k_0}x)\left| \downarrow \right\rangle $下可写成如下更简洁的形式^[16,17]:

其中, $ {\sigma _i}\, (i = x, y, z) $是新基矢下的泡利自旋算符, $ \alpha = \hbar {k_0}/m $为自旋-轨道耦合强度. 仔细观察哈密顿量(2), 系统的动力学由外态和内态两部分贡献, 前者包含位置和动量的变化, 而后者则是自旋的演化. 自旋-轨道耦合强度$ \alpha $承担着连接自旋态和轨道态的作用. 可以预见, 由于存在非零的$ \alpha $, 对外态的操控势必会影响内态, 反之亦然. 在此背景下, 考虑对系统内外态的联合含时操控, 以期获得更加丰富的动力学信息. 具体考虑凝聚体在$ {t_0} $时刻经历一次“晃动”, 与此同时, 作用于自旋的塞曼场$ \eta $由零变化为非零^[32]. 该过程可以归结为哈密顿量(2)中的$ V(x) $和$ \eta $受到如下含时调控:

其中, $ \varTheta (s) $为宗量$ s $的阶跃函数, 满足$ \varTheta (s \gt 0) = 1 $和$ \varTheta (s \lt 0) = 0 $. 注意到, 晃动操作体现在俘获势中心所历经的一个含时高斯脉冲$ {x_0}(t) $; $ \zeta $和$ \tau $分别描述晃动脉冲的峰值和脉宽. 注意到在实际的实验操作中, 塞曼场的快速开启需要耗费有限的时间, 将$ \eta (t) $的开启设定为按照指数调增的时序, 开关特征时间为$ \tau $. 显然$ \tau \to 0 $时, 有$ \eta (t) \to {\eta _0}\varTheta (t - {t_0}) $. 另外, 考虑到实验系统中不可避免的原子间相互作用, 系统完整的动力学演化将由如下GP方程描述^[9]:

式中$ \varPsi = {({\psi _ + }, {\psi _ - })^{\text{T}}} $为旋量波函数; $ {H_{\text{i}}} $是刻画原子间相互作用影响的平均场哈密顿量, 其矩阵形式为^[37]

其中, $ {g_{\sigma \sigma '}}\, (\sigma , \sigma ' = + , - ) $刻画超精细基态原子间的s波相互作用, 其强度可在实验中利用Feshbach共振技术灵活调节. 需要说明, 平均场哈密顿量$ {H_{\text{i}}} $本质上来自于平均场近似^[38], 即将粒子间的相互作用归结为单粒子感受到的平均势场, 其代价是哈密顿量成为单粒子自身波函数的泛函, 原先的线性薛定谔方程变为非线性方程. 如非特殊说明, 本文接下来的数值模拟中将考虑s波相互作用为^[28,29] $ {g_{ + - }} \approx {g_{ + + }} \approx {g_{ - - }} = g $, 并且$ g/\sqrt {{\hbar ^3}\omega /m} = 0.1 $. 将方程(3)代入GP方程(4)中求解, 原则上可以获知任意物理量的动力学细节.

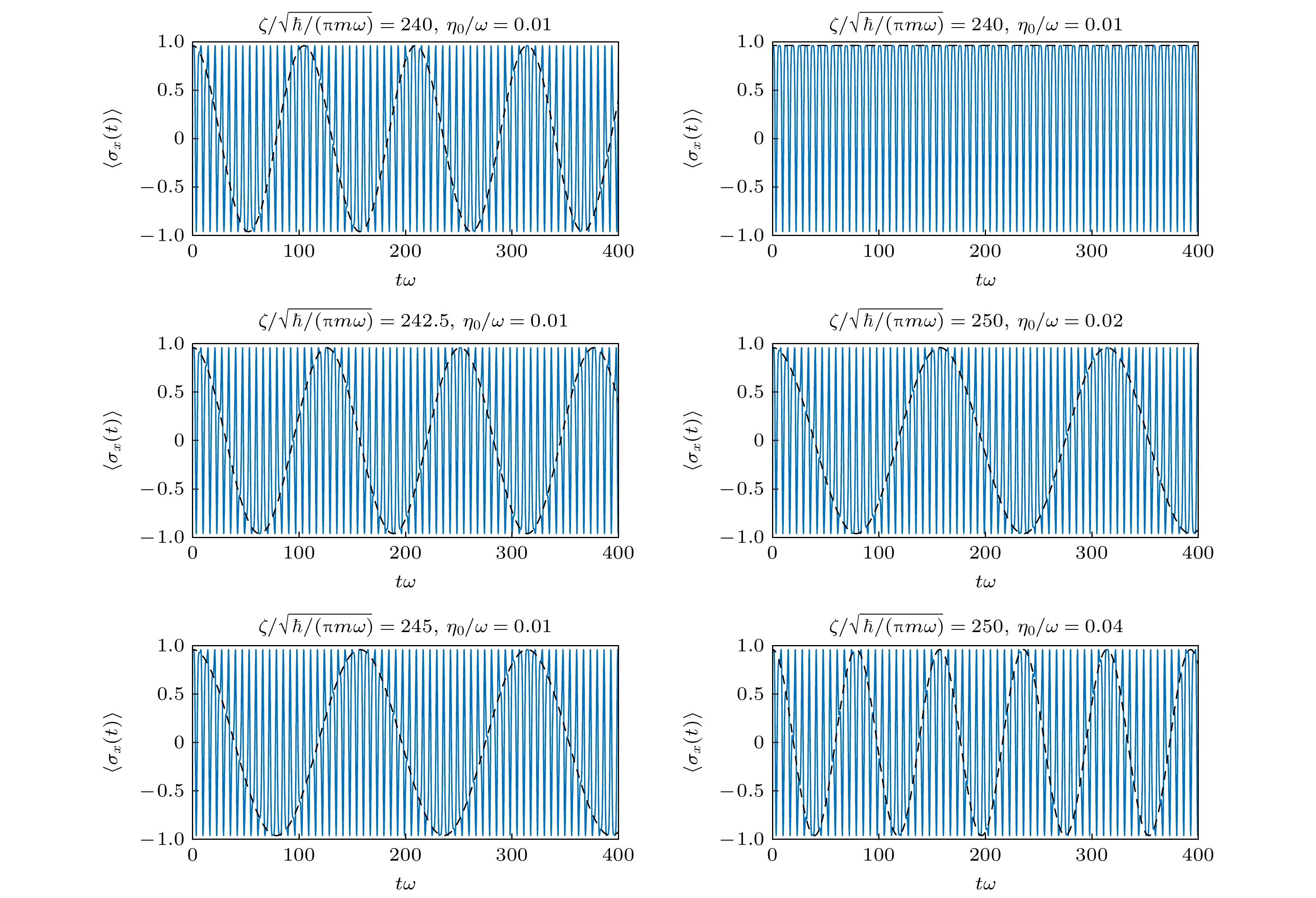
假定初始时刻凝聚体被制备在$ \left| + \right\rangle $和$ \left| - \right\rangle $的某个叠加态上, 研究体系赝自旋对联合含时驱动((3)式)所做出的动力学响应. 图2给出了赝自旋$ \left\langle {{\sigma _x}} \right\rangle $在不同调控参数下的含时演化数值计算结果. 可以看到, 一般而言, 赝自旋以俘获频率$ \omega $为特征频率随时间快速地相干振荡(图中的蓝色实线). 有趣的是, 当参数给定时, 该高频振荡背景上会出现一支低频包络(在图中以黑色虚线标出), 该低频包络的周期与调控参数$ \zeta $和$ {\eta _0} $呈现出某种简单的线性关系. 事实上, 通过将模型作适当简化, 可以在解析上精确得到该关系.

为此, 首先忽略相互作用$ {g_{\sigma \sigma '}}\, $和拉比频率$ \varOmega $对体系的影响, 并对哈密顿量$ {H_0} $施加一含时幺正变换$ U = \exp [ - {\text{i}}m{\omega ^2}A(t)/\hbar ] $, 式中,

其中, $ {A_0} = \sqrt {\text{π}} \tau \zeta $, $ {{\mathrm{erf}}} (s) $是宗量$ s $的误差函数. 经过幺正操作$ U $, 哈密顿量$ {H_0} $变为

从规范变换的角度来看, 哈密顿量(2)通过幺正操作$ U $变为哈密顿量(7)相当于从“长度规范”变换为“速度规范”^[39]. 接下来考虑这样一种强短脉冲极限, 即$ \tau \to 0 $, $ \zeta \to \infty $, 但$ {A_0} $保持为定值^[31]. 在该极限下, 原来的高斯脉冲$ {x_0}(t) $变为$ \delta $型函数, 而含时规范场$ A(t) $变为了简单的阶跃函数$ A(t) = {A_0}\times \varTheta (t - {t_0}) $. 于是, 由哈密顿量(7)所支配的含时动力学问题简化为一个“量子淬火”问题, 即体系在$ t < {t_0} $和$ t \gt {t_0} $时分别由两个不含时的哈密顿量$ {H_ < } $和$ {H_ > } $控制. 更加幸运的是, 注意到$ {\sigma _z} $是守恒量, 这两个不含时的哈密顿量都是精确可解的. 容易发现, 哈密顿量$ {H_ \lt } $有两个简并基态: $ \left| {{\chi _ \pm }(0)} \right\rangle \left| \pm \right\rangle = \exp [ \mp {\text{i}}(m\alpha x)/\hbar ]\left| {{\phi _0}} \right\rangle \left| \pm \right\rangle $, 其中, $ \left| {{\phi _0}} \right\rangle $是一维谐振子势的基态矢量, 满足$ \left\langle {x} \mathrel{\left | {\vphantom {x {{\phi _0}}}} \right. } {{{\phi _0}}} \right\rangle = {[m\omega /({\text{π}}\hbar )]^{1/4}}\times \exp [ - m\omega {x^2}/(2\hbar )] $. 假定系统初态制备在这两个简并基态的某个线性叠加态中, $ \left| {\varPsi (0)} \right\rangle = {C_ + }\left| {{\chi _ + }(0)} \right\rangle \left| + \right\rangle + {C_ - }\left| {{\chi _ - }(0)} \right\rangle \left| - \right\rangle $, 其中$ {C_ \pm } $是叠加系数(简单起见, 假定$ {C_ \pm } $为实数, 当叠加系数为一般的复数时只会给初态增加一个相位因子, 而不影响本文的物理结论). 由于$ {\sigma _z} $守恒, $ \left| {{\chi _ + }(0)} \right\rangle $和$ \left| {{\chi _ - }(0)} \right\rangle $将携带不同的时间积分因子独立演化. 基于此, 可以方便地计算出任意$ t $时刻体系的态矢量:

式中, $ \left| {{\chi _\sigma }(t)} \right\rangle = \exp \Big\{ - \dfrac{{\text{i}}}{\hbar }[m({\omega ^2}{A_0} - {\omega ^2}{A_0}\cos (\omega t) + \sigma \alpha )x - \omega {A_0}\sin (\omega t){p_x}] \Big\} \left| {{\phi _0}} \right\rangle $. 利用(8)式, 可以计算得到$ t $时刻的自旋:

式中, $ \varLambda = 2(m{\omega ^2}{A_0}\alpha /\hbar - {\eta _0}) $, $ \varpi = 2 m\omega {A_0}\alpha /\hbar $.

(9)式是量子淬火条件下的精确解, 观察该公式可以发现, 自旋的高频相干振荡由$ \varpi \sin (\omega t) $项贡献, 而约化参数$ \varLambda $影响低频调制, 具体关系将在3.2节通过分析自旋频谱得到.

通过观察$ \left\langle {{\sigma _x}(t)} \right\rangle $的傅里叶频谱$ {S_x}(\nu ) = \displaystyle \int_{{t_0}}^{{t_0} + {T_{\text{L}}}} {\left\langle {{\sigma _x}(t)} \right\rangle {{\text{e}}^{ - {\text{i}}\nu t}}} {\text{d}}t/{T_{\text{L}}} $来分析赝自旋的动力学响应信息, 其中$ {T_{\text{L}}} $是一个较长的时间间隔. $ {S_x}(\nu ) $通常是复函数, 为了方便讨论, 对其实部进行研究. 将(9)式代入$ {S_x}(\nu ) $并取实部可以计算得到:

其中$ {{\text{J}}_n}(\varpi ) $是$ n $阶第一类贝塞尔函数, $ {\varepsilon _0} = 1/2 $, $ {\varepsilon _n} = 1 $(其中$ n = 1, 2, 3, \cdots $). 由(10)式可知, 自旋频谱$ {S_x}(\nu ) $在

处会出现峰值, 图2中的低频包络即对应于频率$ \nu = {\nu _{\min }} = \min (\left| {k\omega \pm \varLambda } \right|) $.

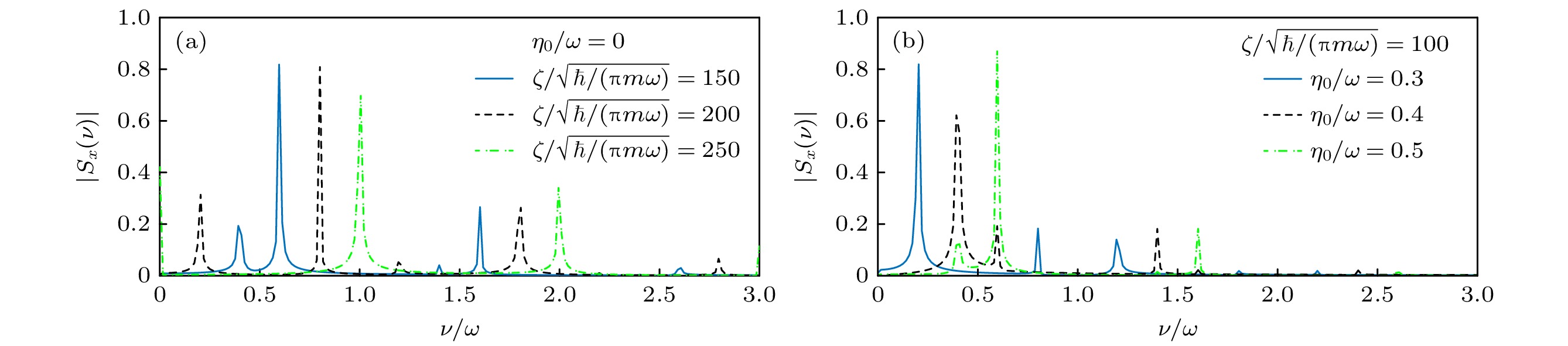
作为本文的重要结论之一, (10)式建立了自旋频谱谱峰与凝聚体多个内外态参数的严格关系. 除了丰富自旋-轨道耦合的相关物理外, 该结果的一个潜在的应用方向是面向物理量测量的量子计量学^[4–6]. 例如, 当已知$ \omega , \zeta , \alpha , {\eta _0} $四个参数当中的3个时, 可基于(11)式, 对另外一个未知参数进行测量或校准.

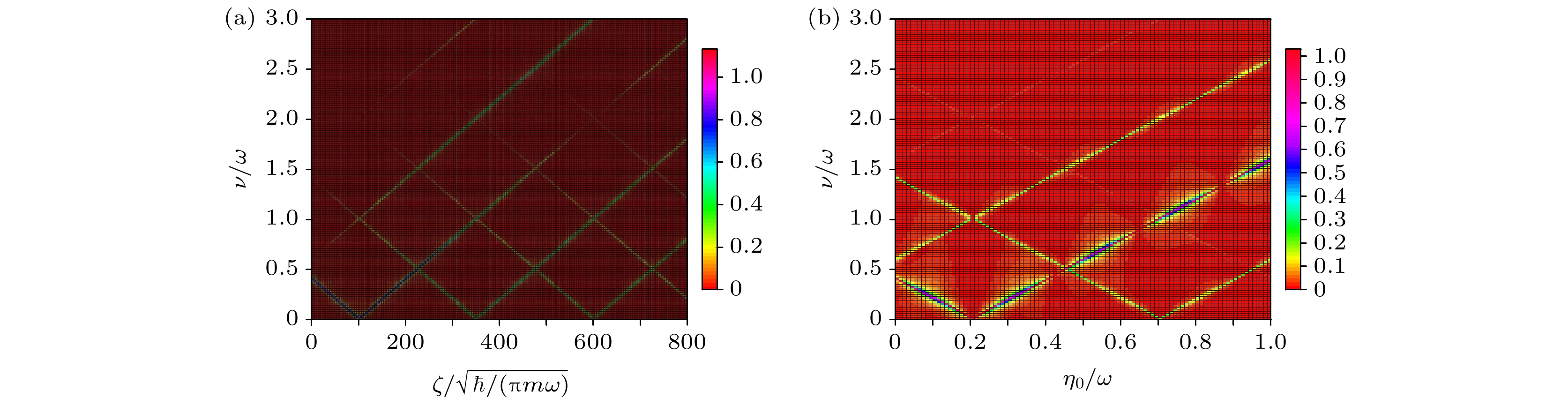
为了佐证(11)式的结论, 对GP方程(4)进行了直接数值积分. 图3展示了计算得到的固定$ \omega , \alpha , {\eta _0} $变化$ \zeta $, 以及固定$ \omega , \zeta , \alpha $变化$ {\eta _0} $的自旋频谱$ \left| {{S_x}(\nu )} \right| $. 可以看到, 谱峰对调控参数的响应规律完全符合(11)式. 图4(a), (b)分别画出了$ \zeta {\text{ - }}\nu $平面和$ {\eta _0}{\text{ - }}\nu $平面上$ \left| {{S_x}(\nu )} \right| $的数值二维图, 所得结果也与(11)式符合得非常好.

为了进一步理清(11)式所刻画的频谱响应背后的物理根源, 分析 “淬火”前后哈密顿量$ {H_ < } $和$ {H_ \gt } $的单粒子能谱. $ {H_ \gt } $的本征态和对应的本征能量可以写为

$ {H_ < } $的本征态和本征能量只需在(12)式和(13)式中令驱动场$ {A_0} $和$ {\eta _0} $为零即可获得. 这里的量子数$ n\, ( = 0, 1, 2, \cdots ) $和$ \sigma \, ( = \pm ) $分别标记轨道态和自旋态, $ \left| {{\phi _n}} \right\rangle $表示一维谐振子势的第$ n $个本征态. 不难发现, 在“淬火”前, 对于每一个轨道能级$ n $, 体系还存在关于自旋取向$ \sigma $的二重简并. 驱动场$ {A_0} $和$ {\eta _0} $破坏了原先关于自旋取向的二重简并, 从而使得轨道能量获得了正比于场强的能级劈裂. 我们仍然假定系统在初始时刻被制备在$ {H_ < } $的两个简并基态的叠加态中, 即$ \left| {\varPsi (0)} \right\rangle = {C_ + }\left| {{\chi _ + }(0)} \right\rangle \left| + \right\rangle + {C_ - }\left| {{\chi _ - }(0)} \right\rangle \left| - \right\rangle $, 则“淬火”后的任意时刻量子态可以按照本征态(12)展开为

其中, $ {N_{n, \sigma }} = \left\langle {{{\psi _{n, \sigma }}}} \mathrel{\left | {\vphantom {{{\psi _{n, \sigma }}} {\varPsi (0)}}} \right. } {{\varPsi (0)}} \right\rangle $. 根据(14)式, 任意时刻的自旋演化可以写为

其中$ {M_{\sigma , \sigma '}}(n, n') = {N_{n, \sigma }}N_{n', \sigma '}^* \langle {{\psi _{n'}^{\sigma '}}} |{{\psi _n^\sigma }} \rangle $ $ (\sigma , \sigma ' = \pm ) $. 考虑到$ {\sigma _x} $的自旋翻转作用且$ {\sigma _z} $在哈密顿量(7)中是守恒量, (15)式中$ {M_{ + , + }}(n, n') = {M_{ - , - }}(n, n') = 0 $. 这样, (15)式中的动力学相位因子将只包含这样的能量差项:

(16)式恰好携带了驱动场的全部信息. 将(15)式进行傅里叶变换, 可得到自旋频谱:

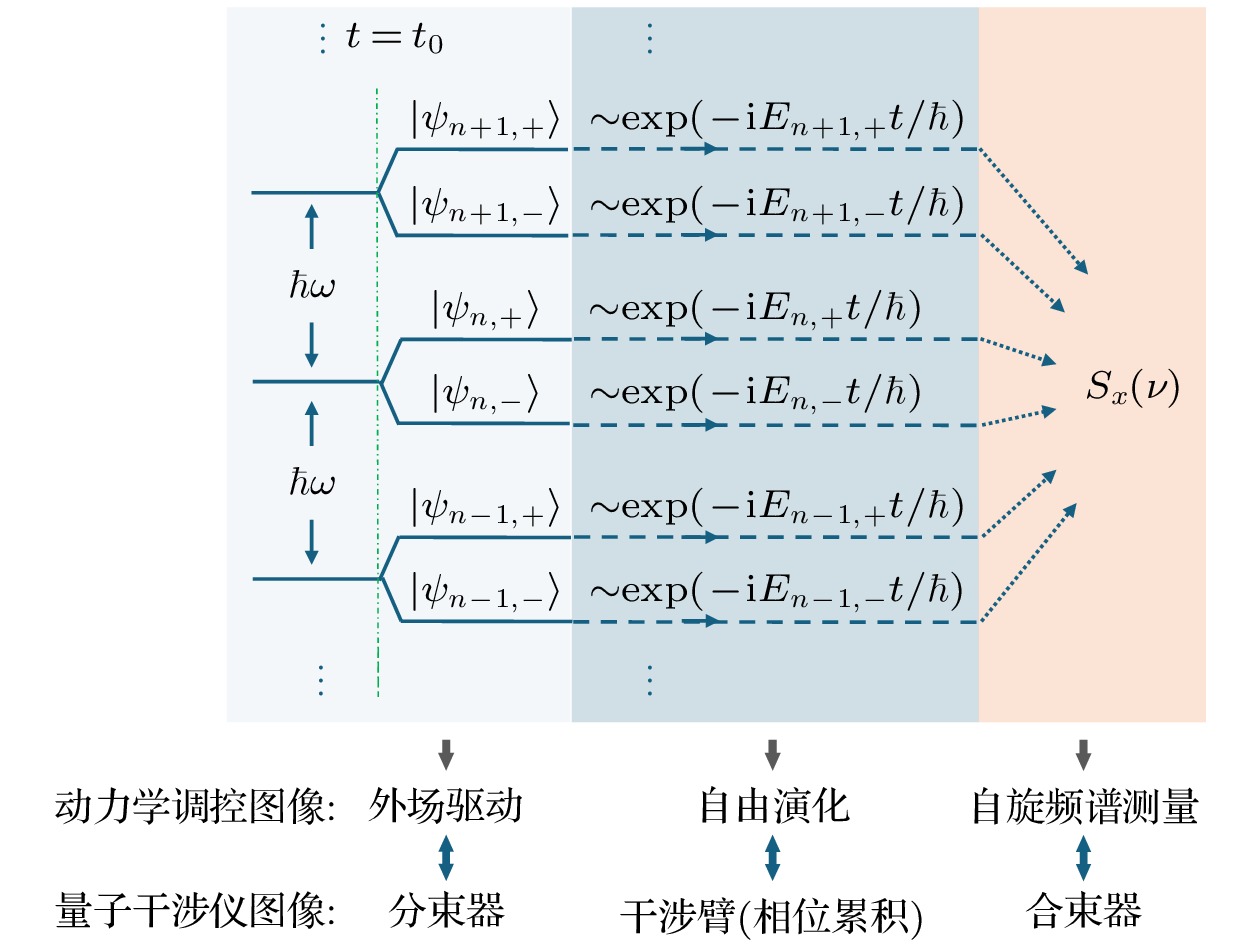
显然, 由于$ {T_{\text{L}}} $较大, (17)式中只有相位因子宗量为零的那些项对积分有贡献, 其他项将随时间快速振荡而干涉相消. 由$ \nu + k\omega - 2\sigma (m{\omega ^2}\alpha {A_0}/\hbar - {\eta _0}) = 0 $, 再次得到谱峰(11)式.

上述基于单粒子能谱建立的动力学图像可以归结为3个部分, 即外场驱动、自由演化和自旋频谱输出. 事实上, 该过程的物理本质是多轨道态的量子干涉, 它可以更方便地纳入到多臂干涉仪的图像中来理解^[40]. 由方程(12)—(14)可知, 外场驱动在$ {t_0} $时刻将初始量子态“分裂”为多个不同的自旋-轨道态, 每个自旋-轨道态携带不同的动力学相位独立演化 (图5). 因此, 外场驱动扮演了干涉仪中分束器的角色, 而“分束”后的一系列自旋-轨道态则充当干涉臂, 它们通过自由演化来完成干涉过程中的相位积累. 干涉仪的合束操作则由对自旋频谱的测量来承担^[41]. 由方程(15)—(17)可知, 自旋频谱的输出过程实则是对满足“同相干涉”(in-phase interference)条件(即(11)式)的那些频率$ {\nu _k} $作挑选, 而其他频率则由于“非同相干涉”(out-of-phase interference)而抑制. 至此, 着眼于自旋频谱对于外场的响应机制, 我们建立了动力学调控图像和量子干涉仪图像, 其对应关系可以用图5进行描述.

目前为止, 本文分析局限于令哈密顿量(2)中$ \varOmega = 0 $, 下面从微扰论的精神出发来简要讨论较小的$ \varOmega $会对系统带来哪些影响. 当$ \varOmega \ne 0 $时, 哈密顿量(7)不再严格可解, 将$ \varOmega /\omega $当作微扰参量, 则准至微扰参量一阶修正的本征态和本征能量可写为

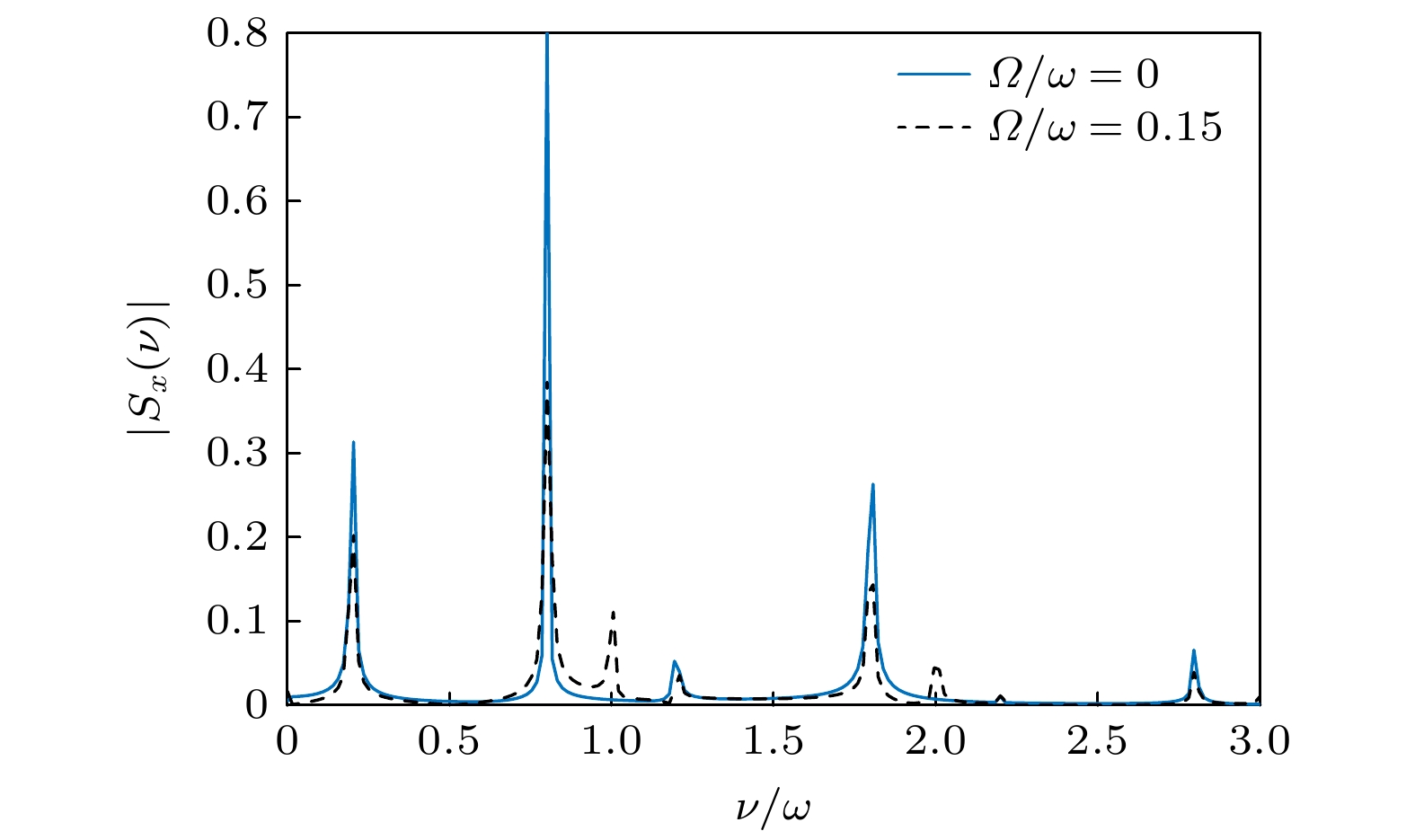
由于$ \varOmega $将自旋相反的状态耦合在一起, (15)式中的动力学相位因子将包含同自旋能量差$ {E_{n, \sigma }} - {E_{n', \sigma }} = k\hbar \omega $的贡献, 权重系数的量级可由(18)式估计为$ {M_{ + , + }}(n, n') = {M_{ - , - }}(n, n') \propto \varOmega /\omega $. 因此, 自旋频谱$ \left| {{S_x}(\nu )} \right| $中将出现一组新的不依赖于外场驱动参数而只取决于俘获频率$ \omega $的边带, 其谱位置为$ \nu = k\omega $. 图6对比了$ \varOmega $取零和非零值时$ \left| {{S_x}(\nu )} \right| $的变化. 可以明显看到$ \varOmega \ne 0 $时$ \left| {{S_x}(\nu )} \right| $在$ \nu = k\omega $处出现了峰值, 与微扰分析完全符合.

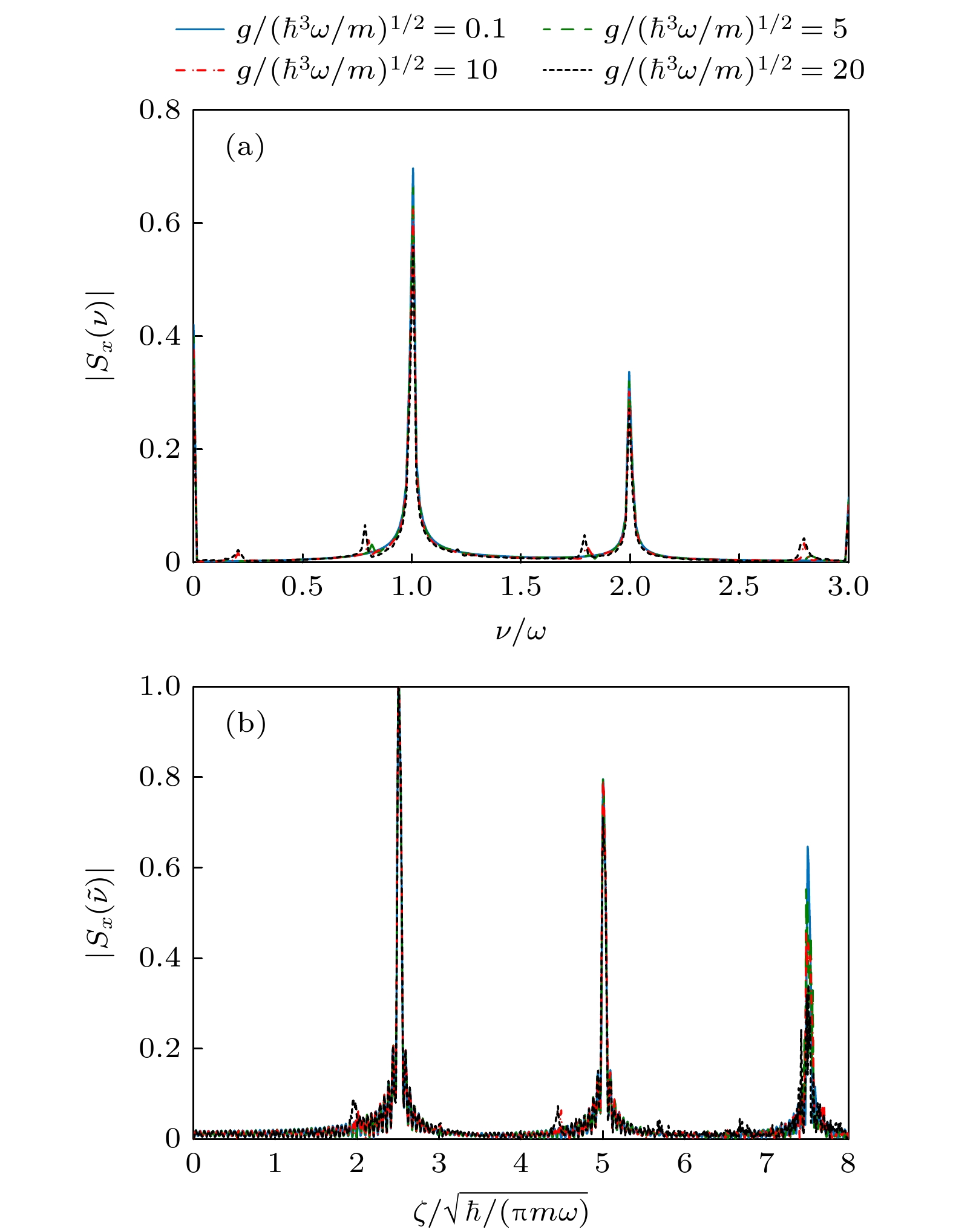
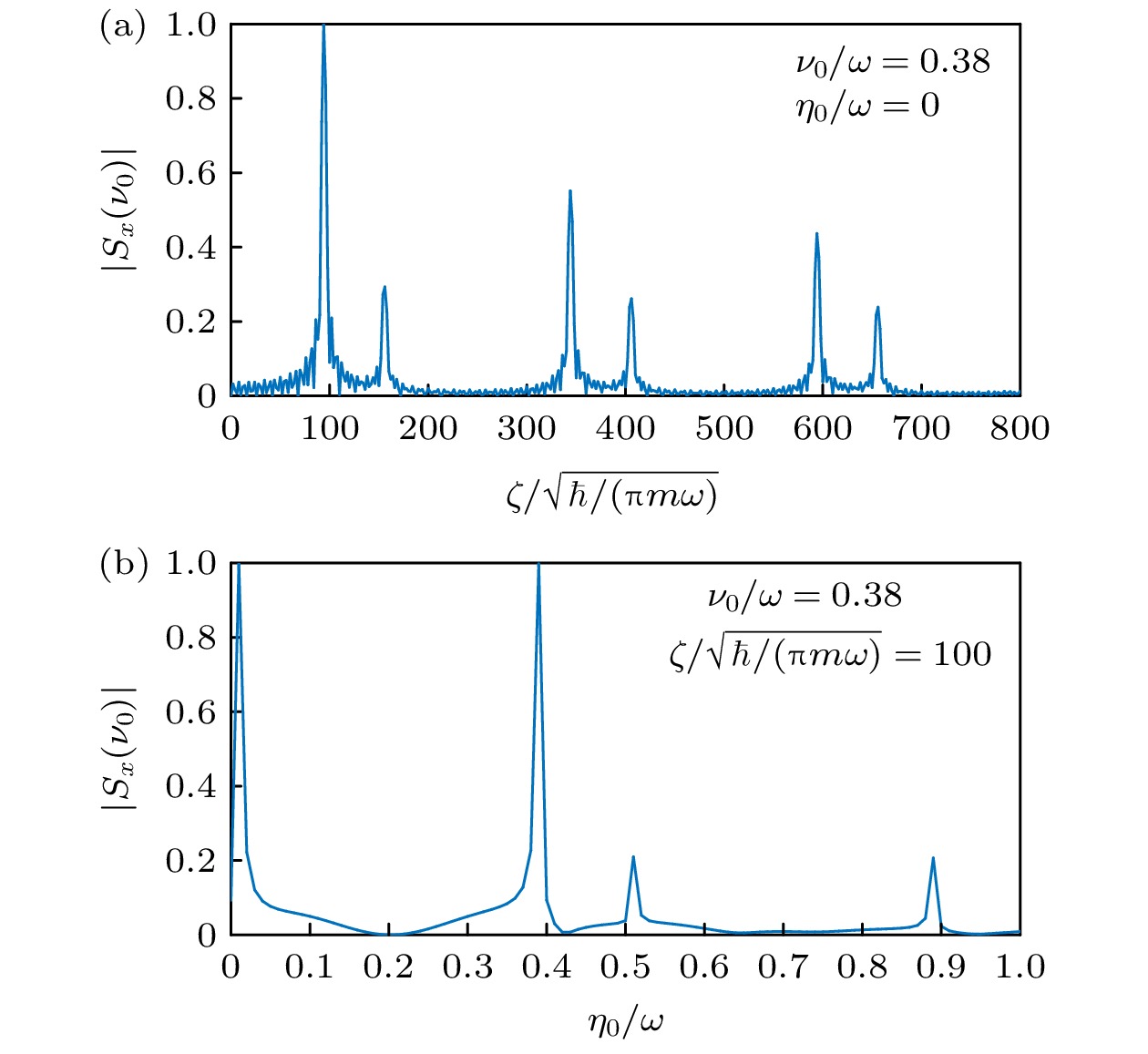
从(11)式出发, 还可以得到一种由外场驱动诱导的动力学共振效应^[31]. 图7所示为自旋在某一频率$ \nu = \tilde \nu $处的取值$ \left| {{S_x}(\tilde \nu )} \right| $随外场参数的变化. 可以看到, 当固定其余参数时, 不论变化$ \zeta $还是$ {\eta _0} $, $ \left| {{S_x}(\tilde \nu )} \right| $均出现两组共振峰, 分别对应(20)式中的$ R_ + ^k $和$ R_ - ^k $($ R = \zeta , {\eta _0} $). 利用(11)式可以很容易得到这些共振峰位置:

由(20)式可知, 两组共振峰的相对间距, 即$ R_ + ^k - R_ - ^k $($ R = \zeta , \eta $)正比于$ \tilde \nu $. 而每组共振峰等间距排列, 对于驱动参数$ \zeta $和$ {\eta _0} $, 其间距分别为$ \Delta \zeta = \zeta _ \pm ^{k + 1} - \zeta _ \pm ^k = \hbar /(2\sqrt {\text{π}} m\omega \tau \alpha ) $和$ \Delta \eta = \eta _ \pm ^{k + 1} - \eta _ \pm ^k = \omega /2 $. 显然, 对共振峰间距$ \Delta \zeta $和$ \Delta \eta $的测量提供了另一种校准体系参数$ \alpha $和$ \omega $的方案.

本节将对动力学调控的一些细节作进一步阐述和讨论.

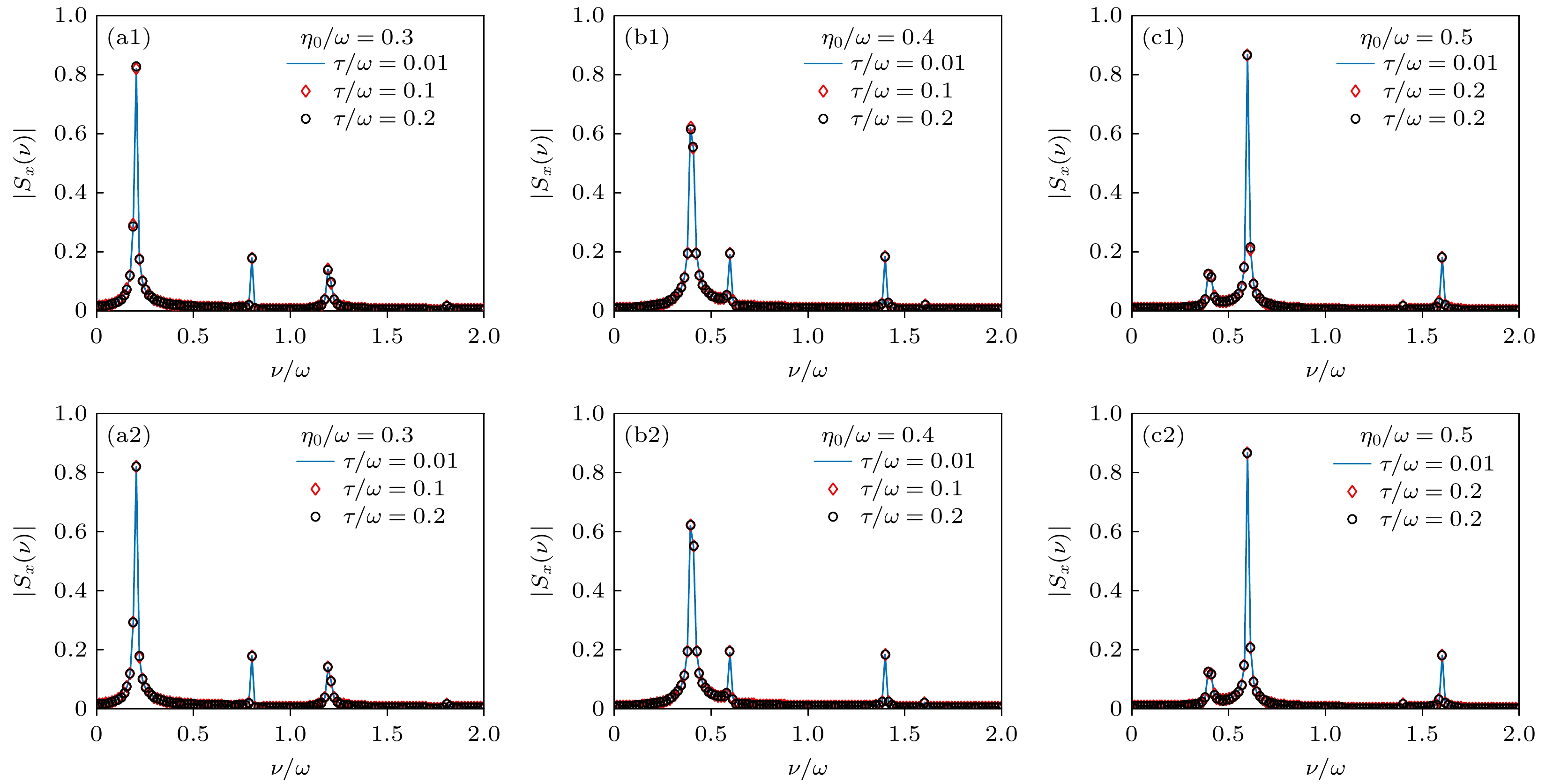
本文方案里, 对BEC的晃动体现在俘获势中心所历经的一个短时脉冲$ {x_0}(t) $. 前文的数值计算中, 已假定晃动脉冲为高斯型, 且脉冲时间宽度固定为$ \tau = 0.01/\omega $ . 事实上, 只要保证晃动脉冲的时间宽度$ \tau $相较于系统的特征振荡时间尽可能短(即$ \tau \ll 1/\omega $), 文中所述的关于自旋动力学相应的物理图像依然适用. 图8(a1)—(c1)比较了脉冲时间宽度$ \tau $取不同值时的自旋频谱. 可以看到, 在时间宽度高至$ \tau = 0.2/\omega $时, 自旋频谱的特征依然没有明显改变. 显然, 在此条件下, 脉冲的波形选取也是任意的. 本质上, BEC晃动的相关参数最终归结于(6)式中的$ {A_0} $. 可将$ {A_0} $一般性地写为$ {A_0} = \varGamma \tau \zeta $, 不同的脉冲波形仅影响前置因子$ \varGamma $. 例如, 对于(3)式中的高斯型脉冲, 前置因子为$ \varGamma = \sqrt {\text{π}} $; 对于如下方波:

前置因子为$ \varGamma = 1 $. 图8(a2)—(c2)给出了短时脉冲为(21)式所描述方波时的自旋响应频谱. 与图8(a1)—(c1)对比可以发现, 该结果与高斯型脉冲的结果完全一致. 这种对脉冲波形选取的任意性客观上也增加了相关实验的灵活度.

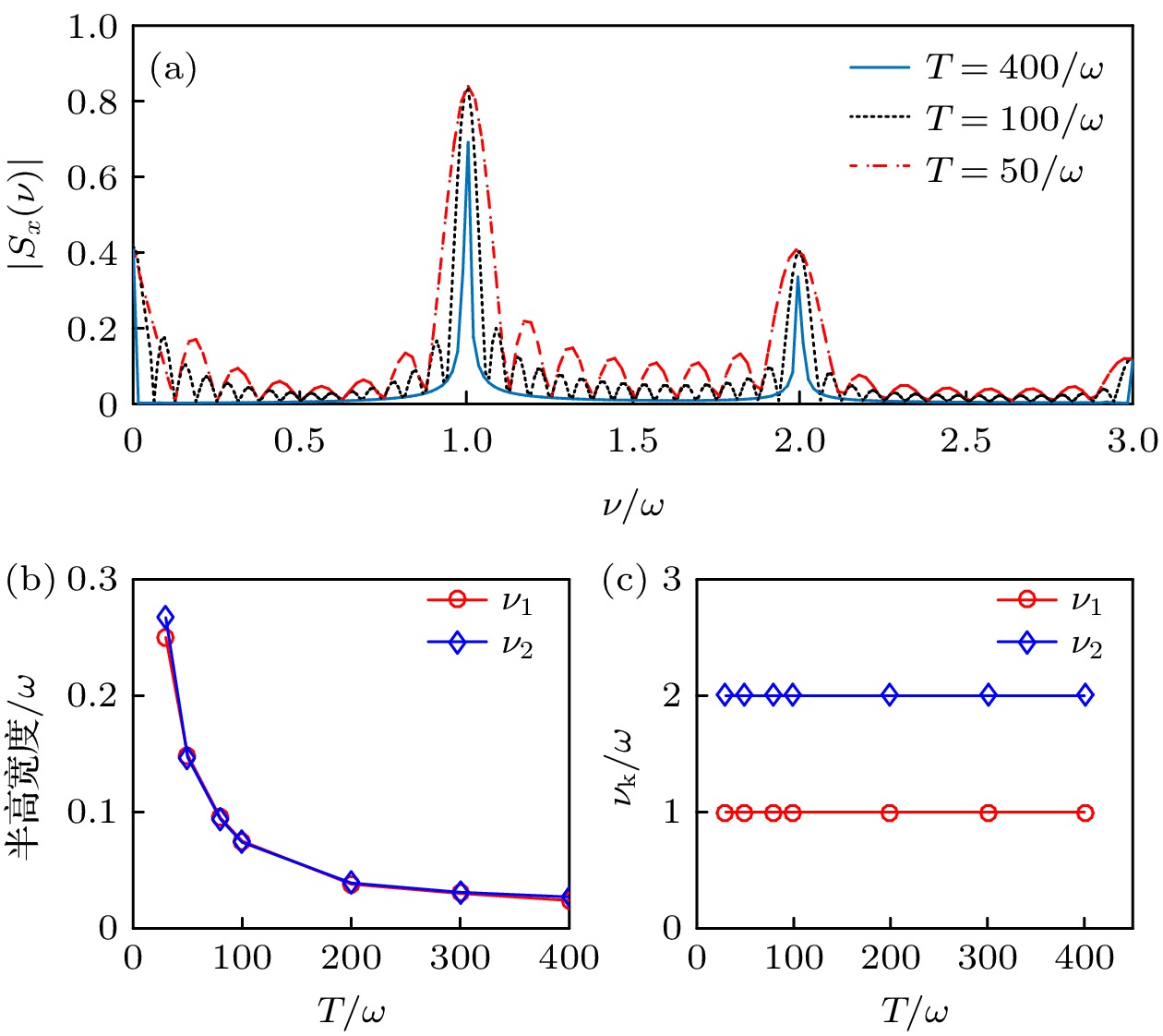
(11)式的获得客观上要求$ T \gg 1/\omega $. 在此条件下, 改变积分时间将起到调控自旋频谱中的谱峰宽度的作用. 图9(a)给出其他参数条件固定时改变积分时间自旋频谱的变化. 可以看到, 随着积分时间缩短, 谱峰宽度随之增大但位置不变. 图9(b)定量地给出$ {\nu _1} $和$ {\nu _2} $两个谱峰的半高宽$ {h}_{半} $随积分时间的变化. 随着T增大, 半高宽均展现出幂律衰减的特征. 与之对比, 谱峰的峰值位置依然由(11)式决定, 不随T的变化而变化(见图9(c)). 因此, 通过合理调整积分时间可以更方便地在实验中观测到自旋响应信号.

本文的核心物理图像来自于凝聚原子不同内外态之间的量子相干性, 这种相干性建立在粒子间无相互作用的背景上. 原子间相互作用体现在GP方程(4)的参数$ g $中. 自旋频谱在不同相互作用$ g $下的变化由图10(a)给出. 可以看到, 对于相互作用大至$ g/\sqrt {{\hbar ^3}\omega /m} = 20 $, 自旋频谱的主要 特征几乎没有发生改变(可见的变化是在某些频 率处出现了相互作用诱导的微弱的次级峰), 特别是谱峰位置依然服从(11)式. 说明此时的原子间相互作用尚不足以破坏本文基于量子相干的物 理图像. 图10(b)给出了在频率$ \tilde \nu = \omega $处的自旋 频谱随晃动参数展示出的共振效应. 随着相互作 用增大, 晃动幅值$ \zeta $较大的共振峰出现显著削弱迹象(峰值位置仍未改变), 而其他共振峰几乎没有明显变化. 这表明凝聚体的自旋响应在强晃动调控下将对原子间相互更为敏感. 因此, 将晃动幅值限制在较小范围内将使得体系对相互作用的鲁棒性 更强.

针对本文提出的对凝聚体施加的晃动操作, 一种可行的实验实现方案是在原先的俘获BEC基础上再施加一梯度磁场, 从而使得BEC感受到随磁场梯度变化的非零合力^[42]. 具体地, 在梯度磁场作用下, 俘获势变为

其中$ {\mu _B} $是玻尔兹曼因子, $ {m_{\text{F}}} $是磁量子数, $ {g_{\text{F}}} $是朗德因子, $ \partial B/\partial x $是磁场梯度. 于是, 谐振子俘获势的快速晃动等价于相应地改变磁场梯度.

为了进一步展示本文方案的实验可行性, 对实验中涉及的一些相关参数进行简要估计. 对于$ ^{87}{\text{Rb}} $原子形成的BEC, 其俘获频率可以设置为$ \omega \sim 2{\text{π}} \times 40 \;{\text{Hz}} $^[27,29]. 相应地, 晃动脉宽和积分时间可以分别选为$ \tau \sim 0.2/\omega \approx 0.8\;{\text{ms}} $和$ T = 50/\omega \approx 200\;{\text{ms}} $. 本文中使用的一维相互作用系数$ g $可由其三维形式推知为$ g = {g_{{\text{3D}}}}/{l_y}{l_z} $^[29,37], 其中$ {g_{{\text{3D}}}} = 4\rho {V_{0}}{\text{π}}{\hbar ^2}{a_{\text{s}}}/m $是三维相互作用系数, $ {a_{\text{s}}} $为s波散射长度, $ \rho $和$ {V_0} $分别为原子数密度和凝聚体体积; $ {l_{y, z}} = \sqrt {\hbar /m{\omega _{y, z}}} $是俘获势的横向特征长度. 我们选择冷原子实验的特征参数$ {g_{{\text{3D}}}}\rho /\hbar = 1\;{\text{kHz}} $^[23]和$ \rho = {10^{14}}{\text{ c}}{{\text{m}}^{ - 3}} $, 以及$ ({\omega _y}, {\omega _z}) = 2{\text{π}} \times (134, 178)\, {\text{Hz}} $^[29], 并代入$ ^{87}{\text{Rb}} $原子参数$ m = 1.44 \times {10^{ - 25}}\; {\text{kg}} $, 可得$ g/\sqrt {{h^3}\omega /m} \sim 0.03 $. 由6.3节分析可知, 该相互作用远不足以破坏文中所使用的单粒子物理图像. 综合以上分析, 本文所预言的自旋动力学响应原则上可以在当前实验条件下被观测到.

如前所述, 作为本文所给出的自旋频谱响应效应的一个可能的潜在应用, $ \omega , \zeta , \alpha , {\eta _0} $等参数可通过动力学的方式测量或校准. 以自旋轨道耦合强度$ \alpha $为例简要讨论其测量精度的估算. 实验中, 待测参数可通过对自旋频谱的峰值位置测量而获得, 于是参数的测量精度将反映在自旋频谱的峰值位置精度中. 作为一种定量估计, 可认为当谱峰位置随参数的变化等于该峰的半高宽时为其测量精度极限. 按照这种精神, 参照方程(11), 可得精度估值公式$ \Delta \nu =2 m{\omega }^{2}{A}_{0}\Delta \alpha /\hbar \geqslant {h}_{半} $. 由6.2节分析可知, 半高宽$ {h}_{半} $随积分时间$ T $增大而幂律减小: $ {h}_{半}\approx C{T}^{-\beta } $, 其中无量纲参数$ C $和$ \beta $可通过数值拟合来确定. 于是得到自旋-轨道耦合强度$ \alpha $的 测量精度满足$ \Delta \alpha \geqslant C\hbar /(2 m{\omega ^2}{A_0}{T^\beta }) $. 可见增大晃动幅值或积分时间均可提高$ \alpha $的测量精度. 作 为一个估算的例子, 我们考虑实验中的特征参 数$ {A_0} = 2.5\sqrt {\hbar /m{\omega ^3}} $, $ \omega \approx 2{\text{π}} \times 40 {\text{Hz}} $, $ m = 1.44 \times {10^{ - 25}}\;{\text{kg}} $, $ T = 50/\omega \approx 200\;{\text{ms}} $, $ {k_0} = 8 \times {10^6}\;{{\text{m}}^{{{ - 1}}}} $. 另外, 对图9(b)作幂律拟合可得$ C \approx 5.2 $和$ \beta \approx 0.9 $. 将以上参数代入$ \alpha $的精度公式, 可估算出测量的相对精度为$ \Delta \alpha /\alpha \sim 6 \times {10^{ - 3}} $.

本文提出了一种自旋-轨道耦合玻色凝聚体的自旋频谱对外场驱动的动力学响应效应. 该效应由对凝聚体的快速晃动和外加的迅变塞曼场来驱动. 通过对模型作适当简化, 我们在解析上精确导出了自旋频谱对外场参数的响应关系. 对GP方程的数值积分结果与解析表达式符合得很好. 将该频谱响应的物理本质归因于多自旋-轨道态之间的量子干涉, 并给出了动力学演化在量子干涉仪背景下的物理图像. 文章的最后对方案的实验可行性及相关参数进行了讨论与估计. 进一步的研究包括将本文的自旋-轨道耦合机制推广到更高维度, 并设计出更广义的含时调控方案.