高级搜索

融合注意力机制的卷积网络单像素成像

,  ,  , 

downloadPDF

上一篇

下一篇

王翔, 周义深, 张轩阁, 陈希浩. 融合注意力机制的卷积网络单像素成像[J]. 物理学报, 2025, 74(8): 084202-1. doi: 10.7498/aps.74.20250010
引用本文: 王翔, 周义深, 张轩阁, 陈希浩. 融合注意力机制的卷积网络单像素成像[J]. 物理学报, 2025, 74(8): 084202-1. doi: 10.7498/aps.74.20250010
shu
Xiang WANG, Yishen ZHOU, Xuange ZHANG, Xihao CHEN. Convolutional network single-pixel imaging with fusion attention mechanism[J]. Acta Physica Sinica, 2025, 74(8): 084202-1. doi: 10.7498/aps.74.20250010
Citation: Xiang WANG, Yishen ZHOU, Xuange ZHANG, Xihao CHEN. Convolutional network single-pixel imaging with fusion attention mechanism[J]. Acta Physica Sinica, 2025, 74(8): 084202-1. doi: 10.7498/aps.74.20250010
shu

融合注意力机制的卷积网络单像素成像

  • 辽宁大学物理学院, 沈阳　110036

    • 通讯作者: xi-haochen@163.com

  • 中图分类号: 42.30.Va, 42.30.Wb, 89.20.Ff, 42.30.-d

Convolutional network single-pixel imaging with fusion attention mechanism

  • School of Physics, Liaoning University, Shenyang 110036, China

    • Corresponding author: E-mail: xi-haochen@163.com

  • MSC: 42.30.Va, 42.30.Wb, 89.20.Ff, 42.30.-d

  • 摘要: 提出了一种基于物理驱动的融合注意力机制的新型卷积网络单像素成像方法. 通过将结合通道与空间注意力机制的模块集成到一个随机初始化的卷积网络中, 利用单像素成像的物理模型约束网络, 实现了高质量的图像重建. 具体来说, 将空间与通道两个维度的注意力机制集成为一个模块, 引入到多尺度U-net卷积网络的各层中, 通过这种方式, 不仅可以利用注意力机制在三维数据立方中提供的关键权重信息, 还充分结合了U-net网络在不同空间频率下强大的特征提取能力. 这一创新方法能够有效捕捉图像细节, 抑制背景噪声, 提升图像重建质量. 实验结果表明, 针对低采样率条件下的图像重建, 与传统非预训练网络相比, 融合注意力机制的方案不仅在直观上图像细节重建得更好, 而且在定量的评价指标(如峰值信噪比和结构相似性)上均表现出显著优势, 验证了其在单像素成像中的有效性与应用前景.
    Abstract: This paper presents a novel convolutional neural network-based single-pixel imaging method that integrates a physics-driven fusion attention mechanism. By incorporating a module that combines both channel attention mechanism and spatial attention mechanism into a randomly initialized convolutional network, the method utilizes the physical model constraints of single-pixel imaging to achieve high-quality image reconstruction. Specifically, the spatial and channel attention mechanism are combined into a single module and introduced into various layers of a multi-scale U-net convolutional network. In the spatial attention mechanism, we extract the attention weight features of each spatial region of the pooled feature map by using convolution. In the channel attention mechanism, we pool the three-dimensional feature map into a single-channel signal and input it into a two-layer fully connected network to obtain the attention weight information for each channel. This approach not only uses the critical weighting information provided by the attention mechanism in the three-dimensional data cube but also fully integrates the powerful feature extraction capabilities of the U-net network across different spatial frequencies. This innovative method can effectively capture image details, suppress background noise, and improve image reconstruction quality. During the experimental phase, we employ the optical path of single-pixel imaging to acquire bucket signals for two target images, "snowflake" and "basket". By inputting any noisy image into a randomly initialized neural network with attention mechanism, and using the mean square error between simulated bucket signal and actual bucket signal, we physically constrain the convergence of the network. Ultimately, we achieve a reconstructed image that adheres to the physical model. The experimental results demonstrate that under low sampling rate conditions, the scheme of integrating the attention mechanism can not only intuitively reconstruct image details better, but also demonstrate significant advantages in quantitative evaluation metrics such as peak signal-to-noise ratio (PSNR) and structural similarity (SSIM), confirming its effectiveness and potential application in single-pixel imaging.
  • 加载中

  • 图 1  实验方案图

    Figure 1.  Experimental schematic diagram

    下载: 全尺寸图片 幻灯片

    图 2  融合注意力机制的U-net卷积神经网络结构示意图　(a) U-net结构的卷积网络; (b) CBAM模块结构总览; (c)空间注意力机制模块; (d)通道注意力机制模块

    Figure 2.  Schematic diagram of U-net convolutional neural network structure with integrated attention mechanism: (a) Convolutional neural networks of a U-net architecture; (b) overall structure of CBAM; (c) spatial attention module; (d) channel attention module

    下载: 全尺寸图片 幻灯片

    图 3  融合注意力机制与原始U-net网络重建方案在不同采样率下的结果

    Figure 3.  Results of the fusion attention mechanism and the original U-net reconstruction scheme under different sampling rates

    下载: 全尺寸图片 幻灯片

    图 4  不同采样率下SSIM的对比

    Figure 4.  Comparison of SSIM at different sampling rates

    下载: 全尺寸图片 幻灯片

    图 5  不同采样率下PSNR的对比

    Figure 5.  Comparison of PSNR at different sampling rates

    下载: 全尺寸图片 幻灯片

    图 6  不同迭代次数下PSNR与损失函数的变化对比　(a)两种方案重建图像的PSNR随迭代次数的变化; (b)本文方案的损失函数在不同初始学习率下随迭代次数的变化

    Figure 6.  Comparison of PSNR and loss function under different iterations: (a) The PSNR of the reconstructed images of the two schemes varies with iterations; (b) the loss function of our scheme varies with iterations under different initial learning rates.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Kilcullen P, Ozaki T, Liang J 2022 Nat. Commun. 13 7879 doi: 10.1038/s41467-022-35585-8
    [2] Hahamovich E, Monin S, Hazan Y, Rosenthal A 2021 Nat. Commun. 12 4516 doi: 10.1038/s41467-021-24850-x
    [3] Shapiro J H 2008 Phys. Rev. A 78 061802 doi: 10.1103/PhysRevA.78.061802
    [4] Ferri F, Magatti D, Gatti A, Bache M, Brambilla E, Lugiato L 2005 Phys. Rev. Lett. 94 183602 doi: 10.1103/PhysRevLett.94.183602
    [5] Wang F, Wang C, Deng C, Han S, Situ G 2022 Photon. Res. 10 104 doi: 10.1364/PRJ.440123
    [6] Pan L, Shen Y, Qi J, Shi J, Feng X 2023 Opt. Express 31 13943 doi: 10.1364/OE.484874
    [7] Song K, Bian Y, Wang D, Li R, Wu K, Liu H, Qin C, Hu J, Xiao L 2024 Laser & Photonics Rev. published online 2401397
    [8] Zhao X S, Yu C, Wang C, Li T, Liu B, Lu H, Zhang R, Dou X, Zhang J, Pan J W 2024 Appl. Phys. Lett. 125 211103 doi: 10.1063/5.0232210
    [9] Karpowicz N, Zhong H, Xu J, Lin K I, Hwang J S, Zhang X C 2005 Semicond. Sci. Tech. 20 S293 doi: 10.1088/0268-1242/20/7/021
    [10] Simões M, Vaz P, Cortez A F V 2024. arXiv: 2411.03907 [physics.ins-det]
    [11] Shwartz S 2021 Sci. Bull. 66 857 doi: 10.1016/j.scib.2021.01.019
    [12] Olbinado M P, Paganin D M, Cheng Y, Rack A 2021 Optica 8 1538 doi: 10.1364/OPTICA.437481
    [13] Clemente P, Durán V, Tajahuerce E, Andrés P, Climent V, Lancis J 2013 Opt. Lett. 38 2524 doi: 10.1364/OL.38.002524
    [14] Jiang W, Yin Y, Jiao J, Zhao X, Sun B 2022 Photon. Res. 10 2157 doi: 10.1364/PRJ.461064
    [15] Gibson G M, Sun B, Edgar M P, Phillips D B, Hempler N, Maker G T, Malcolm G P A, Padgett M J 2017 Opt. Express 25 2998 doi: 10.1364/OE.25.002998
    [16] Zhou L, Xiao Y, Chen W 2023 Opt. Express 31 23027 doi: 10.1364/OE.489808
    [17] Xu Y, Lu L, Saragadam V, Kelly K F 2024 Nat. Commun. 15 1456 doi: 10.1038/s41467-024-45856-1
    [18] Li J, Li X, Yardimci N T, Hu J, Li Y, Chen J, Hung Y C, Jarrahi M, Ozcan A 2023 Nat. Commun. 14 6791 doi: 10.1038/s41467-023-42554-2
    [19] Li S, Liu X, Xiao Y, Ma Y, Yang J, Zhu K, Tian X 2023 Opt. Express 31 4712 doi: 10.1364/OE.473659
    [20] Zheng P, Dai Q, Li Z, Ye Z, Xiong J, Liu H C, Zheng G, Zhang S 2021 Sci. Adv. 7 eabg0363 doi: 10.1126/sciadv.abg0363
    [21] Katz O, Bromberg Y, Silberberg Y 2009 Appl. Phys. Lett. 95 131110 doi: 10.1063/1.3238296
    [22] López-García L, Cruz-Santos W, GarcíaArellano A, Filio-Aguilar P, Cisneros-Martínez J A, Ramos-García R 2022 Opt. Express 30 13714 doi: 10.1364/OE.451656
    [23] Zhang Z, Ma X, Zhong J 2015 Nat. Commun. 6 6225 doi: 10.1038/ncomms7225
    [24] Donoho D 2006 IEEE Trans. Inf. Theory 52 1289 doi: 10.1109/TIT.2006.871582
    [25] Duarte M F, Davenport M A, Takhar D, Laska J N, Sun T, Kelly K F, Baraniuk R G 2008 IEEE Signal Process Mag. 25 83 doi: 10.1109/MSP.2007.914730
    [26] Huang L, Luo R, Liu X, Hao X 2022 Light Sci. Appl. 11 61 doi: 10.1038/s41377-022-00743-6
    [27] Figueiredo M A T, Nowak R D, Wright S J 2007 IEEE J. Sel. Top. Signal Process. 11 586
    [28] Pioneers A 2024 Nat. Mach. Intell. 6 1271 doi: 10.1038/s42256-024-00945-0
    [29] 查文舒, 李道伦, 沈路航, 张雯, 刘旭亮 2022 力学学报 54 543 doi: 10.6052/0459-1879-21-617 Zha W S, Li D L, Shen L H, Zhang W, Liu X L 2022 Chinese Journal of Theoretical and Applied Mechanics 54 543 doi: 10.6052/0459-1879-21-617
    [30] Zhang H, Wang J, Zhang Y, Du X, Wu H, Zhang T 2024 Astronomical Techniques and Instruments 1 1
    [31] van Leeuwen C, Podareanu D, Codreanu V, Cai M X, Berg A, Zwart S P, Stoffer R, Veerman M, van Heerwaarden C, Otten S, Caron S, Geng C, Ambrosetti F, Bonvin A M J J 2020 arXiv: 2004.03454[cs.CE]
    [32] Barbastathis G, Ozcan A, Situ G 2019 Optica 6 921 doi: 10.1364/OPTICA.6.000921
    [33] Ruget A, Moodley C, Forbes A, Leach J 2024 Opt. Express 32 41057 doi: 10.1364/OE.533343
    [34] Wetzstein G, Ozcan A, Gigan S, Fan S, Englund D, Soljačić M, Denz C, Miller D A B, Psaltis D 2020 Nature 588 39 doi: 10.1038/s41586-020-2973-6
    [35] Lyu M, Wang W, Wang H, Wang H, Li G, Chen N, Situ G 2017 Sci. Rep. 7 17865 doi: 10.1038/s41598-017-18171-7
    [36] Zhang X, Deng C, Wang C, Wang F, Situ G 2023 ACS Photonics 10 2363 doi: 10.1021/acsphotonics.2c01537
    [37] Li J, Li Y, Li J, Zhang Q, Li J 2020 Opt. Express 28 22992 doi: 10.1364/OE.399065
    [38] Wang F, Wang C, Chen M, Gong W, Zhang Y, Han S, Situ G 2022 Light Sci. Appl. 11 1 doi: 10.1038/s41377-021-00680-w
    [39] Peng L, Xie S, Qin T, Cao L, Bian L 2023 Opt. Lett. 48 2527 doi: 10.1364/OL.486078
    [40] Liu H, Bian L, Zhang J 2023 Opt. Laser Technol. 157 108600 doi: 10.1016/j.optlastec.2022.108600
    [41] Liu X, Han T, Zhou C, Huang J, Ju M, Xu B, Song L 2023 Opt. Express 31 9945 doi: 10.1364/OE.481995
    [42] Hammernik K, Küstner T, Yaman B, Huang Z, Rueckert D, Knoll F, Akçakaya M 2023 IEEE Signal Process Mag. 40 98
    [43] Wang P, Chen P, Yuan Y, Liu D, Huang Z, Hou X, Cottrell G W 2017. arXiv: 1702.08502[cs.CV]
    [44] Ulyanov D, Vedaldi A, Lempitsky V 2020 IJCV 128 1867 doi: 10.1007/s11263-020-01303-4
    [45] Ren W, Nie X, Peng T, Scully M O 2022 Opt. Express 30 47921 doi: 10.1364/OE.478695
    [46] Zhang H, Sindagi V, Patel V M 2020 IEEE Trans. Circuits Syst. Video Technol. 30 3943 doi: 10.1109/TCSVT.2019.2920407
    [47] Lv W, Xiong J, Shi J, Huang Y, Qin S 2021 J. Intell. Manuf. 32 441 doi: 10.1007/s10845-020-01584-z
    [48] Zhang H, Wang Z, Liu D 2014 IEEE Transactions on Neural Networks and Learning Systems 25 1229 doi: 10.1109/TNNLS.2014.2317880
    [49] Baozhou Z, Hofstee P, Lee J, Al-Ars Z 2021 arXiv: 2108.08205 [cs.CV]
    [50] Karim N, Rahnavard N 2021 arXiv: 2107.01330[cs.CV]
    [51] Hoshi I, Shimobaba T, Kakue T, Ito T 2020 Opt. Express 28 34069 doi: 10.1364/OE.410191
    [52] Stollenga M, Masci J, Gomez F, Schmidhuber J 2014 arXiv: 1407.3068[cs.CV]
    [53] Zhang Y, Li K, Li K, Wang L, Zhong B, Fu Y 2018 arXiv: 1807.02758[cs.CV]
    [54] Liao X, He L, Mao J, Xu M 2024 Remote Sensing 16 1688 doi: 10.3390/rs16101688
    [55] Yu W K, Wang S F, Shang K Q 2024 Sensors 24 1012 doi: 10.3390/s24031012
    [56] Ronneberger O, Fischer P, Brox T 2015 arXiv: 1505.04597[cs.CV]
    [57] Meng Z, Yu Z, Xu K, Yuan X 2021 arXiv: 2108.12654 [eess.IV]
    [58] Ferri F, Magatti D, Lugiato L A, Gatti A 2010 Phys. Rev. Lett. 104 253603 doi: 10.1103/PhysRevLett.104.253603
    [59] Lin J, Yan Q, Lu S, Zheng Y, Sun S, Wei Z 2022 Photonics 9 343 doi: 10.3390/photonics9050343
  • 加载中
图( 7)
计量
  • 文章访问数:  65
  • HTML全文浏览数:  65
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-01-03
  • 刊出日期:  2025-04-20

融合注意力机制的卷积网络单像素成像

  • 收稿日期:  2025-01-03

摘要: 提出了一种基于物理驱动的融合注意力机制的新型卷积网络单像素成像方法. 通过将结合通道与空间注意力机制的模块集成到一个随机初始化的卷积网络中, 利用单像素成像的物理模型约束网络, 实现了高质量的图像重建. 具体来说, 将空间与通道两个维度的注意力机制集成为一个模块, 引入到多尺度U-net卷积网络的各层中, 通过这种方式, 不仅可以利用注意力机制在三维数据立方中提供的关键权重信息, 还充分结合了U-net网络在不同空间频率下强大的特征提取能力. 这一创新方法能够有效捕捉图像细节, 抑制背景噪声, 提升图像重建质量. 实验结果表明, 针对低采样率条件下的图像重建, 与传统非预训练网络相比, 融合注意力机制的方案不仅在直观上图像细节重建得更好, 而且在定量的评价指标(如峰值信噪比和结构相似性)上均表现出显著优势, 验证了其在单像素成像中的有效性与应用前景.

English Abstract

    全文HTML

    1.   引　言

    • 单像素成像(single-pixel imaging, SPI)是近年来快速发展的一种新型计算成像技术[1]. 与传统使用阵列探测器的成像技术不同, 它是一种间接成像技术, 通过一组空间模式按时序调制的光场来照射目标, 使用无空间分辨能力的单像素探测器(single-pixel detector, SPD)捕获被目标透射或反射的光场强度, 最后利用预制的调制散斑和单像素测量数据通过各种反演算法重建目标图像[2]. 由于SPI仅采用单像素探测器捕获信号[3], 因此它在检测灵敏度[4]、光谱响应范围[5]和成像成本[6]等方面都比传统成像技术具有显著优势. 在过去十多年有关SPI的研究中, 工作波长范围已从最初的可见光波段逐步扩展至紫外[7]、红外[8], 甚至太赫兹波段[9]. 此外, SPI技术在X射线[10]和粒子源成像[11]中的应用已经获得了广泛的研究和探索. SPI技术的优异性能也促进了其在医学成像[12]、生物成像[13]、三维成像[14]、气体成像[15]、透视成像[16]、高光谱成像[17]、全息成像[13]、缺陷检测[18]、遥感[19]和光学加密[20]等领域的广泛应用和研究热潮. 然而, SPI技术面临减少计算时间与保证图像质量的双重挑战. 高质量成像需大量空间模式, 导致采样与重建时间增加, 尤其在大规模或动态场景中更为突出. 通用调制模式(如随机散斑[21]、哈达玛基[22]、傅里叶基[23])适应性较差, 需更多模式确保图像质量, 而优化算法在有限模式下难以恢复高质量图像. 压缩感知(compressed sensing, CS)[24]结合光学、数学与优化理论[25], 以更少模式提高SPI速度[26], 但其迭代优化框架计算资源消耗大, 处理时间受场景复杂度影响, 且子奈奎斯特采样引发的图像质量下降仍是难题[27].

      2024年诺贝尔物理学奖授予John Hopfield和Geoffrey Hinton, 表彰他们在人工神经网络和机器学习领域的开创性贡献[28]. 实际上物理学不仅是深度学习(deep leaning, DL)神经网络的基础, 而且神经网络反过来也促进了物理学的发展, 包括深度学习助力物理方程的求解[29]、天体物理学与天文数据分析[30]、数值计算与模拟[31]、以及深度学习与光学成像技术的结合[32]等. 其中在SPI领域[33], DL相比传统图像重建算法, 不仅显著加速了重建过程, 还在低采样率和复杂环境下表现出卓越的重建质量[34;35]. 这些研究包括超分辨SPI[36]、通过散射介质的SPI[37]、光子级SPI[38]、基于SPI的光学加密[39]及无图像传感[40]等. 此外, 基于DL的SPI技术在目标分类[41]、图像分割和目标检测[38]等复杂感知任务中得到成功应用. DL技术在SPI中的应用主要分为数据驱动和物理驱动神经网络两大类[42]. 数据驱动神经网络在SPI中取得了较好的表现, 但通常依赖大规模训练数据, 且在噪声较大或数据缺失的情况下效果较差, 限制了其实际应用[43]. 为了解决这些问题, 物理驱动型神经网络通过结合深度图像先验(deep image prior, DIP)理论[44], 能够实现高质量的图像重建, 且不依赖于大量数据集. 然而, 这些方法在处理复杂图像、捕捉高频细节和降低低采样率下的重建误差方面仍面临困难[45].

      目前卷积神经网络(convolutional neural network, CNN)[46]、生成对抗网络(generative adversarial network, GAN)[47]、循环神经网络(recurrent neural network, RNN)[48]等深度学习模型已在SPI中取得了一定突破, 但各自也存在局限性. CNN在处理复杂场景时容易忽略关键信息, 影响重建精度[49]; GAN虽然在超分辨率和抗散射成像中表现优异, 但在低采样下的细节恢复能力不足[50]; RNN适用于动态场景, 但处理大规模数据时存在困难[51]. 近年来注意力机制[52]也被引入到深度学习框架中, 且已经在Transformer等模型上展现出巨大的优势. 本文以探索注意力机制在基于非训练物理驱动SPI过程中的应用为目的, 提出了融合注意力机制与U-net卷积网络的方案. 在SPI任务中注意力机制可以通过动态调整网络的关注区域, 使其更加精准地聚焦于图像中的关键信息, 从而提升图像重建的质量和分辨率[53]. 通过动态调整网络的关注区域, 注意力机制能够帮助网络自适应地关注最重要的图像部分, 尤其在分辨率提升、噪声抑制和模糊恢复[54]、光学加密[55]等任务中展现了独特优势.

      本文提出了一种将注意力机制融合到卷积神经网络中的SPI重建方案, 通过将空间注意力机制和通道注意力机制两个维度的信息引入到网络的各层结构中, 进一步提升非预训练物理驱动神经网络重建图像的质量. 具体来说, 将结合空间与通道两个维度的注意力机制模块集成到多尺度U-net卷积网络[56]中, 利用注意力机制在三维数据立方中提供的权重信息与U-net网络在各个空间频率的特征提取能力实现高质量的图像重建. 大量的实验结果表明, 本文提出的融合注意力机制的方案相比于传统的基于非预训练网路SPI的重建方案在图像峰值信噪比与结构相似性等指标上展现出巨大优势.

    2.   原　理

      2.1.   实验方案

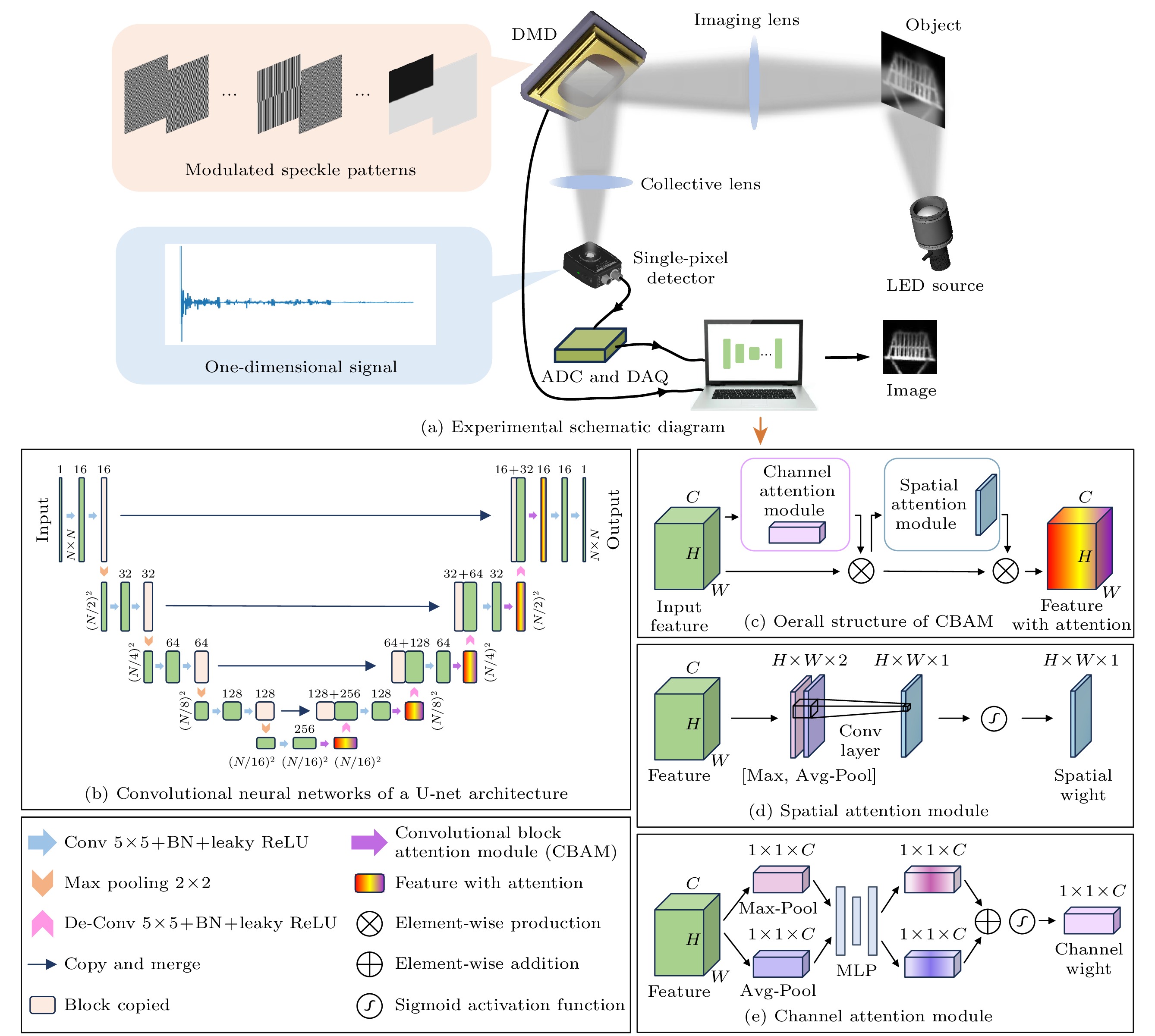
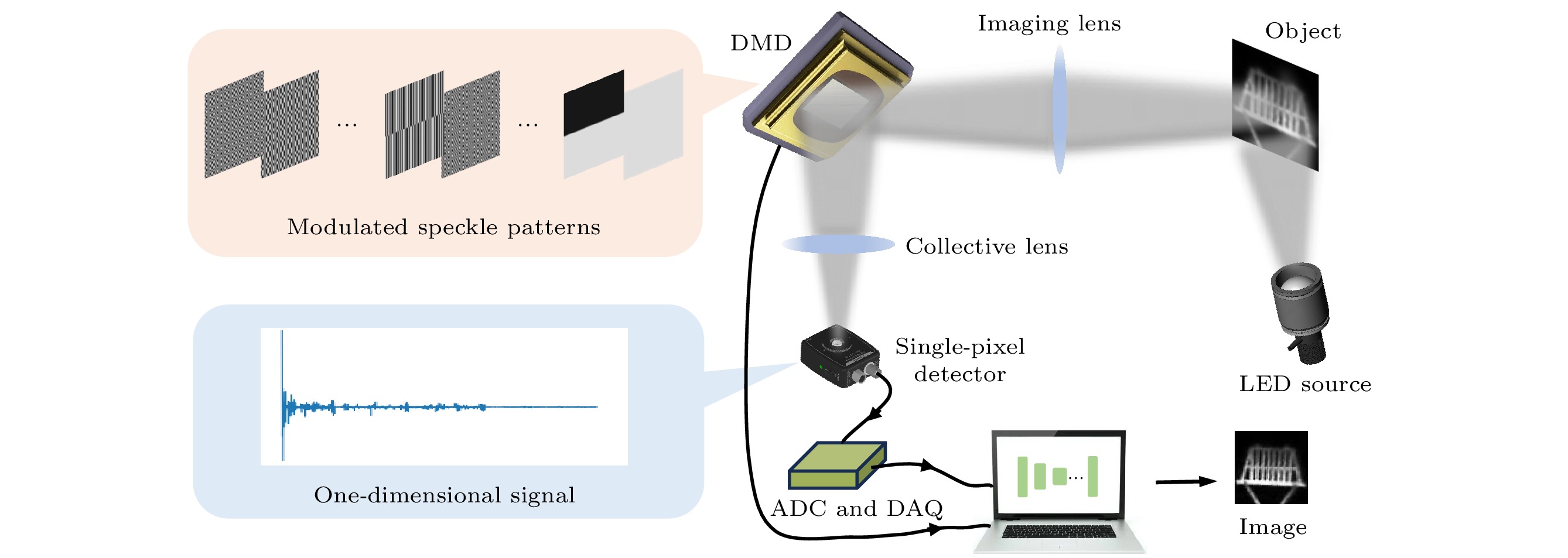
    • 实验光路如图 1所示, 实验将单像素成像与CNN网络相结合, 通过将物理过程嵌入CNN的生成器中, 实现单像素成像的重建. 来自LED光源的白光光束照射到目标物体上, 其反射光线经由一个透镜(f = 10 cm)成像到数字微镜装置(DMD)上. 哈达玛矩阵作为调制矩阵在实验前加载到DMD上, DMD通过预先储存的二进制调制掩膜图案控制其单个微镜翻转, 其中每个微镜可以相对于阵列平面单独定向在±12°, 对应于二值掩膜的“0”“1”像素值. 其中一束携带调制矩阵信息的DMD反射光束经过准直透镜, 被桶探测器收集生成一维桶信号$ {I_{\mathrm{m}}} $, 该信号代表系统的真实采样结果. 然后将桶探测器连接到模数转换器(ADC)进行数字化. 最后通过数据采集卡(DAQ)将这些数字信号储存在计算机中, 用于重建图像. 在具体的实验过程中, 将DMD的调制频率设置为20 Hz, 并将DAQ的数据采集频率调整为1 kHz, 也就是说对应于每一张调制掩膜, 可以收集到50个采样数据, 最终将这些数据的平均作为此调制掩膜的光强信号.

      • 2.2.   图像重建

    • 假设像素化的目标物体图像为$ T(x, y) $, 共包含N个像素点. 在SPI中, 将一系列调制掩膜图案$ P_i(x, y) $加载到DMD上用来对携带物体信息的光束进行空间调制, 其中$ i=1, 2, \cdots, M $代表掩膜的数量. 桶探测器收集到的经DMD调制后的一维光强信号可以表示为

      而整个实验测量过程还可以等价地表示为

      其中$ \boldsymbol I $表示由$ I_{i} $组成的M行列向量, $ \boldsymbol T $表示由离散化的目标图像伸展形成的N行列向量, $ \boldsymbol P $则是表示所有调制掩膜的$ M \times N $矩阵. 在SPI中, $ \left\{ {{I_j}} \right\}_{j = 1}^M, \left\{ {{P_j}} \right\}_{j = 1}^M $用于重建图像. 传统的SPI重建方法通过涨落和调制掩膜之间的关联性重建图像, 定义为[35]

      其中$ \langle \cdot \rangle $表示对物理量求平均值. 与传统的迭代算法相比, 基于数据驱动DL的重建方法被证明能够有效地避免巨大的计算负担并获得高质量的重建结果[50]. 将SPI的成像物理模型集成到随机初始化的非训练的CNN中, 以通过在网络优化期间与成像物理过程交互来获得高质量重建图像[57], 这允许在数据准备和图像重建中的低时间消耗. 目标图像的重建公式可以由以下函数表示:

      (4)式中, 神经网络的输入z可以是使用传统SPI重建方法获得的模糊图像, 或者是与调制模式相同大小的任意图像. $ P{R_\theta }\left( z \right) $表示方程中描述的SPI的物理过程. 在迭代过程中, 网络将找到合适的参数$ {\theta ^ * } $来优化其网络结构. $ \mathrm{TV} $是改善重建图像质量的全变分正则化约束, ζ用来平衡正则化在重建过程中的权重, 始终将其设置为$ 10^{-9} $. 当网络的输出$ \widetilde O = {R_\theta }\left( z \right) $通过SPI的成像物理过程时, 将获得网络估计的一维桶信号, 可以表示为

      $ {\tilde I} $也可使用迭代差分值代替原始值[58], 以与实验中检测到的桶信号的操作保持一致, 可以表示为

      式中, $ S_j= \displaystyle\sum P_j $表示第j个调制模式所有像素的和. 综上, (4)式可以改写成

      其中, $ \| \tilde{I}_j^t - I_j^{\prime t} \|^2 $表示实验测量的桶信号和非训练神经网络估计的桶信号之间的误差, 本文将其作为网络的损失函数. 在迭代操作期间不断更新神经网络权重, 以最小化桶信号之间的误差. 误差越小, 估计的桶信号越接近真实桶信号, 网络输出越接近目标对象图像.

      重建过程具体可分为四个步骤. 步骤1: 将SPD收集的一维桶信号y、调制掩膜H和目标对象的任意图片z输入到随机初始化的非预训练神经网络中; 步骤2: 对y进行迭代差分处理以消除测量噪声和环境噪声; 步骤3: 将网络的输出$ {\widetilde O} $与SPI的成像物理过程融合, 以获得网络估计的桶信号$ {\tilde I} $, 并对其进行迭代差分处理, 然后计算出损失值; 步骤4: 选择一个合适的优化器来更新神经网络权重, 以最小化损失函数. 重复迭代步骤3和4以获得网络的最佳权重和最佳重建图像.

      • 2.3.   网络结构

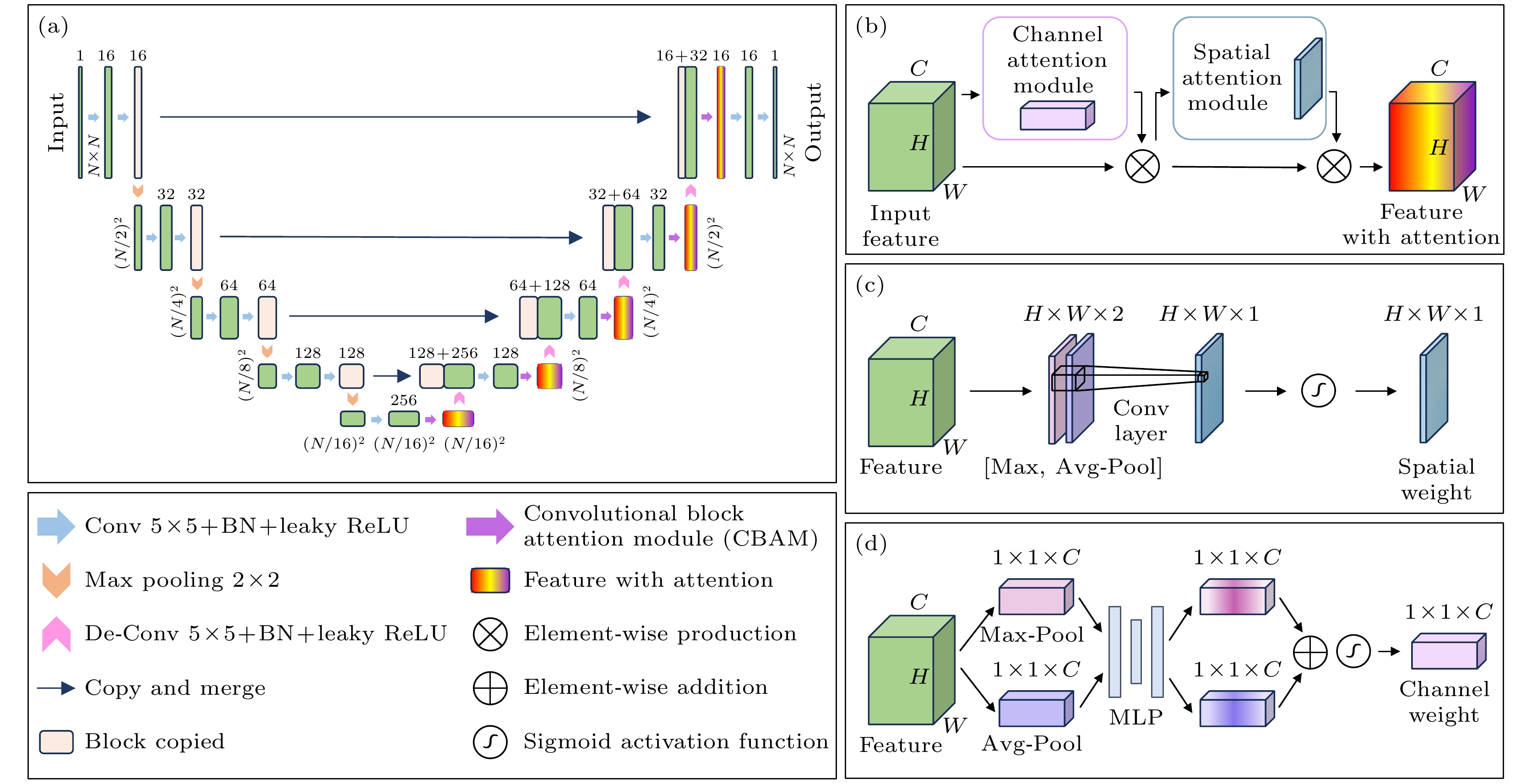
    • 重建方案中使用的网络结构如图 2所示. 其中的主体是名为U-net的经典纯CNN[59], 其基本结构如图 2(a)所示. 作为一个经典的多尺度CNN, 其包含编码器与解码器两部分, 整体呈现“U”字形的架构. 左侧的编码器接收大小为$ N \times N $的随机输入图, 通过一系列卷积操作提取特征(每个卷积层由5 × 5卷积核、批归一化(batch normaliza tion)和leaky ReLU激活函数三部分组成). 具体来说, 首先将输入图片两次经过卷积层, 并利用16个不同的卷积核将灰度图像的通道数扩充为16, 以此来提取目标图片的高频信息. 接着将特征图按照$ 2 \times 2 $最大池化(max pooling)的方式进行下采样, 之后又通过两层32卷积核数的卷积层得到略低于最顶层频率的图片信息. 之后一直按照这样的方式实现对目标图像各种空间频率特征的层层提取, 直到特征图的空间维度减小到$ N/16 \times N/16 $. 由于采用最大池化的方式进行下采样, 从上至下得到的空间频率信息是依次递减的, 最下层对应最低的空间频率, 由于自然图像一般具有平滑低频的特点, 编码器从上至下对应的通道数是逐渐增大的. 解码器是与编码器相互对称的结构, 通过卷积层提取信息, 通过反卷积操作(de-convolution)逐步上采样, 将空间分辨率恢复到原始大小, 并通过跳跃连接(skip connections)将编码器的特征与解码器的特征融合, 以保留高分辨率特征, 避免池化时的信息损失, 从而改善图像重建质量. 在网络末端, 解码器输出大小为$ N \times N $的高分辨率图像. U-Net的对称结构及其跳跃连接设计使其能够高效捕获局部和全局特征, 可以有效地进行图像重建任务.

      在特征图通过解码器的卷积层过后, 令其进入一个名为卷积块注意力机制(CBAM)的模块. CBAM是一种用于增强特征表达能力的模块, 由通道注意力模块(channel attention module, CAM)和空间注意力模块(spatial attention module, SAM)两部分组成. SAM旨在空间维度识别特征图中的重要区域, 通过赋予不同空间位置以不同的权重值来优化网络的特征表达能力. 假设输入特征图尺寸为$ H \times W \times C $, 其中C为通道数量. 该模块首先通过最大池化(max pool)和平均池化(avg pool)在通道维度上进行池化操作, 生成两个单通道的特征图, 然后将二者堆叠为尺寸$ H \times W \times 2 $的特征图. 随后输入到一个单卷积核的卷积层中得到单通道的输出. 为了将此输出表示为不同空间位置的注意力权重, 最后使用了sigmoid激活函数将其映射到(0, 1)区间, 由此得到输入数据空间维度的注意力权重. CAM通过捕捉各通道之间的重要性程度优化特征表达. 对每个通道的特征图分别进行整个空间维度内的全局平均池化和最大池化操作, 生成两个全局描述向量, 大小为$ 1 \times 1 \times C $. 这两个向量经过两个全连接层处理, 先降低维度至$ C/2 $, 再恢复至原始通道数C. 最后将二者相加并通过Sigmoid激活函数生成每个通道的权重, 用于描述各通道的重要性. 当特征图通过CBAM模块时, 首先将CAM的结果与特征图各通道对应相乘, 再将所得到的结果放入SAM中, 最终的输出是SAM结果与通道注意力作用后特征图在空间维度对应相乘, 并在通道维度进行广播(broadcast), 这样就得到了含有两个维度注意力机制的输出.

    3.   结果与讨论

    • 为了验证所提方法的有效性, 对原始CNN重建方案以及融合了注意力机制的网络重建方案在不同采样率下的重建结果进行比较. 采用峰值信噪比(PSNR)和结构相似性(SSIM)两种常用指标对重建质量进行定量分析, 并对重建图像与真实图像的差异进行了比较. PSNR的计算公式为

      其中$ \mathrm{MAX} $为图像的最大像素值, $ \mathrm{MSE} $为均方误差, 定义为

      其中, $ J(a, b) $和$ {K(a, b)} $分别表示真实图像和重建图像, a和b为图像的行列坐标. SSIM是用于评估两幅图像之间相似性的标准, 广泛应用于图像处理领域, 用以衡量图像质量. SSIM基于亮度、对比度和结构三方面的对比, 计算公式如下:

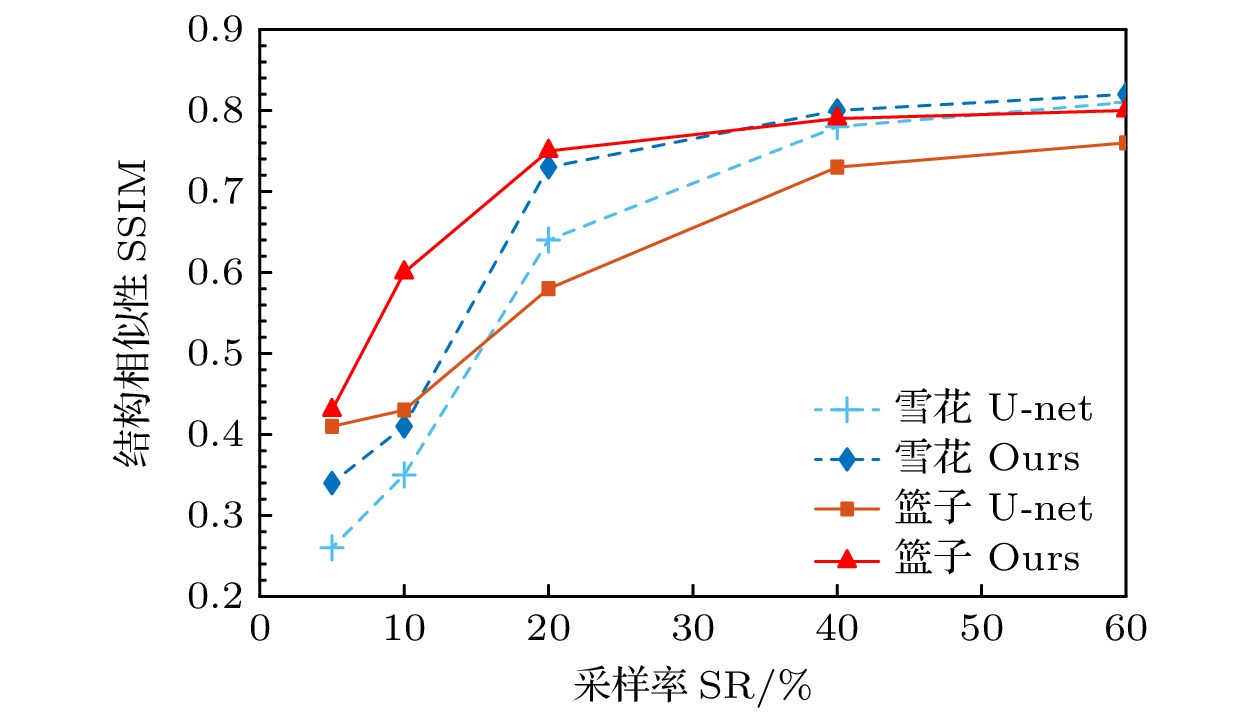
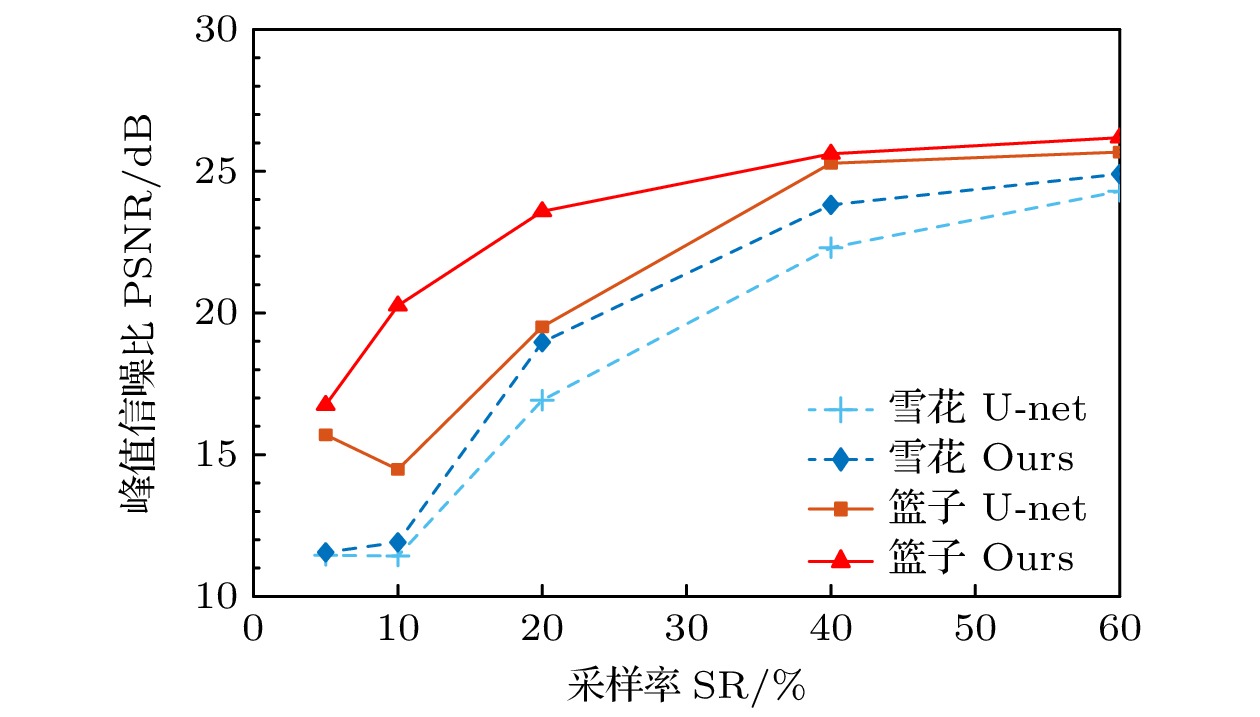
      其中, J和K为待比较的两幅图像, $ {\mu _J} $和$ {\mu _K} $为它们的平均亮度, $ {\sigma _J} $和$ {\sigma _K} $为标准差, $ {\sigma _{JK}} $为两幅图像的协方差, $ {c_1} $和$ {c_2} $为避免分母为零的小常数. SSIM的取值范围为$ \left[ { - 1, 1} \right] $, 值为1时表示两幅图像完全相似.

      在具体的实验中, 利用SPI的光路分别对“篮子”和“雪花”两种目标物体进行成像, 并分别利用随机初始化的U-net卷积网络和融合U-net网络与注意力机制的重建方案恢复图像, 以此来比较所提方案的重建效果. 使用Adam优化器, 并设置初始学习率为0.01, 默认迭代次数为600, 不同采样率(sampling rate, SR)下的图像重建表现如图 3所示(将融合注意力机制的重建方案用“Ours”表示). 实验中采样率定义为$ \mathrm{SR}= M/N \times 100{\text{%}} $, 即重建图像使用到的散斑数与目标物体的像素数的百分数比值. 根据图中的结果, 融合注意力机制的神经网络在重建图像的PSNR和SSIM随采样率的变化中表现显著优于未加入注意力机制的U-net网络. 对于雪花图像和篮子图像, 融合注意力机制方法在低采样率(${\rm SR} < 0.3 $)下提升尤为显著, 表现出更高的PSNR, 表明注意力机制能够更好地恢复图像细节和信噪比. 在高采样率(SR≥0.4)下, 本文的方案与传统U-Net的差距逐渐缩小, 表明基础网络在高采样率时已具备较强的重建能力. 加入注意力机制的网络能够更好地捕捉关键特征, 增强图像细节的恢复能力, 特别是在低采样率条件下表现优异.

      在不同采样率下重建图像的SSIM和PSNR变化趋势对比分别如图 4和图 5所示, 融合注意力机制(Ours)的模型在“雪花”和“篮子”图像的重建中, SSIM与PSNR的值显著高于不加注意力机制(U-Net)的模型. 随着采样率(SR)从5%增加到60%, SSIM与PSNR值逐步上升, 本文方案在低采样率(SR = 10%—20%)时提升效果尤为显著, 尤其对更复杂的“雪花”图像表现更强. 注意到图 5中SR = 10%时的PSNR甚至小于5%采样率的结果, 但10%采样率对应的结构相似性更高, 可能是网络在更新参数时更趋向于优先提升结构相似性指数. 而在高采样率(SR≥40%)时, 两个指标的值趋于平稳, 但本文的重建方法仍保持领先, 说明注意力机制能够有效提升图像结构相似性和峰值信噪比, 特别适用于低采样率和复杂数据情形, 对提升图像重建质量具有重要意义.

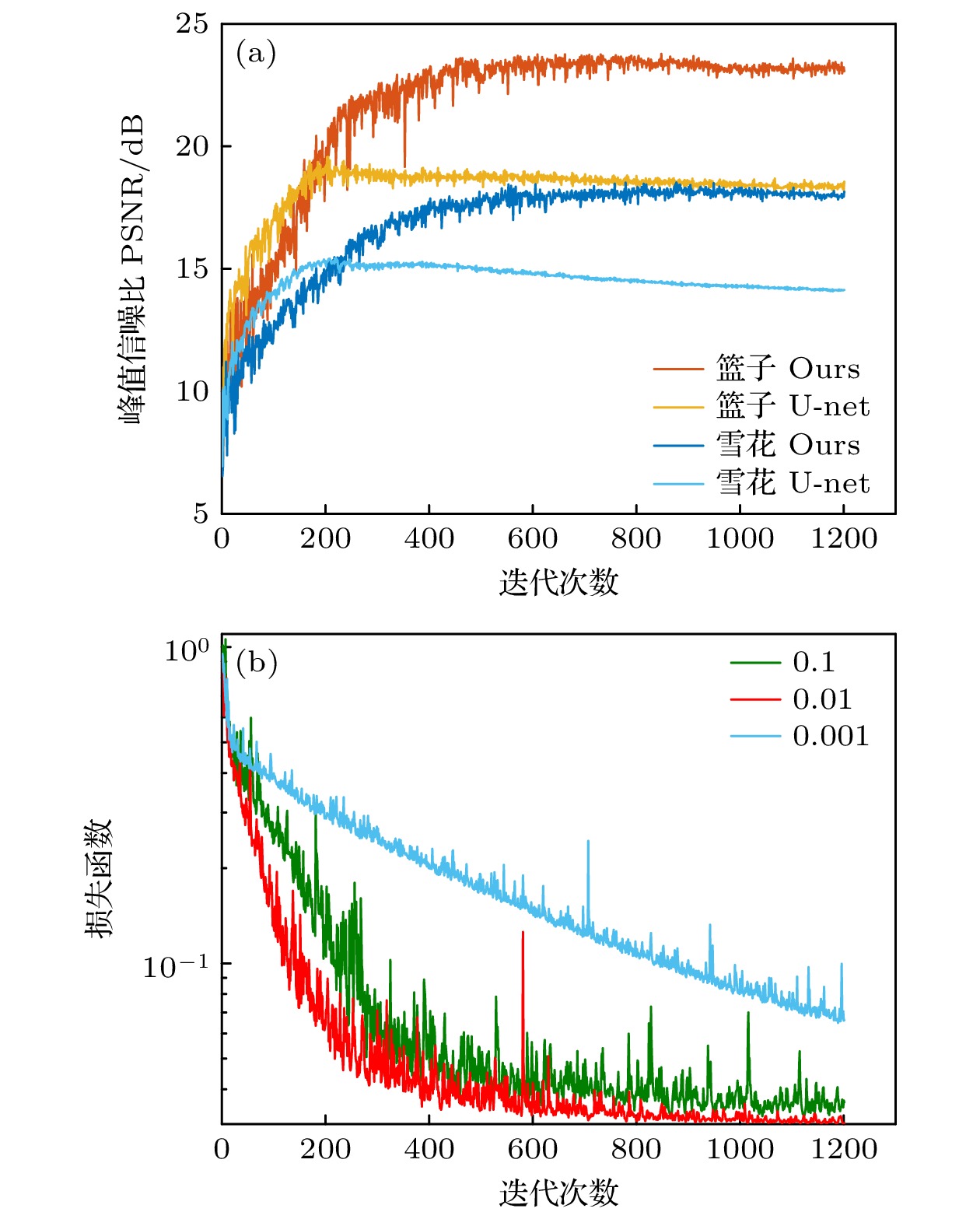
      重建图像的质量随网络迭代次数的变化也是一个重要的问题, 使用不同方案、不同初始学习率时图像的PSNR与网络损失函数的变化如图 6所示. 图 6(a)给出了在SR = 20%时, 本文方案与原始U-net网络重建结果的PSNR对比, 可以看到, 虽然在迭代次数较少(< 200)时原始的U-net展现出略微的优势, 但随着网络的进一步迭代, 注意力机制对数据特征的挖掘能力被逐渐显示出来, 实现了图像PSNR的巨大提升.

      为了比较本文提出的网络模型在不同初始学习率下的表现, 并探索最优初始学习率, 我们进行了多种学习率下的重建, 结果如图 6(b)所示. 首先, 在初始学习率[0.1, 0.001]区间范围内的损失函数均能下降至$ 10^{-2} $左右并得到不错的重建结果, 说明本文的方案具有不错的收敛性. 另外, 大量的实验结果表明学习率为0.01左右时的重建效果最好, 且与目标图像无关, 因此将其设定为网络默认的初始学习率.

      实验结果表明, 融合注意力机制的模型在“篮子”和“雪花”两个图像的重建质量上均优于不加注意力机制的U-Net模型, 尤其在低采样率(SR = 10%—20%)时表现尤为显著. 从视觉效果来看, 融入注意力机制模型能够更好地保留图像的纹理和结构细节, 而U-Net模型在低采样率下出现明显的模糊现象. 在PSNR方面, 两个数据集的PSNR值均随采样率增加而提升, 在低采样率时, 本文方案对“篮子”和“雪花”方案的提升巨大, 而在高采样率(SR = 60%)时, 融入注意力机制模型的PSNR仍保持略高于U-Net的水平, 说明注意力机制在不同采样率下均具有稳定的性能提升. SSIM方面, 本文方案同样在所有采样率下表现出更高的结构相似性, 特别是在“雪花”图像低采样率(SR = 5%)条件下, 融入注意力机制的SSIM显著高于U-Net, 体现了注意力机制在稀疏数据条件下恢复图像结构的能力. 融入注意力机制的模型能够通过更好地提取全局和细节特征, 在低采样率的重建任务中展现出显著优势, 对于提升图像质量和模型适应性具有重要意义.

    4.   结　论

    • 本文提出了一种融合注意力机制的CNN模型, 用于单像素成像任务, 通过将通道注意力机制与空间注意力机制两个维度的信息融入到U-net卷积网络的多尺度特征层中, 实现了高质量的SPI重建. 实验测试了其在不同采样率和迭代次数下的图像重建性能, 结果表明在相同学习率或是相同采样率下, 融合注意力机制的卷积神经网络模型在单像素成像任务中都表现出了更优越的性能, 显著提升了重建图像的PSNR和SSIM值. 本文研究为单像素成像技术中重建算法的进一步发展提供了一种高效且可靠的方案, 尤其适用于采样率受限的实际应用场景. 但目前的方案在网络迭代初期的表现略显不足, 如何进一步优化网络结构和训练方案仍是一个有待解决的问题. 在未来研究中, 可进一步优化网络结构并比较注意力机制在其他神经网络中的表现, 或是探索其在实时成像和高光谱成像中的潜在应用价值.

    参考文献 (59)

目录

/

返回文章
返回