首页
登录
注册
-
大气风场作为表征大气动力学和光化学的关键参数, 是揭示高层大气物理现象及其演化规律, 研究高层大气与低层大气之间动量、能量和成分传递过程, 建立天气预报模式等不可缺少的基础数据, 在航空航天、环境气候、天气预报等领域发挥着重要作用[1–5]. 多普勒差分干涉仪(Doppler asymmetric spatial heterodyne interferometer, DASH)是一种新型的被动测风仪器[6,7], 具有高光通量、高相位灵敏度和无需精密扫描结构等优点, 因此在中高层大气风场测量中占据了重要地位, 成为大气科学研究和空间探测中不可或缺的技术手段[8–12].
多普勒差分干涉仪通过测量大气气辉谱线的多普勒频移导致的干涉图的相位变化量来获得风速信息[7]. 由于大气谱线的多普勒频移非常微小, 其引起的干涉图相位变化量通常为几十mrad, 要实现精确的风速测量, 干涉仪必须具备极高的相位检测精度及相位稳定度[13]. 然而, 在实际应用中, 环境温度的波动和机械振动等外界因素可能导致探测器相对于干涉仪发生相对位移, 导致采集到的干涉图发生漂移, 在相位反演过程中引入额外的相位变化量, 从而影响风速测量的准确性[13,14]. 因此, 如何精确地检测和校正干涉图的漂移, 成为提升风速测量精度的关键挑战之一[15].
针对这一问题, 目前已提出了多种成像漂移检测方法. 2020年, Marr等[15,16]针对ICON卫星的MIGHTI仪器的热机械效应引起的图像漂移开展研究, 提出在干涉仪一臂的光栅上蚀刻周期性的刻槽, 对探测器像面上刻槽形成的图像进行高精度建模, 利用模型拟合刻槽信号的位置来监测干涉仪像面漂移量. 该模型包含数十个拟合参数, 在实际操作中存在计算量大, 数据拟合复杂等问题. 2022年, 张亚飞等[17]提出逐段拟合刻槽图像边缘来检测成像漂移量, 虽降低了对模型的依赖性, 但需要对图像边缘进行多次分段拟合, 计算效率低. 此外, 该方法对边缘清晰度和噪声较为敏感, 限制了其实用性. 综上所述, 这些方法虽在特定条件下有效, 但在算法复杂度、模型依赖性和通用性方面仍存在显著局限. 因此, 仍需开发更高效、更普适的检测与校正方法.
为克服以上不足, 本文提出了一种对刻槽图像进行全局拟合的新算法, 能实现对多普勒差分干涉仪像面漂移的精确检测. 首先对光栅刻槽设计进行优化, 在刻蚀光栅刻槽时, 将刻槽所在光栅区域的基底完全贯穿, 使得该部分位置无法发生衍射和反射, 因此探测器像面上刻槽所对应成像区域仅为另一臂光栅的衍射光, 无干涉现象发生. 当对刻槽图像进行建模时, 可大大简化模型, 减少拟合参量的数目, 显著提升计算效率. 本文仿真分析了刻槽信号信噪比对检测精度的影响, 并对模型参数敏感性进行定量化分析. 基于近红外多普勒差分干涉仪样机的连续热稳定性测试数据进行了像面热漂移监测实验, 验证了该方法的实用性.
-
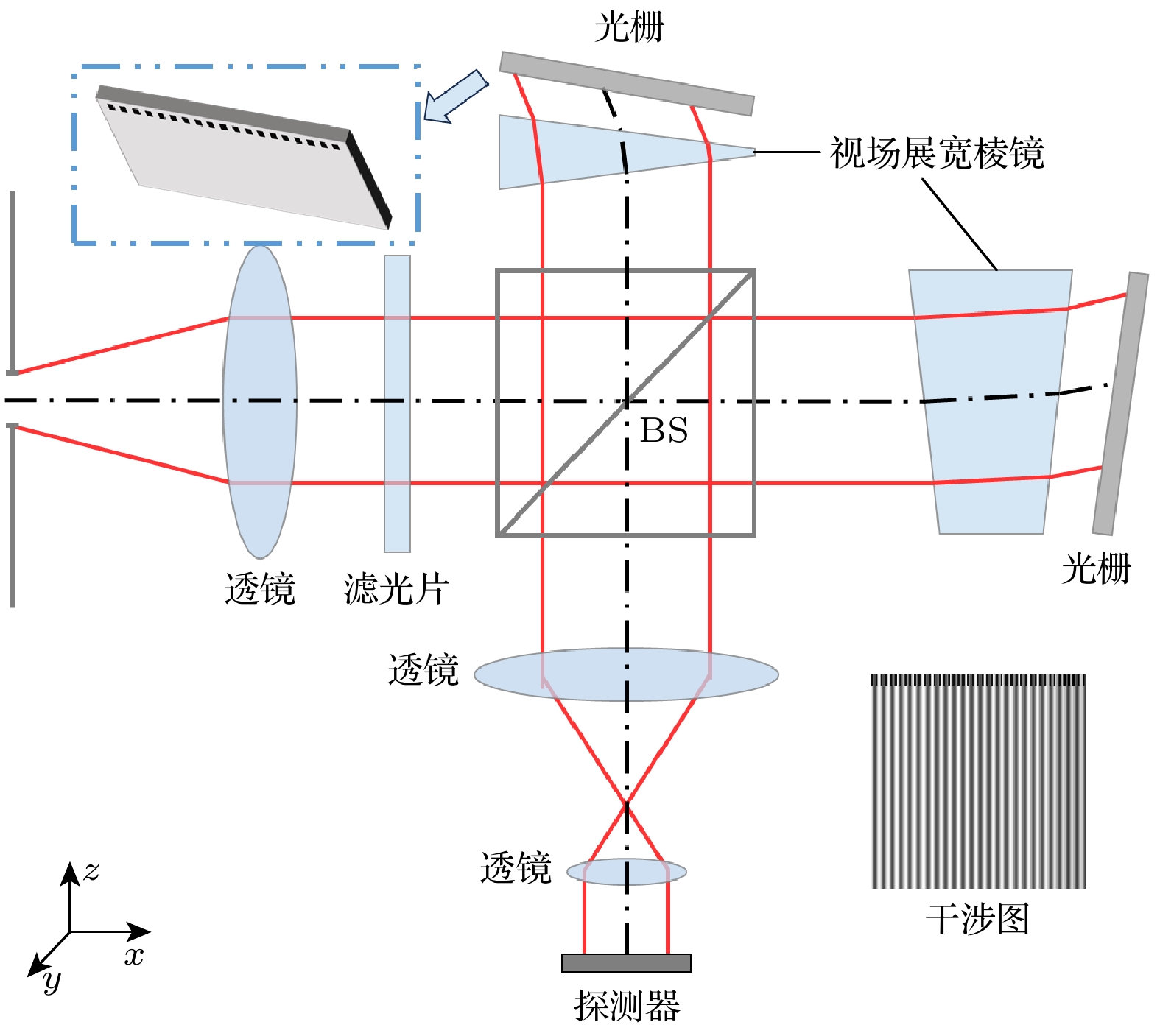
图1所示为DASH的示意图, 其是迈克耳孙干涉仪的变形. 与迈克耳孙干涉仪不同的是, DASH用闪耀光栅替代两臂的反射镜, 并且两臂相对于分束器呈不对称分布, 以增大基础光程差. 如图1所示, 入射光经准直器准直后进入干涉仪, 然后被分束器分成两个波面, 分别照射到两臂的闪耀光栅上[7]. 经过光栅的衍射后, 两个衍射波面在分光镜处重新汇聚, 形成菲索干涉条纹, 由阵列探测器记录. 探测器坐标系的x轴与光栅衍射方向一致, z轴与光轴方向一致, 理想情况下, 干涉条纹仅在x轴方向表现出空间调制, 如图1中的干涉图所示. 探测器(x, y)位置处的干涉图强度可表示为[18]
其中, B(σ)为入射光谱分布函数, f = 4(σ–σL)tanθL表示条纹的空间频率, σ是入射光的波数, σL是光栅的Littrow波长, θL是光栅的Littrow角, Δd表示两臂非对称量. 通过测量干涉图的相位变化量可反演风速信息, 相移与风速之间的关系可以表示为
其中, φv和φ0分别表示有风和零风干涉图的相位, Δσ表示大气谱线的多普勒频移, v表示大气风速. 在实际测量中, 环境温度变化、平台震动、干涉仪结构变化等均会导致探测器相对于干涉仪发生“错位”现象, 具体表现为干涉图在像面上发生整体漂移[19,20]. 在相位反演中, 该偏移会引入额外的相位变化量, 从而影响风速测量结果. 受成像漂移影响的相移可表征为
其中, Dshift1和Dshift2分别表示零风和有风情况下干涉仪像面漂移量,
${\phi _{{\text{pexel}}}} $ 表示探测器每像元对应的干涉条纹相位. 为提高风速反演的准确性, 需对干涉图成像漂移量进行精确检测.通过在干涉仪的一臂光栅上沿着衍射方向利用激光蚀刻周期性的刻槽可实现干涉图像位移检测[15], 如图1中蓝色方框所示, 黑色部分为光栅刻槽. 在刻槽外部, 入射光正常衍射, 在探测器上形成干涉条纹, 在刻槽内部, 由于激光处理的影响, 光栅表面和基底被破坏, 导致入射光无法形成衍射, 探测器相应位置仅接收另一臂光栅的衍射光. 探测器像面上刻槽图案为刻槽内外信号的叠加, 如图1中干涉图顶部区域所示. 当探测器相对于干涉仪发生位移时, 刻槽图案产生相应的位移, 因此可以通过检测刻槽图案位置变化量来确定像面漂移量.
-
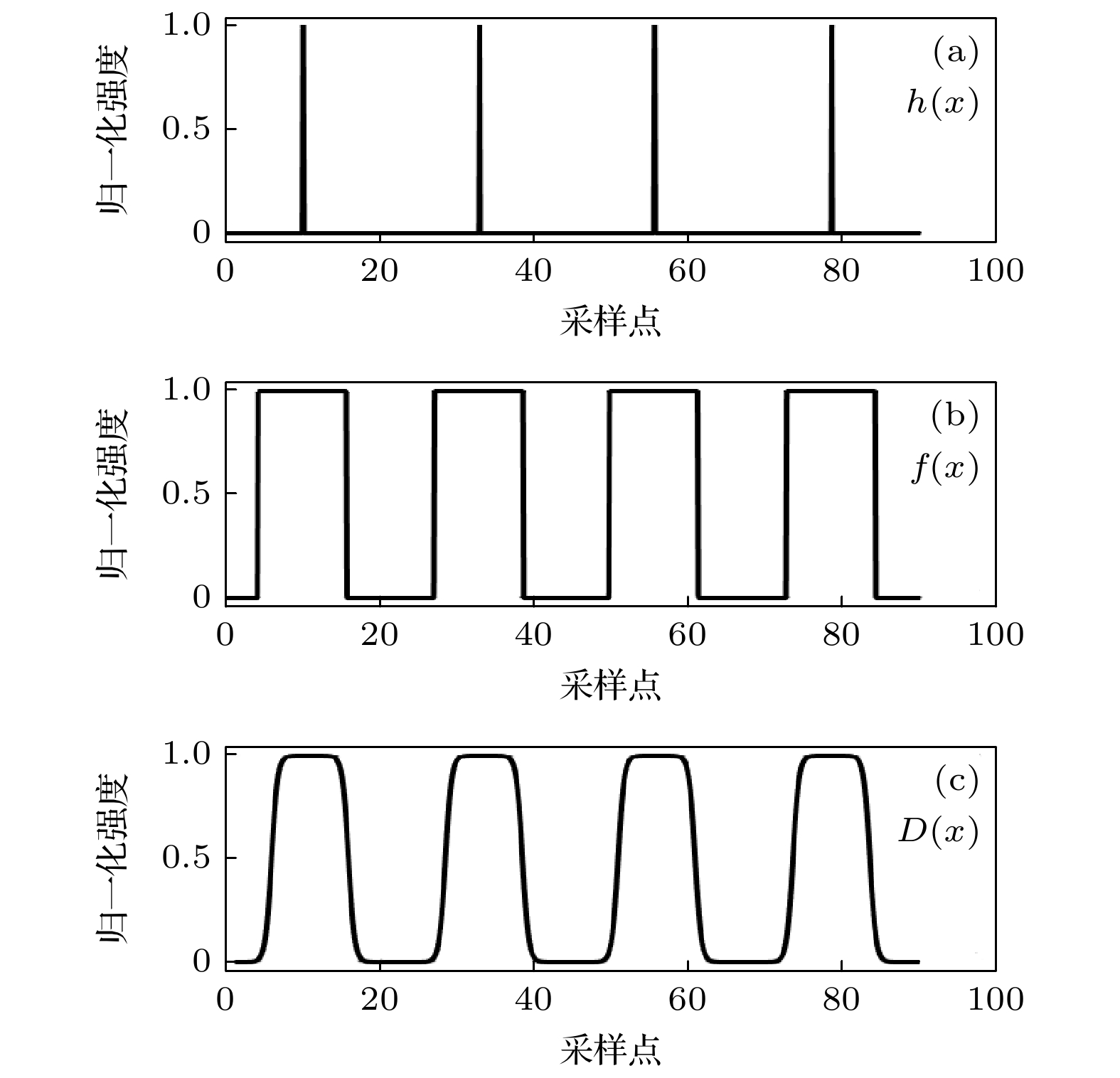
根据光栅刻槽形态分布及信号参数构造模型, 利用模型拟合刻槽图像的位置, 刻槽图像的偏移量即为干涉仪成像漂移量. 由于刻槽具有周期分布特性, 刻槽区域与无刻槽区域交替分布, 因此刻槽的形状和位置的分布可以用方波函数f(x)表示, 方波函数为梳状函数h(x) (见图2(a))与矩形函数rect(x) (图2(b))的卷积,
其中, h(x)表示梳状函数, δ表示脉冲函数, x为采样点位置, xsize为采样点数目, Nnotches为脉冲数目, 代表了刻槽的数量. a0是最重要的参数, 其用于调整刻槽结构的起始位置. rect(x)表示矩形函数, Wnotches表示矩形函数的宽度, 决定了刻槽区域的宽度. 方波函数f(x)变化范围为0—1, 当h(x) = 1时, 表示无刻槽区域, 当h(x) = 0时, 表示刻槽区域.
受限于系统调制函数及刻蚀工艺, 刻槽成像信号边缘通常并非理想的锐利过渡, 而是变得平滑. 因此需引入高斯核对方波函数进行卷积处理, 进而模拟真实的刻槽图像. 高斯核及刻槽形状可以表示为
其中, g(y)表示高斯核, σ为标准差, 其决定了高斯核的展宽程度, 用于表征刻槽图像边缘平滑度. y为高斯核的采样点数, 其与方波周期相关, 通常情况下采样点数为方波周期内样本点数的1—2倍, 确保高斯核能够充分平滑方波边缘, 同时不显著改变方波的整体结构. D(x)则表示经过高斯核卷积后的刻槽形状, 如图2(c)所示, 其能更真实地反映刻槽边缘的模糊特性.
当入射光为大气气辉时, 刻槽形成的图像本质上是由刻槽区域与无刻槽区域的信号相互叠加而成的复杂光学信号分布, 该图案结合了干涉条纹的分布特征与刻槽结构的几何特性. 为了精确描述刻槽图像, 对其进行整体建模, 信号可以表示为
其中, Iout(x)表示无刻槽区域的信号, 它代表了光栅在无结构破坏的情况下, 光束在探测器上形成的干涉条纹, Iout(x)可以使用干涉图中临近刻槽图案的条纹信号来表示. 相反, Iin(x)则对应于刻槽内的信号, 通常情况下, Iin(x)强度较低且起伏较小, 可以对刻槽图案的下包络进行拟合获得. 通常情况下, 为了提高数据的分辨率, 在建模过程中对Iout(x)和Iin(x)进行插值, 将数据扩展至原来的1000倍大小.
(8)式中的刻槽信号模型包含3个关键参数, 这些参数与干涉仪的物理特性密切相关, 不受环境变化的影响, 分别为矩形函数的宽度Wnotches、高斯核的标准差σ以及梳状函数中的脉冲数量Nnotches. 这3个参数可通过大量的定标数据获得, 如用自然光照射光栅刻槽, 此时刻槽外无干涉现象发生, 刻槽图像与D(x)一致, 可选取若干个周期的刻槽图像对3个参数进行拟合. 为了减小随机误差, 以多次测量的平均值作为最终参数值.
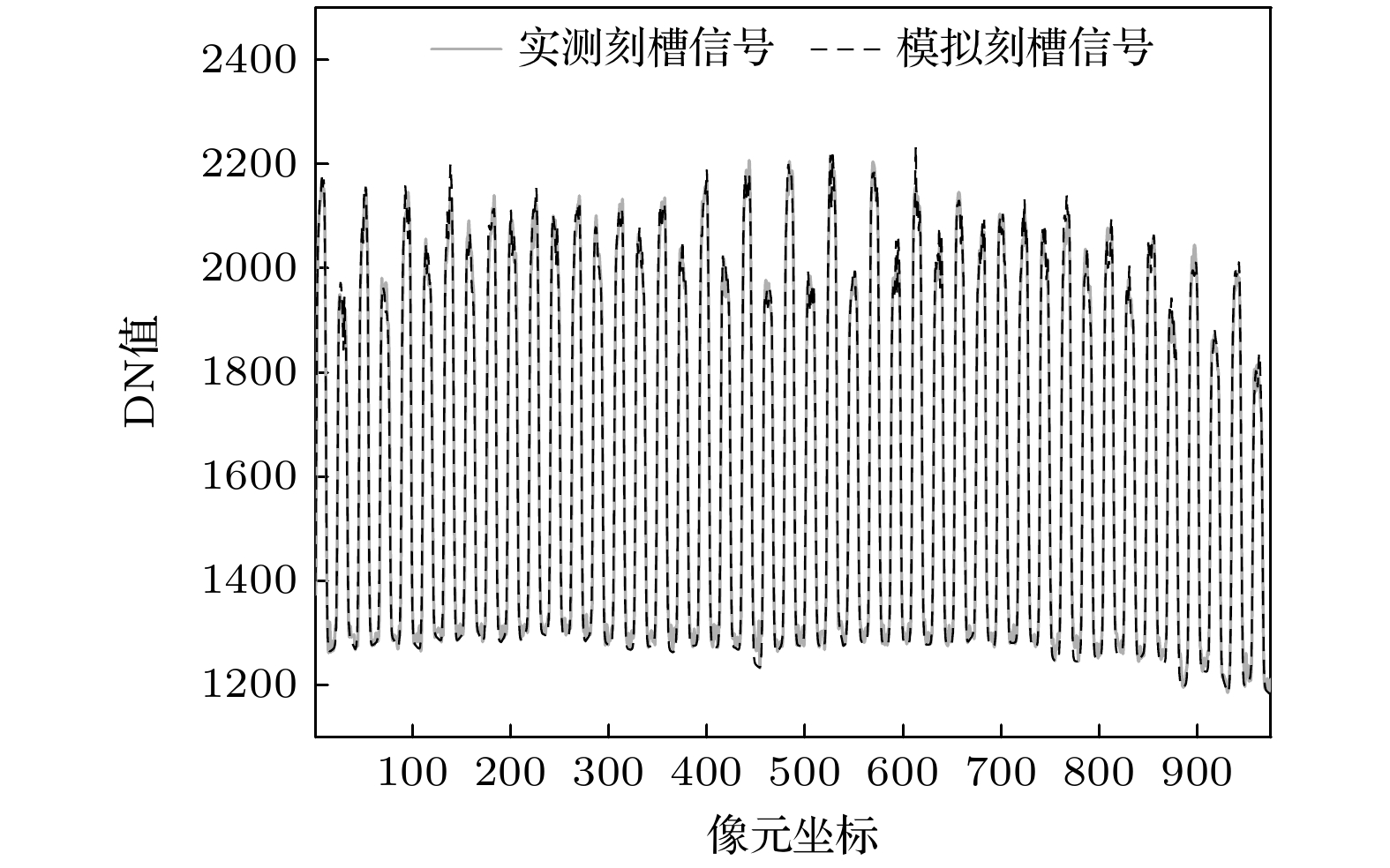
当获得最优的Wnotches, σ, Nnotches值后, 将其作为已知参数, 为刻槽的起始位置a0设定初始估计值, 仿真生成刻槽信号I(x), 结合实测刻槽信号Ireal(x)构造误差函数
其中, a0为待拟合参数向量, 通过最小化误差函数E(a0), 利用梯度下降法, 找到最优a0, 使得I(x)与Ireal(x)达到最佳拟合. 如图3所示, 实线为实测的刻槽信号, 虚线为根据最优参数值所得模拟刻槽信号, 可以看到两个信号基本一致.
-
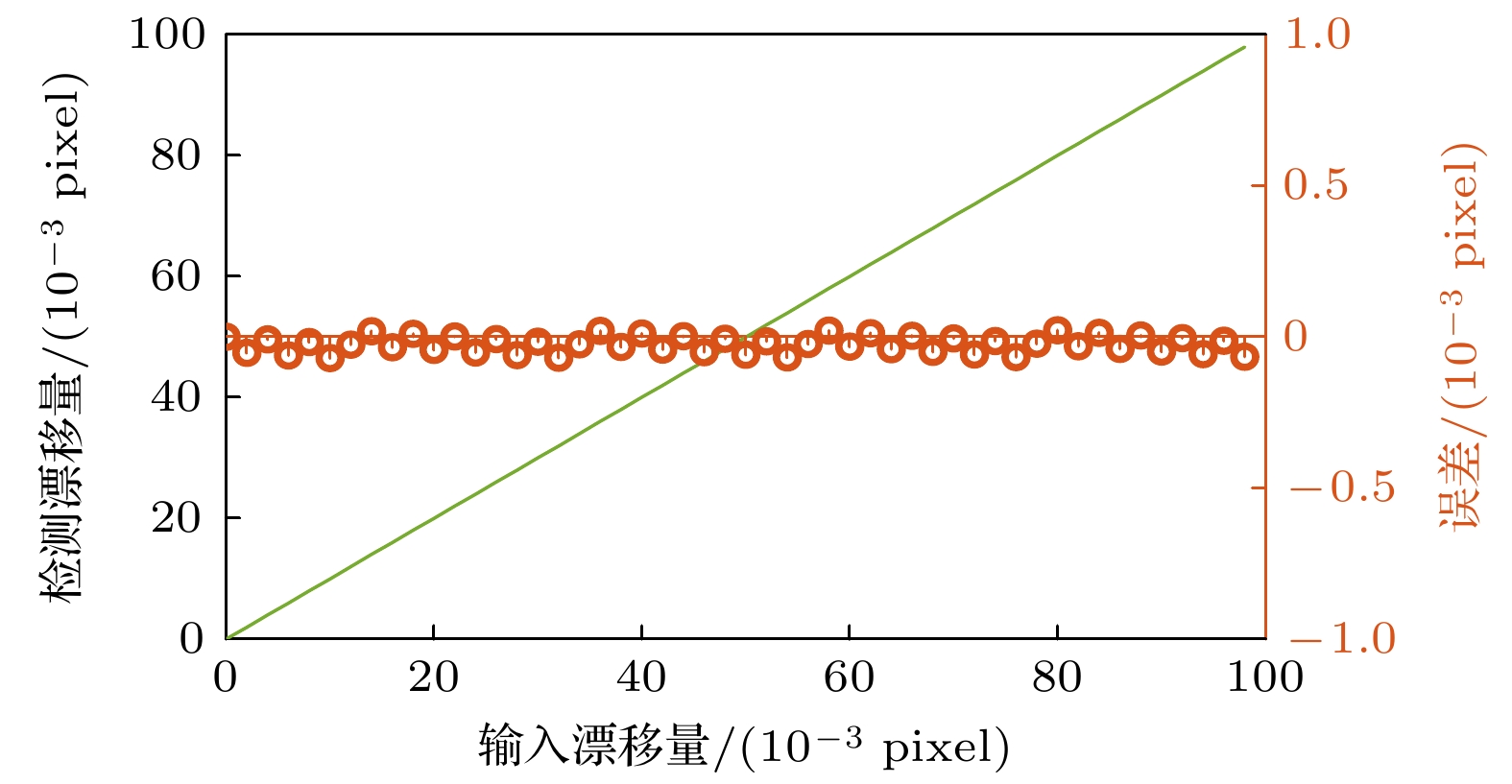
为验证成像漂移检测模型的精度, 本文通过仿真模拟不同成像漂移条件下的刻槽图案进行分析, 仿真参数如表1所示. 探测目标为O2(0-1)带867.7 nm谱线, 干涉仪基础光程差为49.87 mm, 探测器分辨率为2048×2048像元. 根据仪器参数生成对应的干涉条纹, 并利用(4)—(7)式生成刻槽形状函数, 结合(8)式进一步生成刻槽信号. 设定刻槽信号的成像漂移范围为0—100/1000 pixel, 步长为2/1000 pixel, 共生成50帧不同成像漂移量的刻槽信号. 随后, 采用第2节所提出的方法拟合每帧信号的成像位置, 并计算其相对于 第1帧信号的相对成像漂移量. 结果如图4所示, 输入漂移量与检测成像漂移量呈高度线性相关, 相关系数达到1. 图4右坐标轴显示拟合误差均小于0.01/1000 pixel, 对应的成像漂移误差检测小于0.07 nm, 表明该方法具有极高的检测精度.
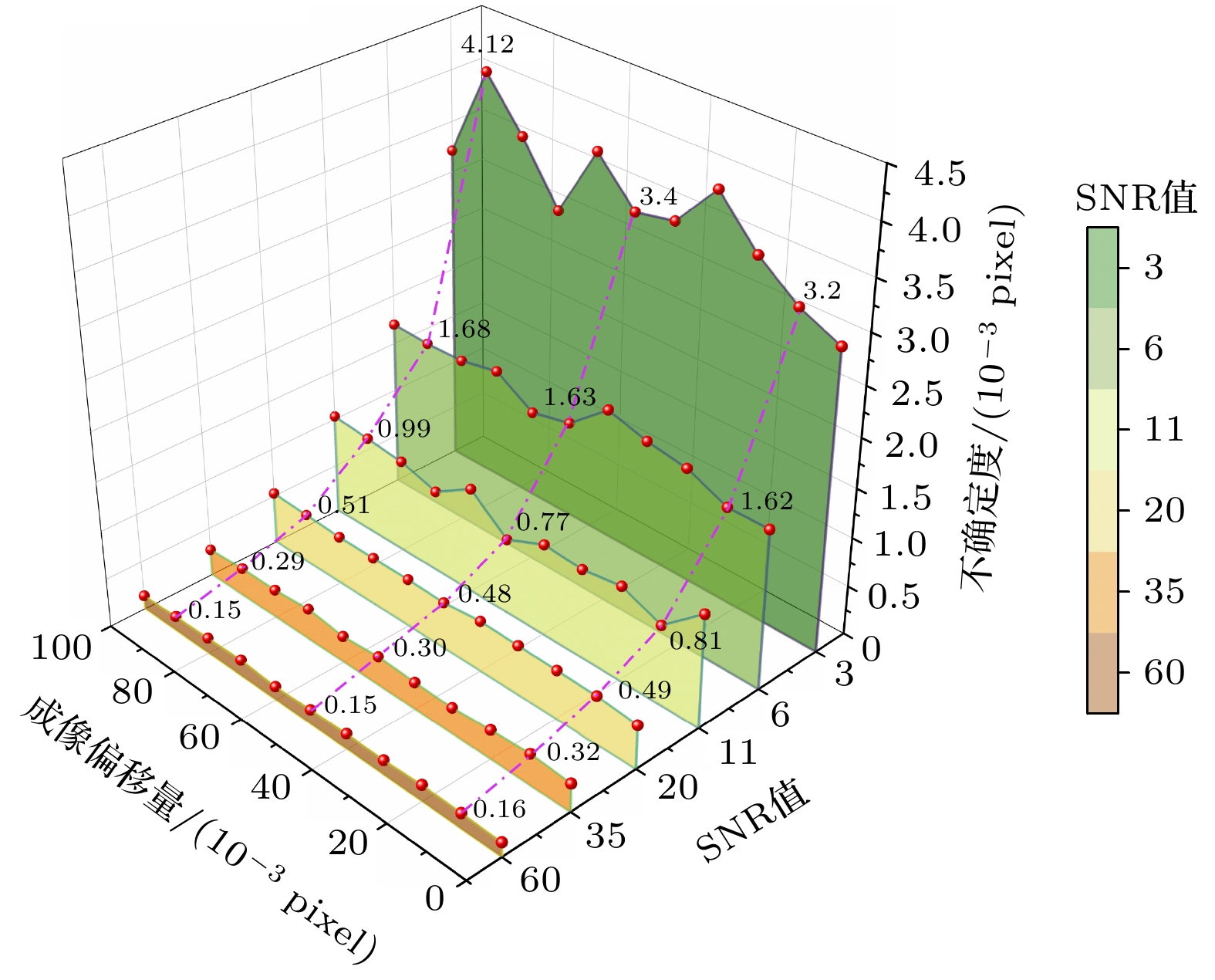
为评估信号信噪比(SNR)对检测精度的影响, 采用蒙特卡罗方法进行仿真实验. 信噪比定义为: SNR = S/N, 其中S为信号强度, N为噪声的标准差. 实验过程中, 生成6组不同SNR的刻槽信号(SNR = 3, 6, 11, 20, 35, 60), 每组包含11幅具有不同成像漂移量的刻槽信号. 为降低随机性对结果的影响, 在每组SNR和漂移量条件下均进行500次仿真, 并对成像漂移进行检测. 随后, 计算检测漂移量与输入偏移量之间的偏差, 并以500次检测误差的标准差作为拟合不确定度的衡量指标.
图5所示为不同信噪比与成像漂移量对拟合不确定度的影响. 结果表明, 拟合不确定度随着信噪比的提高逐渐减小并趋于稳定. 在低信噪比条件下(如SNR = 6), 拟合不确定度随成像漂移量的增加略有波动, 最大可达4.12/1000 pixel, 对应的成像漂移误差为26.78 nm; 而当信噪比提高至SNR ≥11时, 拟合不确定度显著降低, 并在所有成像漂移量范围内稳定保持在1/1000 pixel以内, 对应的成像漂移为6.5 nm以内. 这表明该方法在高信噪比条件下具备良好的抗噪性能和高检测精度.
成像偏移的检测精度受拟合参数准确度的影响, 其中包括矩形函数宽度Wnotches (表征光栅刻槽宽度)、高斯函数标准差σ (表征刻槽图像边缘平滑度), 以及脉冲数目Nnotches (表征刻槽数目)的估计误差. 这些误差源于测量噪声、环境变化或仪器稳定性不足, 可能导致刻槽模型的准确性下降, 从而引起成像漂移拟合结果偏差. 为系统地评估这些误差的影响, 本文进行参数敏感性分析, 通过引入相对误差这一指标来量化拟合参数对真值的偏离程度. 对信噪比SNR = 100的刻槽信号进行300次仿真模拟, 考察各参数在不同相对误差下对检测结果的影响. 这一分析方法旨在明确对检测精度至关重要的参数控制要求, 提升检测的可靠性与精确性.
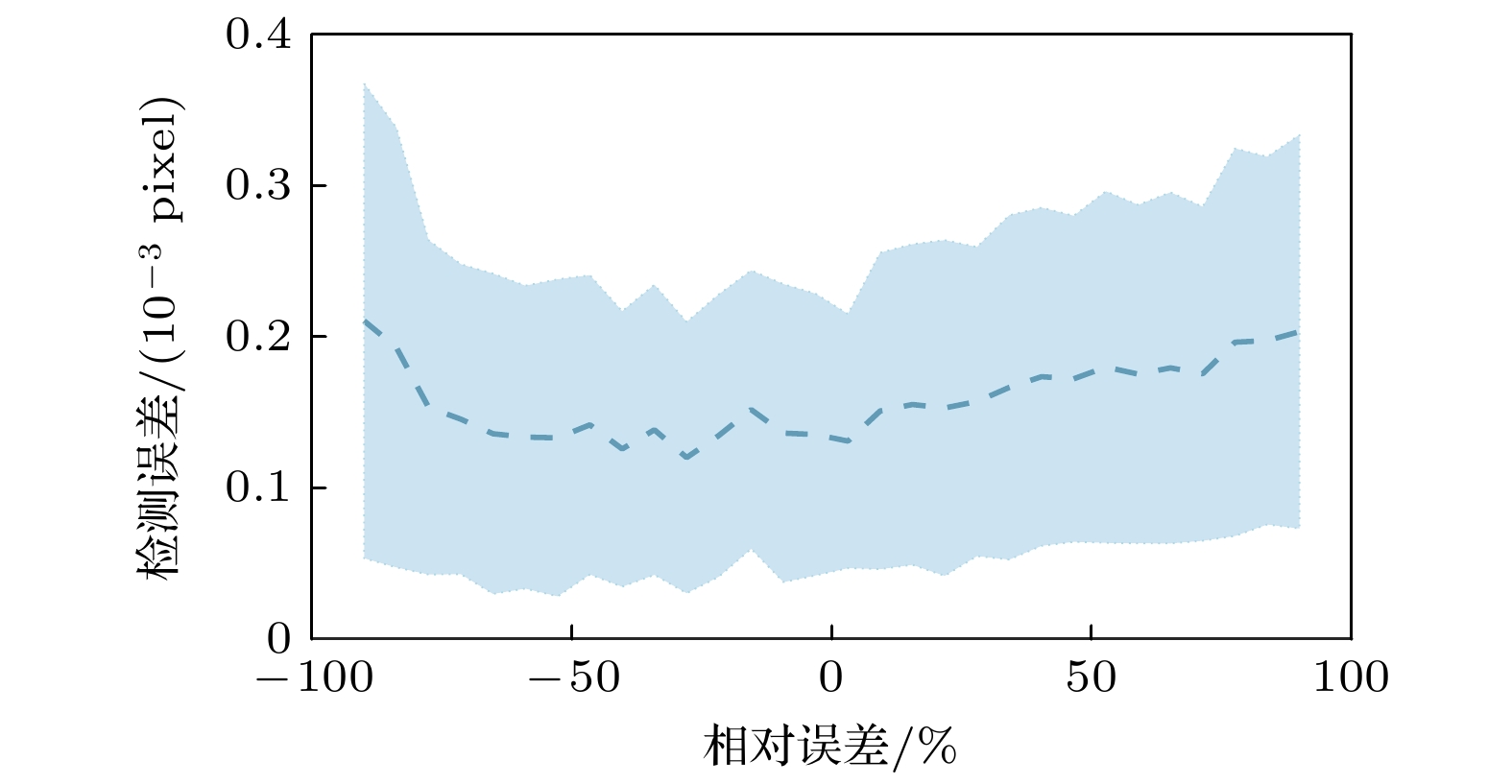
图6展示了高斯函数标准差σ(表征刻槽边缘平滑度)的拟合误差对测量精度的影响, 虚线表示多次测量的平均误差, 蓝色区域表示多次测量结果的标准差, 表征其测量不确定度. 当相对误差在 ±90% 范围内时, 拟合误差的波动幅度较小, 稳定在0.2/1000 pixel, 对应1.30 nm, 且不确定度也基本保持不变, 均小于0.4/1000 pixel, 对应2.60 nm. 这一结果表明, 在一定范围内, σ参数的拟合误差不会对成像漂移检测结果产生显著偏差, 说明该方法对σ具有较高的容忍度, 要求较为宽松.
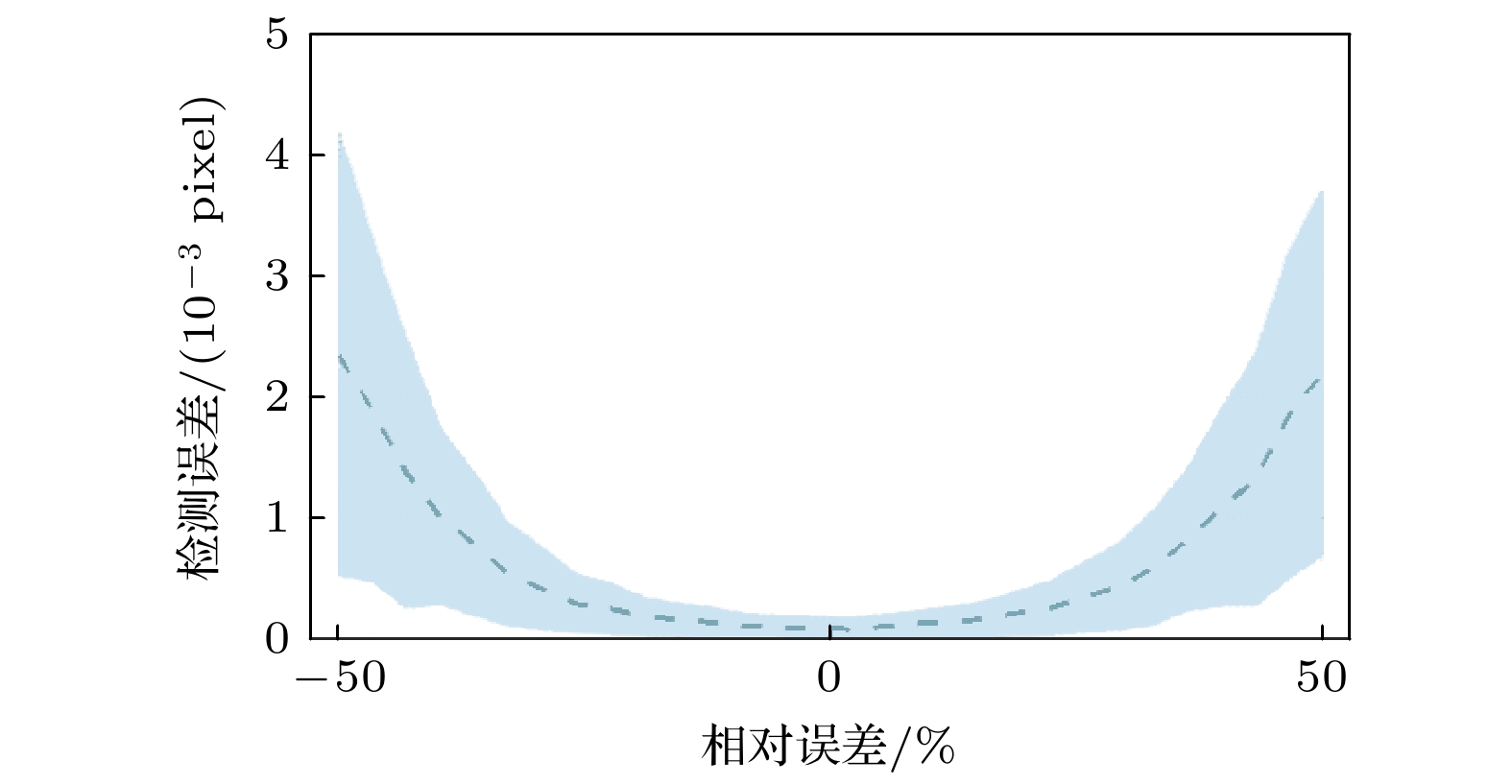
相比之下, 如图7所示, 矩形函数宽度Wnotches(表征光栅刻槽宽度)的拟合误差对成像漂移拟合结果产生了显著影响, 当相对误差较小时, 测量误差保持在约0.5/1000 pixel, 对应3.2 nm, 且测量不确定度较低. 然而, 当相对误差逐渐增至50%时, 检测精度下降, 误差呈现出非线性增长趋势, 最大可达2.5/1000 pixel, 对应16.25 nm, 此外误差带也逐步扩展, 表现出更大的不确定性. 值得注意的是, 拟合误差曲线相对于中心呈现出较高的对称性, 这表明在正负相对误差条件下, 系统对Wnotches参数变化的响应基本一致, 未出现显著的方向偏差. 此外, 为实现1/1000 pixel (6.5 nm)的检测精度, 需将矩形函数宽度拟合误差准确控制在±40%内.
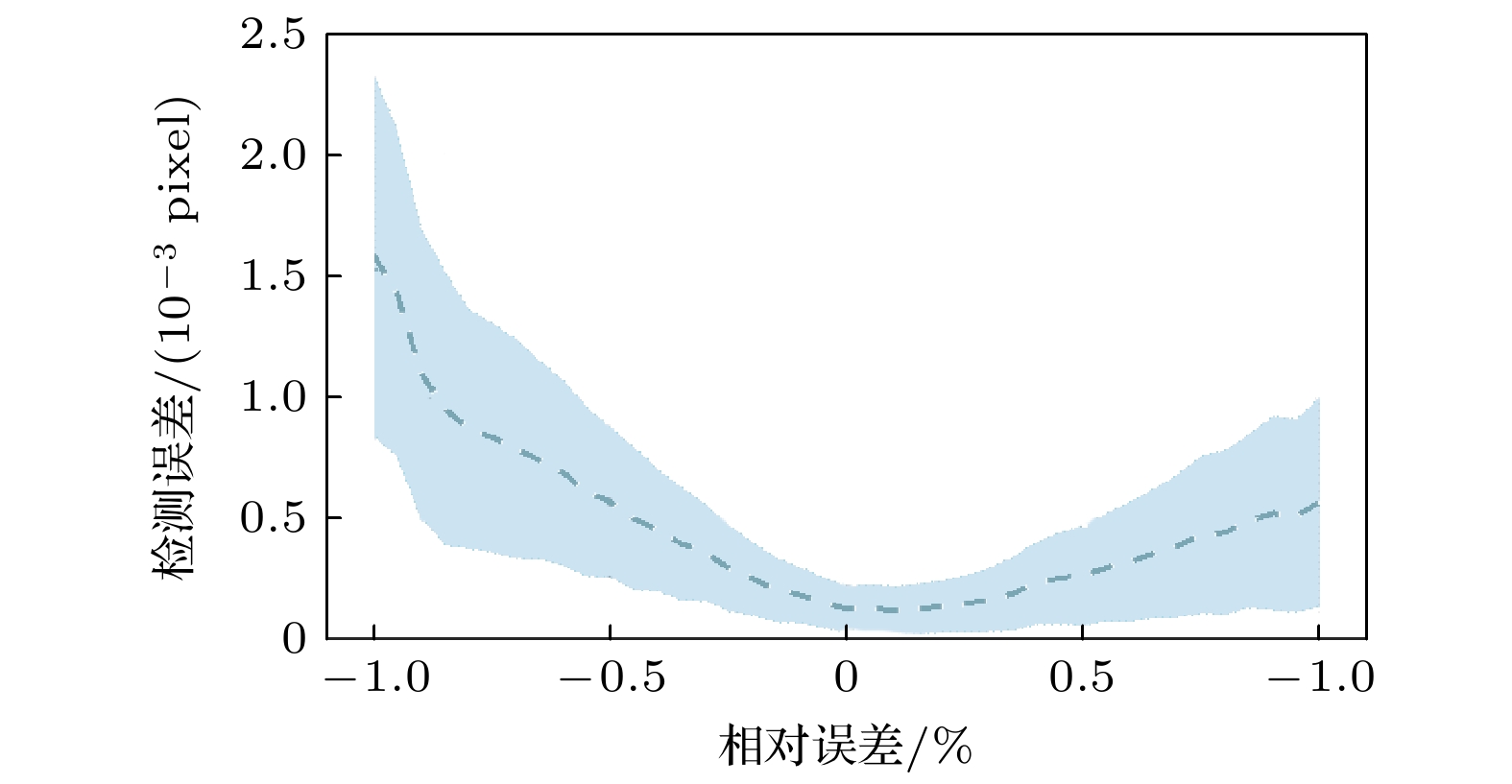
从图8可以看出, 脉冲数目Nnotches (表征刻槽数目)的拟合误差对测量结果影响较大, 尤其是在相对误差达到±0.5%以上时, 检测误差迅速上升, 且呈现出不确定性扩大的趋势. 此外, 误差随 Nnotches的误差增大呈现出不对称特性, 负误差条件下拟合偏差更大, 最高可达1.5/1000 pixel, 对应9.7 nm. 当相对误差控制在0.7%时, 成像误差可控制在1/1000 pixel以内, 对应6.5 nm.
综合各参数的影响, 表明矩形函数宽度Wnotches和脉冲数目Nnotches是影响成像漂移检测精度的关键因素, 这些参数对拟合误差的敏感性较高, 必须在成像拟合中严格控制其误差, 以确保检测结果的可靠性. 相比之下, 参数σ在系统中具有更高的容忍度, 在一定的误差范围内, 其对成像漂移拟合的影响相对较小.
-
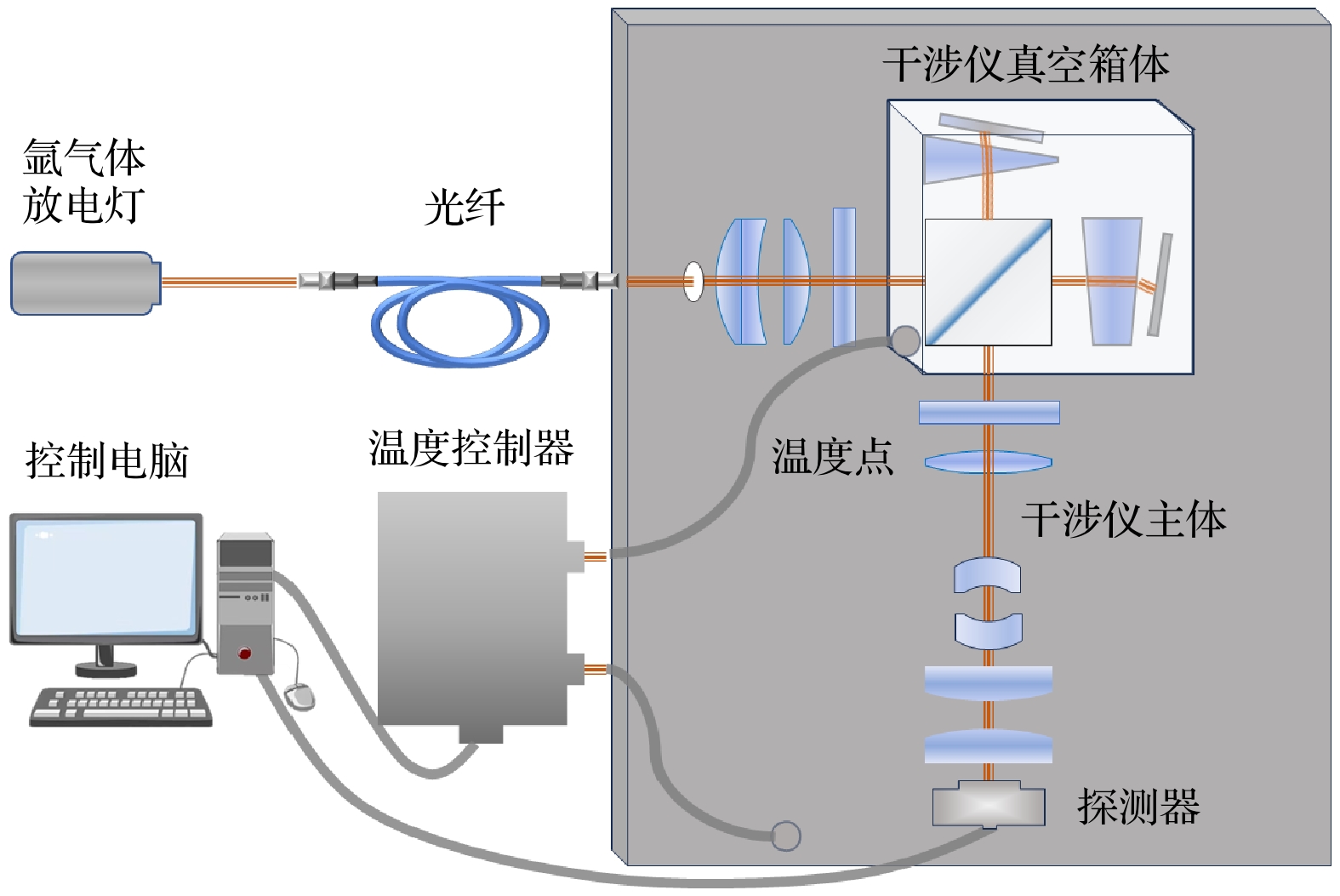
为了验证本文所提成像漂移检测算法的检测精度, 基于近红外多普勒差分干涉仪样机的连续热稳定性测试数据, 开展了像面热漂移监测实验. 实验装置如图9所示, 包括光源模块, 干涉仪模块, 温度控制与读取模块及数据采集模块. 光源为氩气体放电灯, 波长为866.794 nm, 光源由光纤引入前置镜, 经干涉仪调制后成像于探测器像面上. 干涉仪主体置于真空箱体内, 箱体内部配备了加热板, 并由温控仪精确调节温度, 以模拟实际应用环境中温度变化对成像漂移的影响. 实验过程中, 干涉仪外部环境温度数据以及干涉图均由控制电脑实时采集和处理.
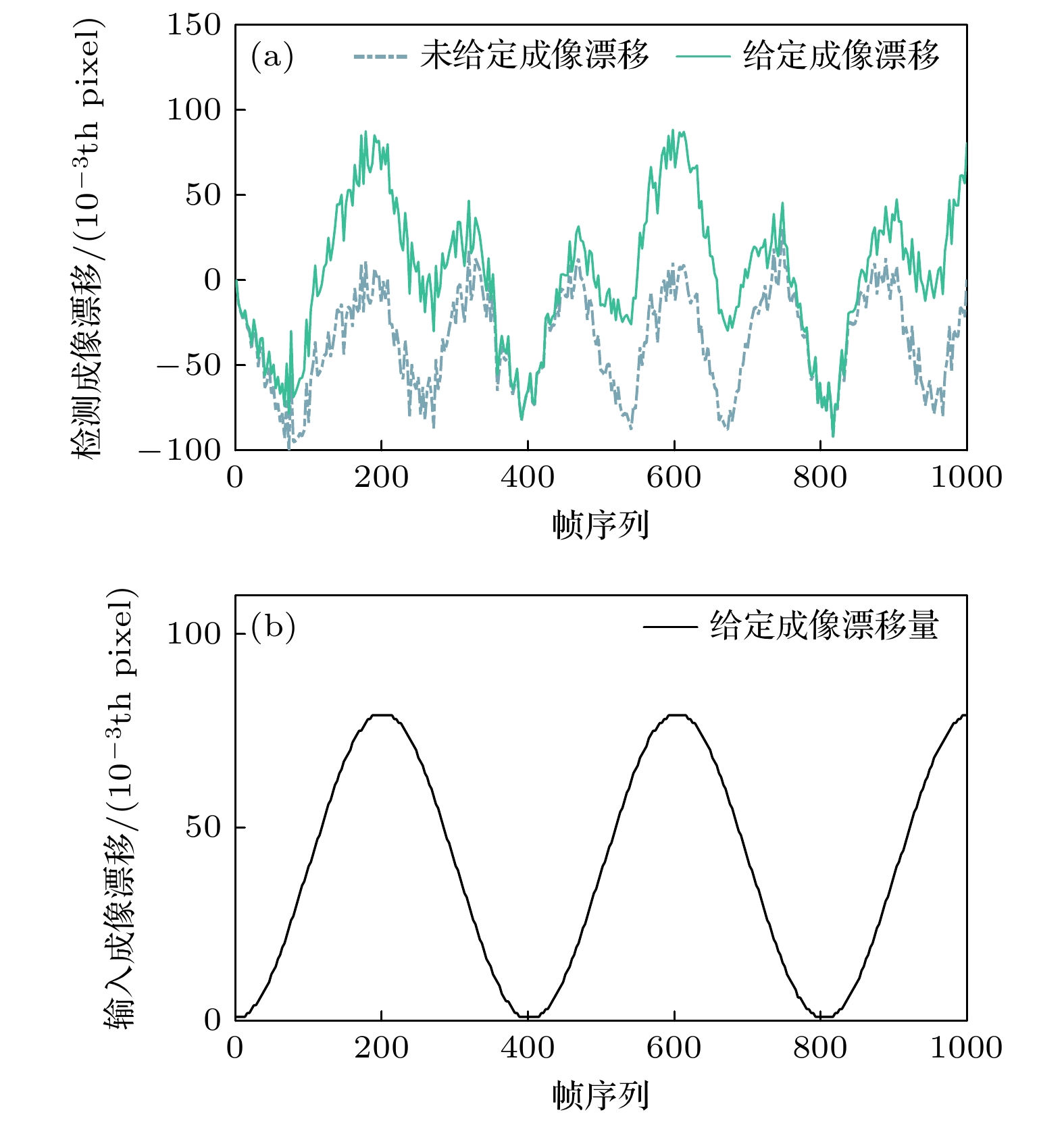
通过调节温控仪改变仪器温度, 采集一系列不同温度下的刻槽图像, 并利用第2节所述方法计算每帧刻槽图像的成像位置, 并计算每帧图像相对于第一帧图像的成像漂移量, 结果如图10(a)中蓝色虚线所示, 可以看到成像漂移量呈现波动状态. 为了验证所提出方法的精度与有效性, 人为给每帧刻槽图像施加固定的成像漂移量, 漂移方向设定为水平方向, 幅度范围为 0—80/1000 pixel, 施加的漂移量随帧序列变化呈现正弦波形, 如图10(b)所示. 基于所提出的成像漂移检测方法, 对人为施加成像漂移量的刻槽图像进行拟合, 成像漂移量如图10(a)中绿色实线所示.
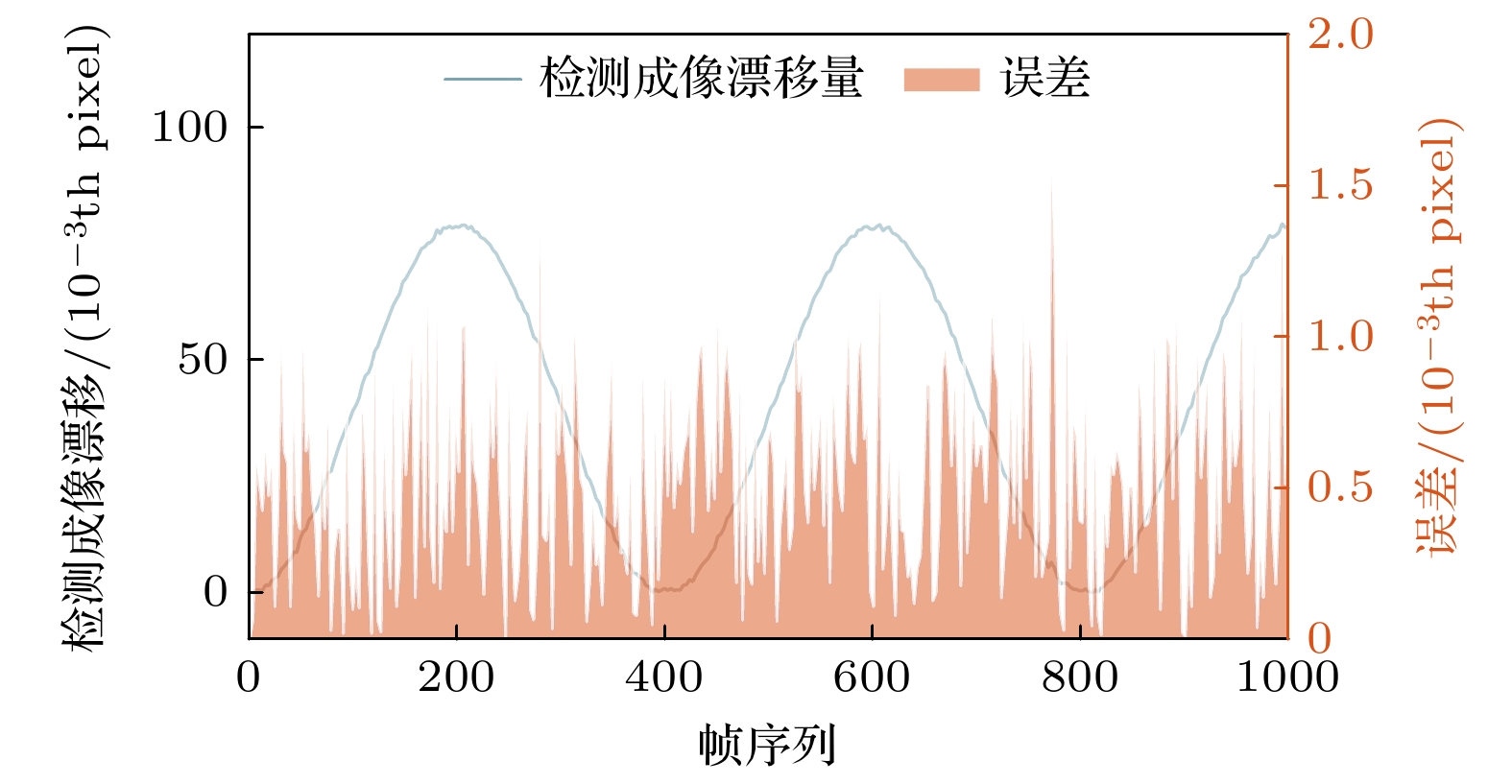
通过进一步计算图10(a)中两组数据的差值, 得到如图11所示的蓝线, 该曲线反映了人为给定成像漂移量的检测值, 计算该曲线与图10(b)中曲线之间的差值, 误差结果如红色区域所示. 分析结果表明, 检测值与给定漂移量(图10(b))在趋势上高度一致, 同时, 检测误差始终保持在9.96 nm(1.53/1000 pixel)以内. 这一结果充分证明, 该方法能够准确地检测出成像漂移量, 并具有极高的精度与稳定性, 误差范围极小, 满足实际应用中对高精度成像漂移检测的严格要求.
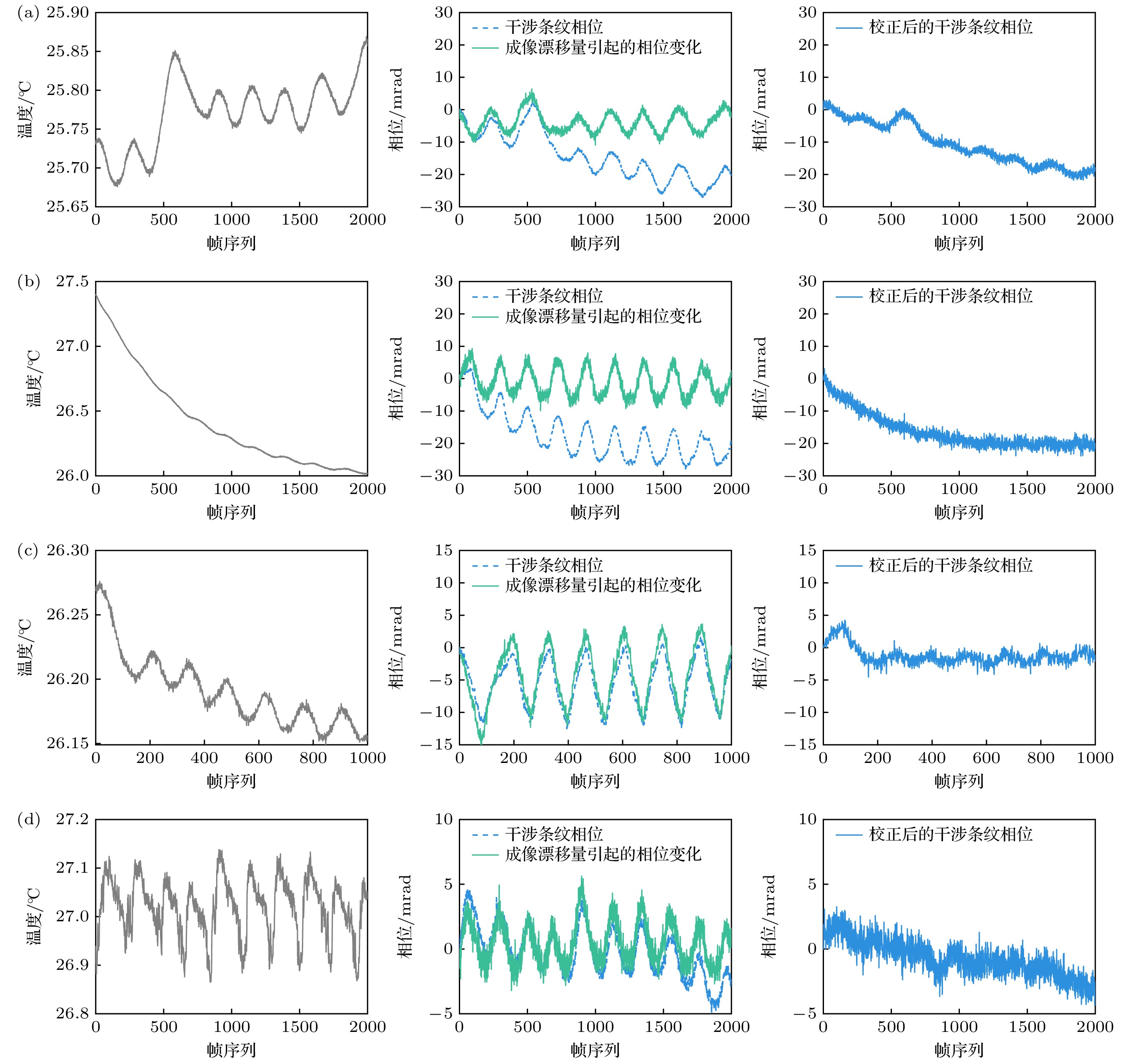
进一步, 通过调控温控仪改变温度曲线, 采集不同温度条件下的干涉图, 并利用第2节所述方法计算每帧图像的成像位置和干涉条纹相位. 4组实验结果如图12所示, 灰色线表示干涉仪温度数据, 蓝色虚线为干涉条纹相位, 其值通过提取多行干涉信号的平均值并进行相位反演获得, 随后计算每帧相位相对于初始帧的变化量. 绿色线表示每帧刻槽图像相对于第一帧的成像漂移量, 通过干涉图每像元的相位变化量进一步转换为成像漂移引起的相位变化量. 蓝色实线则表示经过成像漂移校正后的干涉条纹相位.
由图12可见, 温度、干涉条纹相位与成像漂移量三者存在显著关联性. 温度与干涉条纹相位在整体变化趋势上保持一致, 随着温度升高, 干涉条纹相位呈增加趋势, 温度降低时则相反, 尤其在温度短时剧烈波动时, 条纹相位的波动幅度同步增强. 这表明温度变化通过影响干涉仪的光学路径或器件热膨胀效应, 直接导致了条纹相位的变化. 然而, 在某些时间区段, 当温度表现为单向变化叠加周期性振荡时, 干涉条纹相位的变化却主要表现为局部振荡, 如图12(b)所示. 这种现象表明, 温度的影响机制较为复杂, 可能涉及多种效应的叠加作用, 包括热膨胀、结构变形以及其他环境因素的综合影响, 导致不同因素之间的相互制约, 使相位的响应特征在整体趋势与局部波动上有所差异.
成像漂移量导致的相位变化与干涉条纹相位在局部波动上呈现较高的一致性, 尤其是在温度快速变化区间, 二者的波动幅度同步增加. 然而, 从长期观测数据来看, 成像漂移量与干涉条纹相位的变化并非完全同步, 如图12(a), (b)中所示, 干涉图相位除了局部振荡之外, 整体趋势还呈现出大幅度的下降, 这种不一致性源于二者虽然均受温度变化驱动, 但由于物理性质及响应机制的不同, 导致其整体趋势存在一定差异.
经过成像漂移校正后, 干涉条纹相位的局部波动得到有效抑制, 呈现出更加平滑的变化趋势. 这表明温度引起的成像漂移主要表现为局部振荡特性. 为定量分析干涉条纹相位在校正前后局部波动的改善程度, 对相位进行去基线处理, 并采用均方根误差(root mean square error, RMSE)作为衡量指标以量化波动幅度. 校正前, 四组数据的干涉条纹相位RMSE分别为3.44, 3.74, 3.67 mrad和1.37 mrad; 校正后, RMSE显著降低至1.54, 0.68, 0.85 mrad和0.67 mrad. 上述结果表明, 本文提出的方法能够有效消除温度变化引起的成像漂移, 显著提高干涉条纹相位的稳定性和测量精度.
-
本文提出了一种基于全局拟合的成像漂移监测方法, 以解决多普勒差分干涉仪在风速测量中因环境温度波动引起的像面漂移问题. 通过优化光栅刻槽设计, 并对探测器像面上的刻槽图案进行建模与全局拟合, 成功实现了干涉仪成像漂移量的高精度检测与校正. 优化后的光栅刻槽设计简化了模型, 显著提高了检测精度和计算效率. 首先对刻槽信号信噪比对检测精度进行仿真分析, 结果显示当刻槽信噪比高于11时, 成像漂移量为0—100/1000 pixel的信号的检测不确定度均优于6.5 nm. 对模型拟合参数敏感性分析表明, 刻槽数目和宽度拟合误差对检测精度影响较大, Nnotches和Wnotches的相对变化量小于40%和0.7%的情况下, 检测误差保持在6.5 nm以内, 而刻槽图像边缘平滑度拟合误差对结果影响较小, 这验证了所提出方法的高精度和参数鲁棒性. 在近红外多普勒差分干涉仪样机的连续热稳定性测试实验中, 通过对实验数据施加人为设定的像面漂移量进行验证, 检测结果与输入漂移量高度一致, 拟合误差维持在9.96 nm内. 此外, 通过调节干涉仪温度, 获得4组不同温度曲线下的干涉图, 结果显示, 干涉图相位、成像漂移量和环境温度的变化趋势高度一致, 且经成像漂移校正后的干涉图相位局部周期振荡显著减弱. 实验验证该方法能够有效校正由温度变化引起的图像偏移, 提升干涉图像的相位稳定性, 并在多个实际测试场景中展现出良好的适应性, 显示其在高精度成像漂移检测领域具有重要的应用价值.
基于全局拟合的多普勒差分干涉仪成像漂移检测方法
A method of monitoring image shift based on global fitting Doppler heterodyne interferometer
-
摘要: 大气风场在全球气候研究和空间探测中具有重要作用, 多普勒差分干涉仪作为新型被动测风干涉仪, 其通过测量大气气辉谱线的多普勒频移引起的相位变化量来反演大气风速, 但环境温度波动会导致像面相对于干涉仪发生漂移, 从而影响风场测量结果. 本文提出一种在光栅上刻蚀周期性刻槽, 并对其成像图案进行建模与全局拟合以实现高精度成像漂移检测的方法. 对刻槽图像的信噪比及模型参数拟合误差对检测结果的影响进行仿真分析, 结果表明, 图像信噪比、刻槽数量拟合精度与刻槽宽度拟合精度是影响检测精度的关键因素, 而刻槽图像边缘的平滑度的拟合精度对检测结果影响较小. 在近红外多普勒差分干涉仪的热稳定实验中, 通过对实验所测数据人为施加漂移量, 并进行成像漂移监测, 结果表明该方法能够实现9.96 nm的检测精度. 此外, 经成像漂移校正后的干涉图相位的局部振荡显著减弱, 表明该方法能有效检测与校正成像漂移, 显著提升干涉图像相位稳定性, 为高精度风速测量提供了可靠保障.Abstract: Accurate atmospheric wind field measurements are critical for understanding global climate dynamics and facilitating space exploration. Doppler asymmetric spatial heterodyne interferometer (DASH) is used to measure atmospheric wind speed through detecting the phase changes in interferograms induced by Doppler shifts of airglow emission lines. However, environmental temperature fluctuations and mechanical vibrations often cause imaging plane to shift, thereby introducing phase deviations, and degrading the measurement accuracy. In this study, a novel method of monitoring global fitting-based imaging shift is proposed. By etching periodic notches on the diffraction grating surface, the method models and fits the notch patterns formed on the detector plane to achieve precise imaging shift detection and correction. The optimization of notch signal modeling significantly reduces the number of fitting parameters, thus improving computational efficiency and detection precision. Through extensive simulations, the influences of signal-to-noise ratio (SNR) and model parameter variation on detection accuracy are analyzed. The results indicate that when the SNR exceeds 11, the detection uncertainty is still below 6.5 nm. Sensitivity analysis reveals that the detection error stays within acceptable limits when the variations of notch number and notch width are controlled within 40% and 0.7%, respectively, while the influence of edge smoothness parameter of notch pattern is negligible. To validate the performance of the method, the thermal stability is tested by using a near-infrared DASH prototype. The experimental results demonstrate a strong correlation between interferogram phase shifts, imaging plane shifts, and environmental temperature variations. After applying the proposed correction method, local phase fluctuations in the interferogram are significantly reduced, thus the phase stability is improved. Further, artificially applied imaging shifts are accurately detected with errors consistently below 9.96 nm, thereby confirming the reliability and precision of this method. All in all, the proposed method effectively detects and corrects the imaging plane shifts caused by temperature variations, enhancing interferogram phase stability and ensuring high-precision wind speed measurements. This method provides a robust and computationally efficient solution for reducing imaging shifts in DASH systems, and has great potential applications in atmospheric wind field measurement and space-based observation.
-
-
图 1 DASH原理图, 右下角为干涉图(顶部为刻槽图像)
Figure 1. Schematic of a DASH interferometer. The interferogram is located at the lower right (The top area is notch pattern).
图 2 (a)梳状函数; (b)梳状函数卷积矩形函数后的方波函数; (c)方波函数卷积高斯核后的刻槽形状
Figure 2. (a) The comb function; (b) the square wave function after the comb function convolved with the rectangle function; (c) the notch signal after the square wave function convolved with Gaussian kernel.
图 5 不同信噪比、不同成像漂移量下的成像漂移检测不确定度
Figure 5. Uncertainty of imaging shift measurement under different SNR and different imaging shift.
图 6 SNR = 100时, 高斯函数标准差σ的拟合误差对测量精度的影响
Figure 6. Influence of fitting error of standard deviation σ of Gaussian function on measurement accuracy when SNR = 100
图 7 SNR = 100下, 矩形函数宽度Wnotches的拟合误差对测量精度的影响
Figure 7. Influence of fitting error of rectangle function width Wnotches on measurement accuracy when SNR = 100.
图 8 SNR = 100下, 脉冲数目Nnotches的拟合误差对测量精度的影响
Figure 8. Influence of fitting of pulse number Nnotches on measurement accuracy when SNR = 100.
图 10 (a)实验中所测刻槽图像的成像漂移量(蓝色虚线), 对所测图像人为给定成像漂移量后对应的检测结果(绿色实线); (b)对实验中所测每一帧刻槽图像叠加固定的成像漂移量
Figure 10. (a) The imaging shift of the notch image measured in the experiment (blue dashed line), and the corresponding detection result of the notch image measured in the experiment after artificially superimposing the imaging shift amount (green solid line); (b) the fixed imaging shift is superimposed on each frame of notch image measured in the experiment.
图 11 蓝线为图10(a)中两信号的差值, 即对人为给定漂移量的检测值, 红线为检测误差, 即检测成像漂移量与人为给定成像漂移量间的差值
Figure 11. The blue line is the difference between the two signals in Fig.10 (a), that is, the measurement of the artificially given amount of shift. The red line is the measurement error, that is, the difference between the measured image shift and the input image shift.
图 12 近红外多普勒差分干涉仪样机的连续热稳定性测试数据, 灰色线为温度数据, 蓝色虚线为干涉条纹相位, 绿色线为成像漂移引起的相位变化, 蓝色实线为成像漂移校正后的干涉条纹相位
Figure 12. Thermal stability test data of the near infrared DASH prototype, the gray line is temperature data, the blue dashed line is fringe phase, the green line is phase change caused by imaging shift, and the blue solid line is fringe phase after imaging shift correction.
表 1 仿真参数
Table 1. Simulation parameters.
参数 数值 系统参数 波长/nm 867.16 光程差/mm 49.87 光栅参数 Littrow 波数/nm 868.24 光栅阶数 1 光栅闪耀角/(°) 10 光栅衍射效率 70% 探测器参数 像元数 2048×2048 量子效率 0.75 像元尺寸/μm 6.5 刻槽信号参数 刻槽数量 111.81 刻槽宽度/μm 59.52 
下载: 导出CSV
-
[1] Shepherd G G 2015 Acta Astronaut. 115 206 doi: 10.1016/j.actaastro.2015.05.015 [2] Dhadly M, Sassi F, Emmert J, Drob D, Conde M, Wu Q, Makela J, Budzien S Nicholas A 2023 Astron. Space Sci. 9 1050586 doi: 10.3389/fspas.2022.1050586 [3] 唐远河, 崔进, 郜海阳, 屈欧阳, 段晓东, 李存霞, 刘丽娜 2017 物理学报 66 130601 doi: 10.7498/aps.66.130601 Tang Y H, Cui J, Gao H Y, Qu O Y, Duan X D, Li C X, Liu L N 2017 Acta Phys. Sin. 66 130601 doi: 10.7498/aps.66.130601 [4] 冯玉涛, 傅頔, 赵增亮, 宗位国, 余涛, 盛峥, 朱亚军 2023 光学学报 43 0601011 Feng Y T, Fu D, Zhao Z L, Zong W G, Yu T, Sheng Z, Zhu Y J 2023 Acta Opt. Sin. 43 0601011 [5] Zhang S P, Thayer J P, Roble R G 2004 J. Atmos Sol-terr. Phys. 66 105 doi: 10.1016/j.jastp.2003.09.011 [6] Englert C R, Harlander J M, Babcock D D, Stevens M H, Siskind D E 2006 Proc. SPIE 6303 63030T doi: 10.1117/12.681704 [7] Englert C R, Babcock D D, Harlander J M 2006 Appl. Opt. 46 7297 [8] Harlander J M, Englert C R, Emmert J T, Babcock D D, Roesler F 2010 Opt. Express 18 26430 doi: 10.1364/OE.18.026430 [9] 肖旸, 冯玉涛, 文镇清 2022 光子学报 51 16 Xiao Y, Feng Y T, Wen Z Q 2022 Acta Photon. Sin. 51 16 [10] Harding B J, Chau J L, He M, Englert C R, Harlander J M, Marr K D, Makela J J, Clahsen M, Li G, Ratnam M V, Rao S V B, Wu Y J J, England S L, Immel T J 2021 J. Geophys. Res. Space Phys. 126 e2020JA028947 doi: 10.1029/2020JA028947 [11] Englert C R, Harlander J M, Brown C M, Makela J J, Marr K D, Immel T J In Fourier Transform Spectroscopy Lake Arrowhead, California, United States, March 1–4, 2015 pFM4A-1 [12] Stevens M H, Englert C R, Harlander J M, England S L, Marr K D, Brown C M, Immel T J 2018 Space Sci. Rev. 214 4 doi: 10.1007/s11214-017-0434-9 [13] Harlander J M, Englert C R, Brown C M, Marr K D, Miller I J, Zastera V, Bach B W, Mende S B 2017 Space Sci. Rev. 212 601 doi: 10.1007/s11214-017-0374-4 [14] Englert C R, Brown C M, Bach B, Bach E, Bach K, Harlander J M, Seely J F, Marr K D, Miller I 2017 Appl. Opt. 56 2090 doi: 10.1364/AO.56.002090 [15] Marr K D, Thayer A S, Englert C R, Harlander J M 2020 Opt. Eng. 59 013102 [16] Englert C R, Harlander J M, Marr K D, Harding B J, Makela J J, Fae T, Brown C M, Venkat Ratnam M, Vijaya Bhaskara Rao S , Immel T J 2023 Space Sci. Rev. 219 27 [17] 张亚飞, 冯玉涛, 傅頔, 畅晨光, 李娟, 白清兰, 胡炳樑 2022 物理学报 71 084201 doi: 10.7498/aps.71.20212086 Zhang Y F, Feng Y T, Fu D, Chang C G, Li J, Bai Q L, Hu B L 2022 Acta Phys. Sin. 71 084201 doi: 10.7498/aps.71.20212086 [18] Zhang Y F, Feng Y T, Fu D, Wang P C, Sun J, Bai Q L 2020 Chin. Phys. B 29 104204 doi: 10.1088/1674-1056/ab9de8 [19] 傅頔, 畅晨光, 孙剑, 李娟, 武魁军, 冯玉涛, 刘学斌 2022 光学学报 42 18 Fu D, Chang C G, Sun J, Li J, Wu K J, Feng Y T, Liu X B 2022 Acta Opt. Sin. 42 18 [20] Wei D K, Zhu Y J, Liu J L, Gong Q C, Kaufmann M, Olschewski F, Knieling P, Xu J Y, Koppmann R, Riese M 2020 Opt Express 28 19887 doi: 10.1364/OE.394101 -
计量
- 文章访问数: 77
- HTML全文浏览数: 77
- PDF下载数: 0
- 施引文献: 0