在标准物理模型中, 中微子是一种质量极小的费米子, 与其他物质粒子之间的相互作用只有弱亚原子力和引力, 这种弱相互作用的特性也导致它们能够穿过大量普通物质. 中微子振荡的现象早在半个多世纪前就被提出^[1,2]. 迄今为止, 一些实验利用太阳中微子^[3,4]、大气中微子^[5]、反应堆中微子^[6,7]以及加速器产生的中微子^[8,9], 已经获取了关于不同中微子味之间相互转变的确凿实验证据. 中微子和反中微子同时产生, 并能以三种不同的味态被探测到, 即电子(e)中微子、μ子中微子和τ子中微子. 中微子味态是质量本征态的线性组合. 中微子振荡描述了中微子在传播过程中能够从一种给定的味态类型转换成另一种味态类型, 即三种味态在传播过程中可以相互转化. 中微子振荡也意味着中微子具有确定的质量. 近年来, 关于中微子振荡的参数准确测量与分析吸引了大量理论和实验方面的研究^[10-12]. 为了验证中微子振荡的量子性, 研究者们考虑了Leggett-Garg不等式^[13,14], 该不等式被称为Bell不等式的“时间模拟”, 能够测试在不同时间测量的单个系统的关联函数. 研究表明, 实验观察到的中微子振荡的振荡概率可以违反Leggett-Garg不等式施加的经典极限. 由于中微子的弱相互作用, 在中微子振荡过程中产生的退相干效应相较于其他在量子信息处理过程中被广泛应用的粒子系统中的退相干效应要更弱一些. 在量子信息科学与粒子物理学深度融合的前沿研究领域, 探寻中微子于未来量子信息处理进程中所具备的潜在应用价值, 一个关键的部分就是利用量子资源理论对中微子振荡的量子特性进行量化分析.

量子资源理论为研究量子物理学中的不同现象提供了一个通用性极强且功能强大的框架^[15]. 一个统一且定义严谨的量子资源理论框架能够助力我们研究诸多相关量子问题, 例如在施加约束条件下量子态的表征量化以及操控^[16,17], 还有不同量子关联度量之间的权衡关系^[18-21]. 量子纠缠、量子相干和量子非局域性等是量子资源理论中最基本的概念, 可以用量子资源理论的工具进行严格的度量和表征^[22-25]. 它们在量子信息处理中有许多潜在的应用, 包括量子隐形传态^[26,27]、量子密码学^[28,29]、量子计算^[30,31]、量子密钥分发^[32,33]等. 此外, 量子资源理论中的权衡关系对于多粒子系统中量子关联的量化和分类具有重要意义. 量子信息理论中常见的权衡关系有量子关联的单配性关系^[34,35]和完全互补性关系^[36,37]. 单配性关系主要是基于各种量子关联度量, 探究它们在多体系统中的分配和信息转移关系. 完全互补关系可以将量子系统中的各种量子关联联系起来, 为研究量子关联之间的相互作用(如纠缠和量子相干)提供有效途径. 熵不确定性关系对于探究量子系统的不确定度具有重要意义, 能展现中微子振荡在量子通信中的潜在应用价值. 这些量子关联度量和权衡关系对于探究中微子系统的量子资源特性具有重要的研究意义, 第3节和第4节会展示出它们在三味中微子系统中的具体研究.

量子信息理论在中微子振荡中的研究主要基于量子资源度量和资源分配特性, 例如纠缠和量子相干, 它们通常可以用味态跃迁概率来表示. 在关于中微子振荡的量子特性的诸多研究中, 众多对中微子振荡的量子性验证工作主要聚焦于Leggett-Garg不等式^[14,38,39]. 然而, 用Leggett-Garg不等式检验中微子振荡的量子性存在一些局限性, 主要在于它只能作为判断量子相干性的定性准则. 因此, 违反Leggett-Garg不等式不是量化相干性度量的良好指标. 随后, Song等^[40]提出利用量子资源理论中的$ l_1 $范数相干度量对中微子传播中的量子相干性进行定量分析, 精准地量化了中微子振荡中的相干性. 此后, 利用$ l_1 $范数相干对中微子振荡的相干性研究吸引了众多研究者们的关注^[41-45]. 纠缠作为一种最基本的量子资源, 存在多种量化方法. 近年来, 研究者们用各式各样的纠缠度量方式来量化中微子振荡中的量子性^[46-52]. 其中, 对于三味中微子振荡的纠缠量化, Li等^[51]利用真正的多体纠缠度量, 包括广义的几何测量^[53,54]、three-π纠缠^[55]、多体共生纠缠^[56]、并发填充(concurrence fill)^[57]等, 通过对比分析, 得到了量化三味中微子振荡系统纠缠最优的度量方式. 此外, Blasone等^[58]通过单配性关系构建的剩余纠缠量化了三味中微子振荡的纠缠. 其他类型的量子关联对中微子振荡量子性的研究也受到了众多科研工作者的关注, 包括量子导引^[59]、量子失谐^[49,50]、Bell非局域性^[60,61]、 量子相干的非局域性优势^[62,63]、熵不确定性关系^[64,65]等. 对中微子振荡的量子特性研究, 除了上述提到的量子资源, 利用量子资源理论的权衡关系对中微子振荡在量子信息理论中的研究也具有重要意义. Li等^[60]和Wang等^[66]基于各种量子关联的单配性关系研究了三味中微子振荡中的量子资源分配和转化关系. Blasonet等^[58]和Bittencourt等^[67]利用完全互补性关系研究了量子关联(例如纠缠和相干)在中微子振荡中的相互作用. 这些权衡关系在三味中微子振荡中的研究都会在第4节展示.

近年来, 对中微子振荡的量子特性研究除了以上提到的量子资源及其权衡关系, 还有其他方面的量子理论在该领域的贡献和探索. 限于篇幅, 本文仅概述三味中微子振荡中的量子资源特性研究, 主要基于常见的量子资源度量以及量子资源间的权衡关系和互补性关系.

中微子振荡描述的是在中微子传播过程中, 三种不同的中微子味态之间的振荡概率相互转换的现象. 在这种情况下, 可以将中微子振荡的每一个味态作为一个量子比特系统来研究, 此时三味中微子振荡系统就可以看作是一个三量子比特的物理系统. 因此, 可以在量子资源理论框架下研究中微子振荡的多体量子资源特性. 对于中微子振荡的量子特性研究主要基于平面波近似和波包方法下的中微子振荡模型进行研究, 本节主要介绍平面波近似和波包方法下的三味中微子振荡模型.

在标准的三味中微子振荡模型中, 三种类型的中微子味态$ \left|v_{{\mathrm{e}}}\right\rangle $, $ \left|v_{\text{μ}}\right\rangle $, $ \left|v_{\text{τ}}\right\rangle $是其质量本征态$ \left|\nu_{1}\right\rangle $, $ \left|\nu_{2}\right\rangle $, $ \left|\nu_{3}\right\rangle $的线性叠加, 可以表示为^[68,69]

式中$ {k} = 1, 2, 3, \; \alpha = {\mathrm{e}}, {\text{μ}}, {\text{τ}} $. $ U_{\alpha k}^{*} $是轻子混合矩阵U中元素的复共轭形式, 该混合矩阵U被叫作Pontecorvo-Maki-Nakagawa-Sakata矩阵, 它可以用三个混合角和一个CP违反相位表示^[70]:

式中$ c_{i j} \equiv \cos \theta_{i j}, \; s_{i j} \equiv \sin \theta_{i j} $. 中微子质量本征态$ \left|v_{k}\right\rangle $是能量为$ E_k $的哈密顿量的本征态, 其随时间演化的质量本征态$ \left|v_{k}(t)\right\rangle $可以表示为

式中$ \left|v_{k}(0)\right\rangle $表示$ t = 0 $时刻的质量本征态. 该式呈现了中微子质量本征态随时间以平面波的形式演化. 利用混合矩阵U, 可以将中微子味本征态的时间演化与中微子质量本征态的时间演化联系起来, 表达式为

通过用味本征态来表示质量本征态, 即$ \left|v_{k}\right\rangle = \displaystyle\sum\nolimits_{\beta} U_{\beta k}\left|v_{\beta}\right\rangle $, (4)式可以表示成

在三味中微子振荡情形下, (5)式可以展开成下列形式:

式中$ a_{\alpha \beta}(t) = \displaystyle\sum\nolimits_{k} U_{\alpha k}^{*} {\mathrm{e}}^{-{\mathrm{i}} E_{k} t / \hbar} U_{\beta k} $是味α到味β的转化振幅, 构成了所谓的味演化矩阵$ {\boldsymbol{U}}_{{\mathrm{f}}}(t) $的元素. 在矩阵运算中, $ \boldsymbol{\nu}_{\alpha}(t) \equiv\left(\nu_{{\mathrm{e}}}(t) \nu_{{\text{μ}}}(t) \nu_{\text{τ}}(t)\right) $由味演化矩阵$ {\boldsymbol{U}}_{{\mathrm{f}}}(t) $与t = 0时刻的味态联系起来, 即$ \boldsymbol{\nu}_{\alpha}(t) = {\boldsymbol{U}}_{{\mathrm{f}}}(t) \boldsymbol{\nu}_{\alpha}(0) $.

已知初始为α味中微子, 在振荡过程中探测到β味中微子的概率为

化简后可得到下列形式^[71]:

式中$ \Delta m_{k l}^{2} = m_{k}^{2}-m_{l}^{2} $, E是中微子的能量, $ {L} \approx {ct} $(c为自由空间中的光速)为中微子源与探测器之间的距离. 值得注意的是生存概率$ P_{\alpha \beta } = \left|a_{\alpha \alpha}(t)\right|^{2} $和振荡概率$ P_{\alpha \beta } = \left|a_{\alpha \beta}(t)\right|^{2} $满足$ P_{\alpha \alpha }+P_{\alpha \beta } = 1 $. 为了方便计算, (8)式中的$ \sin ^{2}\left(\Delta m_{i j}^{2} \dfrac{L c^{3}}{4 \hbar E}\right) $可以写成

式中, $\Delta m_{i j} $表示质量平方差, 单位为eV; L表示中微子传播距离, 单位为km; E表示中微子能量, 单位为GeV. 这里中微子味态可以被映射为

因此中微子味态的跃迁概率变化可以视为三量子比特的状态随着时间发生演化, 即

本节主要回顾波包方法^[72,73]下的中微子振荡理论. 原则上, 中微子系统的状态是由纯态描述的, 例如(4)式中的状态. 通过使用波包方法, 描述中微子态$ \rho_{\alpha}(x, t) $演化的密度矩阵依赖于时间和位置, 这种矩阵通过对时间积分, 可以得到^[52]

式中, $ f_{j k}(x) = \exp \bigg[-{\mathrm{i}} \dfrac{\Delta m_{j k}^{2} x}{2 E}-\left(\dfrac{\Delta m_{j k}^{2} x}{4 \sqrt{2} E^{2} \sigma_{x}}\right)^{2}\bigg] $. 通过建立标识关系, 可以方便地用中微子振荡的味态特征态来表示$ \rho_{\alpha}(x) $, 即$ \left|v_{\alpha}\right\rangle = \left|\delta_{\alpha {\mathrm{e}}}\right\rangle_{{\mathrm{e}}}\left|\delta_{\alpha {\text{μ}}}\right\rangle_{\text{μ}}\left|\delta_{\alpha {\text{τ}} }\right\rangle_{\text{τ}} $. 结合$ \left|v_{i}\right\rangle = \displaystyle\sum\nolimits_{\alpha} U_{\alpha i}\left|v_{\alpha}\right\rangle $, 可以得到

式中, $ F_{\beta \gamma}^{\alpha} = \displaystyle\sum\nolimits_{k j} U_{\alpha j}^{*} U_{\alpha k} f_{j k}(x) U_{\beta j} U_{\gamma k}^{*} $($ k, j = 1, 2, 3; \beta, \gamma = {\mathrm{e}}, {\text{μ}}, {\text{τ}} $). 密度矩阵(15)式是一个混态, 可以写成:

由${\boldsymbol{ \rho}}_{\alpha}(x) $描述的中微子在位置x转变为η味中微子的概率为

本节介绍量子信息理论在三味中微子振荡中的具体研究, 主要包括基本的量子资源度量, 例如纠缠、相干和非局域性等.

量子纠缠作为最基本的量子资源, 对于量化中微子振荡的量子性具有重要意义. 对于三味中微子振荡, 现有一些研究利用不同的纠缠度量来量化中微子在振荡过程中的纠缠演化. Svetlichny^[74]利用几种真正的多体纠缠度量对三味中微子系统的纠缠进行了量化, 其中主要包括广义的几何测量(GGM)^[53,54]、three-π纠缠^[55]、多体共生纠缠(GMC)^[56]、并发填充(concurrence fill)^[57]等. 为了介绍这四种纠缠度量在中微子系统中的具体研究, 需要简述这些纠缠度量的数学表达式. 首先广义几何度量被定义为给定状态与不是真正多方纠缠的所有状态的集合的优化距离, 它可以度量任意粒子数的纯态的纠缠, 对任意一个N体纯态$ \left|\psi_{N}\right\rangle $, 其计算方法如下:

式中$ \lambda_{I: L} $是$ \left|\psi_{N}\right\rangle $两体划分I∶L中的最大施密特系数.

three-π纠缠是基于负熵^[75]的单配性关系构建的剩余纠缠, 对于一个三体系统, 其数学表达式为

其中$ \pi_{A} = N_{A(B C)}^{2}-N_{A B}^{2}-N_{A C}^{2} $, $ \pi_{B} = N_{B(A C)}^{2}- N_{B A}^{2}-N_{B C}^{2} $, $ \pi_{C} = N_{C(A B)}^{2}-N_{C A}^{2}-N_{C B}^{2} $是剩余纠缠, $ \ N_{A(B C)} $是三体系统在两体划分A和BC下的负熵, $ N_{A B} $和$ N_{A C} $分别表示子系统AB和子系统AC的负熵.

真正的多体共生纠缠是一种基于众所周知的并发纠缠的量化多体纠缠的计算方法. 对于三比特纯态$ |\psi\rangle_{A B C} $, 多体共生纠缠可以表示为^[56]

2021年, Xie和Eberly^[57]基于海伦公式, 引入了一种三粒子纠缠三角测度的concurrence fill方法. 与其他三体纠缠方法相比, concurrence fill有两个优点: 1) 包含更多的信息; 2)它总是平滑的. 而其他的纠缠度量包含一个取最小值的过程, 这将导致出现具有非解析特征的峰值. Xie和Eberly^[57]提出了一个concurrence三角形的概念, 其中三角形三条边的长度是这个量子系统的三个二部共生纠缠的平方. 然后将concurrence fill定义为并发三角形面积的平方根. 基于此, 给出了concurrence fill的表达式:

其中$ C_{A(B C)}^{2},~ C_{B(A C)}^{2} ,~ C_{C(A B)}^{2} $分别为$ 2[1-\text{Tr}({\boldsymbol{\rho}}_{A}^{2})] $, $ 2[1-\text{Tr}({\boldsymbol{\rho}}_{B}^{2})] $, $ 2[1-\text{Tr}({\boldsymbol{\rho}}_{C}^{2})] $. Q是半周长, 系数$ 16 / 3 $确保$ 0 \leqslant F_{A B C} \leqslant 1 $.

接着就可以用(21)式, 分别求出它们在三味中微子振荡中的纠缠. 当考虑初始$ t = 0 $时刻为电子中微子时, 其三味中微子振荡演化状态为

对于$ \left|\psi_{{\mathrm{e}}}(t)\right\rangle $, 广义的几何测量(GGM)、three-π纠缠、多体共生纠缠(GMC)、concurrence fill在三味中微子振荡中的纠缠表达式分别为

其中,

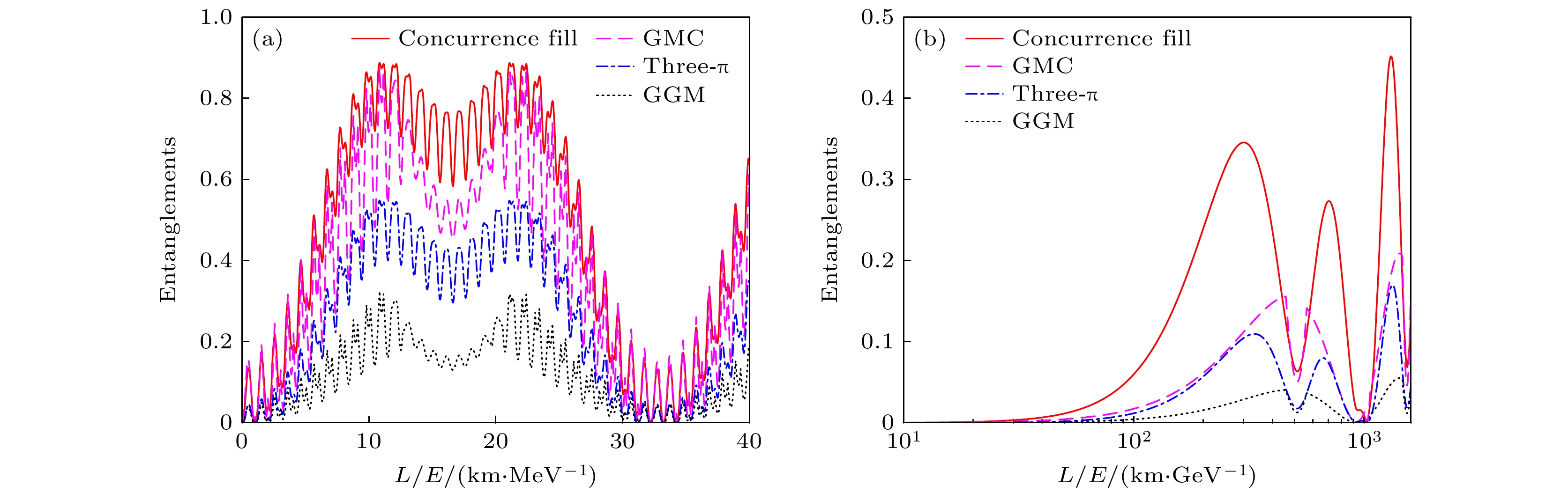
同样也可以求出μ子中微子振荡中的纠缠表达式. 通过对比分析, 可以发现这几种纠缠度量方式在三味中微子振荡中的具体演化方式, 就可以得到量化三味中微子振荡中纠缠的最佳方法. 如图1所示, 四个纠缠度量演化趋势相同, 均为先升后降. 然而, 它们在中微子传播过程中所包含的信息量不同. 对于初始电子中微子振荡, concurrence fill可达到最大值0.89, 而GGM, three-π和GMC三种纠缠度量达到的纠缠最大值分别为0.32, 0.55和0.88. 对于三味中微子振荡的纠缠度量, 与其他三种纠缠度量相比, concurrence fill是一种更自然的度量方式, 原因有两个方面: 1) concurrence fill随比率L/E的变化更平滑, 因为它考虑了所有的两部分纠缠. GGM和GMC具有非解析尖端, 这是由于表达式中的非解析最小参数, 它缺少对整体的纠缠分布的考虑. 2)在电子和μ子中微子传播过程中, concurrence fill包含了更多的量子资源. concurrence fill总是大于或等于其他三个纠缠度量方法. 所有这些特性都使concurrence fill在量子资源理论中, 对于三味中微子振荡中的纠缠量化, 是一种优秀的纠缠度量方式.

除了上述几种真正的多体纠缠度量方式, 还存在其他的纠缠度量可用于对三味中微子纠缠的量化. Li等^[65]利用三体形成纠缠^[76]、三体共生纠缠^[77]和三体并发负熵^[76]从理论和实验两个方面探究了三味中微子振荡中的纠缠特性, 揭示了它们在三味中微子振荡中的层级关系. 其中, 实验方面主要基于对大亚湾中微子和MINOS中微子合作组公布的中微子振荡实验数据进行分析. 研究结果表明, 对于电子中微子振荡, 三体共生纠缠是比三体形成纠缠和三体负熵更合适的纠缠度量, 它能捕获更多的量子资源, 而对于μ子中微子振荡, 三体共生纠缠和三体负熵都比三体形成纠缠更适合量化中微子振荡系统中的纠缠. 此外, Li等^[65]基于冯·诺依曼熵的单配关系构建的剩余纠缠, 通过对其三个剩余纠缠求平均构建多体纠缠, 以确保所构建的纠缠度量在味排序改变下保持不变. 通过该方式构建的多体纠缠熵也可以量化三味中微子振荡的纠缠.

三味中微子振荡的相干性可以用定性和定量两种方法来研究. Leggett-Garg不等式可以作为一种定性标准, $ l_1 $范数可以作为定量度量. 本节从这两个方面来介绍三维中微子振荡中的量子相干性.

1985年Legget与Garg提出了Leggett-Garg不等式, 该不等式主要有两个基本假设: 宏观实在性和非破坏性测量^[72,73]. 第一个假设意味着在系统上执行测量只会显示已存在的值, 即系统总是处于宏观可区分状态中的一个; 第二个假设意味着可以在不改变系统状态及其后续演化的情况下对系统进行测量. 基于这两个假设, 得到的是一系列的不等式. Leggett-Garg不等式的最简单形式由参数$ K_3 $构造, 其定义为

其中$ C\left(t_{i}, t_{j}\right) = \langle\hat{Q}\left(t_{i}\right) \hat{Q}\left(t_{j}\right)\rangle $, $ \hat{Q}(t) $是一个二分可观测量, 它只能取两个离散值中的一个, 通常由+1和–1标记. 因此, 违反Leggett-Garg不等式可以证明量子相干性的存在.

Naikoo等^[78]探究了介质、电荷共轭和宇称破坏效应同时存在的情况下, 三种味中微子振荡的Leggett-Garg不等式. 在该项研究中, 主要聚焦于Leggett-Garg不等式的$ K_3 $参数, 通过使用T2K^[79], NOνA^[80]和未来实验DUNE^[81]中的参数数据来检验Leggett-Garg不等式的有效性. 当考虑初始中微子状态为μ子中微子, 并选择相等的时间间隔$ \left(t_{0} = 0, t_{1} = t, t_{2} = 2 t\right) $时, Leggett-Garg不等式中的$ K_3 $项变为以下相关函数的和:

为了计算出时间关联函数C, 选取的二分可观测量为$ \hat{Q} = 2\left|\nu_{\alpha}\right\rangle\left\langle\nu_{\alpha}\right|-1 $, 如果中微子状态仍处于初始状态$ \left|\nu_{{\text{μ}}}\right\rangle $, 结果为+1, 反之则为–1. 最终可以直接计算出关联函数^[78]

$ U_{{\mathrm{f}}}^{i j} $是味演化矩阵$ {\boldsymbol{U}}_{{\mathrm{f}}} $中的元素, $ \bar{U}_{{\mathrm{f}}}^{i j} = U_{{\mathrm{f}}}^{i j *} $是$ U_{{\mathrm{f}}}^{i j} $的复共轭. 结合(13)式和(14)式, 得到$ K_3 $项为

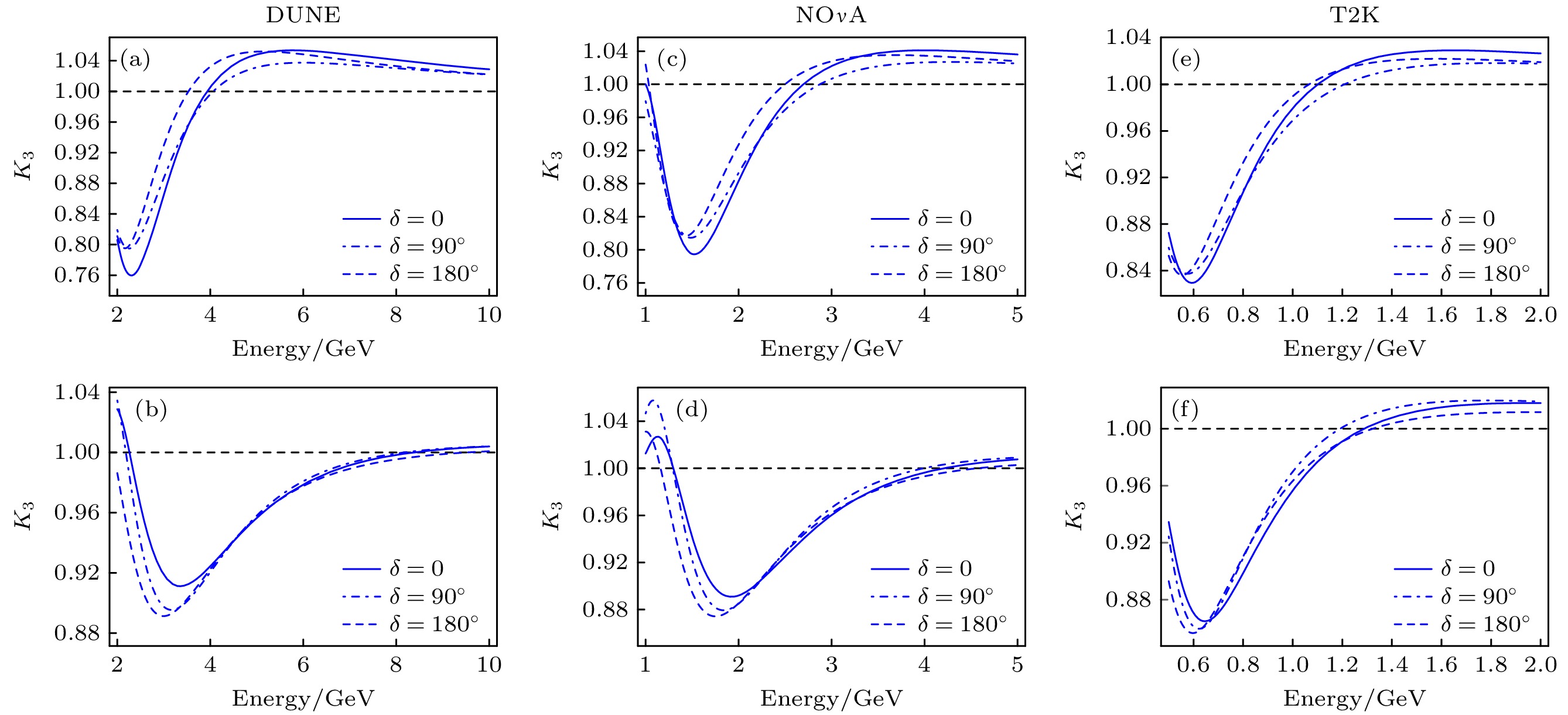
值得注意的是, 当$ \alpha = 0.5, \;\beta = 0 $时, Leggett-Garg不等式恢复到平稳极限. Formaggio等^[82]和Naikoo等^[83]研究了在平稳条件下中微子振荡中的Leggett-Garg不等式. 图2展示了$ K_3 $对于三个不同实验设置的能量变化, 其中δ取值不同得到$ K_3 $的不同变化. 和反中微子振荡相比, 中微子振荡情况下的$ K_3 $在更多的能量区间总是大于1, 即违反Leggett-Garg不等式的现象更加突出. 违反Leggett-Garg不等式可以解释为量子性的存在, 因为量子性是唯一与Leggett-Garg不等式原理相矛盾的理论. 如果进行测量的量子态是哈密顿量本征态的相干叠加, 则揭示了这种量子性. 反之则意味着这个量子态没有足够的相干性.

此外, Fu和Chen^[39]分析了基于大亚湾实验参数下的三味中微子振荡中的Leggett-Garg不等式. Gangopadhyay和Sinha^[84]分析了振荡参数对Leggett-Garg不等式违反的影响.

虽然违反Leggett-Garg不等式可以证明相干性的存在, 然而即使存在量子相干, 也有可能看不到任何参数空间的Leggett-Garg不等式违反. 相反, 如果有足够的相干性就能观察到Leggett-Garg不等式的违反. 所以Leggett-Garg不等式不是量化相干性的一个良好指标. Song等^[40]于2018年提出了利用量子资源理论中的相干性度量的方 法来量化三味中微子振荡中的相干性. 对于中微 子振荡来说, $ l_1 $范数相干是最容易计算的相干性度量, 它等于给定密度矩阵的所有非对角元素的总和, 即

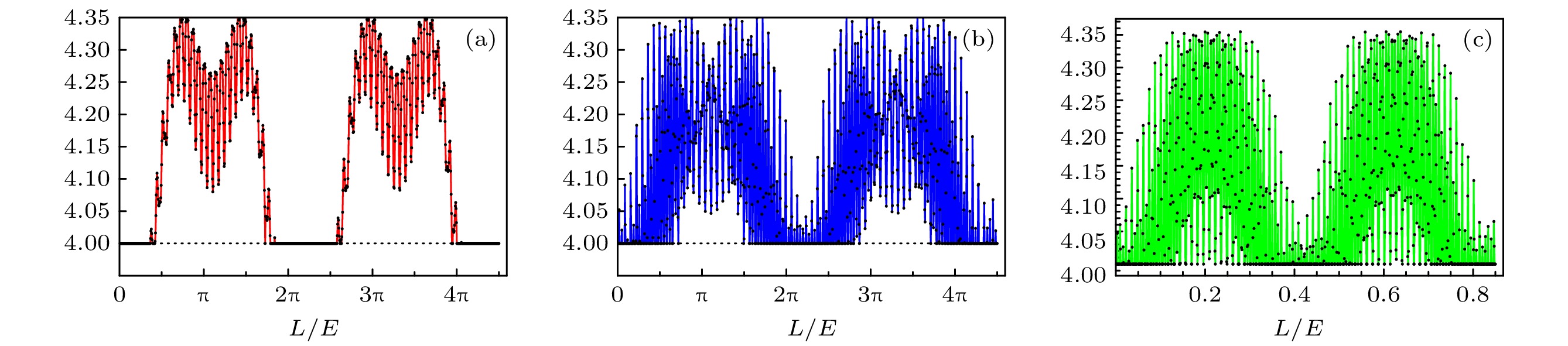
C的最大值由$ {\cal{C}}_{\max } = d-1 $限定, 其中d是密度矩阵ρ的维度. 在三味中微子振荡情形下, C的最大值为2. 对于三味电子和μ子中微子振荡, 其$ l_1 $范数相干可以由振荡概率表示:

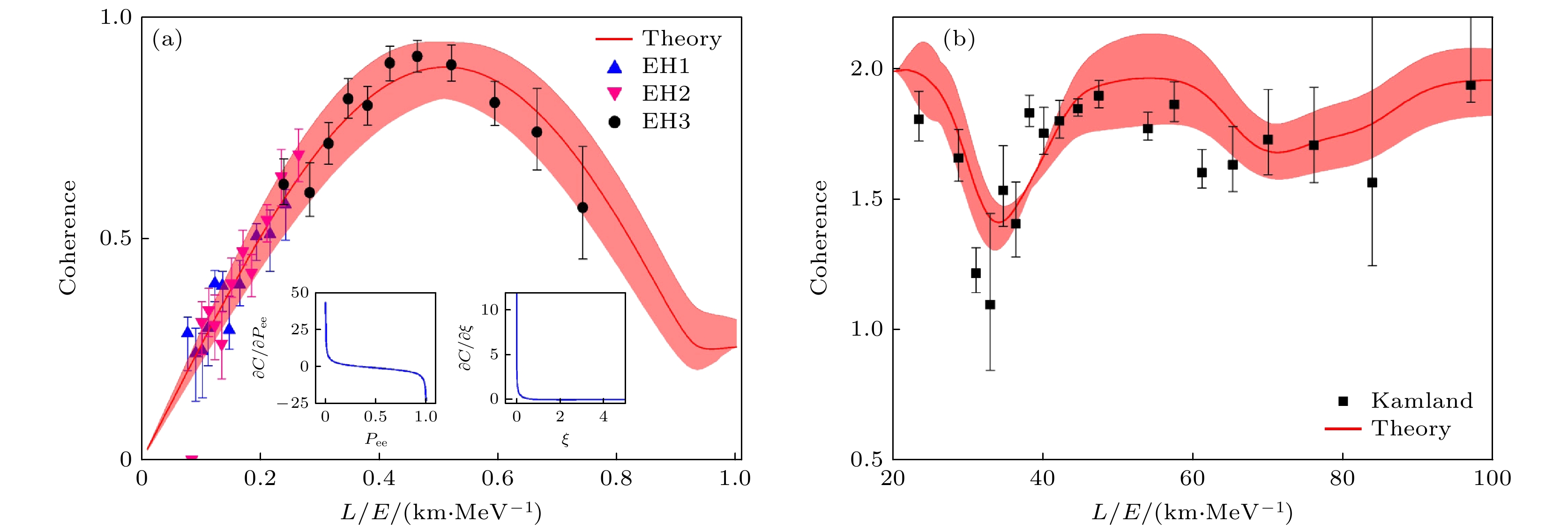
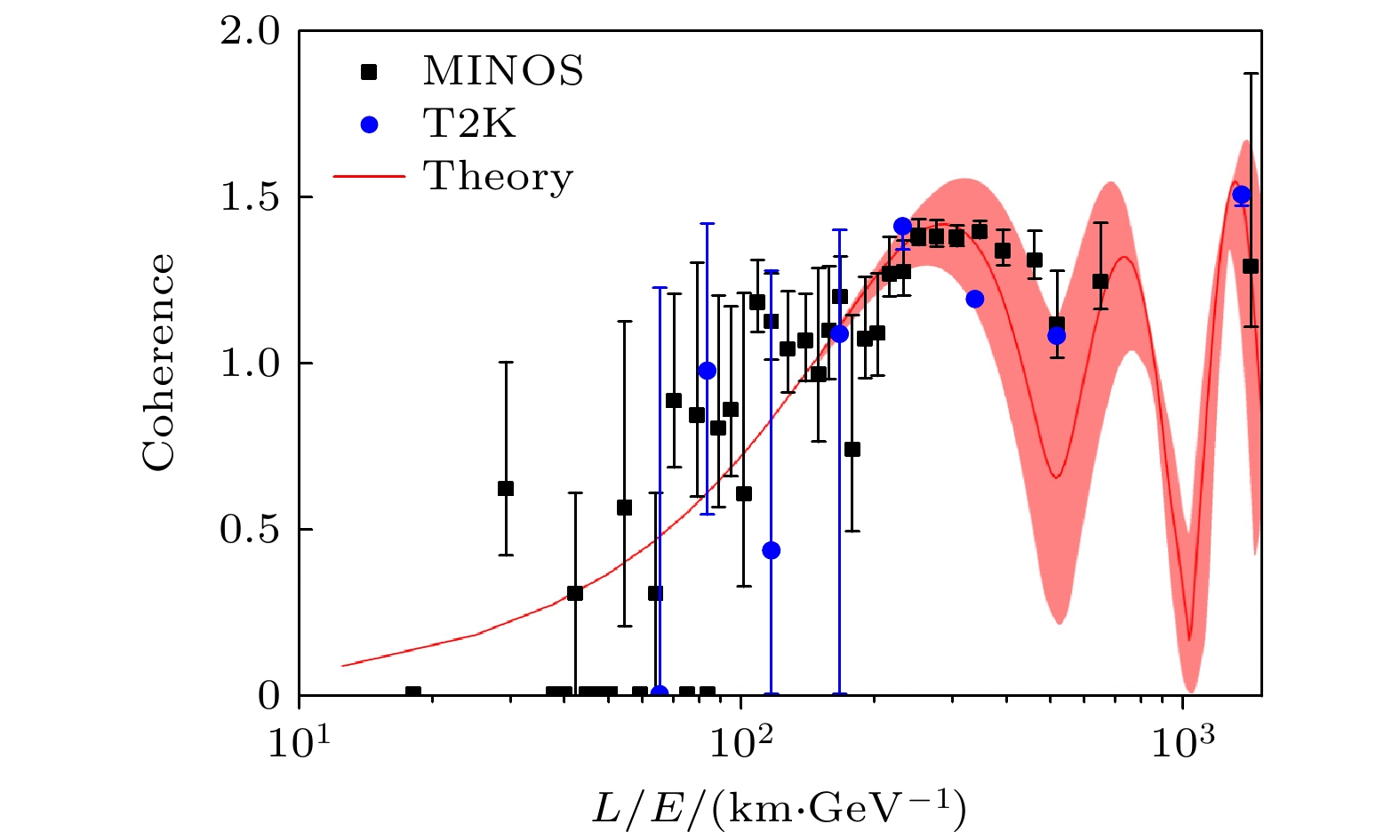
当两个振荡概率与生存概率均为1/3时, 三味中微子振荡相干性达到最大值为2. 而当两个振荡概率与复活概率相比很小时, 相干性将接近于零. 此外, 如图3(a)中的插图所示, 相干关于复活概率偏导数表明$ P_{{\mathrm{e e}}}(t) $的微小变化将会导致相干的剧烈变化, 对应插图中复活生存概率小于0.1和大于0.9的相干变化. 为了量化所测量的相干性, 实验上复活概率可以由各个中微子实验合作组给定, 而$ \xi = P_{{\mathrm{e}} {\text{τ}}}(t) / P_{{\mathrm{e}} {\text{μ}}}(t) $是由理论预测确定的. 当$ \xi > 0.5 $时, 相干随ξ的变化平缓; 当$ \xi < 0.5 $时, 相干随ξ的变化较为剧烈. 对于大亚湾中微子振荡, 相干可达到约0.8, 即使振荡概率小于10%, 对于KamLAND下的三味中微子振荡, 其相干性普遍较高, 甚至最大值可以达到2, 这意味着更多的量子资源可以用于KamLAND实验中的中微子振荡. 对于三味μ子中微子振荡, 如图4所示, 理论相干性表现出更复杂的行为, 其峰值出现在概率$ P_{{\text{μ}} {\text{μ}}}(t) $和$ P_{{\text{μ}} {\text{τ}}}(t) $相同的点上. MINOS相干性的实验数据分布在理论预测线附近, 这与相干性的理论预测是一致的. 另一方面, T2K相干性的实验数据也与理论符合得很好. 以上结果都表明$ l_1 $范数相干可以成为量化数千公里宏观距离上三味中微子振荡中相干性的可靠工具, 证明了中微子是一种除了光子以外可以适用于长距离量子通信的基本粒子.

三味中微子振荡过程中, 其贝尔非局域性, 即一种模态非局域性是否持久? 针对这个问题, Banerjee等^[50]利用贝尔不等式的衍生形式Mermin不等式和Svetlichny不等式对其进行了研究. Mermin不等式是Bell不等式的一种推广形式, 它的违反表明了多体系统中各方之间存在标准的非局域相关性^[85]. 这意味着对于一个三体系统, 概率分布P不能写成局部形式:

这里λ是共享局部变量; $ a_{1}, a_{2}, a_{3} $是测量结果. 然而, 这并不能确保真正的多方非局域性. 如果任意两个子系统是非局部相关的, 但与第三个子系统不相关, 则仍然可以违反Mermin不等式. 为了探索真正的非局部相关性, 基于混合非局域-局域实在论^[74]的Svetlichny不等式是一个不错的选择, 如下所示:

其中B代表两体划分部分. 对于一个三比特量子系统, Mermin不等式参数$ M_3 $^[86]和Svetlichny不等式参数^[87]定义为

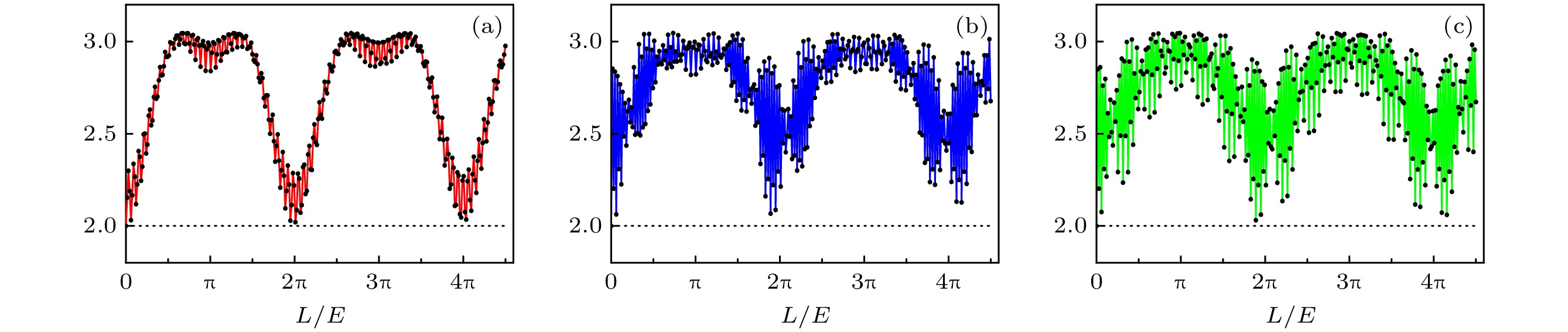
其中X和$ X^{\prime}(X = A, B, C) $对应于每个量子位的两种不同的测量设置. 两种参数的经典界限分别为$ M_{3} \leqslant 2 $和$ S_{3} \leqslant 4 $. 值得注意的是, 对于Mermin不等式的违反, 至少有一个两体部分必须具有非局域相关性, 而Svetlichny不等式只有在所有各方都具有非局域相关性时才会被违反. 如图5和图6所示, 对于初始三种味(即电子中微子、μ子中微子、τ子中微子)的中微子振荡, $ M_3 $的经典界限在各个情形中均被突破, 这意味着在系统中存在剩余非局域性. 而对于$ S_3 $的经典界限, 三种味的中微子振荡均存在未突破的参数区间. 也就是存在真正的多体非局域性缺失的情况. 有趣的是, 对于初始电子中微子振荡, 在其未检测到真正的多体非局域性的时间演化区间, 另外两种味的中微子, 可以观察到更强的振荡行为. 虽然真正的多体非局域关联在时间演化中主要存在(反过来表明存在真正的三方纠缠), 但也存在其消失的特定演化区间.

本课题组研究了引力效应下三维中微子振荡中的非局域性, 通过改变引力效应的强度来得到不同引力效应下的Svetlichny不等式的违反程度, 结果表明在引力效应存在时, 三味中微子振荡过程中所呈现出的真正三方非局域特性将会发生显著变化, 具体表现为既可能出现增强的态势, 也可能出现被削弱的情况^[61].

不确定性原理被视为量子世界的一个重要特征, 它通常与经典世界中的对应情况有所不同. Renes和Boileau^[88]提出了基于熵的三体不确定性关系:

其中$ S(\hat{R} \mid B) $和$ S(\hat{S} \mid C) $是条件冯·诺依曼熵, $ S(\hat{R} \mid B) = S(\rho_{\hat{R} B})-S(\rho_{B}) $, $ q_{{\mathrm{M U}}} = -\log _{2} c(\hat{R}, \hat{S}) $. $ c = \max _{i, j}\{|\langle\varPhi_{i}^{\hat{R}} \mid \psi_{j}^{\hat{S}}\rangle|^{2}\} $代表可观测量$ \hat{R} $和$ \hat{S} $对应本征态$ |\varPhi_{i}^{\hat{R}}\rangle $和$ |\varPhi_{i}^{\hat{S}}\rangle $的最大重叠.

Li等^[65]利用熵不确定性关系进一步揭示了三味中微子振荡的量子特征. 为了更好地探索三味中微子振荡中的熵不确定性关系, Li等^[65]基于下列不等式:

其中$ {\mathbb{X}} $, $ {\mathbb{Y}} $, $ {\mathbb{Z}} $是三个非对易算符. 通过相加可以得到总的熵不确定性关系:

在此, 不相容测量的总不确定度为$ {\cal{U}} = S({\mathbb{X}} | B)+ S({\mathbb{Y}} | B) + S({\mathbb{Z}} | B) + S({\mathbb{X}} | C) + S({\mathbb{Y}} | C) + S({\mathbb{Z}} | C) $.

在初始电子中微子振荡中, 总熵不确定度为^[65]

其中$ H_{\mathrm{bin}}\left(\lambda_{1}\right) = -\lambda_{1} \log _{2} \lambda_{1}-\left(1-\lambda_{1}\right) \log _{2}\left(1-\lambda_{1}\right) $, $ \lambda_{1} = \dfrac{1}{2}(1-\sqrt{(P_{{\mathrm{e e}}}+P_{{\mathrm{e}} {\text{μ}}})^{2}+2(P_{{\mathrm{e e}}}-P_{{\mathrm{e}} {\text{μ}}}) P_{{\mathrm{e}} {\text{τ}}}+P_{{\mathrm{e}} {\text{τ}}}^{2}}) $. 类似地, 可得到μ子中微子振荡中总的不确定度:

其中,

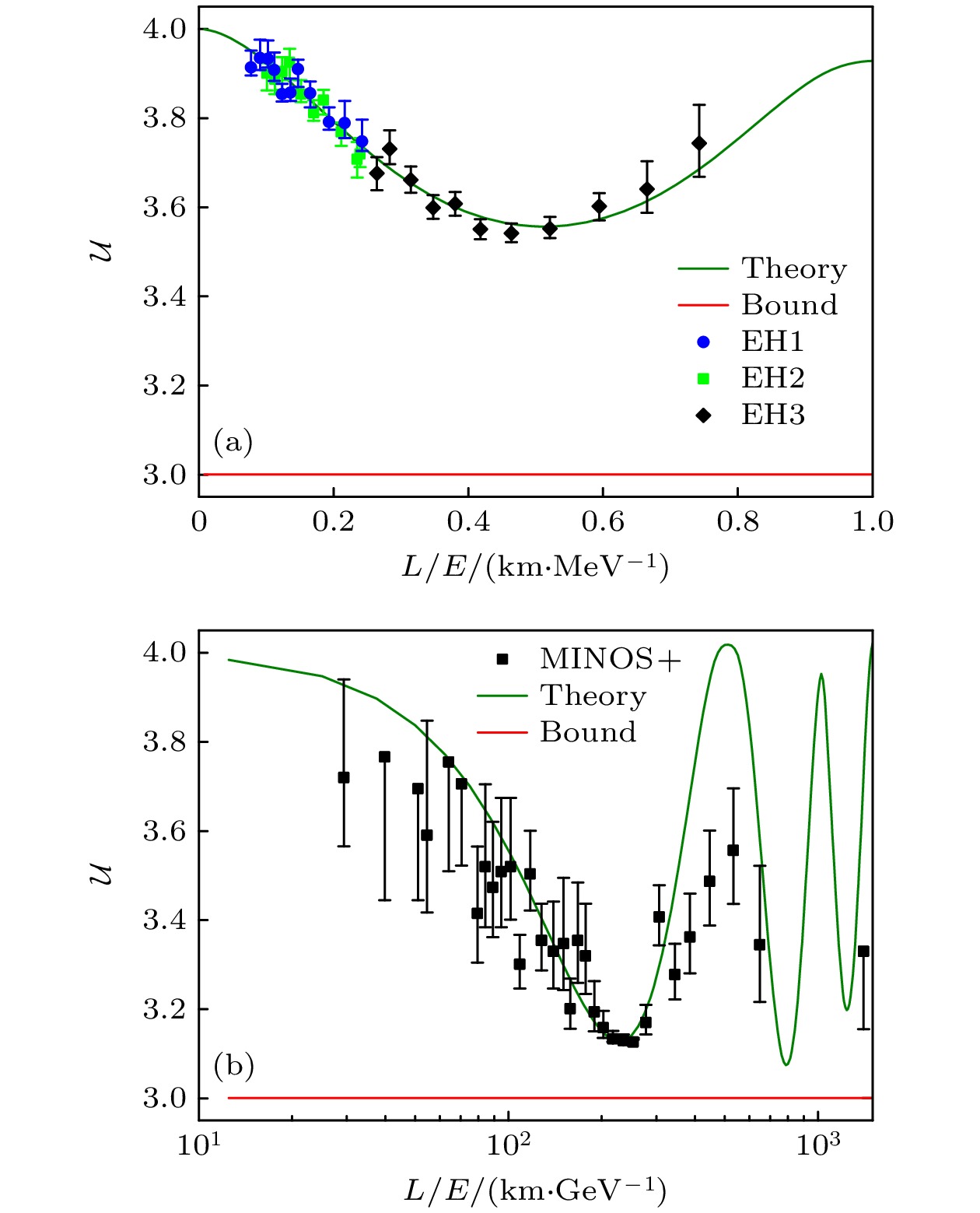
如图7所示, 从理论和实验两个方面分析了由(46)式所描述的总的熵不确定度$ {\cal{U}} $在三味中微子振荡中的变化. 熵不确定度在电子和μ子中微子振荡中呈现先减小后增大的趋势且均大于其最低边界, 这表明由(44)式描述的熵不确定性关系在三味中微子振荡中总是成立. 此外, Li等^[65]还研究了三味中微子振荡中熵不确定度与纠缠的关系, 他们发现在中微子传播过程中熵不确定度和纠缠之间呈现出反关联的变化趋势, 当纠缠在振荡中达到最大值时, 熵不确定度达到最小值. 从理论上讲, 这是因为量子纠缠的本质是一种非经典关联, 原则上量子关联越强, 测量的不确定度越小, 即纠缠越大, 测量的不确定度越小, 反之亦然. Blasone等^[63]和Wang等^[64]在两味中微子振荡中也证明了这一理论. 不确定性的降低以及纠缠的增加使得中微子系统能够提供更多的量子资源. 因此, 展现出较高的量子特性将有利于实现中微子中不相容测量的较小不确定度.

在研究多体系统量子相关的过程中, 最重要的性质之一是单配性, 它描述了多体系统中不同组成部分之间共享关联资源的约束条件^[34]. 例如, 在三体系统中, A和B双方之间的相关性越强, A和C双方之间的相关性就越少, 它们表现出互补的行为. 单配性关系为研究多体系统的量子关联结构提供了有效途径. 我们团队^[66]利用各种量子关联的单配性关系分析了三味中微子系统中的量子关联的分配和转化, 主要基于形成纠缠^[89]、量子失谐^[90]以及几何失谐^[91]等量子关联.

对于任意两体纯态$ |\psi\rangle_{A B} $, 形成纠缠被定义为

这里$ \rho_{{A}} = \text{Tr}_{{B}}\left(|\psi\rangle_{{AB}}\langle\psi|\right) $, $ \mu_{j} $是$ \rho_{{A}} $的本征值. 对于两体混态$ \rho_{A B} $, 利用凸顶构造的方法, 可以得到两体混态的形成纠缠

这里最大化是取遍所有的纯态分解$ \rho_{A B} = \displaystyle\sum\nolimits_{i} p_{i}\left|\phi_{i}\right\rangle_{A B}\left\langle\phi_{i}\right| $, 其中$ p_{i} $表示纯态分解的概率, 对于一个三量子比特系统, 基于形成纠缠平方的单配性关系由下列等式描述^[92]:

其中$ E_{{\mathrm{f}}}\left(\rho_{A \mid B C}\right) $量化的是A与BC之间的纠缠, $ E_{{\mathrm{f}}}\left(\rho_{A B}\right) $和$ E_{{\mathrm{f}}}\left(\rho_{A C}\right) $是A与B(C)之间的纠缠.

除了纠缠, 量子失谐也是一个主要的量子关联度量, 其被定义为

这里$ \widetilde{S}\left(\rho_{A} \mid \rho_{B}\right) = \min _{\left\{M_{j}^{B}\right\}} \sum\nolimits_{j} p_{j} S\left(\rho_{A \mid j}\right) $是测量诱导的量子条件熵. $ \left\{M_{j}^{B}\right\} $是在子系统B上执行的投影测量. 基于失谐平方的单配性关系如下^[19]:

另一方面, 量子失谐的几何测度被定义为两体系统AB的给定量子态与最近的经典态之间的最小平方希尔伯特-施密特距离^[91]

其中最小值是在经典态集合Ω上取得的, 这里的距离是2-范数的平方, 也被称为希尔伯特-施密特范数. 对任意的三比特纯态, 几何失谐的单配性关系被描述为^[93]

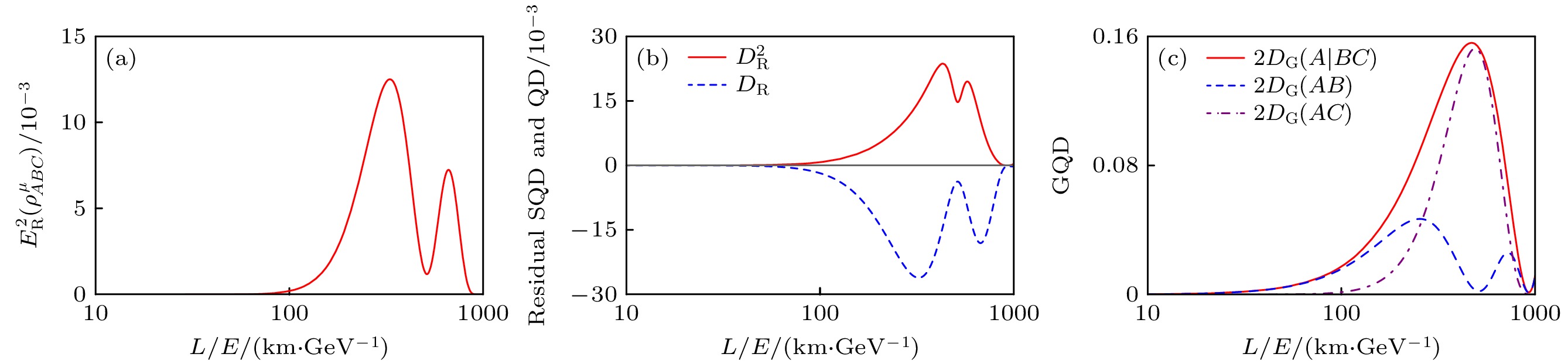
为了更好地验证三味中微子振荡的单配性关系, 我们构建了剩余关联度量. 对于三味电子中微子振荡, 基于以形成纠缠和失谐单配性关系的剩余关联如下:

对于几何失谐, 通过计算, 我们得到了$ D_{\mathrm{G}}(\rho^{\mathrm{e}}_{A\mid BC}) = 2 P_{{\mathrm{ee}}}(P_{{\mathrm{e}}{\text{τ}} }+P_{{\mathrm{e}}{\text{μ}}}) $, $ D_{\mathrm{G}}(\rho^{\mathrm{e}}_{AC}) = 2 P_{{\mathrm{ee}}}P_{{\mathrm{e}}{\text{τ}} } $, $ D_{\mathrm{G}}(\rho^{\mathrm{e}}_{AB}) \; + D_{\mathrm{G}}(\rho^{\mathrm{e}}_{AC}) = D_{\mathrm{G}}(\rho^{\mathrm{e}}_{A\mid BC}) $. 所以几何失谐在三味中微子振荡中满足:

类似地可以得到μ子中微子振荡中的上述三种量子关联的单配性关系.

如图8和图9所示, 形成纠缠的平方、量子失谐的平方、几何量子失谐在三味中微子振荡中均呈现出单配性行为. 这些关系的成立会限制中微子振荡中的关联演化, 即在中微子传播过程中, 系统中A与BC之间的关联提供了一个严格的界限来限制子系统AB和AC之间的关联. 这种限制使得在中微子振荡中, 两个子系统之间的关联演化产生了互补行为. 在这些单配性关系中, 我们发现量子失谐的平方在中微子振荡中具有单配性, 而量子失谐本身在这种情况下不具有单配性, 这表明对中微子振荡中单配性性质的研究本质上依赖于对合适关联度量的选择. 对于几何量子失谐, 其单配性关系在三味中微子系统中是饱和的, 也就是说, 由几何量子失谐度量的单个子系统与三味中微子振荡系统其余子系统之间的关联包含了简化后的成对中微子子系统的关联. 研究结果还表明, 剩余关联是一种合理的度量方式, 它不仅能够清晰地刻画中微子振荡中量子关联的结构, 还能对中微子振荡中单配性关系所施加的约束进行量化. 这些单配性关系有助于更好地理解三味中微子系统中关联的分布情况, 并为研究量子通信中的信息交流及信息转换提供了一种有效的途径.

对于三味中微子振荡中的单配性研究, 除了上述量子关联的单配性关系, Li等^[60]基于量子相干和两体非局域性的单配性关系研究了相干和非局域性在中微子系统中的分配和转化. 此外, 近期 我们基于量子纠缠研究了三味中微子振荡中的完全单配性关系^[61], 该关系包含了三味中微子系 统中整体以及所有两体子系统之间的纠缠, 在此 情形下, 不仅能够以一种有效的方式探究多体关联, 而且还可以更加详细地研究三味中微子振荡中量子关联的分布.

在多体量子系统中, 完全互补性关系^[94]可以将不同的量子资源联系起来, 例如纠缠、相干、失谐. 完全互补性关系为理解量子系统局域和非局域方面的相互作用提供了一种有效途径. Blasone等^[58]从完全互补性关系的角度研究了中微子振荡中不同量子关联的演化. 为了更好地介绍三味中微子振荡中的完全互补性关系的应用, 接下来简单回顾下完全互补性关系.

给定一个两量子比特纯态, 对于子系统k的完全互补性关系如下:

其中$ {\cal{P}}_{k} $是系统的可预见性, 与系统的先验(未经性测量)的粒子性行为有关; $ {\cal{V}}_{k} $是可见度, 与系统的相干有关; $\cal{C} $是共生纠缠, 用来量化子系统k与另一个子系统之间的纠缠. 对于三体纯态系统, 完全互补性关系由以下形式描述:

其中$ P_{\mathrm{hs}}\left(\rho_{A}\right) = \displaystyle\sum\nolimits_{i = 0}^{d_{A}-1}\left(\rho_{i i}^{A}\right)^{2}-\frac{1}{d_{A}} $是可预见性度量, $ C_{\mathrm{hs}}\left(\rho_{A}\right) = \displaystyle\sum\nolimits_{i \neq k}^{d_{A}-1}\left|\rho_{i k}^{A}\right|^{2} $是希尔伯特-施密特量子相干性(一种可见性的测量方法), $ C_{\mathrm{hs}}^{n l}\left(\rho_{A \mid B C}\right) $是A和BC的非局域相干.

如果将(58)式中的单个子系统转化成两体子系统AB, 完全互补性关系描述为

其中, $ S_{{\mathrm{vn}}} $是冯·诺依曼熵, 代表子系统AB的纠缠; $ C_{{\mathrm{re}}} $是相对熵相干; $ P_{{\mathrm{vn}}} $是可预测性度量. 与单个子系统的局域相干相比, 两体子系统的局域相干不会消失. 后文也将探讨中微子系统的这种效应.

对于三体混态情形, 子系统AB的完全互补性关系形式如下:

其中, $ I_{A B: C}\left(\rho_{A B C}\right)\; =\; S_{\mathrm{vn}}\left(\rho_{A B}\right)\;+\;S_{\mathrm{vn}}\left(\rho_{C}\right)\;- S_{\mathrm{vn}}\left(\rho_{A B C}\right) $, $ S_{A B \mid C}\left(\rho_{A B C}\right) = S_{\mathrm{vn}}\left(\rho_{A B C}\right)-S_{\mathrm{vn}}\left(\rho_{C}\right) $.

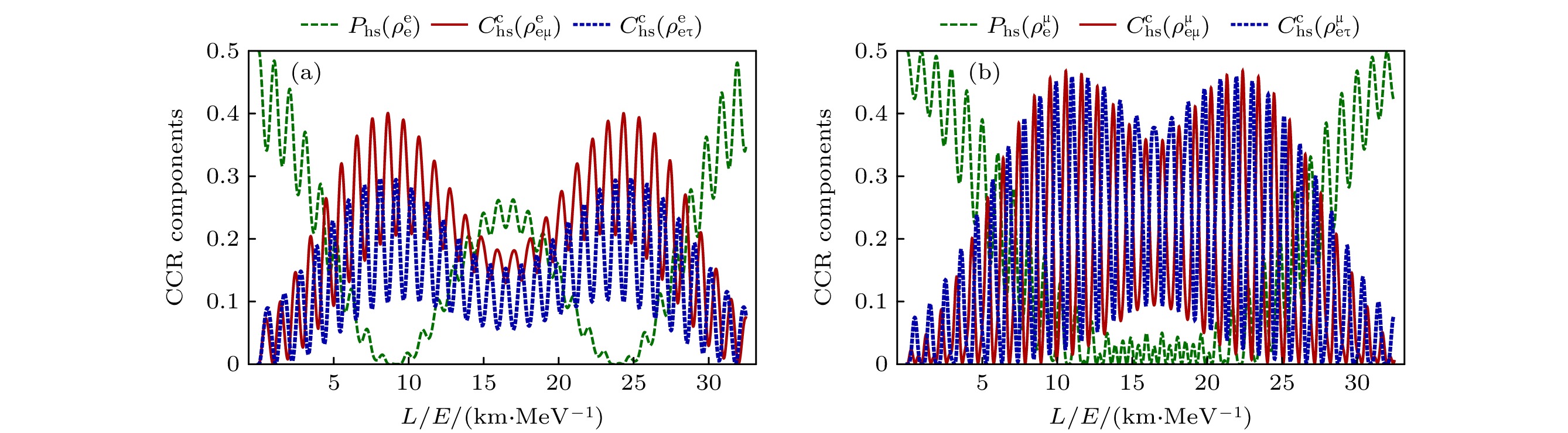
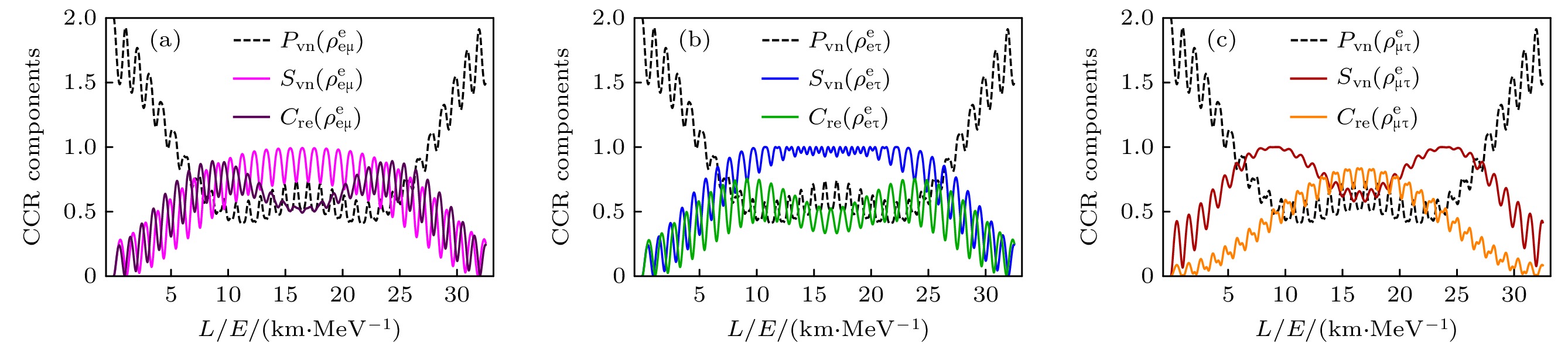
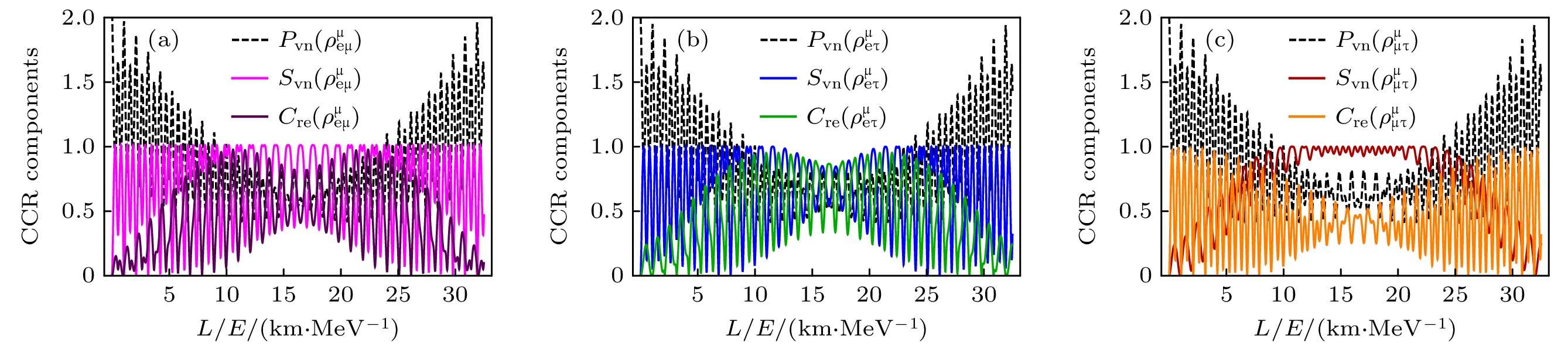
在(13)式描述的三味中微子态中, $ C_{\mathrm{hs}}^{n l}(\rho_{{\mathrm{e}} \mid {\text{μ}} {\text{τ}} }^{\alpha}) = C_{{\mathrm{h s}}}\left(\rho_{{\mathrm{e}} {\text{μ}}}^{\alpha}\right)+C_{{\mathrm{h s}}}\left(\rho_{{\mathrm{e}} {\text{τ}} }^{\alpha}\right) $总是成立, 也就是说子系统e和$ {\text{μ}}{\text{τ}} $之间的非局域相干等于子系统$ {\mathrm{e}}{\text{μ}} $和${\mathrm{ e}}{\text{τ}} $两体关联之和. 因此(58)式可以写成以下形式:

其中, $ C_{{\mathrm{h s}}}\left(\rho_{{\mathrm{e}} {\text{μ}}}^{\alpha}\right) = \left[a_{\alpha {\mathrm{e}}}(t) a_{\alpha {\text{μ}}}(t)^{*}\right]^{2}+\left[a_{\alpha {\text{μ}}}(t) a_{\alpha {\mathrm{e}}}^{*}(t)\right]^{2} $, $ C_{{\mathrm{h s}}}\left(\rho_{{\mathrm{e}} {\text{τ}} }^{\alpha}\right) = \left[a_{\alpha {\mathrm{e}}}(t) a_{\alpha {\text{τ}} }^{*}(t)\right]^{2}+\left[a_{\alpha {\text{τ}} }(t) a_{\alpha {\mathrm{e}}}^{*}(t)\right]^{2} $. 由该等式描述的完全互补性关系如图10所示, e和μ之间共享的两体关联大于e和τ之间的两体关联. 因此, 相干项$ C_{{\mathrm{h s}}}\left(\rho_{{\mathrm{e}} {\text{μ}}}^{{\mathrm{e}}}\right) $相对于$ C_{{\mathrm{h s}}}\left(\rho_{{\mathrm{e}} {\text{τ}}}^{e}\right) $在互补性关系中做出了更为突出的贡献. 而对于μ子中微子振荡的情况, 难以区别$ C_{{\mathrm{h s}}}\left(\rho_{{\mathrm{e}} {\text{μ}}}^{{\text{μ}}}\right) $和$ C_{{\mathrm{h s}}}\left(\rho_{{\mathrm{e}} {\text{τ}}}^{{\text{μ}}}\right) $之间的主导贡献, 两者之间呈现一种反关联关系.

针对子系统$ {\mathrm{e}}{\text{μ}} $, 可以求出由(59)式描述的完全互补性关系的相关项:

图11和图12分别给出了由(59)式描述的完全互补性关系中的相关项在电子和μ子中微子振荡中的演化. 对于$ {\mathrm{e}}{\text{μ}} $和$ {\mathrm{e}}{\text{τ}} $子系统, 可预测性度量$ P_{{\mathrm{vn}}} $、相对熵相干$ C_{{\mathrm{re}}} $、纠缠熵$ S_{{\mathrm{vn}}} $三者均呈现出强烈的振荡行为, 而对于$ {\mathrm{e}}{\text{τ}} $子系统, 纠缠熵$ S_{{\mathrm{vn}}} $会达到一个稳定振荡, 即在最大值附近发生微小振荡变化, 这种行为在较长的时间演化区间内会持续存在. 这种稳定振荡行为可能对量子信息任务很有用.

本文主要回顾了三味中微子振荡中的一些量子性研究. 首先阐述了三味中微子常见的振荡模型, 主要基于平面波和波包方法下的中微子振荡. 之后着重介绍了三味中微子振荡中具体的量子性研究, 从量子信息理论中的资源理论中的关联度量和权衡关系两个方面进行介绍分析. 在中微子振荡量子资源特性的研究中, 回顾了纠缠、相干、非局域性和不确定度等常见的资源度量在中微子系统中的具体表现, 揭示了它们在三味中微子振荡中的演化特征. 在三味中微子振荡的纠缠研究中可以通过对比不同的纠缠度量在三味中微子振荡中的具体表现, 得到中微子振荡中最优的纠缠量化方式. 对于中微子振荡的相干性, 可以利用Leggett-Garg不等式和资源理论中的相干性度量分别进行定性和定量分析. Mermin不等式和Svetlichny不等式呈现了三味中微子振荡中的模态非局域性的具体表现. 熵不确定性关系解释了中微子振荡中熵不确定度和量子关联之间的反关联关系. 最后简要介绍了单配性关系和完全互补性关系等权衡关系在三味中微子振荡中的具体应用, 单配性关系和完全互补性关系对于研究中微子系统中量子资源的分配和转移具有重要研究意义.

这些资源度量和权衡关系与许多量子信息处理任务直接相关, 不仅在揭示中微子振荡的内在量子特征方面具有不可或缺的作用, 而且对于挖掘中微子作为量子信息处理潜在资源的可能性具有关键的研究价值. 在中微子量子信息理论这一研究领域, 基本物理效应下的中微子振荡的量子性研究目前吸引了众多研究者的关注, 例如引力效应对中微子振荡相干性的影响^[95]和非标准相互作用对中微子振荡中量子关联的影响^[96]. 在该研究背景下, 还可以研究基础物理效应存在时, 中微子振荡中量子资源间的分配关系及不确定关系的变化行为. 此外, 考虑PMNS矩阵中的CP违反相位对中微子振荡量子性的影响也是一个值得探讨的课题. 当引入中微子的自旋性质以及手性振荡时, 中微子可以看作一个超纠缠态^[97], 其中自旋、手性以及味态可以看作中微子超纠缠态中不同的自由度, 那么利用量子资源理论可以研究中微子超纠缠态不同自由度之间的相互作用. 最后, 在量子场论的框架下, 研究中微子振荡的量子性也是一个具有重要意义的研究方向, Blasone等^[98]探讨了中微子振荡中的Leggett-Garg不等式. 对中微子量子性的研究, 众多科研工作者正持续深入地进行探索与钻研, 不断推动着该领域边界的拓展与理论的深化. 虽然考虑到目前的技术, 中微子的操纵是一个巨大的挑战, 但对中微子振荡的量子特性研究是迈向中微子量子信息处理的重要一步.