钙钛矿量子点是一种新型纳米材料, 融合了钙钛矿和量子点的特性. 钙钛矿材料因其独特的ABX₃结构和出色的光电性能而广为人知, 而量子点作为纳米级半导体材料, 具有尺寸效应, 能够通过调整尺寸来调控其光吸收. 钙钛矿量子点结合了这两种材料的优势, 因此在材料科学领域受到了广泛的关注. 在国内外的研究中, 钙钛矿量子点的制备方法和特性研究已取得了一系列重要进展. 通过不同的合成方法, 研究人员可以实现对钙钛矿量子点的精确控制^[1-3], 改变其形貌和结构, 从而实现对其光学和电学性能的调控^[4,5]. 此外, 钙钛矿量子点在太阳能电池^[6-12]、发光二极管^[13-17]、光催化^[18,19]等方面的应用研究也取得了显著成果, 为其在光电子学领域的应用奠定了重要基础. 钙钛矿量子点因其独特的光电特性, 在光吸收领域引起了广泛的研究兴趣. 因此, 研究材料的光吸收物理机制已经成为制备高性能和高转化率太阳能电池的关键, 而极化子效应光吸收是首要解决的问题.

极化子光吸收是控制钙钛矿材料光电特性的重要光激发态. 通过化学方法调整钙钛矿量子点(QD)之间的相互作用, 可以操纵极化子特性, 影响其空间扩散、热极化子冷却和内在寿命. 钙钛矿量子点在光、氧气、湿度和热等方面的稳定性是当前研究的焦点之一. 稳定性问题直接影响钙钛矿量子点在光电器件中的商业化应用. 由于铅基钙钛矿的毒性问题, 研究者们正在积极探索无铅或少铅的钙钛矿材料, 以期达到更高的环境和健康安全标准^[8]. 钙钛矿量子点的尺寸效应使其发光峰窄化, 光致发光效率提高^[14], 这为实现高清显示、荧光生物标记等应用提供了新的可能性. 卤化物钙钛矿量子点在光电探测器领域展现出与商用Si基探测器相媲美甚至更优的性能^[20]. 研究团队通过有机配体结构设计, 实现了钙钛矿量子点固体薄膜的原位可控制备, 这对于高性能导电半导体量子点固体薄膜的制备具有重要意义^[21]. 通过原位表征技术和第一性原理理论计算, 研究者们对钙钛矿量子点的热稳定性进行系统性分析, 揭示了不同组分钙钛矿量子点的热分解机理^[22]. 钙钛矿量子点在发光二极管(LED)中的应用研究取得了进展, 实现了高量子效率的蓝光发射钙钛矿LED. 此外, 诸多研究人员计算了极化子与钙钛矿量子点的材料耦合常数、声子频率等因素的关系^[23], 以及这些因素对极化子的光吸收系数和光学性质影响^[13]. 并且, 发现钙钛矿量子点因其独特的电子结构和可调谐的带隙^[24], 在光电领域展现出巨大的应用潜力. 特别是, 极化子在调控钙钛矿量子点的光吸收和发光性能中扮演着关键角色^[25]. 在理论计算部分, 将采用密度泛函理论和多体微扰理论等量子力学方法, 计算钙钛矿量子点中极化子的能级结构和光吸收截面^[26]. 这些问题都与材料中极化子效应息息相关, 但目前对于钙钛矿量子点中极化子光吸收的探讨还不够系统, 尤其是其在光电探测器、发光二极管和太阳能电池等光电器件方面的研究.

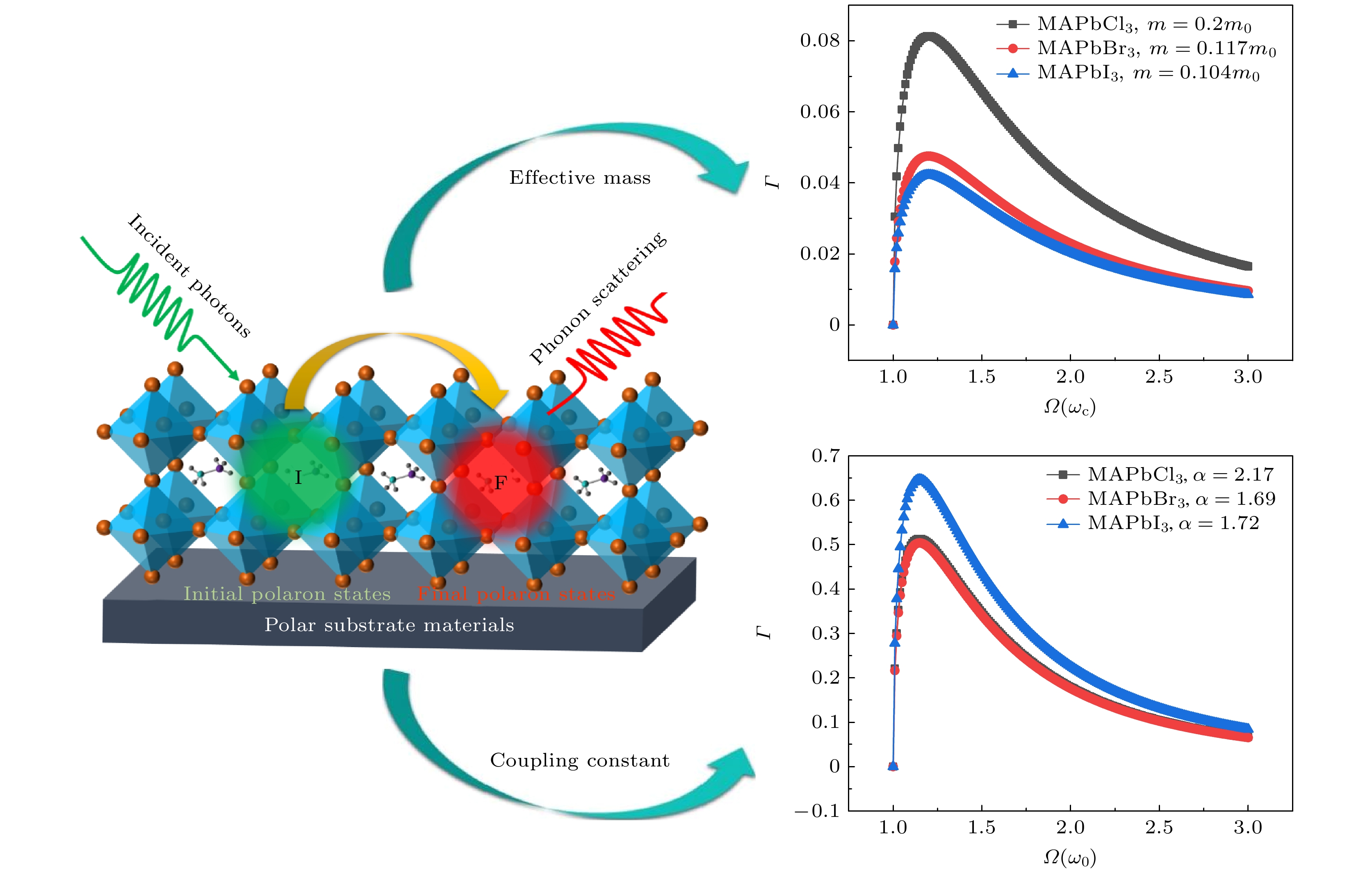
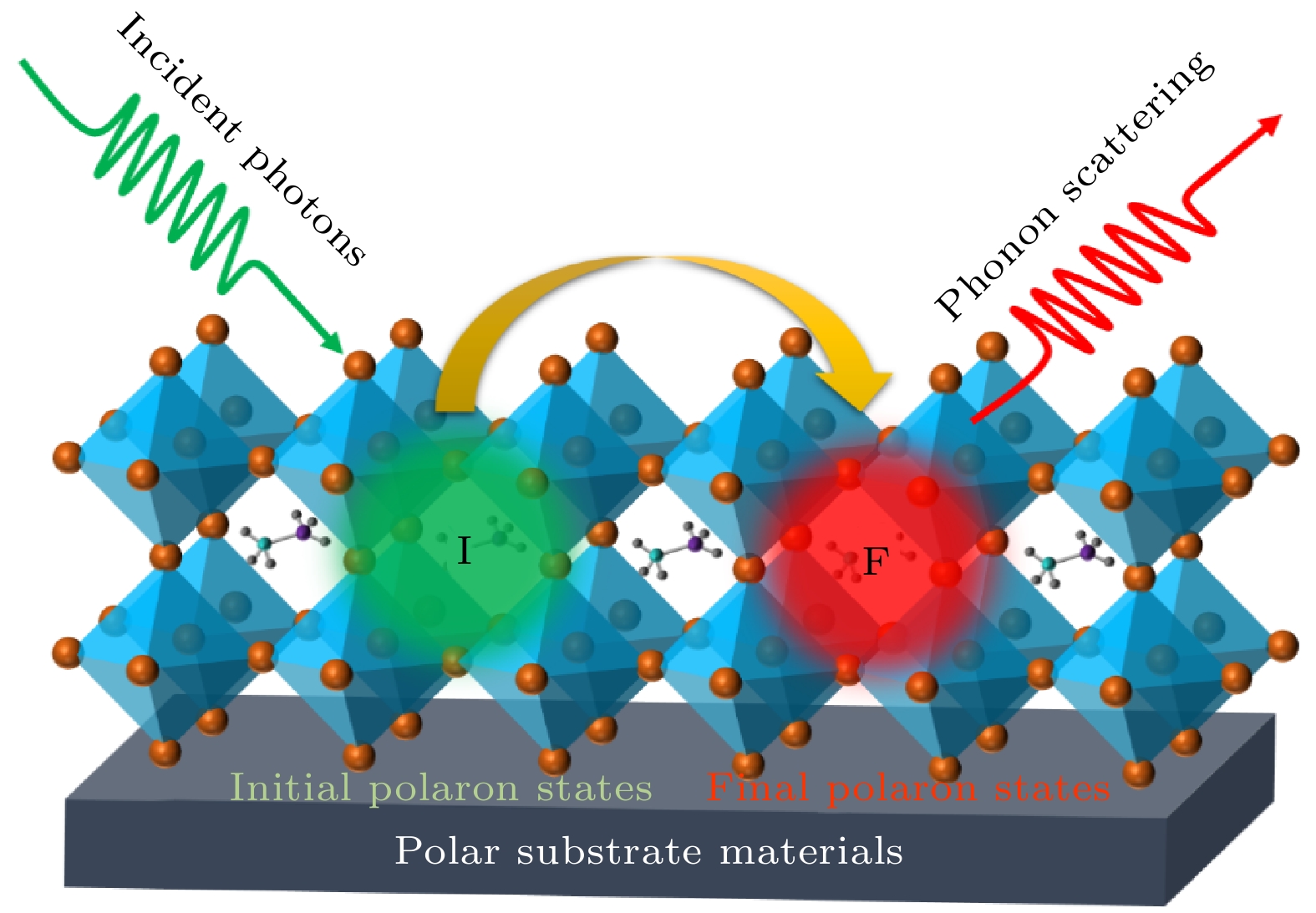
本文旨在通过Larsen变换和Lee-Low-Pines (LLP)幺正变换探究钙钛矿量子点中极化子的光学性质, 建立极化子光吸收模型(如图1所示), 计算光吸收系数与电子-声子相互作用常数之间的关系, 从理论上证实材料中极化子效应的存在. 通过对极化子光吸收性质的深入理解, 可以为钙钛矿量子点在光电领域的应用提供坚实的理论基础和实验依据.

在磁场作用下, 电子在钙钛矿量子点材料中运动, 与钙钛矿晶格相互作用, 极化子的哈密顿量表示为

式中, ${\textit{π}} $表示磁场下的电子动量, $r$表示质量为$m$的电子的位置坐标算符, $a_k^\dagger $和${a_k}$是波矢${\boldsymbol k}$和能量$\hbar {\omega _0}$光学声子的产生和湮灭算符, ${\omega _{\text{c}}}$表示磁场频率, ${V_k}$表示相互作用矩阵, ${{{{\textit{π}} ^2}}}/({{2 m}})$表示电子动能, 其中磁场作用下电子动量为

式中, ${\boldsymbol p}$表示电子的动量算符, ${{\boldsymbol{e}}_x}$为$x$方向基矢量.

电子与声子相互作用的矩阵:

式中, $\alpha $表示电子-声子耦合常数, (1) 式极化子哈密顿量变换为

首先对哈密顿量(1)进行表象变换, 选取幺正变换为

进行第一次幺正变换$ \mathbb{H} = \mathbb{U}_1^{ - 1}H{\mathbb{U}_1} $, 新表象下的哈密顿量:

进行Larsen变换 $ {\mathbb{U}_2} = \exp\left( {{\text{i}}{p_x}{p_y}/m{\omega _{\text{c}}}} \right) $ , 先对坐标$ y $进行变换:

代入哈密顿量$ \mathbb{H} $可得出:

再引进线性组合算符$ {p_y} = \dfrac{{\sqrt {m\hbar {\omega _{\text{c}}}} }}{{\sqrt 2 }}\left( {{b^ + } + b} \right) $, $ y = {\text{i}}\dfrac{{\sqrt \hbar }}{{\sqrt {2 m{\omega _{\text{c}}}} }}\left( {b - {b^ + }} \right) $. 哈密顿量$ \mathbb{H}' $变为

进行第二次幺正变换, 变换矩阵为

可以得出电子在晶格中与声子相互作用, 晶格发生形变形成极化子, 表象发生变化后的哈密顿量:

极化子光吸收求解:

光吸收跃迁矩阵如下:

可分成平行方向和垂直方向进行计算:

分成两个方向计算吸收系数:

当极化矢量平行于磁场:

由于低温情况($ kT \ll \hbar {\omega _0} $)没有热激发的光学声子, 并且忽略了实声子的吸收概率^[27], 因此, (17)式变为

再对其进行一次幺正变换

将基态和末态作用在变换后的哈密顿量得到基态和末态的能量:

吸收系数为

为了能够很简洁说明问题, 取极化单位$ a_{8}= m=1 $, 光吸收系数表达式可以简化为

当极化矢量垂直于磁场时:

进行第一次幺正变换$ {\mathbb{U}_1} = \exp\left( { - \displaystyle\sum\nolimits_{{k}} {{\text{i}}{\boldsymbol{k}} \cdot {\boldsymbol{r}}a_{{k}}^\dagger {a_{{k}}}} } \right) $和Larsen变换$ {\mathbb{U}_2} = \exp\left( {{\text{i}}{p_x}{p_y}/m{\omega _{\text{c}}}} \right) $,

其中在新的表象中, $ {p_z} $是运动(动量)常数, 当T = 0时可以得到$ {p_z} = 0 $.

定义产生$ b^{4} $和湮灭$ b $算符, 引进这样的算符来定义电子的产生和湮灭:

跃迁矩阵:

对跃迁矩阵进行第二次幺正变换:

哈密顿量变为

对哈密顿量进行变分:

得出变分参数:

相应声子产生和湮灭算符为

定义基态$ \left|\dot{i}^{\prime \prime}\right\rangle $

现在对$ M' = \left\langle {i'} \right| - {\text{i}}\hbar {\omega _{\text{c}}}\left[ {{\text{i}}\displaystyle\frac{{\sqrt {m\hbar {\omega _{\text{c}}}} }}{{\sqrt {2} }}\left( {b - {b^\dagger }} \right) + \displaystyle\sum\limits_k {\hbar {k_x}a_k^\dagger {a_k}} } \right] + \displaystyle\sum\limits_k {\hbar {k_y}\left( {{V_k}{a_k} - V_{_k}^*a_k^\dagger } \right)} \left| {f'} \right\rangle $进行变换:

当回旋频率小于光学声子频率($ {\omega _{\text{c}}} < {\omega _0} $)可能的末态存在两种情况: 第1种情况极化子吸收一个光子由基态能级跃迁到第一个朗道能级, 末态为

初态能量:

末态能量:

这时跃迁能量为磁场的能量 :

极化子光吸收系数为

第2种情况极化子吸收一个光子由基态能级跃迁到一个声子能级, 末态为

初态能量:

末态能量:

此时跃迁能量为声子能量和声子反作用于电子的能量:

对应的吸收系数^[28]为

由此, 对应光吸收系数解释了磁场提供极化子光吸收的能量和声子提供光吸收能量两种过程问题.

为了更好地说明两种物理机制, 选取3种不同钙钛矿量子点材料参数如表1所列.

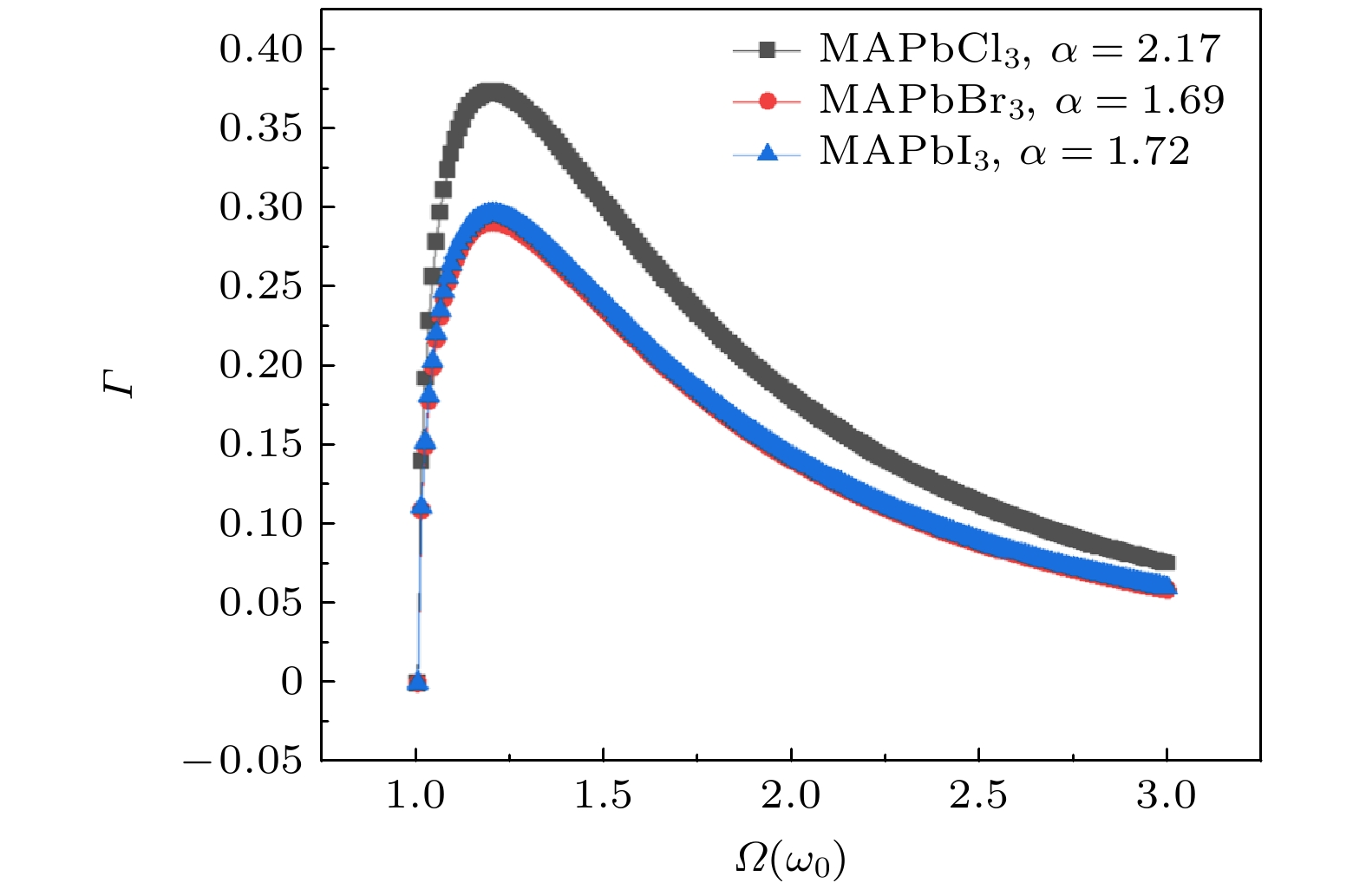
图2为3种不同类型的钙钛矿材料MAPbBr₃, MAPbI₃, MAPbCl₃的极化子光吸收系数. 从图2可以看到, 钙钛矿量子点中极化子光吸收的理论研究主要集中在对极化子形成机制光学性质的深入探讨. 通过理论模拟和计算, 可以揭示钙钛矿量子点中极化子的产生机理, 并预测其在光学响应中的行为^[7]. 基于密度泛函理论和紧束缚模型, 可以计算得出极化子的光学谱特性和能级结构^[29], 从而为实验研究提供理论指导. 钙钛矿量子点中极化子光吸收的理论研究不仅可以帮助解释实验现象, 还有助于设计新型光电器件^[3]和光学材料^[30]. 基于模型得出了极化子的光学谱特性和能级结构. 这些结果不仅与理论计算相符, 还为新型光电器件的构建提供了理论指导. 特别是, 通过计算不同卤族元素组成的钙钛矿材料MAPbBr₃, MAPbI₃, MAPbCl₃的极化子特性, 可发现电子-声子耦合常数的增加会导致光吸收幅度的增大.

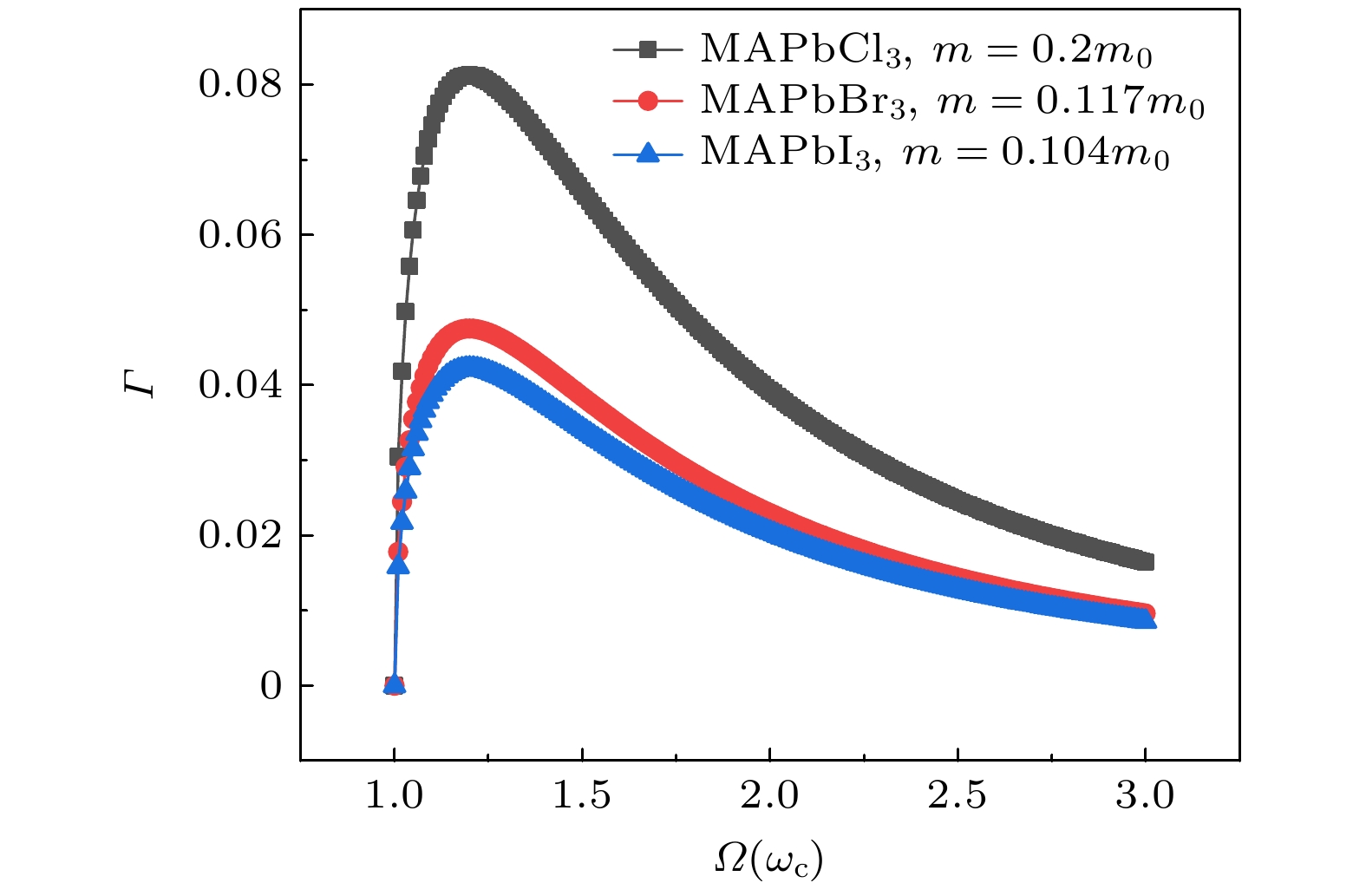
图3表明当极化子吸收一个光子, 从基态级跃迁到第一朗道能级时光吸收系数, 此时把光子能量传递给电子, 发生跃迁, 而这一过程中光学声子完全参与, 但仅仅是与电子耦合, 以极化子形式表现出来. 并且, 这种效应在磁场作用下的跃迁表现会更加明显, 因为磁场的回旋频率决定了基态能级和第一朗道能级直接的跃迁能量, 这一点可以从(40)式给出. 根据(41)式可以看出回旋频率小于光子频率时, 极化子从基态能级跃迁到第一朗道能级的光吸收幅度随着有效质量的增大而增大. 这是由于磁场的影响, 电子与声子耦合增强, 有效质量增大, 导致极化子光吸收幅度增大.

图4表示极化子吸收了一个光子, 由基态能量跃迁到一个声子能级, 就相当于释放出一个声子, 而这一过程中声子能量和电子作用晶格声子的动能提供了跃迁的能量. 其中, 电子和声子的局域耦合称为极化子耦合^[9]. 极化子是一种由载流子和光学声子耦合形成的状态. 当光照射到晶体时, 晶体中的载流子与声子相互作用, 而且与光子进行能量交换, 形成新的准粒子形式^[10]将能量转移. 这种耦合机制可通过调控载流子浓度、晶体结构和外加电场等手段进行调控^[16].

极化子效应在材料科学和器件应用中具有潜在应用. 通过电子-声子耦合, 可以实现光学调控和器件性能的优化^[11]. 例如, 通过调控电子与声子的能量和频率, 可以实现光电器件的频率选择性以及提高转换效率. 通过电子与声子的耦合, 还可以实现能量传输和信息处理的新型方法^[31], 如极化子逻辑门^[12]等.

综上所述, 钙钛矿量子点中极化子光吸收的实验研究为这一新型材料的应用奠定了基础. 通过深入探究其光学特性和光吸收机制, 研究人员可以更好地设计和制备具有特定功能的钙钛矿量子点, 拓展其在光电器件和生物医学领域 的应用潜力^[32]. 未来的研究方向包括进一步优化实验条件、探索 新型结构的钙钛矿量子点, 并结合理论模拟研究, 全面理解和利用极化子光吸收特性, 以促进该领 域的发展与创新. 总之, 钙钛矿量子点中极化子光吸收的理论研究为设计新型光电器件和光学材料提供了重要的理论基础. 未来的研究可以进一步 探索极化子在不同条件下的动态行为^[33], 以及它们在实际光电器件中的应用, 如太阳能电池、光电探测器^[28,34]和发光二极管等. 通过不断的理论创新和实验验证, 钙钛矿量子点在光电领域的应用前景将更加广阔.

本文通过幺正变换方法, 建立了光吸收模型, 发现钙钛矿量子点极化子光吸收的相关理论机制. 数值模拟计算了钙钛矿量子点中极化子光吸收能级差和光吸收系数. 结果表明, 电子在MAPbBr₃, MAPbI₃, MAPbCl₃三种不同卤族元素钙钛矿材料中运动, 与晶格相互作用形成极化子效应. 电子-声子耦合常数和有效质量会导致光吸收幅度的差异. 这一结果为钙钛矿量子点材料的光电性能优化提供了新思路, 并为极化子光吸收的物理机制在光电器件和多学科交叉领域方面指明了应用方向.