-
二维过渡金属二硫化合物(two-dimensiona transition-metal dichalcogenide, 2D-TMD)材料的能带结构中的局部能量极值点, 即能谷, 对材料的电学性质有直接影响而受到研究者的关注[1–3]. 除了传统的电荷与自旋自由度外, 谷作为一种新的自由度, 在信息处理和存储方面具有巨大的潜力. 一般来说, 二维六边形晶格的谷出现在布里渊区的K与K' 点, 非磁性材料的时间反演对称性导致谷简并. 目前谷研究的重点是如何稳定地操纵载流子, 打破谷中的平衡, 从而产生谷极化[4,5].
谷自由度的操控是实现谷电子学和自旋电子学应用的关键, 而解除谷简并则是利用这一自由度处理和存储谷电子信息的前提条件. 已有的研究表明外加磁场[6–8]、光学斯塔克效应[9]、磁性原子掺杂[10–12]、磁近邻相互作用[13–16]等方法是实现平衡态谷退简并的有效方法. 此外, 谷物理研究的另一个主要趋势是利用圆偏振光场产生非平衡的谷极化. 这一现象的机理基于谷光学选择定则[17], 并在2012年由Mak等[18]在单层MoS2中通过实验验证, 利用圆偏振光的光泵浦可以实现完全的动态谷偏振. 在此基础上, Liu等[19]进一步利用全光路径探索了H相和T相共存的WSe2中磁场可控的谷极化, 为实现谷动态操控提供了新的思路. 通过塞曼场施加磁场诱导非平衡自旋态被认为是调节谷动力学的基本方法. 然而, 通过外加磁场获得大的谷极化, 需要施加巨大的磁场, 1 T的磁场只能产生0.1—0.2 meV的塞曼分裂[6,8,20], 这使得其在实验上难以实现. 随着纳米科技的迅速发展, 范德瓦耳斯异质结构(van der Waals heterostructures, vdWHs)作为一种新型的二维材料复合体系, 为设计和调控电子、自旋特性提供了一个丰富的平台. 而构建vdWHs已经成为了拓展二维材料应用潜能的常见手段, 如Abid等[21] 研究了2H和1T晶型物中黑磷烯、Janus 单层(MXY: M = Mo, W 和 X/Y = S, Se, Te)及其相应的vdWHs, 在 1T 相中, 原本属于半导体的MoSSe和WSSe 在各自的异质结构表现出金属特性; Mehdipour和Kratzer[22]通过构建具有不同硫族原子序列和不同堆叠模式的MoSeTe和WSeTe双层, 得到其可调节净偶极矩强度和 Rashba 效应; Sattar等[23]研究发现Janus Pt基二硫族化合物(如SPtSe)在磁近邻作用下会产生谷和大的谷极化. 在vdWHs中, 邻近效应为定制邻近材料的电子能带结构提供了一种可控的方法. 通过精确调控谷自由度, 可以实现对电子态的精细控制, 这对于开发新型电子器件和量子信息技术具有重要意义. Norden等[24]在实验中成功利用 EuS 衬底的邻近效应, 在 WS2/EuS 中实现大的谷极化, 比外部磁场获得的极化高出两个数量级. 尽管已有研究团队对2D-TMD材料如WTe2和WSe2的磁近邻效应进行了理论探索[25,26], 但目前对于二维Janus材料的磁近邻效应的研究仍然相对匮乏.
近年来, 具有天然对称性破缺的二维Janus材料引起了人们的广泛关注. 打破面外反演对称已经成为激发新的电子特性的一种选择, 从而扩大TMD的应用范围[27]. 空间反演对称性破缺是K与K' 谷不等价的必要条件, 因此具有天然对称性破缺二维Janus是一种有前景的谷电子材料. 随着实验技术的快速发展, Janus 结构不再仅是一个理论模型. 最近的研究显示, 在实验中已经成功合成 Janus MoSSe[28,29], BiTeCl[30], WSSe[31]和CrSSe[32]等材料. 此外, 已有许多Janus材料被预测其拥有优异的自旋电子与谷电子特性, 如Guo等[33]研究发现铁谷材料FeClF可产生约109 meV的谷极化; Zhang等[34]的研究表明MnSeTe和 MnSTe单层具有稳定的高自旋极化、室温铁磁性和大的垂直磁各向异性; Chen等[35]预测2H-CeBrCl是理想的铁谷材料, 其自发谷极化为 29.1 meV. WSeTe作为一种典型的Janus材料, 其独特的特性使其在 与磁性材料形成vdWHs时, 相较于传统的2D-TMD材料如WTe2和WSe2, 提供了更为丰富的设计选择. 此外, 异质结构中不同原子层间的界面相互作用对谷极化的影响是一个值得深入研究的问题.
本文基于第一性原理计算, 系统研究了WSeTe/CrI3 vdWHs的电子性质, 分析了其不同堆叠方式的谷极化差异及产生的物理机制. 并通过施加垂直应变与改变衬底磁矩方向对WSeTe/CrI3谷极化进行调控. 总结了不同层间距与衬底磁矩方向对K与K' 谷极化大小的调控规律, 为设计和实现基于谷自由度的新型电子器件提供理论基础和 指导.
-
本工作中使用密度泛函理论(density functional theory, DFT)进行完全相对论的第一性原理计算, 所有计算均使用第一性原理软件包VASP (Vienna ab-initio simulation package)[36]. 首先采用混合泛函方法HSE06获得了精确的能带结构, 通过计算确定Perdew-Burke-Ernzerhofer (PBE)交换关联泛函只低估带隙, 对能带形状无影响, 因此在计算中选取PBE交换关联泛函, 平面波函数截断能为500 eV, 能量收敛标准为10–6 eV, 每个原子的受力标准小于0.01 eV/Å; 使用Grimme等[37]提出的DFT-D3方法描述垂直异质结层间的范德瓦耳斯相互作用; 结构优化计算采用9×9×1的Monkhorst-pack k点网格[38]. 在面外方向上设置15 Å的真空层用以减少周期性边界条件造成的杂散影响. 为了验证材料的稳定性, 利用密度泛函微扰理论(DFPT)计算了声子色散. 为了准确描述Cr原子3d轨道电子的强相关效应, 计算过程中采用简化的DFT+U方法[39], U = 2.2 eV[26]. 为了进一步阐明谷特性, 使用Kubo公式通过VASPBERRY计算Berry曲率[40]. Berry曲率定义为
其中,
${f_n}$ 是费米狄拉克分布函数,$ |\psi \rangle $ 是特征值为$ {E_n} $ 的布洛赫波函数,${{\boldsymbol{\nu}} _{x(y)}}$ 是沿$x/y$ 方向的速度矢量. 通过改变层间距d, 在异质结表面施加垂直应变, 固定界面处原子的z坐标以保证层间距. -
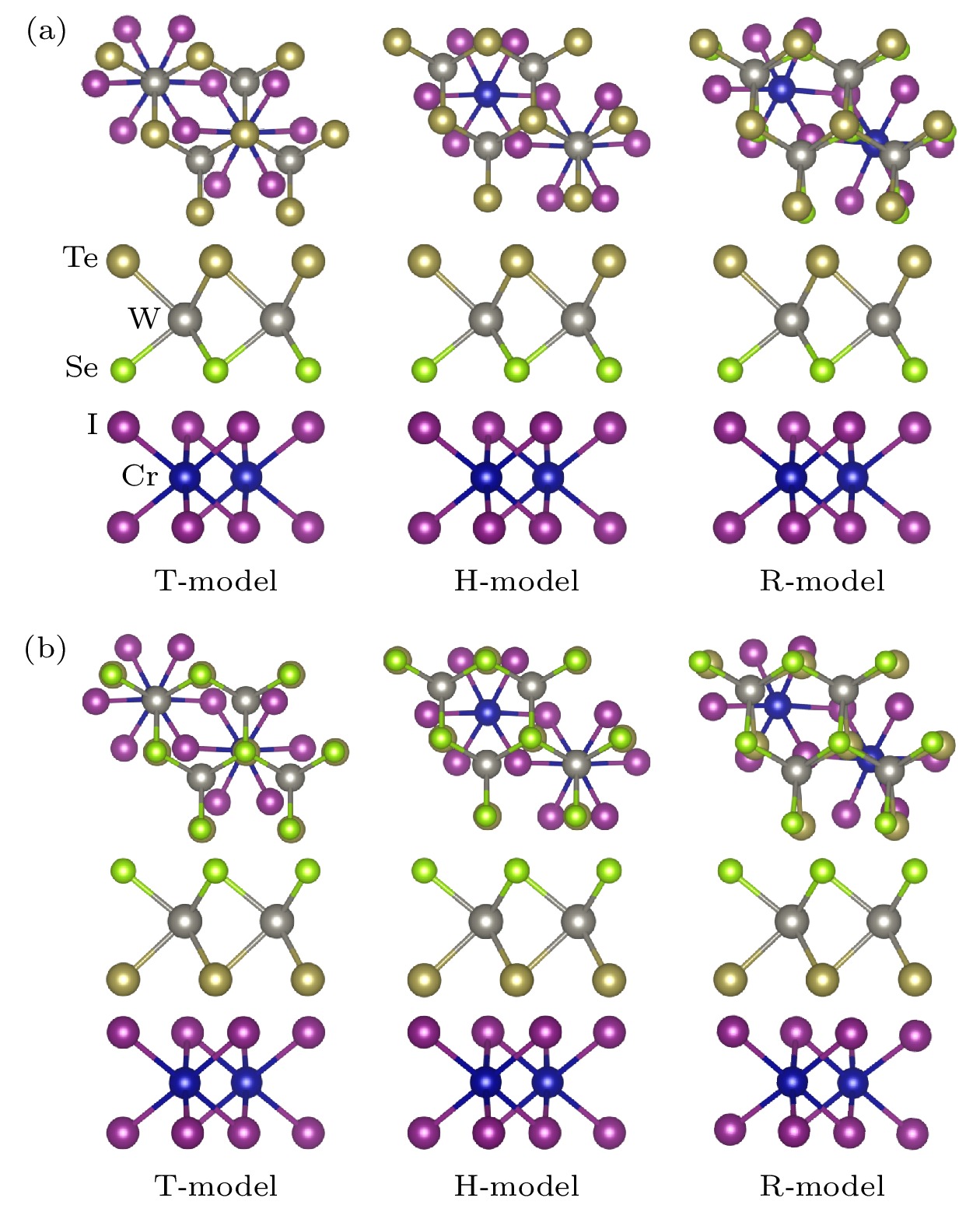
单层Janus材料WSeTe具有2H相和1T' 相两种稳定结构[41]. 2H相的WSeTe相比于1T'相具有更好的稳定性[22]. 单层WSeTe与CrI3的晶格参数分别为3.44 Å和6.96 Å, 与文献[41,42]的理论结果相符. 本文选择2H相的WSeTe与CrI3磁性衬底构建WSeTe/CrI3异质结, 利用磁近邻效应打破时间反转对称性, 实现能谷退简并. WSeTe/CrI3异质结采用了2×2×1 的WSeTe与1×1×1 的CrI3, 晶格失配大约在2%. WSeTe/CrI3异质结有3种堆叠方式, 分别为T(top), H(hollow)和R(random)[26], 每种堆叠方式有两种接触面, 分别记为Te和Se构型, 如附录图A1所示. 结合能
${E_{\text{b}}}$ 定义为其中,
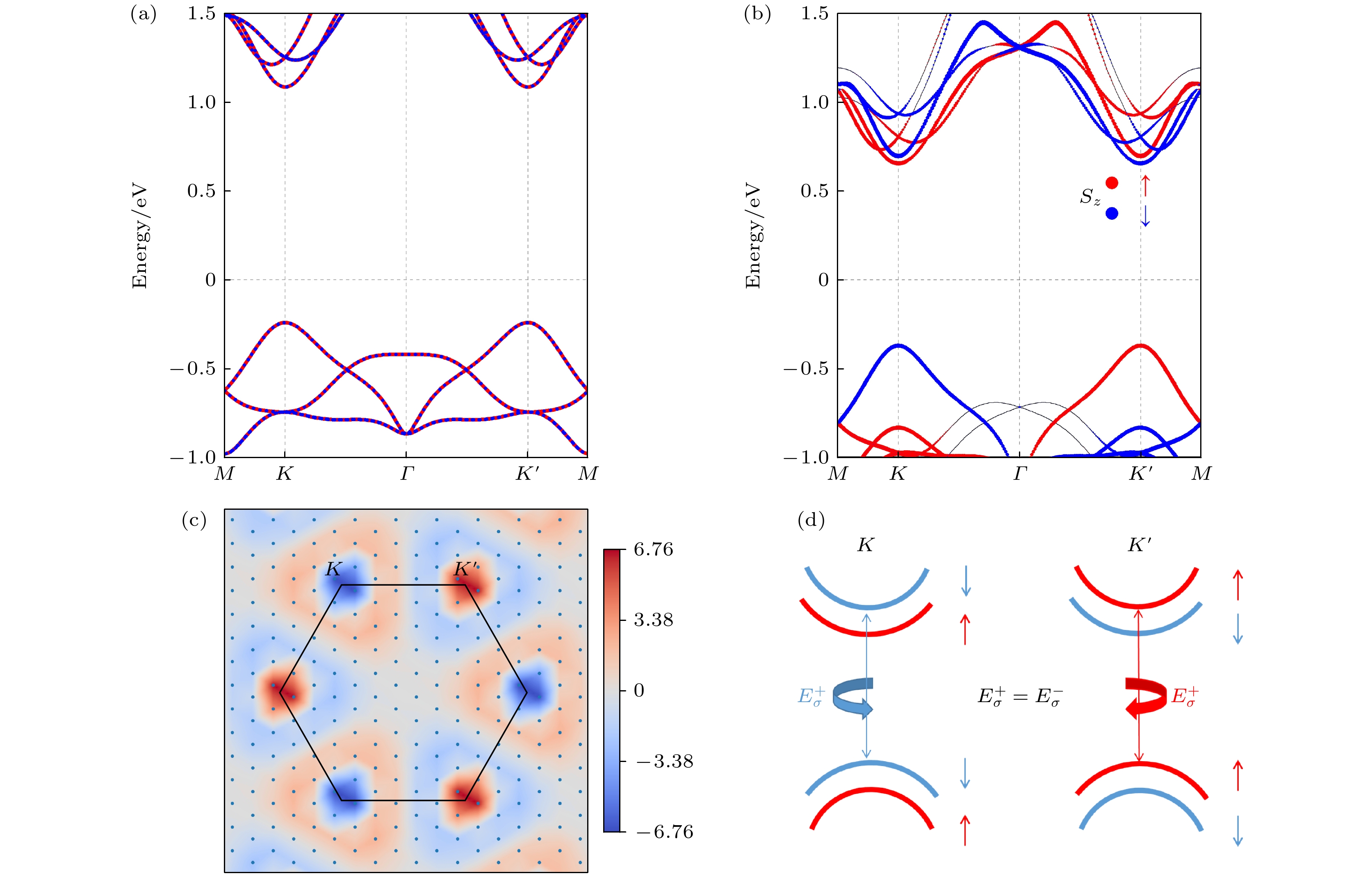
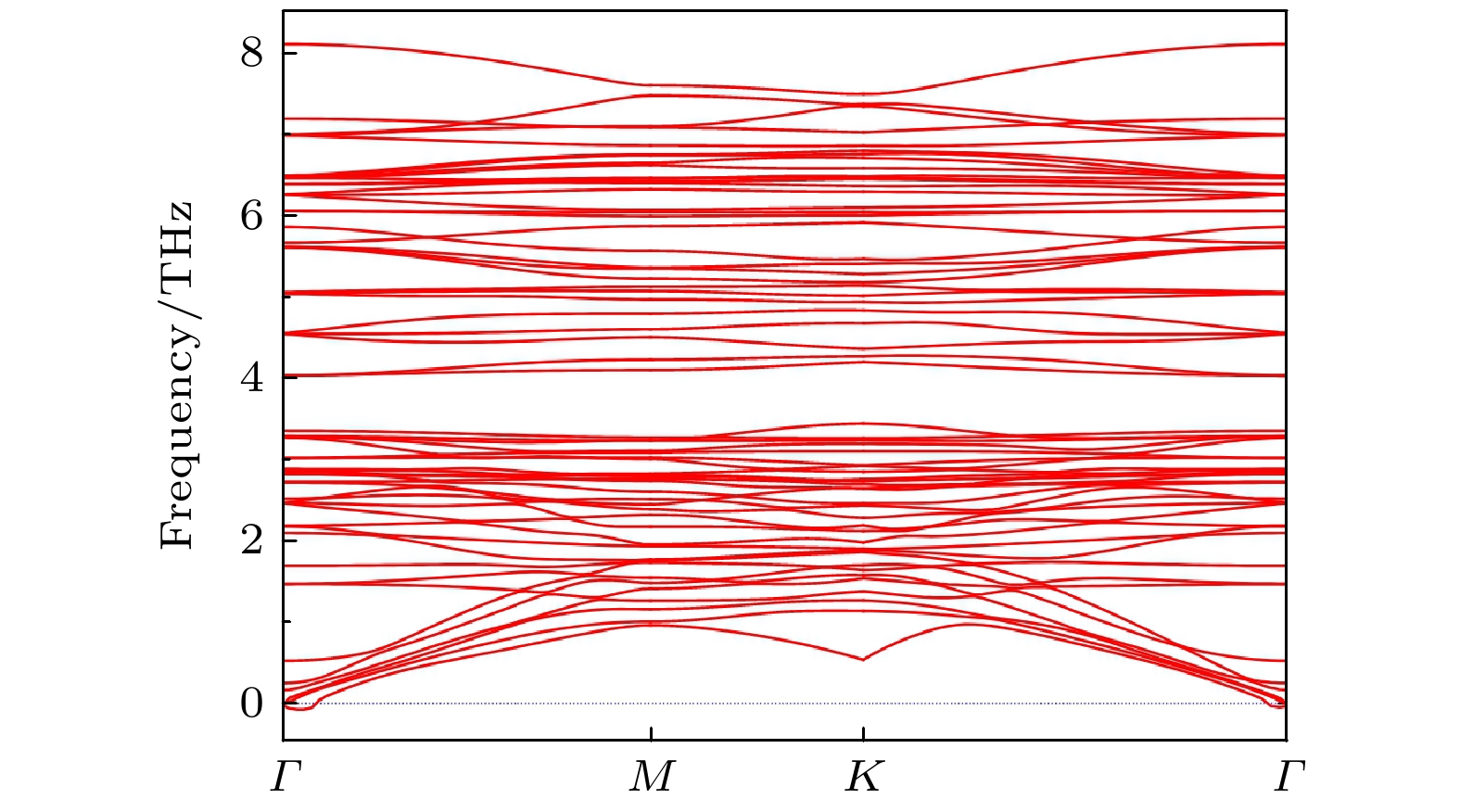
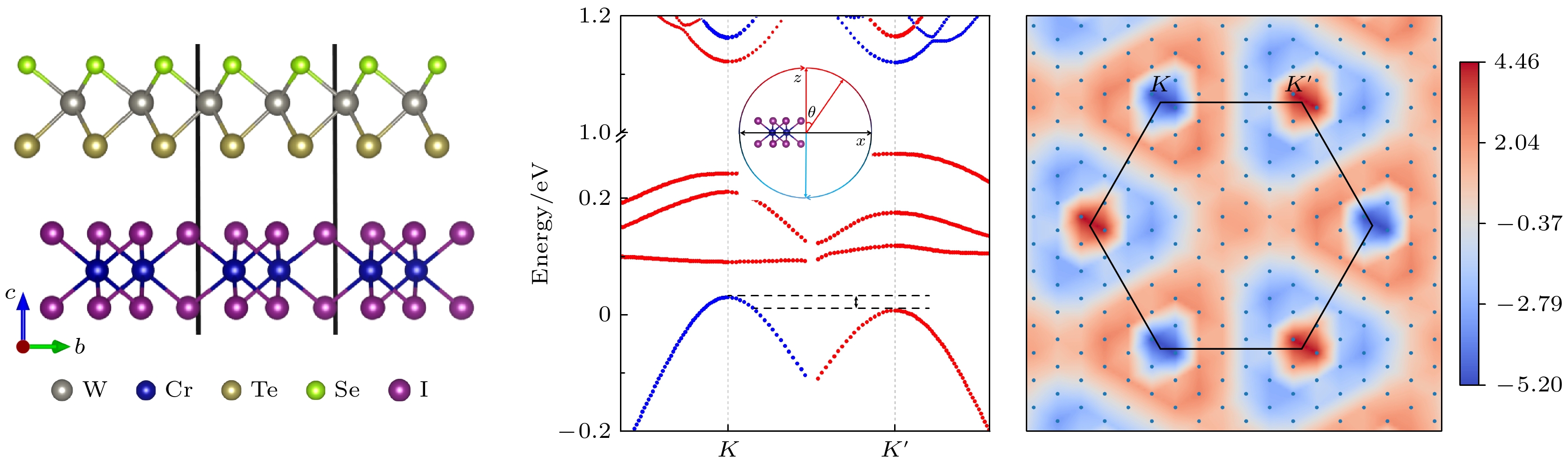
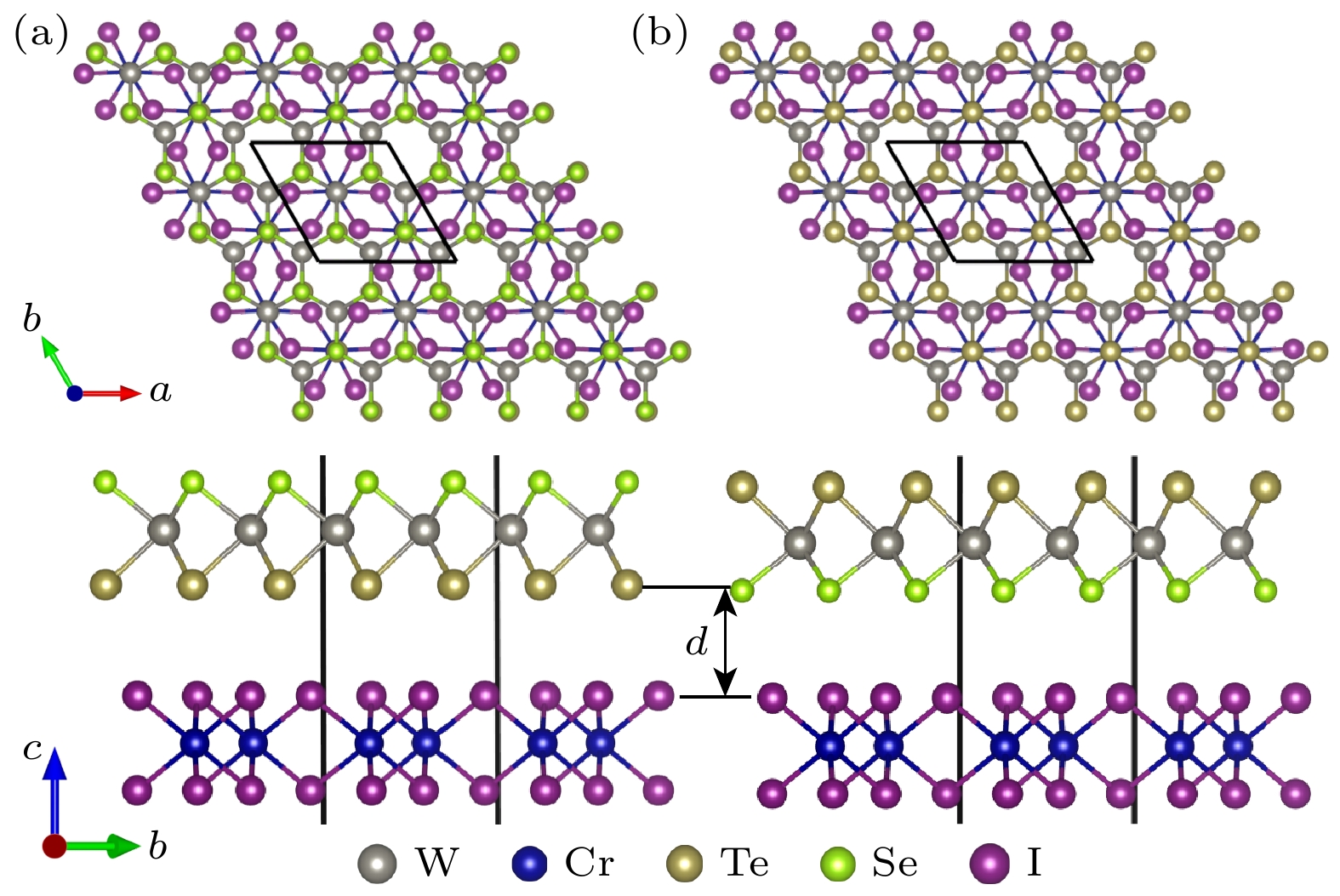
$E_{{\text{WSeTe/Cr}}{{\text{I}}_{3}}}^{}$ 为异质结的总能,$E_{{\text{WSeTe}}}^{}$ 为WSeTe的能量,${E_{{\text{Cr}}{{\text{I}}_{3}}}}$ 为CrI3的能量. 结合能为负值, 这说明结构是稳定的. 表A1表明T型堆叠的WSeTe/CrI3异质结具有较低的结合能, 因此后续的计算采用T堆叠. 为了验证异质结的动态稳定性, 计算声子色散曲线, 结果见附录图A2. 声子谱在Γ点附近出现一个大约0.06 THz 的小虚频率, 这在许多二维系统中观察到[26,43–45], 它们预计不会显著影响结构的整体稳定性. HSE06的能带结果如附录图A3所示. WSeTe/CrI3的T堆叠结构如图1所示, 图中黑色线框表示异质结晶胞. 在T堆叠中, CrI3单胞中的两个Cr原子排列在一个W原子和一个Te或Se原子之下, 位于WSeTe层的立体六边形对位, 可以有效地传递Cr原子的磁有序. 将异质结的层间距定义为层间原子I与Te/Se的Z方向距离, 如图中标注d所示. Te构型的WSeTe/CrI3异质结的俯视图与侧视图如图1(a)所示, 上层为WSeTe, 下层为CrI3, 层间距为3.8 Å. 图1(b)所示为接触面为Se原子层的WSeTe/CrI3的俯视图和侧视图, 层间距为3.6 Å.单层 2×2 WSeTe 能带如图2(a)和图2(b)所示, 图中展示了有、无自旋-轨道耦合(spin-orbit coupling, SOC)两种情况的结果. WSeTe在不考虑SOC的情况下带隙为1.33 eV, K与K' 存在直接带隙, K与K' 处的能谷保持自旋简并, 如图2(a)所示. 在SOC的作用下, WSeTe 能带出现分离, K与K' 处的直接带隙减小为1.02 eV, 如图2(b)所示. 计算结果与已有的研究一致[46]. Janus WSeTe虽然具有天然的空间反转对称性破缺, 但由于时间反演对称性的保护, K与K' 处的能谷保持简并且未出现自旋分裂. 在SOC的作用下, 原本自旋简并的能带出现塞曼分裂, K与K' 价带处的分裂大小远大于导带, 但K与K' 处的能谷仍然简并,
$ {E_ \downarrow }(K) = {E_ \uparrow }(K' ) $ , 如图2(b)所示. 通过进一步研究动量分解的Berry曲率, 在K与K' 点具有等值且符号相反的Berry曲率, 侧面验证了其能谷的简并与不等价, 如图2(c)所示. 由于WSeTe存在的强SOC, 在K与K' 谷处带间光学跃迁中遵循谷相关选择规则. 此外, 圆偏振光的能量是相等的($E_\sigma ^ + = E_\sigma ^ - $ ), 如图2(d)所示. 将谷极化定义为单层WSeTe能谷简并, 不存在谷极化. 使能谷退简并的方法之一是引入磁场, 打破时间反转对称性. 由此, 引入磁性衬底CrI3, 对T堆叠方式WSeTe/CrI3异质结的能带结构进行进一步分析.
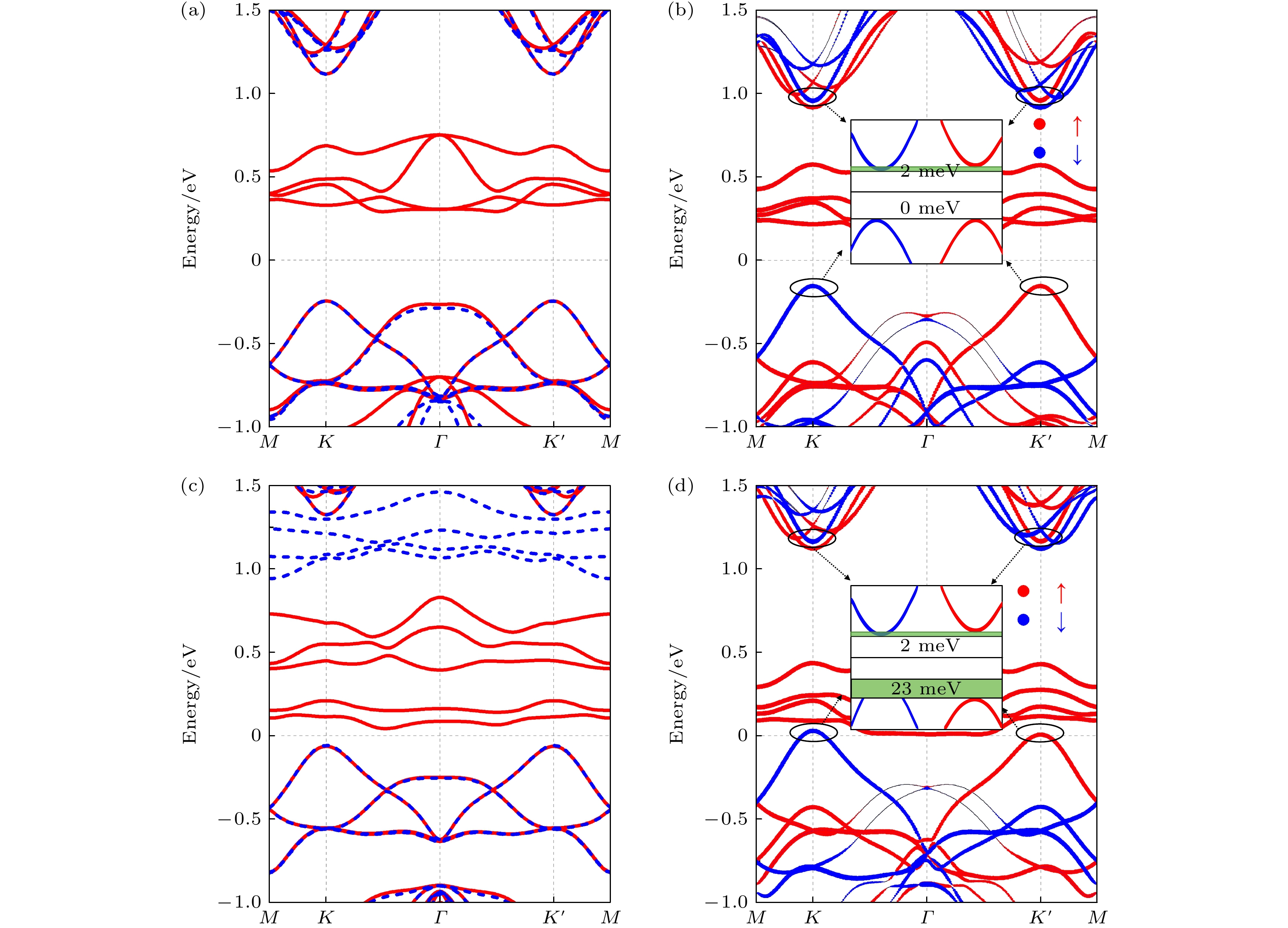
WSeTe/CrI3异质结T堆叠方式下Se与Te构型的能带结构计算结果如图3所示. WSeTe的能带形状在异质结中得到了很好的保留, K与K' 处的能谷依然存在. 其中图3(a), (c)分别展示的是Se, Te构型未考虑SOC的能带. 在不考虑SOC情况下, 由WSeTe层主导的能谷部分代表自旋向下的蓝色虚线与自旋向上的红线部分始终重合, 保持自旋简并. 在SOC的作用下, WSeTe/CrI3能谷处的能带出现塞曼分裂. 此外, K与K' 的能谷由于磁性衬底的加入, 层间耦合作用带来的磁近邻效应打破了时间反演对称性使能谷发生了退简并,
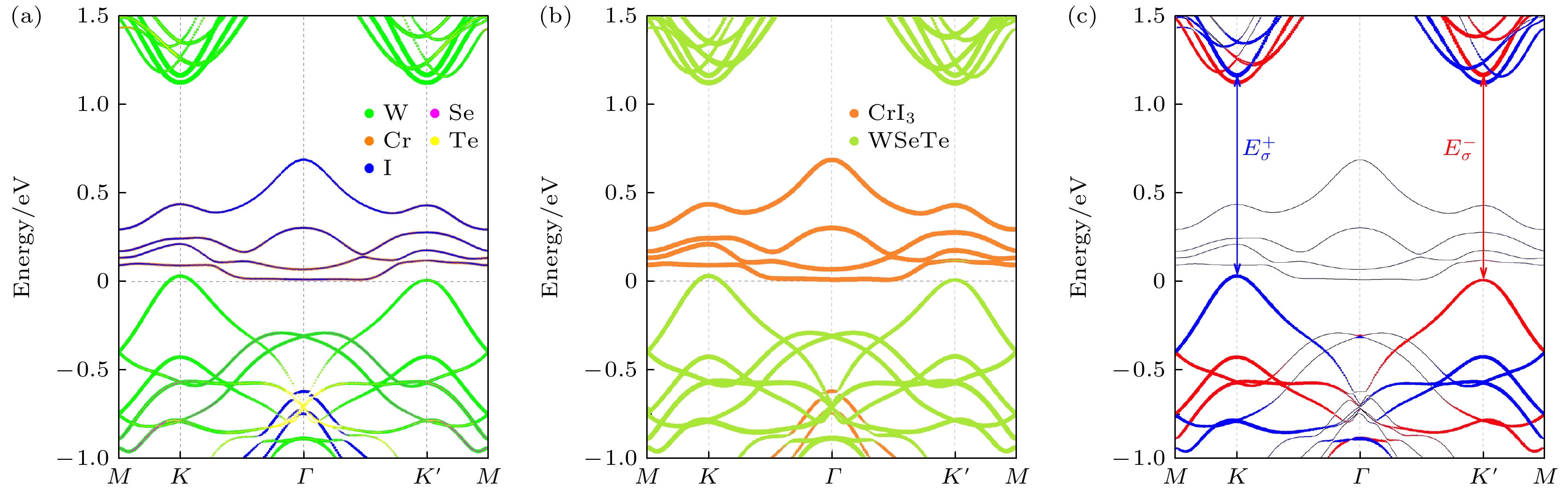
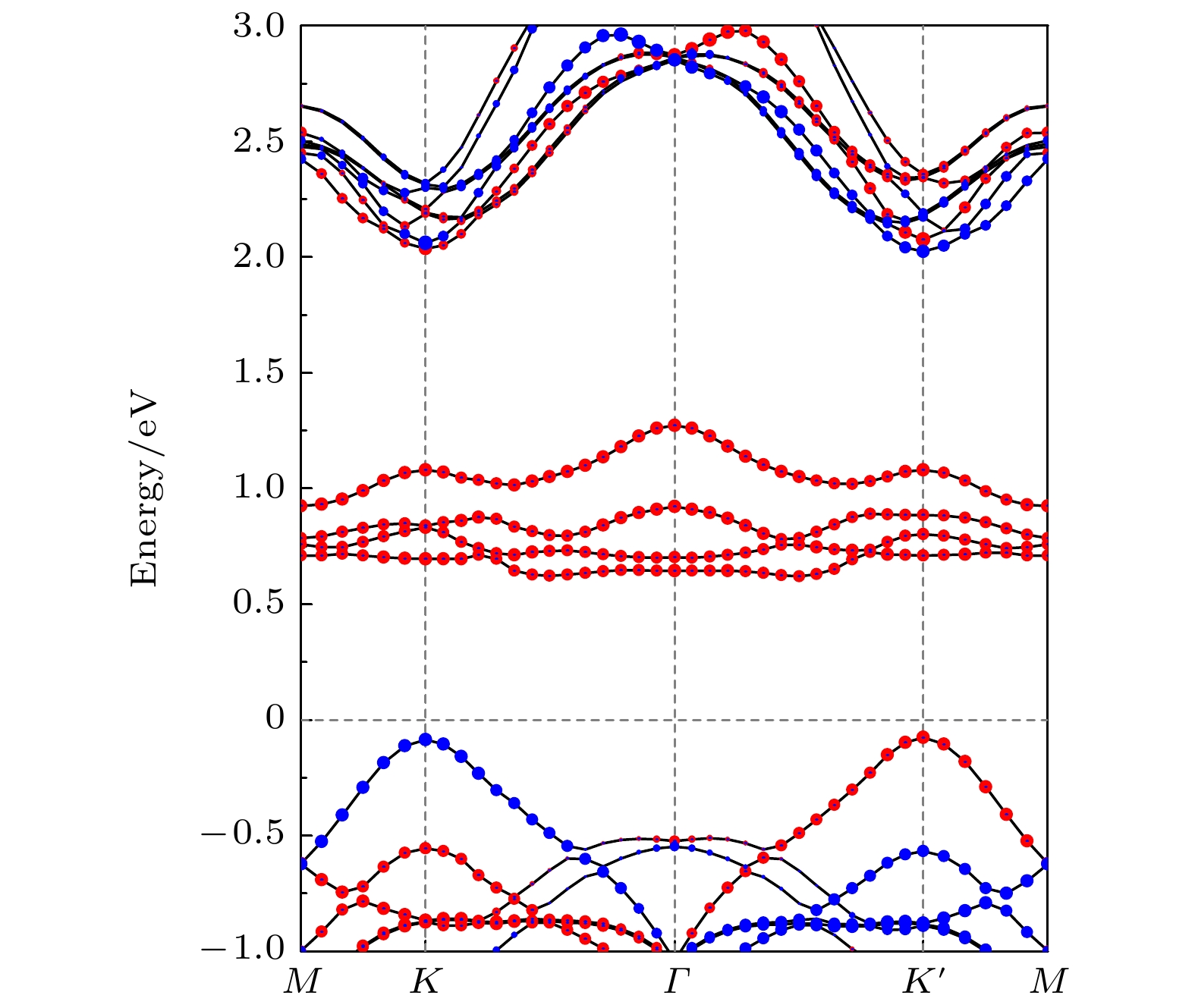
$ {E_ \downarrow }(K) \ne {E_ \uparrow }(K' ) $ , 如图3(b), (d)所示. Se构型的异质结在导带处出现大约2 meV的劈裂, 如图3(b)所示. 对于Te构型的异质结, 衬底CrI3的加入导致WSeTe在K与K' 处的能谷不再简并, 不仅在导带处出现大约2 meV的谷劈裂, 并且在价带处的能谷出现了更为明显的谷劈裂, K处谷为0.030 eV, K' 处为0.007 eV, 产生了大约23 meV的劈裂, 如图3(d)所示. 最终Se, Te构型异质结产生的谷极化分别为2 meV, 25 meV.Te构型WSeTe/CrI3异质结的原子投影能带如图4(a)所示. 可以看出, 能谷部分主要由W原子贡献, 导带与价带能谷间的能带主要由Cr原子贡献. 由图4(b)的层投影能带可以直观看出CrI3与WSeTe在能带中的贡献, WSeTe的能带形状得到了很好的保留. 由于WSeTe的能谷主要由过渡金属W贡献, 将Te构型WSeTe/CrI3能带对W原子Sz方向进行投影, 分别对应于自旋向上与自旋向下, 如图4(c)所示. K与K' 处的能谷具有相反的自旋态, 这种差异导致K与K' 处的能谷满足光学选择定则, 即可通过不相等的光学跃迁来区分能谷, 这使其有希望成为谷电子学领域应用的候选材料. Te构型相对于Se构型在价带出现较大谷劈裂的可能原因是Te堆叠下由W元素贡献的K' 价带谷与CrI3存在轨道杂化, 导致谷下移, 与K处价带谷形成大约23 meV劈裂. 由于杂化只能发生在相同的自旋通道的轨道之间, 因此具有相反自旋态的K处价带谷没有发生杂化. 而Se堆叠下W元素贡献的带与Cr元素贡献的带能量差距较大, 因此未发生杂化, 只产生了由层间磁近邻效应带来的K与K' 处发生在导带底大约2 meV的谷劈裂.
-
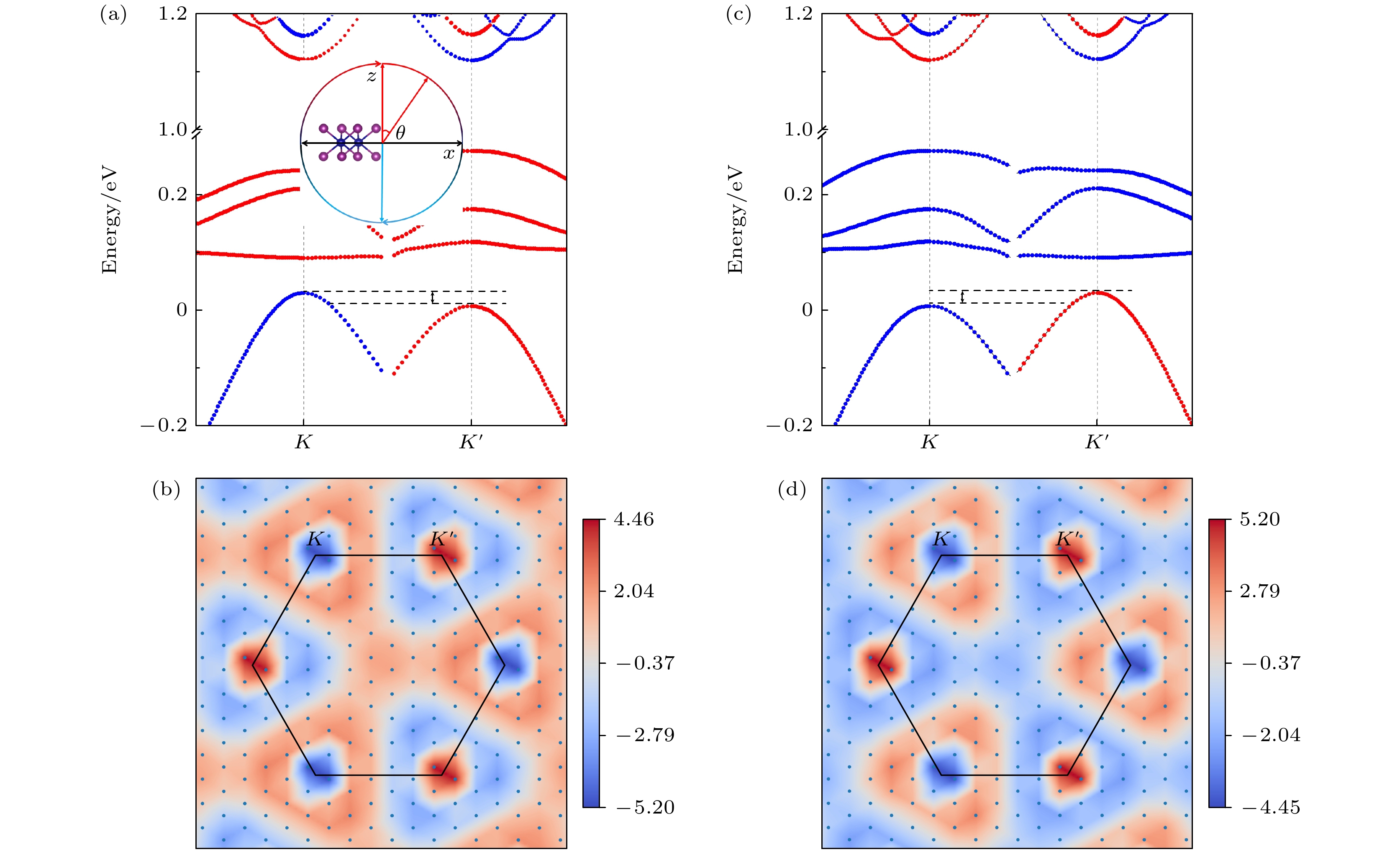
以上Te和Se构型异质结的计算结果中Cr原子的初始磁矩方向都为+Z (θ = 0°)方向. 已有研究结果表明衬底磁矩方向的设定也会影响能谷[26] , 通过比较不同自旋方向的能量得到异质结的易磁化轴是面外方向, 这与单层CrI3易磁化轴方向一致. 为了分析衬底磁矩方向对异质结能谷的调控, 对0°—360°不同磁矩方向的能谷进行对比 分析. 首先对θ = 0°和θ = 180°两种面外相反磁矩方向的能谷进行分析. 此外, 为了确认θ = 0°和θ = 180°磁矩方向WSeTe/CrI3异质结的Berry曲率, 使用VASPBERRY代码计算其Berry曲率[40]. 0°与180°(对应于+Z与–Z方向)磁矩方向的能带与Berry曲率如图5所示, 图5(a)中插图表示设定的磁矩方向, 将面外+Z方向定义为θ = 0°(360°). K 和K' 谷中具有相反的符号, 这表明这些谷中存在不同的伪磁场. 当磁矩方向θ由0°旋转为180°, K与K' 处的能谷劈裂大小不变方向转向, 如图5(a)和图5(c)所示. 谷劈裂方向反转的原因可能是磁矩方向的反转导致由CrI3主导的能带自旋方向反转, 由于杂化只能发生在方向相同的自旋通道, 因此, 原本发生在K' 价带谷处的杂化消失. CrI3自旋方向的反转导致在K价带谷W与Cr的eg轨道发生杂化, 最终导致谷劈裂与谷极化的方向反转. 为了进一步分析, 对两种模型的Berry曲率计算, 结果符合预期, 两种磁矩方向在K与K' 处的Berry曲率具有相反的值, 相当于K与K' 的能带进行了翻转, 结果如图5(b)和图5(d)所示.
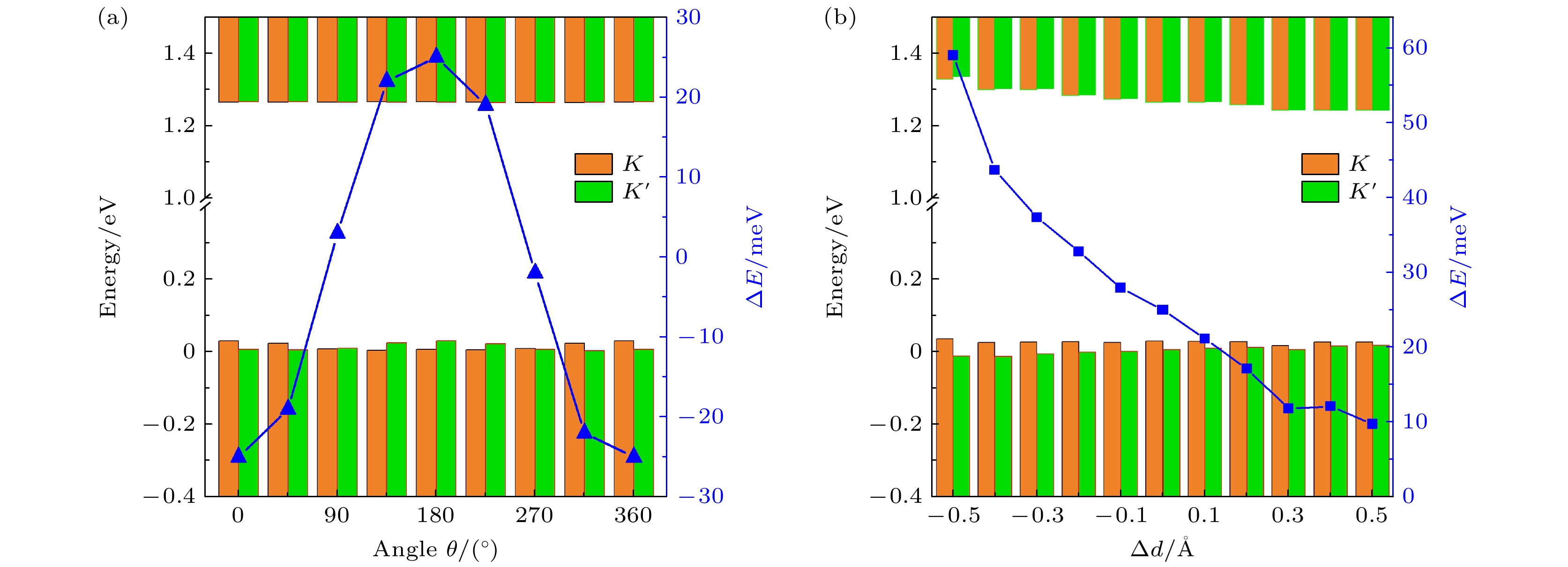
为了更全面地分析衬底磁矩方向对异质结能谷的调控, 对0°—360°不同磁矩方向下的能谷进行对比, 所有K与K' 能谷对比以及谷劈裂大小随磁矩方向变化规律如图6(a)所示. 图中柱状图代表不同磁矩方向下的能谷相对费米能级的能量, 蓝色线条代表不同磁矩方向谷极化
$\Delta {E_\sigma }$ 的大小. 导带部分能谷差异不大, 价带能谷在磁矩方向为0°和180°时差距最大, 对应于+Z与–Z方向. 磁矩方向为0°与180°时的$\Delta {E_\sigma }$ 具有极值, 分别为–25 meV和+25 meV. 随着磁矩方向由0°至180°的反转, K与K' 能谷也进行了反转, 由此谷极化的方向也发生正负反转, 大小几乎不变. 当磁矩方向平行于XY面, 即在面内90°和270°时谷极化为零. 随着磁矩360°旋转, 可控制谷极化在–25—25 meV变化, 由此可见改变磁矩方向是控制谷极化大小和方向的有效手段.为了探究层间距与谷劈裂之间的关系, 对Te构型的异质结施加不同垂直应变并分析其K与K' 能谷, 磁矩方向设置为+Z(θ = 0°). 从原始层间距改变–0.5—+0.5 Å的能谷情况如图6(b)所示, 其中横坐标表示层间距变化大小, 柱状图表示不同层间距下的能谷相对于费米能级的大小. 改变层间距会导致面内晶格常数变化, 但其变化幅度不大, 在1%以内. 对比本征WSeTe/CrI3, 随着层间距减小, 导带的能谷逐渐上移. 价带的能谷变化相较于导带更大, 由I和Te介导的Cr和W之间的交换耦合明显增强. 因此, 价带K处谷上移, K' 处谷下降, 最终导致异质结整体谷极化
$\Delta {E_\sigma }$ 的增大. 随着层间距逐渐增大, 导带能谷向下移动, 价带处K与K' 处的能谷劈裂逐渐减小并趋于相等. 可能的原因是一旦层间距离过大, 层间耦合变弱, 导致W原子与CrI3的eg轨道之间的杂化减弱. 整体的$\Delta {E_\sigma }$ 随层间距变化的规律如图6(b)中蓝线所示, 层间距减小0.5 Å,$\Delta {E_\sigma }$ 的值可由24.96 meV变为58.90 meV, 获得大幅增涨, 而增大层间距0.5 Å导致$\Delta {E_\sigma }$ 的值由24.96 meV变为9.74 meV, 减小了1/2以上. 可见通过施加垂直应变改变层间距是调控谷极化大小的有效方式. -
基于以上理论计算, 验证了WSeTe/CrI3是一种潜在的理想谷电子材料, 其具有较大的本征谷极化. 不同构型的异质结产生的谷极化大小差异较大, T堆叠方式下的Te构型产生的谷极化远大于Se构型. 这是由于Te构型下W元素贡献的K' 价带谷与CrI3存在轨道杂化, 导致谷下移. 改变衬底磁矩方向可以有效调控谷极化的大小和方向. 这是由于价带谷与CrI3的轨道杂化只能发生相同自旋通道, 而改变磁矩方向可使自旋方向发生改变, 从而调控谷极化. 通过模拟施加垂直应变减小层间距可以使得磁性衬底CrI3与WSeTe间的磁近邻效应增强, 实现对谷极化的大小调控.
-
本文通过第一性原理计算研究了WSeTe和CrI3的结构和电子能带结构. 单层WSeTe在布里渊区顶点K与K' 处存在一对简并能谷, 通过Berry曲率计算验证了能谷简并但不等价. 通过构建WSeTe/CrI3异质结可以解除谷简并, 为利用谷自由度处理和存储谷电子信息提供了可能. 计算了两种不同构型的范德瓦耳斯异质结构的能带, 不同构型所产生的谷极化大小有所差异, 可利用界面原子种类改变异质结构型来调控异质结的谷极化. T堆叠方式下Te构型由于W与CrI3发生轨道杂化, 所产生的谷极化远大于Se构型. 垂直应变改变层间距是调控WSeTe/CrI3异质结谷极化大小的有效方式. 此外, 通过改变衬底磁矩方向不仅能有效调控谷极化的大小, 而且可以调控谷极化的方向. 将磁矩方向由面外0°旋转至180°会得到相反的谷极化, K与K' 处的Berry曲率值发生相互交换. 本文研究结果在谷自由度操作为处理和存储量子信息提供了一种新的理论范例, 为谷电子学方面的应用提供了更多的选择.
-
WSeTe/CrI3范德瓦耳斯异质结能谷的调控
Valley manipulation in WSeTe/CrI3 van der Waals heterostructures: A first-principles study
-
摘要: 范德瓦耳斯异质结构为设计二维材料的电子、自旋特性提供了丰富的平台. 解除谷简并是利用谷自由度处理和存储谷电子信息的必要条件, 二维范德瓦耳斯异质结构中的邻近效应为定制邻近材料的电子能带结构提供了可控的方法. 本文基于第一性原理计算, 研究了 WSeTe /CrI3 范德瓦耳斯异质结的电子能带结构. 通过施加垂直应变与改变衬底磁矩方向对能谷进行调控. 单层WSeTe在K与K' 存在一对简并能谷, 在自旋-轨道耦合作用与磁性衬底CrI3邻近效应作用下会产生较大的谷劈裂和谷极化. 异质结产生的谷极化为25 meV. 施加垂直应变可以有效地调节能谷极化, 减小层间距可以增大谷极化. 此外, 衬底磁矩方向变化可以有效调控谷极化的方向和大小. 本文研究结果为谷自由度的调控提供了一个有效的方法, 为谷电子学和自旋电子学的应用提供了新的途径.Abstract: The valley degree of freedom, besides charge and spin, can be used to process information and perform logic operations as well, with the advantage of low power consumption and high speed. The effective manipulation of valley degrees of freedom is essential for their practical applications in valleytronics and spintronics. In this work, the effective strategy is investigated for the valley manipulation of the WSeTe/CrI3 van der Waals heterojunction with about 2% lattice mismatch by the first-principles calculations. The valley degree of freedom in WSeTe can be modulated by the magnetism of Cr atoms in the substrate via the magnetic proximity effect, including the vertical strain method and the rotation of the magnetic moments of Cr atoms. First-principles calculations are performed by using the VASP software package with the generalized gradient approximation functional in PerdewBurke-Ernzerhof (PBE) form. The spin-orbit coupling is considered when calculating the band structure to investigate the valley properties. The dependence of valley polarization on both vertical strain and the substrate’s magnetic moment direction has been systematically analyzed. There are two different stacking configurations for the WSeTe/CrI3 heterojunction with Te/Se atoms at the interface, namely Te-stacking and Se-stacking. Although single-layer WSeTe does not have valley polarization, the Te-stacked and Se-stacked WSeTe/CrI3 heterojunctions exhibit valley polarizations of 25 meV and 2 meV, respectively, which is influenced by spin-orbit coupling and the proximity effect of the magnetic substrate CrI3, indicating the importance of the stack configuration. The Te-stacked configuration of the heterojunction has a larger valley polarization due to stronger orbital hybridization between W atoms in WSeTe layer and Cr atoms in CrI3 layer. The application of vertical strain, which effectively tunes the interlayer distance, significantly regulates the valley polarization. Specifically, the valley polarization is increased to 59 meV when the interlayer distance decreases by 0.5 Å, while it decreases to 10 meV when the interlayer distance increases by 0.5 Å. Additionally, when the magnetic moment of the CrI3 substrate rotates by 360°, the valley polarization changes between –25 meV and 25 meV. It reaches a maximum value when the magnetic moment is aligned along the out-of-plane direction. This study demonstrates that the valley degree of freedom in the WSeTe/CrI3 van der Waals heterojunction can be effectively manipulated by adjusting the interlayer distance through vertical strain and by controlling the magnetic moment direction of the substrate. These findings provide valuable insights into the design and application of valleytronic and spintronic devices based on two-dimensional van der Waals heterostructures.
-
Key words:
- valley /
- heterojunction /
- magnetic proximity /
- first principles .
-

-
图 3 WSeTe/CrI3异质结能带图 (a)不考虑SOC的Se构型; (b)考虑SOC的Se构型; (c)不考虑SOC的Te构型; (d)考虑SOC的Te构型; 蓝色虚线代表自旋向下, 红色实线代表自旋向上; 插图为能谷放大视图
Figure 3. Band structures of WSeTe/CrI3: (a) The band structures of Se model without SOC; (b) the band structures of Se model with SOC; (c) the band structures of Te model without SOC; (d) the band structures of Te model with SOC, the blue dashed lines represent spin-down, and the red lines represent spin-up. The insets are enlarged local views.
图 4 WSeTe/CrI3异质结Te构型的投影能带图 (a)原子投影能带; (b) CrI3与WSeTe层投影能带; (c) W原子Sz方向自旋投影能带, 其中红色和蓝色代表自旋向上和向下的能带,
${E_\sigma }$ 代表导带谷到价带谷的能量差Figure 4. Projected band structures of the Te-model WSeTe/CrI3 heterojunction: (a) Atom projected band structures; (b) layer projected band structures of CrI3 and WSeTe; (c) projected band structures of W along the Sz direction of spin, where the red and blue circles correspond to spin-up and spin-down bands,
${E_\sigma }$ represents the energy difference from the conduction band valley to the valence band valley.图 5 K与K' 附近能带与Berry曲率 (a)磁矩+Z (θ = 0°)方向的能带, 插图为磁矩方向示意图; (b) 磁矩+Z (θ = 0°)方向的Berry曲率; (c)磁矩–Z (θ = 180°)方向的能带; (d)磁矩–Z (θ = 180°)方向的Berry曲率; 红色和蓝色代表自旋向上和向下的能带
Figure 5. Bands and Berry curvature near the K and K' points: (a) Band structures for the magnetic moment along the +Z (θ = 0°) direction, with an inset diagram illustrating the direction of the magnetic moment; (b) Berry curvature for the magnetic moment along the +Z (θ = 0°) direction; (c) bands structures for the magnetic moment along the –Z (θ = 180°) direction; (d) Berry curvature for the magnetic moment along the –Z (θ = 180°) direction; the red and blue circles correspond to spin-up and spin-down bands.
图 6 (a)不同Cr磁矩方向的能谷及谷极化大小, 其中蓝色线条代表不同磁矩方向下的谷极化; (b)不同层间距下能谷及谷极化大小, 其中蓝色线条代表不同层间距下的谷极化
${\text{|}}\Delta {E_\sigma }{\text{|}}$ 大小; 橙色和绿色柱状图分别表示了K与K' 处谷的能量Figure 6. (a) Valley and valley polarization for different Cr magnetic moments, where blue lines represent the valley polarization under different magnetization angles; (b) valley and valley polarization under different interlayer distance, where blue lines represent the valley polarization magnitudes at different interlayer distance. The orange and green bar charts indicate the energy of the valleys at the K and K' , respectively.
表 A1 6种不同结构的晶格常数、层间距和结合能
Table A1. Lattice constant, interlayer distance, and binding energy for six different models.
堆叠方式 晶格常数a = b/Å 层间距d/Å 结合能Eb/eV T-Te 6.84 3.79 –3.59 T-Se 6.84 3.61 –3.58 H-Te 6.83 3.85 –3.52 H-Se 6.83 3.67 –3.51 R-Te 6.84 3.78 –3.58 R-Se 6.84 3.52 –3.58 -
[1] Gunawan O, Shkolnikov Y P, Vakili K, Gokmen T, De Poortere E P, Shayegan M 2006 Phys. Rev. Lett. 97 186404 doi: 10.1103/PhysRevLett.97.186404 [2] Rycerz A, Tworzydło J, Beenakker C W J 2007 Nat. Phys. 3 172 doi: 10.1038/nphys547 [3] Sun Z H, Guan H M, Fu L, Shen B, Tang N 2021 Acta Phys. Sin. 70 027302 [孙真昊, 管鸿明, 付雷, 沈波, 唐宁 2021 物理学报 70 027302] doi: 10.7498/aps.70.20201415 Sun Z H, Guan H M, Fu L, Shen B, Tang N 2021 Acta Phys. Sin. 70 027302 doi: 10.7498/aps.70.20201415 [4] Schaibley J R, Yu H, Clark G, Rivera P, Ross J S, Seyler K L, Yao W, Xu X 2016 Nat. Rev. Mater. 1 16055 doi: 10.1038/natrevmats.2016.55 [5] Xiao D, Liu G B, Feng W, Xu X, Yao W 2012 Phys. Rev. Lett. 108 196802 doi: 10.1103/PhysRevLett.108.196802 [6] Aivazian G, Gong Z, Jones A M, Chu R L, Yan J, Mandrus D G, Zhang C, Cobden D, Yao W, Xu X 2015 Nat. Phys. 11 148 doi: 10.1038/nphys3201 [7] MacNeill D, Heikes C, Mak K F, Anderson Z, Kormanyos A, Zolyomi V, Park J, Ralph D C 2015 Phys. Rev. Lett. 114 037401 doi: 10.1103/PhysRevLett.114.037401 [8] Srivastava A, Sidler M, Allain A V, Lembke D S, Kis A, Imamoğlu A 2015 Nat. Phys. 11 141 doi: 10.1038/nphys3203 [9] Xu S, Si C, Li Y, Gu B L, Duan W 2021 Nano Lett. 21 1785 doi: 10.1021/acs.nanolett.0c04670 [10] Cheng Y C, Zhang Q Y, Schwingenschlögl U 2014 Phys. Rev. B 89 155429 doi: 10.1103/PhysRevB.89.155429 [11] Ramasubramaniam A, Naveh D 2013 Phys. Rev. B 87 195201 doi: 10.1103/PhysRevB.87.195201 [12] 张德贺, 周文哲, 李奥林, 欧阳方平 2021 物理学报 70 096301 doi: 10.7498/aps.70.20201888 Zhang D H, Zhou W Z, Li A L, Ouyang F P 2021 Acta Phys. Sin. 70 096301 doi: 10.7498/aps.70.20201888 [13] Qi J S, Li X, Niu Q, Feng J 2015 Phys. Rev. B 92 121403 doi: 10.1103/PhysRevB.92.121403 [14] Zhang Q, Yang S A, Mi W, Cheng Y, Schwingenschlogl U 2016 Adv. Mater. 28 959 doi: 10.1002/adma.201502585 [15] Zheng G B, Zhang B, Duan H M, Zhou W Z, Ouyang F P 2023 Physica E 148 115616 doi: 10.1016/j.physe.2022.115616 [16] 邓霖湄, 司君山, 吴绪才, 张卫兵 2022 物理学报 71 147101 doi: 10.7498/aps.71.20220326 Deng L M, Si J S, Wu X C, Zhang W B 2022 Acta Phys. Sin. 71 147101 doi: 10.7498/aps.71.20220326 [17] Yao W, Xiao D, Niu Q 2008 Phys. Rev. B 77 235406 doi: 10.1103/PhysRevB.77.235406 [18] Mak K F, He K, Shan J, Heinz T F 2012 Nat. Nanotechnol. 7 494 doi: 10.1038/nnano.2012.96 [19] Liu H, Zhang Z, Li Y, Wu Y, Wu Z, Li X, Zhang C, Xu F, Kang J 2023 Adv. Photon. Nexus 2 026007 doi: 10.1117/1.apn.2.2.026007 [20] Stier A V, McCreary K M, Jonker B T, Kono J, Crooker S A 2016 Nat. Commun. 7 10643 doi: 10.1038/ncomms10643 [21] Abid A, Haneef M, Ali S, Dahshan A 2022 J. Solid State Chem. 311 123159 doi: 10.1016/j.jssc.2022.123159 [22] Mehdipour H, Kratzer P 2024 Phys. Rev. B 109 085425 doi: 10.1103/PhysRevB.109.085425 [23] Sattar S, Larsson J A, Canali C M, Roche S, Garcia J H 2022 Phys. Rev. B 105 L041402 doi: 10.1103/PhysRevB.105.L041402 [24] Norden T, Zhao C, Zhang P, Sabirianov R, Petrou A, Zeng H 2019 Nat. Commun. 10 4163 doi: 10.1038/s41467-019-11966-4 [25] Hu T, Zhao G D, Gao H, Wu Y B, Hong J S, Stroppa A, Ren W 2020 Phys. Rev. B 101 125401 doi: 10.1103/PhysRevB.101.125401 [26] Zhang W L, Zhu H R, Zhang W Q, Wang J, Zhang T T, Yang S R, Shao B, Zuo X 2024 Appl. Surf. Sci. 647 158986 doi: 10.1016/j.apsusc.2023.158986 [27] Ye Y, Xiao J, Wang H L, Ye Z L, Zhu H R, Zhao M, Wang Y, Zhao J H, Yin X B, Zhang X 2016 Nat. Nanotechnol. 11 598 doi: 10.1038/nnano.2016.49 [28] Lu A Y, Zhu H R, Xiao J, Chuu C P, Han Y, Chiu M H, Cheng C C, Yang C W, Wei K H, Yang Y, Wang Y, Sokaras D, Nordlund D, Yang P, Muller D A, Chou M Y, Zhang X, Li L J 2017 Nat. Nanotechnol. 12 744 doi: 10.1038/nnano.2017.100 [29] Zhang J, Jia S, Kholmanov I, Dong L, Er D, Chen W, Guo H, Jin Z, Shenoy V B, Shi L, Lou J 2017 ACS Nano 11 8192 doi: 10.1021/acsnano.7b03186 [30] Hajra D, Sailus R, Blei M, Yumigeta K, Shen Y, Tongay S 2020 ACS Nano 14 15626 doi: 10.1021/acsnano.0c06434 [31] Trivedi D B, Turgut G, Qin Y, Sayyad M Y, Hajra D, Howell M, Liu L, Yang S, Patoary N H, Li H, Petric M M, Meyer M, Kremser M, Barbone M, Soavi G, Stier A V, Muller K, Yang S, Esqueda I S, Zhuang H, Finley J J, Tongay S 2020 Adv. Mater. 32 2006320 doi: 10.1002/adma.202006320 [32] Yang S Y, Shi D R, Wang T, Yue X Y, Zheng L, Zhang Q H, Gu L, Yang X Q, Shadike Z, Li H, Fu Z W 2020 J. Mater. Chem. A 8 25739 doi: 10.1039/D0TA08012H [33] Guo S D, Zhu J X, Yin M Y, Liu B G 2022 Phys. Rev. B 105 104416 doi: 10.1103/PhysRevB.105.104416 [34] Zhang L, Zhao Y, Liu Y, Gao G 2023 Nanoscale 15 18910 doi: 10.1039/D3NR04627C [35] Chen Y K, Zhao X S, An Y K 2024 Phys. Rev. B 109 125421 doi: 10.1103/PhysRevB.109.125421 [36] Kresse G, Furthmuller J 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169 [37] Grimme S, Antony J, Ehrlich S, Krieg H 2010 J. Chem. Phys. 132 154104 doi: 10.1063/1.3382344 [38] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 doi: 10.1103/PhysRevB.13.5188 [39] Dudarev S L, Botton G A, Savrasov S Y, Humphreys C, Sutton A P 1998 Phys. Rev. B 57 1505 doi: 10.1103/PhysRevB.57.1505 [40] Kim H J https://github.com/Infant83/VASPBERRY [2024-7-11] [41] Hu T, Jia F H, Zhao G D, Wu J Y, Stroppa A, Ren W 2018 Phys. Rev. B 97 235404 doi: 10.1103/PhysRevB.97.235404 [42] Webster L, Yan J A 2018 Phys. Rev. B 98 144411 doi: 10.1103/PhysRevB.98.144411 [43] Ma Z, Huang P, Li J, Zhang P, Zheng J X, Xiong W, Wang F, Zhang X W 2022 npj Comput. Mater. 8 11 doi: 10.1038/s41524-022-00697-8 [44] Zhang H J, Li Y F, Hou J H, Du A J, Chen Z F 2016 Nano Lett. 16 6124 doi: 10.1021/acs.nanolett.6b02335 [45] Shao Y, Shao M, Kawazoe Y, Shi X, Pan H 2018 J. Mater. Chem. A 6 10226 doi: 10.1039/C8TA00635K [46] Yang C, Li J, Liu X L, Bai C L 2023 Phys. Chem. Chem. Phys. 25 28796 doi: 10.1039/D3CP03331G -


 首页
首页 登录
登录 注册
注册



 下载:
下载: