-
雷达散射截面(radar cross section, RCS)是物体在雷达照射下所产生回波强度的一种物理量, 是衡量目标隐身能力强弱的最重要指标. 随着雷达探测技术的发展, 通过RCS减缩从而降低目标的可探测性, 已成为雷达隐身技术的研究前沿[1-8]. 实现RCS减缩的传统方法主要是改变目标的形状结构[6]及使用吸波材料[7,8]. 形状结构的改变会影响目标的机动性能, 而吸波材料通常存在厚度较大、质量较重和成本昂贵等问题. 超材料具有轻薄、成本低、可实现电磁波灵活调控等传统雷达吸波材料不具备的优良特性, 为目标RCS减缩提供了全新的设计思路[9-27].
超材料是由亚波长尺寸单元按照特定规律排列而形成的人工材料, 可实现自然界材料无法实现的奇异电磁特性. 超表面是超材料的二维形态, 通过在平面上排列亚波长尺寸的结构单元实现与三维超材料类似的电磁特性. 应用于隐身技术的超表面, 通常可分为吸波型超表面[9-11]和散射型超表面[12-25]. 吸波型超表面主要通过将电磁波能量转换为热能实现隐身效果, 但存在能量热转换引起红外频段被探测概率升高的弊端. 2011年, Yu等[12]提出了广义斯涅尔定律, 基于这一定律, Gao等[13]设计了由 V 形单元组成的超表面, 通过改变单元几何形状及排列方式, 可以有效地操纵电磁波的散射特性. 散射型超表面通常可分为单波束型、多波束型和漫反射型超表面[14]. 单波束散射超表面适用于单基地雷达探测, 通过将主要回波能量转移到非威胁方向, 即可实现单站RCS减缩. 而随着雷达探测组网的发展, 在双/多基地雷达探测下, 探测信号的发射与接收将处于不同位置, 能量转移这类“拆东墙补西墙”的隐身方式将不再适用. 因此, 增加散射波束数量成为实现双站RCS减缩的关键途径, Paquay等[15]用AMC单元及棋盘排列结构, 实现了4波束的相位对消功能, 获得了窄带单站RCS减缩效果. 基于上述工作, 研究人员通过进一步改进单元的相位带宽, 实现了单站RCS减缩带宽的拓展[16,17]. 然而, 有限数量散射、固定方向传播的波束限制了棋盘结构对消超表面在全空间双站RCS减缩中的应用.
2014年, Cui等[18]提出了数字编码超表面, 利用1 bit和2 bit数字相位, 实现了散射波束全空间漫反射效果, 这类数字编码超表面可将能量重新分配在全空间各个角度, 从而降低每个方向被探测的概率. 2017年, Liu等[19]使用遍历算法优化1 bit数字编码超表面的单元编码序列, 在频带5.5—7.37 GHz内实现了10 dB以上的单站RCS减缩和漫反射. 这类数字编码相位分布具有设计逻辑简单、优化维度低、参数少等优势, 但其整行/列的编码优化策略, 使得其表面相位分布自由度低, 波束发散程度有限. 全局优化相位则是将超表面 的反射相位分布视作高维的多目标优化问题, 通过全局搜索方法在给定的目标函数下迭代寻优, 可 打破整行/列的固有优化模式, 使相位分布更加 多样, 波束控制更加灵活自由. Fu等[20]提出了基于Pancharatnam-Berry单元的双频带1 bit数 字相位, 利用遗传算法(genetic algorithm, GA)对超表面相位分布优化, 实现了9.26—12.87 GHz与14.84—19.35 GHz双频带的漫反射效果; Li等[21]提出了一种基于透射、吸收与极化转换的2 bit数字超表面, 利用SA并结合天线阵列理论优化相位分布, 在4.4—16.3 GHz实现了 10 dB以上的RCS减缩. Qi等[22]通过卷积操作优化单元设计, 同时用粒子群算法(particle swarm optimization, PSO)对2 bit单元相位分布优化, 实现了15.5—40 GHz的RCS减缩. 面对多参数、多目标的复杂问题, 采用传统优化算法往往存在计算开销大、易陷入局部最优等效率低、性能差的问题. 为此, 近年来有研究通过引入机器学习实现超表面的相位分布优化设计[14,23-25]. Tao等[24]实现了基于神经网络的波束调控超表面设计, 通过学习相位分布与反射波束的复杂关系, 使用训练好的模型成功对散射波进行调控和预测, 准确率达到了94%; 杨雨欣[25]介绍了一种基于VGG网络的卷积神经网络模型, 实现了对单波束的调控, 准确率达到了96%. 但上述工作仅对单波束和多波束进行调控, 并未将具有全空间最值特性的复杂双站RCS减缩问题作为优化目标.
鉴于此, 本文提出了一种基于卷积神经网络的双站RCS减缩超表面设计方法, 以实现全空间均匀的漫反射效果和双站RCS减缩. 该方法采用模拟退火混合粒子群算法(PSO-SA)结合天线阵列理论优化相位分布, 将优化后的相位分布作为特征提取对象, 同时构建了包含双站RCS损失、相位分布损失和正则化损失的自定义损失函数, 从而充分挖掘相位分布与回波散射峰值之间的复杂关系, 得到最优相位分布. 在对样本数据进行训练后, 训练损失曲线和验证损失曲线基本一致, 表明模型具有良好的稳定性和泛化能力, 可以直接根据输入的随机相位快速得到经过模型优化后的相位分布. 通过将随机初始相位多次输入至训练完成的模型中, 其结果标准差仅为0.013, 说明模型具有良好的鲁棒性. 仿真与实测结果表明: 在预设中心频点处, 相较于传统优化算法, 双站 RCS值由5.2 dBms降低至3.8 dBms, 减缩效果提升了26.92%; 且在7.26—10.74 GHz可实现10 dB 以上的双站RCS减缩, 相比传统优化算法减缩效果提升17.2%. 综上, 基于深度卷积神经网络的相位分布优化方法, 能够使散射波在全空间每个角度都达到低能量状态, 从而进一步提升双站RCS减缩性能, 同时具备输入到输出的毫秒级响应能力, 有望为雷达组网探测下目标隐身性能的提升提供新的设计思路.
-
样本的质量很大程度上会影响模型的性能, 因此, 本节旨在对比不同算法对相位分布优化的效果. 通过评估GA, PSO, 杂交粒子群算法(PSO-GA)以及PSO-SA对双站RCS的减缩效果, 选取高质量样本. 根据天线阵列理论[28,29], 对于一个由
$ N \times M $ 个单元组成的超表面阵列, 其远场散射电场可以表示为其中θ和φ分别是散射波的俯仰角和方位角;
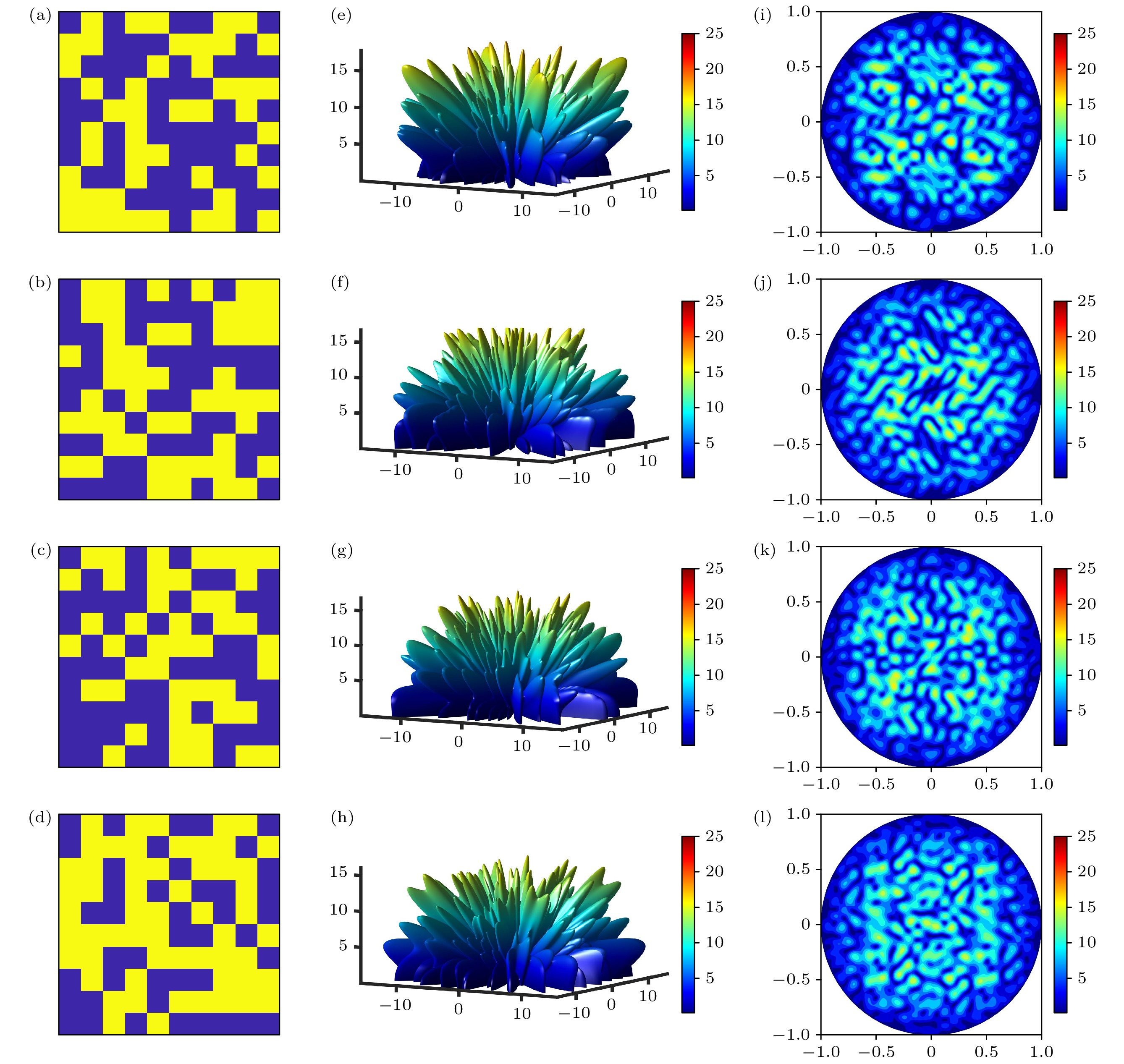
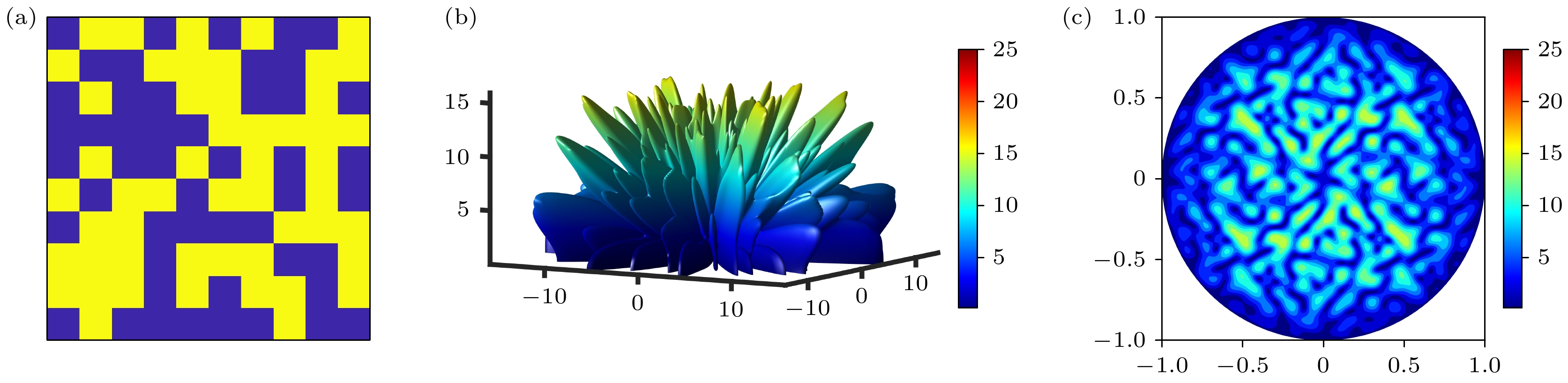
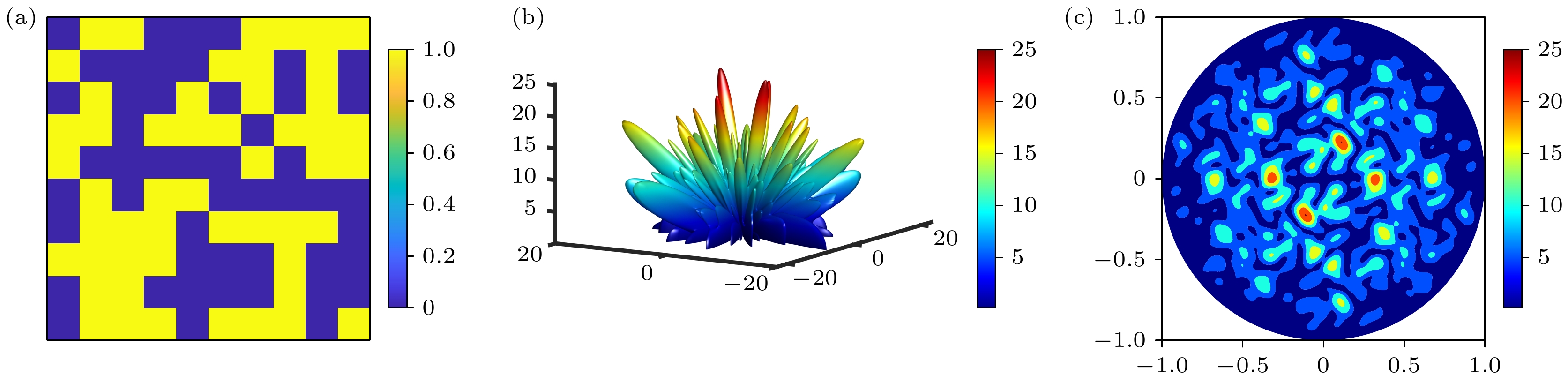
$ \theta_i $ 和$ \varphi_i $ 分别是入射波的俯仰角和方位角;$ f_{\mathrm{s}}(\theta , \varphi ) $ 为单元的方向性函数;$ \varphi (m, n) $ 是单元的反射相位;$ k = 2\pi /\lambda $ 是自由空间的波数, λ为波长; D (mm)为超表面的单元周期. (1)式考虑了入射波和散射波之间的角度关系, 适用于任意入射和散射角度的组合, 体现了双站RCS的特性. 从电磁波传播理论的角度, 超表面单元的反射相位$ \varphi (m, n) $ 通过调控散射波的相位延迟, 影响远场电场的相干叠加. 当相位分布呈现随机性或特定梯度时, 不同单元的散射波在远场发生相长或相消干涉, 从而改变能量在空间中的分布. 例如, 周期性相位分布会导致能量集中在特定方向(如镜面反射方向), 而优化后的相位分布可通过破坏相位的空间相干性, 使散射能量分散至全空间各角度, 降低双站RCS的峰值. 在电磁波垂直入射时, 超表面的远场散射与相位分布$ \varphi (m, n) $ 和单元周期D相关. 因此, 可以通过改变超表面的相位分布来控制远场散射方向图. 在确定超表面单元周期D的前提下, 优化相位分布可以实现对超表面远场分布的快速控制. 在双站RCS减缩目标下, 优化算法旨在最小化远场散射函数的峰值, 因此适合该问题的适应度函数定义如下:全空间均匀散射的实现依赖于相位分布的去相关特性. 优化算法通过引入二值化相位编码(0°与180°), 在超表面相邻单元间形成剧烈的相位跳变, 导致散射波前畸变, 这种畸变使远场散射波在空间上产生多波束干涉, 统计上表现为能量均匀分布, 从而在双站探测中降低任意方向的RCS值. 以火控雷达的主要工作频段X波段(8—12 GHz)为预设频率, 确定单元尺寸为30 mm, 超表面阵面大小为300 mm × 300 mm. 使用“0”和“1”分别表示1 bit数字相位中0°和180°两种反射相位, 对各算法的初始相位分布进行统一设置. 使用Random函数生成的随机相位作为对照组, 根据(1)式, 可以得到随机相位分布及其三维(3D)远场图和二维(2D)远场图, 如图1所示. 经过上述 GA[30], PSO[31], PSO-GA和PSO-SA[32]四种算法对该随机相位优化后的结果作为实验组, 得到的相位分布及其3D 远场图和2D远场图如图2所示.
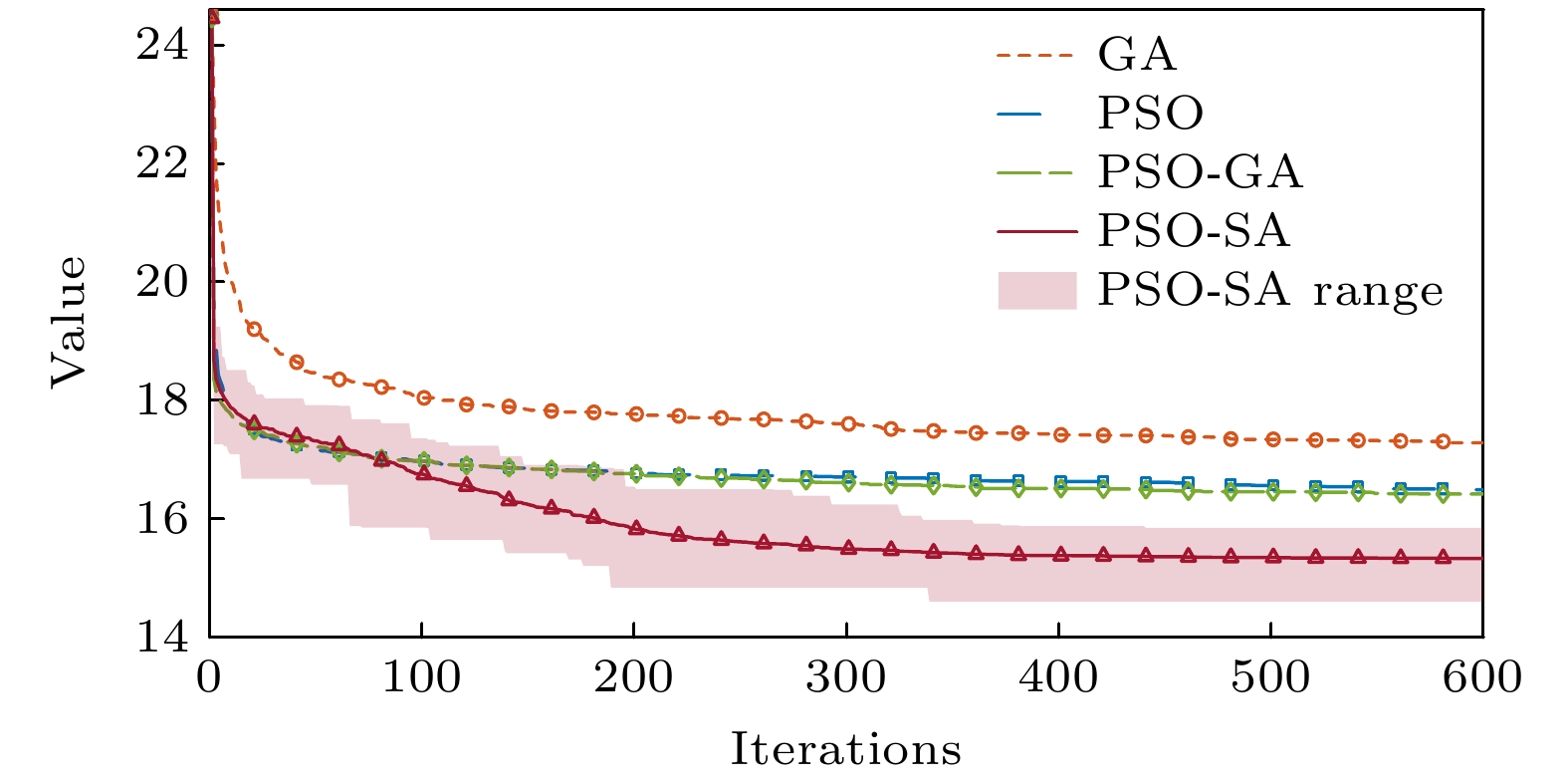
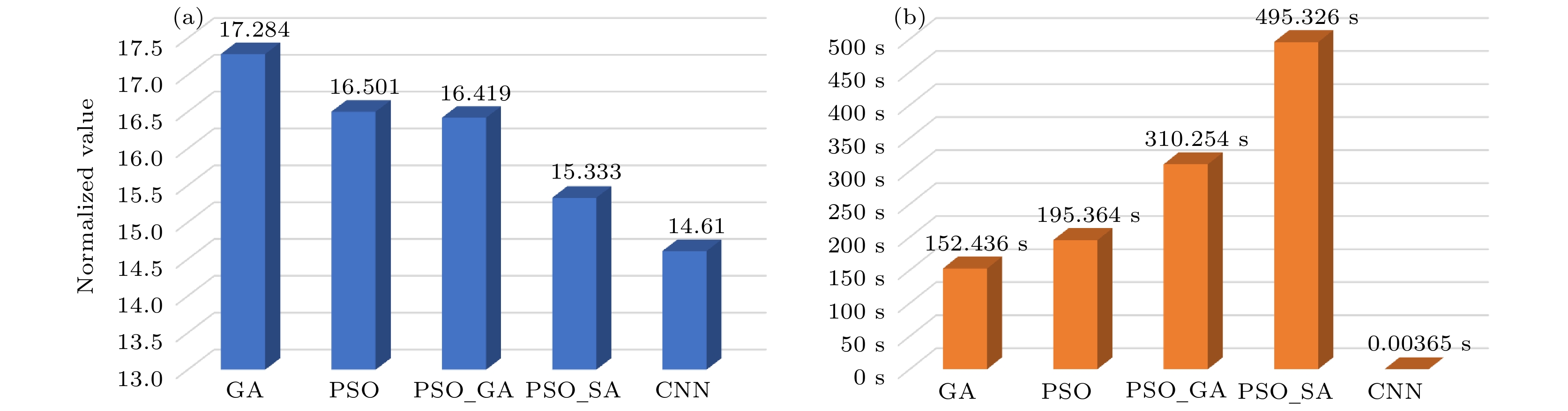
可以看出, 无论哪种优化算法相比对照组都可以实现更好的漫反射效果. GA通过遗传机制(选择、交叉、变异)逐步逼近最优解; PSO利用群体智能, 每个粒子随当前最优解移动; PSO-GA则在迭代过程中随机选取粒子进行杂交, 增强全局搜索能力; PSO-SA结合了PSO的全局搜索与SA的局部优化优势, 更易获得全局最优解. 经实验组各算法对相位分布优化后, 双站RCS值(远场散射峰值)分别降低至17.284, 16.501, 16.419和15.333(对照组为24.455). 为确保结果不失一般性, 累计执行100次运算, 每次运行时均记录RCS值随迭代次数的变化曲线并取平均, 结果如图3所示, 其中红色阴影区域表示在100次独立实验中, 每个 迭代步骤的最大值和最小值之间的范围. 该范围展示了不同实验运行中的变化, 图例中阴影区域标记为‘PSO-SA Range’. 相比PSO-SA, 其他算法在全局最优搜索过程中存在易陷入局部最优而导致性能较差的问题. 尽管通过PSO-SA优化后得到的RCS值最低, 但其运行时间长, 计算资源消耗大. 为兼顾性能与效率, 本文采用CNN学习样本特征, 进一步优化相位分布, 同时提升运算速率. 为了确保输入样本的质量, 选择PSO-SA对随机相位优化, 并将优化后的相位分布及其对应的远场散射峰值作为特征提取对象. 鉴于设备计算能力的限制, 共生成了3300个数据样本, 因此, 模型基于小样本的架构进行搭建.
-
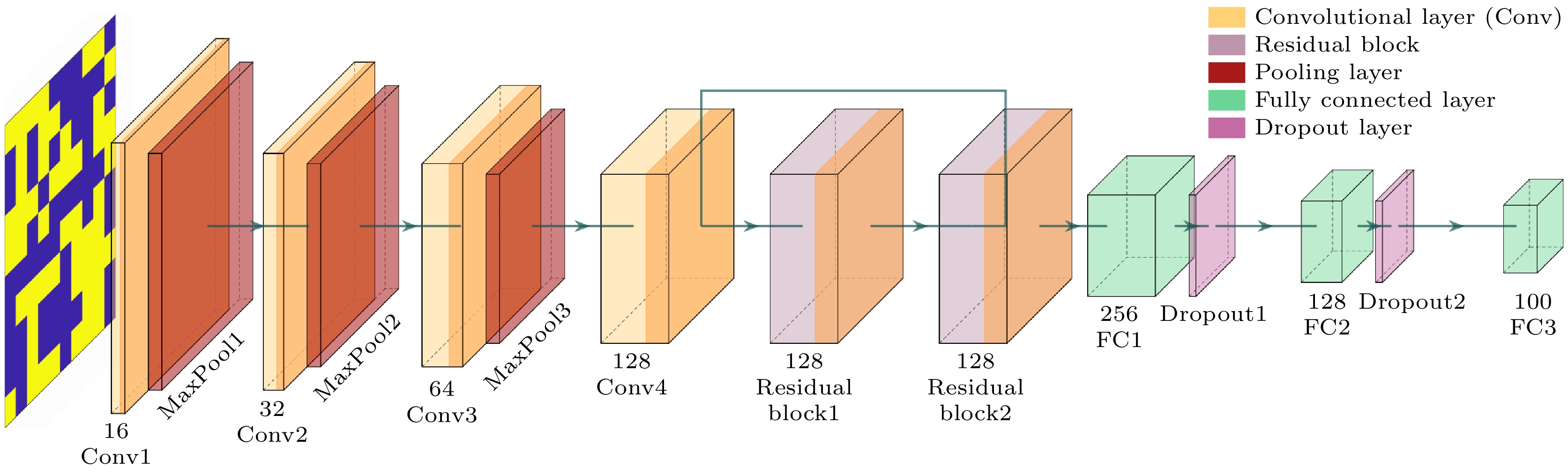
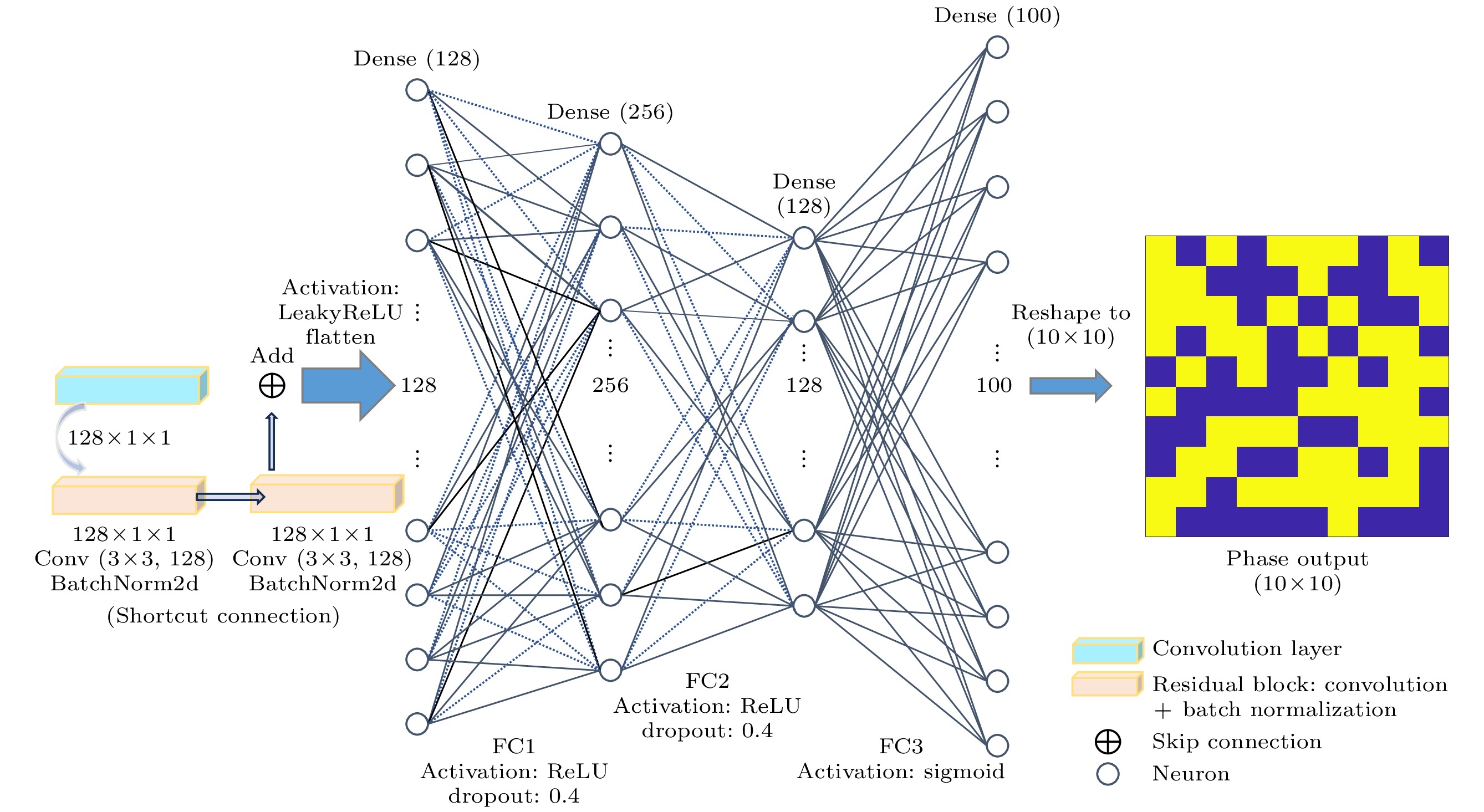
CNN模型如图4所示, 由卷积特征提取模块、残差增强模块、全连接优化模块组成. 具体包括: 输入层、四层卷积层、两个残差块、全连接层以及输出层. 输入输出均为
$ 1\times 10\times 10 $ 的相位矩阵, 其中卷积层用于提取输入数据的空间特征, 残差块用于增强模型的非线性表达能力, 全连接层用于将特征映射为相位分布. -
输入层的输入为
$ 1 \times 10 \times 10 $ 的初始相位分布矩阵, 使用“0”和“1”分别表示1 bit数字相位中0°和180°两种反射相位. -
卷积特征提取模块包括卷积层和池化层, 分别用于特征提取和降维. 卷积层通过在输入矩阵上滑动同一个卷积核(即权重共享), 对不同局部区域进行卷积运算, 从而提取局部特征并逐层捕获相位分布的空间特性. 卷积层的步长(stride)及填充操作(padding)均默认为1. 池化层则在卷积层之后对特征图进行降维处理, 减少空间尺寸, 降低参数量和计算复杂度. 这一过程有助于消除冗余信息, 使后续网络层能更高效地学习样本特征.
第一层卷积(conv1)输出16个特征图, 通过对输入数据使用
$ 3\times 3 $ 的卷积核, 生成大小为$ 16 \times 10 \times 10 $ 的特征图, 其表达式为[33]其中
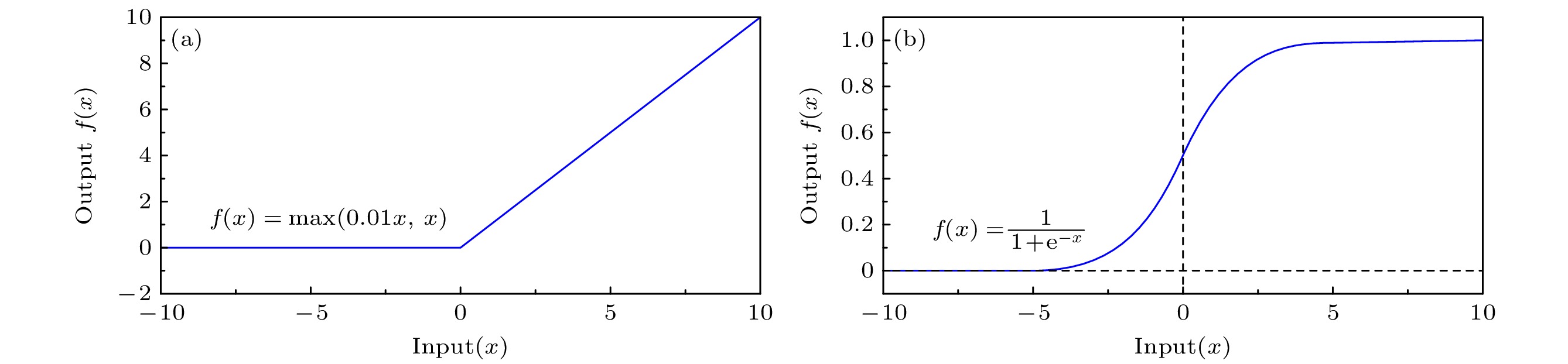
$ {{{\boldsymbol{W}}}^{(1)}} $ 为第一层的卷积核权重矩阵,$ {{b}^{(1)}} $ 为偏置,$ * $ 为卷积运算,$ f(\cdot ) $ 为激活函数 Leaky ReLU, 激活函数的表达式为[34]其中, α 是 x 为负数时的一个系数, 用来控制负斜率的角度, 默认值为 0.01. 使用 Leaky ReLU 激活函数可以缓解梯度消失的问题, 同时提升了模型的非线性表达能力, 其函数如图5(a)所示. 批量归一化(BatchNorm)用于对卷积层的输出进行标准化处理, 使特征的均值为 0, 方差为 1, 加快了模型的收敛速度并提高网络的稳定性, BatchNorm的计算公式为[35]
其中,
$ x_{{\mathrm{B}}} $ 为输入特征, μ和$ {{\sigma }^{2}} $ 分别为小批量数据(mini-batch)的均值和方差, ε为防止除零的常数. 随后, 对特征图进行大小为$ 2 \times 2 $ 、步幅为2的最大池化(max pooling)操作, 将特征图尺寸缩小为$ 16 \times 5 \times 5 $ . 最大池化通过在每个池化窗口(R)内选择最大值来减少空间维度, 并提升特征的鲁棒性. 其计算公式如下:其中, X为输入特征图,
$ Y_{ij} $ 表示池化后在位置$ (i, j) $ 的输出特征. R大小为$ 2 \times 2 $ , 定义了窗口内的偏移范围. 在位置$ (i, j) $ 处的输出$ Y_{ij} $ 取决于输入特征图在对应池化窗口内的最大值.第二层卷积(conv2)将特征图数量扩展至32 个, 使用了
$ 3\times 3 $ 卷积核, 并通过最大池化减少特征图的空间尺寸, 输出的特征图尺寸为$ 32\times 2\times 2 $ . 第三层卷积(conv3)进一步将特征图数量扩展至 64个, 经过$ 3\times 3 $ 的卷积核和最大池化后, 特征图尺寸变为$ 64\times 1\times 1 $ . 第四层卷积层(conv4)将特征图数量扩展到128个, 使用$ 3 \times 3 $ 的卷积核, 输出特征图大小为$ 128 \times 1 \times 1 $ . -
在卷积特征提取模块之后, 网络引入了两个残差块(residual block1, residual block2), 每个残差块由两个卷积层组成, 每个卷积层包括
$ 3 \times 3 $ 的卷积核. 通过“跳跃连接”(shortcut connection), 保留输入特征的同时学习特征变化, 提高网络的表达能力并加速训练收敛. 残差块的输出计算公式为式中,
$ {{\boldsymbol{W}}}^{(1)} $ 和$ {{\boldsymbol{W}}}^{(2)} $ 分别为两个卷积层的权重矩阵,$ {b}^{(1)} $ 和$ {b}^{(2)} $ 为相应的偏置项,$ {y}^{({\mathrm{in}})} $ 为残差块的输入特征. 通过“跳跃连接”, 输入特征$ {y}^{({\mathrm{in}})} $ 直接与卷积运算后的结果相加, 残差块能够在学习特征变化的同时保留原始特征. 该模块不仅有助于学习新的特征, 还有效缓解了梯度消失问题, 从而提升模型的训练效果和精度. -
经过卷积和残差块的特征提取后, 通过全连接层进一步整合处理特征信息, 以生成最终的相位分布. 其结构包括展平操作(flatten)、全连接层和输出层, 如图6所示.
通过展平操作, 尺寸为
$ 128 \times 1 \times 1 $ 的特征图被转换为具有128个神经元的一维向量, 从而使后续全连接层能够以标准的一维形式处理输入特征, 便于整合经过卷积和池化后提取的特征.展平后的特征向量被输入至第一层全连接层(FC1), 该层包含256个神经元. 通过全连接操作, 聚合来自不同空间位置和通道的特征, 以捕获输入数据的全局信息. 为了增强模型的非线性表达能力, FC1采用ReLU激活函数[34]. 为应对小样本训练中的过拟合风险, 模型引入了Dropout机制. 丢弃率过低可能无法有效抑制过拟合, 而丢弃率过高则会削弱模型的学习能力. 考虑模型的架构特点与小样本数据的特性, 丢弃率设置为0.4. 这意味着在训练过程中, 随机丢弃40%的神经元, 以减少模型对特定特征的过度依赖, 从而提高泛化能力. Dropout的计算过程如下[36]
其中, r为服从伯努利分布的随机向量, 其元素取值为0或1, 用于随机屏蔽部分神经元. 图中以虚线标示了丢弃率为0.4的Dropout操作, 直观体现了在训练过程中随机丢弃部分神经元的机制.
第二层全连接层(FC2)包含128个神经元, 同样采用ReLU激活函数和Dropout操作. 此层进一步降低特征维度, 同时保留最重要的信息.
第三层全连接层(FC3)将前两层的输出特征进一步整合, 并转换为100个神经元的输出. 该层的作用在于将聚合的特征转换为最终的相位分布, 生成预测结果. 为了保证输出的相位值符合物理 意义, 采用了Sigmoid激活函数[37], 将每个输出值限制在
$ (0, 1) $ 的范围内. 函数图如图5(b)所示. Sigmoid函数的表达式如下: -
输出层将第三层全连接层(FC3)的结果映射为最终的相位矩阵, 尺寸为
$ 1 \times 10 \times 10 $ . -
本数据集包含随机生成的
$ 10\times10 $ 相位分布和通过PSO-SA优化后的相位分布及其双站RCS值. 相位分布以二进制形式(0和1)表示, 直接作为模型的输入和目标输出. 数据集按8∶2比例划分为训练集和验证集[14,23-25], 并在加载过程中随机打乱, 以提高泛化能力和防止过拟合. -
根据前期训练结果, 同时保证模型收敛, 训练周期(epoch)设置为600次, 批量大小(batch size)设置为64. 在小样本条件下, 优化器采用AdamW优化器[38], 初始学习率设置为0.001, 权重衰减因子为0.01, 以确保模型在训练过程中收敛稳定并通过L2 正则化抑制过拟合[39]. 同时采用学习率调度器(ReduceLROnPlateau)[40], 当验证集上的损失在连续15个epoch中不再下降时, 将学习率降低20%. 此外, 引入了早停策略, 若验证损失在连续40个epoch中没有得到改善, 则停止训练. 这些策略确保模型不会过度拟合, 同时能够在适当的时候自动减小学习率以获得更优的结果.
-
本设计构建了自定义损失函数: 双站RCS损失、相位分布损失和正则化损失. 通过这种设计, 不仅使模型有效地学习相位分布的特征, 还确保其具备减缩电磁散射峰值的物理意义, 从而在满足物理约束的同时实现数值上的稳定性.
根据(2)式, 双站RCS损失旨在最大限度地减缩CNN优化后的远场散射峰值. 借助该策略, 模型在训练初期能够迅速收敛. 即使在学习到样本特征之后, 该策略仍然激励模型进一步降低散射峰值, 使其在一定程度上探索更优的相位分布, 从而实现RCS的进一步减缩. 其损失定义如下:
相位分布损失用于衡量模型输出的相位分布与目标相位分布之间的误差. 该损失能够在训练初期加快模型收敛速度, 从而在后期能够探索更优相位分布. 损失采用二元交叉熵(binary cross-entropy)计算, 定义如下:
其中,
$ \hat{y}_i $ 表示模型预测的相位值,$ y_i $ 为目标相位值, 通过最小化该损失来确保模型生成的相位分布具备良好的精度. 为使模型输出更倾向于确定的0或1值, 并降低数值模糊性, 引入正则化损失. 定义如下:其作用在于鼓励输出趋于二值化, 从而提高相位分布在实际应用中的有效性. 最终的损失函数为双站 RCS损失、相位分布损失和正则化损失的加权和, 用于捕捉电磁波散射特性、相位分布的合理性以及输出的二值性. 损失函数的表达式为
其中,
$ \gamma_{{\mathrm{RCS}}} $ ,$ \gamma_{{\mathrm{Phase}}} $ 和$ \gamma_{{\mathrm{Reg}}} $ 为权重参数, 用于控制各损失项在优化目标中的相对重要性. 通过调整权重, 使模型能够在减缩RCS、匹配相位分布和增强二值性之间实现动态平衡. 在本设计中,$ \gamma_{{\mathrm{Phase}}} $ 通常设置为较小的值, 以确保相位分布对模型优化的影响适度, 而$ \gamma_{{\mathrm{RCS}}} $ 和$ \gamma_{{\mathrm{Reg}}} $ 相对较大, 确保输出结果在有效减缩RCS的过程中, 仍符合物理特性并保持良好的可控性.为保证损失函数权重参数取值的合理性, 在此进行了消融实验, 结果如表1所列, 可以看出: 仅使用
$ \gamma_{{\mathrm{RCS}}} \cdot {\mathrm{Loss}}_{{\mathrm{RCS}}} $ 会导致模型收敛过慢甚至无法收敛, 同时存在二值化模糊问题; 仅使用$ \gamma_{{\mathrm{Phase}}} \cdot {\mathrm{Loss}}_{{\mathrm{Phase}}} $ 会导致输出结果与样本结果高度 一致, 无法进一步探索更优相位分布; 使用$ \gamma_{{\mathrm{RCS}}} \cdot {\mathrm{Loss}}_{{\mathrm{RCS}}} + \gamma_{{\mathrm{Phase}}} \cdot {\mathrm{Loss}}_{{\mathrm{Phase}}} $ 收敛速度提升且能够进一步降低RCS, 但同时也存在二值化模糊问题; 加入$ \gamma_{{\mathrm{Reg}}} \cdot {\mathrm{Reg}} $ 显著提升二值化, 故最终权重($ \gamma_{{\mathrm{RCS}}} $ = 0.5,$ \gamma_{{\mathrm{Phase}}} $ = 0.1,$ \gamma_{{\mathrm{Reg}}} $ = 1.5)通过网格搜索确定, 平衡了物理约束与优化目标. -
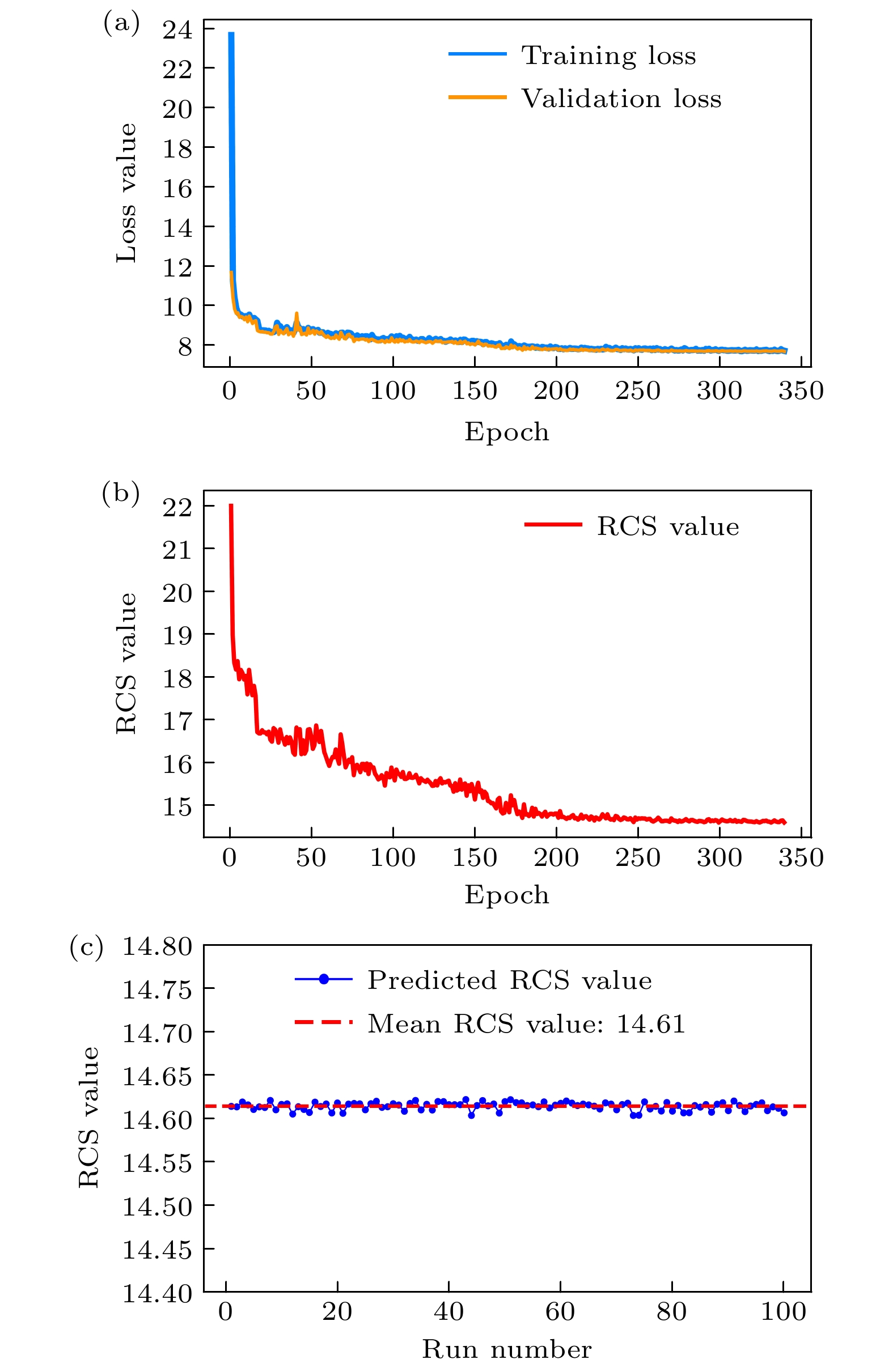
实验环境配置如表A1所示. 图7(a)展示了模型的训练损失和验证损失的迭代曲线, 模型在前期的学习阶段能够有效提取数据特征, 并在后期收敛至稳定的状态. 图7(b)展示了模型在训练过程中RCS值的变化趋势, 可以看出在训练初期RCS值从较高值迅速下降, 并在后期趋于平稳. 图7(c)展示了模型在不同随机初始相位下100次的运行结果, 蓝色曲线表示每次运行得到的RCS值, 红色虚线表示RCS的均值, 根据标准差公式:
其中,
$ {{x}_{i}} $ 是第i次运行得到的RCS值,$ \bar{x} $ 为均值, 通过计算得到标准差为0.013. 这表明模型对输入的初始条件变化具有较高的鲁棒性, 能够在多种不同的条件下保持良好的优化效果.图8(a)—(c)展示了CNN优化后的相位分布及其3D和2D远场图, 图9(a)和图9(b)则比较了各类算法的优化效果及运行时间. 结果表明, CNN在相位分布优化方面优于传统方法. 尽管 PSO-SA结合了全局搜索与局部优化, 但由于计算资源或迭代次数的限制, 同时也存在陷入局部最优解问题, 而CNN通过自定义损失函数(包括双站RCS损失、相位分布损失和正则化损失)的约束, 不仅拟合PSO-SA的优化结果, 在一定程度上能够进一步探索降低远场散射峰值的可能性, 通过这种多目标优化机制, 有助于CNN突破样本的局部最优, 找到更有效的相位分布组合, 进一步提升RCS减缩效果. 此外, 正则化损失(鼓励二值化相位)与RCS损失的联合优化促使模型在物理约束下找到更高效的相位分布, 这使得CNN能够在复杂的物理约束下优化相位分布, 达到更优的RCS 减缩效果. 值得注意的是, 在收敛速度上, 生成一个
$ 10\times 10 $ 相位分布仅需$ 3.65\times10^{-3}\; {\mathrm{s }}$ , 而传统算法则需耗时 3—8 min. 在大规模超表面设计(如卫星表面、舰艇表面等大规模阵列应用)中, 传统算法的计算时间将呈指数级增长, 因此采用CNN可显著提升超表面相位分布优化的效率. -
为进一步验证理论结果的有效性, 通过CST全波仿真, 对PEC板、随机初始、PSO-SA优化及CNN优化相位分布在减缩双站RCS方面的效果进行了定量分析.
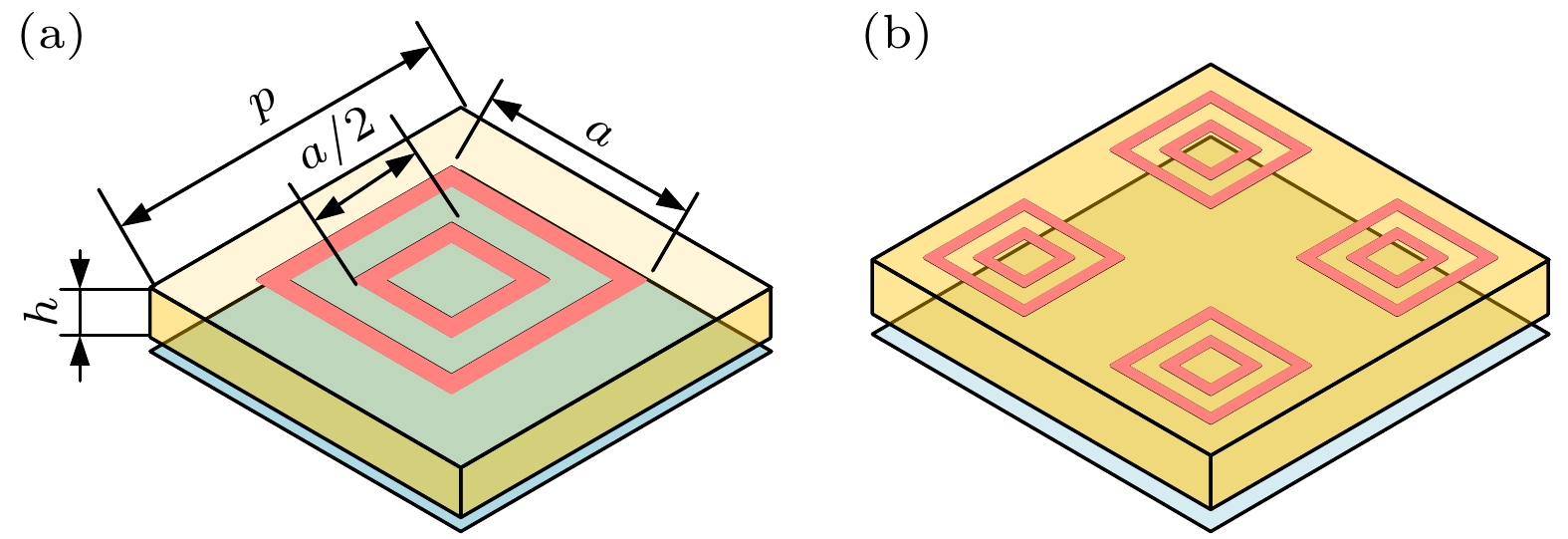
本研究中的超表面单元采用双环结构[41], 如图10(a)所示. 通过参数扫描发现, 当双环的尺寸参数分别为
$ a = 4.2\text{ mm} $ 和$ a = 8\text{ mm} $ ,$ p = 15\;\text{mm} $ ,$ h = 5\text{ mm} $ 时, 该单元在中心频率9 GHz下的反射相位差为$ 178^\circ $ , 基本满足“0”和“1”单元的相位需求. 基于上述参数设计, 通过CST和Matlab联合仿真, 利用单元结构及其相位分布构建完整的超表面阵列排布, 以分析其电磁特性. 如图10(b)所示, 引入$ 2 \times 2 $ 子阵单元, 用于模拟集中具有相似相位的单元场景, 使仿真结果尽可能接近周期边界条件下的单元仿真. 图11展示了不同相位分布在频率为9 GHz下垂直入射的远场散射特性, 以对比 PEC板、随机初始、PSO-SA优化及CNN优化相位分布的电磁响应性能.如图11所示, 在垂直入射时不同相位分布对远场散射特性的影响显著: 相比于PEC板和随机生成的相位分布, PSO-SA优化后的相位分布在远场散射方面已有明显改善, 而通过CNN得到的相位分布进一步优化了散射特性, 使远场散射更加均匀. 为验证该方法能否实现雷达回波全空间均匀散射, 当入射角(与法线夹角)为 30°, 45°, 60°时, PEC 板、经CNN优化后的相位分布图及其CST全波仿真得到的3D和2D远场图如图12所示. 由于单元角度色散和阵列耦合效应, 导致仿真结果与预设频点(9 GHz)存在频偏. CST仿真数据中, 双站RCS减缩效果最佳的频点为8.4 GHz.
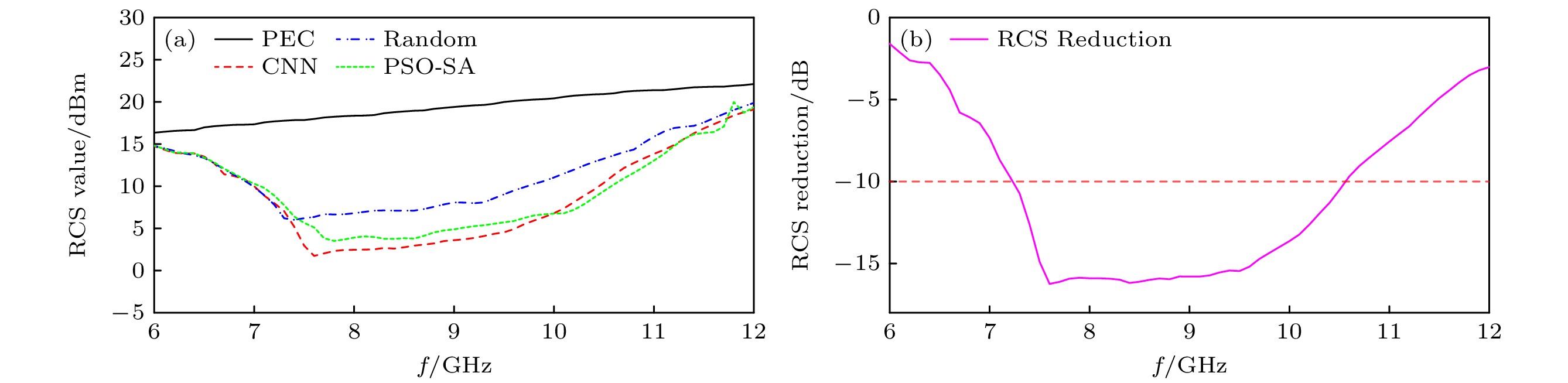
图13展示了在图11相位分布中, 6—12 GHz频段内的RCS值、CNN相比PEC板的RCS减缩值, 其中, 入射角垂直入射, 接收角为全空间(0°—180°) RCS最大值方向的角度(根据双站RCS全空间最值特性定义). 从图13(a)可以看出, 在7—10 GHz频段内, 通过CNN得到的相位分布成功实现了RCS的进一步缩减. 相比于传统算法, 在9 GHz处, 双站RCS值由5.2 dBms降低至3.8 dBms, 减缩效果提升了26.92%. 从图13(b)可以看出, 在7.2—10.7 GHz处, 实现了10 dB以上的双站RCS减缩. 其总体提升效果可通过(15)式计算可得:
其中,
$ {{R}_{{\mathrm{PSO\text-SA}}}}(i) $ 为在i频点处, 通过PSO-SA优化相位分布后得到的双站RCS值. 同理$ {{R}_{{\mathrm{CNN}}}}(i) $ 为在i频点处, 通过CNN优化相位分布后得到的双站RCS值, 其中i为6—12, 采样间隔为0.1, 通过计算, 可以得到其总体减缩效果提升了 17.2%.为验证结果的正确性, 在此对比了CNN预测结果以及CST全波仿真结果. 根据公式:
其中, RCSR为RCS减缩值(RCS reduction)(单位dB),
$ {{F}_{{\mathrm{Theory}}}} $ ,$ {{F}_{{\mathrm{PEC}}}} $ 分别为优化后得到相位分布和PEC板的RCS值. 当$ {{F}_{{\mathrm{Theory}}}} $ = 14.61,$ {{F}_{{\mathrm{PEC}}}} $ = 100 dB. CNN预测的RCSR为16.7 dB, CST仿真结果为15.9 dB, 与理论分析基本符合. -
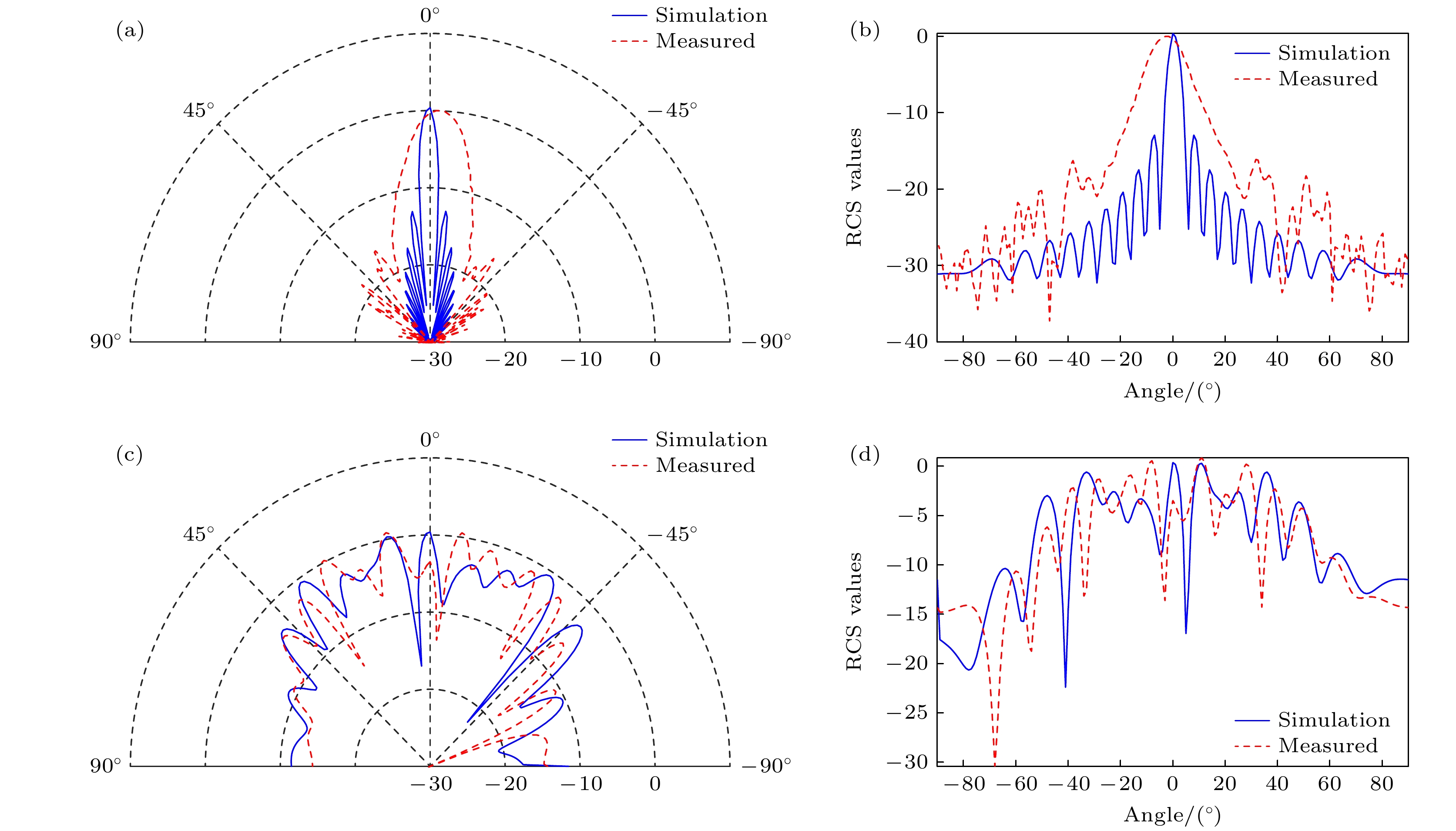
为验证理论计算与全波仿真结果的准确性, 对图8(a)所示相位分布的超表面进行了实物加工与测试, 图14(a)和图14(b)展示了加工后的样品及其测试环境. 超表面阵列尺寸为300 mm × 300 mm; 厚度为5 mm; 中间层介质采用 F4BM265, 介电常数为2.65; 覆铜厚度为1 OZ. 加工后的样品委托西安恒达微波技术开发有限公司进行测试, 测试 环境为6 m × 4 m × 4 m的微波暗室, 天线校准采用标准增益喇叭法, 测试前通过空腔反射验证 背景噪声低 –40 dB, 测试主要使用E8364B矢量网络分析仪、HD-2018DRHA10S 迷你双脊喇叭发射天线、HD-100SGAH20N和 HD-84SGAH20+S标准增益接收天线, 以及 HD-AP15 AAT小暗室转台.
在测试过程中, 网络分析仪用于测量超表面的 S参数, 发射天线向超表面发射电磁波, 接收天线则安装在小暗室转台上, 通过精确调节接收天线的角度与位置, 可以准确捕获超表面的电磁散射幅值. 在测试环境中, 发射端与接收端位于不同位置, 构建双站RCS测试环境, 以验证本方法在优化超表面相位分布, 实现双站RCS减缩方面的有效性.
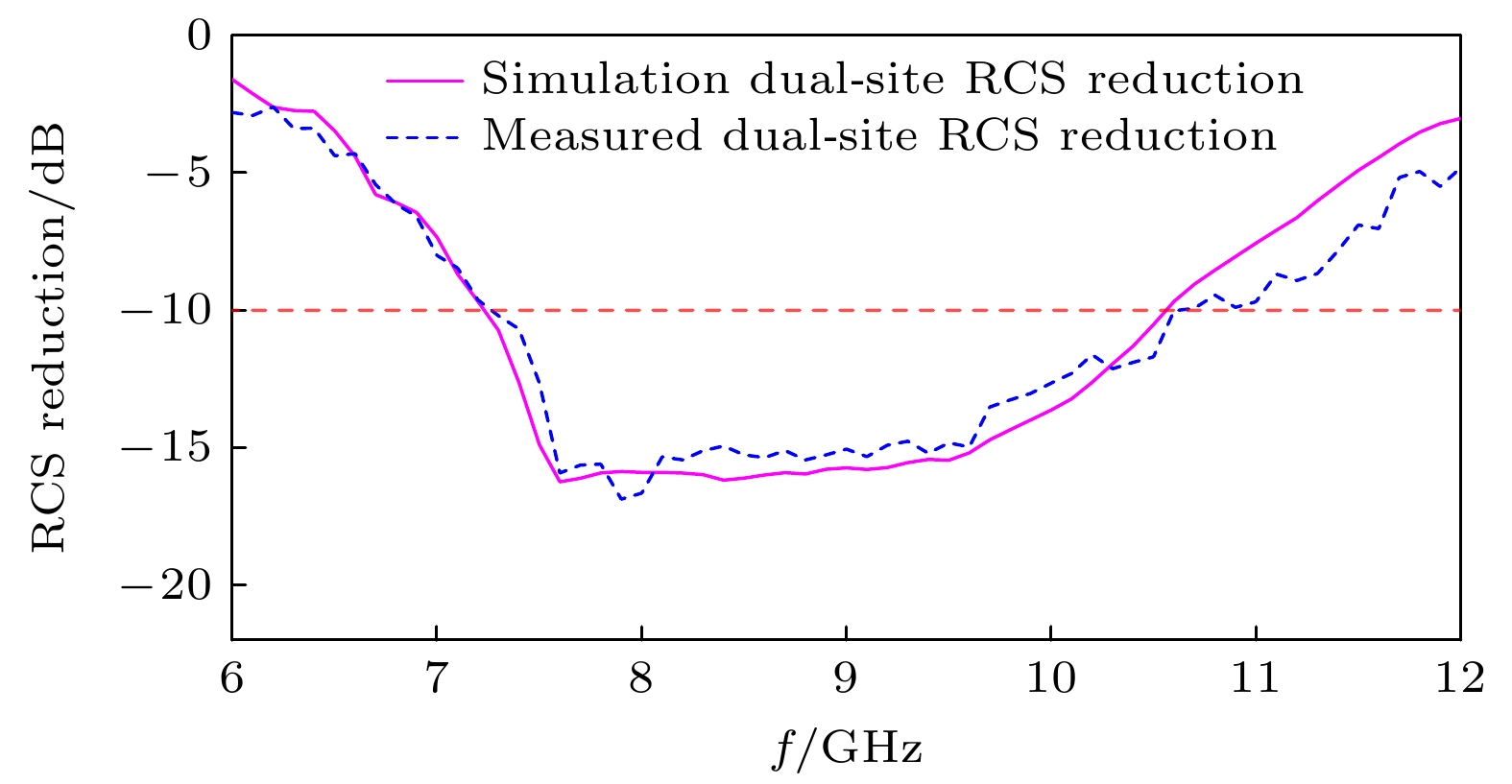
图15(a)—(d)展示了在9 GHz频率下, 入射角为垂直入射, 接收角为全空间(0°—180°) RCS 最大值方向的角度(根据双站RCS全空间最值特性定义), PEC板与加工后样品的1D远场图, 并对比了全波仿真与实测结果. 结果表明, 无论是全波仿真还是实测结果, 经过CNN优化的相位分布均实现了漫反射效果. 在6—12 GHz频段内, 对样品与其同尺寸的金属板分别进行了实测. 在测试过程中, 使用矢量网络分析仪和天线测量系统, 确保数据的准确性与可靠性. 同时, 对数据进行归一化预处理, 得到的双站RCS减缩随频率变化曲线如图16所示. 与全波仿真结果相比, 实测结果在 7.26—10.74 GHz频段内, 可实现10 dB以上的双站RCS减缩, 实测结果与全波仿真结果基本符合. 部分频偏和幅度差异是由于仿真设置中, 入射波为理想平面波, 实测中为喇叭天线的点源, 而暗室受尺寸限制, 不能完全满足远场条件, 同时, 样品的加工精度和实验装置的设计也是引起误差的原因之一. 实测结果与全波仿真结果验证了本方法对超表面相位优化分布和实现双站RCS减缩的有效性与可行性.
-
本文提出了一种基于小样本条件下CNN的超表面相位分布优化设计方法, 可快速高效地实现宽带双站RCS减缩. 该方法通过利用PSO-SA与天线阵列理论生成样本数据, 并结合卷积特征提取、残差增强与全连接优化模块, 配合自定义损失函数学习样本特征, 实现对超表面散射波束最大值的有效降低. 与现有研究相比, 本文的创新性主要体现在全空间特性建模与多物理约束融合, 将全空间散射峰值作为优化目标, 实现全空间能量均匀散射; 提出了一种包含双站RCS损失、相位分布损失和正则化损失的自定义目标函数, 直接关联电磁散射物理特性与深度学习优化过程. 理论计算、全波仿真与样品测试结果表明, 在预设中心频点处, 相较于传统优化算法, 本方法设计的超表面双站RCS减缩效果可提升26.92%. 在7.26—10.74 GHz宽带范围内实现了10 dB以上的双站RCS减缩, 总体减缩效果提升17.2%. 该方法可解决目前RCS减缩及漫反射超表面设计中存在的效率不高、性能较差等问题, 有望为大规模阵列双站RCS减缩超表面相位分布优化提供更优效果、更快速度、更少资源占用的设计新思路.
感谢西安恒达微波技术开发有限公司提供的样品测试服务.
-
基于卷积神经网络的双站雷达散射截面减缩超表面设计
Design of bistatic radar cross section reduction metasurface based on convolutional neural networks
-
摘要: 随着雷达组网技术的发展成熟, 未来电磁隐身对抗中双站雷达散射截面(radar cross section, RCS)减缩将比单站更为重要. 人工电磁超表面为双站RCS减缩提供了全新的技术途径. 然而, 受制于大规模阵列优化耗时及双站RCS减缩全空间最值特性, 目前的双站 RCS 减缩超表面设计还存在效率不高、性能较差的问题. 鉴于此, 本文提出了一种小样本条件下的卷积神经网络(convolutional neural network, CNN)方法, 通过定向优化超表面相位分布, 实现雷达回波全空间均匀散射, 从而达到双站 RCS 减缩效果. 本方法结合了卷积特征提取、残差增强与全连接优化模块, 配合自定义损失函数, 可高效捕捉漫反射相位与 RCS 全空间最值的多维度复杂关系. 理论计算、全波仿真和样品测试结果表明, 在7.26—10.74 GHz 频段内, 利用本方法设计的超表面可实现10 dB以上的双站RCS减缩, 相比传统优化算法减缩效果提升17.2%, 且优化效率显著提高, 有望为武器装备的全空间电磁隐身提供新的技术思路.
-
关键词:
- 超表面 /
- 双站雷达散射截面减缩 /
- 卷积神经网络
Abstract: Radar cross section (RCS), a crucial physical quantity that characterizes the backscattering intensity of targets under radar illumination, is the primary metric for assessing stealth capabilities. With the development of radar detection technologies, RCS reduction has become a forefront research topic in radar stealth, aiming to minimize target detectability. With the maturity of radar networking technology, the bistatic radar RCS reduction is becoming increasingly important in future electromagnetic stealth countermeasures compared with the monostatic radar RCS reduction. Artificial electromagnetic metasurfaces have introduced innovative technical approaches for realizing the bistatic radar RCS reduction. However, current metasurface designs still face challenges related to inefficiency and suboptimal performance, mainly due to the time-consuming nature of large-scale array optimization and the global extremum characteristics of bistatic radar RCS reduction. To overcome these limitations, this study proposes a few-shot convolutional neural network (CNN)-based approach, which achieves uniform full-space radar echo scattering by directionally optimizing metasurface phase distributions, thereby enabling effective bistatic radar RCS reduction. This approach integrates convolutional feature extraction, residual enhancement, and fully connected optimization modules with a customized loss function to efficiently capture the complex multidimensional relationships between diffuse reflection phases and the full-space RCS extrema. Theoretical calculations, full-wave simulations, and experimental tests show that the metasurface designed with this approach can achieve over 10 dB of Bistatic Radar RCS reduction in a frequency range from 7.26 GHz to 10.74 GHz. The method also ensures uniform diffuse reflection across the full space for various incidence angles (30°, 45°, 60°). Compared with traditional optimization algorithms, this method enhances RCS reduction by 17.2% while significantly improving computational efficiency. This approach provides a promising new technical paradigm for achieving full-space electromagnetic stealth in advanced weapon systems. -

-
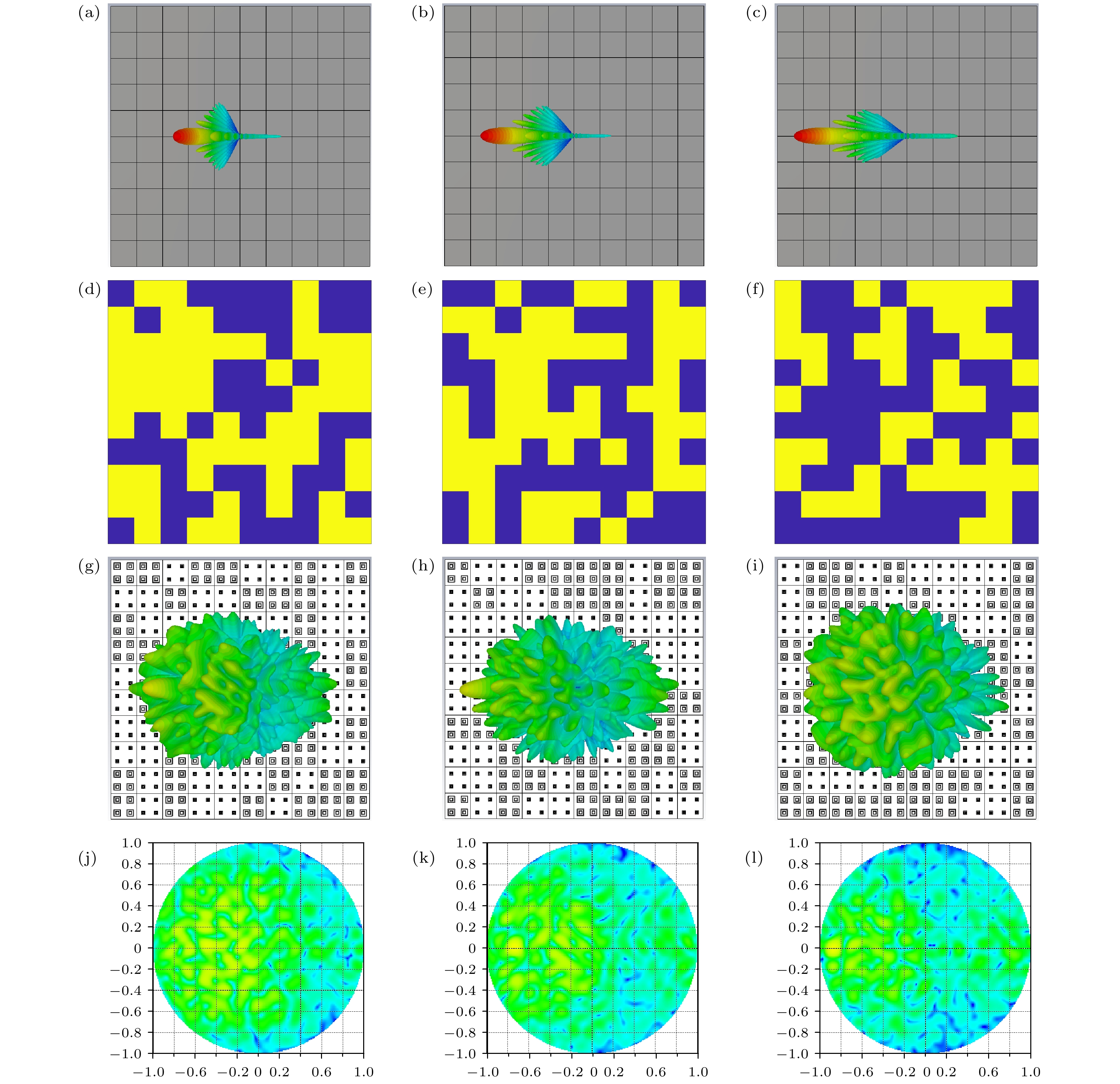
图 2 (a)—(d) GA, PSO, PSO-GA, PSO-SA优化后的相位分布; (e)—(h) 优化相位分布后的3D远场图; (i)—(l)优化相位分布后的2D远场图
Figure 2. (a)–(d) Phase distributions optimized by GA, PSO, PSO-GA, and PSO-SA; (e)–(h) 3D far-field patterns of the optimized phase distributions; (i)–(l) 2D far-field patterns of the optimized phase distributions
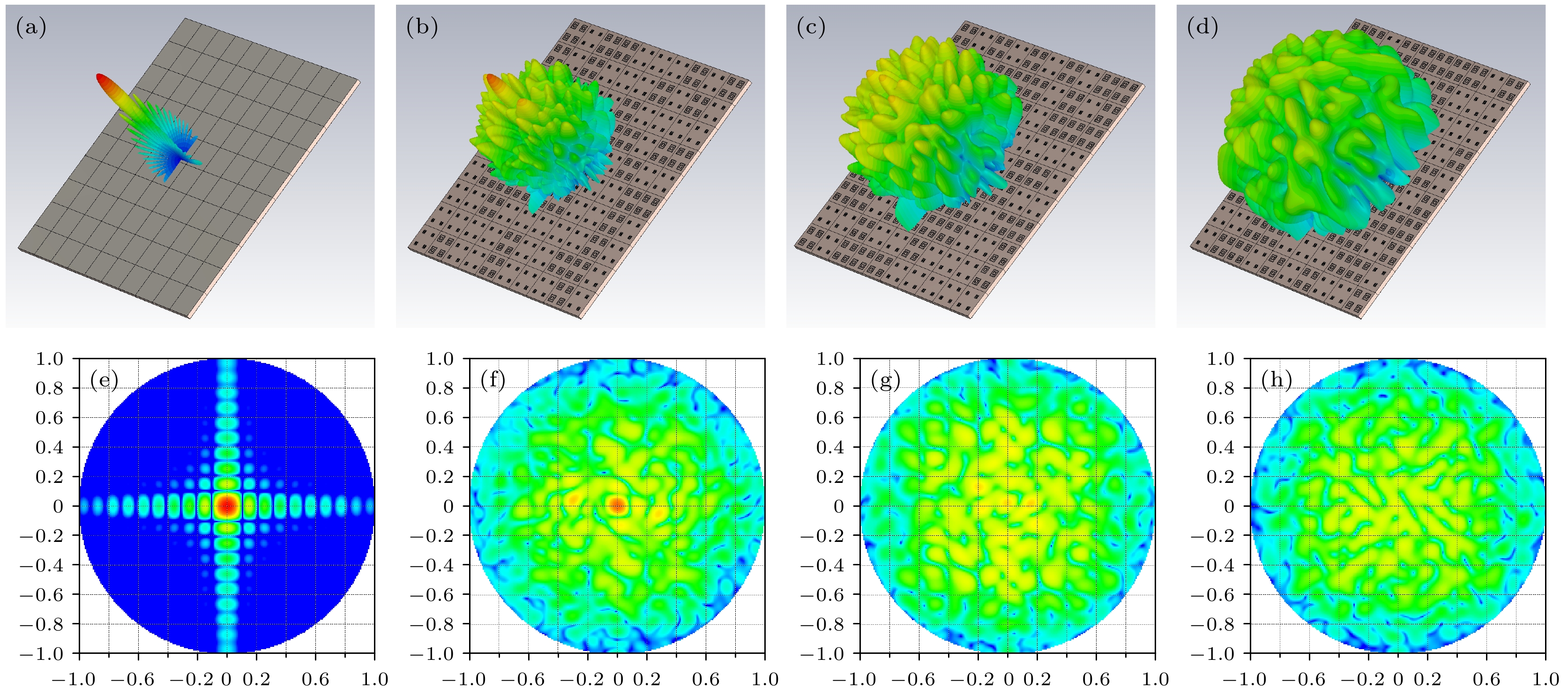
图 11 (a)—(d) PEC, 随机, PSO-SA 优化, CNN 优化相位分布后的3D远场图; (e)—(h) PEC, 随机, PSO-GA优化, CNN优化相位分布后的2D远场图
Figure 11. (a)–(d) 3D far-field patterns after phase distribution optimization by PEC, Random, PSO-SA, and CNN, respectively; (e)–(h) 2D far-field plots after phase distribution optimization by PEC, Random, PSO-SA, and CNN respectively
图 12 入射角分别为30°, 45°, 60°时 (a)—(c) CST 全波仿真 PEC 板的3D远场图; (d)—(f) CNN优化后的相位分布; (g)—(i) CNN优化后的相位分布在CST全波仿真的3D远场图; (j)—(l) CNN优化后的相位分布在CST全波仿真的2D远场图
Figure 12. Incident angles of 30°, 45°, 60°: (a)–(c) 3D far-field patterns of CST full-wave simulation of PEC plates; (d)–(f) phase distribution optimized by CNN; (g)–(i) 3D far-field patterns of CST full-wave simulation with CNN-optimized phase distribution; (j)–(l) 2D far-field patterns of CST full-wave simulation with CNN-optimized phase distribution
表 1 损失函数不同权重参数效果对比
Table 1. Comparison of the effects of different weight coefficients of the loss function.
权重参数 参数取值 RCS 值 $ \gamma_{{\mathrm{RCS}}} $ 0.1, 0.5, 1.0, 1.5 15.5, 14.7, 14.6, 14.6 (收敛速度慢) $ \gamma_{{\mathrm{Phase}}} $ 0.1, 0.3, 0.7, 1.0 16.8, 16.3, 16.2, 16.0 (无法减缩RCS) $ \gamma_{{\mathrm{RCS}}} $ +$ \gamma_{{\mathrm{Phase}}} $ (0.1, 0.1), (0.5, 0.1), (0.5, 0.3)··· 16.3, 14.8, 15.6··· (二值化模糊) $ \gamma_{{\mathrm{RCS}}} $ +$ \gamma_{{\mathrm{Phase}}} $ +$ \gamma_{{\mathrm{Reg}}} $ (0.5, 0.1, 0.5), (0.5, 0.1, 1), (0.5, 0.1, 1.5)··· 14.8, 14.7, 14.6··· 表 A1 实验环境配置
Table A1. Experimental environment configuration.
名称 配置信息 开发语言 Python 3.9 框架 PyTorch 1.10.0 + CUDA 12.0 CPU Intel Core i9 GPU GeForce RTX 4060 Laptop GPU (8G) 内存 8 G NumPy 1.21.3 Matplotlib 3.9.2 torchvision 0.13.0 Pandas 1.3.3 -
[1] Rao G A, Mahulikar S P 2002 Aeronaut. J. 106 629 doi: 10.1017/S0001924000011702 [2] Ball R E, Albrecht R S, Horne R L 2003 The Fundamentals of Aircraft Combat Survivability: Analysis and Design (2nd Ed.) (Reston: AIAA) pp8–56 [3] Westwick P 2019 Stealth: The Secret Contest to Invent Invisible Aircraft (Oxford: Oxford University Press) pp5–42 [4] Singh H, Antony S, Jha R M 2016 Plasma-based Radar Cross Section Reduction (Singapore: Springer) pp1–46 [5] Knott E F 2012 Radar Cross Section Measurements (New York: Springer) pp12–36 [6] Knott E F, Schaeffer J R, Tuley M T 2004 Radar Cross Section (2nd Ed.) (Reston: SciTech Publishing) pp4–22 [7] Kim S H, Lee S Y, Zhang Y, Park S J, Gu J 2023 Adv. Sci. 10 2303104 doi: 10.1002/advs.202303104 [8] Ananth P B, Abhiram N, Krishna K H, Nisha M S 2021 Mater. Today Proc. 47 4872 doi: 10.1016/j.matpr.2021.06.196 [9] Ye D, Wang Z, Xu K, Li H, Huangfu J, Wang Z, Ran L 2013 Phys. Rev. Lett. 111 187402 doi: 10.1103/PhysRevLett.111.187402 [10] Wang J, Yang R, Ma R, Tian J, Zhang W 2020 IEEE Access 8 105815 doi: 10.1109/ACCESS.2020.3000042 [11] Liu Y, Zhao X 2014 IEEE Antennas Wirel. Propag. Lett. 13 1473 doi: 10.1109/LAWP.2014.2341299 [12] Yu N, Genevet P, Kats Ma, Aieta F, Tetienne J P, Capasso F, Gaburro Z 2011 Science 334 333 doi: 10.1126/science.1210713 [13] Gao X, Han X, Cao W P, Li H O, Ma H F, Cui T J 2015 IEEE Trans. Antennas Propag. 63 3522 doi: 10.1109/TAP.2015.2434392 [14] Abdullah M, Koziel S 2022 IEEE Trans. Microwave Theory Tech. 70 264 doi: 10.1109/TMTT.2021.3105677 [15] Paquay M, Iriarte J C, Ederra I, Gonzalo R, Maagt P de 2007 IEEE Trans. Antennas Propag. 55 3630 doi: 10.1109/TAP.2007.910306 [16] Chen W, Balanis C A, Birtcher C R 2015 IEEE Trans. Antennas Propag. 63 2636 doi: 10.1109/TAP.2015.2414440 [17] Sang D, Chen Q, Ding L, Guo M, Fu Y 2019 IEEE Trans. Antennas Propag. 67 2604 doi: 10.1109/TAP.2019.2891657 [18] Cui T J, Qi M Q, Wan X, Zhao J, Cheng Q 2014 Light Sci. Appl. 3 e218 doi: 10.1038/lsa.2014.99 [19] Liu X, Gao J, Xu L, Cao X, Zhao Y, Li S 2016 IEEE Antennas Wirel. Propag. Lett. 16 724 doi: 10.1109/LAWP.2016.2601108 [20] Fu C, Han L, Liu C, Lu X, Sun Z 2021 IEEE Trans. Antennas Propag. 70 2352 doi: 10.1109/TAP.2021.3112618 [21] Li W, Huang N, Kang Y, Zou T, Ying Y, Yu J, Zheng J, Qiao L, Li J, Che S 2024 IEICE Electron. Express 21 20240246 doi: 10.1587/elex.21.20240246 [22] Qi W J, Yu C, Du J L, Zhao Y J 2022 Int. J. RF Microwave Comput. Aided Eng. 32 23306 doi: 10.1002/mmce.23306 [23] Koziel S, Abdullah M 2020 IEEE Trans. Microwave Theory Tech. 69 2028 doi: 10.1109/TMTT.2021.3061128 [24] Tao S, Pan X T, Li M K, Xu S H, Yang F 2020 IEEE J. Emerg. Sel. Top. Circuits Syst. 10 114 doi: 10.1109/JETCAS.2020.2972764 [25] 杨欣雨 2023 硕士学位论文 (南京: 东南大学) Yang X Y 2023 M. S. Thesis (Nanjing: Southeast University [26] 袁方, 毛瑞棋, 高冕, 郑月军, 陈强, 付云起 2022 物理学报 71 084102 doi: 10.7498/aps.71.20212174 Yuan F, Mao R Q, Gao M, Chen Q, Fu Q Y 2022 Acta Phys. Sin. 71 084102 doi: 10.7498/aps.71.20212174 [27] Yuan F, Wang G M, Xu H X, Cai T, Zou X J, Pang Z H 2017 EEE Antennas Wirel. Propag. Lett. 16 3188 doi: 10.1109/LAWP.2017.2768129 [28] Han X M, Xu H J, Chang Y P, Lin M, Zhang W Y, Xin W 2020 IEEE Access 8 162313 doi: 10.1109/ACCESS.2020.3021650 [29] Zhou Y, Cao X Y, Gao J, Li S, Liu X 2017 Electron. Lett. 53 1381 doi: 10.1049/el.2017.2414 [30] Katoch S, Chauhan S S, Kumar V 2021 Multimed. Tools Appl. 80 8091 doi: 10.1007/s11042-020-10139-6 [31] Wang D S, Tan D P, Liu L 2018 Soft Comput. 22 387 doi: 10.1007/s00500-016-2474-6 [32] Pan X, Xue L, Lu Y, Sun N 2019 Multimed. Tools Appl. 78 29921 doi: 10.1007/s11042-018-6602-4 [33] Dumoulin V, Visin F 2016 arXiv:1603.07285 [stat.ML] [34] Xu B, Wang N Y, Chen T Q, Li M 2015 arXiv: 1505.00853 [cs.LG] [35] Bjorck N, Gomes C P, Selman B, Weinberger K Q 2018 arXiv: 1806.02375 [cs.LG] [36] Srivastava N, Hinton G, Krizhevsky A, Sutskever I, Salakhutdinov R 2014 J. Mach. Learn. Res. 15 1929 [37] Dubey S R, Singh S K, Chaudhuri B B 2022 Neurocomputing 503 92 doi: 10.1016/j.neucom.2022.06.111 [38] Zhou P, Xie X, Lin Z, Yan S 2024 IEEE Trans. Pattern Anal. Mach. Intell. 46 6486 doi: 10.1109/TPAMI.2024.3382294 [39] Shi G, Zhang J, Li H, Wang C 2019 Neural Process. Lett. 50 57 doi: 10.1007/s11063-018-9883-8 [40] Al-Kababji A, Bensaali F, Dakua S P 2022 arXiv: 2202.06373 [cs.CV] [41] Yuan F, Xu H X, Jia X Q, Wang G M, Fu Y Q 2020 IEEE Trans. Antennas Propag. 68 2463 doi: 10.1109/TAP.2019.2940503 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: