-
被完全限制在辐射波的连续谱中而不与它们相互作用的波被称为连续体中的束缚态(bound states in the continuum, BICs), 这是一种独特的全受限模式[1,2]. 由于其能在纳米尺度上对局域电场产生强烈的增强引起了现代纳米光子学界的广泛关注[3]. BIC的概念最初起源于量子力学, 1929年由冯⋅诺依曼和威格纳以薛定谔方程为基础提出[4]. 此后在波动物理学的不同领域得到广泛研究, 包括声学、微波、水波和纳米光子学[5–15]. 2008年, BIC的概念首次被引入光学领域[16]. 此后, 纳米光子晶体薄板、光波导阵列、超构表面等各种光学结构相继通过BIC实现了高品质因子(quality factors, Q)共振[17–19]. 近年来由于可以定制材料和结构, 纳米光子结构已经成为了一个特别有吸引力的平台. 理想的BIC由于与自由空间辐射完全解耦和, 因此具有理论上无限大的品质因子, 辐射寿命趋于无穷大[20], 在光谱上表现为法诺共振的共振线宽消失, 能量被局域在纳米结构内部. BIC可以根据解耦合的物理机制分为两类: 一类是由系统参数的连续调节导致意外解耦合的偶然型 BIC[9,21]; 另一类是由于空间对称性的破缺导致离散模式和连续辐射模式解耦合的对称保护型束缚态 (symmetry-protected BIC, SP-BIC)[22]. 在光子晶体板中, 带结构的光线以上的模式由于与扩展模式的连续体耦合, 通常是辐射的. 然而, 由于它们的模式轮廓与外部传播模式之间的对称性不匹配, 某些束缚态甚至可存在于带结构的光线以上. 在光子晶体能带的Γ点处, 当工作频率低于衍射极限时, 唯一的辐射状态是法向的平面波[23], 其电磁场分布在绕z轴旋转180°下为奇态, 即C2对称, 因此在Γ点处的任何偶数模态都是BIC[24], 因为它们的模态分布与出射波之间的重叠为零. 由于SP-BIC较为常见和易于实现, 已被发现于各种光子微纳米结构中, 如波导[25,26]、光栅[27,28]和超表面[29]. 对称保护BIC是一种理想的BIC, 其不向外辐射能量, 线宽为零, 因此在光谱中无法被检测到. 在实际的应用中通常在系统中引入非对称因素(如偏心孔、劈裂、折射率不均匀、高度倾斜等)打破结构的对称性导致SP-BIC与连续体辐射之间耦合, 建立辐射通道, 使SP-BIC转化为准束缚态(quasi-BIC, QBIC). QBIC可认为是一种发生在BIC附近具有有限但巨大Q因子的漏模, 可以极大地增强局域场和光与物质相互作用, 在透射谱上表现为具有尖锐的法诺线型. 同时其无需特殊的耦合机制即可被外部光源直接激发. 目前, QBIC机制已用于各种应用, 如滤波器[3]、激光器[30]、非线性器件[24]和传感器[31]等.
近十年来, 由于超表面的易调谐性以及相当的鲁棒性引起了广泛关注. 已经证明, Q因子的剧烈变化可以通过调整光子晶体结构单元的不对称性来实现[32]. 其中, 传统基于贵金属的超表面由于存在高欧姆损耗的固有缺陷不可避免地具有低Q因子[33,34]. 全介质超表面由于具有灵活的可调性、低欧姆损耗、强局域性和超紧凑结构的特性有望成为等离子体超表面结构的优秀替代品. 截至目前, 许多支持QBIC高Q共振的超表面结构已经被提出, 比如倾斜的介质脊[35]、介质分裂环[36]和不等尺度的介质立方体[37]. 在实际的应用中, 基于介质环境变化引起的光共振的光谱形状、共振波长和强度变化的光学传感已被成功证明[19,38]. 对于在超表面上形成的QBIC, 由于电场在晶胞内的强局域性, 其共振波长通常对周围环境的折射率有很强的依赖[39], 这一特性通常被用来实现光学传感. QBIC的高Q因子可以为光学传感器带来高灵敏度和更大优值.
过去几十年, 光学在生物传感上的应用在生物化学和医学领域引起了极大的关注[40–42]. 特别是在细胞扫描成像和生物蛋白的检测识别方面. 然而, 传统的基于电化学的生物传感技术, 设备和检测步骤通常比较繁琐. 例如, 在使用透射电子显微镜观察和分析细胞和生物蛋白时, 时间和材料上的成本十分高昂, 同时样品制备过程复杂, 这些弊端限制了其在基础研究中的应用[43,44], 传统的基于荧光标记法的生物传感方式也具有需要复杂的仪器设备和标记物、不可实时检测、对样本具有一定的损伤、成本昂贵的缺点. 相对而言, 光学生物传感技术具有较低的侵入性克服了上述不足. 此外, 由于光学生物传感器具有相对稳定且不导电的传感元件, 其在复杂环境下也表现出较强的优势, 如强电场、强电波或极端温度条件[45,46]. 近年来, 许多新的生物传感光学机制被提出, 例如微腔[47]、表面等离子体[48]以及微纳米悬浮通道谐振器[49]等. 尽管这些新方法在某些领域已经显示出实际的应用潜力, 它们仍然存在一些固有的缺陷, 如高电阻损耗、复杂的结构设计以及低可调性. 作为一种独特的增强光-物质相互作用的新机制, 支持QBIC的全介质超表面在生物传感领域上的应用潜力尚未得到充分挖掘. 目前, 对BIC传感器的研究主要集中在折射率和温度变化的基本传感上[50,51], 在生物传感上的研究较少, 同时传感参数也相对较低. 因此, 提出一种新的无标记、快速和实时、更高灵敏、更低成本的高效检测生物蛋白的方法是有必要的.
本文提出了一种在支持高质量磁偶极子(magnetic dipole, MD) QBIC共振的全介质超表面上检测生物蛋白的可能方法, 其Q因子高于105. 通过引入偏心孔的方式打破面内结构对称, SP-BIC转变为具有超高Q因子的QBIC, 伴有巨大的局部场增强. 同时, 相比于传统等离子体超表面其具有更低的欧姆损耗和更高的可调谐性. 通过控制不对称参数的数值, 能够灵活地控制QBIC模式的谱线宽度, 理论上能够提高品质因子到任意的数值, 从而实现传感性能的提升和调节. 通过调节, 其优值FOM可高达1711.05 RIU–1, 高于许多基于其他传统方法的已报道的成果. 高FOM的传感性能赋予了该传感器在检测生物蛋白时更高的准确性, 能够更精确地探测微小的折射率变化, 从而提供更加可靠的检测结果, 可以看出这种基于QBIC的生物传感器具有优异的性能. 此外简单的设计允许该传感器适应各种复杂的检测环境, 进一步扩展了其在生物医学检测领域的应用前景. 本文研究成果展示了这种新型传感器的潜力. 这种高Q因子的全介质超表面设计有望在未来的生物传感器开发中发挥重要作用, 为高灵敏度和高精度的生物检测提供新的途径.
-
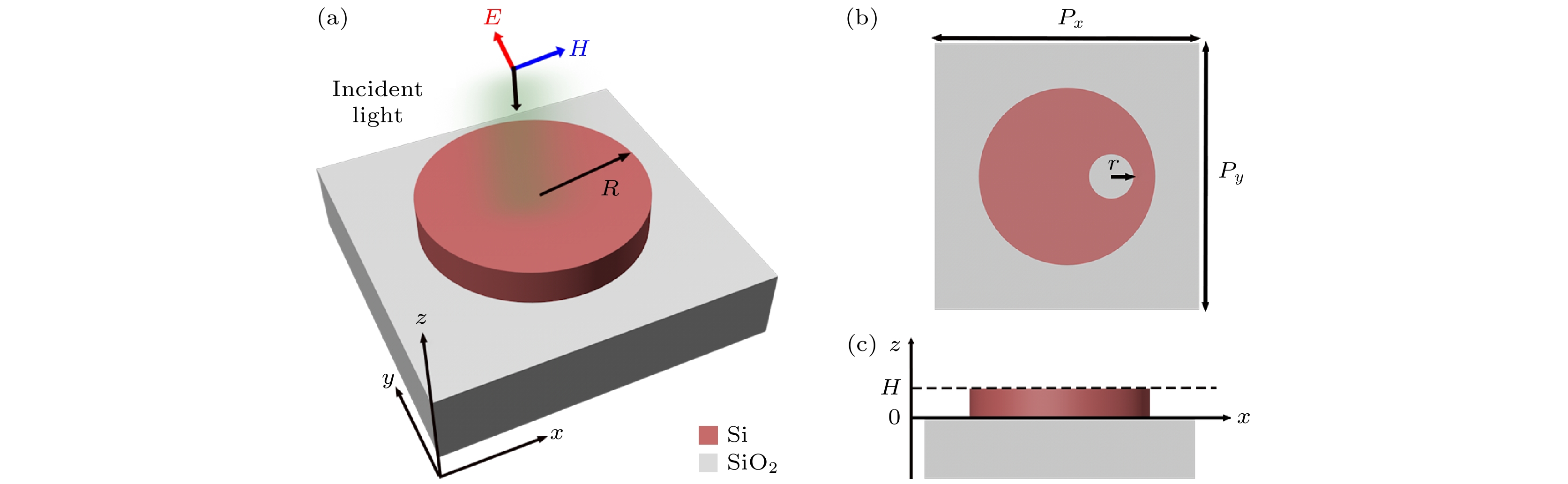
所设计的全介质超表面结构最小结构单元如图1所示. 半径R = 300 nm, 高度H = 100 nm的硅纳米圆盘放置在厚度为1000 nm的玻璃衬底上. 结构单元的周期尺寸为Px = Py = 900 nm. 在距离纳米圆盘中心150 nm的固定距离内引入一个半径r可变的偏心孔, 示意图如图1(b)所示. 平面内对称性被打破, 允许建立辐射通道和共振态从对称保护的BIC过渡到准BIC, 通过改变半径r的大小来调控结构的不对称性进而实现对准BIC共振的调控. 模拟计算在商业软件Lumerical FDTD Solutions中进行, 采用时域有限差分法(finite-difference time-domain method, FDTD)进行数值模拟, 该方法已被证明是对电磁相互作 用问题提供准确预测的有效手段[52]. 系统光源 设置为1400—1700 nm的近红外平面波沿–z轴入射, 电场和磁场分别沿y轴和x轴极化, 因此在 x-y平面上采用周期边界条件, 在z方向上采用完美匹配层. 为了模拟方便硅和玻璃的折射率分别设置为3.48和1.5, 背景设置为折射率为1的均匀 背景.
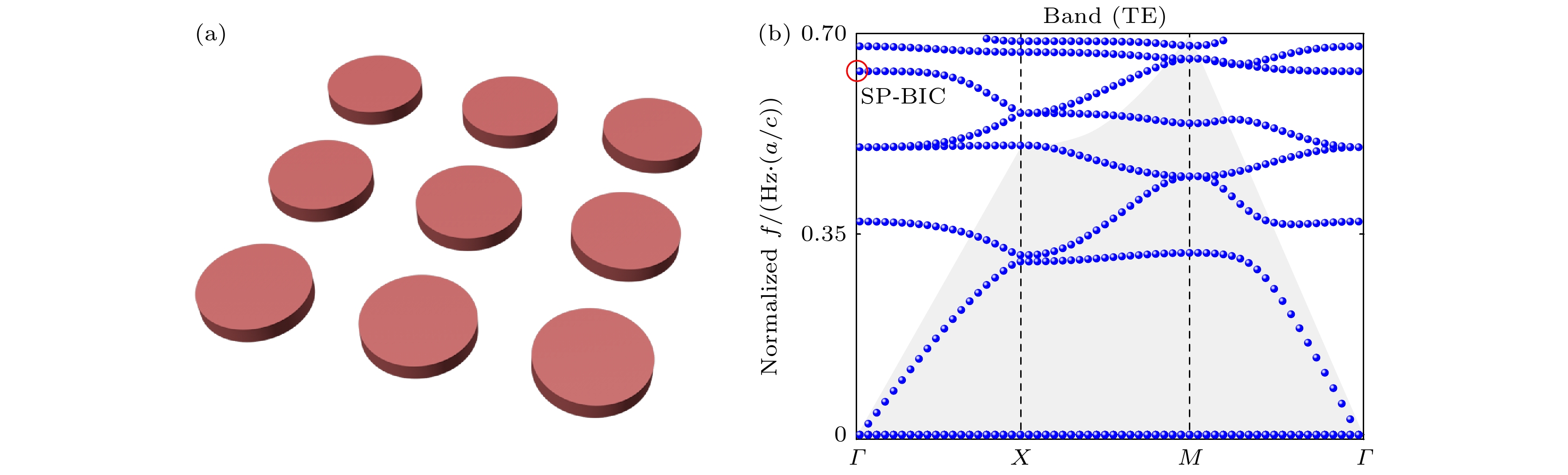
如图2(a)所示, 首先考虑的是无衬底的具有C2对称性的硅纳米盘组成的理想独立的周期阵列. 为寻找BIC, 使用偶极子云激发周期阵列支持的所有可能的共振模式[53], 得到的光子带结构如图2(b)所示, SP-BIC的位置在图中用红圈标出, 处于第一布里渊区的Γ点, 并位于近红外二区的频率范围内. 其相应频率低于给定周期结构的衍射极限, 这种情况下唯一的辐射通道是沿法向传播的平面波[23]. SP-BIC模式的电磁场矢量在C2对称性下为奇数, 由于对称性不匹配, 共振模式变得完全受限不再与自由空间的其他辐射通道耦合, 进而导致理论上的无限Q因子[22,54]. 当引入缺陷打破平面内对称性时辐射通道会被打开, 这样SP-BIC将会转变为QBIC, 具有有限且巨大的Q因子, 并在光学响应光谱中表现为明显的法诺特征.
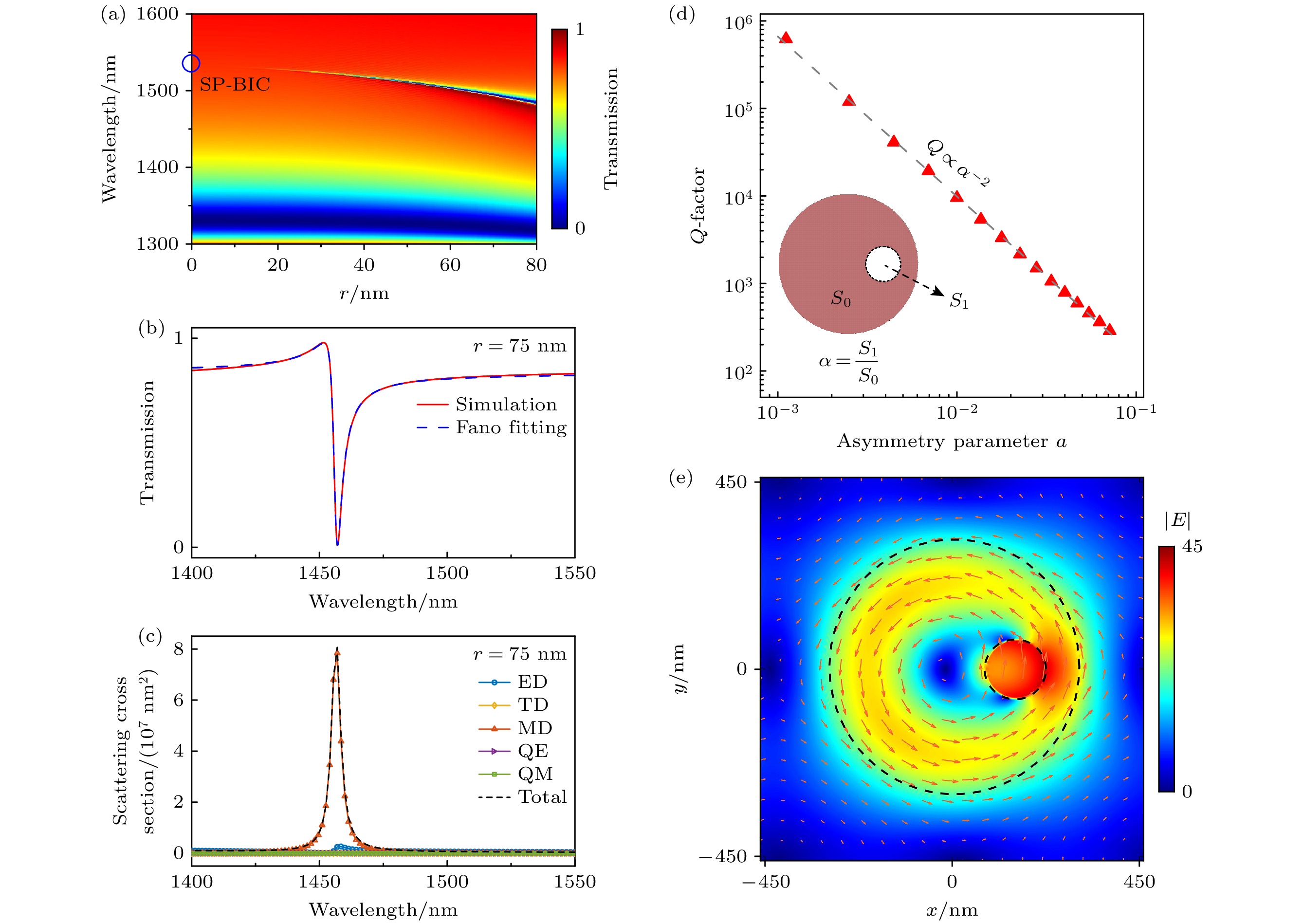
在实际情况中, 周期排列的硅纳米盘不可能悬浮在空气当中, 所以这里引入一个低损耗指数的玻璃衬底, 基底的存在会导致受束缚的少量能量从 衬底中打开的辐射通道泄漏出去, 进而造成Q因子的减小[24]. 然而提出的结构所支持的SP-BIC具有相当的鲁棒性[55], 衬底的存在并不会造成很大影响. QBIC共振与辐射泄漏密切相关, 因此可以通过控制几何参数来调节辐射速率和传输线宽. 随着偏心孔半径的增大, QBIC共振时的透射谱的线宽逐渐增大, 为了更直观地展示SP-BIC到QBIC的转变, 计算了随着偏心孔半径变化而变化的透射光谱如图3(a)所示. 从图3(a)可以看出, 当偏心孔半径r为0时传输线宽也为零, 意味着共振峰消失, 没有能量从束缚态泄漏到自由空间连续态, 对应的Q因子为理论上的无穷大. 而当r增大时, 传输倾角会出现轻微的蓝移和展宽, QBIC与连续自由空间辐射模式发生能量交换, 表现为尖锐的法诺共振[32]. 如图3(b)所示, 考虑r = 75 nm的单一情况, 从图3(b)可以看出, 透射谱在λ = 1458.11 nm处呈现出不对称线形和窄的凹陷, 这与经典的耦合模理论(coupled-mode theory, CMT)框架下的法诺线形吻合得较好, 为了说明这一点使用经典的法诺公式对透射谱进行拟合[56,57]:
其中ω0为谐振中心频率, γ是共振线宽, T0是背景散射参数, A0是连续态与离散态的耦合系数, q是Breit-Wigner-Fano参数, 决定共振曲线的非对称性, 根据拟合公式可以计算出Q = ω0/γ [58]. 如图3(d)所示, 计算了不同偏心孔半径条件下QBIC模式的Q因子并画出了其与不对称参数的函数对应关系, 这里不对称参数α定义为偏心孔面积(记为S1)与原始硅圆盘面积(记为S0)的比值:
为了更直观地看出Q因子和不对称参数α之间的关系, 图中坐标用log10-log10标度绘制, 从图3(d)可以看出, 在适当的范围内Q因子和α具有明显的反二次方关系[32]:
其中Q0是超表面结构所确定的常数, 与不对称参数α无关. 结果表明, 随着偏心孔半径的变化, 硅纳米盘所支持的QBIC谐振的Q因子的调控范围超过3个数量级, 可以在很大程度上主动调节耦合效率和Q因子的大小, 同时如此大的Q因子也为实现高分辨率的光学生物传感器提供了巨大的应用前景. 为了更进一步探究QBIC共振的辐射机理, 如图3(c)所示, 通过对r = 75 nm时的光学共振响应进行散射截面的多级分解[59,60], 发现MD的辐射功率最大, 其他极子共振的贡献都十分微弱, 进一步说明这种QBIC辐射状态由MD响应绝对主导, 其代表了系统中与出射波耦合的辐射通道. 图3(e)为r = 75 nm时相应的x-y平面上的电场的近场分布. 从图3(e)可以看出, 在偏心孔处, 电场得到了巨大的增强, 表明沿–z方向的入射光被磁偶极子振荡强烈的捕获在了超表面内, 同时巨大的Q因子可以显著增强局域光与物质的相互作用. 叠加的箭头表示平面内循环分布的位移电流, 这是磁偶极子共振的典型特征[61,62].
在实际的制造过程中, 高Q因子超表面对工艺制造要求很高, 因为它们的近场耦合效应对制造误差十分敏感, 制造缺陷会导致更多的光辐射到自由空间造成Q因子的减小. 因此实现高Q因子需要减小由于制造误差造成的散射损失. 虽然本研究仅限于仿真层面, 但近期的一些文献已经为我们的实验可行性提供了进一步的支持. 2024年, Hu等[63]展示了基于QBIC的可调谐长方体阵列超表面的实际制造, 实验与仿真结果一制. 对于本文提出的超表面结构的制备, 首先利用低压物理气相 沉积(low-pressure physical vapor deposition, LPCVD)在SiO2衬底上沉积硅膜, 然后将ZEP520抗蚀剂均匀旋涂在样品上并进行烘烤. 接下来通过电子束光刻(electron beam lithography, EBL)和电感耦合等离子体蚀刻(inductively coupled plasma etching, ICP), 可以获得所需的超表面. 最后, 在去除抗蚀剂后进行等离子体清洗. 只需几个简单的工艺, 就可以制造出所需的超表面.
-
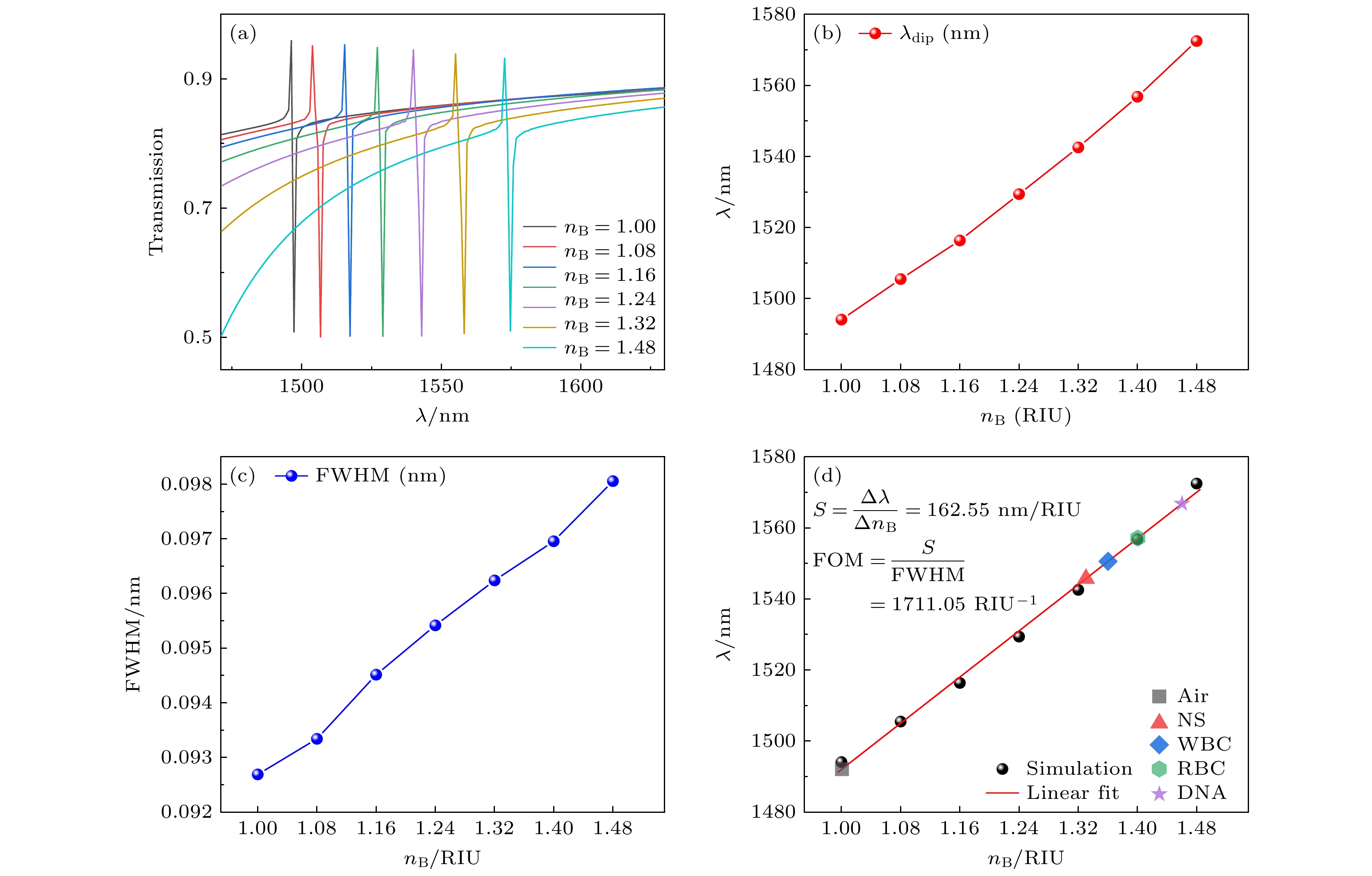
所提出的超表面结构所支持的QBIC共振模式对应的波长位于近红外二区范围内, 这个范围内的光波常用于生物和医学检测. 通常超表面结构的共振波长位置也会随着周围介电常数的改变而改变, 随着有效折射率的增加在透射谱上会出现红移现象[64]. 因此, 本文的研究也具有作为生物传感器的潜力. 此处首先通过改变背景环境折射率来模拟研究不同生物成分(不同生物成分的折射率记为RI)对QBIC共振的影响. 在默认条件下的背景为理想空气, 所以背景折射率(记为nB)设置为nB = 1. 在偏心孔半径的选择上, 虽然半径r越小所获得的Q因子越大共振线宽越窄, 对应的优值越大. 但考虑到随着半径r的减小共振峰的幅值信号也会随之减小, 当r = 0时共振峰也将完全消失, 在实际应用中不利于探测仪器的探测. 在经过对比筛选后, 这里偏心孔的半径r = 25 nm. 根据图3(d)中的Q-α关系, 这时的Q因子可以达到惊人的105级别. 如图4(a)所示, 透射光谱随着背景折射率的增大会有明显的红移现象, 这是因为背景折射率的增大会导致超表面结构单元整体有效折射率的增大. 在这里背景折射率nB的变化范围为1.00—1.48, 许多生物成分的折射率处在在这一范围内, 例如: 生理盐水(NS, RI = 1.33)、白细胞(WBC, RI = 1.36)、红细胞(RBC, RI = 1.40)和蛋白质、RNA或DNA (RI = 1.46) [65–67]. 为了更进一步研究这种性能, 分析了透射谱的共振峰波长位置(λdip)和半高全宽(FWHM)和nB的关系, 结果如图4(b), (c)所示. 从图4可知, λdip和FWHM与背景折射率nB之间具有线性关系, 利用这一线性依赖关系可以实现对生物成分折射率的传感. 灵敏度S和优值FOM是衡量传感器特性的两个重要指标. 对于折射率传感器, 灵敏度S定义为[51]:
其中Δλ为共振波长位置的变化量, ΔnB为背景折射率的变化量, S的单位为nm/ RIU. 优值FOM为
其中FWHM为透射谱谐振峰的半高全宽, FOM的单位为RIU–1. 对应于图4(b)中的数据, 在r = 25 nm的条件下, 传感器的性能表征为S = 165.22 nm/RIU, FOM = 1711.05 RIU–1.
表1为本文提出的超表面结构与已有文献中提出的结构在传感性能上的对比. 可以看出本文所设计的结构在具有较高灵敏度的同时, 也具有较高的FOM和Q因子. 与此同时, 所设计的超表面作为处于自由空间的光学平台为生物传感操作提供了更大的便利, 同时结构设计简单为实际的刻蚀制备省去了许多麻烦.
-
综上所述, 本文提出了一种新型全介质超表面结构, 以实现对生物蛋白质的折射率传感. 这种超表面由置于玻璃衬底上的周期性排列的偏心孔硅圆盘构成, 可以支持一个连续介质中对称保护的束缚态. 当超表面的面内对称性被破坏时, SP-BIC会转化为具有高Q因子的QBIC, 从而实现具有尖锐不对称线型的法诺共振. 这种共振峰的灵敏度对周围折射率变化非常敏感, 因此可以用于生物折射率的精确传感. 基于高Q因子的QBIC, 这种超表面能够实现生物折射率传感的灵敏度和优值分别达到162.55 nm/RIU 和1711.05 RIU–1, 高于许多现有研究. 在高FOM传感性能的基础上, 该超表面相比传统的等离子体超表面具有更低的欧姆损耗和更高的可调谐性. 因此, 这种超表面在细胞扫描成像和生物蛋白质折射率测量方面展示了显著的应用潜力, 能够提供更高的检测灵敏度和更广泛的适用性.
基于准连续体束缚态的近红外高Q全介质超表面生物传感器
Near-infrared high-Q all-dielectric metasurface biosensor based on quasi-bound state in continuum
-
摘要: 近年来, 连续体中的束缚态因具有极强的促进光与物质相互作用的能力, 是实现具有超高品质因子的光学共振的理想平台, 成为研究的热点. 本工作设计了一个单元胞由硅圆盘构成的全介质超表面, 在此超表面上观察到一个对称保护的束缚态, 当面内对称性被破坏时, 其可以转化为具有高质量品质因子的准束缚态. 随着背景折射率的改变, 共振峰的位置随之变化, 通过这一原理实现了一种生物折射率传感器. 由于品质因子和不对称参数成二次反比关系, 通过调节不对称参数, 品质因子也会发生改变, 从而实现传感性能的提升和调节. 经过调节, 该超表面的折射率传感灵敏度和优值分别达到162.55 nm/RIU和1711.05 RIU–1, 高于大部分的现有报道结果. 本工作的高品质因子全介质超表面设计为高灵敏度和高精度的生物检测提供了新的途径.Abstract: In recent years, bound states in the continuum (BICs) have become a hot research topic because of their strong ability to facilitate light-matter interactions, and they are also an ideal platform for realizing optical resonances with ultra-high quality factors (Q). Nowadays, BICs have been found to exist in various photonic microstructures and nanostructures such as waveguides, gratings, and metasurfaces, among which metasurfaces have attracted much attention due to their ease of adjustment and considerable robustness. Traditional precious metal-based metasurfaces inevitably have low Q-factors due to the inherent defect of high ohmic losses. In contrast, due to lower ohmic losses, all-dielectric metasurfaces can be an excellent alternative to metallic metasurface structures. In this work, an all-dielectric metasurface is designed, with a silicon disc as the unit cell, and symmetric protected BIC (SP-BIC) is observed on the metasurface. When introducing eccentric holes to break the symmetry in the structural plane (QBIC), the SP-BIC can be transformed into a quasi-BIC, with radiation dominated by magnetic dipoles and has a high-quality Q-factor. For QBICs formed on the metasurface, the resonance wavelength is usually greatly dependent on the refractive index of the surroundings due to the strong localization of the electric field within the cell. As the refractive index of the background changes, the positions of the resonance peaks change accordingly, and identification sensing of some biological components is achieved by this principle. This metasurface-based bio-refractive index sensor is less invasive in free space and is expected to overcome the drawbacks of traditional electrochemical-based biosensing technologies, which have cumbersome detection steps and high time and material costs. In terms of sensing parameters, due to the quadratic inverse relationship between the quality factor and asymmetric parameters, by adjusting the asymmetric parameters, the quality factor will also change, thereby enhancing and adjusting the sensing performance. After adjusting, the refractive index sensing sensitivity and figure of merit of this metasurface reach 162.55 nm/RIU and 1711.05 RIU–1, respectively, which are higher than those achieved in many other existing studies. This high Q-factor all-dielectric metasurface design provides a new avenue for achieving high-sensitivity and high-precision bio-detection.
-

-
图 1 (a) 所提出的全介质超表面示意图, 结构参数为Px = Py = 900 nm, R = 300 nm, H = 100 nm, 玻璃衬底的厚度设定为1000 nm; (b) 在距离盘中心150 nm的固定距离内引入一个半径r可变的偏心孔以破坏结构的C2对称性; (c) 硅纳米盘超表面的前视图
Figure 1. (a) Schematic of the proposed all-dielectric metasurface, the structural parameters are Px = Py = 900 nm, R = 300 nm, H = 100 nm, and the thickness of the glass substrate is set to 1000 nm; (b) an off-centered hole with variable radius r is introduced at a fixed distance of 150 nm from the center of the disc to break the C2 symmetry of the structure; (c) front view of the silicon nanodisc metasurface.
图 2 (a) 由周期排列的硅纳米盘阵列组成的超表面示意图; (b) 计算出图(a)中周期排列的硅纳米盘阵列的光子带结构, 灰色阴影表示位于自由空间光锥下方的区域, 被困的对称保护的BIC位置用红圈标记
Figure 2. (a) Schematic of a metasurface consisting of periodically aligned arrays of silicon nanodiscs; (b) calculated photonic band structure of the periodically aligned silicon nanodisk array in panel (a), grey shading indicates the region located below the free-space light cone, the location of the trapped symmetrically protected BIC is marked with a red circle.
图 3 (a) 玻璃衬底上硅纳米盘超表面的透射谱相对于偏心孔半径的变化, SP-BIC的对应位置使用篮圈标记; (b)在r = 75 nm时的透射光谱, 以及与法诺公式拟合曲线的对比; (c) 在r = 75 nm时, 硅超表面共振的多级展开, 可以看出在共振波长位置处MD响应占绝对的主导地位; (d) Q因子和不对称参数α的关系, 为直观反映两者之间的关系采用对数坐标绘制; (e) 在r = 75 nm的情况下共振时的x-y平面电场分布图像, 红色箭头表示面内循环位移电流
Figure 3. (a) Transmission spectrum of the silicon nanodisk metasurface on a glass substrate concerning the radius of the off-centered hole, the corresponding position of the SP-BIC is marked using a basket circle; (b) transmission spectrum at r = 75 nm and comparison with the fitted curve of Fano’s formula; (c) the multilevel unfolding of the silicon metasurface resonance at r = 75 nm shows that the MD response is dominant at the resonance wavelength position; (d) the relationship between the Q-factor and the asymmetry parameter α, which is plotted in logarithmic coordinates to visualize the relationship; (e) image of the x-y plane electric field distribution at resonance in the case of r = 75 nm, with the red arrows indicating the in-plane circulating displacement currents.
图 4 (a)不同背景折射率下的透射光谱; (b)共振波长随背景折射率的变化; (c)半高宽FWHM随背景折射率的变化; (d)对共振波长随背景折射率红移变化的线性拟合, 灵敏度S和优值FOM根据拟合梯度计算, 在拟合直线中标记了多种生物成分的RI
Figure 4. (a) Transmission spectra at different background refractive indices; (b) variation of resonance wavelength with background refractive index; (c) variation of half-height width FWHM with background refractive index; (d) linear fit to the variation of resonance wavelength with background refractive index redshift, the sensitivity S and the superior value FOM are calculated from the fitted gradient, the RIs of multiple biological components are labeled in the fitted straight line.
表 1 不同机制超表面结构传感性能和本研究的对比
Table 1. Comparison of the sensing performance of different mechanisms of metasurface structures and the present study.
Mechanism Materical Q-factor S/
(nm·RIU–1)FOM/
RIU–1Reference Surface
plasmonAu 121 250 28 [68] Surface
plasmonAu ~40 450 28.8 [69] Surface
plasmonAu ~8 170 1.3 [70] SP-BIC Si 3326 145 389 [71] SP-BIC Si 8428 160 575 [72] SP-BIC Si3N4 ~103 178 445 [73] Fano resonance TiO2 5126 186.96 721 [74] Accidental BIC GaP <104 135 <103 [39] SP-BIC Si 16506 162.55 1711.05 This work -
[1] Sadreev A F 2021 Rep. Prog. Phys. 84 055901 doi: 10.1088/1361-6633/abefb9 [2] Koshelev K, Bogdanov A, Kivshar Y 2019 Sci. Bull. 64 836 doi: 10.1016/j.scib.2018.12.003 [3] Huang L J, Li G Q, Gurarslan A, Yu Y L, Kirste R, Guo W, Zhao J J, Collazo R, Sitar Z, Parsons G N, Kudenov M, Cao L Y 2016 ACS Nano 10 7493 doi: 10.1021/acsnano.6b02195 [4] Neumann J V, Wigner E P 1929 Phys. Z 30 465 doi: doi:10.1007/978-3-662-02781-3_20 [5] Tong H, Liu S Y, Zhao M D, Fang K J 2020 Nat. Commun. 11 5216 doi: 10.1038/s41467-020-19091-3 [6] Linton C M, McIver P 2007 Wave Motion 45 16 doi: 10.1016/j.wavemoti.2007.04.009 [7] Marinica D C, Borisov A G, Shabanov S V 2008 Phys. Rev. Lett. 100 183902 doi: 10.1103/PhysRevLett.100.183902 [8] Plotnik Y, Peleg O, Dreisow F, Heinrich M, Nolte S, Szameit A, Segev M 2011 Phys. Rev. Lett. 107 183901 doi: 10.1103/PhysRevLett.107.183901 [9] Hsu C W, Zhen B, Lee J, Chua S L, Johnson S G, Joannopoulos J D, Soljačić M 2013 Nature 499 188 doi: 10.1038/nature12289 [10] Monticone F, Alù A 2014 Phys. Rev. Lett. 112 213903 doi: 10.1103/PhysRevLett.112.213903 [11] Gomis-Bresco J, Artigas D, Torner L 2017 Nat. Photonics 11 232 doi: 10.1038/nphoton.2017.31 [12] Kodigala A, Lepetit T, Gu Q, Bahari B, Fainman Y, Kanté B 2017 Nature 541 196 doi: 10.1038/nature20799 [13] Doeleman H M, Monticone F, den Hollander W, Alù A, Koenderink A F 2018 Nat. Photonics 12 397 doi: 10.1038/s41566-018-0177-5 [14] Li Z Y, Chang H N, Lai J M, Song F L, Yao Q F, Liu H Q, Ni H Q, Niu Z C, Zhang J 2023 J. Semicond. 44 082901 doi: 10.1088/1674-4926/44/8/082901 [15] Salmanogli A 2023 J. Semicond. 44 052901 doi: 10.1088/1674-4926/44/5/052901 [16] Bulgakov E N, Sadreev A F 2008 Phys. Rev. B 78 075105 doi: 10.1103/PhysRevB.78.075105 [17] Romano S, Zito G, Lara Yépez S N, Cabrini S, Penzo E, Coppola G, Rendina I, Mocellaark V 2019 Opt. Express 27 18776 doi: 10.1364/OE.27.018776 [18] 刘会刚, 张翔宇, 南雪莹, 赵二刚, 刘海涛 2024 物理学报 73 047802 doi: 10.7498/aps.73.20231514 Liu H G, Zhang X Y, Nan X Y, Zhao E G, Liu H T 2024 Acta Phys. Sin. 73 047802 doi: 10.7498/aps.73.20231514 [19] Srivastava Y K, Ako R T, Gupta M, Bhaskaran M, Sriram S, Singh R 2019 Appl. Phys. Lett. 115 151105 doi: 10.1063/1.5110383 [20] Liu D J, Wu F, Yang R, Chen L, He X Y, Liu F 2021 Opt. Lett. 46 4370 doi: 10.1364/OL.422771 [21] Koshelev K, Favraud G, Bogdanov A, Kivshar Y, Fratalocchi A 2019 Nanophotonics 8 725 doi: 10.1515/nanoph-2019-0024 [22] Lee J, Zhen B, Chua S L, Qiu W, Joannopoulos J D, Soljačić M, Shapira O 2012 Phys. Rev. Lett. 109 067401 doi: 10.1103/PhysRevLett.109.067401 [23] Hsu C W, Zhen B, Stone A D, Joannopoulos J D, Soljačić M 2016 Nat. Rev. Mater. 1 1 [24] Xu L, Zangeneh Kamali K Z, Huang L J, Rahmani M, Smirnov A, Camacho-Morales R, Ma Y X, Zhang G Q, Woolley M, Neshev D, Miroshnichenko A E 2019 Adv. Sci. 6 1802119 doi: 10.1002/advs.201802119 [25] Paddon P, Young J F 2000 Phys. Rev. B 61 2090 doi: 10.1103/PhysRevB.61.2090 [26] Bulgakov E N, Sadreev A F 2014 Opt. Lett. 39 5212 doi: 10.1364/OL.39.005212 [27] Barrow M, Phillips J 2020 Opt. Lett. 45 4348 doi: 10.1364/OL.397779 [28] Zong X Y, Li L X, Liu Y F 2021 Opt. Lett. 46 6095 doi: 10.1364/OL.446950 [29] Jain A, Moitra P, Koschny T, Valentine J, Soukoulis C M 2015 Adv. Opt. Mater. 3 1431 doi: 10.1002/adom.201500222 [30] Wang Y H, Fan Y B, Zhang X D, Tang H J, Song Q H, Han J C, Xiao S M 2021 ACS Nano 15 7386 doi: 10.1021/acsnano.1c00673 [31] Chen Y, Zhao C, Zhang Y Z, Qiu C W 2020 Nano Lett. 20 8696 doi: 10.1021/acs.nanolett.0c03506 [32] Koshelev K, Lepeshov S, Liu M, Bogdanov A, Kivshar Y 2018 Phys. Rev. Lett. 121 193903 doi: 10.1103/PhysRevLett.121.193903 [33] Alipour A, Farmani A, Mir A 2018 IEEE Sensors J. 18 7047 doi: 10.1109/JSEN.2018.2854882 [34] Kong Y, Cao J J, Qian W C, Liu C, Wang S Y 2018 IEEE Photonics J. 10 6804410 doi: 10.1109/JPHOT.2018.2881264 [35] Bezus E A, Bykov D A, Doskolovich L L 2018 Photon. Res. 6 1084 doi: 10.1364/PRJ.6.001084 [36] Zeng T Y, Liu G D, Wang L L, Lin Q 2021 Opt. Express 29 40177 doi: 10.1364/OE.446072 [37] Al-Ani I A M, As’Ham K, Huang L, Miroshnichenko A E, Hattori H T 2021 Laser Photonics Rev. 15 2100240 doi: 10.1002/lpor.202100240 [38] Xiang J, Chen J, Lan S, Miroshnichenko A E 2020 Adv. Opt. Mater. 8 2000489 doi: 10.1002/adom.202000489 [39] Li Z T, Panmai M, Zhou L D, Li S L, Liu S M, Zeng J H, Lan S 2023 Appl. Surf. Sci. 620 156779 doi: 10.1016/j.apsusc.2023.156779 [40] Chen C, Wang J 2020 Analyst 145 1605 doi: 10.1039/C9AN01998G [41] Sharma S, Kumari R, Varshney S K, Lahiri B 2020 Reviews in Physics 5 100044 doi: 10.1016/j.revip.2020.100044 [42] Wang Z, Tan C H, Peng M, Yu Y Y, Zhong F, Wang P, He T, Wang Y, Zhang Z H, Xie R Z, Wang F, He S J, Zhou P, Hu W D 2024 Light. Sci. Appl. 13 277 doi: 10.1038/s41377-024-01640-w [43] Roingeard P, Raynal P I, Eymieux S, Blanchard E 2019 Rev. Med. Virol. 29 e2019 doi: 10.1002/rmv.2019 [44] Caucheteur C, Villatoro J, Liu F, Loyez M, Guo T, Albert J 2022 Adv. Opt. Photon. 14 1 doi: 10.1364/AOP.444261 [45] Polz L, Dutz F J, Maier R R J, Bartelt H, Roths J 2021 Optics & Laser Technology 134 106650 [46] Valušis G, Lisauskas A, Yuan H, Knap W, Roskos H G 2021 Sensors 21 4092 doi: 10.3390/s21124092 [47] Toropov N, Cabello G, Serrano M P, Gutha R R, Rafti M, Vollmer F 2021 Light Sci. Appl. 10 42 doi: 10.1038/s41377-021-00471-3 [48] Azzouz A, Hejji L, Kim K H, Kukkar D, Souhail B, Bhardwaj N, Brown R J C, Zhang W 2022 Biosens. Bioelectron. 197 113767 doi: 10.1016/j.bios.2021.113767 [49] Li Q, Meng J P, Li Z 2022 J. Mater. Chem. A 10 8107 doi: 10.1039/D2TA00075J [50] Wang J, Kühne J, Karamanos T, Rockstuhl C, Maier S A, Tittl A 2021 Adv. Funct. Mater. 31 2104652 doi: 10.1002/adfm.202104652 [51] Guo L H, Zhang Z X, Xie Q, Li W X, Xia F, Wang M, Feng H, You C L, Yun M J 2023 Appl. Surf. Sci. 615 156408 doi: 10.1016/j.apsusc.2023.156408 [52] https://www.lumerical.com/tcad-products/fdtd/ for FDTD method. [53] Johnson S G, Joannopoulos J D 2001 Opt. Express 8 173 doi: 10.1364/OE.8.000173 [54] Xu T, Wheeler M S, Nair S V, Ruda H E, Mojahedi M, Aitchison J S 2008 Appl. Phys. Lett. 93 241105 doi: 10.1063/1.3046124 [55] Zhen B, Hsu C W, Lu L, Stone A D, Soljačić M 2014 Phys. Rev. Lett. 113 257401 doi: 10.1103/PhysRevLett.113.257401 [56] Limonov M F, Rybin M V, Poddubny A N, Kivshar Y S 2017 Nat. Photonics 11 543 doi: 10.1038/nphoton.2017.142 [57] Miroshnichenko A E, Flach S, Kivshar Y S 2010 Rev. Mod. Phys. 82 2257 doi: 10.1103/RevModPhys.82.2257 [58] Yang Z J, Hao Z H, Lin H Q, Wang Q Q 2014 Nanoscale 6 4985 doi: 10.1039/c3nr06502b [59] Hinamoto T, Fujii M 2021 OSA Continuum. 4 1640 doi: 10.1364/OSAC.425189 [60] Alaee R, Rockstuhl C, Fernandez-Corbaton I 2018 Opt. Commun. 407 17 doi: 10.1016/j.optcom.2017.08.064 [61] Wang X, Duan J, Chen W, Zhou C, Liu T, Xiao S 2020 Phys. Rev. B 102 155432 doi: 10.1103/PhysRevB.102.155432 [62] Li Z, Xie M, Nie G, Wang J, Huang L 2023 J. Phys. Chem. Lett. 14 10762 doi: 10.1021/acs.jpclett.3c02763 [63] Hu H, Lu W, Antonov A, Berté R, Maier S A, Tittl A 2024 Nat. Commun. 15 7050 doi: 10.1038/s41467-024-51340-7 [64] Zhou C B, Liu G Q, Ban G X, Li S Y, Huang Q Z, Xia J S, Wang Y, Zhan M S 2018 Appl. Phys. Lett. 112 101904 doi: 10.1063/1.5020576 [65] Maji P S, Shukla M K, Das R 2018 Sensor. Actuat. B: Chem. 255 729 doi: 10.1016/j.snb.2017.08.031 [66] Bankapur A, Zachariah E, Chidangil S, Valiathan M, Mathur D 2010 PLOS ONE 5 e10427 doi: 10.1371/journal.pone.0010427 [67] Tuchin V V, Zhestkov D M, Bashkatov A N, Genina E A 2004 Opt. Express, OE 12 2966 doi: 10.1364/OPEX.12.002966 [68] Chen J, Yuan J, Zhang Q, Ge H M, Tang C J, Liu Y, Guo B N 2018 Opt. Mater. Express 8 342 doi: 10.1364/OME.8.000342 [69] Gao B W, Wang Y L, Zhang T Z, Xu Y, He A X, Dai L, Zhang J S 2019 ACS Nano 13 9131 doi: 10.1021/acsnano.9b03406 [70] Sun F, Yang W C, Du C L, Chen Y X, Fu T Y, Shi D N 2020 Plasmonics 15 949 doi: 10.1007/s11468-019-01115-4 [71] Li H, Yu S L, Yang L, Zhao T G 2021 Optics Laser Technology 140 107072 doi: 10.1016/j.optlastec.2021.107072 [72] Song S, Yu S L, Li H, Zhao T G 2022 Laser Phys. 32 025403 doi: 10.1088/1555-6611/ac46cf [73] Zito G, Sanità G, Alulema B G, Yépez S N L, Lanzio V, Riminucci F, Cabrini S, Moccia M, Avitabile C, Lamberti A, Mocella V, Rendina I, Romano S 2021 Nanophotonics 10 4279 doi: 10.1515/nanoph-2021-0396 [74] Liu H G, Zheng L, Ma P Z, Zhong Y, Liu B, Chen X Z, Liu H T 2019 Opt. Express 27 13252 doi: 10.1364/OE.27.013252 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: