-
加速器在科学和工业领域有着非常广泛的应用[1]. 受现有技术手段在物理尺度、制备复杂度所引发的高昂成本等诸多因素掣肘[2,3], 国内外学者对介电激光加速器(DLA)的光栅结构设计展开了深入研究. 20世纪80年代, 研究者们首次利用太赫兹辐射和金属光栅证明了亚相对论电子的逆史密斯-珀塞尔效应, 尽管梯度很低(~keV/m)[4]. 同时, 二氧化硅等一系列介电材料具有高达GV/m的材料损伤阈值[5,6], 理论上DLA可以提供高达GV/m的加速梯度[7,8]. 作为一类二维光子晶体微纳光学器件, DLA光栅的材料特性、几何参数与光场分布直接决定了加速区域的电场分布, 从而影响粒子束的运动规律[9–11]. 2013年斯坦福直线加速器中心在石英玻璃制成的对偶光栅结构中观测到高达300 MeV/m的加速梯度[12]. 随研究不断深入, 目前DLA的加速梯度已经非常接近1 GV/m[13]. 但现阶段DLA领域的大多数优化研究多集中在结构优化和加速性能研究[14–18]. 由于现阶段多采用1 μm左右的近红外波长的激光作为DLA入射光源, 对应设计的光栅结构加速通道更小, 可加速的粒子数量较少. Siemann等[19]在800 nm波段设计了半个波长的光栅结构, 但结果表明仅有2%的电子束流能通过加速通道. 马克斯普朗克量子光学研究所在790 nm波段在单个石英玻璃光栅结构的近表面激发加速场[20,21]. 相较于近红外光栅结构, 长波红外光栅结构尺寸更大, 且更易于加工. 此外, 较大的粒子加速通道能够加速更多粒子, 进而提高粒子束电流和亮度. 同时, 长波红外光栅结构对于粒子加速有更高的能量转换效率, 受长距离加速的限制, 现阶段有关DLA光栅加速器设计的研究主要集中在近红外波段[22,23], 缺乏对于长波红外波长DLA结构设计的研究.
目前, 介电光栅加速器的主流设计方法主要依赖于人工调参和单一的参数化扫描优化. 其局限性在于其优化效率低、设计参数经验依赖性强, 可迁移性较差, 且难以快速适应复杂的实验需求, 这些缺陷限制了DLA的结构优化. 随着人工智能技术的发展, 深度学习技术在光电微纳器件设计领域开始获得应用[24–29]. 与传统设计方法相比, 深度学习能够通过自动学习数据中的复杂模式, 可以从复杂的多维参数下精准提取有效特征参数, 极大提高了结构设计的参数可靠性同时降低了计算量, 从而实现对加速器设计参数的高效优化.
本研究提出了一种基于深度学习的长波红外介电光栅加速器的设计方法, 采用9.6 μm的长波红外波长作为介电光栅加速器的入射光源, 综合考虑几何参数、材料特性、光场分布等多个关键因素. 几何参数设计方面, 建立了包含几何参数、材料性质、光场能量等多个参数的综合特征评估方法, 使用GANDALF模型作为深度学习的框架, 并对目标粒子能量增幅指标进行精准预测, 综合选取最大能量增幅对应的结构参数, 以实现长波红外介电光栅加速器结构的优化设计. 通过对比C(金刚石), CaF2, ZnSe三种材料探究材料特性对于长波红外介电光栅加速器加速效果的影响并选出最优结构. 同时, 与近红外光栅结构进行对比, 进一步验证了长波红外介电光栅加速器的高能量转换效率. 结果表明, C材料的光栅结构加速器加速效果最优, 粒子能量增幅高达99.5 keV, 同比增长19.9%, 并且可实现100%的加速相位, 束斑半径14.5 μm. 长波红外光栅结构加速通道宽度为2.88 μm, 加速的平均粒子束电流为20.4 fA, 对比近红外光栅结构高出了6.9倍, 长波红外光栅结构加速的粒子束亮度与近红外光栅结构相当, 这表明尽管长波红外光栅结构的尺寸显著大于近红外光栅结构, 其聚焦能力依然能够保持在相同水平. 本研究为长波红外高净增益介电光栅加速器的设计及发展提供了潜在的技术路线.
-
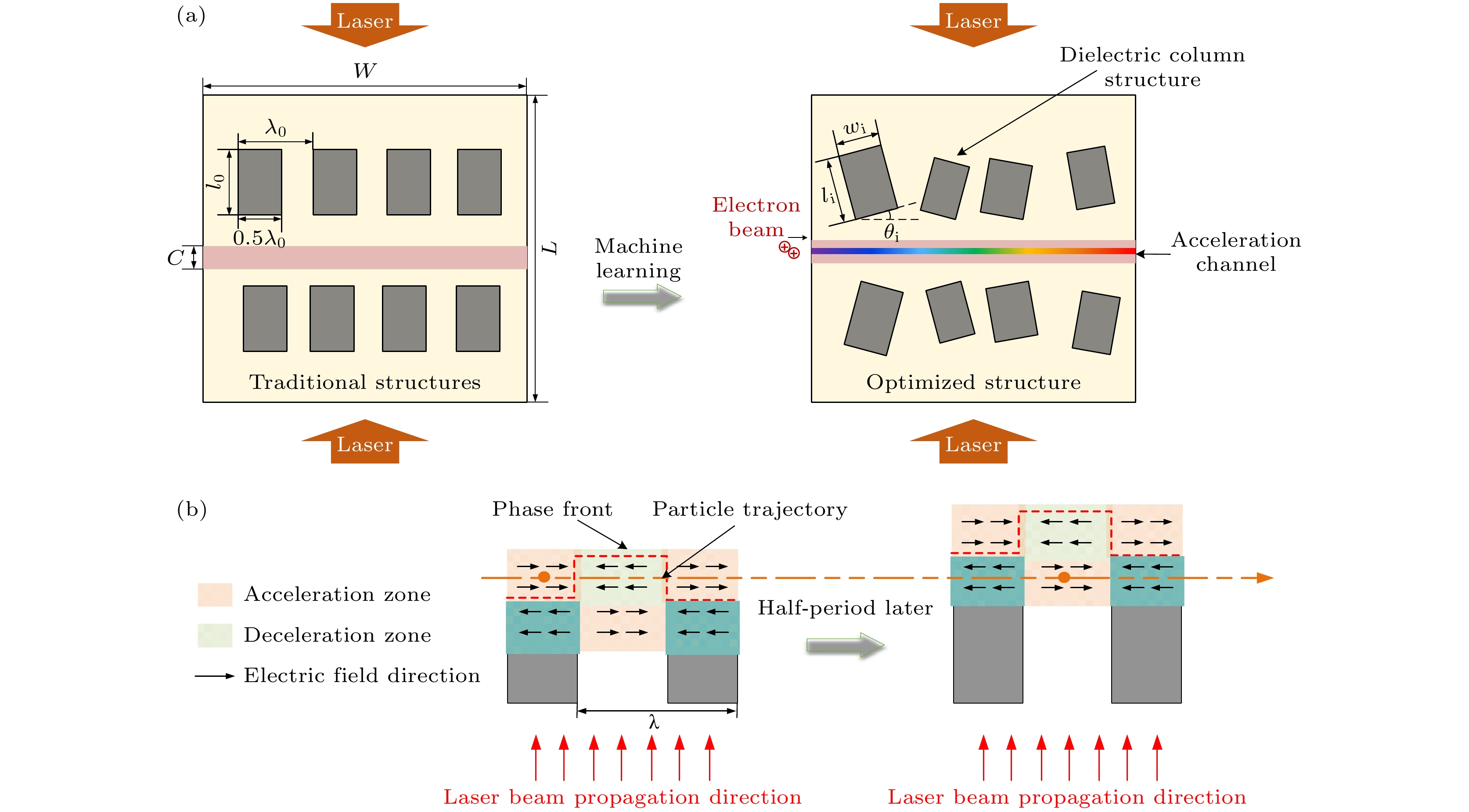
介电光栅加速器的加速效果受多重因素的共同作用. 在设计光栅结构时, 必须综合考虑几何参数、材料特性、光场分布等多个关键因素. 其中, 几何参数的合理选择是决定加速效果的关键因素之一. 当光栅结构设计中提取的几何参数较单一时, 粒子在经过电场加速后速度膨胀, 粒子速度与入射激光的波前相位匹配失衡, 会直接导致粒子在部分区域被减速. 与近红外光栅加速器的结构设计相比, 长波红外光栅具有更大的结构尺寸和更宽的粒子加速通道, 这使得其能够加速更多的粒子, 从而显著提升加速粒子束的电流并增强束流亮度. 由于长波红外光栅的尺寸较大, 粒子加速距离增大, 常规的单一参数设计不能适用在长波红外光栅的结构设计中. 为确保长波红外介电光栅加速器在持续加速过程中保持稳定的加速效果, 本文采用由多个独立单元组成的光栅结构作为研究对象. 加速器结构如图1(a)所示, 粒子加速通道位于器件结构中央, 介电柱排列于加速通道的两侧, 将关于加速通道对偶的一对介电柱视为一组, 每组介电柱的结构参数以参数阵列Di = [li, wi, θi]表示, 参数数值相对独立, 它们的几何尺寸和空间分布之间均无明显相关性. 光栅加速器中光栅尺寸与粒子束半径的匹配是影响加速效果的重要因素之一. 光束在传播过程中产生的衍射扩散现象可用菲涅耳衍射公式来近似表达, 当菲涅耳数大于1时, 衍射效应较弱, 波前保持平直, 光斑扩展受到较小影响; 反之则衍射效应显著, 光斑容易扩展且失真. 因此在介电光栅加速器设计中, 设置4组介电柱区域增大横向光场调制区域, 菲涅耳数远大于10, 使激光能量约束在主波导模式内, 抑制由衍射引起的光斑扩展, 从而维持稳定的加速电场分布.
光栅加速器的持续性加速原理如图1(b)所示, 激光脉冲在介电柱内的传播速度小于近邻的真空柱内的速度, 这会导致粒子加速通道内两个近邻区域的电场相位不同步, 如果调节介电柱的几何特征使得临近区域内电场分布产生π的相位差, 就可以让粒子受到持续性的加速推动力. 而在几何参数单一的光栅结构中, 介电柱的几何尺寸大多相同且位置分布呈现周期性, 粒子在经过电场加速后速度膨胀, 此时粒子速度与入射激光的波前相位匹配失衡, 导致粒子在近半数区域被减速. 而本研究中设计的加速器中每一组介电柱均可通过调整参数阵列Di构成独立单元, 实现对发射激光的波前控制, 更易于实现粒子的持续性加速. 这种可调节性强的光栅结构数据结构较大, 而传统的单一数值计算方法耗时久, 经验性依赖强, 不适用于本研究中的光栅结构优化设计. 因此, 本研究将基于GANDALF模型的深度学习技术对这一复杂光栅结构进行设计与优化.
-
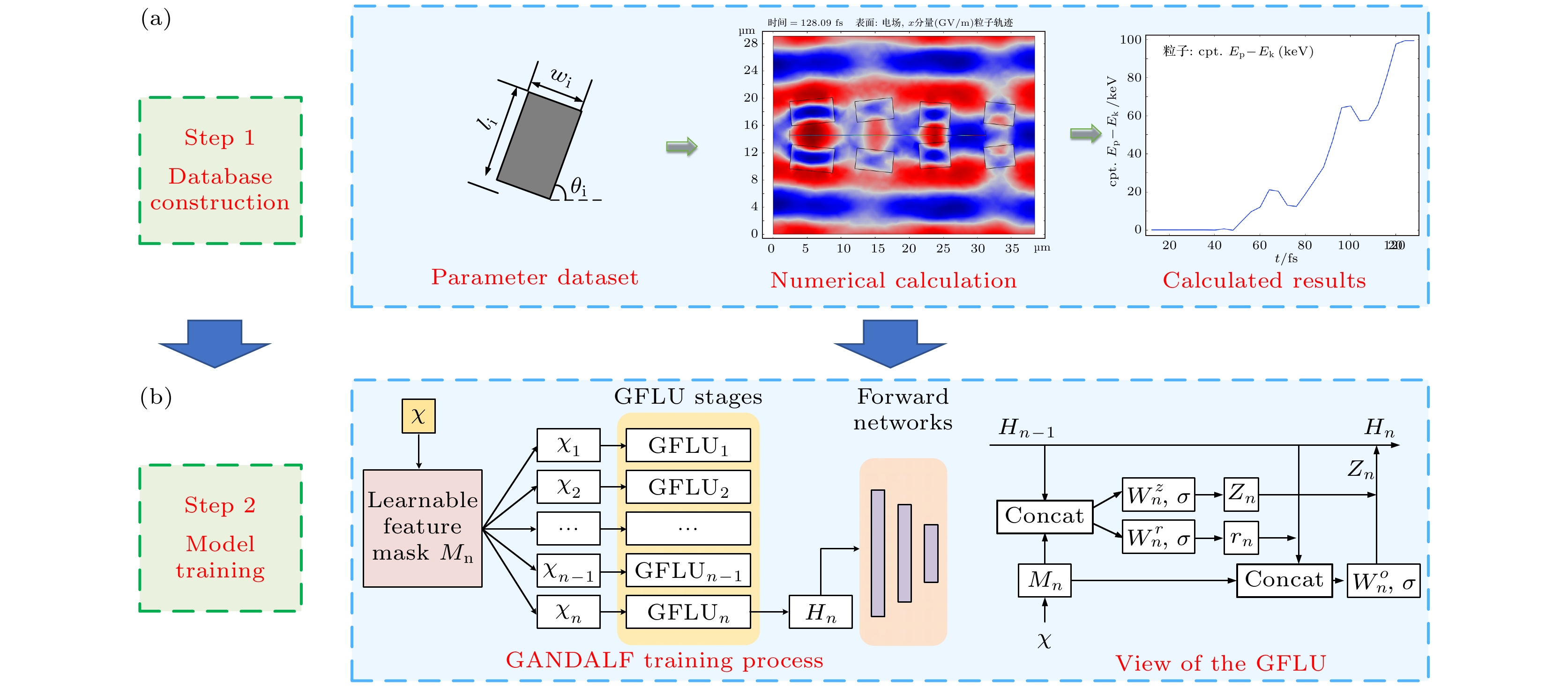
在本研究中, 我们采用一种基于GANDALF模型的深度学习方法作为技术框架, 该方法的优势在于能够有效处理高维度数据和非线性关系. 通过先进的特征学习技术优化特征表示, 显著提升了模型的泛化能力和预测准确性. 此外, GANDALF模型的灵活性使其能够适应不同的数据分布和噪声条件, 增强对复杂系统的解析能力. 本研究涉及的特征参数复杂且均无明显相关性, 因此需采用深度学习技术对于这种复杂的数据进行处理. 基于GANDALF模型的深度学习方法如图2所示. 本研究中采用的深度学习方法分为两个阶段. 第1步是构建数据库. 首先, 设置加速器模型参数(图2(a)), 入射激光光源选取CO2激光, CO2激光有四大主支(9.2, 9.6, 10.2, 10.6) μm, 9.6 μm波段具有更密集的谱线和更宽的谱宽, 理论上可实现亚皮秒至皮秒级的超短脉冲, 符合介电激光加速器中对入射光源的要求, 因此本研究选用9.6 μm作为入射激光波长[30,31]. 初始粒子注入能量为500 keV. 为降低衍射效应, 模型几何尺寸L和W分别为29 μm和38. 4 μm. 每组介电柱的设计参数用参数矩阵Di =[li, wi, θi]表示. 其次, 本研究的参数扫描范围是基于经典周期性光栅结构的物理准则和初步数值模拟结果共同决定的: 传统结构的介电柱长度为
$ {l}_{i}=\lambda /2\left(n-1\right) $ , 介电柱的占空比为波长的1/2, 旋转角度为0°, 本文设计并在此基础上围绕关键参数的中心值进行±10%的增减, 再通过数值模拟法二次筛选, 最终确定参数较优区间: 长度参数li从3 μm变化到3.7 μm, 间隔为0.1 μm; 宽度wi从4.5 μm变化到5.2 μm, 间隔为0.1 μm; 旋转角θi从–6°变化到6°, 间隔为1°; 将几何参数与光场强度等多个参数交叉组合作为数据集. 数值模拟法采用商用电磁场有限元分析软件进行数值计算. 此外, 基于C, CaF2, ZnSe三种材料的电场损伤阈值和热响应特性, 本研究同时对以上3种材料的最优结构参数进行探究. 3种材料的折射率参考文献[10].第2步, 在研究的第2阶段, 将收集到的数据输入至深度学习模型, 旨在建立多个介电柱设计参数与粒子能量增幅之间的映射关系. 同时, 对建立的深度学习模型进行评估, 确保其可靠性. 在模型验证通过后, 将测试集数据输入已经训练好的深度学习模型, 对每组特定参数对应的粒子能量增幅进行预测. 最终, 基于粒子能量增幅最大的结果, 将选出对应的最优结构参数, 作为本研究光栅结构模型的优化方案, 从而实现加速器结构的优化设计. 图2(b)所示为本研究提出的粒子能量增幅预测模型, 该模型通过采用复杂网络集成实现目标的精准预测. 用于特征深度自动学习的门控自适应网(GANDLF)模型主要由两部分模块组成: 门控功能学习单元(GFLU)和多层感知(MLP). 每个GFLU阶段使用可学习的特征掩码(Mn)来选择重要特征. 特征掩码通过应用稀疏变换来生成, 这种变换使用了t-softmax函数. t-softmax函数相比于传统softmax函数, 额外引入了温度参数(t), 从而能够控制输出的稀疏程度. 具体来说, 给定输入向量
$\boldsymbol x = (x_1, x_2, \cdots, x_n) $ , t-softmax函数的计算公式如下:当t取较小值时, 指数函数的放大效应增强, 使得最大值所对应的特征权重显著增大, 而其他较小的特征权重趋近于零, 从而实现稀疏化选择. 这一特性使得t-softmax特别适用于特征筛选任务, 能够突出少数关键特征, 同时减少冗余信息的干扰, 提高模型的学习效率. 除了特征掩码机制, GFLU包含重置门(rn)和更新门(zn), 重置门决定了从上一阶段隐藏状态中遗忘多少信息, 而更新门则决定了当前阶段特征表示的更新程度. 通过这种方式, GFLU可以动态调整特征选择和表示学习的过程, 同时, GFLU的每一层都具有独特的权重矩阵, 允许不同的层在学习过程中关注不同的特征子集. 这种层次结构使得特征表示能够逐步优化, 从而提高模型的性能. 在GFLU模块之后, 特征表示被传递到一个标准的多层感知器(MLP). 在GANDALF模型中, MLP作为最后的预测层对特征表示进行进一步处理. 经过多个GFLU阶段后得到的特征表示(H)被输入到一个标准的K层MLP中. MLP的作用是将经过GFLU优化后的特征映射到最终的输出维度. MLP用于将经过GFLU处理的特征表示转换为最终的预测结果. 为有效评估基于GANDALF的深度学习模型, 本文引入了均方误差(MSE)和决定系数(R2), 并选用MSE作为损失函数. 模型的优化器使用Adam.
-
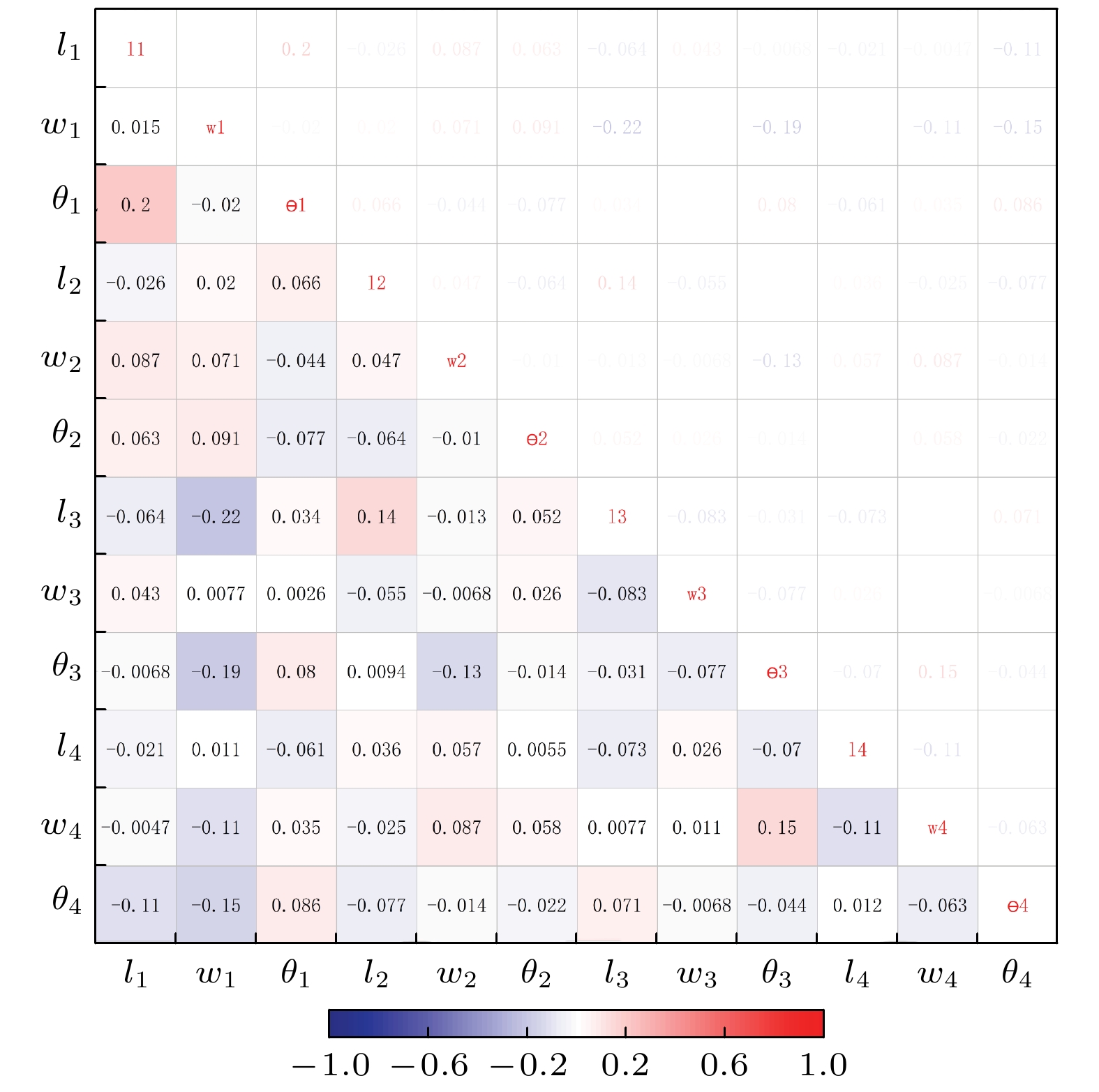
本研究所提出的深度学习模型具有预测能力, 能够准确预测复杂参数下建立其输入DLA的粒子能量增幅. 同时GANDALF模型可以在复杂信息中筛选参数并和输出之间的有效联系, 从而实现复杂结构光栅加速器的设计. 模型的数据集以介电柱的几何参数Di作为输入, 粒子能量增幅作为输出. 为保证模型的可靠性, 我们将数据集随机划分成训练集: 测试集: 验证集为7∶2∶1的比例. 如图3所示, 为验证本研究中所设计提取特征参数的合理性, 我们选取设计中介电柱的12个特征参数进行person相关性分析, 数值均低于0.3, 该结果表明特征参数间相对独立无明显相关性, 模型使用的数据集具有统计可靠性.
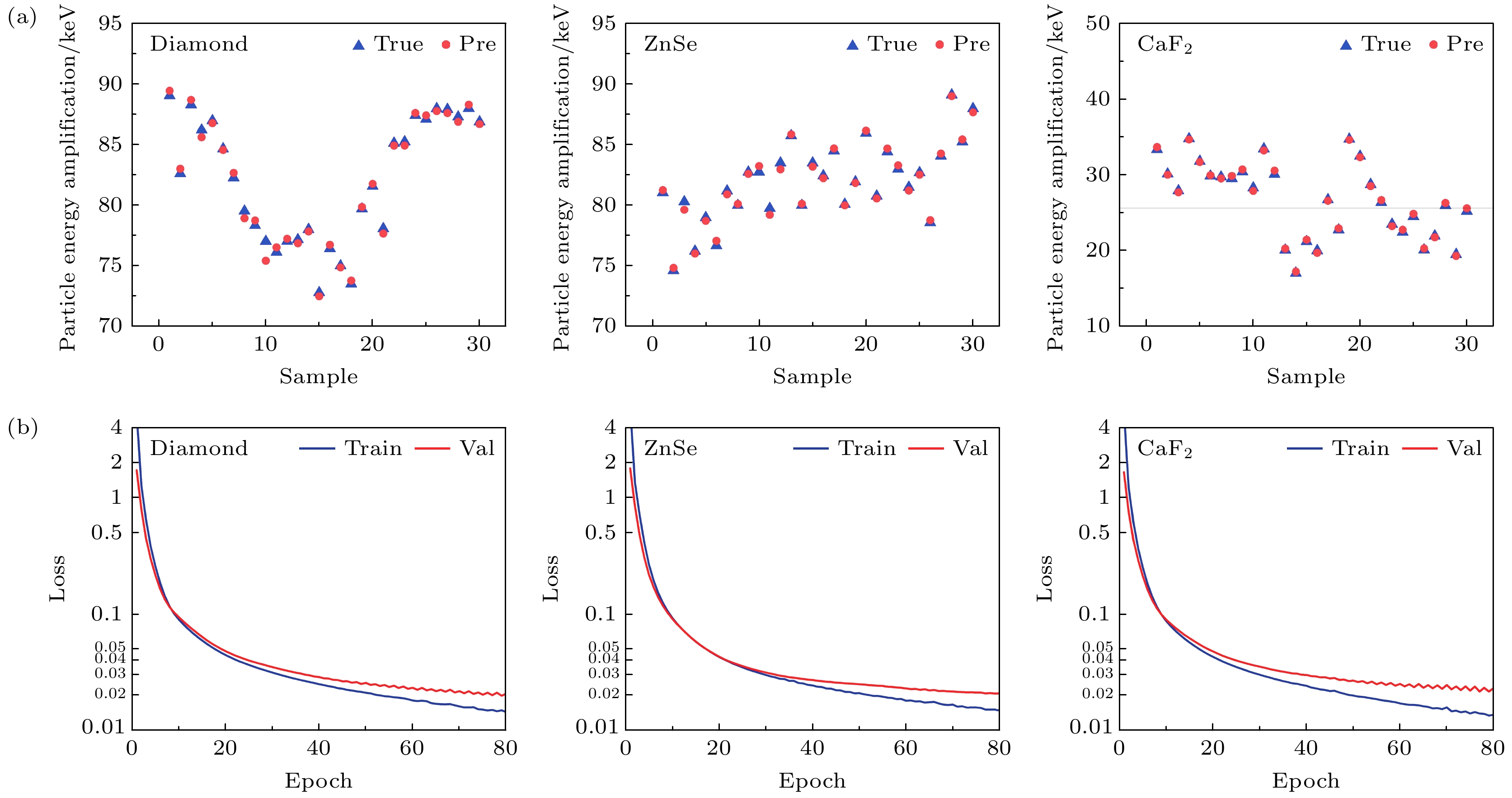
采用获得的数据集训练本研究中的深度学习模型, 为更精准地评估深度学习模型的预测性能, 在C, CaF2, ZnSe三种材料中分别随机挑选30个样本数据对GANDALF模型进行测试. 测试结果如图4(a)所示, 对模型预测的准确性进行合理评估, 3组数据集下的R2分别为0.983, 0.979, 0.974, 这表明模型在各个数据集上的拟合效果非常好, 能够充分捕捉到数据的内在趋势和模式. 具体而言, 高R2值显示出模型对数据的高解释能力, 意味着模型预测的值与实际观察值之间的差异极小, 且误差较为一致. 虽然3组R²值有些微差异, 表明虽然在各个数据集上的预测性能有所差异, 但模型依然能够有效地捕捉不同数据集的特征, 展示了较强的泛化能力和稳定性. 该结果进一步验证了模型的高效性和对复杂数据模式的适应性. 模型损失函数如图4(b)所示, 结果表明, 随着训练轮次增加, 训练集和验证集的损失函数值均稳定下降, 且在达到收敛时, 损失值均低于0.03, 并且非常接近. 该现象表明模型在训练过程中有效拟合了数据, 且具有较好的泛化能力. 损失函数的收敛性和低值反映出训练集和验证集的误差趋于一致, 避免了过拟合的发生. 此外, 训练集和验证集损失接近的趋势也进一步证明了模型的稳定性与鲁棒性, 表明模型对未知数据的预测能力较强, 且在优化过程中能够实现有效的误差最小化. 基于GANDALF的深度学习模型在此预测目标下表现较为优秀. 以上结果均表明模型能够准确预测粒子能量增幅, 预测值和真实值数据高度重叠且匹配良好, 证明本研究中的深度学习模型具有较高的稳定性和很好的鲁棒性.
-
在长波红外光栅加速器结构设计中, 综合考虑了几何参数、材料特性、光场分布等多个关键因素对加速效果的影响. 其中几何参数的选取由深度学习技术完成. 在验证GANDALF模型可靠性的基础上, 将不同的几何参数组合输入到已经训练完成的深度学习模型, 对每组参数所对应的粒子能量增幅进行预测. 综合选取粒子能量增幅最大时所对应的模型结构参数作为本研究光栅结构模型的最优几何参数, 以金刚石为例最优几何参数如表1所示.
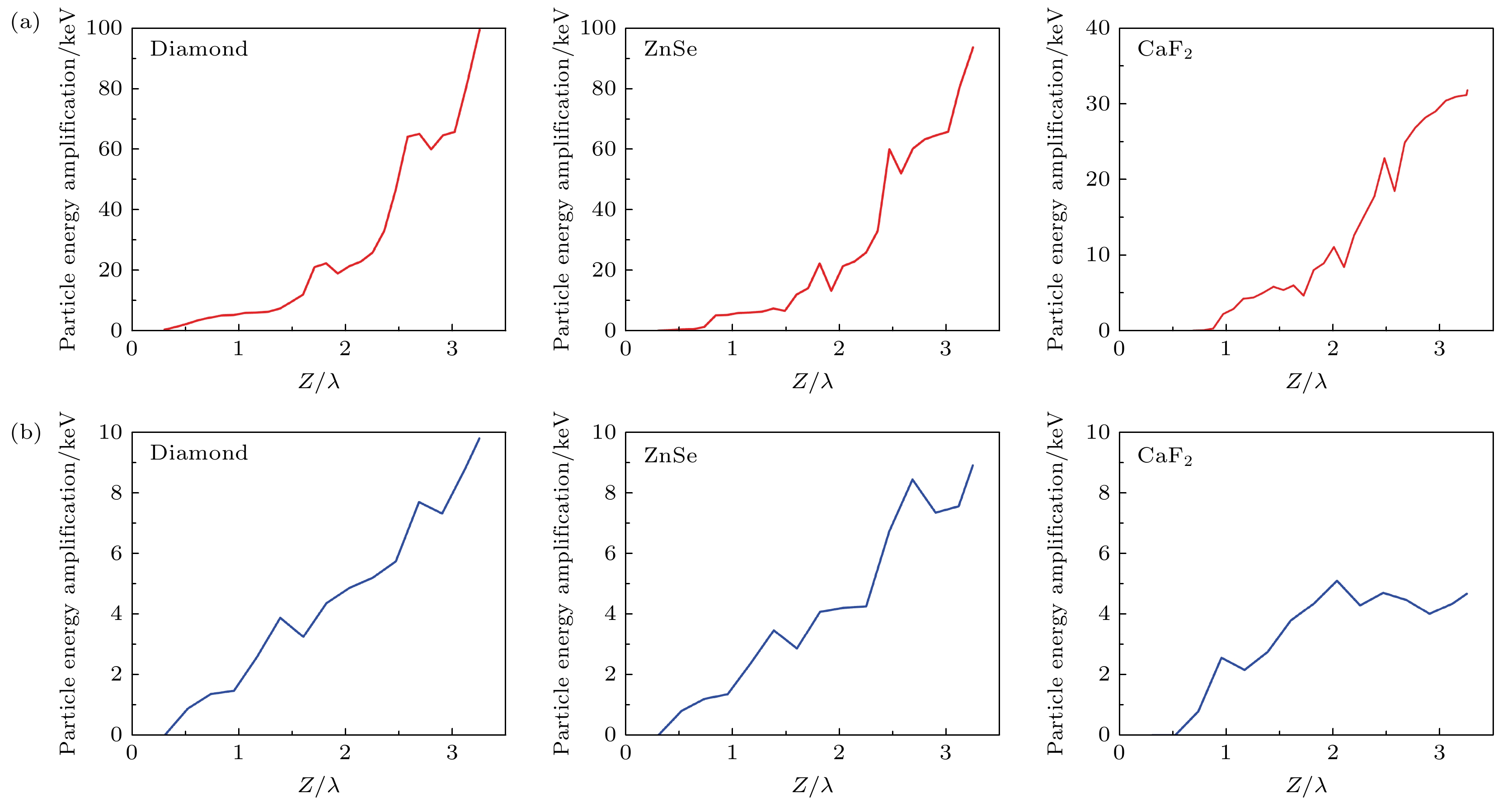
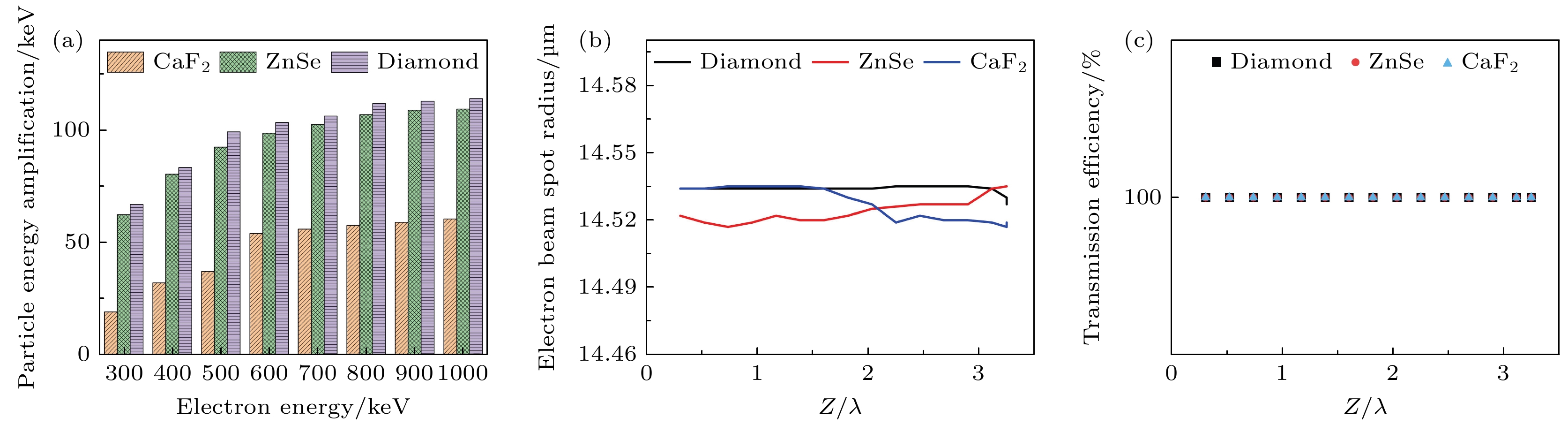
为了研究长波红外介电光栅加速器的材料特性对加速效果的影响, 我们比较了C, CaF2, ZnSe三种不同折射率的材料对粒子加速效果的影响, 如图5(a)所示. 结果表明, 在C, CaF2, ZnSe三种材料中, C结构的长波红外光栅加速器对粒子的加速效果最好, 粒子能量增幅99.5 keV, 同比粒子初始能量增幅为19.9%. 为进一步验证9.6 μm长波红外波长下介电光栅加速器的优异性能, 本文选取了常规近红外波长(800 nm)下相同材料的光栅加速器作为对照组, 如图5(b)所示. 在3种不同折射率材料的对比实验中, 近红外波段加速器在不同折射率材料中表现出与长波红外加速器相似的加速规律, 3种不同折射率材料对近红外采用C材料的加速器表现最佳, 实现了9.67 keV的能量增幅, 同比粒子初始能量增幅1.95%, 但与长波红外下加速效果较差的CaF2光栅结构对比, 粒子能量增幅仅为是长波红外波长下CaF2结构的26.1%.
从长波红外波长和近红外波长的加速器材料对比实验结果表明, 在长波红外波长下, 表现较差的CaF2光栅结构加速器对比近红外波长下表现较好的C光栅结构加速器的能量转换效率高出近5倍, 这说明了长波红外波长下的光栅加速器件能够在较长的区间内实现持续性加速, 极大地提高了粒子束质量. 同时, 通过对比3种不同材料组合下的加速结果, 说明由高折射率材料组成的介电光栅加速器的粒子能量增幅相较于由低折射率材料组成的光栅加速器更高. 一方面, 由斯涅尔定律可知, 激光入射高折射率材料时光线的折射角度更大, 能够聚焦成更小的光斑. 这会使得光束在激光加速区域内的能量密度增大, 从而提高加速电场的强度; 另一方面, 在高折射率材料中, 光束的传播速度变慢, 光束会在更小的区域内聚焦, 这意味着光束在加速区的空间分布会更加集中, 减少了衍射带来的扩展, 从而有利于产生有效的驻波形式的加速场. 本研究设计的长波红外光栅结构能够在较长区域内实现粒子的持续性加速, 极大提升了粒子能量转换效率, 提高了粒子束质量.
为了全面探究不同参数对光栅加速器的影响, 本文研究了3种材料在不同初始能量注入时的加速效果, 如图6(a)所示. 结果表明随着初始注入粒子能量的增大, C和ZnSe结构的粒子能量增幅在注入能量800 keV之前一直保持持续上升随后逐渐饱和, CaF2结构的粒子能量增幅在注入能量600 keV之后增长速率变缓. 图6(b), (c)分别表现了不同材料下基于GANDALF模型选择出的介电光栅加速器产生粒子的束流半径以及传输效率, 3种材料下的光栅结果均能产生束斑半径为14.5 μm的高能粒子束, 并且传输效率达到100%. 该束斑半径仅为光栅结构尺寸的约1/2, 这表明在加速过程中, 粒子束能够保持较高的聚焦度. 这一较小的束斑半径表明粒子束在空间上具有高度集中性, 有效提高了束流的能量密度, 从而促进了粒子加速和材料加工中的精度与效率提升. 更小的束斑半径意味着束流的发散角度较小, 这对于粒子束在长距离传输中的稳定性和精确度至关重要, 尤其是在需要高精度加速和长距离传输的应用场景中, 如高能物理实验和先进材料科学研究. 此外, 该聚焦特性在光栅加速器中展现出优异的空间分辨率和束流质量, 进一步证明了设计的优越性.
在实际应用中, 与近红外光相比, 长波红外光栅结构尺寸更大, 更易于加工. 这种大尺度光栅结构具有两个关键优势: 其一, 加速通道横向尺寸的显著增大使得加速器能够同时加速更高密度的 粒子束, 单位时间传输电荷量(粒子束电流I)实现量级提升, 从而提升束流亮度; 其二, 更大曲率半径的光栅结构可降低空间电荷效应对束流品质 的影响, 有利于维持横向发射度的稳定性. 束流亮度是表征单位体积内粒子通量密度的物理量, 是 衡量加速器品质的核心指标. 束流亮度在实际应用中可以显著提高实验的灵敏度和碰撞率. 例如, 在粒子对撞机、同步辐射源, 以及激光等离子体加速器等, 粒子束电流和亮度的提高直接影响实验的效率和准确性. 尤其在医学领域, 高亮度束流使得研究人员能够获得更加精确和高效的质子治疗效果和更高分辨率的X射线图像. 束流亮度数学表达式如下:
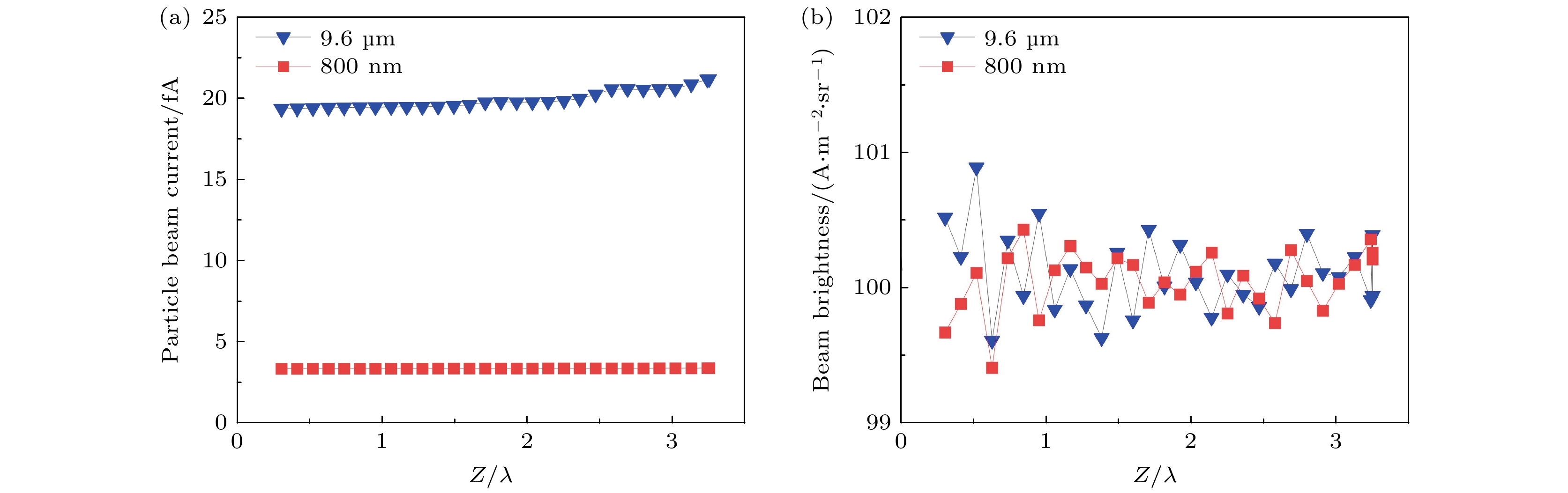
如图7所示, 本文对比研究了金刚石材料下9.6 μm长波红外结构和800 nm近红外结构的粒子束电流以及粒子束亮度.
结果表明, 9.6 μm长波红外光栅结构加速粒子束电流的上升趋势明显快于800 nm近红外光栅结构加速粒子束电流, 说明长波红外光栅结构的能量转换效率高, 能实现更好的加速性能. 长波红外光栅结构加速的平均粒子束电流为20.4 fA, 对比近红外光栅结构加速的平均粒子束电流高出了6.9倍. 图7(b)显示, 长波红外光栅结构加速的粒子束亮度与近红外光栅结构相当, 表明尽管长波红外光栅结构的尺寸显著大于近红外光栅, 其聚焦性能仍能保持在相同水平. 对于高能物理实验(如粒子碰撞实验), 提高束流亮度可以显著增强实验的灵敏度和碰撞率, 从而提供更多的碰撞事件用于数据采集. 此结果证明了长波红外光栅结构的优异性能, 并表明其在实际应用中相较于近红外光栅结构具有更显著的优势.
-
本工作提出了一种基于深度学习技术的长波红外介电光栅加速器结构设计方法. 将深度学习技术与光栅结构优化相结合, 实现了高性能的长波红外加速器结构设计. 该设计方法采用综合特征评估对目标粒子能量增幅指标进行预测, 训练集和验证集误差均低于0.03, 利用斯皮尔曼相关系数对数据库的有效性进行评估, 结果表明特征参数间相对独立无明显相关性, 随后预测得到最优粒子能量增幅, 进而实现介电光栅加速器结构的优化设计. 本文所设计的C (金刚石)光栅加速器粒子能量增幅增加了99.5 keV, 同比粒子能量增幅19.9%. 加速后粒子束流传输效率100%, 束斑半径14.5 μm. 本研究设计的长波红外光栅结构与近红外光栅结构进行对比, 长波红外光栅结构加速的平均粒子束电流为20.4 fA, 对比近红外光栅结构加速的平均粒子束电流高出了6.9倍且粒子束亮度与近红外光栅结构相当. 本研究对基于光子芯片的粒子加速器的设计提供有益的参考. 本研究为一维光子晶体的设计以及亚波长结构的复杂光电器件设计提供了一种新的设计思路.
基于深度学习的长波红外介电光栅加速器结构设计
Deep learning-based design of long-wave infrared dielectric grating accelerator structures
-
摘要: 电介质激光加速器作为一种微型加速器, 其结构设计直接影响加速粒子束的能量增益和束流品质. 多数设计基于波长约1 μm的近红外激光驱动光源. 采用10倍波长的长波红外激光作为驱动光源, 有望在保持加速梯度的前提下获得更高束流品质. 受长距离加速限制, 相关波段下的结构设计仍较为缺失. 为此, 本研究提出一种基于深度学习技术的长波红外介电光栅加速器结构设计方法, 建立包含几何参数、材料性质、光场能量等多个参数的综合评估方法, 通过精准预测粒子能量增幅, 综合提取最优粒子能量增幅对应的结构参数以实现结构设计. 结果表明, 本研究所设计的光栅加速器粒子能量增幅高达99.5 keV, 同比增长19.9%, 可实现100%的传输效率, 束斑半径14.5 μm, 加速的平均粒子束电流为20.4 fA, 比近红外光栅结构高出了6.9倍, 且粒子束亮度与近红外光栅结构相当. 本研究为长波红外高净增益介电光栅加速器的设计提供了潜在的技术路线, 同时为复杂光电器件结构设计提供一个新思路.Abstract: Dielectric laser accelerators (DLAs), as compact particle accelerators, rely critically on their structural design to determine both the energy gain and beam quality of accelerated bunches. Although most existing DLAs are driven by near-infrared lasers with a wavelength of approximately 1 μm, the use of long-wave infrared (LWIR) lasers at a wavelength ten times that of this wavelength indicates that it is possible to achieve excellent beam quality without sacrificing acceleration gradient. To address the lack of optimized structural designs in the LWIR band where long-distance acceleration poses unique challenges—we introduce a deep learning–based design method for LWIR dielectric grating accelerator structures. Our approach integrates geometric parameters, material properties, and optical-field energy metrics into a unified evaluation framework and uses a surrogate model to predict particle energy gain with high precision. Optimal structural parameters are then extracted to realize the final design. The simulation results show that the energy gain is 99.5 keV (a year-over-year increase of 19.9%), the transmission efficiency is 100%, the beam spot radius of 14.5 μm, and the average beam current is 20.4 fA, which is 6.9 times higher than similar near-infrared gratings, while maintaining equivalent beam brightness. This work provides a feasible technical route for designing high-netgain LWIR dielectric grating accelerators and a novel framework for optimizing the structure of complex optoelectronic devices.
-
Key words:
- dielectric laser accelerators /
- grating structures /
- long-wave infrared /
- deep learning .
-

-
图 1 介电光栅加速器设计方案及其持续性加速原理示意图 (a)介电光栅加速器的结构设计及相关参数; (b)介电光栅加速器的持续性加速原理
Figure 1. Schematic of the dielectric grating accelerator design and its continuous acceleration mechanism: (a) Structural design and related parameters of the dielectric grating accelerator; (b) principle of continuous acceleration in the dielectric grating accelerator.
图 4 预测结果和模型性能评估 (a)预测结果; (b)损失函数. 其中蓝色数据点代表数值计算的真实值, 红色数据点表示GANDALF模型预测值
Figure 4. Prediction results and model performance evaluation: (a) Prediction results; (b) loss function. The blue data points represent the real value of numerical calculation, and the red data points represent the predicted value of Gandalf model.
图 5 不同波长下C, CaF2, ZnSe介电光栅加速器加速效果对比及性能评估 (a) 9.6 μm不同材料光栅加速器加速效果; (b) 800 nm不同材料光栅加速器加速效果
Figure 5. Comparison of acceleration performance and evaluation of dielectric grating accelerators for Diamond, CaF2, and ZnSe at different wavelengths: (a) Acceleration performance of grating accelerators for different materials at 9.6 μm; (b) acceleration performance of grating accelerators for different materials at 800 nm.
图 6 C, CaF2, ZnSe光栅结构加速器的粒子加速性能评估 (a)不同初始注入能量下粒子能量增幅的变化; (b)束斑半径随横向位移的变化; (c)粒子束流的传输效率
Figure 6. Particle acceleration performance evaluation of diamond, CaF2, and ZnSe grating structure accelerators: (a) Variation of particle energy amplification at different initial injection energies; (b) variation of beam spot radius with transverse displacement; (c) transmission efficiency of particle beam current.
图 7 金刚石材料长波红外光栅结构与近红外光栅结构加速粒子电流及粒子束亮度对比 (a)不同波长下结构加速粒子电流对比; (b)不同波长下粒子束亮度对比
Figure 7. Comparison of particle current and beam brightness accelerated by diamond material long-wave infrared and near-infrared grating structures: (a) Comparison of particle current accelerated by grating structures at different wavelengths; (b) comparison of beam brightness at different wavelengths.
表 1 金刚石材料光栅加速器最优几何参数
Table 1. Optimal geometric parameters of diamond material for grating accelerators.
Geometric parameter i Value li/μm 1 3.56 2 3.08 3 3.67 4 3.15 wi/μm 1 6.36 2 5.47 3 4.51 4 4.51 θi 1 –5.4 2 –6 3 4 4 6 -
[1] Zhang Y, Fang W C, Huang X X, Tan J H, Wang C P, Zhao Z T 2021 Nucl. Sci. Tech. 32 38 doi: 10.1007/s41365-021-00869-z [2] Tantawi S G, Dolgashev V, Higashi Y, Dolgashev V A, Cary J R, Kemp M A 2010 AIP Conf. Proc. 1299 29 [3] Higo T, Higashi Y, Matsumoto S, Yokoyama K, Doebert S, Grudiev A, Riddone G, Wuensch W, Zennaro R, Adolphsen C, Dolgashev V, Jensen A, Laurent L, Tantawi S G, Wang F, Wang J W 2010 Proc. 14th Adv. Accel. Concepts Wksp.Annapolis, USA, June 13–19, 2010 [4] Mizuno K, Ono S, Shimoe O 1975 Nature 253 184 doi: 10.1038/253184a0 [5] Soong K, Byer R L, Colby E R, England R J, Peralta E A 2012 AIP Conf. Proc. 1507 516 [6] Agustsson R, Arab E, Murokh A, O’Shea B, Ovodenko A, Pogorelsky I, Rosenzweig J, Solovyov V, Tilton R 2015 Opt. Mater. Express 5 2835 doi: 10.1364/OME.5.002835 [7] Cesar D, Maxson J, Musumeci P, Shen X, England R J, Wootton K P 2018 Nucl. Instrum. Methods A 909 252 doi: 10.1016/j.nima.2018.01.012 [8] Plettner T, Byer R L, Montazeri B 2011 J. Mod. Opt. 58 1518 doi: 10.1080/09500340.2011.611914 [9] Hughes T, Veronis G, Wootton K P, England R J, Fan S 2017 Opt. Express 25 15414 doi: 10.1364/OE.25.015414 [10] Tompkins H G, Tigner E L S 1993 Refractive Index of Optical Materials in the Infrared (Academic Press [11] Plettner T, Lu P P, Byer R L 2006 Phys. Rev. ST Accel. Beams 9 111301 doi: 10.1103/PhysRevSTAB.9.111301 [12] Peralta E A, Soong K, England R J, Colby E R, Wu Z, Montazeri B, McGuinness C, McNeur J, Leedle K J, Walz D, Sozer E B, Cowan B, Schwartz B, Travish G, Byer R L 2013 Nature 503 91 doi: 10.1038/nature12664 [13] Cesar D, Custodio S, Maxson J, Musumeci P, Shen X, Threlkeld E, England R J, Hanuka A, Makasyuk I V, Peralta E A, Wootton K P, Wu Z 2018 Commun. Phys. 1 46 doi: 10.1038/s42005-018-0047-y [14] Lin X E 2001 Phys. Rev. ST Accel. Beams 4 051301 doi: 10.1103/PhysRevSTAB.4.051301 [15] Cowan B M 2008 Phys. Rev. ST Accel. Beams 11 011301 doi: 10.1103/PhysRevSTAB.11.011301 [16] Mei X, Zha R, Pan Y, Wang S, Sun B, Lei C, Ke C, Zhao Z, Wang D 2023 Ultrafast Sci. 3 0050 doi: 10.34133/ultrafastscience.0050 [17] Plettner T, Byer R L, McGuinness C, Hommelhoff P 2009 Phys. Rev. ST Accel. Beams 12 101302 doi: 10.1103/PhysRevSTAB.12.101302 [18] Plettner T, Byer R L 2008 Phys. Rev. ST Accel. Beams 11 030704 doi: 10.1103/PhysRevSTAB.11.030704 [19] Siemann R H 2004 Phys. Rev. ST Accel. Beams 7 061303 doi: 10.1103/PhysRevSTAB.7.061303 [20] Breuer J, Graf R, Apolonski A, Hommelhoff P 2014 Phys. Rev. ST Accel. Beams 17 021301 doi: 10.1103/PhysRevSTAB.17.021301 [21] Breuer J, Hommelhoff P 2014 Nucl. Instrum. Methods Phys. Res. A. 740 114 doi: 10.1016/j.nima.2013.10.078 [22] Breuer J, McNeur J, Hommelhoff P 2014 J. Phys. B At. Mol. Opt. Phys. 47 234004 doi: 10.1088/0953-4075/47/23/234004 [23] Black D S, Zhao Z X, Leedle K J, Miao Y, Byer R L, Fan S, Solgaard O 2020 Phys. Rev. Accel. Beams. 23 114001 doi: 10.1103/PhysRevAccelBeams.23.114001 [24] He Y F, Sun B, Ma M J, Li W, He Q Y, Cui Z H, Wang S Y, Zhao Z Q 2022 Nucl. Sci. Tech. 33 120 doi: 10.1007/s41365-022-01101-2 [25] Ma W, Xu Y H, Xiong B, Deng L, Peng R W, Wang M, Liu Y M 2022 Adv. Mater. 34 2110022 doi: 10.1002/adma.202110022 [26] Liu X H, Wang P, Xiao C Y, Fu L C, Xu J, Zhang D, Zhou H, Fan T X 2023 Adv. Funct. Mater. 33 2212068 doi: 10.1002/adfm.202212068 [27] Zhang Q, Liu C, Wan X, Zhang L, Liu S, Yang Y, Cui T J 2019 Adv. Theory Simul. 2 1800132 doi: 10.1002/adts.201800132 [28] Wang C Q, Cheng X G, Wang R, Hu X, Wang C H 2024 Laser Photonics Rev. 18 2300958 doi: 10.1002/lpor.202300958 [29] Lei Z D, Xu Y D, Zhao Y, Wang D 2024 Photon. Res. 12 123 doi: 10.1364/PRJ.505991 [30] Polyanskiy M N, Babzien M, Pogorelsky I V 2015 Optica 2 675 doi: 10.1364/OPTICA.2.000675 [31] Pogorelsky I V, Babzien M, Ben-Zvi I, Skaritka J, Polyanskiy M N 2016 Nucl. Instrum. Methods Phys. Res. A 829 432 doi: 10.1016/j.nima.2015.11.126 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: