水蒸气凝结作为自然界中常见的相变过程, 在物质传递和能量传递过程中扮演着至关重要的角色, 被广泛应用于各类工业生产过程中, 如电力生产^[1,2]、化工生产^[3,4]、生物制药^[5,6]、智能制造^[7,8]等领域. 在凝结过程中常伴随液滴的成核、生长、合并、弹跳等现象, 且能量转化机制较为复杂^[9]. 凝结现象由于独特的能量转化机制和多尺度协同调控的特点, 为了更好地控制水蒸气凝结的进行, 学者们从不同的尺度出发不断深入研究.

针对水蒸气滴状凝结过程的研究, 液滴的尺寸集中在宏观、介观尺度^[10–13]. 欧阳袁渊^[14]通过实验构造了不同微柱结构以制备更加疏水的表面, 结果表明通过光刻技术制备的微柱结构疏水表面比光滑的疏水表面拥有更大的接触角和更小的运动角, 即疏水性能更加优良, 且微柱结构的存在使得液滴在其表面形成Cassie状态更加利于液滴自运动和自清洁. 费媛媛等^[15]制备了具有微方孔结构的梯度能表面, 发现随着微方孔边长的梯度变化会使得冷凝的液滴在梯度能表面形成不同的形态. Wang等^[16]利用格子Boltzmann方法模拟研究微结构表面上水蒸气的凝结换热, 发现对于不同尺度的结构表面而言, 微柱阵列表面上的传热系数较纳米结构表面提高26.4%, 并且随着微柱间距的增大传热系数随之减小. Aminian等^[17]利用模拟的方式研究在圆管表面上设置不同疏水-亲水的混合表面, 使液滴呈现Cassie状态和Wenzel状态, 结果表明一般情况下在圆管表面上Wenzel状态比Cassie状态具有更好的传热能力.

针对微观尺度表面, 学者们开展了纳米液滴在平板、阵列纳米结构等简单表面上的润湿行为及凝结过程研究^[18–21]. Huang等^[22]利用分子动力学模拟了铜基底纳米柱阵列表面上氩蒸气的凝结情况, 发现壁面过冷度的增大, 会使得纳米柱阵列中的液滴可以从底部移至顶部; 柱间距密集会抑制纳米阵列底部凝结, 而更倾向于上部进行凝结. 王浩杰等^[23]利用分子动力学方法模拟研究硅表面不同粗糙纳米结构表面上的润湿行为, 结果表明二级结构表观接触角优于光栅形、方柱形、梯形等不同粗糙壁面, 并且在相同条件下二级结构的表观接触角可达到152.25°. Wang等^[24]利用分子动力学方法模拟研究水蒸气在含有亲水点疏水平板上的凝结过程, 结果表明亲水点越大的疏水平板, 液滴凝结成核的速度越快; 在亲水点大小一定的情况下, 随着亲水点密度的增大, 可以提高凝结成核的概率, 然而随着亲水点密度的继续增大, 凝结成核位点之间相互竞争抑制的现象越明显, 抑制单个液滴的生长. Shi等^[25]利用分子动力学方法模拟研究纳米波纹表面上水的成核和生长情况, 发现不同的表面形态对水蒸气凝结具有耦合效应, 水蒸气更易在势能分布较低的凹形结构成核; 凝结液滴更易在平面发生自移动与合并; 凸形结构则可以控制液滴的平均大小. Nurrohman等^[26]采用分子动力学研究了铜表面覆盖石墨烯微结构对水蒸气凝结的影响, 发现石墨烯覆盖度的降低有利于水蒸气的凝结, 在相同覆盖度下, 微结构分布更加均匀有利于提高水蒸气凝结效率和传热性能. Wei等^[27]采用分子动力学研究了不同浓度水蒸气在不同润湿状态下的凝结行为, 结果表明水蒸气浓度的增大, 对亲水和超亲水表面的影响较大, 而对疏水和超疏水表面的影响较小.

目前对于更为复杂的纳米结构表面(如二级微结构、结构缺陷、亲疏水表面等)的研究较为稀缺. 因此本研究采用分子动力学的模拟方法, 从微观尺度出发以探讨较为复杂的不同二级微结构对水蒸气凝结的影响, 以提高凝结传热速率, 并且为设计更加高效、稳定的凝结功能表面提供一定的结构优化思路和参考.

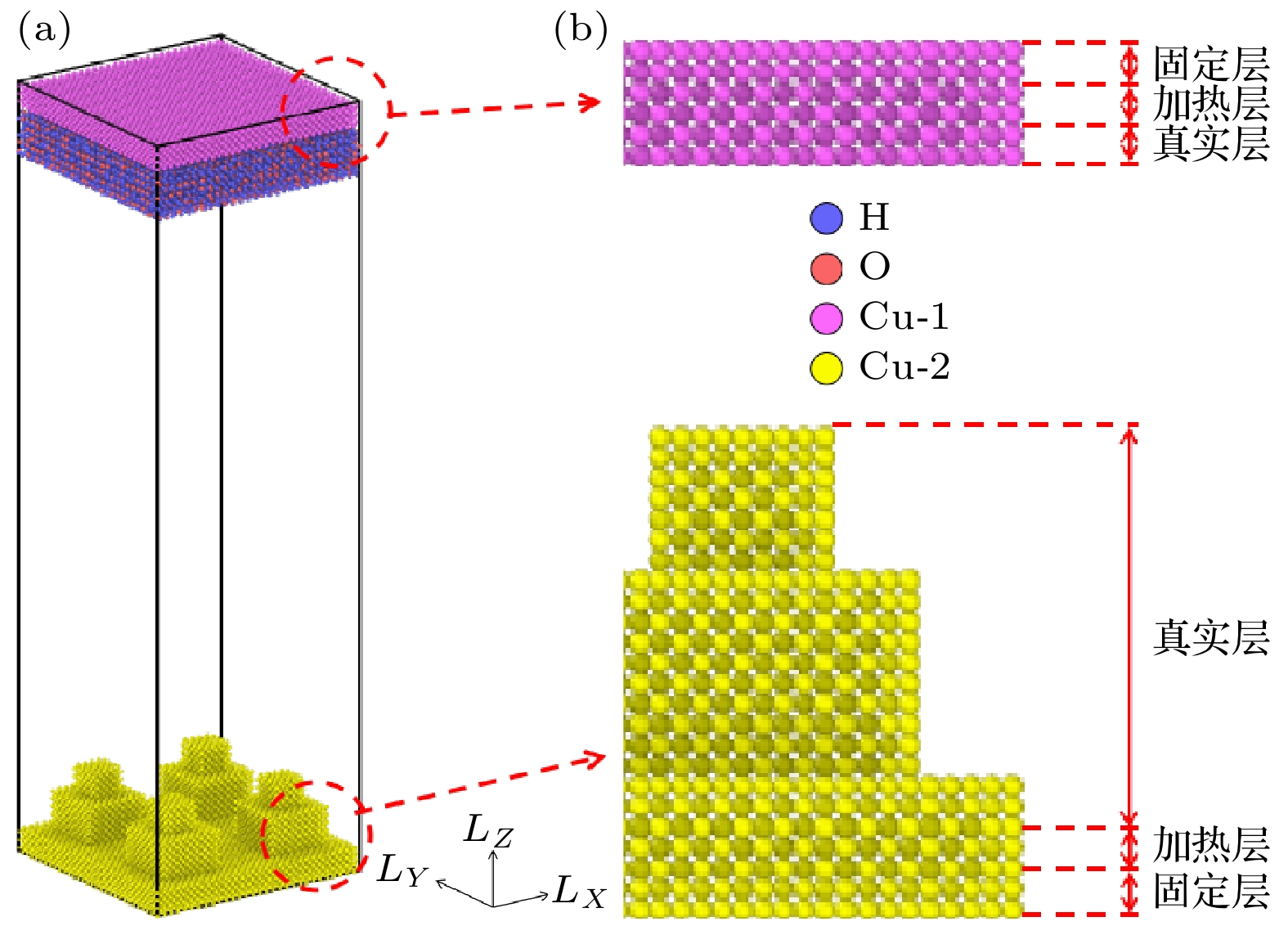
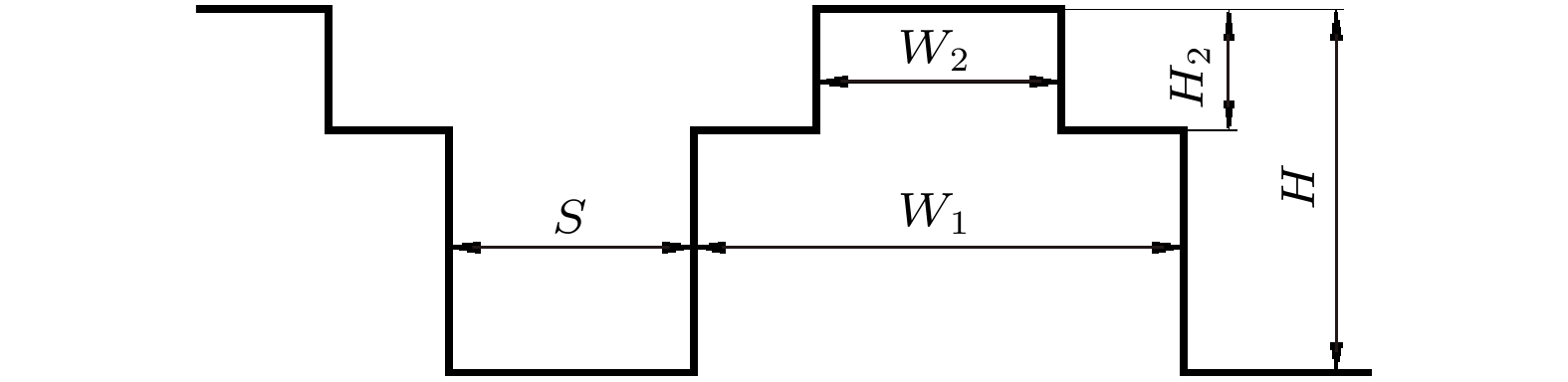
基于分子动力学(MD)方法采用Lammps软件进行不同二级微结构表面的水蒸气凝结模拟. 研究思路为上方固体金属板持续加热液膜, 使水分子受热蒸发而给下方提供源源不断稳定的水分子, 在下方不同二级微结构固体金属板表面遇冷凝结. 固体壁面为铜材质, 铜原子采用面心立方(FCC)晶体结构(晶格常数为3.615 Å, 即面心立方晶体结构的边长a = 3.615 Å). 如图1所示为二级微结构的基础结构单元, 在第1级微结构上叠加第2级微结构而成, 所涉及的结构参数主要有第1级柱宽度W₁ = 8a, 第2级柱宽度W₂ = 4a, 柱间距S = 8a, 总柱高度H = 8a, 第2级柱高度H₂ = 8a, 以及微柱的形状: 矩形-矩形(第1级微结构-第2级微结构).

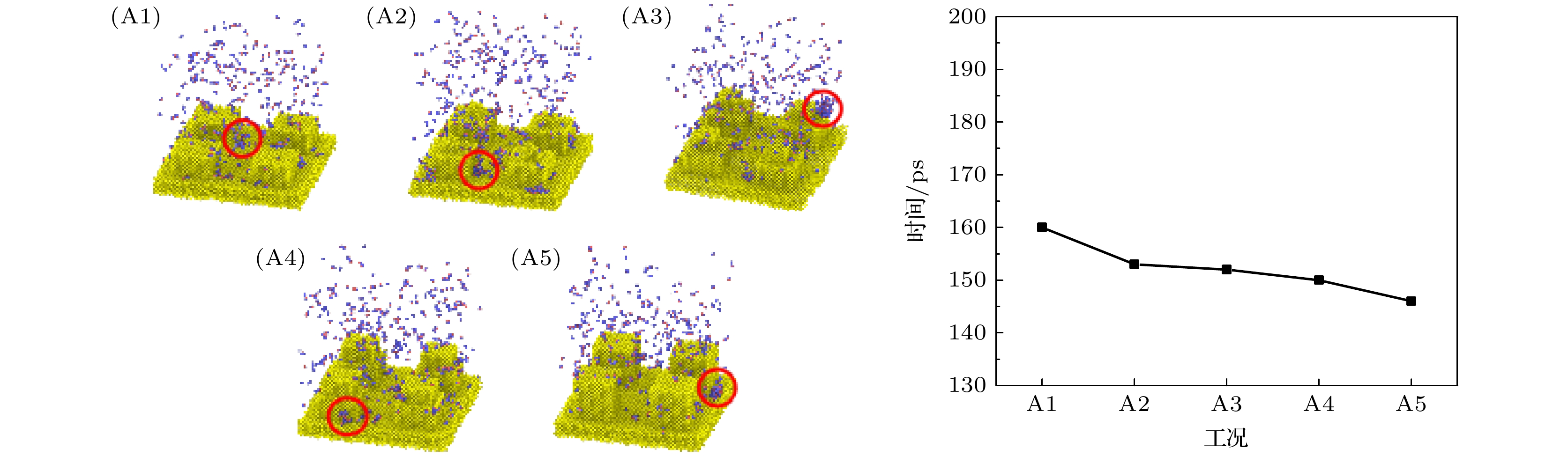
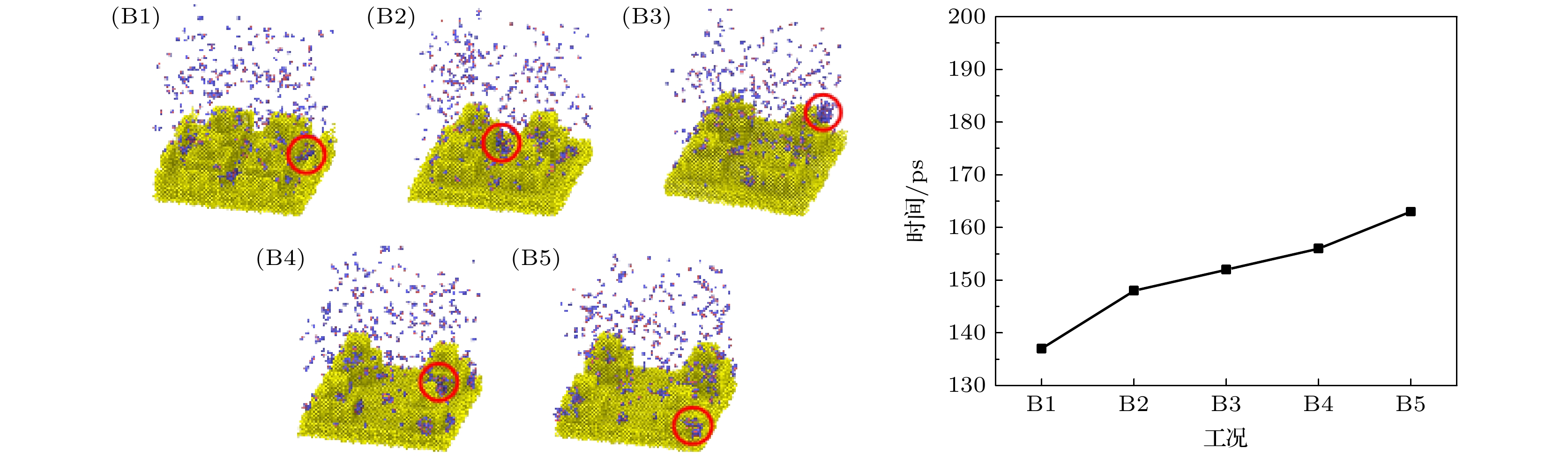
图2(a)所示为调整第2级柱宽W₂为0, 2a, 4a, 6a, 8a构建工况A1—A5; 图2(b)所示为调整柱间距S为4a, 6a, 8a, 10a, 12a构建工况B1—B5; 为了反映第2级柱高度占总柱高度的比例大小, 引入柱高比β概念. 柱高比β为第2级柱高度与总柱高度之比, 计算方法如(1)式所示:

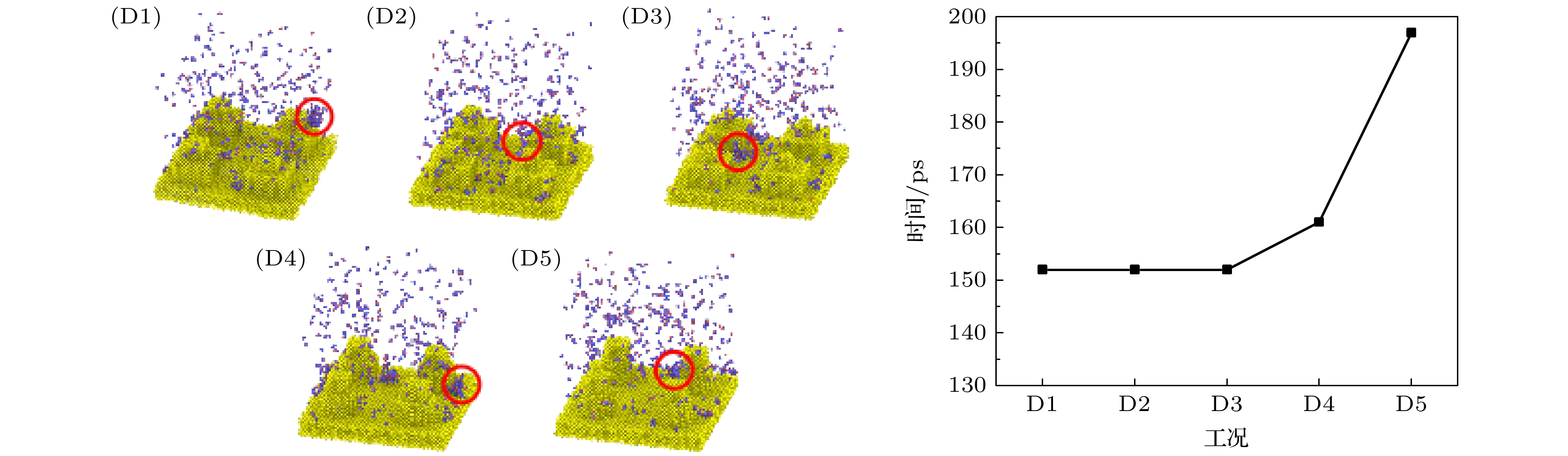
图2(c)所示为调整柱高比β为0, 0.25, 0.50, 0.75, 1.00构建工况C1—C5. 图2(d)所示为由于二级微结构为下方第1级、上方第2级微结构叠加而成, 因此通过调整各自最小单元的参数w, h和角度, 使微结构单元结构改变为矩形(rectangle, 简记为R)、圆柱(cylinder, 简记为C)或圆台(frustum of a cone, 简记为F), 调整柱结构分别为R-R, R-C, R-F, C-R, F-R (对应简记为D1—D5)来进行研究.

通过二级微结构的基础单元建立二级微结构表面水蒸气凝结的物理模型, 图3(a)所示为该模型由上下两层固体金属板和液膜构成, 其中上下两层固体金属板为不同亲疏水性的铜原子, 液膜为水分子. 整体的模拟盒子尺寸为L_X × L_Y × L_Z = 30a×30a×100a. 其中, 上方固体金属板的初始结构为L_X × L_Y × L_Z = 30a×30a×3a, 由铜原子-1 (简记为Cu-1)采用面心立方晶体(FCC)构成, 计算得到上方固体金属板共包含10800个铜原子. 下方固体金属板为本文研究对象, 初始结构为L_X × L_Y × L_Z = 30a×30a×11a, 由铜原子-2 (简记为Cu-2)采用面心立方晶体构成, 晶格常数为3.615 Å, 铜原子数量随工况不同而发生变化, 总共包含15352—22424个铜原子. 液膜内水分子的饱和密度为0.997 g/cm³, 由8624个水分子组成, 均匀地放置在上方固体金属板表面上.

模拟过程中, 铜原子的相互作用力势函数采用兰纳-琼斯势^[28] (Lennard-Jones势, 简记为L-J势), 该势函数的表达形式为

其中E_ij为L-J势函数; ε为势阱深度; r_ij为原子i和j之间的距离, r_c为截断半径, σ为原子间碰撞距离.

综合考虑水的各种热力学、结构性质表现, 水分子选择TIP4P模型. 本文所用模拟参数见表1.

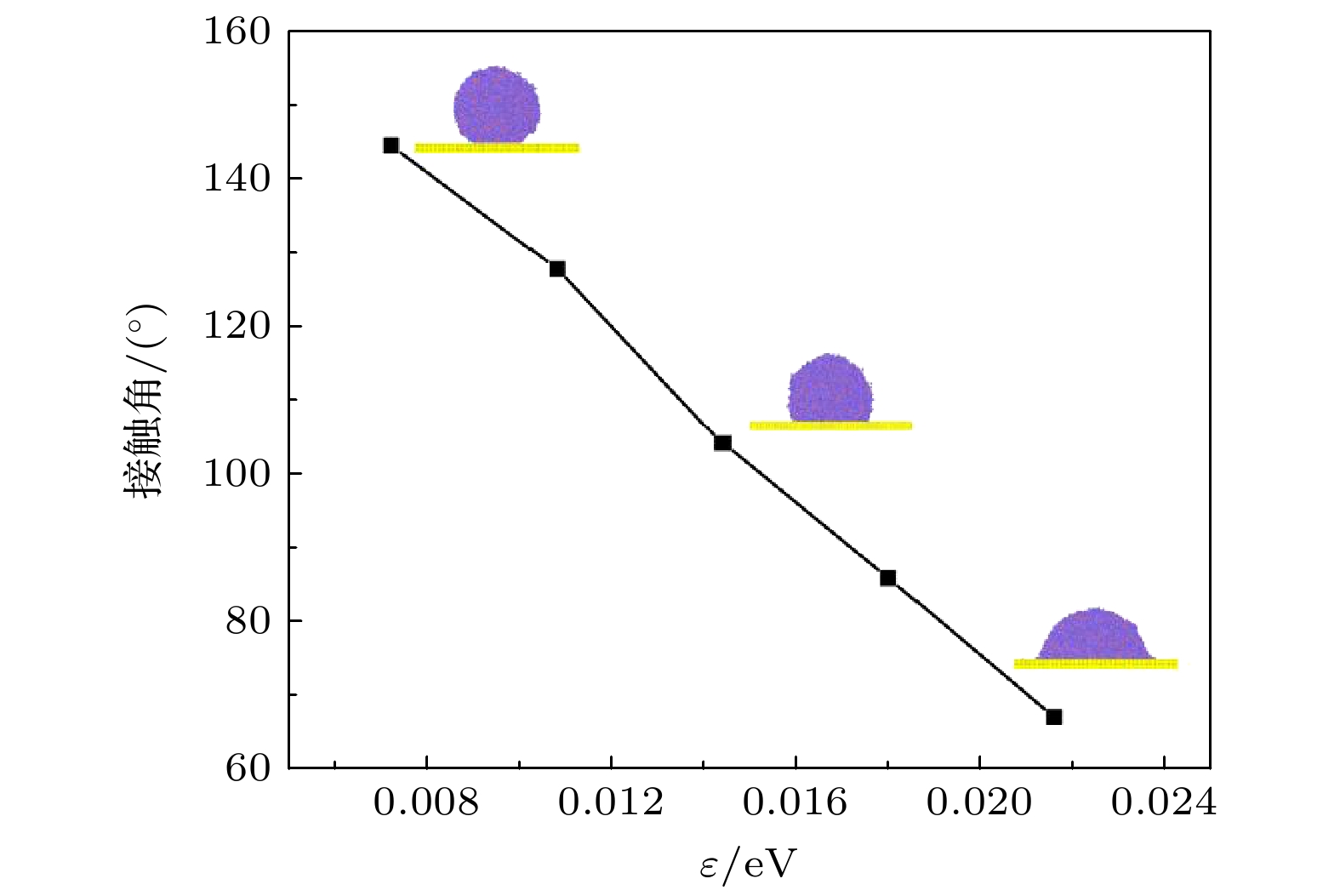
通过间接的改变势阱深度ε数值大小, 可以改变铜表面的浸润性, 分别选择势阱深度为0.0072, 0.0108, 0.0144, 0.0180和0.0216. 模拟得到接触角(液滴稳定在光滑表面上时)随势阱深度变化曲线, 如图4所示, 得到势阱深度与接触角呈线性关系, 随着势阱深度的增大, 接触角减小. 为了使上方铜原子更快提供加热后的水分子, 下方铜原子较快的凝结, 分别选择ε为0.216和0.144, 对应接触角67.1°和104.2°.

在模拟过程中为防止原子从模拟盒子上方逃逸, 在X和Y方向采用周期性边界条件, 在Z方向采用固定边界条件. 模拟时间步长为∆t = 0.001 ps, 计算过程采用velocity-verlet算法求解运动方程.

在模拟过程中为了保证模型的准确性和真实性, 本文对上下两层固体金属板分别进行了分块处理, 如图3(b)所示. 将金属板分为3个计算区域, 依次是固定层、加热层和真实层. 固定层主要用于模拟体系的边界, 将铜原子固定在这一层, 以防止模拟过程中体系发生漂移或者变形. 加热层是对体系进行加热处理的区域, 通过调整温度等参数, 来影响分子或者原子在受到不同温度时的不同运动变化. 真实层也叫原子层, 为所研究的对象本身, 在这一层中调整模型结构来模拟不同的微结构变化. 其中固定层、加热层的厚度均为a, 为节约计算和导热时长, 真实层厚度设置为a; 下方则根据所模拟的二级微结构不同, 厚度发生变化.

控制整个体系温度恒定为300 K基础上, 在整个模拟过程依次进行能量最小化、弛豫和模拟过程. 首先能量最小化, 让系统的初始势能降到最低, 排除模型可能存在的不合理情况, 使模拟结果更加准确可靠. 其次进行弛豫, 让系统内各分子间的动能和势能进行有效的转换, 达到相对稳定的动态平衡. 对整个系统采用等温等体积系综(NVT)维持体系温度为定值300 K, 采取Langevin方法控制体系温度, 弛豫过程进行1000 ps后到达平衡. 达到平衡态后, 将金属板真实层及液膜切换为微正则系综(NVE), 上方加热层温度调整为500 K, 用于加热水分子提供水蒸气, 下方加热层不做改变. 模拟过程进行2000 ps.

对于模拟所建立的模型, 针对水蒸气凝结的模拟分别从液滴全过程形态、铜板初始化温度变化及凝结水密度变化3个方面进行模型验证, 以确保后续模拟的准确性和可靠性.

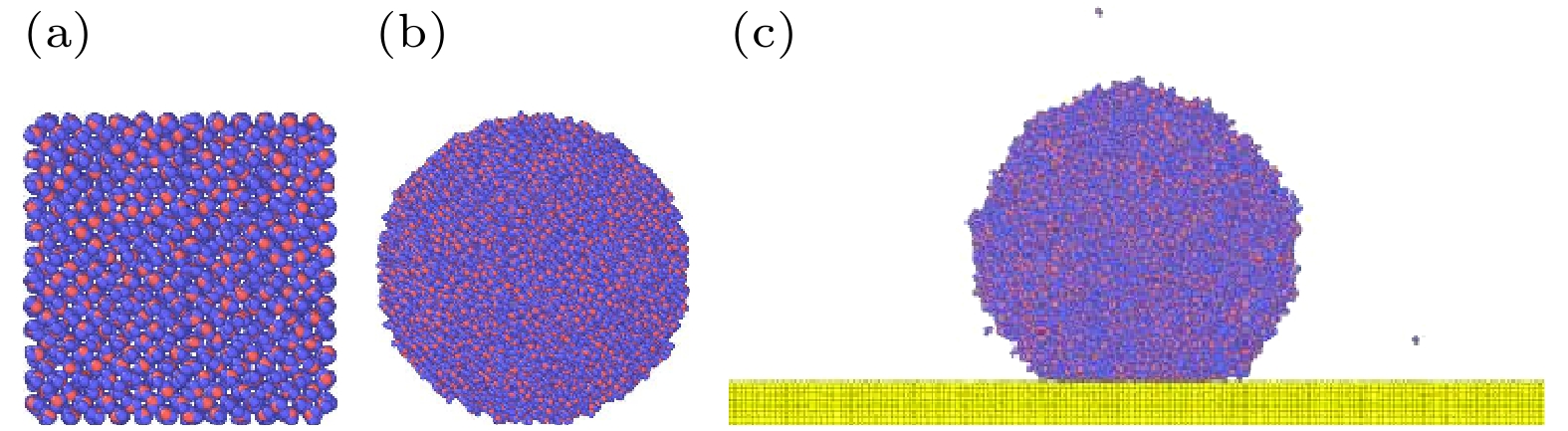
首先, 选择铜板及环境温度为300 K的室温环境下, 液滴的初始结构为正方体, 其边长为100 Å. 图5所示分别为不同时刻下液滴所展现的不同形态. 从初始时刻所设置的正方体液滴由于表面张力的作用, 液体表面分子间存在相互吸引力, 使得液滴尽可能减小其表面积, 从而收缩成一个球体. 随后收缩的球体与铜板接触, 由于液滴与铜板表面之间存在相互作用力, 使得液滴在固体表面形成稳定的接触角.

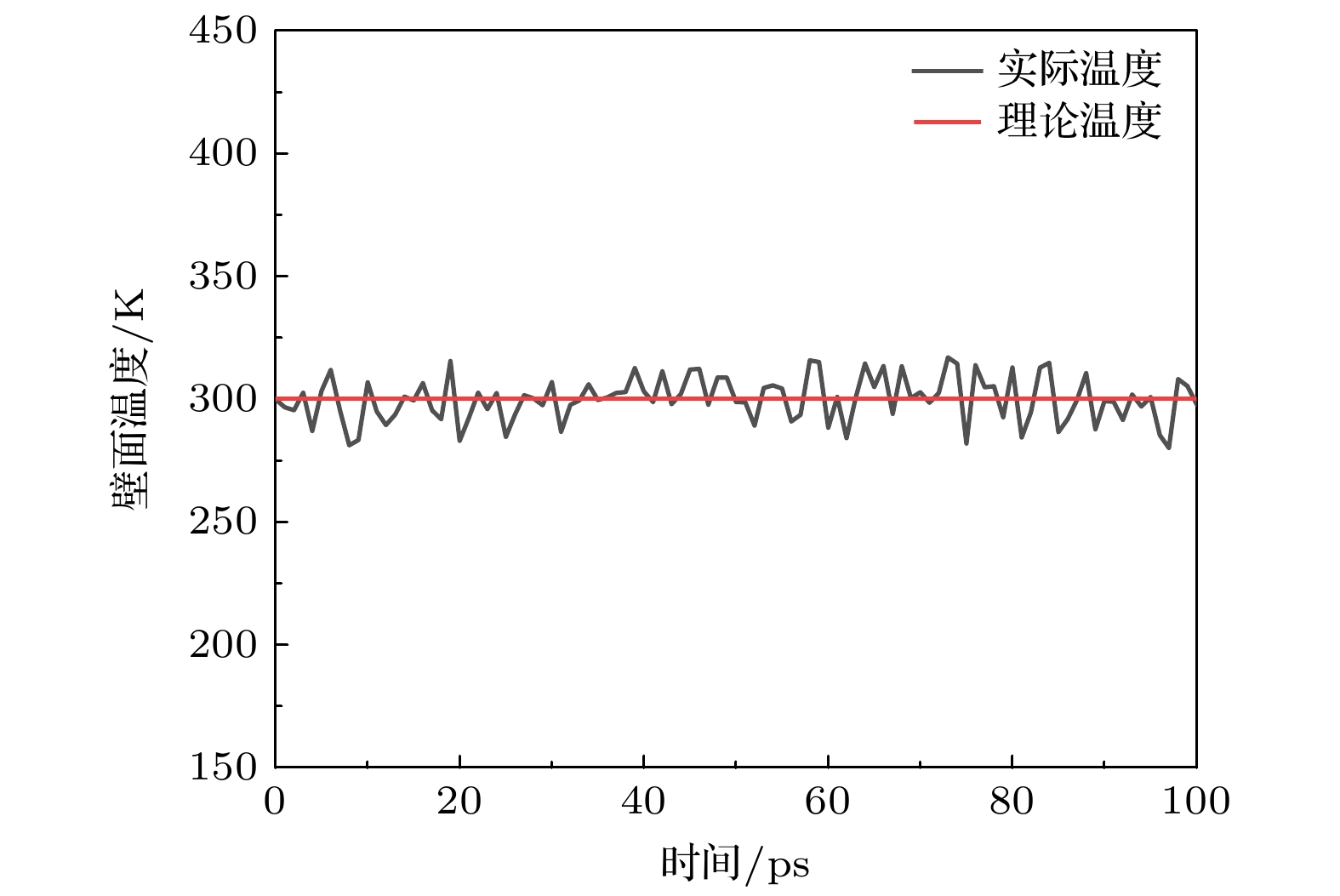
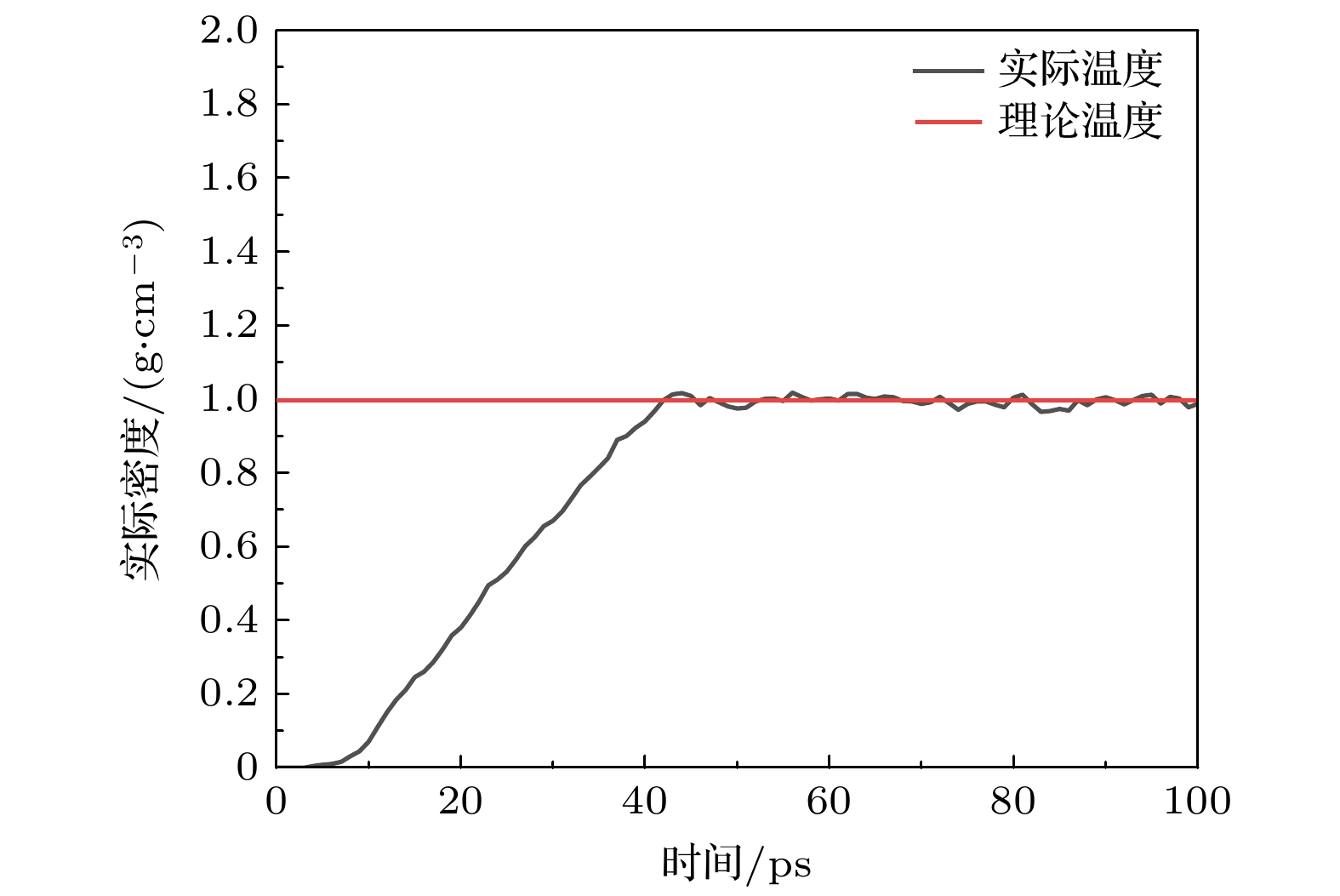
其次, 对于铜板初始化温度变化及凝结水密度变化的模型验证, 所选择的模型与工况与后文模拟所选择的工况相同. 上方铜板500 K, 底部铜板300 K, 通过监测底部铜板温度随时间变化及底部铜板上所凝结水分子的密度来进行验证. 图6所示为底部铜板壁面真实层温度随时间的变化, 由于在设置过程中是对加热层温度进行设置, 那么有效的控温以及导热至关重要, 故对真实层温度进行统计, 经过计算, 最大相对误差为4.64%, 在合理范围内. 如图7所示为底板凝结水分子的密度随时间变化图, 随着时间的推移, 底部铜板表面逐渐凝结水分子. 查文献^[29]得到常压、温度为300 K时水的密度为0.997 g/cm³, 当密度趋于稳定后, 对于所模拟的铜板水分子的平均密度进行统计, 经过计算, 最大相对误差为3.16%, 在合理范围内. 综合模拟结果与理论分析, 证明模型的合理性和可靠性.

凝结水分子总数作为表征气液相变过程的重要参数, 直接反映凝结过程中水分子从气相向液相发生转变的总量, 有助于量化相变过程中的水蒸气凝结速率, 对优化凝结表面提供依据.

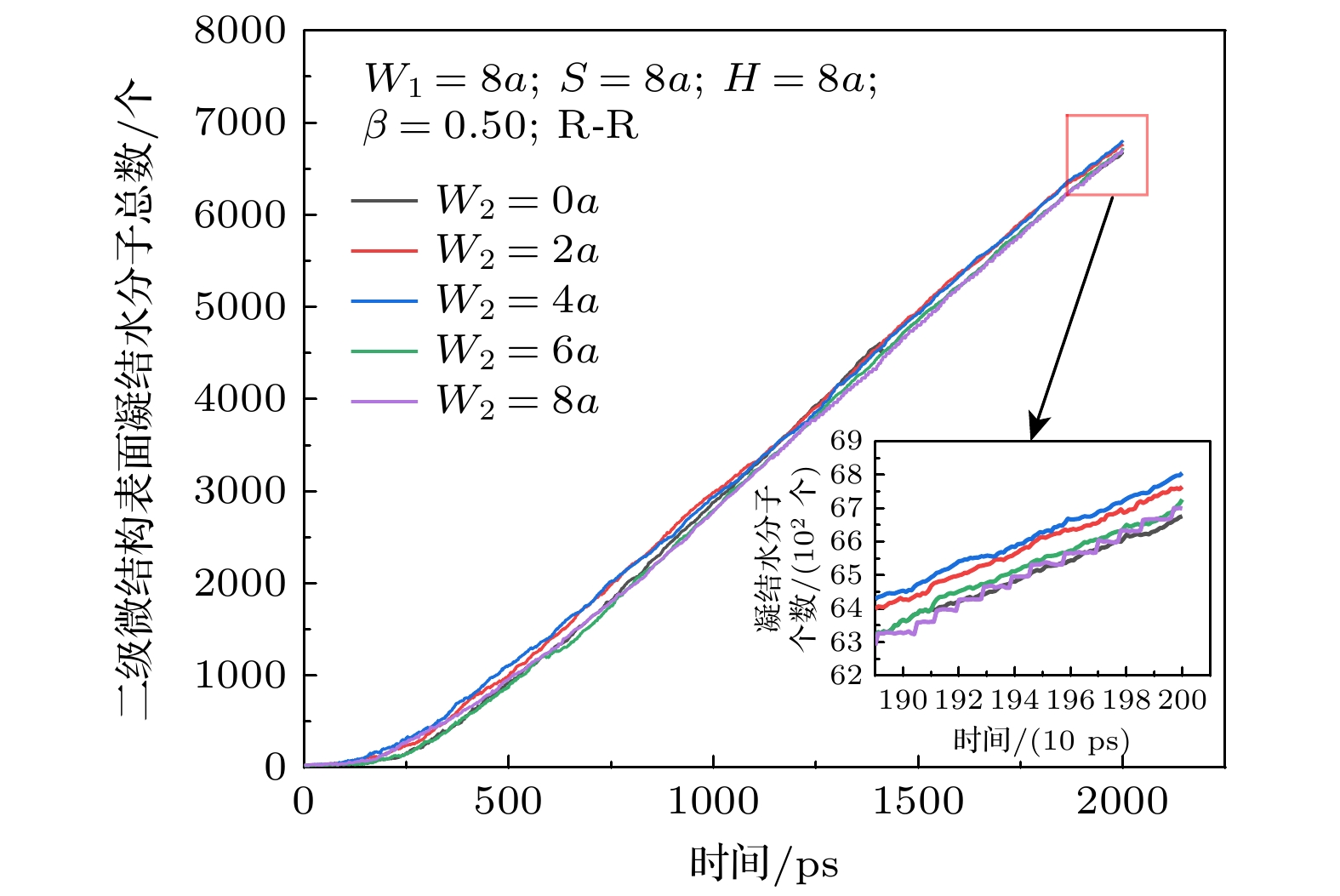
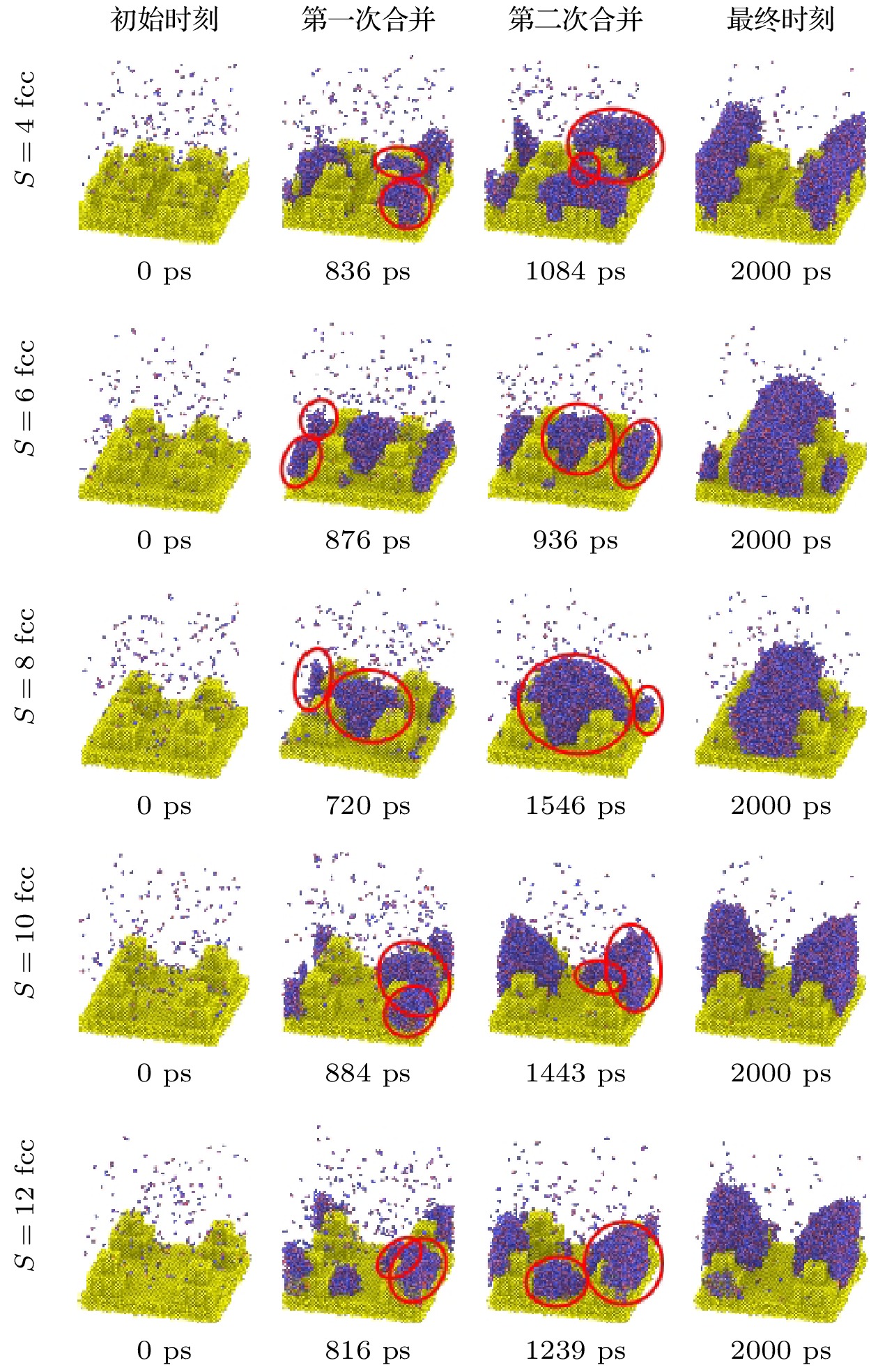
如图8所示, 模拟得到随着宽度的增大系统总凝结水分子量先增大后减小, 在所模拟范围内最佳柱宽度为工况A3(W₂ = 4a). 工况A1和A5均低于其余工况的凝结量. 说明在相同条件下, 额外增大第2级微结构或总柱高度相同条件下, 二级微结构可以比单一一级微结构凝结更多的水分子. 分析原因为液滴不仅仅在第1级微结构微柱侧壁发生凝结, 还会在第1, 2级转折处发生, 同时液滴主要在第1级微结构附近产生凝结核并发生凝结. 由于第2级微结构的存在, 液滴会在第2级微结构处发生合并和弹跳从而加快凝结的进行.

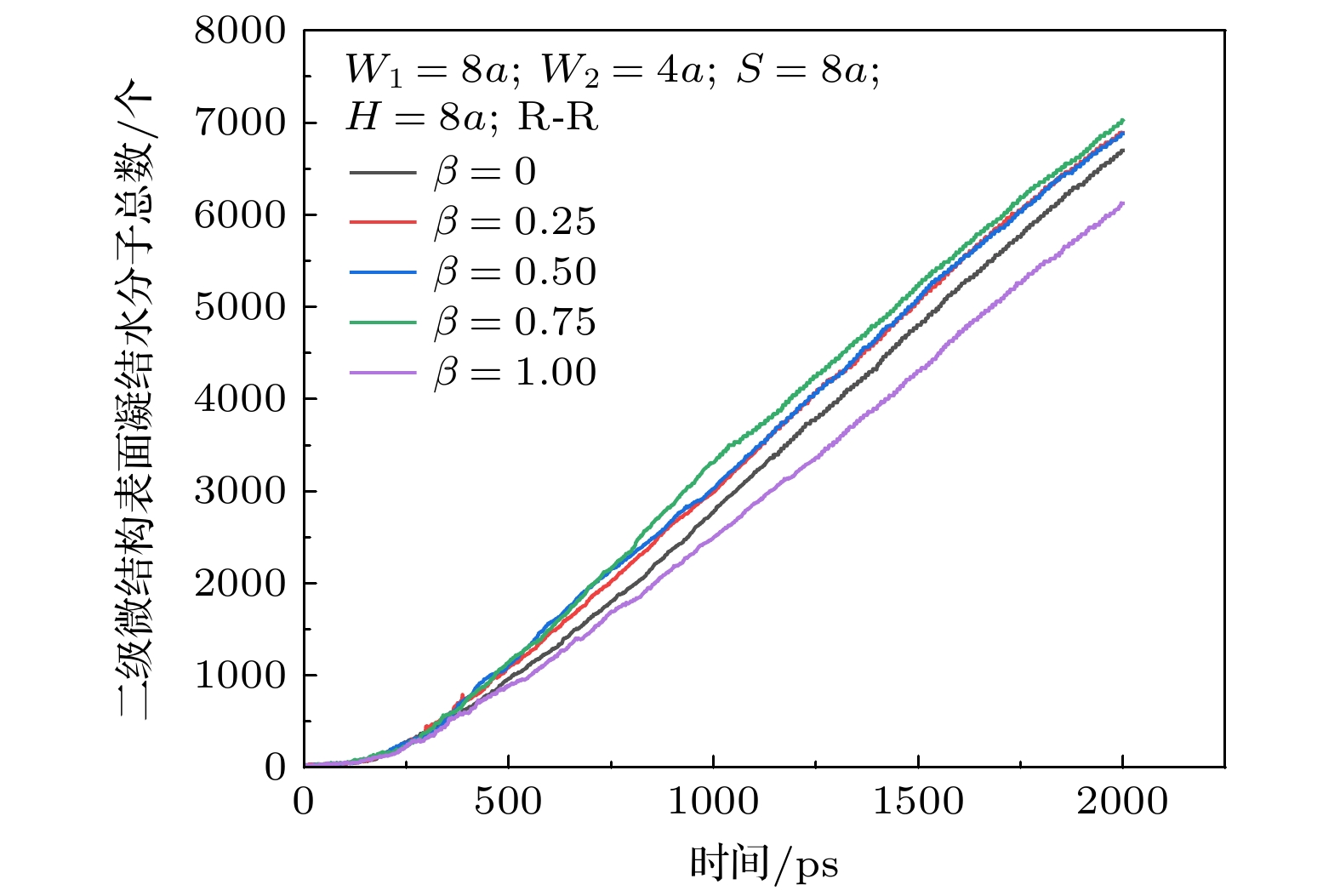
如图9所示, 随着柱高比的增大, 总凝结水分子量先增大后急剧减小, 在所模拟范围内最佳柱宽度为工况C4(β = 0.75), 含第2级微结构的模型凝结水分子量均大于一级微结构的模型. 分析原因为工况C1—C4随着柱高比增大, 第2级微结构高度增大, 传热热阻减小增强换热, 且一二级微结构转折区域更低, 凝结液滴可以更快运动到上方而裸露下方成核区域, 从而使得总凝结水分子量增大. 工况C5微结构变细表面积变小且柱间距S变大, 表面积变小使得换热能力下降阻碍热量的传导, 同时相同条件下柱间距与总凝结水分子量呈反比, 柱间距变大凝结总数降低, 在两者共同作用下, 总凝结水分子量出现急剧减少.

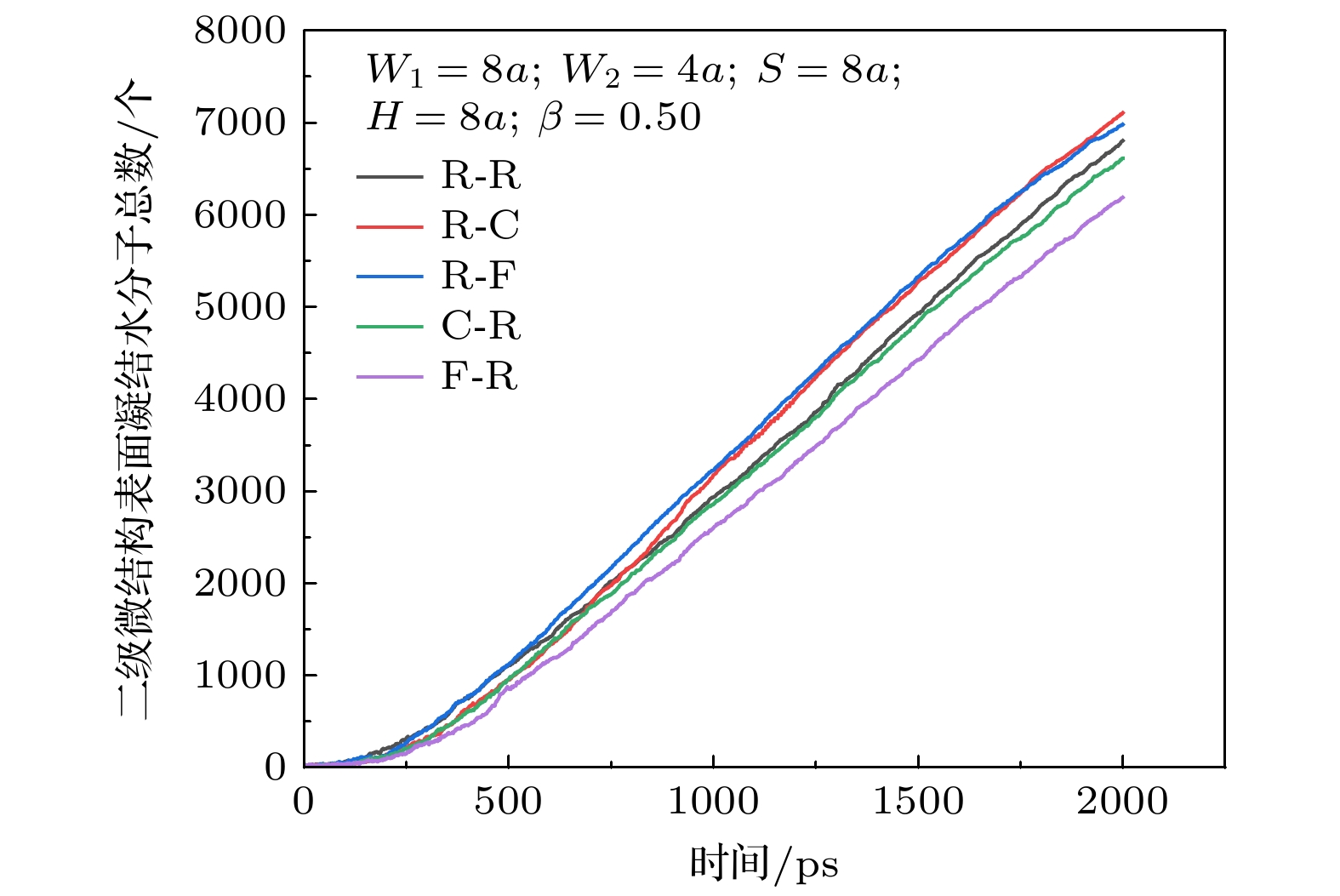
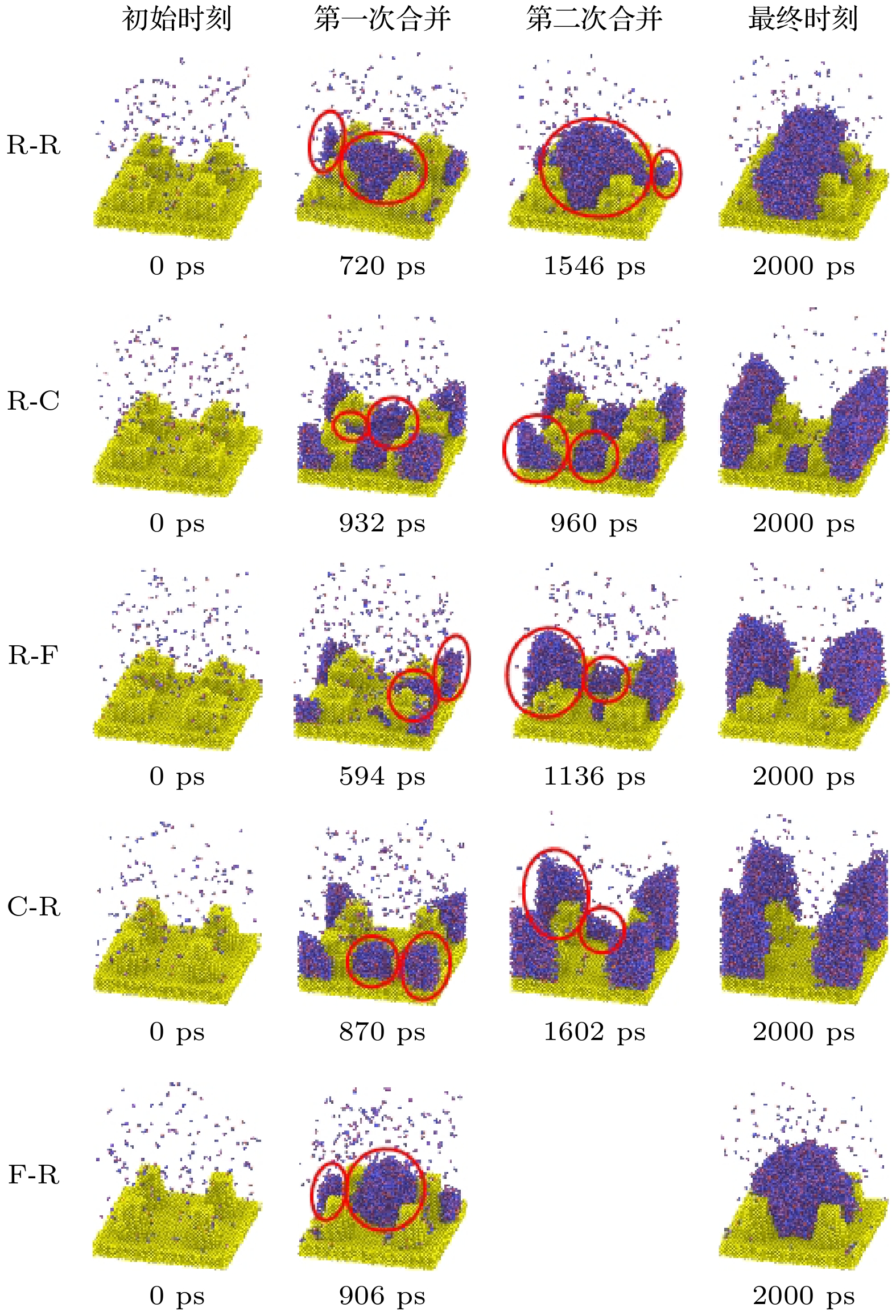
如图10所示, 选择工况D1(R-R)作为对比项. 当第2级结构替换为圆柱、圆台时, 总凝结水分子量均增大, 而当第1级结构替换为圆柱、圆台时, 总凝结水分子量均减小. 分析原因, 由于第2级微结构的替换, 微结构体积减小, 并且观察到液滴包裹在微结构表面, 体积减小的铜原子区域被水分子替代, 使得液滴可以更好的在第2级微结构上有更大的区域支撑, 从而停留并纵向生长, 而裸露更多下方区域继续进行凝结. 但是并非表面积越小越好而是存在一个临界值, 过大不利于液滴的“停留”, 过小不利于与壁面进行导热. 而随着第1级微结构的替换, 由于水蒸气凝结过程主要的成核和生长是发生在第1级微结构区域的, 当第1级微结构的表面积和体积减小时, 减少了铜板对于水分子能量的传递, 从而抑制水分子在第1级微结构区域的凝结总量.

通过对比工况D1, D2和D3可以得到第2级微结构形状对凝结能力的提升关系: C > F > R. 对比工况D1, D4和D5得到第1级微结构形状对凝结能力的提升关系: R > C > F. 依照此种关系, 最佳结构应为R-C与结果相符, 从而证明凝结能力受第1和第2级微结构的共同作用且在某些调整中可相互叠加各自的优势.

成核时间的长短直接影响凝结过程的开始速度和液滴的形成效率, 研究成核时间有助于了解凝结初始阶段的特性.

如图11所示, 随着宽度的增大, 成核时间缩短. 随着第2级微结构宽度的增大, 由于柱体表面积增大, 可以为凝结过程提供更大的固-液接触面积, 有效降低固-液界面处的温度梯度, 使柱体拥有更好的热传导性能, 下表面区域温度更快降低, 水分子更容易聚集, 促进成核, 缩短成核所需时间.

如图12所示, 随着柱间距的增大, 成核时间延长. 当柱间距增大, 微柱之间的相对距离变大, 抑制局部低温区域形成, 并且柱间距的增大, 能垒增大, 水蒸气成核过程受到更大的阻力, 从而减少了形核点的数量. 柱间距较小时, 自由运动到凝结区域的水分子在较小柱间距内有更大概率与微结构表面发生碰撞, 从而由于相互作用力的存在产生凝结, 有利于能量的传递和成核. 然而, 在较大的柱间距下, 水蒸气与微柱表面的接触概率降低, 能量传递效率降低, 导致成核时间增长.

如图13所示, 不同柱结构条件下, 成核时间随着微结构形状变化而增长. 通过分析第1级微 结构为矩形时的工况D1—D3, 成核时间不随第2级微结构形状而变化. 而改变第1级微结构形状时的工况D1, D4和D5, 成核时间发生变化. 从矩形变为圆柱和圆台, 相同尺寸下, 接触面积逐渐减小, 表面对于水分子的吸引力减弱, 液滴成核时间逐渐延长. 第1级微结构形状变化直接影响液滴合并时间.

液滴合并会显著改变液滴尺寸分布与数量, 进而影响凝结的整体效果. 由于模拟时长均为2000 ps, 那么在有限的模拟时间内由于部分工况所设计的结构受限, 抑制水蒸气凝结的进程, 微结构表面上的液滴不能够发生两次合并. 所以在分析合并时间时, 认为此工况的平均合并时间大于1000 ps, 以进行后续分析.

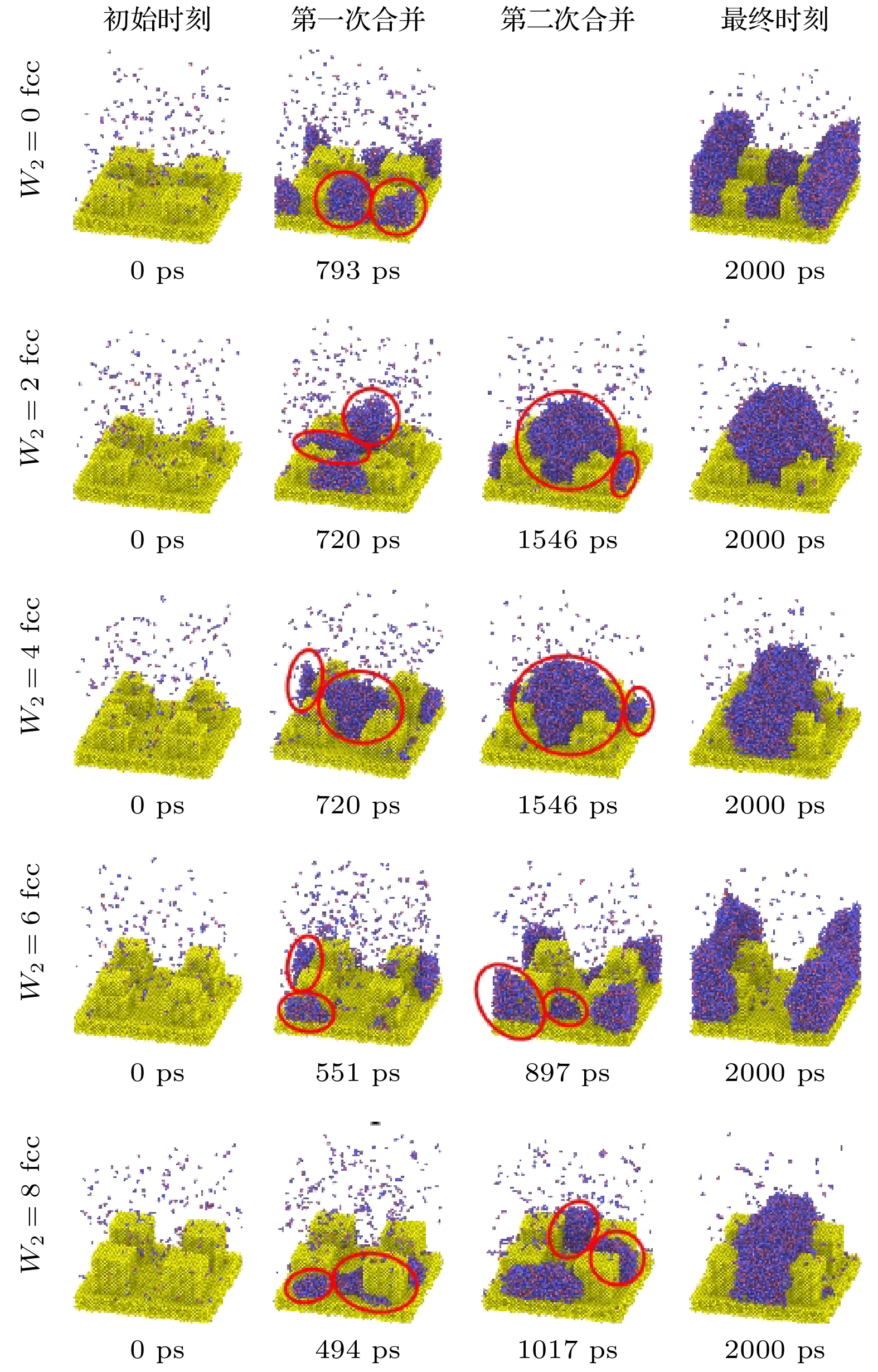
第2级柱宽度存在临界柱宽度, 平均合并时 间随着柱宽度增大, 先加快后减慢. 如图14所示, 柱宽度从0到8a, 两次液滴平均合并时间分别为仅发生一次合并, 725 ps, 697 ps, 354 ps, 436 ps. 柱宽度为0 时, 微结构表面为一级微结构, 水分子与铜接触面积较小, 相互作用力弱, 且成核时间长, 液滴生长缓慢, 延长了合并时间. 随着第2级柱 宽度增大, 液滴能够停留在能垒更低的第1和第 2级微结构交界处, 促进液滴运动, 从而使得合 并时间缩短. 同时, 由于临界柱宽度的存在使得 合并时间出现陡降. 而随着第2级柱宽度进一步增大, 由二级微结构回归一级微结构, 能垒最低处 的缺失, 使得液滴只能在底部发生合并, 合并时间减缓.

如图15所示, 柱间距从4a到12a, 平均合并时间分别为474, 392, 697, 644, 538 ps. 柱间距较小时, 成核的液滴运动受到限制, 无法快速发生合并; 柱间距适当增大时, 使得液滴可以定向发生运动, 合并概率增大, 合并时间缩短; 随着间距的增大, 液滴运动的自由度增大, 合并概率降低, 合并时间延长; 随着间距的进一步增大, 可凝结成核区域受限, 液滴更容易集中在特定的成核区域附近, 从而增大了合并概率, 合并时间缩短.

如图16所示, 随着柱形状的变化, 使得两次液滴平均合并时间分别为697, 404, 492, 721和 仅发生一次合并. 随着第2级微结构变化, 时间先缩短后延长. 由于过大或过小的第2级微结构不 利于液滴在此处停留, 从而不同程度抑制合并进行. 而随着第1级微结构变化, 时间逐渐延长. 第1级微结构作为主要成核区域, 直接影响凝结的 进行. 随着结构的变化, 微结构表面积减小, 导热性能降低, 能垒增大, 从而使得平均合并时间逐渐延长.

最大凝结液滴的大小与分布会直接影响微结构表面的热传递效率和液滴的脱落行为, 较大的液滴会覆盖更多的凝结表面, 抑制小液滴生成. 而促进液滴不断脱落有助于微结构表面持续进行换热, 提高凝结效率.

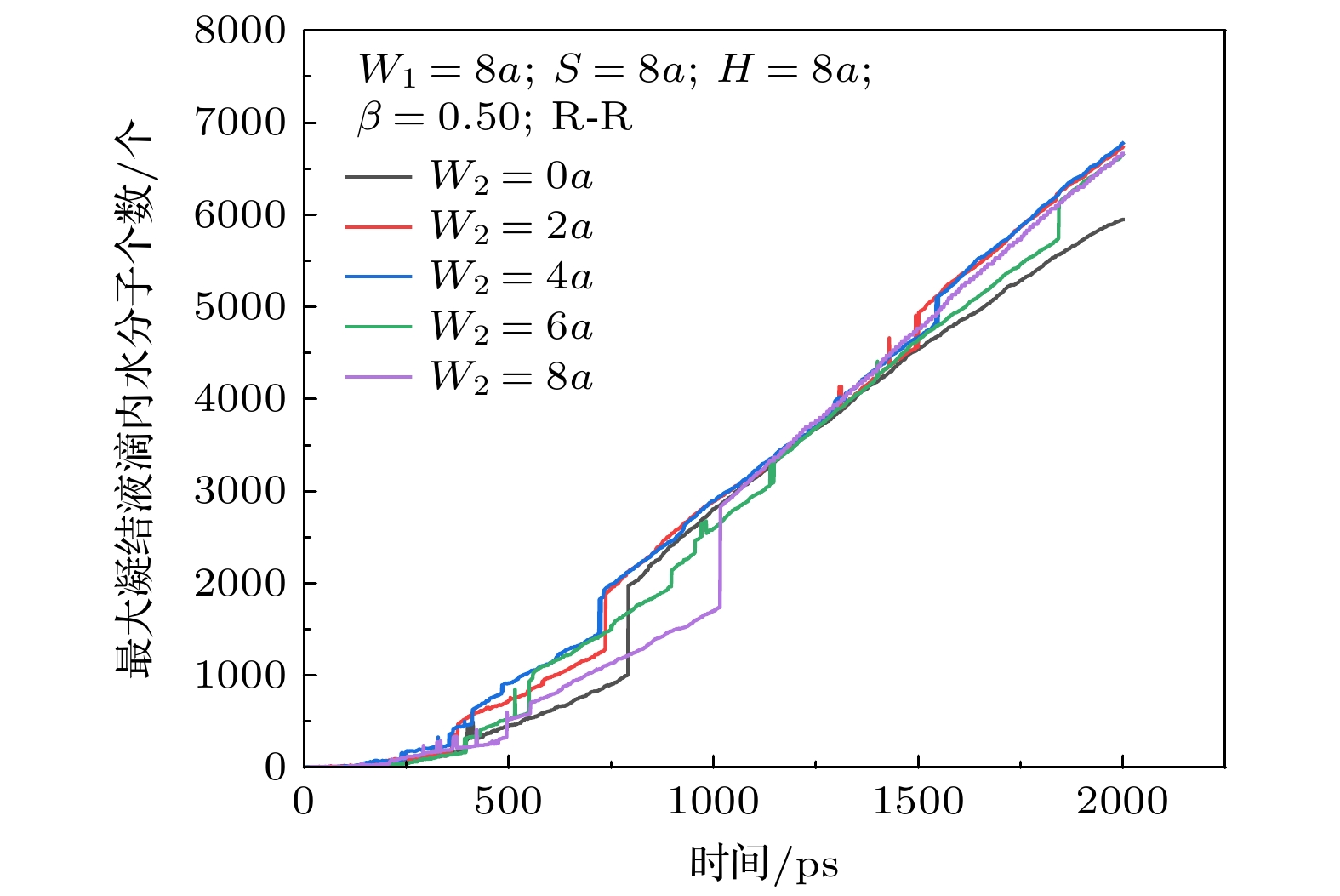
如图17所示, 对于最大液滴而言, 随着微结构宽度的增大, 液滴内水分子量同样先增大后减小. 工况A1和A5均出现一次阶跃, 工况A2和A3出现两次阶跃, 工况A4出现5次阶跃. 阶跃的出现是由于在此时刻下大小两个液滴发生合并, 使得最大液滴内水分子总数发生了阶跃, 而阶跃的高度即液滴合并时小液滴内水分子个数. 故工况A1和A5仅出现一次液滴合并, 工况A2和A3出现两次液滴合并, 工况A4出现五次液滴合并. 且各工况均发生最后一次合并后, 工况A2—A5增长率相同, 工况A1斜率低于其他工况. 由于二级微结构的存在液滴可以更好地纵向生长而裸露出更多区域进行凝结核的生成, 使得合并频率增大. 工况A1最终形成一大一小两个液滴, 二级柱宽为0时, 没有第2级微结构的存在, 液滴未发生明显运动仅依靠凝结空气中的水分子, 故最大凝结液滴明显低于其他工况. 虽然工况A4虽然合并频率最高, 但单次合并阶跃高度减小, 抑制了液滴的生长. 比较工况A2和A3, 工况A2较先完成两次合并而趋于稳定的半球形, 工况A3则由于表面张力的作用处于聚并的非稳定状态, 在该形态变化的过程中表面张力的变化给液滴提供一定的动能, 使其可以小距离运动并合并微结构表面上的更多水分子.

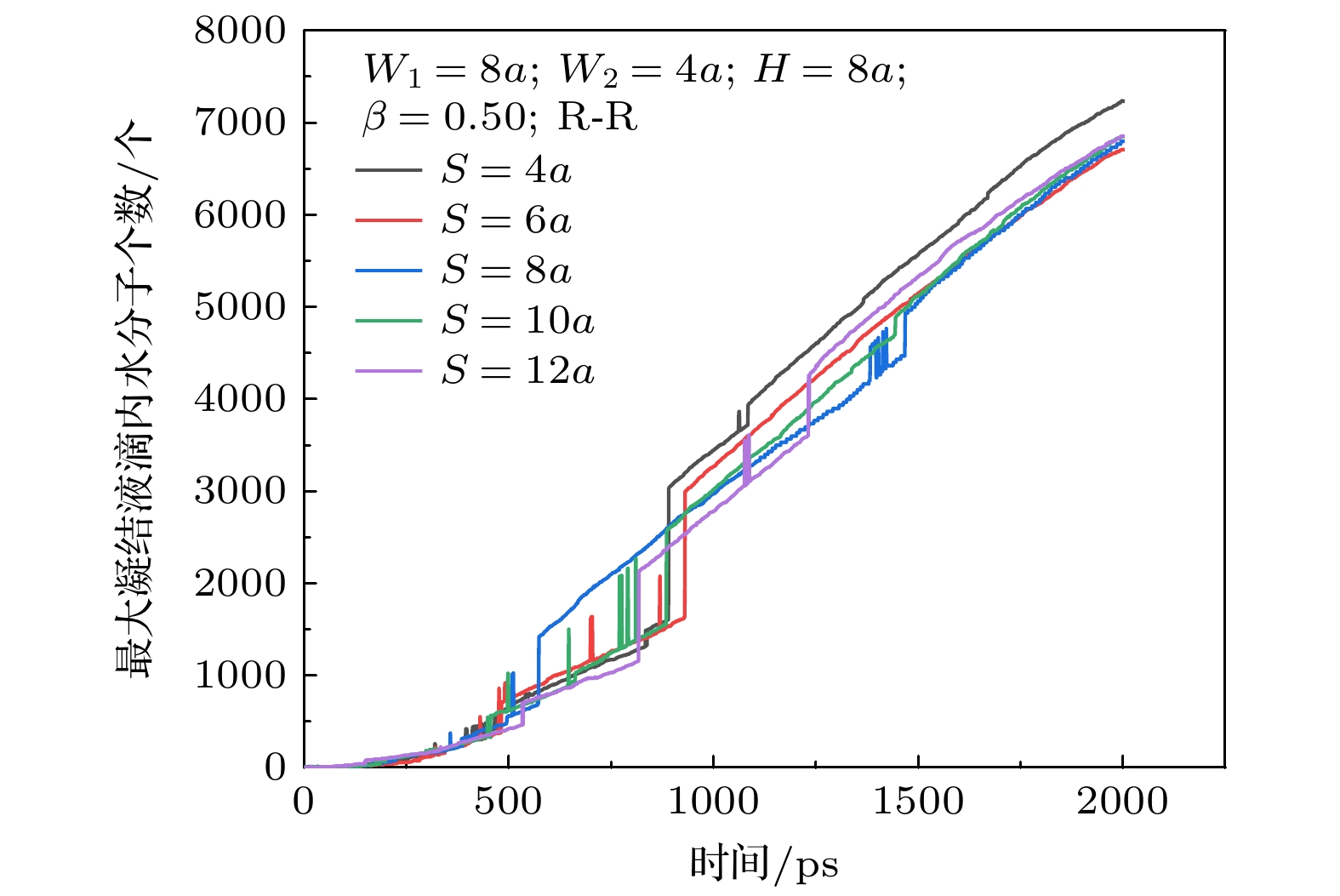
如图18所示, 随着柱间距的增大, 最大凝结液滴受柱间距影响凝结水分子总数同样出现下降趋势. 且仅工况B1(S = 4a)最大凝结液滴内水分子总数最高, 其余水分子总数无明显区别. 由于工况B1发生4次液滴合并, 较快裸露出凝结表面, 使得其水分子数量高于其他工况. 对于其余工况分别发生两次合并, 使得水分子量无明显区别, 而影响其总量变化的原因是发生第2次合并的时间, 较早发生合并的液滴在表面张力的作用下发生多次震荡与小距离的移动, 在这个过程中液滴运动并吸引更多的水分子发生凝结.

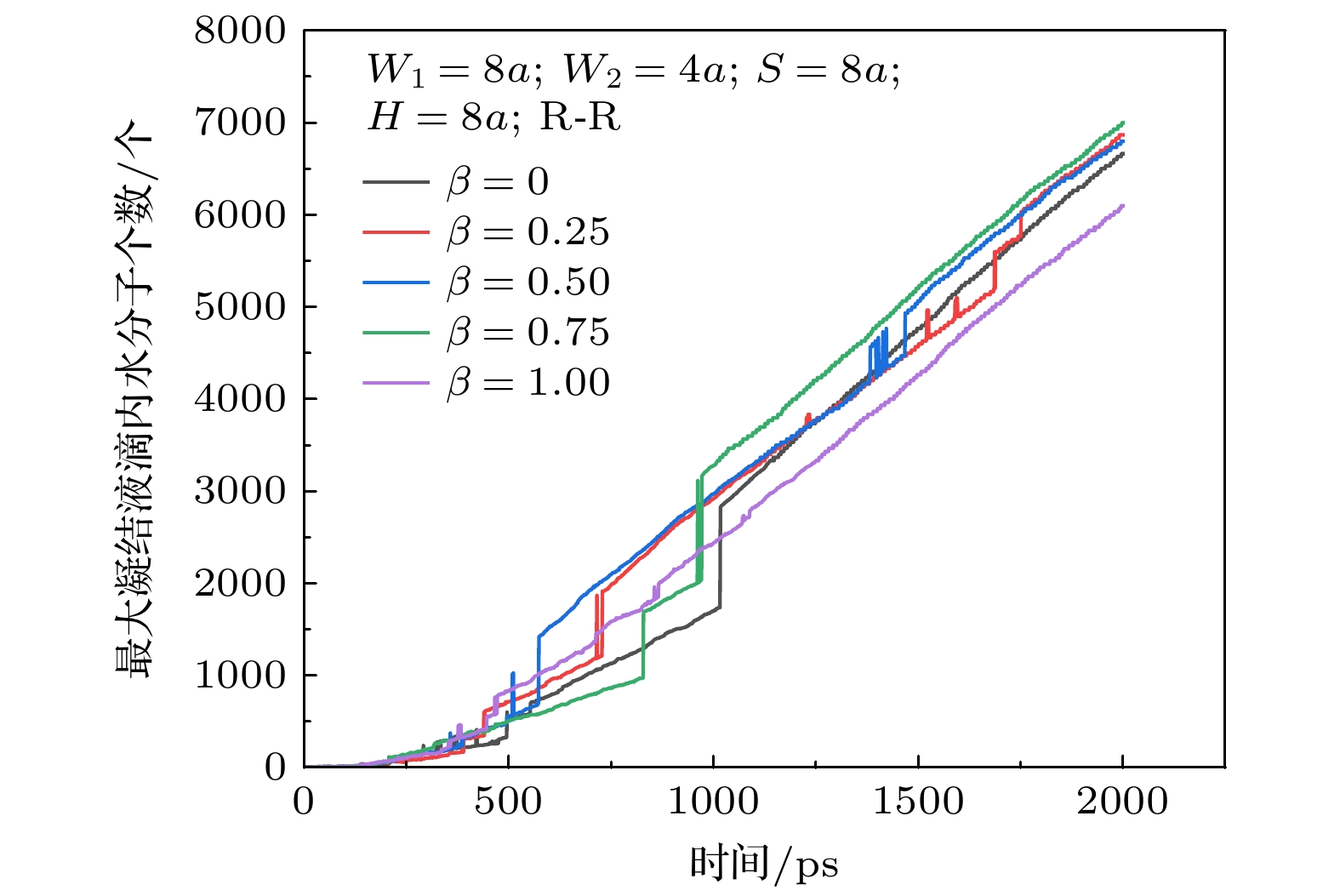
如图19所示, 随着柱高比的增大, 最大凝结液滴内水分子总数同样出现先增大后急剧减小趋势. 工况C1发生1次合并, 而C2—C4均发生两次合并, 且合并小液滴大小逐渐变大、两次合并发生时间逐渐缩短, 促进凝结的进行. 工况C5由于微结构变细液滴横向生长, 未发生明显合并, 仅依靠自然凝结, 从而凝结效率较低.

本文采用分子动力学的方法模拟了不同柱宽度、柱间距、柱高比和柱结构的二级微结构表面水蒸气凝结所产生的现象, 通过分析液滴成核与合并时间、水蒸气凝结快照、凝结水分子总数及最大凝结液滴内水分子总数, 考察不同二级微结构对水蒸气凝结的影响, 主要得到以下结论.

1)在相同条件下, 二级微结构可以比单一一级微结构凝结更多的水分子.

2)随着柱宽度的增大, 系统总凝结水分子量先增大后减小, 成核时间缩短, 在所模拟范围内最佳柱宽度为W₂ = 4a.

3)随着柱间距的增大, 系统总凝结水分子量呈现降低趋势, 成核时间延长, 平均合并时间先减小后增大再减小. 在所模拟范围内最佳柱间距为S = 4a. 然而对于模拟范围外情况未进行进一步的模拟与分析, 有待进一步的研究与探讨.

4)在总柱高度一定的条件下, 随着柱高比的增大, 系统总凝结水分子量先增大后减小, 平均合并时间先增大后减小, 在所模拟范围内最佳柱高比为β = 0.75.

5)第2级微结构形状对凝结能力的提升: C > F > R, 第1级微结构形状对凝结能力的提升: R > C > F.

6)二级微结构表面的凝结能力受第1和第2级微结构的共同作用, 并且在某些调整中可相互叠加各自的优势, 值得更加深入的探讨.