首页
登录
注册
-
受激布里渊散射(stimulated Brillouin scattering, SBS)是由强激光与介质声波相互作用产生的复杂非线性光学现象, 主要通过三波耦合方程近似描述[1]. SBS具有高增益因子和较大的散射截面, 在各种非线性竞争中占据有利地位, 是产生高峰值功率短脉冲的有效手段, 在能源动力、光学通信、生物医学、海洋遥感等领域应用广泛[2–9]. 尤其在海洋环境参数遥感探测领域, SBS频移和线宽特性在海洋温盐剖面探测及声速反演中发挥着重要作用[10,11], 对于海洋三维遥感的发展极具价值. SBS光脉冲的时域特性可以评价信号光束质量及峰值功率大小, 通过对斯托克斯(Stokes)散射光脉冲进行数值研究, 能够量化SBS产生条件, 为优化受激布里渊散射激光雷达(SBS-LiDAR)系统、提升系统探测性能提供理论依据.
Maier等[12]最早对CS2、甲苯的SBS脉冲研究已经证明了SBS瞬时信号功率可以超过激光功率. Hon[13]依据受激拉曼散射(stimulated Raman scattering, SRS)中的脉宽压缩理论, 提出了SBS脉宽压缩的半经典理论, 该理论认为SBS脉冲宽度与泵浦光功率负相关, 泵浦光功率越大, 脉冲宽度越窄. Eichler等[14]对聚焦光束下的SBS声波分布进行理论模拟, 发现散射脉冲宽度随入射功率的增加逐渐增大, 形状也越来越接近入射脉冲. 徐德[15]利用耦合波方程建立了一维瞬态SBS数值模型, 分析了水的SBS脉冲波形从产生到饱和过程. 刘照虹[16]在研究组合式脉冲压缩技术时从耦合波方程出发绘制了水中SBS脉冲随泵浦能量的变化. 从对SBS脉冲的研究结果来看, Stokes脉宽随入射能量变化的相关结论并不一致, 这主要是由于理论模拟均是在不同的条件参数下进行, 而介质参数、泵浦光参数、环境条件、SBS单元结构等均会影响散射结果[17–22]. 目前关于Stokes散射波形研究系统多采用聚焦结构, 集中于声子寿命短的气体(如SF6、氩气、甲烷等)、有机溶液和液态氟碳化物中, 对于水中Stokes散射脉冲特性的数值研究结果缺乏系统的报道.
本文针对SBS-LiDAR系统优化和性能提升的需求, 利用时域SBS模型研究了系统参数和系统结构对水中SBS光谱的影响, 讨论了聚焦与非聚焦情况下Stokes脉冲波形, 并给出温度与两种情况的Stokes脉宽变化之间的关系, 研究结果对受激布里渊散射激光雷达海洋遥感探测具有重要意义.
-
SBS是典型的声光相互作用过程, 依据麦克斯韦(Maxwell)方程组和纳维-斯托克斯方程(Navier-Stokes), 水中入射光、散射光和声波三波耦合的偏微分方程可表示为[1]
其中
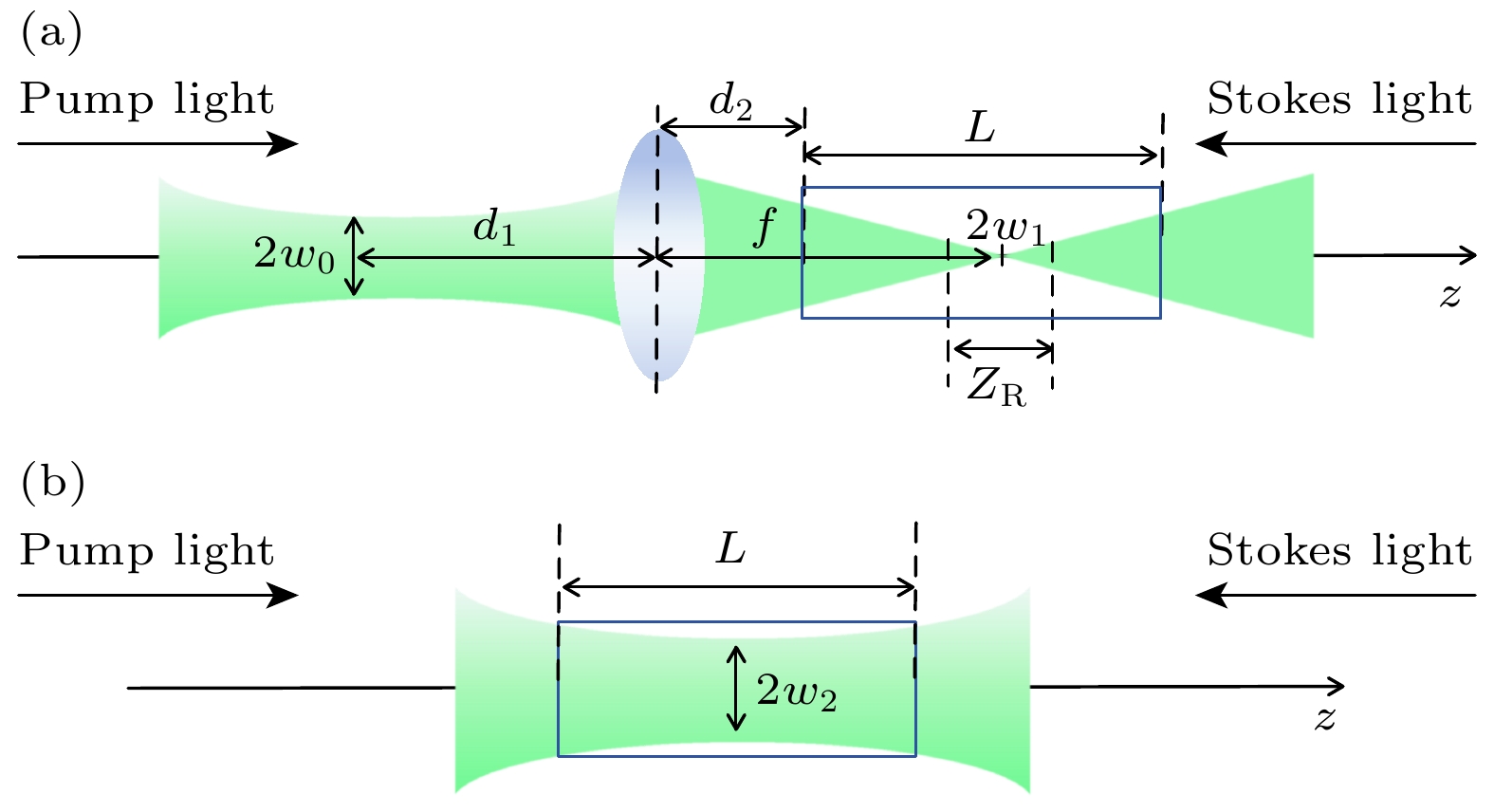
${{\boldsymbol{E}}_{\text{p}}}$ 和${{\boldsymbol{E}}_{\text{s}}}$ 分别代表入射光场和散射光场;${\boldsymbol{\rho}} $ 为声波场;$n$ 为水的折射率;$c$ 为真空中光速;$\alpha $ 为水的衰减系数;${\omega _{\text{p}}}$ 和${\omega _{\text{s}}}$ 分别为入射光和散射光的角频率;${\gamma _{\text{e}}}$ 为水中电致伸缩系数;${{{\rho}} _0}$ 为水的初始密度;$\varGamma $ 为声阻尼系数;${\varepsilon _0}$ 为真空中的介电常数;${{\boldsymbol{k}}_{\text{a}}}$ 为声波的波矢量;${\upsilon _{\text{a}}}$ 为声速. 令${g_{\text{p}}} = {{\omega _{\text{p}}}{\gamma _{\text{e}}}} /{4 cn{{{\rho}} _0}}$ ,${g_{\text{s}}} = {{{\omega _{\text{s}}}{\gamma _{\text{e}}}} {/ } {4 cn{{{\rho}} _0}}}$ ,${g_{\text{a}}} = {{{\varepsilon _0}{k_{\text{a}}}{\gamma _{\text{e}}}} {/ } {4{\upsilon _{\text{a}}}}}$ , (1)式、(2)式、(3)式表示为水中SBS光束传输结构如图1所示, Nd:YAG激光器发出的脉冲光以高斯光束的形式沿z方向向前传播, 其初始束腰半径为
${\omega _0}$ , 根据水池前有无聚焦透镜可分为聚焦与非聚焦结构. 聚焦结构下光束光斑面积较小, 光束经过焦距为f的透镜汇聚到长度为L的水池中时, 光斑半径为${\omega _1}$ , 瑞利长度为${Z_{\text{R}}}$ . 初始束腰与聚焦透镜之间的距离为${d_1}$ , 透镜与水池之间的距离为${d_2}$ . 而在非聚焦结构下水池中光束的光斑半径为${\omega _2}$ .只考虑其纵向光功率密度的变化, 入射光振幅可表示为
其中r为场上任一点到中心光轴的径向距离,
$\omega \left( z \right)$ 为振幅在峰值幅度1/2处的光斑半径. 假设水中光束束腰位置为${z_0}$ , 对于聚焦结构来说, 光束截面积减小, 且随z不断变化:相比于聚焦结构, 非聚焦泵浦下的光束较为发散, 其光斑大小与传输距离有关. 假设光束束腰在水池中距离激光初始发射位置为
$l$ , 那么其光斑半径为从(7)式可以看出, 以高斯函数传输的光束, 其振幅与某一点的光束截面半径呈负相关, 即与光束截面积σ的平方根负相关. 因此, (4)式和(5)式中的入射光与散射光振幅可以用高斯光振幅与截面积平方根的乘积来表示. 令
${g_{\text{s}}} \approx {g_{\text{p}}} = {g_1}$ ,${g_{\text{a}}} = {g_2}$ , 由(6)式可得对于SBS的起振方式, 采用分布式热噪声模型[23], 这是目前研究SBS光束传输最常用的模型, 它认为介质内均匀分布的随机噪声是SBS的激励源. 对耦合波方程计算求解采用有限时域差分(finite difference time domain, FDTD)方法[24], 将SBS整个作用区域进行网格化处理, 时间步长为
$\Delta t$ , 位置步长为$\Delta z$ , 处理后的耦合波方程组为其中,
${G_1} = {{n\Delta z} {/ } {c\Delta t}}$ ,${G_2} = {{{g_1}{g_2}\Delta z\Delta t} {/ } 2}$ ,${G_3} = {\alpha \Delta z} {/ } 2$ ; m为时间下标, j为位置下标;$ q_j^m $ 为积分离散化处理的结果, 表示为在利用(13)式和(14)式求解的过程中, 需要依据一定的边界条件, 假设激光从初始发射端z = 0输入, 一直到z = L处强度达到峰值, 散射光在z = 0位置出射, 满足的边界条件为
其中
$E_{\rm p max}$ 表示入射光峰值幅度,${{{E}}_{{\text{s0}}}}$ 为Stokes噪声振幅. 依据SBS-LiDAR系统和介质水的物理性质[8,25–27], 初始输入参数设置如表1所列. -
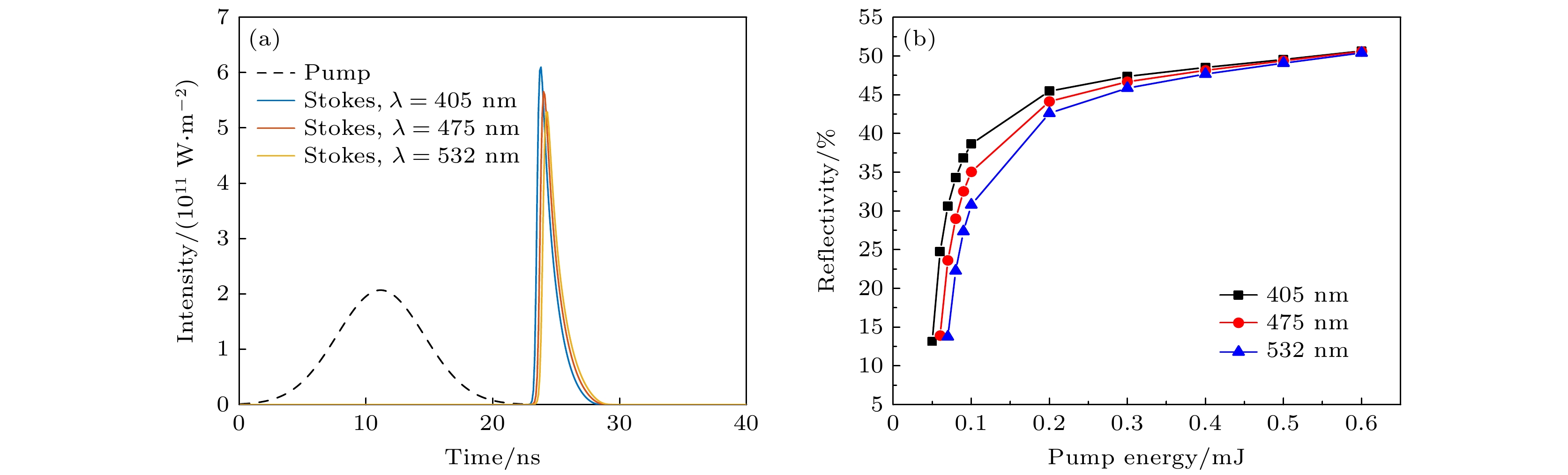
在实际的测量系统中, 光源的性质(如激光波长、脉宽)和聚焦深度是影响SBS脉冲特性的主要因素, 在这里给出了聚焦结构SBS在不同入射波长、激光脉宽以及焦距下的时域脉冲变化. 图2(a)显示了不同入射波长作用时的SBS脉冲波形图, 选取海洋探测常用的蓝绿激光波段405, 475, 532 nm. 由图2(a)可以看到, 波长不同时, Stokes峰发生位置不同, 峰值强度也不同, 波长越短, 产生位置越靠前, 峰值功率密度越大. 如果把Stokes峰值强度与入射光峰值强度的比值定义为反射率, 从图2(b)可以看到, 入射波长越短, 反射率越高, 阈值越小. 短波长光束光子能量高, 更容易诱导水中弹性声波产生, 增强其非线性极化响应以启动SBS, 因此所需入射能量较小. 在所给参数条件下, 随着入射能量的增加, 反射率呈现开始迅速增加而后逐渐趋于平缓的变化情况.
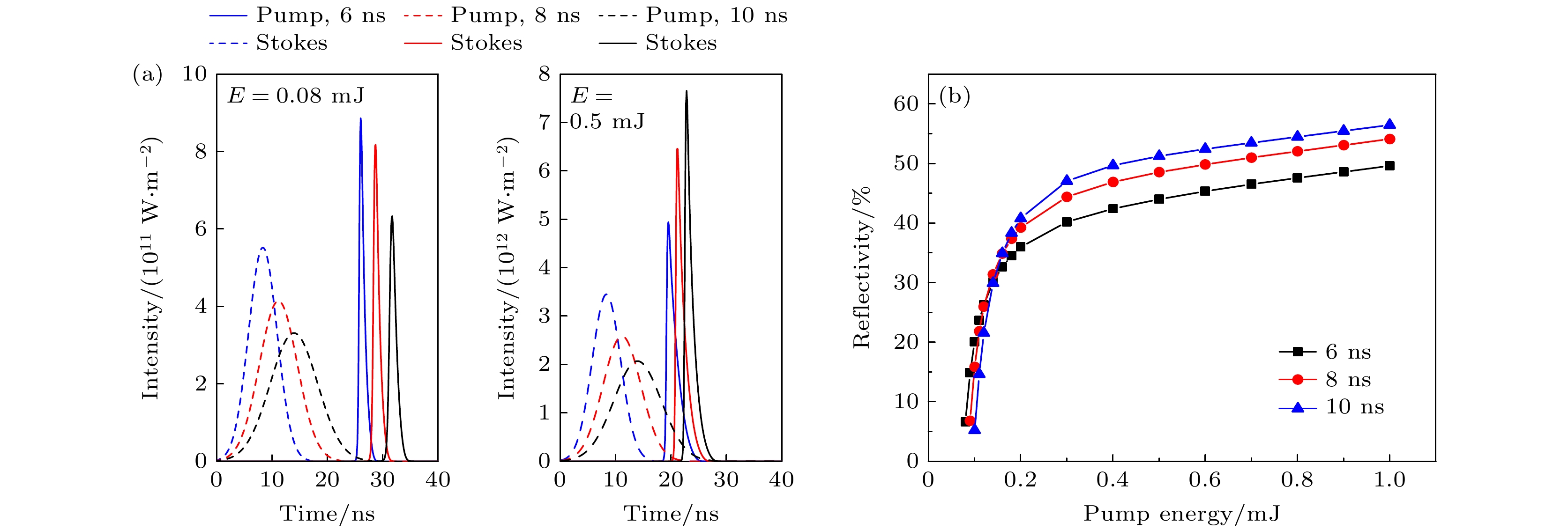
分别模拟脉宽为6, 8, 10 ns下的SBS脉冲波形, 结果如图3(a)所示. 可以看出, 在固定的单脉冲输入能量下, 激光脉宽越小, Stokes散射峰出现越早, 而散射峰峰值功率在不同能量下呈现出不同变化. 当入射能量较小时, 短脉冲光产生的Stokes散射信号强; 当入射能量较大时, 长脉冲光产生的Stokes散射信号强. 这是由于短脉冲光峰值功率高, 在低能量情形下, 脉冲上升沿光子更容易满足SBS阈值, 产生强Stokes散射信号. 在入射能量较大时, 长脉冲光上升沿光子同样满足SBS阈值, 短脉冲光的优势不再明显, 而长脉冲光由于与水的相互作用时间更长, 光子与声子作用概率增加, 能够累积更多的散射信号. 从图3(b)可以看出, 入射光脉宽较大时, SBS阈值较大, 当Stokes信号反射率约大于30%后, 长脉冲光对信号的累积作用才能体现. 对于相同的入射激光脉宽来说, 在阈值能量附近SBS反射率迅速增加, 而后增长逐渐缓慢.
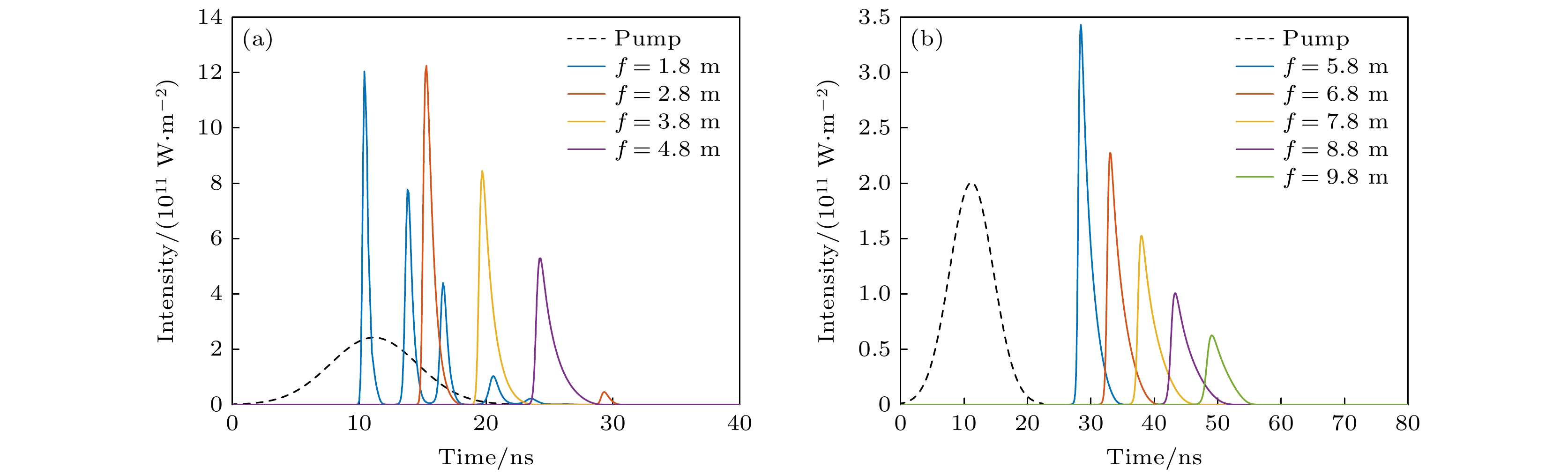
图4为焦距对SBS脉冲的影响, 在不改变其他参数的情况下, 设置水池长为10 m. 由图4可以看到, 当聚焦深度较小时, Stokes峰值功率较大, 且伴随多个振荡峰出现. 随着焦距的增加, Stokes散射峰值功率急剧下降, 其脉冲前沿逐渐变得平缓, 尾部逐渐拖长, SBS阈值能量增加, 反射率逐渐下降. 聚焦深度越大, Stokes脉冲建立时间越晚, 振荡峰消失, SBS脉冲保持良好的相位共轭保真度. 由于聚焦结构会使得焦点附近的光功率密度远大于其他位置的功率密度, 当聚焦到介质前端时, 入射泵浦功率在介质中的损耗非常小, 因此在焦点附近极易激发SBS, 造成入射光在短时间内迅速消耗又迅速补充, 出现多个振荡次峰. 直到其功率不能满足SBS阈值时, 这种在入射光与Stokes光之间反复、迅速的能量转换过程才会停止.
-
为激发介质中的SBS, 通常利用提高入射光强度来增加系统增益的原理, 在介质前端增加单透镜或者组合透镜, 形成聚焦SBS结构, 而焦点附近过大的功率密度不仅会对实验系统造成损坏, 还可能带来自聚焦效应, 降低信噪比, 这对激光能量有很大的限制. 从3.1节数值模拟的结果可知, 聚焦深度还会对SBS脉冲波形相位共轭保真度带来一定的影响. 因此, 在实验过程中需要对聚焦位置进行精确控制. 非聚焦结构同样能产生受激布里渊散射, 且能够大幅度提升系统能量的注入, 适用于高功率强激光系统的光束传输, 但光束具有发散性. 通过比较聚焦与非聚焦结构下的时域SBS信号, 讨论两种情况下Stokes散射峰值强度、脉冲宽度的变化对实验中两种结构的选择以及规避相应的缺陷有重要意义.
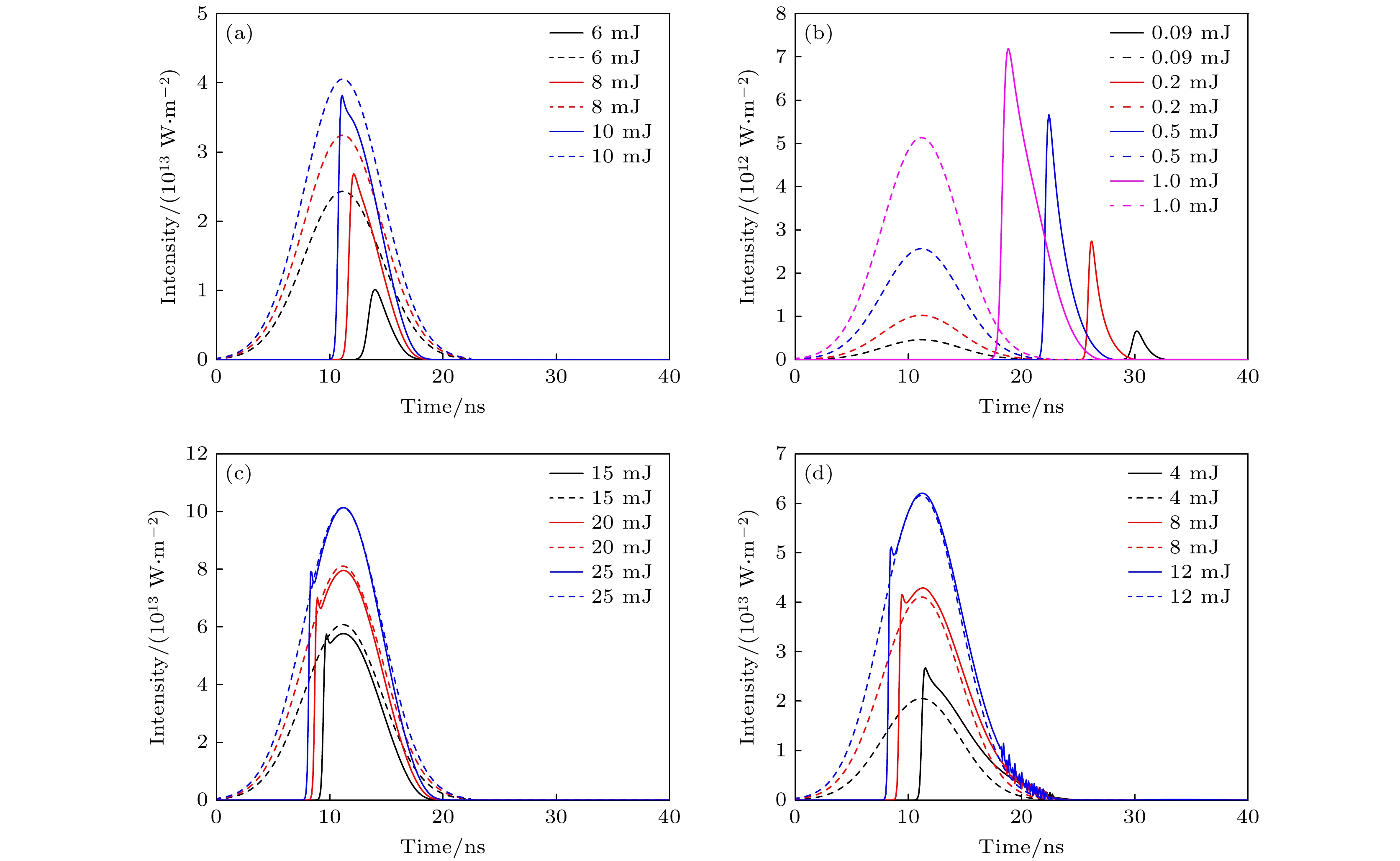
图5描述了相同参数下非聚焦与聚焦两种结构产生的Stokes脉冲波形. 由于入射能量相同时, 聚焦结构和非聚焦结构光束直径差异大, 当入射光斑大小为2.5 mm时, 聚焦光束(f = 4.5 m)在水中的光斑大小为434 μm; 非聚焦光束在传输路径上逐渐发散, 在水中相同位置光斑大小为2.65 mm, 两者激发的SBS状态不同. 因此, 在这里给出的是从阈值能量开始的SBS脉冲波形变化. 从图5(a), (c)可以看出, 随着入射能量的增加, SBS系统内入射光场和Stokes散射光场随之增强, 但由于非聚焦结构中斜向散射光在与后向共轭散射光的竞争中被放大, 光束在空间上具有一定的发散角, 因此需要更高的注入能量才能满足SBS阈值条件. 当入射能量为4.5 mJ时, SBS刚刚发生, 入射光与Stokes散射光之间的能量转移是一个缓慢变化的过程, 即使增大能量也很难获得高峰值功率的短脉冲. 图5(b), (d)显示了聚焦状态下的SBS脉冲波形. 对比非聚焦情况, 其阈值能量更低, 随着入射能量的增加, Stokes散射光峰值功率急剧增加, 出现峰值远高于入射光的短脉冲, 散射光的产生位置也随着入射光的增大而前移. 这是由SBS的阈值特性导致的. 无论是聚焦结构还是非聚焦结构, Stokes光脉冲会随着能量的增加最终趋于入射光波形, 但均保持陡峭的脉冲前沿这一特征.
当入射光强度
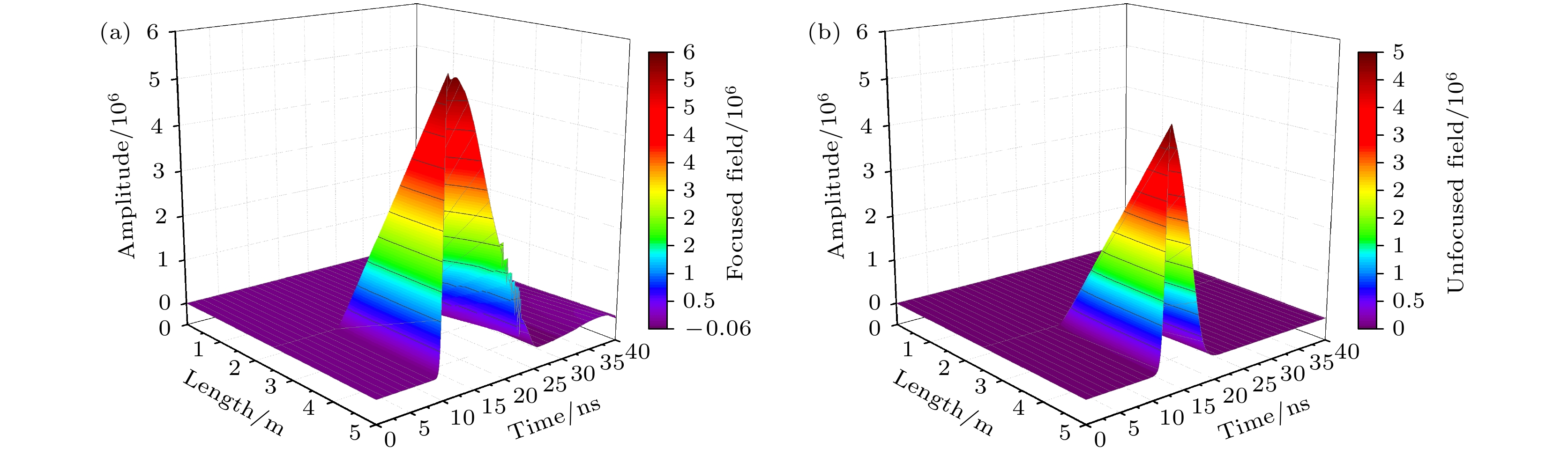
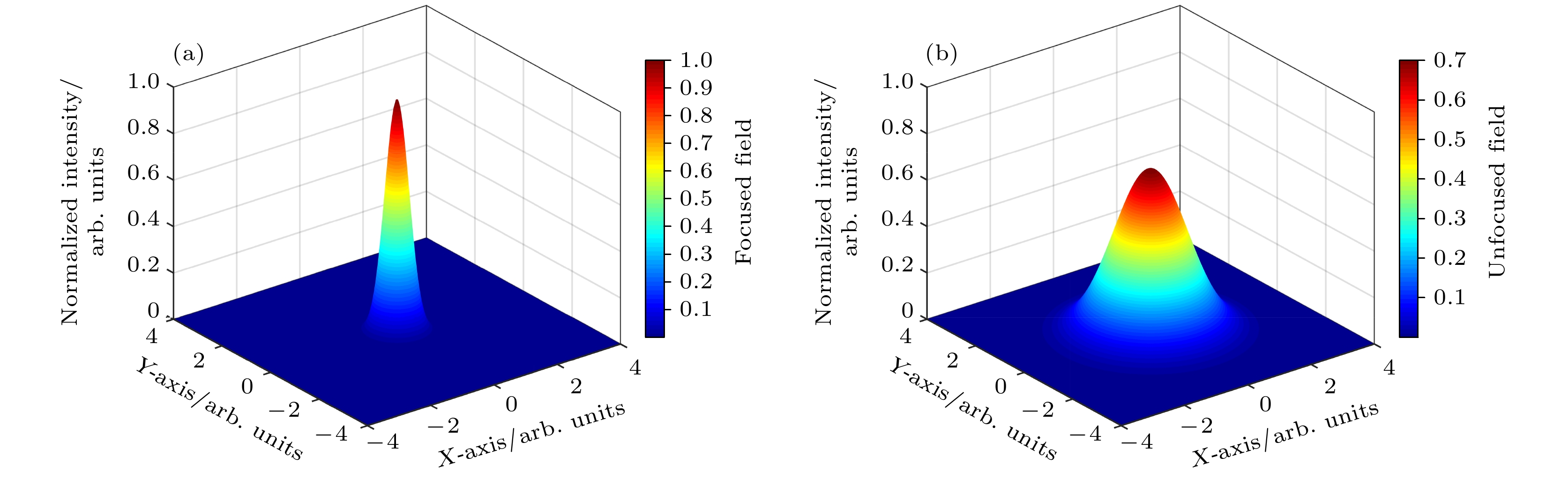
${I_{{\text{input}}}} = 3.08 \times {10^{13}}{\text{ W/}}{{\text{m}}^{2}}$ , 水池长度为5 m时, 聚焦与非聚焦条件对应的Stokes散射光振幅变化如图6所示. 从图6可以看出, 聚焦SBS可以获得更大的峰值强度, 在9.5 ns处, SBS开始发生, 脉冲峰值幅度可达$5.90 \times {10^6}$ , 峰值强度为$3.48 \times {10^{13}}{\text{ W/}}{{\text{m}}^{2}}$ , 反射率为77.13%. 而非聚焦SBS在11 ns附近开始产生, 脉冲峰值幅度为$4.92 \times {10^6}$ , 峰值强度为$2.42 \times {10^{13}}{\text{ W/}}{{\text{m}}^{2}}$ , 反射率为25.71%. 图7展示了相同条件下两种结构产生的信号光斑在空间上的归一化强度分布, 当在水中传输4.5 m时, 聚焦结构产生SBS信号强度约为非聚焦结构的1.4倍. -
增益系数是决定SBS信号放大能力的重要参数, 与介质本身物理特性, 如声子寿命、声速及密度等有关. 水中SBS增益系数可表示为[25]
式中,
${\gamma _{\text{e}}}$ 为电致伸缩系数,${\omega _{\text{s}}}$ 为布里渊散射角频率,$ \rho_0\boldsymbol{ } $ 为密度,$n$ 为折射率,$c$ 为真空中的光速,${\upsilon _{\text{a}}}$ 为声速,$\Delta {\nu _{\text{B}}}$ 为布里渊线宽, 这些介质物理参量均与温度有关[28–30]. 其中布里渊线宽$\Delta {\nu _{\text{B}}}$ 决定了SBS频率响应范围, 进而影响散射信号脉冲宽度, 其大小为声子寿命${\tau _{\text{B}}}$ 的倒数, 水中声子寿命与密度${{\rho_0}} $ 、黏度$\eta $ 和声波矢$ \boldsymbol{k}_{\text{a}} $ 有关[31].当温度变化时, 水的黏性改变引起声子寿命及增益系数的变化会对Stokes光脉冲宽度及脉冲能量产生影响. 因此, 根据增益系数与温度的依赖关系可以获得不同温度下Stokes散射光脉冲特性. 实验研究表明水中SBS增益系数与温度正相关, SBS增益系数随温度变化的经验关系为[26]
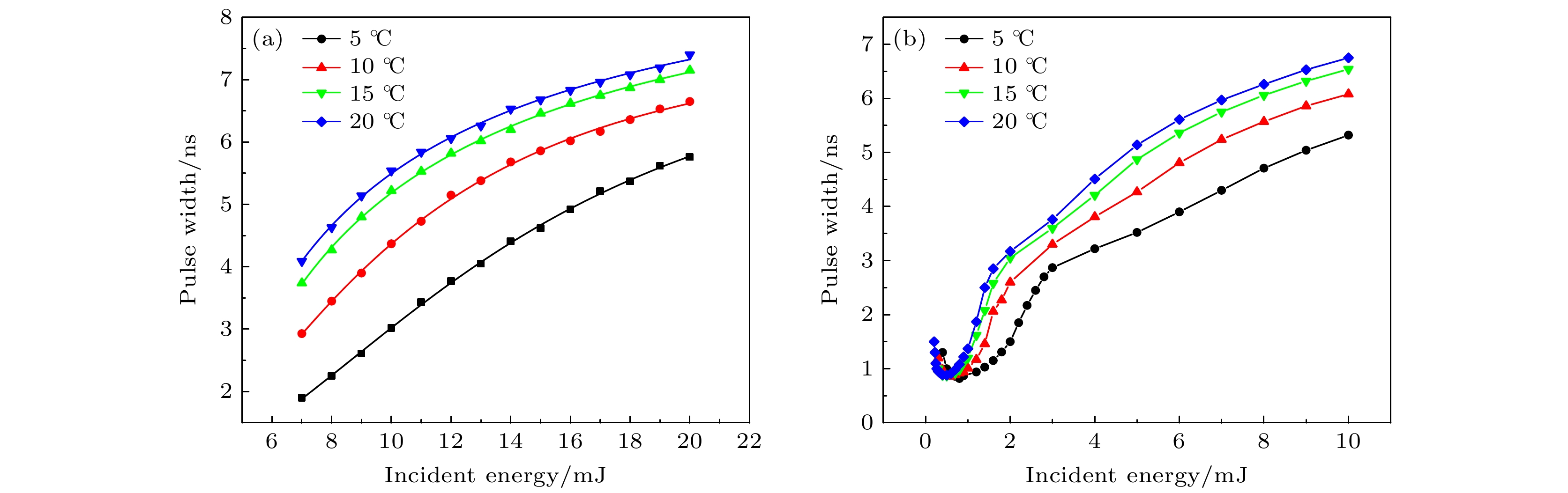
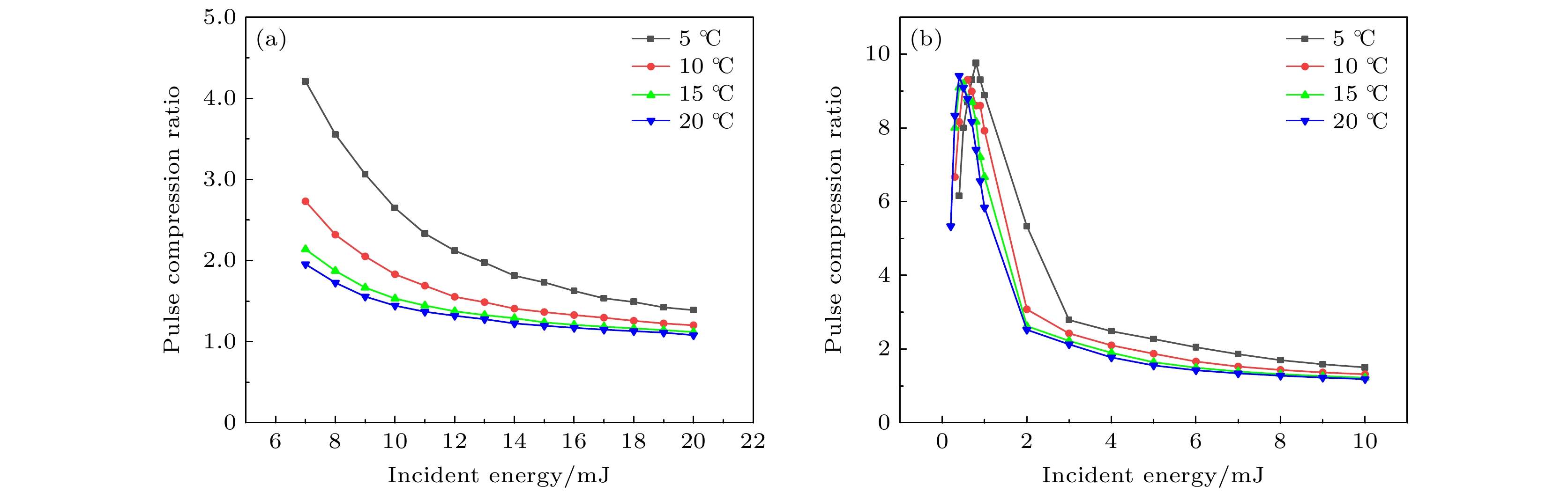
图8给出了聚焦与非聚焦状态下Stokes散射光脉冲宽度随入射能量的变化情况, 能量范围为SBS从发生到饱和. 从图8(a)看出, 非聚焦结构的Stokes散射光脉宽随着入射能量的增加持续增大, 温度越高, 脉冲宽度越大, 且温度带来的这种影响逐渐减小. 图8(b)为聚焦结构的SBS脉冲波形随能量变化关系, 在入射光较弱时, Stokes散射光脉宽随着能量的增加而减小, 当能量超过一定值时, 脉冲不会继续压缩而是逐渐展宽, 这使得脉宽压缩具有一最佳值. 该现象主要是由于入射光强度在刚满足SBS阈值条件时, 散射光与入射光可以充分作用, 形成高功率短脉冲. 当入射光峰值功率密度超过一定的值后, 随着Stokes散射脉冲产生位置逐渐向前移动, 介质中散射光与入射光的相互作用长度逐渐减小, 导致其脉冲前沿在介质内的停留时间缩短, 不能被充分压缩. 在其前沿过早地离开介质后, 入射能量在介质内有仍大量剩余, 进而放大了脉冲后沿, 使得整个Stokes脉冲展宽. 同样, 随着温度的升高, 这种脉冲压缩作用逐渐减弱, 在低温时具有更好的压缩效果. 根据(20)式, SBS频率响应范围与声子寿命成反比, 低温时水的黏性大, 声波衰减增加, 声子寿命减小, SBS频率响应范围增加. 由傅里叶变换关系可知时域Stokes散射光脉冲宽度减小, 研究结果与水中不同温度SBS脉宽的实测结果表现一致[20]. 图9显示了不同温度下入射光脉宽与散射光脉宽的比值. 可以看到, 在5 ℃时聚焦SBS结构存在最大脉宽压缩比为9.75, 获得了0.82 ns的散射光, 两种结构的比值最终都趋近于1.
-
本文通过对不同系统参数及聚焦场与非聚焦场的时域SBS进行研究, 分析了脉冲宽度随入射能量的变化. 结果表明: 在高输入输出情况下, 短入射波长和较大的激光脉宽更容易产生高峰值功率散射光, 聚焦深度则需要根据实际情况选择, 短焦距下SBS功率大, 容易出现次峰干扰, 长焦距下SBS功率小, 光谱信号保真度好. 因此, SBS-LiDAR在短距离信号探测时需解决好次峰干扰及光谱展宽问题. 对于非聚焦结构, 入射光能量增大, Stokes脉宽增加. 对于聚焦结构, Stokes光随入射能量的增加出现脉宽压缩的现象, 在低温时能量稍高于阈值处脉宽值最小, 脉宽的压缩意味着信号峰值功率增大, 为避免接收器件的损坏应根据实验环境灵活设置衰减. 本文研究内容为改善受激布里渊散射激光雷达系统探测性能提供重要参考.
受激布里渊散射海洋激光雷达时域脉冲特性
Time-domain pulse characteristics of stimulated Brillouin scattering ocean lidar
-
摘要: 受激布里渊散射激光雷达探测技术具有高分辨、高信噪比、强抗干扰能力等优势, 在海水温-盐-声多参数联合测量方面具有重要应用前景. 受激布里渊散射是一个非线性动态过程, 其发生位置、峰值强度、谱线形状等随时间而变化. 本文基于分布式噪声模型对不同激光波长、脉宽及焦距的水中受激布里渊散射时域信号进行了理论模拟及分析, 研究了聚焦与非聚焦两种结构产生的Stokes脉冲特性. 结果表明: 波长越短, Stokes散射光的峰值功率越高, 在低入射能量时短脉冲获得更强的散射光, 而高入射能量时, 长脉冲更具优势, 焦距越大, 散射光峰值功率越低, 脉冲保真度越好; 随着入射能量的增加, 非聚焦结构的Stokes散射光脉冲宽度不断增加, 聚焦结构的Stokes散射光脉宽先减小后增大, 且存在受温度和能量影响的最佳压缩值, 低温时, Stokes散射光脉宽在阈值能量附近具有更好的压缩效果. 研究结果对提升受激布里渊散射激光雷达探测性能具有重要意义.Abstract: Stimulated Brillouin scattering lidar (SBS-LiDAR) technology possesses significant advantages such as high resolution, high signal-to-noise ratio, and strong anti-interference capacity, making it highly promising for simultaneous measurements of temperature, salinity, and sound velocity in seawater. Stimulated Brillouin scattering (SBS) is a nonlinear dynamic process characterized by temporal variations in its occurrence location, peak intensity, and spectral shape. Through numerical simulations of Stokes pulse, the conditions for SBS generation can be quantitatively determined, thereby establishing a theoretical foundation for optimizing lidar systems and enhancing their detection capabilities. Existing studies on Stokes pulses typically focus on specific experimental configurations under varying parameters, including medium properties, pump laser characteristics, and ambient environmental factors. There are still significant discrepancies in reported conclusions regarding the relationship between incident energy levels and pulse width variations, particularly in water-based environments where systematic research on the Stokes scattering pulse characteristics is clearly insufficient. In this study, a distributed noise model is used to theoretically simulate and analyze the time-domain signals of SBS in water at different laser wavelengths, pulse widths, and focal lengths. The characteristics of Stokes pulses generated by focused and non-focused configurations are investigated. The results indicate that under the same conditions, shorter incident wavelength produces significantly higher peak power of Stokes scattering light. The Stokes scattering light exhibits significant energy-dependent behavior: at low input energy, short pulse generates stronger scattering signal due to enhanced nonlinear interaction efficiency, while at high input energy, longer pulse exhibits excellent performance by maintaining temporal coherence. The larger focal length results in lower peak power but better pulse fidelity. As the incident energy increases, the pulse width of Stokes scattering light in the non-focused configuration exhibits a continuous increase. In contrast, for the focused configuration, the pulse width initially decreases and then increases, exhibiting an optimal compression value influenced by temperature and energy. At lower temperatures, the Stokes pulse width exhibits excellent compression performance near the threshold energy. Therefore, reducing secondary peak interference and suppressing spectral broadening are critical technical challenges that must be systematically addressed for short-range SBS-Lidar applications. In low-temperature detection scenarios, dynamic attenuation control becomes essential to prevent thermal stress-induced damage to photodetectors. These findings are of great significance in enhancing the performance of SBS-LiDAR system.
-
Key words:
- stimulated Brillouin scattering /
- lidar /
- distributed noise model /
- time-domain pulse waveform .
-
-
图 1 水中SBS光束传输 (a)聚焦结构; (b)非聚焦结构
Figure 1. SBS beam transmission in water: (a) Focused structure; (b) unfocused structure.
图 2 入射波长对时域SBS信号的影响 (a) SBS脉冲波形; (b)反射率
Figure 2. Effect of incident wavelength on SBS temporal profile: (a) SBS spectral line; (b) reflectivity.
图 3 脉宽对时域SBS信号的影响 (a) SBS脉冲波形; (b)反射率
Figure 3. Effect of pulse width on SBS temporal profile: (a) SBS spectral line; (b) reflectivity.
图 5 SBS时域波形图 (a), (c)非聚焦结构; (b), (d)聚焦结构
Figure 5. SBS temporal profiles: (a), (c) Unfocused structure; (b), (d) focused structure.
图 6 Stokes散射光的振幅变化 (a)聚焦结构; (b)非聚焦结构
Figure 6. Amplitude variation of Stokes light: (a) Focused structure; (b) unfocused structure.
图 7 Stokes散射光空间归一化光强分布(z = 4.5 m) (a)聚焦结构; (b)非聚焦结构
Figure 7. Normalized intensity of the Stokes light (z = 4.5 m): (a) Focused structure; (b) unfocused structure.
图 8 不同温度下Stokes散射光脉宽随能量的变化 (a)非聚焦结构; (b)聚焦结构
Figure 8. Variation of the pulse width of Stokes light with the incident energy at different temperatures: (a) Unfocused structure; (b) focused structure.
图 9 脉宽压缩比变化 (a)非聚焦结构; (b)聚焦结构
Figure 9. Changes in pulse width compression ratio: (a) Unfocused structure; (b) focused structure.
表 1 数值模拟参数设置
Table 1. Parameter setting for numerical simulation.
参数 数值 参数 数值 波长/nm 532 增益系数/(cm·GW–1) 3.8 脉宽/ns 8 折射率 1.333 光斑尺寸/mm 2.5 声子寿命/ps 200 介质池长/m 5 衰减系数/m–1 0.06 
下载: 导出CSV
-
[1] Shen Y R 1984 The Principles of Nonlinear Optics (New York: Wiley [2] Eliasson B, Senior A, Rietveld M, Phelps A D R, Cairns R A, Ronald K, Speirs D C, Trines R M G M, McCrea I, Bamford R, Mendonça J T, Bingham R 2021 Nat. Commun. 12 6209 doi: 10.1038/s41467-021-26305-9 [3] Zhao Y, Lei A, Kang N, Li F, Li X, Liu H, Lin Z, Yin H, Xu Y, Yi Y, Xu Z 2024 Phys. Rev. E 110 065206 doi: 10.1103/PhysRevE.110.065206 [4] Gonzalez-Herraez M, Song K Y, Thévenaz L 2005 Appl. Phys. Lett. 87 081113 doi: 10.1063/1.2033147 [5] Wei W, Yi L L, Jaouèn Y, Morvan M, Weisheng H 2015 Opto-Electronics and Communications Conference (OECC) Shanghai, China June 28–July 2, 2015 p1 [6] Ballmann C W, Thompson J V, Traverso A J, Meng Z, Scully M O, Yakovlev V V 2015 Sci. Rep. 5 18139 doi: 10.1038/srep18139 [7] Ballmann C W, Meng Z, Traverso A J, Scully M O, Yakovlev V V 2017 Optica 4 124 doi: 10.1364/OPTICA.4.000124 [8] Shi J, Ouyang M, Gong W, Li S, Liu D 2008 Appl. Phys. B 90 569 doi: 10.1007/s00340-007-2866-5 [9] Shi J, Xu J, Guo Y, Luo N, Li S, He X 2021 Phys. Rev. Appl 15 054024 doi: 10.1103/PhysRevApplied.15.054024 [10] Xu N, Liu Z, Zhang X, Xu Y, Luo N, Li S, Xu J, He X, Shi J 2021 Opt. Express 29 36442 doi: 10.1364/OE.443151 [11] Shi J, Xu N, Luo N, Li S, Xu J, He X 2022 Opt. Express 30 16419 doi: 10.1364/OE.457095 [12] Maier M, Rother W, Kaiser W 1967 Appl. Phys. Lett. 10 80 doi: 10.1063/1.1754860 [13] Hon D T 1981 Opt. Lett. 5 516 doi: 10.1364/OL.5.000516 [14] Eichler H J, Menzel R, Sander R, Smandek B 1992 Opt. Commun. 89 260 doi: 10.1016/0030-4018(92)90170-V [15] 徐德 2008 硕士学位论文 (杭州: 浙江大学) Xu D 2008 M. S. Thesis ( Hangzhou: Zhejiang University [16] 刘照虹 2018 博士学位论文 (哈尔滨: 哈尔滨工业大学) Liu Z H 2018 Ph. D. Dissertation (Harbin: Harbin Institute of Technology [17] 哈斯乌力吉, 吕志伟, 滕云鹏, 刘述杰, 李强, 何伟明 2007 物理学报 56 878 doi: 10.7498/aps.56.878 Hasi W L J, Lv Z W, Teng Y P, Liu S J, Li Q, He W M 2007 Acta Phys. Sin. 56 878 doi: 10.7498/aps.56.878 [18] 郭少锋, 陆启生, 李强, 程湘爱, 邓少永, 曾学文 2004 强激光与粒子束 16 1106 Guo S F, Lu Q S, Li Q, Cheng X A, Deng S Y, Zeng X W 2004 High Power Laser Part. Beams 16 1106 [19] 邓少永, 郭少锋, 陆启生, 程湘爱 2005 物理学报 54 3164 doi: 10.7498/aps.54.3164 Deng S Y, Guo S F, Lu Q S, Cheng X A 2005 Acta Phys. Sin. 54 3164 doi: 10.7498/aps.54.3164 [20] He X, Tang Y, Shi J, Liu J, Cheng W, Mo X 2012 J. Mod. Opt. 59 1410 doi: 10.1080/09500340.2012.717117 [21] 龚华平, 吕志伟, 林殿阳, 刘松江 2007 物理学报 56 5263 doi: 10.7498/aps.56.5263 Gong H P, Lü Z W, Lin D Y, Liu S J 2007 Acta Phys. Sin. 56 5263 doi: 10.7498/aps.56.5263 [22] Zhu L, Bai Z, Chen Y, Jin D, Fan R, Qi Y, Ding J, Yan B, Wang Y, Lu Z 2022 Opt. Commun 515 128205 doi: 10.1016/j.optcom.2022.128205 [23] Boyd R W, Rzaewski K, Narum P 1990 Phys. Rev. A 42 5514 doi: 10.1103/PhysRevA.42.5514 [24] Levent S 2014 Electromagnetic Modeling and Simulation (IEEE) (New York: Wiley-IEEE Press) pp407–513 [25] Schiemann S, Ubachs W, Hogervorst W 1997 IEEE J. Quantum Electron. 33 358 doi: 10.1109/3.556004 [26] Shi J, Tang Y, Wei H, Zhang L, Zhang D, Shi J, Gong W, He X, Yang K, Liu D 2012 Appl. Phys. B 108 717 doi: 10.1007/s00340-012-5142-2 [27] Feng C, Xu X, Diels J C 2017 Opt. Express 25 12421 doi: 10.1364/OE.25.012421 [28] Hirschberg J G, Byrne J D, Wouters A W, Boynton G C 1984 Appl. Opt. 23 2624 doi: 10.1364/AO.23.002624 [29] Millard R C, Seaver G 1990 Deep Sea Res. Part A 37 1909 doi: 10.1016/0198-0149(90)90086-B [30] Roquet F, Madec G, McDougall T J, Barker P M 2015 Ocean Modell. 90 29 doi: 10.1016/j.ocemod.2015.04.002 [31] Damzen M J, Vlad V, Babin V, Mocofanescu A 2003 Stimulated Brillouin Scattering: Fundamentals and Applications (London: Institute of Physics Publishing) pp1–190 -
计量
- 文章访问数: 74
- HTML全文浏览数: 74
- PDF下载数: 1
- 施引文献: 0