量子纠缠是量子信息处理^[1,2]、量子通信^[3,4]、量子计算^[5,6]、量子隐形传态^[7,8]、量子网络构建^[9,10]等过程的核心资源. 在构建量子网络的过程中, 由于每个物理系统都有其各自的优势, 往往需要将不同的物理系统(即不同的频率)关联在一起组成混合量子网络体系, 以便于它们能最大程度地发挥各自的优势. 腔光力系统中的机械振子和腔磁力系统中的磁振子都可以作为中介使得不同的物理系统之间产生关联(纠缠), 利用腔光(磁)力系统制备不同模式之间纠缠态的各种方案得到了广泛的关注和研究^[9,11–17]. 光磁力系统^[18–22]将腔光力系统和腔磁力系统结合起来, 可以同时包含磁致伸缩和辐射压力两种色散耦合机制, 使得系统具有丰富的模式和灵活的可调性, 因此, 基于光磁力系统的量子态制备方案成为了更好的选择. 2023年, 由一个微波腔、一个光学腔和一个制作成微桥结构的YIG (yttrium-iron-garnet)晶体组成的光磁力系统被提出和研究, 其中, 微桥表面附着了一个小的高反射镜垫作为光学腔的另一个腔镜, 当采用红失谐激光场驱动光学腔、蓝失谐微波场驱动磁振子模式时, 可以获得稳定的光-微波纠缠^[18]. 基于上述光磁力系统, 考虑微波腔增益的类PT对称的情况, 可以获得光微波纠缠、光磁纠缠和微波-声子纠缠的增 强^[19]. 采用双模压缩光场分别驱动两个相同的混合光磁力系统, 光模之间的纠缠通过光力耦合转移到声子之间, 再通过磁力耦合(磁致伸缩)转移到磁振子之间, 最后通过磁偶极相互作用转移到两个微波模式之间^[20]. 在混合二能级原子系综的光磁力系统中, 光力耦合产生的光力纠缠通过磁力耦合和Tavis-Cummings耦合转移至原子和磁振子之间, 从而制备原子-磁子纠缠^[21]. 因此, 混合光磁力学系统是制备涉及磁振子、光子、微波光子、声子和原子等的宏观量子态的理想平台之一.

随着量子信息技术的快速发展, 对纠缠度的要求越来越高, 因此, 量子纠缠的增强成为了一个重要的课题. 相干反馈^[23–26]作为一种增强纠缠的有效方法, 其基本原理是将携带腔内关联信息的部分输出场再次输入到系统, 从而获得关联增强的效果, 该方法在各种产生量子纠缠的系统中均得到了广泛的研究^[27–31]. 在腔光力系统中引入相干反馈回路不仅可以增强光力纠缠, 还可以扩大系统稳定区的参数范围^[27]. 双色驱动包含两个机械振子的腔光力系统, 与腔模发生光力耦合的两个机械振子之间会产生纠缠, 引入相干反馈可以显著增强两个机械振子之间的纠缠^[28]. 在上述腔光力系统中, 增加一个辅助腔, 再将辅助腔的输出反馈回系统中, 也可以显著地增强两个机械振子之间的纠缠^[29]. 利用非简并光参量放大器(NOPA)产生纠缠光束的过程中, 将双端输出的纠缠光束反馈回输入端, 可以获得纠缠的增强^[30]. 在双模压缩微波场驱动的双腔磁力系统中, 微波模之间的纠缠通过磁偶极相互作用转移到两个磁振子之间, 将两个腔磁力系统的输出微波场反馈回各自的系统中, 可以获得两个磁振子之间纠缠的显著增强^[31].

本文提出了利用相干反馈的光磁力系统获得光-微波纠缠和光磁纠缠的有效增强的方案, 并讨论分析了纠缠增强效果的参数依赖性. 研究结果显示, 相干反馈不仅能够有效地增强纠缠, 还能够扩大纠缠的参数范围, 减少纠缠受环境条件的影响. 该研究对于混合量子网络的构建及纠缠调控等方面, 提供了重要的理论依据.

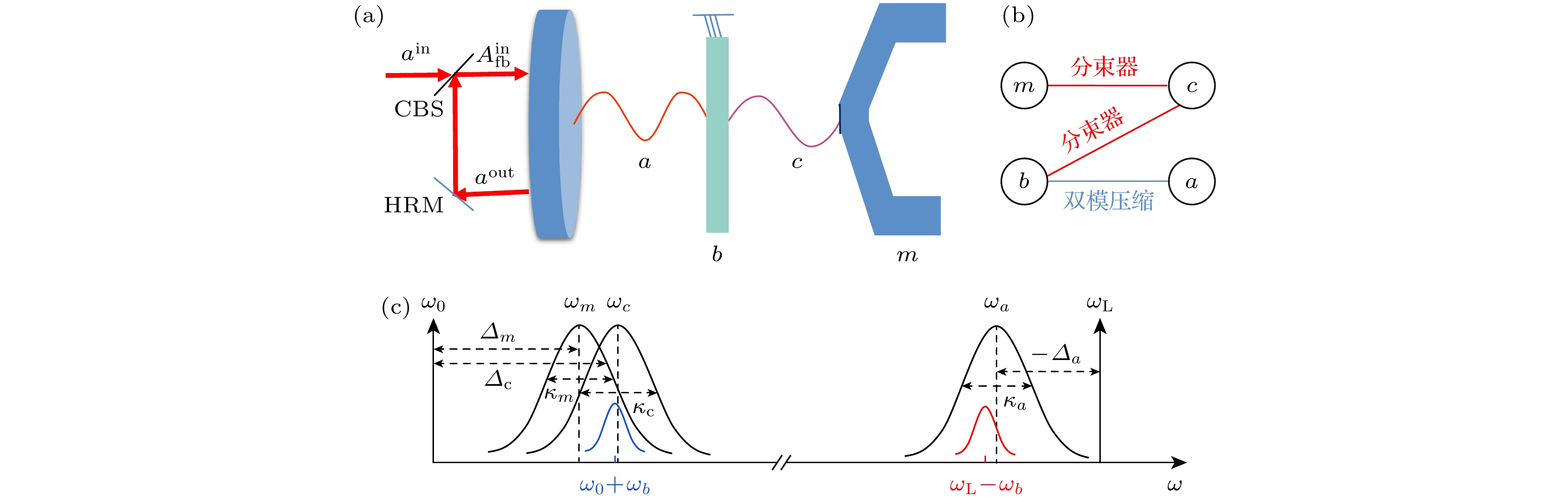
我们考虑的光磁力系统如图1(a)所示, 在一个输入输出腔镜和一个附有高反射镜的YIG桥之间插入一个薄膜, 使得薄膜与左边的腔镜构成光学腔、与右边的YIG桥构成微波腔, 腔镜的左端是一个相干反馈回路. 其中, 两侧的腔模与薄膜之间通过辐射压力发生相互作用, 右侧YIG桥中被微波驱动激发的磁振子与微波发生磁偶极相互作用, 而左侧的光学腔模与右侧的微波腔模则通过薄膜中介产生间接关联. 我们主要关注的是光磁纠缠和光-微波纠缠, 因此没有考虑YIG激发的声子, 这在调整偏置磁场方向的条件下是合理的^[32]. 磁振子m (频率为$ {\omega _m} $、衰减率为$ {\kappa _m} $)、微波模c (频率为$ {\omega _c} $、衰减率为$ {\kappa _c} $)、机械振子b (频率为$ {\omega _b} $、衰减率为$ {\gamma _b} $)、光模a (频率为$ {\omega _a} $、衰减率为$ {\kappa _a} $)之间的相互作用如图1(b)所示, 其中蓝色和红色实线分别表示所连接模式之间存在双模压缩型和分束器型相互作用. 该光磁力系统的频率关系如图1(c)所示, 微波和磁振子模式在微波驱动场的(蓝)反斯托克斯边带$ {\omega _0} + {\omega _b} $附近共振, 光模在激光驱动场的(红)斯托克斯边带$ {\omega _{\text{L}}} - {\omega _b} $附近共振, 其中$ {\omega _{\text{L}}} $和$ {\omega _0} $分别表示驱动激光场和驱动微波场的频率, $ {\varDelta _a} = {\omega _a} - {\omega _{\text{L}}} $, $ {\varDelta _c} = {\omega _c} - {\omega _0} $, $ {\varDelta _m} = {\omega _m} - {\omega _0} $分别为光学腔模、微波腔模和磁振子模式相对于各自驱动场的失谐.

图1(a)所示的光磁力系统的哈密顿量可表示为$ \left( {\hbar = 1} \right) $

第一行的四项依次表示光学腔模、微波腔模、磁振子和机械振子(薄膜)的自由哈密顿量, 其中, $ a\left( {{a^\dagger }} \right), {\text{ }}c\left( {{c^\dagger }} \right), {\text{ }}m\left( {{m^\dagger }} \right) $分别是光子、微波光子和磁振子的湮灭(产生)算符, 满足对易关系$ [o, {o^\dagger }] = 1 $, $ o = a, {\text{ }}c, {\text{ }}m $; $ q $和$ p $是机械振子的无量纲位置和动量算符, 满足对易关系$ [q, p] = i $. 第二行的前两项分别表示薄膜与左侧的光学腔模和右侧的微波腔模之间的辐射压力相互作用(耦合强度分别为$ {g_{ab}} $和$ {g_{cb}} $), 第二行的第三项表示微波与磁振子之间的磁偶极相互作用(耦合强度为$ {g_{cm}} $). 第三行的两项依次表示磁振子和光学腔的驱动项, $ \varOmega = \dfrac{{\sqrt 5 }}{4}\gamma \sqrt N {H_{\text{d}}} $是磁振子和微波驱动场耦合的拉比 频率^[9], 其中, $ \gamma $是磁振子的磁旋比, $ N $是YIG晶体中的总自旋数, $ {H_{\text{d}}} $是驱动磁场的振幅. $ E = \sqrt {2{\kappa _a}{P_{\text{L}}}/(\hbar {\omega _{\text{L}}})} $为光学腔与驱动激光的耦合强度, 其中, $ {\kappa _a} $是光学腔的衰减率, $ {P_{\text{L}}}({\omega _{\text{L}}}) $是激光场的功率(频率).

根据(1)式中的哈密顿量, 考虑噪声项和阻尼项, 可以得到系统的朗之万方程:

式中, $ {a^{{\text{in}}}}, {\text{ }}{c^{{\text{in}}}}, {\text{ }}{m^{{\text{in}}}} $分别为光学腔模、微波腔模和磁振子的输入噪声算符, 它们的噪声关联函数可以统一表示为$ \langle {{o_{{\text{in}}}}(t)o_{{\text{in}}}^\dagger ({t'})} \rangle = [ {{N_o}({\omega _o}) + 1} ]\delta (t - {t'}) $和$ \langle {o_{{\text{in}}}^\dagger ({t'}){o_{{\text{in}}}}(t)} \rangle = [ {{N_o}({\omega _o})} ]\delta (t - {t'}) $, 机械振子的噪声算符$ \xi (t) $的噪声关联可以表示为$ \langle \xi (t)\xi ({t'})\; + \xi ({t'})\xi (t) \rangle {/ } 2 = {\gamma _b}[ {2{N_b}({\omega _b} + 1)} ]\delta (t - {t'}) $. 各个模式的平均热激发数可以统一表示为$ {N_j} = [ \exp ( \hbar {\omega _j}/{k_{\text{B}}}T - 1 ) ]^{ - 1}$, $ j=o,b $, 其中T是环境温度, $ {k}_{{\mathrm{B}}} $是玻尔兹曼常数.

当光磁力系统受到强场驱动时, 可将朗之万方程中的每个物理量都写成稳态平均值加起伏的形式, 即$ o=\langle o\rangle +\delta o, {q}=\langle q\rangle +\delta q, p=\langle p\rangle +\delta p $, 可以得到线性化的朗之万方程, 其稳态解可以解出:

其中$ {\tilde \varDelta _a} = {\varDelta _a} - {g_{ab}}\left\langle q \right\rangle $, $ {\tilde \varDelta _c} = {\varDelta _c} + {g_{cb}}\left\langle q \right\rangle $是考虑了由辐射压力的机械位移引起的频移后光模和微波光模的有效失谐量. 光学腔模、微波腔模、磁振子及其输入噪声算符的正交振幅和正交相位由各自模式的产生和湮灭算符定义:

进一步可以得到各个模式的正交振幅和正交位相的起伏满足的方程, 用矩阵形式表示为

其中, $ {\boldsymbol{U}}( t ) = [ \delta {X_a}( t ), \delta {Y_a}( t ), \delta {X_c}( t ), \delta {Y_c}( t ), \delta {X_m}( t ), \delta {Y_m}( t ), \delta q( t ), \delta p( t ) ]^{\text{T}} $是各个物理量的正交分量的起伏, 由于线性化的动力学特征和量子噪声的高斯性质, 系统各模式之间的关联可以由一个$ 8 \times 8 $的协方差矩阵表征, 该协方差矩阵$ {\boldsymbol{V}} $可以通过求解Lyapunov方程来确定:

其中, 协方差矩阵的矩阵元定义为$ {V_{ij}} = {1}/{2}\times \langle {{u_i}( t ){u_j}( {{t'}} ) + {u_j}( {{t'}} ){u_i}( t )} \rangle,\; \;( {i, j = 1, 2, \cdots, 8} ) $; D为噪声关联矩阵, 由$ {D_{ij}}\delta ( {t - {t'}} )\; =\; \langle {n_i}( t ){n_j}( {{t'}} )\; + {n_j}( {{t'}} ){n_i}( t ) \rangle {/ } 2 $来定义.

我们采用Logarithmic Negativity^[33,34]来量化系统中的两体纠缠:

其中$ {\eta ^ - } = {\text{mineig}}\left| { \bigoplus _{j = 1}^2\left( { - {{\boldsymbol{\sigma}} _y}{\boldsymbol{P}}{{\boldsymbol{V}}_4}{\boldsymbol{P}}} \right)} \right| $是部分转置协方差矩阵$ {\boldsymbol{P}}{{\boldsymbol{V}}_4}{\boldsymbol{P}} $的最小辛本征值; $ {{\boldsymbol{\sigma}} _y} $为泡利矩阵; $ {{\boldsymbol{V}}_4} $是包含所求两个模式的$ 4 \times 4 $的协方差矩阵; $ {\boldsymbol{P }}= {\mathrm{diag}}\left( {1, - 1, 1, 1} \right) $是部分转置操作.

对于未加相干反馈回路的情况, $ {n}_{1}(t)= [\sqrt{2{\kappa }_{a}}{X}_{a}^{\text{in}}(t), \sqrt{2{\kappa }_{a}}{Y}_{a}^{\text{in}}(t), \sqrt{2{\kappa }_{c}}{X}_{c}^{\text{in}}(t), $ $ \sqrt{2{\kappa }_{c}}{Y}_{c}^{\text{in}}(t), \sqrt{2{\kappa }_{m}}{X}_{m}^{\text{in}}(t), \sqrt{2{\kappa }_{m}}{Y}_{m}^{\text{in}}(t), 0, \xi (t)]^{\text{T}} $是相应的噪声项, 相应的系数矩阵$ {{\boldsymbol{A}}_1} $和噪声关联矩阵$ {{\boldsymbol{D}}_1} $表示为

其中, $ {G_{ab}} = {\mathrm{i}}\sqrt 2 {g_{ab}}\langle q \rangle $, $ {G_{cb}} = {\mathrm{i}}\sqrt 2 {g_{cb}}\langle q \rangle $, 分别是有效的光力和微波-机械振子耦合强度.

由图1(a)可知, 相干反馈后的输入光场可以表示为$ A_{\rm fb}^{{\text{in}}} = r{{\mathrm{e}}^{{\mathrm{i}}\theta }}{a^{{\text{out}}}} + \mu {a^{{\text{in}}}} $, 其中$ r $为可控分束器的反射系数, $ \mu $为其透射系数, $ r $与$ \mu $的关系满足$ {r^2} + {\mu ^2} = 1 $; $ \theta $为可控分束器的反射和透射之间的相位差. 考虑输入输出关系$ {a^{{\text{out}}}} = \sqrt {2{\kappa _a}} a - {a^{{\text{in}}}} $, 相干反馈后的输入光场可以进一步表示为$ A_{\rm fb}^{{\text{in}}} = \sqrt {2{\kappa _a}} r{{\mathrm{e}}^{{\mathrm{i}}\theta }}a + a_{\rm fb}^{{\text{in}}} $, 其中, $ a_{\rm fb}^{{\text{in}}} = ( {\mu - r{{\mathrm{e}}^{{\mathrm{i}}\theta }}} ){a^{{\text{in}}}} $是加入 相干反馈回路后的输入噪声项, 其噪声关联为$ \langle {a_{\rm fb}^{{\text{in}}}(t)a_{\rm fb}^{{\text{i}}{\mathrm{n}}\dagger }({t'})} \rangle = |\mu-r\mathrm{e}^{\mathrm{i}\theta}|^2[N_a(\omega_a)+1]\delta(t-t') $以及$ \langle {a_{\rm fb}^{{\text{in}}\dagger }({t'})a_{\rm fb}^{{\text{in}}}(t)} \rangle = {| {\mu - r{{\mathrm{e}}^{{\mathrm{i}}\theta }}} |^2}{N_a}( {{\omega _a}} )\delta (t - {t'}) $. 由于输入光场发生了改变, 朗之万方程(2)中关于光学腔模a的部分变为

式中$ \varDelta _a' = {\varDelta _a} - 2{\kappa _a}r{\text{sin}}\theta $和$ \kappa _a' = {\kappa _a}\left( {1 - 2 r{\text{cos}}\theta } \right) $为加入相干反馈后光模的等效失谐和衰减率; a的稳态解变为$ {a_{\text{s}}} = {E}/({{{\mathrm{i}}\tilde \varDelta _a' + \kappa _a'}}) $, 其中$ \tilde \varDelta _a' = {\tilde \varDelta _a} - 2{\kappa _a}r\sin\theta $为考虑机械振子频移和相干反馈后光模的总有效失谐量.

对于加入相干反馈回路后, $ {n}_{2}\left(t\right)\;=\;\Big[\sqrt{2{\kappa }_{a}{\left|\mu -r{{\mathrm{e}}}^{{\mathrm{i}}\theta }\right|}^{2}}{X}_{a}^{\text{in}}\left(t\right), \;\sqrt{2{\kappa }_{a}{\left|\mu -r{{\mathrm{e}}}^{{\mathrm{i}}\theta }\right|}^{2}}{Y}_{a}^{\rm in} (t), \sqrt{2{\kappa }_{c}}{X}_{c}^{\text{in}}\left(t\right), \sqrt{2{\kappa }_{c}}{X}_{c}^{\text{in}} (t), {\sqrt{2{\kappa }_{m}}{X}_{m}^{\text{in}}(t), \sqrt{2{\kappa }_{m}}{Y}_{m}^{\text{in}}(t), 0, \xi (t) \Big]}^{\text{T}} $是相应的噪声项, 相应的系数矩阵$ {{\boldsymbol{A}}_2} $和噪声关联矩阵$ {{\boldsymbol{D}}_2} $ 表示为

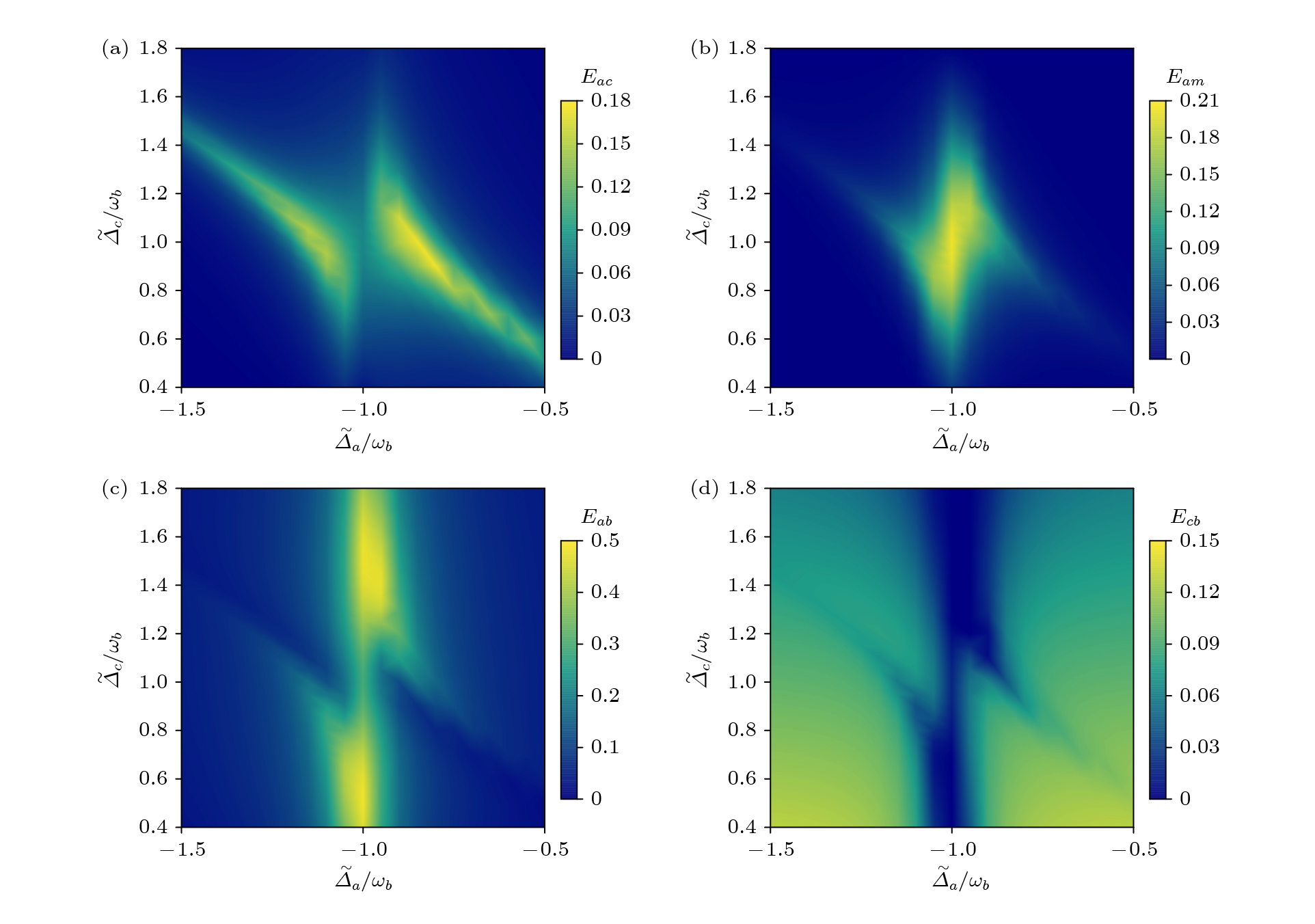
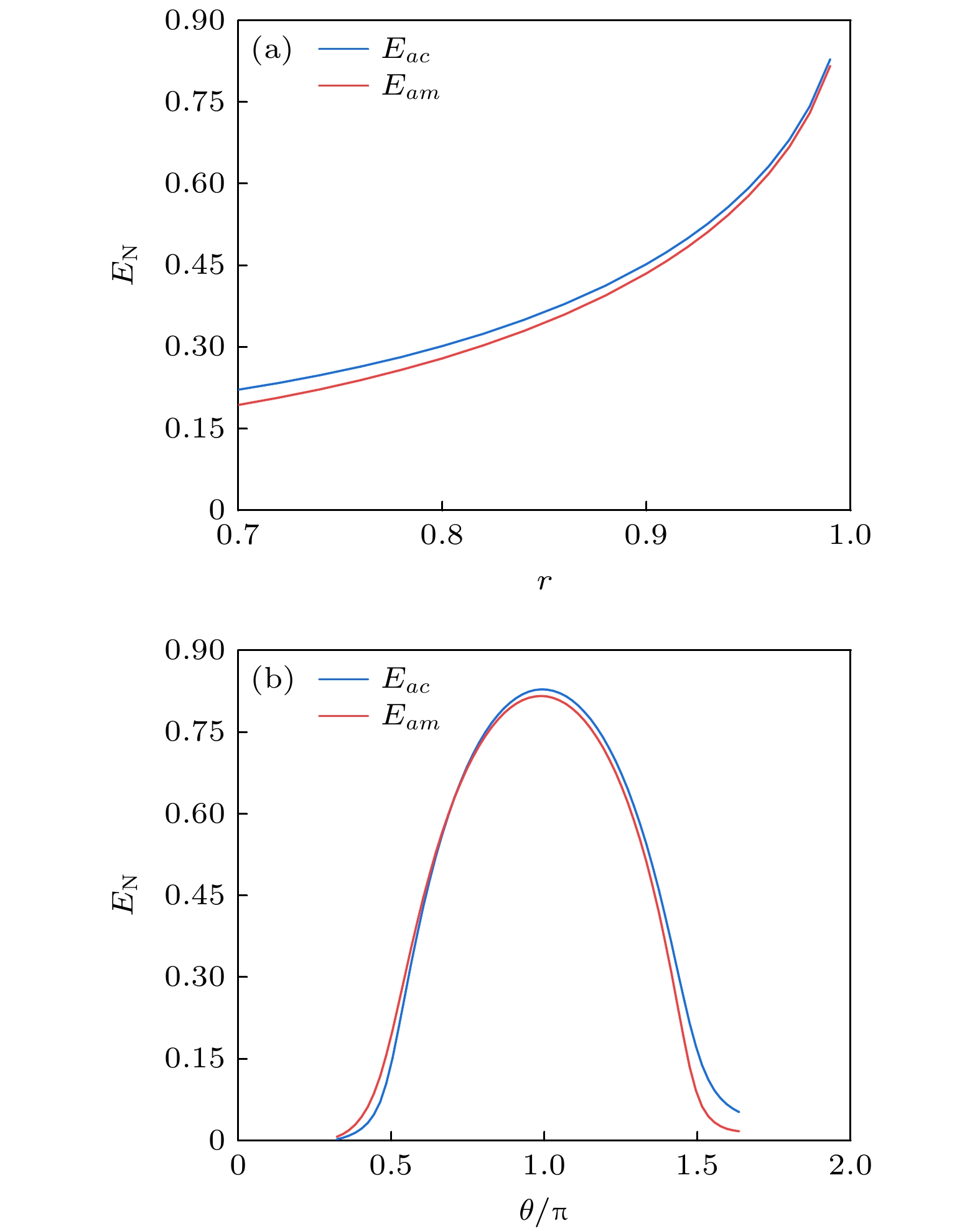
未加反馈回路时, 各个模式之间的纠缠随有效失谐$ {\tilde \varDelta _a} $与$ {\tilde \varDelta _c} $的变化如图2所示. 选用的参数为: $ {\varDelta _m} = {\omega _b} $, $ {\omega _m} = {\omega _c} = 2\pi \times 10{\text{ }}{\mathrm{GHz}} $, $ {\omega _b} = 2\pi \times 40{\text{ MHz}} $, $ {\lambda _a} = 1064{\text{ nm}} $, $ {\kappa _a} = {\kappa _c} = {\kappa _m} = 2\pi \times 1{\text{ MHz}} $, $ {g_{cm}} = 2\pi \times 4{\text{ MHz}} $, $ {G_{cb}} = $$ 2{\text{π}} \times 8{\text{ MHz}} $, $ {G_{ab}} = 2\pi \times 1{\text{ MHz}} $, $ T = 0.01{\text{ K}} $. 从图2可以看出: 光力耦合在蓝失谐条件下产生的纠缠E_ab, 通过红失谐条件下微波腔模c和机械振子b之间的分束器相互作用(态转移)机制转移到了光模a与微波模c之间, 如图2(a)所示; 进一步通过磁振子m与微波模c之间的分束器(磁偶极)相互作用转移到了光模a和磁振子m之间, 如图2(b)所示, 在$ {\tilde \varDelta _a} = - {\omega _b} $(斯托克斯边带)附近、$ {\tilde \varDelta _c} = {\omega _b} $(反斯托克斯边带)附近时, E_ab主要转移到E_am中; 在$ {\tilde \varDelta _c} = {\omega _b} $附近而$ {\tilde \varDelta _a} $离开$ - {\omega _b} $时, E_ab主要转移到E_ac中; 在$ {\tilde \varDelta _a} = - {\omega _b} $附近而$ {\tilde \varDelta _c} $离开$ {\omega _b} $时, E_ab可以很好地保留; E_cb对应的是纠缠转移, 与保留的纠缠E_ab的强弱正好相反. 为了最大程度地把E_ab转移到E_ac和E_am中, 取$ {\tilde \varDelta _a} = - 0.9{\omega _b} $, $ {\tilde \varDelta _c} = {\omega _b} $, 其他参数与图2相同, 可以得到加入相干反馈回路后的光-微波纠缠和光磁纠缠随反射系数$ r $和相位$ \theta $的变化, 如图3所示.

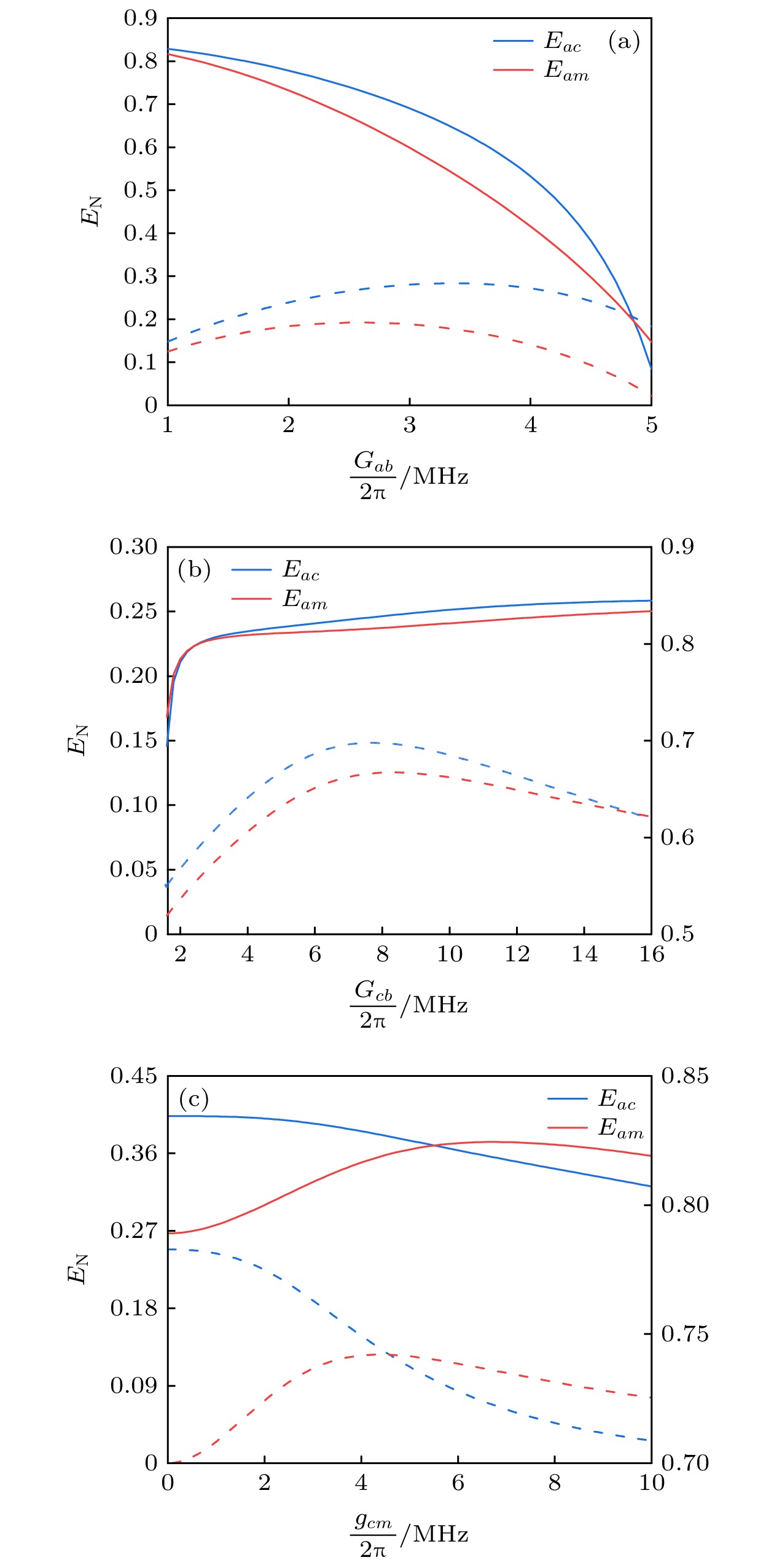
从图3可以看出, 当可控分束器的反射率从50% ($ r = 0.71 $)增加至98% ($ r = 0.99 $)时, 由于输出光场的利用率越来越高, E_ac和E_am均能得到显著提升; 此外, E_ac和E_am对于相位的变化也非常敏感, 在$ \theta = {\text{π}} $时均可达到纠缠最大. 加入相干反馈回路后, E_ac和E_am随反射系数$ r $和相位$ \theta $的变化趋势基本一致是因为纠缠的来源是一样的, 都是来自于光模和声子之间的纠缠, 考虑实验可行的条件, 选择$ r=0.99, \theta =\pi $, 可以得到最优的相干反馈对纠缠的提升效果. 为了更全面地比较加入相干反馈前后的光-微波纠缠E_ac和光磁纠缠E_am, 我们需要分析它们随不同参数的变化关系.

E_ac和E_am随各个耦合强度的变化如图4所示, 虚线和实线分别表示加入反馈前和加入反馈后的纠缠情况. 从图4(a)可以看出, 随着光力耦合强度G_ab的增大, 未加反馈时的E_ac和E_am呈现先增大后减小的趋势. 这是因为产生的光力纠缠E_ab逐渐增加, 转移到E_ac和E_am的纠缠也增加, 但是当G_ab增大到一定程度时, 声子模b主要与光模a发生相互作用, 与微波模c的相互作用减弱, 导致纠缠转移的减少. 从图4(b)可以看出, 随着微波-机械振子的耦合强度G_cb的增加, 未加反馈时的E_ac和E_am也表现出先增大后减小的趋势. 这是因为纠缠转移能力的增加使得转移到E_ac和E_am的纠缠增加, 但是增加到一定程度, 声子模b主要与微波模c发生相互作用, 与光模a的相互作用减弱, 导致产生的纠缠减少. 从图4(c)可以看出, 随着微波-磁子耦合强度g_cm增大时, 未加反馈时的E_ac逐渐减小, E_am先增加后减小. 这是因为E_ac逐渐转移到E_am. 从图4可看出, 加入相干反馈后, E_ac和E_am都得到了大幅度的提升, 只是不同的耦合强度对应的提升幅度不同.

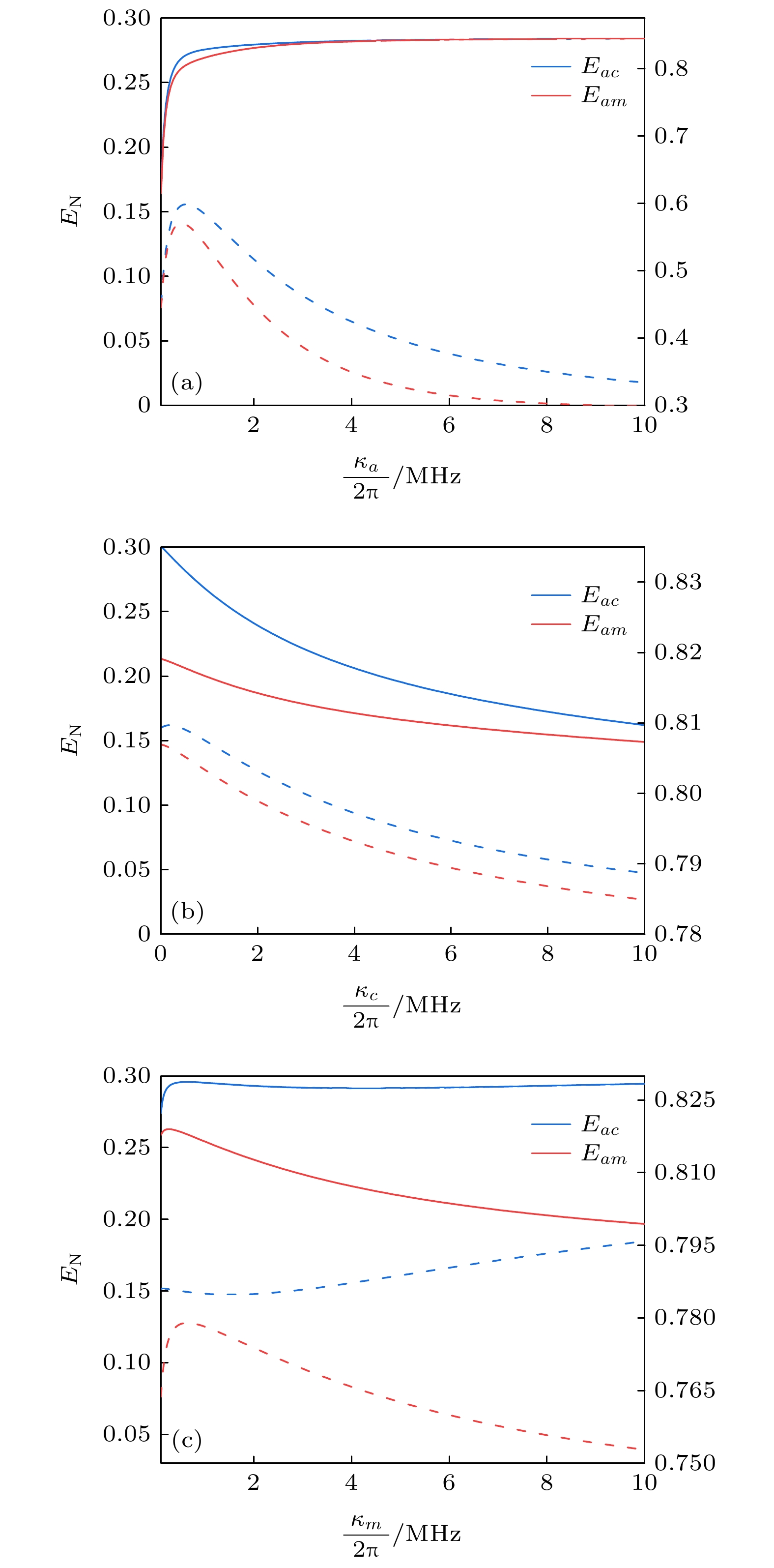
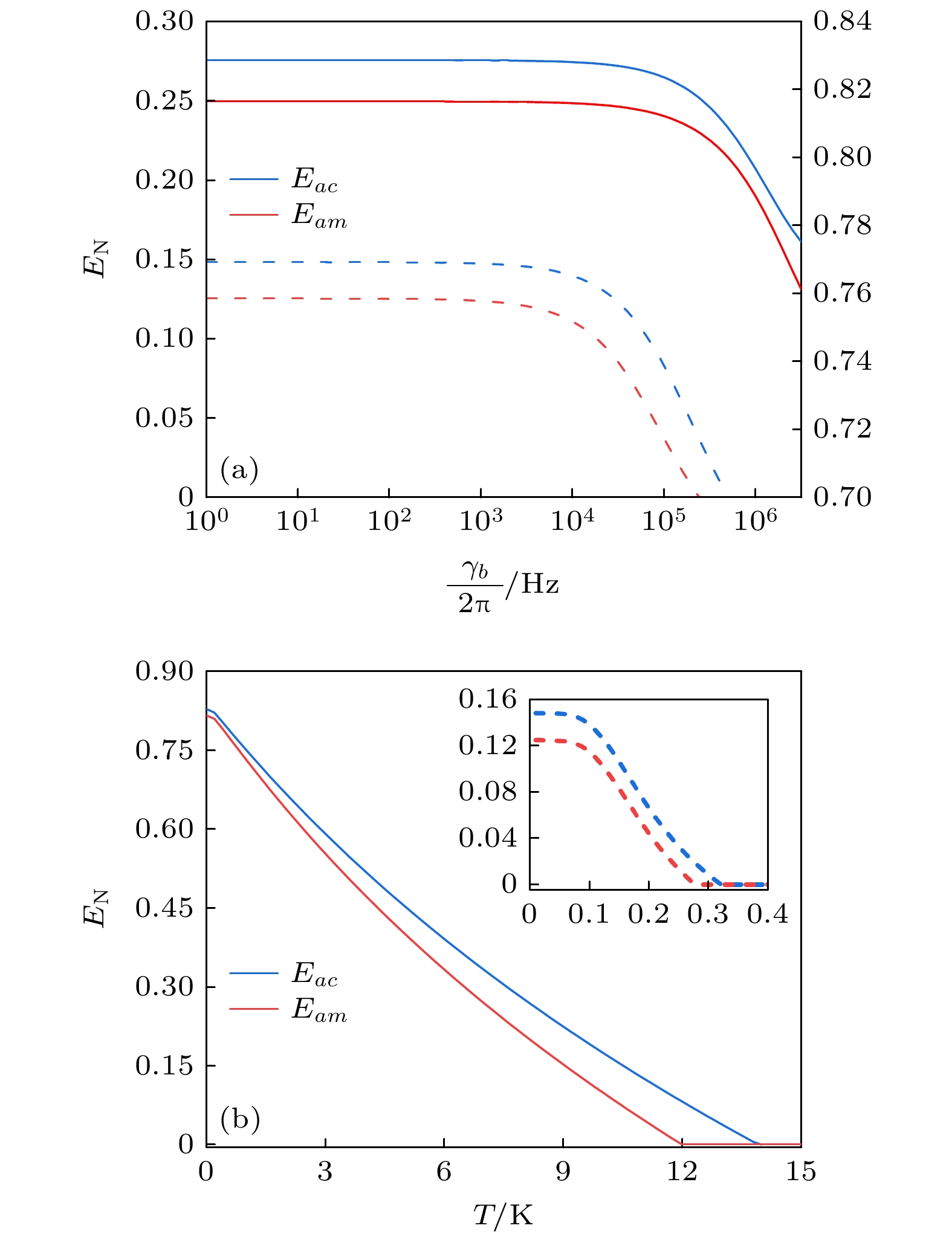
E_ac和E_am随各个衰减率的变化如图5所示, 虚线和实线分别表示加入反馈前和加入反馈后的纠缠情况. 从图5(a)可以看出, 随着$ {\kappa _a} $的增加, 未加反馈时的E_ac和E_am会短暂增加然后逐渐减小, 这是因为$ {\kappa _a} $较小时, 耗散耦合是有利于纠缠产生的, 只是衰减率较大时, 耗散引起的退相干会占据主导地位, 从而导致纠缠减小; 但是, 加入反馈后, 随着$ {\kappa _a} $的增加, E_ac和E_am等不仅能够显著地提升, 而且能够有效地保持这种纠缠增强效果, 这是因为考虑反馈后的等效光模衰减率对纠缠的影响发生了变化. 从图5(b)可以看出, 随着$ {\kappa _c} $的增加, 加入反馈前后的E_ac和E_am均逐渐减小, 且变化趋势相同, 加入反馈后的纠缠也有显著提升. 从图5(c)可以看出, 由于$ {\kappa _m} $的增加对E_ac到E_am的纠缠转移所起的作用由积极变为消极, 未加反馈时的E_am先短暂增加后逐渐减小, E_ac先轻微减小后逐渐增加, 加入反馈后, 纠缠显著增强, 且变化趋势相同.

E_ac和E_am随机械振子的衰减率和温度的变化如图6所示, 虚线和实线分别表示加入反馈前和加入反馈后的纠缠情况. 从图6可以看出, 相干反馈的引入不仅使纠缠显著增强而且对机械振子的衰减率和温度的变化能在很大程度上免疫, 尤其是光磁纠缠E_am可以在12 K以下很好的保持. 这说明相干反馈的引入不仅可以有效地提升纠缠, 而且可以有效地提升纠缠抗环境干扰的能力, 使得系统能够在更广泛的参数范围内稳定运行. 需要说明的是: 本文所有的结果都是在系统处于稳定时得到的, 由系数矩阵$ {A_k}\left( {k = 1, {\text{ }}2} \right) $的特征值的实部为负数来保证的.

我们提出了一种利用相干反馈的光磁力系统增强光-微波纠缠和光磁纠缠的方案, 详细地分析了纠缠产生和纠缠转移的物理机制和条件, 得到了纠缠优化的参数条件, 并在此基础上详细地比较了加入相干反馈前后的光-微波纠缠和光磁纠缠随不同参数的变化关系. 研究结果表明, 加入相干反馈后, 在较宽的参数范围内, 光-微波纠缠和光磁纠缠均可获得较大幅度的提升, 并且这种提升效果可以很好的保持. 我们的研究结果不仅为实现混合量子网络提供了有力的理论支持, 还为光学控制、设计、检测和传输磁振子状态提供了更多的可能性, 便于未来能够更加灵活地操控和利用磁振子的量子特性.