首页
登录
注册
-
随着压电超声换能器应用领域的不断拓展, 对其性能要求也越来越高, 尤其是在超声加工、工业液体处理、超声清洗等大功率应用领域, 不仅要求换能器的功率容量大, 还需要其具有较高的工作效率. 在使用单个压电超声换能器的应用场景中, 一般通过增大换能器的辐射面积来提高其功率容量, 但辐射面积的增大, 会使换能器因泊松效应产生严重的耦合振动, 对主辐射方向上的工作效率产生不利的影响[1–3]. 大功率压电超声换能器的性能优化研究本质上是一个复杂的系统优化问题, 因为其性能指标之间, 常常相互制约. 因此, 如何在提高换能器辐射面积情况下, 有效降低耦合振动对换能器其他性能指标的不利影响, 是大功率压电超声换能器研究中亟需解决的问题[4–6].
研究发现, 在大功率换能器中设计合理的声学表面结构[7–11]和缺陷结构[12–16], 不仅可以有效抑制杂散振动模态, 提高设备的工作精度, 还可以大幅提高换能器辐射面的位移振幅, 提高工作效率, 保证设备在大功率使用环境中的性能. 基于此, 本文提出了表面与缺陷调控型压电超声换能器的研究, 旨在建立大功率压电超声换能器设备优化设计的新理论和新方法, 提高设备的设计效率和成功率, 推动压电超声换能器的进一步实际应用.
-
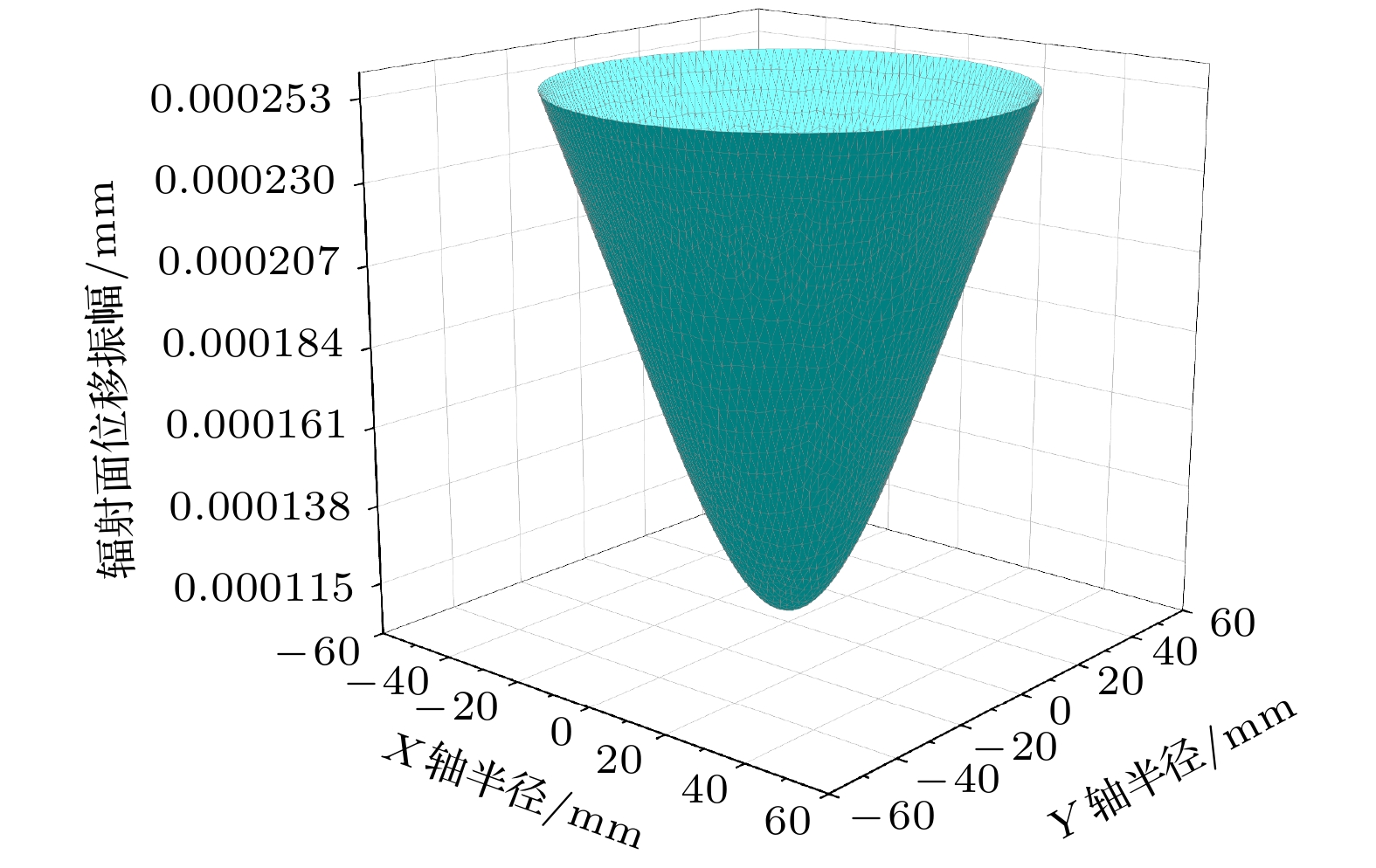
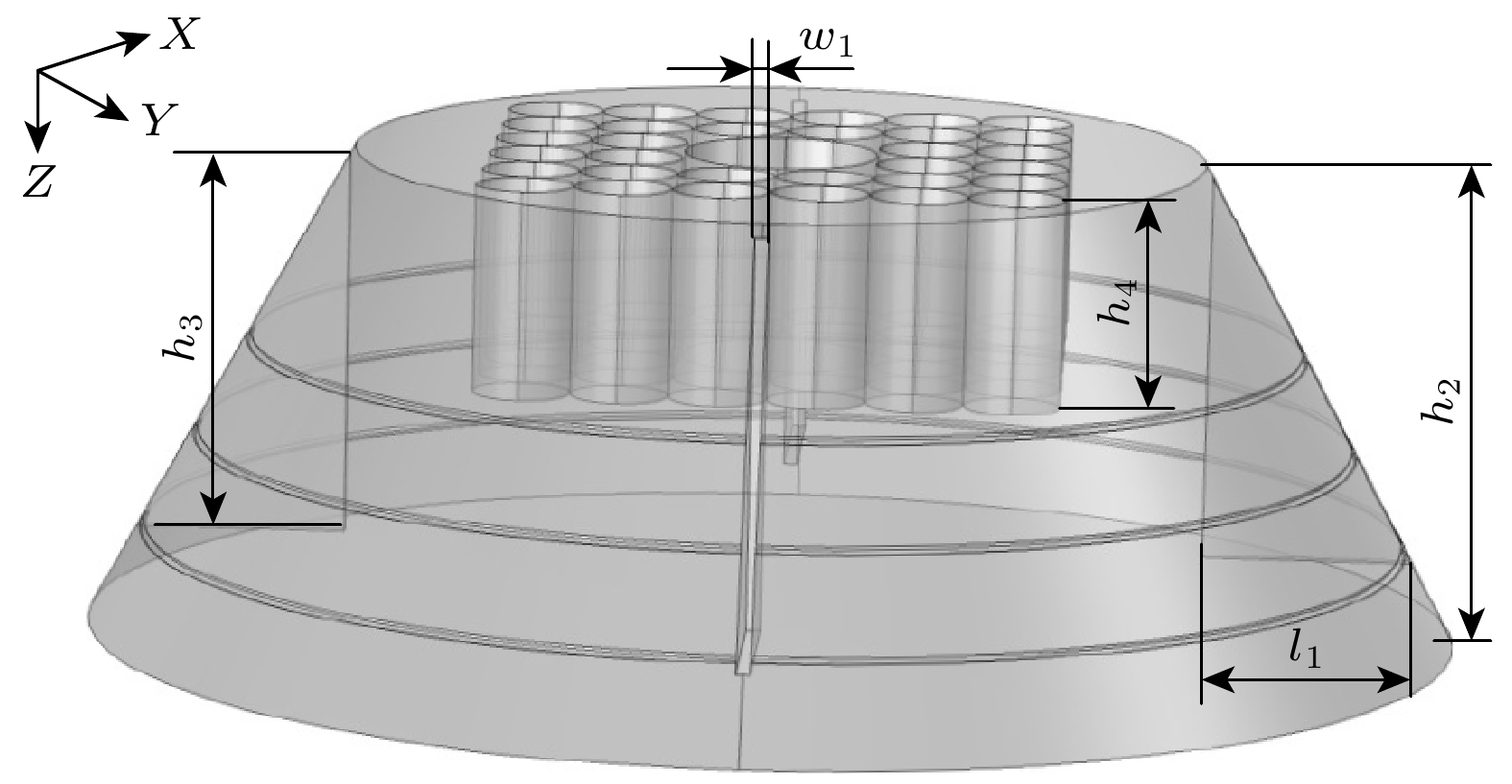
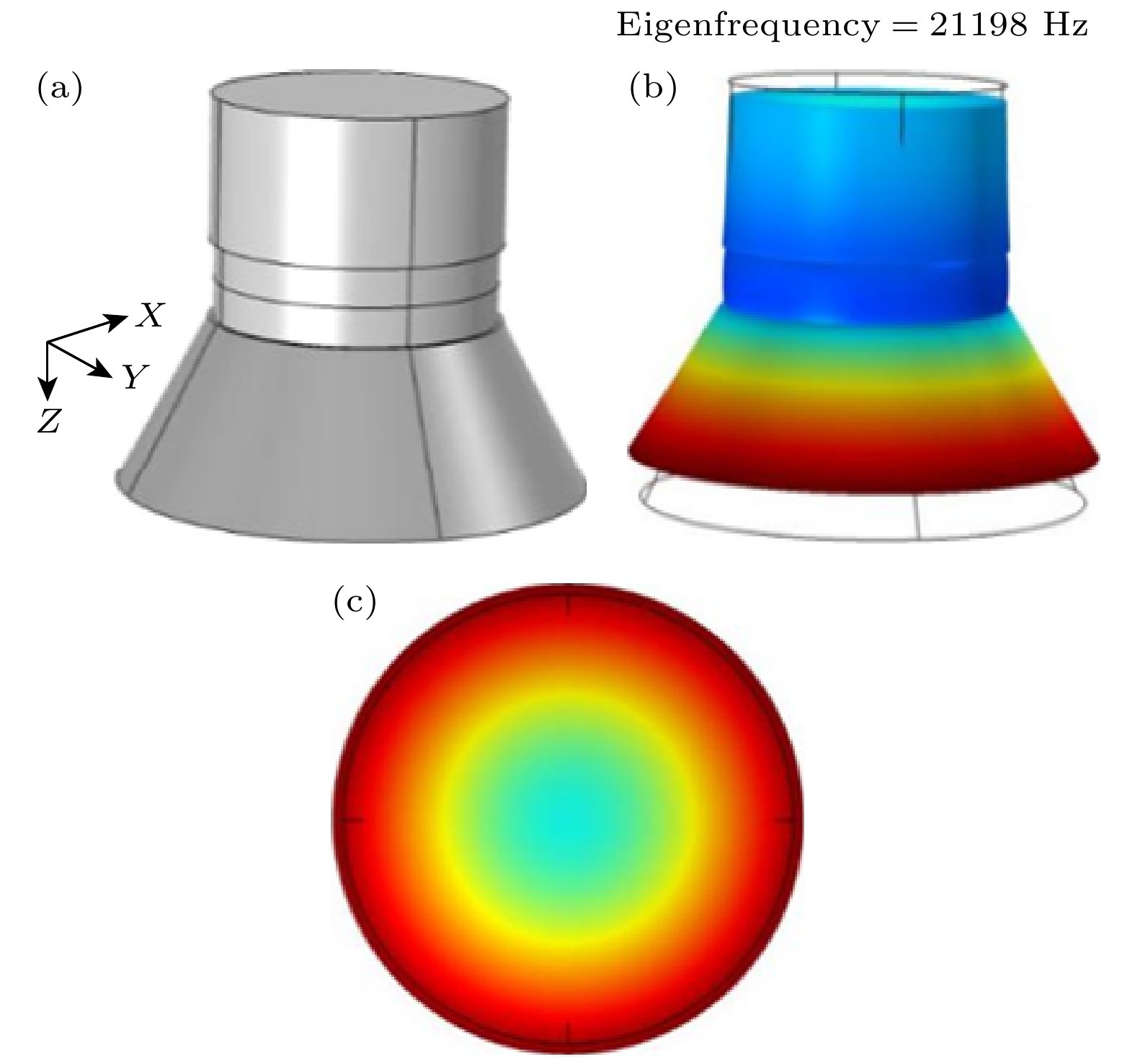
为了验证优化方法的适应性和可行性, 本文选取复杂的大尺寸纵振夹心式压电超声换能器为例进行研究. 该换能器的工作频率为21 kHz, 超声振动能量沿图1中的Z轴(纵向)进行传播, 换能器的材料和几何结构参数如表1所列, 换能器辐射面的位移振幅如图2所示.
从图2可以看出, 耦合振动导致压电超声换 能器辐射面输出的位移振幅变化范围为0.1040× 10–3—0.2550 × 10–3 mm. 根据
可求得换能器的辐射面位移振幅平均值Aave = 0.1963×10–3 mm、位移振幅分布均匀度Du =23.04%. 即换能器的辐射面位移振幅不仅较小, 而且分布非常不均匀, 中心位移振幅较小, 边缘位移振幅较大.
为了改善换能器的性能, 研究团队曾利用缺陷结构[17]、管柱结构[18]对换能器进行优化(换能器的材料和几何结构尺寸均保持不变), 研究成果均能在一定程度上对耦合振动进行控制, 提高换能器设备的工作效率(提高换能器辐射面的位移振幅)和工作精度(提高换能器辐射面的位移振幅分布均匀度). 但因为换能器的尺寸较大, 换能器辐射面输出的位移振幅仍不尽人意, 且优化设计方案基本采用经验试错法[19], 设计的主观性强、可预见性低、设计周期长和成功率低. 为了更好地控制耦合振动, 进一步提高换能器辐射面的位移振幅, 提高设计效率和成功率, 本研究将可以降低能量损耗、提高超声能量传输效率的声表面结构和缺陷结构进行结合, 并利用数据分析工具, 通过“基于声子晶体声表面结构和缺陷结构对大功率超声换能器设备进行理性设计——高效的仿真和实验——数据分析技术”的深度融合, 建立大功率超声换能器设备优化设计的新方法, 提出了一种更加高效的换能器设计模式.
-
在完美的周期或准周期结构中引入缺陷会导致禁带中出现窄带宽的透射峰, 引发局域化效应[20]. 而声学表面结构是通过在材料表面加工的周期性孔、凹槽或凸起结构来实现对弹性波的调控, 激发能量局域化现象[21,22]. 研究者曾利用刚性板上雕刻的周期槽阵列来激发结构调制的声表面波, 实现了声准直和声学反常透射现象[23,24]. 通过设计合理的缺陷和声表面结构, 可以激发声波的强局域化效应, 且这种局域化效应可通过改变缺陷和声学表面的几何结构参数来有效地操纵, 为声波控制工程中的各种功能器件提供思路. 因此, 本文在换能器中引入缺陷结构和声学表面结构, 以此构造具有单向高透射率、低损耗、高能量传输效率、高品质因数的大功率压电超声换能器.
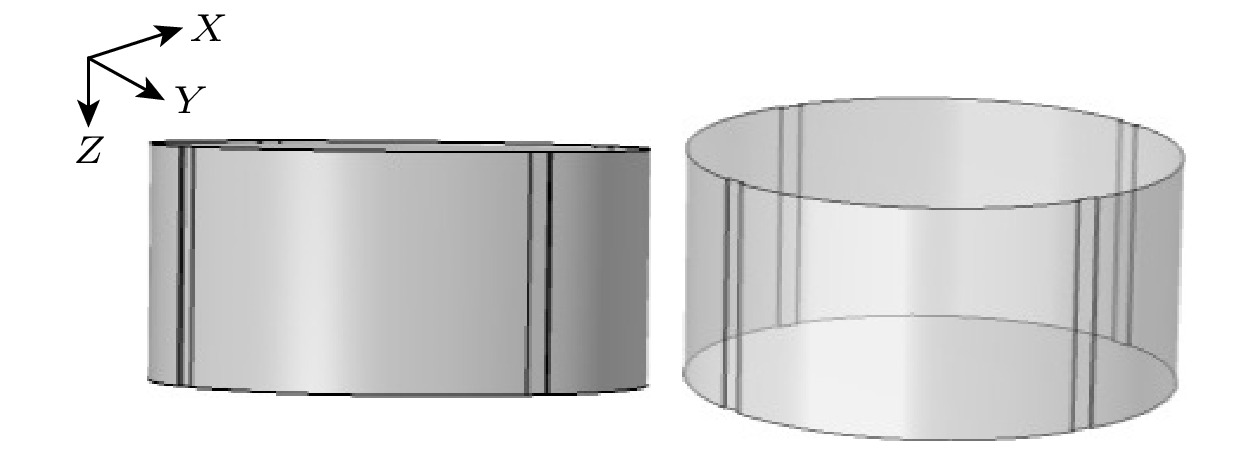
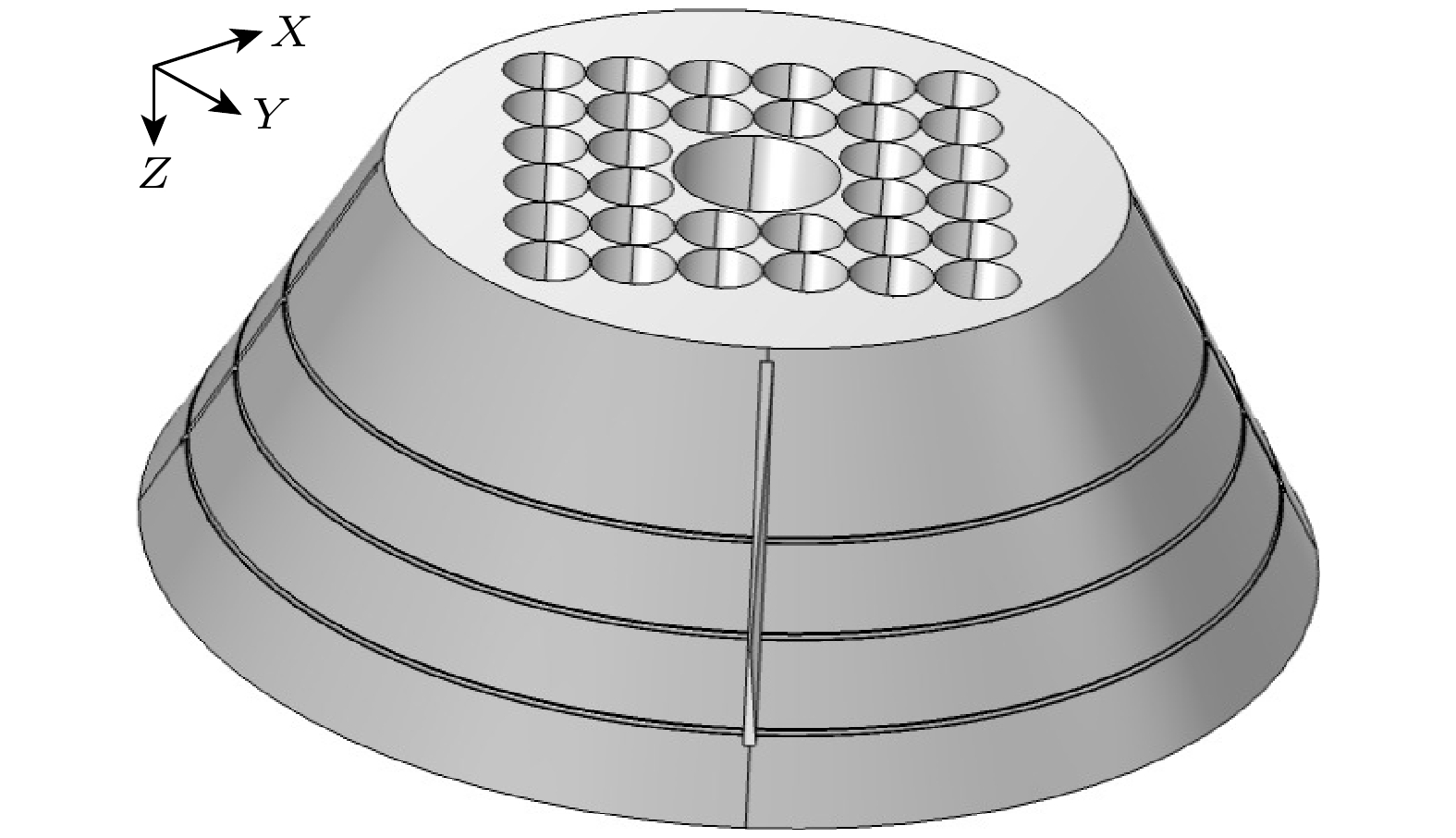
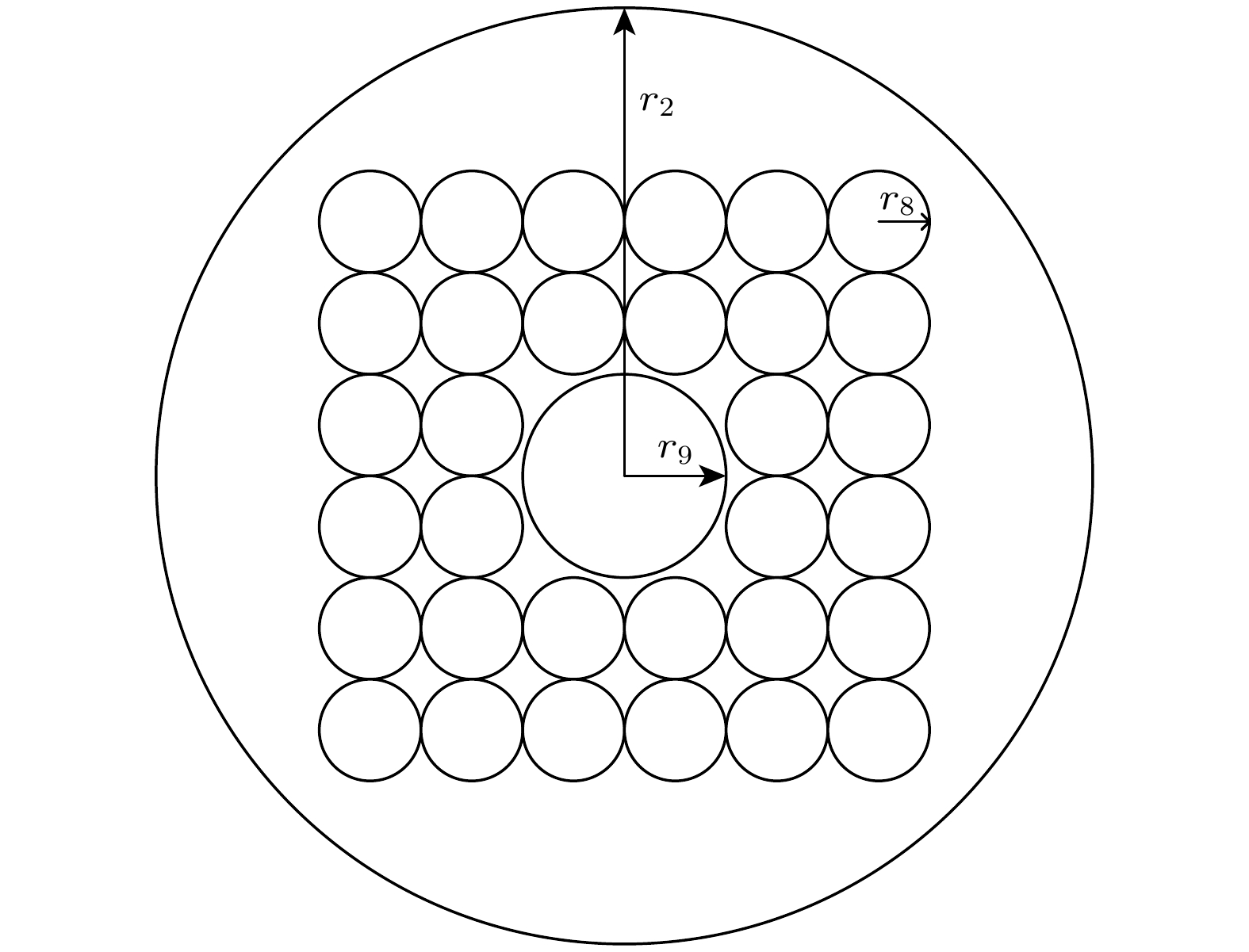
在压电超声换能器的后盖板(半径为r1, 高度为h1)表面上, 加工4个高度为h、长度为l、厚度为w的凹槽, 在换能器的前盖板(上底面半径为r2、下底面半径为r3、高度为h2)的表面上, 加工3个外半径为r4, r5, r6, 内半径为r7的环状体槽. 同时, 在前盖板上, 加工4个长度为l1、宽度为w1、高度为h3楔形体孔; 6行6列与Z轴平行的、半径为r8、高度为h4的空气圆柱体孔, 圆柱体孔按正方晶格排列在6063-T83铝中, 并将中心4个空气圆柱体合并成一个半径为r9、高度为h4的空气圆柱体孔, 形成空气-铝二维正方晶格近周期声子晶体点缺陷结构. 后盖板的结构如图3所示, 前盖板的结构如图4所示, 优化后的前盖板的俯视图和侧视图分别如图5和图6所示.
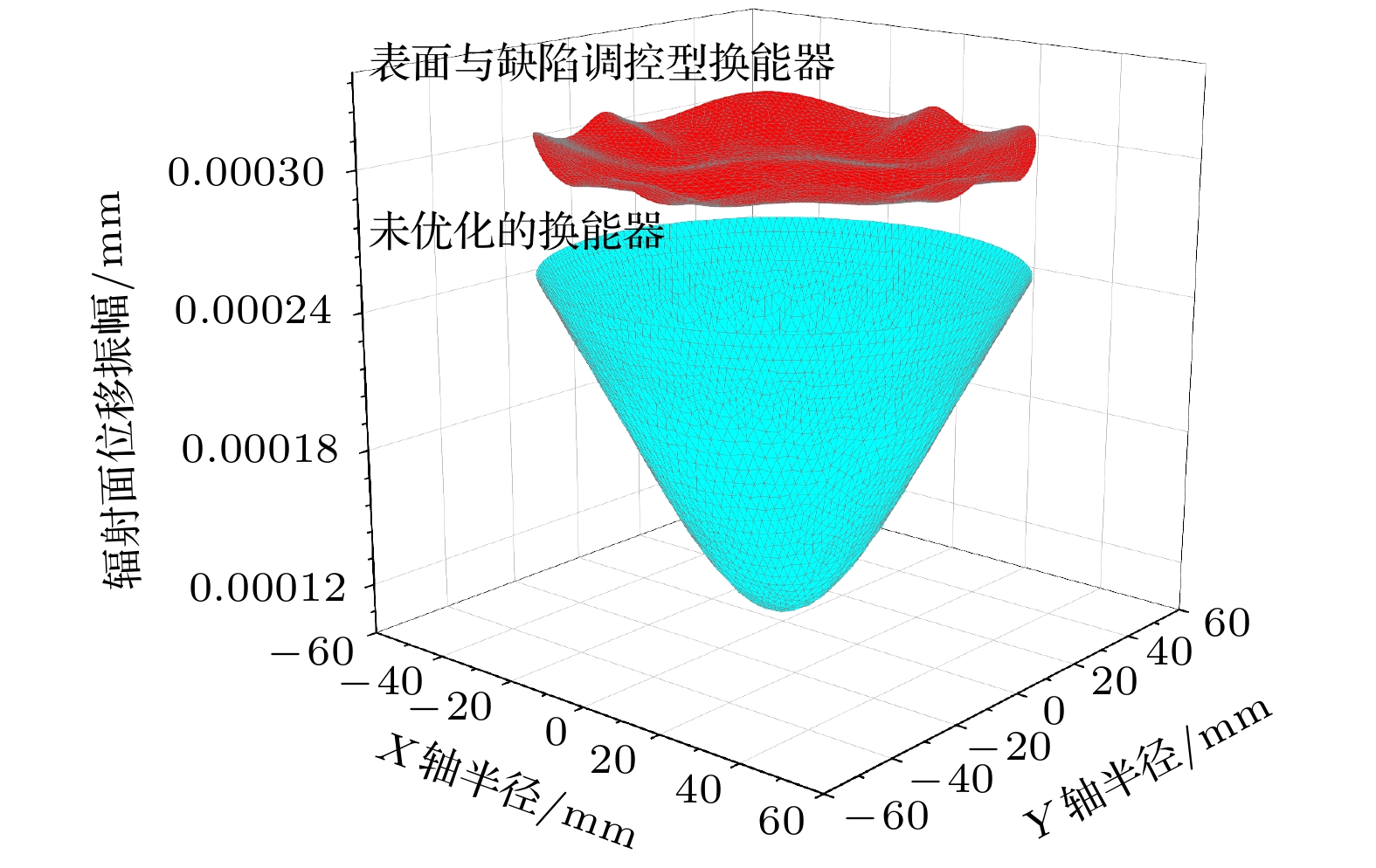
表面与缺陷调控型大功率压电超声换能器的材料和几何结构参数与图1所示的模型相同, 如表1所列. 设后盖板上加工的凹槽的长度l = 3 mm、厚度w = 0.5 mm, 高度h = 30 mm. 设前盖板上加工的3个环状体槽的外半径(从上至下)r4 = 28.6 mm, r5 = 42.4 mm, r6 = 46.2 mm, 内半径r7 = 0.3 mm. 设前盖板上加工的4个楔形体孔的长度l1 = 15.24 mm、宽度w1 = 1 mm、高度h3 = 28 mm; 6行6列正常散射体空气圆柱孔的半径r8 = 3.5 mm、高度h4 = 15 mm, 缺陷散射体空气圆柱孔的半径r9 = 7 mm. 在COMSOL Multiphysics中建立表面与缺陷调控型大功率压电超声换能器的模型(如图7(a)所示), 并计算其振动特性, 结果如图7(b)所示, 计算表面与缺陷调控型大功率压电超声换能器辐射面的位移振幅, 并与未优化的换能器进行比较, 结果如图8所示.
从图8可以看出, 相比于未优化的换能器, 表面与缺陷调控型大功率压电超声换能器辐射面位移振幅以及振幅分布均匀度均得到了大幅提升. 根据(1)式和(2)式, 可求得表面与缺陷调控型换能器辐射面位移振幅平均值Aave = 0.3015 × 10–3 mm、位移振幅分布均匀度Du = 93.56%. 即
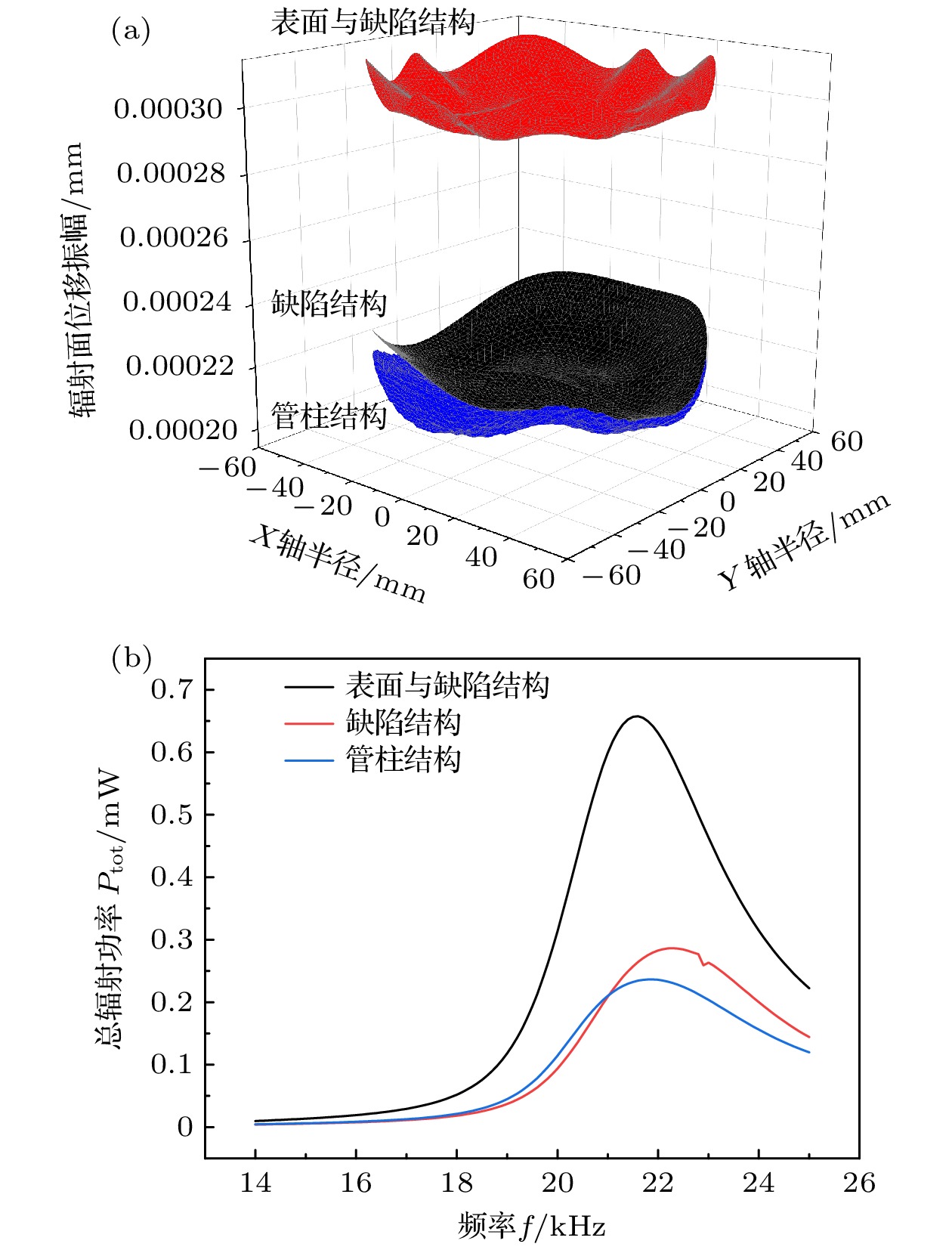
$ {({A}_{\text{ave}}{)}_{表面与缺陷}}/{({A}_{\text{ave}}{)}_{未优化}} = {0.3015}/{0.1963}=1.536 $ ,$ {({D}_{\text{u}}{)}_{表面与缺陷}}/{({D}_{\text{u}}{)}_{未优化}} = {93.56{\text{%}} }/{23.04{\text{%}}}=4.061 $ .为了更加清晰地看到表面与缺陷调控型换能器在性能上的优越性, 将利用缺陷结构、管柱结构、表面与缺陷结构优化的换能器的辐射面位移振幅、振幅分布均匀度、总辐射功率(水域)进行对比, 结果如图9(a), (b)和表2所示.
-
目前, 市场对压电超声换能器设备的需求越来越多样化, 但国内大多厂商难以提供多功能和灵活性[25]. 通过设计合理的声表面和缺陷结构的材料、几何结构、位置等属性, 可以对换能器的性能属性进行灵活的调控, 但灵活设计也带来了一定的弊端, 过多的设计参数势必会增加设计的复杂度. 若仍然沿用传统的经验试错法, 会成倍的增加设计周期, 大幅降低设计效率. 为了提高设计效率, 从实验室、仿真软件、设备厂商、客户需求分析等渠道挖掘压电超声换能器相关的数据, 经过清洗、集成、转换和消减后, 利用数据分析软件分析声学表面结构(表面凹槽、环状体槽等)和缺陷结构的配置对换能器设备频率特性和工作效率等性能影响的原因和规律, 建立压电超声换能器性能的预测模型, 实现设备的智能设计[26].
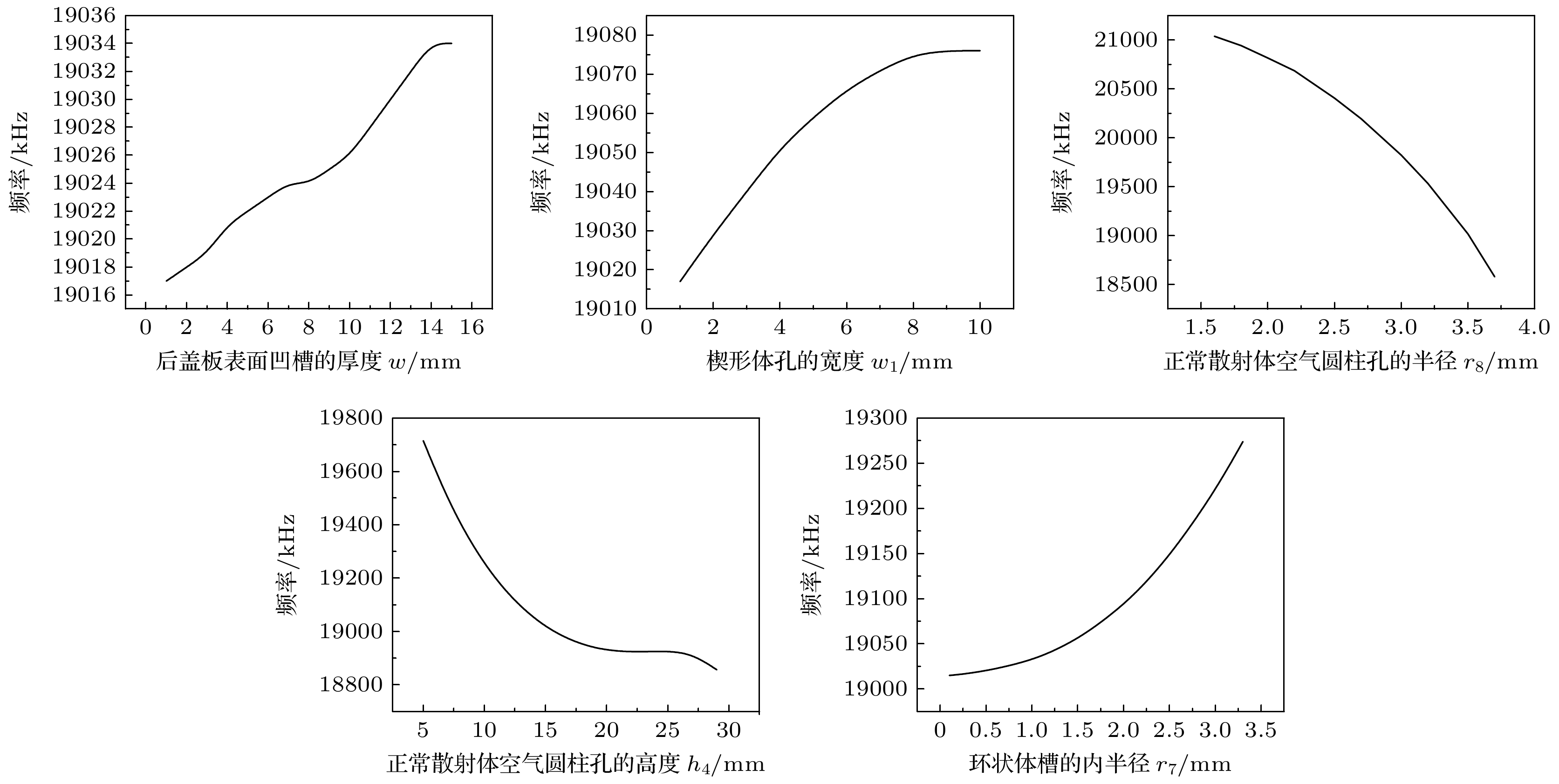
表面与缺陷调控型大功率压电超声换能器中, 表面凹槽、楔形体孔和空气圆柱体孔等均会对换能器的性能产生影响. 因此, 本文使用SPSS软件分析了后盖板表面凹槽的厚度w, 楔形体孔的宽度w1, 正常散射体空气圆柱孔的半径r8、高度h4, 环状体槽的内半径r7对换能器纵向谐振频率f、辐射面位移振幅平均值Aave(mm)、辐射面位移振幅分布均匀度Du的影响规律, 建立表面与缺陷调控型大功率压电超声换能器的性能预测模型:
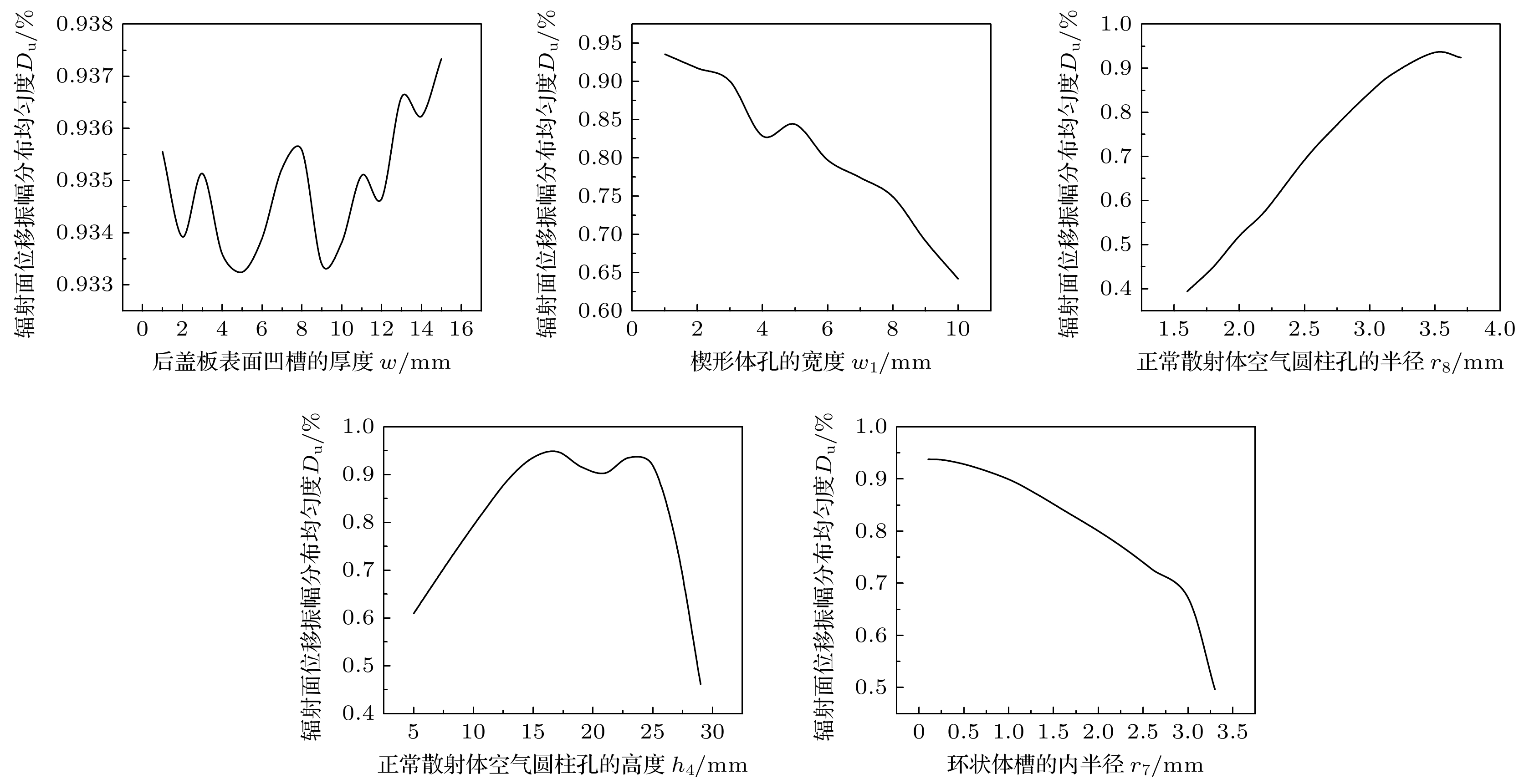
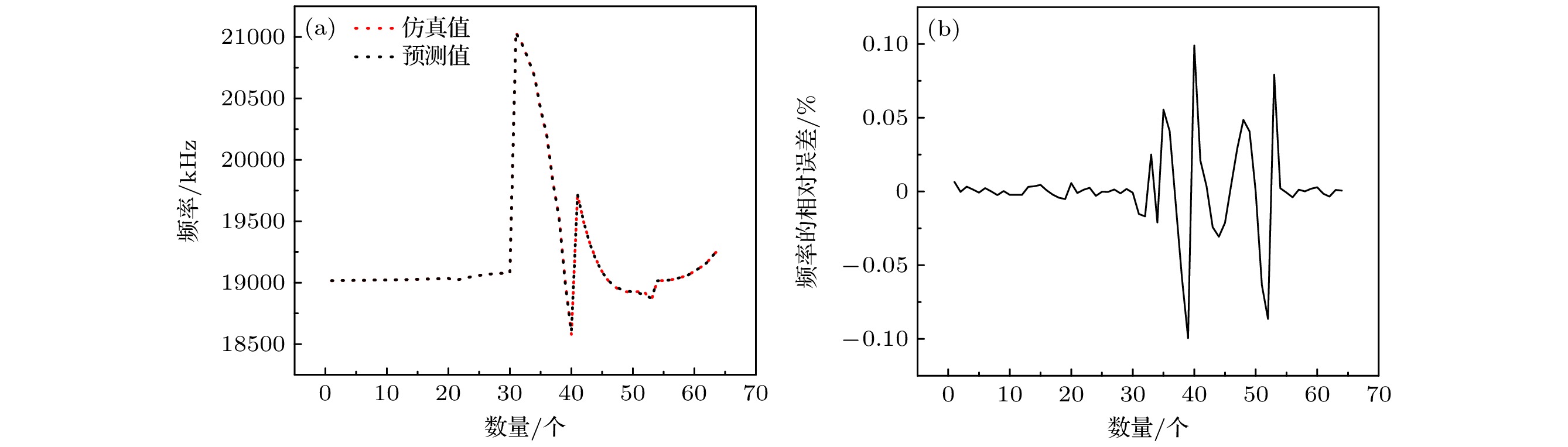
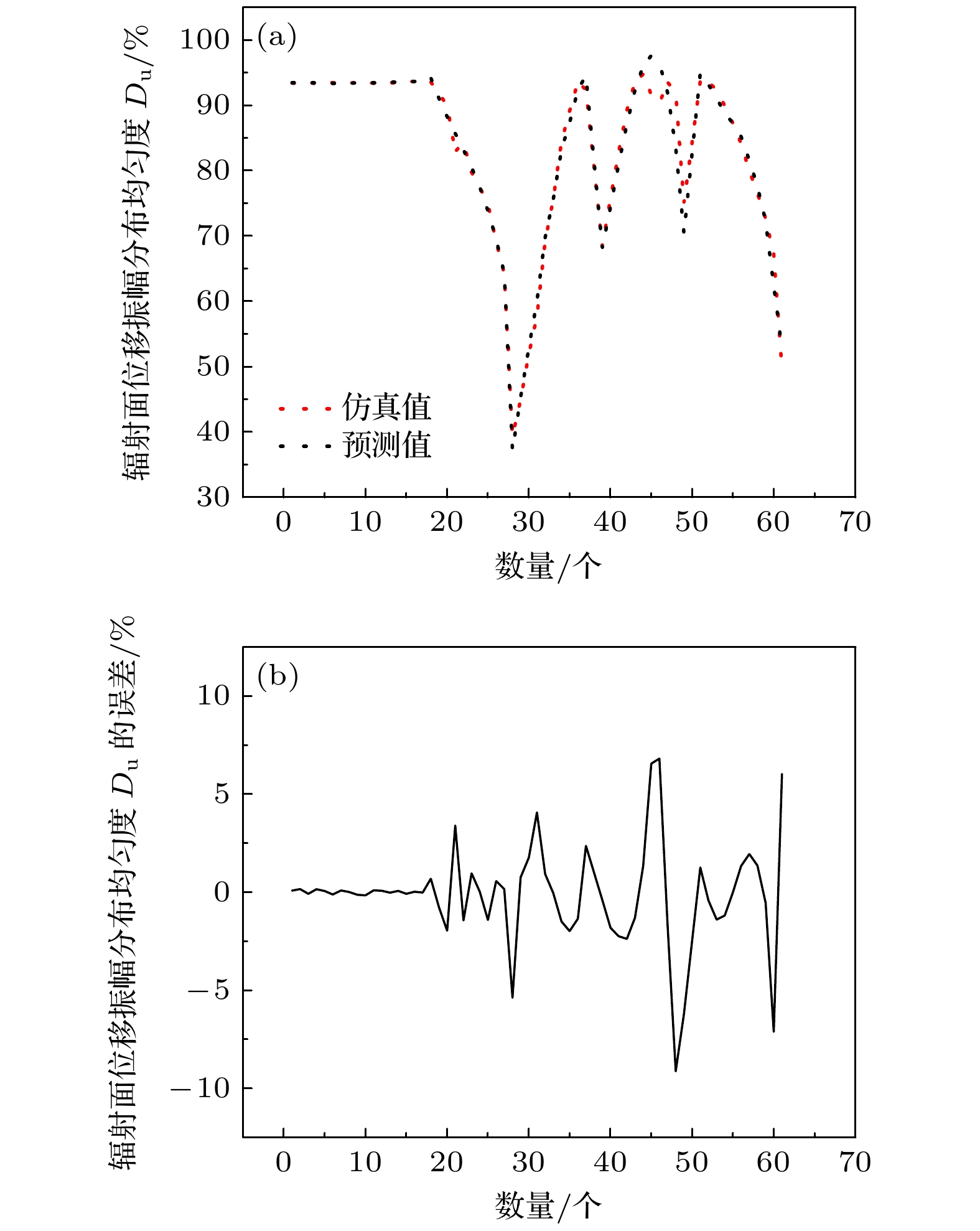
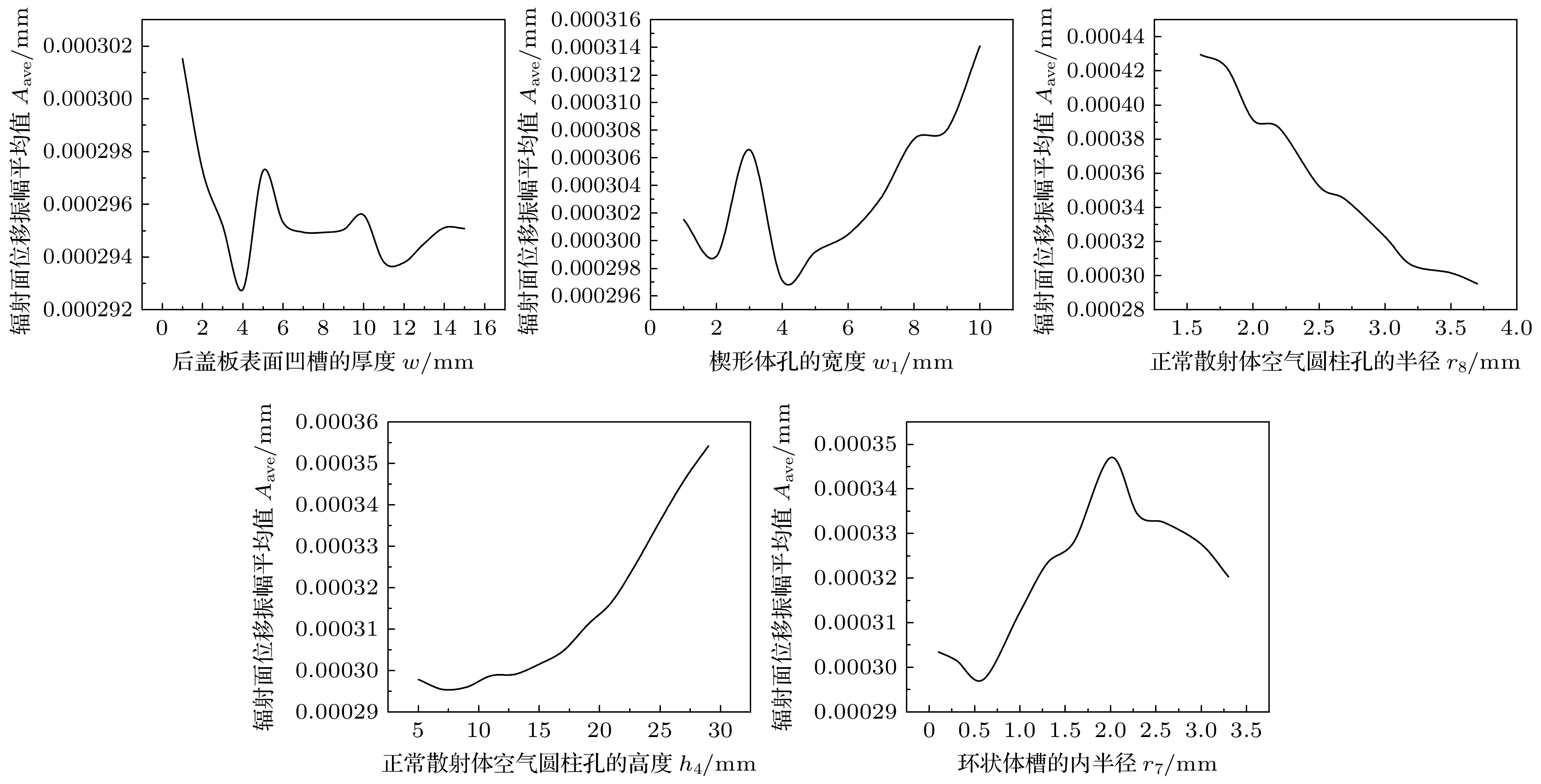
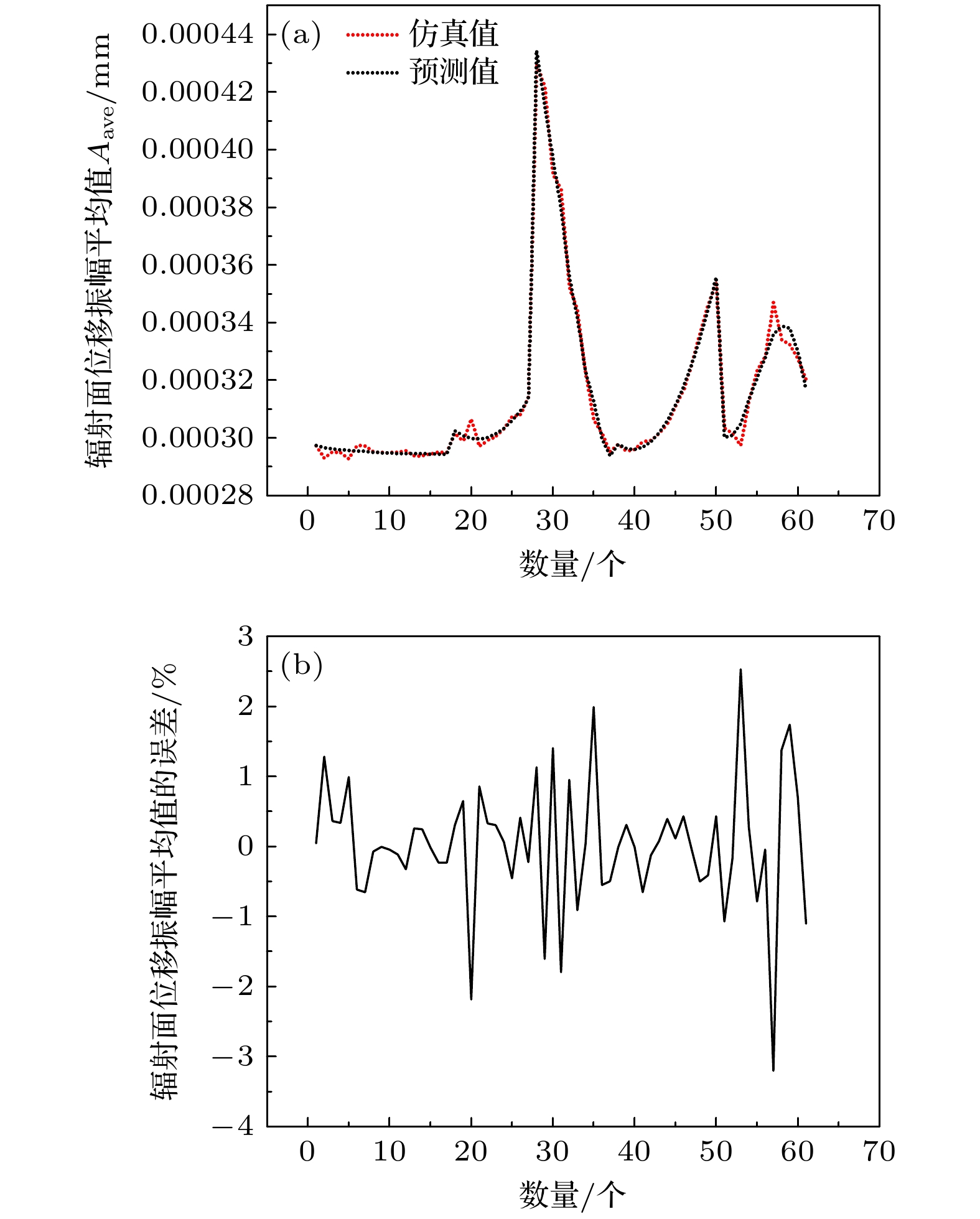
表3—表5给出了当变量为w, w1, h4, r7, r8时, 利用模型(3)—(7)得到的各个常数的预测值. 将COMSOL计算的仿真结果(图10—图12)和公式(3)—(7)的预测结果进行对比, 结果如图13—图15所示. 从图10—图12可以看出, 后盖板表面凹槽的厚度w, 楔形体孔的宽度w1, 正常散射体空气圆柱孔的半径r8、高度h4, 环状体槽的内半径r7都能对换能器纵向谐振频率f、辐射面位移振幅平均值Aave(mm)、辐射面位移振幅分布均匀度Du产生影响, 但是各个性能指标之间存在相互制约关系, 因此, 为实现多变量约束下压电超声换能器性能的均衡最优, 最终确定了各个参数的最佳取值范围: 当后盖板表面凹槽的厚度w≥1 mm 且≤3 mm、楔形体孔的宽度w1 ≥ 1 mm 且≤3 mm、正常散射体空气圆柱孔的半径r8 ≥ 3.2 mm 且≤3.7 mm、正常散射体空气圆柱孔的高度h4 ≥ 15 mm 且≤25 mm、环状体槽的内半径r7 ≥ 0.1 mm 且≤1 mm时, 表面与缺陷调控型大功率压电超声换能器的性能可达到较为理想的状态.
另外, 由图13可知, 纵向谐振频率f的仿真值和预测值的相对误差在±1%以内; 由图14可知, 辐射面位移振幅平均值Aave的仿真值和预测值的相对误差在±3%以内; 由图15可以看出, 辐射面位移振幅分布Du的仿真值和预测值的相对误差在±10%以内(经过数据清洗, 剔除了受耦合作用影响较大的极个别点). 即, 预测误差均控制在±10%以内, 模型可以获得较高的预测准确度.
-
加工表面与缺陷调控型压电超声换能器和未经优化的换能器, 如图16所示. 对换能器的输入电阻抗、辐射面位移振幅和振幅分布情况在实验室中进行实验测试以评估换能器的性能.
-
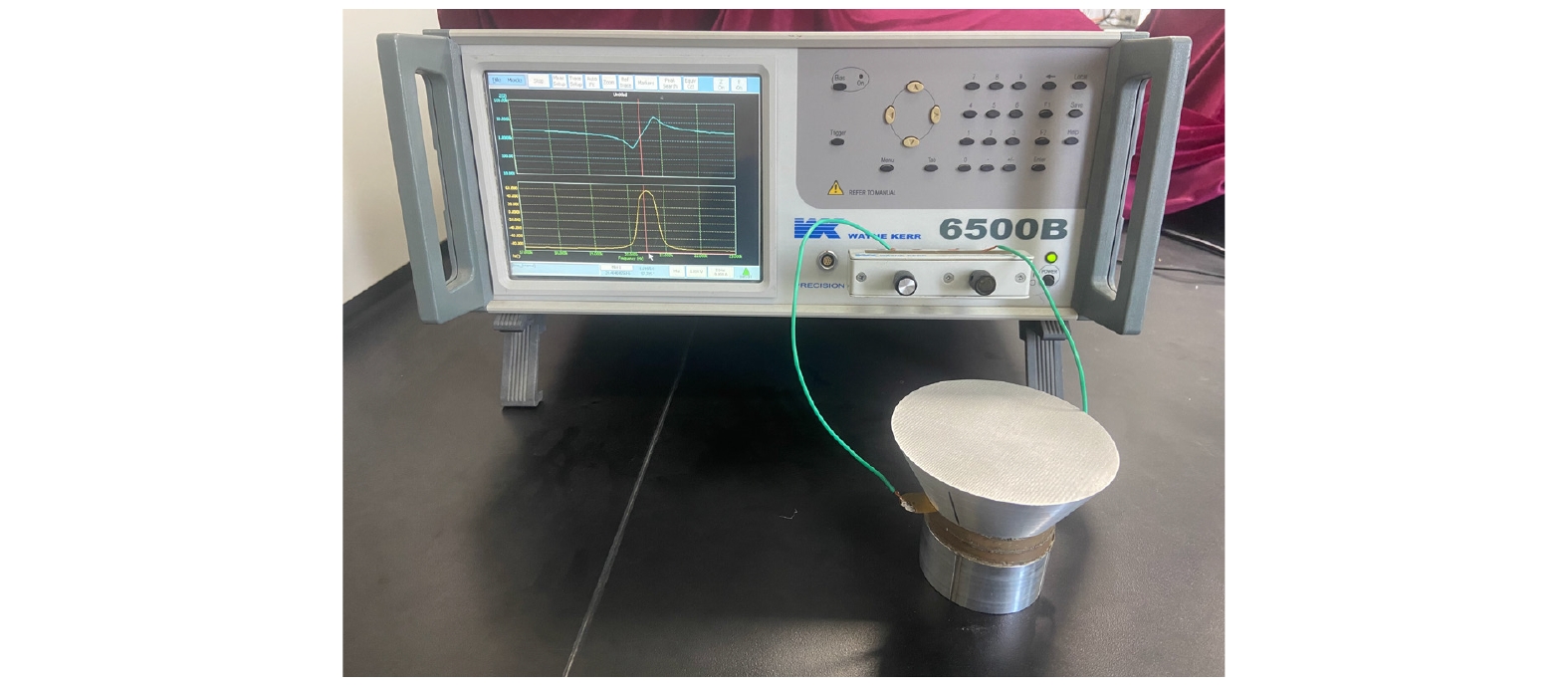
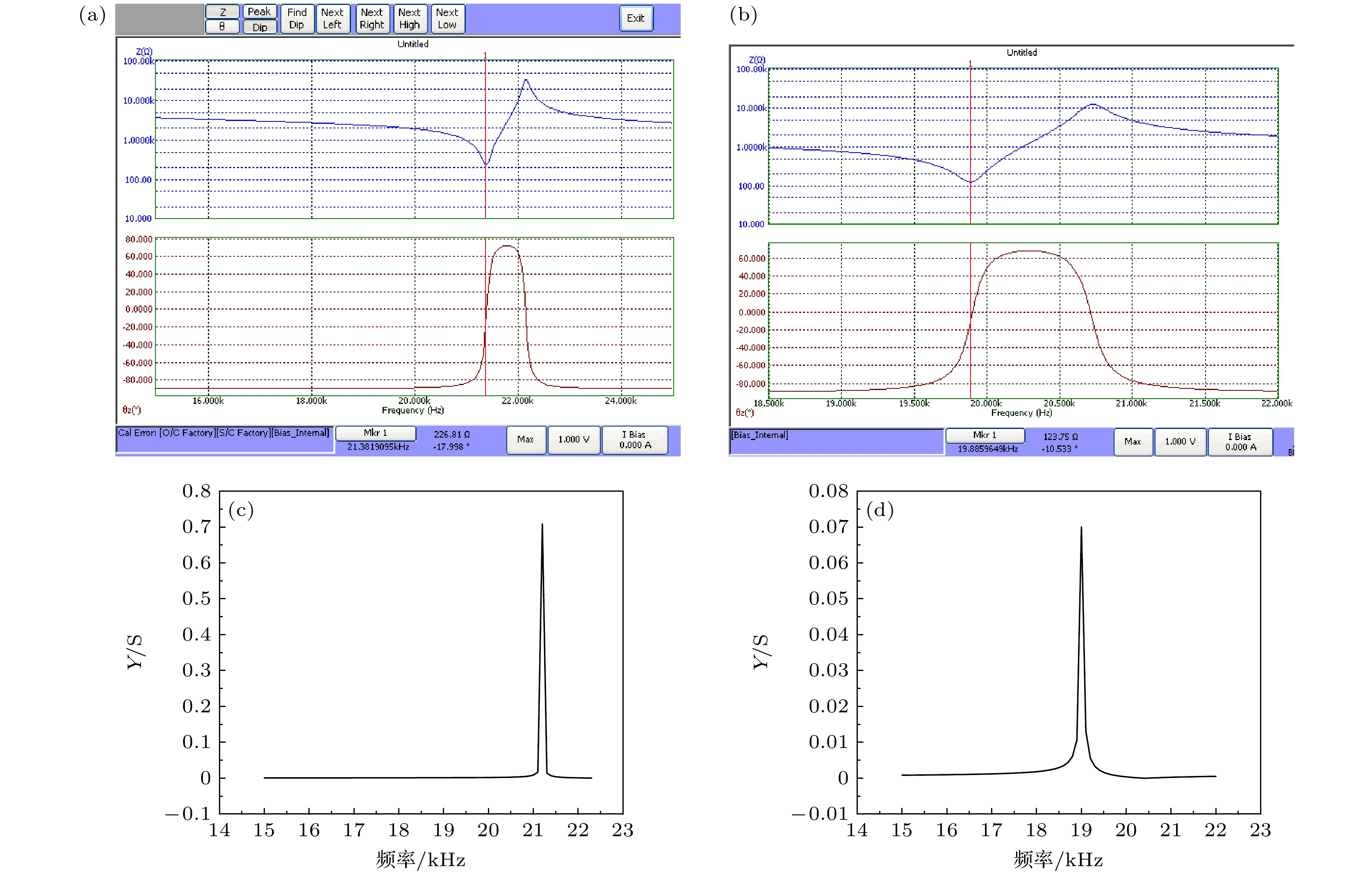
使用6500B精密阻抗分析仪对加工的样品设备(未优化的换能器、表面与缺陷调控型压电超声换能器)的阻抗特性进行测量, 记录测量所得数据, 测量过程如图17所示. 分析仪测量的未优化的换能器的纵向谐振频率为21.382 kHz(如图18(a)所示), 表面与缺陷调控型换能器的纵向谐振频率为19.886 kHz (如图18(b)所示). COMSOL仿真软件计算所得的未优化的换能器的纵向谐振频率为21.198 kHz (如图18(c)所示), 表面与缺陷调控型换能器的纵向谐振频率为19.017 kHz (如图18(d)所示). 计算可得, 未优化的换能器的纵向谐振频率的仪器测量值和仿真计算值的误差为0.86054%, 表面与缺陷调控型换能器的纵向谐振频率的仪器测量值和仿真计算值的误差为4.3699%. 误差均在可接受的范围内, 表明仿真模型和实验设计都相对准确.
-
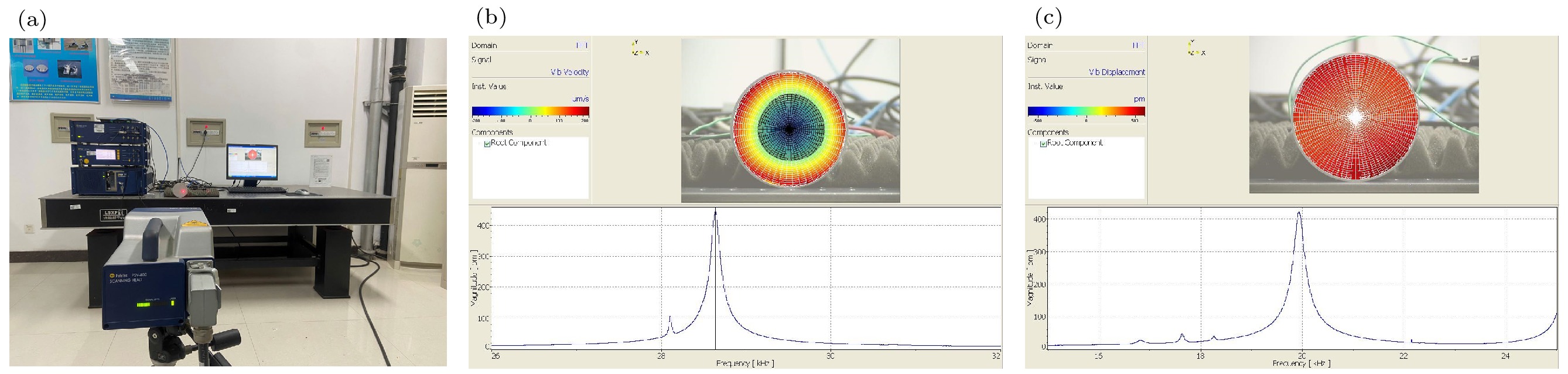
调节好PSV-400全场扫描式激光测振仪的参数后, 启动仪器对未优化的换能器、表面与缺陷调控型换能器表面的振速、位移分布及变化进行测量, 仿真计算和实验中换能器均使用额定电压1 V的电信号进行激励, 测量过程如图19(a)所示, 测量所得的振动信息分别如图19(b), (c)所示.
从图19可以看出, 表面与缺陷调控型压电超声换能器的位移共振峰所对应的频率为19.9375 kHz, 与阻抗分析仪的测量结果基本一致; 扫描获得的辐射面振动信息也与仿真结果保持一致, 且相比于未优化的压电超声换能器, 表面与缺陷调控型压电超声换能器的辐射面位移振幅分布均匀度获得了大幅提升. 仿真实验的结果与实际实验的数据验证了设计理论的准确性, 证明表面与缺陷调控型结构对换能器的性能优化是有效的. 而仿真和实验结果非常一致, 也验证了论文研究方案的可行性, 可将其推广到具体工程应用的场景中.
-
本文基于声子晶体声表面结构和缺陷结构对大功率超声换能器进行理性设计, 建立大功率超声换能器优化设计的新方法, 提出了一种更加高效的换能器设计模式, 并得到以下结论:
1)表面与缺陷调控型大功率压电超声换能器辐射面位移振幅是未优化换能器的1.54倍, 位移振幅分布均匀度是未优化换能器的4.06倍, 有效提升了换能器的性能.
2)利用数据分析软件分析声学表面结构和缺陷结构的配置对换能器性能影响的原因和规律后, 建立的压电超声换能器性能的预测模型的预测值与仿真实验计算所得的仿真值和预测值的相对误差在±10%以内, 模型具有较高的预测准确度.
3)利用6500B精密阻抗分析仪和PSV-400全场扫描式激光测振仪对加工的样品设备进行测试, 发现仿真和实验结果一致, 进一步验证了论文所提的研究方案的可行性, 为大功率压电超声换能器的优化提供一种新的解决思路.
表面与缺陷调控型大功率压电超声换能器
Surface and defect controlled high power piezoelectric ultrasonic transducers
-
摘要: 在大功率压电超声换能器中设计合理的声子晶体缺陷结构, 可以实现对杂散振动模态的有效抑制. 但当换能器尺寸较大时, 声子晶体缺陷结构对换能器设备辐射面的位移振幅改善情况仍不理想. 如何既能有效抑制有害振动, 又能保证换能器的工作效率, 提高换能器辐射面的位移振幅, 一直都是功率超声领域亟待解决的难题. 研究发现, 声学表面结构可以实现能量的单向传输, 更好地降低能量损耗, 提高能量传输的效率. 基于此, 本文提出了表面与缺陷调控型大功率压电超声换能器的研究. 通过在换能器中设计合理的缺陷和声表面结构, 激发声波的强局域化效应, 实现声学反常透射, 大幅提高换能器纵向辐射声功率. 同时利用数据分析技术, 对声学表面结构和缺陷结构的材料成分、几何结构参数对换能器性能的影响进行分析, 建立大功率压电超声换能器的性能预测模型, 实现换能器的优化设计. 从定量研究的角度出发, 系统性地提出一种大功率压电超声换能器优化设计的新理论和新方法. 仿真和实验证明, 本研究可以提高大功率压电超声换能器的创新设计能力和设计的智能化水平, 使得换能器在大功率应用环境中振动模态更加单一, 大幅提高了辐射面的位移振幅和振幅分布均匀度.
-
关键词:
- 声表面和缺陷调控 /
- 大功率压电超声换能器 /
- 局域化效应 /
- 性能预测
Abstract:Researches have shown that a reasonably designed phononic crystal defect structure in high-power piezoelectric ultrasonic transducers can effectively suppress stray vibration modes. However, when the size of the transducer is large, the improvement of the displacement amplitude of the radiation surface of the transducer device by the phononic crystal defect structure is still not so ideal. How to effectively suppress harmful vibrations while ensuring the operational efficiency of transducers and enhancing the displacement amplitude of their radiating surfaces has always been a challenging problem in the field of power ultrasonics that needs to be solved urgently. Researches have found that acoustic surface structures can achieve unidirectional energy transmission, effectively reduce energy loss, and enhance the efficiency of energy transmission. Based on this, the high-power piezoelectric ultrasonic transducers with surface and defect regulation are investigated in this work. By designing reasonable defects and acoustic surface structures in the transducer, strong localization effects of sound waves can be excited to achieve acoustic anomalous transmission, significantly increasing the longitudinal radiated sound power of the transducer. At the same time, a data analysis technique is used to analyze the influence of material composition and geometric parameters of acoustic surface structure and defect structure on the performance of transducers, and a performance prediction model is established for high-power piezoelectric ultrasonic transducers, ultimately achieving optimized design of transducers. In this study, a new theory and method are systematically proposed for optimizing the design of high-power piezoelectric ultrasonic transducers quantitatively. Simulation and experimental results show that the innovative design capability and intelligent level of high-power piezoelectric ultrasonic transducers can be improved, making the vibration mode of the transducer more singular in high-power application environments, and thus significantly improving the displacement amplitude and amplitude distribution uniformity of the transducer radiation surface. -
-
图 1 大功率压电超声换能器的结构和振型图 (a) 结构图; (b)振型图; (c) 辐射面位移分布图
Figure 1. Structure and vibration mode diagram of high-power piezoelectric ultrasonic transducer: (a) Structural diagram; (b) vibration mode diagram; (c) displacement distribution diagram of radiation surface.
图 2 未优化换能器的辐射面位移振幅
Figure 2. Radiation surface displacement amplitude of unoptimized transducer.
图 3 优化后的后盖板的结构示意图
Figure 3. Structural schematic diagram of optimized rear cover plate.
图 4 优化后的前盖板的结构示意图
Figure 4. Structural schematic diagram of optimized front cover plate.
图 5 优化后的前盖板的结构示意图(俯视图)
Figure 5. Structural schematic diagram of optimized front cover plate (top view).
图 6 优化后的前盖板的结构示意图(侧视图)
Figure 6. Structural schematic diagram of optimized front cover plate (side view).
图 7 表面与缺陷调控型大功率压电超声换能器的结构模型图和振型图 (a) 换能器结构模型图; (b)振型图
Figure 7. Structural model diagram and vibration mode diagram of surface and defect controlled high-power piezoelectric ultrasonic transducer: (a) Structural model diagram of transducer; (b) vibration mode diagram.
图 8 优化后的换能器和未优化的换能器的辐射面位移振幅对比图
Figure 8. Comparison of displacement amplitude of radiation surface between optimized and unoptimized transducers.
图 9 三种换能器性能对比图 (a) 辐射面位移振幅和分布均匀度对比图; (b) 总辐射功率对比图
Figure 9. Comparison chart of three types of transducer performance: (a) Comparison diagram of displacement amplitude and distribution uniformity of radiation surface; (b) comparison chart of total radiated power.
图 10 不同的属性参数对纵向谐振频率f的影响
Figure 10. Influences of different attributes parameters on the longitudinal resonance frequency f.
图 12 不同的属性参数对辐射面位移振幅分布Du的影响
Figure 12. Influences of different attribute parameters on the amplitude distribution Du of radiation surface displacement.
图 13 纵向谐振频率f的仿真值和预测值的对比及相对误差
Figure 13. Comparison and relative error between simulated and predicted values of longitudinal resonant frequency f.
图 15 辐射面位移振幅分布Du的仿真值和预测值的对比及相对误差
Figure 15. Comparison and relative error between simulated and predicted values of Du.
图 11 不同的属性参数对辐射面位移振幅平均值Aave的影响
Figure 11. Influences of different attribute parameters on the average displacement amplitude Aave of the radiation surface.
图 14 辐射面位移振幅平均值Aave的对比及相对误差
Figure 14. Comparison and relative error of average amplitude Aave of radiation surface displacement.
图 18 输入电阻抗与谐振频率的测量 (a) 未优化的换能器的测量结果; (b) 表面与缺陷调控型换能器的测量结果; (c) 未优化的换能器的仿真导纳曲线图; (d)表面与缺陷调控型换能器的仿真导纳曲线图
Figure 18. Measurement of input impedance and resonant frequency: (a) Measurement results of an unoptimized transducer; (b) measurement results of surface and defect controlled transducers; (c) simulation admittance curve of unoptimized transducer; (d) simulation admittance curve of surface and defect controlled transducers.
图 19 换能器辐射面位移振幅分布的实验测量 (a) 测量过程; (b) 测量得到的未优化换能器的表面数据; (c) 测量得到的优化后的换能器的表面数据
Figure 19. Experimental measurement of displacement amplitude distribution of transducer radiation surface: (a) Measurement process; (b) surface data of unoptimized transducers obtained through measurement; (c) the surface data of the optimized transducer obtained through measurement.
表 1 压电超声换能器的材料和几何结构参数
Table 1. Materials and geometric structure parameters of piezoelectric ultrasonic transducer.
部件 材料属性 形状 半径/mm 半径/mm 高/mm 后盖板 AISI 4340 钢 等截面圆柱 31 31 30 压电陶瓷圆环(两片) PZT-4压电陶瓷 等截面圆环 7 (内径) 30 (外径) 8 前盖板 6063-T83铝 圆台 31 (上底) 50 (下底) 35 
下载: 导出CSV
表 2 三种换能器性能对比表
Table 2. Performance comparison table of three transducers.
换能器 位移振幅Aave/mm 分布均匀度Du
/%总辐射功率
/mW缺陷结构 0.2180 × 10–3 87.73 0.04818 管柱结构 0.2109 × 10–3 90.56 0.04904 表面与缺陷结构 0.3015 × 10–3 93.56 0.1181 比值(表面与缺陷/缺陷) 1.384 1.066 2.450 比值(表面与缺陷/管柱) 1.430 1.033 2.407
下载: 导出CSV
表 3 纵向谐振频率f的预测模型(单位Hz)
Table 3. Predictive model for longitudinal resonant frequency f of slot structures (Unit: Hz).
A B C D 后盖板表面凹槽厚度w/mm 19015.485 1.544 –0.09065 0.004986 楔形体孔的宽度w1 /mm 19003.333 13.94 –0.4575 –0.02117 正常散射体空气圆柱孔半径r8/mm 21299.902 –36.52 0.000 –50.71 空气圆柱孔的高度h4/mm 20530.792 –202.5 8.669 –0.1261 环状体槽的内半径r7/mm 19015.083 2.116 11.49 3.530
下载: 导出CSV
表 4 辐射面位移振幅平均值Aave的预测模型
Table 4. Prediction model for the average displacement amplitude Aave of the radiation surface.
A B C D 后盖板表面凹槽厚度w/ mm 0.0002939 6.991×10–6 0.000 0.000 楔形体孔的宽度w1/mm 3.048×10–4 –2.717×10–6 3.576×10–7 0.000 正常散射体空气圆柱孔半径r8/mm 6.102×10–4 –1.155×10–4 0.000 2.187×10–6 空气圆柱孔的高度h4/mm 3.063×10–4 –2.397×10–6 1.375×10–7 1.373×10–10 环状体槽的内半径r7/mm 3.005×10–4 –4.852×10–6 2.407×10–5 –6.396×10–6
下载: 导出CSV
表 5 辐射面位移振幅分布均匀度Du的预测模型
Table 5. Prediction model for the uniformity of displacement amplitude distribution Du on the radiation surface.
A B C D 后盖板表面凹槽厚度w/mm 0.9355 –0.0004441 3.130×10–5 4.060×10–7 楔形体孔的宽度w1/mm 0.9798 –0.04139 0.003935 –0.0003165 正常散射体空气圆柱孔半径r8/mm –0.3622 0.4834 0.000 –0.009487 空气圆柱孔的高度h4/mm 0.5726 –0.004406 0.003738 –0.0001257 环状体槽的内半径r7/mm 0.9600 –0.1010 0.05795 –0.01953
下载: 导出CSV
-
[1] Lin S Y 2004 J. Acoust. Soc. Am. 115 182 doi: 10.1121/1.1635836 [2] 刘世清, 姚晔 2008 机械工程学报 44 239 doi: 10.3901/JME.2008.10.239 Liu S Q, Yao Y 2008 J. Mecha. Engi. 44 239 doi: 10.3901/JME.2008.10.239 [3] Chen C, Dong Y L, Wang S, Hu L Q, Lin S Y 2022 J. Acoust. Soc. Am. 151 2712 doi: 10.1121/10.0010287 [4] 许龙, 王威震, 龚涛, 李果, 赵伦, 周光平, 梁召峰 2024 振动与冲击 43 287 doi: 10.13465/j.cnki.jvs.2024.08.033 Xu L, Wang W Z, Gong T, Li G, Zhao L, Zhou G P, Liang Z F 2024 J. Vibration Shock 43 287 doi: 10.13465/j.cnki.jvs.2024.08.033 [5] Wu Z Z, Zhang Z, Wu D G, Chen Y H, Hu F, Guo C X, Tang L J 2024 Actuators 13 177 doi: 10.3390/act13050177 [6] Wang S, Lin S Y 2021 Ultrasonics 111 106299 doi: 10.1016/j.ultras.2020.106299 [7] He Z J, Jia H, Qiu C Y, Peng S S, Mei X F, Cai F Y, Peng P, Ke Manzhu Liu Z Y. 2010 Phys. Revi. Lett. 105 074301 doi: 10.1103/PhysRevLett.105.074301 [8] Christensen J, Fernandez-Dominguez A I, De Leon-Perez F, Martin-Moreno L, Garcia-Vidal F J 2007 Nat. Phys. 3 851 doi: 10.1038/nphys774 [9] 冯俊瑾 2023 博士学位论文 (成都: 电子科技大学) Feng J J 2023 Ph. D. Dissertation (Chengdu: University of Electronic Science and Technology of China [10] Zhou Y, Lu M H, Liang F, Xu N, Chen Y F, Zhu Y Y, Zhu S N, Ming N B 2010 Phys. Revi. Lett. 104 164301 doi: 10.1103/PhysRevLett.104.164301 [11] Liu F, Cai F, Ding Y, Liu Z 2008 Appl. Phys. Lett. 92 103504 doi: 10.1063/1.2896146 [12] 卢一铭, 曹东兴, 申永军, 陈许敏 2021 力学学报 53 1114 doi: 10.6052/0459-1879-20-436 Lu Y M, Cao D X, Shen Y J, Chen X M 2021 Chin. J. Theo. Appl. Mech. 53 1114 doi: 10.6052/0459-1879-20-436 [13] 孙伟彬, 王婷, 孙小伟, 康太凤, 谭自豪, 刘子江 2019 物理学报 68 234206 doi: 10.7498/aps.68.20190260 Sun W B, Wang T, Sun X W, Kang T F, Tan Z H, Liu Z J 2019 Acta Phys. Sin. 68 234206 doi: 10.7498/aps.68.20190260 [14] 朱兴一, 钟盛, 叶安珂, 邓富文, 吴睿, 俞悟周 2014 人工晶体学报 43 2852 doi: 10.3969/j.issn.1000-985X.2014.11.016 Sun W B, Wang T, Sun X W, Kang T F, Tan Z H, Liu Z J 2014 J. Synt. Crys. 43 2852 doi: 10.3969/j.issn.1000-985X.2014.11.016 [15] 侯丽娜, 侯志林, 傅秀军 2014 物理学报 63 034305 doi: 10.7498/aps.63.034305 Hou L N, Hou Z L, Fu X J 2014 Acta Phys. Sin. 63 034305 doi: 10.7498/aps.63.034305 [16] 高东宝, 曾新吾 2013 国防科技大学学报 35 129 doi: 10.3969/j.issn.1001-2486.2013.05.022 Gao D B, Zeng X W J 2013 J. Nati. Univ. Defen. Tech. 35 129 doi: 10.3969/j.issn.1001-2486.2013.05.022 [17] 林基艳, 林书玉, 徐洁, 王升, 钟兴华 2023 中国科学: 物理学 力学 天文学 53 254311 doi: 10.1360/SSPMA-2022-0171 Lin J Y, Lin S Y, Xu J, Wang S, Zhong X H 2023 Sci. Sin. Phys. Mech. As. 53 254311 doi: 10.1360/SSPMA-2022-0171 [18] 林基艳, 林书玉 2023 物理学报 72 094301 doi: 10.7498/aps.72.20230195 Lin J Y, Lin S Y 2023 Acta Phys. Sin. 72 094301 doi: 10.7498/aps.72.20230195 [19] 孙琢刚 2023 博士学位论文 (秦皇岛市: 燕山大学) Sun Z G 2023 Ph. D. Dissertation (Qinhuangdao: Yanshan University [20] 刘婷 2022 博士学位论文 (哈尔滨: 哈尔滨工程大学) Liu T 2022 Ph. D. Dissertation (Harbin: Harbin Engineering University [21] 李雪锋 2011 硕士学位论文 (南京: 南京大学) Li X F 2011 M. S. Thesis (Nanjing: Nanjing University [22] 张蒙 2019 硕士学位论文 (沈阳: 沈阳航空航天大学) Zhang M 2019 M. S. Thesis (Shenyang: Shenyang University of Aeronautics and Astronautics [23] 郭梦萍 2019 硕士学位论文 (南京: 南京理工大学) Guo M P 2019 M. S. Thesis (Nanjing: Nanjing University of Science and Technology [24] 谢素君 2017 硕士学位论文 (吉首: 吉首大学) Xie S J 2017 M. S. Thesis (Jishou: Jishou University [25] 毛宇宸, 沈建东, 刘涛, 杨嘉倩, 豆涵杰, 张汪洋, 牟笑静 2024 压电与声光 46 617 doi: 10.11977/j.issn.1004-2474.2024.05.001 Mao Y C, Shen J D, Liu T, Yang J Q, Dou H J, Zhang W Y, Mou X J 2024 Piez. & Acous. 46 617 doi: 10.11977/j.issn.1004-2474.2024.05.001 [26] 郭万里 2022 硕士学位论文 (天津: 河北工业大学) Guo W L 2022 M. S. Thesis (Tianjin: Hebei University of Technology -
计量
- 文章访问数: 32
- HTML全文浏览数: 32
- PDF下载数: 0
- 施引文献: 0