-
高能量密度物质是指能量密度大于
$ 10^{11} \ \mathrm{J}/ \mathrm{m}^{3} $ 或等效压强超过1 Mbar (1 Mbar = 1011 Pa)的一种极端物质状态, 这种状态被认为存在于恒星、大型行星内部以及超新星爆炸中, 也短暂存在于人工核聚变反应过程中, 是天体物理和可控核聚变科学等领域的核心研究课题, 已逐渐成为国际物理学新兴的重要方向之一[1,2]. 如何在实验室条件下制备物质状态良好可控、参数范围宽广、物态特性精确可测的高能量密度物质, 是当前该领域面临的最为迫切的核心问题. 目前, 实验室制备高能量密度物质的途径有强激光、Z箍缩(Z-pinch)、化学爆轰以及强流重离子束等驱动方式. 然而基于大型离子加速器装置的强流重离子束驱动产生的高能量密度物质具有以下突出特性: 样品体积大、空间分布均匀、材料种类多样、实验重复性好与实验频率高等. 通过改变束靶耦合的参数条件, 该加载途径能够实现准等熵压缩与准等容加热不同的方式, 在大的参数空间内开展相关的研究, 可极大地提升实验研究的精确性与系统性. 在高能量密度物理的研究中, 基于大型加速器装置的驱动方式将发挥重要作用, 成为科学家们探索未知世界的有力工具[1–7].在国际上基于大型加速器装置开展重离子束驱动的高能量密度物理的研究机构和装置有: 美国LBNL的NDCX-II、俄罗斯ITEP的TWAC和德国GSI的FAIR等. 我国“十二五”规划重大科技基础设施强流重离子加速器装置(high intensity heavy-ion acelerator facility, HIAF)项目[7], 提出了利用超高功率的强流重离子束驱动方式开展实验室高能量密度物理研究工作, 拟引出束流强度可达1012 ppp (particle per pulse) 的U离子束, 单离子能量可达0.5—1 GeV/u, 束团长度仅为50—200 ns, 束斑尺寸为1 mm水平. 如图 1所示[5], 并在HIAF上规划和建设高能量密度物理实验研究的终端, 发展了相关的制备技术与诊断技术等, 期待为我国的高能量密度物理研究注入新的活力. 表 1对比了FAIR装置使用重离子加热和膨胀(HIHEX)技术[8]以及HIAF装置可分别产生的重离子束的束流参数[1,3]. HIAF装置不仅能够提供更高电荷态与更大流强范围的重离子束流, 在离子束脉宽、能散、焦斑尺寸等方面更具有优势, 因此可以用于产生更为极端的物质状态. 随着国际形式的剧烈变化, FAIR项目进展非常缓慢, 而HIAF装置在可预见的未来一段时间, 将成为国际上唯一的利用强流高能重离子束驱动产生高能量密度物质的实验装置, 开展系统性稠密等离子体、高压新材料等特性的研究工作. 如何在实验之前, 发展和利用流体动力学计算程序, 针对HIAF上的束流参数与束靶耦合实验开展高精度模拟计算工作, 并理论预测高能量密度物质的基本行为, 探索其物态参数的变化规律, 揭示物质基本结构、相变和物理性质间的关联性, 具有极其重要的意义和价值. 该计算工作也将对未来的系列实验提供关键性的参考结果与前瞻性的技术指导.
本文利用Aardvark程序开展了流体动力学模拟计算[9], 构建了不同参数条件下铀离子束与靶物质相互作用后的靶物质状态演化的数据库, 获得了不同束靶相互作用条件下的单位质量的能量沉积、温度、密度和压强等物态参数的时空演化规律. 随着束流强度的不断增加, 靶状态参数呈现出非线性变化, 预测有冲击波的生成; 未来基于短脉冲束、高流强密度等的HIAF平台, 可开展跨越稠密物质特性到强冲击波输运过程的研究工作. 本文首先介绍了利用HIAF装置研究高能量密度物理的发展机遇, 接着详细阐述了铀离子束与靶物质相互作用机制, 其次利用Aardvark程序对该过程进行了模拟与计算, 展示了相应的模拟结果, 最后对研究进行了总结.
-
Aardvark程序是具有精细状态方程的辐射流体动力学程序, 可以描述等离子体随时间演化的过程图像, 有关该程序的具体描述可以参考文献[9]. 该程序以3个流体力学控制方程为基础: 1)连续性方程
$ \dfrac{\text{d}\rho}{\text{d}t} + \rho\nabla\cdot\boldsymbol{v} = 0 $ , 2) 动量方程$ \rho\dfrac{\text{d}\ \boldsymbol{v}}{\text{d}t} = -\nabla P+ \rho\boldsymbol{\mathbf{F\boldsymbol{ }}} $ , 3) 能量方程$ \rho\dfrac{\text{d}e}{\text{d}t}=-P\nabla\boldsymbol{\cdot v}\ + \nabla \cdot \boldsymbol{q}+\rho \dot{q} $ . 其中, ρ是流体密度, v是流体速度, P是压力, F是单位质量的体力, q是热通量矢量,$\rho \dot{q} $ 代表能量源项. 基于拉格朗日坐标系并使用交错网格技术, 以物质的状态方程(EOS)作为基本的数据库开展相关的模拟计算. Aardvark程序的设计是根据实验中可能发生的各类实际物理过程, 对其进行了合理的模块化设计, 将整个程序分为材料构型模块、流体力学模块、能量输入与沉积模块、光子辐射输运模块和物性参数模块[10–12]. 其中重离子束驱动的高能量密度物理所涉及的能量输入与沉积模块的关键是对单粒子的能量损失$ {\mathrm{d}}E/{\mathrm{d}}x $ 进行建模. 通常单粒子的阻止本领近似为入射离子能量和靶物质状态(密度与温度)的函数[13,14]. 单离子的阻止本领函数确定后, 就可以由离子束流的相关参数(例如重离子束脉冲包含的离子数、脉冲宽度、离子束半高全宽、离子束入射方向等)计算重离子束每一时刻在靶材料任意位置处的能量沉积功率, 并将其作为能量源项耦合到能量方程中. 针对高能重离子束驱动方式特点以及能量沉积的具体情况, Aardvark程序采用的单离子阻止本领模型是标准阻止模型(standard stopping model, SSM). 它是Bohr-Bethe-Bloch能损公式的一个高温扩展, 该模型可以较为准确地描述高速离子入射到高温物质时的能损, 且在温度较低时, 模型结果也能与经典的Bohr-Bethe-Bloch公式一致. 在高温等离子体环境中, 离子束的阻止能力主要由等离子体靶中的束缚电子和自由电子与入射离子的相互作用决定, 且束缚电子和自由电子对离子束能损的贡献具有独立性. 同时, 等离子体靶中的离子对阻止过程的贡献相对微弱, 因此可以将阻止本领主要归因于电子的贡献. Aardvark程序通过阻止本领(stopping power)的修正和近似来匹配具体的实际应用场景[15]. 该计算程序通过数值方法可以对流体力学方程进行离散化处理并添加适当的边界条件, 求解出物质的物态参数, 如温度、密度和压强等所需的关键量. 通过改变初始模拟参数, 如初始靶状态、离子束参数、材料种类和结构参数等, 用于模拟不同实验条件下束靶耦合过程以及产生的高能量密度靶物质的动态演化图像. -
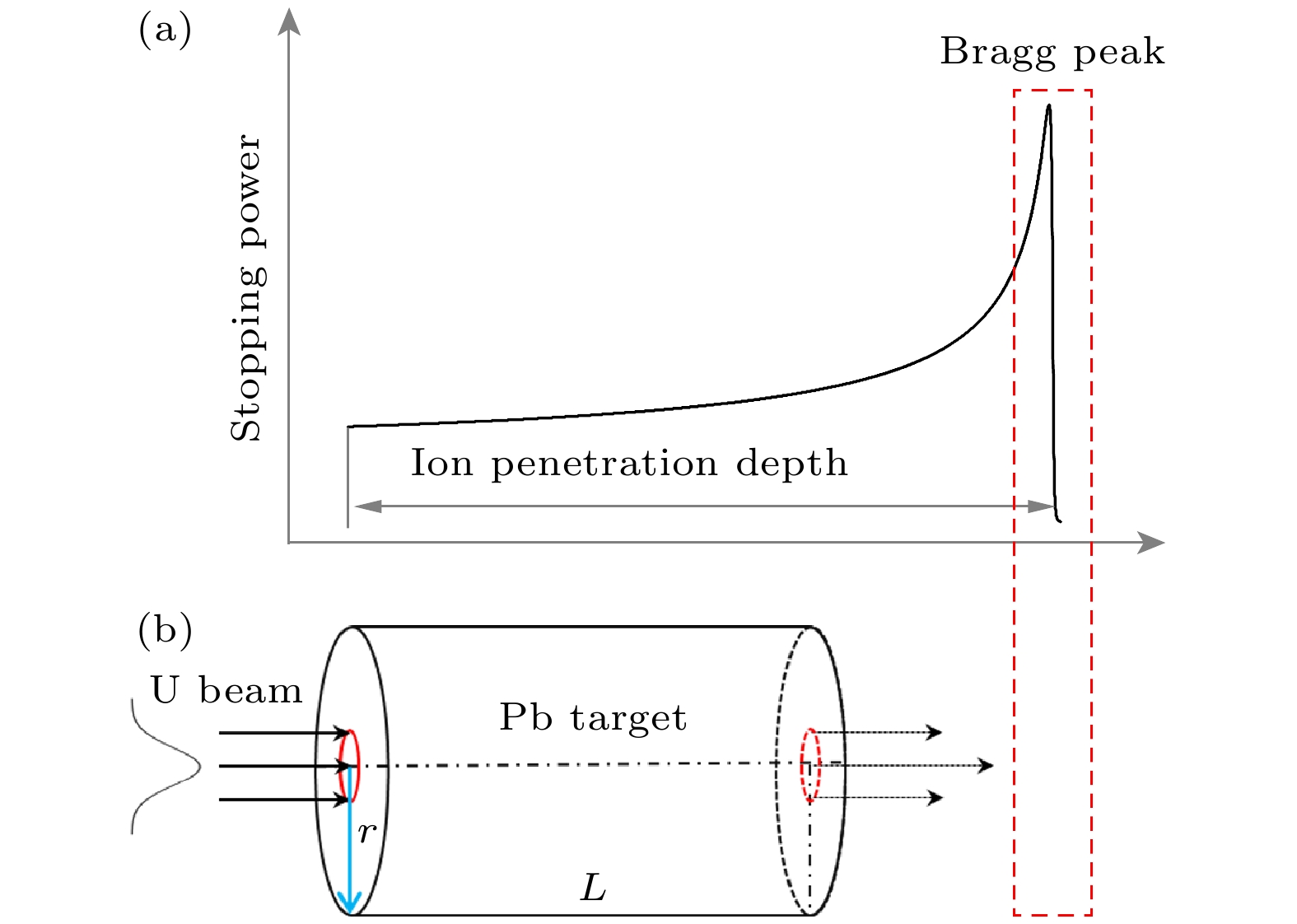
如前文所述, HIAF工程建设进展顺利, 预计在2026年出束并开展第一轮实验工作. 目前在实验设计方面, 拟利用高能238U92+离子束作为驱动束, 其能量为1 GeV/u, 高斯型束斑直径为1 mm, 脉冲长度100 ns, 离子束流强 1 × 1011 ppp (particle per pulse)入射圆柱型铅靶, 入射点为靶轴心; 靶为固体铅, 长度为5 mm, 半径4 mm. 如图 2所示的离子束打靶设计方案, 铀离子束从一侧入射到圆柱形靶, 并从另外一侧穿出, 对于能量为1 GeV/u的铀离子束, 在固态铅靶中的离子射程超过1 cm, 因此离子布拉格峰(红色虚线框)将位于靶材之外, 在靶材料内部, 离子的能量沉积体现很好的坪区特性. 对于几个毫米的穿行范围, 高能U离子束的束散仅在微米量级, 综上, 实现了大体积铅靶样品的均匀加热. 基于上述离子路径方向能量均匀沉积的设定, 下面重点考虑垂直于离子路径, 即圆柱靶径向方向r (蓝色实线)的单位质量的能量沉积与产生的靶物质参数(温度、压强与密度)的含时演化过程图像.
-
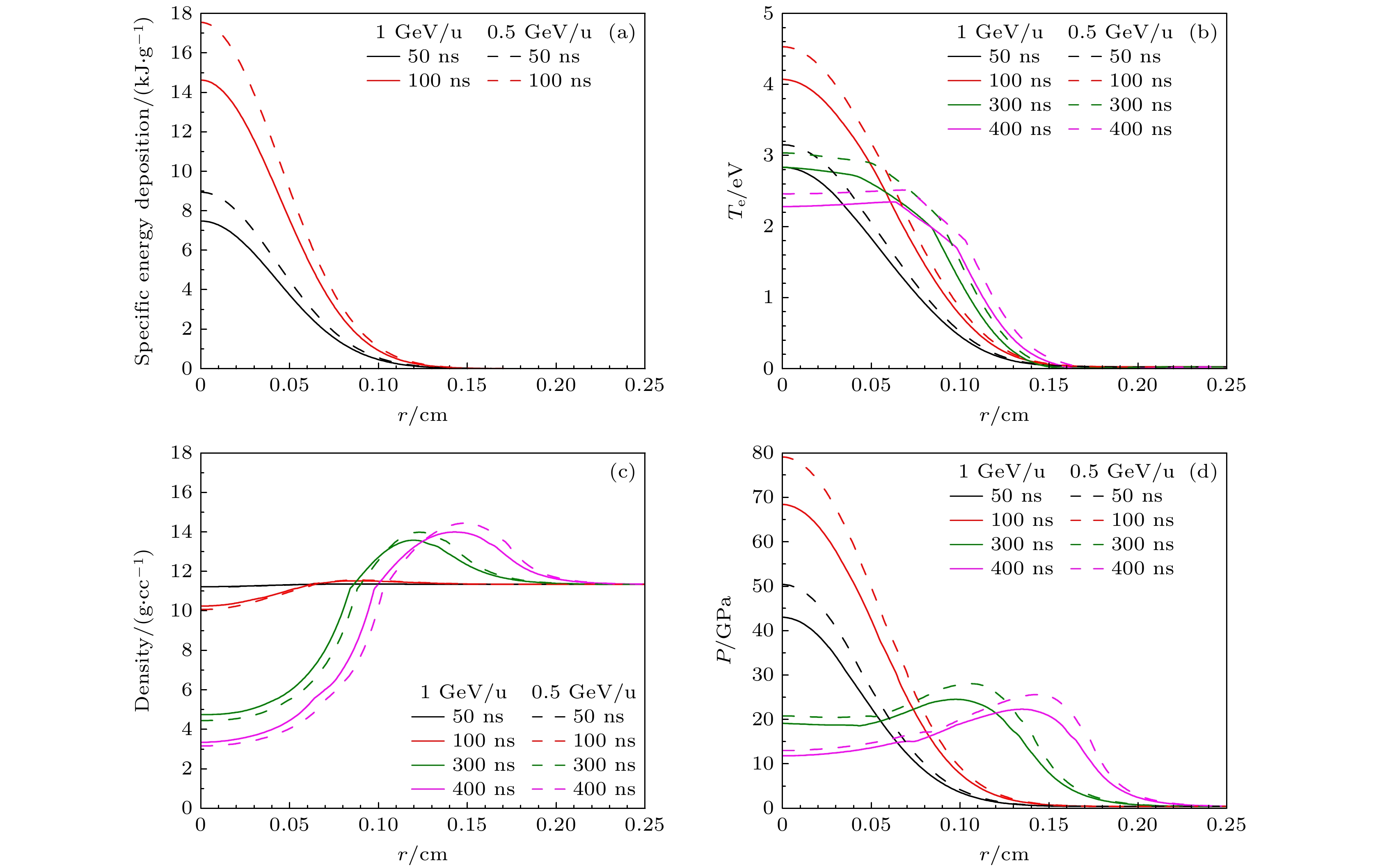
利用上述Aardvark程序, 模拟了强聚焦U束轰击圆柱型Pb靶条件下可产生的物质状态, 结果包括离子束单位质量的能量沉积、靶物质的温度、密度和压强的含时演化过程. 需要特别说明的是模拟计算中所需的靶物质的状态方程由改进的第一性原理分子动力学方法计算获得, 该方法将基于密度泛函理论的计算拓展到了keV温度范围, 且保留了低温区和高温区的计算一致性, 十分适合用来精确计算高能量密度物理中的宽温度区域的状态方程[16,17]. 图 3展示了在束团强度为
$ 1 \times 10^{11}\;{\rm ppp} $ , 脉冲长度为100 ns下, 能量分别为500 MeV/u和1 GeV/u的U92+离子束入射造成的靶物质状态参数沿圆柱径向r方向的演化过程. 图中500 MeV/u与1 GeV/u的束流条件相比, 整体的状态参数曲线的变化趋势是一致的, 但是铅靶达到的单位质量的能量沉积、温度、密度和压强数值都要高. 这是由于500 MeV/u离子束的坪区能损率较高, 导致靶物质中的能量沉积更高[1]. 由于离子束脉冲呈现高斯分布, 即在离子束脉冲作用时间内, 单位质量的能量沉积、温度和压强也呈现高斯分布. 图3(a)展示了离子束单位质量的能量沉积随半径的演化特性. 随着入射离子束作用时间的延长, 单位质量的能量沉积持续增加, 并在脉冲结束时达到最大值. 图3(b)展示了靶物质中电子温度随半径的变化. 在离子束作用期间, 靶物质中的电子被持续加热, 直至100 ns (即束流结束时), 靶物质温度达到最高值, 如图3(d)所示, 此时压强也同步达到最大值. 然而, 尽管温度和压强显著升高, 但靶物质整体仍基本保持初始的固体密度状态. 离子束作用结束后, 热传导效应开始显现, 靶物质温度逐渐降低. 如图3(c)所示, 靶物质轴心处因加热而膨胀, 产生一系列向外传播的压缩波, 同时推动物质向外运动, 导致中心密度下降. 靶物质密度沿半径方向呈现出先增加后逐渐减小的趋势, 压强的变化也表现出类似的特征. 另一个值得关注的现象是温度和压强在轴心附近形成的平台. 这表明在重离子束作用下, 通过重离子束的坪区能损特色结合高斯型束流包络, 可以在靶子轴心处制备一种大空间体积的高度均匀的极端物质状态区域. 结合温度、压强和密度的状态参数结果, 表明利用强流重离子束驱动方式, 能在实验室环境制备一种大体积空间均匀的低温高压高密的特殊物质状态, 即温稠密物质状态, 其存在于行星内核区域, 比如: 地球(外核为液态, 温度达5000 K以上, 压强超过100 GPa; 内核为固态, 温度达6000 K, 压强超过了300 GPa)、木星(温度达20000 K, 压强3000 GPa). 因此, 该理论模拟揭示了重离子束驱动产生高能量密度物质研究具有的特色, 而HIAF装置将为实验室探索行星内核的物态性质等工作提供特有的条件支持.为表明Aardvark程序设计的合理性和准确性, 表 2分别对比了利用Aardvark程序与二维流体力学BIG2程序在相同束流条件下靶物质轴心处的特征物态参数[18]. 其中基于Godunov数值方案的BIG2程序的可靠性已经被德国GSI (Helmholtz-Zentrum für Schwerionenforschung, 重离子研究中心)的相关实验所证实, 具有较好的可靠性[19–28]. Aardvark程序已经能够模拟激光情况, 而离子束与靶物质的相互作用过程也能给出清晰的模拟结果. 可以发现, 相比BIG2程序的结果, 靶子物态参数的变化图像是高度一致的, 其演化趋势同图 3的结果类似, 所以Aardvark程序具备较高的可信度. 进一步对比表 2数值, 发现对单位质量的能量沉积和压强, Aardvark程序计算的结果比BIG2程序计算的略高, 而温度和密度数值略微偏低, 这些数值之间的偏差不超过30%. 我们分析认为, 这种偏差的主要原因在于两个程序分别采用了不同的电子能损计算模型以及靶物质状态方程数据库. 其一, Aardvark辐射流体力学程序采用的是改进的第一性原理分子动力学方法计算得到的状态方程数据库, 而BIG2程序采用半经验模型的EOS或者调用SESAME数据库, 这两者具有高度的一致性. 其二, BIG2程序采用的能量沉积值是由SRIM方法计算得到, 而Aardvark程序采用了高温扩展模型—SSM[22,29,30]. 通过对比表明, 在一定的误差范围内, Aardvark程序能给出合理的物质状态参数变化的过程和具体数值, 对于未来指导实验设计具有重要的价值和意义. 但同时也说明, 开展高精度实验的迫切性, 对于验证和发掘我们自己模型的准确性也是非常重要的.
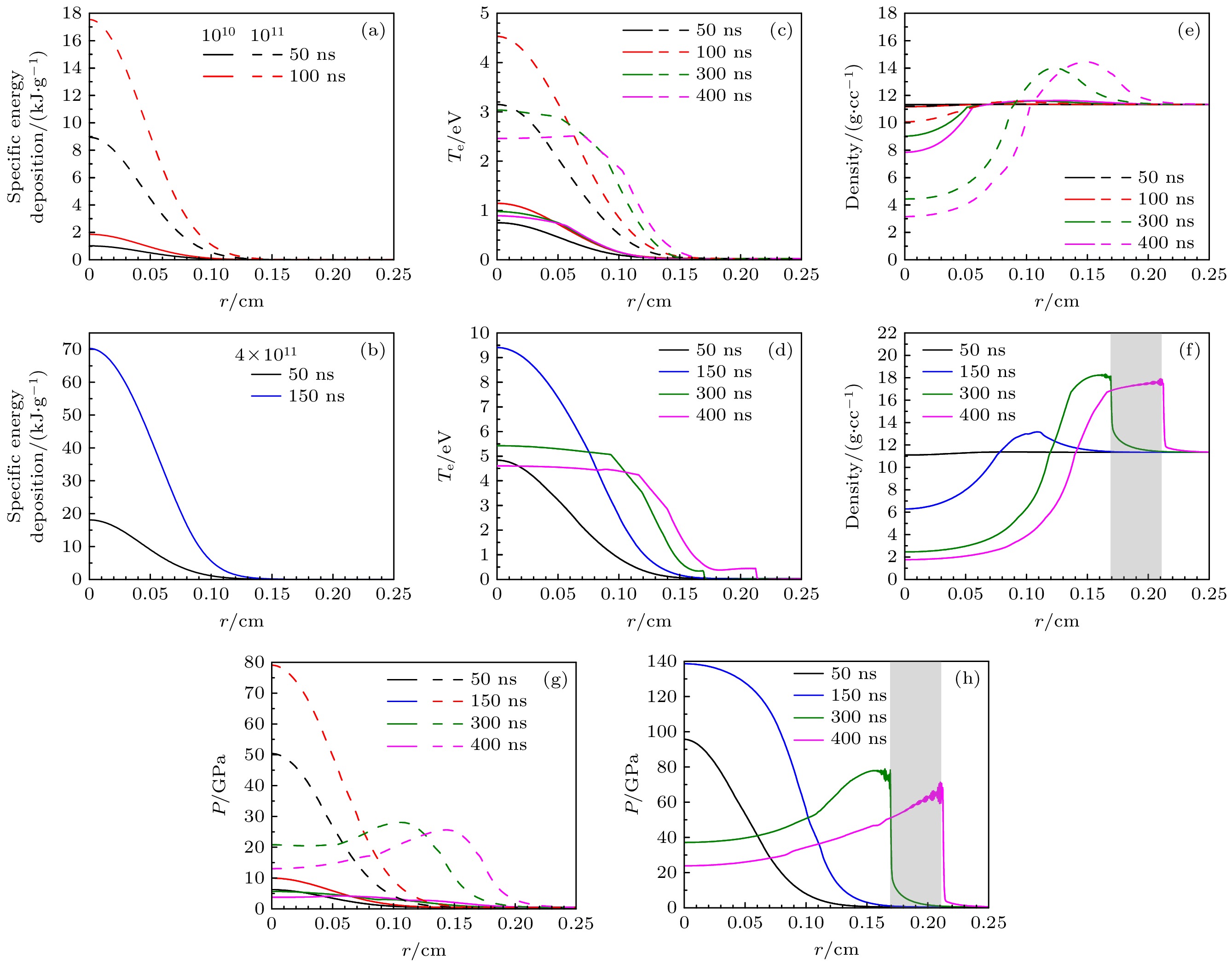
图4(a), (c), (e), (g)展示了入射U离子束能量为500 MeV/u, 脉冲长度为100 ns的条件下, 分别在束流强度为1 × 1010, 1 × 1011 ppp时的物态参数的含时演化过程. 随着束流强度的增加, 靶物质轴心处的压强从10 GPa迅速跃升至80 GPa, 温度也从1 eV显著升高至4.5 eV, 从而使靶物质的状态在温稠密物质区域内呈现出连续的演变过程. 随着束流强度的增加, 单位时间内作用于靶材料的能量输入显著提升, 进而导致单位质量的能量沉积大幅增加. 这一过程不仅显著提升了靶物质的温度, 还使其内部压强急剧升高. 因此, 束流强度对靶物质的状态参数具有极为显著的影响. 为进一步深入研究离子束流强度对靶物质物态参数的影响, 对离子束流强度提升至4 × 1011 pppp的情况进行了详细计算. 在图4(b), (d), (f), (h)中, 可以观察到在演化后期靶物质的状态参数出现了剧烈变化, 即为冲击波(图中阴影区域). 这种高速冲击波能够使介质的压强、温度和密度在波前发生显著的跳跃式变化, 反映了其在极端条件下对材料的强烈作用. 通过系统模拟计算发现, 随着离子束流强度的持续增加, 材料局部的温度会迅速升高, 热膨胀效应显著增强. 这一过程进一步引发了材料内部辐射压强的显著提升, 并显著加快了冲击波的传播速度. 与激光方式相比, 重离子束能够在材料内部较深的位置沉积能量, 并实现更高的冲击压力. 这一特性使其在研究和处理大体积材料的内部状态方面展现出独特的优势. 未来在HIAF装置的实验中借助冲击波所产生的高能量密度环境, 有望更深入地探究材料的结构和物态参数的变化.
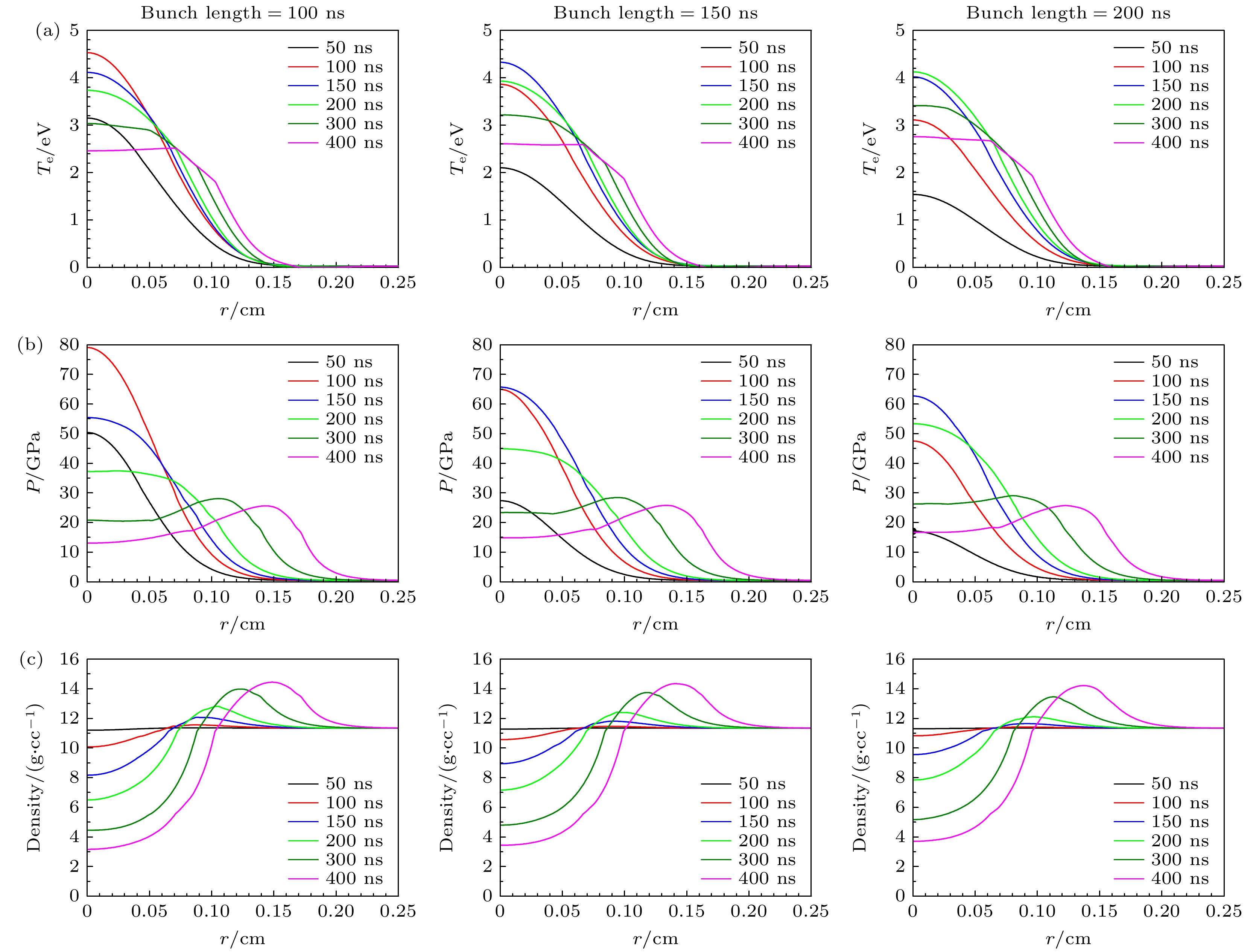
图5展示了在离子束能量为500 MeV/u, 束流强度为1 × 1011 ppp, 在不同离子束脉冲长度下(分别为100, 150和200 ns), 靶物质状态参数的演化过程曲线. 从图5(a)可以看出, 随着离子束流脉冲时间的增加, 靶物质中电子的温度逐渐降低. 对应图5(b)显示, 轴心处靶物质达到的最大压强值也随着脉冲时间的增加而降低. 图5(c)描绘了靶物质的密度演化曲线, 其变化相对较小, 整体趋势不明显. 值得注意的是, 当脉冲长度为200 ns时, 轴心处最大压强在约150 ns时达到峰值, 而非脉冲末端. 这是因为束团脉冲过长, 前150 ns的能量沉积导致靶心区温度急剧升高, 引发快速流体膨胀, 密度急剧下降. 而后续50 ns的束流因靶区密度减低, 能量沉积效率显著降低, 无法进一步提升压强. 此外, 若离子束的束斑半径较小且脉冲宽度过大, 因流体运动的时间尺度远小于脉冲宽度, 靶物质在脉冲初期即发生飞散. 这种情况下, 离子束无法有效加热样品, 已加热的样品热量会部分向外传递并耗散, 导致离子束能量无法充分沉积, 靶材料的温度只能升至较低水平, 从而产生能量损耗. 总体而言, Aardvark程序能够实现靶物质状态参数的广泛且精细调控, 为高能量密度物质状态的研究提供了一种高效且精确的模拟工具.
-
为了研究不同靶材料在极端条件下的状态演化规律, 基于Aardvark程序开展了铀离子束与圆柱型固体靶(Pb, Al, Au和LiF)相互作用的数值模拟研究. 其模拟参数为: 离子束脉冲时间为100 ns、高斯型束斑直径为1 mm、离子束能量为500 MeV/u. 表 3列出了在不同离子束流强度下, 各靶物质轴心区的峰值状态参数(温度、密度、压强和单位质量的能量沉积). 以铅(Pb)为例, 其轴心区温度在束流强度
$ 10^{9} $ ppp时, 靶物质的温度远高于其熔点(600.6 K), 导致物质从固态转变为液态. 这一相变现象表明, 低熔点材料在相对较低的温度下即可发生部分或完全熔化, 从而影响其整体压强. 当材料熔化时, 能量更多地用于相变过程, 而非进一步提升压强. 类似的现象在金(Au, 熔点1337 K)中亦被观察到: 当轴心温度接近熔点时, 压强的上升速率随束流强度增加相比于温度而趋缓. 这些结果表明, 在极端条件下, 材料的熔化行为对单位质量的能量沉积和压强变化具有重要影响. 本工作为强流重离子束与靶物质相互作用的多尺度建模提供了关键数据支撑, 尤其为HIAF装置上高能量密度物理实验的靶设计优化奠定了理论基础. -
本文利用Aardvark程序, 针对HIAF装置的束靶实验参数空间, 模拟了铀离子束与多种靶物质的相互作用过程, 通过与现有程序的比较, 验证了该程序在预测高能量密度物质状态研究中的可靠性. 通过模拟计算, 详细记录了靶物质的单位质量的能量沉积、温度、密度和压强状态参数的含时演化图像, 并建立了相应的模拟参数数据库, 为理解实验中高能量密度物质状态的产生过程提供了重要的理论支持. 随着离子束流强度的增加, 靶物质被迅速加热, 可引起靶物质的相变和冲击波的产生等现象. 计算结果表明, 在重离子驱动方式下, 产生的高能量密度物质在轴心处能够形成大体积、空间分布均匀的温稠密物质区域, 在实验研究方面具有特殊优势. 该工作为未来在HIAF装置上开展的高精度、系统性的高能量密度物理实验研究提供了重要的理论支持.
利用Aardvark程序预测HIAF上强流重离子束驱动产生的高能量密度物质状态
Aardvark program predicted high-energy density matter induced by intense heavy ion beams at HIAF
-
摘要: 强流重离子束驱动产生的高能量密度物质具有大体积、状态均匀、材料种类多样等显著特色, 为高能量密度物理研究提供了新的研究途径. 我国“十二五”规划建设的强流重离子加速器装置(HIAF)正加速推进, 将为重离子束驱动的高能量密度物理实验研究提供独特的实验平台与新的机遇. 本文基于HIAF上重离子束流参数特点, 利用自主研发的一维辐射流体程序Aardvark进行了数值模拟计算, 预测了铀离子束与铅靶相互作用下可产生的物质状态. 结果清晰展示了重离子束能量加载过程中, 靶物质的单位质量的能量沉积、温度、压强和密度的含时演化图像, 以及靶物质轴心处产生的大面积均匀区. 研究发现随着重离子束流强度的逐步提升, 靶物质的温度等状态参数呈现出非线性的增长趋势, 靶物质内部还引发了冲击波现象. 本研究还构建了铀离子束与多种靶物质相互作用产生的靶物质状态参数的数据库. 相关模拟数据不仅为HIAF上重离子束驱动的高能量密度物理实验研究规划提供重要的前期理论指导, 而且为深入研究高能量密度物质的产生、演化及其特性等提供了关键的理论支持. 该工作将为推动我国在强流重离子束驱动的高能量密度物理领域的研究工作发挥重要作用.
-
关键词:
- 强流重离子束 /
- 高能量密度物质 /
- 流体动力学 /
- Aardvark程序 /
- 强流重离子加速器装置
Abstract:The unique properties of heavy-ion beam-driven high-energy density matter (HEDM), characterized by macroscale uniformity, extended volumetric dimension, and material diversity, present novel opportunities for advancing high-energy density physics (HEDP). The High-Intensity Heavy-Ion Accelerator Facility (HIAF), a cornerstone project which is initiated during China’s 12th Five-Year Plan, is currently being accelerated in construction. After completion, it will become a primary platform for experimental research on the HEDP phenomenon induced by intense heavy-ion beams. In this work, a self-developed 1D radiation hydrodynamics code, Aardvark, is used to simulate the interaction dynamics between uranium ion beams and cylindrical targets under HIAF-relevant beam parameters. The results show time-evolution images of specific energy deposition, temperature, pressure, and density of the target material in the radial direction during heavy-ion beam energy loading. By comparing the state of matter produced by the ion beam hitting the target at different beam energy and intensity, a interesting phenomenon is observed, i.e. a plateau region of temperature and pressure are formed near the axis center. This result indicates that under the action of the heavy-ion beam, a substantially homogeneous region is formed in the axis center the target material, further elucidating the salient characteristics of the heavy-ion beam-driven high energy density material, i.e. homogeneous state. The state parameters of the target matter undergo significant changes in the process, for a beam duration of 150 ns and a beam intensity of 4 × 1011 ppp (particle per pulse) and beam energy of 500 MeV/u. A sharp discontinuity in pressure and density occurs, forming a phenomenon known as a shock wave. Thereby, systematic modulation of heavy ion beam parameters enables investigation into the generation and propagation dynamics of shock waves. This study further constructs a systematic database that meticulously records the state parameters of target materials when uranium ion beams interact with various types of targets. The relevant simulation data provide important theoretical guidance for planning heavy-ion beam-driven high-energy density physics experiments at HIAF and crucial theoretical support for in-depth research on the generation, evolution, and properties of high-energy density matter. These advances in calculation position HIAF as a transformative platform for detecting extreme-state substances, with is of direct implications in studying inertial confinement fusion and modeling astrophysical plasma. -

-
图 2 根据HIAF上的铀离子束与铅靶作用的设计方案示意图 (a) 离子束打靶的能量沉积示意图; (b)铀离子束与圆柱型铅靶作用的示意图. 红色虚线区域表示能量沉积最大的位置即布拉格峰
Figure 2. Schematic diagram of the design scheme based on the interaction of the uranium ion beam and the lead target on the HIAF: (a) Schematic diagram of the energy deposition of the ion beam target; (b) schematic diagram of the interaction of the uranium ion beam with a cylindrical lead target. The red dotted line area indicates the location where the energy is deposited the most, the Bragg peak.
图 3 不同束团能量下, 束团强度为1 × 1011 ppp, 长度为100 ns的物态参数随半径的变化规律 (a) 离子束单位质量的能量沉积; (b) 电子温度; (c) 密度; (d) 压强
Figure 3. Variation of the beam parameters with radius at different beam energy levels, with a beam intensity of 1 × 1011 ppp and a length of 100 ns: (a) Specific energy deposition; (b) Te; (c) density; (d) P
图 4 束团能量为500 MeV/u时的物态参数 (a), (c), (e), (g)不同束流强度(1 × 1010, 1 × 1011 ppp)下物态参数的对比, 脉冲长度为100 ns; (b), (d), (f), (h)脉冲长度为150 ns, 束流强度为4 × 1011 ppp的物态参数演化
Figure 4. Matter state parameters when the beam energy is 500 MeV/u: (a), (c), (e), (g) The comparison of matter state parameters under different beam intensities (1 × 1010, 1 × 1011 ppp), with a bunch length of 100 ns; (b), (d), (f), (h) the evolution of matter state parameters with a bunch length of 150 ns and a beam intensity of 4 × 1011 ppp.
表 1 重离子加速器装置参数对比
Table 1. Comparison of parameters of heavy ion accelerator device.
HIHEX@FAIR HEDP@HIAF Ion $ \mathrm{U}^{28+} $ $ \mathrm{U}^{92+} $ E/AGeV $ 2\ $ $ 0.8—1\ $ Intensity/ppp $ 2 \times 10^{12} \ $ $ (0.1—2) \times 10^{12} \ $ Pulse length/ns 50 $ 50—100 \ $ $ \Delta {E} / {E} $ $ \pm 1 {\text{%}} $ $ \pm 0.5{\text{%}} $ Beam spot size/mm $ 1 \ $ $ 0.5—1 \ $ 表 2 Aardvark程序与BIG2程序[18]的物态参数对比
Table 2. Comparison of the state parameters of the Aardvark program and the BIG2 program[18].
Code Pulse
lengths
/nsE/ $ (\mathrm{kJ} \cdot \mathrm{g}^{-1}) $ $ {T}_{\mathrm{e}} /\mathrm{K} $ $\rho/$ $ ({\rm g} \cdot {\rm cm}^{-3}) $ P/GPa BIG2 100 14.8 58000.0 10.2 75.0 150 14.0 55000.0 9.3 58.0 Aardvark 100 19.1 55205.0 9.9 84.4 150 18.9 52613.7 8.8 69.4 表 3 离子束流强变化时, 不同材料的靶物质在轴心处产生的靶物质状态参数的极值
Table 3. Maximum values of the state parameters of target materials at the axis as ion beam intensity changes.
Target Intensity
/ppp$\rho/({\rm g}{\cdot}{\rm cm}^{-3}) $ $ {P}/\mathrm{GPa} $ $ {T_{{\mathrm{e}}}}/\mathrm{K} $ $ E/(\mathrm{kJ}{\cdot}\mathrm{g}^{-1}) $ Target Intensity
/ppp$\rho/({\rm g}{\cdot}{\rm cm}^{-3}) $ $ {P}/\mathrm{GPa} $ $ {T_{{\mathrm{e}}}}/\mathrm{K} $ $ E/(\mathrm{kJ}{\cdot}\mathrm{g}^{-1}) $ Pb $ 10^9 $ 11.33 1.48 2561.12 0.17 Al $ 10^9 $ 2.69 0.90 1089.32 0.26 $ 10^{10} $ 11.18 9.98 13279.05 1.86 $ 10^{10} $ 2.65 4.02 4952.81 2.57 $ 10^{11} $ 10.07 79.09 52577.75 17.54 $ 10^{11} $ 2.26 22.81 24508.74 25.95 $ 10^{12} $ 7.65 441.22 209187.11 177.03 $ 10^{12} $ 1.13 93.63 91883.41 264.66 Au $ 10^9 $ 19.21 7.75 1617.67 0.18 LiF $ 10^9 $ 2.63 0.63 696.27 0.23 $ 10^{10} $ 18.50 49.24 10909.41 1.76 $ 10^{10} $ 2.59 3.49 4293.67 2.28 $ 10^{11} $ 16.74 172.76 56315.57 17.54 $ 10^{11} $ 2.25 20.8 22396.72 23.08 $ 10^{12} $ 10.27 574.96 199485.15 178.75 $ 10^{12} $ 1.16 88.5 87265.98 235.73 -
[1] 赵永涛, 张子民, 程锐, Hoffmann Dieter, 马步博, 王友年, 王瑜玉, 王兴, 邓志刚, 任洁茹, 刘巍, 齐伟, 齐新, 苏有武, 杜应超, 李福利, 李锦钰, 杨杰, 杨建成, 杨磊, 肖国青, 吴栋, 何斌, 宋远红, 张小安, 张世政, 张琳, 张雅, 张艳宁, 陈本正, 陈燕红, 周征, 周贤明, 周维民, 赵红卫, 赵全堂, 赵宗清, 赵晓莹, 胡章虎, 弯峰, 栗建兴, 徐忠锋, 高飞, 唐传祥, 黄文会, 曹树春, 曹磊峰, 盛丽娜, 康炜, 雷瑜, 詹文龙 2020 中国科学: 物理学 力学 天文学 50 112004 doi: 10.1360/SSPMA-2020-0275 Zhao Y T, Zhang Z M, Cheng R, Hoffmann D, Ma B B, Wang Y N, Wang Y Y, Wang X, Deng Z G, Ren J R, Liu W, Qi W, Qi X, Su Y W, Du Y C, Li F L, Li J Y, Yang J, Yang J C, Yang L, Xiao G Q, Wu D, He B, Song Y H, Zhang X A, Zhang S Z, Zhang L, Zhang Y, Zhang Y N, Chen B Z, Chen Y H, Zhou Z, Zhou X M, Zhou W M, Zhao H W, Zhao Q T, Zhao Z Q, Zhao X Y, Hu Z H, Wan F, Li J X, Xu Z F, Gao F, Tang C X, Huang W H, Cao S C, Cao L F, Sheng L N, Kang W, Lei Y, Zhan W L 2020 Sci. Sin.-Phys. Mech. Astron. 50 112004 doi: 10.1360/SSPMA-2020-0275 [2] 程锐, 张晟, 申国栋, 陈燕红, 张延师, 陈良文, 张子民, 赵全堂, 杨建成, 王瑜玉, 雷瑜, 林平, 杨杰, 杨磊, 马新文, 肖国青, 赵红卫, 詹文龙 2020 中国科学: 物理学 力学 天文学 50 112011 doi: 10.1360/SSPMA-2020-0265 Cheng R, Zhang S, Shen G D, Chen Y H, Zhang Y S, Chen L W, Zhang Z M, Zhao Q T, Yang J C, Wang Y Y, Lei Y, Lin P, Yang J, Yang L, Ma X W, Xiao G Q, Zhao H W, Zhan W L 2020 Sci. Sin.-Phys. Mech. Astron. 50 112011 doi: 10.1360/SSPMA-2020-0265 [3] 任洁茹, 王佳乐, 陈本正, 徐皓, 张艳宁, 魏文青, 徐星, 马步博, 胡忠敏, 尹帅, 冯建华, 宋莎莎, 张世政, Hoffmann Dieter, 赵永涛 2021 强激光与粒子束 33 012005 doi: 10.11884/HPLPB202133.200339 Ren J R, Wang J L, Chen B Z, Xu H, Zhang Y N, Wei W Q, Xu X, Ma B B, Hu Z M, Yin S, Feng J H, Song S S, Zhang S Z, Hoffmann D, Zhao Y 2021 High Power Laser and Particle Beams 33 012005 doi: 10.11884/HPLPB202133.200339 [4] Ren J R, Zhao Y T, Cheng R, Xu Z F, Xiao G Q 2017 Nucl. Instrum. Methods Phys. Res., Sect. B 406 703 doi: 10.1016/j.nimb.2017.03.018 [5] 赵红卫 2024 现代物理知识 36 42 Zhao H W 2024 Mod. Phys. 36 42 [6] Sharkov B Y, Hoffmann D H, Golubev A A, Zhao Y T 2016 Matter Radiat. Extremes 1 28 doi: 10.1016/j.mre.2016.01.002 [7] 赵红卫, 徐瑚珊, 肖国青, 夏佳文, 杨建成, 周小红, 许怒, 何源, 马新文, 杨磊, 陈旭荣, 唐晓东, 赵永涛, 孙志宇, 王志光, 胡正国, 张军辉, 马力祯, 原有进, 詹文龙 2020 中国科学: 物理学 力学 天文学 50 112006 doi: 10.1360/SSPMA-2020-0248 Zhao H W, Xu H S, Xiao G Q, Xia J W, Yang J C, Zhou X H, Xu N, He Y, Ma X W, Yang L, Chen X R, Tang X D, Zhao Y T, Sun Z Y, Wang Z G, Hu Z G, Zhang J H, Ma L Z, Yuan Y J, Zhan W L 2020 Sci. Sin.-Phys. Mech. Astron. 50 112006 doi: 10.1360/SSPMA-2020-0248 [8] Hoffmann D H H, Fortov V E, Lomonosov I V, Mintsev V, Tahir N A, Varentsov D, Wieser J 2002 Phys. Plasmas 9 3651 doi: 10.1063/1.1498260 [9] 廖棱锐, 刘浩, 杨咏乐, 莫崇杰, 陈良文, 张晟, 程锐, 张平, 康炜 2024 计算物理 41 1 Liao L R, Liu H, Yang Y L, Mo C J, Chen L W, Zhang S, Cheng R, Zhang P, Kang W 2024 Chin. J. Comput. Phys. 41 1 [10] 彭惠民 2008 等离子体中辐射输运和辐射流体力学 (北京: 国防工业出版社) 第243—253页 Peng H M 2008 Radiation Transport in Plasma and Radiation Hydrodynamics (Beijing: National Defense Industry Press) pp243–253 [11] Atzeni S, Meyer-ter Vehn J 2004 The Physics of Inertial Fusion: Beam Plasma Interaction, Hydrodynamics, Hot Dense Matter (Vol. 125) (Oxford: OUP) pp371–408 [12] Mihalas D, Weibel-Mihalas B 1985 Foundations of Radiation Hydrodynamics ( Oxford: OUP) pp235-258 [13] 王友年, 马腾才 2020 计算物理 7 235 doi: 10.19596/j.cnki.1001-246x.1990.02.014 Wang Y N, Ma T C 2020 Chin. J. Comput. Phys. 7 235 doi: 10.19596/j.cnki.1001-246x.1990.02.014 [14] 张智猛, 齐伟, 崔波, 张博, 洪伟, 周维民 2023 计算物理 40 210 doi: 10.19596/j.cnki.1001-246x.8609 Zhang Z M, Qi W, Cui B, Zhang B, Hong W, Zhou W M 2023 Chin. J. Comput. Phys. 40 210 doi: 10.19596/j.cnki.1001-246x.8609 [15] Couillaud C, Deicas R, Nardin P, Beuve M A, Guihaumé J M, Renaud M, Cukier M, Deutsch C, Maynard G 1994 Phys. Rev. E 49 1545 doi: 10.1103/PhysRevE.49.1545 [16] Blöchl P E, Parrinello M 1992 Phys. Rev. B 45 9413 doi: 10.1103/PhysRevB.45.9413 [17] Zhang S, Wang H W, Kang W, Zhang P, He X T 2016 Phys. Plasmas 23 042707 doi: 10.1063/1.4947212 [18] Cheng R, Lei Y, Zhou X M, Wang Y Y, Chen Y H, Zhao Y T, Ren J R, Sheng L N, Yang J C, Zhang Z M, Du Y C, Gai W, Ma X W, Xiao G Q 2018 Matter Radiat. Extremes 3 85 doi: 10.1016/j.mre.2017.11.001 [19] Fortov V, Goel B S, Munz C D, Ni A L, Shutov A, Vorobiev O Y 1996 Nucl. Sci. Eng. 123 169 doi: 10.13182/NSE96-A24181 [20] Tahir N A, Hoffmann D H H, Kozyreva A, Shutov A, Maruhn J A, Neuner U, Tauschwitz A, Spiller P, Bock R 2000 Phys. Rev. E 61 1975 doi: 10.1103/PhysRevE.61.1975 [21] Tahir N A, Lomonosov I V, Borm B, Piriz A R, Shutov A, Neumayer P, Bagnoud V, Piriz S A 2017 ApJS 232 1 doi: 10.3847/1538-4365/aa813e [22] Tahir N A, Shutov A, Lomonosov I V, Piriz A R, Neumayer P, Bagnoud V, Piriz S A 2018 ApJS 238 27 doi: 10.3847/1538-4365/aadd4c [23] Tahir N A, Shutov A, Neumayer P, Bagnoud V, Piriz A R, Deutsch C 2022 Eur. Phys. J. Plus 137 273 doi: 10.1140/epjp/s13360-022-02476-2 [24] Tahir N A, Shutov A, Lomonosov I V, Piriz A R, Wouchuk G, Deutsch C, Hoffmann D, Fortov V 2006 High Energy Density Phys. 2 21 doi: 10.1016/j.hedp.2006.02.001 [25] Tahir N A, Stöhlker T, Shutov A, Lomonosov I V, Fortov V E, French M, Nettelmann N, Redmer R, Piriz A R, Deutsch C, Zhao Y, Zhang P, Xu H, Xiao G, Zhan W 2010 New J. Phys. 12 073022 doi: 10.1088/1367-2630/12/7/073022 [26] Tahir N A, Deutsch C, Fortov V E, Gryaznov V, Hoffmann D H H, Kulish M, Lomonosov I V, Mintsev V, Ni P, Nikolaev D, Piriz A R, Shilkin N, Spiller P, Shutov A, Temporal M, Ternovoi V, Udrea S, Varentsov D 2005 Phys. Rev. Lett. 95 035001 doi: 10.1103/PhysRevLett.95.035001 [27] Tahir N A, Shutov A, Neumayer P, Bagnoud V, Piriz A R, Lomonosov I V, Piriz S A 2021 Phys. Plasmas 28 032712 doi: 10.1063/5.0037943 [28] Tahir N, Lomonosov I, Borm B, Piriz A, Neumayer P, Shutov A, Bagnoud V, Piriz S 2017 Contrib. Plasma Phys. 57 493 doi: 10.1002/ctpp.201700076 [29] Tahir N A, Adonin A, Deutsch C, Fortov V E, Grandjouan N, Geil B, Grayaznov V, Hoffmann D H H, Kulish M, Lomonosov I V 2005 Nucl. Instrum. Methods Phys. Res. A 544 16 doi: 10.1016/j.nima.2005.01.178 [30] Tahir N A, Neumayer P, Lomonosov I V, Shutov A, Bagnoud V, Piriz A R, Piriz S A, Deutsch C 2020 Phys. Rev. E 101 023202 doi: 10.1103/PhysRevE.101.023202 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: