首页
登录
注册
-
随着微通道在材料、芯片、航空航天等领域的广泛应用, 其传热传质特性已成为目前研究的热点. 微通道内的质量运输是由压差驱动的, 此过程通常受气体可压缩性、表面粗糙度、稀薄效应等多因素[1–3]的独立或耦合影响, 会引起管内气流加速、流态转化[4]、温降压降、流动壅塞[5]等复杂现象, 这都对流道内沿程流动模拟及运输流量预测带来了挑战.
目前关于微通道质量运输特性的理论及数值研究有很多. ANSI N14.5[6]中提出了用于预测微圆管气体泄漏流量的计算公式, 考虑了连续流以及壅塞流等流动情况. 而后Anderson等[7]实验验证了此计算公式的预测能力, 实验采用的管径范围小于250 μm, 发现当质量流量小于1 atm·cm3/s时, 连续流的计算结果与实验吻合性较好, 而壅塞流条件下的计算结果比实验结果高4个数量级. Chen等[8]采用Baldwin-Lomax双层湍流模型求解可压缩湍流边界层方程, 当管径在100 μm量级时, 数值模拟得到的流量预测结果高于实验值与理论值. Asako等[9,10]提出基于任意拉格朗日欧拉方法求解二维可压缩动量和能量方程, 模拟气体可压缩性影响下管流完全发展阶段的沿程流动参数分布; 文献[11–13]基于此方法研究了层流、层流-湍流以及全湍流条件下质量流量、平均速度等随雷诺数(Re)的变化, 发现层流状态下
$f\cdot Re$ 计算值与实验值存在较大偏差, 全湍流状态下依据Blasius方程计算得到的质量流量计算值与实验值吻合较好. Lijo等[14]基于三维、稳态条件下的雷诺平均Navier-Stokes方程, 研究了流动壅塞而导致的微通道内的流动特性的影响, 发现当上游压力一定, 仅改变背压时, 高压比可以使出口马赫数达到超声速状态, 当压力条件相反时的研究暂未涉及. Wang等[15]通过积分方法求解一维可压缩流动方程, 采用Colebrook关系式湍流摩擦系数计算结果求解质量流量, 并与文献[11]中数值模拟与实验结果进行了对比, 得到了相同的结论. 努森数Kn是用于描述气体分子自由程与特征长度之间关系的无量纲数, 用以判断气体的稀薄程度, 以上理论公式或数值方法基础均为连续介质假设, 即Kn < 0.001, 而当管径达到1 μm量级或背压接近于真空时, Kn通常大于0.001, 即流动处于滑移流与稀薄流范围内[16], 此时基于传统Navier-Stokes (N-S)方程求解方法已不再适用, 目前常用解决方法为基于N-S方程框架, 采用壁面速度滑移与温度跳跃边界条件代替无滑移边界条件[17]. Yovanovich和Khan [18]基于分子流至最小努森数以及最小努森数至连续流两种流态范围内的圆形与矩形截面微通道, 通过新定义的无量纲质量流率提出Poiseuille-Knudsen数值模型, 对一阶滑移条件[19]和二阶滑移条件[20]得到的研究结果进行修正, 发现在上述两种流态范围内对于相同特征尺度的两种微通道内质量运输流量几乎是等效的, 偏差值小于1.6%. 此外, 对于Kn > 0.1的流动, 直接采用分子动力学或气体动理学方法描述流动和传热行为也是目前的研究热点, 例如DSMC (the direct simulation Monte Carlo)方法[21,22]、适用于全流域的UGKS (unified gas-kinetic scheme)方法[23,24]等.与数值计算方法研究相关的实验进展均集中在摩擦系数的测量与变化规律研究, 这是因为数值计算中采用的摩擦系数计算模型是基于实验总结的, 且直接影响运输质量预测结果的准确性. Hong等[25]通过实验验证了达西摩擦系数与范宁摩擦系数公式的准确性, 发现在气体可压缩性影响下范宁摩擦系数与理论值吻合较好, 而达西摩擦系数则偏高. Celata等[26]研究了长径比对微圆管内转捩 雷诺数的影响, 发现不同长径比条件下转捩雷诺数均大于2000, 且未表现出明显的相关性, 而对于 矩形截面, 不同纵横比条件下转捩雷诺数则存在较为明显的差异[27]. 文献[28,29]通过测量出口附近的质量流量和局部压力来确定局部摩擦系数、全局平均摩擦系数、雷诺数等参数, 并发现随着雷诺数的增大测量的质量流量略有增大, 并在转捩期间趋于平稳. 此外, 微圆管表面粗糙度也会对摩擦系数及转捩雷诺数产生显著的影响[30,31]. 目前研究结果表明, 在多种因素的影响下, 摩擦系数时常与莫迪图中理论公式与经验结果存在差异, 即便这种差异是微小的, 也可能会对质量流量的预测带来可观的误差.
综上, 在连续介质范围内, 目前已采用的数值计算模型均集中在二维、三维角度, 而计算模型和求解的复杂性意味着更大的计算花费, 这对工程应用实则是不利的. 此外, 数值计算与实验结果表明, 当管内流动涉及转捩与湍流时, 预测结果仍然存在较大误差, 对于误差来源, 目前的分析与认识还存在一定局限性.
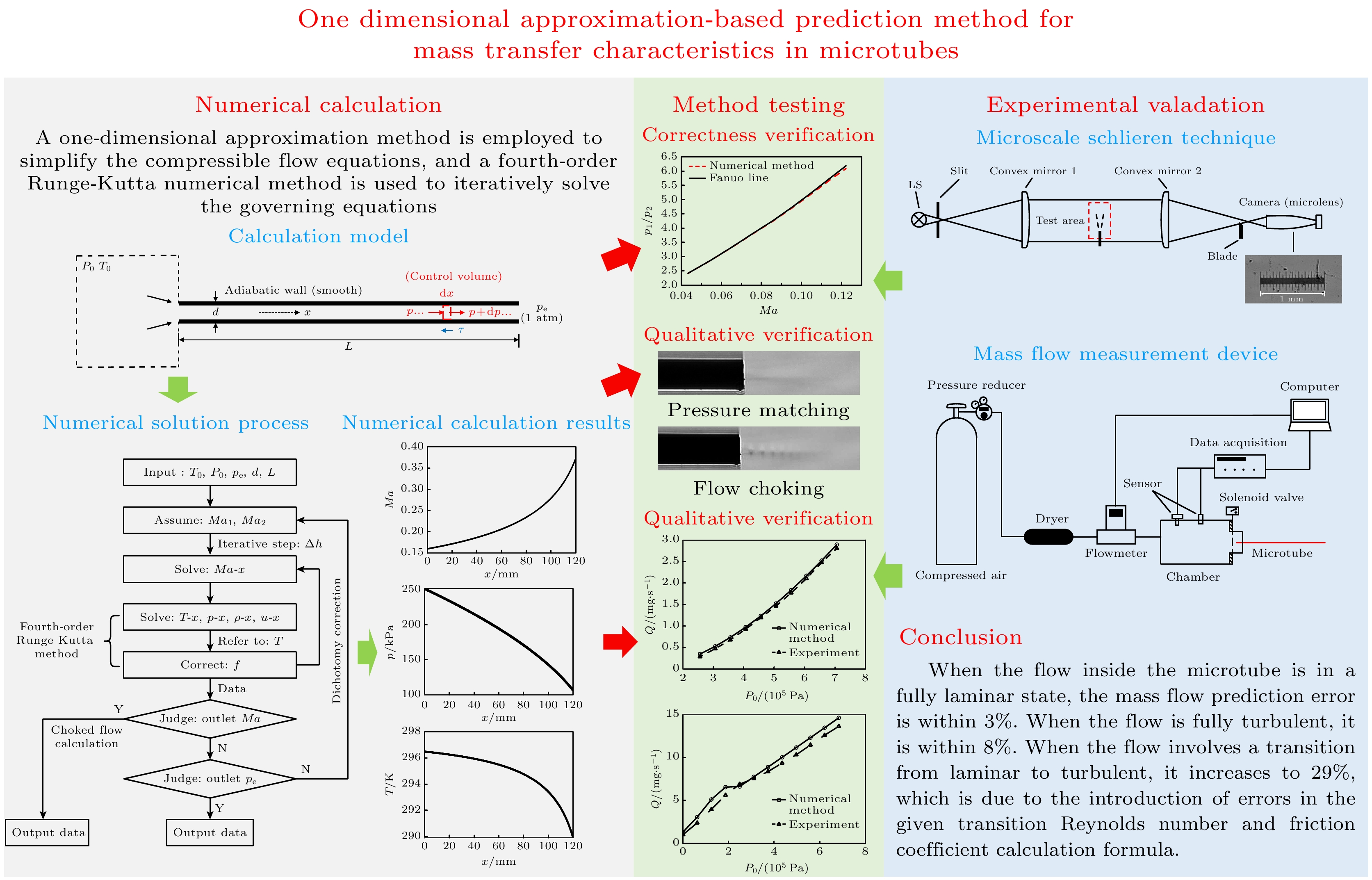
针对目前研究的不足, 本文提出采用一维处理法建立适用的计算模型及数值求解算法, 并结合实验方法进行合理性验证及误差分析, 该方法在保证预测精度的同时, 可简化理论模型并提高计算效率, 能够为工程应用提供参考与依据.
-
一维处理法是指流动参数在流线法向的变化率相比于流线方向可忽略时所采用的近似处理方法. 对于微尺度直管, 其管轴曲率半径远大于管道直径, 且充分发展条件下各截面速度型近乎不变, 当采用一维处理方法近似时, 各截面流动参数代表的均为该截面的平均属性, 这种近似带来的误差很小.
-
图1所示为微圆管计算模型的示意图. 当管壁暴露在环境中, 且上游总温与环境温度相同时, 在可压缩条件下对于导热率较低的管壁材料, 环境输入热量对流动的影响可忽略, 流动应近似为绝热过程, 故采用绝热壁假设; 直管上游相对于下游为高压, P0 和T0分别代表上游的滞止压力和滞止温度, 在压差驱动下气体经过微直管排入大气环境中(出口背压pe = 1 atm); 工质为干燥空气, 并假设其比热比γ为常数.
理论分析采用控制体方法(见图1), 考虑连续流体, 直管内的流动满足质量守恒条件, 采用其微分形式为
其中ρ为密度, u为速度.
由完全气体绝热条件下的能量方程和动量方程可得
其中, R为空气气体常数, A为截面面积, τ为剪应力, Aw为剪应力作用的壁面面积, T为静温, p为静压. 依据剪应力可以得到直管内摩擦系数f的定义:
又由完全气体状态方程和马赫数Ma的定义, 将其整理为微分形式:
联立方程(1)—(6), 整理可以得到关于Ma, p, T, ρ, u五项流动参数的控制方程组:
其中, d表示直管的水力直径, 当直管等截面时, 水力直径即为其自身管径; 方程组中每个方程的右侧均含有摩擦系数f, 求解中将其作为已知量, 计算方法依据现有的摩擦系数公式(7)和(8)给出, 层流至湍流过渡的临界雷诺数规定为2300 [32,33].
当Re ≤ 2300时, 采用经典的层流阻力系数计算公式:
当Re > 2300时, 依据实际壁面条件, 采用适用于光滑管的Blasuis阻力系数计算公式:
当内壁为粗糙表面则可采用考虑壁面粗糙度的Cole-brook公式[34].
考虑微分方程组中关于马赫数的微分方程, 仅包含了马赫数与流向位置两个参数, 若已知入口马赫数参数, 则可以采用数值方法进行迭代求解, 从而得到沿程的马赫数分布; 依据可压缩流动的处理方法, 滞止压力与当地静压、滞止温度与当地静温之间的关系为关于马赫数的函数, 则在已知滞止压力和滞止温度的前提下, 入口处的静压、静温与马赫数是一一对应的, 进而可以迭代求解其余4个流动参数方程.
-
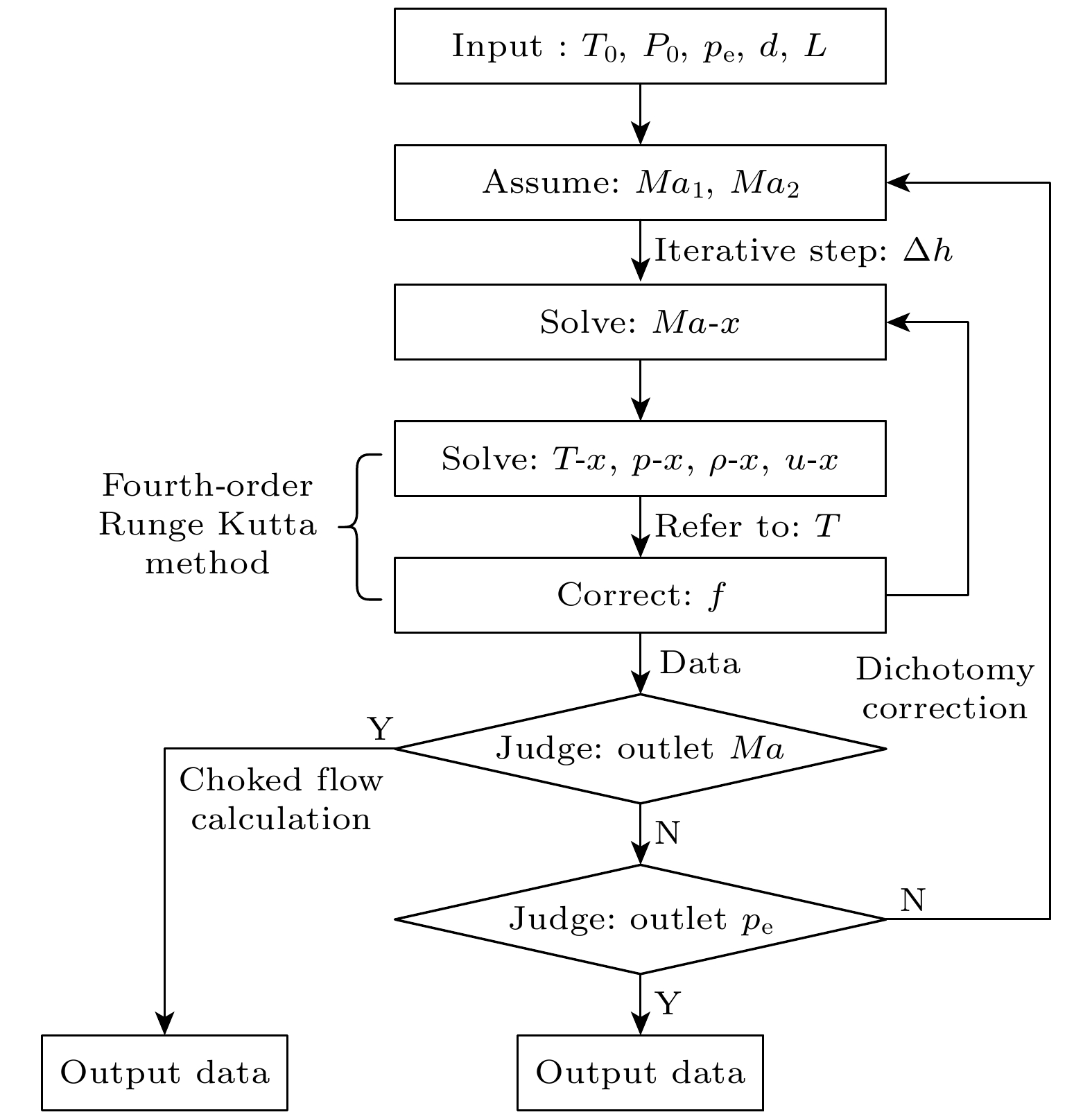
图2为求解控制方程组的数值计算流程图. 初始输入量为上游滞止压力、滞止温度、出口静压、直管截面直径以及长度. 其中, 滞止压力与滞止温度可提供入口的边界条件, 出口静压可为迭代结果提供判断条件.
由于绝热过程中接近出口处压力膨胀速度会出现骤增现象, 其对于马赫数的变化非常敏感, 入口马赫数提法采用假设两端极限马赫数(Ma1 = 0, Ma2 = 0.99), 随迭代次数进行二分法修正, 此方法可有效缩短代码运行时间.
当入口马赫数给定时, 采用具有四阶精度的Runge Kutta方法进行近似求解, 计算步长即为沿管长方向dx的长度, 每一个步长的计算中存在逻辑顺序, 马赫数为静压与静温计算的必要条件, 进而求得密度与速度参数, 不同计算步长的摩擦系数依据动力黏性系数变化修正, 直至计算至直管出口, 得到5个流动参数关于流向位置的数据, 即完成一次迭代过程.
又依据热力学第二定律中绝热过程的熵增原理以及控制方程组中的等式右侧中分母项可知, 微圆管内亚声速条件下的加速过程存在极限马 赫数(Malim = 1), 可以认为当出口达到极限马赫数时即直管内发生了流动壅塞, 此后无论如何增 大上游滞止压力, 出口马赫数不变. 因此迭代计算的判断条件是基于出口马赫数与出口压力同时控制的. 非壅塞条件下应为静压匹配条件, 判断精度小于0.1%; 壅塞条件下出口马赫数已知为1, 判断精度小于0.1%, 此时无需使用压力判断条件. 由于不同算例的运行时间会随收敛条件及计算步长而改变, 经过测试统计, 在 Intel Core i5-10210U处理器、LPDDR3 2133 MHz 8 GB内存以及512 GB NVMe PCIe高速固态硬盘的硬件条件, 以及本文采用的收敛精度和计算步长条件下, 算例实际计算时间均短于2 min.
-
本节基于范诺线参数比方程与数值计算结果对比验证数值计算方法的正确性, 并采用实验测试的方法对数值计算结果进行定性和定量验证, 检验物理计算模型的有效性和预测精度.
-
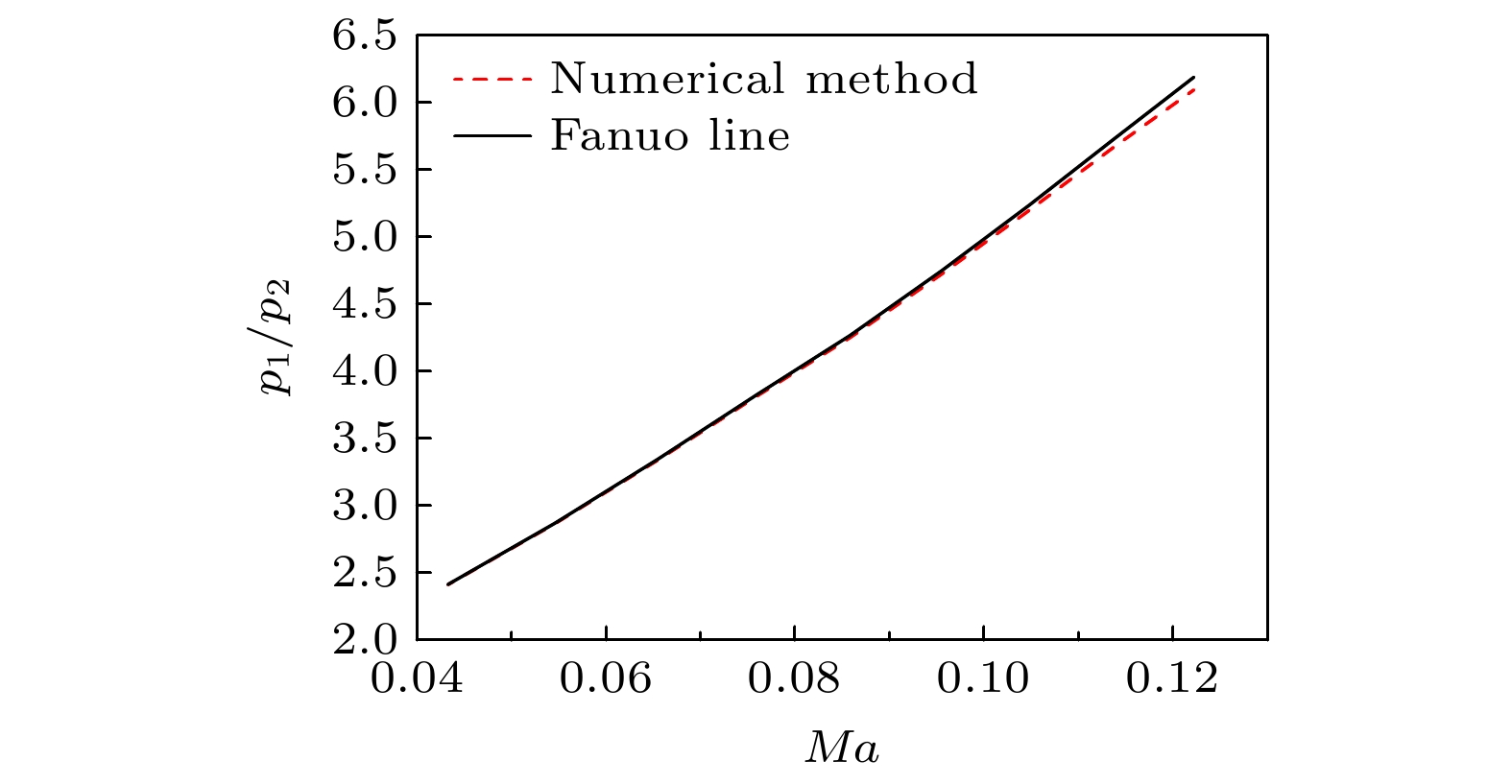
范诺线是描述等截面摩擦管流中气体状态变化的曲线, 不同状态下气体参数(如压力、温度、密度等)之间的比值均可以表示为与马赫数Ma之间的函数关系. 因此可以通过对比数值计算方法得到的参数比结果与范诺线理论结果来检验数值计算方法的正确性.
由2.2节可知, 通过数值方法可以求解给定初始条件下微圆管由入口至出口的沿程流动参数, 包括马赫数、静压、静温等. 选取静压比数据作为验证参数. 将每个计算工况下入口马赫数表示为Ma1, 出口马赫数表示为Ma2, 入口静压表示为p1, 出口静压表示为p2. 根据范诺线[35]静压比计算公式, 静压比与马赫数关系式如下:
其中比热比γ = 1.4.
验证采用算例的工况条件如下: P0 = 256—656 kPa(∆P0 = 50 kPa), T0 = 298 K, pe = 106 kPa, d = 100 μm, L = 120 mm. 将数值计算得到的Ma1和Ma2代入公式可得到理论静压比, 图3给出了理论静压比与数值计算得到的静压比的对比. 从图3可知, 数值计算方法与范诺线理论结果吻合性较好, 其最大误差小于1.5%, 故可证明本文采用的数值计算方法是正确的.
-
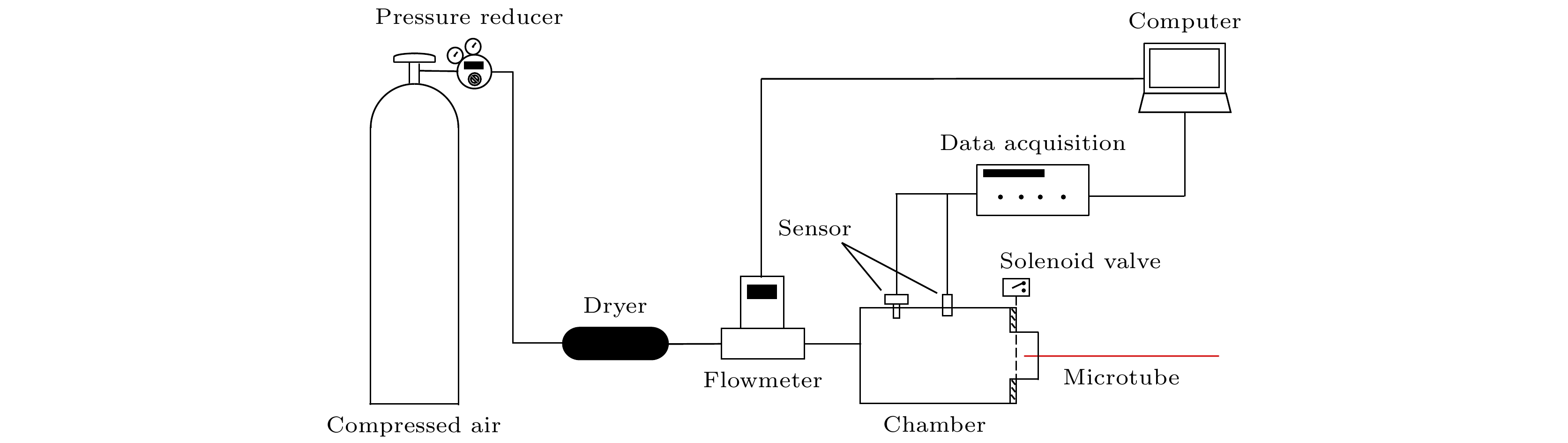
为验证本文中采用的物理计算模型的有效性, 依据数值计算方法中涉及的参数条件, 设计了微圆管实验测试系统, 可测量不同滞止压力驱动下微圆管的运输流量, 如图4所示.
实验气路采用高压气瓶供气, 工质为压缩空气, 高压气瓶出口设置数显减压器以调节腔室内的滞止压力. 减压后的气体工质需要经过干燥处理才可进入流量计. 流量计量程为0—1 slm (standard litre per minute), 最大耐压为3 MPa, 精度为±0.2% F.S, 屏显数据为1 atm (1 atm = 1.01325×105 Pa)和25 ℃条件下的实时流量. 流量计与高压腔室相连, 高压腔室的容积远大于直管的气体泄漏量, 即直管运输流量时腔室内的压力波动可忽略, 腔室内设置了NS-2型压力传感器和K型热电偶来测量腔室内的滞止压力与滞止温度, 压力传感器量程为1 MPa, 精度为±0.25% F.S, 热电偶测温精度为±0.1 ℃. 为减小测量的随机误差, 腔室内滞止压力与环境压力均由同一压力传感器测得. 直管材料为石英, 其内表面为光面, 管径尺寸均采用电子显微镜进行校准, 如图5所示.
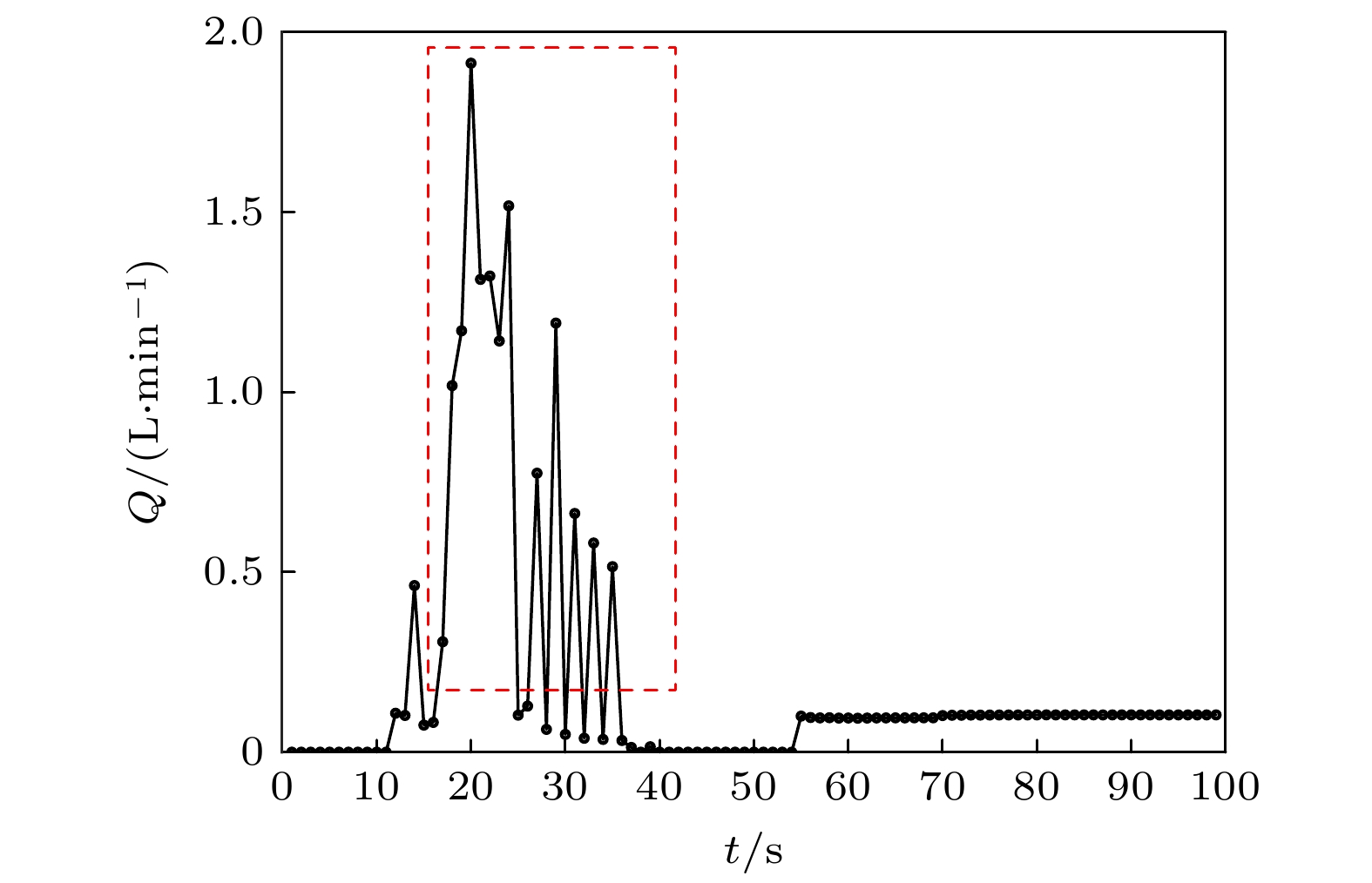
为验证整套实验装置的气密性, 且方便调节腔室内滞止压力, 腔室与直管之间设置了截止阀, 通过典型时间序列下的流量数据, 可反映实验流程, 如图6所示.
实验开始前, 截止阀关闭, 此时流量为0, 而后调节减压器向腔室增压, 如图6中红色框所示, 当腔室内的滞止压力达到预设条件时, 减压器后的压力与腔室内压力应保持一致, 此时流量重新归零, 即证明实验系统气密性良好. 实验开始时, 打开截止阀, 经过短暂的气路调整过程, 流量计数据即达到稳定状态, 此时流量计数据即为直管向外运输的空气的质量流量. 通过改变滞止压力和控制滞止温度, 即可得到不同滞止压力时直管的运输流量.
-
由2.2节可知, 小压差条件下, 直管中流动马赫增大的同时, 气流膨胀导致静压衰减, 直至在出口处与出口静压达到压力匹配的状态, 而当上下游压差足够大时, 直管中则会出现壅塞现象, 此时理论上出口马赫数达到1, 出口处静压大于环境静压, 表现为欠膨胀状态. 因此, 实际出口处的工况可定性验证绝热假设以及数值计算方法关于壅塞流计算的合理性.
-
纹影技术是利用光在非均匀密度场中因折射率不同而出现光程差, 进而导致图像局部明暗变化的原理, 实现密度场流动显示的实验方法. 本文利用此方法测试非壅塞与壅塞条件下直管出口的实际工况.
图7为实验采用的透射式纹影光路原理图. 纹影系统包含光源、狭缝、平凸透镜、刀口以及配有显微镜头的相机. 光源与狭缝共同产生矩形“起始光源”, 平凸透镜的焦距为250 mm, 透镜的直径为60 mm, 将过狭缝后点光源位于透镜焦距位置时, 可使经过透镜的光平行穿过测试区域, 测试区域由图中红色虚线框表示, 其范围为实验中测试的直管的出口直径的10倍以上; 而后光经过第2个透镜形成对称下游光路, 调整刀口位置使其恰好位于下游光路中光源的像的位置, 此时光路的灵敏度最高. 由于实验中采用的直管尺寸在100 μm量级, 为保证足够的放大倍数和图像分辨率, 需使用显微镜头采集图像, 实验中图像分辨率为5.46 μm/pixel, 分辨率测试结果如图8所示, 图中标尺的最小刻度为50 μm, 黑色斑点为镜头或标定板上的灰尘颗粒所致.
-
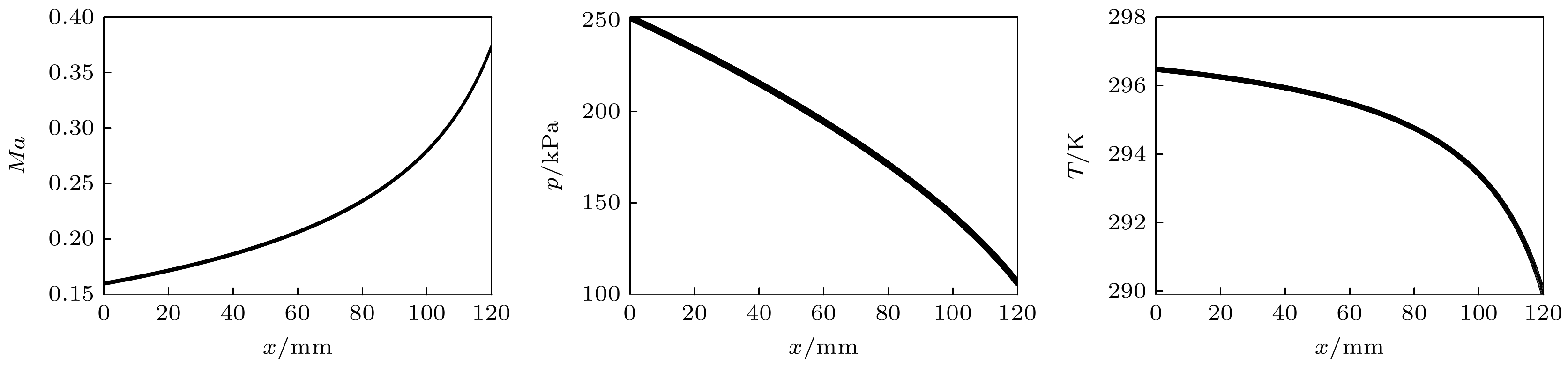
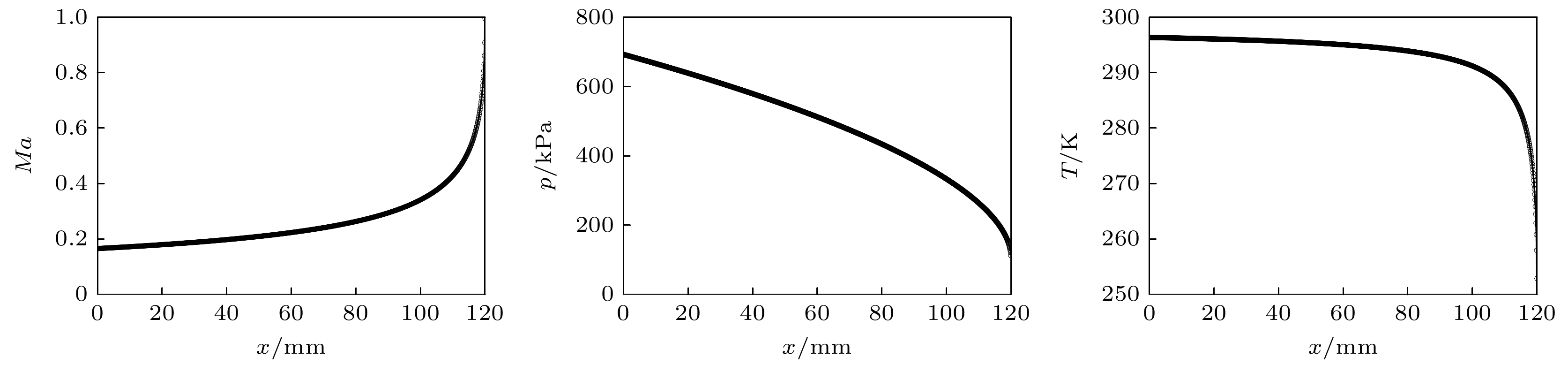
表1列出了数值计算与纹影实验的工况条件. 图9和图10分别为Case 1和Case 2条件下通过数值计算得到的沿管长向的马赫数、静压以及静温的变化曲线.
由图9和图10计算结果知: 当滞止压力为256 kPa时, 出口马赫数为0.374, 出口处静压为106 kPa, 此工况下出口处为压力匹配状态; 当滞止压力升高至706 kPa时, 出口马赫数为1, 出口静压为112 kPa, 此工况下为流动壅塞状态.
图11为Case 1和Case 2出口处的纹影实验结果. 纹影图像定性地证明了计算结果的合理性. 黑色区域为管壁, 管外径为800 μm. 当滞止压力为256 kPa时, 如图11(a)所示, 直管内流动处于非壅塞状态, 出口处工况为压力匹配状态, 未出现任何波系结构, 由于绝热过程中沿管长方向静温有所下降, 即出口处的密度应大于环境密度, 故可观察到较微弱的明暗变化. 而当滞止压力升高至706 kPa时, 如图11(b)所示, 直管出口出现了激波串结构. 这说明直管出口处已达到声速, 且出口静压应大于环境静压, 即流动处于欠膨胀状态, 经过出口之后气流继续膨胀加速, 达到超声速状态, 而后在气流压缩减速过程中, 则会出现连续的激波结构, 这与计算结果中得到的流动壅塞状态是吻合的. 故可定性说明, 文中采用的绝热假设以及关于非壅塞与壅塞流动的处理方法是合理的.
-
由2.2节计算流程可知, 可通过数值方法得到密度与速度的沿程数据, 则由(9)式可得直管出口的质量流量:
对不同内径以及不同滞止压力条件下直管的运输质量流量进行计算和实验测试, 计算和实验条件保持一致, 如表2所列.
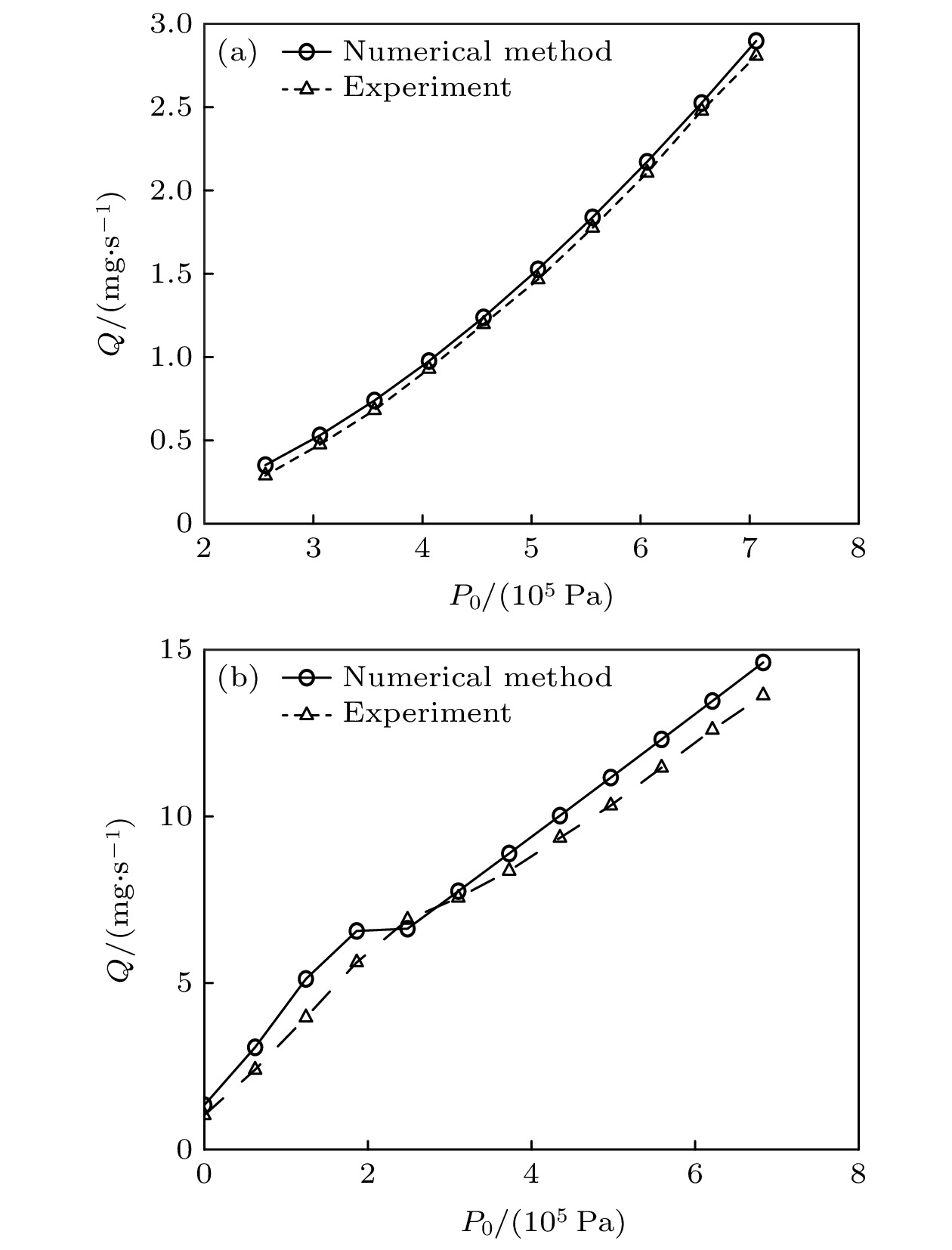
图12为直管内径d = 100 μm和200 μm时不同滞止压力对应的质量流量数据, 每个系列实验中滞止压力的增量均为50 kPa. 由于d = 100 μm条件下实际质量流量相对于流量计量程偏小, 与流量计测量不确定度属于同一量级, 为减小分析误差故舍弃P0 = 156 kPa和P0 = 206 kPa两组数据.
从图12可以得到, 当d = 100 μm时, 数值计算与实验的结果吻合得较好, 不同滞止压力条件下偏差值均小于2%, 流量与滞止压力之间近似呈幂次关系. 而当d = 200 μm时, 数值计算与实验的结果则出现明显的误差, 最大偏差出现在滞止压力为306 kPa时, 偏差值达到了29%, 滞止压力继续增大时, 偏差值减小, 均能控制在8%之内. 数值计算结果中, 在滞止压力为156—256 kPa范围内, 流量与滞止压力之间近似为幂次关系, 而在256—356 kPa范围内, 数据点偏离此关系, 且出现流量滞止现象, 随着滞止压力继续增大, 流量重新开始增大, 并呈线性增长的趋势; 在实验结果中, 并未出现极端的流量滞止现象, 但在206—406 kPa变化范围内, 流量增长的斜率逐渐减小, 此后流量增长趋势也近似于线性关系, 这与数值计算的结果趋势吻合.
-
对于摩擦力为唯一驱动势的一维流动, 流动参数的变化由摩擦力引起. 而在数值求解中摩擦系数是作为输入量给定的, 其偏差将直接导致预测误差的产生. 本研究采用的摩擦系数计算公式(7)和(8)均是在不可压条件下得到, 但实际微圆管中的流动具有可压缩性, 其在较高马赫数条件下对摩擦系数的影响实际无法忽略. 此外, 转捩雷诺数决定了层流至湍流的转捩点, 此处摩擦系数会出现间断式升高, 转捩雷诺数规定的偏差也是误差来源之一. 本节基于摩擦系数及转捩雷诺数对预测误差产生的原因开展分析.
-
由于绝热条件下管内流动的雷诺数沿管长方向不断变化, 故只能得到全局的平均摩擦系数. 首先提出基于一维方法的实际管内平均摩擦系数的计算方法.
将平均摩擦系数定义为
定义最大管长Lmax为绝热条件下某一起始马赫数加速至极限马赫数所需要的最短长度, 将2.1节中控制方程组中关于马赫数与x坐标的微分关系式改写成以下形式:
因此, 假设已知一段长度的直管入口以及出口的马赫数, 则可以求得这段长度范围内的平均摩擦系数:
对于实验而言, 我们有已知量
$ \dot m $ , P0, T0, pe, 由于直管内每个截面的质量流量为常数, 可由下列方程组求解得到实际入口马赫数:又根据2.1节微分方程组中, 可以整理出压力与马赫数的积分形式:
求解得
由(14)式可以求得出口处的马赫数, 代入(12)式和(13)式即可求得直管内的实际平均摩擦系数. 对于数值计算的平均摩擦系数, 只需按求解步长将(11)式离散即可.
-
依据4.1节中平均摩擦系数求解方法, 可以得到d = 100 μm和200 μm时不同滞止压力对应的计算摩擦系数与实际摩擦系数, 如图13所示.
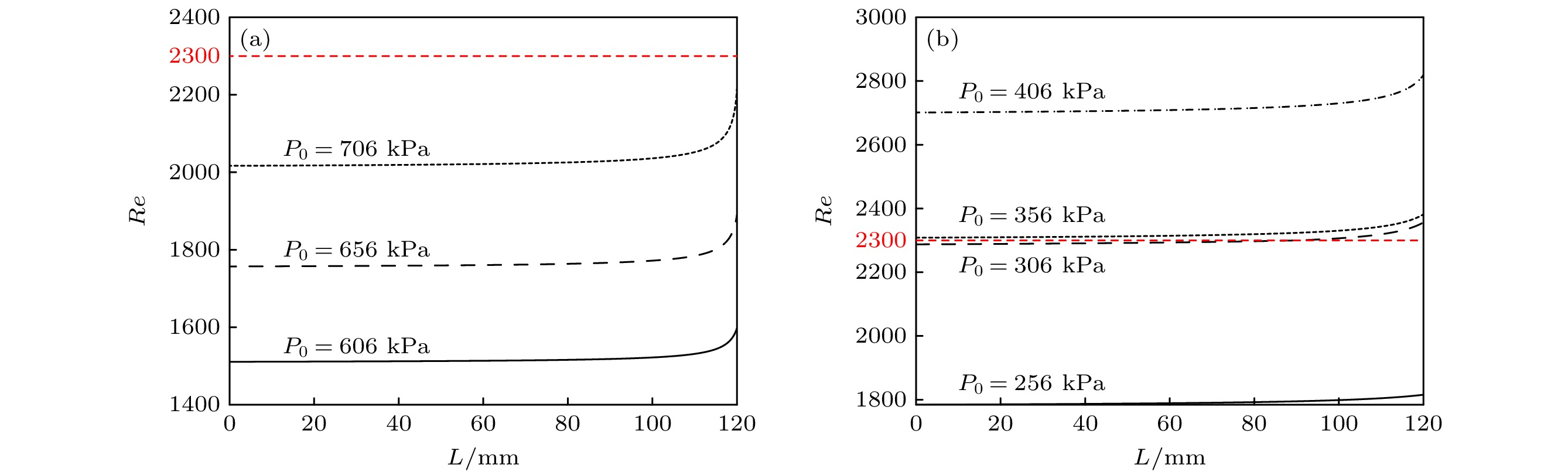
由图13结果可知, 当d = 100 μm和200 μm时, 实验数据得到的实际摩擦系数大于计算摩擦系数, 因此实验测得的质量流量比数值计算结果小, 这与图12结果反映的整体规律吻合. 为进一步解释随滞止压力变化偏差的变化规律, 统计了由数值计算得到的不同滞止压力时沿程的雷诺数分布.
由图14可知, 当d = 100 μm时, 不同滞止压力时直管内的雷诺数应小于计算时规定的层流至湍流的转捩雷诺数2300, 因此该工况下直管内均保持层流状态. 当滞止压力较小时, 管内流动压缩性较弱, 直管内沿程的雷诺数几乎不变, 而层流的摩擦系数计算公式为反比例函数, 即随雷诺数增大, 摩擦系数变化的斜率会减小. 由图12结果, 实验结果比计算结果的偏差均在3%左右, 故表现在平均摩擦系数的偏差则是随着滞止压力的提升而逐渐减小, 这解释了图13(a)中平均摩擦系数的误差来源.
当d = 200 μm时, 数值计算结果与实验结果均出现了流量滞止或者流量增量变缓, 而后过渡至线性变化的现象. 依据图13(b)与图14(b)中的结果, 此现象均是由于层流至湍流的过渡过程导致摩擦系数增大而引起的. 从数值计算结果来看, 当滞止压力由256 kPa升高至306 kPa时, 直管内流动状态由全层流转变为层流与湍流混合的状态, 滞止压力继续增大至356 kPa时, 则为全湍流状态, 在此范围内平均摩擦系数表现为增大的趋势, 也对应了流量滞止现象出现的压力范围.
d = 100 μm时的结果证明了在全层流状态下质量流量与滞止压力的符合相同的幂次增长趋势. 但在d = 200 μm时, 实验与计算值最大偏差反而出现在滞止压力为206 kPa与256 kPa时, 此时计算结果中沿程雷诺数均小于2300, 质量流量符合幂次增长规律, 但实验值从206—256 kPa开始质量流量的增长规律便不符合幂次增长规律, 质量流量的增量随滞止压力升高保持不变或逐渐减小, 此时管内的平均摩擦系数应比理论上全层流状态要高. 这说明实际管内流态并非为理论上的全层流流动, 即以雷诺数为2300作为层流至湍流的转捩雷诺数的假设不合理, 实际的转捩点应是提前的, 这与部分已有的研究结论吻合[2,36]. 此外, 当滞止压力高于406 kPa时, 理论与实际管内均为全湍流, 此时实际的平均摩擦系数比计算的摩擦系数是要大的, 即光滑管的假设与实际直管在湍流状态下的摩擦系数存在偏差. 在转捩雷诺数与经验公式的共同控制下, 导致了在涉及层流至湍流过渡的工况下质量流量预测出现了较大的偏差.
可见, 数值计算中关于摩擦系数的给定方法是质量流量预测误差的主要来源, 包括了经验公式的准确性以及转捩雷诺数的判断. 层流摩擦系数公式是经过数学推导得来, 数值方法与实验的对比验证了全层流状态下质量流量预测的精度较高, 预测误差在3%以内; 全湍流状态下光滑管Blasius湍流摩擦系数公式存在一定误差, 预测误差在8%以内. 而当流动过程中包含层流至湍流的过渡过程时, 在转捩点和湍流经验公式的共同控制下, 预测精度下降, 误差提高至29%.
此外, 依据经典Moody图[37,38]中摩擦系数与雷诺数的变化规律可知, 由层流至湍流的过渡过程中摩擦系数随雷诺数连续增大, 并非间断式增长. 但针对此过程中摩擦系数的计算目前尚未有统一的经验公式, 故而在计算中通常忽略过渡过程, 而直接采用湍流摩擦系数公式代替, 这使得摩擦系数计算值应比实际过渡过程要大. 因此也解释了实验中当出现转捩情况时平均摩擦系数增大的速度比计算结果要小的现象.
-
本文采用一维近似处理方法简化可压缩流动方程组, 建立了适用于微圆管质量运输特性预测的计算模型和数值计算方法, 结合范诺线方程及实验方法对数值计算方法的正确性和物理计算模型的有效性进行了检验, 并详细分析了预测误差来源. 主要得到以下结论: 依据范诺线参数比理论结果检验了数值计算方法的正确性. 对比典型驱动压差条件下微圆管出口工况的计算与纹影结果, 证明了数值方法关于流动壅塞预测的合理性, 并依据全局平均摩擦系数分析了数值计算方法的误差来源.
1)依据范诺线参数比理论结果检验了数值计算方法的正确性, 数值计算结果误差在1.5%以内; 通过直管出口工况的密度场变化特征, 定性验证了绝热假设与一维近似处理方法的合理性, 在大压差条件下, 直管出口处可以达到声速, 即流动壅塞状态.
2)质量流量预测精度方面, 在全层流状态下, 数值方法的预测误差可以控制在3%以内, 全湍流状态下光滑管假设误差在8%以内, 当流动过程包含层流至湍流过渡过程时, 误差提高至29%.
3)数值计算误差是由转捩雷诺数以及湍流摩擦系数经验公式共同引起的, 实际管内的转捩雷诺数比计算规定的转捩雷诺数要小, 再加之湍流摩擦系数计算存在偏差, 使得当管内流动包含过渡过程时质量流量预测误差较大.
综上研究可以看出, 转捩雷诺数以及湍流状态下摩擦系数的修正和标定是影响质量流量预测精度的关键因素. 而目前关于摩擦系数的实验标定普遍基于等温流动假设得来, 此假设仅适用于极低马赫数条件, 对于高雷诺数情形存在误差, 合理性受限, 这是后续研究中需解决的重要问题.
基于一维处理法的微圆管质量运输特性预测方法
One-dimensional approximation-based method of predicting mass transfer characteristics in microtubes
-
摘要: 微通道传热传质相关基础问题在新材料、微电子、航空航天等工程领域具有重要的科研需求. 本文针对微圆管内质量运输特性预测问题开展了数值方法研究及实验测量验证. 采用一维近似处理方法简化可压缩流动方程组, 建立了适用于微圆管质量运输特性预测的数值计算方法, 结合范诺线方程及实验方法对数值计算方法的正确性和物理计算模型的有效性进行检验, 并详细分析预测误差来源. 结果表明, 依据范诺线参数比理论结果与数值计算结果证明了数值计算方法的正确性. 对比典型驱动压差条件下微圆管出口工况的计算与纹影结果, 证明了数值方法关于流动壅塞预测的合理性. 在质量流量预测方面, 全层流阶段质量流量预测误差在3%以内, 全湍流状态下的预测误差在8%以内, 而当微圆管内流动包含层流至湍流的过渡过程时, 预测误差则提高至29%, 这是由于给定的转捩雷诺数以及摩擦系数计算公式的误差引入而造成的.Abstract:
The fundamental issues related to heat and mass transfer in microchannels have significant research needs in various engineering fields, such as new materials, microelectronics, and aerospace. This paper addresses the problem of predicting mass transport characteristics within microtubes by developing numerical methods, conducting experimental measurements for validation, and analyzing prediction errors. A one-dimensional approximation method is employed to simplify the compressible flow equations, and a fourth-order Runge-Kutta numerical method is also used to iteratively solve the governing equations. A theoretical calculation method suitable for predicting mass transport characteristics in microtubes is established. This method can calculate various flow parameters along the length of the microtube and can handle different flow conditions, such as static pressure matching or flow choking at the outlet. Subsequently, by comparing the numerical calculation results with the theoretical results of the Fanuo line parameter ratio, the correctness of the numerical calculation method is verified. Also, Schlieren experiments and a self-designed mass flow measurement device are used to qualitatively and quantitatively verify the effectiveness of physical computing models. Under typical driving pressure differences, the qualitative agreement between the calculated and schlieren results for the outlet conditions of the microtube demonstrate the rationality of the numerical method in terms of static pressure matching and flow choking calculations. Regarding mass flow prediction, comparisons between theoretical calculations and experimental measurements under different driving pressures reveal that when the flow inside the microtube is in a fully laminar state, the mass flow prediction error is within 3%. When the flow is fully turbulent, the prediction error is within 8%. However, when the flow involves a transition from laminar to turbulent, the prediction error increases to 29%. During the numerical calculations, based on existing research results, the formula for transition Reynolds number and the turbulent friction factor are set as input parameters. However, the analyses of the Reynolds numbers along the length of the microtube and the average friction factors under different conditions show that the actual transition Reynolds number in the microtube is lower than the value set in the numerical calculations. Additionally, there is a significant discrepancy between the calculated turbulent friction factor and the actual value. Moreover, during the transition from laminar to turbulent flow, the friction factor should increase continuously with the Reynolds number increasing, but the in the numerical calculations the turbulent friction factor is directly used to represent this process. These factors are the main reasons for the larger mass flow prediction errors when the flow involves transition and turbulence. -
Key words:
- one-dimensional processing method /
- mass transfer /
- numerical prediction /
- friction coefficient .
-
-
图 3 数值计算方法与范诺线方程求解p1/p2对比
Figure 3. Comparison of numerical calculation methods and van Gogh line equations for p1/p2.
图 9 Case 1直管内沿程Ma, p, T分布
Figure 9. Distribution of Ma, p, and T along the tube of Case 1.
图 10 Case 2直管内沿程Ma, p, T分布
Figure 10. Distribution of Ma, p, and T along the tube of Case 2.
图 12 数值计算与实验测量质量流量结果对比 (a) 系列 1 (d = 100 μm); (b) 系列 2 (d = 200 μm)
Figure 12. Comparison of mass flow rate results of numerical calculation and experimental measurement: (a) Series 1 (d = 100 μm); (b) Series 2 (d = 200 μm).
图 13 不同滞止压力时的平均摩擦系数 (a) d = 100 μm; (b) d = 200 μm
Figure 13. Average friction coefficient at different stagnation pressures: (a) d = 100 μm; (b) d = 200 μm.
图 14 不同滞止压力时的沿程雷诺数 (a) d = 100 μm; (b) d = 200 μm
Figure 14. Reynolds numbers along the tube at different stagnation pressures: (a) d = 100 μm; (b) d = 200 μm.
表 1 工况条件
Table 1. Operating conditions.
Case P0/kPa T0/K pe/kPa d/μm L/mm 1 256 298 106 200 120 2 706 298 106 200 120 
下载: 导出CSV
表 2 计算与实验条件
Table 2. Calculation and experimental conditions.
Series P0 /kPa T0 /K pe /kPa d/μm L/mm 1 256—706 298 106 100 120 2 156—706 298 106 200 120
下载: 导出CSV
-
[1] van den Berg H R, ten Seldam C A, van den Gulik P S 1993 J. Fluid. Mech. 246 1 doi: 10.1017/S0022112093000011 [2] Lorenzini M, Morini G L, Salvigni S 2010 Int. J. Therm. 49 248 doi: 10.1016/j.ijthermalsci.2009.07.025 [3] Fang X, Yue X A, An W Q, Feng X G 2019 Microfluid. Nanofluidics. 23 5 doi: 10.1007/s10404-018-2175-9 [4] Reynolds O 1883 Philos. Trans. 174 935 doi: 10.1098/rstl.1883.0029 [5] Kawashima D, Yamada T, Hong C, Asako Y 2016 J. Mech. Eng. 230 420 doi: 10.1177/0954406215614598 [6] American National Standard Institute. ANSI N14.5 2022 Radioactive Materials Leakage Teats on Packages for Shipment [7] Anderson B L, Carlson R W, Fischer L E 1994 Predicting the Pressure Driven Flow of Gases through Micro-capillaries and Micro-orifices (Washington, DC: Nuclear Regulatory Commission [8] Chen C S, Kuo W J 2004 Numer. Heat. Transfer. 45 85 doi: 10.1080/1040778049026737 [9] Asako Y, Nakayama K, Shinozuka T 2005 Int. J. Heat. Mass. Transfer. 48 4985 doi: 10.1016/j.ijheatmasstransfer.2005.05.039 [10] Asako Y, Pi T, Turner S E, Faghri M 2003 Int. J. Heat. Mass. Transfer. 46 3041 doi: 10.1016/S0017-9310(03)00074-7 [11] Murakami S, Toyoda K, Asako Y 2021 J. Fluids. Eng. 134 111301 doi: 10.1115/1.4051422 [12] Hong C, Asako Y, Suzuki K, Faghri M 2012 Numer. Heat. Transfer. 61 163 doi: 10.1080/10407782.2012.638513 [13] Hong C, Tanaka G, Asako Y, Katanoda H 2018 Int. J. Heat. Mass. Transfer. 121 187 doi: 10.1016/j.ijheatmasstransfer.2017.12.104 [14] Lijo V, Kim H D, Setoguchi T 2012 Int. J. Heat. Mass. Transfer. 55 701 doi: 10.1016/j.ijheatmasstransfer.2011.10.040 [15] Wang H, Xing J, Sun Z, Gu H, Sun X, Wang Y 2023 AEST 57 74 doi: 10.7538/yzk.2022.youxian.0015 [16] Agrawal A, Kushwaha H M, Jadhav R S 2020 Microscale Flow and Heat Transfer (New York: Springer [17] Shome B 2023 Phys. Fluids 35 122004 doi: 10.1063/5.0174929 [18] Yovanovich M M, Khan W A 2020 J. Thermophys. Heat. Trans. 34 792 doi: 10.2514/1.T5914 [19] Valougeorgis D 2007 Phys. Fluids 19 091702 doi: 10.1063/1.2780192 [20] Barber R W, Emerson D R 2006 HTE 27 3 doi: 10.1080/01457630500522271 [21] Bykov N Y, Zakharov V V 2022 Phys. Fluids. 34 057106 doi: 10.1063/5.0089628 [22] Wang X D, Li Y, Gao Y, Gao C G, Fu W C 2023 Aerospace 10 126 doi: 10.3390/aerospace10020126 [23] Xu K, Huang J C 2010 J. Comput. Phys. 229 7747 doi: 10.1016/j.jcp.2010.06.032 [24] Guo Z L, Xu K, Wang R J 2013 Phys. Rev. E 88 033305 doi: 10.1103/PhysRevE.88.033305 [25] Hong C, Yamada T, Asako Y, Faghri M 2012 Int. J. Heat. Mass. Transfer. 55 4397 doi: 10.1016/j.ijheatmasstransfer.2012.04.008 [26] Celata G P, Lorenzini M, Morini G L, Zummo G 2009 Int. J. Heat. Fluid. Flow. 30 814 doi: 10.1016/j.ijheatfluidflow.2009.02.015 [27] Rehman D, Barattini D, Hong C, Morini G L 2021 Exp. Fluids 62 52 doi: 10.1007/s00348-021-03137-3 [28] Rehman D, Morini G L, Hong C 2019 Micromachines 10 171 doi: 10.3390/mi10030171 [29] Hong C, Asako Y, Morini G L, Faghri M 2024 Exp. Therm. Fluid. Sci. 155 111196 doi: 10.1016/j.expthermflusci.2024.111196 [30] Brackbill T, Kandlikar S 2007 Proceedings of the International Conference on Nanochannels, Microchannels and Minichannels Puebla, Mexico, June 18−20, 2007 p509 [31] Eckhardt B, Schneider T M, Hof B, Westerweel J 2007 Annu. Rev. Fluid. Mech. 39 468 doi: 10.1098/rsta.2008.0217 [32] Morini G L, Lorenzini M, Salvigni S 2006 Exp. Therm. Fluid. Sci. 30 733 doi: 10.1016/j.expthermflusci.2006.03.003 [33] Du D, Li Z, Guo Z 2000 Sci. China. Technol. Sci. 43 171 doi: 10.1007/BF02916887 [34] Sonnad J R, Goudar C T 2006 J. Hydraul. Eng 132 863 doi: 10.1061/(ASCE)0733-9429(2006)132:8(863) [35] 左克罗, 霍夫曼 著 (王汝涌 译) 气体动力学(上册) (北京: 国防工业出版社) Zucrow M J, Hoffman J D (translated by Wang R Y) 1984 Gas Dynamics (Vol. 1) (Beijing: National Defense Industry Press [36] Tang G H, Li Z, He Y L, Tao W Q 2007 Int. J. Heat. Mass. Transfer. 50 2282 doi: 10.1016/j.ijheatmasstransfer.2006.10.034 [37] Moody L F 1944 T. ASME 66 671 doi: 10.1115/1.4018140 [38] Avci A, Karagoz I 2019 Eur. J. Mech. B. Fluids 78 182 doi: 10.1016/j.euromechflu.2019.07.007 -
图( 15) 表( 2)
计量
- 文章访问数: 41
- HTML全文浏览数: 41
- PDF下载数: 0
- 施引文献: 0