首页
登录
注册
-
低频水声定向发射技术具有广泛的应用前景, 可发挥探测鱼群、海底环境监测、水下通信等功能. 然而低频声波由于其波长较长, 衍射效应明显, 很难实现声波的定向传播[1].
弯张换能器是目前应用最广泛的低频大功率辐射声源, 其工作原理是由纵向伸缩振动振子或径向脉动圆环驱动具有振幅放大效应的壳体产生弯曲振动来辐射声能. 由于壳体弯曲振动模频率更低, 且具有振幅放大效应, 因此该类换能器可以兼备低频、小尺寸、大功率的工作特性. 已有的弯张换能器工作频率范围大多在300—3000 Hz, 这些换能器的几何尺寸一般远小于工作波长, 且壳体大部分表面同相振动, 从经典声学的角度来看这类换能器都将充当单极子, 并在所有方向上均匀发射声能[2]. 这对有限尺寸声源发射低频定向声波构成了根本障碍, 从而阻碍了声学换能器的有效缩小.
为了使弯张换能器实现低频指向性发射, Moosad等[3]研究了使用反声障板使3 kHz Ⅳ型弯张换能器获得定向发射的可行性, 但障板会导致换能器的尺寸增大2—3倍, 且无法在深水中使用. Butler[4]通过给两组驱动振子分别施加不同的电压设计了指向性Ⅶ型弯张换能器. 随后, Zhang等[5,6]将这种双激励方式应用到了Ⅴ型弯张换能器中, 这导致电路系统的配置更加复杂, 且会大大增加整个发射系统的体积重量和成本, 还很难实现大功率发射, 这也是这些研究很少讨论声源级的原因. Wang等[7]设计了一种单面辐射的弯张换能器, 波长约为换能器最大尺寸的7倍, 但单个换能器也是全指向性的, 仍然需要组成圆形阵列来实现心形指向性, 频率不变的情况下换能器的体积重量增大了4—8倍, 且需要配备多台功放使用. 蓝宇等[8,9]利用非对称辐射面搭配非对称激励方式, 提出了指向性四边形弯张换能器, 莫喜平[10]提出了凹凸球冠帽复合壳体结构指向性弯张换能器, 但结构均较复杂, 且目前对利用非对称壳体实现指向性的研究较少, 缺乏对其工作机制和调控手段的探讨. 因此设计一种仅采用单路电信号驱动, 无需相控与加权的低频指向性弯张换能器并给出其优化研究很有必要[11,12].
本研究提出了一种凹凸梁结构, 可以使换能器在ka < 1 (k为波数,
$ a $ 为换能器最大尺寸的一半)的低频段实现心形指向性, 为弯张换能器的 低频定向发射提供了新思路. 建立了凹凸梁型低 频指向性弯张换能器有限元模型, 探讨了其指向性形成机制, 研究了各结构参数对换能器性能的影响, 同时从谐振频率、发送电压响应(transmitting voltage response, TVR)、前后声压比(front-to-back ratio, FBR)、指向性、空间均匀度、带宽等参数出发对换能器进行全面优化设计, 可充分发掘其应用潜力. 设计的凹凸梁型低频指向性弯张换能器使用起来更加轻便, 成本更低, 且与双激励方式在单一权系数条件下的指向性调控能力相当. -
Ⅳ型弯张换能器是目前应用最广泛的弯张换能器之一, 其通常由一个椭圆形的壳体和沿主轴方向放置的纵向振子组成, 由于结构设计的对称性, 该类换能器通常只有偶次阶模式被激发[13]. 因Ⅳ型弯张换能器长轴方向比短轴方向的振动位移小且面积占比小, 因此端部的反相辐射可忽略不计, 换能器可近似看作等效单极子球源. 若要激发Ⅳ型弯张换能器的偶极模式, 目前最具代表性的研究是Butler等[14–16]提出的双激励方法. 该方法通过将驱动振子设计成两组机械并联单元, 并在电路上独立驱动, 从而激发出奇数阶偶极模式. 但其本质是壳体受压电振子的一阶弯曲模式影响而产生的刚体运动. 此时压电振子内部出现剪切应力, 在大功率模式下会导致功能材料的机械损伤, 影响换能器的大功率发射. 在驱动方式上, 需要两路电信号驱动, 并且随频率变化调整幅度加权系数, 甚至需要配合相位参数的调控. 在换能器结构上采用了两套压电驱动振子, 增大了体积重量, 两路电信号驱动增加了电系统配置, 同时应用起来也不够方便. Ⅶ型弯张换能器与Ⅳ型同理, 只是将外凸壳体变成了内凹壳体, 使得工作深度更深[17].
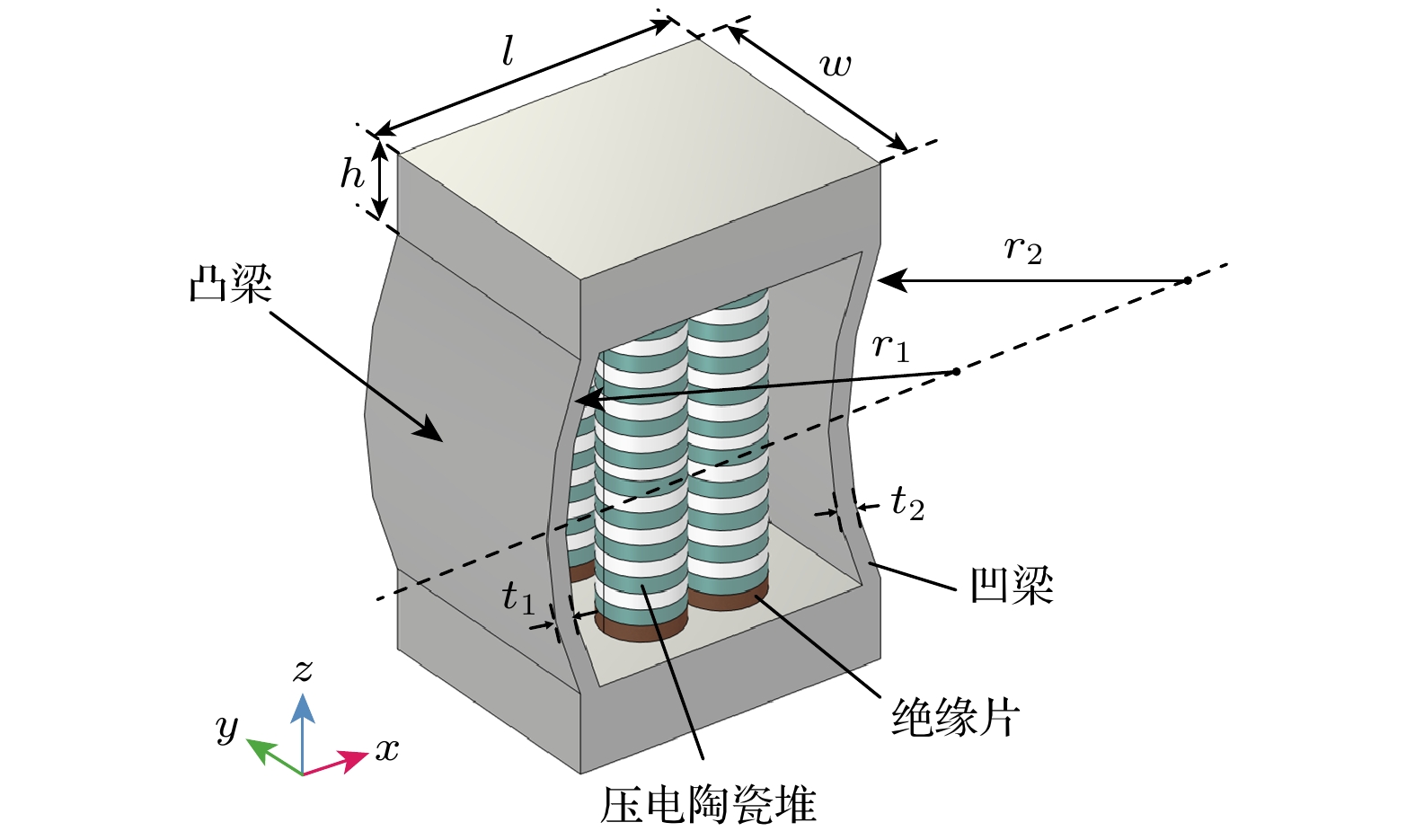
为了解决上述问题, 本文提出了一种新结构低频指向性弯张换能器, 可以利用凹凸壳体的非对称性产生固有的单极子模态和偶极子模态, 并使两种模态按一定比例在同一频率处叠加形成心形指向性[18]. 换能器结构如图1所示, 主要包括压电陶瓷组成的驱动振子和非对称金属壳体. 其中, 非对称金属壳体由外凸型弯曲梁和内凹型弯曲梁通过方形侧壁连接而成, 类似于单侧Ⅶ型弯张换能器和单侧Ⅳ型弯张换能器组合而成的复合结构. 振子装配体由一组或多组压电陶瓷堆组成, 陶瓷堆的数量由陶瓷片的尺寸以及壳体内部空间决定, 这里采用4组直径为40 mm的压电陶瓷堆, 工作时所有压电陶瓷片电学上并联连接, 仅采用单路电信号激励.
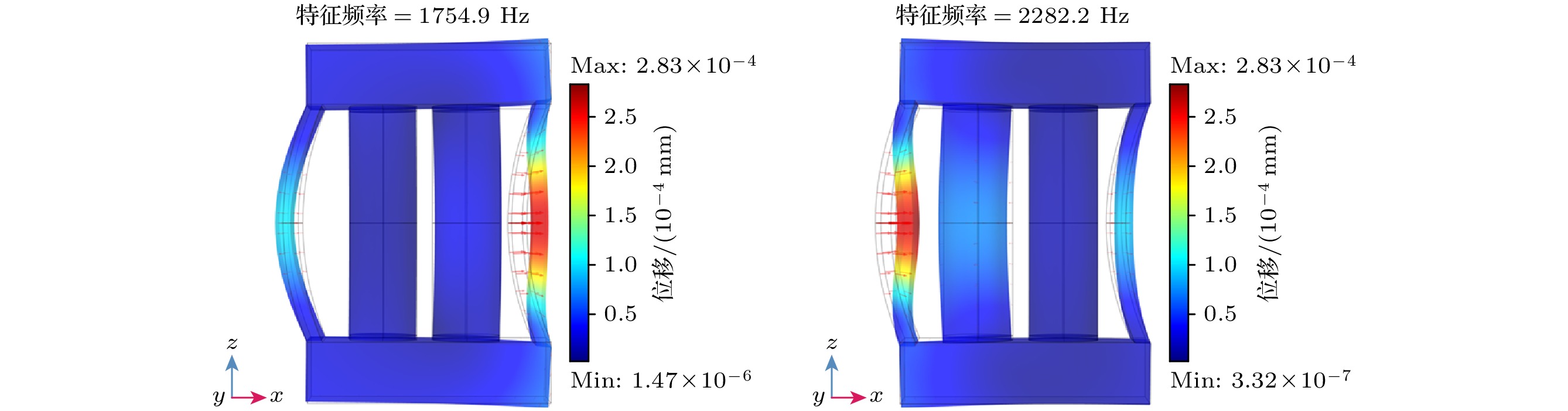
图2为换能器的前两阶振动模态位移矢量, 图中黑色线框为结构原型状态. 前两阶模态谐振频率为1754.9 Hz和2282.2 Hz. 可见, 第1阶谐振模态以凹梁振动为主, 带动凸梁做反向运动, 且靠近凹梁一侧的压电陶瓷堆产生与凹梁同向的弯曲振动; 第2阶谐振模态以凸梁振动为主, 带动凹梁做同向运动, 且靠近凸梁一侧的压电陶瓷堆产生与凸梁反向的弯曲振动. 凸梁和凹梁的振动均可等效为两端约束的弯曲梁的一阶振动, 即中心位移最大, 两端位移最小. 由于上述振型图是模态分析的结果, 当换能器在水中工作时, 壳体的振动形式更加复杂.
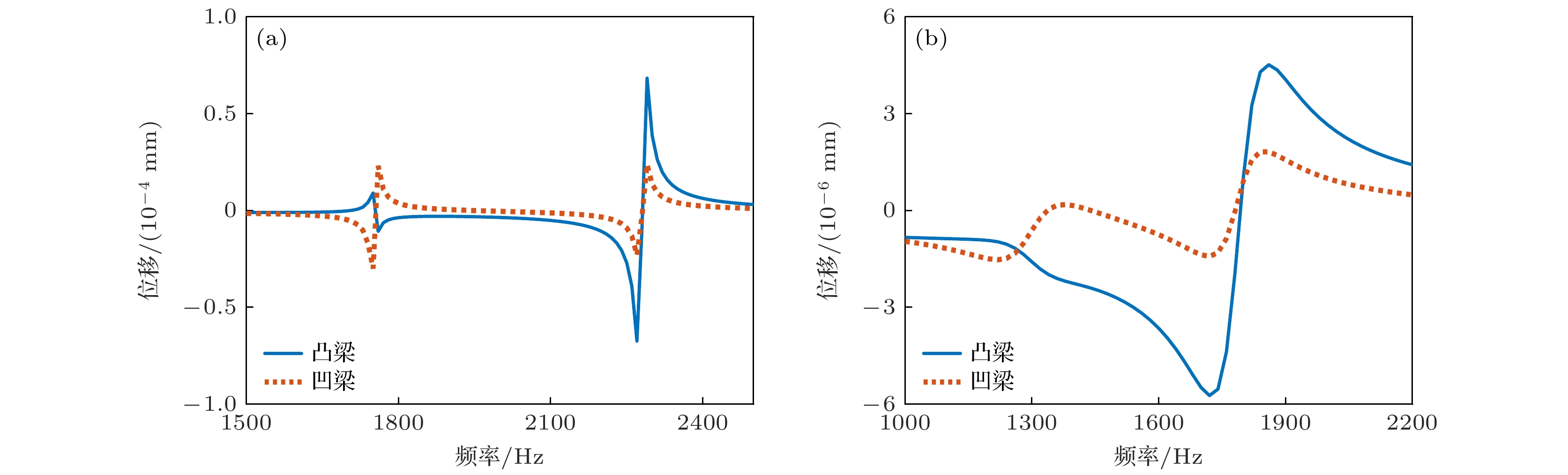
为进一步分析换能器在空气中的振动响应, 换能器凹梁和凸梁辐射面中心点法向位移随频率变化的响应曲线如图3(a)所示. 从图3(a)可以看出, 空气中由于换能器的振动Q值比较高, 两个谐振点处的响应带宽较窄. 在第1阶谐振点处, 凹凸梁反向振动, 且凹梁振幅大于凸梁振幅, 换能器实现类单极子模态工作; 在第2阶谐振点处, 凹凸梁同向振动, 且凸梁振幅大于凹梁振幅, 换能器实现类偶极子模态工作, 与模态分析结果一致. 但由于两种模态谐振频率差较大, 模态叠加效果并不明显. 图3(b)为换能器在水中的凹凸梁辐射面中心点法向位移随频率变化的响应曲线. 与空气中的结果不同, 受水中辐射阻抗的影响, 换能器的谐振频率显著降低. 由于水中换能器的振动Q值降低, 两个谐振点处的响应带宽变宽. 同时两种模态的频率差减小, 双梁振动的耦合作用增强, 使得在两个谐振点之间的中间频段, 凹梁运动受到抑制, 凸梁运动得到增强, 换能器以双梁同向运动的类偶极子工作模态为主. 除此以外, 可以看到换能器的二阶谐振峰比一阶谐振峰更加尖锐, 即换能器二阶模态的机械Q值更高, 振动位移更大, 与偶极子模态特性一致.
-
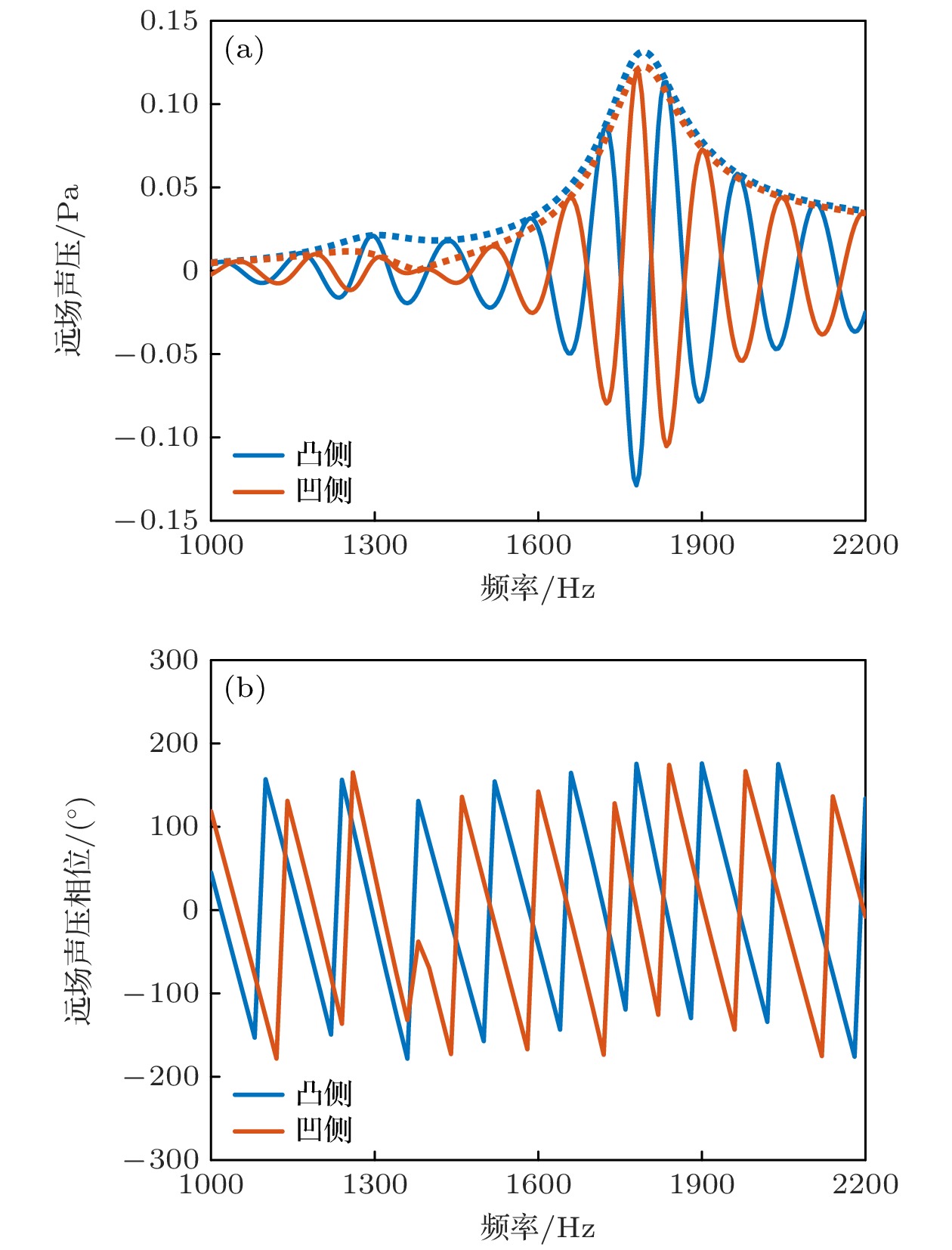
了解了换能器的振动机理, 接下来还需要对换能器的辐射声场进行研究. 由于换能器壳体的不对称性, 在压电陶瓷的厚度模式振动激励下, 凹凸梁主要以同向振动为主, 无法单独产生理想的单极子辐射声场和偶极子辐射声场, 换能器在两种振动模态的耦合作用下形成复杂的辐射声场[19]. 图4(a), (b)分别给出了换能器水中凹侧和凸侧距离声中心10 m处的声压以及相位的频响曲线, 可以看到, 在小于1300 Hz的低频段, 换能器凹凸两侧声压基本同相, 以单极子辐射声场为主, 换能器基本表现为全向工作特性. 随着频率的升高, 换能器凹凸两侧声压趋于反相, 偶极子模态输出比例增大. 在中间的过渡频段, 可以保证偶极子等效辐射源之外还可以剩余单极子声源辐射分量, 使得换能器两侧 声压比提高, 并在1375 Hz处凹侧相位发生突变, 此时两侧声压比达到最大值, 凹侧声压几乎为零, 凸侧声压增强, 从而形成单向指向性.
结合2.1节的研究结果, 可以确定换能器的凹梁-凸梁耦合振动机制直接影响声场中单极子模态与偶极子模态分量的能量分布特性, 进而对换能器的低频指向性性能起到关键作用. 与双激励法中将各阶模态权重量化为不同驱动振子电压大小的思路不同, 本研究提出通过调整凹凸壳体的几何参数实现模态权重调控的方法. 为揭示结构参数对换能器辐射特性的影响规律, 下一步将系统开展关键参数与换能器电声参数的关联性研究, 通过参数敏感性分析明确结构优化方向, 为低频指向性换能器的设计提供理论依据.
-
换能器的单极子和偶极子模态的形成与凹凸梁的振幅和相位有关, 又因为换能器的尺寸远小于波长, 因此可将换能器等效为如图5所示的两个振幅和相位不等的球源, 且两个球源的振动幅度和相位均与频率相关, 可通过复数形式将其声场统一表示为[20]
其中,
$ {A}_{1}\left(f\right), {A}_{2}\left(f\right) $ 为频率相关的振动幅度,$ \Delta \phi \left(f\right) $ 为频率相关的相位差,$ k = {2{\mathrm{\pi }}f}/{c} $ .在远场条件下(
$ r\gg d $ ),$ {r}_{1} \approx r - {d}/{2}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\theta $ ,$ {r}_{2}\approx r+ {d}/{2}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\theta $ , (1)式可进一步简化为引入幅度比
$ \alpha \left(f\right)=\dfrac{{A}_{2}\left(f\right)}{{A}_{1}\left(f\right)} $ 和归一化幅度$ A\left(f\right)= {A}_{1}\left(f\right) $ , (2)式可改写为1)换能器工作在一阶谐振频率
$ {f}_{1} $ 时,$ {{\Delta }}\phi \left({f}_{1}\right)= 0 $ ,$ \alpha \left({f}_{1}\right)=1 $ , 则:若
$ k\left({f}_{1}\right)d\ll 1 $ , 则$ {\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\left(k\left({f}_{1}\right){d}/{2}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\theta \right)\approx 1 $ , 声场近似为全指向性(单极子模式).2)换能器工作在二阶谐振频率
$ {f}_{2} $ 时,$ \Delta \phi \left({f}_{2}\right)= {\mathrm{\pi }}, \alpha \left({f}_{2}\right)=1 $ , 则:若
$ k\left({f}_{2}\right)d\ll 1 $ , 则$ {\mathrm{s}}{\mathrm{i}}{\mathrm{n}}\left(k\left({f}_{2}\right)\dfrac{d}{2}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\theta \right)\approx k\left({f}_{2}\right)\times \dfrac{d}{2}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\theta $ , 声场近似为偶极子指向性.3)换能器工作在一二阶谐振频率之间时, 相位差
$ {{\Delta }}\phi \left(f\right) $ 和幅度比$ \alpha \left(f\right) $ 随频率变化:在某一频率
$ {f}_{0} $ 处$ \alpha \left({f}_{0}\right) $ 达到最大值, 同时相位差$ {{\Delta }}\phi \left({f}_{0}\right) $ 介于$ 0 $ 和$ {\mathrm{\pi }} $ 之间. 此时声场为单极子与偶极子的混合模式, 指向性呈现复杂瓣状结构. 为量化频率对幅度和相位的影响, 假设幅度比随频率变化满足 Lorentzian 型共振:其中,
$ {\alpha }_{0} $ 为基线振幅比,$ C $ 为振幅系数,$ \varGamma $ 为半峰全宽.假设相位差随频率线性过渡:
其中,
$ {f}_{1} $ 和$ {f}_{2} $ 分别为一阶和二阶频率,$ {f}_{1}\leqslant f\leqslant {f}_{2} $ .当
$ \alpha \left(f\right)=1, {{\Delta }}\phi \left(f\right)={{\mathrm{\pi }}}/{2}, kd=1 $ 时, 指向性函数可简化为此时换能器可以产生典型的心形指向性波束. 因此, 双球源模型的声场表达式可完整描述全指向性、偶极指向性及过渡频段的耦合模式特性. 其中, 所有常数项均可通过数值模拟得到具体数值. 通过调节
$ \alpha \left(f\right) $ ,$ {{\Delta }}\phi \left(f\right) $ 和$ kd $ , 可实现从单极子到偶极子的平滑过渡, 并在特定条件下实现心形指向性. 该方法为换能器的指向性调控提供了理论框架, 有助于理解低频指向性换能器的工作原理. -
基于第2节的理论分析可知, 换能器的低频指向性性能由单极子与偶极子模态的耦合作用主导, 而耦合特性直接受换能器结构参数的影响. 通过参数化建模与数值仿真, 系统研究了包括侧壁长度(
$ l $ )、侧壁宽度($ w $ )、侧壁高度($ h $ )、凸梁曲率半径($ {r}_{1} $ )、凸梁厚度($ {t}_{1} $ )、凹梁曲率半径($ {r}_{2} $ )、凹梁厚度($ {t}_{2} $ )在内的7个关键结构参数对换能器TVR, FBR及指向性的影响规律. 首先定义了初始几何参数(如表1所示), 并基于控制变量法逐一调整目标参数, 其余参数保持不变. 参数范围参考了典型弯张换能器的设计经验, 确保结构合理性与可加工性.单极子与偶极子模态的耦合强度可通过换能器TVR曲线的前两阶谐振频率差值(
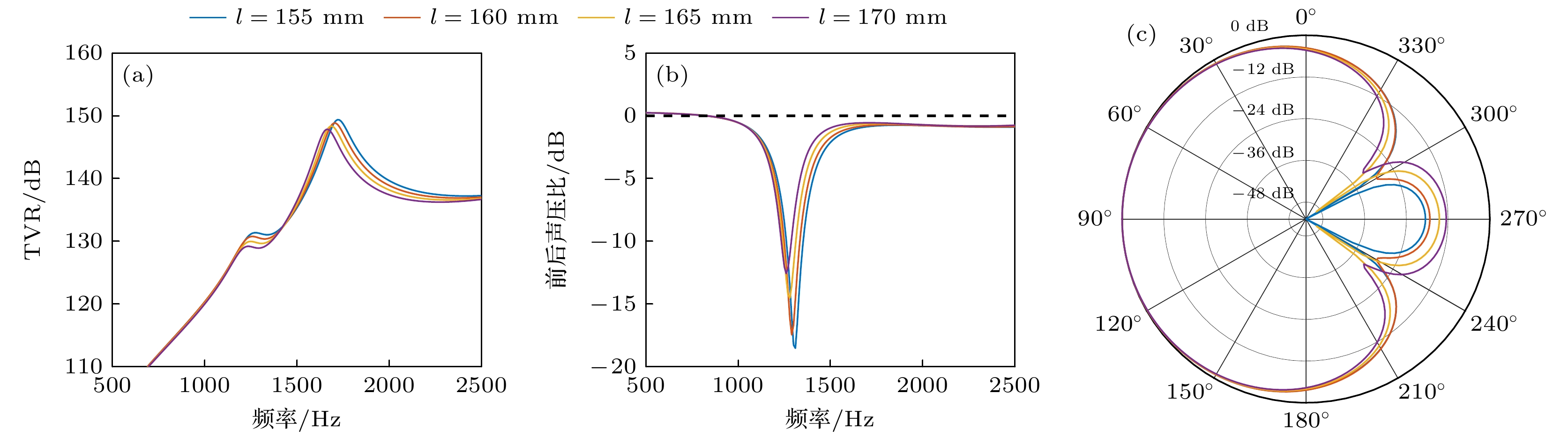
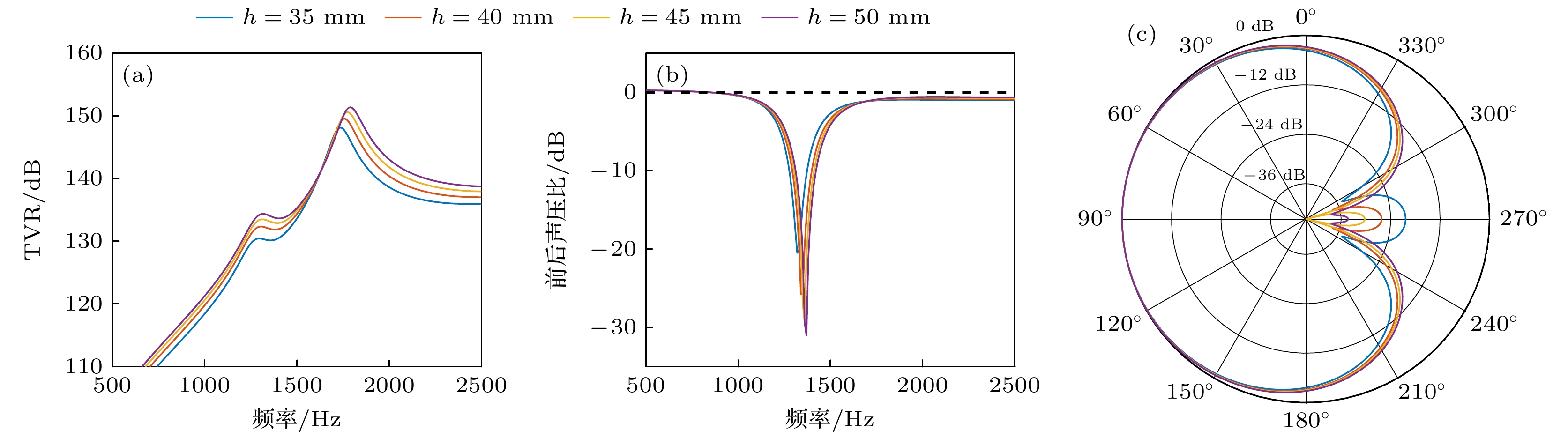
$ {{\Delta }}f={f}_{2}-{f}_{1} $ )及其峰值幅值来表征. 理论上, TVR峰值幅值越大, 表明对应模态分量的能量占比越高; 而前两阶谐振频率越接近, 则说明单极子与偶极子模态的耦合效应越强. 图6(a)所示为不同侧壁长度$ l $ 下换能器凸侧的TVR曲线, 随着$ l $ 的增大, 换能器的前两阶谐振频率$ {f}_{1} $ 和$ {f}_{2} $ 及其对应的TVR峰值均呈现下降趋势, 但前两阶谐振频率差值$ {{\Delta }}f $ 基本保持不变. 这一现象表明,$ l $ 主要影响换能器的整体刚度分布, 导致谐振频率向低频偏移, 但对单极子与偶极子模态的耦合强度影响较小. 结合图6(b), (c)的分析结果可以看出, 随着侧壁长度$ l $ 的增大, FBR峰值所在的频率逐渐向低频偏移, 同时FBR峰值(负值)呈现增大趋势, 即其绝对值减小. 此外, 在最大|FBR|频率处, 换能器的指向性也随$ l $ 的增大而减弱. 这一现象表明,$ l $ 的增大会削弱换能器的指向性性能, 同时使其最大|FBR|向低频移动.图7和图8分别探究了侧壁宽度
$ w $ 及高度$ h $ 对换能器性能的影响. 结果表明, 当$ w $ 从130 mm增至160 mm时, 前两阶TVR峰值及对应谐振频率的波动幅度小于3% (见图7(a)), FBR峰值所在频率向低频偏移60 Hz (见图7(b)), |FBR|由28.3 dB降至19.6 dB (图7(c)). 类似地,$ h $ 从35 mm增至50 mm时, 前两阶谐振频率仅微幅升高, 分别从1290 Hz增至1310 Hz, 从1740 Hz增至1790 Hz, 对应TVR峰值提升约3 dB (见图8(a)); FBR峰值所在频率向高频偏移50 Hz (见图8(b)), |FBR|则从20.5 dB提升至31 dB (见图8(c)). 上述结果表明, 尽管侧壁参数通过调节整体刚度对指向性产生一定影响, 但其对单极子-偶极子模态耦合的贡献有限, 换能器的TVR起伏较大且指向性最优时的响应较低.凸梁曲率半径
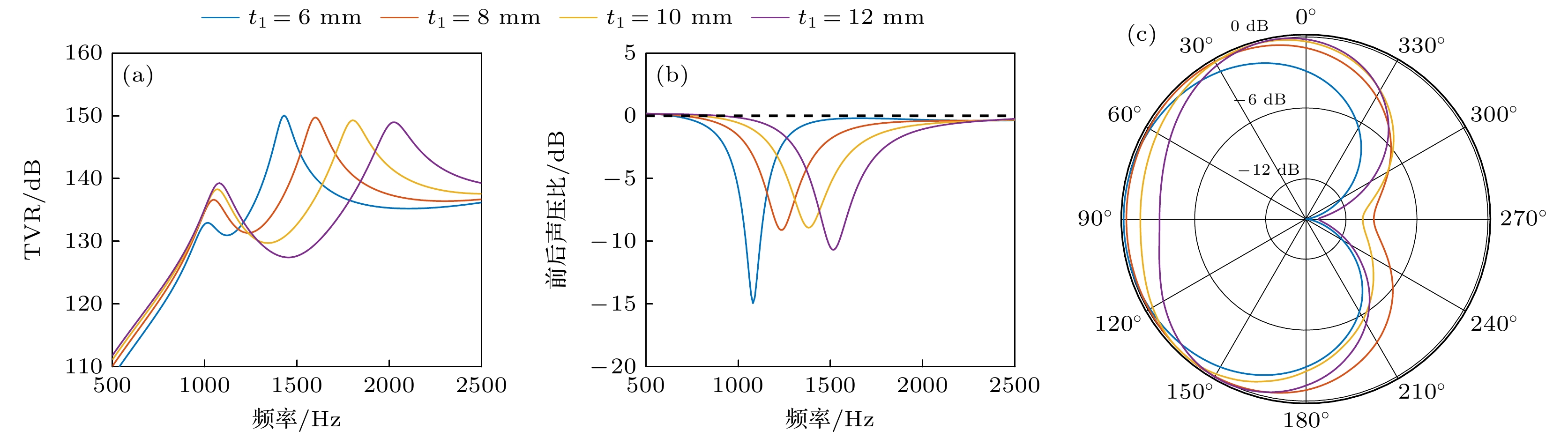
$ {r}_{1} $ 与厚度$ {t}_{1} $ 对偶极子模态特性呈现显著调控作用. 当$ {r}_{1} $ 由150 mm增至300 mm时, 一阶谐振频率基本保持不变, 而二阶谐振频率从2040 Hz显著降至1740 Hz (图9(a)). 这一非对称频移表明, 凸梁曲率半径的增大会降低其局部弯曲刚度, 从而削弱偶极子模态的高频振动能量. 与此同时, 最大FBR所在频率从1510 Hz降至1380 Hz (图9(b)), |FBR|从22 dB降低至10 dB(图9(c)). 类似地, 当$ {t}_{1} $ 从6 mm增至12 mm时, 二阶谐振频率从1430 Hz显著升至2020 Hz (图10(a)). 这一现象主要源于凸梁弯曲刚度的显著增强, 导致偶极子模态的振动频率升高. 尽管厚度增大也会引入附加质量, 但$ m\propto {t}_{1},\; k\propto {{t}_{1}}^{3} $ , 因此其对频率的影响远小于刚度效应. 这也导致FBR峰值所在频率从1080 Hz显著升至1520 Hz (图10(b)), |FBR|从15 dB降至9 dB (图10(c)). 进一步分析表明, 厚度增大导致凸梁轴向刚度提升, 抑制了偶极子模态与单极子模态的耦合效应, 使得主辐射方向由凸侧偏移至侧壁方向(图10(c)), 不再满足心形指向性要求. 上述结果揭示了凸梁参数通过局部刚度重构调控偶极子模态能量分布的物理机制.凹梁曲率半径
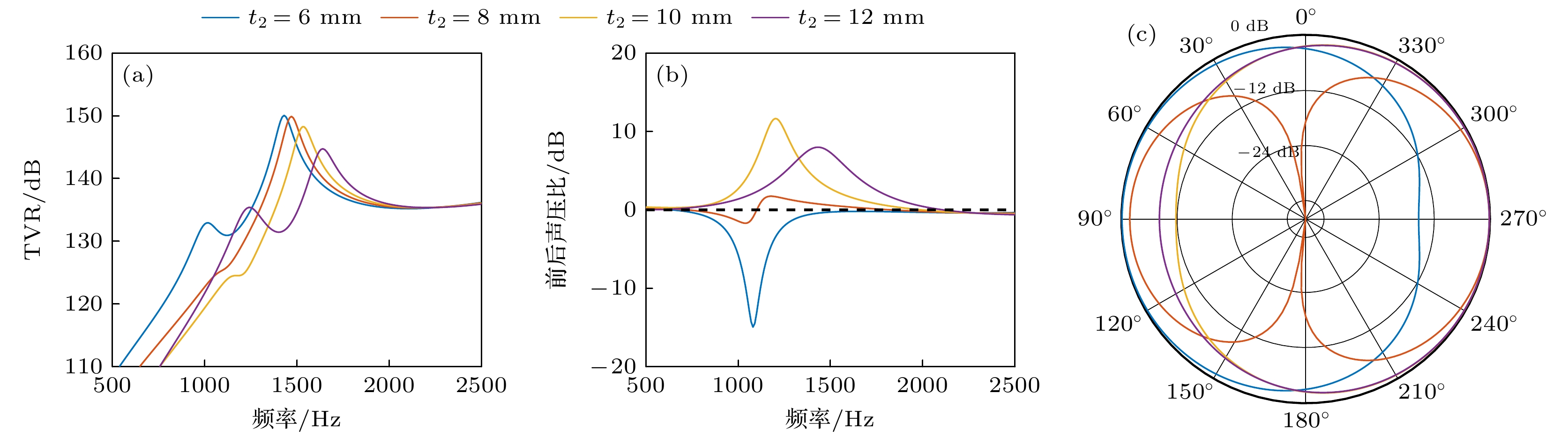
$ {r}_{2} $ 与厚度$ {t}_{2} $ 主要影响单极子模态特性. 当$ {r}_{2} $ 由150 mm增至300 mm时, 一阶谐振频率从1410 Hz降至1250 Hz, TVR峰值降低8 dB (135 dB→127 dB), 二阶谐振影响不大(图11(a)). FBR峰值所在频率同步向低频偏移190 Hz(1510 Hz→1320 Hz) (图11(b)), |FBR|从22.4 dB升至31.6 dB又降至14.3 dB (图11(c)). 该现象表明, 增大曲率半径会降低凹梁弯曲刚度, 虽然有利于提高换能器的低频特性, 但使得单极子模态分量减少且耦合效应减弱, 不利于换能器指向性的形成. 类似地,$ {t}_{2} $ 从6 mm增至12 mm时, 一阶频率由1010 Hz升至1240 Hz, TVR峰值呈现先降后升的非单调变化(132.9 dB→124.5 dB→135.4 dB), 二阶谐振频率从1430 Hz升至1640 Hz, TVR峰值从150 dB降至144.7 dB (图12(a)), FBR峰值所在频率从1080 Hz升至1430 Hz (图12(b)), 且主辐射方向由凸侧逐步过渡到凹侧(图12(c)). 上述结果不仅揭示了凹梁参数通过局部刚度重构调控单极子模态能量分布的物理机制, 还明确了其对偶极子模态振动特性的影响, 表明凹梁参数在换能器的振动特性调控中起到了核心作用.综合图6—图12的分析可知, 侧壁结构参数对换能器性能的整体影响较弱, 这是由于侧壁结构远离凹凸梁的弯曲振动核心区域, 其刚度与质量分布对单极子-偶极子模态耦合的贡献较小, 因此优化设计应聚焦于凹凸梁的关键几何参数. 其中, 凸梁参数主导偶极子模态分量, 凹梁参数则主要影响单极子模态分量, 这与第2节理论分析中单极-偶极模态耦合由壳体弯曲刚度主导的结论一致. 本研究还为低频指向性换能器的结构设计提供了明确的参数敏感度排序: 凹梁参数>凸梁参数>侧壁参数. 这一发现为低频指向性弯张换能器的多目标优化设计提供了重要理论依据, 并强调了模态解耦分析在低频定向声学器件开发中的关键作用.
-
低频指向性换能器的优化设计需同时满足低频、强指向性、高TVR及宽带的性能要求, 以适应水下目标探测、海洋环境监测等具体应用场景. 为量化优化目标, 基于2 kHz以下低频指向性换能器的典型应用需求, 设定了以下性能约束条件: |FBR| > 20 dB, TVR > 140 dB re 1 μPa·m, –6 dB带宽 > 400 Hz. 优化后的换能器结构参数如表2所示.
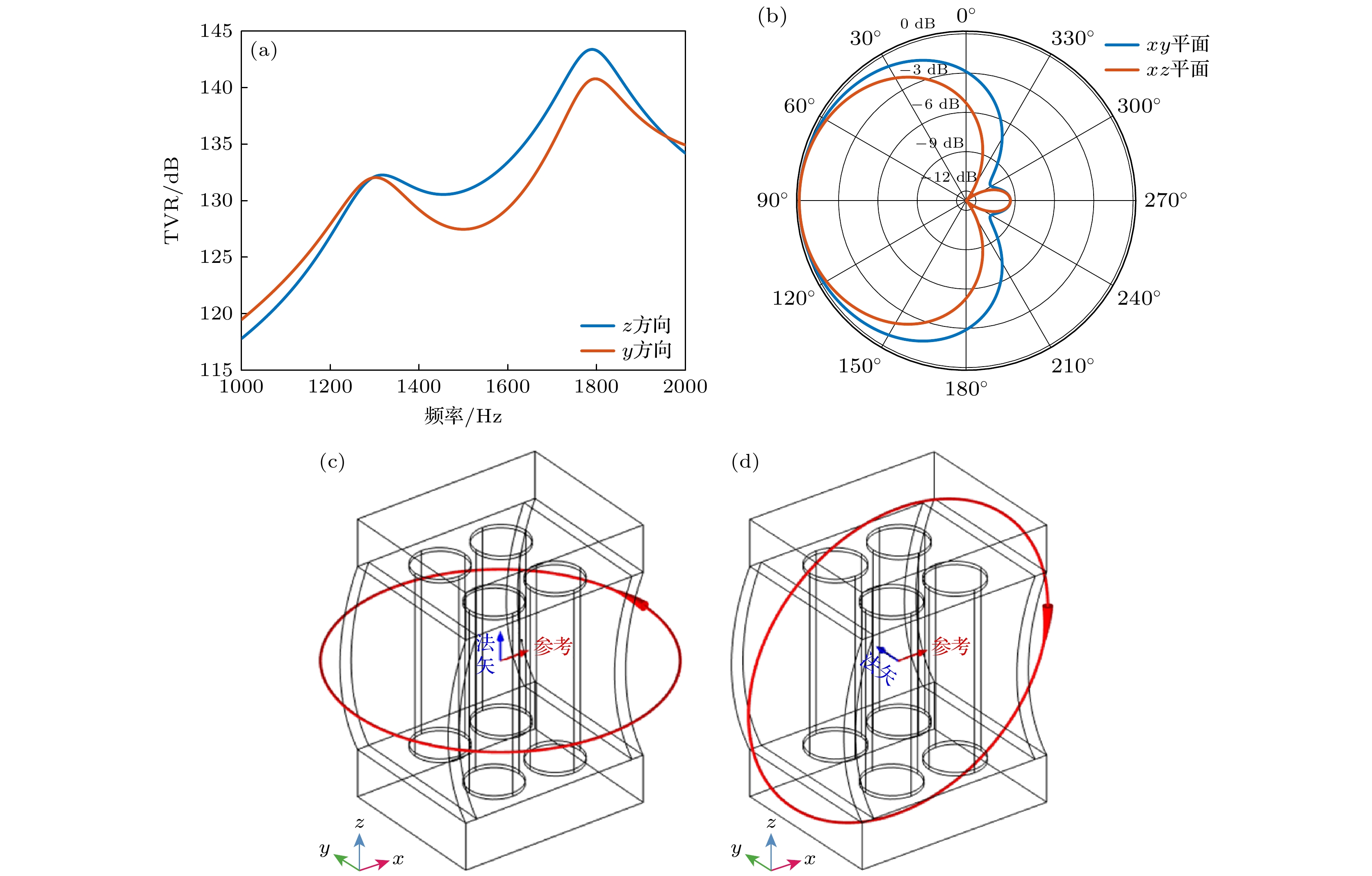
由于换能器结构的非对称性, 辐射声场在yz平面呈现显著的空间分布不均匀现象. 如图13(a)所示, 在两谐振峰之间的工作频段内, 换能器z方向与y方向的TVR差异达4 dB以上, 图13(b)进一步研究了换能器xy平面和xz平面的二维指向性差异, 图13(c), (d)以红色圆圈标明了换能器xy平面与xz平面的几何位置关系. 针对声场非均匀性问题, 传统方法通常采用附加声学障板以改善指向性[21], 然而, 这种方式对本研究提出的凹凸梁结构低频指向性换能器并不适用. 因此本研究在优化过程中还重点关注了换能器的辐射声场空间均匀度, 发现只有当
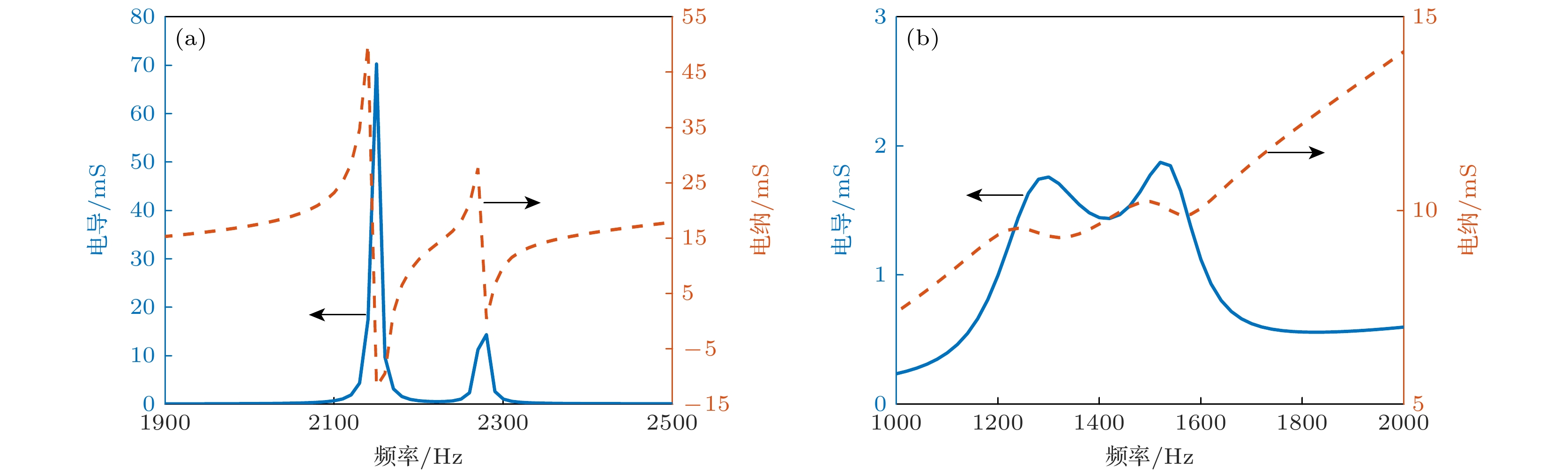
$ {{t}_{2}}/{{t}_{1}} > 1 $ 时, 才能满足声场在yz平面的均匀辐射. 如图14所示的优化结果表明, 通过协同调控凹凸梁的结构参数, 可在保证结构紧凑性(最大尺寸<λ/4)的前提下实现换能器的性能提升. 此时, 换能器的前两阶谐振峰处的响应值差距减小, 响应曲线更加平坦, TVR最大值为145.9 dB; 在一二阶模态之间的工作频段内, 换能器y方向与z方向的响应曲线基本重合, 说明yz平面的声场空间分布均匀度较好; 换能器在1480 Hz处实现最大|FBR|为27 dB的心形指向性.图15所示为优化后的换能器的导纳特性曲线. 在不同介质中, 换能器的导纳曲线表现出显著差异. 对比图15(a), (b)可知, 当换能器置于空气中时, 由于空气密度较小, 共振质量视为可忽略因素. 然而, 在水等高密度流体中, 共振质量的影响不可忽视, 其将导致换能器的发射共振频率相较于空气中有所降低, 这一现象在电导曲线上表现为峰值向低频方向移动, 同时峰值幅度也相应减小. 换能器在空气中的一阶谐振频率为2150 Hz, 电导值为70.3 mS, 二阶谐振频率为2280 Hz, 电导值为14.4 mS. 换能器在水中的一阶谐振频率为1300 Hz, 电导值为1.8 mS, 二阶谐振频率为1520 Hz, 电导值为1.9 mS.
图16(a)所示为提出的凹凸梁型低频指向性弯张换能器与传统Ⅳ型、Ⅶ型弯张换能器的TVR对比结果. 该对比实验在严格控制变量的条件下进行, 保证各换能器的最大外形尺寸、辐射面积及驱动振子参数保持完全一致. 结果表明, 本研究设计的换能器有效工作频带介于传统Ⅳ型与Ⅶ型结构之间, 且具有更宽的工作带宽. 值得注意的是, 在整个有效工作频段内, 该换能器的TVR值均显著优于两种传统结构, 展现出更优的机电转换效率. 即便近年来传统Ⅳ型和Ⅶ型弯张换能器经过持续结构优化, 其2 kHz以下低频段的TVR响应仍普遍低于145 dB量级[22–25]. 这一对比充分说明, 本研究所采用的凹凸梁型结构在实现低频指向性提升的同时, 并未以牺牲换能器响应特性为代价, 反而在关键性能指标上实现了突破.
图16(b)对比了凹凸梁型换能器与传统双激励法低频指向性Ⅳ型弯张换能器的压电陶瓷堆径向弯曲位移量. 结果显示, 该设计使压电陶瓷堆的弯曲振动幅度显著降低, 这一特性差异也揭示了两种技术方案的本质区别: 传统双激励法通过激发陶瓷堆的弯曲振动驱动壳体刚体位移, 而本方案则利用壳体自身的弯曲振动实现多模态耦合. 这种方式将主要应力集中区域从压电陶瓷材料转移至壳体结构, 可有效避免压电陶瓷的疲劳失效, 对于提升大功率发射状态下的器件可靠性具有重要意义.
-
本文设计了一种凹凸梁型低频指向性弯张换能器, 通过分析其振动特性以及辐射特性, 揭示了换能器的指向性形成机理并建立等效双球源模型. 研究结构参数对换能器性能的影响规律, 并进行优化设计. 对优化后的换能器性能进行讨论并与其他已有的研究工作进行对比, 论证了本设计的优势. 主要结论如下.
1) 本文提出的新结构低频指向性弯张换能器, 凸凹梁在振动模式上具有固有的法向位移反相的工作特性, 通过结构参数调控, 可以使二者在单一振子驱动下, 输出幅度满足一定差值关系, 可等效为单极子与偶极子的模态叠加, 实现指向性辐射.
2) 结构参数对换能器性能的影响呈现显著差异, 按参数敏感度排序为: 凹梁参数>凸梁参数>侧壁参数, 且只有凹凸梁的厚度比大于1时, 才能显著提高换能器yz平面的空间均匀度. 其中, 凹梁参数主导单极子模态分量占比, 凸梁参数主导偶极子模态分量占比.
3) 凹凸梁型低频指向性弯张换能器最大TVR为145.9 dB, 可以在1480 Hz附近(ka < 1)实现|FBR|最大27 dB的心型指向性发射, 这与双激励方式在单一权系数条件下的指向性调控能力相当, 且发射能力优于传统Ⅳ型和Ⅶ型弯张换能器.
4) 不同于传统双激励法通过激发陶瓷堆的弯曲振动驱动壳体刚体位移, 本研究利用壳体自身的弯曲振动实现多模态耦合, 从而将剪切应力集中区域从有源材料转移至金属壳体, 可有效避免有源材料的疲劳失效.
总之, 这种通过结构的非对称设计来实现换能器多模态联合应用与同频激发的方式, 不仅可以有效避免现有的双激励和加障板方式应用复杂的问题, 还可以提升大功率发射状态下的换能器可靠性, 且结构更加紧凑, 应用成本更低, 为弯张换能器实现低频指向性发射提供了新思路.
凹凸梁型低频指向性弯张换能器
Low-frequency directional flextensional transducer with concave-convex beam
-
摘要: 弯张换能器的尺寸远小于波长, 从而阻碍了紧凑型水声换能器产生定向波束. 针对传统的指向性弯张换能器电路驱动的幅度相位调控的复杂性问题, 本文提出一种指向性弯张换能器结构, 采用外凸型弯曲梁与内凹型弯曲梁复合而成的非对称壳体结构实现低频指向性发射, 可简化换能器的配套电路系统, 便于应用且成本更低. 本文从换能器的振动和辐射特性分析入手, 揭示了指向性形成机理并建立了等效双球源模型. 采用数值模拟的方法分析了主要结构参数对换能器谐振频率、发送电压响应、前后声压比及指向性的影响. 通过优化设计, 换能器在1240—1660 Hz的工作频段内最大发送电压响应为145.9 dB, 可在单电路驱动下产生前后声压比最大27 dB的心型指向性波束, 并且大大降低了有源材料的剪切应力, 可有效避免大功率发射时有源材料的疲劳失效, 为低频水声定向发射提供了一种更便捷的方法.Abstract: The dimensions of flextensional transducers are much smaller than the wavelength, thereby hindering the generation of directional beams by compact underwater acoustic transducers. To address the complexities of amplitude and phase modulation in circuit-driven traditional directional flextensional transducers, a directional flextensional transducer structure is proposed in this work. By implementing an asymmetric composite shell configuration combining concave and convex curved beams, the low-frequency directional radiation is achieved while simplifying peripheral driving circuits, thereby improving the operational convenience and cost-effectiveness. Through an analysis of the vibration characteristics and radiation mechanisms, this study elucidates the principle of directional generation. The concave and convex beams of the flextensional transducer exhibit an intrinsic operational characteristic of opposite-phase normal displacement in their vibration modes. By adjusting structural parameters, the amplitude output from the two beams under a single actuator drive can satisfy a specific differential relationship, effectively resulting in the modal superposition of a monopole and a dipole, thereby achieving directional radiation. By using a Lorentzian resonance fitting function and a linear fitting function, the relationship between the frequency-dependent amplitude ratio and phase difference of sound pressure for the concave and convex beams is established, forming an unequal amplitude, unequal phase dual-spherical source radiation model for the transducer, thereby providing a theoretical framework for controlling the directivity of the transducer. Through numerical simulations, the effects of the transducer sidewall parameters, as well as the thicknesses and curvature radii of the concave and convex beams, on the transducer’s resonance frequency, transmitting voltage response, front-to-back sound pressure ratio, and directivity are analyzed. Sensitivity ranking of the structural parameters is also presented. Finally, the optimization of transducer’s performance is discussed and compared with that in other existing research, showing the advantages of this design. Specifically, the transducer achieves a maximum transmitting voltage response of 145.9 dB within the operating frequency band from 1240 Hz to 1660 Hz. Under single-circuit drive, a cardioid-shaped directional beam with a maximum front-to-back sound pressure ratio of 27 dB is produced. Furthermore, the shear stress on the active material is significantly reduced, effectively preventing fatigue failure of the active material during high-power emission. This provides a more convenient method for achieving low-frequency underwater acoustic directional emission.
-
Key words:
- flextensional transducer /
- low-frequency directional beam /
- cardioid directivity /
- modal coupling .
-
-
图 3 换能器在(a)空气中和(b)水中的凹凸梁辐射面中心点法向位移
Figure 3. Normal displacement at the center of the radiating surface of the arched beam for the transducer in (a) air and (b) water.
图 4 换能器水中凹侧和凸侧距离声中心10 m处的(a)声压及(b)相位频响曲线
Figure 4. (a) Sound pressure and (b) phase frequency response curves at 10 m from the acoustic center for the concave and convex sides of the transducer in water.
图 5 凹凸梁型低频指向性弯张换能器等效双球源模型
Figure 5. Equivalent dual-spherical source model of the concave-convex beam low-frequency directional flextensional transducer.
图 6 侧壁长度
$ l $ 对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性Figure 6. Effect of sidewall length
$ l $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 7 侧壁宽度
$ w $ 对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性Figure 7. Effect of sidewall width
$ w $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 8 侧壁高度
$ h $ 对换能器的影响 (a) TVR, (b) FBR; (c) 最大指向性Figure 8. Effect of sidewall height
$ h $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 9 凸梁曲率半径
$ {r}_{1} $ 对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性Figure 9. Effect of convex beam curvature radius
$ {r}_{1} $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 10 凸梁厚度
$ {t}_{1} $ 对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性Figure 10. Effect of convex beam thickness
$ {t}_{1} $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 11 凹梁曲率半径
$ {r}_{2} $ 对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性Figure 11. Effect of concave beam curvature radius
$ {r}_{2} $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 12 凹梁厚度
$ {t}_{2} $ 对换能器的影响 (a) TVR; (b) FBR; (c) 最大指向性Figure 12. Effect of concave beam thickness
$ {t}_{2} $ on the transducer: (a) TVR; (b) FBR; (c) maximum directivity.
图 13 (a) 换能器z方向和y方向的TVR曲线对比; (b) 换能器在1480 Hz处的xy平面和xz平面指向性图; (c) 换能器xy平面示意图; (d) 换能器xz平面示意图
Figure 13. (a) Comparison of TVR curves in the z-direction and y-direction of the transducer; (b) directivity patterns in the xy-plane and xz-plane at 1480 Hz; (c) schematic diagram of the xy-plane of the transducer; (d) schematic diagram of the xz-plane of the transducer.
图 14 (a) 优化后的换能器凹侧、凸侧、z方向、y方向的TVR曲线; (b) 1480 Hz处的指向性图
Figure 14. (a) TVR curves of the concave side, convex side, z-, and y-directions of the optimized transducer; (b) directivity pattern at 1480 Hz.
图 15 (a) 优化后的换能器空气中导纳曲线; (b) 优化后的换能器水中导纳曲线
Figure 15. (a) Admittance curve of the optimized transducer in air; (b) admittance curve of the optimized transducer in water.
图 16 (a) 优化后的换能器和传统Ⅳ型、Ⅶ型弯张换能器的TVR对比; (b)优化后的换能器和传统采用双激励法实现低频指向性的Ⅳ型弯张换能器的压电振子径向位移对比
Figure 16. (a) Comparison of TVR between the optimized transducer and traditional Class IV and Class VII flextensional transducers; (b) comparison of radial displacement of piezoelectric vibrators between the optimized transducer and the traditional Class IV flextensional transducer achieving low-frequency directivity using dual-drive excitation.
表 1 换能器结构参数优化范围
Table 1. Optimization range of the transducer structure parameters.
参数 取值范围/mm 步长/mm $ l $ 155—170 5 $ w $ 130—160 10 $ h $ 35—50 5 $ {r}_{1} $ 150—300 50 $ {t}_{1} $ 6—12 2 $ {r}_{2} $ 150—300 50 $ {t}_{2} $ 6—12 2 
下载: 导出CSV
表 2 换能器优化后的结构参数
Table 2. Structural parameters of the transducer after optimization.
参数 值/mm 参数 值/mm $ l $ 160 $ {t}_{1} $ 7 $ w $ 160 $ {r}_{2} $ 300 $ h $ 40 $ {t}_{2} $ 13 $ {r}_{1} $ 200 换能器总高度 236
下载: 导出CSV
-
[1] Fan X D, Zhu Y F, Liang B, Cheng J C, Zhang L K 2018 Phys. Rev. Appl. 9 034035 doi: 10.1103/PhysRevApplied.9.034035 [2] 刘永平, 莫喜平, 柴勇, 张运强, 崔斌 2019 声学学报 6 1060 Liu Y P, Mo X P, Chai Y, Zhang Y Q, Cui B 2019 Acta Acust. 6 1060 [3] Moosad K P B, Chandrashekar G, Joseph M J, Sharma D, Kumar N 2011 Appl. Acoust. 72 127 doi: 10.1016/j.apacoust.2010.10.003 [4] Butler S C 2010 160th Meeting Acoustical Society of America Cancun, Mexico, November 15–19, 2010 p030001 [5] Zhang J, Hladky-Hennion A C, Hughes W J, Newnham R E 2001 Ultrasonics 39 91 doi: 10.1016/S0041-624X(00)00055-X [6] Zhang J, Newnham R E 2003 US Patent 6 614 143 [7] Wang Q M, Fan J, Lan Y, Zhou T F 2022 J. Acoust. Soc. Am. 151 2223 doi: 10.1121/10.0009579 [8] 蓝宇, 王秋木, 李宽 2017 中国专利 107452365A Lan Y, Wang Q M, Li K 2017 CN Patent 107452365A [9] 李宽 2015 硕士学位论文 (哈尔滨: 哈尔滨工程大学) Li K 2015 M. S. Thesis (Harbin: Harbin Engineering University [10] 莫喜平 2020 哈尔滨工程大学学报 41 1500 doi: 10.11990/jheu.202007105 Mo X P 2020 J. Harbin Eng. Univ. 41 1500 doi: 10.11990/jheu.202007105 [11] 夏铁坚, 范进良, 刘强, 周利生, 王照霞 2005 中国声学学会2005年青年学术会议论文集 中国杭州, 2005 第588页 Xia T J, Fan J L, Liu Q, Zhou L S, Wang Z X 2005 Proceedings of the CYCA'05 Hangzhou, China, 2005 p588 [12] Zhang X Z, Wu C F, Gong W, Wang K, Mo X P, Chai Y 2024 Appl. Phys. Lett. 124 022901 doi: 10.1063/5.0181748 [13] 滕舵 2016 水声换能器基础 第113页 Teng D 2016 Fundamentals of Hydroacoustic Transducers (Northwestern Polytechnical University Press) p113 [14] Butler S C, Butler A L, Butler J L, Cavanagh G H 1997 J. Acoust. Soc. Am. 102 308 doi: 10.1121/1.419609 [15] Butler S C, Butler A L 1992 J. Acoust. Soc. Am. 92 2977 doi: 10.1121/1.404362 [16] Butler J L, Butler A L 2003 J. Acoust. Soc. Am. 115 658 [17] 李杰, 顾磊, 吉辰 2024 舰船电子工程 44 214 doi: 10.3969/j.issn.1672-9730.2024.05.042 Li J, Gu L, Ji C 2024 Ship Electron. Eng. 44 214 doi: 10.3969/j.issn.1672-9730.2024.05.042 [18] 赵智勇, 王祖杰 2009 水雷与战舰防护 17 15 Zhao Z Y, Wang Z J 2009 J. Underwater Acoust. 17 15 [19] Zhang X Z, Chai Y, Mo X P 2022 16th Symposium on Piezoelectricity, Acoustic Waves, and Device Applications Nanjing, China, October 11-14, 2022 p691 [20] 张海澜 2012 理论声学(北京: 高等教育出版社) 第410页 Zhang H L 2012 Theoretical Acoustics (Beijing: Higher Education Press) p410 [21] 胡久龄 2009 硕士学位论文 (哈尔滨: 哈尔滨工程大学) Hu J L 2009 M. S. Thesis (Harbin: Harbin Engineering University [22] Moosad K P B, Krishnakumar P, Chandrashekar G, Vishnubhatla R M R 2007 Appl. Acoust. 68 1280 [23] 刘慧生, 张运强, 崔斌 2017 声学与电子工程 1 33 doi: 10.3969/j.issn.2096-2657.2017.01.009 Liu H S, Zhang Y Q, Cui B 2017 Acoust. Electron. Eng. 1 33 doi: 10.3969/j.issn.2096-2657.2017.01.009 [24] 李志强, 莫喜平, 张运强, 崔斌, 潘耀宗, 李鹏 2015 声学技术 6 566 Li Z Q, Mo X P, Zhang Y Q, Cui B, Pan Y Z, Li P 2015 Acoustical Technology 6 566 [25] 卢苇, 叶皓棠 2025 声学学报 50 149 doi: 10.12395/0371-0025.2023091 Lu W, Ye H T 2025 Acta Acust. 50 149 doi: 10.12395/0371-0025.2023091 -
计量
- 文章访问数: 26
- HTML全文浏览数: 26
- PDF下载数: 1
- 施引文献: 0