与传统激光相比, 涡旋光束携带有轨道角动量(orbital angular momentum, OAM), 并且由于OAM具有无限多的彼此正交的本征态, 可以形成无限维的希尔伯特空间^[1], 因此涡旋光束能极大地满足大容量、高速水下无线光通信的需求. 然而, 由于海洋湍流的存在, 携带OAM的涡旋光束在海水中传输时不可避免地受到湍流影响, 产生波前畸变和OAM模态间相互串扰的现象^[2–6], 从而导致通信性能下降. 因此, 研究海洋湍流对涡旋光束水下传输的影响以及提高基于涡旋光束的水下无线光通信系统性能成为了新热点, 国内外学者在该领域相继开展了大量的研究工作.

王明军等^[7]研究了完美涡旋(perfect vortex, PV)光束、拉盖尔-高斯(Laguerre-Gaussian, LG)光束和贝塞尔高斯(Bessel-Gaussian, BG)光束在各向异性海洋湍流下的传输特性, 并分析了这3种光束在海洋湍流中传输时的探测概率和信道容量. 刘昌勋等^[8]搭建实验系统, 对具有自聚焦效果的艾里光束和普通的高斯光束在海水信道中的传输进行对比分析, 结果表明, 艾里光束在海水信道中的光束质量保持能力和抗光束抖动能力要明显优于高斯光束, 证明了艾里光束在水下光通信中具有更优越的性能. Karimi等^[9]在2008年提出的一种超几何高斯类型的涡旋光束-超几何高斯二型(hypergeometric-Gaussian type-II, HyGG-II)光束, 并研究证明在所有已知的有限功率近轴模族中, HyGG-II模具有最低的光束发散度, 且随着径向变量的增大, 光束振幅向外围呈指数下降^[10]. 但到目前为止, 尚未发现研究证明HyGG-II光束适于在海水中传输的相关报道. 此外, 能否通过使用聚焦透镜来提高该光束的通信性能也有待研究.

基于上述原因, 本文首先利用Rotov近似和惠更斯菲涅耳衍射原理推导得到了使用聚焦透镜之后HyGG-II光束在海洋湍流中的信道容量表达式, 随后详细分析了不同光源参数和海洋湍流参数对聚焦HyGG-II光束信道容量的影响, 同时也对聚焦HyGG-II光束和非聚焦HyGG-II光束、LG光束的信道容量进行对比, 并通过分析聚焦HyGG-II光束的光强分布解释了聚焦透镜对信道容量增强的原因. 所得研究结果对实际水下无线光通信系统的设计具有一定的借鉴和指导意义.

为了研究聚焦透镜对HyGG-II光束在海洋湍流中的传输性能的影响, 从而验证通过使用聚焦透镜能够提高基于HyGG-II光束的通信系统的信道容量, 首先对在源平面位置加入聚焦透镜后该光束的信道容量表达式进行推导. 在柱坐标系下, HyGG-II光束在源平面的复振幅可表示为^[9]

其中, $ {r_0} = $$ |\boldsymbol r_0|$, $ {\boldsymbol r_0} $$ = \left( {x, y} \right) $是源平面上的二维位置矢量; $ {\theta _0} $为方位角; $ {\omega _0} $表示初始波束的束腰半径; $ {m_0} $是HyGG-II光束的OAM指数; $ p $是HyGG-II光束的空心度参数, 为了保证该光束的功率是有限的, $ p $需要满足条件$ p \geqslant - \left| {{m_0}} \right| $. 当$ p $=0时, HyGG-II光束可等效为阶数为0的LG涡旋光束^[11]. (1)式中的$ {}_1{F_1}\left( {a, b;c} \right) $表示合流超几何函数, 其级数展开式为^[12]

将(2)式代入(1)式之后可得

当在源平面位置放置聚焦透镜时, HyGG-II光束通过聚焦透镜之后的复振幅可以表示为

式中, $ k = 2{\text{π}}/\lambda $是波数, $ \lambda $是波长, $ f $为聚焦透镜的焦距.

根据惠更斯-菲涅耳积分, 可以得到经过聚焦透镜之后HyGG-II光束(简称为聚焦HyGG-II光束)传输到任意位置的复振幅为

其中, $ r $和$ \theta $分别是距离为z处的接收平面上的径向和方位角坐标.

将(4)式代入(5)式, 并利用如下积分公式^[12]:

J(·)为贝塞尔函数, 可得

为了进一步简化计算, 接下来利用以下积分式^[12]对(7)式进行化简:

此时(7)式可改写为

其中, $ \Gamma \left( \cdot \right) $为伽马函数, $ \beta = \dfrac{1}{{{\omega _0^2}}} - \dfrac{{{\text{i}}k}}{{2 z}} + \dfrac{{{\text{i}}k}}{{2 f}} $.

基于Rytov近似原理, 聚焦HyGG-II光束在海洋湍流中传播的复振幅为

式中$ \varPsi (r, \theta , z) $是由海洋湍流引起的复相位扰动.

在湍流影响下, 聚焦HyGG-II光束不同OAM模式之间存在相互干扰, 此时接收平面处的复振幅可以被表示为各种OAM模式的叠加^[13]:

其中$ {a_m}(r, z) $为叠加系数, 其表达式为

将(10)式代入(12)式并对海洋湍流进行系综平均, 可以推导得到聚焦HyGG-II光束的OAM模式概率密度为

进一步利用波结构函数的二次近似^[14], 即:

其中$ {\rho _0} $为海洋湍流的空间相干长度, 其表达式为^[15]

式中, $ {\phi _n}\left( \kappa \right) $是海洋湍流空间折射率功率谱, 本文采用的是Nikishov各向同性折射率功率谱模型^[16]. $ \kappa $是空间频率, $ \varepsilon $表示单位质量动能耗散率, $ \eta $表示湍流内尺度, $ {\chi _{\text{t}}} $表示海水温度均方差耗散率, $ \tau $为温度与盐度波动导致折射率变化时其所做贡献的比率, 简称温度盐度贡献比或温盐比.

将(9)式、(14)式和(15)式代入(13)式后可得

再进一步利用积分式^[12]:

对(16)式进行化简, 可以得到最终的OAM模式概率密度解析表达式为

其中, $ {{\text{I}}_{m - {m_0}}}\left( \cdot \right) $表示第一类修正贝塞尔函数.

为了得到聚焦HyGG-II光束在海洋湍流中传输时的信道容量, 首先需要计算其探测概率. 通过利用(18)式的OAM模式概率密度, 可得聚焦HyGG-II光束的探测概率为

其中, $ \displaystyle \int_0^\infty {\langle {{{\left| {{a_m}(r, z)} \right|}^2}} \rangle r{\text{d}}r} $表示接收到的模式数为m的OAM模式对应的能量, $\displaystyle \int_0^\infty {\langle {{{\left| {{a_{m'}}(r, z)} \right|}^2}} \rangle r{\text{d}}r} $是光束携带的总能量.

涡旋光束的信道容量表达式为^[17,18]

其中, $ H\left( {{m_0}} \right) $是信源熵, $ H\left( {{m_0}|m} \right) $是条件熵, 可以利用探测概率$ p\left( {m|{m_0}} \right) $对其进行计算. 假设发射端等概率的发送不同OAM模式, 其模式范围为$ {m_0} \in \left[ { - N, N} \right] $, 通过推导可得聚焦HyGG-II光束在海洋湍流中传输时信道容量的最终表达式为

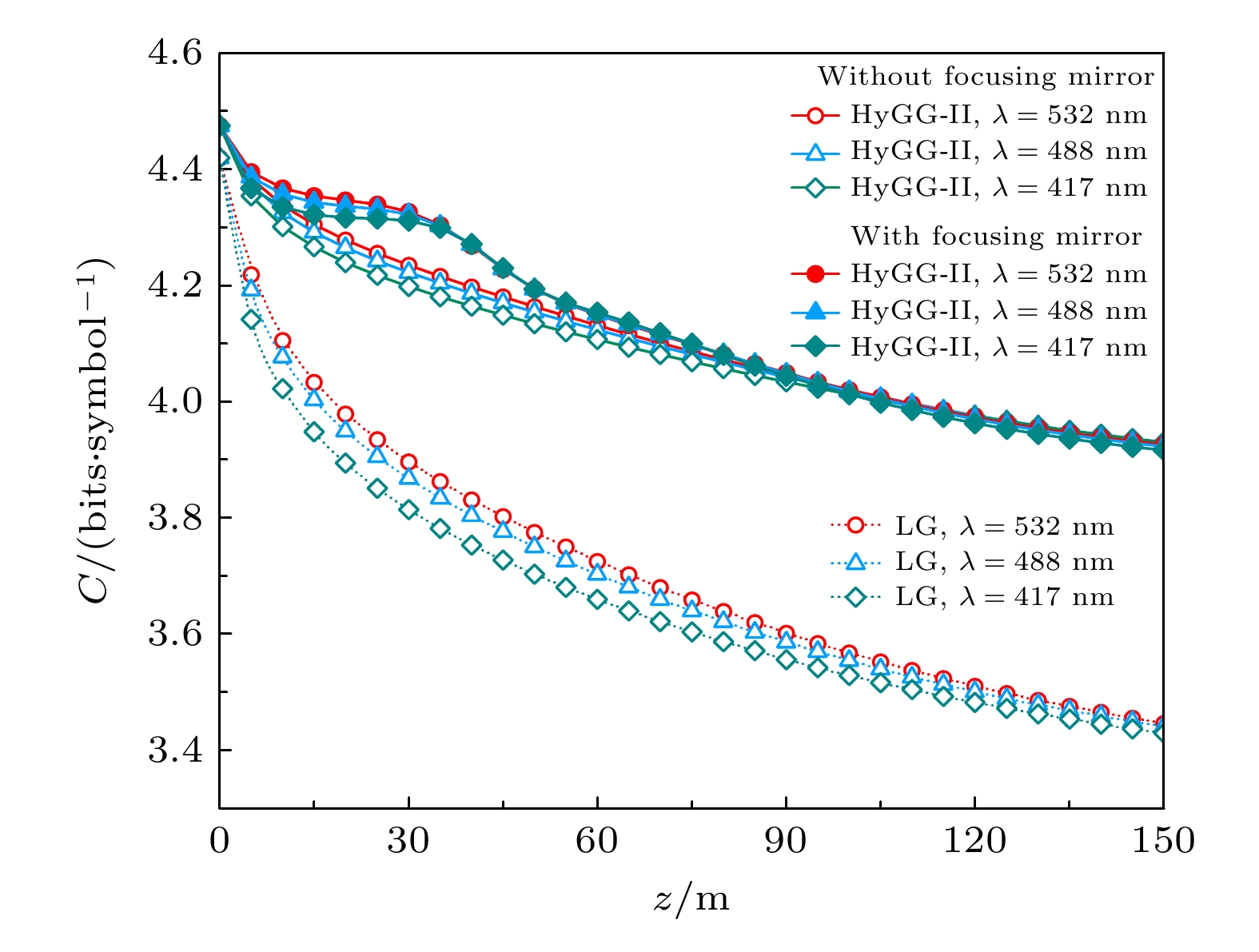
根据前面的理论模型, 本节对聚焦透镜对HyGG-II光束信道容量的影响进行研究, 并与未使用透镜时的信道容量以及其与LG光束的信道容量进行对比分析, 以验证HyGG-II光束适于水下传输, 并证明聚焦透镜对其信道容量具有提升效果. 除非另外说明, 本节在仿真过程中使用的主要参数如下: $ {\omega _0} = 4 \times {10^{ - 3}}{\text{m}} $, $ {m_0} = 1 $, $ p = 2 $, $ f = 50 {\text{ m}} $, $ \lambda = 532 {\text{ nm}} $, $ z = 30 {\text{ m}} $, $ \varepsilon = {10^{ - 5}}{{\text{ m}}^{2}}{\text{/}}{{\text{s}}^{3}} $, $ \eta = {10^{ - 3}}{\text{ m}} $, $ {\chi _{\text{t}}} = {10^{ - 7}}\;{{\text{K}}^{2}}{\text{/s}} $, $ \tau = - 3 $.

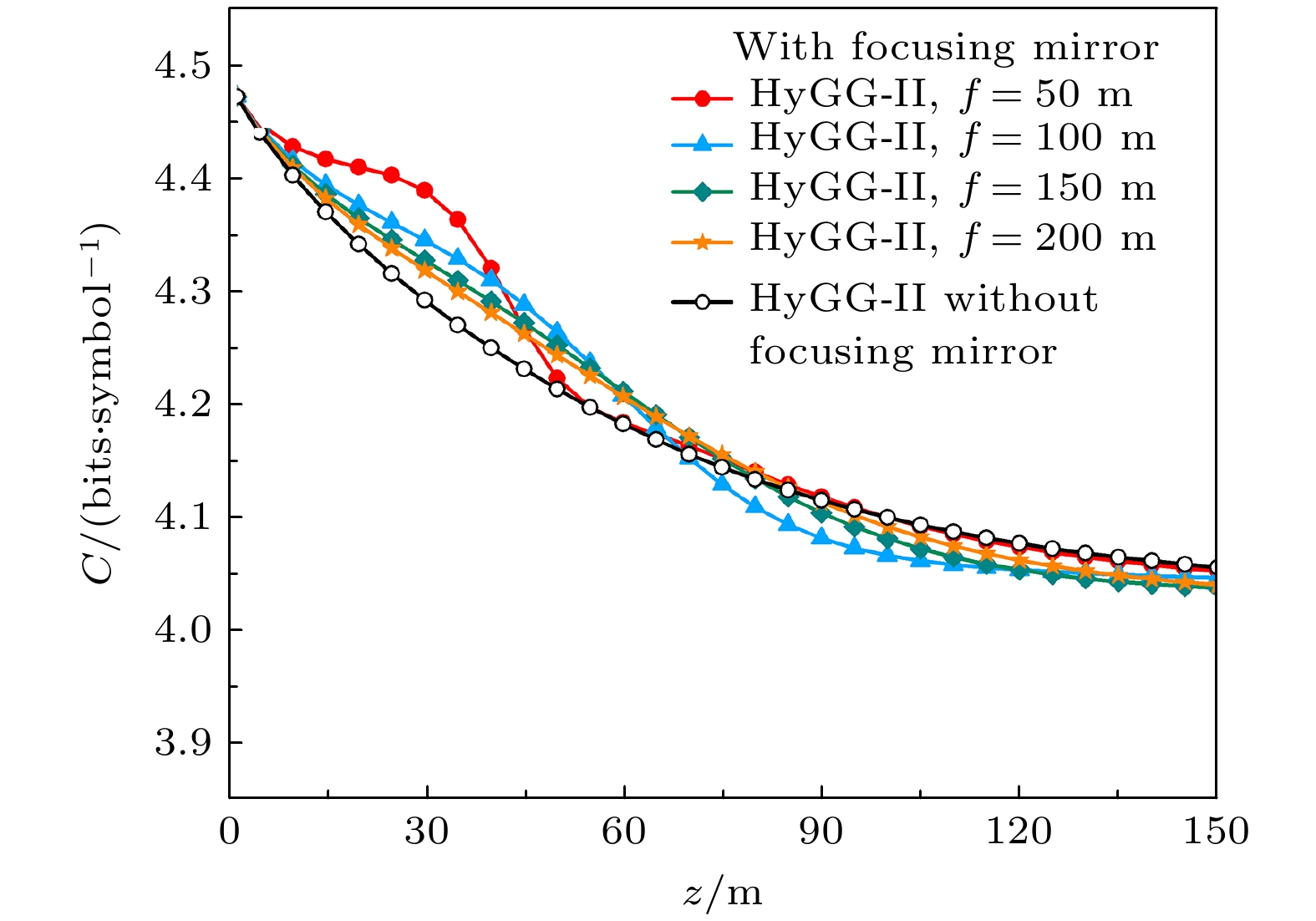
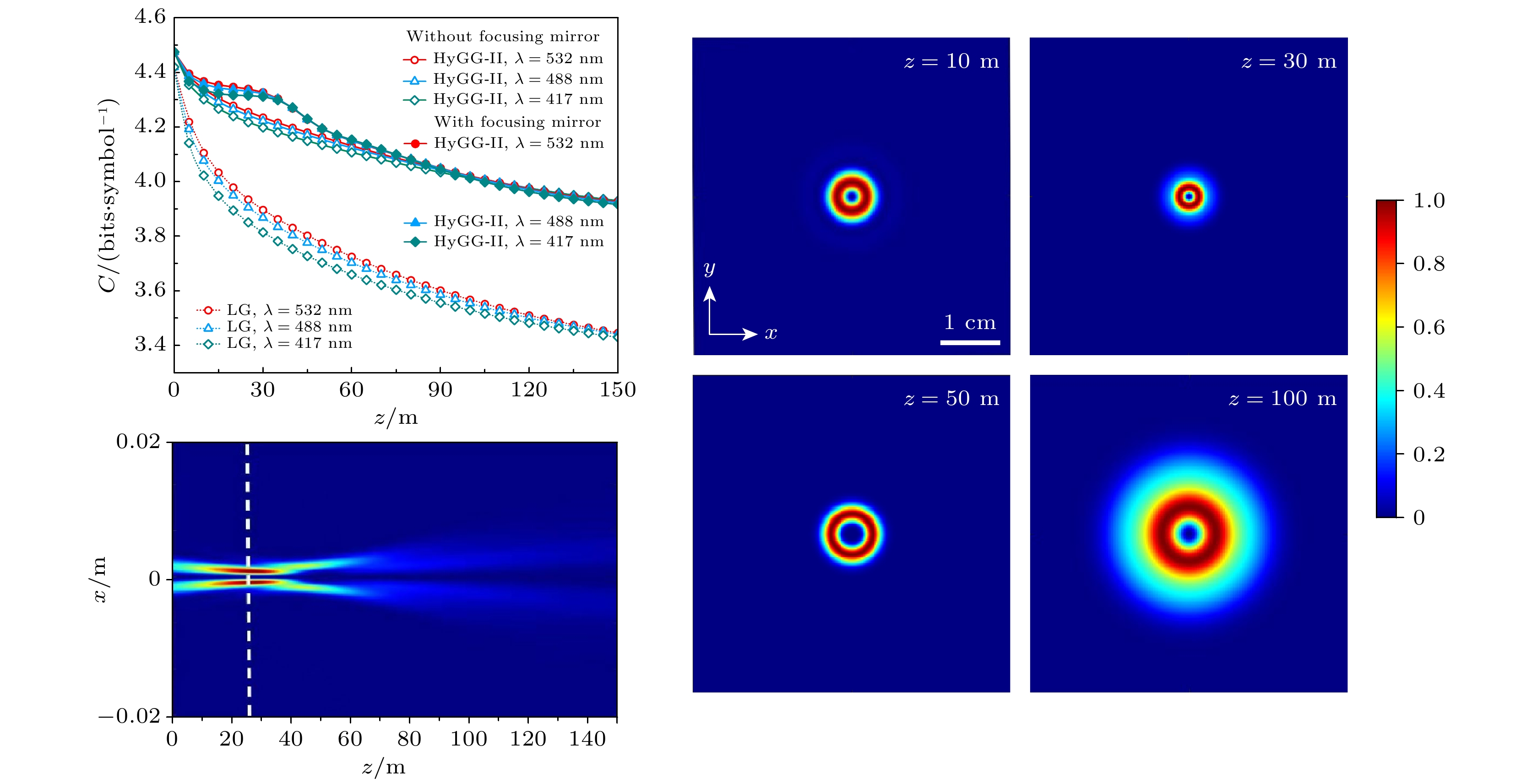
首先仿真了不同波长$ \lambda $时聚焦HyGG-II光束、非聚焦HyGG-II光束和LG光束的信道容量C随传输距离z的变化, 结果如图1所示. 可以看出, 3种涡旋光束的信道容量均随传输距离的增大而减小, 并且波长越小信道容量相对减小的越快, 此结果与文献[6,7]报道的结果相似. 产生这种现象的主要原因是随着传输距离的增大或者波长的减小, 空间相干长度$ {\rho _0} $减小, 湍流引起的模式串扰变严重, 从而导致信道容量减小. 与LG光束相比, 在相同传输距离下无论是否使用聚焦透镜HyGG-II光束的信道容量都明显要高, 这表明HyGG-II光束具有更好的抗湍流干扰能力. 此外, 对比聚焦和非聚焦HyGG-II光束的信道容量结果可以发现, 通过在源平面位置加入聚焦透镜确实可以提高信道容量, 但信道容量的增强却受传输距离限制(约百米), 这意味着无法通过使用聚焦透镜对较远接收位置处的信道容量进行改善. 从图1还可看出, 存在一个最佳接收位置(约30 m), 此处聚焦透镜对信道容量的增强效果最好. 虽然使用聚焦透镜存在着上述传输距离的限制, 但由于目前已报道的水下无线光通信实验的传输距离大都也为几十米^[19–23], 所以这种距离限制对于实际通信系统而言几乎没有影响.

为了研究聚焦透镜的不同焦距是否会对信道容量产生影响, 仿真了当波长取532 nm, 焦距 f 分别取50, 100, 150, 200 m时HyGG-II光束的信道容量随传输距离z的变化, 结果如图2所示. 从图2可以看出, 不同 f 的聚焦透镜对HyGG-II光束的信道容量增强效果也不同. 例如, 当f = 50 m时, 在z约为30 m处信道容量的增强达到最大, 此时聚焦HyGG-II光束的信道容量为4.2769, 比不使用聚焦透镜提高了4.77%. 但随着 f 的增大, 聚焦和非聚焦HyGG-II光束之间的信道容量最大差值减小, 且最大差值对应的接收位置会向远距离传输方向偏移. 例如当使用 f = 100, 150, 200 m的聚焦透镜时, 信道容量的最大增强效率分别为3%, 2.07%和1.58%, 对应的位置分别约为40, 41, 45 m. 由此可知, 实际中可根据接收机的位置相应调整 聚焦透镜的焦距, 从而获得更好的信道容量增强 效果.

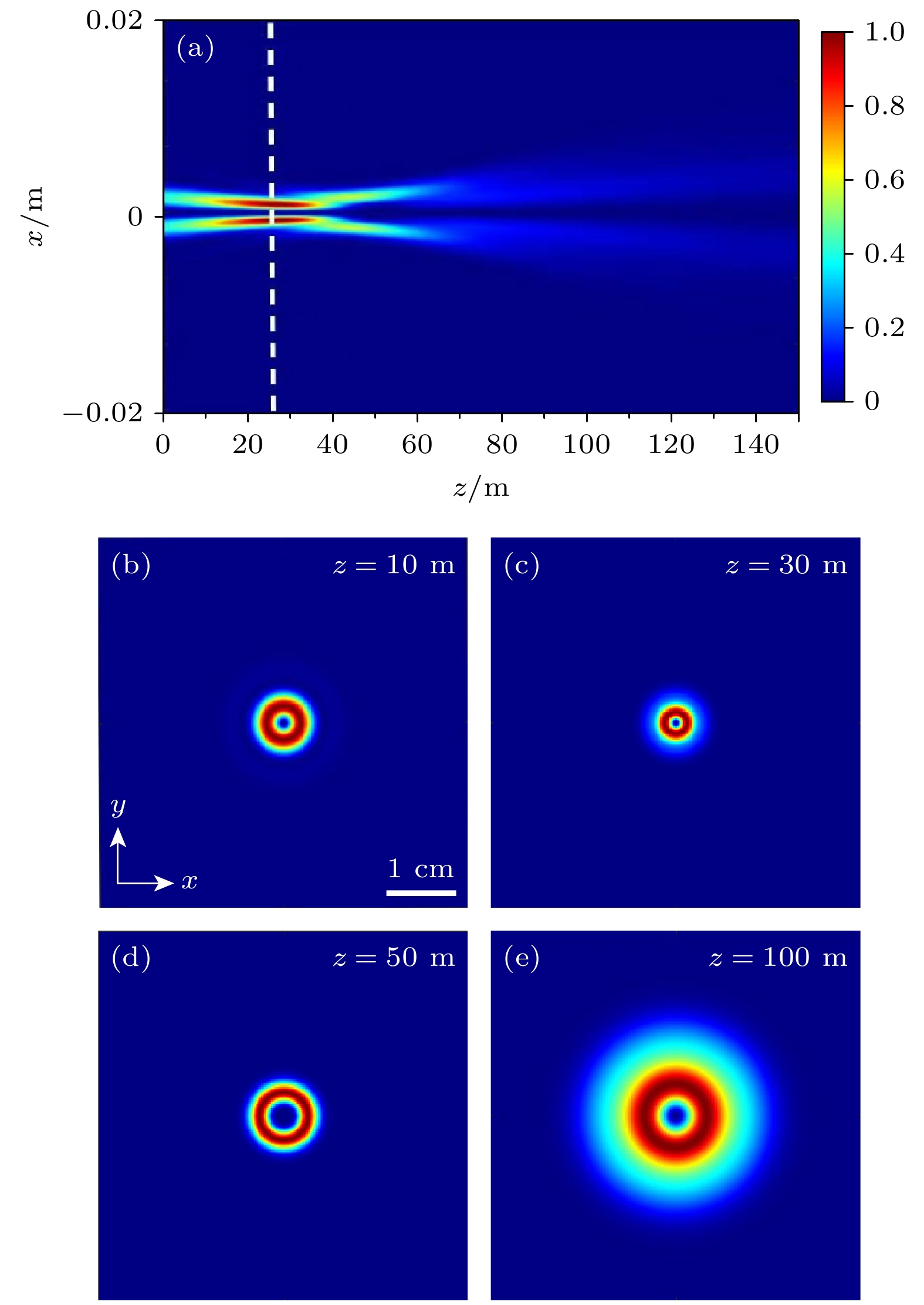
为了探究聚焦透镜只能在一定的传输距离范围内才能改善信道容量的原因, 研究了当焦距为50 m时聚焦HyGG-II光束的光强随传输距离z的变化, 结果如图3所示. 从图3可以明显看出, 随着z的增大, 光束产生了先会聚、随后逐渐发散的现象, 即聚焦透镜使HyGG-II光束的光强会聚在一定的传输距离范围之内. 在图3中, z约为30 m时HyGG-II光束会聚的最强, 表现为中心亮环半径最小且归一化光强值最大. 随着z的继续增大, 中心亮环半径逐渐变大, 归一化光强值逐渐变小, 且光环发散程度越来越大. 当传输距离接近百米时, HyGG-II光束的发散已经较严重, 并且归一化光强值也很低, 此时聚焦透镜对HyGG-II光束的传输几乎不起任何作用. 从上述分析可知, 图1表现出的信道容量增强效果受传输距离的影响, 与聚焦透镜对HyGG-II光束的会聚效果有关, 在透镜起到光强会聚作用的传输距离范围内, 信道容量都能够得到一定程度的改善, 且可以在光强汇聚最强的位置附近获得最好的信道容量增强效果, 这可以为实际设计基于HyGG-II光束的水下无线光通信系统提供一定的指导.

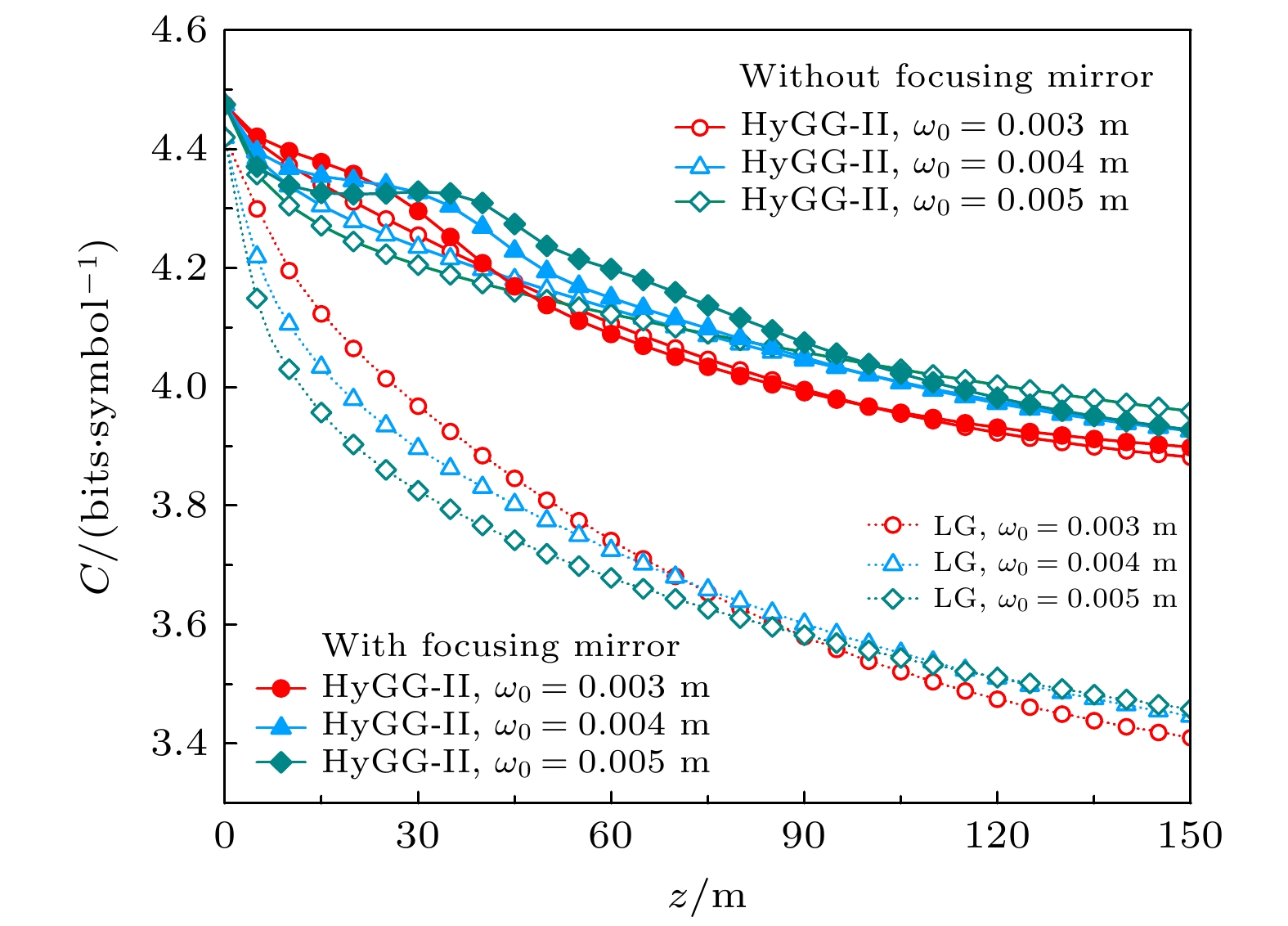
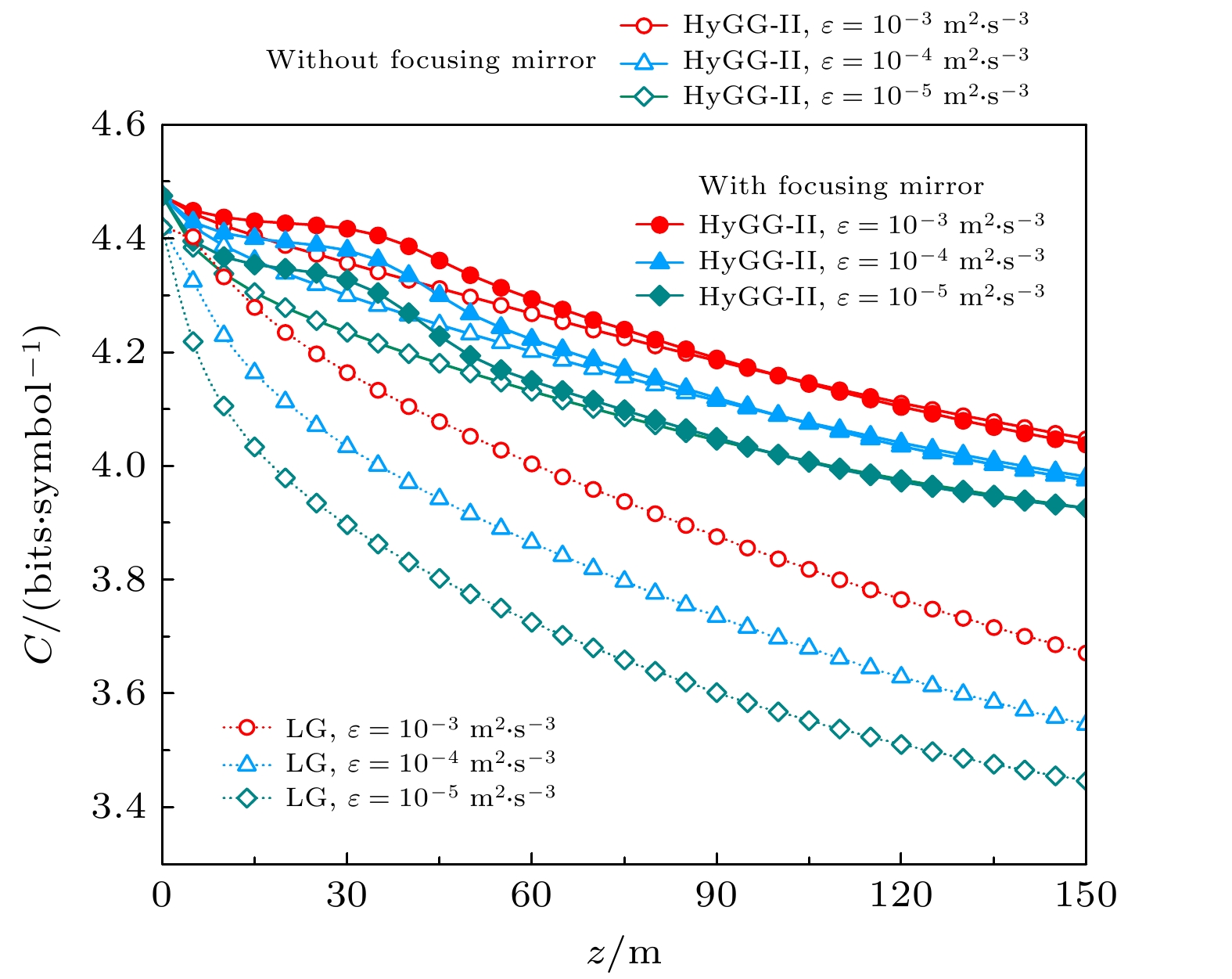
接下来分析不同束腰半径$ {\omega _0} $对聚焦HyGG-II光束、非聚焦HyGG-II光束和LG光束信道容量的影响, 结果如图4所示. 可以看出, 随着$ {\omega _0} $的增大, 信道容量获得增强时所对应的传输距离范围, 以及聚焦透镜对信道容量的最大增强效果都随之增大. 因此如果想在较远的接收位置处获得更好的信道容量特性, 可以将HyGG-II光源的束腰半径参数设置成较大的值. 从图4还可以看出, 不同$ {\omega _0} $下信道容量得到最大增强时所对应的位置是不一样的, 如$ {\omega _0} = $3, 4, 5 mm时, 最大增强位置分别约为25, 30, 35 m. 这意味着束腰半径参数与聚焦透镜的焦距参数类似, 在实际也可以根据具体要求的传输距离, 通过调整束腰半径参数来获得相对最优的信道容量. 与LG光束相比, 不同$ {\omega _0} $时无论是否使用聚焦透镜HyGG-II光束的信道容量都明显要好, 这与图1结论相同.

因为海洋湍流是影响水下无线光通信系统性能的主要因素之一, 所以下面将详细分析不同海洋湍流参数对HyGG-II光束信道容量的影响. 图5给出了不同单位质量动能耗散率$ \varepsilon $下聚焦HyGG-II光束、非聚焦HyGG-II光束和LG光束的信道容量随传输距离z的变化. 如图5所示, 相同传输距离下随着$ \varepsilon $的增大, HyGG-II光束的信道容量随之变大, 但聚焦透镜对信道容量的增强效果却越来越小. 由于$ \varepsilon $可以反映海洋湍流的强度, $ \varepsilon $越大代表海洋湍流越弱, 因此上述结果表明在强海洋湍流中HyGG-II光束的信道容量较差, 但此时使用聚焦透镜却可以获得比在弱海洋湍流环境下更好的信道容量增强效果. 与LG光束相比, 相同条件下HyGG-II光束的信道容量较好, 且随着$ \varepsilon $的减小二者之间的差距变大, 这意味着在强海洋湍流环境中HyGG-II光束的抗湍流干扰能力比LG光束更好.

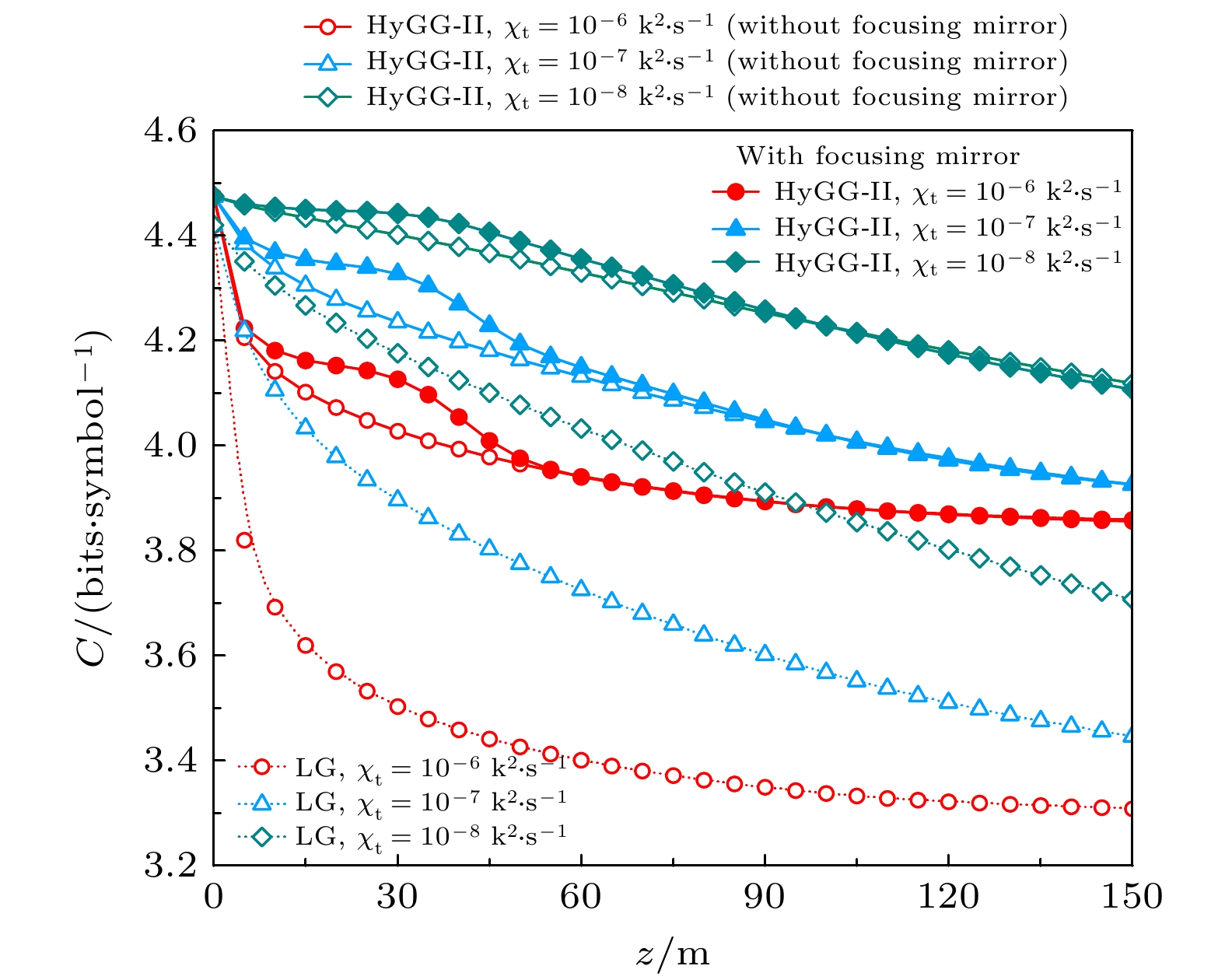
与单位质量动能耗散率$ \varepsilon $类似, 温度均方差耗散率$ {\chi _{\text{t}}} $也是反映海洋湍流强度的一个重要参数, 其值越大代表着湍流越强. 因此图6仿真了$ {\chi _{\text{t}}} $分别为10^–6, 10^–7, 10^–8 K²/s时3种光束的信道容量随传输距离的变化. 可以看出, $ {\chi _{\text{t}}} $对3种光束信道容量的影响与$ \varepsilon $相似, 即$ {\chi _{\text{t}}} $越大(湍流越强)信道容量越小, 但聚焦透镜的增强效果却越好. 分析认为上述现象的产生可归因为: 弱海洋湍流对HyGG-II光束的信道容量特性影响很小, 所以使用聚焦透镜后虽能对信道容量再进行改善, 但改善的空间却有限. 而在强海洋湍流环境中, HyGG-II光束的信道容量特性本身较差, 所以此时通过使用聚焦透镜可对原本较差的信道容量起到较显著的增强效果. 与图5类似, 不同温度均方差耗散率条件下HyGG-II光束的信道容量都比LG光束的更好.

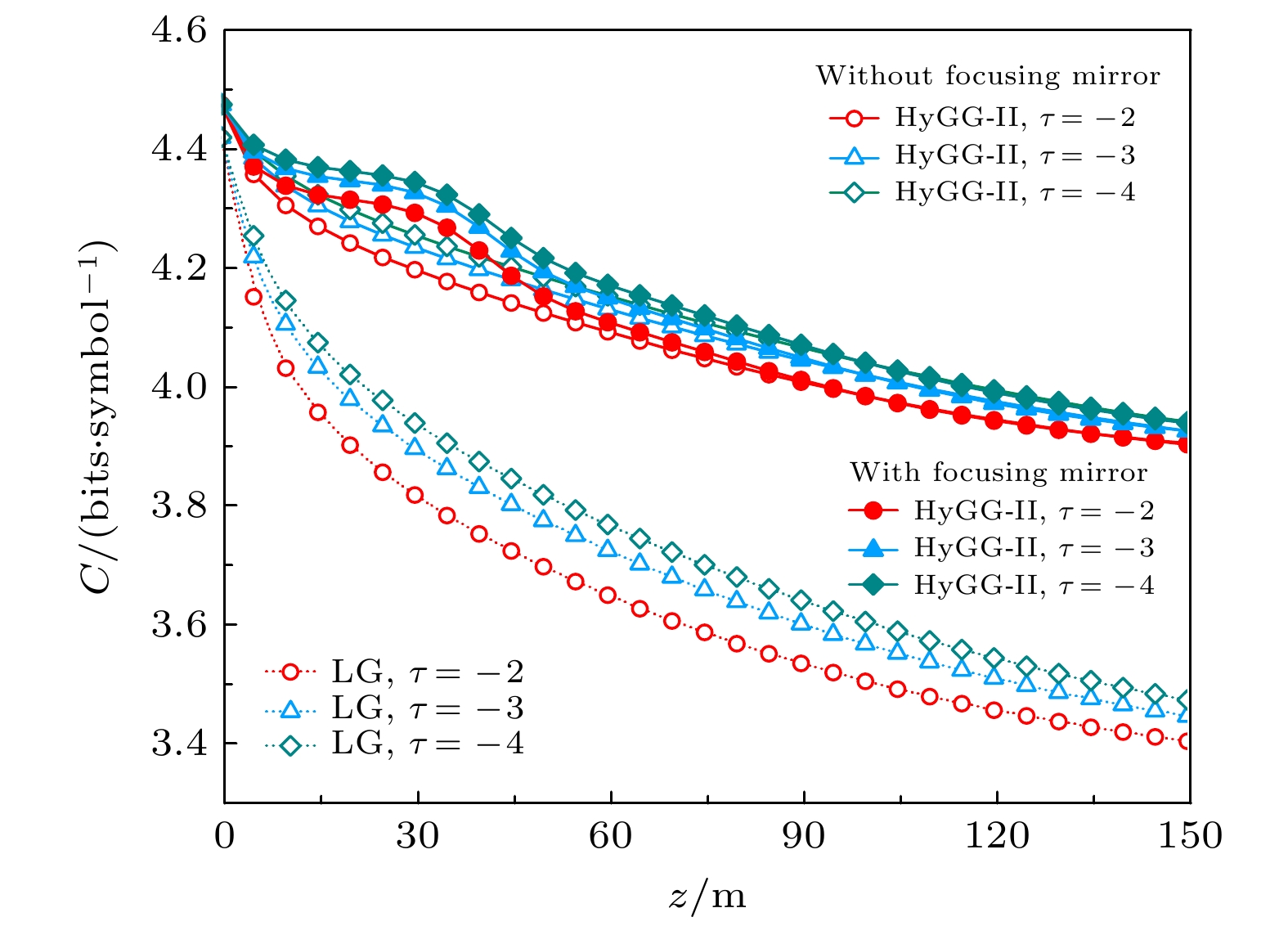
除单位质量动能耗散率和均方温度耗散率之外, 海洋湍流还受温度与盐度的波动影响. 如第2节所述, 这种影响可以用温度盐度贡献比$ \tau $来表示. $ \tau $值范围为0—-5, 当$ \tau \to 0 $时, 代表海洋湍流主要由盐度波动主导; 当$ \tau \to - 5 $时, 代表海洋湍流主要由温度波动主导. 图7所示为不同$ \tau $时聚焦HyGG-II光束、非聚焦HyGG-II光束和LG光束的信道容量随传输距离的变化. 可以看出, 3种光束都是在盐度波动占主导的海洋湍流中传输时信道容量相对更好. 此外, 对于HyGG-II光束而言, 不同$ \tau $时通过使用聚焦透镜都能对信道容量进行增强, 且增强效果接近.

本文分析了HyGG-II光束在海洋湍流中传输时的信道容量特性, 并研究了通过使用聚焦透镜来提升信道容量的方法, 同时还将HyGG-II光束与LG光束进行对比. 首先, 基于Rytov近似和广义惠更斯菲涅耳原理推导得到在源平面位置加入聚焦透镜之后HyGG-II光束在海洋湍流中传输时的信道容量解析表达式, 随后详细分析了不同光源参数(焦距、波长和束腰半径)和海洋湍流参数(单位质量动能耗散率、温度均方差耗散率和温度盐度贡献比)对信道容量的影响. 结果表明, 相同条件下无论是否使用聚焦透镜, HyGG-II光束的信道容量都比LG光束的明显要好, 并且在强海洋湍流环境中HyGG-II光束表现出比LG光束更优秀的抗湍流干扰能力. 使用聚焦透镜之后, HyGG-II光束的信道容量在约百米的传输距离范围之内都能够被不同程度地增强. 通过分析聚焦HyGG-II光束的光强随传输距离的分布发现, 最佳信道容量增强效果出现在HyGG-II光束会聚最强的位置附近. 在实际中为了获得较好的信道容量特性, 可以采用增大HyGG-II光束的波长或根据具体接收距离优化调整焦距和束腰半径的方法. 本文的研究结果能够对提高海洋湍流环境下基于涡旋光束的水下通信系统性能提供参考和借鉴.