首页
登录
注册
下载:
-
光电离是非常重要的微观原子过程之一, 其对原子(或离子)能级、波函数和内部电子关联的变化非常敏感, 因此可以作为理解复杂物理系统结构的工具. 在激光等离子体、惯性约束聚变等离子体以及天体等离子体的温度密度范围内开展光电离过程的研究是很有意义的[1,2]. 对于光电离过程的相关研究还可以为天体和实验室等离子体中不透明度的计算提供基本原子参数[3,4]. 在热稠密等离子体中, 离子与周围粒子之间存在复杂的多体相互作用, 这将显著改变离子的原子结构和动力学性质. 具体来说, 等离子体环境效应会削弱原子核对束缚电子的吸引, 导致光电离阈值发生红移. 同时, 考虑屏蔽的库仑势得到的光电离截面会体现部分低能特征, 例如势形共振, Cooper极小, 近零能增强, 低能Wigner阈值定律、虚态共振、Combet-Farnoux极小等[5,6].
对于等离子屏蔽引起的截面低能特征的研究可以解释截面的线型, 从而用于等离子体光谱诊断. 目前为止, 已有很多工作主要应用德拜模型(Debye Hückel, DH)[7,8]研究了阈值附近光电离截面的重要低能特征. Sahoo等[9]基于复坐标旋转法计算了等离子体环境中碱金属原子 Li 和 Na的光电离截面, 他们发现强屏蔽效应显著改变了电离阈值附近的光电离截面. 随着屏蔽效应的增强, Na光电离截面的Cooper极小值向高能方向移动. Qi等[10]研究了非相对论的类氢离子基态和n ≤ 3激发态的光电离截面, 并详细讨论了低能截面特征, 如势形共振、Cooper极小、低能增强等. Lin等[11]利用复坐标旋转法研究了德拜等离子体中, 偶极子和四极子光电离截面均出现的势形共振和Cooper极小. 然而在热稠密等离子体中, 非弹性碰撞如三体复合的贡献将变得重要, 不能被忽略[12]. 因此, 为了精确处理具有较大温度和密度范围的温/热稠密等离子体, 我们提出了原子态分辨(atomic-state-dependent, ASD)屏蔽模型[13], 该模型可以准确描述等离子体中带电粒子之间的相互作用, 包括电子简并效应. 对于热稠密等离子体, ASD模型考虑了包含三体复合的非弹性碰撞过程产生的负能电子密度分布的贡献, 这对于描述热稠密等离子体中的不同原子性质非常重要, 如谱线移动[13]、电离势下降[12]和光电离截面[14]. 另外, 在弱耦合及强简并极限条件下, ASD模型计算得到的电子密度可以分别收敛到DH和离子球(ion sphere, ISP)[15]模型, 因此ASD模型适用于广泛的等离子体温度密度范围.
本文应用ASD模型研究了热稠密等离子体中Fe25+离子基态及激发态的低能光电离截面, 分析了屏蔽势、连续波函数以及能级布居随等离子体密度的变化. 由于光电离截面的低能特征与电子波函数以及跃迁矩阵元直接相关, 因此本文通过这些参数分析了不同等离子体条件下基态和激发态不同光电离截面低能特征的形成及其影响, 包括势形共振、Cooper极小、低能增强、Combet-Farnoux极小. 本文主要考虑在太阳辐射层的等离子体温度条件下(~200 eV), 改变等离子体密度来研究不同等离子体环境对于光电离截面的影响. 如无特别提及, 下文均采用原子单位.
-
在中等耦合及强耦合等离子体中, 等离子体粒子之间的耦合增强, 简并效应变得尤为重要, 而ASD模型可以考虑这些效应. 在ASD模型中, 首先假设等离子体的自由电子处于平衡状态且可以通过费米狄拉克分布描述为
式中, μ是等离子体自由电子的化学势,
$ \varPhi (r) $ 是处于r位置的总有效势, p是电子的动量, Te是等离子体电子温度. 除了一般的弹性碰撞之外, 在热稠密等离子体中, 非弹性碰撞特别是三体复合也是很重要的, 因此准确模拟屏蔽效应时应该被考虑. ASD模型的电子密度包含电子与靶态离子之间的三体复合过程. 由于离子的束缚电子之间的简并效应, 被俘获的电子只能分布在外壳层未占据的轨道上, 这些电子被称为负能电子. 为简单起见, 假设等离子体自由电子处于平衡状态, 并应用稳态近似来获得给定自由电子温度和密度中的负能态分布. 因此具有特定束缚态j的原子可以通过靶离子的三体复合形成, 其数密度$ n_{{\text{atom}}}^j $ 可以通过速率方程确定:其中
$ {\alpha _j} $ ,$ {\beta _j} $ ,$ {K_{j'j}} $ 和$ {K_{jj'}} $ 分别是电子碰撞电离、三体复合、激发, 以及退激发的速率系数.由于复合电子与初始束缚电子之间的简并效应, 负能电子更容易被填充在未被占据的外壳层轨道, 导致其动量大于
$ \sqrt {2{m_{\text{e}}}[{\varepsilon _{\text{b}}} - \varPhi (r)]} $ . 因此总等离子体电子密度表示为其中,
$ \chi (p, r) $ 是通过求解速率方程(2)得到的非平衡系数, 详细的描述见文献[13]及其补充材料[16],$ {\varepsilon _{\text{b}}} $ 是最外层束缚电子的轨道能量, 其显著影响目标离子的负能电子分布. (3)式的第2项对应于后文中的自由电子模型, 表示自由电子密度的费米-狄拉克分布, 只考虑动量p > p0的自由电子, 且$ {p_0}(r) = \sqrt {2{m_{\text{e}}}\varPhi (r)} $ .进一步可以得到靶态离子总的有效势:
式中,
$ \delta \rho (r) = \rho (r) - {\rho _{\text{e}}} $ 是嵌入靶离子引起的等离子体电子密度涨落,$ {\rho _{\text{b}}}(r) $ 是束缚电子密度. 当给定电子温度Te和平均电子密度$ {\rho _{\text{e}}} $ 时, 相互依赖的$ \varPhi (r) $ 和$ \delta \rho (r) $ 就可以用迭代的方法计算得到. 关于ASD模型势的详细推导见文献[13]及其补充材料[16].最终, ASD模型中电子-离子相互作用, 包括核势和等离子体屏蔽产生的外场, 可以描述为
-
将以上ASD屏蔽势代入类H离子Dirac哈密顿量中:
式中c是光速, α 和β 是Dirac 矩阵, p是动量算符.
束缚和连续态的自旋轨道波函数:
式中,
$ {P_{g, k}}(Z;r) $ 和$ {Q_{g, k}}(Z;r) $ 分别是径向波函数的大小分量. 对于束缚态, g = n, n是主量子数; 对于连续态, g = ε,$ \varepsilon = {({k^2}{c^2} + {c^4})^{1/2}} - {c^2} $ 是连续电子的动能.$ {\chi _{km}}(\theta , \varphi ) $ 是自旋角向函数, 表达式为其中
$ \left\langle {\left. {lm - \sigma {1}/{2}\sigma } \right|l{1}/{2}jm} \right\rangle $ 是Clebsch-Gordan 系数,$ {\text{Y}}_l^{m - \sigma }(\theta , \varphi ) $ 是球谐函数,$ {\phi ^\sigma } $ 是旋量基函数.将单电子哈密顿量分离变量后得到角向和径向两部分, 角向部分可以通过Racah代数来直接计算, 而径向部分满足Dirac方程. 以下为类H离子的束缚和连续波函数满足的耦合Dirac方程:
对于束缚态,
$ {E_{gk}} < 0 $ 表示束缚电子的轨道能量; 对于连续态,$ {E_{gk}} > 0 $ 表示连续电子的动能. 通过求解Dirac方程可以得到束缚和连续电子的径向波函数. 该方程是非线性耦合方程, 可以通过自洽场求解. 束缚和连续径向波函数的正交条件满足:其中
$ {\delta _{nn'}} $ 和$ \delta (\varepsilon - \varepsilon ') $ 是克罗内克δ函数.需要说明的是, 本文基于改进的GRASP2K程序包进行多组态Dirac-Hartree-Fock (MCDHF)理论计算, 以获得相对论束缚态波函数和能量[17,18]. 基于CONTWVSA程序包, 通过相对论WKB近似对连续态波函数进行归一化[19,20].
得到束缚和连续态波函数之后, 计算总角动量为ja的初态a到末态连续态b的相对论总光电离截面:
式中α 是精细结构常数,
$ {{{\text{d}}{f_{ab}}} {/ } {{\text{d}}\varepsilon }} $ 是振子强度密度:$ {\psi _{nk}} $ 和$ {\psi _{\varepsilon k'}} $ 分别是初态和末态电子的波函数.$ {\widehat {\boldsymbol{O}}^{(L)}} $ 是阶为L的多极辐射场算符. 偶极跃迁(L=1)的跃迁矩阵元$ \langle {{\psi _{nk}}\| {{{\widehat {\boldsymbol{O}}}^{(L)}}} \|{\psi _{\varepsilon k'}}} \rangle $ 形式为式中
$ {\overline M _{ab}} $ 是跃迁积分, 由Grant[21]给出. -
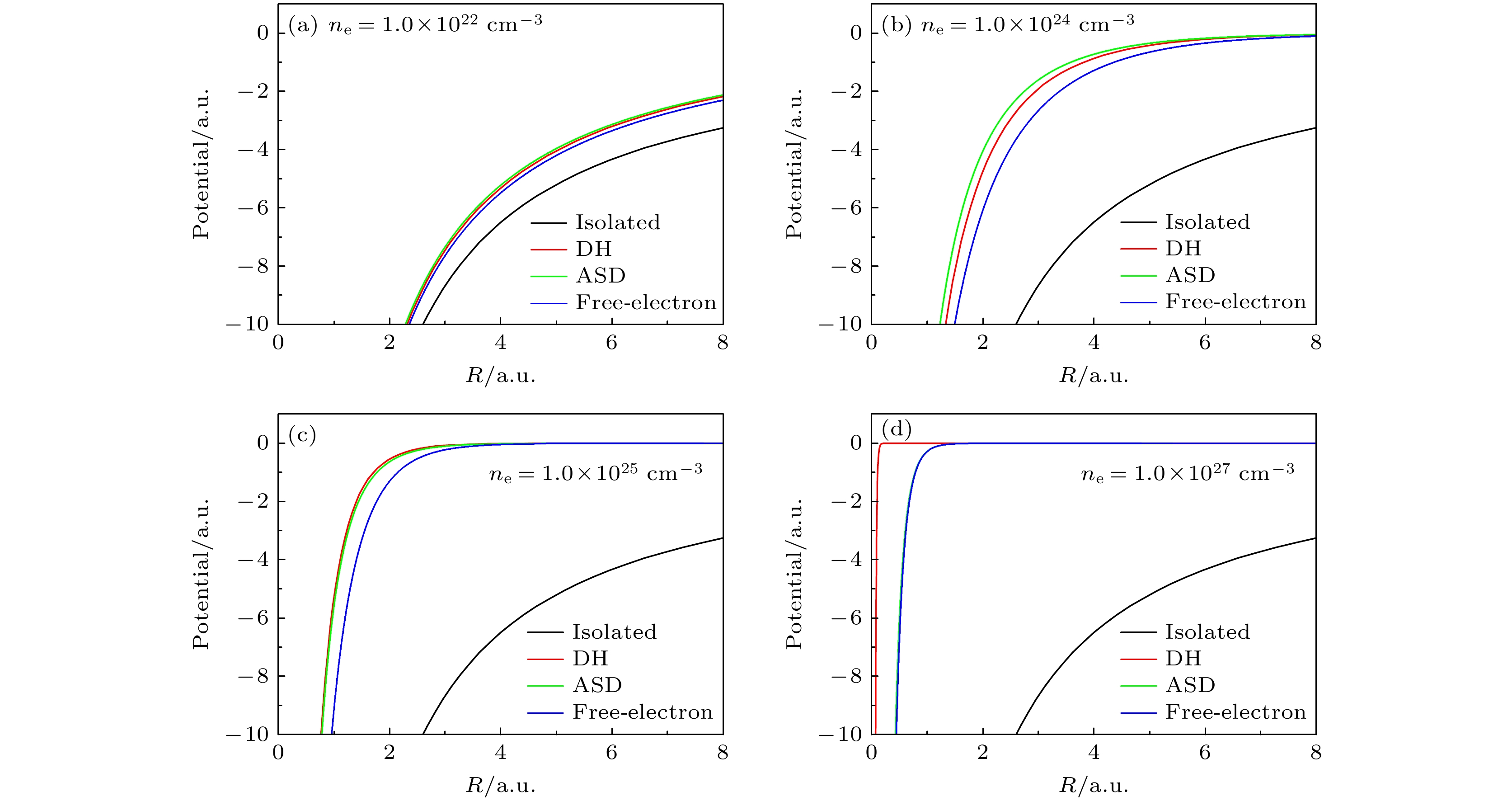
不同屏蔽模型考虑了不同的效应, 因此产生不同的屏蔽势. 图1所示为孤立的(isolated)、原子态分辨(ASD)模型的Fe25+离子基态势能, 并和自由电子(free-electron)、DH屏蔽模型的结果进行比较. 可以看到, 当密度开始增大, ASD模型的势能比DH模型大, 然而密度继续增大, DH模型的势能逐渐反超ASD模型的, 这是因为DH模型的密度分布为玻尔兹曼分布的一阶线性近似, 没有考虑稠密等离子体中的简并效应, 因此高估了屏蔽效应. 而ASD模型通过考虑负能电子分布包含了简并效应, 因此当密度继续增加, 简并效应增强时, 其屏蔽势的增加没有DH模型多. 对于自由电子模型, 可以看到其势能随着密度的变化始终小于ASD模型, 且和ASD模型之间的差异随密度先增大后减小. 这是因为密度增大, 耦合增强, 负能电子密度增大; 而密度继续增大, 简并效应开始增强, 负能电子密度减小, 最终ASD模型的势能收敛到自由电子模型.
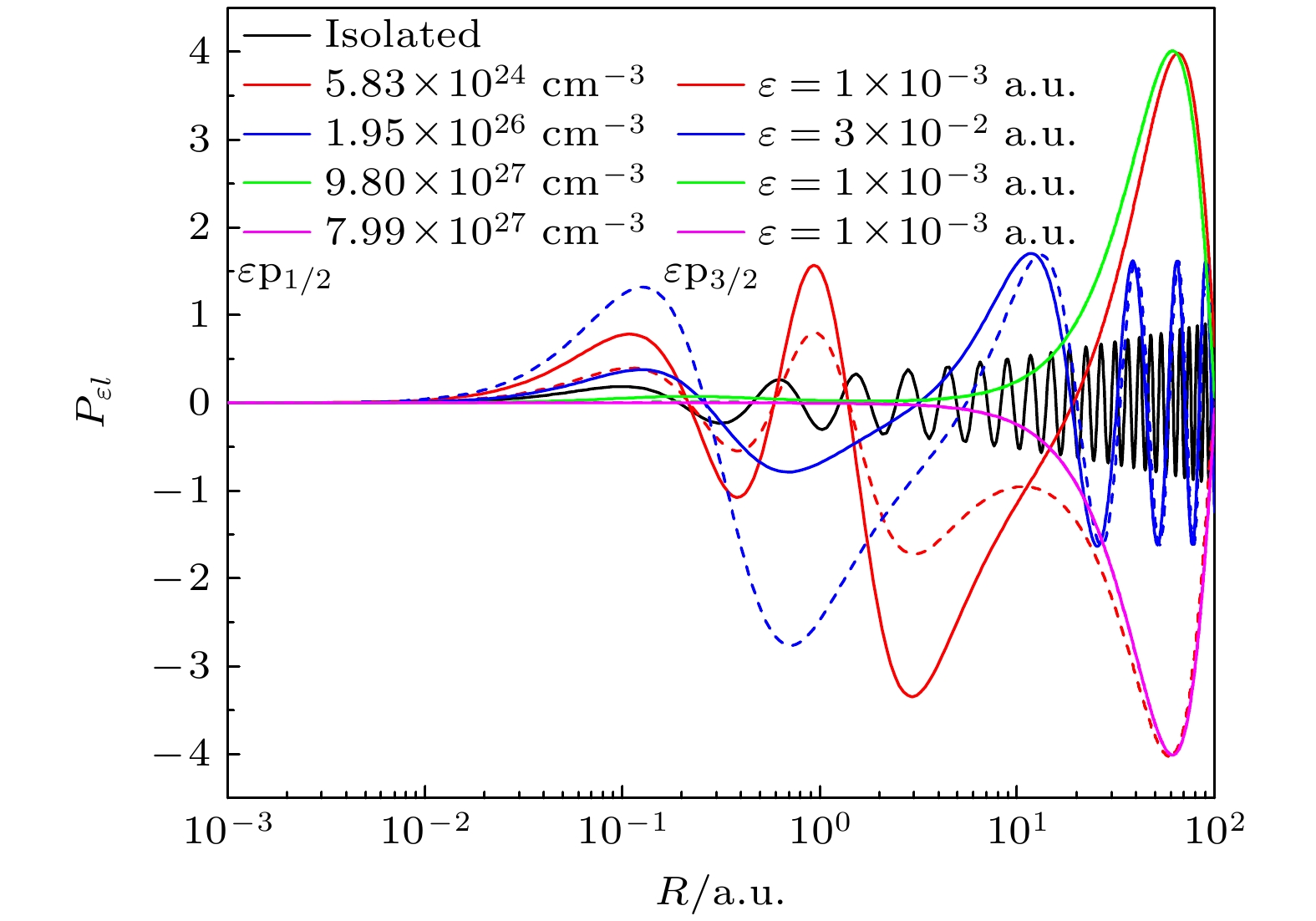
等离子体屏蔽效应会造成束缚和连续电子波函数发生变化, 从而影响它们的重叠积分. 图2所示为等离子体电子温度固定时不同电子密度的连续态波函数. 可以看到, 连续态波函数随等离子体密度变化十分敏感, 表现为振幅和相位的显著增加. 等离子体电子密度为1.95×1026 cm–3时, 连续电子εp3/2的振幅比εp1/2大, 而密度为5.83×1024 cm–3时连续电子εp1/2的振幅却比εp3/2大, 这与对应准束缚态进入连续态的先后顺序有关[22]. 此外, 密度为5.83×1024 cm–3时, 连续波函数出现的异常增大将会导致耦合矩阵元也突然增大, 最终体现为截面出现势形共振峰. 当连续电子的角动量l>0时, 其会短暂地停留在有效势的离心势垒中, 造成连续电子波函数相位突变, 最终导致电离阈值附近的截面显著增大, 即为势形共振.
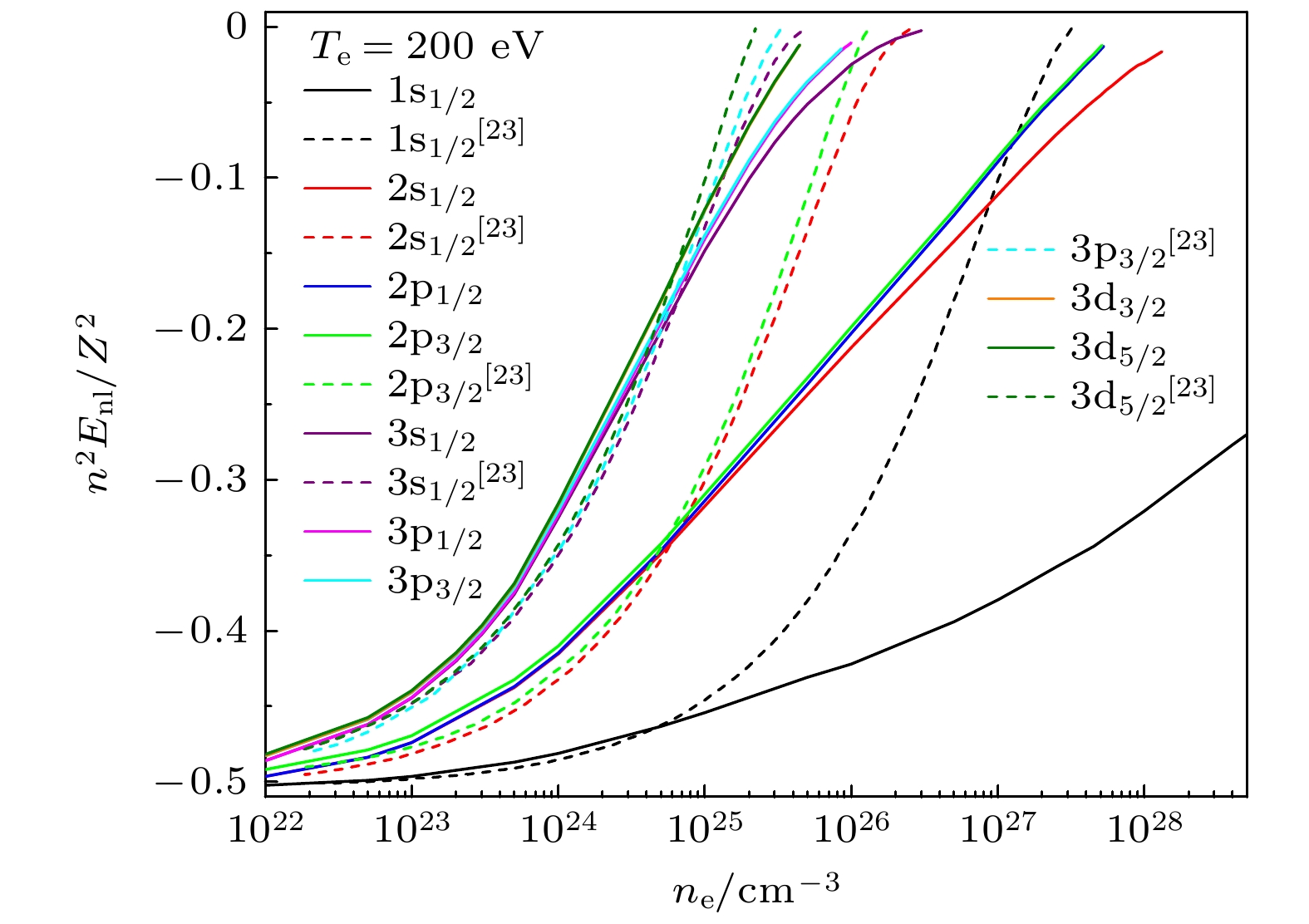
等离子体屏蔽效应导致束缚电子的能级布居逐渐向外移动, 密度增大直到超过临界值时, 束缚电子进入连续态, 这里的临界值即为束缚电子能量为0时对应的屏蔽环境[22,23]. 图3所示为Fe25+离子1s, 2s, 2p1/2, 2p3/2的标度能级随电子密度的变化. 从图3可以发现, 等离子体屏蔽导致nl态的能级简并解除, 即原本简并的nl态能级开始分裂, 且nl态的能级分裂随着密度的增大而逐渐增大. 而nlj态的能级随密度增大而逐渐减小, 如2p1/2和2p3/2的能级分裂随密度增大而减小. 等离子体屏蔽模型不同, 束缚态能级进入连续态时的临界密度不同, 因此对应的截面低能线型也会沿着能量推移. 从图3可以看到, ASD模型的能级进入连续态比DH模型慢. 这是因为密度较高时, DH模型没有考虑等离子体中电子的简并效应, 产生的屏蔽效应偏高, 因此能级进入连续态更快[15].
-
本文在相对论偶极近似下计算了光电离过程的跃迁矩阵元和截面. 相对论近似下的光电离跃迁通道表示为: nlj → ε, l±1, j' (n和l分别是主量子数和轨道角动量量子数, ε是被电离连续电子的能量). 一般在大部分能量范围内, l + 1波的跃迁几率比l – 1波的跃迁几率大1个数量级. 在孤立的单电子Coulomb系统中, 光电离截面是ε的单调函数[24]. 而在屏蔽的单电子Coulomb系统中, 由于电子密度主要分布的径向区域中自洽场的非库仑特性(屏蔽效应[25]), 截面不再随ε单调变化, 这也是屏蔽相互作用的短程势体现.
等离子体环境中, 对于相对论近似下的光电离截面, 在临界密度附近的密度区域, 会发生如势形共振、Cooper极小、虚态共振(虚态截面增强)等现象. 图4为Fe25+离子基态1s→εp1/2和1s→εp3/2分立跃迁通道的光电离截面及总截面. 总截面由同一初态束缚态分立的跃迁通道的光电离截面叠加. 发现基态截面出现势形共振峰, 其中单峰来自一个光电离跃迁通道, 双峰来自两个通道, 这是精细能级分裂的结果, 也受电子密度的影响, 因此单双峰的出现是相对论光谱的一个重要特征. 势形共振是光电离截面的重要低能特征之一, 被定义为: 连续电子的角动量大于0时, 它会短暂地停留在有效势的离心势垒中, 造成连续电子波函数的相位出现π弧度的变化, 最终导致电离阈值附近的截面显著增大. 此外, 低能阈值附近时, 考虑屏蔽后的每个跃迁通道的截面都服从Wigner阈值定律[10,26], 即截面和能量存在正比例关系
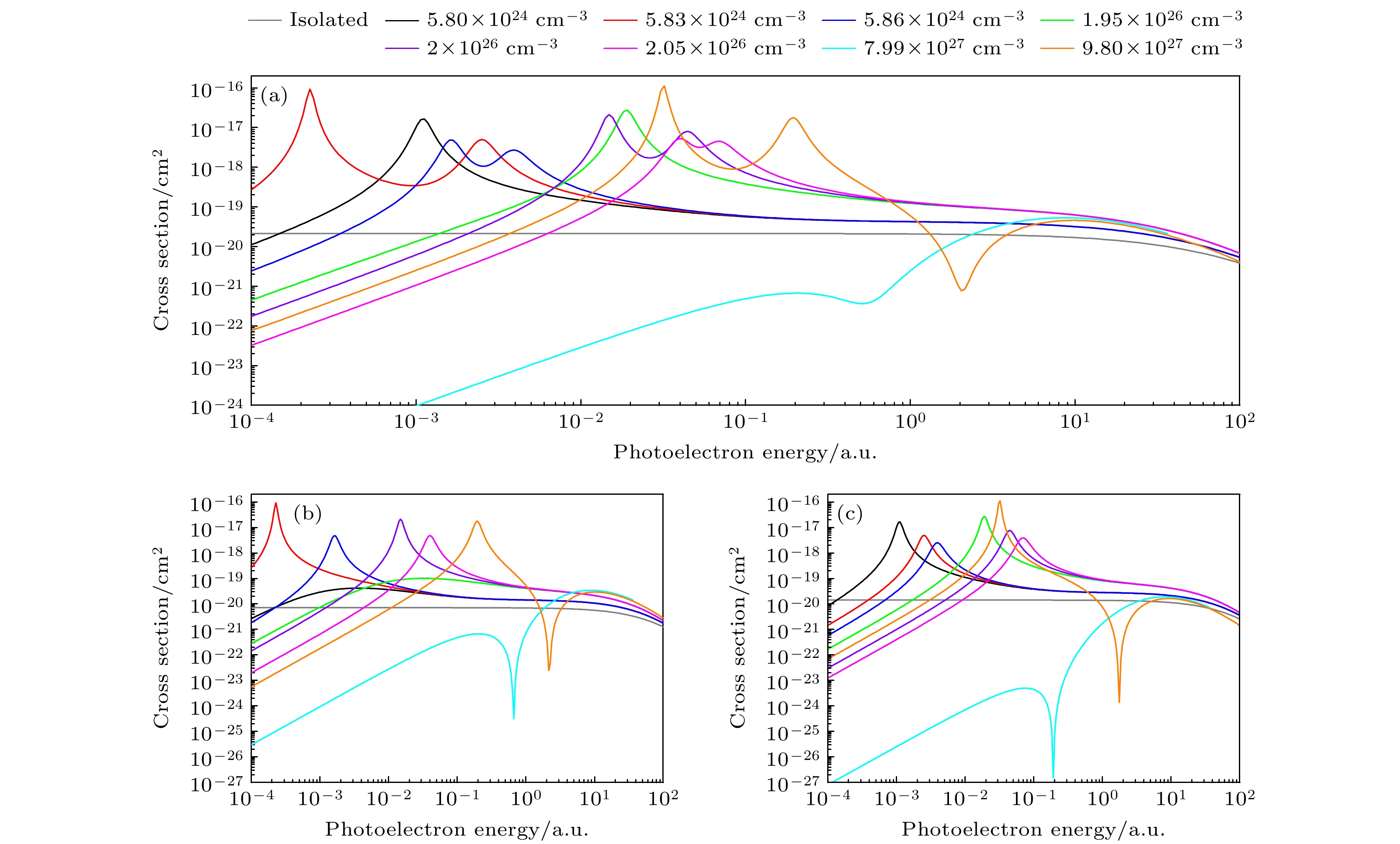
$ \sigma \propto {k^{2 l' + 1}} $ , 其中$ k = \sqrt {2\varepsilon } $ . 对于1s→εp1/2跃迁通道, l' = 1, 因此$ \sigma \propto {\left( {2\varepsilon } \right)^{3/2}} $ .图5所示为Fe25+离子2s激发态的光电离截面. 可以看到2s的光电离截面也出现了单峰和双峰的势形共振现象. 图中密度为5.83×1024 cm–3时, 2s→εp1/2和2s→εp3/2通道的截面在ε = 1×10–3 a.u.附近出现势形共振峰, 对应的εp1/2和εp3/2连续电子波函数在相同光电子能量处出现相位突变, 如图2所示. 同样, 密度为1.95×1026 cm–3时, 2s→εp3/2通道的截面在ε = 3×10–2 a.u.附近出现势形共振峰, 对应图2中连续电子波函数在该光电子能量附近出现相位突变. 此外能量较大时, 密度为7.99×1027 cm–3和9.80×1027 cm–3的截面出现了Cooper极小. Cooper极小出现在初态波函数节点数(n – l – 1)≥1的跃迁通道中, 且在临界值附近. 当密度大于临界值时, Cooper极小值经常与势形共振直接相关, 并在光电子能量高于离心势垒顶端时出现; 当密度小于临界值时, 由于ε(l + 1) 连续态的波函数在离心势垒顶端附近的相位发生改变, 只有Cooper极小值出现. 图5中2s截面中Cooper极小值出现的原因为: 初态束缚态波函数有1个节点, 影响偶极耦合矩阵元
$ \left\langle {nl\left| r \right|\varepsilon , l + 1} \right\rangle $ , 导致偶极矩阵元在阈值附近经过0, 这表现为光电离截面出现一个很深的极小值.为了分析截面出现势形共振和Cooper极小时偶极矩阵元的表现, 图6分别给出了电子密度为5.8×1024, 7.99×1027和9.8×1027 cm–3时2s1/2激发态的偶极矩阵元. 观察图5可以发现, 密度为5.8×1024 cm–3时, 2s→εp3/2通道的截面出现势形共振峰, 而2s→εp1/2通道没有. 这两个跃迁的偶极矩阵元也是如此. 密度为7.99×1027 cm–3时, 2s→εp1/2和2s→εp3/2通道的矩阵元均经过0值, 这体现为对应截面出现Cooper极小. 密度为9.8×1027 cm–3时2s→εp1/2和2s→εp3/2通道的光电离截面同时出现了势形共振峰和Cooper极小现象. 这两个通道的跃迁矩阵元在该密度下出现了极大的谷, 这是势形共振导致的谷, 掩盖了随后出现的cooper极小导致的变化.
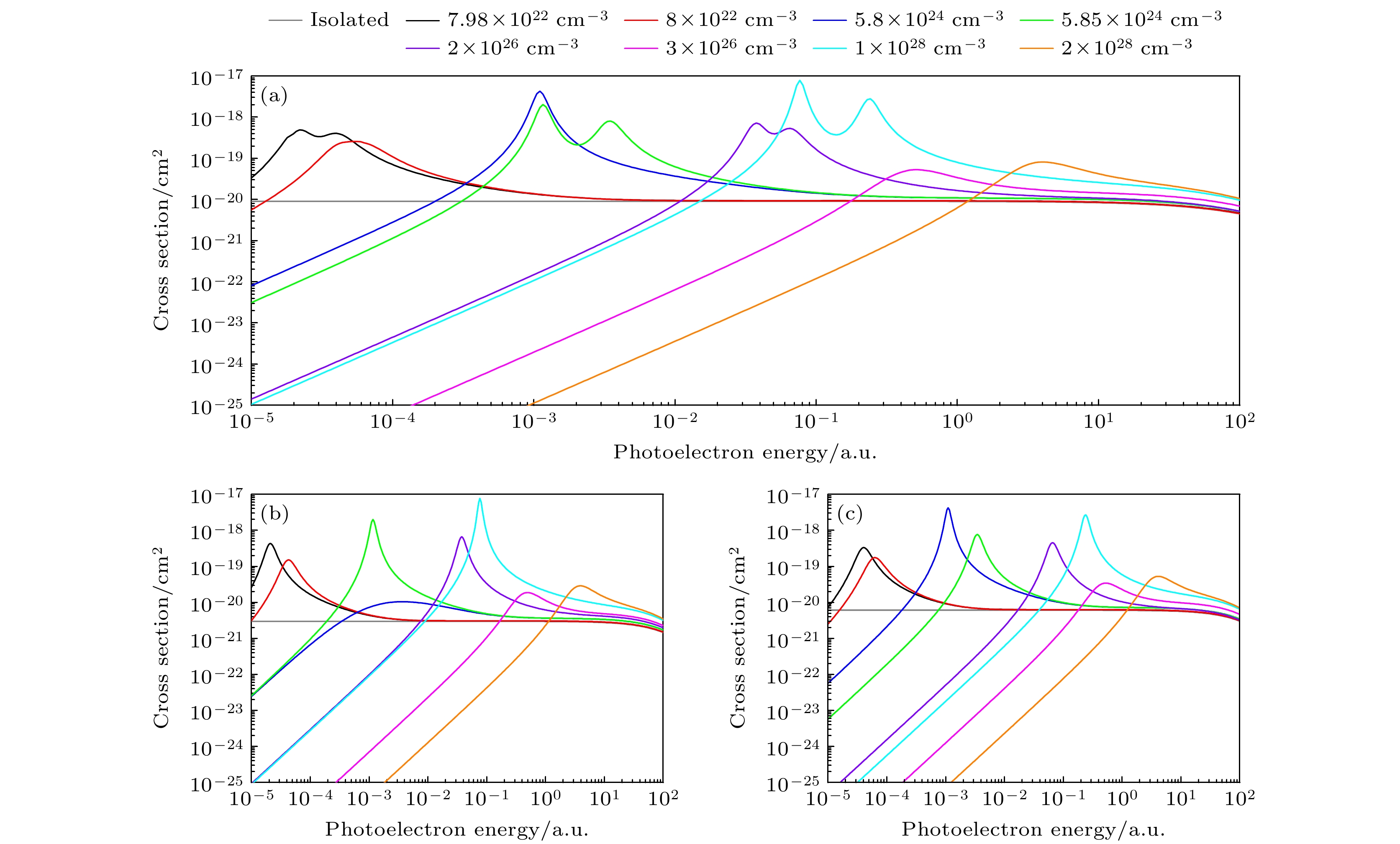
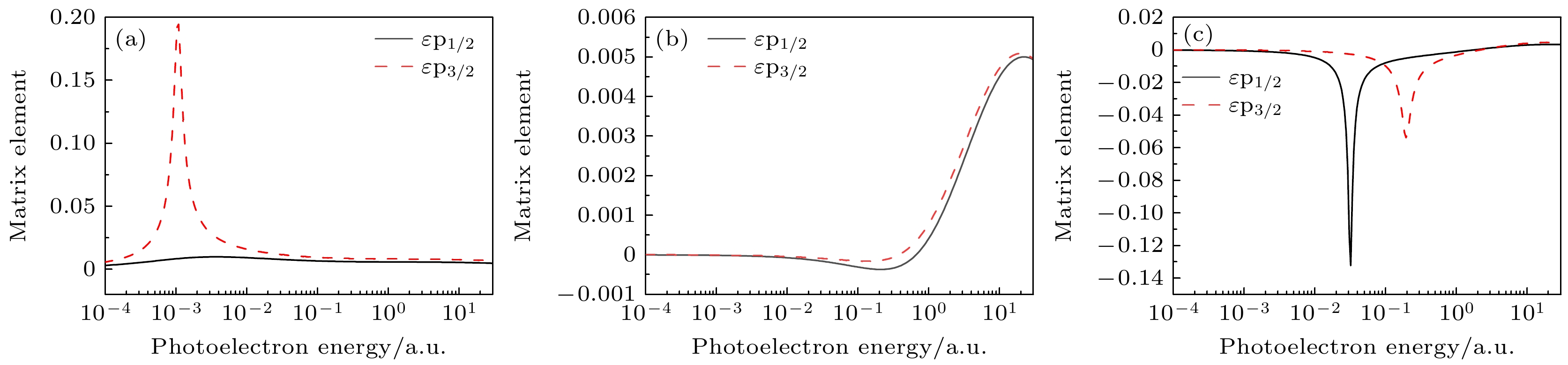
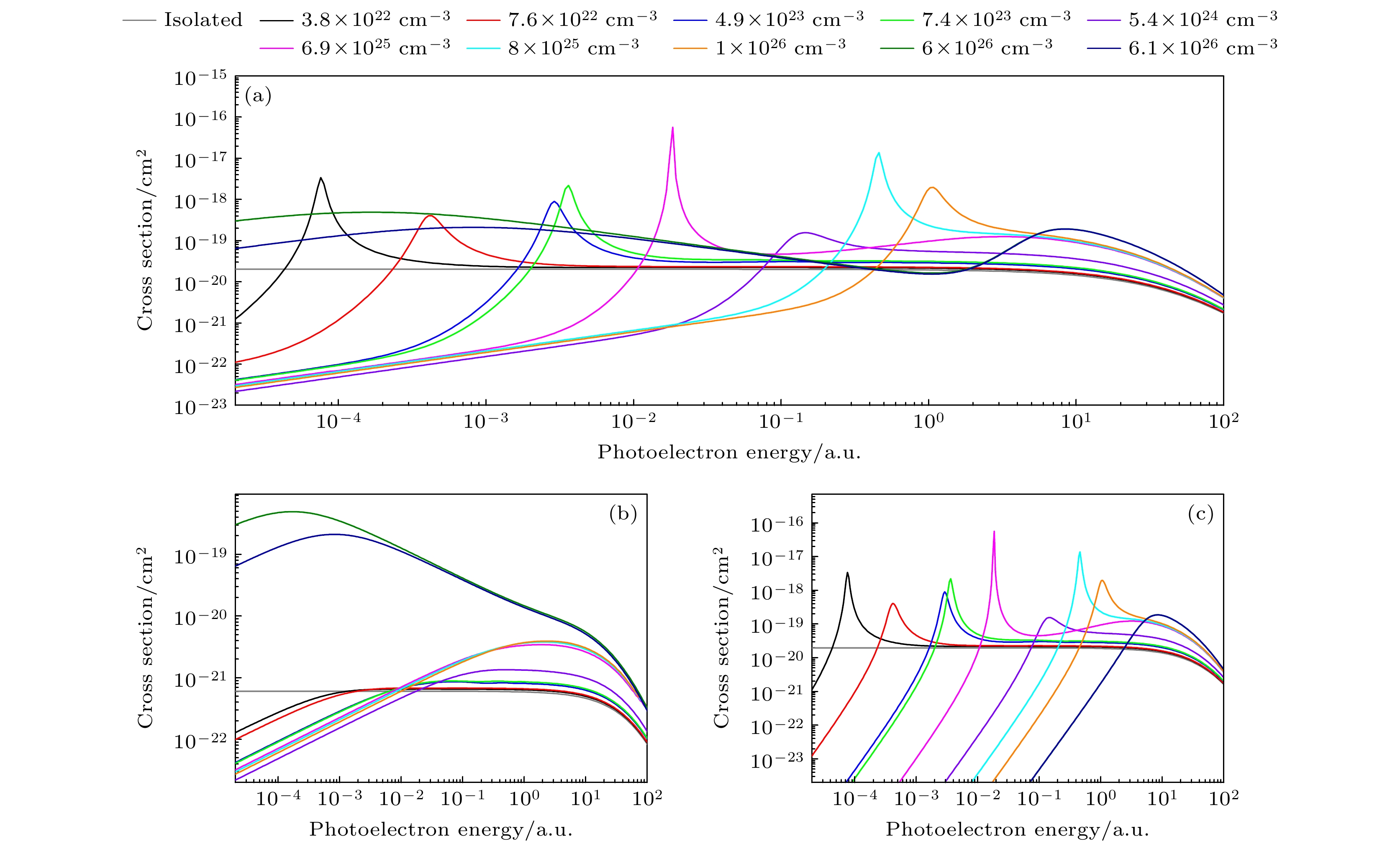
图7所示为Fe25+离子2p1/2激发态的光电离截面. 首先, 2p1/2→εs1/2跃迁通道表现出普通的截面特征. εs1/2态连续电子的角动量l = 0, 有效势单调增大, 并且没有离心势垒, 因此截面不会出现势形共振峰[27]. 密度为6.0×1026和6.1×1026 cm–3时, 2p1/2→εs1/2跃迁通道在近零能区有又高又宽的截面增强现象, 即近零能增强, 而叠加2p1/2→εd3/2跃迁通道后得到总的2p1/2光电离截面在能量更高时出现一个较宽的极小值, 即为Combet-Farnoux极小. 近零能增强是指在每个能级的临界屏蔽长度附近的近零能截面出现增强现象. 这个现象和短程势中连续态s波的波函数性质有关, 即在一定屏蔽条件下该短程势支持束缚态或虚态(能量为正值)特征的近零能态, 一般偶极跃迁末态有s态电子的截面才有可能会出现近零能增强, 继而出现Combet-Farnoux极小现象. 低能截面增强出现在任意ns1/2的临界密度附近[23]. 需要说明的是, Combet-Farnoux极小原本是孤立系统中光电离截面的特征之一, 它出现的现象是在总截面出现一个浅的(非零)最小值. Qi等[10]首次采用DH模型在等离子体中离子的光电离截面中发现这一现象. 图7中出现是由密度为6.0×1026和6.1×1026 cm–3的2p1/2→εs1/2截面的近零能增强引起的. 图中2p1/2→εs1/2通道除了密度为6.0×1026和6.1×1026 cm–3(在3s1/2的临界密度3.0×1026 cm–3附近)的截面有低能增强现象外, 其他密度条件下如6.9×1025和8×1025 cm–3的截面在能量较大时也出现增强, 显示了又高又宽的极大值, 这是虚态共振现象, 对应的近零能态3s1/2即为一个虚态[28,29].
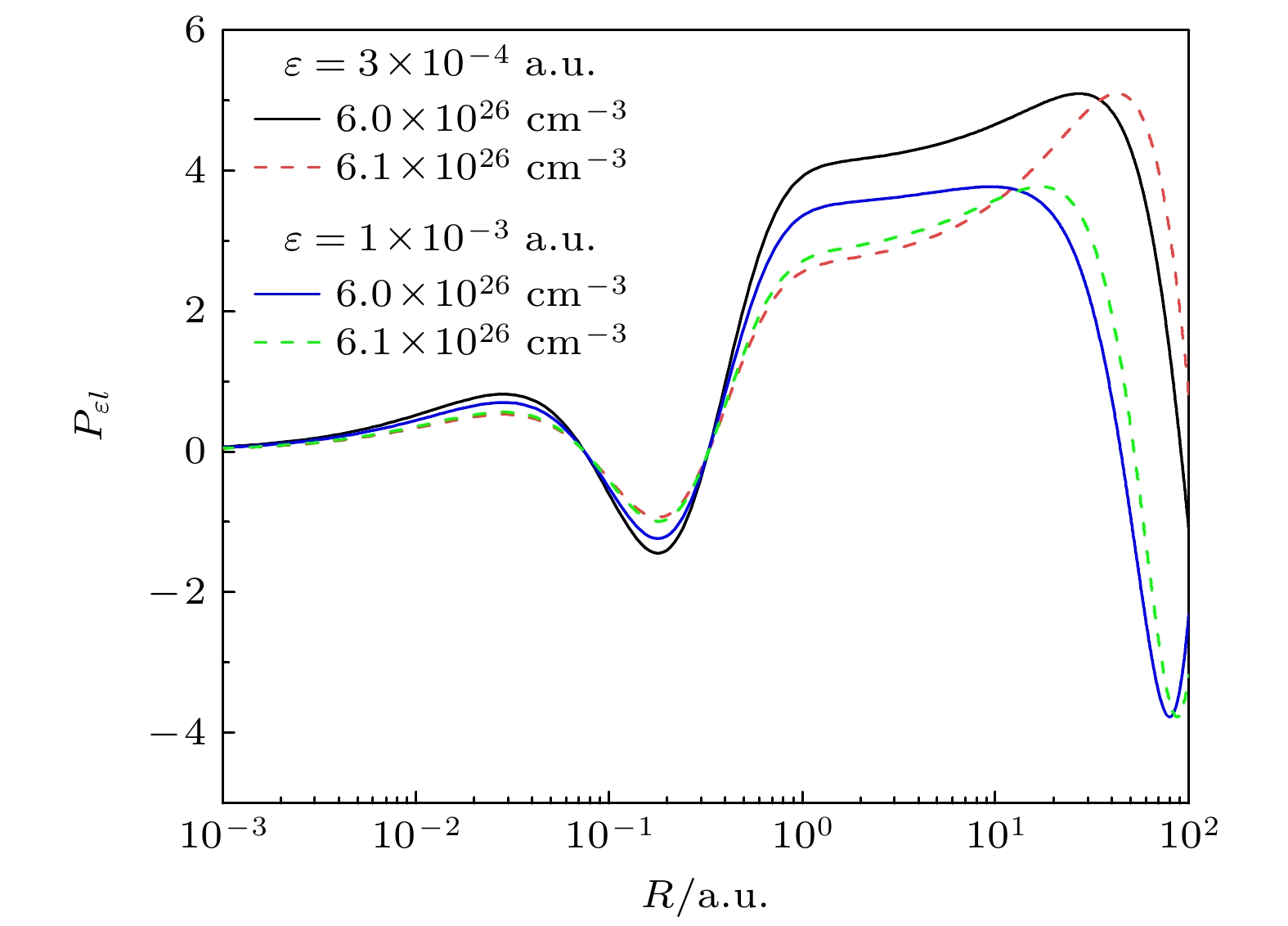
图8给出了Fe25+离子εs1/2连续电子的波函数. 通过比较ε = 3×10–4 a.u. 和ε = 1×10–3 a.u. 两种光电子能量时电子密度分别为ne = 6.0×1026 cm–3和ne = 6.91×1026 cm–3的连续电子波函数, 可以充分解释图7讨论过的2p1/2→εs1/2通道的低能截面增强现象. εs1/2 连续电子波函数的径向大分量很大, 这将导致连续电子波函数和束缚电子波函数叠加之后的矩阵元也很大, 最终在相同光电子能量处出现很大的截面.
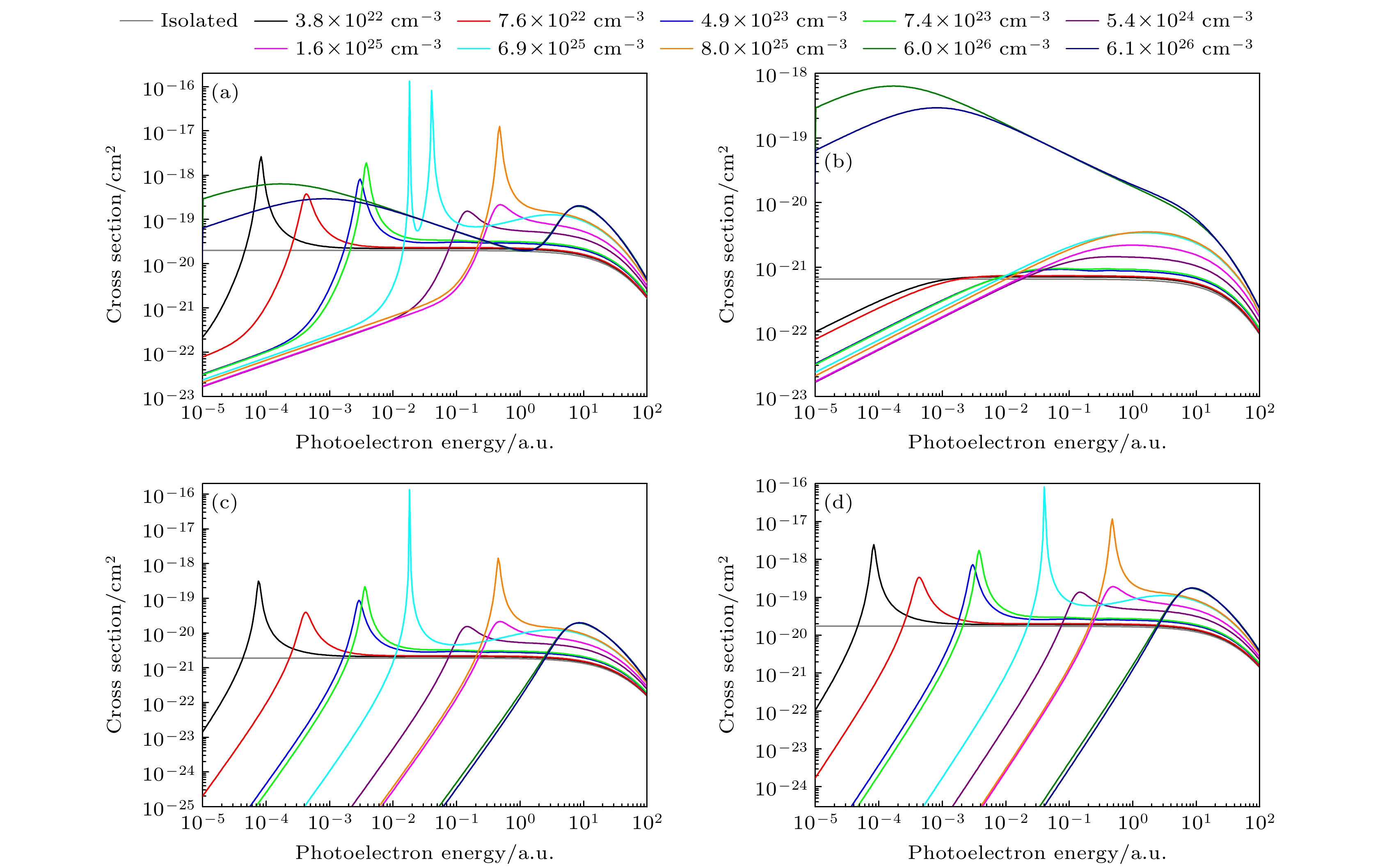
图9所示为Fe25+离子激发态2p3/2的光电离截面. 可以看到, 2p3/2的截面和2p1/2的截面有相同的低能特征, 且同一密度时总截面共振峰的能量位置也很接近. 2p3/2→εd3/2和2p3/2→εd5/2跃迁通道的低能截面特征的能量位置也很接近, 但是截面的数值有较大差异. 同一密度时2p3/2→εd3/2和2p3/2→εd5/2的截面数值的差异只与精细结构分裂有关. 密度为6.9×1025 cm–3时, 截面由2p1/2单峰共振变成2p3/2的双峰共振, 这是精细能级沿着能量增大的方向移动的结果.
-
本文采用原子态分辨屏蔽模型, 计算了热稠密等离子体中Fe25+离子的有效势、连续电子波函数、能级和光电离截面. 研究了固定电子温度时Fe25+离子基态及激发态光电离截面随等离子体密度的变化规律, 详细分析了等离子体屏蔽导致截面线型出现的经典低能特征及其形成原因. 相比较传统的德拜模型, ASD模型进一步考虑了电子简并效应和非弹性碰撞过程的影响, 能够更加准确地描述温热稠密等离子体的屏蔽效应. 研究发现由于电子简并效应的影响, ASD模型在高密度等离子体条件下屏蔽效应比DH模型更弱, 表现为ASD模型的束缚电子进入连续态比DH模型更慢. 对于光电离过程, 低能阈值附近, 屏蔽后的光电离截面服从Wigner阈值定律, 截面随光电子能量单调增加. 能量逐渐增大, 等离子体屏蔽引起的低能特征出现, 同时引起截面变化. 具体来说, 势形共振和低能增强导致对应能区的截面显著增加, 而Cooper极小和Combet-Farnoux极小导致对应能区的截面显著减小. 研究截面的低能特征对于认识和理解光电离过程的物理性质是很有意义的. Fe是天体物理中重要的元素, 本文采用原子态分辨屏蔽模型计算得到的中高能区的截面数据可以为天体物理和实验室相关的热稠密等离子体的研究提供理论和数据支持.
热稠密等离子体中Fe25+离子光电离截面的低能特征
Low-energy characteristics of photoionization cross section for Fe25+ ion embedded in hot dense plasma
-
摘要: 采用原子态分辨(atomic-state-dependent, ASD)屏蔽模型, 研究了热稠密等离子体中Fe25+离子光电离截面的低能特征. 等离子体屏蔽会减弱核和束缚电子之间的相互作用, 导致束缚电子逐渐进入连续态. 对于光电离过程, 屏蔽效应改变束缚和连续电子的波函数, 进一步改变重叠积分和跃迁矩阵元, 最终引起截面出现低能特征. 相比于传统的德拜模型, ASD模型进一步考虑了电子简并效应和非弹性碰撞过程的影响, 能够更加准确地描述温热稠密等离子体的屏蔽效应. 基于ASD模型, 研究发现, 低能阈值区, 截面服从Wigner阈值定律; 能量逐渐增大时截面出现低能增强、势形共振、Cooper极小、Combet-Farnoux极小等低能特征, 导致对应能区的截面显著增大或减小, 继而改变光电子谱的性质. 本工作研究了热稠密等离子体中离子的光电离过程, 可以为天体和实验室中热稠密等离子体的研究提供理论和数据支持.Abstract: Complex multi-body interactions between ions and surrounding charged particles exist in hot and dense plasmas, and they can screen the Coulomb potential between the nucleus and electrons and significantly change the atomic structures and dynamic properties, thereby further affecting macroscopic plasma properties such as radiation opacity and the equation of state. Using the atomic-state-dependent (ASD) screening model, we investigate the photoionization dynamics of Fe25+ ions in hot and dense plasma. The photoionization cross section for all transition channels and total cross sections of n ≤ 2 states for Fe25+ ions are studied in detail, and the low-energy characteristics induced by plasma screening are also investigated. Compared with the classical Debye Hückel model, the ASD model introduces degeneracy effects through inelastic collision processes, resulting in higher plasma density requirements for bound electrons to merge into the continuum. Near the threshold, the photoionization cross section obeys the Wigner threshold law after considering the screening effect. As the energy increases, the cross sections show low-energy characteristics such as shape resonance, Cooper minimum, low-energy enhancement, and Combet-Farnoux minimum, which can significantly increase or reduce the cross section of the corresponding energy region. For example, the low-energy enhancement in the 2p→εs1/2 channel increases the cross section by several orders of magnitude, drastically changing the properties of the photoelectron spectrum. It is significant to study the low-energy characteristics for understanding the physical properties of the photoionization cross section. Fe is an important element in astrophysics. The cross section results in the medium and high energy regions calculated by the ASD model in this work can provide theoretical and data support for investigating hot and dense plasmas in astrophysics and laboratory.
-
Key words:
- atomic-state-dependent /
- photoionization cross section /
- plasma screening .
-
-
图 1 Fe25+离子基态的势能, Te = 200 eV, isolated表示孤立Fe25+离子的势能
Figure 1. Potential energy V(r) of Fe25+ ion at four electron densities ne and the temperature Te = 200 eV, the potential energy of the free Fe25+ ion is also plotted and represented as isolated.
图 2 采用ASD模型得到的εp1/2(实线), εp3/2(虚线)的连续波函数, Te = 200 eV
Figure 2. The radial wavefunction of εp1/2 (solid lines), εp3/2 (dashed lines) of continuous electrons from the ASD model, the electron temperature Te = 200 eV.
图 3 Fe25+离子基态及n ≤ 3激发态标度能级随电子密度的变化, 实线为ASD模型的结果, 虚线为Xie等[23]采用DH模型的计算结果
Figure 3. Scaled energies of ground and n ≤ 3 excited states of Fe25+ ion as a function of electron density for a fixed plasma temperature Te = 200 eV, the solid line is the result of ASD model, and the dotted line is the calculation result from DH model adopted by Xie et al.[23].
图 4 不同等离子体密度时Fe25+离子的基态光电离截面 (a) 1s总截面; (b) 1s→εp1/2; (c) 1s→εp3/2; 温度Te = 200 eV
Figure 4. Behavior of (a) total 1s, (b) individual 1s→εp1/2, and (c) 1s→εp3/2 photoionization cross sections of the Fe25+ ion as functions of the photoelectron energy for the plasma with temperature Te = 200 eV.
图 5 不同等离子体密度时Fe25+离子2s激发态的光电离截面 (a) 2s1/2总截面; (b) 2s1/2→εp1/2; (c) 2s1/2→εp3/2; 温度Te = 200 eV
Figure 5. Behavior of (a) total 2s1/2, (b) individual 2s1/2→εp1/2, and (c) 2s1/2→εp3/2 photoionization cross sections of the Fe25+ ion as functions of the photoelectron energy for a plasma with temperature Te = 200 eV.
图 6 Fe25+离子2s1/2激发态密度为 (a) 5.8×1024 cm–3, (b) 7.99×1027 cm–3和 (c) 9.8×1027 cm–3的偶极矩阵元, 温度Te = 200 eV
Figure 6. Dipole matrix elements of 2s1/2 excited state of Fe25+ ion with densities (a) 5.8×1024 cm–3, (b) 7.99×1027 cm–3, and (c) 9.8×1027 cm–3. Te = 200 eV.
图 7 不同等离子体密度时Fe25+离子 (a) 2p1/2总截面, (b) 2p1/2→εs1/2截面以及(c) 2p1/2→εd3/2光电离截面, 温度Te = 200 eV
Figure 7. Behavior of (a) total 2p1/2, (b) individual 2p1/2→εs1/2, and (c) 2p1/2→εd3/2 photoionization cross sections of the Fe25+ ion as functions of the photoelectron energy for the plasma with temperature Te = 200 eV.
图 8 Fe25+离子εs1/2连续电子波函数的径向大分量, 温度Te = 200 eV
Figure 8. Large component of radial wavefunctions of εs1/2 continuous electron. Here the electron temperature is 200 eV.
图 9 不同等离子体密度时Fe25+离子2p3/2激发态的光电离截面 (a) 2p3/2总截面; (b) 2p3/2→εs1/2; (c) 2p3/2→εd3/2; (d) 2p3/2→εd5/2; 温度Te = 200 eV
Figure 9. Behavior of (a) total 2p3/2, (b) individual 2p3/2→εs1/2, (c) 2p3/2→εd3/2, and (d) 2p3/2→εd5/2 photoionization cross sections of the Fe25+ ion as functions of the photoelectron energy for the plasma with temperature Te = 200 eV.
-
[1] Astapenko V A, Lisitsa V S 2024 Matter Radiat. Extremes 9 057801 doi: 10.1063/5.0210407 [2] Alkhimova M, Skobelev I, Pikuz T, et al. 2024 Matter Radiat. Extremes 9 067205 doi: 10.1063/5.0212545 [3] Berrington K A, Burke P G, Butler K, Seaton M J, Storey P J, Taylor K T, Yan Y 1987 J. Phys. B: At. Mol. Phys. 20 6379 doi: 10.1088/0022-3700/20/23/027 [4] Hummer D G, Berrington K A, Eissner W, Pradhan A K, Saraph H E, Tully J A 1993 A& A 279 298 [5] Tong X M, Li J M, Pratt R H 1990 Phys. Rev. A 42 5348 doi: 10.1103/PhysRevA.42.5348 [6] Zhao L B, Ho Y K 2004 Phys. Plasmas 11 1695 doi: 10.1063/1.1650351 [7] Debye P, Hückel E 1923 Phys. Z. 24 185 [8] Salzmann D 1998 Atomic Physics in Hot Plasmas (Oxford: Oxford University Press [9] Sahoo S, Ho Y K 2006 Phys. Plasmas 13 063301 doi: 10.1063/1.2200290 [10] Qi Y Y, Wang J G, Janev R K 2009 Phys. Rev. A 80 063404 doi: 10.1103/PhysRevA.80.063404 [11] Lin C Y, Ho Y K 2010 Phys. Plasmas 17 093302 doi: 10.1063/1.3480641 [12] Wu C S, Zhou F Y, Yan J, Gao X, Wu Y, Zeng C H, Wang J G 2024 Chin. Phys. Lett. 41 085202 doi: 10.1088/0256-307X/41/8/085202 [13] Zhou F Y, Qu Y Z, Gao J W, Ma Y L, Wu Y, Wang J G 2021 Commun. Phys. 4 1 doi: 10.1038/s42005-020-00504-0 [14] Lu S M, Zhou F Y, Xie L Y, Ma Y L, Zhao G P, Gao X, Wu Y, Wang J G 2024 Phys. Rev. E 109 055205 doi: 10.1103/PhysRevE.109.055205 [15] Ichimaru S 1982 Rev. Mod. Phys. 54 1017 doi: 10.1103/RevModPhys.54.1017 [16] https://www.nature.com/articles/s42005-021-00652-x [2025-1-1] [17] Dyall K G, Grant I P, Johnson C T, Parpia F A, Plummer E P 1989 Comput. Phys. Commun. 55 425 doi: 10.1016/0010-4655(89)90136-7 [18] Jönsson P, He X, Froese Fischer C, Grant I P 2007 Comput. Phys. Commun. 177 597 doi: 10.1016/j.cpc.2007.06.002 [19] Tews M G, Perger W F 2001 Comput. Phys. Commun. 141 205 doi: 10.1016/S0010-4655(01)00208-9 [20] Perger W F, Halabuka Z, Trautmann D 1993 Comput. Phys. Commun. 76 250 doi: 10.1016/0010-4655(93)90136-Z [21] Grant I P 1974 J. Phys. B: Aom. Molec. Phys. 7 1458 doi: 10.1088/0022-3700/7/12/007 [22] Zhao G P, Xie L Y, Liu L, Wang J G, Janev R K 2018 Phys. Plasmas 25 083302 doi: 10.1063/1.5042295 [23] Xie L Y, Wang J G, Janev R K 2014 Phys. Plasmas 21 063304 doi: 10.1063/1.4882244 [24] Bethe H A, Salpeter E E 1957 Quantum Mechanics of One- and Two-Electron Atoms (New York: Academic Press [25] Fano U, Cooper J W 1968 Rev. Mod. Phys. 40 441 doi: 10.1103/RevModPhys.40.441 [26] Wigner E P 1948 Phys. Rev. 73 1002 doi: 10.1103/PhysRev.73.1002 [27] Bylicki M, Stachów A, Karwowski J, Mukherjee P K 2007 Chem. Phys. 331 346 doi: 10.1016/j.chemphys.2006.11.003 [28] Joachain 1975 Quantum Collision Theory (New York: American Elsevier [29] Taylor J R 1972 Scattering Theory (New York: John Wiley -
计量
- 文章访问数: 141
- HTML全文浏览数: 141
- PDF下载数: 6
- 施引文献: 0