在目标与背景红外辐射强度对比度低的情况下, 将偏振特性差异结合到强度探测中可显著提高系统的探测与识别能力^[1–5]. 飞行器目标经过高温尾焰传输后的红外偏振辐射是红外探测设备对导弹、无人机等飞行器进行探测、识别、跟踪、告警的重要特征依据. 考虑到真实发动机试验昂贵、操作复杂等因素, 数值仿真方法具有成本低、操作简单、结果具有可参考性等诸多优点^[6], 是研究红外偏振光在高温尾焰中传输特性的主要手段之一.

近年来, 以数值仿真的方式对不同介质中偏振光传输特性的研究有很多, 主要研究介质包括: 大气、气溶胶、烟雾、水体. 1) 大气介质. 王子谦等^[7]提出了一种混浊大气偏振模式的建模方法, 以三维天球大气模型为基础, 用Monte Carlo法模拟太阳光在大气中的传输过程. 王威等^[8]利用简化的双层大气模式模拟实际大气, 建立了基于RT3的大气偏振模型. 提汝芳等^[9]针对近地面水平方向偏振观测, 基于单次散射假设, 仿真计算了不同气溶胶光学厚度条件下的大气偏振辐射传输特性. 2) 气溶胶. Pust和Shaw^[10]研究了无云天气的可见光和近红外偏振度. 胡帅等^[11]系统给出了矢量辐射传输Monte Carlo模型, 分析了气溶胶形状、入射光偏振状态对光波退偏振度、透过率及反射率的影响. 3) 烟雾. van der Laan等^[12]分析了圆偏振光较线偏振光在雾环境中的传输优势. 王开鹏^[13]基于Monte Carlo法, 针对不同类型的微粒体系, 仿真了宽波段下不同偏振光(圆偏振和线偏振) 在雾天环境下的动力学演化过程. 张肃等^[14]针对烟雾环境中烟雾浓度对偏振光传输特性的影响, 用Monte Carlo法建立仿真模型并对偏振传输理论进行分析. 4) 水体. 曾祥伟等^[15]基于偏振子午面Monte Carlo法, 提出一种散射环境中前向传输光子偏振态的统计方法. 吴琼等^[16]用Monte Carlo法对水下蓝绿高斯光束传输过程进行仿真, 分析海水类型、传输距离和发散角等因素对接收功率及脉冲响应的影响. 目前关于不同类型偏振光(圆偏振光、线偏振光)在不同介质(大气、气溶胶、烟雾和水体)中的偏振辐射传输特性研究已较为完善. 然而大部分关于气体偏振辐射传输特性的研究均聚焦于可见光波段, 且研究对象大多为大气环境. 少量研究虽探讨了红外波段气体辐射特性的改变, 但缺少针对偏振特性的研究, 更缺乏对高温尾焰这种特殊气体环境中红外偏振辐射传输特性的研究.

针对上述分析, 本文通过Monte Carlo法对红外偏振光在高温尾焰中的传输过程进行了建模, 并利用HITRAN数据库计算了H₂O在2.5—3.3 μm波段和CO₂在4—5 μm波段的吸收系数, 模拟光子在尾焰空间的多次散射过程, 从微观层面分析发生碰撞事件时每个光子运动余弦和振动余弦的变化, 结合偏振度、透过率计算原理来统计光子特性, 根据仿真结果对比了不同传输距离下辐亮度透过率和偏振度的改变, 并分析了尾焰温度、压强、尾焰气体组分浓度和探测波长对红外偏振光传输特性的影响.

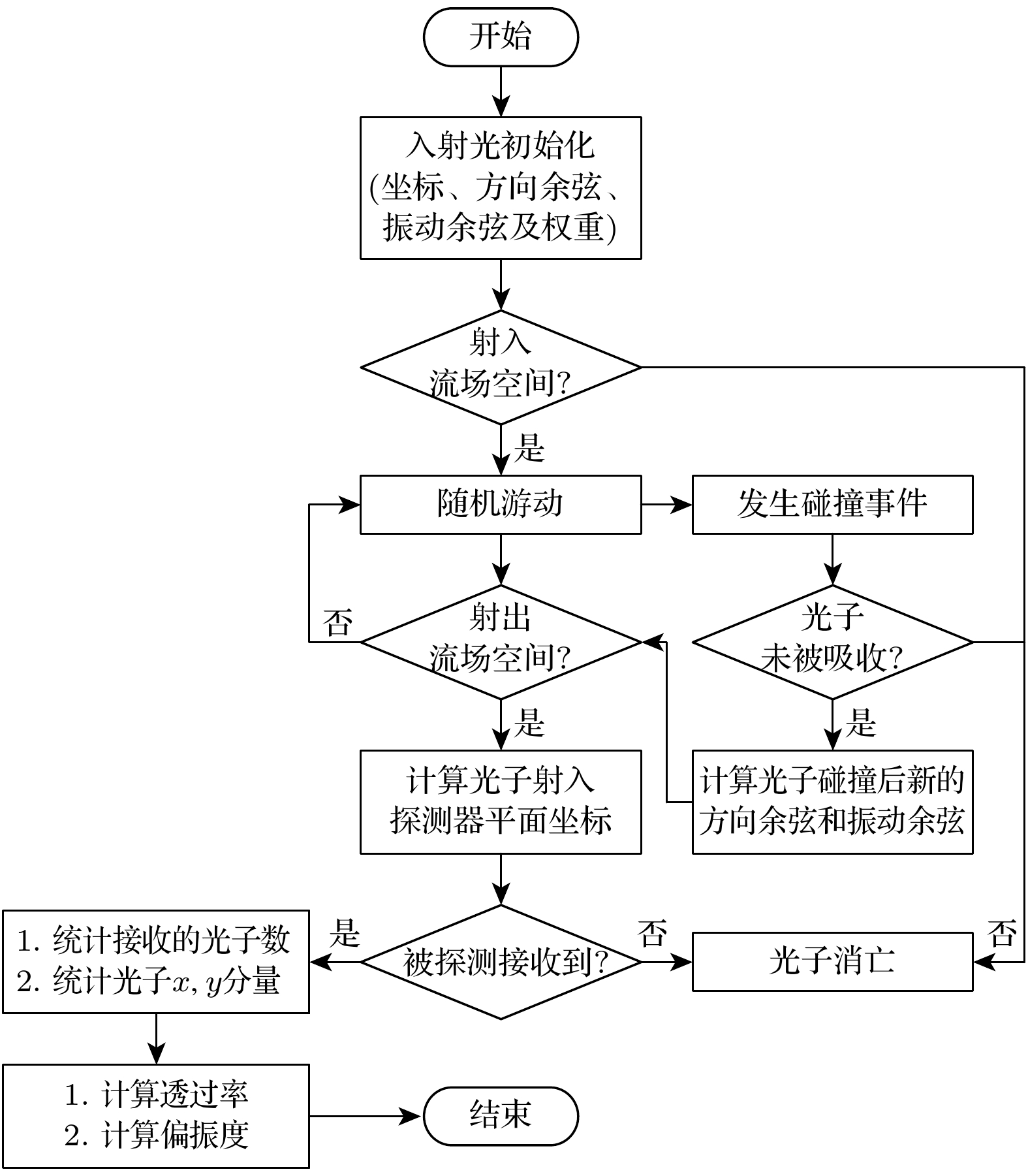
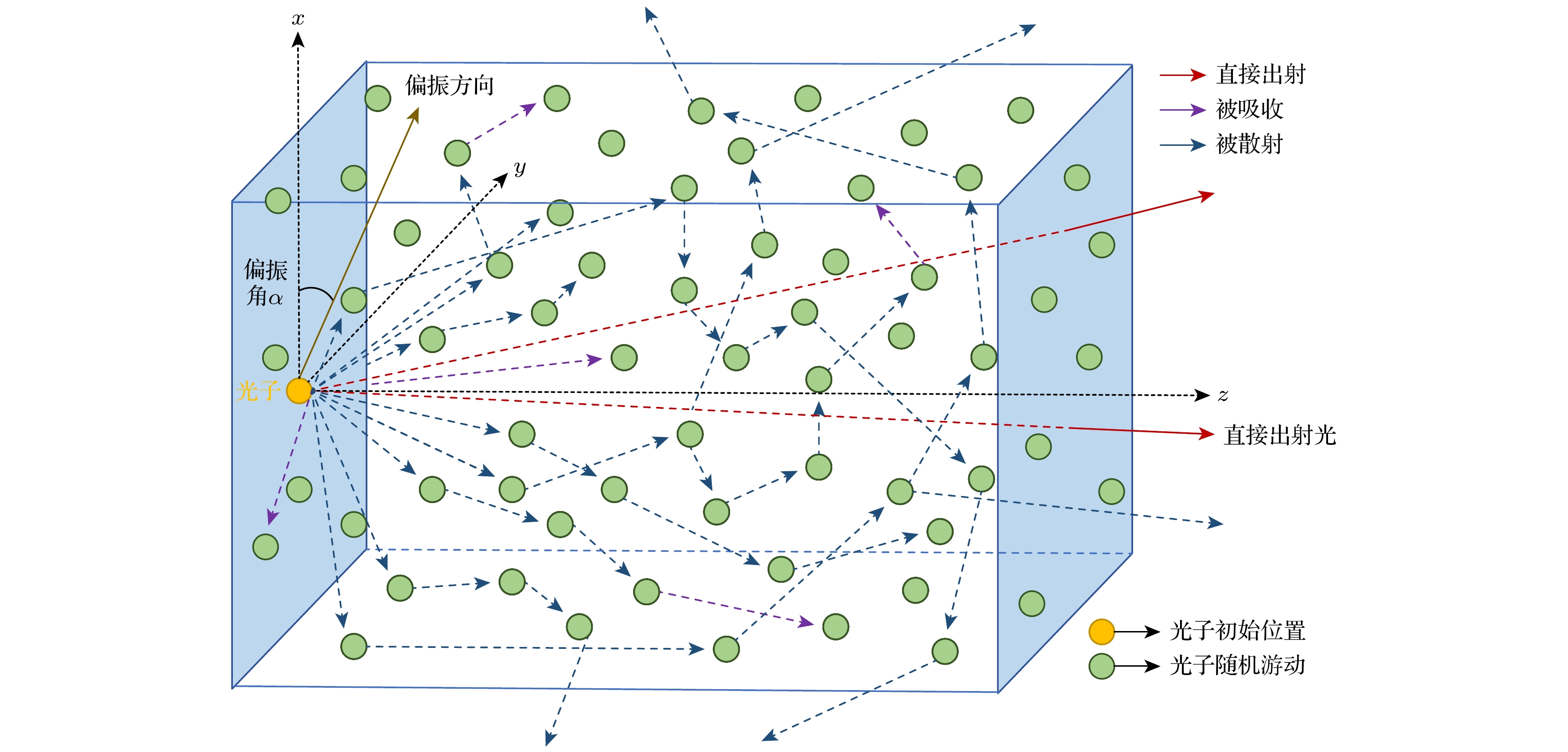
图1为Monte Carlo模拟中光子在尾焰空间的随机运动过程示意图. Monte Carlo法求解红外偏振辐射传输的基本思想是模拟光子在尾焰空间中的运动, 其运动过程可分解为若干个光子与气体分子的多次碰撞, 碰撞的结果包括发射、吸收和散射等一系列独立且随机的子过程, 需建立每个子过程的概率模型进行求解. 图2为Monte Carlo法的基本流程图. 点光源发射一定数量的光子, 假设每个光子携带的初始能量权重为1. 首先初始化每个光子的位置坐标、能量、方向余弦和振动余弦信息. 根据光子的初始位置和方向余弦判断光子能否射入尾焰空间. 若能, 模拟光子在尾焰中的随机游动过程, 即光子在尾焰空间中与气体分子的多次碰撞过程. 接着, 根据每次碰撞事件发生前的位置坐标、方向余弦和振动余弦计算下一次发生碰撞事件的位置坐标和碰撞后新的方向余弦和振动余弦. 最后统计探测面接收到的光子数及光子最大振动方向分量和最小振动方向分量, 用以计算透过率和偏振度. 光子携带能量的随机运动过程由高温尾焰的物理参数决定, 如温度、压强、气体组分浓度等.

光子在尾焰空间中与气体分子的多次碰撞过程主要模拟光子的散射与吸收过程, 下文具体阐述了相关模拟过程.

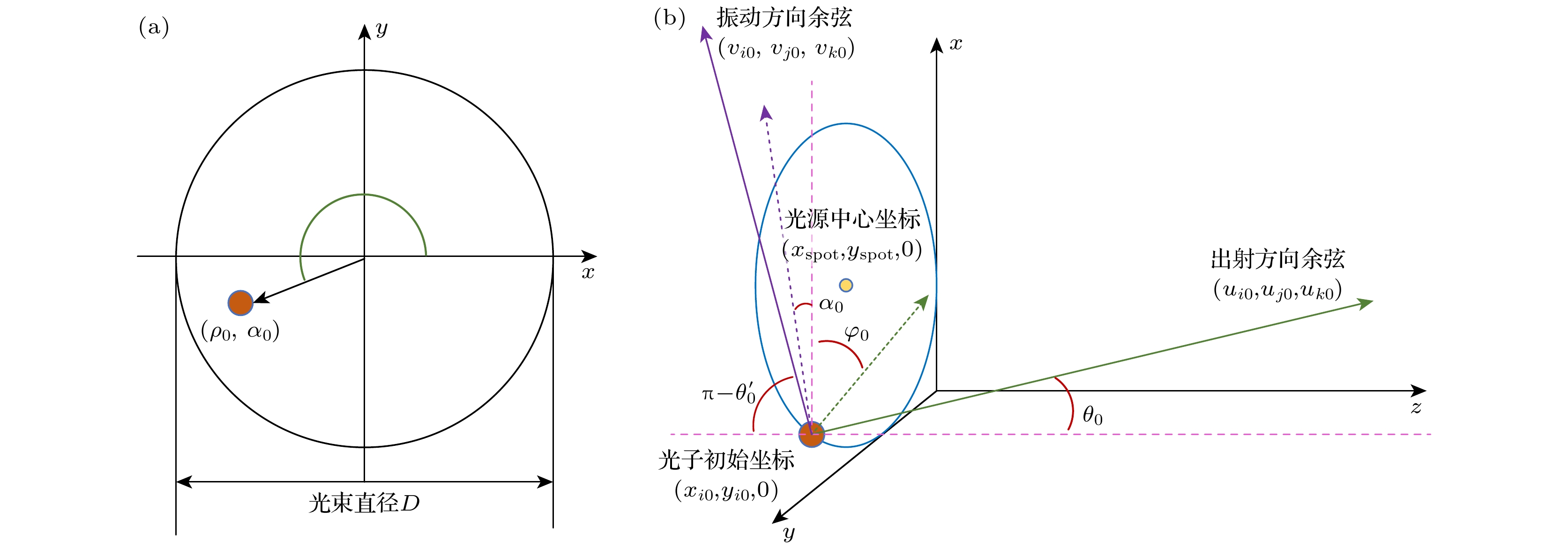
如图3所示, 红外偏振光点光源$ ({x_{{\mathrm{spot}}}}, {y_{{\mathrm{spot}}}}, 0) $发出的光子的起始位置$ ({x_{i0}}, {y_{j0}}, 0) $服从正态分布.光束初始平面为z = 0, 沿着z轴正方向传播, 光束发散角为$ {\theta _{\max }} $, 光束偏振角为$ {\alpha _0} $, 光束直径为D, 光子初始权重为1, $ ({\theta _0}, {\varphi _0}) $为光子初始运动方向的天顶角及方位角, $ (\theta _0', {\alpha _0}) $为光子初始振动方向的天顶角及方位角. 则光子初始发射时的坐标$ ({x_{i0}}, {y_{j0}}, {z_{k0}}) $、出射方向余弦$ ({u_{i0}}, {u_{j0}}, {u_{k0}}) $和振动方向余弦$ ({v_{i0}}, {v_{j0}}, {v_{k0}}) $可表示为

其中, $ ({\rho _0}, {\alpha _0}) $为光子在z = 0平面的极坐标, $ ({\theta _0}, {\varphi _0}) $为光子初始运动方向的天顶角及方位角, $ (\theta _0^\prime, {\alpha _0}) $为光子初始振动方向的天顶角及方位角.

光子的概率分布以高斯函数$ \exp [ { - {r^2}/{{\left( {D/2} \right)}^2}} ] $形式从中心向外平滑地减小, 所以光子的起始发射位置和起始发射方向满足:

其中, $ {\theta _{\max }} $为光束发散角; D为光束直径; $ {r_{{\alpha _0}}},\; {r_{{\varphi _0}}}, {r_{{\theta _0}}} $为互相独立的[0, 1]范围内随机数; $ {r_{{\rho _0}}} $为$ [{{\mathrm{e}}^{ - 1}}, 1] $范围内的随机数.

由于出射方向余弦$ ({u_{i0}}, {u_{j0}}, {u_{k0}}) $和振动方向余弦$ ({v_{i0}}, {v_{j0}}, {v_{k0}}) $始终垂直, 振动方向方位角$ {\alpha _0} $为偏振角, 计算振动方向的天顶角$ \theta _0^\prime $时满足:

在这个模块中, 光子与气体分子的单次碰撞过程分为三种情况: 光子与气体分子未发生碰撞直接射出尾焰空间; 光子与气体分子碰撞后被吸收; 光子与气体分子碰撞后改变运动状态继续在尾焰空间中运动.

光子在尾焰内部传播时, 遇到H₂O, CO₂, NO等气体存在被吸收的概率, 不同温度压强状态下不同气体组分的红外吸收系数的值可由HITRAN数据库计算得到^[17,18]. 光子在气体分子空间中发生碰撞后被吸收的概率为

其中, $ {\mu _{{\mathrm{absorb}}}} $是尾焰总气体的红外吸收系数, 由HITRAN库计算得到, d是光子发生碰撞前运动的距离.

高温尾焰空间属于多粒子分散系统, 其中散射介质总的吸收系数计算表达式为

其中, $ {x_1}, {x_2}, \cdots{x_n} $表示第几种粒子在整个散射系统里的相对体积分数, $ {x_1} + {x_2} + \cdots + {x_n} = 1 $; $ u_{e1}, u_{e2},\cdots u_{en} $分别为第几种粒子的吸收系数.

Monte Carlo是通过概率统计方法直接模拟光在气体空间中的传输过程. 这种方法将光的散射过程视为光子随机游动并与气体分子发生碰撞的结果. 每次光子碰撞后行进的距离称为自由程, 其大小与气体的吸收系数密切相关. 已知光子的起始位置和起始运动方向后, 需要给定光子本次移动的步长, 才能确定光子的下一个落脚点. 光子连续散射两次的过程间, 能量的变化遵循比尔定律$ I = {I_0}{{\mathrm{e}}^{ - {\mu _{\mathrm{t}}}z}} $, 设两次连续散射运动距离(光子自由程)为$ \Delta z $:

其中, $ \Delta z $范围在$ \left[ {0, \infty } \right) $, ζ是随机生成的$ \left( {0, 1} \right] $之间的数, $ {\mu _{\mathrm{t}}} $是尾焰气体介质的吸收系数.

当光子传输的自由程l确定后, 由当前光子所处位置(x, y, z)和运动方向单位向量$ ({u_x}, {u_y}, {u_z}) $推定光子抵达的下一个散射点坐标$ (x', y', z') $:

若计算出的下一次散射点位置在尾焰气体空间内, 则发生下一次碰撞. 反之, 下一次碰撞事件并不会发生, 光子直接射出尾焰空间.

当光子与尾焰空间内气体分子发生碰撞时, 生成一个[0, 1]范围内的随机数$ {\tau _0} $, 若满足$ {\tau _0} \leqslant {\tau _{{\mathrm{absorb}}}} $, 则光子被吸收; 反之, 光子与气体分子碰撞后被散射出去. 若光子此次碰撞事件后被散射, 则生成[0, 1]范围内的随机数ζ, 并根据尾焰气体介质的吸收系数$ {\mu _{\mathrm{t}}} $计算出下一次碰撞事件发生的随机步长l. 散射后根据随机步长l计算出下一次发生碰撞事件的点位$ (x', y', z') $, 若该点位超出尾焰空间, 则下一次碰撞事件不存在, 判断为光子直接射出尾焰空间. 尾焰空间模拟为一个长方体, 空间内各点坐标满足:

其中, $ ({x_{{\mathrm{fluent}}}}, {y_{{\mathrm{fluent}}}}, {z_{{\mathrm{fluent}}}}) $是尾焰空间的中心点坐标; $ {l_{{\mathrm{length}}}} $, $ {l_{{\mathrm{width}}}} $, $ {l_{{\mathrm{height}}}} $分别为尾焰空间的长度、宽度和高度.

光子的生存周期的终止只有两种情况, 一种是光子被气体分子吸收, 另一种是光子逃逸出尾焰介质的边界. 否则, 光子持续在尾焰空间中与气体分子发生碰撞, 碰撞后的运动方向由瑞利散射角度得出.

在运用Monte Carlo方法处理辐射传输问题时, 对空间散射方向的采样计算尤为关键. 目前, 主流的实现方式有两种: 其一是两步抽样法^[19,20], 即通过两次随机抽样来确定运动方向; 其二是一步抽样法^[21], 一次随机抽样即可确定所有角度. 本文基于后一种方法, 提出了一种用于随机采样散射角及运动方位角的计算策略.

红外光子与气体分子的碰撞过程实际上是光子的单次散射过程. 散射通常分为瑞利散射、米氏散射和几何光学散射三种, 一般采用无量纲尺度参数$ k = 2\pi r/\lambda $作为散射种类的判别标准. 气体分子的半径r比红外光的波长λ小得多, 此时$ k < 0.1 $, 需用瑞利散射来模拟计算光子碰撞后的散射角度.

描述瑞利散射的原始方程$ S\left( {\lambda, \theta, h} \right) $可以分为两个变量. 一个是散射系数$ \beta \left( {\lambda, h} \right) $, 表示散射强度; 一个是相位函数$ \gamma \left( \theta \right) $(与散射的几何结构有关)控制散射方向:

相位函数$ \gamma \left( \theta \right) $可以用$ S\left( {\lambda, \theta, h} \right) $除以$ \beta \left( {\lambda, h} \right) $得到:

其中, $ \gamma \left( \theta \right) $是偶极子的形状, $ {3}/{{(16\pi) }} $用作归一化因子, θ是散射角度. 因此, 光子与气体分子单次碰撞后的散射角度θ的概率公式$ P(\theta ) $与$ \left( {1 + {{\cos }^2}\theta } \right) $因子密切相关:

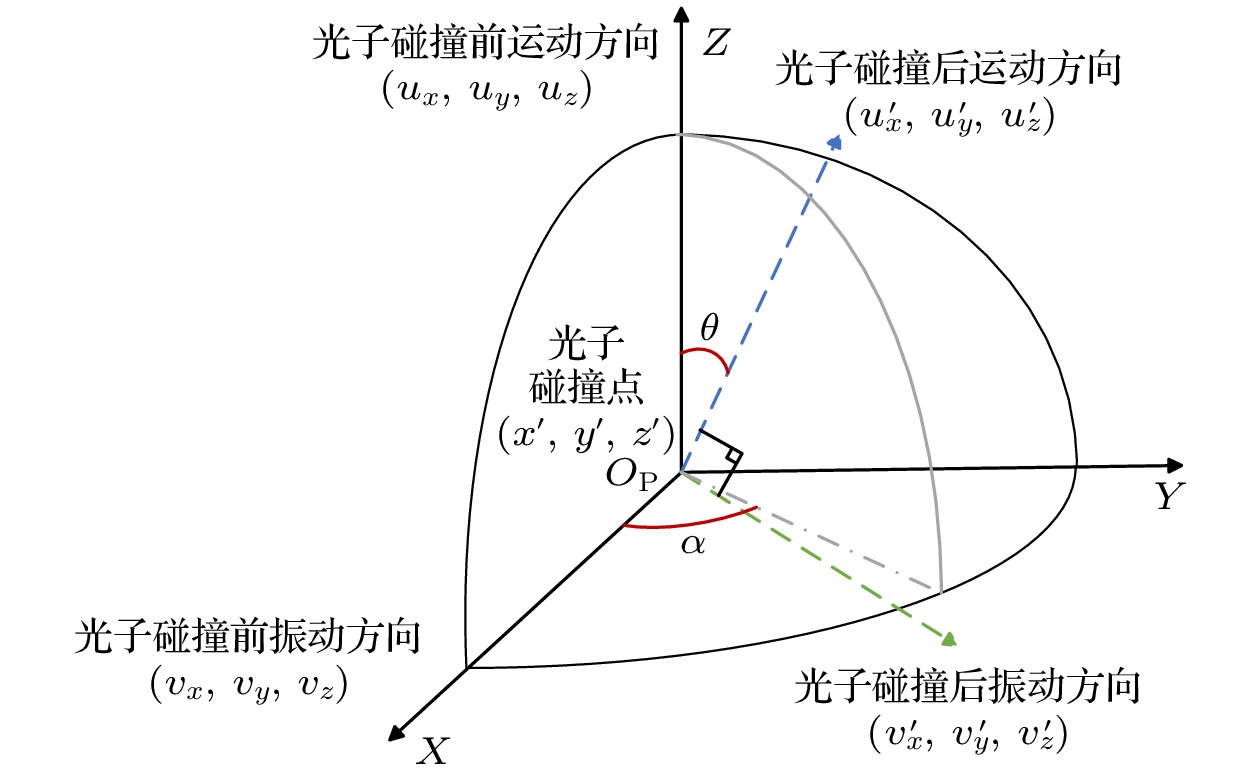
给[0, 180°]间的180个整数角度一个$ P(\theta ) $的概率值. 每个θ代表的概率区间为[0, $ P\left( 0 \right) $], [$ P\left( 0 \right) $, $ P\left( 0 \right) + P\left( 1 \right) $], [$ P\left( 0 \right) + P\left( 1 \right) $, $ P\left( 0 \right) + P\left( 1 \right) + P\left( 2 \right) $]···, 以此类推. 给定一个0—1的随机数, 散射角度θ为随机数落在区间对应的角度. 再随机生成一个0—360的整数随机数, 作为运动方位角α的值.

图4为散射过程角度变化示意图. 以光子碰撞点$ (x', y', z') $为坐标原点, 碰撞事件发生前光子运动方向$ ({u_x}, {u_y}, {u_z}) $为z轴, 光子振动方向$ ({v_x}, {v_y}, {v_z}) $为x轴建立右手坐标系作为光子坐标系$ {O_{\mathrm{P}}} \text- XYZ $. 在光子坐标系中, 天顶角θ和方位角α构成碰撞后的运动方向$ (\cos \alpha \sin \theta, \sin \alpha \sin \theta, \cos \theta ) $, 天顶角$ (\theta + 90) $°和方位角α构成碰撞后光子的振动方向$ (\cos \alpha \cos \theta, \sin \alpha \cos \theta, - \sin \theta ) $.

根据原始坐标系$ {O_{\mathrm{L}}} \text- XYZ $和每次碰撞发生时的光子坐标系$ {O_{\mathrm{P}}} \text- XYZ $计算坐标系间的旋转平移矩阵$ {{\boldsymbol{R}}_{\mathrm{T}}} = \left[ {\begin{array}{*{20}{c}} {{r_{11}}}&{{r_{12}}}&{{r_{13}}}&{{t_1}}\\ {{r_{21}}}&{{r_{22}}}&{{r_{23}}}&{{t_2}}\\ {{r_{31}}}&{{r_{32}}}&{{r_{33}}}&{{t_3}}\\ 0&0&0&1 \end{array}} \right] $, 然后根据$ {{\boldsymbol{R}}_{\mathrm{T}}} $、 光子坐标系$ {O_{\mathrm{P}}}\text{-}XYZ $下光子碰撞后的运动方向 向量$ (\cos \alpha \sin \theta, \sin \alpha \sin \theta, \cos \theta ) $和振动方向向量$ (\cos \alpha \cos \theta, \sin \alpha \cos \theta, - \sin \theta ) $计算出原始坐标系下光子碰撞后的运动方向向量$ (u_x', u_y', u_z') $和振动方向向量$ (v_x', v_y', v_z') $为

设探测器平面单位法向量为$ ({l_x}, {l_y}, {l_z}) $, 中心点坐标$ ({x_{\mathrm{d}}}, {y_{\mathrm{d}}}, {z_{\mathrm{d}}}) $, 尺寸为a cm$ \times $a cm, 计算每个从尾焰空间中出射的光子的运动轨迹与探测器平面的交点$ ({x_{\mathrm{p}}}, {y_{\mathrm{p}}}, {z_{\mathrm{p}}}) $, 判断光子是否能被探测器接收到的标准为

若光子当前发生碰撞事件后, 判定发生下一次碰撞事件的位置超过尾焰空间, 则表明光子直接射出尾焰空间. 接着, 判断从尾焰空间中出射的光子是否能被探测器接收到. 若能, 统计每个射出空间且能被探测器接收到的光子的能量和振动方向向量.

计算程序中, 每个光子的初始权重为1, 光子能量只存在被完全吸收的情况, 并不存在传输路径中的衰减, 因此用统计到的总的接收光子数表示探测器接收到的光强的大小. 光子经过尾焰空间的辐亮度透过率ρ用接收光子数/总出射光子数表示.

偏振度是描述光或电磁波的偏振状态的量化指标. 偏振度依据电矢量在不同方向上的强度来定义:

其中, P表示偏振度, $ {I_{\max }} $为某一部分偏振光沿某一方向上所具有的能量最大值, $ {I_{\min }} $为在其垂直方向上具有的能量最小值.

出射光的偏振度由接收的所有光子叠加计算得到, 光子的数量、 每个光子的能量(或波长、频率)和振动方向对计算结果有贡献. 假设每个光子一开始都有一个数值为1的能量权重, 最后接收到的光子在原始坐标系XOY平面上计算振动方向的x, y分量, x分量的方向设置为与初始振动方位角方向一致. 偏振度DOP计算公式为

本文红外Monte Carlo偏振辐射传输模型程序包运行的硬件配置为: CPU: 12th Gen Intel(R) Core(TM) i7-12700处理器, 2.10 GHz; 内存: 16 GB; 硬盘: 1 TB; 网卡: 千兆网卡. 操作系统: Windows10 64位; 开发工具: Microsoft Visual Studio 2022. 气体红外吸收系数计算程序包的开发工具为python 3.10, 配置了HITRAN库开源的hapi.py文件.

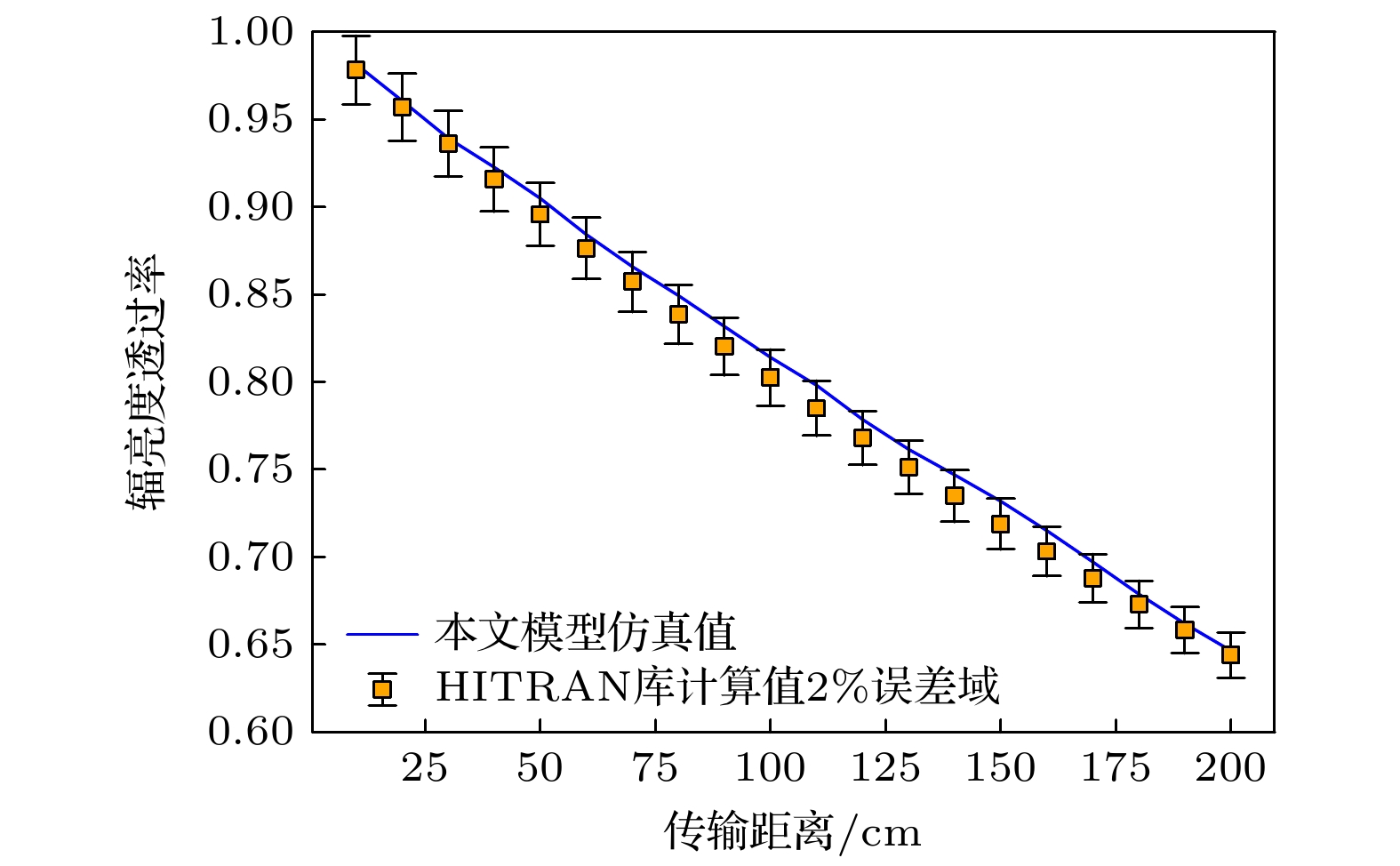
为了验证Monte Carlo模型的准确性, 设定一组实验参数进行仿真, 并对比HITRAN库关于透过率的计算结果. 假设红外线偏振光入射, 入射光波长为1.96 μm. 尾焰空间由20% CO₂和80%空气组成的, 温度为1500 K, 压强为20 atm (1 atm =1.01×10⁵ Pa). 分别模拟并统计传输距离为10, 20, 30, ···, 200 cm的散射粒子出射光透过率和偏振度变化, 模拟光子数设为$ 10^{8} $个, 本模型与HITRAN库关于辐亮度透过率的计算结果对比如图5所示. 结合图5误差数据, 本文研究方法和HITRAN库的计算结果基本一致, 误差保持在2%以内, 验证了本文模型在模拟光粒子散射过程中对偏振辐射特性分量统计的准确性.

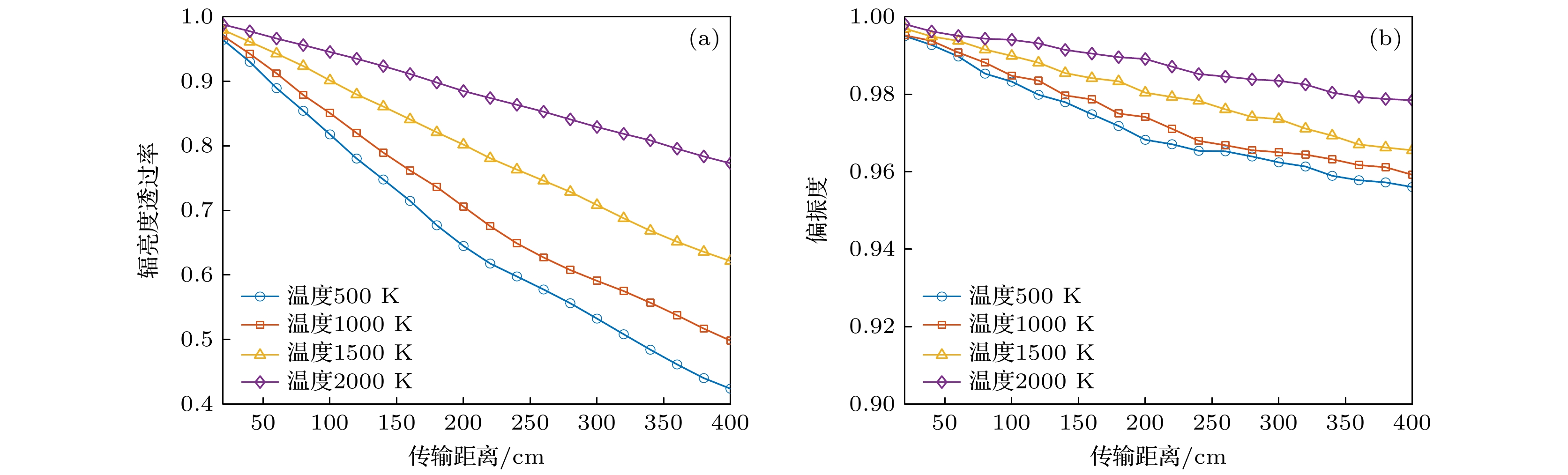
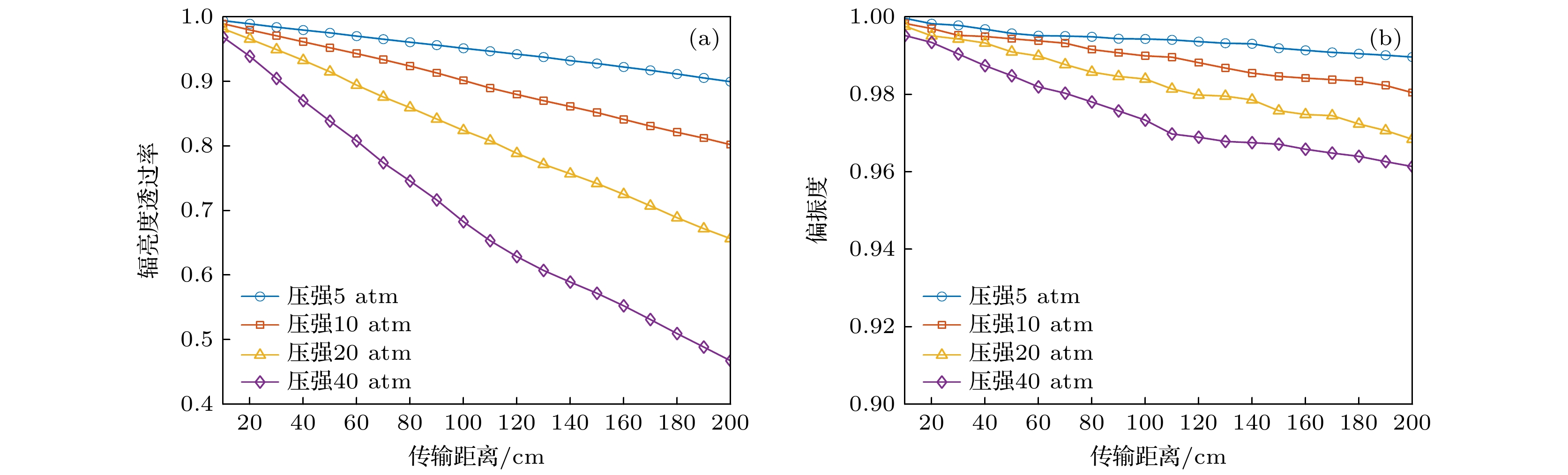
本节模拟了20% CO₂和80%空气组成的立方体尾焰空间温度分别为500, 1000, 1500, 2000 K (压强为10 atm)和压强分别为5, 10, 20, 40 atm (温度为1500 K)时对光波传输特性的影响, 尾焰空间横截面尺寸为1 m × 1 m, 尾焰空间起点平面为XOY平面. 模拟过程中取光波为线偏振光, 光束直径为10 mm, 发散角为0°, 偏振角为90°, 光束中心点坐标为(0.5, 0.5, 0) cm, 探测波长为1.96 μm, 传输距离为$ 0 —4 $m, 模拟光子数为$ 10^{8} $个. 探测接收面尺寸为1 cm × 1 cm, 与光束入射面平行, 探测接收面中点坐标(0.5, 0.5, $ {z_{\mathrm{l}}} $) cm, $ {z_{\mathrm{l}}} $为光束传输距离. 辐亮度透过率和偏振度图像如图6和图7所示.

由图6和图7可知, 光波辐亮度透过率随着距离增大而减小, 偏振度变化规律相同. 随着距离增大, 温度和压强对辐亮度透过率和偏振度的影响更为显著, 其中温度和压强对透过率的影响强于偏振度. 分析原因可知, 对于辐亮度透过率而言, 传输距离增大, 尾焰空间光学厚度增加, 可能发生碰撞散射事件的概率增加, 碰撞后被吸收的概率和改变传输方向不能被探测器接收的概率同步增大. 同时多次散射效应的增强, 使得碰撞造成的散射特性差异被积累放大, 光束偏振度随距离增加而减小. 根据模拟结果可知, 透过率和偏振度的斜率由开始的陡峭逐渐过渡到平缓, 说明辐亮度透过率和偏振度与传输距离呈指数衰减的关系; 随着温度的升高, CO₂气体的吸收系数减小, 其对红外辐射的吸收逐渐减弱, 光波辐亮度透过率和偏振度的衰减程度越来越小; 而在压强不断增大过程中, 辐亮度透过率和偏振度不断减小, 这是因为压强升高, 单位立方米空间内CO₂分子数量增多, 即相同传输距离条件下发生碰撞事件的可能性增大, 光子被吸收和散射的概率增大(图中曲线存在一定波动, 这是光子统计脉动造成的). 需说明的是, 并非所有气体吸收谱线的峰值吸收系数均随温度的升高而减小, 这与气体分子类型、温度范围、谱线位置等因素有关^[22].

液体发动机尾流一般由高温气体组成, 燃料不同其尾流组分也有所不同, 尾流中H₂O和CO₂气体成分占绝大多数. 除此之外, 极化是导致红外分子吸收的一个重要因素, 极性气体或者有极性键的气体红外吸收特性很强, 如H₂O, CO₂, NO, NO₂, OH. 如果既不是极性气体, 又没有极性键, 比如N₂, O₂, 则红外吸收特性很弱. 因此, 掌握发动机尾流中的H₂O和CO₂气体红外光谱吸收特性具有重要意义和价值.

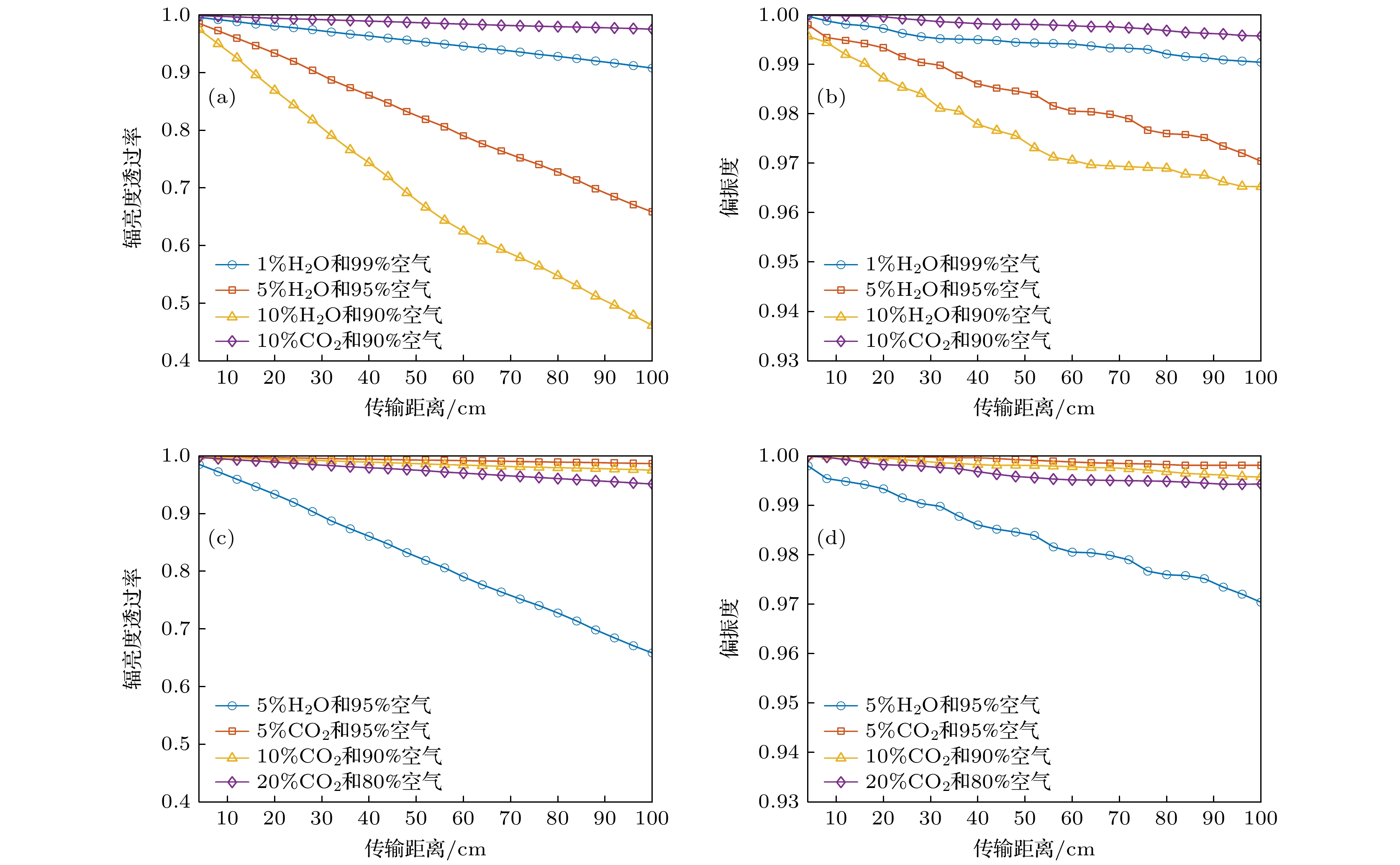
本节不仅模拟了温度1500 K、压强5 atm时, H₂O气体体积分数分别为1%, 5%, 10%情况下对光波偏振辐射传输特性的影响, 并选取体积分数为10%的CO₂作为对照. 还模拟了相同温度压强时, CO₂气体体积分数分别为5%, 10%, 20%情况下对光波偏振辐射传输特性的影响, 并选取体积分数为5%的H₂O作为对照. 其余仿真条件与3.2节一致. 辐亮度透过率和偏振度图像如图8所示.

由图8可知, 对于同种气体的不同浓度情况, 随着气体浓度的增加, 光波辐亮度透过率和偏振度的衰减程度增大. 其中不同气体组分浓度对透过率的影响强于偏振度. 主要原因是随着气体组分和浓度的变化, 尾焰空间的红外吸收系数改变, 随机步长分布概率改变, 气体分子碰撞后发生散射或吸收的概率也随之改变, 光子传输特性改变. 由图8(a)可得, 传输距离为100 cm时, 5% H₂O透过率为0.66, 10% H₂O透过率为0.46. 此时10% H₂O的吸收系数是5% H₂O的2倍, 但10% H₂O透过率的衰减度0.54不足5% H₂O透过率衰减度0.34的2倍. 根据图8(b)可得, 传输距离为100 cm时, 5% H₂O偏振度为0.97, 10%H₂O偏振度为0.965. 此时10% H₂O的吸收系数是5% H₂O的2倍, 但10% H₂O的退偏度0.035不足5% H₂O的退偏度0.03的2倍. 因此辐亮度透过率和偏振度与尾焰空间气体的吸收系数呈指数衰减关系. 研究探测波长1.96 μm处相同浓度的H₂O和CO₂气体对红外线偏光的影响时, HITRAN库计算得CO₂的红外吸收系数比H₂O低, 此时光波透过率和偏振度对H₂O气体的敏感性更强.

H₂O气体主要吸收峰的波长分别为1.38, 1.87, 2.53, 6.3, 18 μm. 不同温度下, H₂O气体的吸收峰中心波长位置几乎没有变化, 只是吸收系数数值大小发生变化. CO₂气体的吸收峰位置分别为2.7, 4.3, 15 μm. 其中4.3 μm处的吸收系数最大, 5 μm处的次之, 2.7 μm处的最小. 不同温度的CO₂气体吸收峰波长位置相同^[23]. 故本文选取H₂O气体的2.5—3.3 μm和CO₂气体的4—5 μm波段进行研究.

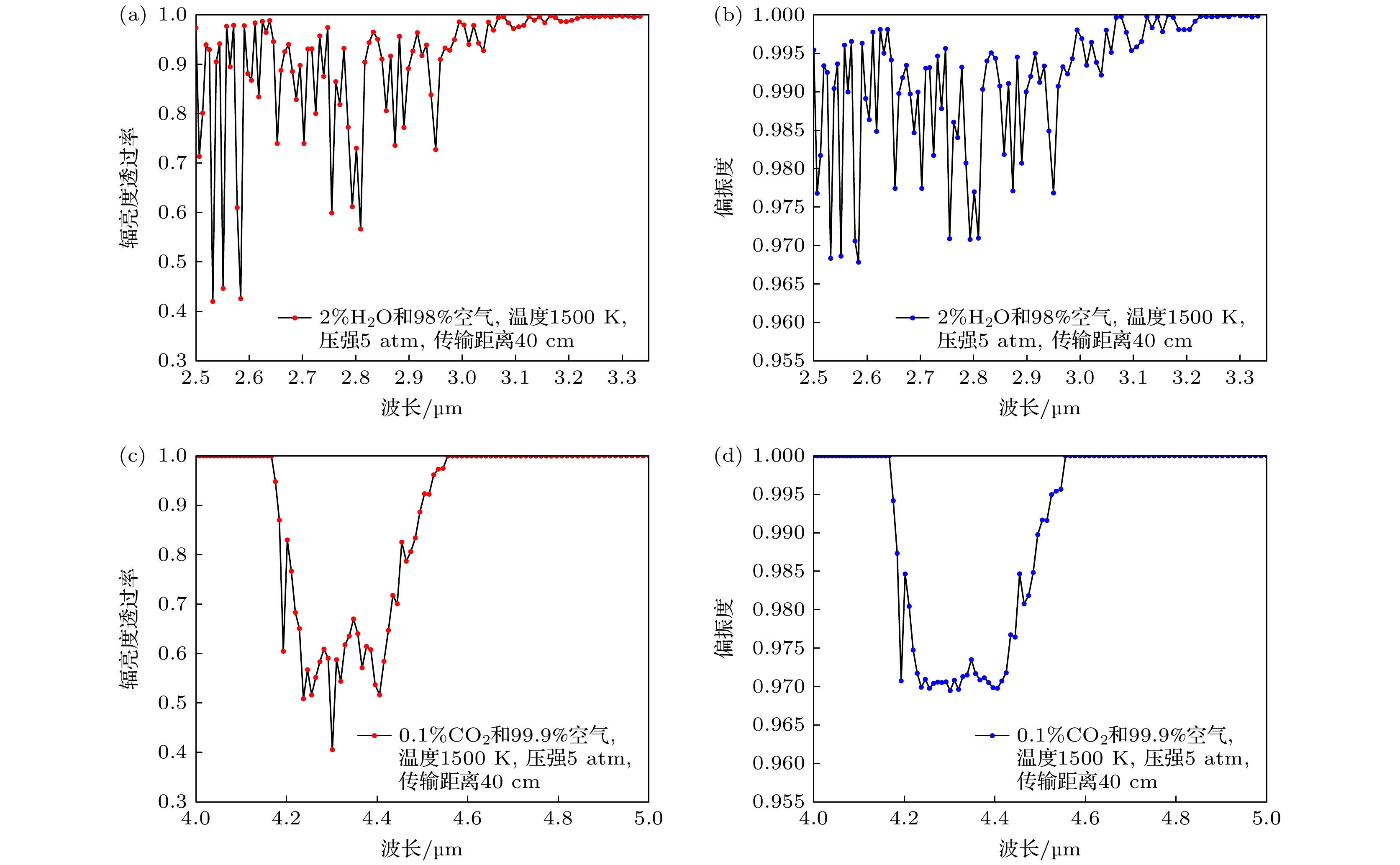
本节模拟了温度1500 K、压强5 atm时, 2% H₂O气体在2.5—3.3 μm波段和0.1%CO₂气体在4—5 μm波段对偏振辐射传输特性的影响, 其余仿真条件与3.2节一致. 辐亮度透过率和偏振度图像如图9所示.

对于2% H₂O和98%空气组成的尾焰空间, H₂O气体主要吸收峰出现在2.53 μm, 透过率波谷出现在2.53 μm, 数值约为0.42. 然而此时, 偏振度的波谷却出现在2.58 μm, 数值约为0.967, 与H₂O气体主要吸收峰出现在2.53 μm略有出入, 但是总体上偏振度变化的规律与透过率一致, 故可认为这一现象是光子统计脉动造成的. 整体上光波偏振度在2.5—3.3 μm波段随着波长的变化规律与辐亮度透过率相同, 其中波长对透过率的影响强于偏振度, 在2.5—3 μm波段H₂O气体对光波透过率和偏振度的影响波动较大, 而在3—3.3 μm波段H₂O气体对光波透过率和偏振度的影响趋于平缓; 对于0.1% CO₂和99.9%空气的尾焰空间, 透过率的波谷出现在4.3 μm, 数值约为0.4, 偏振度的波谷也出现在4.3 μm, 数值约为0.969, 与CO₂气体主要吸收峰出现在4.3 μm的现象一致. 整体上光波偏振度在4—5 μm波段随着波长的变化规律与辐亮度透过率相同, 其中波长对透过率的影响强于偏振度, CO₂气体对光波透过率和偏振度的影响主要分布在4.18—4.58 μm波段, 而在4—4.18 μm和4.58—5 μm波段CO₂气体对光波透过率和偏振度几乎没有影响.

本文基于Monte Carlo法建立了高温尾焰红外偏振辐射传输特性仿真模型. 根据HITRAN库计算气体红外吸收特性参数, 使用Monte Carlo法解决偏振辐射传输问题, 结合透过率、偏振度计算原理, 最终讨论了传输距离、尾焰温度和压强、尾焰气体组分浓度和探测波长对红外偏振光传输特性的影响, 主要得到以下结论.

1)本文研究方法和HITRAN库关于辐亮度透过率的计算结果误差基本保持在2%以内, 验证了本文模型在模拟光粒子散射过程中对偏振辐射特性分量统计的准确性.

2)随着传输距离增大, 温度和压强对光波偏振辐射传输特性的影响更为显著. 压强与透过率和偏振度呈负相关, 温度的影响与气体的类型、温度范围等因素有关.

3)辐亮度透过率和偏振度与尾焰空间气体的吸收系数和传输距离呈指数衰减关系.

4)探测波长不同, 光波的偏振辐射传输特性也存在差异, 其变化与气体的红外吸收特性光谱有关.

本文为红外偏振光在均匀分布的尾焰空间中的偏振辐射传输特性研究提供了理论依据. 由于尾焰传输特性还受到分布不均匀的温度压强等因素的干扰, 下一步研究重点为完善理论模型, 考虑尾焰分层特性对传输特性的影响.