高级搜索

超冷原子气体中的孤子共振与反共振调控

,  ,  , 

downloadPDF

上一篇

下一篇

何章明, 翟德训, 朱钱泉, 潘湘. 超冷原子气体中的孤子共振与反共振调控[J]. 物理学报, 2025, 74(11): 110501-1. doi: 10.7498/aps.74.20250177
引用本文: 何章明, 翟德训, 朱钱泉, 潘湘. 超冷原子气体中的孤子共振与反共振调控[J]. 物理学报, 2025, 74(11): 110501-1. doi: 10.7498/aps.74.20250177
shu
Zhangming HE, Dexun ZHAI, Qianquan ZHU, Xiang PAN. Regulation of resonance and anti-resonance of soliton in ultracold atomic gases[J]. Acta Physica Sinica, 2025, 74(11): 110501-1. doi: 10.7498/aps.74.20250177
Citation: Zhangming HE, Dexun ZHAI, Qianquan ZHU, Xiang PAN. Regulation of resonance and anti-resonance of soliton in ultracold atomic gases[J]. Acta Physica Sinica, 2025, 74(11): 110501-1. doi: 10.7498/aps.74.20250177
shu

超冷原子气体中的孤子共振与反共振调控

  • 湖南工业大学理学院, 株洲　412007

    • 通讯作者: E-mail: qianquanzhu@126.com.; 

  • 中图分类号: 05.45.Yv, 03.75.Mn, 03.75.Lm

Regulation of resonance and anti-resonance of soliton in ultracold atomic gases

  • School of Science, Hunan University of Technology, Zhuzhou 412007, China

    • Corresponding author: E-mail: qianquanzhu@126.com.; 

  • MSC: 05.45.Yv, 03.75.Mn, 03.75.Lm

  • 摘要: 考虑周期性驱动的谐振势阱, 通过数值模拟研究了超冷原子气体中的孤子性质. 结果有趣地发现: 当孤子位于势阱中心时, 在特定的频率驱动下, 孤子的幅度振荡产生共振现象, 其振荡幅度随着谐振势阱囚禁频率的增大而增大, 共振频率随着孤子初始幅度的增大而增大; 当孤子位于势阱边缘时, 孤子运动的共振、反共振和准周期振荡也能被观察到. 此外, 通过调节驱动频率可实现孤子运动的共振与反共振之间的转换. 相关结果可为超冷原子气体的精确调控提供帮助.
    Abstract: Kapitza’s pendulum is an inverted pendulum that is dynamically stabilized by rapidly driving its pivot point. Many applications of Kapitza stabilization in quantum systems have been proposed, such as optical molasses, the stability of optical resonators, preparation of molecular ions, the breaking of translation symmetry, the periodically driven sine-Gordon model, polariton Rabi oscillation, and the stabilization of bright solitons in a Bose-Einstein condensate. In particular, Kapitza stabilization can be used to trap particles. The most notable example of such an application is the Paul trap.Recently, the Kapitza trap was created by superimposing time-tuned focused laser beams to produce a periodically driven harmonic potential for ultracold atomic gases. This work opens up new possibilities to study Floquet systems of ultracold atomic gases. So we consider the periodically driven harmonic potential, and investigate the properties of soliton in ultracold atomic gases by numerical simulations. It is found interestingly that when a soliton is located at the center of the harmonic potential, a resonance phenomenon of soliton amplitude oscillation occurs at a specific driven frequency. In addition, the oscillation amplitude increases with the increase of the trapping frequency of the harmonic potential, and the resonance frequency increases with theaugment of soliton initial amplitude.The change of driven frequency and initial phase has a significant effect on soliton motion when the soliton is located at the edge of the harmonic potential. When the initial phase is zero, there is a characteristic driven frequency. For the case where the driven frequency is equal to the characteristic frequency, soliton motion exhibits periodic oscillations. For the case where the driven frequency is slightly lower than the characteristic frequency, the resonance of soliton oscillation can be found. When the driven frequency is slightly higher than the characteristic frequency, the anti-resonance of soliton oscillation can be found. In addition, it is found that the characteristic driven frequency increases linearly with the increase of the trapping frequency of the harmonic potential. When the initial phase is not equal to zero, the irregular oscillation, quasi-periodic oscillation, and periodic oscillation can be observed with the increase of driven frequency. When the driven frequency is equal to a specific value, the resonance of soliton oscillation can also obtained. Furthermore, the fast driving has no effect on the motion trajectory of solitons. These results can help to precisely control ultracold atomic gases.
  • 加载中

  • 图 1  超冷原子气体的概率密度演化图

    Figure 1.  The evolution of the ultracold atom gases probability density.

    下载: 全尺寸图片 幻灯片

    图 2  不同驱动频率下孤子的幅度变化图　(a) $\omega = 0.5$; (b) $\omega = 1.5$; (c) $\omega = 1.0$

    Figure 2.  The change of soliton amplitude under different driven frequency: (a) $\omega = 0.5$; (b) $\omega = 1.5$; (c) $\omega = 1.0$.

    下载: 全尺寸图片 幻灯片

    图 3  不同的囚禁频率下的孤子的幅度变化图　(a) ${\omega _x} = 5\pi \; {\text{Hz}}$; (b) ${\omega _x} = 4\pi \; {\text{Hz}}$; (c) ${\omega _x} = 3\pi \; {\text{Hz}}$; (d) ${\omega _x} = 2\pi \; {\text{Hz}}$; (e) ${\omega _x} = $$ 1\pi \; {\text{Hz}}$; (f) ${\omega _x} = 0.9\pi \; {\text{Hz}}$

    Figure 3.  The change of soliton amplitude under different trapping frequency of harmonic potential: (a) ${\omega _x} = 5\pi \; {\text{Hz}}$; (b) ${\omega _x} = 4\pi \; {\text{Hz}}$; (c) ${\omega _x} = 3\pi \; {\text{Hz}}$; (d) ${\omega _x} = 2\pi \; {\text{Hz}}$; (e) ${\omega _x} = 1\pi \; {\text{Hz}}$; (f) ${\omega _x} = 0.9\pi \; {\text{Hz}}$.

    下载: 全尺寸图片 幻灯片

    图 4  共振频率随孤子的初始幅度变化图

    Figure 4.  The resonance frequency varying with the soliton initial amplitude.

    下载: 全尺寸图片 幻灯片

    图 5  超冷原子气体中孤子运动的周期性振荡

    Figure 5.  The periodic oscillation of soliton in the ultracold atom gases.

    下载: 全尺寸图片 幻灯片

    图 6  $\phi = 1.57$时不同驱动频率下孤子运动轨迹图　(a) $\omega = 0$; (b) $\omega = 0.003$; (c) $\omega = 0.06$; (d) $\omega = 0.088$; (e) $\omega = 0.1$; (f) $\omega = $$ 0.27$; (g) $\omega = 1.0$; (h) $\omega = 2.0$

    Figure 6.  The trajectories of soliton with different driven frequencies at $\phi = 1.57$: (a) $\omega = 0$; (b) $\omega = 0.003$; (c) $\omega = 0.06$; (d) $\omega = $$ 0.088$; (e) $\omega = 0.1$; (f) $\omega = 0.27$; (g) $\omega = 1.0$; (h) $\omega = 2.0$.

    下载: 全尺寸图片 幻灯片

    图 7  孤子振荡的分布图

    Figure 7.  The distribution of soliton oscillation.

    下载: 全尺寸图片 幻灯片

    图 8  $\phi = 0$时不同驱动频率下孤子运动轨迹图 (a) $\omega = 0$; (b) $\omega = 0.06$; (c) $\omega = 0.208$; (d) $ \omega=0.209 $; (e) $\omega = 0.21$; (f)$\omega = 2.0$

    Figure 8.  The trajectories of soliton with different driven frequencies at $\phi = 0$: (a) $\omega = 0$; (b) $\omega = 0.06$; (c) $\omega = 0.208$; (d) $ \omega=0.209 $; (e) $\omega = 0.21$; (f) $\omega = 2.0$.

    下载: 全尺寸图片 幻灯片

    图 9  特征驱动频率${\omega _t}$随谐振势阱的囚禁频率变化图

    Figure 9.  The characteristic driven frequency ${\omega _t}$varying with the trapping frequency of harmonic potential.

    下载: 全尺寸图片 幻灯片
  • [1] Weitenberg C, Simonet J 2021 Nat. Phys. 17 1342 doi: 10.1038/s41567-021-01316-x
    [2] Bukov M, D’Alessio L, Polkovnikov A 2015 Adv. Phys. 64 139 doi: 10.1080/00018732.2015.1055918
    [3] Eckardt A 2017 Rev. Mod. Phys. 89 011004 doi: 10.1103/RevModPhys.89.011004
    [4] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 doi: 10.1103/RevModPhys.91.015006
    [5] Oka T, Kitamura S 2019 Annu. Rev. Condens. Matter Phys. 10 387 doi: 10.1146/annurev-conmatphys-031218-013423
    [6] 焦宸, 简粤, 张爱霞, 薛具奎 2023 物理学报 72 060302 doi: 10.7498/aps.72.20222306 Jiao C, Jian Y, Zhang A X, Xue J K 2023 Acta Phys. Sin. 72 060302 doi: 10.7498/aps.72.20222306
    [7] Zhao W L, Liu J 2024 Phys. Rev. A 109 052215 doi: 10.1103/PhysRevA.109.052215
    [8] Zhang L, Ke Y G, Lin L, Lee C H 2024 Phys. Rev. B 109 184313 doi: 10.1103/PhysRevB.109.184313
    [9] Chen L, Zhu F, Zhang Y B, Pu H 2025 Phys. Rev. A 111 L011303 doi: 10.1103/PhysRevA.111.L011303
    [10] Kamal H, Kemp J, He Y C, Fuji Y, Aidelsburger M, Zoller P, Yao N Y 2024 Phys. Rev. Lett. 133 163403 doi: 10.1103/PhysRevLett.133.163403
    [11] Zhou L W, Chen C, Gong J B 2016 Phys. Rev. B 94 075443 doi: 10.1103/PhysRevB.94.075443
    [12] Kapitza P L 1951 Usp. Fiz. Nauk 44 7 doi: 10.3367/UFNr.0044.195105b.0007
    [13] Bagnato V S, Bigelow N P, Surdutovich G I, Zílio S C 1994 Opt. Lett. 19 1568 doi: 10.1364/OL.19.001568
    [14] Torosov B T, Della Valle G, Longhi S 2013 Phys. Rev. A 88 052106 doi: 10.1103/PhysRevA.88.052106
    [15] Gilary I, Moiseyev N, Rahav S, Fishman S 2003 J. Phys. A: Math. Gen. 36 L409
    [16] Citro R, Dalla Torre E G, D’Alessio L, Polkovnikov A, Babadi M, Oka T, Demler E 2015 Ann. Phys. 360 694 doi: 10.1016/j.aop.2015.03.027
    [17] Smirnova O, Spanner M, Ivanov M Y 2003 Phys. Rev. Lett. 90 243001 doi: 10.1103/PhysRevLett.90.243001
    [18] Rajagopal S V, Fujiwara K M, Senaratne R, Singh K, Geiger Z A, Weld D M 2017 Ann. Phys. 529 1700008 doi: 10.1002/andp.201700008
    [19] Voronova N S, Elistratov A A, Lozovik Y E 2016 Phys. Rev. B 94 045413 doi: 10.1103/PhysRevB.94.045413
    [20] Martin J, Georgeot B, Guéry-Odelin D, Shepelyansky D L 2018 Phys. Rev. A 97 023607 doi: 10.1103/PhysRevA.97.023607
    [21] Park S J, Andersen H K, Mai S, Arlt J, Sherson J F 2012 Phys. Rev. A 85 033626 doi: 10.1103/PhysRevA.85.033626
    [22] Eckardt A, Weiss C, Holthaus M 2005 Phys. Rev. Lett. 95 260404 doi: 10.1103/PhysRevLett.95.260404
    [23] 何章明, 张志强 2016 物理学报 65 110502 doi: 10.7498/aps.65.110502 He Z M, Zhang Z Q 2016 Acta Phys. Sin. 65 110502 doi: 10.7498/aps.65.110502
    [24] Abdullaev F Kh, Caputo J G, Kraenkel R A, Malomed Boris A 2003 Phys. Rev. A 67 013605 doi: 10.1103/PhysRevA.67.013605
    [25] Goldman N, Dalibard J 2014 Phys. Rev. X 4 031027
    [26] Jiang J, Bernhart E, Röhrle M, Benary J, Beck M, Baals C, Ott H 2023 Phys. Rev. Lett. 131 033401 doi: 10.1103/PhysRevLett.131.033401
    [27] Zhang X F, Yang Q, Zhang J F, Chen X Z, Liu W M 2008 Phys. Rev. A 77 023613 doi: 10.1103/PhysRevA.77.023613
    [28] Kengne E, Liu W M 2018 Phys. Rev. E 98 012204 doi: 10.1103/PhysRevE.98.012204
  • 加载中
图( 9)
计量
  • 文章访问数:  23
  • HTML全文浏览数:  23
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-14
  • 刊出日期:  2025-06-05

超冷原子气体中的孤子共振与反共振调控

  • 收稿日期:  2025-02-14

摘要: 考虑周期性驱动的谐振势阱, 通过数值模拟研究了超冷原子气体中的孤子性质. 结果有趣地发现: 当孤子位于势阱中心时, 在特定的频率驱动下, 孤子的幅度振荡产生共振现象, 其振荡幅度随着谐振势阱囚禁频率的增大而增大, 共振频率随着孤子初始幅度的增大而增大; 当孤子位于势阱边缘时, 孤子运动的共振、反共振和准周期振荡也能被观察到. 此外, 通过调节驱动频率可实现孤子运动的共振与反共振之间的转换. 相关结果可为超冷原子气体的精确调控提供帮助.

English Abstract

    全文HTML

    1.   引　言

    • Floquet调控是通过时间周期性驱动调控系统, 经过长时间演化后形成一个稳定的Floquet态, 其在超冷原子物理、光晶格和固体物理中有广泛的应用[1–5], 是当前凝聚态物理学领域的研究热点之一[6–11]. 在经典物理中, 与Floquet调控类似的模型是卡皮查摆, 通过振荡产生一个平均值为零的振荡力, 使不稳定的定点转变为稳定的不定点, 如通过周期性的振荡调控使小球在高点保持平衡[12]. 这种稳定机制被称为卡皮查稳定. 近年来, 卡皮查摆在量子系统方面有大量的应用, 如光学黏团[13]、光学谐振腔的稳定性[14]、激光囚禁[15]、周期性的驱动Sine-Gordon模型[16]、分子离子的制备[17]、平移对称性的破缺[18]、极化基元的拉比振荡等[19]. 值得一提的是, 通过调节外部势阱或原子间相互作用, 卡皮查摆在玻色-爱因斯坦凝聚体(Bose-Einstein condensate, BEC)中也能实现. 研究发现, 通过类似卡皮查摆的振荡调节光晶格势阱, 可以阻止原子间为相互排斥作用的BEC在晶格中扩散, 使BEC保持长时间的稳定[20]; 也可调控BEC中的Landau-Zener遂穿和BEC的分裂行为[21]; 还可以观察到BEC中从超流态到莫特绝缘体态的转变[22]; 周期性的调控线性势, 可控制BEC中双孤子之间的相互作用[23]. 此外, 调节原子间相互作用周期性振荡可防止 BEC的崩塌[24].

      实验中, 可利用卡皮查稳定性来囚禁粒子, 如Paul阱[25]. 最近周期性驱动的谐振势阱即“卡皮查阱”在超冷原子气体中成功实现, 为了研究中性原子气体的Floquet调控提供一种新的可能[26]. 在此, 我们考虑超冷原子气体中囚禁于周期性驱动的谐振势中, 研究其中的孤子性质. 结果有趣地发现: 当孤子位于势阱中心时, 在特定的频率驱动下, 孤子的幅度振荡产生共振现象. 而当孤子位于势阱边缘时, 驱动频率和初始相位的变化对孤子运动有 重要影响. 当初始相位为零($\phi = 0$)时, 存在一个特征驱动频率${\omega _{\text{t}}}$. 当驱动频率等于特征频率${\omega _{\text{t}}}$时, 孤子运动呈周期性振荡; 当驱动频率小于特征频率${\omega _{\text{t}}}$时, 孤子运动产生共振现象; 当驱动频率大于特征频率${\omega _{\text{t}}}$时, 孤子运动产生反共振现象. 当初始相位$\phi = 1.57$时, 可通过调节驱动频率使孤子运动从无规则振荡到准周期振荡再到周期性振荡的转变, 并且当驱动频率等于特定值时, 孤子运动也可产生共振现象

    2.   模　型

    • 考虑超冷原子气体囚禁于周期性驱动的谐振势阱中, 基于GP(Gross-Pitaevskii)理论, 其性质可用下面无量纲化的方程来描述[27,28]:

      其中, $\psi $为描述超冷原子气体的波函数; 势阱驱动圆频率$\omega $和初始相位$\phi $为常数; $\lambda = {\omega _x}/{\omega _ \bot }$, ${\omega _x}$和$ {\omega _ \bot } $分别为谐振势阱的轴向和横向囚禁频率. 非线性系数$g = 2 N{a_{\text{s}}}/{a_ \bot }$, N为超冷原子气体中总的原子数目, $ {a_{\text{s}}} $为超冷原子的S-波散射长度, 谐振子横向特征长度$ {a_ \bot } = \sqrt {\hbar /M{\omega _ \bot }} $, M表示原子质量. 方程(1)中无量纲化参量为$ X = {a_ \bot }x $, $ T = 2 t/{\omega _ \bot } $. 基于当超冷原子气体的实验, 超冷原子气体中总原子数目和谐振势阱的横向囚禁频率分别选取N = 5000, $ {\omega _ \bot } = {\text{π}} \times 100 $ Hz.

    3.   孤子幅度的共振现象

    • 考虑周期性驱动的谐振势阱后, 采用Crank-Nicolson方法来数值研究其中超冷原子气体中的孤子性质, 无量纲的GP方程(1)的初始条件选取如下:

      其中$b$和${x_0}$为常数, ${x_0}$表示孤子初始位置, 孤子的初始幅度$A = 4{b^2}$.

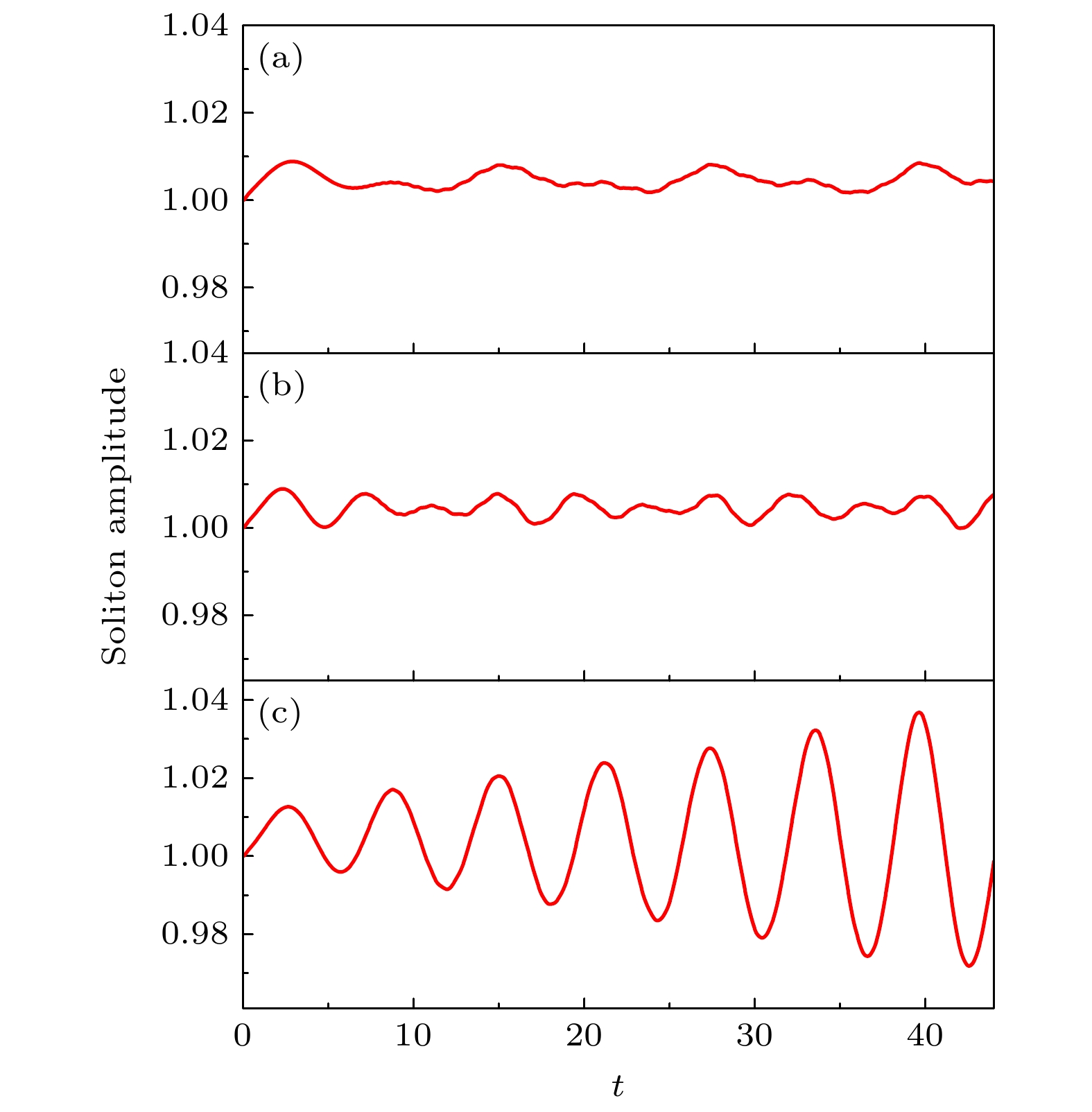
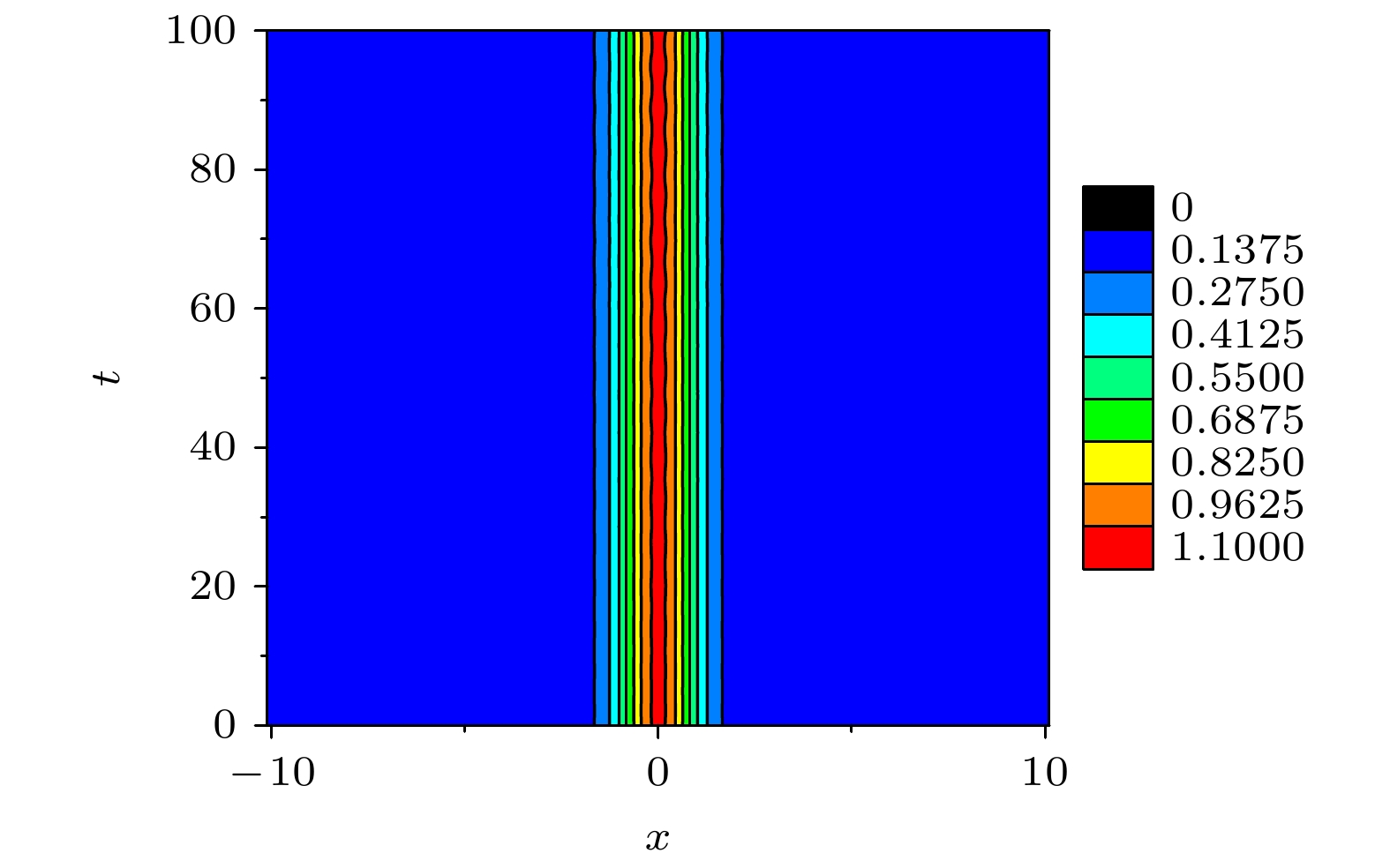
      为了对比, 首先考虑驱动圆频率$\omega $为零, 其他参数选取为: 驱动的初始相位常数$\phi = 1.57$, 相互作用常数$g = 2.0$, 谐振势囚禁频率${\omega _x} = 6{\text{π}}$ Hz, 孤子的初始位置x0 = 0, 初始幅度常数$b = 0.5$, 相应的超冷原子气体的概率密度演化如图1所示. 从图1可看到, 随着时间的推移, 超冷原子气体中孤子在谐振势阱中心位置保持稳定, 孤子幅度保持不变. 接下来考虑驱动圆频率增大到$\omega = 0.5$, 其他参数保持不变, 相应的孤子幅度变化如图2(a)所示. 从图2(a)可看到, 孤子的幅度产生振荡现象. 随着驱动圆频率继续增大到$\omega = 1.5$, 从图2(b)可看到孤子的幅度产生无规则振荡现象, 与图2(a)相比, 图2(b)孤子幅度的振荡频率增大. 而当驱动频率$\omega = 1.0$时, 从图2(c)有趣地看到, 孤子的幅度也产生振荡, 并且在时间上具有周期性, 其振荡的幅度随时间延长. 这一现象表明孤子幅度变化产生了共振现象. 图2(c)中孤子幅度振荡周期$T \approx 6.28$, 振荡圆频率${\omega _1} = 2{\text{π}}/T = 1.0$. 此时孤子幅度振荡的圆频率与驱动频率相同, 从而产生共振.

      为了研究谐振势阱囚禁频率对孤子幅度共振现象的影响. 选取驱动频率$\omega = 1.0$, 驱动的初始相位常数$\phi = 1.57$, 相互作用常数$g = 2.0$, 孤子的初始位置x0 = 0, 初始幅度常数为$b = 0.5$, 不同囚禁频率下的孤子幅度变化如图3所示. 当谐振势阱囚禁频率分别为${\omega _x} = 5{\text{π}}\; {\text{Hz}}$, ${\omega _x} = 4{\text{π}}\; {\text{Hz}}$, ${\omega _x} = 3{\text{π}}\; {\text{Hz}}$和 ${\omega _x} = 2{\text{π}}\; {\text{Hz}}$时, 分别从图3(a)—(d)可看到, 孤子幅度振荡的频率没有发生变化, 而振荡的幅度随着囚禁频率的减小而减小. 这些结果表明孤子幅度振荡的共振现象可通过调节谐振势阱囚禁频率来控制. 当${\omega _x} = 1{\text{π}}\; {\text{Hz}}$时, 从图3(e)可看到, 孤子幅度的振荡变化已经非常小, 而当${\omega _x} = 0.9{\text{π}}\; {\text{Hz}}$时, 从图3(f)可看到, 孤子的幅度已经几乎不变. 图3(e), (f)中的结果表明, 谐振势阱的囚禁频率存在着一个临界值. 在图3中可以选取${\omega _x} = {\text{π}}\; {\text{Hz}}$为临界值, 当囚禁频率高于临界值时, 孤子的幅度才会产生共振现象.

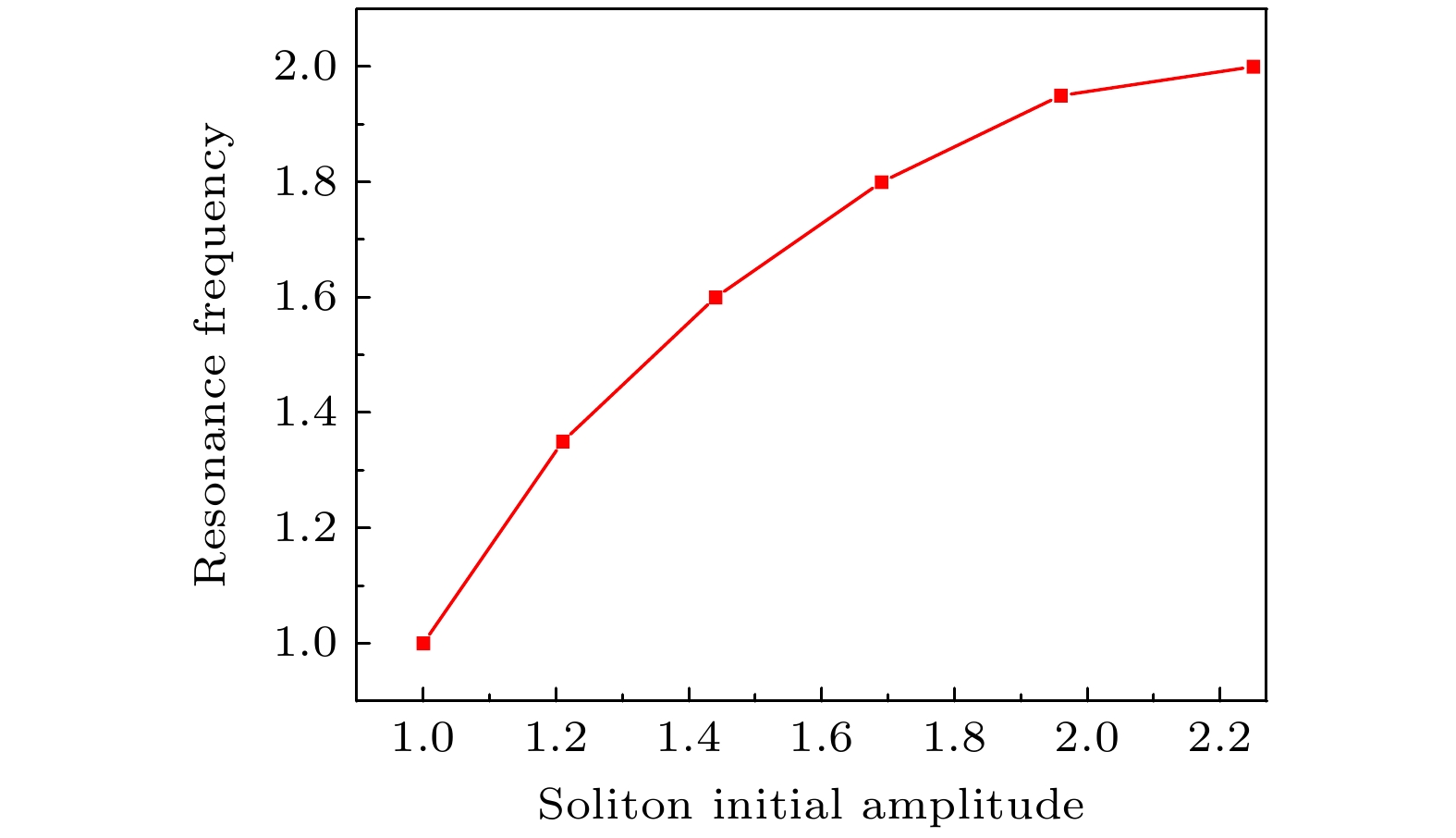
      接下来计算了初始幅度不同的孤子的共振现象, 选取驱动的初始相位常数$\phi = 1.57$, 相互作用常数$g = 2.0$, 孤子的初始位置x0 = 0. 不同初始幅度孤子的共振频率如图4所示. 从图4看到, 随着孤子初始幅度的增大, 共振频率也随之增大.

    4.   孤子运动的共振与反共振现象

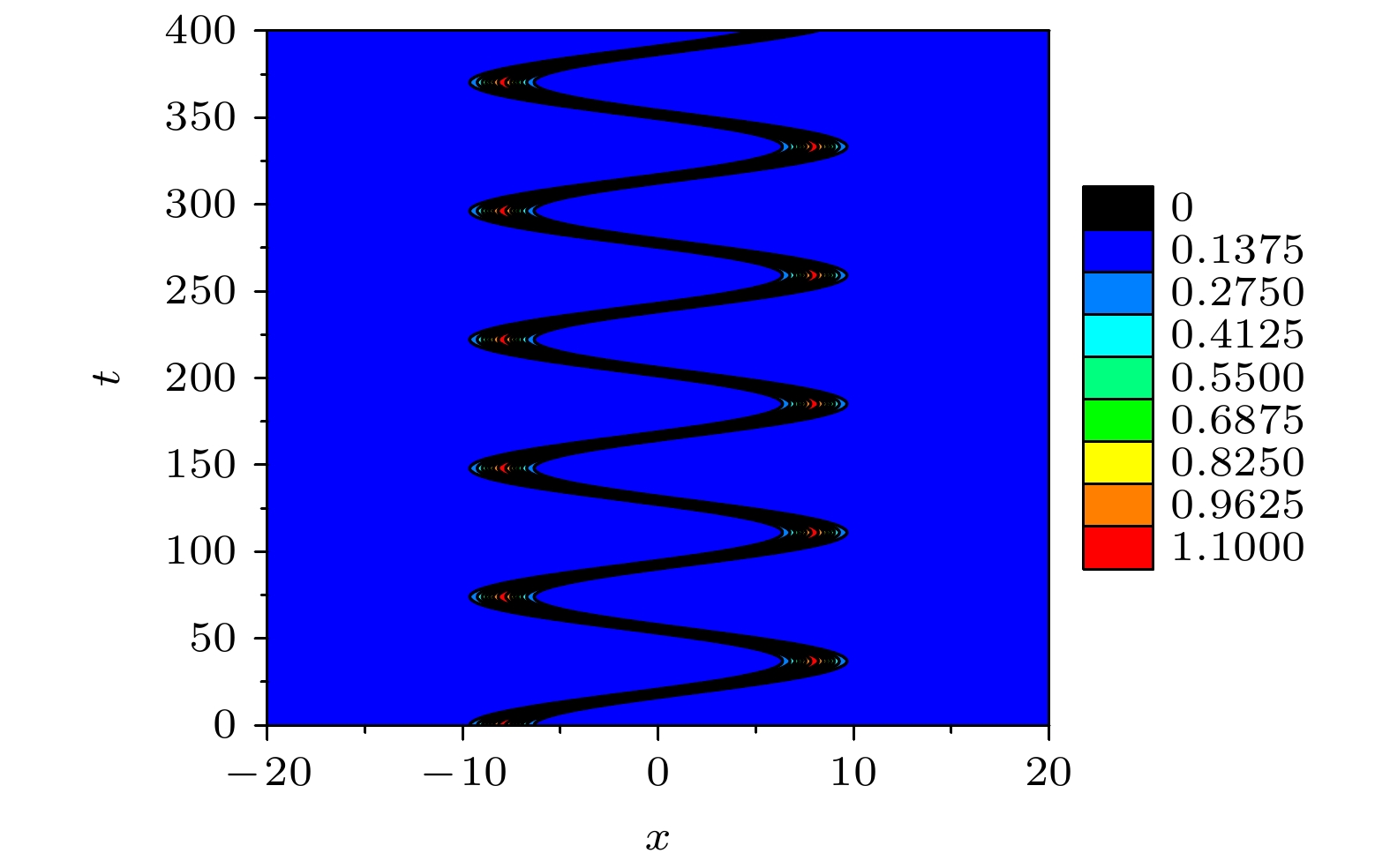
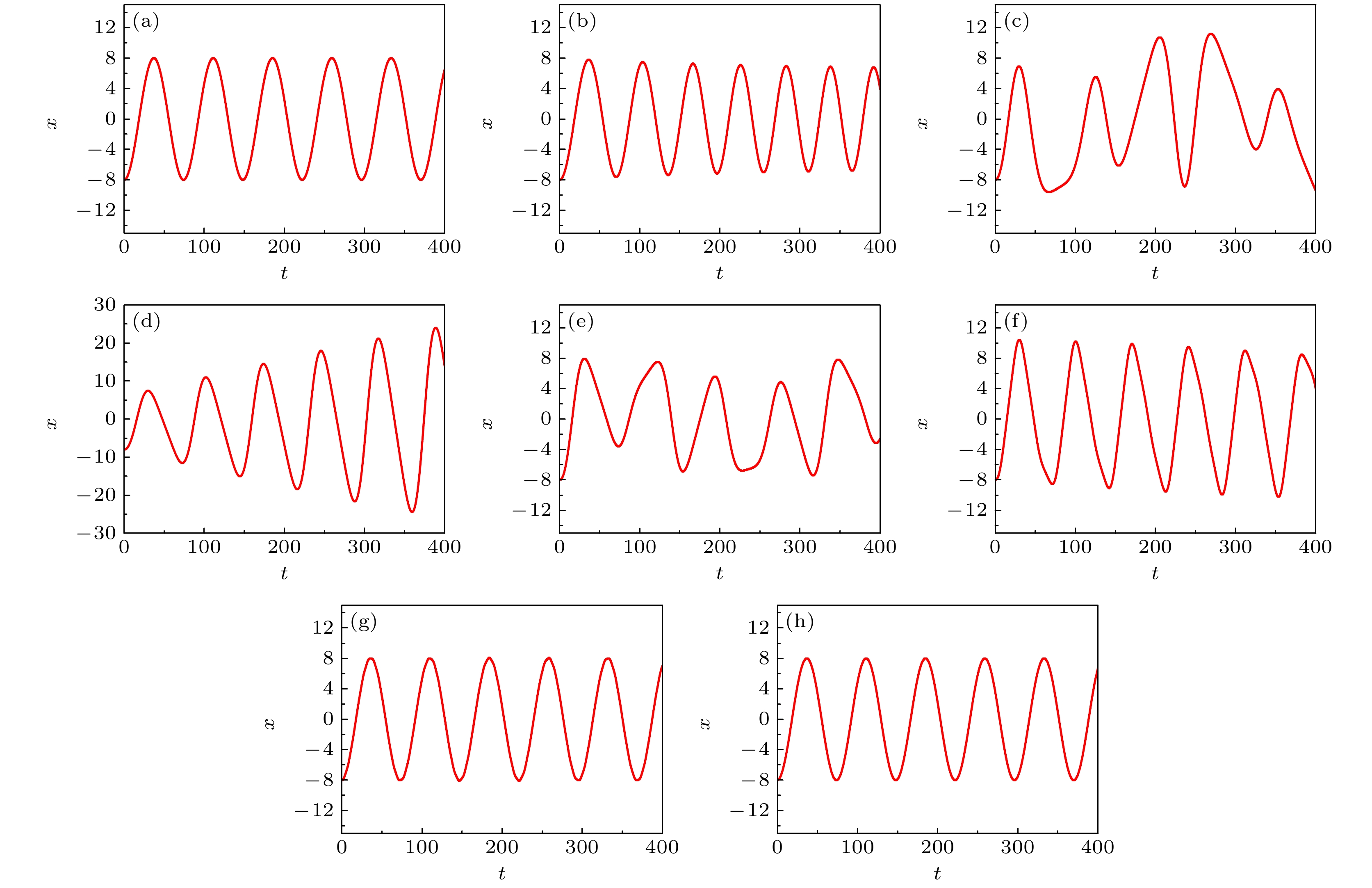
    • 为了研究周期驱动频率和相位变化对孤子运动轨迹的影响, 首先选取初始相位常数$\phi = 1.57$, 相互作用常数$g = 2.0$, 孤子的初始位置${x_0} = - 8.0$, 谐振势囚禁频率${\omega _x} = 6{\text{π}}$ Hz, 初始幅度常数为$b = 0.5$. 当驱动频率$\omega = 0$时, 超冷原子气体的概率密度随时间演化如图5所示. 从图5可看到, 孤子在谐振势阱中产生了一个周期性振荡. 此时, 孤子的运动轨迹如图6(a)所示, 从图6(a)看到, 振荡频率约为0.088, 孤子运动的范围从x = -8.0到x = 8.0. 当驱动频率$\omega = 0.003$时, 孤子的运动轨迹如图6(b)所示, 从图中可发现孤子从初始位置${x_0} = - 8.0$出发, 在$t \approx 70$时, 孤子只能回到$x \approx - 7.6$; 在$t \approx 135$时, 孤子只能回到$x \approx - 7.3$; 在$t \approx 195$时, 孤子只能回到$x \approx - 7.0$; 在$t \approx 255$时, 孤子只能回到$x \approx - 6.7$. 这表明在非常小的频率驱动下, 孤子运动仍然产生了振荡, 并且振荡频率越来越快, 但是振荡的幅度越来越小, 这是因为随着时间的延长, 谐振势阱的强度一直增大. 随着驱动频率增至$\omega = 0.06$时, 从图6(c)可看到, 孤子运动产生无规则振荡. 当驱动频率$\omega = 0.088$时, 即驱动频率等于图6(a)中驱动频率为零时孤子运动的振荡频率, 从图6(d)可有趣地看到, 当两个频率相等时, 孤子运动也产生共振现象, 随着时间的推移, 孤子运动的振荡幅度越来越大, 振荡频率仍约为0.088. 当驱动频率$\omega = 0.01$时, 从图6(e)可看到, 孤子的共振现象消失, 呈无规则振荡. 继续增大驱动频率$\omega = 0.27$时, 从图6(f)可看到, 当时间在$0 < t < 30$范围内, 孤子朝x轴正方向运动, 当$t \approx 30$, 孤子到达位置为$x \approx 10.5$, 当时间在$30 < t < 70$范围内, 孤子朝x轴负方向运动, 当$t \approx 70$, 孤子到达位置为$x \approx - 8.4$. 接下来时间$70 < t < 100$范围内, 孤子朝x轴正方向运动, 当$t \approx 100$, 孤子到达位置为$x \approx 10.2$, 当时间在$100 < t < 140$范围内, 孤子朝x轴负方向运动, 当$t \approx 140$, 孤子到达位置为$x \approx - 9.1$. 类似现象在其他的时间段内也能观察到. 这表明孤子产生了特殊振荡, 其中朝x轴正方向运动的时长为30, 朝x轴负方向运动的时长为40, 同时孤子振荡整体在向x轴负方向偏移. 不同于图6(a)中孤子的周期性振荡, 我们把这种孤子的特殊振荡称为准周期振荡. 接下来继续增大驱动频率, 如$\omega = 1.0$和$\omega = 2.0$, 相应的孤子运动轨迹如图6(g), (h)所示. 从图6(g), (h)看到, 孤子的运动又恢复了周期性振荡, 并且振荡频率约为0.088, 运动轨迹和振荡频率与图6(a)中驱动频率$\omega = 0$时一致. 这表明快速驱动对孤子运动没有影响.

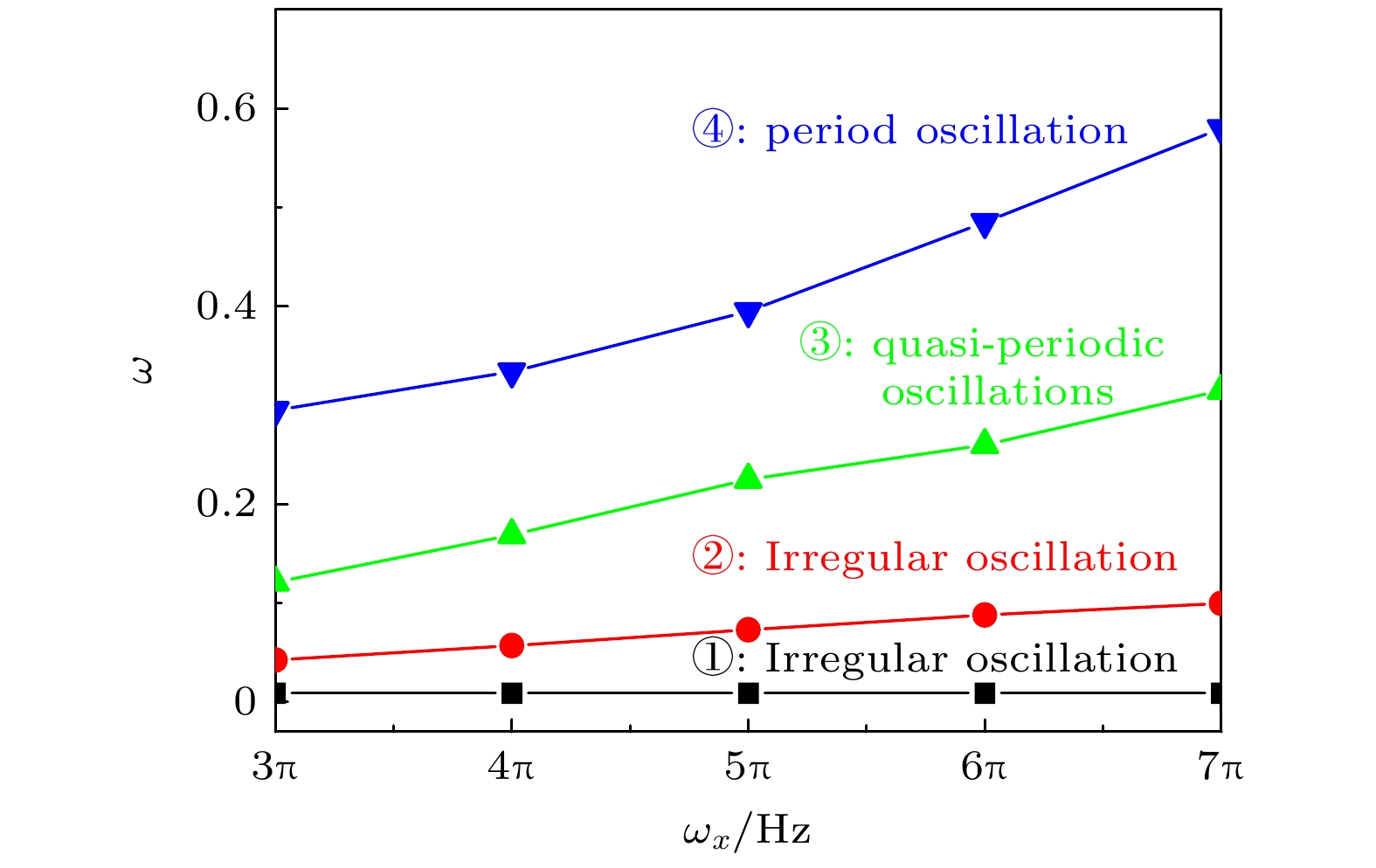
      图6中的结果表明, 可通过调节驱动频率使孤子运动从无规则振荡到准周期振荡再到周期性振荡的转变, 并且当驱动频率等于特定值时还可产生共振现象. 为了研究谐振势阱对孤子振荡转换行为的影响, 选取初始相位常数$\phi = 1.57$, 相互作用常数$g = 2.0$, 孤子的初始位置${x_0} = - 8.0$, 初始幅度常数$b = 0.5$, 不同驱动频率和谐振势阱中孤子无规则振荡、准周期振荡和周期性振荡的分布如图7所示. 在图7中, 驱动频率选取范围为$0.01 \leqslant \omega \leqslant 0.7$. 图7中黑色方块点线代表驱动频率为$\omega = 0.01$; 红色圆点线表示特征共振驱动频率随谐振势阱囚禁频率的变化, 当驱动频率等于红色圆点线的特征共振驱动频率时, 可观察到孤子运动的共振现象; 绿色上三角点线和蓝色下三角点线代表是临界驱动频率, 当驱动频率小于绿色上三角点代表的临界频率时, 孤子振荡为无规则振荡; 当驱动频率大于绿色上三角点代表的临界频率时而小于蓝色下三角点代表的临界频率时, 孤子振荡为准周期振荡; 当驱动频率大于蓝色下三角点代表的临界频率时, 孤子运动呈周期性振荡. 黑色方块点线和红色圆点线之间为区域①, 红色圆点线和绿色上三角点线之间为区域②, 绿色上三角点线和蓝色下三角点线之间为区域③, 蓝色下三角点线之上为区域④. 当驱动频率位于区域①和②时, 孤子振荡为无规则振荡; 当驱动频率位于区域③时, 孤子的振荡为准周期振荡; 当驱动频率位于区域④时, 孤子的振荡为周期性振荡.

      接下来选取初始相位常数$\phi = 0$, 其他参数与图5一致, 不同驱动频率下孤子的运动轨迹如图8所示. 当驱动频率$\omega = 0$时, 从图8(a)看到, 孤子在谐振势阱中产生了周期性振荡, 孤子运动的范围从x = –8.0到x = 8.0, 振荡频率约为0.121. 孤子振荡频率比图6(a)中孤子的振荡频率大, 这是因为驱动频率$\omega = 0$时, 囚禁势为谐振势阱$V\left( x \right) = \left[ {1 + \cos \left( \phi \right)} \right]{\lambda ^2}{x^2}/2$, 当$\phi = 1.57$时, $V\left( x \right) \approx {\lambda ^2}{x^2}/2$, 而当$\phi = 0$时, $V\left( x \right) = {\lambda ^2}{x^2}$, 即$\phi = 0$时谐振势阱强度要高于$\phi = 1.57$时, 所以图8(a)中孤子运动振荡频率比图6(a)中孤子运动的振荡频率大. 当驱动频率增至$\omega = 0.06$时, 从图8(b)中看到, 孤子运动产生无规则振荡. 当驱动频率$\omega = 0.208$时, 从图8(c)中可有趣的看到, 孤子运动产生共振现象, 随着时间的推移, 孤子运动的振荡幅度越来越大; 而当驱动频率$\omega = 0.209$时, 从图8(d)可看到, 孤子在谐振势阱中产生周期性振荡, 孤子运动的范围从x = –8.0到x = 8.0, 振荡频率约为0.105, 孤子振荡频率比图8(a)中驱动频率$\omega = 0$时孤子振荡频率要小; 随着驱动频率继续增加$ \omega=0.21 $时, 从图8(e)中可有趣地看到孤子运动也产生振荡, 但是随着时间的推移, 孤子运动的振荡幅度越来越小, 这是一种典型的反共振现象. 当驱动频率$\omega = 2.0$时, 从图8(e)可看到, 孤子的运动又恢复了周期性振荡, 并且振荡频率约为0.088, 比图8(a)中驱动频率$\omega = 0$时孤子的振荡频率要小, 而与图6(a)中驱动频率$\omega = 0$时孤子的振荡频率一致, 这也表明快速驱动对孤子的运动轨迹没有影响.

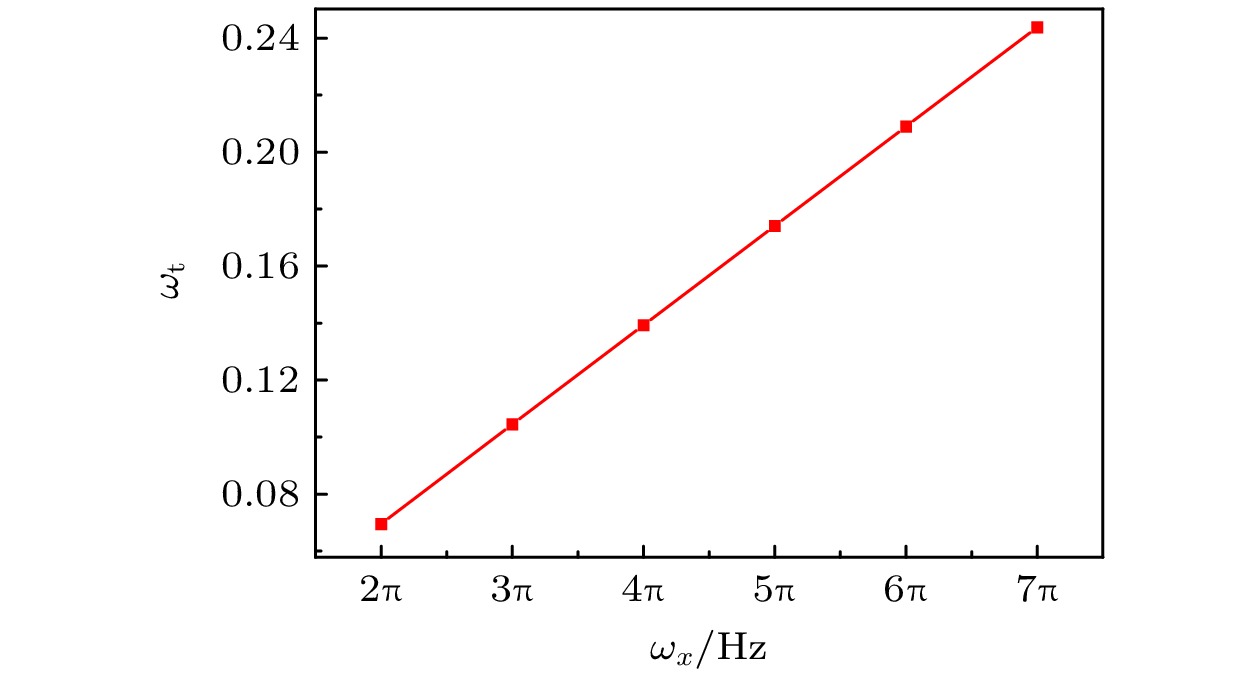
      对比图8(c)—(e)中所示的孤子运动轨迹, 结果表明存在一个特征驱动频率${\omega _{\text{t}}}$. 当驱动频率等于特征频率时, 孤子运动呈周期性振荡; 当驱动频率小于特征频率时, 孤子运动产生共振现象; 当驱动频率大于特征频率时, 孤子运动产生反共振现象. 在图8中可以得到特征驱动频率${\omega _{\text{t}}} = 0.209$. 此外, 我们还计算得到了不同谐振势阱中的特征驱动频率, 如图9所示. 从图9可看到, 特征驱动频率${\omega _{\text{t}}}$随着谐振势阱囚禁频率的增大而线性增大.

    5.   结　论

    • 考虑超冷原子气体囚禁于周期性驱动的谐振势阱中, 数值研究了其中的孤子性质. 结果发现: 在特定的频率驱动下, 当孤子位于势阱中心时, 孤子的幅度振荡产生共振现象, 其振荡幅度随着谐振势阱囚禁频率的增大而增大, 共振频率随着孤子初始幅度的增大而增大. 而当孤子位于势阱边缘时, 驱动频率和初始相位的变化对孤子运动有重要影响. 当初始相位为零($\phi = 0$)时, 存在一个特征驱动频率${\omega _t}$. 当驱动频率等于特征频率时, 孤子运动呈周期性振荡; 当驱动频率小于特征频率时, 孤子运动产生共振现象; 当驱动频率大于特征频率时, 孤子运动产生反共振现象. 通过进一步计算发现, 特征驱动频率${\omega _t}$随着谐振势阱囚禁频率的增大而线性增大. 当初始相位$\phi = 1.57$时, 可通过调节驱动频率使孤子运动从无规则振荡到准周期振荡再到周期性振荡的转变, 并且当驱动频率等于特定值时, 孤子运动还可产生共振现象. 此外, 快速驱动对孤子的运动轨迹没有影响. 相关结果可为超冷原子气体中孤子的精确调控提供一定的参考价值.

    参考文献 (28)

目录

/

返回文章
返回