高级搜索

运动光格中非线性作用随时空变化的玻色-爱因斯坦凝聚体的混沌时空动力学

, 

downloadPDF

上一篇

下一篇

李飞, 李文武. 运动光格中非线性作用随时空变化的玻色-爱因斯坦凝聚体的混沌时空动力学[J]. 物理学报, 2025, 74(11): 110302-1. doi: 10.7498/aps.74.20241604
引用本文: 李飞, 李文武. 运动光格中非线性作用随时空变化的玻色-爱因斯坦凝聚体的混沌时空动力学[J]. 物理学报, 2025, 74(11): 110302-1. doi: 10.7498/aps.74.20241604
shu
Fei LI, Wenwu LI. Chaotic spatiotemporal dynamics of Bose-Einstein condensates with nonlinear time- and space-varying interactions in moving optical lattices[J]. Acta Physica Sinica, 2025, 74(11): 110302-1. doi: 10.7498/aps.74.20241604
Citation: Fei LI, Wenwu LI. Chaotic spatiotemporal dynamics of Bose-Einstein condensates with nonlinear time- and space-varying interactions in moving optical lattices[J]. Acta Physica Sinica, 2025, 74(11): 110302-1. doi: 10.7498/aps.74.20241604
shu

运动光格中非线性作用随时空变化的玻色-爱因斯坦凝聚体的混沌时空动力学

  • 湖南第一师范学院物理系, 长沙　410205

    • 通讯作者: E-mail: lifeipaper@163.com.; 

  • 中图分类号: 03.75.Lm, 03.75.Kk, 05.45.Ac, 05.45.Gg

Chaotic spatiotemporal dynamics of Bose-Einstein condensates with nonlinear time- and space-varying interactions in moving optical lattices

  • Department of Physics, Hunan First Normal University, Changsha 410205, China

    • Corresponding author: E-mail: lifeipaper@163.com.; 

  • MSC: 03.75.Lm, 03.75.Kk, 05.45.Ac, 05.45.Gg

  • 摘要: 本文研究运动光格中非线性作用随时空变化的玻色-爱因斯坦凝聚体的混沌时空动力学. 在运动光格势强度和非线性作用调制强度较小的情况下, 系统满足微扰条件, 将Melnikov函数法应用于理论分析, 得到了系统的Melnikov时空混沌判据. 当系统不满足微扰条件时, 数值模拟表明, 对于原子间呈吸引作用的玻色-爱因斯坦凝聚体, 非线性作用调制强度的增大可以加深系统的时空混沌程度. 在某些参数区域, 非线性作用调制频率对系统时空动力学行为具有重要影响. 进一步的数值研究结果揭示, 较大的化学势不仅可以抑制吸引系统的时空混沌, 还可以抑制排斥系统的时空混沌. 基于以上研究结果, 在实验中可以根据需要规避或引发玻色-爱因斯坦凝聚系统的时空混沌.
    Abstract: The dynamical behaviors of Bose-Einstein condensates (BECs) depend largely on the nonlinear interactions between BEC atoms. The advancement of experimental techniques enables the rapid and effective modulation of the nonlinear interactions through Feshbach resonance technique. At present, both the nonlinear time-varying interaction and nonlinear space-varying interaction have been realized, respectively, thus making it possible to simultaneously modulate the nonlinear interactions in time and space through the combination of techniques. It will provide more options to conduct various studies by manipulating the BECs. Therefore, BECs with time- and space-varying interactions must possess unique advantages in studying BEC dynamics.This paper focuses on the chaotic spatiotemporal dynamics of BECs with nonlinear time- and space-varying interactions in moving optical lattices. When the intensities of the moving optical lattice potential and the modulation of the nonlinear interaction are small, the system satisfies the perturbation conditions and the Melnikov-function method is used in the theoretical analyses to obtain the Melnikov spatiotemporal chaotic criterion of the system. When the system does not meet the perturbation conditions, numerical simulations show that for a BEC with an attractive atomic interaction, increasing the modulation intensity of the nonlinear interaction can deepen the degree of spatiotemporal chaos in the system. In certain parameter regions, the modulation frequency of the nonlinear interaction can have a significant influence on the spatiotemporal dynamical behavior of the system. Further numerical research results show that larger chemical potentials can suppress the spatiotemporal chaos not only in the attractive BEC but also in the repulsive BEC. Based on the above research results, spatiotemporal chaos in BEC system can be avoided or triggered off in experiments as needed.
  • 加载中

  • 图 1  改变非线性作用调制强度过程中庞加莱截面的演化, 其他参数和初始条件设置为$ \tilde \mu = 0.8 $, $ \tilde v = 2.0 $, $ \tilde I = 0.23 $, $ {\tilde g_0} = - 0.75 $, $ \omega = 0.4 $, $ A(0) = 0.26 $, $ \dot A(0) = 0 $

    Figure 1.  Evolution of Poincaré sections in the process of changing the modulation intensity of the nonlinear interaction. The other parameters and initial conditions are set as $ \tilde \mu = 0.8 $, $ \tilde v = 2.0 $, $ \tilde I = 0.23 $, $ {\tilde g_0} = - 0.75 $, $ \omega = 0.4 $, $ A(0) = 0.26 $, $ \dot A(0) = 0 $.

    下载: 全尺寸图片 幻灯片

    图 2  增大化学势过程中相图的演化　(a)—(c)图对应的化学势$ \tilde \mu $的值分别为1.7, 2.5, 10; 其他参数和初始条件与图1(d)相同

    Figure 2.  Evolution of phase portraits with the increase of chemical potential: The values of the chemical potential $ \tilde \mu $ corresponding to (a)–(c) are 1.7, 2.5, and 10, respectively. The other parameters and initial conditions are the same as Fig. 1(d).

    下载: 全尺寸图片 幻灯片

    图 3  不同$ \omega $值对应的庞加莱截面　(a), (a') $ \omega = 29.999 $; (b), (b') $ \omega = 30 $; (c), (c') $ \omega = 30.00001 $; 其他参数和初始条件与图1(d)相同

    Figure 3.  The Poincaré sections for different values of $ \omega $: (a), (a') $ \omega = 29.999 $; (b), (b') $ \omega = 30 $; (c), (c') $ \omega = 30.00001 $. The other parameters and initial conditions are the same as Fig.1 (d).

    下载: 全尺寸图片 幻灯片

    图 4  不同$ \omega $值时的相图和对应的庞加莱截面　(a), (a') $ \omega = 1 $; (b), (b') $ \omega = 2.2 $; (a), (b)是相图; (a'), (b')是对应的庞加莱截面; 参数和初始条件设置为$ \tilde \mu = 2.11 $, $ \tilde v = 2.0 $, $ \tilde I = 0.25 $, $ {\tilde g_0} = {\tilde g_1} = - 0.7 $, $ A(0) = 0.28 $, $ \dot A(0) = 0 $

    Figure 4.  The phase portraits and corresponding Poincaré sections for different values of $ \omega $: (a), (a') $ \omega = 1 $; (b), (b') $ \omega = 2.2 $; (a), (b) are phase portraits; (a'), (b')　are the corresponding Poincaré sections. The parameters and initial conditions are set as $ \tilde \mu = 2.11 $, $ \tilde v = 2.0 $, $ \tilde I = 0.25 $, $ {\tilde g_0} = {\tilde g_1} = - 0.7 $, $ A(0) = 0.28 $, $ \dot A(0) = 0 $.

    下载: 全尺寸图片 幻灯片

    图 5  $ \tilde \mu = 30 $时的相图, 其他参数和初始条件与图4(b)相同

    Figure 5.  The phase portrait for $ \tilde \mu = 30 $. The other parameters and initial conditions are the same as Fig.4(b).

    下载: 全尺寸图片 幻灯片

    图 6  原子间呈排斥作用的BEC系统的混沌相图和对应的$ A(\zeta ) $混沌时空演化曲线, 参数和初始条件为$ \tilde \mu = 3 $, $ \tilde v = $$ 1 $, $ \tilde I = 0.9 $, $ {\tilde g_1} = 0.6 $, $ {\tilde g_0} = 0.7 $, $ \omega = 1.2 $, $ A(0) = 0.6 $, $ \dot A(0) = 0 $

    Figure 6.  The chaotic phase portrait and corresponding chaotic spatiotemporal evolution curve of $ A(\zeta ) $ of a BEC system with a repulsive interaction between atoms. The parameters and initial conditions are set as $ \tilde \mu = 3 $, $ \tilde v = 1 $, $ \tilde I = 0.9 $, $ {\tilde g_1} = 0.6 $, $ {\tilde g_0} = 0.7 $, $ \omega = 1.2 $, $ A(0) = 0.6 $, $ \dot A(0) = 0 $.

    下载: 全尺寸图片 幻灯片

    图 7  $ \tilde \mu = 40 $时的相图, 其他参数和初始条件与图6相同

    Figure 7.  The phase portrait for $ \tilde \mu = 40 $. The other parameters and initial conditions are the same as Fig.6

    下载: 全尺寸图片 幻灯片
  • [1] Anderson M H, Ensher J R, Matthews M R, E Wieman C, Cornell E A 1995 Science 269 198 doi: 10.1126/science.269.5221.198
    [2] Davis K B, Mewes M O, Andrews M R, van Druten N J, Durfee D S, Kurn D M, Ketterle W 1995 Phys. Rev. Lett. 75 3969 doi: 10.1103/PhysRevLett.75.3969
    [3] Efremidis N K, Sears S, Christodoulides D N, Fleischer J W, Segev M 2002 Phys. Rev. E 66 046602 doi: 10.1103/PhysRevE.66.046602
    [4] Dahan B M, Peik E, Reichel J, Castin Y, Salomon C 1996 Phys. Rev. Lett. 76 4508 doi: 10.1103/PhysRevLett.76.4508
    [5] Anderson B P, Kasevich M A 1998 Science 282 1686 doi: 10.1126/science.282.5394.1686
    [6] Liu S, Xiong H, Xu Z, Huang G 2003 J. Phys. B 36 2083 doi: 10.1088/0953-4075/36/10/316
    [7] 高吉明, 狄国文, 鱼自发, 唐荣安, 徐红萍, 薛具奎 2024 物理学报 73 130503 doi: 10.7498/aps.73.20240376 Gao J M, Di G W, Yu Z F, Tang R A, Xu H P, Xue J K 2024 Acta Phys. Sin. 73 130503 doi: 10.7498/aps.73.20240376
    [8] Pachos J K, Knight P L 2003 Phys. Rev. Lett. 91 107902 doi: 10.1103/PhysRevLett.91.107902
    [9] Morsch O, Müller J H, Cristiani M, Ciampini D, Arimondo E 2001 Phys. Rev. Lett. 87 140402 doi: 10.1103/PhysRevLett.87.140402
    [10] Bhattacherjee A B, Pietrzyk M 2008 Cent. Eur. J. Phys. 6 26
    [11] Choi D I, Niu Q 1999 Phys. Rev. Lett. 82 2022 doi: 10.1103/PhysRevLett.82.2022
    [12] Wu B, Niu Q 2001 Phys. Rev. A 64 061603(R doi: 10.1103/PhysRevA.64.061603
    [13] Cristiani M, Morsch O, Müller J H, Ciampini D, Arimondo E 2002 Phys. Rev. A 65 063612 doi: 10.1103/PhysRevA.65.063612
    [14] Liu J, Fu L B, Ou B Y, Chen S G, Choi D I, Wu B, Niu Q 2002 Phys. Rev. A 66 023404 doi: 10.1103/PhysRevA.66.023404
    [15] Choi D I, Niu Q 2003 Phys. Lett. A 318 558 doi: 10.1016/j.physleta.2003.09.066
    [16] Trombettoni A, Smerzi A 2001 Phys. Rev. Lett. 86 2353 doi: 10.1103/PhysRevLett.86.2353
    [17] Berg-Sørensen K, Mølmer K 1998 Phys. Rev. A 58 1480 doi: 10.1103/PhysRevA.58.1480
    [18] Holthaus M 2000 J. Opt. B: Quantum Semiclassical Opt. 2 589 doi: 10.1088/1464-4266/2/5/306
    [19] Cerimele M M, Chiofalo M L, Pistella F, Succi S, Tosi M P 2000 Phys. Rev. E 62 1382 doi: 10.1103/PhysRevE.62.1382
    [20] Scott R G, Martin A M, Fromhold T M, Bujkiewicz S, Sheard F W, Leadbeater M 2003 Phys. Rev. Lett. 90 110404 doi: 10.1103/PhysRevLett.90.110404
    [21] Filho V S, Gammal A, Frederico T, Tomio L 2000 Phys. Rev. A 62 033605(R doi: 10.1103/PhysRevA.62.033605
    [22] Hai W H, Lee C H, Chong G S, Shi L 2002 Phys. Rev. E 66 026202 doi: 10.1103/PhysRevE.66.026202
    [23] Li F, Shu W X, Jiang J G, Luo H L, Ren Z Z 2007 Eur. Phys. J. D 41 355 doi: 10.1140/epjd/e2006-00247-3
    [24] Li F, Shu W X, Luo H L, Ren Z Z 2007 Chin. Phys. 16 650 doi: 10.1088/1009-1963/16/3/016
    [25] Li F, Ren Z Z, Luo H L, Shu W X, Wu Q 2007 Commun. Theor. Phys. 48 107 doi: 10.1088/0253-6102/48/1/023
    [26] 李飞, 张冬霞, 李文斌 2011 物理学报 60 120304 doi: 10.7498/aps.60.120304 Li F, Zhang D X, Li W B 2011 Acta Phys. Sin. 60 120304 doi: 10.7498/aps.60.120304
    [27] Li F, Zhang D X, Rong S G, Xu Y 2013 J. Exp. Theor. Phys. 117 800 doi: 10.1134/S1063776113130141
    [28] Li F, He Z J, Li W W 2023 Commun. Theor. Phys. 75 035501 doi: 10.1088/1572-9494/acaef8
    [29] Li F, Li W W, He Z J 2023 Rom. J. Phys. 68 103
    [30] Chong G S, Hai W H, Xie Q T 2004 Phys. Rev. E 70 036213 doi: 10.1103/PhysRevE.70.036213
    [31] 王冠芳, 傅立斌, 赵鸿, 刘杰 2005 物理学报 54 5003 doi: 10.3321/j.issn:1000-3290.2005.11.005 Wang G F, Fu L B, Zhao H, Liu J 2005 Acta. Phys. Sin. 54 5003 doi: 10.3321/j.issn:1000-3290.2005.11.005
    [32] Zhu Q Q, Hai W H, Rong S G 2009 Phys. Rev. E 80 016203 doi: 10.1103/PhysRevE.80.016203
    [33] 王力, 刘静思, 李吉, 周晓林, 陈向荣, 刘超飞, 刘伍明 2020 物理学报 69 010303 doi: 10.7498/aps.69.20191648 Wang L, Liu J S, Li J, Zhou X L, Chen X R, Liu C F, Liu W M 2020 Acta Phys. Sin. 69 010303 doi: 10.7498/aps.69.20191648
    [34] 王青青, 周玉珊, 王静, 樊小贝, 邵凯花, 赵月星, 宋燕, 石玉仁 2023 物理学报 69 010308 doi: 10.7498/aps.72.20222195 Wang Q Q, Zhou Y S, Wang J, Fan X B, Shao K H, Zhao Y X, Song Y, Shi Y R 2023 Acta Phys. Sin. 69 010308 doi: 10.7498/aps.72.20222195
    [35] Ruprecht P A, Edwards M, Burnett K, Clark C W 1996 Phys. Rev. A 54 4178 doi: 10.1103/PhysRevA.54.4178
    [36] Denschlag J H Simsarian, J E , Häffner H, McKenzie C, Browaeys A, Cho D, Helmerson K, Rolston S L, Phillips W D 2002 J. Phys. B 35 3095 doi: 10.1088/0953-4075/35/14/307
    [37] Mellish A S, Duffy G, McKenzie C, Geursen R, Wilson A C 2003 Phys. Rev. A 68 051601(R doi: 10.1103/PhysRevA.68.051601
    [38] Fallani L, Cataliotti F S, Catani J, Fort C, Modugno M, Zawada M, Inguscio M 2003 Phys. Rev. Lett. 91 240405 doi: 10.1103/PhysRevLett.91.240405
    [39] Kagan Y, Surkov E L, Shlyapnikov G V 1997 Phys. Rev. Lett. 79 2604 doi: 10.1103/PhysRevLett.79.2604
    [40] Cornish S L, Claussen N R, Roberts J L, Cornell E A, Wieman C E 2000 Phys. Rev. Lett. 85 1795 doi: 10.1103/PhysRevLett.85.1795
    [41] Kevrekidis P G, Theocharis G, Frantzeskakis D J, Malomed B A 2004 Phys. Rev. Lett. 90 230401 doi: 10.1103/PhysRevLett.90.230401
    [42] Theocharis G, Schmelcher P, Kevrekidis P G, Frantzeskakis D J 2005 Phys. Rev. A 72 033614 doi: 10.1103/PhysRevA.72.033614
    [43] Abdullaev F K, Garnier J 2005 Phys. Rev. A 72 061605(R doi: 10.1103/PhysRevA.72.061605
    [44] He J R, Li H M 2011 Phys. Rev. E 83 066607 doi: 10.1103/PhysRevE.83.066607
    [45] Avelar A T, Bazeia D, Cardoso W B 2009 Phys. Rev. A 79 025602(R doi: 10.1103/PhysRevA.79.025602
    [46] Wang D S, Hu X H, Liu W M 2010 Phys. Rev. A 82 023612 doi: 10.1103/PhysRevA.82.023612
    [47] Beitia J B, García V M P, Vekslerchik V, Konotop V V 2008 Phys. Rev. Lett. 100 164102 doi: 10.1103/PhysRevLett.100.164102
    [48] Arroyo Meza L E, de Souza Dutra A, Hott M B 2012 Phys. Rev. E 86 026605 doi: 10.1103/PhysRevE.86.026605
    [49] Arroyo Meza L E, Souza Dutra A de, Hott M B 2013 Phys. Rev. E 88 053202 doi: 10.1103/PhysRevE.88.053202
    [50] Cardoso W B, Leão S A, Avelar A T, Bazeia D, Hussein M S 2010 Phys. Lett. A 374 4594 doi: 10.1016/j.physleta.2010.09.037
    [51] Wang D S, Song S W, Xiong B, Liu W M 2011 Phys. Rev. A 84 053607 doi: 10.1103/PhysRevA.84.053607
    [52] Wang D S, Song S W, Liu W M 2012 Journal of Physics: Conference Series 400 012078 doi: 10.1088/1742-6596/400/1/012078
    [53] He J R, Yi L 2014 Phys. Lett. A 378 1085 doi: 10.1016/j.physleta.2014.01.050
    [54] Rong S G, Hai W H, Xie Q T, Zhong H H 2012 Chaos 22 033109 doi: 10.1063/1.4733304
    [55] Parker N G, Proukakis N P, Barenghi C F, Adams C S 2004 Phys. Rev. Lett. 92 160403 doi: 10.1103/PhysRevLett.92.160403
    [56] Parker N G, Proukakis N P,Barenghi C F, Adams C S 2004 J. Phys. B 37 S175 doi: 10.1088/0953-4075/37/7/063
    [57] Proukakis N P, Parker N G, Barenghi C F, Adams C S 2004 Phys. Rev. Lett. 93 130408 doi: 10.1103/PhysRevLett.93.130408
    [58] Gardiner S A, Jaksch D, Dum R, Cirac J I, Zoller P 2000 Phys. Rev. A 62 023612 doi: 10.1103/PhysRevA.62.023612
    [59] Machholm M, Pethick CJ, Smith H 2003 Phys. Rev. A 67 053613 doi: 10.1103/PhysRevA.67.053613
    [60] Goldstein E V, Meystre P 1999 Phys. Rev. A 59 1509 doi: 10.1103/PhysRevA.59.1509
    [61] Goldstein E V, Meystre P 1999 Phys. Rev. A 59 3896 doi: 10.1103/PhysRevA.59.3896
    [62] Ling H Y 2001 Phys. Rev. A 65 013608 doi: 10.1103/PhysRevA.65.013608
    [63] 刘式适, 刘式达 2012 物理学中的非线性方程 (第二版)(北京: 北京大学出版社)第68页 Liu S K, Liu S D 2012 Nonlinear Equations in Physics (2nd edition) (Beijing: Peking University Press) p68
    [64] Li F, Zhou B J, Shu W X, Luo H L, Huang Z Y, Tian L 2008 Eur. Phys. J. D 50 75 doi: 10.1140/epjd/e2008-00201-5
    [65] Stavans J, Heslot F, Libchaber A 1985 Phys. Rev. Lett. 55 596 doi: 10.1103/PhysRevLett.55.596
    [66] Bishop A R, Forest M G, McLaughlin D W, Overman II E A 1986 Physica D 23 293 doi: 10.1016/0167-2789(86)90137-5
  • 加载中
图( 7)
计量
  • 文章访问数:  30
  • HTML全文浏览数:  30
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-11-18
  • 刊出日期:  2025-06-05

运动光格中非线性作用随时空变化的玻色-爱因斯坦凝聚体的混沌时空动力学

    通讯作者: E-mail: lifeipaper@163.com.; 
  • 湖南第一师范学院物理系, 长沙　410205
  • 收稿日期:  2024-11-18

摘要: 本文研究运动光格中非线性作用随时空变化的玻色-爱因斯坦凝聚体的混沌时空动力学. 在运动光格势强度和非线性作用调制强度较小的情况下, 系统满足微扰条件, 将Melnikov函数法应用于理论分析, 得到了系统的Melnikov时空混沌判据. 当系统不满足微扰条件时, 数值模拟表明, 对于原子间呈吸引作用的玻色-爱因斯坦凝聚体, 非线性作用调制强度的增大可以加深系统的时空混沌程度. 在某些参数区域, 非线性作用调制频率对系统时空动力学行为具有重要影响. 进一步的数值研究结果揭示, 较大的化学势不仅可以抑制吸引系统的时空混沌, 还可以抑制排斥系统的时空混沌. 基于以上研究结果, 在实验中可以根据需要规避或引发玻色-爱因斯坦凝聚系统的时空混沌.

English Abstract

    全文HTML

    1.   引　言

    • 玻色-爱因斯坦凝聚体(BEC)在实验中的实现[1,2]激发了学界研究BEC的热情. 此后, 该领域的研究成果大量涌现. 在这些研究工作中, 光学晶格中的BEC因其便于研究周期势中相干物质的动力学行为而引起了越来越多的关注. 光学晶格可以通过两个或多个激光束的干涉来创建[3]. 1996年, Dahan等[4]成功地将BEC加载到了光学晶格中. 两年后, Anderson和Kasevich [5]也实现了类似的实验. 此后, 研究者们对静态或移动光学晶格中BEC的系列物理现象进行了实验和理论研究, 如量子相变[5–7]、量子计算和量子信息[8]、布洛赫振荡[9,10]、物质波输运[11]、朗道-齐纳隧穿[5,12–15]、凝聚体基态加速[11,16–20]、混沌[21–32]、孤子[33,34]以及BEC对弱移动光学势的响应[35]. 2002年, Denschlag等[36]发表了系列关于移动光学晶格中BEC的实验结果. 2003年, Mellish等[37]提出了一种通过非绝热方法将BEC加载到弱运动光学晶格基态的方案; Fallani等[38]报道了在一维运动光晶格中膨胀的BEC的透镜效应. 由于BEC系统在光学晶格中展现出了丰富的动力学特性, 这个领域仍存在许多悬而未决的问题需要研究.

      众所周知, BEC动力学行为在很大程度上取决于BEC原子间非线性相互作用是吸引力还是排斥力及其强弱[39,40]. 实验技术的进步使得可以通过Feshbach共振技术快速有效地改变原子间非线性相互作用. 目前, 不但已经实现了时间调制的非线性相互作用[39–41], 而且还实现了空间调制的非线性相互作用[42,43].

      单独对非线性作用进行空间调制的过程是需要时间的, 在这个过程中非线性作用有可能随着时间发生改变; 而单独对非线性作用进行时间调制的过程中, 非线性作用也有可能因空间位置不同而不同. 这两种情况都意味着非线性作用可以同时随时空变化. 值得关注的是, 单独对非线性相互作用进行时间或空间调制的成功, 为通过技术结合实现同时对非线性相互作用进行时间和空间调制提供了可能, 这也为操控BEC系统开展各类研究提供了更多的选择. 所以, 非线性作用随时空变化的BEC在研究物理系统动力学行为方面必然具有独特的优越性.

      事实上, 文献[44–54]在BEC的研究中引入同时随时间和空间变化的非线性相互作用, 并详细讨论了BEC的一些物理性质. 非线性相互作用随时间和空间变化的系统必定具有非常独特和有趣的性质, 但研究相对较少[44]. 本文将同时随时间和空间变化的非线性相互作用引入BEC, 并研究其混沌时空动力学行为特点.

      本文结构如下: 第2节运用Melnikov函数法对BEC系统进行理论分析, 得到系统的Melnikov时空混沌判据; 第3节对BEC系统不满足微扰条件的情形进行数值模拟, 讨论了系统时空混沌行为及其控制; 第4节给出了文章总结和一些讨论. 本文的研究基于非线性薛定谔方程(Gross-Pitaevskii(GP)方程), 它的解通常是宏观量子波函数. 由宏观量子波函数演化导致的混沌又被称为宏观量子混沌[22].

    2.   微扰系统的Melnikov混沌判据

    • 描述绝对零度附近BEC动力学演化特征的宏观量子波函数满足平均场GP方程 [55–57]

      其中$\hbar $是普朗克常量, $m$是原子质量, $\mu $是化学势, 其通常是温度和BEC原子总数的函数, $g$是考虑了玻色子产生的平均场效应的非线性作用参数, $g \gt 0$表示原子间呈排斥作用, $g \lt 0$表示原子间呈吸引作用.

      考虑具有如下形式的外部囚禁势${V_{{\text{ext}}}}$[30,36,58]:

      很明显, 囚禁势${V_{{\text{ext}}}}$为一运动光格势, 由沿$x$轴相向传播的两束激光形成. $k$为激光波矢, 运动光格势的速度被确定为$v = \delta /(2 k)$[36], $\delta $是两个激光束之间的频率差, $ {\varOmega _1}(t) $和$ {\varOmega _2}(t) $分别是两束激光的拉比频率, $ \varDelta $是共振失谐量. 考虑$ {\varOmega _1}(t) = {\varOmega _2}(t)= {\varOmega _0} $的情形, 囚禁势改写为$ {V_{{\text{ext}}}} = - I[1 - \cos (2 kx + \delta t)] $, 其中$ I = \hbar \varOmega _0^2/(2\varDelta ) $. 本文将$ I = \hbar \varOmega _0^2/(2\varDelta ) $作为光格势的强度. 采取与文献[59]一样的处理方式, 忽略常数项, 囚禁势被简化为$ {V_{{\text{ext}}}} = I\cos (2 kx + \delta t) $. 由此可得如下GP方程:

      对GP方程采用行波解已被证明是研究BEC的有效手段[60–62]. 在本文考虑的系统中, 由于凝聚体随运动光格势移动, 所以关注GP方程的行波解, 并将其设为

      则凝聚原子总数$ N = {\displaystyle\int_{ - \infty }^{ + \infty } {\left| {A(\xi )} \right|} ^2}{\text{d}}\xi $. 其中$ A(\xi ) $和$ B(\xi ) $为实函数, $ \alpha $和$ \beta $为待定实数, 时空变量$ \xi = x + vt $[30,36], 这意味着行波与光格势运动速度相同. 行波解(3)表明BEC系统中的物质波类似于布洛赫波.

      将解(3)式代入方程(2)后, 引入以下无量纲参量:

      可得如下方程组:

      方程(5)和(6)中$ A $已经被以$ \sqrt k $为单位归一化. 对(6)式积分可得$ {\text{d}}B/{\text{d}}\zeta {=}C/{A^{2}}-(\tilde v/2 + \tilde \alpha ) $[32], 其中$ C $为由初始条件决定的积分常数. 显然, $ B $对时空变量$ \zeta $的一阶导数为$ A $的非线性函数, 同时亦隐含$ B $是时空变量的非线性函数. 令$ B(\xi ) + \alpha x + \beta t = \theta $, 则BEC波函数位相对空间坐标$ x $的一次导数为$ {\text{d}}\theta /{\text{d}}x = k(C/{A^{2}}-\tilde v) $. 根据量子力学基本原理, 对于质量为$ m $的粒子, 其超流速度为$ \hbar /m $乘以粒子波函数位相对空间坐标的一次导数. 所以, 在本文考虑的一维BEC系统中, 凝聚原子的超流速度为$ (\hbar /m){\text{d}}\theta /{\text{d}}x = \hbar k(C/{A^{2}}-\tilde v)/m $. 显然, 波函数位相对空间坐标的一次导数对BEC原子的超流速度具有决定性作用.

      根据文献[32], 适当选取初始条件可使$ C = 0 $, 则$ {\text{d}}B/{\text{d}}\zeta = - (\tilde v/2 + \tilde \alpha ) $. 这表明$ B(\zeta ) $也可以是时空变量$ \zeta $的一次函数. 调节系统参数可以使

      成立[30], 从而消除方程(5)中的位相参数, 方程中将只出现原GP方程参数和运动光格参数. 与位相参数相比, 这些参数相对容易获取. 将(7)式代入方程(5)后化简得

      (8)式是一个典型的杜分方程[63]. 因此, 接下来将用杜分方程分析方法研究系统的时空动力学行为. 如引言所述, 考虑时空变化的非线性相互作用, 设$ \tilde g = {\tilde g_0} + {\tilde g_1}\sin (\omega \zeta ) $, $ {\tilde g_0} $为无调制时的非线性作用参数, $ {\tilde g_1} $为非线性作用调制强度, $ \omega $为调制频率. 对于微扰情形, $ {\tilde g_1} $是一个小量. 随后可得

      在理论分析中, 令$ {\tilde g_1} \sim \tilde I $, 这意味着与它们同一量级的项可以视为对系统的微扰. 因此, 方程(9)可以写成:

      根据参考文献[63], 当$ \tilde \mu - {\tilde v^2}/4 > 0 $和$ {\tilde g_0} \gt 0 $时, 可得(10)式无扰情形的异宿解:

      其中$ {\zeta _0} $是由初始条件决定的常数.

      众所周知, Melnikov分析法被认为是分析混沌的标准方法, 其提供一种有效的判据来近似确定各种动力学系统的混沌阈值(Melnikov分析法是一级近似方法). Melnikov分析法常被用于判断动力学系统中同宿和异宿混沌的存在与否.

      在理论分析中研究系统的异宿混沌. 根据Melnikov分析法, 系统的Melnikov函数可以表示为

      将解(11)式应用于Melnikov函数(12)式并计算积分, 可得一个显性的Melnikov函数:

      Melnikov函数也称为Melnikov距离, 用于测量庞加莱截面上稳定流形和不稳定流形之间的距离. 如果Melnikov函数存在简单零点, 那么异宿点附近区域内的稳定流形和不稳定流形将发生横截相交, 从而导致Smale马蹄混沌的出现[26,60].

      具有简单零点的Melnikov函数必须满足以下条件[26,64]:

      根据条件(14)式, 可得

      此处分析系统参数满足条件(15)式和(16)式的可能性. 化学势通常是温度和凝聚原子总数的函数, 在实际系统中, 两者都是可变的. 通过精确地调节激光波矢$ k $和两束激光之间的频率差$\delta $, 可以有效地调节光格势的速度$ \tilde v $; 激光强度$ \tilde I $很容易改变; 频率$ \omega $可以通过调节形成Feshbach共振的激光频率进行调制. 所以, 根据上述讨论, 可以找到一组满足条件(15)式和(16)式的系统参数, 使庞加莱截面上的稳定流形和不稳定流形发生横截相交, 从而出现Smale马蹄混沌. 对于实际系统而言, 可以依据条件(15)式和(16)式来引发或规避混沌. 在混沌理论中, 通常把条件(16)式称为Melnikov混沌判据[26,64]. 对于本文考虑的系统而言, 也可以把(15)式和(16)式称为Melnikov时空混沌判据.

      有意思的是, $ (\tilde \mu - {\tilde v^2}/4) $和$ {\tilde g_0} $的正负决定系统无扰解是异宿解还是同宿解, 系统受扰情形对应地存在出现异宿或同宿混沌的可能性. 前面的理论分析讨论了系统的异宿混沌. 同宿混沌的讨论与此类似, 本文不再赘述.

    3.   非微扰数值计算

    • 在第2节中应用Melnikov分析法从理论上研究了BEC系统的异宿混沌, 获得了系统微扰情形的Melnikov时空混沌判据. 前面已经指出, Melnikov分析法是一级近似方法. 当系统不能满足微 扰条件时, 上述理论方法将无效. 在这种情况下, 可以通过数值模拟画出系统的相图、庞加莱截面 或$ A(\zeta ) $时空演化曲线来分析BEC的时空动力学行为. 根据非线性动力学理论, 如果系统处于规 则(周期性)状态, 则相图上出现一条或多条相轨道, 庞加莱截面由一个或多个点组成, $ A(\zeta ) $时空 演化曲线形状呈简单的周期性重复; 当系统处于准周期状态时, 相图上出现数量稍多, 彼此简单交叉、结构并不复杂的相轨道分布图, 庞加莱截面为闭合曲线, $ A(\zeta ) $时空演化曲线形状仍呈周期性 重复; 当系统处于混沌状态时, 相轨道彼此交叉, 形成复杂的相空间结构, 难以确定轨道的周期性, 对应的庞加莱截面由随机分布的点组成, 形成混 沌海, $ A(\zeta ) $时空演化曲线形状不再呈周期性重复. 在多数情况下, 根据相图、庞加莱截面和$ A(\zeta ) $时空演化曲线中的任意一种图像就能确定系统的动力学状态. 在实际研究中, 可以基于简单、明了、易 辨的原则选用其中的某一种图像对系统的时空动力学状态展开讨论. 但是, 在某些临界条件下, 单独根据相图、庞加莱截面和$ A(\zeta ) $时空演化曲线中的某一种图像无法确定系统的动力学状态, 就需要综合至少两种图像展示的特征才能够做出科学的判断.

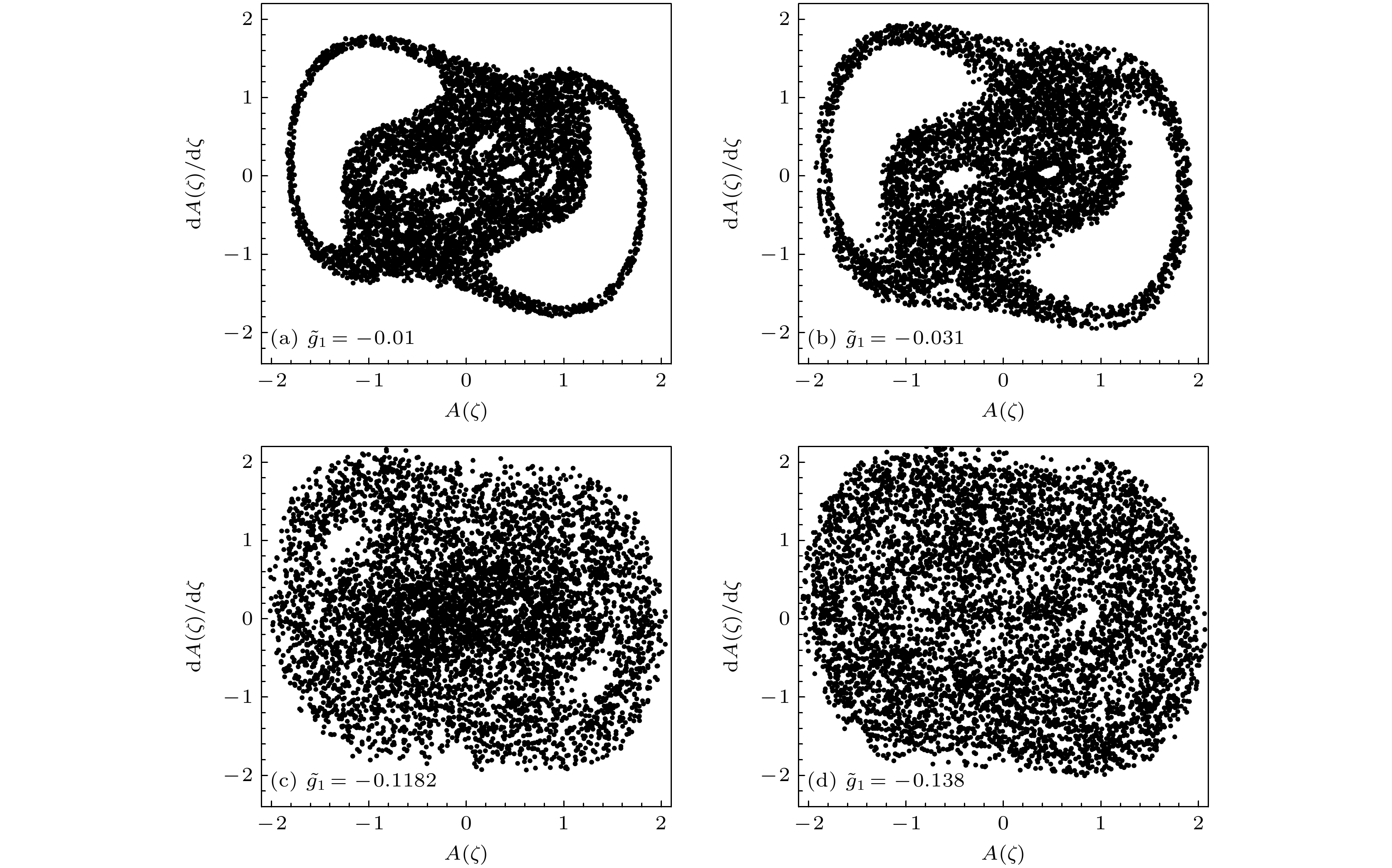
      我们感兴趣的是系统的稳态, 因此在画图时忽略了从$ \zeta = 0 $到$ \zeta = 500 $的瞬态过程. 设参数和初始条件为$ \tilde \mu = 0.8 $, $ \tilde v = 2.0 $, $ \tilde I = 0.23 $, $ {\tilde g_0} = - 0.75 $, $ \omega = 0.4 $, $ A(0) = 0.26 $, $ \dot A(0) = 0 $, 对于不同的$ {\tilde g_1} $值, 图1所示为$ (A, \dot A) $平面上的一组庞加莱截面(取点间隔为$ \Delta \zeta = {\text{π}} $). 当$ {\tilde g_1} = - 0.01 $时, 从图1(a)可以看出, 庞加莱截面上的点在有限区域内呈随机分布, 形成混沌海, 混沌海包围着两个大岛和几个小岛; 当$ {\tilde g_1} $的值被调制到$ - 0.031 $时, 部分小岛消失, 只剩下两个小岛和两个大岛, 如图1(b)所示. 当$ {\tilde g_1} $值被进一步调制到$ - 0.1182 $时, 两个小岛近乎消失, 两个大岛边界已经模糊且所占区域大幅减小, 见图1(c). 当$ {\tilde g_1} $被调制到$ - 0.138 $时, 图1(d)显示, 所有岛屿都消失, 混沌海连成了一个整体. 必须指出的是, 混沌海中岛屿附近可以存在非混沌运动, 即周期运动或准周期运动. 岛屿面积不断缩小直至消失, 说明岛屿附近的非混沌运动在逐步转变为混沌运动; 与此同时, 混沌运动不断向新的区域扩散, 导致混沌海面积增大, 庞加莱截面上点的分布更加杂乱无章, 这是一个混沌程度不断加深的过程. 本文中混沌程度是指庞加莱截面上点分布的无序性程度以及混沌海在庞加莱截面上所占面积大小. 上述庞加莱截面的演化表明, 随着非线性作用调制强度$ |{\tilde g_1}| $的增大, BEC系统时空混沌区域不断扩大, 混沌程度不断加深, 最后系统进入到了一个全域混沌的状态.

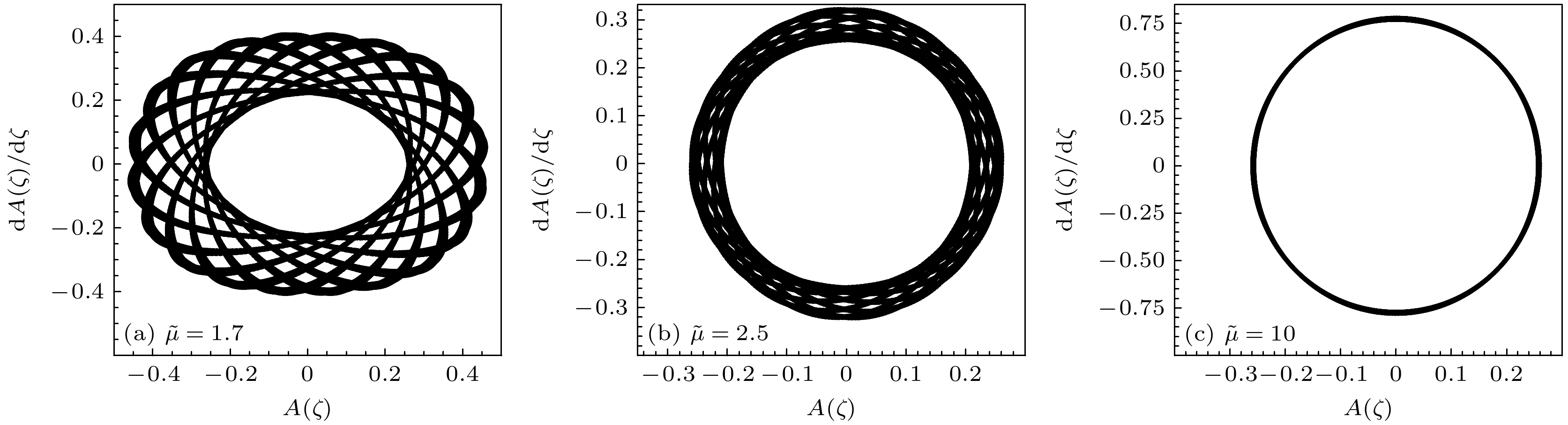
      文献[21]指出, 混沌可以影响BEC的稳定性, 甚至会导致BEC塌缩. 在数值模拟过程中, 研究发现增大化学势$ \tilde \mu $可以有效抑制混沌. 考虑图1(d)的情形. 保持其他参数和初始条件与图1(d)相同, 增大化学势$ \tilde \mu $到$ 1.7 $, 相图上出现了典型的准周期轨道(多周期轨道), 见图2(a), 这意味着混沌已经消失, 系统进入了准周期状态(多周期状态); 当化学势$ \tilde \mu $增至$ 2.5 $, 图2(b)显示相平面上的准周期轨道呈紧密分布, 所占相平面区域明显缩小, 这体现出系统向单周期状态转变的趋势; 当化学势$ \tilde \mu $增至$ 10 $时, 图2(c)的相平面上只出现了一条周期轨道, 系统进入一个时空单周期状态. 图2中相图的演化表明, 较大的化学势会抑制系统的时空混沌, 并使系统由时空混沌状态经准周期路径进入时空单周期规则状态. 准周期路径是混沌状态和规则状态之间转化的重要途径之一 [65,66].

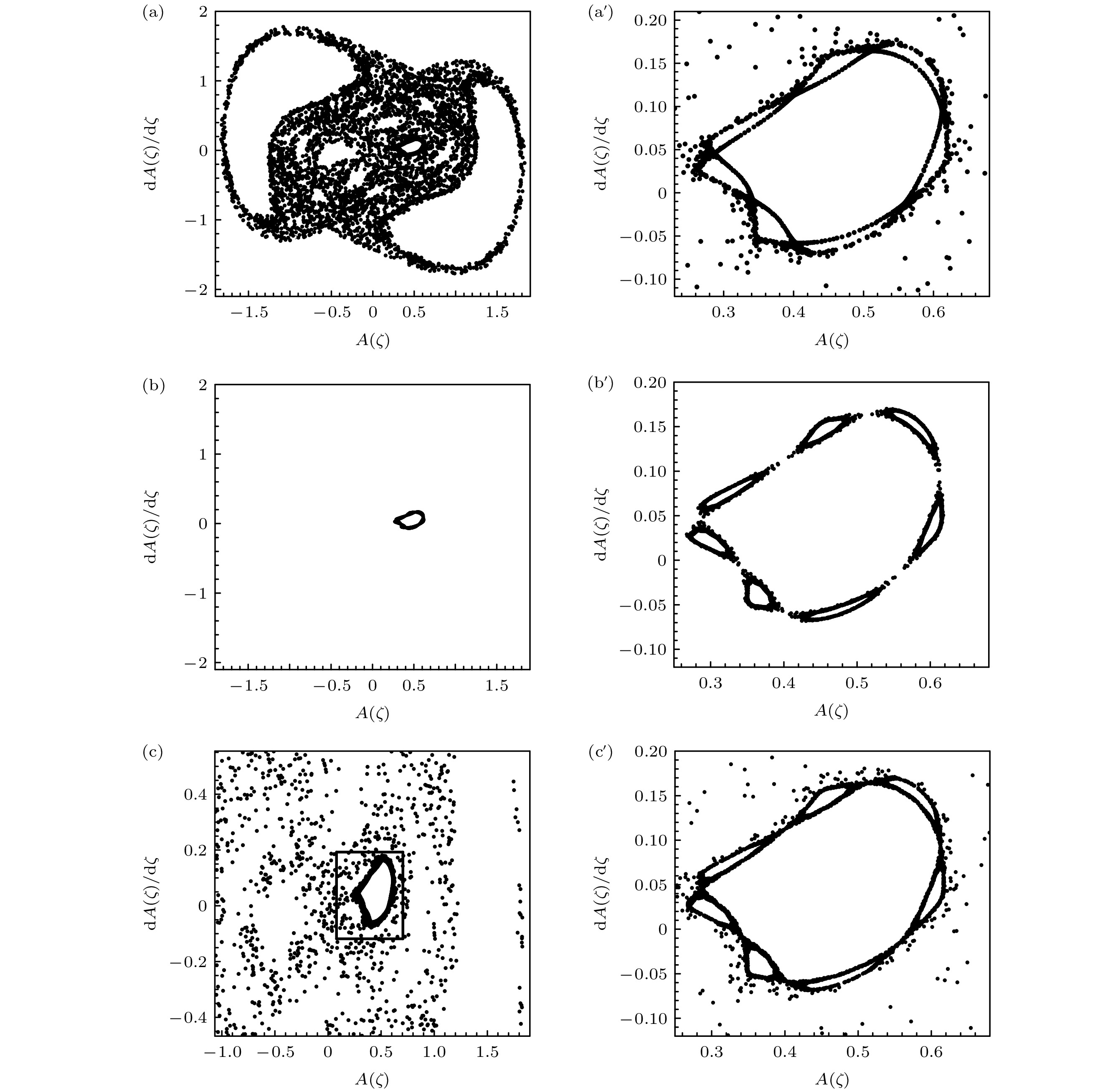
      现在讨论非线性作用调制频率$ \omega $对系统的影响. 依然考虑图1(d)的情形. 保持其他参数和初始条件与图1(d)相同, 使调制频率$ \omega $从$ 0.4 $增至30. 在这个过程中, 每隔$ \varDelta \omega = 0.001 $画出一个庞加莱截面. 每一个$ \omega $值对应的庞加莱截面都表明系统处于时空混沌状态. 当$ \omega $增至$ 29.999 $的时候, 系统庞加莱截面与图1(a)的情形相似, 见图3(a). 对图中小框内的部分庞加莱截面结构放大后发现, 小框内的环由7个靠得很近的混沌岛组成, 见图3(a'). 有意思的是, 当$ \omega $进一步增至$ 30 $的时候, 庞加莱截面上的绝大多数点都收缩到了7个混沌岛边界线上, 只有极少数点分布在7个混沌岛周围, 见图3(b), (b'). 图3(b')是图3(b)的放大图. 与图3(a)中庞加莱截面混沌海所占面积相比, 图3(b)中7个混沌岛和点的分布范围大幅减小. 这说明BEC原子分布范围大幅收缩. 但是, 当调制频率$ \omega $由$ 30 $小幅增至$ 30.00001 $后, 庞加莱截面上的点即从7个混沌岛边界线及附近扩散到了大片区域, 见图3(c). 对图3(c)中小框内图形结构放大后发现, 7个混沌岛依然存在, 并未融合在一起, 各混沌岛的大小和形状与图3(a'), (b')的情形基本相同, 差别不显著, 见图3(c'). 图3中庞加莱截面的演化表明, 在某些参数区域内, BEC系统的时空动力学行为对调制频率$ \omega $十分敏感. 调制频率$ \omega $的细微变化即可使系统时空动力学行为发生显著改变.

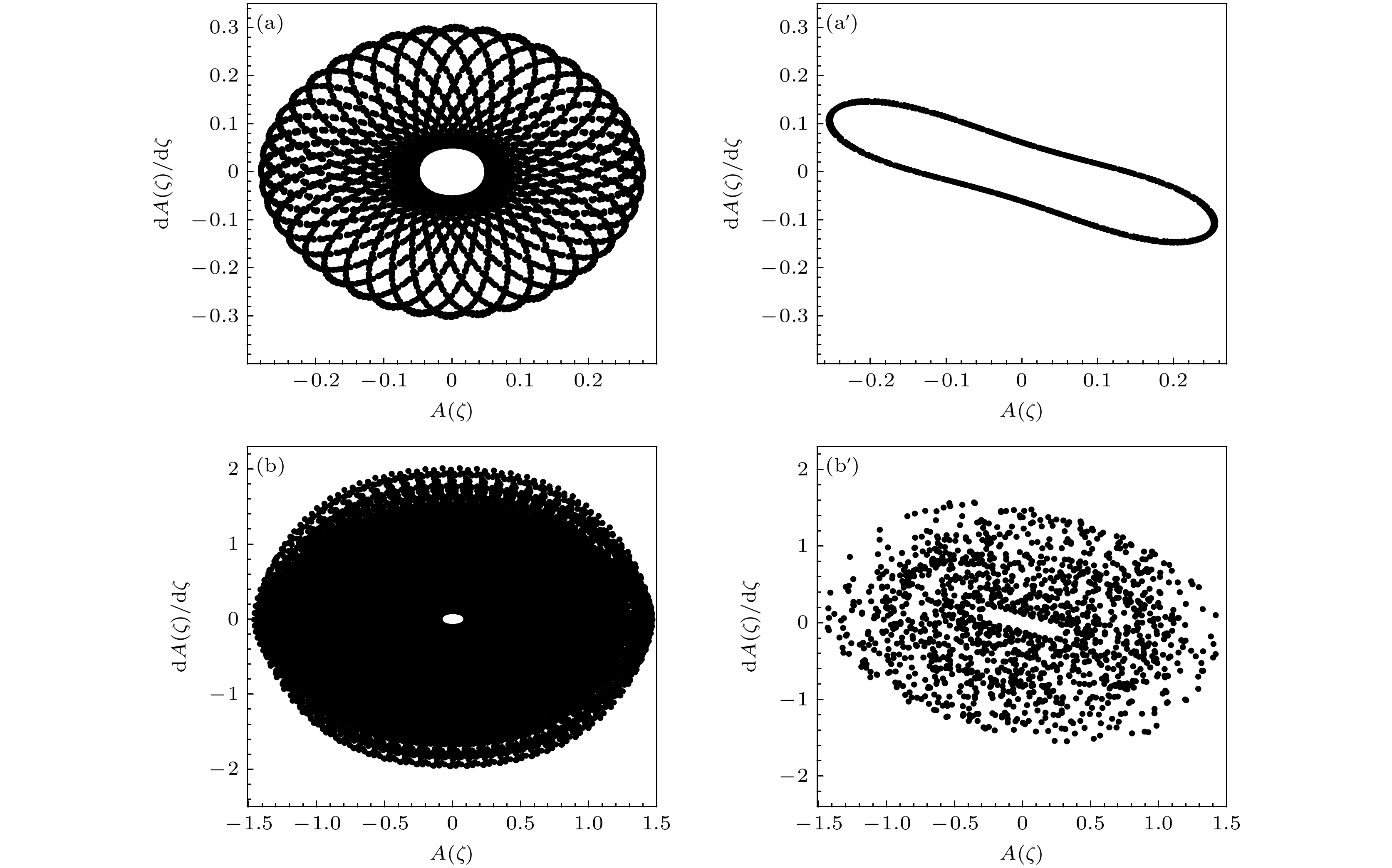
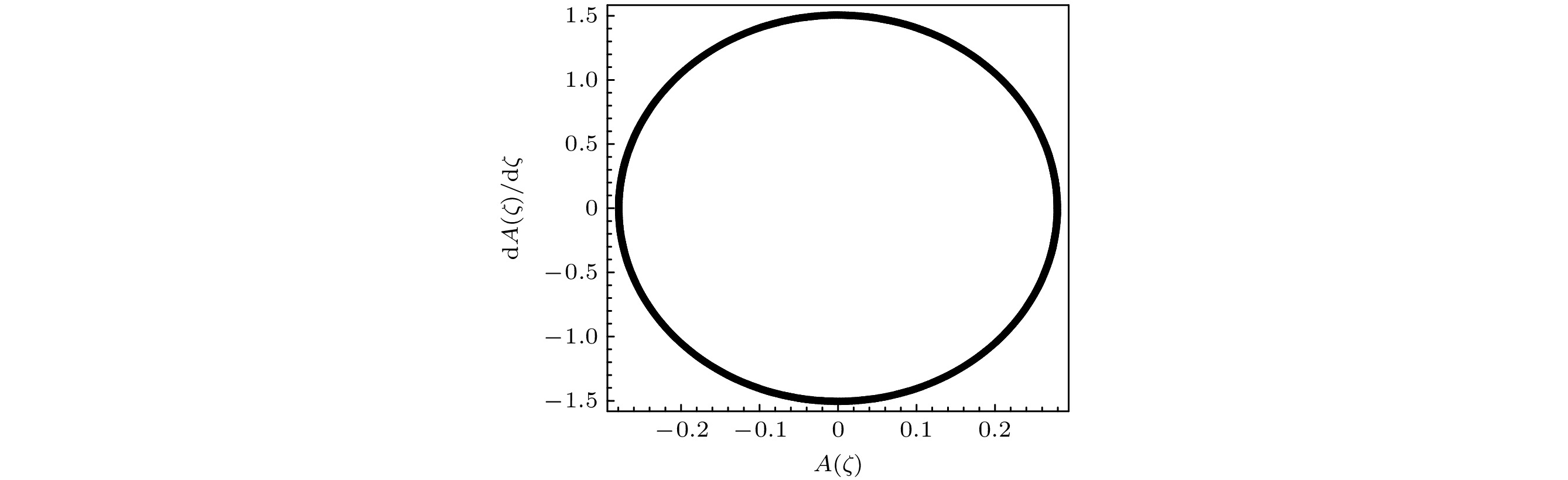
      在上述参数条件下, 调制$ \omega $无法实现系统在混沌和非混沌状态之间的转变. 但是, 数值模拟结果表明, 改变参数条件后, 通过调制$ \omega $可以实现这种转变. 另设参数和初始条件为$ \tilde \mu = 2.11 $, $ \tilde v = 2.0 $, $ \tilde I = 0.25 $, $ {\tilde g_0} = {\tilde g_1} = - 0.7 $, $ A(0) = 0.28 $, $ \dot A(0) = 0 $, 我们对不同的$ \omega $值画出了系统的相图和庞加莱截面. 当$ \omega = 1 $时, 图4(a)中的相图和图4(a')中对应的庞加莱截面都表明系统处于典型的准周期(多周期)状态. 当$ \omega $增至$ 2.2 $时, 图4(b)显示相平面上的相轨道呈密集分布, 难以确定系统是处于混沌状态还是准周期状态, 但是从图4(b')中对应的庞加莱截面上出现的一片混沌海可以断定此时系统已经从准周期状态进入混沌状态. 图4表明, 在某些参数条件下, 调制频率$ \omega $的变化可以实现系统在混沌状态和准周期态(非混沌态)之间的转变. 与图2的情形类似, 保持图4(b)中的参数和初始条件不变, 将化学势$ \tilde \mu $增至$ 30 $, 混沌亦会被彻底抑制, 相图中只出现一条周期轨道, 见图5.

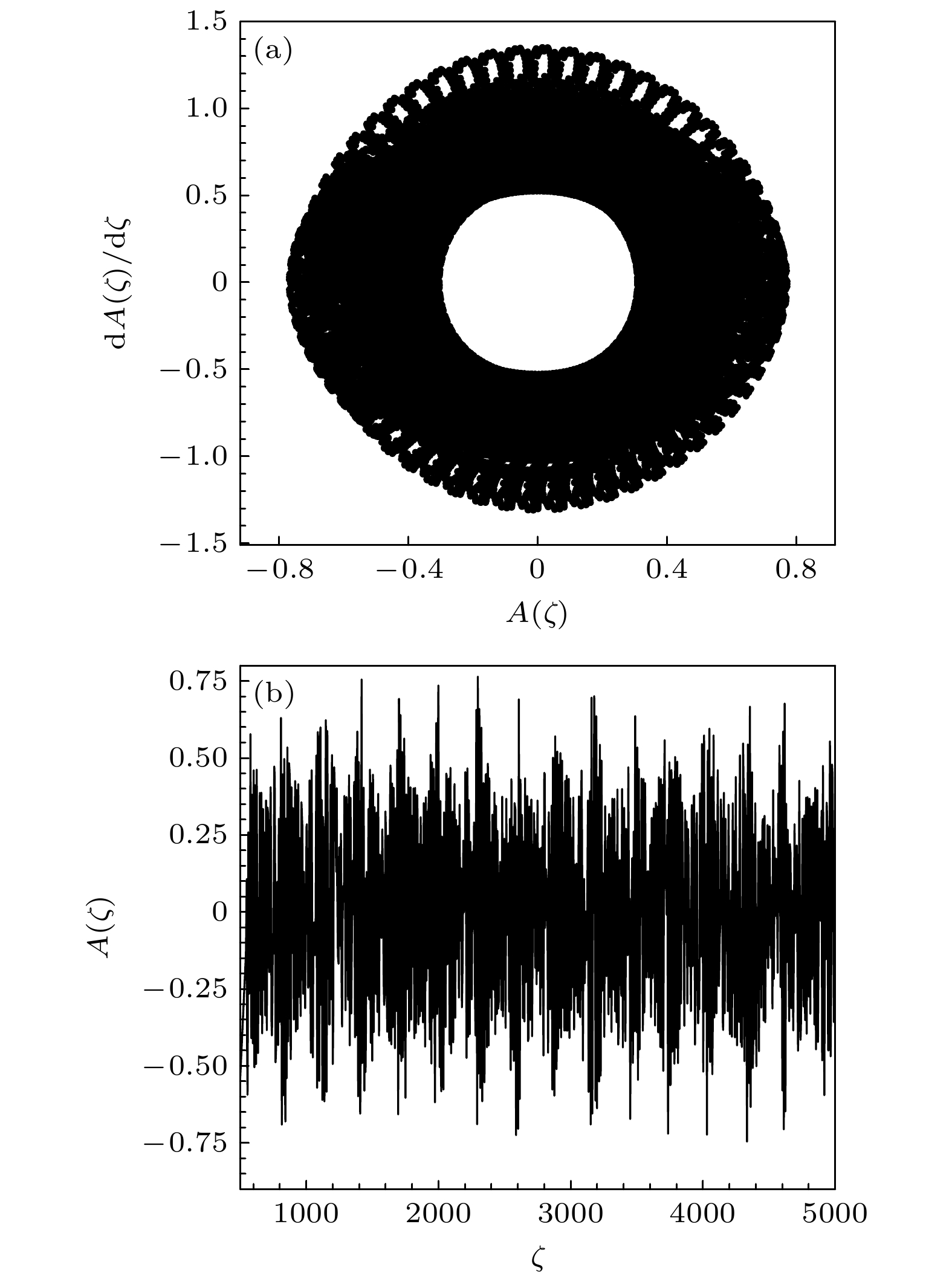
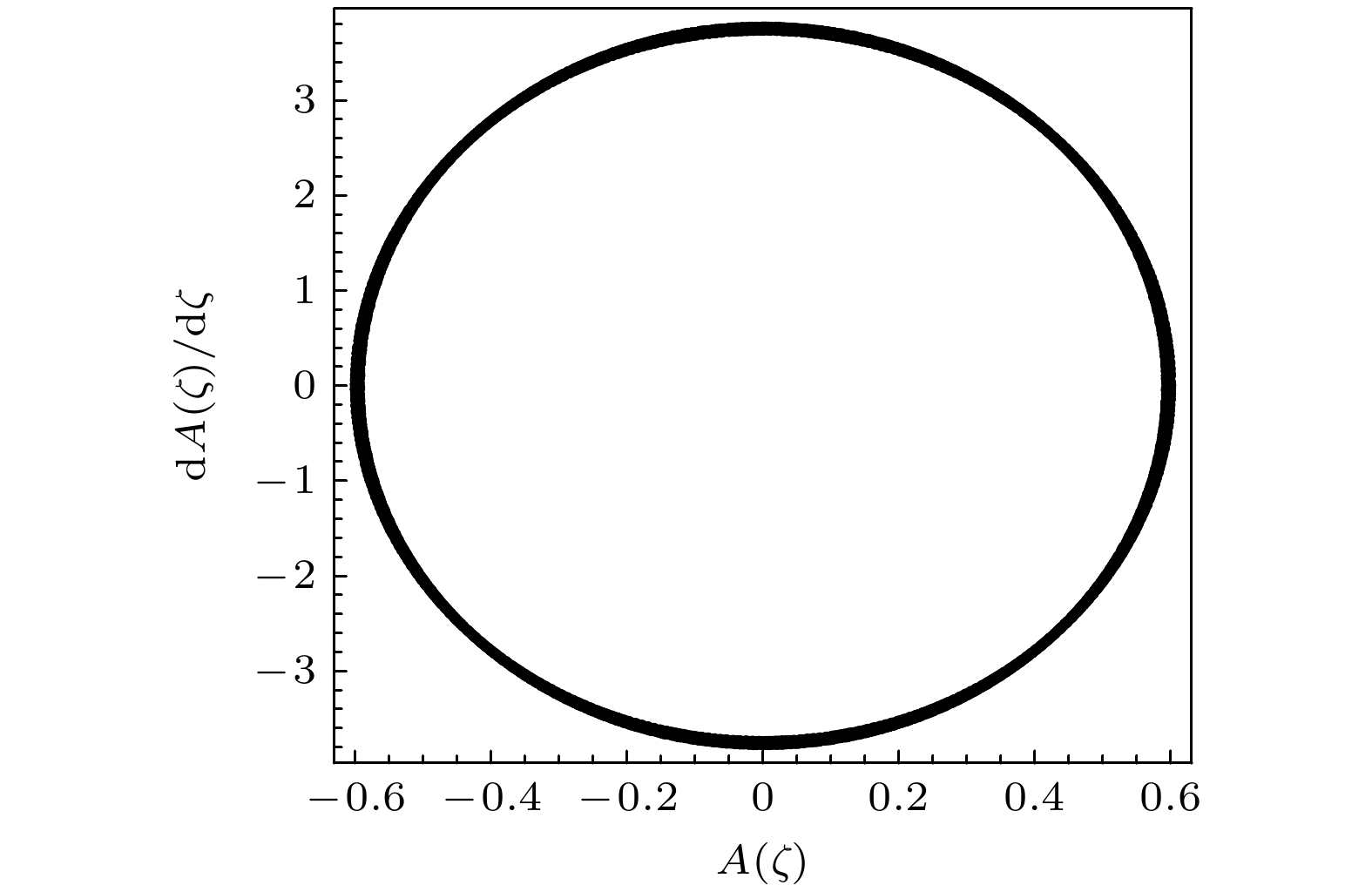
      上文对原子间呈吸引作用的BEC系统的时空动力学特征进行了数值讨论. 此处考虑原子间呈排斥作用的情形. 设定参数和初始条件为$ \tilde \mu = 3 $, $ \tilde v = 1 $, $ \tilde I = 0.9 $, $ {\tilde g_1} = 0.6 $, $ {\tilde g_0} = 0.7 $, $ \omega = 1.2 $, $ A(0) = 0.6 $, $ \dot A(0) = 0 $, 图6所示为系统的相图和相应的时空演化曲线, 从相图展示的清晰特征和相应的$ A(\zeta ) $时空演化曲线可知系统处于混沌状态. 数值模拟显示, 与吸引系统一样, 大化学势能有效抑制混沌; 保持图6中其他参数和初始条件不变, 仅把$ \tilde \mu $增至40, 只有一条周期轨道出现在相平面上(见图7), 混沌完全消失, 这表明BEC系统处于时空单周期状态.

    4.   结　论

    • 本文研究了运动光格中具有时空变化非线性作用的BEC系统的混沌时空动力学. 混沌通常被认为与BEC的稳定性和塌缩有关[21]. 因此, 研究BEC中的混沌具有重要意义. 对于微扰系统, 采用Melnikov方法进行理论分析, 得到Melnikov混沌判据. 根据该判据, 可以得到微扰系统出现异宿混沌的条件.

      当系统不满足微扰条件时, 庞加莱截面的演化表明, 随着非线性作用调制分量强度的增大, 系统时空混沌程度不断加深. 在不同的参数区域内, 调制频率$ \omega $对系统行为影响是不同的. 在某些参数区域内, BEC系统的时空动力学行为对调制频率$ \omega $十分敏感, $ \omega $的细微变化即可使系统时空动力学行为发生显著改变; 在另外的一些参数区域内, 改变调制频率可以实现系统在混沌态和非混沌态之间的转变. 数值模拟揭示, 较大的化学势不仅可以抑制吸引系统的混沌, 还可以抑制排斥系统的混沌.

      既然随时间或空间周期(余弦和正弦)变化的非线性作用已经在实验上得到实现, 那么随着实验技术的进步, 通过技术上的结合, 同时随时间和空间作周期(余弦和正弦)变化的非线性作用必定可以实现, 这将极大地推动玻色-爱因斯坦凝聚领域的研究. 非线性作用随时空变化的系统无疑具有独特且有趣的物理性质, 但迄今为止对此类系统的研究相对较少, 成果不多[44]. 因此, 这个领域内还有很多研究工作可做.

    参考文献 (66)

目录

/

返回文章
返回