量子纠缠是量子物理中最为独特的现象之一, 它揭示了量子世界与经典物理的根本区别. 自爱因斯坦、波多尔斯基和罗森提出EPR佯谬以来, 量子纠缠的研究引发了对量子力学基础的广泛探讨. 贝尔不等式的实验验证进一步确认了纠缠现象的真实性, 并加深了我们对这一非经典现象的理解^[1-4]. 尽管量子纠缠在微观尺度上的实验验证已经十分成熟^[5,6], 但在宏观系统中, 纠缠常常表现得极为微弱, 给观测带来了巨大挑战^[7-11]. 尤其是当纠缠态的某一分量非常小时, 实验设备的误差可能掩盖这些微弱信号, 使其难以检测. 弱纠缠态的检测因此成为了量子信息领域的重要课题. 在多个领域, 弱纠缠的探测具有潜在的重大应用. 例如, 在生物系统中, 有研究推测生物分子可能在某些条件下产生量子纠缠, 这可能揭示量子效应在生命过程中扮演的角色^[12-14]. 同样, 在宇宙学和引力波研究中, 弱纠缠的存在可能为我们理解量子力学与引力的结合提供关键线索^[15-19]. 成功探测这些微弱的量子纠缠现象, 能够帮助我们在复杂系统中发现新的量子效应, 推动量子物理和其他学科的发展.

为了解决弱纠缠检测中的难题, 最近提出了一种新的方法, 即基于量子导引的弱纠缠判据^[20]. 这种方法通过放大微弱的纠缠信号, 能够在设备精度有限的情况下有效识别弱纠缠态. 与传统的纠缠检测方法相比, 基于量子导引的弱纠缠判据对微弱纠缠信号更加敏感, 尤其是在资源受限的实验条件下, 表现出明显的优势.

本文在线性光学实验平台上对基于量子导引的弱纠缠判据进行了实验验证. 实验结果显示, 该方法在检测微弱纠缠态方面具有很高的灵敏度, 验证了其理论预测的正确性, 并展示了其在更广泛量子系统中的应用潜力.

量子导引是一种量子非局域性现象, 描述了在量子纠缠体系中, 一个子系统通过选择性测量能够影响另一个远程子系统的状态. 这一现象不仅在理论研究中具有重要意义, 在量子信息技术中也展现了广泛的应用潜力. 基于量子导引的弱纠缠判据考虑的是一类两量子比特纠缠纯态的导引场景, 具体过程如下. 由量子比特A和量子比特B组成的一个两比特量子态$ \rho^{{\mathrm{A B}}}=|\psi\rangle\langle\psi| $可以表示为

其中$ \gamma $是影响纠缠强度的参数(0<$\gamma$<1). 这个量子态也可以在不同的基矢下进行展开, 例如, 当A在$ \left\{|+\rangle, |-\rangle\right\} $基下展开($ |\pm\rangle=\dfrac{1}{\sqrt{2}}(|0\rangle\pm|1\rangle) $), 该量子态可以写为

其中

而当A在$ \{|\varepsilon\rangle, \left|\varepsilon^{\perp}\right\rangle\} $基下展开,

其中$ \varepsilon\in(\pi/4, \pi/2) $, 这个量子态又可以写为

其中

基于前面描述的不同展开形式, 可以进一步定义具体的测量操作. 在量子比特A的测量过程中, 可以选择在两个不同的基下进行测量——$ |+\rangle $, $ |-\rangle $基或者$ |\varepsilon\rangle $, $ |\varepsilon^\perp\rangle $基. 无论在哪个基下, 测量结果都会是+1或–1. 具体而言, 当量子比特A在$ |+\rangle $, $ |-\rangle $基下进行测量时, 测得+1的概率为$ p_+ $, 此时量子比特B会被投影到态$ |\chi_+\rangle $, 对应的投影成功概率记为$ {\cal{P}}_1 $; 测得–1的概率为$ p_- $, 此时量子比特B会被投影到态$ |\chi_-\rangle $, 对应的投影成功概率记为$ {\cal{P}}_2 $. 类似地, 当量子比特A在$ |\varepsilon\rangle $, $ |\varepsilon^\perp\rangle $基下进行测量时, 测得+1的概率为$ p_\varepsilon $, 此时量子比特B会被投影到态$ |\chi_\varepsilon\rangle $, 对应的投影成功概率记为$ {\cal{P}}_3 $; 测得–1的概率为$ p_{\varepsilon^{\perp}} $, 此时量子比特B会被投影到态$ |\chi_{\varepsilon^\perp}\rangle $, 对应的投影成功概率记为$ {\cal{P}}_4 $. 根据量子力学的预言, 这四个投影成功概率$ \{{\cal{P}}_1, {\cal{P}}_2, {\cal{P}}_3, {\cal{P}}_4\} $理论上应该全部等于1, 即:

这意味着, 通过对量子比特A在不同基矢下的测量, 可以成功将量子比特B的状态导引至相应的量子态.

如果试图使用局域隐变量模型来解释上述过程, 则可以构造一个局域隐态$ \tilde{\rho}_{{\mathrm{AB}}} $, 使其尽量模拟量子力学对量子比特A和量子比特B所做预测的结果^[21,22]:

这个态结合了量子比特A在不同基下的测量结果以及量子比特B的投影态, 使用条件概率$ p_+ $, $ p_- $, $ p_\varepsilon $, $ p_{\varepsilon^{\perp}} $来权衡各个可能的投影结果. 在局域隐变量模型下, 通过对局域隐态$ \tilde{\rho}_{{\mathrm{AB}}} $进行同样的测量过程得到四个投影成功概率$ \{\tilde{{\cal{P}}}_1, \tilde{{\cal{P}}}_2, \tilde{{\cal{P}}}_3, \tilde{{\cal{P}}}_4\} $, 在弱纠缠情况下(即$ \gamma $很小时), 结果为

可以观察到, $ \tilde{{\cal{P}}}_1 $, $ \tilde{{\cal{P}}}_2 $和$ \tilde{{\cal{P}}}_4 $都非常接近1, 因此在实验中很难与量子力学预言的$ {\cal{P}}_1 $, $ {\cal{P}}_2 $和$ {\cal{P}}_4 $区分开. 然而, 当$ \tan \varepsilon $较大, 使得$ \gamma^2 \tan^2 \varepsilon $与1相当时, 第三个投影概率$ \tilde{{\cal{P}}}_3 $会显著小于1, 这与量子力学预言的$ {\cal{P}}_3 $产生了明显差异, 可以在实验中方便地检测到. 事实上, 通过检测第三个投影概率的值, 可以有效地区分一个量子态是否具有纠缠. 如果第三个投影概率接近1, 这表明量子态可以实现量子导引, 说明它具备纠缠性质. 而如果第三个投影概率明显小于1, 这与隐变量模型的预言一致, 表明该量子态无法实现量子导引, 也就不具备纠缠. 因此, 基于量子导引的弱纠缠判据正是通过测量第三个投影概率, 判断其是接近1还是显著小于1, 从而判断量子态是否包含纠缠.

上面介绍了基于量子导引的纠缠判据, 下面将与传统的基于纠缠目击者的判据进行比较, 分析它们在测量弱纠缠能力方面的差异. 传统的基于纠 缠目击者的纠缠判据是通过测量一个特定算符的期望值来判断量子态是否含有纠缠. 当测得的期 望值为负数时, 该判据可以确认量子态中含有纠缠. 然而, 实际实验中不可避免地会存在误差, 这使得实际测得的期望值与理想值产生偏差. 在给定误差条件下, 随着纠缠强度的减小(对应$ \gamma $变小), 测得的期望值越来越大, 当测得的期望值变成零时, 基于纠缠目击者的纠缠判据已无法检测出量子态的纠缠. 在基于量子导引的纠缠判据下, 量子模型与经典局域隐变量模型预言的主要差异体现在投影概率$ {\cal{P}}_3 $上. 对于量子模型, 投影概率的理想值为1, 而在经典局域隐变量模型下, 投影概率则为$ {1}/({1 + \gamma^2 \tan^2 \varepsilon}) $. 理论上, 在没有实验误差的情况下, 无论纠缠程度$ \gamma $多小, 实验都能够有效区分这两者. 然而, 实际实验中的误差将导致测得的投影概率会比量子预言的1要小. 在给定误差条件的情况下, 随着纠缠强度的减小(对应$ \gamma $变小), 测得的投影概率会越来越偏离量子预言值1, 当测得的投影概率处于量子预言值和经典预言值正中间的时候, 基于量子导引的纠缠判据已无法测出量子态的纠缠.

下面将在一个具体的测量误差模型^[23,24]下, 对基于量子导引和基于纠缠目击者这两种纠缠检测判据的纠缠分辨能力进行定量比较分析. 对于位于XZ平面的一个量子态$ |\varPhi\rangle=\cos\dfrac{\theta}{2}|0\rangle+ \sin\dfrac{\theta}{2}|1\rangle $, 它的理想投影测量算符为

其中Z, X为泡利算符. 但在考虑测量误差的情况下, 实际的算符可以表示为$ \tilde{X}=qX+\sqrt{1-q^2}Z, \tilde{Z}=qZ-\sqrt{1-q^2}X $, 其中q表示误差带来的不确定度, 由测量精度参数$ \delta $限定, 并满足$ 1\geqslant q\geqslant 1-2\delta $. 此时, 实际的投影测量算符修正为

对于基于量子导引的纠缠判据来说, 在不考虑测量误差的情况下, 弱纠缠态$ |\psi\rangle $的量子比特A被成功投影到$ |\varepsilon\rangle_{\mathrm{A}} $, 则量子比特B被投影到$ |\chi_\varepsilon\rangle_{\mathrm{B}} $的成功概率$ {\cal{P}}_3 $为1. 考虑测量误差时, 量子比特A和量子比特B的投影算符分别修正为

在此情况下, 相应的投影概率修正为

这里取$ \tan\varepsilon \to +\infty $, 此时量子力学和经典隐变量模型对投影概率$ {\cal{P}}_3 $的理论预言具有最大偏差. 相应的投影概率可以进一步简化为

由于$ q_{\mathrm{A}}, q_{\mathrm{B }}\geqslant 1 - 2\delta $, 可推导出, 只要满足$ \gamma> \sqrt{\dfrac{\delta-2\delta^2}{1-2\delta}} $就能确保$ {\cal{P}}^\prime_3> \dfrac{{\cal{P}}_3 +\tilde{{\cal{P}}}_3 }{2} = 0.5 $, 即在这种情况下, 基于量子导引的判据仍然能够检测到纠缠态.

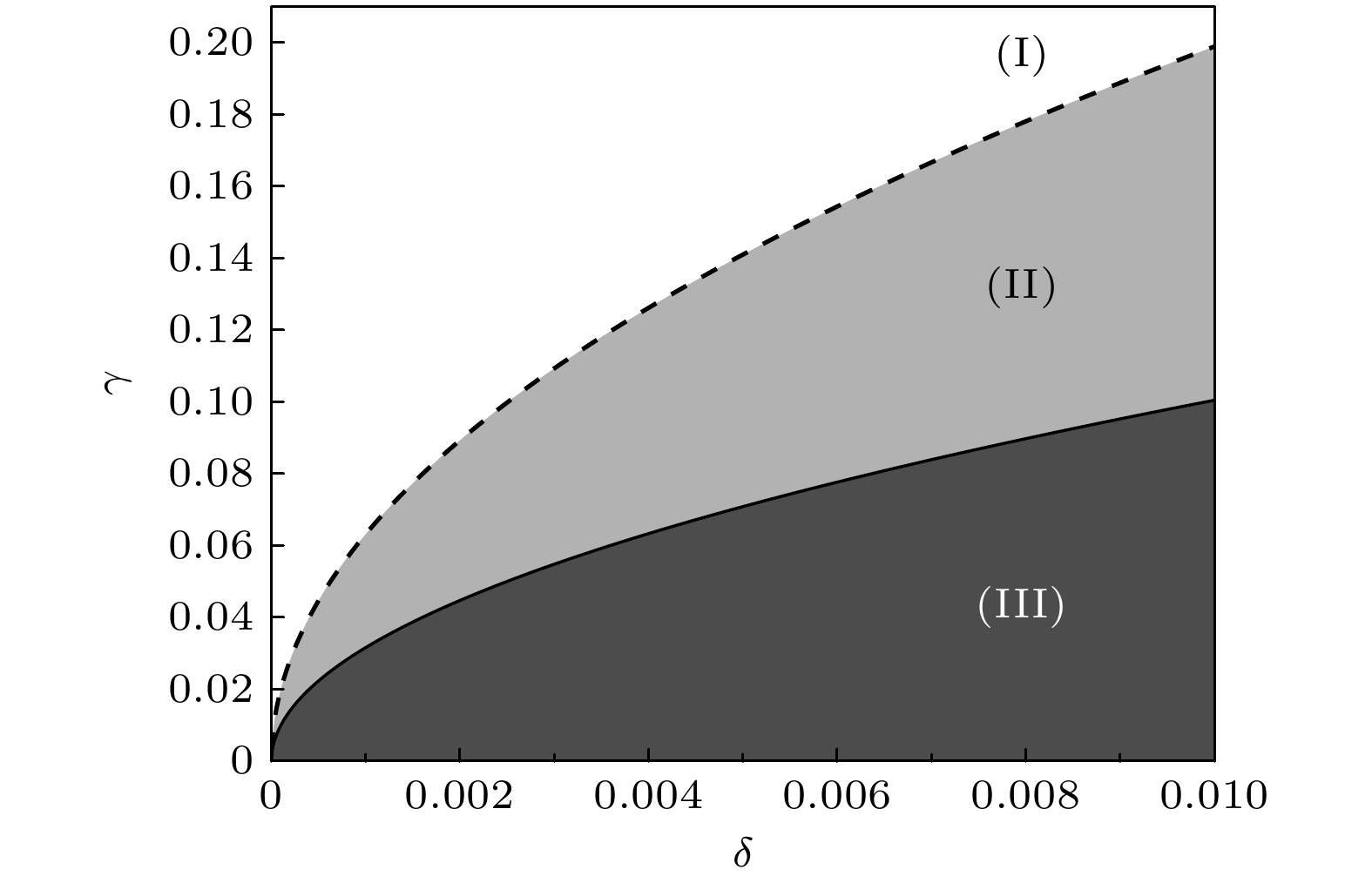
在相同的测量误差模型下, 文献[24]对基于 纠缠目击者的判据进行了分析, 并给出了误差条 件下的经典边界. 在此基础上, 可以证明纠缠目击 者能够有效检测出$ |\psi\rangle $具有纠缠性质的条件为$ \gamma> \sqrt{\dfrac1{2}\Big[{1-\sqrt{1-16\delta(1-\delta)(1-2\delta)^2}}\Big]} $ .

为了比较两种判据的纠缠检测能力, 我们绘制了图1, 展示其检测范围. 从图1可以看出, 基于纠缠目击者的判据仅能检测出区域(I)内的量子态纠缠. 而相比之下, 基于量子导引的判据不仅能检测到区域(I)的纠缠态, 同时还能检测区域(II)内的量子态纠缠. 这表明, 在相同的误差条件下, 基于量子导引的判据在纠缠检测的灵敏度上优于传统的纠缠目击者判据.

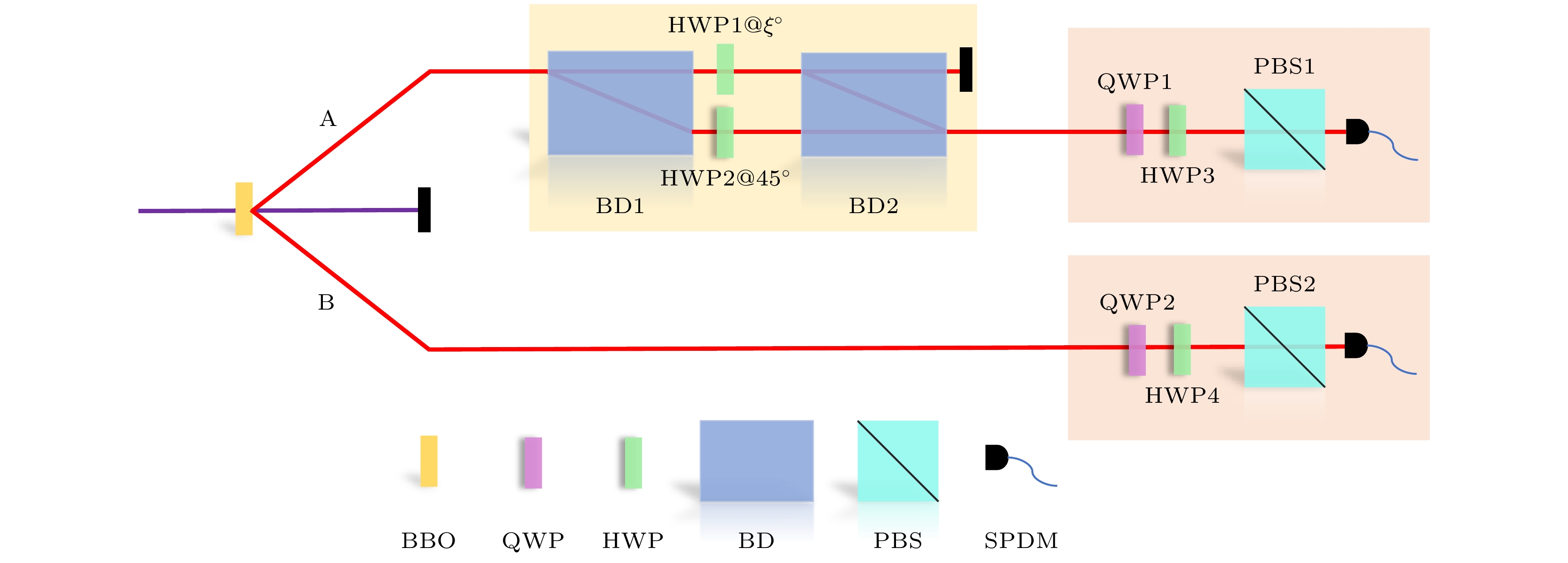
本文工作在线性光学平台上对基于量子导引的弱纠缠判据进行了实验验证. 具体的实验装置如图2所示. 首先, 一束中心波长为390 nm、脉宽为130 fs、重复频率为76 MHz的紫外脉冲激光被聚焦到一块二型相位匹配的硼酸钡(BBO)晶体上, 并在晶体中发生了自发参量下转换(SPDC)过程. 在这一过程中, 会在满足相位匹配条件的情况下沿特定方向出射中心波长为780 nm的简并双光子对. 双光子对同时包含HV和VH两种偏振成分, 其中H和V分别表示水平和竖直偏振. 通过调节这两种成分的相对相位, 可以得到一对偏振纠缠光子对^[25,26]:

接下来, 光子A导入一个由偏振分束位移器(polarizing beam displacer) BD1和BD2以及半波片HWP1和HWP2组成的装置中. 该装置能够独立调节水平(H)偏振和竖直(V)偏振光的透射率. 具体而言, 将半波片HWP2的角度固定为45°, 而半波片HWP1的角度设为$ \sin^{-1}\left(\gamma/\sqrt{1-\gamma^2}\right) $. 经过该装置后, 即可得到我们想要的两光子态:

其中0代表V, 1代表H. 实验中分别制备了$ \gamma= 0.0872 $的弱纠缠态$ |\psi\rangle_{\mathrm{e}} $(保真度为99.37$ {\text{%}} $)以及$ \gamma=0 $的可分态$ |\psi\rangle_{\mathrm{s}} = |0\rangle_{\mathrm{A}} |0\rangle_{\mathrm{B}} $. 由于$ |\psi\rangle_{\mathrm{e}} $和$ |\psi\rangle_{\mathrm{s}} $在形式上非常接近, 为了有效区分这两个量子态, 对它们进行了精确的测量.

具体而言, 光子A和光子B分别通过两个投影测量装置. 每个装置由半波片、四分之一波片、偏振分束器(PBS)以及单光子探测器组成. 通过这些装置, 可以在任意指定的测量基下, 对量子态进行投影测量, 以验证基于导引的弱纠缠判据的有效性.

实验中对光子A在两个不同的基下进行了测量, 并根据测量结果对光子B执行了相应的投影测量. 具体步骤如下.

1) 在$ |+\rangle $, $ |-\rangle $基下的测量

当光子A在$ |+\rangle $, $ |-\rangle $基下进行测量时, 测得+1的概率为$ p_+ $. 在这种情况下, 光子B会被投影到态$ |\chi_+\rangle $, 对应的投影成功概率为$ {\cal{P}}_1 $.

如果光子A测得–1, 其发生的概率为$ p_- $. 此时, 光子B会被投影到态$ |\chi_-\rangle $, 对应的投影成功概率为$ {\cal{P}}_2 $.

2) 在$ |\varepsilon\rangle $, $ |\varepsilon^\perp\rangle $基下的测量

当光子A在$ |\varepsilon\rangle $, $ |\varepsilon^\perp\rangle $基下进行测量时, 测得+1的概率为$ p_\varepsilon $. 在这种情况下, 光子B会被投影到态$ |\chi_\varepsilon\rangle $, 对应的投影成功概率为$ {\cal{P}}_3 $.

如果光子A测得–1, 其发生的概率为$ p_{\varepsilon^{\perp}} $. 此时, 光子B会被投影到态$ |\chi_{\varepsilon^\perp}\rangle $, 对应的投影成功概率为$ {\cal{P}}_4 $.

以上步骤构成了整个量子导引的实验操作. 通过在不同测量基下对光子A进行测量, 并根据结果对光子B进行相应的投影, 就可以确定不同的投影成功概率. 这些成功概率的测量结果, 将用于区分弱纠缠态$ |\psi_{\mathrm{e}}\rangle $与可分态$ |\psi_{\mathrm{s}}\rangle $.

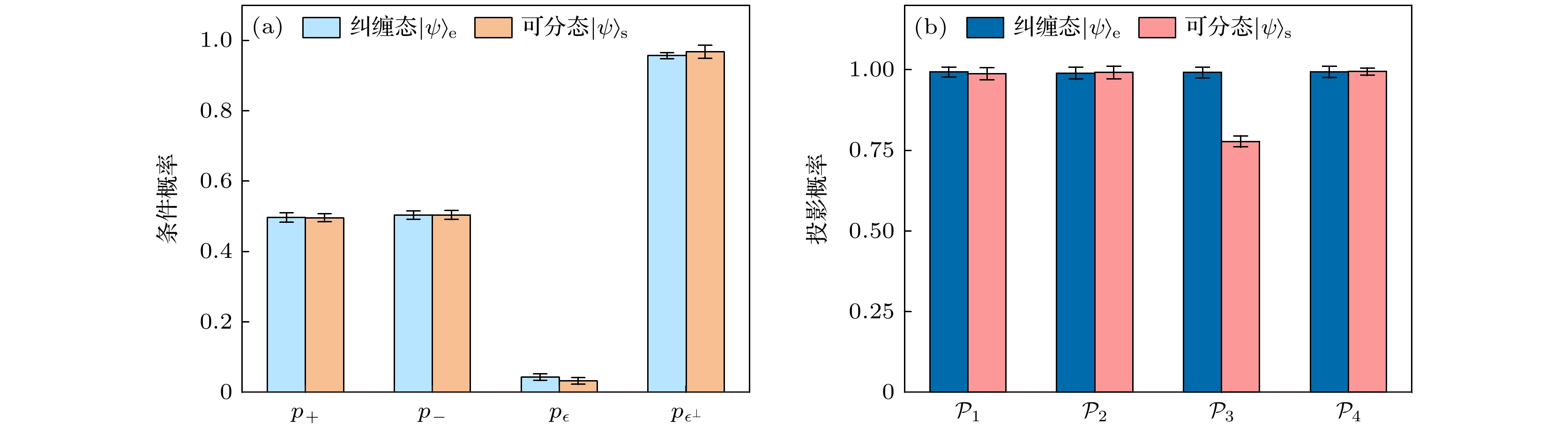
实验中将$ \varepsilon $设为$ \dfrac{9\pi}{20} $($ \tan\varepsilon=6.3 $), 得到的实 验结果如图3所示. 可以看到, 对于条件概率而言, 无论是可分态还是弱纠缠态, 测量结果都十分 接近: $ p_+ $和$ p_- $均接近于$ {1}/{2} $, $ p_\varepsilon $接近于0, 而$ p_{\varepsilon^{\perp}} $接近于1. 基于这些条件概率难以有效区分这两 种量子态. 然而, 它们在投影成功概率方面有显著的差异. 实验结果表明, 对于第一个、第二个和 第四个投影概率, 无论是可分态还是弱纠缠态, 它们的值都接近于1. 但是在第三个投影概率上, 可以观察到明显的不同: 对于纠缠态, 第三个投影 概率接近于1, 具体为$ 0.9921\pm0.0162 $; 而对于 可分态, 第三个投影概率为$ 0.7779\pm0.0172 $, 显著小于1. 因此, 通过对投影概率的测量, 可以方便 地区分纠缠态和可分态, 从而验证弱纠缠态判据的有效性.

接下来, 将$ \varepsilon $设定为$ \dfrac{17\pi}{36} $($ \tan\varepsilon=11.4 $), 并再次进行实验, 结果如图4所示. 类似于之前的实验, 从条件概率的角度来看, 纠缠态与可分态的测量结果依然难以区分. 然而, 在投影成功概率方面, 可以观察到显著的差异. 特别是第三个投影概率, 对于弱纠缠态, 这次的结果为$ 0.5243\pm 0.0162 $, 相较于之前的0.7779进一步降低. 而纠缠态的第三个投影概率仍然维持在$ 0.9952\pm0.0159 $, 这使得两者之间的差异更加明显.

从以上的实验结果可以看到, 基于导引的弱纠缠判据能够清晰地揭示纠缠态与可分态之间的差异, 并且随着$ \varepsilon $逐渐增大(接近$ \pi/2 $), 量子与经典的区分愈加明显(即$ {\cal{P}}_3 $的差异增大). 这一结果与弱纠缠判据的理论预期相一致, 验证了其有效性. 需要注意的是, 随着$ \varepsilon $的增大, 条件概率$ p_\varepsilon $也会相应减小, 因此在计算投影概率$ {\cal{P}}_3 $时, 需要更多的样本来确保测量结果的准确性.

本文在光学系统中对基于量子导引的弱纠缠判据进行了原理性的验证, 展示了该方法在区分弱纠缠态和可分态上的有效性. 弱纠缠态与可分态区分的挑战在于实验设备的误差和统计涨落, 这些因素可能导致测量得到的概率分布与理论理想态产生偏差. 当纠缠态的纠缠程度较弱时, 纠缠态与可分态之间的差异可能非常小, 统计涨落和实验误差容易掩盖这种微弱的差异, 进而增加区分的难度. 通过本实验, 利用基于量子导引的检测方法, 有效放大了弱纠缠态与可分态在实验观测结果上的差异. 实验结果表明, 即使量子态在纠缠非常微弱的情况下, 选择合适的测量基后, 该判据依然能够成功检测出纠缠态. 这一判据在量子信息技术中具有广泛应用前景, 尤其在量子通信和量子计算等领域, 为简便且可靠的纠缠态检测提供有效的新方法.

感谢香港大学计算机系冯田峰博士后的讨论.