高级搜索

具有($ 2 m+1 $)次非线性项和时空变系数的广义($ n+1 $)维薛定谔方程的相似变换和精确解

, 

downloadPDF

上一篇

下一篇

王岗伟, 谭子轩. 具有($ 2 m+1 $)次非线性项和时空变系数的广义($ n+1 $)维薛定谔方程的相似变换和精确解[J]. 物理学报, 2025, 74(11): 110201-1. doi: 10.7498/aps.74.20250225
引用本文: 王岗伟, 谭子轩. 具有($ 2 m+1 $)次非线性项和时空变系数的广义($ n+1 $)维薛定谔方程的相似变换和精确解[J]. 物理学报, 2025, 74(11): 110201-1. doi: 10.7498/aps.74.20250225
shu
Gangwei WANG, Zixuan TAN. Similarity transformations and exact solutions of the generalized ($ n+1 $)-dimensional Schrödinger equation with ($ 2 m+1 $)th order nonlinear terms and spatiotemporally varying coefficients[J]. Acta Physica Sinica, 2025, 74(11): 110201-1. doi: 10.7498/aps.74.20250225
Citation: Gangwei WANG, Zixuan TAN. Similarity transformations and exact solutions of the generalized ($ n+1 $)-dimensional Schrödinger equation with ($ 2 m+1 $)th order nonlinear terms and spatiotemporally varying coefficients[J]. Acta Physica Sinica, 2025, 74(11): 110201-1. doi: 10.7498/aps.74.20250225
shu

具有($ 2 m+1 $)次非线性项和时空变系数的广义($ n+1 $)维薛定谔方程的相似变换和精确解

  • 1.

    河北经贸大学数学与统计学学院, 石家庄　050061

  • 2.

    河北经贸大学微分方程及其应用研究中心, 石家庄　050061

    • 通讯作者: gangwei@hueb.edu.cn; 

  • 中图分类号: 02.30.Jr, 04.20.Jb, 05.45.Yv, 52.35.Mw

Similarity transformations and exact solutions of the generalized ($ n+1 $)-dimensional Schrödinger equation with ($ 2 m+1 $)th order nonlinear terms and spatiotemporally varying coefficients

  • 1.

    School of Mathematics and Statistics, Hebei University of Economics and Business, Shijiazhuang 050061, China

  • 2.

    Center for Differential Equations and Their Applications, Hebei University of Economics and Business, Shijiazhuang 050061, China

    • Corresponding author: gangwei@hueb.edu.cn; 

  • MSC: 02.30.Jr, 04.20.Jb, 05.45.Yv, 52.35.Mw

  • 摘要: 薛定谔型方程是一类十分重要的微分方程. 高维及变系数薛定谔型方程的研究具有一定的价值和意义. 本文利用相似变换推导了($ n+1 $)维($ 2m+1 $)次变系数非线性薛定谔方程的一类新的孤子解, 给出了系数之间满足的关系. 并利用定态薛定谔方程的解, 得到了($ n+1 $)维($ 2m+1 $)次变系数非线性薛定谔方程的明暗孤子解. 最后, 对于特殊的情况, 给出了明暗孤立子解的图像, 并系统分析了孤子解的空间结构和传播特性.
    Abstract: Schrödinger-type equations represent a fundamentally important class of differential equations. Research on high-dimensional variable-coefficient Schrödinger-type equations as important theoretical and practical value, providing critical insights into the dynamics of complex wave phenomena. In this paper, we employ similarity transformations to derive a novel class of soliton solutions for the (n + 1)-dimensional (2m + 1)th-order variable-coefficient nonlinear Schrödinger equation. By extending similarity transformations from lower-dimensional to higher dimensionnal equations, we establish the intrinsic relationships among the equation’s coefficients. Furthermore, utilizing the solutions of the stationary Schrödinger equation and using the balancing-coefficient method, we construct both bright and dark soliton solutions for the (n + 1)-dimensional (2m + 1)th-order variable-coefficient nonlinear Schrödinger equation. Finally, for specific cases, we present graphical representations of the bright and dark soliton solutions and conduct a systematic analysis of their spatial structures and propagation characteristics. Our results indicate that bright solitons exhibit a single-peak structure, while dark solitons form trough-like profiles, further confirming the stability of soliton wave propagation.
  • 加载中

  • 图 1  方程(29)的一种明孤子解, 展示的图像为$ |u|^2 $. 其中$ x_1\in[-10, 10] $, $ t\in[0, 10] $, $ x_2=-3,\; x_3 = 2 $　(a) 三维图; (b) 相位图

    Figure 1.  Bright soliton solution of Eq.(29), shown as $ |u|^2 $, where $ x_1\in[-10, 10] $, $ t\in[0, 10] $, $ x_2=-3,\; x_3 = 2 $: (a) 3-dimensional image; (b) phase image.

    下载: 全尺寸图片 幻灯片

    图 2  方程(29)的一种明孤子解, 展示的图像为$ |u|^2 $. 其中$ x_1\in[-10, 10] $, $ t\in[3, 5] $, $ x_2=-3,\; x_3 = 2 $ 　(a) 三维图; (b) 相位图

    Figure 2.  Bright soliton solution of Eq.(29), shown as $ |u|^2 $, where $ x_1\in[-10, 10] $, $ t\in[3, 5] $, $ x_2=-3,\; x_3 = 2 $: (a) 3-dimensional image; (b) phase image.

    下载: 全尺寸图片 幻灯片

    图 3  方程(30)的一种暗孤子解, 展示的图像为$ |u|^2 $. 其中 $ x\in[-10, 10] $, $ t\in[0, 10] $, $ x_2=-3,\; x_3 = 2 $ 　(a) 三维图; (b) 相位图

    Figure 3.  Dark soliton solution of Eq.(30), shown as $ |u|^2 $, where $ x_1\in[-10, 10] $, $ t\in[0, 10] $, $ x_2=-3,\; x_3 = 2 $: (a) 3-dimensional image; (b) phase image.

    下载: 全尺寸图片 幻灯片

    图 4  方程(30)的一种暗孤子解, 展示的图像为$ |u|^2 $. 其中 $ x\in[-10, 10] $, $ t\in[0, 2] $, $ x_2=-3,\; x_3 = 2 $ 　(a) 三维图; (b) 相位图

    Figure 4.  Dark soliton solution of Eq.(30), shown as $ |u|^2 $, where $ x_1\in[-10, 10] $, $ t\in[0, 2] $, $ x_2=-3,\; x_3 = 2 $: (a) 3-dimensional image; (b) phase image.

    下载: 全尺寸图片 幻灯片
  • [1] Zhong M, Malomed B A, Yan Z 2024 Phys. Rev. E 110 014215 doi: 10.1103/PhysRevE.110.014215
    [2] Malomed B A 2024 Chaos 34 022102 doi: 10.1063/5.0190039
    [3] Kudryashov N A, Nifontov D R, Biswas A 2024 Phys. Lett. A 528 130037 doi: 10.1016/j.physleta.2024.130037
    [4] Wang T Y, Zhou Q, Liu W J 2022 Chin. Phys. B 31 020501 doi: 10.1088/1674-1056/ac2d22
    [5] Lü X, Zhu H W, Yao Z Z, Meng X H, Zhang C, Zhang C Y, Tian B 2008 Ann. Phys. 323 1947
    [6] 公睿智, 王灯山 2023 物理学报 72 100503 doi: 10.7498/aps.72.20230172 Gong R Z, Wang D S 2023 Acta Phys. Sin. 72 100503 doi: 10.7498/aps.72.20230172
    [7] Pérez-García V M, Pardo R 2009 Physica D 238 1352
    [8] Dinh V D 2022 Nonlinear Anal. 214 112587 doi: 10.1016/j.na.2021.112587
    [9] Rizvi S T R, Seadawy A R, Farah N, Ahmad S 2022 Chaos, Solitons Fractals 159 112128 doi: 10.1016/j.chaos.2022.112128
    [10] Yang Z, Zhong W P, Belić, M R 2023 Phys. Lett. A 465 128715 doi: 10.1016/j.physleta.2023.128715
    [11] Djelah G, Ndzana F I I, Abdoulkary S, English L Q, Mohamadou A 2024 Phys. Lett. A 518 129666 doi: 10.1016/j.physleta.2024.129666
    [12] 饶继光, 陈生安, 吴昭君, 贺劲松 2023 物理学报 72 104204 doi: 10.7498/aps.72.20222298 Rao J G, Chen S A, Wu Z J, He J S 2023 Acta Phys. Sin. 72 104204 doi: 10.7498/aps.72.20222298
    [13] 孙斌, 赵立臣, 刘杰 2023 物理学报 72 100501 doi: 10.7498/aps.72.20222416 Sun B, Zhao L C, Liu J 2023 Acta Phys. Sin. 72 100501 doi: 10.7498/aps.72.20222416
    [14] 裴一潼, 王锦坤, 郭柏灵, 刘伍明 2023 物理学报 72 100201 doi: 10.7498/aps.72.20230241 Pei Y T, Wang J K, Guo B L, Liu W M 2023 Acta Phys. Sin. 72 100201 doi: 10.7498/aps.72.20230241
    [15] 温嘉美, 薄文博, 温学坤, 戴朝卿 2023 物理学报 72 100502 doi: 10.7498/aps.72.20222284 Wen J M, Bo W B, Wen X K, Dai C Q 2023 Acta Phys. Sin. 72 100502 doi: 10.7498/aps.72.20222284
    [16] 楼森岳, 郝夏芝, 贾曼 2023 物理学报 72 100204 doi: 10.7498/aps.72.20222418 Lou S Y, Hao X Z, Jia M 2023 Acta Phys. Sin. 72 100204 doi: 10.7498/aps.72.20222418
    [17] Rao J, Mihalache D, Ma M, He J 2024 Phys. Lett. A 493 129244 doi: 10.1016/j.physleta.2023.129244
    [18] 杨佳奇, 刘文军 2023 物理学报 72 100504 doi: 10.7498/aps.72.20222430 Yang J Q, Liu W J 2023 Acta Phys. Sin. 72 100504 doi: 10.7498/aps.72.20222430
    [19] 廖秋雨, 胡恒洁, 陈懋薇, 石逸, 赵元, 花春波, 徐四六, 傅其栋, 叶芳伟, 周勤 2023 物理学报 72 104202 doi: 10.7498/aps.72.20230096 Liao Q Y, Hu H J, Chen M W, Shi Y, Zhao Y, Hua C B, Xu S L, Fu Q D, Ye F W, Zhou Q 2023 Acta Phys. Sin. 72 104202 doi: 10.7498/aps.72.20230096
    [20] Wang G 2016 Appl. Math. Lett. 56 56
    [21] Zhang J, Wang G 2025 Appl. Math. Lett. 159 109286 doi: 10.1016/j.aml.2024.109286
  • 加载中
图( 4)
计量
  • 文章访问数:  34
  • HTML全文浏览数:  34
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-24
  • 刊出日期:  2025-06-05

具有($ 2 m+1 $)次非线性项和时空变系数的广义($ n+1 $)维薛定谔方程的相似变换和精确解

    通讯作者: gangwei@hueb.edu.cn; 
  • 1. 河北经贸大学数学与统计学学院, 石家庄　050061
  • 2. 河北经贸大学微分方程及其应用研究中心, 石家庄　050061
  • 收稿日期:  2025-02-24

摘要: 薛定谔型方程是一类十分重要的微分方程. 高维及变系数薛定谔型方程的研究具有一定的价值和意义. 本文利用相似变换推导了($ n+1 $)维($ 2m+1 $)次变系数非线性薛定谔方程的一类新的孤子解, 给出了系数之间满足的关系. 并利用定态薛定谔方程的解, 得到了($ n+1 $)维($ 2m+1 $)次变系数非线性薛定谔方程的明暗孤子解. 最后, 对于特殊的情况, 给出了明暗孤立子解的图像, 并系统分析了孤子解的空间结构和传播特性.

English Abstract

    全文HTML

    1.   引 言

    • 非线性薛定谔方程(nonlinear Schrödinger equation, NLSE)

      是研究非线性波现象[1]的基本模型, 其中u表示复波包振幅, α控制色散或衍射效应, γ描述非线性相互作用. 在非线性光学[2-4]、流体动力学[5,6]、玻色-爱因斯坦凝聚体[7-9]和等离子体物理学[5]中有广泛的应用. 作为描述色散和非线性之间相互作用的经典方程, NLSE具有多种非线性波特性, 包括孤子[2]、呼吸波[10]和怪波[11,12], 例如孤子干涉过程中的相位演化特性[13]. 文献[14]考虑了特殊的NLSE与Korteweg-de Vries (KdV)方程的耦合系统. 温嘉美等[15]构造了耦合自散焦饱和非线性薛定谔方程. 对高维和高阶NLSE的研究获得越来越多的关注, 楼森岳等[16]使用形变术导出了许多高维可积方程, 高维NLSE对于理解多维、强非线性系统中的复杂波动力学至关重要. 然而, 为这种广义系统构建解析解并分析其性质仍然具有重要的价值.

      孤子解的研究对于高维NLSE尤为重要, 因为孤子是描述局域能量转移和非线性波传播稳定性的核心模型. 明孤子表现为振幅局域化结构, 而暗孤子表现为局域化波谷[17], 以及特殊的明暗孤子混合的特殊孤子[18]. 孤子的稳定性和动态特性为非线性波传播机制提供了深刻的理论见解. 廖秋雨等[19]研究了高维空间光孤子的特性. 尽管已有一些研究, 但高维、高阶、变系数NLSE孤子解的构建和分类仍然不完整, 对其动态行为的深入分析值得进一步探索.

      本文作者王岗伟[20]应用相似变换推导出了(2+1)维的三次非线性薛定谔方程的一组新解. 并在此基础上, 扩展了求解(3+1)维三次非线性薛定谔方程的方法. 本文是对参考文献[20,21]的深入研究和拓展. 当$ n = 3 $和$ m = 1 $时, 退化为参考文献[21]的结果. 当$ n = 2 $和$ m = 1 $时, 简化为参考文献[20]的结果. 因此, 本文给出了更一般的结论, 将薛定谔方程推广为($ n+1 $)维的($ 2 m+1 $)次非线性薛定谔方程

      其中含有与标准薛定谔方程相同的时间项和外势项, 本文考虑更高维的色散效应, 于是将二阶色散项扩展为n阶. 相似地, 将二阶非线性效应扩展为$ (2 m+1) $次, 适用于多体碰撞、高阶极化率、复杂介质等高密度高强度的极端条件, 是超越平均场理论或弱非线性近似的修正. 方程(2)的难点在于对其的相似变换得到的方程组是高维的, 这意味着该方程组的解是相当复杂的. 本文发现低维方程组的方法可以应用到高维方程组中, 它们的解之间有相似的结构.

      采用相似变换[20]结合稳态薛定谔方程, 本文推导出了一类新的($ n+1 $)维的($ 2 m+1 $)次NLSE的孤子解. 自相似解是NLSE研究中的重要方向, 广泛出现在高功率光纤放大器、等离子体涡旋以及非均匀介质中的波传播问题中. 这类解的数学形式通常为

      其中ρ描述波包的自适应演化, 相位函数φ反映群速度与频率偏移的动态调制, 自相似解的构造依赖于变量变换及对称群方法, 并在非均匀系数的NLSE (如带有增益-损耗项或外势场的系统)中展现出特殊的动力学行为. 本文将解分为明孤子和暗孤子, 详细分析它们在不同参数条件下的空间分布、相位结构和稳定性. 通过数值模拟, 展示了孤子解的动态传播特性以及非线性和色散之间的平衡机制, 为研究高维非线性波系统提供了新的理论见解和工具.

      这项工作的主要贡献如下: 基于相似变换, 推导了($ n+1 $)维的($ 2 m+1 $)次NLSE的孤子解, 扩大了高阶非线性波动方程孤子解的研究范围; 通过对孤子的空间结构、相位分布和动态稳定性的系统研究, 确定了它们的不同特征. 通过三维图、相位图直观地展示了解的动态行为, 验证了孤子解的准确性和稳定性; 本研究丰富了高维非线性方程组的理论框架, 为进一步探索高维非线性波动力学提供了一定的理论依据, 并为物理系统中的孤子动力学提供了潜在的应用.

      本文的结构如下: 第2节推导了高维NLSE的新孤子解; 第3节对特殊情况分析了明孤子和暗孤子解, 研究了它们在各种参数下的特性, 并将结果可视化.

    2.   变系数(n+1)维NLSE的相似变换

    • 对于(n+1)维(2m+1)次NLSE,

      利用相似变换[20]

      式中的U为不含时定态薛定谔方程的解, E为分离常量, $ U_{\xi\xi} $为二阶色散项, $ G|U|^{2 m} U $为对应的非线性项, G为常数, 方程如下:

      其中

      缩写为

      将方程(5)和方程(6)代入方程(2), 可以得到

      对U及其导数的不同子项进行分类, 并将它们的系数分别设为零, 得到以下方程组:

      根据方程(10d)和方程(10e), 可知

      从方程(10b)和方程(10c), 可以推出一组解:

      这里的$ p,\; q $是关于t的任意函数.

      将方程(12)代入方程(10a), 可以得到

      这个解的形式为

      其中 $ c_1,\; c_2 $ 都为常数, c 是关于 t 的任意函数, 并且 $ i \ne j, \;j > i $.

      将方程(14)代入方程(10a) 有

      最后, 得到了广义($ n+1 $)维的($ 2 m+1 $)次非线性薛定谔方程的一个新解:

      这里$ p, \;q, \; c $是关于t的任意函数, 并且$ i \ne j, \; j > i $.

    3.   孤子解

      3.1.   明暗孤子解

    • 对于方程(6), 将孤子解的形式设为

      将方程(17)代入方程(6), 得到

      平衡最高阶的系数, 有

      根据方程(18), 可以得到以下方程:

      所以, 可知

      假定

      然后可以得到

      根据方程(5), 设$ q=c = 0 $并得到方程(4)的孤子解为

      这里有

      同理, 它的暗孤子解是

      • 3.2.   解的图像

    • 本文假定

      选取不同的p和σ可以得到大量的孤子解, 本文仅考虑下面的几种情况:

      明孤子解的显式表达式为

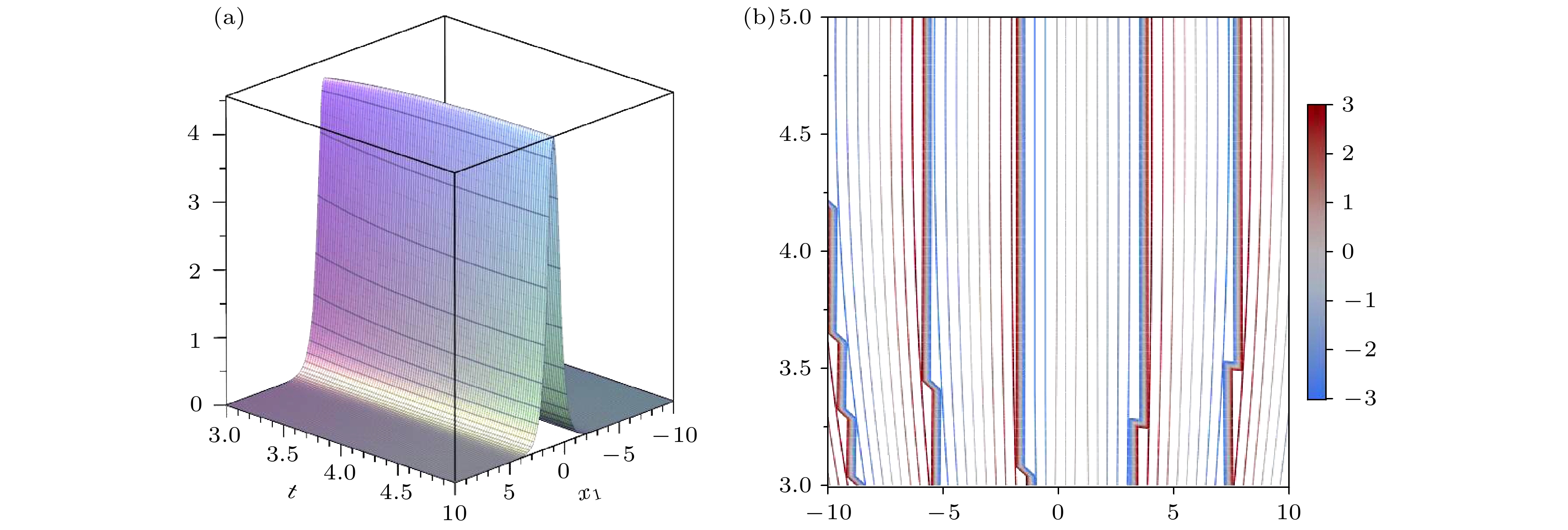
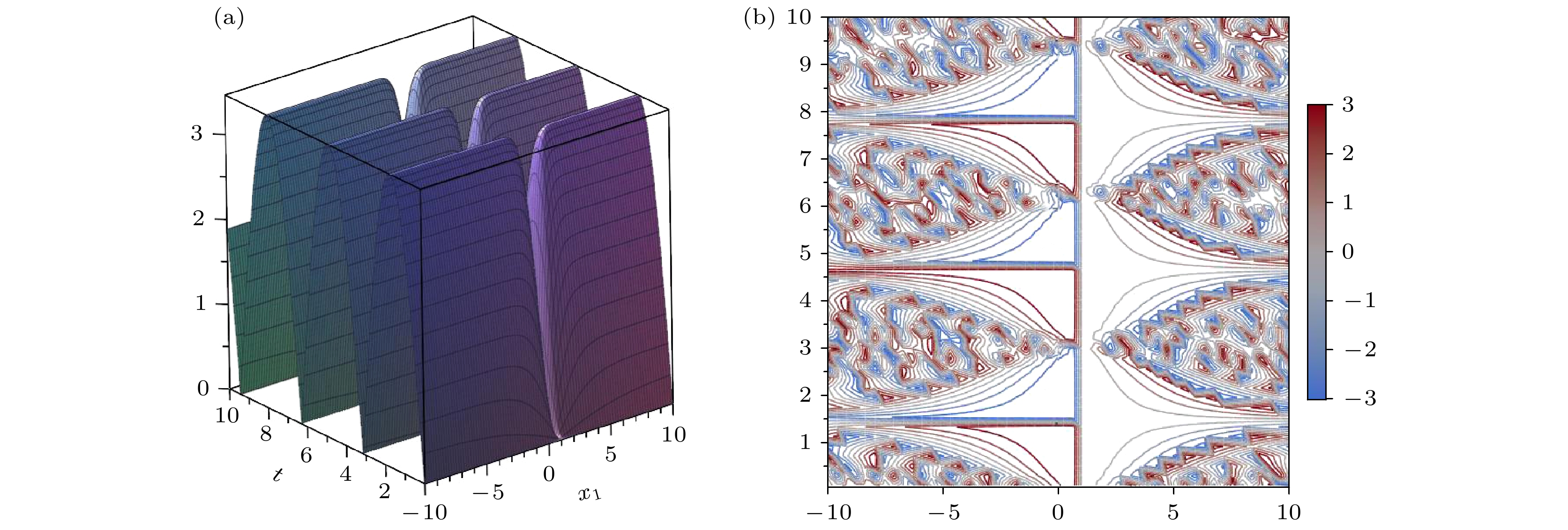
      选定$ p=p_0,\; \sigma=\sigma_0 $, 方程(29)的图像见图1. 选定$ p=p_1,\; \sigma=\sigma_1 $, 方程(29)的图像见图2.

      暗孤子解的显式形式为

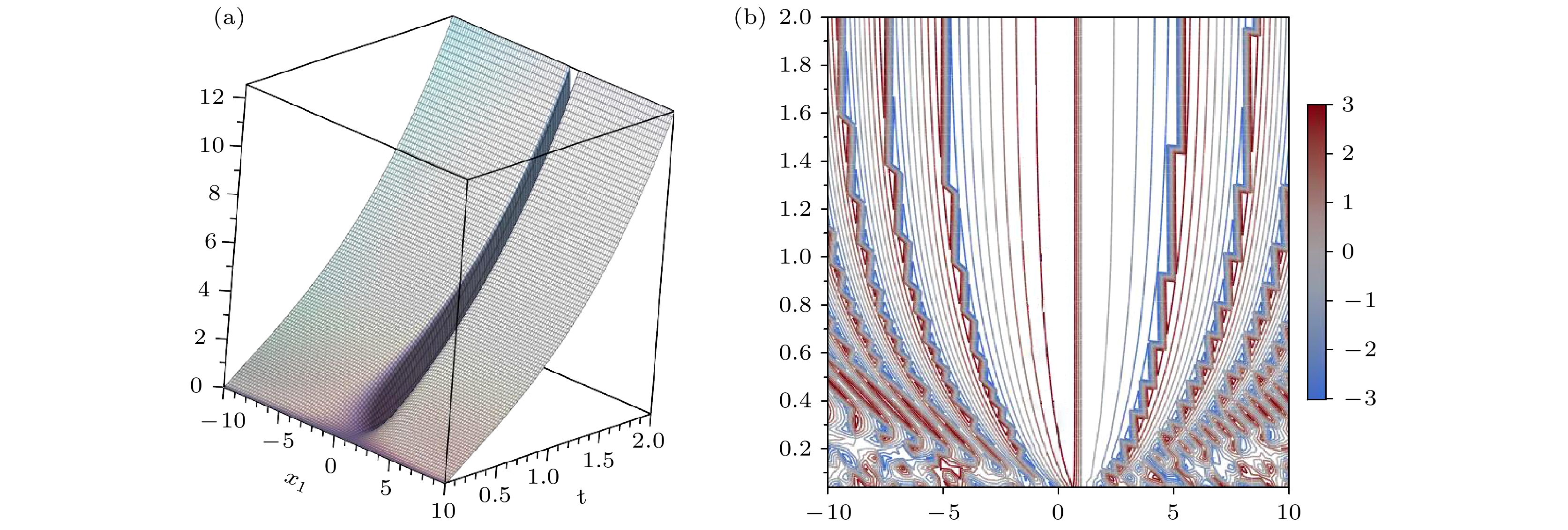
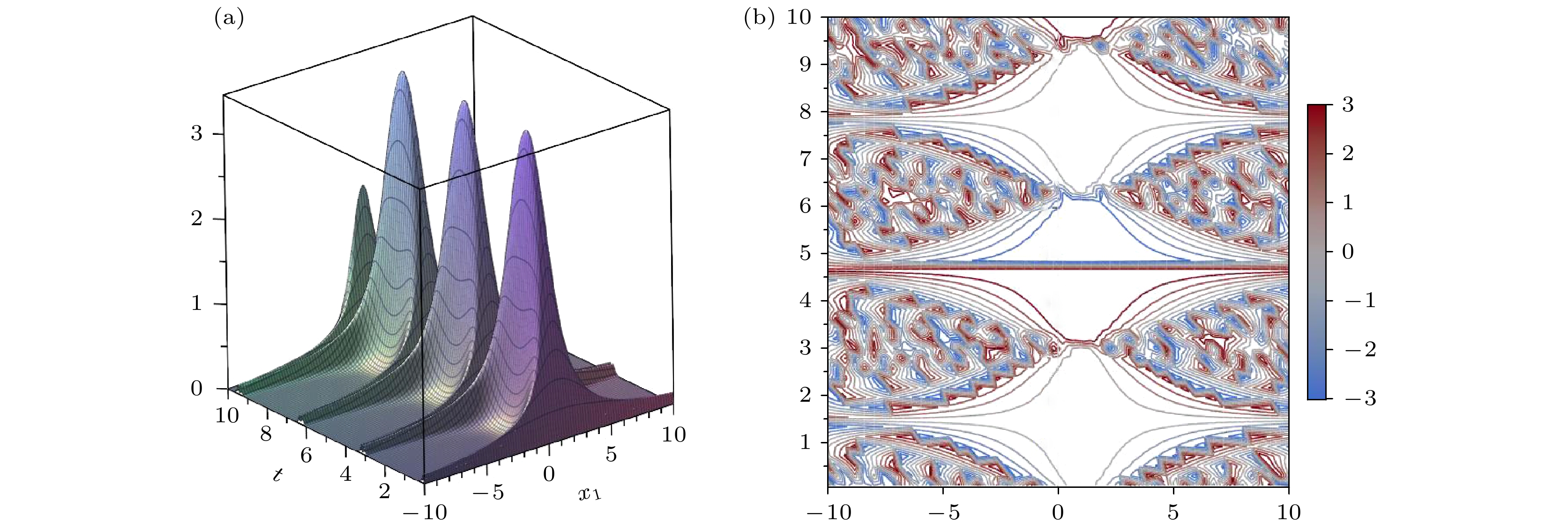
      选定$ p=p_0,\; \sigma=\sigma_0 $, 方程(30)的图像见图3. 选定$ p=p_2,\; \sigma=\sigma_2 $, 方程(30)的图像见图4.

      图1有明显的周期单峰结构和对称性, 与图2一起展示了明孤子解的局域涨落特性. 这样的单峰结构证明了孤子在非线性和色散平衡下的稳定传播. 两者的相位图都反映了孤子的对称性和相位连续性, 均为支持稳定传播的相位梯度分布.

      图3有明显的暗孤子特有的体现能量耗散的槽结构, 并且是周期性的, 描述了暗孤子的动态特性. 图4的三维图像清晰地捕捉到了波谷区域, 体现了孤子的局域性和稳定性.

    4.   结　论

    • 通过使用相似变换, 本研究构建了($ n+1 $)维($ 2 m+1 $)次变系数非线性薛定谔方程的孤子解, 对于特殊情况, 深入研究了其明孤子和暗孤子在各种条件下的传播特性和动态行为. 结果表明, 明孤子表现出稳定传播的局域单峰结构, 而暗孤子表现出能量耗尽的槽结构. 验证了解的准确性和孤子波的稳定性. 这些发现扩大了非线性薛定谔方程孤子解的研究范围, 并为研究高维非线性波的动力学提供了新的视角. 未来的工作将探索更复杂的物理背景下的模型及孤子相互作用和演化.

    参考文献 (21)

目录

/

返回文章
返回