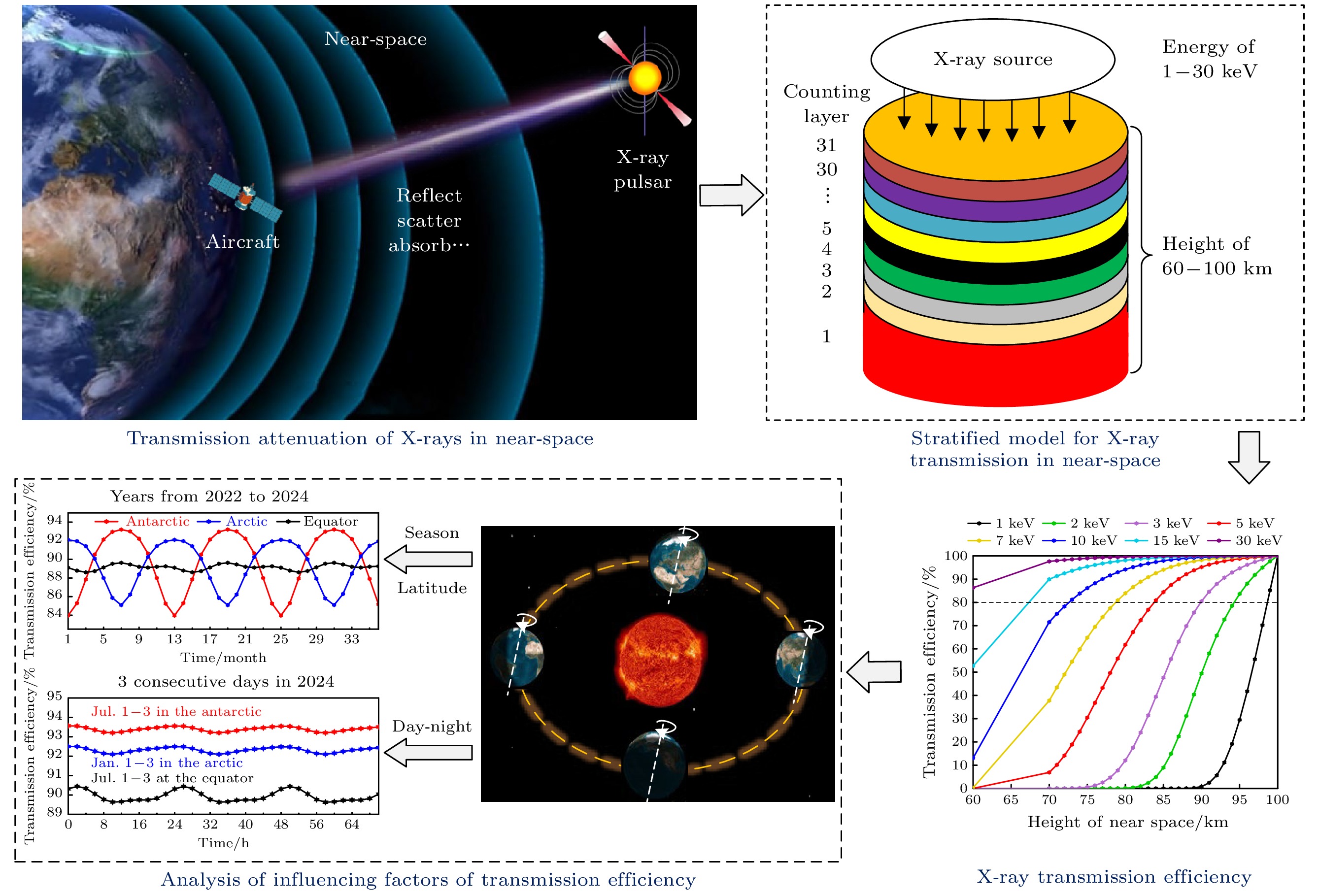
临近空间在空天一体化发展中具有重要的应用价值^[1]. 随着临近空间探索活动日益增多, 临近空间飞行器自主导航变得至关重要. 通过自主导航, 飞行器可摆脱对外部导航系统的过度依赖, 进而实现在信号受干扰、拒止或中断等极端环境下的稳定飞行^[2]. 这不仅拓展了飞行器在军事、民用等领域的应用范围^[3], 还为空天一体化发展筑牢根基, 是推动空天技术迈向更高水平的关键支撑要素.

利用X射线脉冲星进行导航或可成为临近空间飞行器自主导航的技术途径^[4–8]. 脉冲星是快速旋转、高度磁化的中子星^[9–17], 其作为宇宙中的天然灯塔^[18–20], 能够持续稳定地发射周期性信号^[21,22], 且信号覆盖范围广, 可为临近空间飞行器提供全球覆盖且不受地面设施与卫星系统限制的导航基准, 提升导航的自主性^[23–26]. 然而, 将脉冲星应用于临近空间导航面临着诸多难题. 一方面, 脉冲星信号极其微弱, 在穿越临近空间复杂环境时, 易受X射线衰减、大气折射等因素影响, 导致信号捕获与处理难度极大^[27]; 另一方面, 目前对临近空间复杂环境下的脉冲星信号传播特性认知尚浅, 难以构建精准的信号传播模型. 因此, 脉冲星信号在临近空间的衰减特性是决定其能否有效应用于该领域的关键因素.

国内外近年来已将X射线应用于导航通信中, 对其在深空及临近空间黑障区的传输问题开展了相关研究. Henke等^[28]的研究表明: 在真空中, X射线可实现近乎无损耗传播, 为基于X射线的深空通信研究提供了理论支撑. 2007年, Gendreau^[29]开创性地提出了利用X射线作为载波进行深空信息传输的技术构想. 2017年, Li等^[30]从理论层面证实了X射线在等离子体环境下几乎不会出现衰减现象, 这一理论突破为利用X射线实现黑障区通信提供了重要的理论支撑. 2020年, 周围^[31]针对黑障区X射线通信问题, 对X射线与大气的相互作用过程进行了模拟, 并就不同通信链路下X射线的传输特性开展了计算分析. 目前X射线传输特性相关研究大多是为实现X射线通信而开展, 但针对临近空间X射线脉冲星导航(X-ray pulsar-based navigation, XPNAV)需求, X射线脉冲星信号在临近空间的传输特性研究尚属空白.

在开展临近空间X射线脉冲星信号传输特性分析时应合理选择适用于XPNAV的X射线能段, 对临近空间不同高度的光子流量进行修正. 首先确定能段, 由于X射线脉冲星辐射信号经大尺度空间传播, 已衰减为微弱的光子流, 高能观测谱段涵盖0.1—200 keV, 本文针对XPNAV导航需求^[32–35], 主要分析1—30 keV能段的传输效率, 相关分析方法可推广至其他能段. 然后确定高度范围, 小于10 keV的低能段X射线脉冲星信号基本无法穿透60 km以下的大气, 而距地面100 km以上的大气密度非常稀薄, 可被认为是真空或近似真空的环境, 基本不存在X射线衰减, 因此本文选择60—100 km作为临近空间X射线脉冲星信号传输特性研究的高度范围.

本文首先对X射线与带电离子、自由电子等物质的反射、散射、吸收三种作用机理进行分析, 为临近空间X射线传输效率的获取提供了理论基础; 然后根据国际参考电离层模型IRI-2020和大气模型NRLMSIS 2.1得到的电子、大气等密度, 利用MCNP5软件构建了X射线于临近空间60—100 km高度范围的传输分层模型, 对1—30 keV的X射线传输衰减情况进行分析, 给出了临近空间不同高度下脉冲星流量数据的获取方法; 最后从季节和纬度、昼夜等方面分析了临近空间X射线脉冲星信号的传输效率影响因素.

电离层是在太阳高能辐射与宇宙粒子的轰击下产生电离的高层大气, 其结构可依照电子密度的不同而划分为D层、E层、F层^[36]. 本文所研究高度范围基本覆盖D层及E层底部, 因此重点分析这两个区域的电离层特性.

D层位于电离层的最下方, 在60—90 km的高度范围内^[37], 日间电子密度为10⁸—10⁹ m^–3, 主要辐射源为来自太阳的Lyman-α辐射, 所以夜间D层基本消失^[38]. 该层电子密度稀薄, 以离子成分居多, 因受到下层大气影响, 层内电子密度随季节和海拔变化较大^[39]; E层位于90—150 km^[40], 日间电子含量较高, 密度约为2×10¹¹ m^–3, 夜间电子含量较低, 约为2×10¹⁰ m^–3, 主要辐射源为太阳紫外线和软X射线^[41,42]. 电离层的化学组成及电子密度分布特性对X射线在其中的传播具有显著影响.

当X射线穿越临近空间电离层时, 会与其中的物质发生反射、散射及吸收^[43]等效应, 以下分别针对上述几种效应展开分析.

X射线在电离层的反射现象主要源于其与自由电子之间的相互作用, 大气折射系数^[44,45]可表示为

其中${N_{\text{e}}}$是电离层自由电子密度, 单位为m^–3; $f$是X射线频率, 单位为Hz. 由(1)式可得, 随着电子密度${N_{\text{e}}}$的升高, 大气折射系数$n$逐渐降至0, 此时的频率为电磁波进入电离层的临界频率

当入射波频率低于临界值${f_{\text{c}}}$时, 将发生全反射现象, 无法穿透介质层; 当频率高于临界值时, 电磁波将穿透该层, 并发生折射效应; 若频率继续提升至远远超出临界值, 则可实现完全穿透. X射线频段处于10¹⁶—10¹⁹ Hz范围, 显著高于电离层临界频率值, 因此其在大气层中的反射损耗可近似视为零.

X射线散射现象的产生源于其与电子的相互作用, 可分为相干散射和非相干散射^[46]. 相干散射入射线和散射线频率相同、相位固定, X射线能量可有效传输而不会受到损耗. 非相干散射又称康普顿散射, 相较于相干散射, 康普顿散射出射X射线相位差不固定, 且常伴有能量损耗^[47]. 在康普顿散射作用中, 部分能量被自由电子吸收, 表现为散射吸收截面; 另一部分能量传递给散射光子, 表现为纯散射截面; 总散射截面可表示为两者的线性叠加. 本节将阐述康普顿散射中入射光子能量与上述三种截面之间的关联.

散射光子能量可由下式计算:

其中${E_{\text{γ }}}$为入射光子能量, $E_{\text{γ }}'$为散射光子能量, ${m_{\text{e}}}{c^2}$为电子静止能, $c$为光速, $\theta $是散射角. 根据Klein-Nishina公式, 自由电子的康普顿散射总截面可被描述为^[48]

其中$\alpha = \dfrac{{{E_{\text{γ }}}}}{{{m_{\text{e}}}{c^2}}}$, ${r_{\text{e}}}$为电子经典半径. 散射吸收截面$\sigma _{\text{e}}^{\text{a}}$为

纯散射截面$\sigma _{\text{e}}^{\text{b}}$为

各类散射事件的发生概率可由(4)式、(5)式、(6)式进行量化表征^[49].

当X射线光子入射物质并与原子内电子相互作用时, 若光子能量达到或超过电子结合能, 光子便会将自身能量赋予电子而使其逸出, 该现象称为光电吸收. 光电效应发生的概率同样可用截面进行量化表征

其中$\beta $是精细结构常数, 取1/137; ${E_{\text{e}}} = {m_{\text{e}}}{c^2}$; ${E_{\text{γ }}}$是入射X射线光子能量; $Z$是原子序数; ${\sigma _{\text{T}}}$是单电子汤姆逊散射作用截面, 取$6.651 \times {10^{ - 25}}$cm². 由(7)式可知, 光电截面与入射光子能量、原子序数密切相关. 在原子序数恒定的条件下, 光电截面与入射光子能量呈负相关; 当入射光子能量保持不变时, 光电截面与原子序数呈正相关.

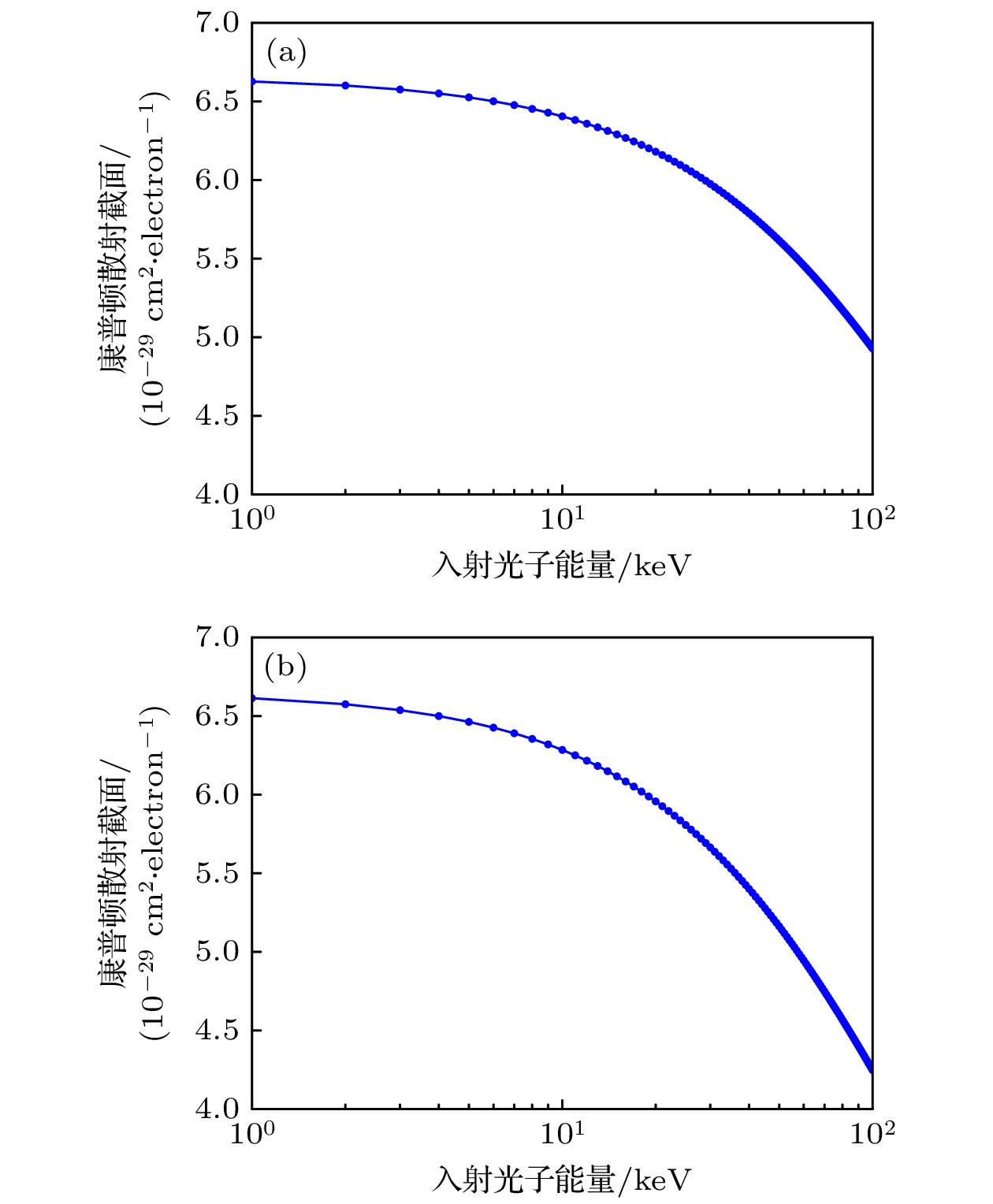
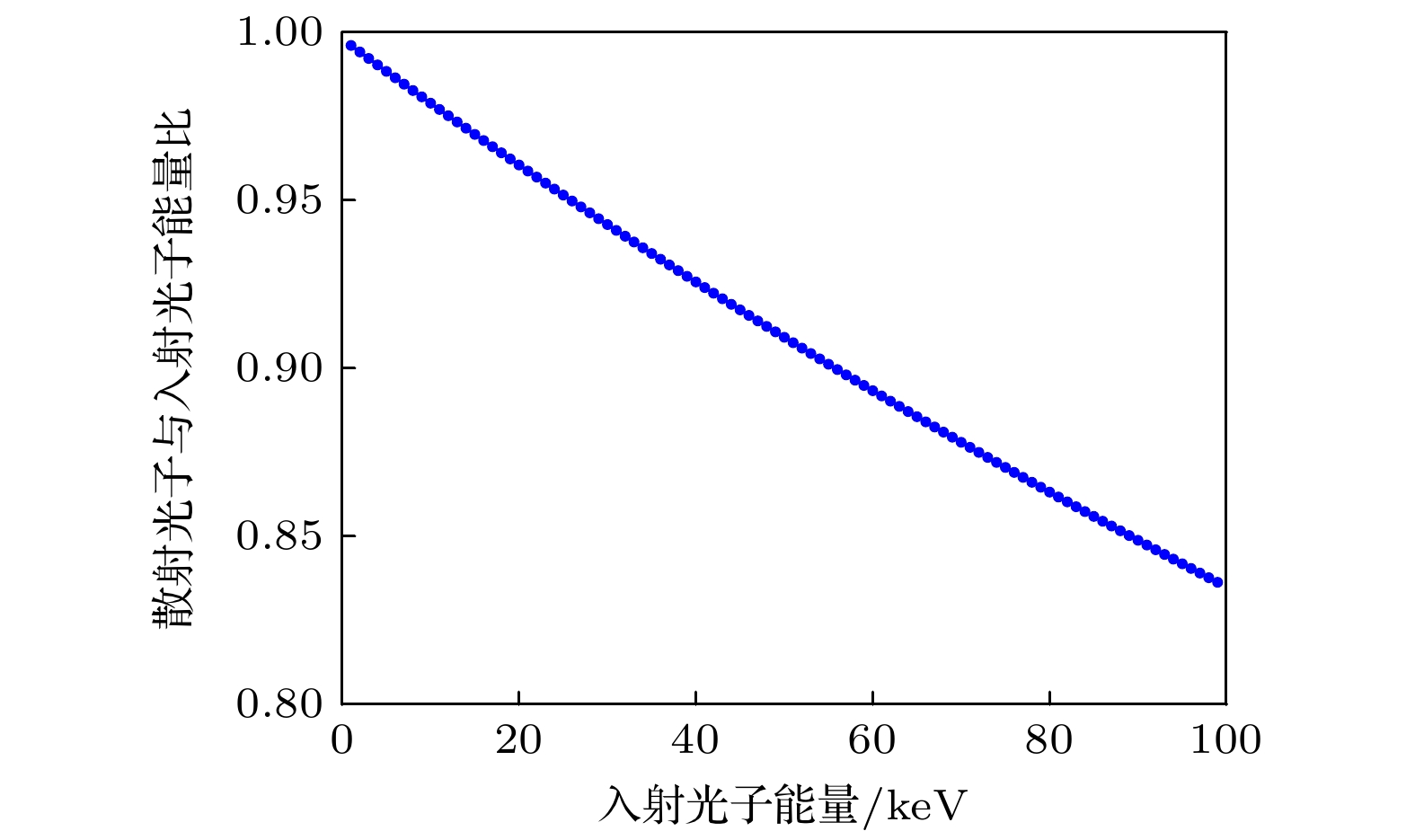
为分析散射光子能量和入射光子能量的关系, 以散射角$\theta $取90°为例, 图1给出了1—100 keV入射X射线能量下, 散射光子与入射光子能量比值的变化规律. 由图1可知, 该比值与入射光子能量呈负相关, 这一现象表明, 对于1—100 keV的X射线, 当能量逐步升高时, 康普顿散射效应会愈发显著.

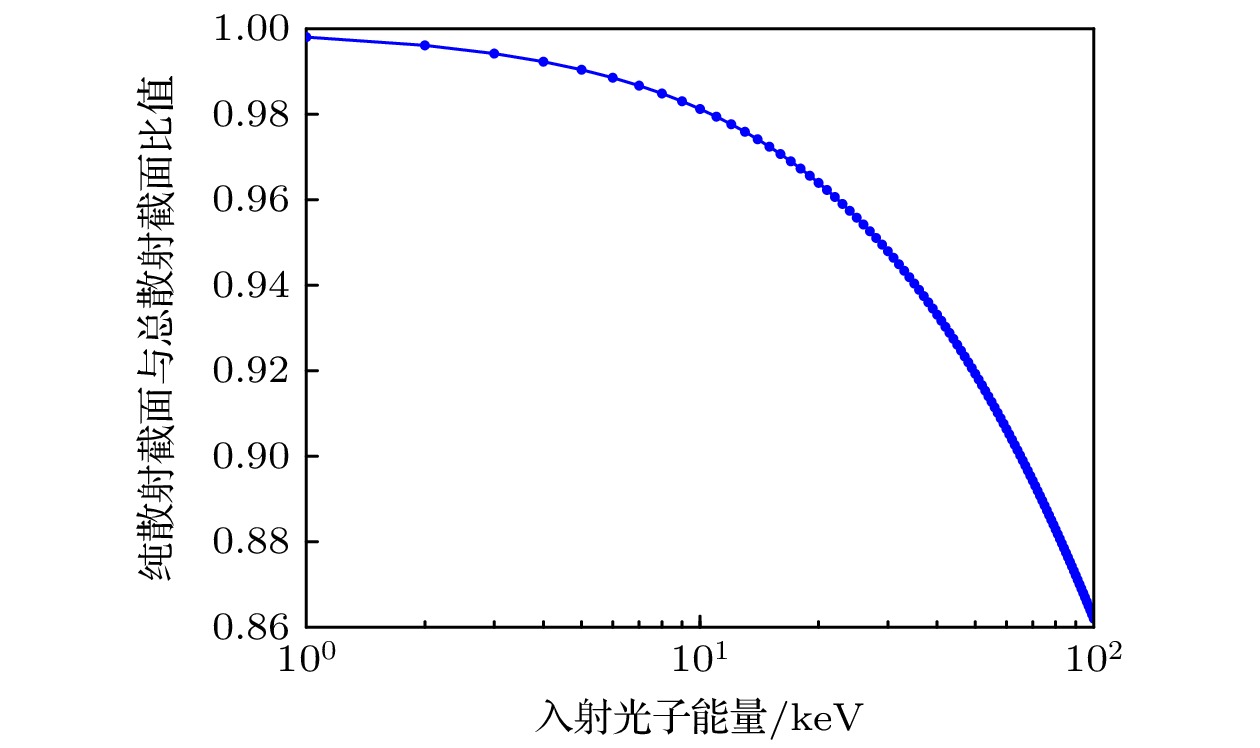
为分析散射截面和入射光子能量的关系, 给出1—100 keV入射X射线光子的总康普顿散射截面和纯散射截面如图2所示. 由此可见, 康普顿散射截面与入射X射线光子能量之间存在负相关关系, 即随着入射X射线光子能量的增加, 康普顿散射截面逐渐减小. 当入射X射线光子能量处于较高水平时, 康普顿散射截面近似与${E^{ - 1}}$成正比. 在通常情况下, 单个电子与光子之间发生康普顿散射的概率相对较低. 然而, 当空间中电子密度显著升高时, 电子与光子发生康普顿散射作用的概率将随之逐步增大.

纯散射截面与总散射截面的变化曲线具有相似性. 图3展示了纯散射截面与总散射截面的比值随入射X射线光子能量的变化情况. 由图3可知, 当入射X射线能量为1 keV时, 该比值高达99%, 表明在此能量下, 康普顿散射所导致的能量损耗程度相对较低; 随着X射线能量的增大, 该比值逐渐下降, 当达到100 keV时, 比值降至86%. 这一变化表明, 随着入射X射线能量的不断升高, 纯散射所占比例逐渐减小, 而散射吸收比例逐渐增大, 即X射线因散射而损耗的能量相应增加. 对于XPNAV而言, 其适用能段大部分处于软X射线范畴, 在该能段下康普顿散射能量损耗并不显著, 因此散射光子能量大多仍处于探测器有效探测范围之内, 这为脉冲星导航技术中X射线信号的有效接收与利用提供了有利条件.

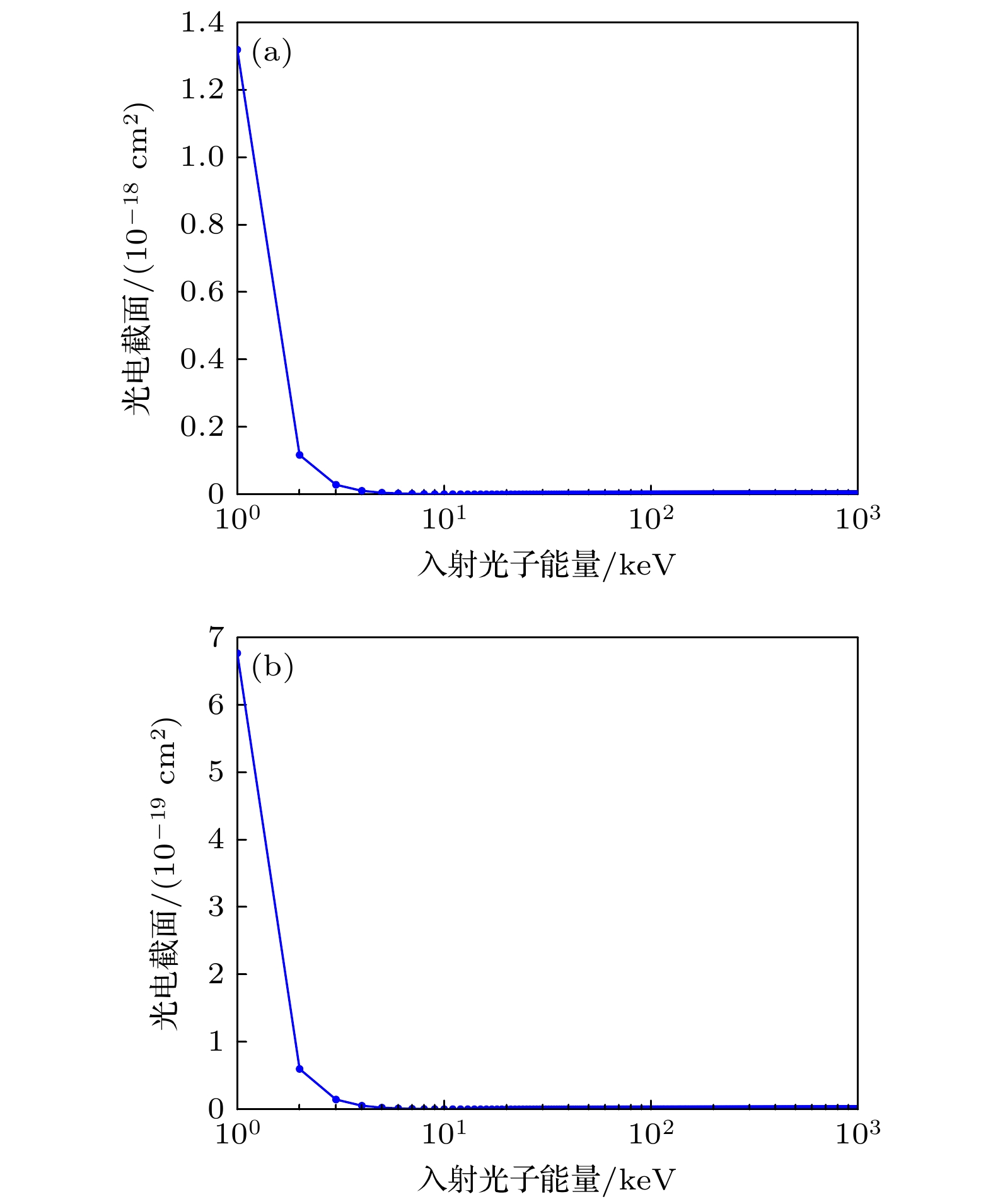
电离层内的大气成分主要为O₂, N₂, NO等, 其在相关分析中被作为独立的氮、氧原子进行处理. 为深入分析光电吸收截面与入射光子能量之间的内在联系, 依据(7)式得到了氧、氮原子的光电吸收截面随X射线能量的变化情况, 如图4所示. 从图4中数据可看出, 氮、氧原子的光电吸收截面变化规律呈现出高度的一致性. 这一现象主要是由于氮、氧原子的原子序数接近, 分别为7和8, 其壳层结构具有一定的相似性, 因此X射线光子与其相互作用时的光电吸收效应截面变化趋势基本一致.

电离层对X射线的吸收符合比尔-朗伯定律^[50]:

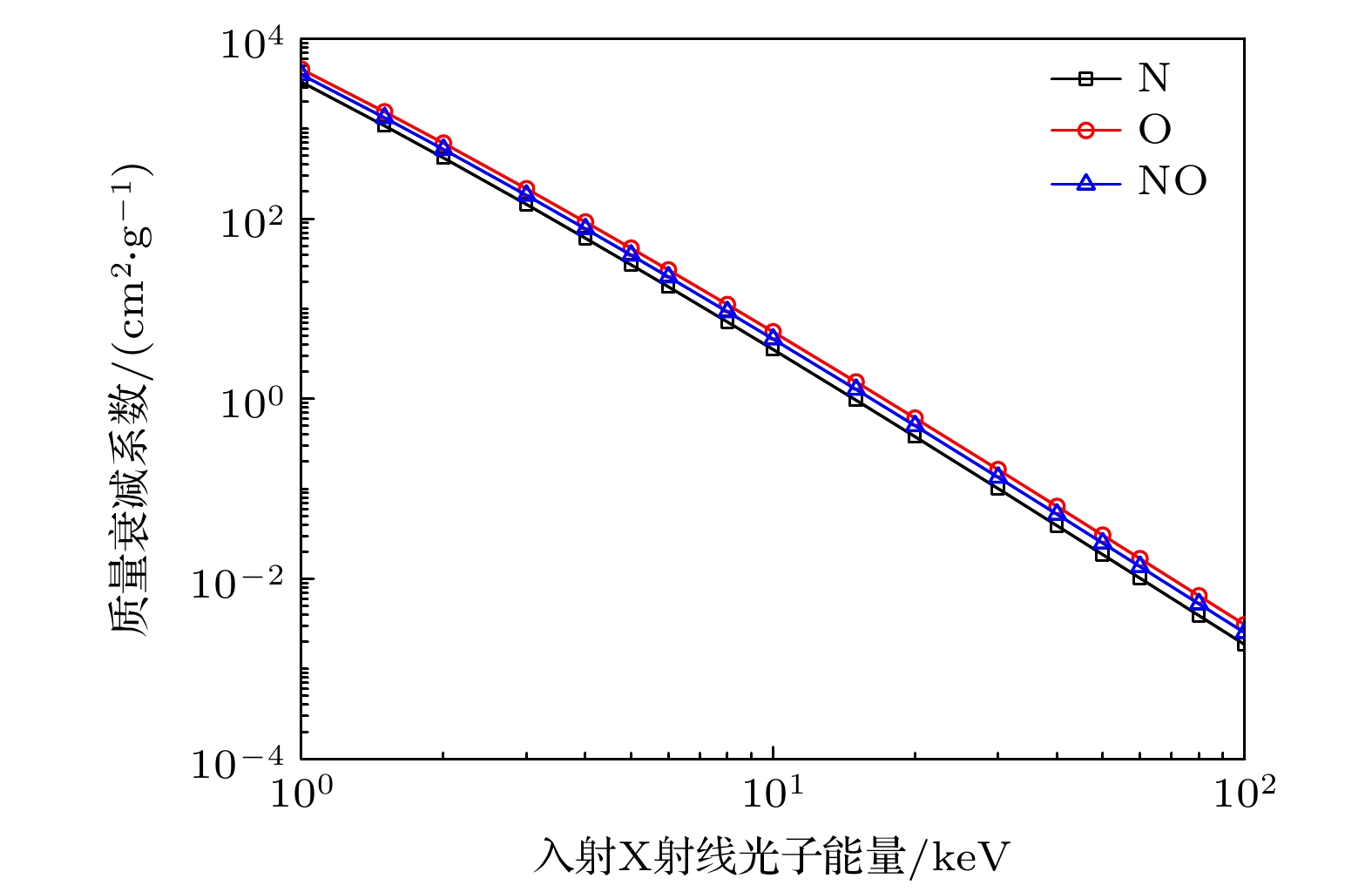
其中${I_0}$表示入射X射线强度; $I$表示出射X射线强度; $\rho $表示电离层内各原子的密度; x代表X射线在电离层中传播的路径长度; ${\mu _{\text{m}}}$为质量衰减系数, 表示单位质量的物质对X射线的吸收能力.

为进一步分析氮、氧原子以及一氧化氮分子等物质对X射线的吸收特性, 通过美国国家标准与技术研究院(National Institute of Standards and Technology, NIST)物理测量实验室给出的光子横截面数据库^[51], 获得其光电吸收质量衰减系数随入射X射线能量的变化曲线, 如图5所示. 由图5可知, 随着X射线能量的逐步增加, 氮、氧以及一氧化氮的质量衰减系数均呈现出逐渐减小的趋势. 这一现象进一步印证了在低能段X射线条件下, 物质对X射线的吸收作用更加显著.

通过对康普顿散射截面与光电吸收截面随入射X射线光子能量变化趋势的深入对比分析可知, 在低能段范围内, 光电吸收截面通常呈现出较大数值, 而随着能量的增加, 康普顿散射截面逐渐占据主导. 在低能段X射线与物质的相互作用过程中, 因光电吸收截面较大, 故以光电吸收作用为主导. 而当X射线能量不断增大时, 康普顿散射截面的下降速度相较于光电吸收截面更为缓慢, 因此在相对数值上逐渐凸显, 进而在各种作用机制中占据主导地位.

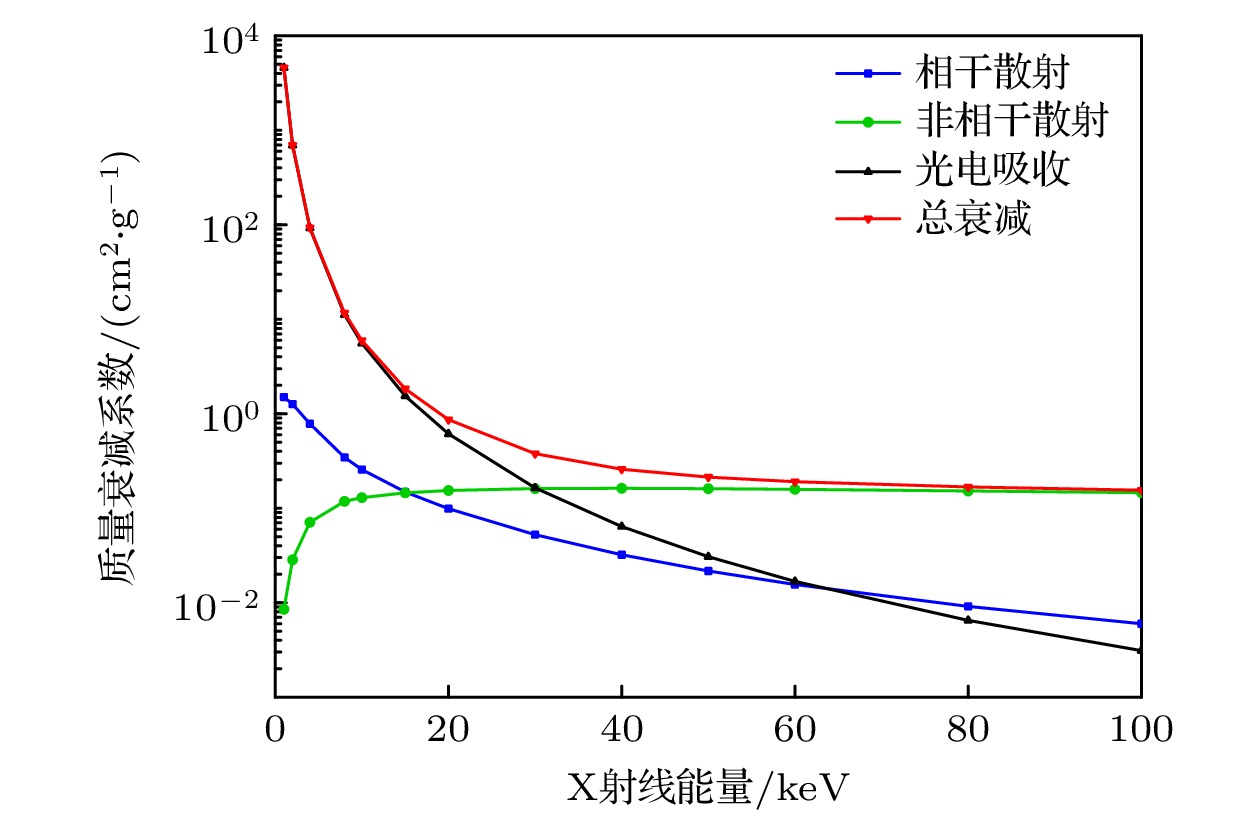
针对X射线的相干散射、非相干散射以及光电吸收过程, 为研究X射线与物质的相互作用机制, 以入射X射线能量作为输入变量分析X射线衰减特性. 详细记录各能段X射线经不同相互作用所产生的质量衰减系数, 其随X射线能量的变化曲线如图6所示. 从图6中数据可知, 随着入射X射线能量逐步增大, 相干散射、光电吸收以及总体的质量衰减系数均呈显著下降趋势, 而非相干散射的质量衰减系数则相反, 此结论与Churazov等^[52]中的研究成果相符. 在低能段X射线(小于20 keV)范畴内, 光电吸收是主要作用形式, 在各种相互作用中占比超出70%, 而随着X射线能量的持续增大, 康普顿散射逐渐上升至主导地位, 在50 keV以上时占比超出75%, 该趋势与前文分析结果一致.

适用于脉冲星导航的X射线能量一般较低(30 keV以下), 反射作用极其微弱, 可忽略不计. 对于该能段的X射线, 光电吸收发挥着主要作用, 相干散射和非相干散射均影响相对较小. 这一特性为研究脉冲星导航中X射线信号的传输与衰减机制提供了依据.

本节首先利用国际参考电离层模型IRI-2020与大气模型NRLMSIS 2.1, 对临近空间高度60—100 km范围内的电子、大气等密度展开全面分析, 为后续X射线在该区域的传输特性研究奠定基础; 然后, 使用MCNP5软件构建了X射线在临近空间的传输分层模型, 并依据电离层模型和大气模型所获取的物理参数, 模拟了X射线在不同计数层中的传播过程; 最后, 分析了1—30 keV能段的X射线光子在临近空间60—100 km高度范围内的传输效率, 给出了导航常用脉冲星在临近空间的流量数据获取方法, 有效地提高了脉冲星导航中信号流量数据的准确性.

1) IRI-2020电离层模型

本文使用国际参考电离层模型IRI-2020获取了电离层不同高度下的电子密度、电子温度、离子温度等月平均数据. 该模型旨在精准刻画地球电离层状态, 能够描述50—1500 km高度电离层参数的全球分布情况, 适用范围涵盖任意时刻、任意日期及各种太阳和地磁活动条件^[53,54].

CCMC Instant Run System为实现IRI-2020模型的在线计算提供了便利平台: 在操作界面中, 将高度范围设定为60—100 km, 步长定义为1 km, 并输入时间、坐标系、经纬度等参数, 即可基于IRI-2020模型生成对应时刻、对应地理位置上空60—100 km高度区间内, 每隔1 km的电离层详细数据. 这为分析电离层特性、划分临近空间X射线传输分层模型计数层高度提供了详实的数据支撑.

以南极中山站(69.4°S, 76.4°E)为例, 由IRI-2020模型获取其协调世界时(Universal Time Coordinated, UTC)2022年2月11日10:00在100 km高度下的电子密度为74731 cm^–3, 经(2)式计算获得了该位置电磁波入射临近空间电离层的临界频率为2.46×10⁶ Hz, 显著低于X射线频率. 因此, 当X射线进入电离层时, 由于其频率远高于临界频率, 在这一过程中基本不会发生反射现象. 与前文通过理论分析所得到的结果高度吻合, 进一步验证了相关理论分析的正确性与可靠性.

2) NRLMSIS 2.1大气模型

本文使用大气模型NRLMSIS 2.1获取60—100 km高度的大气密度. 该模型是大气科学领域中用于描述地球中性大气状态的重要经验模型, 以长期累积的大量观测数据为支撑, 综合纳入了多个影响大气状态的关键要素. 通过对太阳黑子数、射电通量等太阳活动指标以及地磁指数的分析, 结合季节与经纬度、高度等地理参数, 运用复杂的数学公式与经验关系, 精准刻画大气密度、温度及成分等参数, 能够实时、准确地反映大气状态变化情况^[55].

与IRI-2020模型运用方式类似, 在向NRLMSIS 2.1模型输入参数后, 该模型能够精准运算并输出某一特定时刻、特定地理位置上空60—100 km高度范围内的大气密度数据, 这同样也是在建立临近空间X射线传输分层模型中划分计数层高度、对分层模型进行几何建模与材料建模的重要依据.

为分析临近空间60—100 km高度下的X射线传输特性, 本文以NRLMSIS 2.1模型与IRI-2020模型所提供的数据为基础, 利用蒙特卡罗粒子输运软件MCNP5, 建立了X射线在临近空间的传输分层模型. 本研究参考了周围^[31]提出的建模方法, 但针对临近空间XPNAV实际应用场景调整了实验参数, 以适应本文研究需求.

采用蒙特卡罗方法模拟粒子与物质间的相互作用机制, 该方法通过描述概率过程可实现对物理现象的可靠预测. MCNP5软件在模拟光子、电子等粒子输运问题领域具有广泛应用, 可模拟1 keV—1000 MeV能量范围内的电子和光子行为^[56]. 本文从以下两个方面建立临近空间X射线传输模型:

1)几何建模

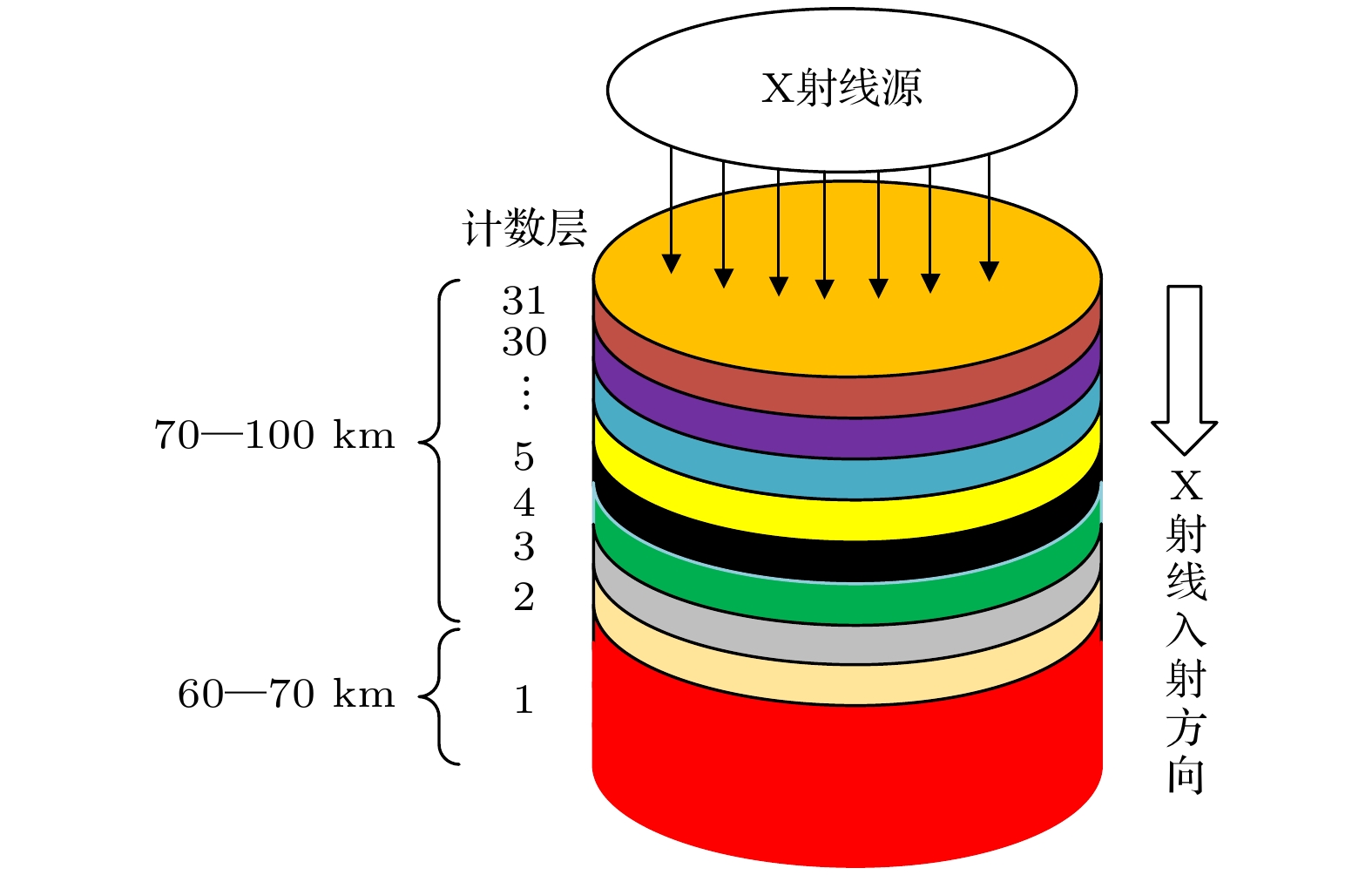
首先进行几何建模, 实现大气分层结构的合理划分, 确保模拟过程中各层的高度、厚度及形状等特征得以准确表征^[57]. 考虑设置半径过大可能导致实测数据无法准确反映该位置真实环境情况的问题, 将60—100 km高度的大气层空间构建为一个半径10 cm、高度40 km的圆柱体结构, 同时将X射线源设定为该圆柱体上方半径10 cm的圆形平面, 如图7所示.

依据IRI-2020模型、NRLMSIS 2.1模型所提供的不同高度电子、大气密度等数据, 对60—100 km高度的大气层再进行精细划分. 由于70—100 km区间离子密度高且变化大, 为提高模型的几何精度, 充分体现不同高度的密度变化, 本文采用1 km为单位进行分层; 而在60—70 km区间内密度低且变化小, 将其单独作为一层. 这不仅有助于在模拟过程中精确界定各层的高度和厚度, 还能准确表征各层的形状特征, 为后续研究提供几何建模基础.

2)粒子源参数与材料建模

粒子源参数包括粒子类型、能量分布、粒子数量与方向等, 是建立临近空间X射线传输模型的基本参数. 材料建模用于确定不同计数层内的空气密度及各原子占比, 使模型中各区域的物理属性能够如实映射真实环境条件. 本文所设置粒子源类型为光子, 能量分布为1—30 keV, 粒子数量为10⁶个, 发射方向竖直向下. 材料建模采用南极中山站上空的环境条件, 不同计数层的空气密度及所含原子占比可由NRLMSIS 2.1模型获得. 与周围^[31]相比, 本文面向临近空间XPNAV应用需求, 针对特定高度范围和导航能段, 构建了自上而下的X射线脉冲星信号传输模型, 模拟了脉冲星信号穿越大气的实际过程.

综上, 本文实现了临近空间X射线传输模型中不同高度空间范畴、空气密度的精细划分与设定, 保障了模拟结果的准确性.

首先, 利用所建模型, 使用MCNP5软件进行模拟, 获得各计数层光子数量. 当粒子抵达不同材料界面, 对涵盖散射、吸收等在内的多种复杂物理过程进行模拟, 记录每个粒子的运动历史和相互作用事件. 通过对大量粒子路径进行统计分析, 获得各计数层光子数量, 以此作为计算传输效率等关键指标的重要依据.

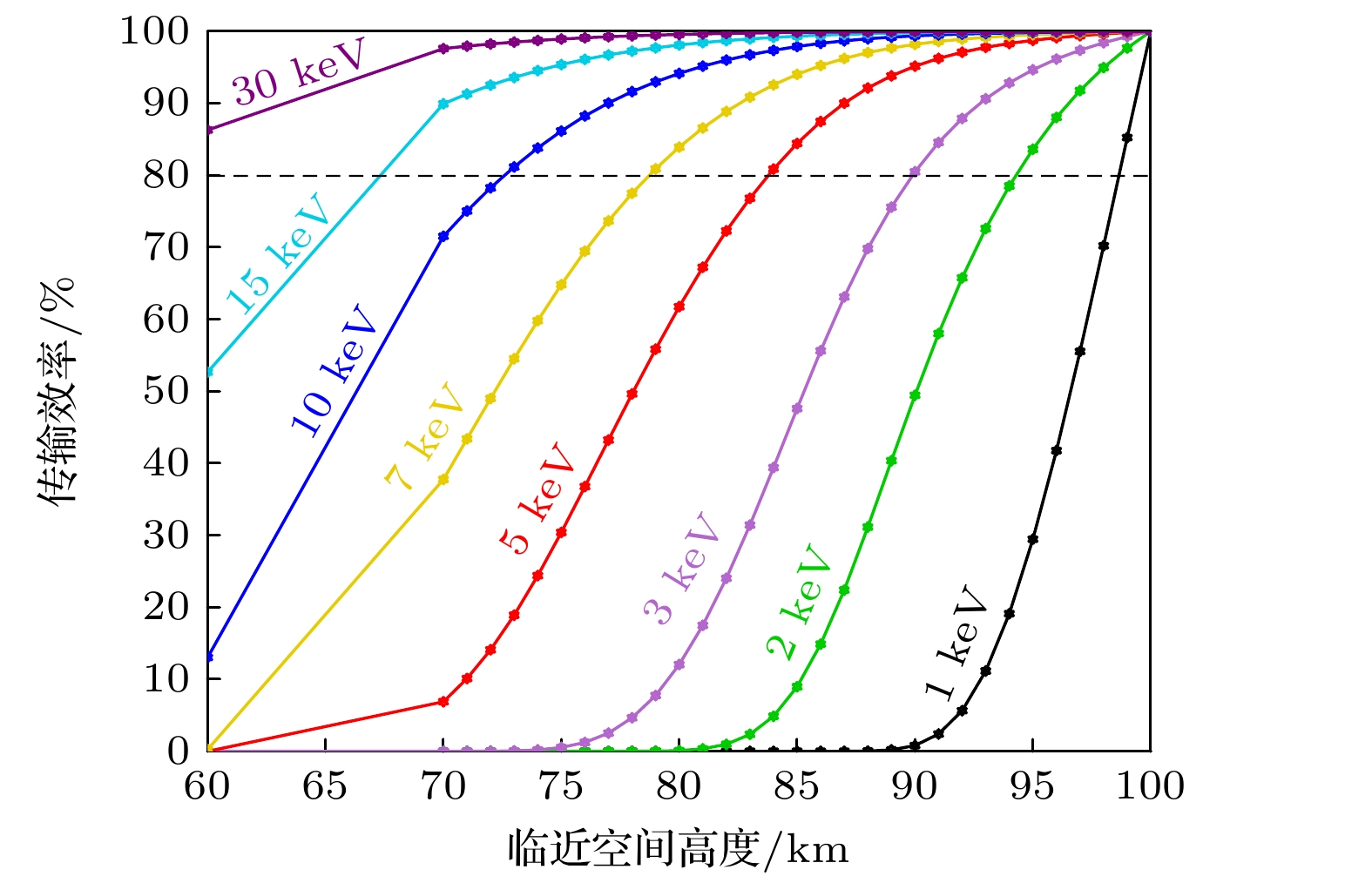
然后, 计算X射线光子传输效率. 根据记录的各层X射线光子数量, 将其与信号发射端的总光子数之比定义为传输效率$ \mu $, 数值越大传输效率越高. 本文基于所提分层模型, 对60—100 km高度处1—30 keV能段的传输效率进行分析. 选取时间为UTC时2022年2月11日10:00, 地点为南极中山站, 结果如图8所示.

由图8可知, 传输效率与高度、X射线能量呈显著正相关, 随着高度的增加以及X射线能量的提升, 传输效率逐渐增大, 与周围^[31]的模拟结果具有相同的变化趋势. 当X射线能量高于10 keV时, 传 输效率通常超过80%; 以10 keV为例, 其在75 km以上传输效率高于85%. 出现这一现象主要有两方面原因, 一方面随X射线能量的升高, 其穿透大气层中物质的能力逐渐增强; 另一方面随高度的增加, X射线经历的衰减减少, 同时大气也更加稀薄, 物质的吸收和散射作用减弱.

最后, 在得到传输效率后, 可根据大气外脉冲星流量参数, 计算出脉冲星在临近空间中的流量数据:

其中$ {\lambda _{\text{s}}} $为X射线脉冲星源流量, $ {\lambda _{\text{n}}} $为X射线脉冲星在临近空间的流量. 表1所列为五颗导航常用脉冲星的流量^[58,59], 所提方法对其他X射线脉冲星同样适用.

电离层的电子密度、大气密度及各种组分具有显著的时空变化特性, 其变化规律与季节、纬度及昼夜等因素密切相关, 作为X射线在临近空间传输的关键介质参数, 它们通过调控X射线和各种粒子的相互作用过程, 直接影响X射线的传输效率. 因此, 本节利用所提传输分层模型, 分别从季节和纬度、昼夜等方面分析了X射线脉冲星信号的传输效率, 给出其分布特征. 同时, 为分析传输效率变化成因, 本节先基于IRI-2020电离层模型与NRLMSIS 2.1大气模型, 对大气密度和电子密度的变化规律进行分析, 然后将传输效率的分布特征与其对比.

根据第3节分析, 由于10 keV的X射线在75 km以上具有较高的传输效率, 本节的分析条件设 为: 能量10 keV; 高度75 km; 地理位置选取: 南极地区(69.4°S, 76.4°E), 北极地区(69.4°N, 76.4°E), 赤道地区(0°, 76.4°E).

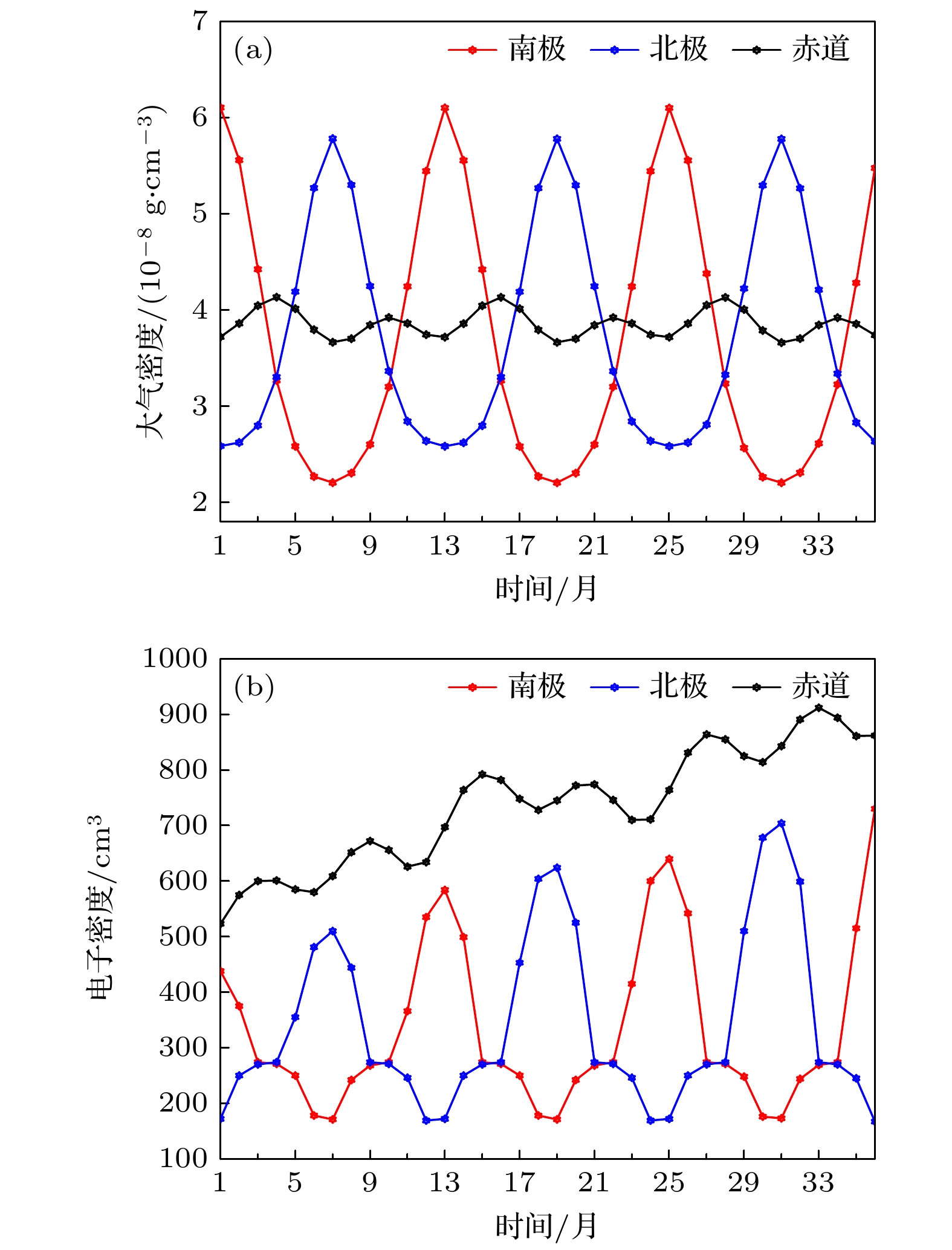
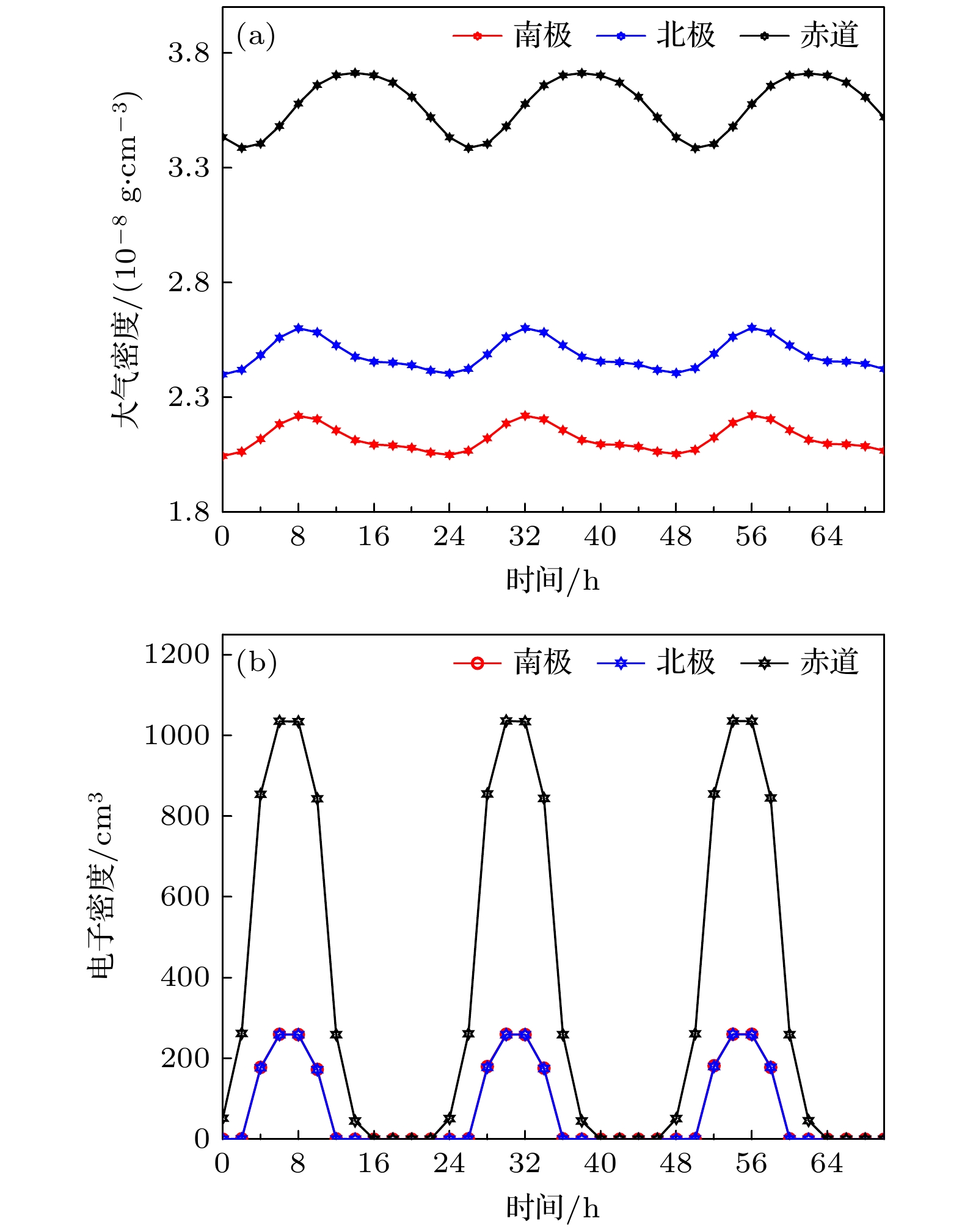
首先, 分析了三个区域的大气密度和电子密度随季节和纬度的变化规律, 给出了2022—2024年连续36个月的大气密度和电子密度, 如图9(a)和图9(b)所示. 可见, 两者在南北极地区的最大值主要出现在当地半球夏季期间, 而赤道带则表现出半年周期性变化, 与文献[60–63]的分析相符.

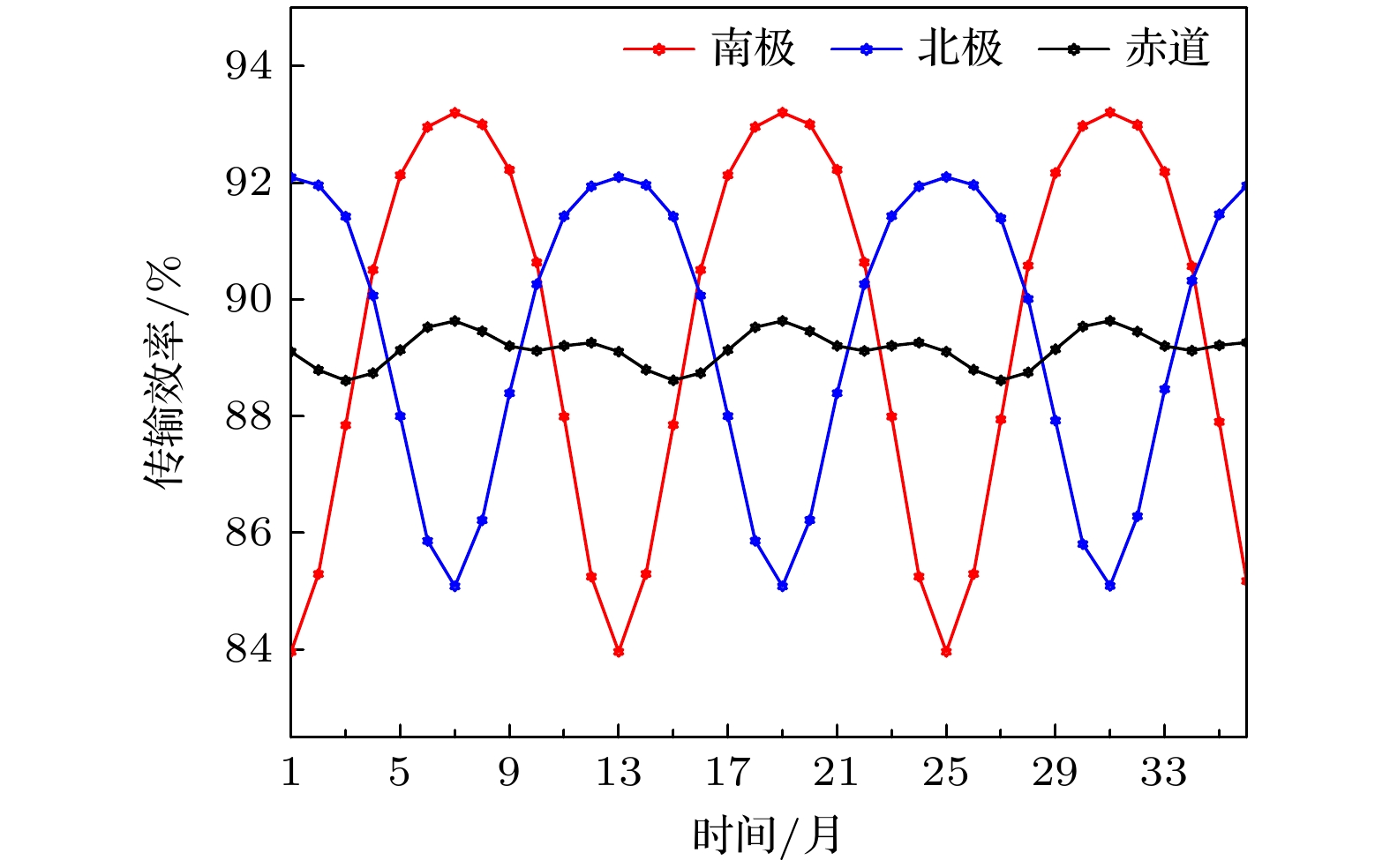
然后, 根据所提传输模型, 给出了10 keV能量X射线在75 km高度传输效率的季节性变化曲线, 如图10所示. 可见X射线传输效率在南北极有着显著的年变化特征, 在赤道地区呈现微弱的半年变化特征. 南极地区传输效率在冬季达到最大值93.20%; 在夏季达到最小值83.96%. 北极地区的季节性变化规律与南极相同, 冬季的传输效率最大值比南极低1.11%. 而赤道地区的传输效率均值为89.15%, 极差为1.02%.

由图9和图10对比可知, 南北极地区在当地夏季大气密度和电子密度升高, 导致X射线与大气粒子的相互作用概率增加, 进一步加剧了X射线衰减, 引起传输效率的降低. 因此, 传输效率与大气密度、电子密度的变化趋势大致相反, 在每年南极地区7月、北极地区1月显著优于同纬度其他时段; 在南极地区1月、北极地区7月最低; 在赤道地区变化不大, 7月达到最优.

本节选取南北极及赤道地区传输效率最高的月份进行分析, 南极和赤道区域为2024年7月1—3日、北极区域为2024年1月1—3日. 由于UTC时无法准确反映各区域的当地实际时间, 本文采用地方时(local time, LT)进行分析. 所选地区均位于东五区, 地方时比UTC时快了约5 h.

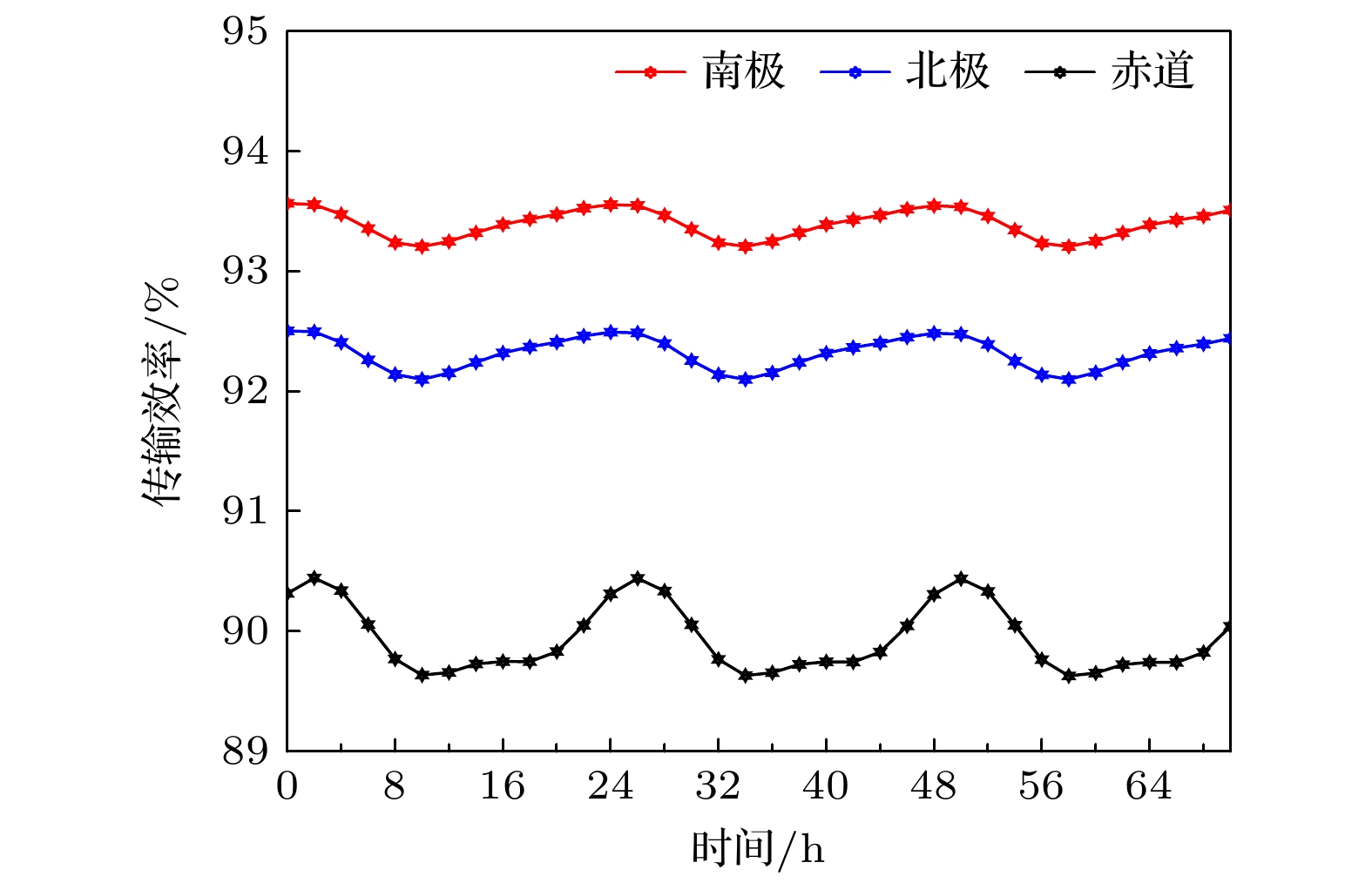
首先, 分析了大气密度和电子密度, 给出了其在三天内各区域的变化情况, 如图11(a)和图11(b)所示. 图中横轴0为UTC时0时, 对应LT时5时. 可以看出, 大气密度与电子密度均呈现显著的日 升夜降特征, 这一趋势与文献[64,65]的论述相符. 两者在凌晨至清晨期间维持较低水平, 到下午升至峰值, 在夜间逐渐减小. 其中, 图11(b)中南极地区和北极地区的变化曲线基本重合.

然后, 根据所提传输模型, 获得了10 keV能量的X射线在两极及赤道地区75 km高度传输效率的昼夜变化曲线, 如图12所示. 由图12可见, 各地区的传输效率均呈现出昼降夜升的日周期性变化. 传输效率在LT时7时(UTC时2时)左右达到最大值, 15时(UTC时10时)降至最低, 南北极及赤道地区的最大传输效率分别为93.57%, 92.50%, 90.44%, 对应的极差分别为0.36%, 0.40%和0.82%. 将图11与图12进行对比, 可见传输效率与大气密度、电子密度的昼夜变化趋势大致相反.

由本节分析可知, 传输效率在南北极及赤道地区凌晨至清晨时段较高, 下午降至最低, 且赤道地区波动幅度略大于两极, 最大不超过0.82%.

针对临近空间X射线脉冲星信号传输特性, 本文首先分析了1—30 keV能量的X射线在60—100 km高度范围内的传输效率, 结果表明传输效率随高度和X射线能量的增加显著提升; 其次, 分析了南北极和赤道地区三年传输效率, 其在南北极有着显著的年变化特征, 在赤道地区呈现微弱的半年变化特征, 于冬季半球处于最大值, 夏季半球处于最小值, 且极地地区波动幅度远高于赤道; 最后, 对南北极及赤道地区连续三日的传输效率进行分析, 结果表明传输效率有周期性的昼降夜升变化, 昼夜波动幅度不超过0.82%. 综上所述, 在南极冬季清晨时段, 10 keV能量的X射线在75 km高度传输效率最高可达93.57%, 较夏季的最低值提升9.61%, 为X射线脉冲星导航在临近空间的应用研究提供了数据支撑.

鉴于篇幅限制, 本文在传输效率影响因素分析中仅给出了赤道和南北极三个代表性地区的结果, 分析方法在其他地区仍适用. 此外, 本文精度受限于IRI-2020电离层模型和NRLMSIS 2.1大气模型, 虽然该模型充分考虑了太阳活动和地磁活动, 但其对传输效率的影响有待进一步研究.