量子绝热控制技术提供了一套控制量子系统的有效思路, 其理论基础是量子绝热定理. 1928年, Born和Fock^[1,2]提出量子体系绝热跟随其能量本征态进行演化的理论. 他们证明: 如果系统特定能量本征值和能谱的其余部分之间有一个能隙, 并且作用在其上给定的含时微扰足够缓慢, 那么系统总能够保持在其相应的瞬时本征态上. 量子绝热定理是量子理论中最重要的结论之一, 在理论和实际中有着十分广泛的应用^[3,4]. 在量子绝热演化中, 受激拉曼绝热通道(stimulated Raman adiabatic passage, STIRAP)过程是实现粒子数布居转移的最有效方案之一^[5]. 1991年, Shore等^[6]展示了在原子或分子中两个离散量子态之间绝热布居转移的有效方法. 该方法很快被推广到具有三个离散量子态的系统中^[7–11]. 两个时滞激光脉冲被应用到一个三能级结构中, 以实现两个更低能级间(通过一个能量更高的中间能级)的完全布居转移. 特别是, 在STIRAP方案中采用的脉冲序列是反直觉的, 即斯托克斯(Stokes)激光脉冲耦合中间态和末态, 先于(但要重叠)泵浦(pump)激光脉冲打开, 而后者耦合初始和中间态. 激光场的强度应足够高, 以便产生多个拉比振荡循环. 量子态间激光诱导的相干性可利用时间延迟进行调节, 保证中间态的瞬时布居几乎为零, 避免辐射衰减引起的布居损耗^[5,6,12]. 为了实现更高效率的转移, 这就要求系统满足特定的绝热条件^[13]. 然而, 满足绝热条件的过程一定是个极其缓慢的过程, 在实际应用中通常具有显著缺点.

为了加快量子绝热过程并保持高转移效率, 研究者们提出了一些新的控制方案, 例如量子绝热捷径(STA)^[14–16]. 该方案已经在很多系统中得到深入的讨论, 如核磁共振自旋系统^[17]、量子点系统^[18]、腔中的原子系统^[19–21]以及超导量子比特系统^[22]等. 在宏观量子系统的操控方面, 研究者们还研究了旋量玻色-爱因斯坦凝聚体的非绝热量子控制^[23,24]. 除此之外, 目前能够加快量子绝热转换的方法还包括无跃迁量子驱动^[25,26]、基于Lewis-Riesenfeld绝热不变量理论^[27,28]、快速向前方法^[29,30]以及非厄密捷径技术^[31–33]等. 这些方法为量子系统布居转移过程的绝热捷径奠定了坚实的理论基础. 最近, 研究人员提出了一种基于动力学量子几何张量对STIRAP进行优化的方法, 其利用最优控制技术沿参数空间测地线路径实施量子态的演化, 以消除或降低过程中的非绝热效应^[34,35]. 这种方法可以显著缩短绝热量子转移过程所需的时间, 并对系统误差和随机误差具有很好的鲁棒性. 然而, 现有研究主要针对失谐为零的非简并三能级系统, 对于有失谐且存在能级简并的多能级系统尚未被研究.

本文旨在研究利用动力学量子几何张量对含单光子失谐的$ {{\Lambda }} $型三能级系统和三脚架型四能级系统中STIRAP技术进行优化. 第2节给出了基于动力学量子几何张量实现多能级STIRAP技术优化控制的一般理论框架. 第3节详细给出对具有单光子失谐的三能级系统的优化方案与计算结果. 第4节给出了对具有失谐的四能级系统的优化方案与计算结果, 重点讨论了四能级系统中简并双暗态的解耦与量子叠加态的快速高效制备. 通过与传统STIRAP方法的比较, 本文展示了优化STIRAP方法在多能级系统量子态布居转移过程中的鲁棒性. 最后给出研究结论.

首先介绍动力学量子几何张量的定义并基于该张量对STIRAP进行优化的一般理论框架(下文称为优化STIRAP或OSTIRAP). 考虑一个由含时哈密顿量$ H\left(t\right) $描述的N维量子系统, 其非简并瞬时本征值和本征态用$ {E}_{n}\left(t\right) $和$ |{E}_{n}\left(t\right)\rangle $表示, 其中1$ \leqslant n\leqslant N $. 根据量子绝热定理, 若体系初始时刻处在系统哈密顿量的第n个本征态上, 只要参数变化足够缓慢, 则体系的末态仍将保持在其第n个绝热本征态. 然而, 对有限时间内的过程, 系统随时间的演化将会产生非绝热跃迁, 从而导致其偏离绝热本征态, 最终影响系统的布居转移效率.

为确定非绝热跃迁的程度, 可在绝热基下将时间演化态展开, 即$ \left|{\psi }_{n}\right(t)\rangle =\displaystyle\sum \nolimits_{l}{c}_{nl}\left(t\right)\left|{E}_{l}\right(t)\rangle $. 态矢量满足的薛定谔方程可被转化为关于态矢振幅的方程:

绝热本征态$ |{E}_{n}\left(t\right)\rangle $的非绝热跃迁程度可以用非绝热跃迁概率$ {P}_{n}^{{\mathrm{T}}}\left(t\right)=\displaystyle\sum\nolimits _{l\ne n}|{c}_{nl}\left(t\right){|}^{2} $来定量描述. 根据高阶绝热近似理论^[36–38], $ {P}_{n}^{{\mathrm{T}}}\left(t\right) $的一阶项存在上下界, 即$ {P}_{n, -}^{{\mathrm{T}}}\left(t\right)\leqslant {P}_{n}^{{\mathrm{T}}}\left(t\right)\leqslant {P}_{n, +}^{{\mathrm{T}}}\left(t\right) $. 其中,

其中$ \tau $是演化过程所需要的时间. $ {\tilde{T}}_{nl} $描述第$ n $个和第$ l $个能级之间的非绝热跃迁率, 其具体形式为

其中, s = t/τ为归一化后的时间. 系统整体非绝热跃迁率为$ {\tilde{T}}_{n}\left(s\right)\equiv {[\displaystyle\sum\nolimits _{l\ne n}|{\tilde{T}}_{nl}(s){|}^{2}]}^{1/2} $. 若系统中参数$ {R}_{p, q}\left(t\right) $ $ (1\leqslant p, q\leqslant {{M}}) $具有时间依赖性, 则系统哈密顿量$ H\left(t\right) $是含时的. 整体非绝热跃迁率可利用动力学量子几何张量来计算, 即^[34,35]:

其中, 动力学量子几何张量$ {D}_{n, pq} $被定义为

作为参数空间的度规, $ {D}_{n, pq} $定量刻画整体非绝热跃迁率, 并在体系整个优化过程中起主导作用^[34]. 为了使演化过程保持在绝热通道中, 应使整体非绝热跃迁率$ {\tilde{T}}_{n}\left(s\right) $为尽可能小的常数. 这将使得时间演化态均匀地偏离绝热本征态, 并导致系统出现绝热共振现象, 即在共振点处系统回到绝热本征态^[39]. 此时(2)式中非绝热跃迁概率的上下界变为$ {P}_{n, \pm }^{{\mathrm{T}}}=\pm 4{\tilde{T}}_{n}^{2}\left(s\right)/{\tau }^{2} $, 与工作时间的平方成反比. 基于$ {\tilde{T}}_{n}\left(s\right) $为常数设计的绝热控制脉冲, 可以在短时间内达到高效率的量子绝热布居转移.

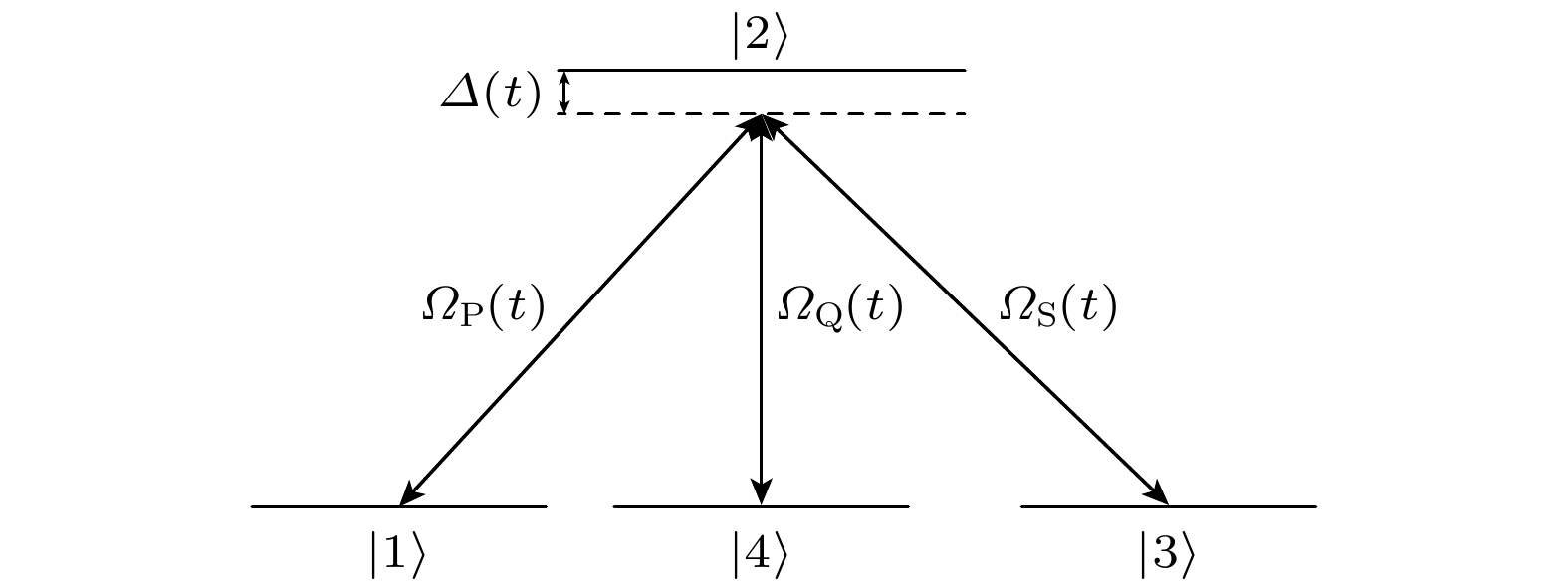
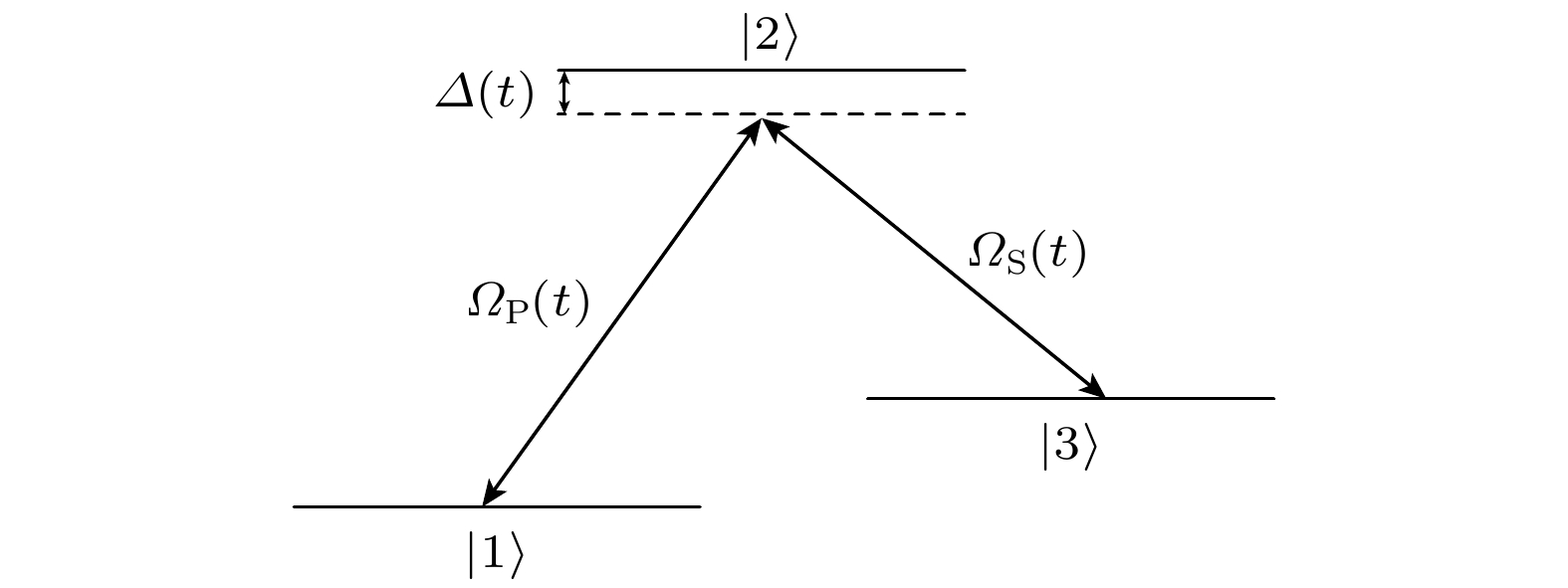
运用上述理论对图1所示的$ {{\Lambda }} $型三能级系统的STIRAP方案进行优化, 以实现系统粒子数布居从态$ |1\rangle $到$ |3\rangle $的快速高效转移. 本文重点讨论存在单光子失谐时基于动力学量子几何张量的三能级系统的优化方案及其计算结果, 其中自然包含了失谐量为零的情况.

在旋转波近似下, 图1所示三能级系统的哈密顿量为^[40–44]

其中, $ {\varOmega }_{{\mathrm{P}}}\left(t\right) $代表耦合态$ |1\rangle $和$ |2\rangle $的泵浦激光脉冲, $ {\varOmega }_{{\mathrm{S}}}\left(t\right) $代表耦合态$ |3\rangle $和$ |2\rangle $的斯托克斯激光脉冲, $ \varDelta \left(t\right) $为单光子失谐量. 该哈密顿量的本征值为$ {\lambda }_{0}= 0 $, $ {\lambda }_{\pm } $=$ \hslash [\varDelta \pm \sqrt{{\varDelta }^{2}+{\varOmega }^{2}}]/2 $, 其中$ \varOmega = \sqrt{{\varOmega }_{{\mathrm{S}}}^{2}+{\varOmega }_{{\mathrm{P}}}^{2}} $. 系统对应的本征态为

其中, 混合角满足$ {\mathrm{tan}}\theta \left(t\right)=\dfrac{{\varOmega }_{{\mathrm{P}}}\left(t\right)}{{\varOmega }_{{\mathrm{S}}}\left(t\right)} $和$ {\mathrm{tan}}2\phi \left(t\right)= \dfrac{\varOmega \left(t\right)}{\varDelta \left(t\right)} $. 本征值$ {\lambda }_{0}=0 $对应的本征态$ \left|{\lambda }_{0}\rangle \right. $被称为暗态, 其余态被称为亮态.

根据(5)式可以计算出有失谐时三能级系统的动力学量子几何张量^[34,35]:

其中,

利用(4)式可得到三能级系统的整体非绝热跃迁率:

(9)式给出了一般情况下系统总的非绝热跃迁率$ {\tilde{T}}_{n}\left(s\right) $. 当$ \varDelta =0 $时, 系统的动力学量子几何张量和整体非绝热跃迁率将退化为无失谐时的相应结果^[34]. 通过保持整体非绝热跃迁率为常数, 绝热演化过程中的非绝热效应可被周期性自消除, 从而导致在相对短的时间内实现绝热转移^[34,39].

利用整体非绝热跃迁率对脉冲进行优化, 使得$ {\tilde{T}}_{n}\left(s\right) $为常数, 计算可以得到一种满足条件的拉比脉冲组合:

此时整体非绝热跃迁率:

该式表明激光脉冲强度$ {\varOmega }_{0} $越大, 整体非绝热跃迁率将越小, 系统布居的转移效率就越高. 当s = 0时, 系统的演化态与暗态重合, 随后也将沿着暗态通道进行演化. 当s = 1时, 系统自然演化到最终的目标态. 由(10)式可知, 在$ s=\left[{\mathrm{0, 1}}\right] $的范围内, 优化脉冲的相位$ \alpha s $将从0变化到$ \alpha $, 优化脉冲相位$ \alpha s $与传统STIRAP过程中的混合角$ \theta = {\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{t}}{\mathrm{a}}{\mathrm{n}}\left({\varOmega }_{{\mathrm{P}}}/{\varOmega }_{{\mathrm{S}}}\right) $等价. 后面的计算取优化脉冲参数$ \alpha ={\mathrm{\pi }}/2 $, 这将使初始布居在态$ \left|1\right.\rangle $的粒子最终能完全转移到态$ \left|3\right.\rangle $上.

基于拉比脉冲形式(10), 可以计算优化脉冲作用下系统布居数的演化结果. 传统STIRAP方案采用如下的高斯型激光脉冲:

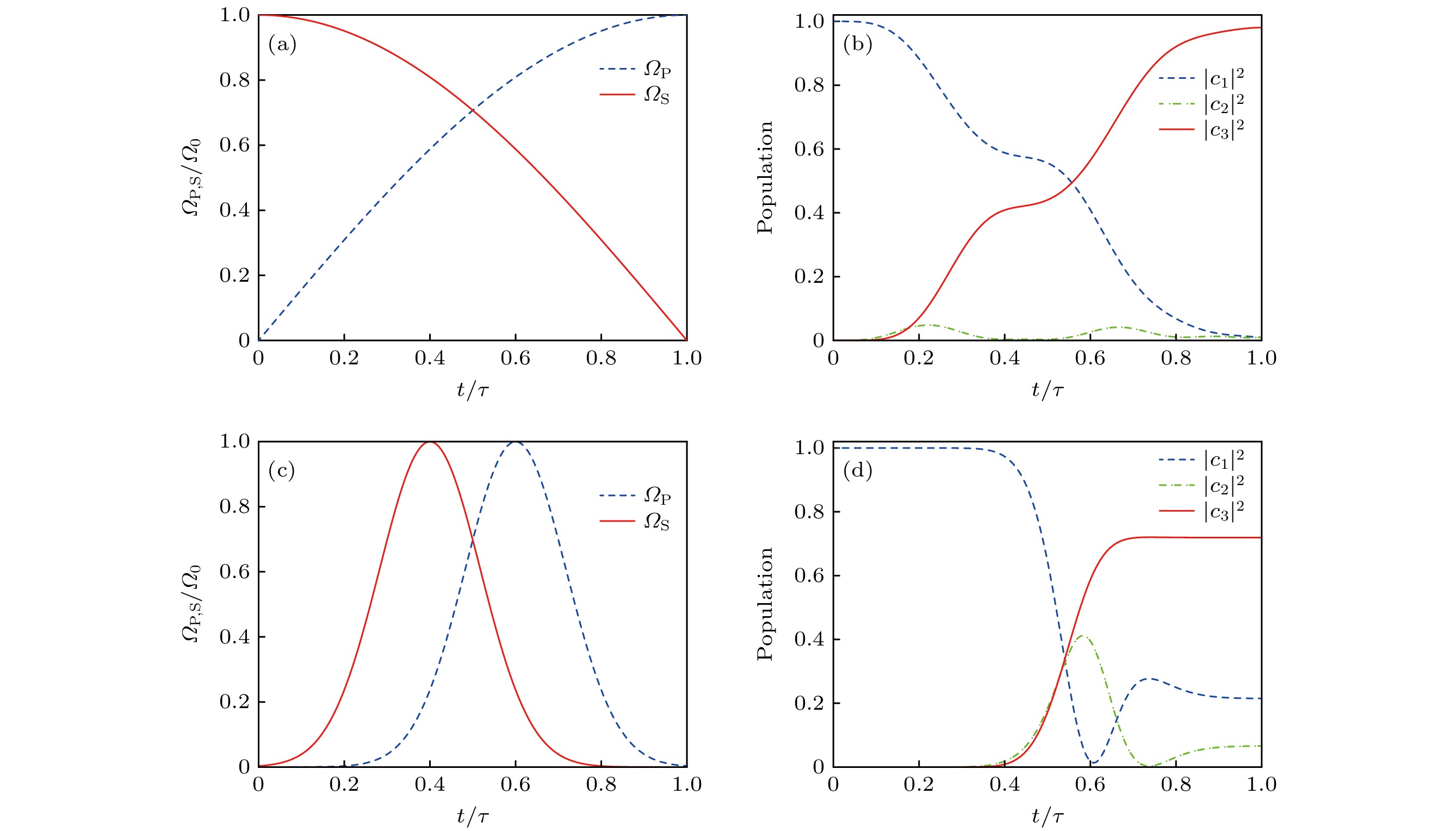
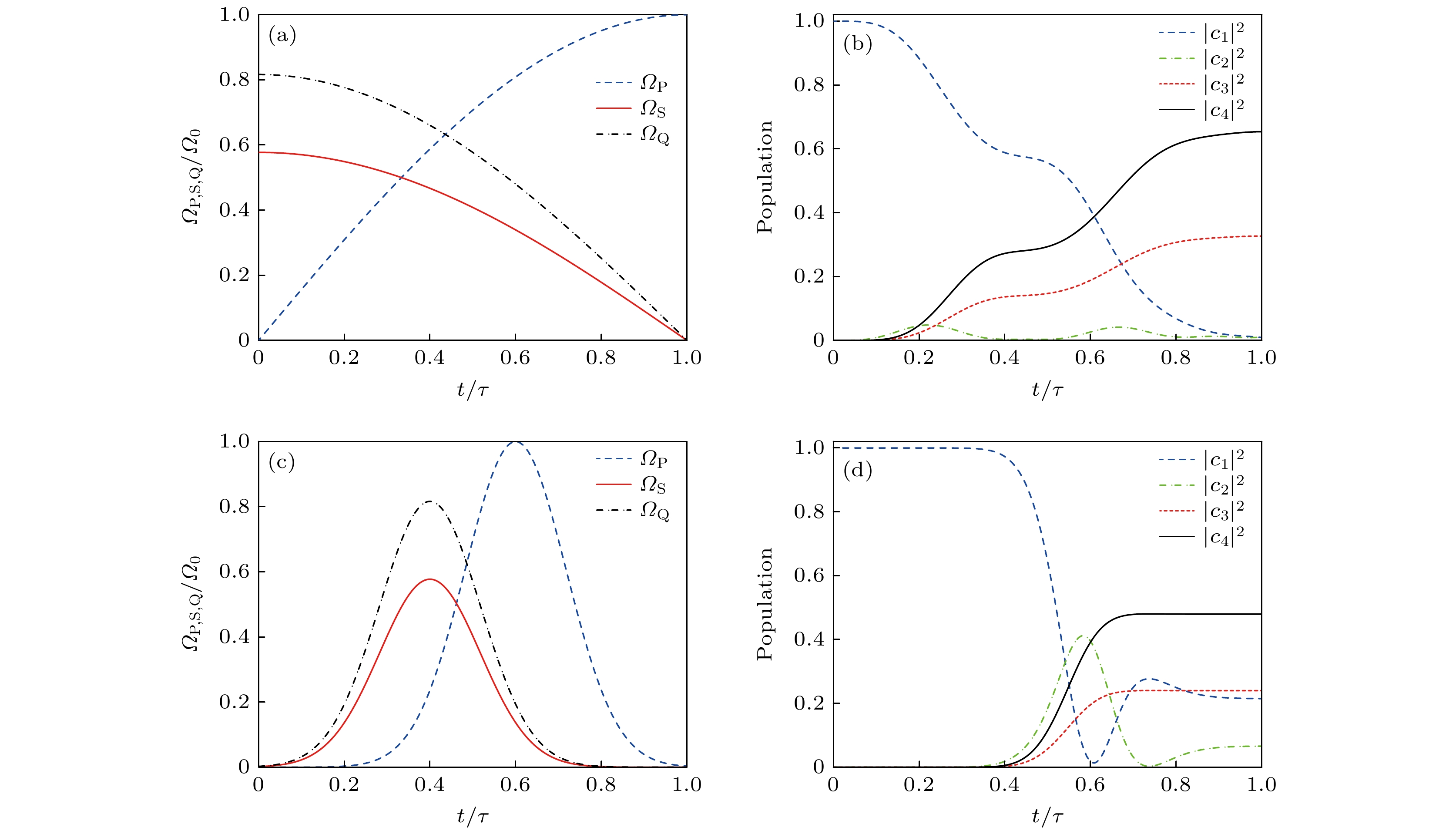
通过比较优化STIRAP和传统STIRAP两种方案的演化结果, 展示采用动力学量子几何张量优化STIRAP的优越性. 计算中设定脉冲半最大全宽$ \sigma =\tau /6 $, 两脉冲的分离时间$ \mu =\tau /10 $.

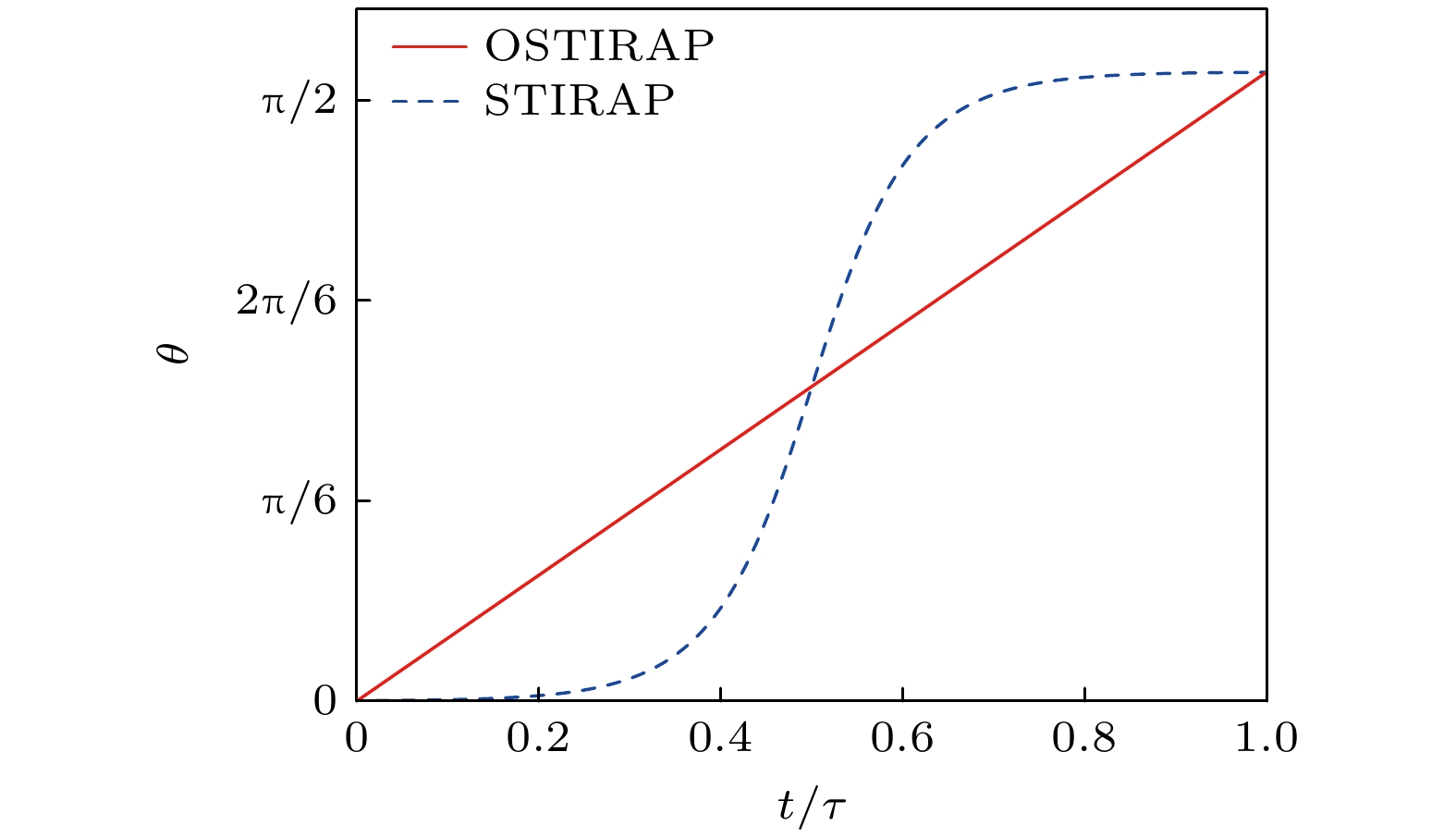
图2(a)和图2(c)分别为优化STIRAP和传统STIRAP的脉冲结构. 优化后的STIRAP脉冲从演化开始时斯托克斯脉冲强度达到最大, 而泵浦脉冲强度为零. 随着演化的进行, 斯托克斯脉冲强度按$ {\mathrm{cos}}\left({\mathrm{\pi }}s/2\right) $的规律减小, 泵浦脉冲强度按$ {\mathrm{s}}{\mathrm{i}}{\mathrm{n}}\left({\mathrm{\pi }}s/2\right) $的方式增大. 相比之下, 传统STIRAP的高斯脉冲结构在演化开始时斯托克斯脉与泵浦脉冲强度均为零, 但斯托克斯脉冲强度将先达到最大, 随后泵浦脉冲强度达到最大, 为反直觉的脉冲序列. 优化STIRAP和传统STIRAP粒子数布居的演化情况如图2(b), (d)所示, 可以看出, 优化后的STIRAP将粒子数布居转移到态$ \left|3\right.\rangle $上的效率达到98%以上, 而传统STIRAP的转移效率约为72%. 原因是系统的工作时间τ较短, 传统STIRAP方案无法较好地满足绝热条件. 优化STIRAP方案中的非绝热跃迁率是一个较小的常数, 因此即使在较短的工作时间内, 非绝热跃迁率也不会很大, 可以很好地实现绝热转移.

我们可以从混合角随时间的变化来进一步考察优化STIRAP和传统STIRAP的区别. 图3给出了两种转移方案中系统混合角随时间的变化情况. 传统STIRAP方案中的混合角$ \theta \left(t\right) $在s从0.3—0.7期间变化率较大, 这将破坏局部绝热条件, 使得系统的非绝热跃迁率升高, 粒子数布居不断转移到亮态通道. 优化STIRAP方案中等效混合角$ \alpha s $, 是一条过原点且斜率为$ \alpha $的直线. 在演化结束时, 有$ \alpha s={\mathrm{\pi }}/2. $

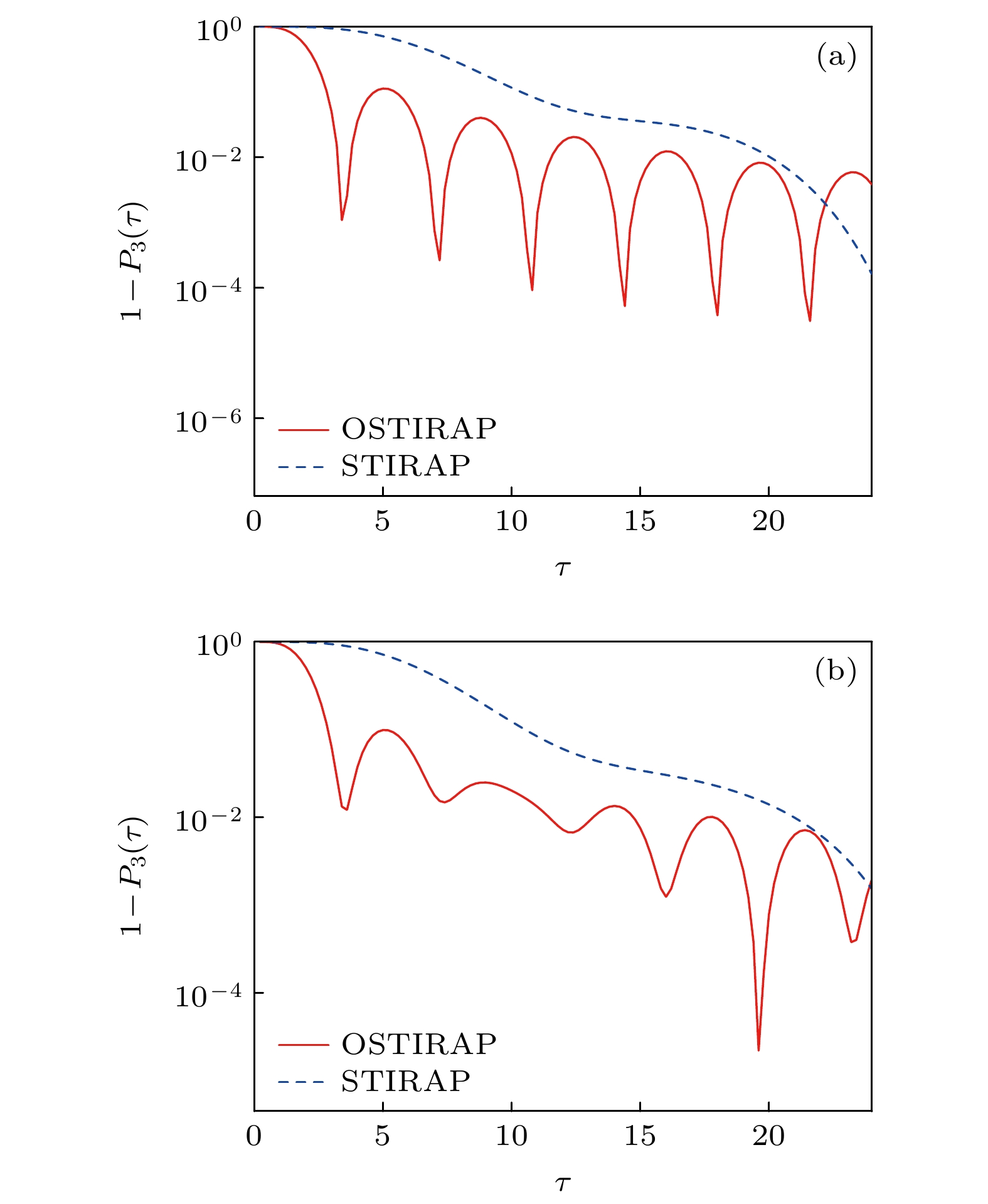
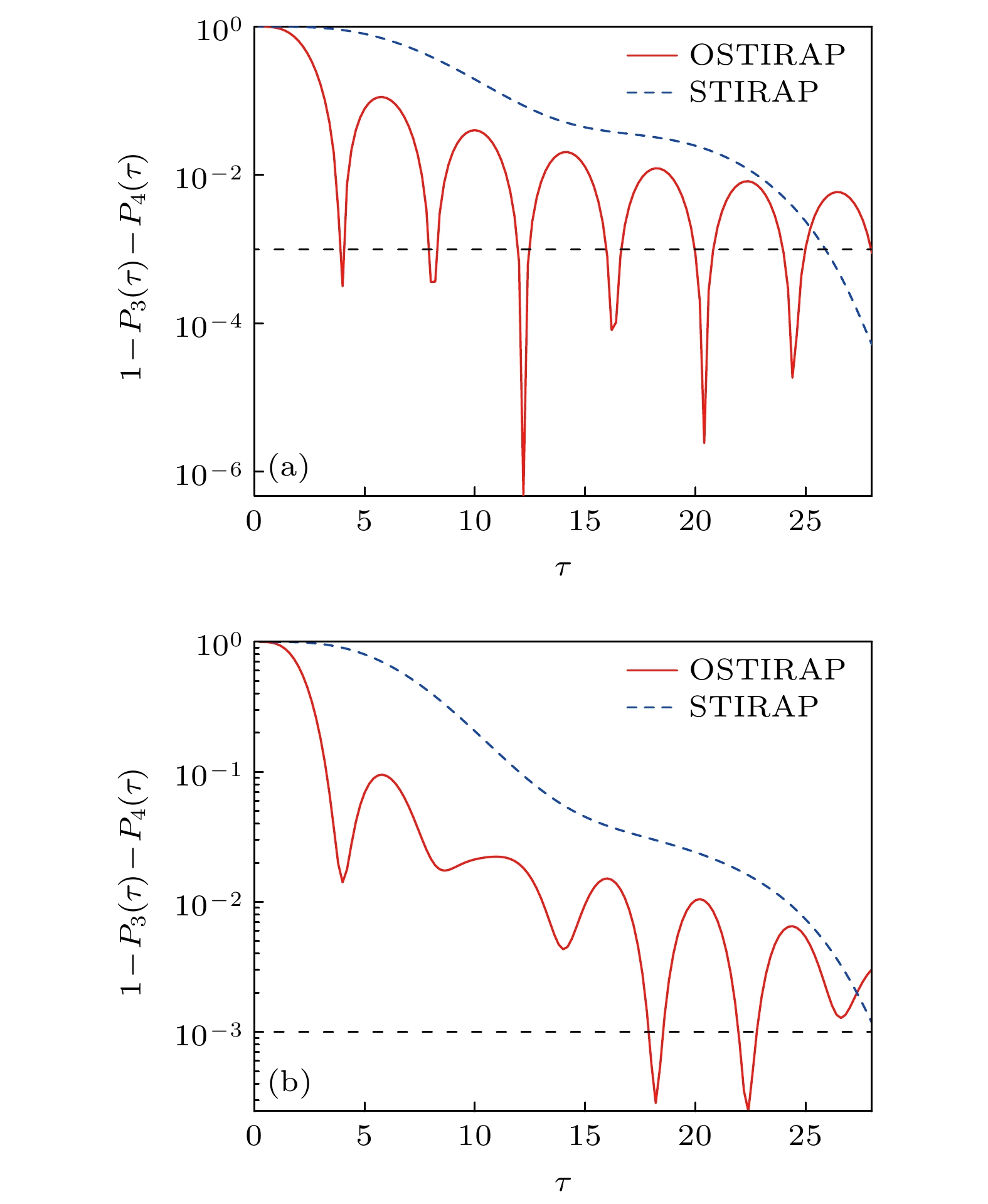
图4(a)给出不存在失谐时, 系统的失真度随脉冲工作时间的变化情况. 失真度定义为总粒子数1减去演化结束后态$ \left|3\right.\rangle $上的粒子数布居. 失真度越小, 表明转移效率越高, 转移过程对参数的变化更稳定. 由图4可知, 优化STIRAP的失真度随τ的变化具有周期性变化的特征, 并随着工作时间的延长, 失真度的最高点逐渐降低, 极低点对应着一系列时间窗口. 选择这些时间窗口内的工作时间, 就可以使得优化STIRAP的失真度保持在$ {10}^{-3} $以下. 例如在第1个时间窗口内, 选择τ = 3.7 μs时, 优化STIRAP的失真度可降到$ {10}^{-3} $以下. 而在采用高斯脉冲的传统STIRAP方案中, 失真度整体呈现缓慢下降趋势, 直到工作时间为23.8 μs才能使转移过程的失真度降到$ {10}^{-3} $以下. 结果表明, 通过选取特定的极低点工作窗口, 优化STIRAP就可以在较短时间内实现近完全的粒子数布居转移. 图4(b)给出存在失谐时失真度随脉冲工作时间的变化情况. 当失谐量不为零时, 优化STIRAP失真度的周期性受到影响, 整体的失真度上移, 但仍存在若干失真度的极低点. 在对应的极低点工作窗口内系统依然能实现较好的布居转移, 使失真度降到$ {10}^{-2} $以下. 总之, 优化STIRAP方法可以在较短的时间窗口内进行较为完全的布居转移, 而失谐量的存在会明显降低过程的转移效率.

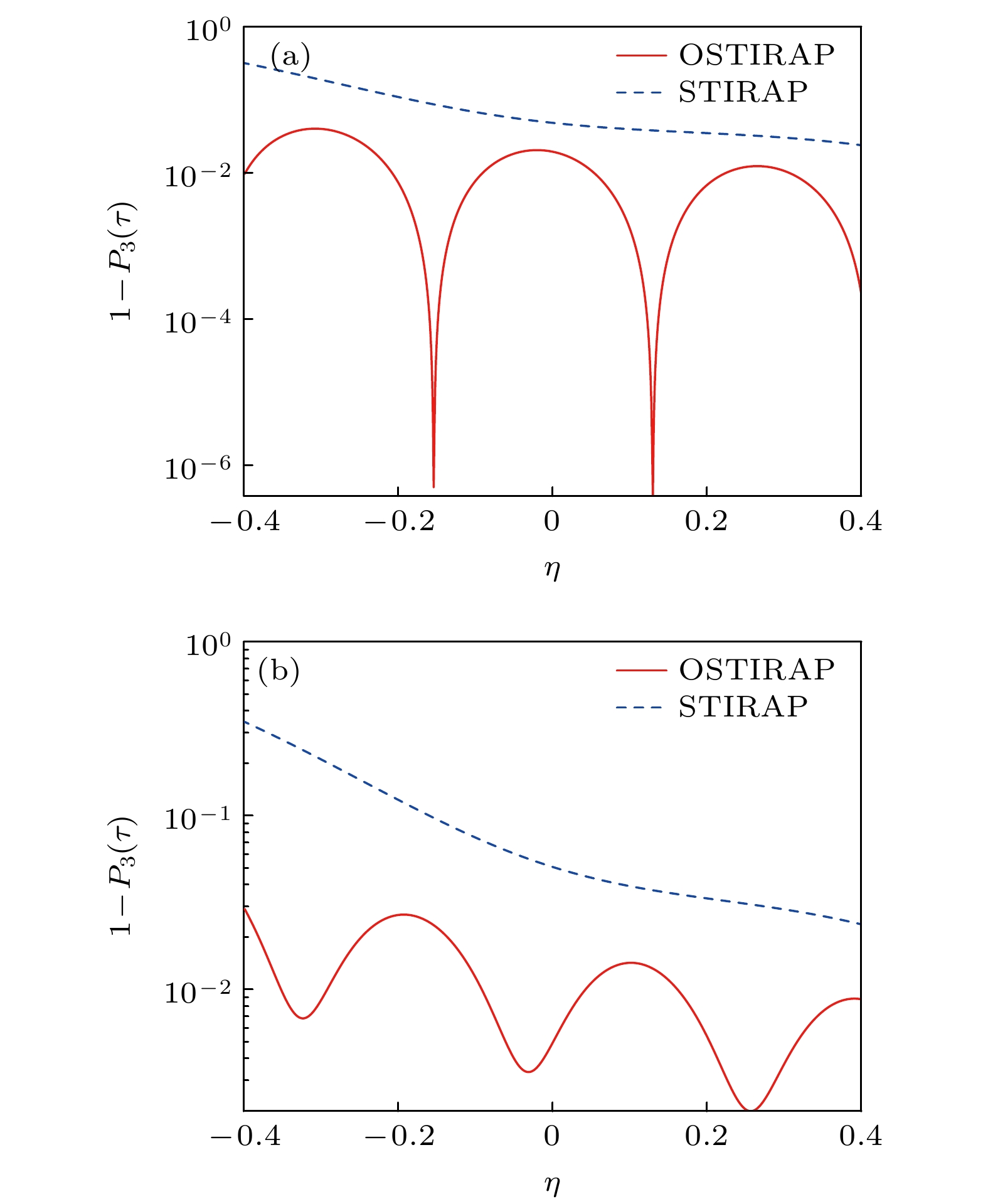
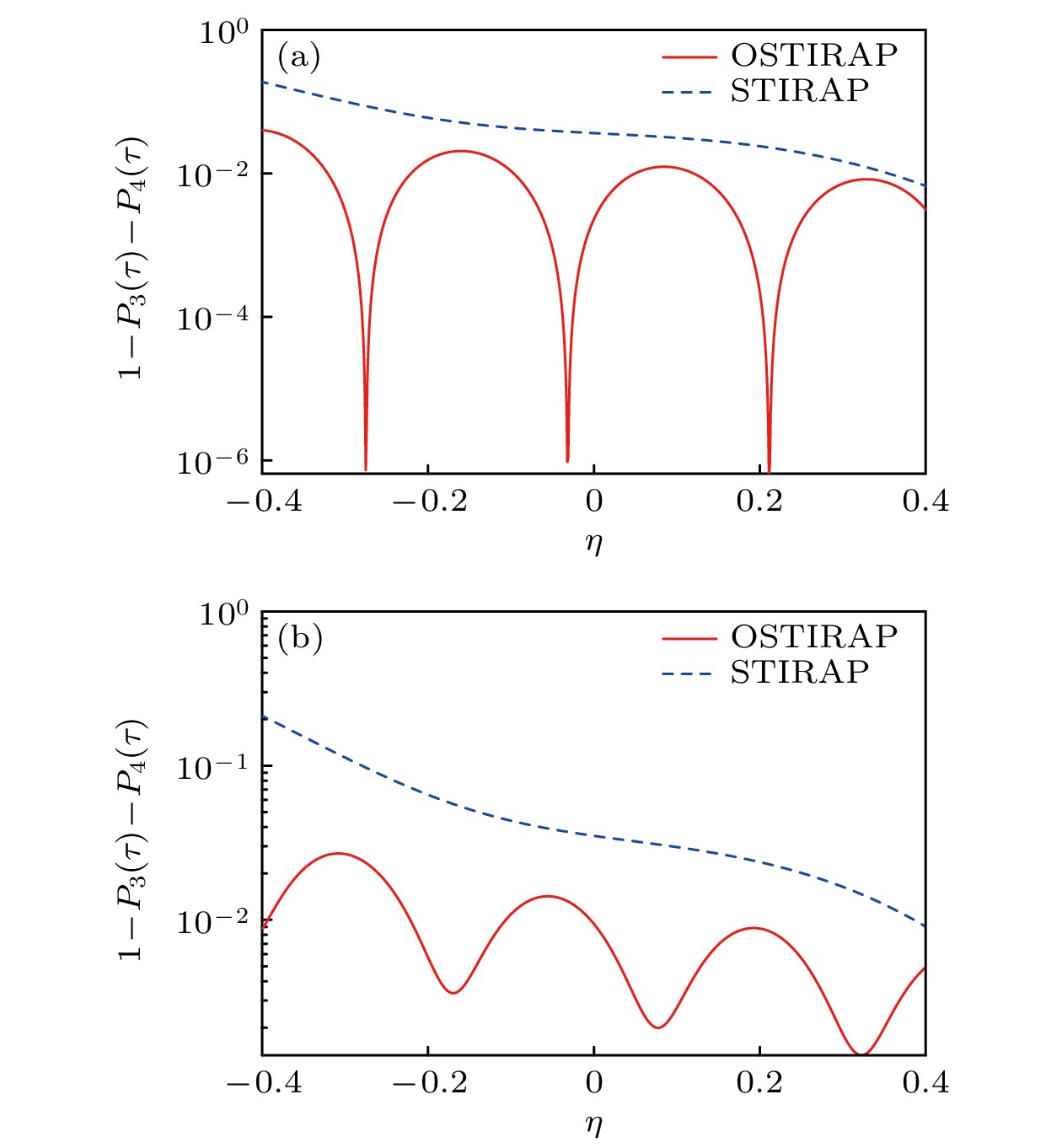
接下来研究优化STIRAP与传统STIRAP方法对系统参数的稳定性. 首先分析脉冲峰值$ {\varOmega }_{0} $的涨落对优化STIRAP的影响. 取脉冲峰值为$ {\varOmega }_{0}\left(1+\eta \right) $. 图5给出失真度随脉冲峰值涨落$ \eta $ 的变化情况. 选取的脉冲工作时间为τ = 7.4 μs, 此工作时间处于图4(a)中第2个时间窗口. 图5(a)给出失谐量$ \varDelta = $0时失真度随η的变化情况. 优化STIRAP的失真度关于$ \eta =0 $分布不对称, 并随$ \eta $的增大而呈现略微降低的趋势. 传统STIRAP方法失真度随着$ \eta $的增大不断减小. 优化STIRAP的失真度始终小于传统STIRAP的失真度. 在$ \eta =-0.15 $和$ 0.13 $处, 优化STIRAP的失真度出现共振极低点, 失真度可降到$ {10}^{-6} $以下. 图5(b)给出失谐量$ \varDelta =2{\mathrm{\pi }}{\mathrm{ }}\;{\mathrm{M}}{\mathrm{H}}{\mathrm{z}} $时失真度随脉冲峰值涨落$ \eta $的变化情况. 可以看到随着失谐量的出现, 优化STIRAP的失真度整体增大, 均值在$ {10}^{-2} $左右, 共振峰明显展宽, 有失谐时优化STIRAP的失真度仍然比传统STIRAP小.

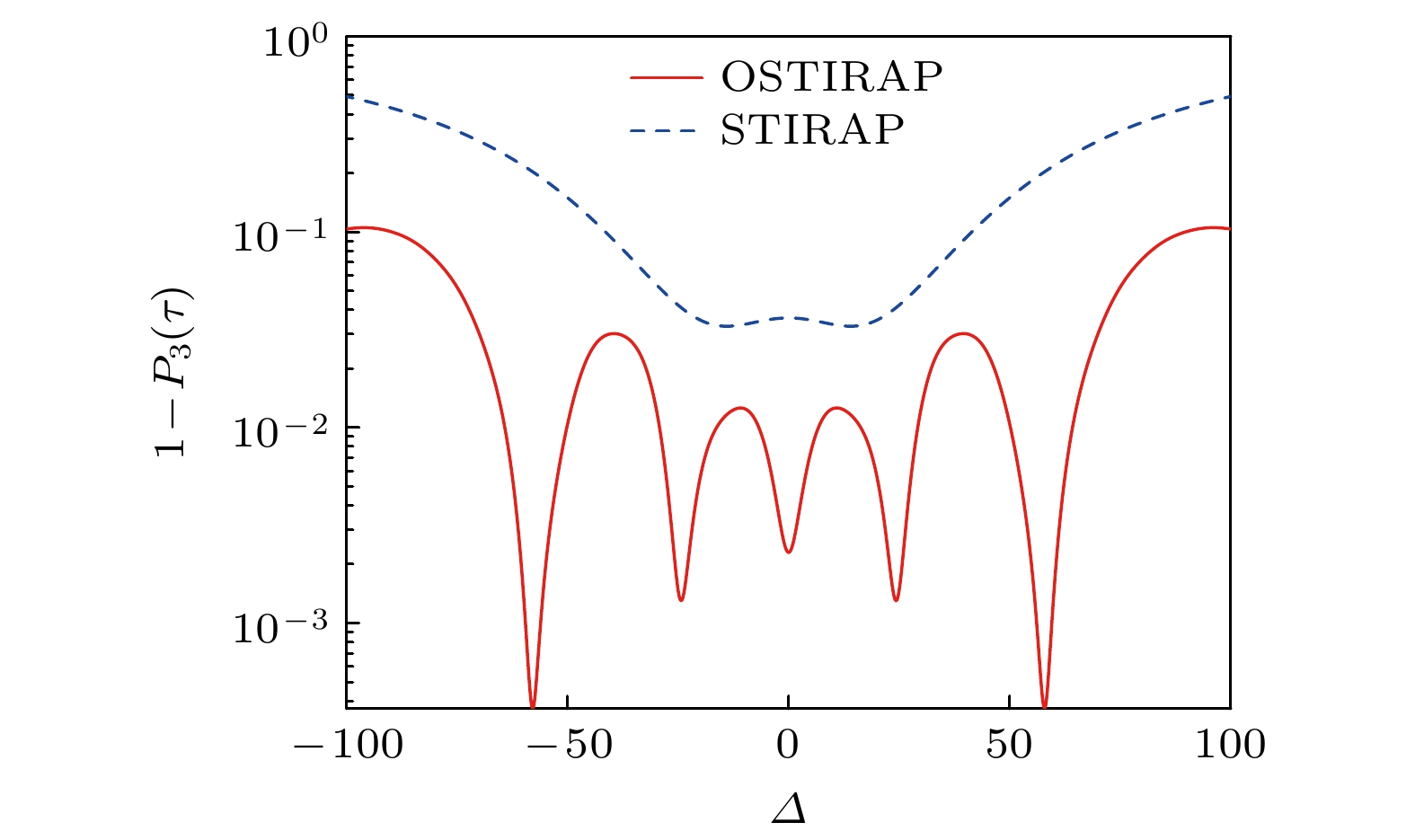
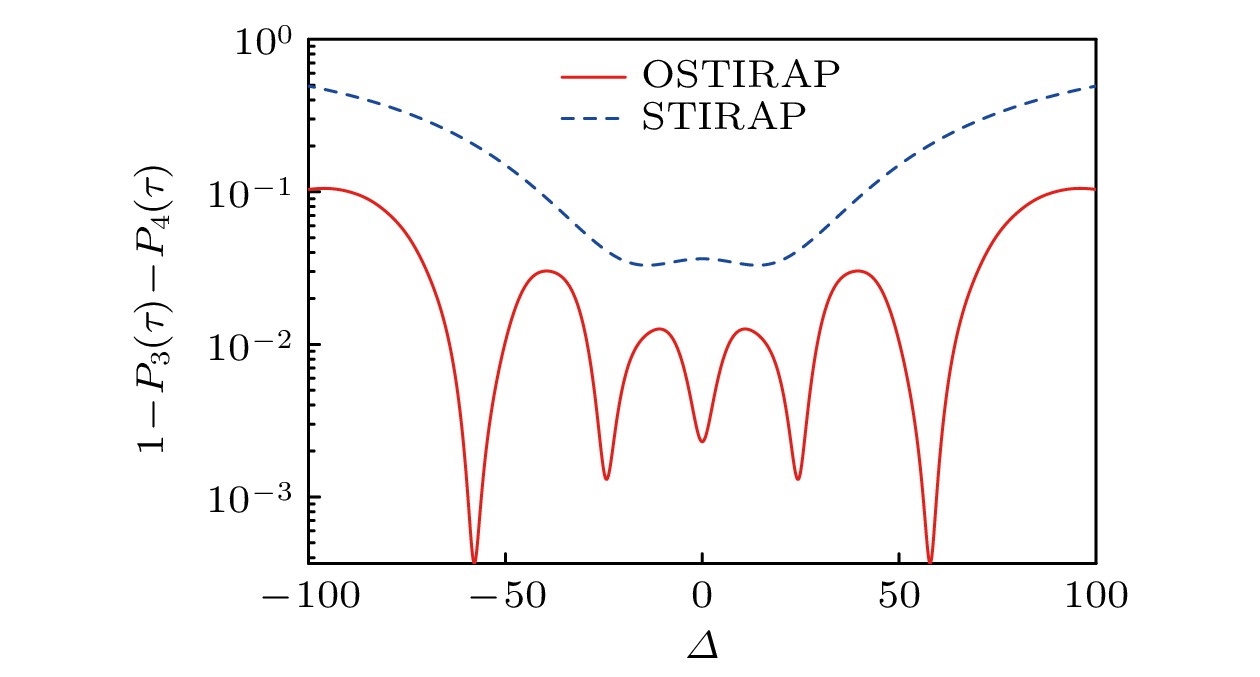
下面考虑失谐量$ \varDelta $的变化对优化STIRAP过程的影响. 同样将失真度作为转移效果的评判标准. 由图6可知, 优化STIRAP方法的失真度随失谐量绝对值的增大而增大, 并呈现一系列共振极低窗口, 使得失真度低于$ {10}^{-2} $. 传统STIRAP方法中, 随着失谐量的增大, 其失真度也随之增大. 在任何失谐量取值下, 传统STIRAP过程的失真度都大于优化STIRAP过程. 另外, 两种情形下的转移趋势关于$ \varDelta $= 0都是对称的.

考虑图7所示三脚架型四能级系统的绝热布居转移过程. 系统可实现从态$ |1\rangle $到态$ |3\rangle $和$ |4\rangle $的粒子数布居转移, 也能形成态$ |3\rangle $和$ |4\rangle $的按任意比例的量子叠加态. 在旋转波近似下, 该四能级系统的哈密顿量为^{[7,12,45–48]}

其中, $ {\varOmega }_{{\mathrm{P}}}\left(t\right) $, $ {\varOmega }_{{\mathrm{S}}}\left(t\right) $和$ {\varOmega }_{{\mathrm{Q}}}\left(t\right) $是耦合基态$ |1\rangle $, $ |3\rangle $和$ |4\rangle $与激发态$ |2\rangle $之间的拉比脉冲. 相比于三能级系统, 四能级系统因其存在两个简并的暗态而使绝热转移变得稍显复杂. 但在一定条件下可将四能级系统变为一个三能级系统进行处理. 本文在此给出四能级系统中消除简并能级影响的一种方法^[5]. 该方法同样适用于相同情况下具有更多能级的系统.

对于以上四能级系统, 它的4个能量本征值分别为$ {\lambda }_{+}=-{\lambda }_{-}={\varOmega}/{2} ,\;\; {\lambda }_{1}={\lambda }_{2}=0 $, 其中$\varOmega = \sqrt{{\varOmega }_{{\mathrm{P}}}^{2}+{\varOmega }_{{\mathrm{S}}}^{2}+{\varOmega }_{{\mathrm{Q}}}^{2}} $. 相应的4个本征态为

其中, 混合角满足

该系统中, 两个为零的本征值$ {\lambda }_{{\mathrm{1, 2}}} $所对应的本征 态$ \left|{\lambda }_{{\mathrm{1, 2}}}\rangle \right. $被称为暗态, 两个不为零的本征值$ {\lambda }_{\pm } $所对应的本征态$ \left|{\lambda }_{\pm }\rangle \right. $被称为亮态. 由于本征值为零的两 个本征态$ \left|{\lambda }_{1}\rangle \right. $和$ \left|{\lambda }_{2}\rangle \right. $是简并的, 即使满足绝热 条件, 它们之间的非绝热耦合也是无法抑制的^[5]. 本征态$ \left|{\lambda }_{1}\rangle \right. $和$ \left|{\lambda }_{2}\rangle \right. $之间的耦合将会严重影响到 最终布居转移的效果, 为此必须找到消除这种耦合的办法.

为建立简并能级之间的关系, 我们将系统从纯态空间变换到本征态空间进行研究. 采用的幺正变换矩阵为^[6]

系统哈密顿量的变换关系为$ \tilde{H}\left(t\right)={U\left(t\right)}^{-1}H\left(t\right)U\left(t\right)+{\mathrm{i}}{\dot{U}\left(t\right)}^{-1}U\left(t\right) $, 代入(14)式可得

本征态满足的薛定谔方程为$ \dfrac{{\mathrm{d}}}{{\mathrm{d}}t}\overrightarrow{\lambda }\left(t\right)=-{\mathrm{i}}\tilde{H}\left(t\right)\overrightarrow{\lambda }\left(t\right) $, 其中$ \overrightarrow{\lambda }\left(t\right)={\left[\left|{\lambda }_{1}\left(t\right)\rangle \right., \left|{\lambda }_{2}\left(t\right)\rangle \right., \left|{\lambda }_{+}\left(t\right)\rangle \right., \left|{\lambda }_{-}\left(t\right)\rangle \right.\right]}^{{\mathrm{T}}} $. 此时若仅需研究$ \left|{\lambda }_{1}\left(t\right)\rangle \right.{\mathrm{与}}\left|{\lambda }_{2}\left(t\right)\rangle \right. $之间的耦合, 则有约化方程:

对约化的薛定谔方程, 可得其一般解:

其中, $ \varTheta \left(t\right)=\displaystyle\int _{-{\mathrm{\infty }}}^{t}{\mathrm{d}}t'\dot{\xi }\left(t'\right){\mathrm{sin}}\vartheta \left(t\right) $.

我们得到了两个简并本征态之间的耦合关系, 其中新的混合角$ \varTheta \left(t\right) $是涉及两个简并本征态变化的关键. 若$ \varTheta \left(t\right)=0 $, 则两个简并态之间的耦合将会消失, 即$ \left|{\lambda }_{{\mathrm{1, 2}}}\left(t\right)\rangle \right.=\left|{\lambda }_{1}\left(-\infty \right)\rangle \right. $, 这将满足绝热转移的要求. 由式(13)可知, 暗态$ \left|{\lambda }_{2}\left(t\right)\rangle \right. $中只有态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $而无态$ \left|1\right.\rangle $, 因此应确保绝热转移始终沿着暗态$ \left|{\lambda }_{1}\left(t\right)\rangle \right. $演化, 把初始布居在态$ \left|1\right.\rangle $上的粒子数高效转移到态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $上, 同时排除$ \left|{\lambda }_{2}\left(t\right)\rangle \right. $的影响. 只要保证$ \dot{\xi }\left(t\right)=0 $, 就可使$ \varTheta \left(t\right)= 0 $, 两简并态之间的非绝热耦合被解除, 演化可以沿着选定的本征态$ \left|{\lambda }_{1}\left(t\right)\rangle \right. $进行. 所以消除两简并态之间非绝热耦合的条件为

我们已经给出了消除简并暗态之间非绝热跃迁的条件, 接下来将进行动力学量子几何张量的优化, 并在最后满足本征态简并消除条件(18)式.

根据(5)式、(12)式和(13)式, 可得暗态$ \left|{\lambda }_{1}\left(t\right)\rangle \right. $的动力学量子几何张量的各分量^[34,35]:

根据(4)式, 我们可以得到整体非绝热跃迁率:

当系统失谐量$ \varDelta $ = 0时, 整体非绝热跃迁率将转化为

整体非绝热跃迁率进行优化需要满足两个条件, 即(18)式和$ {\tilde{T}}_{n1}^{2}\left(s\right) $为常数. 满足这两个条件的脉冲可以实现沿着暗态$ \left|{\lambda }_{1}\left(t\right)\rangle \right. $的绝热演化, 非绝热跃迁的影响将被降到最低. 本文对四能级系统给出一种满足该条件的拉比脉冲组合:

使用上述脉冲组合, 系统整体非绝热跃迁率

优化脉冲中的参量$ \chi $是一个可控参数, 等效于传统STIRAP过程中的混合角$ \xi $. 取另一参数$ \beta ={\mathrm{\pi }}/2 $, 意味系统演化将沿着暗态$ \left|{\lambda }_{1}\left(t\right)\rangle \right. $进行, 最终将初始态$ \left|1\right.\rangle $上的粒子数布居全都转移到态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $上. 又由(13)式可知, 演化结束后态$ \left|3\right.\rangle $上的粒子数布居为$ {{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}}^{2}\chi $, 态$ \left|4\right.\rangle $上的粒子数布居为$ {{\mathrm{s}}{\mathrm{i}}{\mathrm{n}}}^{2}\chi $. 因此可以通过控制脉冲参数$ \chi $来设计演化结束后态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $上的粒子数布居比例, 实现任意比例的态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $的量子叠加.

假定初始状态下所有粒子数全部布居在态$ \left|1\right.\rangle $上. 根据上面给出的脉冲序列进行演化, 若选取参数$ \chi ={\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}(1/3) $时, 最终态$ \left|3\right.\rangle $上粒子数布居为$ {1}/{3} $, 态$ \left|4\right.\rangle $上粒子数布居为2/3. 在传统STIRAP过程中所采用的高斯型脉冲如下:

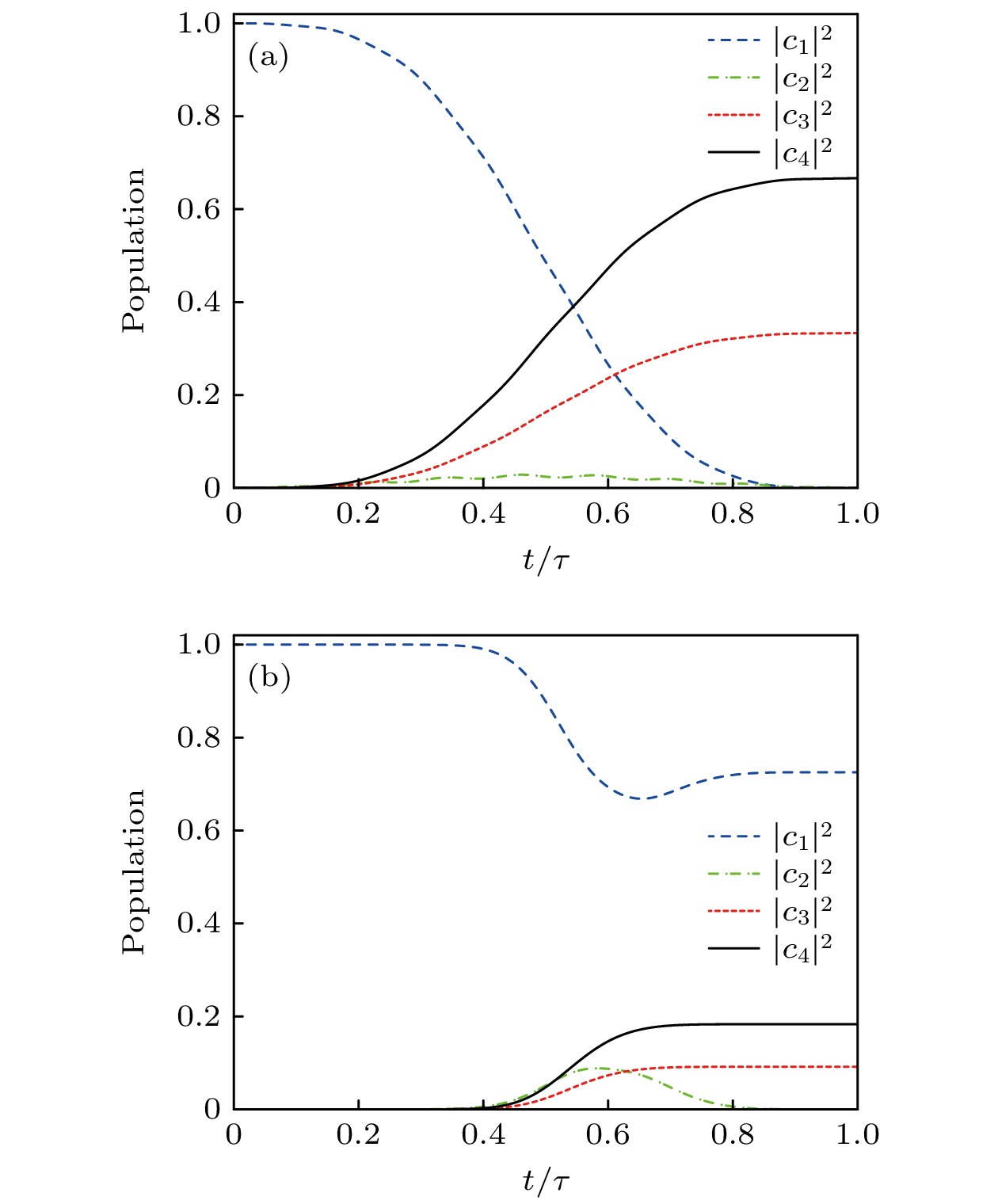
与三能级系统类似, 计算中设定高斯脉冲半最大全宽$ \sigma =\tau /6 $, 两脉冲的分离时间$ \mu =\tau /10 $.

优化STIRAP和传统STIRAP的脉冲结构分别如图8(a), (c)所示. 在优化STIRAP脉冲中, 演化开始时$ {\varOmega }_{{\mathrm{Q}}} $与$ {\varOmega }_{{\mathrm{S}}} $达到最大值而$ {\varOmega }_{{\mathrm{P}}} $为零. 随着演化的进行, $ {\varOmega }_{{\mathrm{Q}}} $与$ {\varOmega }_{{\mathrm{S}}} $逐渐减小, $ {\varOmega }_{{\mathrm{P}}} $逐渐增大. 相比之下, 传统的高斯脉冲结构在演化刚开始时$ {\varOmega }_{{\mathrm{P}}} $, $ {\varOmega }_{{\mathrm{Q}}} $和$ {\varOmega }_{{\mathrm{S}}} $都为零, 随后$ {\varOmega }_{{\mathrm{Q}}} $和$ {\varOmega }_{{\mathrm{S}}} $同时出现, 且保持$ {\varOmega }_{{\mathrm{Q}}}\left(t\right)/ {\varOmega }_{{\mathrm{S}}}\left(t\right) $为常数, 随后$ {\varOmega }_{{\mathrm{P}}} $出现. 图8(b), (d)分别给出优化STIRAP和传统STIRAP粒子数布居的演化过程. 在优化STIRAP演化中, 中间态$ \left|2\right.\rangle $上出现较小的粒子数布居波动, 但这些波动很快就会消失, 最终几乎将所有的粒子数布居转移到态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $上. 因为混合角$ \xi $为常数, 简并暗态之间的非绝热跃迁被抑制, 导致最终实现态$ \left|3\right.\rangle $上粒子数布居为1/3, 态$ \left|4\right.\rangle $上粒子数布居为2/3. 对传统STIRAP过程, 中间态$ \left|2\right.\rangle $上出现了较大的粒子数布居, 表明系统出现了较大的非绝热跃迁, 使得演化没有完全沿着暗态$ {|\lambda }_{1} \rangle $进行. 原因是工作时间τ较小, 传统STIRAP不能满足绝热条件, 导致了较大的非绝热跃迁, 而优化STIRAP方案借助于动力学量子几何张量的优化, 使得非绝热跃迁率为一较小的常数, 因此对演化结果的影响较小.

图9(a)给出失谐量$ \varDelta = $0时失真度随工作时间的变化情况. 这里的失真度定义为1减去演化结束后态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $上的粒子数布居数之和. 失真度越小, 表明系统布居转移越完全. 由图9(a)可知, 优化STIRAP的失真度呈现周期性的变化, 并随着工作时间的延长, 失真度的极高点逐渐下移, 极低点则对应出现一系列时间窗口. 选择这些时间窗口处的工作时间, 可使优化STIRAP的失真度保持在$ {10}^{-3} $以下. 例如在第1个时间窗口内, 选择τ = 4 μs后优化STIRAP的失真度降到$ {10}^{-3} $以下. 而使用高斯脉冲的传统STIRAP方案整体呈现缓慢下降的趋势, 直到工作时间达到25.8 μs才能使STIRAP的失真度降到$ {10}^{-3} $以下. 该结果表明, 优化STIRAP方案完全转移所需的时间小于传统STIRAP方案, 可实现快速高效的布居转移. 图9(b)给出失谐量$ \varDelta =2{\mathrm{\pi }}{\mathrm{ }}\;{\mathrm{M}}{\mathrm{H}}{\mathrm{z}} $时失真度随工作时间的 变化情况. 当失谐量不为零时, 优化STIRAP 方 案失真度的周期性受到影响, 优化STIRAP与传统STIRAP方法的失真度都出现了上移. 但优化STIRAP依然存在可以实现较低失真度的时间窗口. 在对应的极低点工作窗口内, 失真度较低, 依然能实现较完全的布居转移.

上文表明四能级系统中优化STIRAP方案可以实现最终态$ |3 \rangle $和$ |4 \rangle $按任意比例的叠加, 并且转移时间明显短于传统STIRAP方案. 接下来将讨论优化STIRAP方案对于两个系统参数涨落的稳定性.

图10(a)给出失谐量$ \varDelta =0 $时失真度随脉冲峰值涨落$ \eta $的变化情况. 当脉冲峰值涨落$ \eta $不为零时, 实际的脉冲峰值变为$ {\varOmega }_{0}\left(1+\eta \right) $. 从图10可以看到, 优化STIRAP方案对于脉冲峰值涨落变化仍然具有周期性, 但整体上随着脉冲涨落的增大, 失真度逐渐减小. 相比之下, 传统STIRAP方案中失真度随着涨落的增大而减小, 不具有周期性变化的特征. 传统STIRAP方案的失真度整体上都大于优化STIRAP方案的值. 优化STIRAP方案具有的这种周期性特征, 表明存在使用较小的脉冲峰值和工作时间, 能够实现较完全的布居转移. 图10(b)给出失谐量$ \varDelta =2{\mathrm{\pi }}{\mathrm{ }}\;{\mathrm{M}}{\mathrm{H}}{\mathrm{z}} $时失真度随η的变化情况. 从图中可以发现, 随着失谐量$ \varDelta $的出现, 优化STIRAP和传统STIRAP的失真度都整体上移. 优化STIRAP的整体趋势保持不变, 失真度仍然呈现周期性并随着脉冲的增大而下降. 传统STIRAP的失真度随着脉冲峰值的增大而减小, 但仍然大于优化STIRAP. 这表明失谐的增大会使得优化STIRAP方案的布居转移能力有所下降, 但通过选取合适的参数, 仍然可以在短工作时间与低脉冲峰值下实现较完全的布居转移.

图11给出四能级系统中失真度随失谐量$ \varDelta $的变化. 由图11可知, 优化STIRAP方案对失谐量$ \varDelta $的变化同样存在周期性波动, 并且随着失谐量$ \varDelta $的增大, 这种波动也越明显. 这表明失谐量$ \varDelta $越大, 可能会出现失真度较大的情况, 同时也会出现一些失谐量的周期性窗口. 在这些失谐量窗口内, 失真度较低, 并且随着失谐量$ \varDelta $的增大, 这些窗口内较低的失真度将会进一步降低. 这就为优化STIRAP方案在大失谐情况下实现绝热布居转移提供了可能. 传统STIRAP方案则对于失谐量$ \varDelta $没有较好的转移效果. 随着失谐量的增大, 传统STIRAP的失真度升高, 这意味布居转移被抑制, 非绝热跃迁的影响愈发明显.

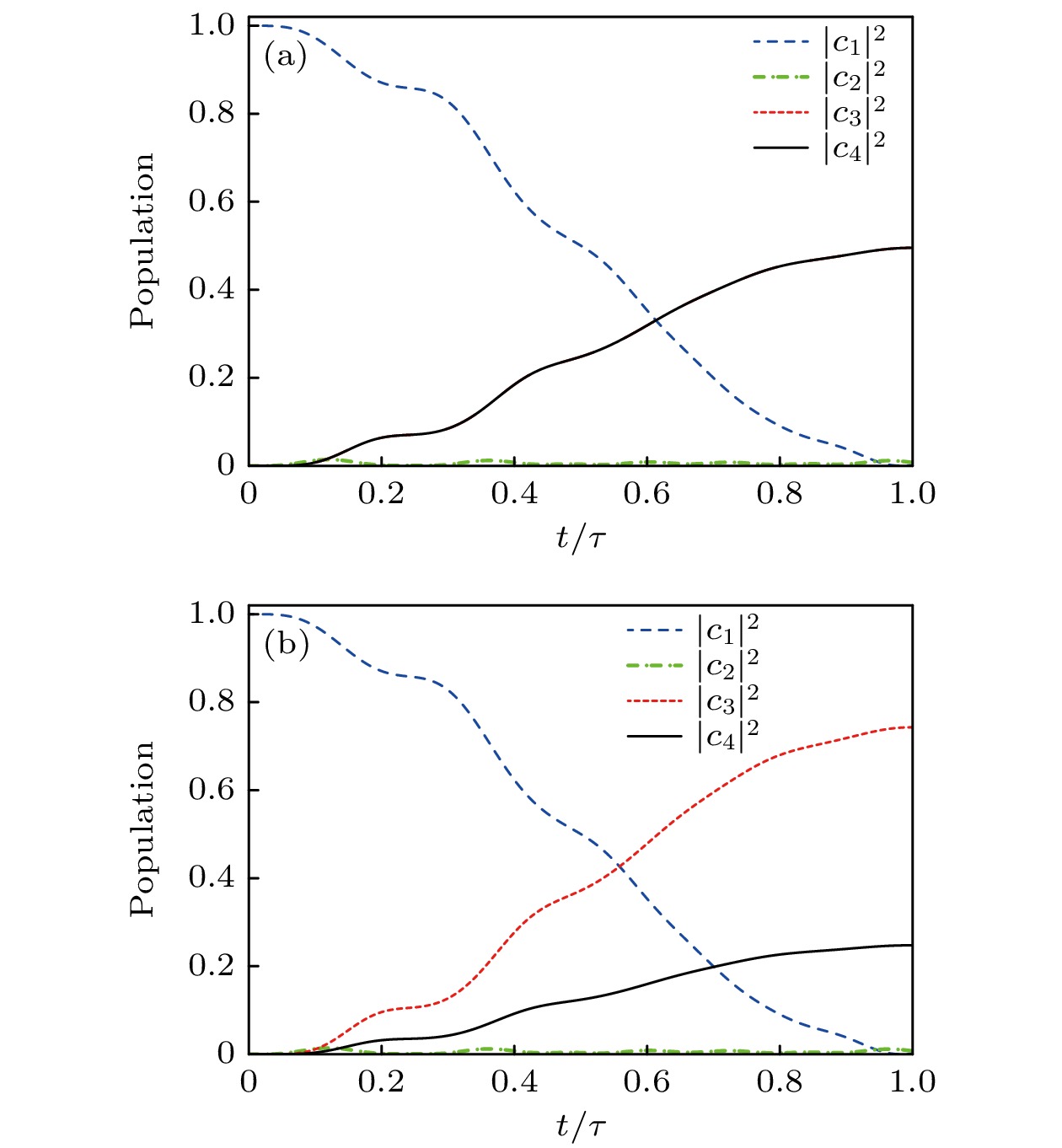
从上文的讨论中不难发现, 优化STIRAP方案具有在短工作时间、低脉冲峰值以及大失谐量情况($ \varDelta > {\varOmega }_{0} $)下实现最终态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $相干叠加的能力, 是相对于传统STIRAP的另一个优势. 这意味着实现特定环境下量子叠加态的制备是可能的. 例如可在工作时间τ = 7.4 μs, 脉冲峰值$ {\varOmega }_{0}= 22.13\;{\mathrm{MHz}} $, 失谐量$ \varDelta =58.1\;{\mathrm{MHz}} $下, 选取脉冲参数$ \chi ={\mathrm{a}}{\mathrm{r}}{\mathrm{c}}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}(1/3) $进行转移, 计算结果如图12所示.

从图12可以看到, 传统STIRAP方案在这种大失谐情况下布居转移并不完全. 大部分粒子数仍然布居在初始态$ \left|1\right.\rangle $上, 而最终态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $上粒子数布居较少. 优化STIRAP方案可以在大失谐情况下实现完全的布居转移. 初始态$ |1 \rangle $上粒子数布居很少, 几乎所有粒子数布居转移到了态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $上, 最终态上的粒子数分布满足预期设定的相干叠加. 在传统STIRAP方案不能较好实现的条件下, 优化STIRAP方案可以实现高效绝热布居转移.

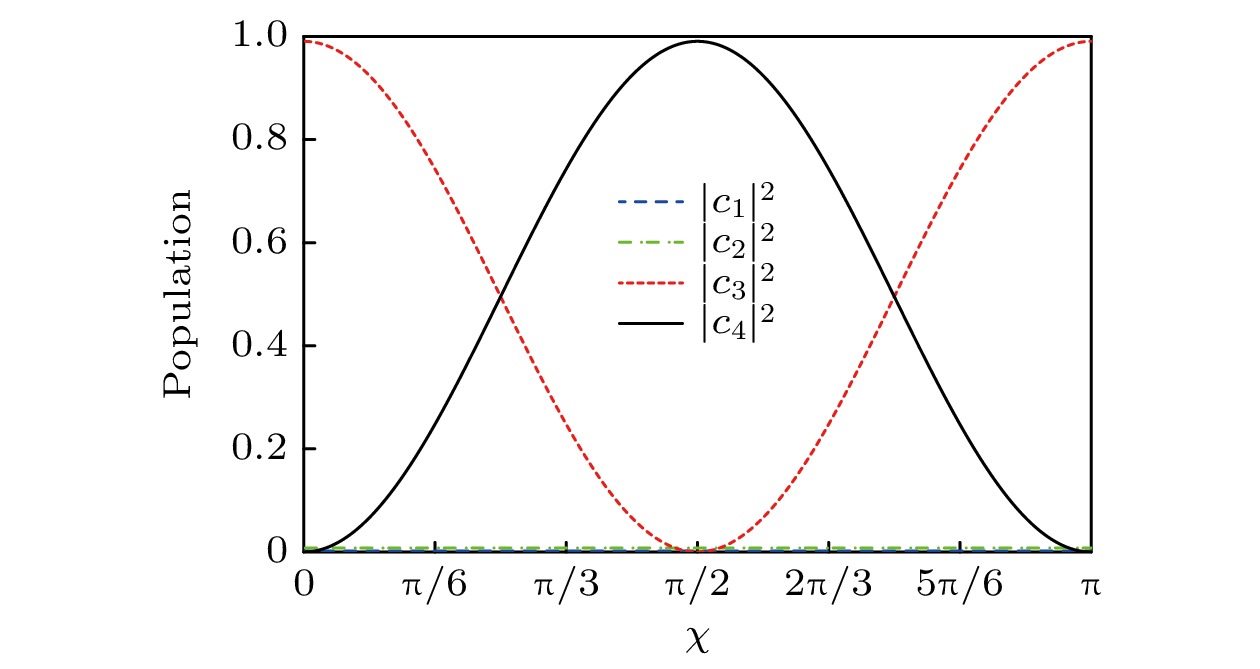
前文提到, 只需控制优化脉冲参数$ \chi $, 就可以控制最终各态上的粒子数布居, 实现各态按任意比例的相干叠加. 下面给出演化终点处态$ \left|3\right.\rangle $, $ \left|4\right.\rangle $上粒子数布居随脉冲参数$ \chi $的变化情况.

由图13可得, 优化STIRAP方案满足(13)式, 即演化结束后在态$ |3 \rangle $上的粒子数布居为$ {{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}}^{2}\chi $, 态$ \left|4\right.\rangle $上的粒子数布居为$ {{\mathrm{s}}{\mathrm{i}}{\mathrm{n}}}^{2}\chi $, 这样就可通过控制脉冲参数$ {\mathrm{\chi }} $来设计最终各态的相干叠加. 图14(a)是脉冲参数$ \chi $= $ {{\mathrm{\pi }}}/{4} $时优化STIRAP的演化结果. 可以看到态$ \left|3\right.\rangle $和$ \left|4\right.\rangle $上粒子布居始终相等, 实现了按1∶1的等比叠加态. 图14(b)给出脉冲参数$ \chi $=$ {\mathrm{\pi }}/4 $时优化STIRAP的演化结果, 最终实现了3∶1的叠加态. 通过选取其他合适参数, 可以实现所需的任意比例量子态的叠加.

本文基于动力学量子几何张量提出了一种对传统STIRAP进行优化的方案. 通过对有无单光子失谐时$ {{\Lambda }} $型三能级系统和三脚架型四能级系统的研究, 展示了优化STIRAP在绝热布居转移过程中的优越性. 一方面, 利用最优控制理论和量子几何张量的定义, 解析推导了使得系统整体非绝热跃迁率为常数的优化拉比脉冲组合. 另一方面, 通过数值计算与传统STIRAP中采用的高斯脉冲组合的结果进行比较, 发现优化STIRAP过程中系统具有更高的转移效率, 对脉冲工作时间、脉冲幅度涨落以及单光子失谐等参数的变化具有更高的稳定性. 优化STIRAP过程随脉冲作用时间、拉比脉冲幅度涨落以及单光子失谐的变化展现绝热共振现象. 在共振窗口处取参数, 可在较短的工作时间、较小的脉冲峰值涨落以及特定的单光子失谐下实现高保真度的粒子布居转移. 尤其是, 针对四能级系统中存在两个简并暗态的问题, 从态矢空间推出了解除简并能级耦合的条件. 通过合理选择脉冲参数, 可实现四能级系统中利用优化STIRAP方案制备具有任意布居占比的量子叠加态. 总之, 本文证明了利用动力学量子几何张量优化的STIRAP方案比传统的STIRAP方案具有更快更高效的绝热布居转移. 本文讨论的方案具有普适性, 可推广研究其他类似多能级系统的布居转移, 为量子系统的优化控制提供必要基础.