高级搜索

准晶势调制的一维p波超导体中的拓扑量子相变

,  , 

downloadPDF

上一篇

下一篇

古燕, 王智鹏, 陆展鹏. 准晶势调制的一维p波超导体中的拓扑量子相变[J]. 物理学报, 2025, 74(10): 100303-1. doi: 10.7498/aps.74.20250137
引用本文: 古燕, 王智鹏, 陆展鹏. 准晶势调制的一维p波超导体中的拓扑量子相变[J]. 物理学报, 2025, 74(10): 100303-1. doi: 10.7498/aps.74.20250137
shu
Yan GU, Zhipeng WANG, Zhanpeng LU. Topological quantum phase transitions in quasicrystalline potential modulated one-dimensional p-wave superconductors[J]. Acta Physica Sinica, 2025, 74(10): 100303-1. doi: 10.7498/aps.74.20250137
Citation: Yan GU, Zhipeng WANG, Zhanpeng LU. Topological quantum phase transitions in quasicrystalline potential modulated one-dimensional p-wave superconductors[J]. Acta Physica Sinica, 2025, 74(10): 100303-1. doi: 10.7498/aps.74.20250137
shu

准晶势调制的一维p波超导体中的拓扑量子相变

  • 1.

    山西工程科技职业大学, 晋中　030619

  • 2.

    湖北民族大学, 恩施　445000

  • 3.

    山西大学理论物理研究所, 光量子技术与器件全国重点实验室, 太原　030006

    • 通讯作者: E-mail: 201712605002@email.sxu.edu.cn

  • 中图分类号: 03.65.Vf, 84.71.Mn

Topological quantum phase transitions in quasicrystalline potential modulated one-dimensional p-wave superconductors

  • 1.

    Shanxi Vocational University of Engineering Science and Technology, Jinzhong 030619, China

  • 2.

    Hubei Minzu University, Enshi 445000, China

  • 3.

    State Key Laboratory of Quantum Optics Technologies and Devices, Institute of Theoretical Physics, Shanxi University, Taiyuan 030006, China

    • Corresponding author: E-mail: 201712605002@email.sxu.edu.cn

  • MSC: 03.65.Vf, 84.71.Mn

  • 摘要: 研究了一维Fibonacci准晶势调制下的p波超导体下的拓扑相变和局域化性质. 在Fibonacci准晶势调制下, 通过计算$Z_2$拓扑不变量确定了系统的拓扑相图. 分析相图指出在Fibonacci准晶势调制下, 系统可以由拓扑平庸超导相进入拓扑安德森超导相. 进一步分析发现, 在某些参数下, 系统会发生多次拓扑安德森超导相转变并伴随零能态的出现. 此外, 还研究了系统的局域化性质, 通过分析分形维度、平均逆参与率序参量, 发现Fibonacci准晶势诱导的拓扑安德森超导相, 其体态的波函数表现出多重分形行为, 这与随机无序诱导出来的传统拓扑安德森超导相完全不同. 该研究结果为一维p波超导体中拓扑相变和局域化转变的研究提供了一些新的理解和参考.
    Abstract: The topological phase transitions and localization properties in a 1D p-wave superconductor under Fibonacci quasi-periodic potential modulation are investigated in this work. By calculating the Z2 topological invariant, the topological phase diagram of the system is determined numerically. It is found that the system can transition from a topologically trivial phase to a topological Anderson superconductor phase through the Fibonacci quasi-periodic modulation. Moreover, under certain parameters, the system undergoes multiple topological Anderson superconductor phase transitions, accompanied by the emergence of zero-energy modes. However, in the case of strong disorder, the topological Anderson superconductor phase is destroyed, indicating that the topological Anderson superconductor phase can be induced only within a finite range of parameters. Furthermore, by calculating and analyzing the fractal dimension and the mean inverse participation ratio (MIPR) order parameter, the localization properties of the system are analyzed. The results show that regardless of how the disorder intensity increases, the fractal dimension values of most eigenstates always remain within a range of 0–1. Subsequently, the variations in the fractal dimensions of all eigenstates for different system sizes are studied. The results show that the fractal dimension values of most eigenstates are away from 0 and 1. These results indicate that the wavefunction in the bulk of the topological Anderson superconductor phase induced by Fibonacci quasi-periodic potential is a critical state wavefunction, with the system overall being in a critical phase. The stability of the critical phase is confirmed by scale behavior of MIPR as shown in Fig. (a). It differs from the traditional topological Anderson superconductor phase induced by random disorder or AA-type quasi-periodic disorder. The results provide new insights into and references for studying topological phase transitions and localization transitions in 1D p-wave superconductors.
  • 加载中

  • 图 1  (a)以拓扑不变量Q大小为背景颜色填充的V-M参数平面的拓扑相图. 颜色条代表$Z_{2}$拓扑不变量Q的大小. 绿色虚线代表拓扑相变点解析解, 由(20)式确定. (b)—(d) 当常数势强度$M=1$, $-3$和$-4$时, 能隙$\varDelta_{\mathrm{g}}$和$Z_{2}$拓扑不变量Q随无序强度V的变化. (b)插图对应的是无序强度$V=0.2$时, L能级对应的波函数分布. 这里, $\varDelta=0.4$和$L=2000$

    Figure 1.  The $Z_{2}$ topological invariant Q as a function of the disorder strength V and constant potential M. The colorbar shows the value of the $Z_{2}$ topological invariant Q. The green dashed line represents the analytical solution of the topological phase transition point, determined by Eq. (20). Energy gap $\varDelta_{\mathrm{g}}$ and the $Z_{2}$ topological invariant Q as a function of V for (b) $M=1$, (c) $M=-3$ and (d) $M=-4$. The wave function distributions corresponding to the L energy levels at a disorder strength of $V=0.2$ in the inset of panel (b). Other parameters: $\varDelta=0.4$ and $L=2000$.

    下载: 全尺寸图片 幻灯片

    图 2  当系统尺寸$L=500$, M分别为(a)$M=1$和(b)$M=-3$时, 分形维度(${\varGamma}_n$)随着本征能量E和无序强度V的变化. 图中的颜色条代表分形维度(${\varGamma}_n$)的大小. (c)当$V=2$且$M=1$时, 不同系统尺寸下, 系统分形维度(${\varGamma}_n$)的值. (d)当$V=2$且$M=-3$时, 不同系统尺寸下, 系统分形维度(${\varGamma}_n$)的值. 其他参数取值为$\varDelta=0.4$

    Figure 2.  The fractal dimension ${\varGamma}_n$ of different eigenstates as a function of the corresponding E and the modulation strength V with $L=500$ for (a)$M=1$ and (b)$M=-3$. (c) The fractal dimensions ${\varGamma}_n$ for different system sizes for $V=2$ and $M=1$. (d) The fractal dimensions ${\varGamma}_n$ for different system sizes for $V=2$ and $M=-3$. Other parameters: $\varDelta=0.4$.

    下载: 全尺寸图片 幻灯片

    图 3  当M分别为(a)$M=1$和(b)$M=-3$时, MNPR在无序强度为$V=1,\;2,\;3 $ 情况下的标度行为. 其他参数$\varDelta=0.4$

    Figure 3.  The scaling behavior of MIPR in (a) $M=1$ and (b) $M=-3$ with $V=1,\; 2,\;3$. Other parameters: $\varDelta=0.4$.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Nakajima S, Takei N, Sakuma K, Kuno Y, Marra P, Takahashi Y 2021 Nat. Phys. 17 844 doi: 10.1038/s41567-021-01229-9
    [2] Thouless D J, Kohmoto M, Nightingale M P, den Nijs M 1982 Phys. Rev. Lett. 49 405 doi: 10.1103/PhysRevLett.49.405
    [3] Hasan M X, Kane C L 2010 Rev. Mod. Phys. 82 3045 doi: 10.1103/RevModPhys.82.3045
    [4] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 doi: 10.1103/RevModPhys.83.1057
    [5] Bansil A, Lin H, Das T 2016 Rev. Mod. Phys. 88 021004 doi: 10.1103/RevModPhys.88.021004
    [6] Xiao T, Xie D, Dong Z, Chen T, Yi W, Yan B 2021 Sci. Bull. 66 2175 doi: 10.1016/j.scib.2021.07.025
    [7] Szameit A, Rechtsman M C 2024 Nat. Phys. 20 905 doi: 10.1038/s41567-024-02454-8
    [8] König M, Wiedmann S, Brüne C, Roth A, Buhmann H, Molenkamp L, Qi X L, Zhang S C 2007 Science 318 766 doi: 10.1126/science.1148047
    [9] Zhang H J, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 doi: 10.1038/nphys1270
    [10] Zhang Y Y, Chu R L, Zhang F C, Shen S Q 2012 Phys. Rev. B 85 035107 doi: 10.1103/PhysRevB.85.035107
    [11] Jiang H, Wang L, Sun Q F, Xie X C 2009 Phys. Rev. B 80 165316 doi: 10.1103/PhysRevB.80.165316
    [12] Li X Q, Zhang H H, Xu H, San H D, Wang X N, Qi S F, Qiao Z H 2024 Phys. Rev. B 109 155427 doi: 10.1103/PhysRevB.109.155427
    [13] Su W P, Schrieffer J R, Heeger A J 1979 Phys. Rev. Lett. 42 1698 doi: 10.1103/PhysRevLett.42.1698
    [14] Song F, Yao S, Wang Z 2019 Phys. Rev. Lett. 123 246801 doi: 10.1103/PhysRevLett.123.246801
    [15] Velury S, Bradlyn B, Hughes T L 2021 Phys. Rev. B 103 024205 doi: 10.1103/PhysRevB.103.024205
    [16] 徐磊, 李沛岭, 吕昭征, 沈洁, 屈凡明, 刘广同, 吕力 2023 物理学报 72 177401 doi: 10.7498/aps.72.20230951 Xu L, Li P L, Lü Z Z, Shen J, Qu F M, Liu G T, Lü L 2023 Acta Phys. Sin. 72 177401 doi: 10.7498/aps.72.20230951
    [17] 关欣, 陈刚 2023 物理学报 72 140301 doi: 10.7498/aps.72.20230152 Guan X, Chen G 2023 Acta Phys. Sin. 72 140301 doi: 10.7498/aps.72.20230152
    [18] Gu Y, Lu Z P 2024 Chin. Phys. B 33 090202 doi: 10.1088/1674-1056/ad59fb
    [19] Li G Q, Wang B H, Tang J Y, Peng P, Dong L W 2023 Chin. Phys. B 32 077102 doi: 10.1088/1674-1056/aca7ef
    [20] Huang A H, Ke S S, Guan J H, Li J, Lou W K 2024 Chin. Phys. Lett. 41 097302 doi: 10.1088/0256-307X/41/9/097302
    [21] Chang Z W, Hao W C, Bustamante M, Liu X 2024 Chin. Phys. Lett. 41 037302 doi: 10.1088/0256-307X/41/3/037302
    [22] Xu Z, Zhang R, Chen S, Fu L, Zhang Y 2020 Phys. Rev. A 101 013635 doi: 10.1103/PhysRevA.101.013635
    [23] Prodan E, Hughes T L, Bernevig B A 2010 Phys. Rev. Lett. 105 115501 doi: 10.1103/PhysRevLett.105.115501
    [24] Cai X M, Lang L J, Chen S, Wang Y 2013 Phys. Rev. Lett. 110 176403 doi: 10.1103/PhysRevLett.110.176403
    [25] Liu J, Potter A C, Law K T, Lee P A 2012 Phys. Rev. Lett. 109 267002 doi: 10.1103/PhysRevLett.109.267002
    [26] Li J, Chu R L, Jain J K, Shen S Q 2009 Phys. Rev. Lett. 102 136806 doi: 10.1103/PhysRevLett.102.136806
    [27] Groth C W, Wimmer M, Akhmerov A R, Tworzydlo J, Beenakker C W J 2009 Phys. Rev. Lett. 103 196805 doi: 10.1103/PhysRevLett.103.196805
    [28] Meier E J, An F A, Dauphin A, Maffei M, Massignan P, Hughes T L, Gadway B 2018 Science 362 929 doi: 10.1126/science.aat3406
    [29] Stützer S, Plotnik Y, Lumer Y, Titum P, Lindner N H, Segev M, Rechtsman M C, Szameit A 2018 Nature 560 461 doi: 10.1038/s41586-018-0418-2
    [30] Borchmann J, Farrell A, Pereg-Barnea T 2016 Phys. Rev. B 93 125133 doi: 10.1103/PhysRevB.93.125133
    [31] Kitaev A Y 2001 Phys. Usp. 44 131 doi: 10.1070/1063-7869/44/10S/S29
    [32] Ivanov D A 2001 Phys. Rev. Lett. 86 268 doi: 10.1103/PhysRevLett.86.268
    [33] Zhu S L, Shao L B, Wang Z D, Duan L M 2011 Phys. Rev. Lett. 106 100404 doi: 10.1103/PhysRevLett.106.100404
    [34] Lindner N H, Berg E, Refael G, Stern A 2012 Phys. Rev. X 2 041002 doi: 10.1103/PhysRevX.2.041002
    [35] Nayak C, Simon S H, Stern A, Freedman M, Sarma S D 2008 Rev. Mod. Phys. 80 1083 doi: 10.1103/RevModPhys.80.1083
    [36] Lang L J, Chen S 2012 Phys. Rev. B. 86 205135 doi: 10.1103/PhysRevB.86.205135
    [37] Hua C B, Chen R, Xu D H, Zhou B 2019 Phys. Rev. B 100 205302 doi: 10.1103/PhysRevB.100.205302
    [38] Hegde S S, Vishveshwara S 2016 Phys. Rev. B 94 115166 doi: 10.1103/PhysRevB.94.115166
    [39] DeGottardi W, Thakurathi M, Vishveshwara S, Sen D 2013 Phys. Rev. B 88 165111 doi: 10.1103/PhysRevB.88.165111
    [40] Wakatsuki R, Ezawa M, Tanaka Y, Nagaosa N 2014 Phys. Rev. B 90 014505 doi: 10.1103/PhysRevB.90.014505
    [41] Jagannathan A 2021 Rev. Mod. Phys. 93 045001 doi: 10.1103/RevModPhys.93.045001
    [42] Aubry S, André G 1980 Ann. Isr. Phys. Soc. 3 18
    [43] Merlin R, Bajema K, Clarke R, Juang F Y, Bhattacharya P K 1985 Phys. Rev. Lett. 55 1768 doi: 10.1103/PhysRevLett.55.1768
    [44] Longhi S 2019 Phys. Rev. Lett. 122 237601 doi: 10.1103/PhysRevLett.122.237601
    [45] Kobiałka A, Awoga O A, Leijnse M, Domański T, Holmvall P, Black-Schaffer A M 2024 Phys. Rev. B 110 134508 doi: 10.1103/PhysRevB.110.134508
    [46] Hu Y C, Kane C L 2018 Phys. Rev. Lett. 120 066801 doi: 10.1103/PhysRevLett.120.066801
    [47] Tong L, Cheng S J, Guo H, Gao X L 2021 Phys. Rev. B 103 104203 doi: 10.1103/PhysRevB.103.104203
    [48] Zhu J X 2016 Bogoliubov-de Gennes Method and Its Applications (Cham: Springer Cham
    [49] Lieb E, Schultz T, Mattis D 1961 Ann. Phys. 16 407 doi: 10.1016/0003-4916(61)90115-4
    [50] Zhang P, Nori F 2016 New J. Phys. 18 043033 doi: 10.1088/1367-2630/18/4/043033
    [51] Akhmerov A R, Dahlhaus J P, Hassler F, Wimmer M, Beenakker C W J 2011 Phys. Rev. Lett. 106 057001 doi: 10.1103/PhysRevLett.106.057001
    [52] Fulga I C, Hassler F, Akhmerov A R, Beenakker C W J 2011 Phys. Rev. B 83 155429 doi: 10.1103/PhysRevB.83.155429
    [53] Roy S, Mishra T, Tanatar B, Basu S 2021 Phys. Rev. Lett. 126 106803 doi: 10.1103/PhysRevLett.126.106803
    [54] Li X, Sarma S D 2020 Phys. Rev. B 101 064203 doi: 10.1103/PhysRevB.101.064203
    [55] Wang Y, Zhang L, Niu S, Yu D, Liu X J 2020 Phys. Rev. Lett. 125 073204 doi: 10.1103/PhysRevLett.125.073204
    [56] Longhi S 2020 Opt. Lett. 45 4036 doi: 10.1364/OL.399742
    [57] Lang L J, Cai X M, Chen S 2012 Phys. Rev. Lett. 108 220401 doi: 10.1103/PhysRevLett.108.220401
    [58] Mourik V, Zuo K, Frolov S M, Plissard S R, Bakkers E P A M, Kouwenhoven L P 2012 Science 336 1003 doi: 10.1126/science.1222360
    [59] Law K T, Lee P A, Ng T K 2009 Phys. Rev. Lett. 103 237001 doi: 10.1103/PhysRevLett.103.237001
    [60] Lin C H, Sau J D, Das Sarma S 2012 Phys. Rev. B 86 224511 doi: 10.1103/PhysRevB.86.224511
    [61] Prada E, San Jose P, Aguado R 2012 Phys. Rev. B 86 180503 doi: 10.1103/PhysRevB.86.180503
    [62] Nichele F, Drachmann A C C, Whiticar A M, O'Farrell E C T, Suominen H J, Fornieri A, Wang T, Gardner G C, Thomas C, Hatke A T, Krogstrup P, Manfra M J, Flensberg K, Marcus C M 2017 Phys. Rev. Lett. 119 136803 doi: 10.1103/PhysRevLett.119.136803
    [63] Kells G, Meidan D, Brouwer P W 2012 Phys. Rev. B 85 060507 doi: 10.1103/PhysRevB.85.060507
    [64] Chen J, Woods B D, Yu P, Hocevar M, Car D, Plissard S R, Bakkers E P A M, Stanescu T D, Frolov S M 2019 Phys. Rev. Lett. 123 107703 doi: 10.1103/PhysRevLett.123.107703
    [65] Yu P, Chen J, Gomanko M, Badawy G, Bakkers E P A M, Zuo K, Mourik V, Frolov S M 2021 Nat. Phys. 17 482 doi: 10.1038/s41567-020-01107-w
  • 加载中
图( 4)
计量
  • 文章访问数:  36
  • HTML全文浏览数:  36
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-02
  • 刊出日期:  2025-05-20

准晶势调制的一维p波超导体中的拓扑量子相变

    通讯作者: E-mail: 201712605002@email.sxu.edu.cn
  • 1. 山西工程科技职业大学, 晋中　030619
  • 2. 湖北民族大学, 恩施　445000
  • 3. 山西大学理论物理研究所, 光量子技术与器件全国重点实验室, 太原　030006
  • 收稿日期:  2025-02-02

摘要: 研究了一维Fibonacci准晶势调制下的p波超导体下的拓扑相变和局域化性质. 在Fibonacci准晶势调制下, 通过计算$Z_2$拓扑不变量确定了系统的拓扑相图. 分析相图指出在Fibonacci准晶势调制下, 系统可以由拓扑平庸超导相进入拓扑安德森超导相. 进一步分析发现, 在某些参数下, 系统会发生多次拓扑安德森超导相转变并伴随零能态的出现. 此外, 还研究了系统的局域化性质, 通过分析分形维度、平均逆参与率序参量, 发现Fibonacci准晶势诱导的拓扑安德森超导相, 其体态的波函数表现出多重分形行为, 这与随机无序诱导出来的传统拓扑安德森超导相完全不同. 该研究结果为一维p波超导体中拓扑相变和局域化转变的研究提供了一些新的理解和参考.

English Abstract

    全文HTML

    1.   引　言

    • 近年来, 寻找新奇的拓扑物态一直是凝聚态物理的基本课题之一[1-5]. 而对拓扑物态的研究中, 最著名的就是拓扑绝缘体的发现, 已经在各类实验系统中得到了证实, 包括超冷原子系统[6]、光子晶体[7]等. 而在实际的拓扑材料中, 拓扑绝缘体也得到了广泛的证实, 如König等[8]在$ {\rm{HgTe}}/{\rm{CdTe}} $量子阱体系中获得了拓扑绝缘体, 而张海军等[9]在$ {\rm{Bi}}_2{\rm{Se}}_3 $材料中也发现了拓扑绝缘体的存在. 而后很多工作基于$ {\rm{HgTe}} $和$ {\rm{Bi}}_2{\rm{Se}}_3 $这些拓扑材料, 对拓扑绝缘体的性质进行了大量研究[10-12]. 而拓扑绝缘体最显著的特征是, 在能隙中具有导电的拓扑边界态[13-21], 其对弱无序扰动具有鲁棒性. 但在强无序条件下, 拓扑边界态会被破坏掉并伴随着安德森局域化转变[22-25]. 但在2009年, 香港大学的沈顺清组[26]和荷兰莱顿大学的Beenakker组[27]在研究中发现, 当体系处于拓扑平庸相时, 加入无序, 随着无序强度的增加, 系统可以从拓扑平庸相转化为拓扑非平庸相, 这种被无序诱导出来的拓扑相被称为拓扑安德森绝缘体. 2018年, 人们在一维冷原子纳米线[28]和二维光子波导阵列[29] 两种不同的人工合成的实验系统中观测到了拓扑安德森绝缘体的存在.

      之后的研究发现, 将无序引入拓扑超导系统, 也能出现无序诱导的拓扑相, 类似地被称为拓扑安德森超导体相[30]. 两者的区别主要在于研究的系统不一样, 拓扑安德森绝缘体主要是在拓扑绝缘体模型中研究, 如一维Su-Schrieffer-Heeger (SSH)模型[28]和二维Haldane模型[11]. 而拓扑安德森超导相主要出现在一维超导体模型中, 比如典型的模型就是一维p波超导体对应的Kitaev链. 一维p波超导体对应的Kitaev链是一类非常重要的拓扑模型, 其拓扑边界态是一对Majorana费米子组成的拓扑零模[31]. 而Majorana费米子遵循非阿贝尔交换统计, 使得其成为实现容错拓扑量子计算的重要参考模型[32-35]. 但在实际的研究中, 由于环境的不稳定性, 会不可避免地引入各种类型无序效应, 所以研究不同类型的扰动对拓扑零模的影响具有十分重要的意义. 如Lang和Chen[36]研究了周期性调制对拓扑零模的影响, 发现随着调制强度的增大, 拓扑非平庸超导相可能会被破坏. 蔡小明等[24]讨论了准晶势调制下一维p波超导体的拓扑相变, 发现随着准晶势的增加, 系统会经历一个拓扑非平庸超导相到拓扑平庸相的转相变, 并伴随着局域化转变. 此外, 周斌等[37]讨论了随机无序调制下的一维二聚化的p波超导体中的拓扑相变, 发现无序强度会诱导出一个拓扑非平庸超导相. 后续进一步对不同无序类型调制的一维p波超导体进行了深入研究[38-40]. 众所周知, 相较于随机无序系统, 准晶系统具有更加多样化的局域化特性. 准晶系统虽然没有周期性, 但是其分布不是杂乱无章的, 而是整体满足长程有序. 换而言之, 其无序势是具有关联性质的. 比较典型的准晶系统有Fibonacci准晶[41]和调制周期为无理数的一维Anbry-André (AA)模型[42]. 但是这两类准晶系统的局域化性质有着明显的区别, Fibonacci准晶是由A和B不同的原子按照特定的排列规律形成的准晶, 原子排列顺序可以表示为B, A, AB, ABA, ABAAB···[41]. 目前, 科学家们按照Fibonacci准晶排列顺序制作出了GaAs-AlAs等超晶格材料[43]. 而Fibonacci准晶对应的体态波函数既不是扩展态也不是局域态, 而是临界态, 其空间波函数分布具有自相似性, 并且态密度分布满足数学上的Cantor集合形式[41]. 一维Anbry-André (AA)模型是在位势调制周期为无理数的系统(一般情况下无理数取值为黄金分割比$ ({\sqrt{5}-1})/{2} $), 该模型具有整体局域化转变的性质. 当在位势强度小于跃迁强度的2倍时, 系统的体态波函数全部为扩展态波函数; 当在位势强度大于跃迁强度的2倍时, 系统的体态波函数全部为局域态波函数[44]. 而且两类准晶系统对拓扑性质的影响也不尽相同, 例如对拓扑超导系统的影响, 有研究表明, 拓扑超导系统中引入Fibonacci准晶势, 可以显著提高系统的拓扑性质, 显著增大存在Majorana费米子束缚态的拓扑能隙[45]或使得Majorana费米子转化为Fibonacci任意子[46]等. 而如果在拓扑超导系统引入AA准晶势, 会发现随着准晶势的增加, 系统的拓扑性质被破坏掉, 而且拓扑的转变点也对应于系统局域化转变点[24], 并且可以在拓扑超导系统中诱导出一个临界相区[47]. 但相对于AA准晶势对一维p波超导体的研究来说, Fibonacci准晶势对一维p波超导体的研究工作较少.

      基于以上研究进展, 本文研究了Fibonacci准晶势调制的一维p波超导体下的拓扑相变和局域化性质. 发现Fibonacci准晶势会诱导出多次拓扑安德森超导相转变并伴随着零能态的出现, 并且给出了拓扑相变点的解析表达式. 此外, 还研究了系统的局域化性质, 发现拓扑安德森超导相对应的体态波函数为具有多重分形特征的临界态.

    2.   理论模型与方法

    • 考虑一维具有Fibonacci准晶势调制的p波超导体, 其哈密顿量如下:

      其中$ {c}_{i}^{\dagger} $($ {c}_{i} $)是费米子的产生(湮灭)算符, $ {n}_{i} = {c}_{i}^{\dagger }{c}_{i} $是粒子数算符, t是最近邻跃迁, Δ为p波配对强度. 在位无序势考虑为Fibonacci准晶势, 可以通过特征函数$ V_{i} $[41]得到:

      这里M代表常数势; V是准晶势调制强度; $ {{\rm{sgn}}[\cdots]} $表示符号函数; ϕ表示任意相位; α为准晶势的调制周期, 为无理数, 为了不失一般性, 取$ \alpha = (\sqrt{5}- 1)/2 $. 如果不考虑在位无序势($ V = 0 $), 当$ |M| = 2 t $时, 对应着能隙的闭合点, 而能隙的闭合点对应着拓扑的相变点. 所以该模型在干净条件下, 拓扑相变点为$ |M| = 2 t $[24]. 如果在位无序势不为零, 则可以通过Bogoliubov-de Gennes (BdG)[48,49]变换将系统的哈密顿量(1)对角化, 这里引入一组准粒子算符:

      式中, L代表系统的尺寸, n是能级指标. 哈密顿量(1)可用准粒子算符表示为$ {H} =\displaystyle \sum\nolimits_{n = 1}^{L}E_{n} ( {\eta}_{n}^{\dagger }{\eta}_{n}- {1}/{2}) $, 其中$ E_{n} $是准粒子的本征能量. 由对角化关系$ \left[ {\eta}_{n}^{\dagger }, H\right] = -E_{n}{\eta}_{n}^{\dagger} $, 得到下面的BdG耦合方程:

      其中, $ {h}_{ij} \;= \;-t\left( \delta_{j, i+1}\;+\;\delta_{j, i-1}\right) \;+\;V_{i}\delta_{ji} $, $ {\varDelta}_{ij}\;= -\varDelta( \delta_{j, i+1}\; -\;\delta_{j, i-1}) $, $ u_{n} \;=\; \left( u_{n, 1},\; \cdots,\; u_{n, L}\right) $, $ \nu_{n} \;= \left( \nu_{n, 1}, \cdots, \nu_{n, L}\right) $. 通过对角化求解BdG方程, 可以得到准粒子的本征能量$ E_n $以及对应本征波函数的$ u_{n} $和$ \nu_{n} $. 由于BdG方程满足粒子-空穴对称性, 即系统的能谱关于零点对称. 而(1)式的哈密顿量通过BdG变化后可以写成如下形式:

      其中${\boldsymbol{ C}} = (c_1, \cdots, c_L, c_1^{\dagger}, \cdots, c_L^{\dagger})^{{\mathrm{T}}} $. 这里C的前L项是电子的湮灭算符, 后L项可以看成空穴的湮灭算符, 相当于整个体系的自由度变成了原来的两倍. 而变化之后的BdG哈密顿量$ {{\boldsymbol{H}}}_{\rm{BdG}} $写成矩阵形式为

      其中, $ {h}_{ij} \;=\; -t\left( \delta_{j, i+1}\;+\;\delta_{j, i-1}\right) \;+\;V_{i}\delta_{ji} $, $ {\varDelta}_{ij} = -\varDelta\left(\delta_{j, i+1}-\delta_{j, i-1}\right) $.

      这里为了识别系统拓扑相变和局域化性质, 可以分别计算下列序参量. 用$ Z_{2} $拓扑不变量(Q)来表征其拓扑性质[50-52]. 而$ Q = {\rm{sgn}} [{\rm{Det}}({\boldsymbol{R}})] $. 当$ Q = -1 $时, 系统处于拓扑超导相, 存在拓扑零模. 当$ Q = 1 $时, 系统处于拓扑平庸相, 不存在拓扑零模. 这里R表示从左端入射得到的反射矩阵, 是散射矩阵S的一部分. 则$ Z_{2} $拓扑不变量用散射矩阵S 来计算, S形式如下:

      其中, $ 2\times 2 $的子块$ {\boldsymbol{R}},\; {\boldsymbol{R}}^{\prime} $和$ {\boldsymbol{T}},\; {\boldsymbol{T}}^{\prime} $分别为在超导体两端的反射和透射矩阵. 散射矩阵S可以通过转移矩阵方法得到. 基于哈密顿量(1), 零能的薛定谔方程给出:

      式中,

      $ \hat{{\boldsymbol{t}}}_{i} = -t{\boldsymbol{\sigma}}_z+{\mathrm{j}}\varDelta {\boldsymbol{\sigma}}_y $, $ \hat{{\boldsymbol{\lambda}}}_{i} = V_i{\boldsymbol{\sigma}}_z $, ${\boldsymbol{ \varPhi}} _{i} = \left( u_{i}, \nu _{i}\right) ^{{\mathrm{T}}} $是第i个格点上准粒子的波函数, $ {\boldsymbol{\sigma}}_{y} $和$ {\boldsymbol{\sigma}}_{z} $分别为y和z组分的泡利矩阵. 在超导体两端($ i = 1 $和L)总的转移矩阵为$ \tilde{{\boldsymbol{W}}} = \tilde{{\boldsymbol{W}}}_{L}\tilde{{\boldsymbol{W}}}_{L-1}\cdots \tilde{{\boldsymbol{W}}}_{2}\tilde{{\boldsymbol{W}}}_{1} $. 通过相似变换U, 把转移矩阵$ \tilde{{\boldsymbol{W}}} $写在新的基矢下[50-52]:

      这里I为$ 2\times 2 $的单位阵. 传输矩阵的矩阵元可以定义左端入射所得到的反射矩阵R和透射矩阵T, 以及表示从右端入射的反射$ {\boldsymbol{R}}' $和透射矩阵$ {\boldsymbol{T}}' $. 根据文献[50-52], 具体关系如下:

      得到R, T, $ {\boldsymbol{R}}' $和$ {\boldsymbol{T}}' $, 即可得到散射矩阵S.

      为了识别系统的局域化特性, 可以计算波 函数对应的逆参与率(inverse participation ratio, IPR)[53], 对第n个能级, IPR的定义如下:

      这里n为能级指标, i为格点指标. 如果波函数是扩展态, 在热力学条件下, IPR的值趋近零. 但对于局域态波函数, 其IPR为一个有限值. 为了研究系统整体的局域化性质, 可以进一步定义其平均值:

      这里$ {\rm{MIPR}} $将所有能级的$ {\rm{IPR}} $进行了求和平均, 从而反映系统整体的局域化性质. 而研究$ {\rm{MIPR}} $的标度行为, 可以确定系统的局域化特性. 如果系统处于局域相, $ {\rm{MIPR}} $保持为一个有限值, 不随系统尺寸变化而变化. 如果系统处于扩展相, $ {\rm{MIPR}} $的值随着1/L线性变化. 如果系统处于临界相, $ \mathrm{MIPR} $随尺寸L变化行为近似为$ \mathrm{MIPR}\propto L^{-\tilde{\tau}} $, 其中$ \tilde{\tau} \in (0, 1) $, 此时系统的波函数为临界波函数, 具有多重分形行为[41,54]. 为了更加直观反映系统局域化性质, 可以进一步定义分形维度$ {\varGamma} $, 对于第n个本征态的分形维度$ {\varGamma}_n $定义如下[55]:

      对于扩展态, $ {\varGamma}_n $的值趋于1; 对于局域态, $ {\varGamma}_n $的值趋于0; 对于临界态, $ {\varGamma}_n $为(0, 1)之间的一个有限值.

      下面的数值计算中考虑t作为能量量纲(t = 1). 这里为了方便计算, 设定$ \phi = 0 $. 通过精确对角化方法求解BdG方程, 可以得到准粒子的本征能量及本征波函数, 进而计算出上述序参量随无序强度V的变化, 分析出系统的性质.

    3.   结果分析与讨论

    • 本节首先选取参数$ \varDelta = 0.4 $作为具体的例子, 通过改变不同的无序强度V和常数势强度M, 计算不同序参量的数值结果, 分别分析系统的拓扑相变和局域化性质. 并且给出系统在V-M参数平面的拓扑相图.

      • 3.1.   拓扑相变

    • 这里, 为了确定拓扑相变点, 首先写出拓扑零能态的本征方程, 形式如下:

      引入局部变换: $ \varPsi_{i} = u_{i}+\nu_{i} $和$ \varPsi'_{i} = u_{i}-\nu_{i} $, 则(16)式可以写为

      将$ \varPsi'_{i} $的方程改写成转移矩阵的形式如下:

      由(18)式的转移矩阵的形式, 可以定义出拓扑零能态局域化长度的表达式如下:

      这里$ ||T|| $为总转移矩阵的范数, 且$ T = \displaystyle\prod\nolimits_{i = 1}^LT_i $. 根据文献[56], 拓扑零能态在拓扑相变点处, 局域化长度λ会产生发散行为($ \lambda \to \infty $), 则对应$ \lambda^{-1} = 0 $. 令(19)式等于0, 可得

      (20)式即拓扑相变点表达式, 如图1(a)中绿色虚线所示.

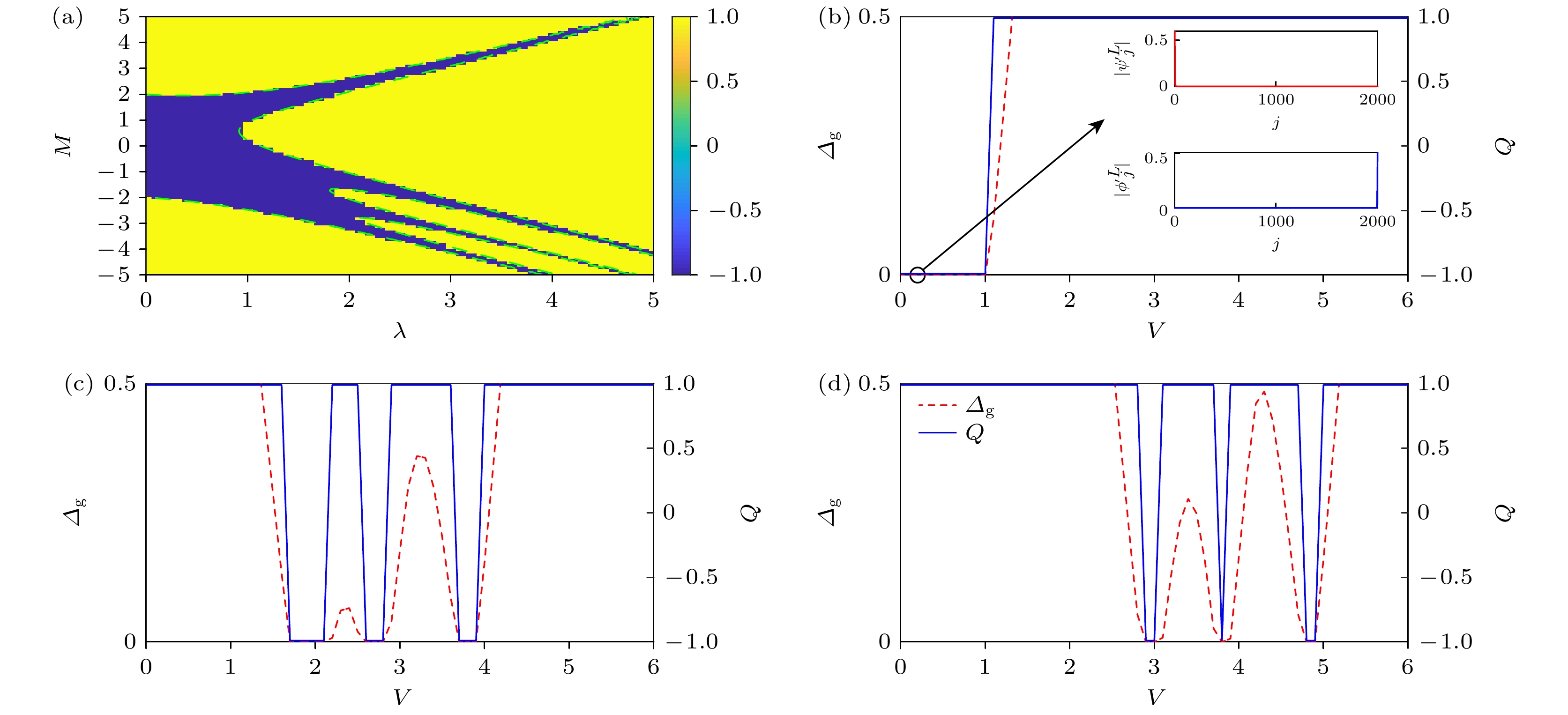
      图1(a)展示了以拓扑不变量Q大小为背景颜色填充的V-M参数平面的拓扑相图. 从图1(a)中可以发现, 当$ V = 0 $, 在$ |M| < 2 $的参数范围内, $ Q = -1 $表明系统处于拓扑非平庸超导相, 系统存在Majorana零模. 而在$ |M| > 2 $的范围内, $ Q = 1 $表明系统处于拓扑平庸相, 不存在Majorana零模. 与不考虑无序时结论一致. 但如果V不为零, 可以发现, 在$ |M| > 2 $的范围内, 随着无序强度V的增加, 拓扑不变量Q的值可以从1突变为–1, 说明无序可以诱导系统进入一个拓扑非平庸相, 即拓扑安德森超导体相. 进一步分析可以发现, 当$ M > 2 $, 随着无序强度V的增加, 系统只会出现一次拓扑安德森超导体转变, 并且随着无序强度V的进一步增加, 所诱导出的拓扑安德森超导体相还是会被无序破坏掉. 但在$ M < -2 $的参数范围内可以发现, 系统会出现多次拓扑安德森超导体相转变, 即第一次被诱导出的拓扑安德森超导体相被无序破坏掉之后, 随着无序强度V的进一步增强, 系统会发生第二次甚至第三次拓扑安德森超导体转变. 并且, 从图1(a)中的结果还可以看到(20)式所描述的拓扑相变点结果, 清晰地分割开了拓扑相区和拓扑平庸区. 这表明数值和解析的结果相符合.

      为了更加清晰地反映出这一现象, 定义能隙$ \varDelta_{\mathrm{g }}= E_{L+1}-E_{L} $, 这里$ E_{L+1} $和$ E_L $分别代表$ L+1 $和L能级的能量, 由于系统具有粒子空穴对称性, 系统的能谱上下对称, 并且出现拓扑零模的能级就是$ L+1 $和L能级. 如果存在拓扑零模, 则$ E_{L+1} $和$ E_L $都为零, $ \varDelta_{\mathrm{g }}$的值也为零, 表明系统处于拓扑相. 但如果拓扑零模被破坏, 则$ \varDelta_{\mathrm{g }}$的值不为零, 表示系统处于拓扑平庸相. 这里分别选取$ M = 1 $, $ -3 $和$ -4 $三个参数点, 绘制出$ \varDelta_{\mathrm{g}} $与拓扑不变量Q随无序强度V的变化, 如图1(b)—(d)所示. 当$ M = 1 $, 无序强度不大时, $ \varDelta_{\rm{g}} $的值为零, 并且对应的拓扑不变量$ Q = -1 $, 表明此时系统处于拓扑非平庸的超导相. 但当V增加到1.1时, $ \varDelta_{\mathrm{g}} $的值不为零, 并且对应的拓扑不变量Q的值从–1跳变至1, 表明系统发生了拓扑相变, 进入到拓扑平庸相, 如图1(b)所示. 这里为了更加直观反映系统的拓扑性质, 当$ M = 1 $时, 选取$ V = 2 $, 画出此时L拓扑零模能级对应的波函数$ {\psi'}^L_j = (u_j^L + v_j^L) $和$ {\phi'}^L_j = (u_j^L-v_j^L) $. 结果如图1(b)插图所示, 可以看到波函数分布在空间两端, 对应着拓扑边界态. 当$ M = -3 $ 或$ -4 $ 时, 开始$ \varDelta_{\mathrm{g}} $的值不为零, 能级能隙始终存在, 并且对应$ Q = 1 $, 说明系统处于拓扑平庸相. 但当V增加到一定值时, $ \varDelta_{\mathrm{g}} $的值为零, 形成拓扑零模. 并且对应拓扑不变量Q从1跳变到–1, 表明系统进入拓扑安德森超导体相. 随着无序强度V增加, 会发现拓扑安德森超导体相被破坏, $ \varDelta_{\mathrm{g }}$的值不为零, 对应拓扑不变量Q又跳变为$ 1 $. 而后继续增加V, $ E_L $和$ E_{L+1} $能级形成的能隙会再次发生闭合, $ \varDelta_{\mathrm{g}} $的值为零, 对应拓扑不变量Q再度跳变为–1. 表明系统会多次进入拓扑安德森超导体相. 并且可以看到, 当无序强度V很大时, 系统还是处于拓扑平庸相, 说明拓扑安德森超导体相只能在有限参数范围内被诱导出来, 对于强无序扰动还是会被破坏掉.

      • 3.2.   局域化性质

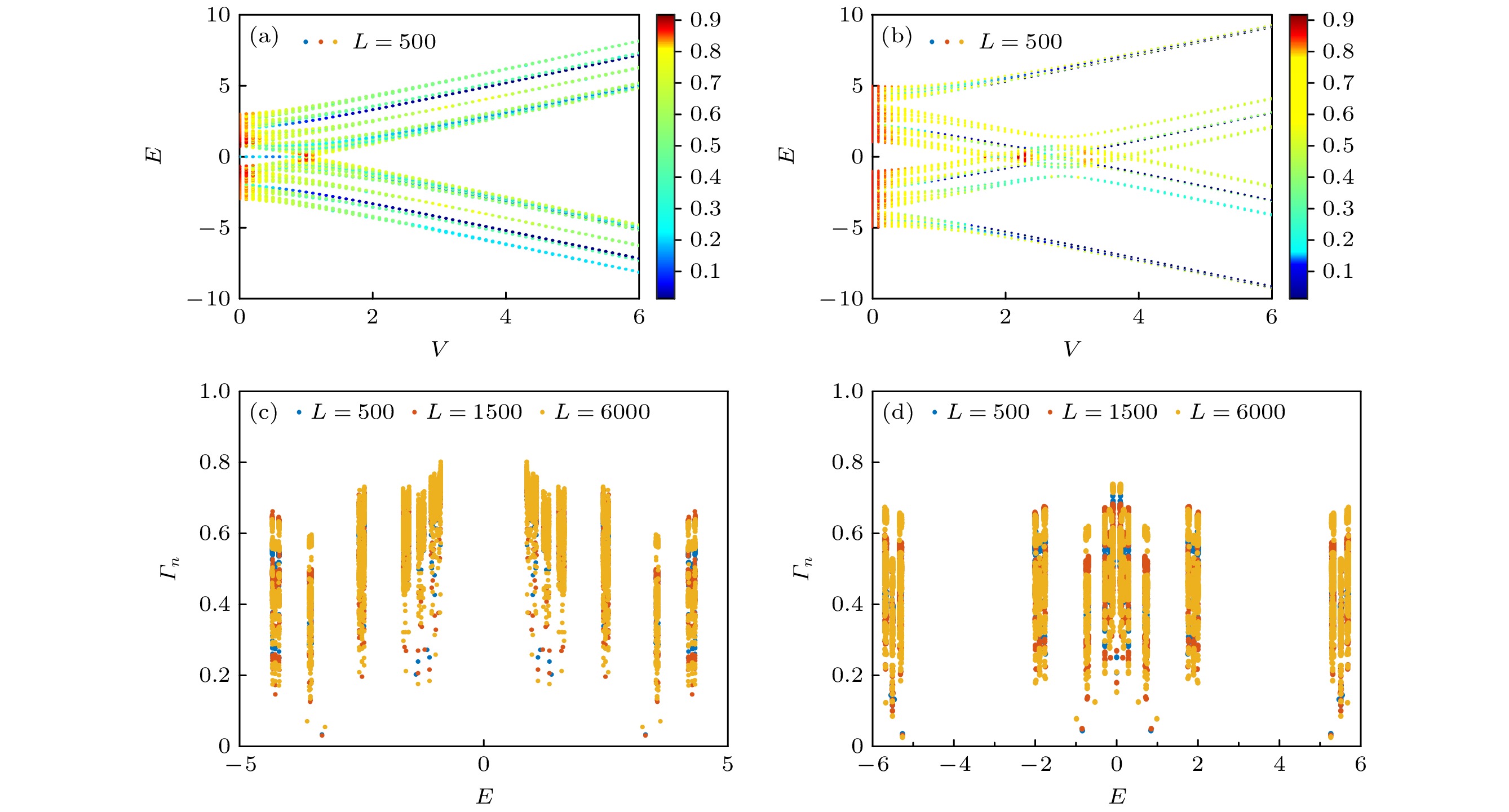
    • 上节通过数值计算各种序参量分析了系统的拓扑相变, 并且给出系统在V-M参数平面的拓扑相图. 一般来说, 由于随机无序诱导出来的拓扑安德森绝缘体或者拓扑安德森超导体, 其体态处于完全局域相, 不存在迁移率边. 但最近的研究表明, 由AA准晶势诱导出的拓扑安德森绝缘体相, 其对应的体态存在局域扩展混合的情况. 众所周知, Fibonacci准晶势形成的系统的波函数是具有多分形特征的临界态. 那么其诱导出的拓扑安德森超导体相对应的体态性质又会发什么样的变化? 为了研究其局域化性质, 本文分别在传统拓扑区和拓扑平庸区选取参数$ M = 1 $和$ -3 $来研究. 相关数值结果如下.

      图2(a), (b)分别显示了当$ M = 1 $和$ M = -3 $时分形维度($ {\varGamma}_n $)随本征能量E和无序强度V的变化. 可以发现, 无论无序强度V如何增加, 系统的本征态的分形维度$ {\varGamma}_n $值基本上都介于(0, 1)之间, 这表明系统整体处于临界相, 所有的本征波函数都是临界态波函数. 当然, 也会发现有少量的本征态的分形维度$ {\varGamma}_n $值趋于$ 0 $, 呈现出局域态的特征. 这是由于在数值计算中, 考虑的是开边界条件, 开边界条件会导致系统存在一些离散的局域态[57]. 而后, 选取$ V = 2 $参数下, 本征态的分形维度$ {\varGamma}_n $随着系统尺寸的变化, 结果如图2(c)和图2(d)所示. 图2(c)显示, 当$ M = 1 $且$ V = 2 $时, 可以发现整体本征态的分形维度$ {\varGamma}_n $不会随着尺寸的增加而发生明显的变化. 除了少数离散局域态的分形维度$ {\varGamma}_n $随着尺寸的增加, 其值向$ 0 $趋近之外, 其余大部分本征态的分形维度$ {\varGamma}_n $维持在(0, 1)之间的值. 当$ M = -3 $且$ V = 2 $时, 根据图1(c)的结果, 此时系统处于拓扑安德森超导体相, 可以发现, 除了诱导出的零模态和少数离散局域态的分形维度$ {\varGamma}_n $随着尺寸的增加, 其值向$ 0 $趋近. 其余大部分本征态的分形维度$ {\varGamma}_n $也为(0, 1)之间的值. 结果表明Fibonacci准晶势诱导的拓扑安德森超导体相的体态为临界态, 这与传统随机无序和AA类型准晶势无序诱导出的拓扑安德森超导体相局域化性质完全不同.

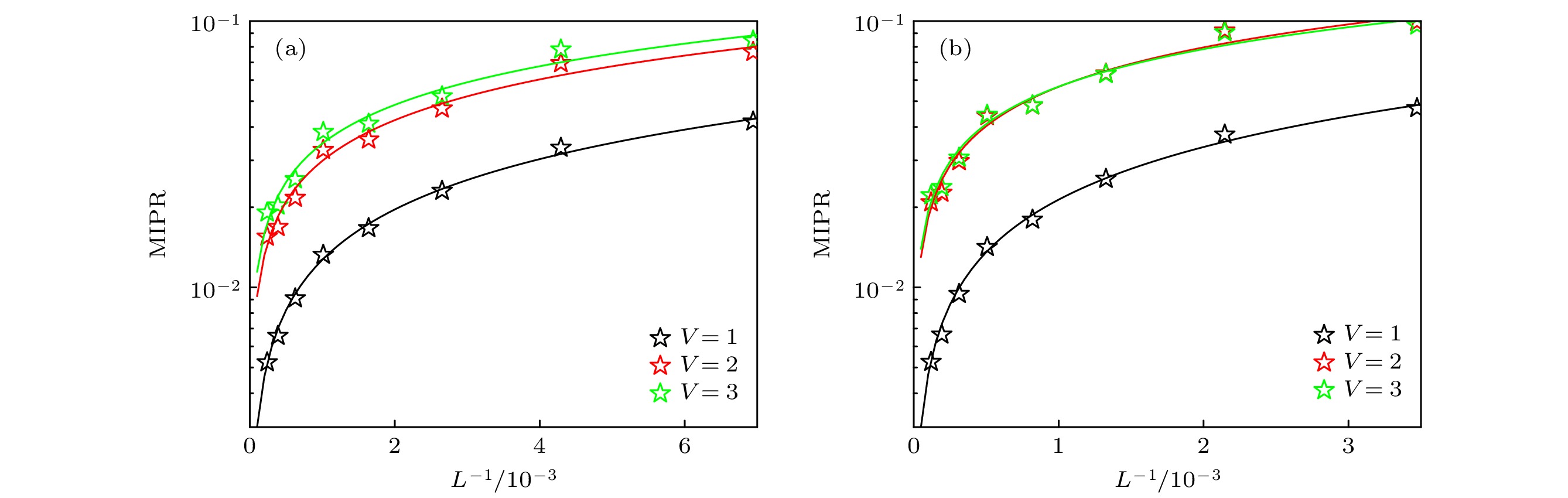
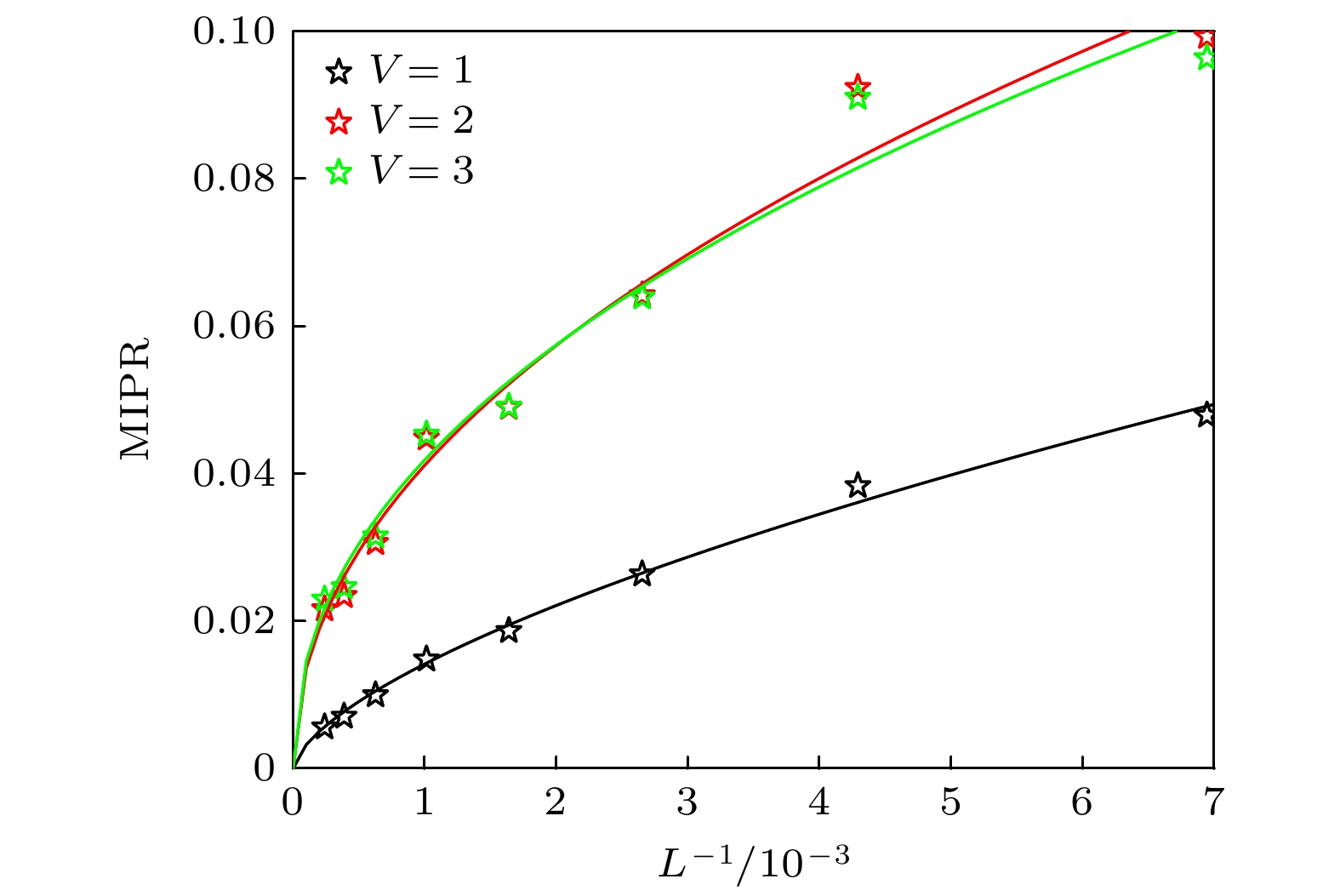
      为了进一步验证上述结果的正确性, 依旧选择$ M = 1 $和$ M = -3 $两种情况分析, 观察MIPR在不同无序强度V下的标度行为, 结果如图3(a)和图3(b)所示.

      当$ M = 1 $时可以发现, 当V分别取1, 2, 3时, MIPR随着尺寸L的增加, 其变化趋势分别可以由$ 0.9733 L^{-0.6283} $, $ 0.9996 L^{-0.5083} $以及$ 0.9688 L^{-0.482} $三条拟合函数描绘出来, 如图3(a)中三条实线所示. MIPR随尺寸L变化的标度行为满足幂函数变化, 说明系统整体处于临界相中. 当$ M = -3 $且V分别取1, 2, 3时, MIPR随着尺寸L的增加变化可以拟合为$ \mathrm{MIPR}\propto 1.193 L^{-0.6417}, 1.137 L^{-0.4805} $和$ 0.9869 L^{-0.4575} $, 如图3(b)中三条实线所示. 该结果也表明系统处于临界相当中. 以上结果表明Fibonacci准晶势诱导的拓扑安德森超导体相的体态都为临界态.

    4.   结　论

    • 本文研究了一维Fibonacci准晶势调制下的p波超导体下的拓扑相变和局域化性质. 通过计算$ Z_2 $拓扑不变量数值确定了系统的拓扑相图, 发现在Fibonacci准晶势调制下, 系统可以由拓扑平庸超导相进入拓扑安德森超导相. 并且在某些参数下, 系统会发生多次拓扑安德森超导相转变并伴随着零能态的出现. 但在强无序情况下, 拓扑安德森超导相还是会被破坏掉, 说明拓扑安德森超导相只会在有限的参数范围内被诱导出来. 此外, 通过计算分析分形维度, 平均逆参与率序参量, 分析了系统的局域化性质. 发现Fibonacci准晶势诱导的拓扑安德森超导相, 其体态的波函数为临界态波函数, 系统整体处于临界相. 并通过平均逆参与率序参量证明了临界相在热力学极限下的稳定性. 这与随机无序或者AA类型的准晶势无序诱导出来的传统拓扑安德森超导相不同. 该研究结果为一维p波超导体中拓扑相变和局域化转变的研究提供了一些新的理解和参考. 实验上, 能够实现一维p波超导体的实验平台就是超导体纳米线系统. 人们通过对超导体纳米线的研究认为, 量子化的零偏压电导峰是Majorana费米子, 即拓扑态出现的标志[58-61]. 通过提高样品的品质, 实验测得费米面处于零能附近的电导率已经接近于$ 2 e^2/h $[62]. 然而, 随着研究的深入, 人们在无Majorana费米子的超导体纳米线系统中同样也发现了零偏压的电导峰, 因此用零偏压电导峰来验证Majorana费米子的方法受到了质疑[63]. 最近的实验表明, 实验材料制备过程杂质或者温度等引入的可能是干扰实验探测Majorana费米子的重要原因[64,65]. 所以如何在有干扰的情况下, 找寻新的探测Majorana费米子的方法, 成为了实验上需要解决的问题.

    参考文献 (65)

目录

/

返回文章
返回