在量子光学领域, 单光子作为光与物质相互作用的理想研究对象, 不仅促进了量子叠加态^[1]和量子纠缠^[2,3]等基本量子现象的发现与验证, 还在量子信息科学中展现出了重要的应用价值. 作为量子信息传输的理想载体之一, 单光子凭借其优异的量子特性, 已广泛应用于量子密钥分发^[4]、量子计量学^[5]和量子信息处理^[6]等领域的研究. 特别值得关注的是, 单光子与量子比特的相干相互作用的研究在探索量子基础物理规律和推动量子信息处理技术等方面均展现出重要科学意义. 然而, 该体系面临的主要挑战在于两者之间的耦合强度通常非常微弱. 腔量子电动力学(QED)系统^[7–11]通过原子和特定量子化腔场的有效耦合, 可实现单光子(量子)层面上的光与物质的强相互作用. 这一独特的强耦合机制^[12,13]已在量子光学^[14,15]、量子信息^[16–18]以及基础物理^[19,20]等多个领域展现出广泛的应用价值. 实验研究中, 经常通过光学微腔技术来降低腔的衰减率^[21–23]以实现强耦合特性. 此外, 环路QED^[24]、半导体微腔^[25]、量子阱波导^[26]等新兴平台在调控系统耦合强度方面也取得了很大进展, 为实现强耦合乃至超强耦合提供了多样化方案.

近期, 受腔光力系统中单光子光力耦合增强方案^[27]的启发, Qin等^[28]和Leroux等^[29]分别提出了基于光学参量放大的原子-腔耦合增强的新方法. 该方案通过非线性参量过程对腔内模式进行压缩, 可使原子与腔内模式耦合强度呈现指数级增强. 这一创新方案显著降低了实现强耦合的技术门槛, 可使系统更容易进入强耦合乃至超强耦合区域^[30,31], 为量子调控提供了新的自由度. 目前, 基于光学参量放大的光与原子相互作用的研究已经取得一系列重要进展, 该机制已被用于压缩激光产生^[32]和原子间偶极-偶极相互作用增强^[33], 还在快速高保真度稳态纠缠制备^[34]及实现高保真的任意相位门实现^[35]等方面展现出独特优势.

系统辐射谱的量子特征及其统计特性是光与物质相互作用的直观体现, 同时也是研究光与物质相互作用的重要方法^[36,37]. 本文基于单光子激发的原子-腔系统, 通过非线性参量过程对腔内模式进行压缩, 研究这一系统中辐射光谱所呈现出的 特征. 腔内模式的压缩程度可通过施加于非线性介质上的驱动场进行调控. 理论计算表明, 随着驱动场强度的增大, 压缩腔模和原子的耦合强度显著增强. 当系统进入强耦合区域时, 原子辐射光谱中 观察到明显的真空拉比劈裂现象, 但光谱积分强度保持相对稳定. 值得注意的是, 随着驱动场强度的增大, 腔的辐射谱表现出更为丰富的物理特性, 不仅出现光谱劈裂现象, 还伴随着显著的强度放大效 应. 这一现象表明在适当的泵浦条件下, 对腔模的压缩能够有效增强腔的辐射光谱强度, 这可以为发展高灵敏度单光子探测^[38,39]技术提供一种新的理论思路.

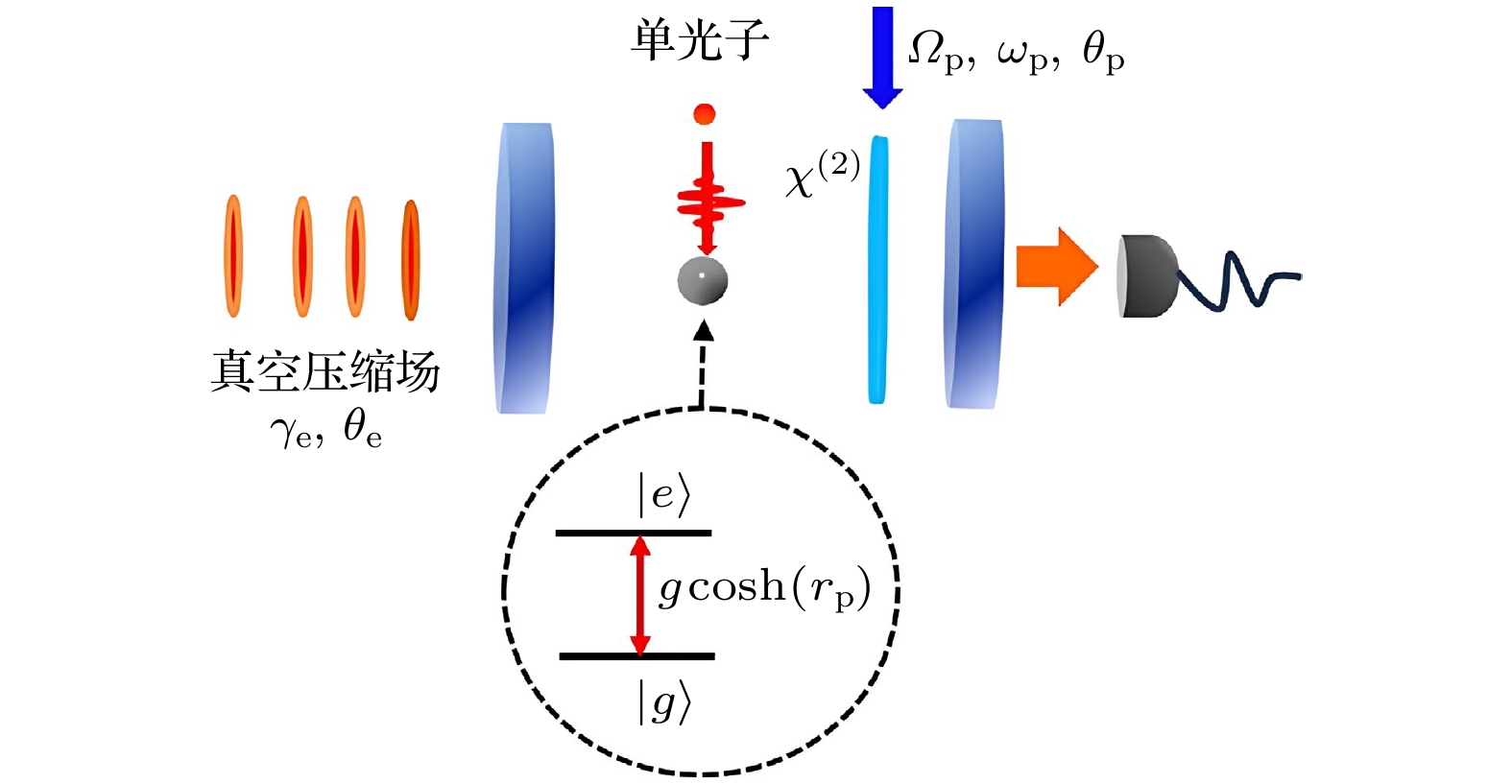
本文研究模型如图1所示, 光腔内包含一个二能级原子和$ \chi^{(2)} $非线性介质, 其中非线性介质受到振幅为$ \varOmega_{{\mathrm{p}}} $, 频率为$ \omega_{{\mathrm{p}}} $, 相位为$ \theta_{{\mathrm{p}}} $的驱动场泵浦. 这一系统的哈密顿量可以表示为$ (\hbar = 1) $:

式中$ \varDelta_{{\mathrm{c}}} = \omega_{{\mathrm{c}}}-\omega_{{\mathrm{p}}}/2 $和$ \varDelta_{{\mathrm{a}}} = \omega_{{\mathrm{a}}}-\omega_{{\mathrm{p}}}/2 $分别为腔模和原子的失谐量; $ a^{\dagger}(a) $为腔模的升(降)算符; $ \sigma_{z} = (\sigma_{+}\sigma_{-}-\sigma_{-}\sigma_{+})/2 $, $ \sigma_{+}(\sigma_{-}) $分别为二能级原子的泡利算符和跃迁算符; g为原子与腔模的耦合强度. 对于方程(1)中的非线性相互作用项, 可利用波戈留玻夫压缩(Bogoliubov squeezing)变换$ a = a_{{\mathrm{s}}}\cosh(r_{{\mathrm{p}}})-{\mathrm{e}}^{-{\mathrm{i}}\theta_{{\mathrm{p}}}}\sinh(r_{{\mathrm{p}}})a^{\dagger}_{{\mathrm{s}}} $进行对角化, 其中参数$ r_{{\mathrm{p}}} = (1/2)\arctan(\varOmega_{{\mathrm{p}}}/\varDelta_{{\mathrm{c}}}) $(为了保证系统的稳定, $ \left |\varOmega_{{\mathrm{p}}}/\varDelta_{{\mathrm{c}}}\right | < 1 $). 变换后的哈密顿形式变为

其中, $ \varDelta_{{\mathrm{s}}} = \varDelta_{{\mathrm{c}}}\sqrt{1-\alpha^{2}} $, $ a_{{\mathrm{s}}}^{\dagger}(a_{{\mathrm{s}}}) $表示压缩腔模的升(降)算符. 在旋转波近似下, 忽略哈密顿量中的反旋转波项后, 可以发现原子和压缩腔模的耦合强度增强为未压缩前的$ \cosh(r_{{\mathrm{p}}}) $倍. 当$ \varOmega_{{\mathrm{p}}}/\varDelta_{{\mathrm{c}}}\approx1 $时, 原子与腔的耦合强度将得到显著提升.

单光子激发时, 系统的初态可表示为

其中$ |1\rangle|0\rangle_{{\mathrm{s}}} $表示原子处于激发态, 压缩腔模处于基态; $ |0\rangle_{j}|0\rangle_{k} $表示耦合原子和腔的真空场处于基态. 在腔QED系统中, Almeida等^[40,41]通过单个三能级原子与经典驱动场及腔模之间的色散相互作用, 能够生成任意腔模压缩态, 并可有效制备如(3)式所示的量子态. 系统任意t时刻的态可表示为

其中, $ c_{{\mathrm{a}}}(t), c_{{\mathrm{s}}}(t), C_{j}(t), B_{k}(t) $是(4)式中相应态的几率振幅, 最后两个求和项代表能量向真空热库的耗散. 光学参量放大能够压缩腔模, 同时也为腔模带来额外的耗散. 为了抵消这一影响, 可将腔与压缩真空场(压缩参数为$ r_{{\mathrm{e}}} $和参考相位为$ \theta_{{\mathrm{e}}} $)耦合. 当压缩参数和参考相位满足$ r_{{\mathrm{e}}} = r_{{\mathrm{p}}} $, $ \theta_{{\mathrm{e}}}+\theta_{{\mathrm{p}}} =\pm n\pi (n = 1, 3, 5, \cdots) $时, 由光学参量放大引起的额外耗散将被完全抵消, 压缩腔模的耗散等效于耦合真空场的情况. 详细推导过程见附录A, 这一结论和文献[28,29]利用主方程推导的结果一致. 在旋转波近似下, 根据(2)式和(4)式可以得到$ c_{{\mathrm{a}}}(t) $和$ c_{{\mathrm{s}}}(t) $的运动学方程为

其中, γ和κ分别表示原子和压缩腔模的耗散. (5)式和(6)式仅基于哈密顿量(2)式的前三项进行推导, 而未包含反旋转波项的贡献. 关于反旋转波项的影响及其物理意义, 将在后续研究中详细讨论.

本文重点讨论系统的辐射谱, 虽然文献[29]利用量子回归理论研究了原子辐射谱, 但并未给出具体的解析形式. 为了进一步研究这一系统, 本文参照文献[42]中的方法, 在单光子激发的系统中研究原子和腔的辐射谱线, 并详细推导出解析形式.

本系统中原子辐射谱$ S_{{\mathrm{a}}} $可表示为

在单光子激发的情况下, 根据系统任意时刻的量 子态(4)式, (7)式中的二阶关联函数可用几率振幅^[42]表示:

所以$ S_{{\mathrm{a}}}(\omega) $可进一步表示为

根据(5)式和(6)式, 以及系统的初态(3)式, 可以给出$ c_{{\mathrm{a}}}(t) $的解析式. 为了更清晰地展示非线性参量驱动对系统的影响, 这里让$ \kappa = \gamma $, $ \varDelta_{{\mathrm{a}}} = 0 $. 在此条件下, 可以得到:

其中$ \beta = \sqrt{4 g^{2}\cosh^{2}(r_{{\mathrm{p}}})+\varDelta_{{\mathrm{s}}}^{2}} $. 将(10)式代入到(9)式中, 并利用关系式

可以得到原子的辐射谱有如下形式:

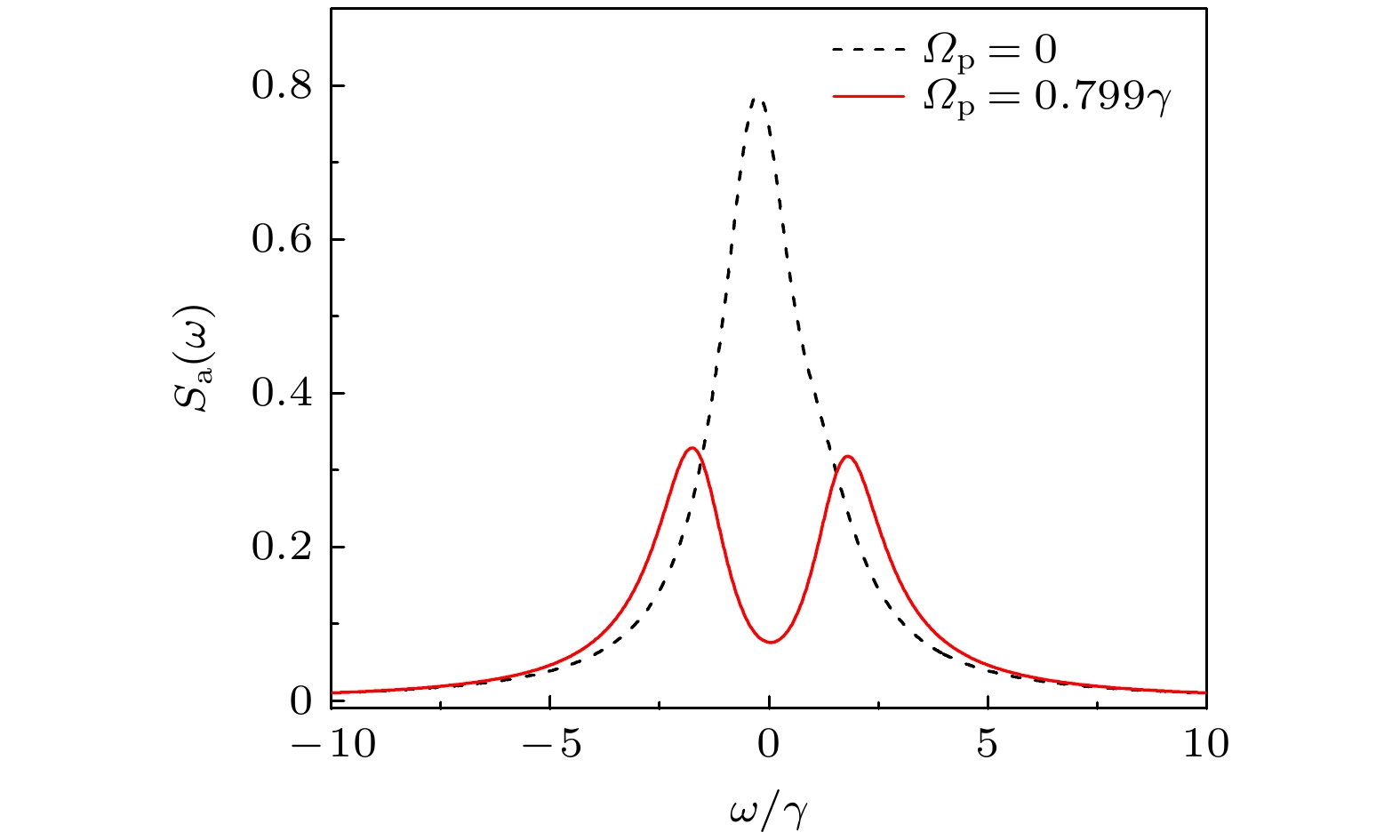
式中的前两项分别对应位于$ \omega = (\beta+\varDelta_{{\mathrm{s}}})/2 $和$ \omega = -(\beta-\varDelta_{{\mathrm{s}}})/2 $的两个峰, 第三项是前两项的相干项. 图2给出了原子的辐射谱.

图2展示了光学参量放大对原子辐射光谱的影响. 在未施加参量驱动泵浦($ \varOmega_{{\mathrm{p}}} = 0 $)时, 原子与腔模的耦合强度为$ g = 0.5\gamma $ ($ g/\gamma < 1 $, 处于弱耦合区域), 两者之间未形成有效的能量交换, 原子的辐射谱以自由辐射为主, 因此原子辐射谱呈现出洛伦兹型的单峰结构. 当参量驱动泵浦强度为$ \varOmega_{{\mathrm{p}}} = 0.799\gamma $时, 腔内模式被压缩, 导致原子与压缩腔模的有效耦合强度增大至$ g\cosh(r_{{\mathrm{p}}}) = 1.62\gamma $(处于强耦合区域). 在这一状态下, 原子和压缩腔模之间出现周期性的能量交换, 导致原子辐射谱线出现劈裂双峰结构. 另外需要指出的是, 根据(12)式的理论结果, 劈裂峰应呈现出非对称结构. 然而, 当$ \varOmega_{{\mathrm{p}}} = 0.799\gamma $时, $ \varDelta_{{\mathrm{s}}}/\beta \approx0.012 $, 从而使得谱线的不对称特征在图2中很难体现. 因此, 如图2中的红色实线所示, 两个劈裂峰在高度和位置上均呈现出近似的对称性分布.

腔的辐射谱$ S_{{\mathrm{c}}}(\omega) $可表示为

为求解基于哈密顿(2)式的二阶关联函数, 这里也需要利用波戈留玻夫压缩变换$ a = a_{{\mathrm{s}}}\cosh(r_{{\mathrm{p}}})- {\mathrm{e}}^{-{\mathrm{i}}\theta_{{\mathrm{p}}}}\sinh(r_{{\mathrm{p}}})a^{\dagger}_{{\mathrm{s}}} $将(13)式中的二阶关联函数中的算符$ a, a^{\dagger} $转换为$ a_{{\mathrm{s}}}, a_{{\mathrm{s}}}^{\dagger} $:

从(14)式可以看到, 非线性参量驱动会显著改变腔的辐射谱特性. 在单光子激发的条件约束下, 系统的动力学行为可由旋转波近似(RWA)主导. 利用(4)式, 忽略反旋转波项, (14)式可以进一步写成:

因此, 腔的辐射谱$ S_{{\mathrm{c}}}(\omega) $可表示为

同样地, 让$ \kappa = \gamma $, $ \varDelta_{{\mathrm{a}}} = 0 $, 根据系统的哈密顿量和系统初态, 可以得到$ c_{{\mathrm{s}}}(t) $的解析式为

其中$ \beta = \sqrt{4 g^{2}\cosh^{2}(r_{{\mathrm{p}}})+\varDelta_{{\mathrm{s}}}^{2}} $. 根据(16)式和(17)式, 可以得到:

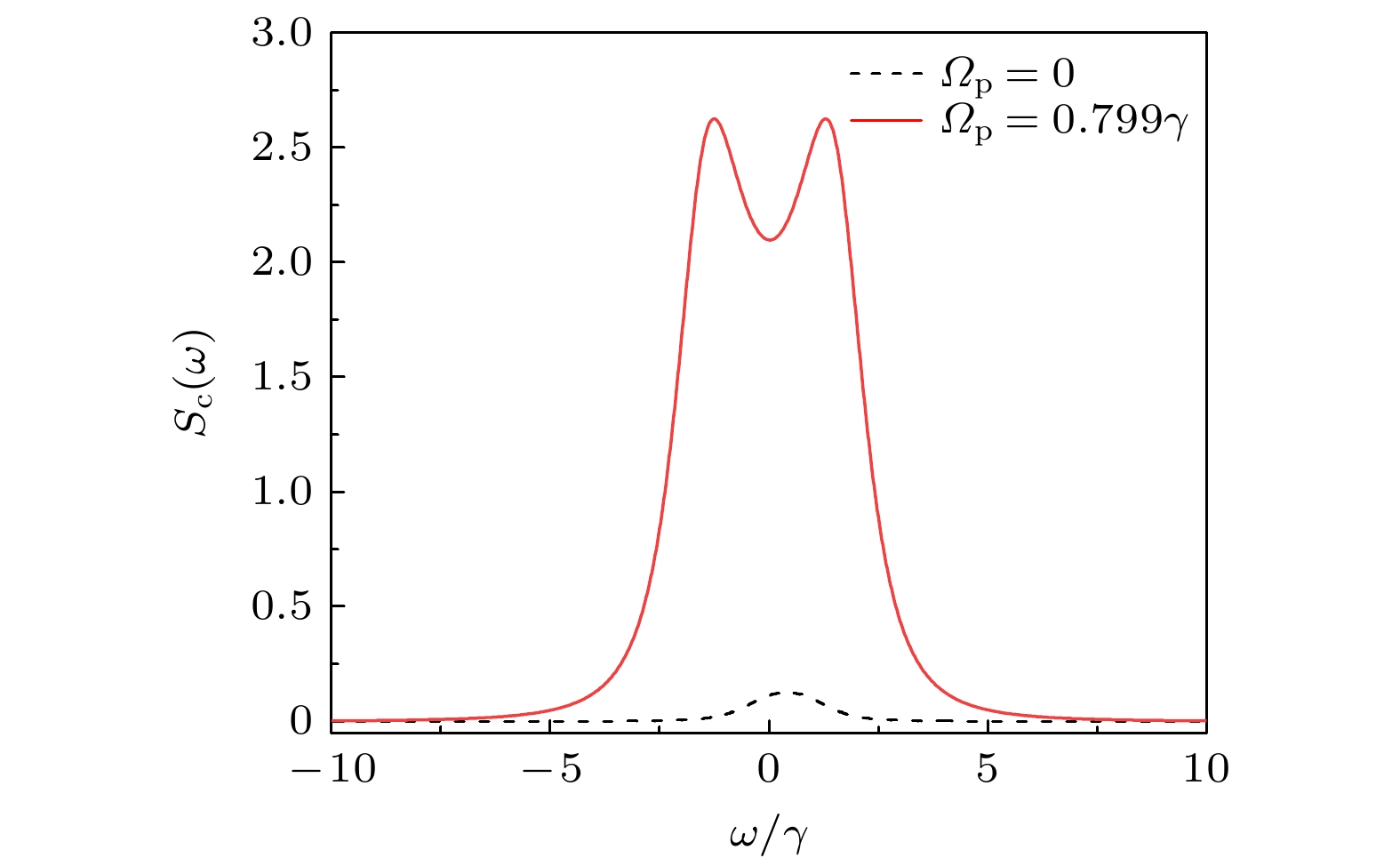
式中前两项分别对应位置在$ \omega = (\beta+\varDelta_{{\mathrm{s}}})/2 $, $ \omega = -(\beta-\varDelta_{{\mathrm{s}}})/2 $且高度相同的两个峰, 第三项是前两项的相干项. 根据(18)式画出腔的辐射谱如图3所示.

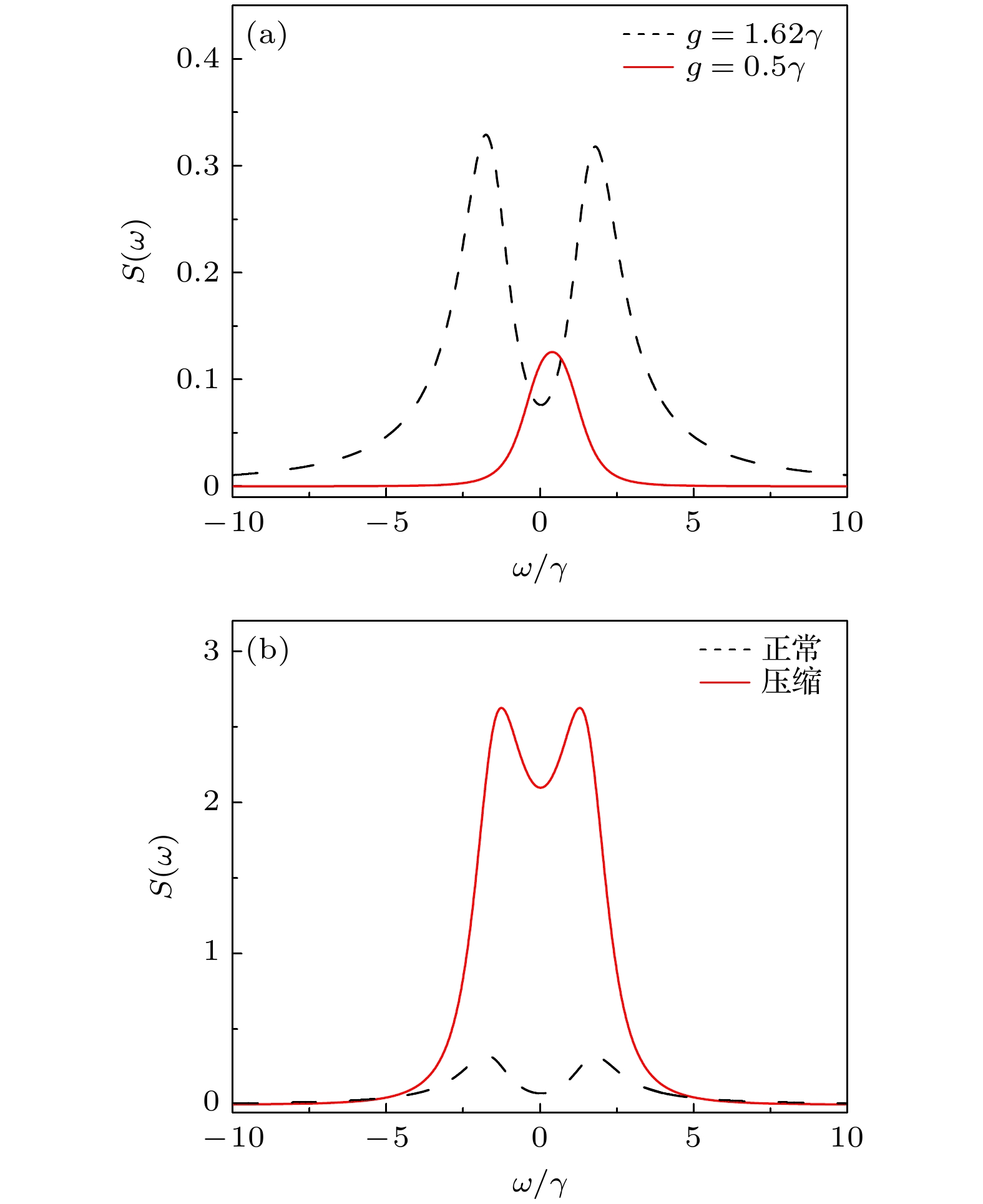
图3清晰地展示了驱动场强度对腔辐射谱的影响. 在未施加驱动泵浦场时($ \varOmega_{{\mathrm{p}}} = 0 $), 原子与腔模的耦合强度为$ g = 0.5\gamma $ ($ g/\gamma < 1 $, 处于弱耦合区域). 在此状态下, 原子与腔模的相互作用非常弱, 因此腔的辐射谱强度很弱, 且由于腔模的失谐量$ \varDelta_{{\mathrm{c}}} = 0.8\gamma $, 辐射谱呈现出非对称的单峰结构. 当驱动场强度增强至$ \varOmega_{{\mathrm{p}}} = 0.799\gamma $时, 原子与腔内压缩模式的耦合强度为$ 1.62\gamma $, 系统进入强耦合区域. 此时, 腔的辐射谱呈现出双峰劈裂特征, 并伴随显著的强度放大现象. 值得注意的是, 虽然原子与腔内模式耦合强度的增加会提升光子转移到腔模的几率, 导致光谱强度的增加, 然而这不是光谱强度被放大的主要原因. 图4比较了未施加驱动泵浦($ \varOmega_{{\mathrm{p}}} = 0 $)且原子与腔耦合强度为$ 1.62\gamma $时的情况(黑色虚线), 来进一步研究非线性参量驱动对辐射谱的影响.

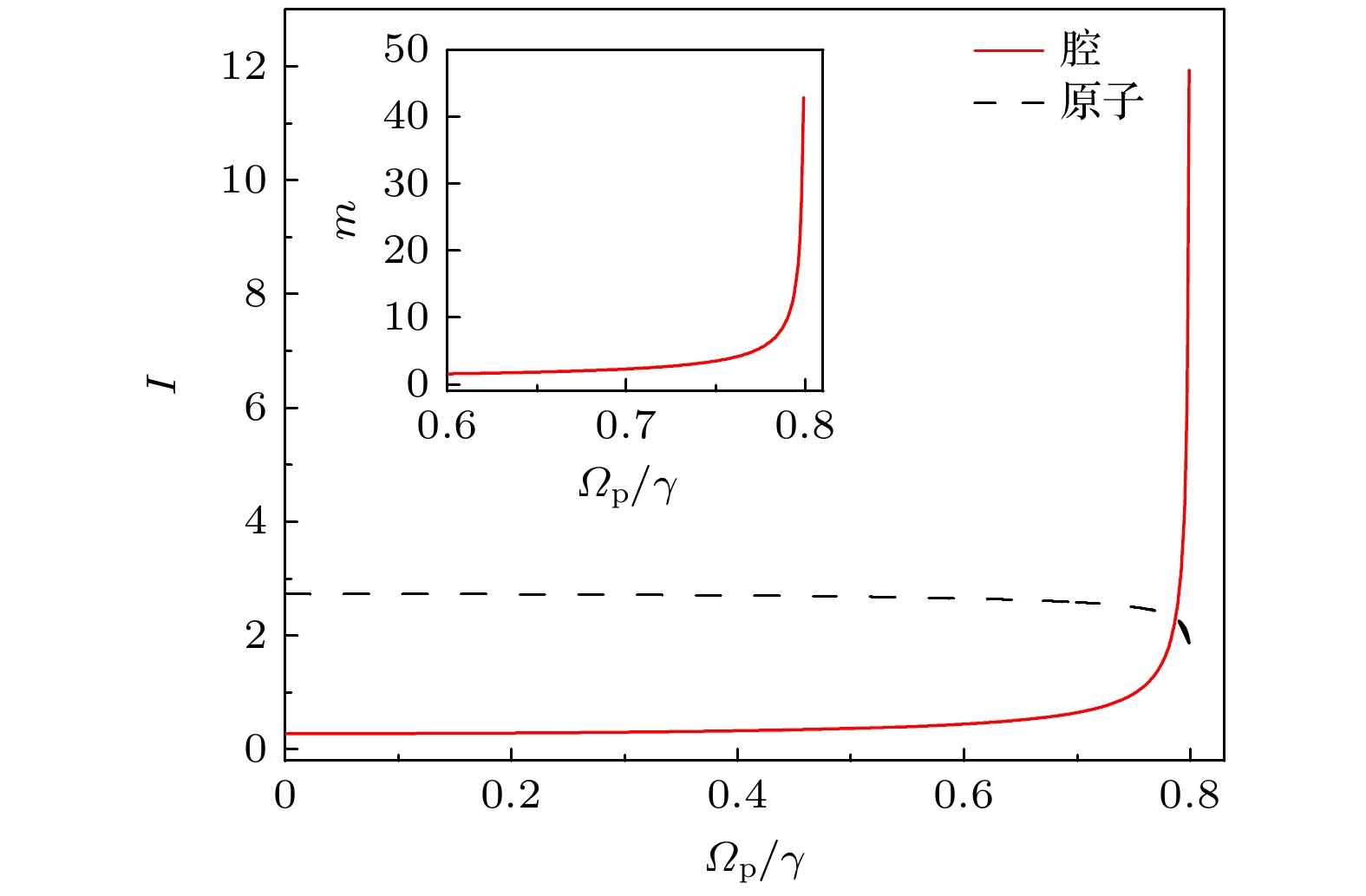
图4(a)展示了在$ \varOmega_{{\mathrm{p}}} = 0 $时, 原子与腔模的耦合强度分别为$ g = 1.62\gamma $和$ g = 0.5\gamma $时的辐射谱. 结果表明, 当$ g = 1.62\gamma $时腔的辐射谱出现劈裂, 强度相较于$ g = 0.5\gamma $的情况显著提高, 这是因为耦合强度的提高提升了原子和腔模的能量交换效率. 进一步, 图4(b)对比了相同有效耦合强度下的腔的辐射谱, 其中红色实线对应$ \varOmega_{{\mathrm{p}}} = 0.799\gamma $(根据(2)式, 原子与腔内模式的耦合强度为$ g\cosh(r_{{\mathrm{p}}}) = 1.62\gamma $), 黑色虚线同图4(a)的参数一致. 显然, 无论是压缩模式还是正常模式, 辐射谱均呈现出劈裂现象. 值得注意的是, 当原子与压缩腔模强耦合时, 光谱强度表现出更为显著的放大效应. 这是因为随着泵浦驱动强度的增加, 原子与压缩腔模的耦合强度随之增加, 提高了压缩腔模被激发的几率. 同时, 驱动场强度的增加也促使更多泵浦光子转换为压缩腔模的单光子态. 通过波戈留玻夫压缩变换还原为腔原始模式时, 压缩腔模中的泵浦光子转换为腔的辐射谱, 从而实现了光谱强度的放大. 为了更直观地展示这种放大特性, 图5比较了原子和腔的辐射谱强度随$ \varOmega_{{\mathrm{p}}} $的变化情况, 其中辐射谱强度定义如下:

从图5可以看到, 随着驱动场$ \varOmega_{{\mathrm{p}}} $的逐渐增大, 原子的光谱强度呈现出缓慢下降的趋势, 但整体变化幅度很小, 说明光学参量放大过程对原子辐射谱强度的影响非常有限. 相比之下, 腔的辐射谱则表现出显著不同的行为, 当$ \varOmega_{{\mathrm{p}}} < 0.7\gamma $时, 辐射谱强度变化不大. 当$ \varOmega_{{\mathrm{p}}} > 0.7\gamma $时, 辐射谱强度开始显著增大. 特别地, 当$ \varOmega_{{\mathrm{p}}}/\varDelta_{{\mathrm{c}}} $接近1时, 辐射谱的强度显示出急剧的放大效应. 在腔QED系统中, 基于量子比特与腔模相互作用的单光子探测得到广泛研究^[43]. 如图5所示, 可通过调节$ \varOmega_{{\mathrm{p}}} $值改变腔的辐射谱强度, 为进一步说明这一性质, 这里定义光谱强度放大因子

其中$ S_{{\mathrm{n}}}(\omega) $为$ \varOmega_{{\mathrm{p}}} = 0 $时腔的辐射谱, $ S_{{\mathrm{c}}}(\omega) $是(18)式描述的与$ \varOmega_{{\mathrm{p}}} $相关的辐射谱. 放大因子m和$ \varOmega_{{\mathrm{p}}} $的关系如图5的嵌入图所示, 放大因子m随着$ \varOmega_{{\mathrm{p}}} $强度的增大呈现出显著的非线性增长特征. 值得注意的是, 当非线性响应区域满足$ \varOmega_{{\mathrm{p}}} > 0.78\gamma $时, 放大因子m急剧增大, 尤其在$ \varOmega_{{\mathrm{p}}} = 0.799\gamma $时, 这一值可以达到43. 因此, 通过调节$ \varOmega_{{\mathrm{p}}} $至临界区域($ \varOmega_{{\mathrm{p}}}\approx\varDelta_{{\mathrm{c}}} $), 可显著增强腔的辐射谱强度, 从而提升单光子的探测几率. 针对本文提出的腔辐射谱放大理论, 现提供一种可能的实验途径. 腔中的二能级原子可采用$ ^{87} {\rm{Rb}}$, 其D1线(波长为795 nm)对应的$ 5 {\mathrm{P}}_{1/2}(\left| F = 2, m_{F} = -2 \right\rangle) $至$ 5 S_{1/2}(\left| F = 2, m_{F} = -2 \right\rangle) $的电偶极跃迁可与腔模发生有效耦合. 为提升单光子的探测效率, 可利用原子系综来替代单个二能级原子, 通过集体增强效应提高系统被单光子激发的几率, 从而确保量子初态的有效制备. 压缩腔场可通过周期性极化的磷酸钛氧钾(PPKTP)晶体来实现, 采用高带宽泵浦的PPKTP晶体可产生带宽达GHz量级的压缩真空库, 这些技术已经广泛应用于实验研究^[44,45], 从物理实现角度确保了理论方案的实验可行性.

本文研究了单光子激发的原子-腔中光学参量放大对系统光谱特性的调控机制. 在该系统中, 外部驱动场对腔内非线性介质的泵浦能够实现腔模压缩. 研究结果表明, 随着驱动泵浦场$ \varOmega_{{\mathrm{p}}} $强度的增大, 原子的辐射谱呈现出双峰劈裂结构, 但其光谱强度保持相对稳定, 仅呈现出微弱衰减. 与之形成对比的是, 腔辐射谱的线型和强度都随$ \varOmega_{{\mathrm{p}}} $增大而发生变化, 不仅出现双峰劈裂现象, 辐射谱强度也能得到显著放大. 该现象的物理机制可归因于参量驱动放大将驱动光转换为特定的压缩模式, 通过波戈留玻夫压缩变换将压缩模式映射回腔的原始模式时, 压缩腔模中的泵浦光子转换为腔的辐射谱, 最终实现腔辐射谱的放大. 本研究有助于加深人们对光学参量放大腔中光与物质相互作用的理解, 并为光信息处理、量子光学中的单光子检测提供了一种新的方案.

系统的哈密顿量(2)式仅描述了腔内模式和原子之间的相互作用, 而未考虑系统的耗散过程. 本附录将根据相互作用表象下的原子与腔同环境相互作用的哈密顿量, 对系统的耗散进行研究. 在旋转波近似下, 表征原子和腔的耗散的相互作用哈密顿量可分别表示为

波戈留玻夫压缩变换可以对角化系统哈密顿量(1). 该对角化过程对原子的耗散特性无影响, 但会显著改变腔的耗散行为. 在波戈留玻夫压缩变换下, 方程(A2)变为

在相互作用表象下, 若腔模耦合的是压缩真空场, 则将(A2)式中的$ c_{j}(c_{j}^{\dagger}) $替换为$ c_{j{\mathrm{s}}}( c_{j{\mathrm{s}}}^{\dagger}) $, 其中

其中, $ r_{{\mathrm{e}}} $和$ \theta_{{\mathrm{e}}} $分别为压缩真空场的压缩参数和参考相位. 则(A3)式可以写为

当$ r_{{\mathrm{e}}} = r_{{\mathrm{p}}} $, $ \theta_{{\mathrm{e}}}+\theta_{{\mathrm{p}}} = \pm n\pi \;(n = 1, 3, 5, \dots) $时, (A5)式可以化简为

(A6)式与方程(A2)形式相同, 即当参量驱动腔模耦合特定条件下的压缩真空场时, 可将其耗散过程等效为压缩腔模耦合自由空间的情况. 正文中(5)式和(6)式也是在这一前提条件下得到的.