-
压缩光场的制备与探测是量子光学领域的重要课题[1-3]. 作为一种非经典的量子态, 压缩光场某一正交分量的不确定性低于相干态的标准量子极限, 这一特性使其在精密测量中展现独特的优势[4]. 早在20世纪70年代, Stoler等[5]首次提出了压缩光场的数学描述, 为该领域奠定了坚实的理论基础. 1985年, 实验首次成功观测到压缩态光场[6], 标志着这一研究从理论迈向实践. 参量下转换(PDC)[7,8]和四波混频(FWM)[9-11]是制备压缩光场的两种主流技术. 近年来, 随着集成光子技术的突破, 芯片级压缩光源[12-14]的开发显著推动了其实用化进程. 在探测方面, 平衡零拍探测[15,16]利用信号光与本振光的干涉, 精确测量了压缩光场的非经典特性. 压缩光场在多个领域展现出重要的应用前景, 在引力波探测中, LIGO和Virgo天文台通过引入压缩光场技术, 有效降低了量子噪声, 大幅提升了探测灵敏度. 同时在保密通信[17-19]、精密计量学[20-23]以及量子计算[24,25]等领域, 压缩光场同样表现出良好的应用潜力.
压缩热态[26-29]与压缩数态[27,30,31]是两种重要的压缩态光场, 近期研究表明光子关联的聚束效应可显著提升成像和干涉图案的可见度[32-36], 甚至超越经典热光性能极限, 可见度接近自发参量下转换产生的纠缠光子对水平. 其研究对于理解量子光学非经典光态及量子信息处理至关重要, 揭示其在提升成像技术和干涉测量[32,33]的潜在优势. 同时, 光场的相干性分析是揭示其量子特性的重要手段[37], 相较于二阶相干函数, 高阶相干性可揭示诸如偏度与峰度等更高阶光子统计分布特征[38], 从而更加全面地反映光场的量子特性. 高阶相干性的深入研究对于区分经典与非经典光源、推动量子成像[39,40]等应用具有重要理论与实践意义. 然而, 关于压缩热态与压缩数态的高阶相干性及聚束效应仍有待分析研究, 其光场的非高斯散射过程及光子聚束的量子统计特性直接关系着在量子精密测量中的性能指标[38]. 其次, 全时延条件下高阶相干性理论框架尚未完善, 难以准确刻画光子全时延情况下高阶相干性的演化.
本文基于多级联HBT探测方案, 分析了压缩热态与压缩数态光场的高阶光子相干性. 理论上, 推导并研究了压缩热态光场在不同压缩参数与平均光子数下的超聚束效应及压缩数态光场在不同压缩参数与压缩光子数下的非经典特性. 进一步研究分析了实际实验条件下考虑背景噪声与探测效率后, 压缩热态光场的高阶光子超聚束效应及压缩数态光场的高阶相干度大范围连续可调性. 此外, 推导并分析了压缩热态光场全时延条件下的高阶相干度变化特性, 为量子信息技术的实际应用提供新的理论洞见.
-
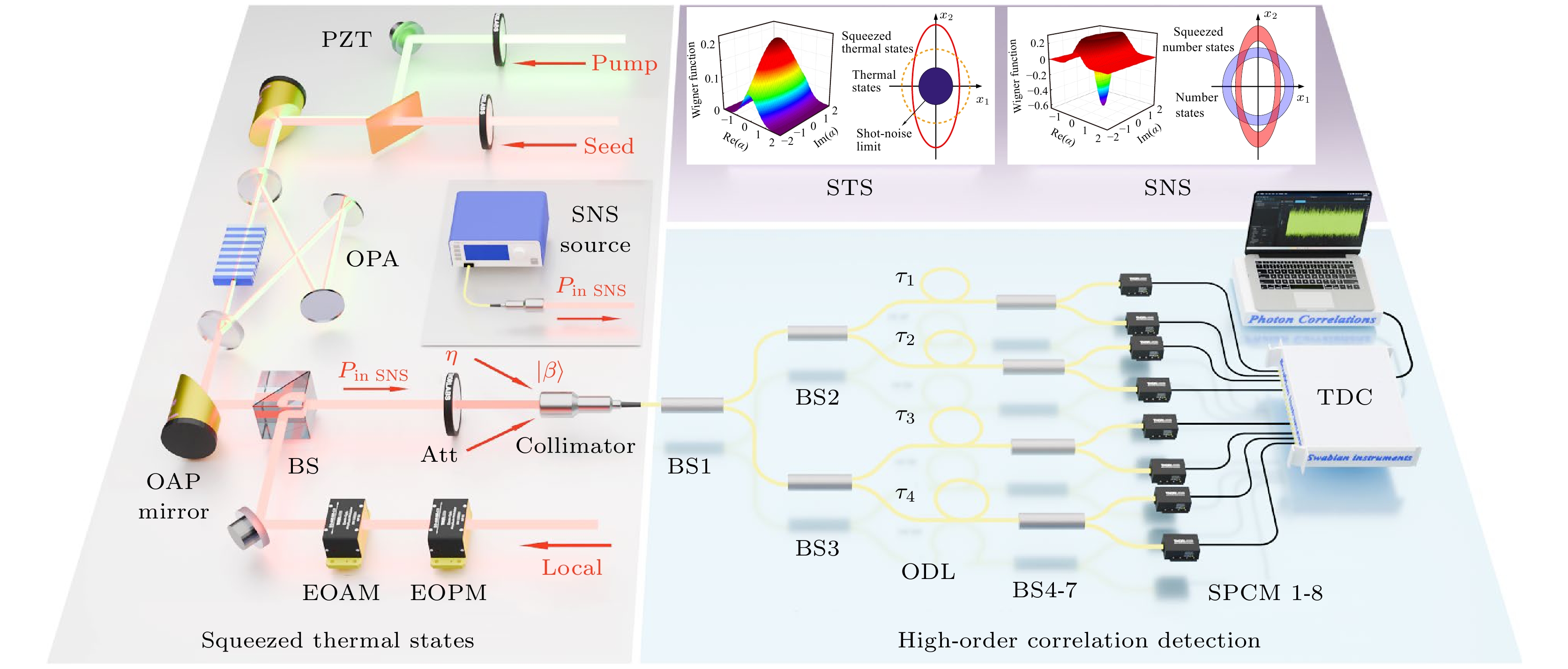
为了分析光场的高阶相干性, 构建8个单光子计数模块(SPCM)组成的多级联HBT(Hanbury Brown-Twiss)测量系统[35,38], 如图1所示. 在该模型中, 压缩光场的入射光子数分布为
${P_{{\text{in}}}}$ , 考虑系统的总探测效率$\eta $ , 包括光的传输效率、收集效率以及探测器效率等. 光场经过衰减器Att后, 部分光子经分束后进入各个探测器进行检测, 考虑背景噪声$\gamma $ , 则与信号光场混合后的光子数分布为信号光通过BS1—BS7的三阶分束进入8个单光子探测器, 最终由8通道高速时间数字转换器采集, 完成高阶相干性测量. 由于单光子探测器的死时间, 每个周期内每个单光子探测器只能响应一次, 故根据响应探测器的数量共有9种联合概率分布:
其中,
$\left( \begin{array}{*{20}{c}} L \\ N \end{array} \right) = \dfrac{{L!}}{{N!\left( {L - N} \right)!}}$ , 每个求和符号对应一个BS光纤分束器, 表示$L$ 个光子被分束为$N$ 和$L - N$ 个, 通过高阶相干函数的定义[41], 由光子数联合分布与产生湮灭算符可得光场零延迟条件下$ m $ 阶关联的表达式如下:其中,
$ \langle {n_1}{n_2} \cdots {n_m}\rangle $ 是在零延迟条件下的联合光子数的期望值,$ \langle {n_i}\rangle $ 表示每个探测器探测到的平均光子数. 利用(3)式, 结合光场的平均光子数, 进一步可得$ m $ 阶零延迟时的高阶相干函数为 -
压缩数态(squeezed number state)是量子光学中重要的非经典光场之一, 其不仅具有压缩光场的非经典性, 而且光子数分布也呈现出独特的振荡特性, 压缩数态可以通过以下公式进行描述:
其中,
$ S(\xi ) $ 是压缩算符, 定义为$ S(\xi ) = \exp ({\xi ^*}{a^2}/2 - \xi {a^\dagger }^2/2) $ , 其中$ \xi (r, \theta ) = r{{\text{e}}^{{\text{i}}\theta }} $ 是一个复压缩参数,$ r $ 表示压缩强度,$ \theta $ 表示压缩相位.为了得到理想条件下各阶光子相干函数, 利用压缩算符与产生湮灭算符的性质[42], 可得各阶算符在压缩数态表象下的平均值为
其中,
$ \theta (n - k) $ 是单位阶跃函数, 仅在$ n - k \geqslant 0 $ 时为1, 将上述结果代入(3)式可得压缩数态在理想情况下零延迟时的各阶相干函数. (7)式为压缩双光子态的二阶与三阶相干函数, 随着压缩参数$ r $ 的增大, 二阶与三阶相干函数均单调递增, 从反聚束效应到聚束效应连续变化:考虑系统的总效率
$\eta $ 以及背景噪声$\gamma $ 对关联探测的影响, 将压缩数态[27]的光子数分布表达式(8)(其中$ {n_{0}} $ 表示被压缩的数态光场的光子数)代入(1)式, 可得在实验条件下零延迟时的各阶相干函数: -
压缩热态(squeezed thermal state)是一种混态光场, 可通过对热态光场进行压缩操作得到. 如图1所示, 实验上可通过光学参量放大器(OPA)制备压缩热态光场. 该装置采用连续波激光器输出长波基频光和短波倍频光, 基频光分为种子光(seed)和本地振荡光(local), 倍频光作为OPA泵浦光(pump). OPA包含PPLN晶体和凹面镜组成的谐振腔, 晶体前表面镀长波高反射和短波透射膜, 后表面镀双波长增透膜. 种子光注入OPA增强信号光输出, 泵浦光驱动PPLN晶体中的参量下转换, 生成压缩态. 相位控制通过电光调制器(EOPM)和压电陶瓷(PZT)锁定相对相位, 确保光场稳定性. 通过调整泵浦功率、优化腔长和相位匹配条件, 控制压缩水平和反压缩噪声, 从而制备具有不同纯度和压缩度的压缩热态光场[43]. 压缩热态光场的表达式如下, 其密度矩阵可通过对压缩数态的密度矩阵根据玻色爱因斯坦分布加权求和来描述[27]:
其中,
$ n $ 为被压缩的数态光场的光子数,$ \alpha $ 为压缩热态光场的平均光子数.为得到理想条件下各阶相干函数, 根据Marian等[28]对各阶算符平均值的表达式, 代入(3)式, 化简得到压缩热态在理想情况下零延迟时的各阶相干函数:
其中,
$A = \alpha + (2\alpha + 1){\text{sin}}{{\text{h}}^2}r$ ,$B = - (2\alpha + 1){{\text{e}}^{{\text{i}}\theta }}\times \sinh r\cosh r$ ,$\varGamma (z)$ 为伽马函数. 根据(11)式可知压缩热态光场的各阶相干函数均大于热态光场, 始终保持超聚束效应. -
压缩热态光场结合了热态光场的混沌统计特性和压缩态光场的非经典相干性, 仅通过零延迟的高阶相干性不能全面反映光场的相干性与聚束效应等信息, 故建立高阶相干度在全时延条件下的函数关系. 洛伦兹谱压缩热态光场的一阶关联函数如下:
其中
${\omega _{0}}$ 为中心频率,${\tau _{0}}$ 为相干时间. 为了得到压缩热态光场的高阶相干函数, 通过高斯场的Isserlis和Wick定理将多时间点的相干函数展开为一阶相干函数的配对和[44]:其中
$ \displaystyle\sum\nolimits_{\text{all}} $ 表示对所有$ m $ 个时间点的全排列, 共有$ m! $ 项,$ \displaystyle\prod\nolimits_{(i, j)}^m {} $ 表示每个排列下$ m $ 个一阶相干函数的乘积,$\langle {O_i}({t_i}){O_j}({t_j})\rangle $ 为一阶关联项, 对于压缩热态光场有如下形式:其中,
$A = \alpha + (2\alpha + 1){\text{sin}}{{\text{h}}^2}r$ ,$B = - (2\alpha + 1) {{\text{e}}^{{\text{i}}\theta }} \times \sinh r\cosh r$ ,${G_{i, j}} = {g^{(1)}}({t_i} - {t_j})$ . 分别可得压缩热态光场的二阶、三阶和四阶全时延相干性如下:如不引入压缩操作, 将不会含有压缩参数的非经典项, 上述结果退化为经典热态光场的二阶、三阶和四阶相干函数.
-
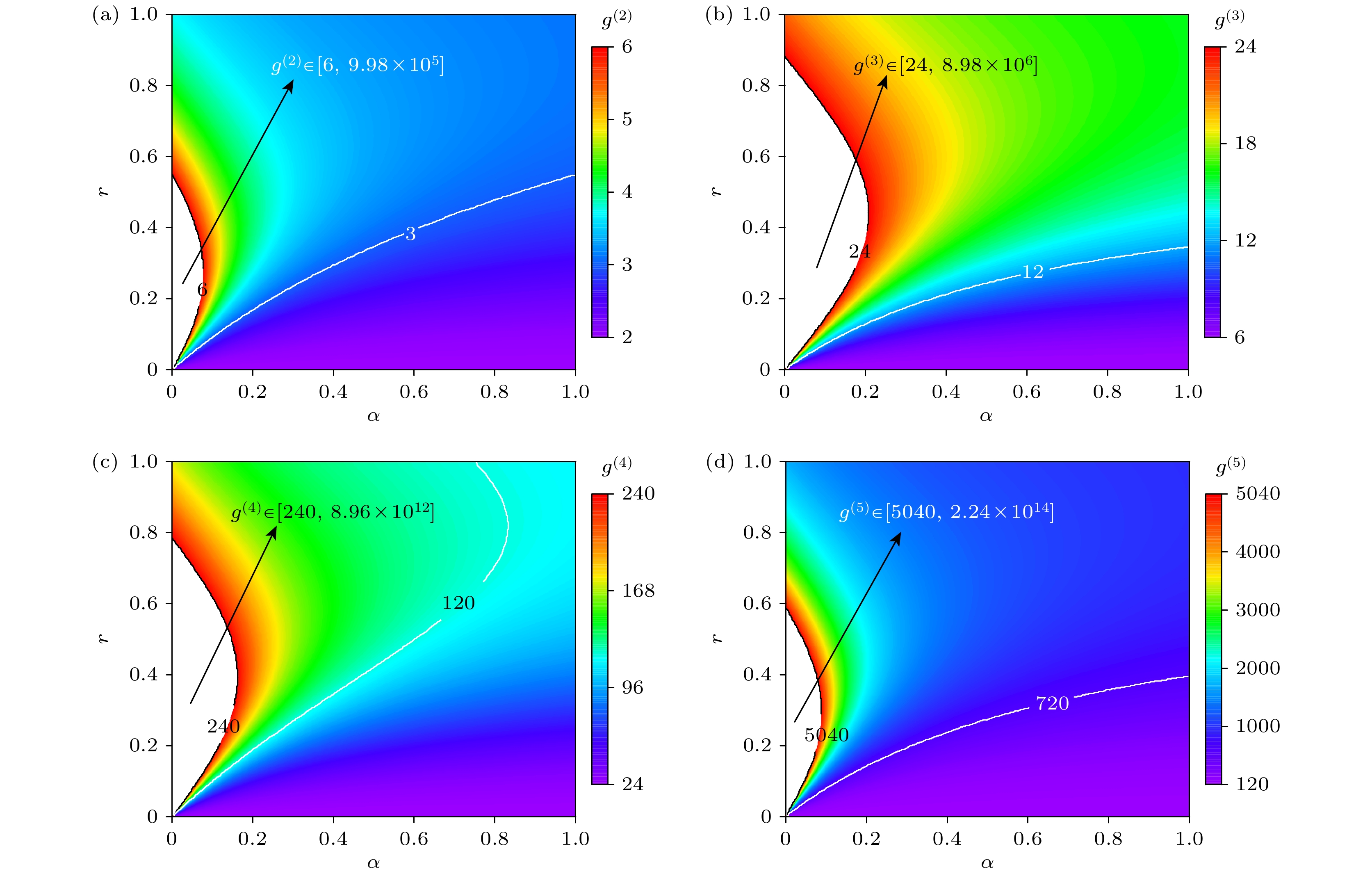
根据(11)式可知压缩热态光场在理想条件下零时延的各阶相干函数
$ {g^{(n)}} $ 与压缩相位$ \theta $ 无关. 图2为理想条件下相位无关压缩热态光场的高阶相干度$ {g^{(n)}} $ 随光场平均光子数$ \alpha $ 和压缩参数$ r $ 变化的超聚束结果. 图2(a)—(d)中彩色渐变区域表示$ {g^{(n)}} $ 逐渐增强的超聚束区域($ {g^{({2})}} $ ∈[2,6],$ {g^{({3})}} $ ∈[6,24],$ {g^{({4})}} $ ∈[24, 240],$ {g^{({5})}} $ ∈[120, 5040])白色区域表示$ {g^{(n)}} $ 迅速增大的超聚束区域($ {g^{({2})}} $ ∈[6, 9.98×105],$ {g^{({3})}} $ ∈[24, 8.98×106],$ {g^{({4})}} $ ∈[240, 8.96×1012],$ {g^{({5})}} $ ∈[5040, 2.24×1014]). 当平均光子数$ \alpha $ 为定值时, 随着压缩参数$ r $ 的增大, 压缩热态的高阶相干度$ {g^{(n)}} $ 先增大到一个极大值, 随后逐渐减小. 平均光子数$ \alpha $ 越小, 压缩热态的高阶相干度$ {g^{(n)}} $ 随压缩参数$ r $ 的变化率越大, 取极大值时的压缩参数$ r $ 也越小. 进一步分析, 当压缩参数$ r $ = 0时, 压缩热态光场退化为热态光场, 其各阶光子关联$ {g^{({2})}} $ ,$ {g^{({3})}} $ ,$ {g^{({4})}} $ ,$ {g^{({5})}} $ 分别等于2, 6, 24, 120, 与热态光场的理论结果一致. 经过压缩算符的作用, 从原本的聚束光场变化为超聚束光场, 原因是压缩热态光场可视为不同光子数的压缩数态光场根据玻色爱因斯坦分布加权求和得到, 而压缩数态光场仅存在与压缩前光子数之差为偶数的光子数分布, 如(8)式所示, 这样的压缩光场的各阶光子关联的聚束效应相较于热态光场聚束效应更强. 当平均光子数$ \alpha $ 和压缩参数$ r $ 均较小时, 各阶相干性出现极强的超聚束效应, 压缩热态光场的$ n $ 阶相干性显著大于热态光场的$ n + 2 $ 阶相干性.类似地, 根据(6)式可得压缩数态光场在理想条件下零延迟时的各阶相干函数
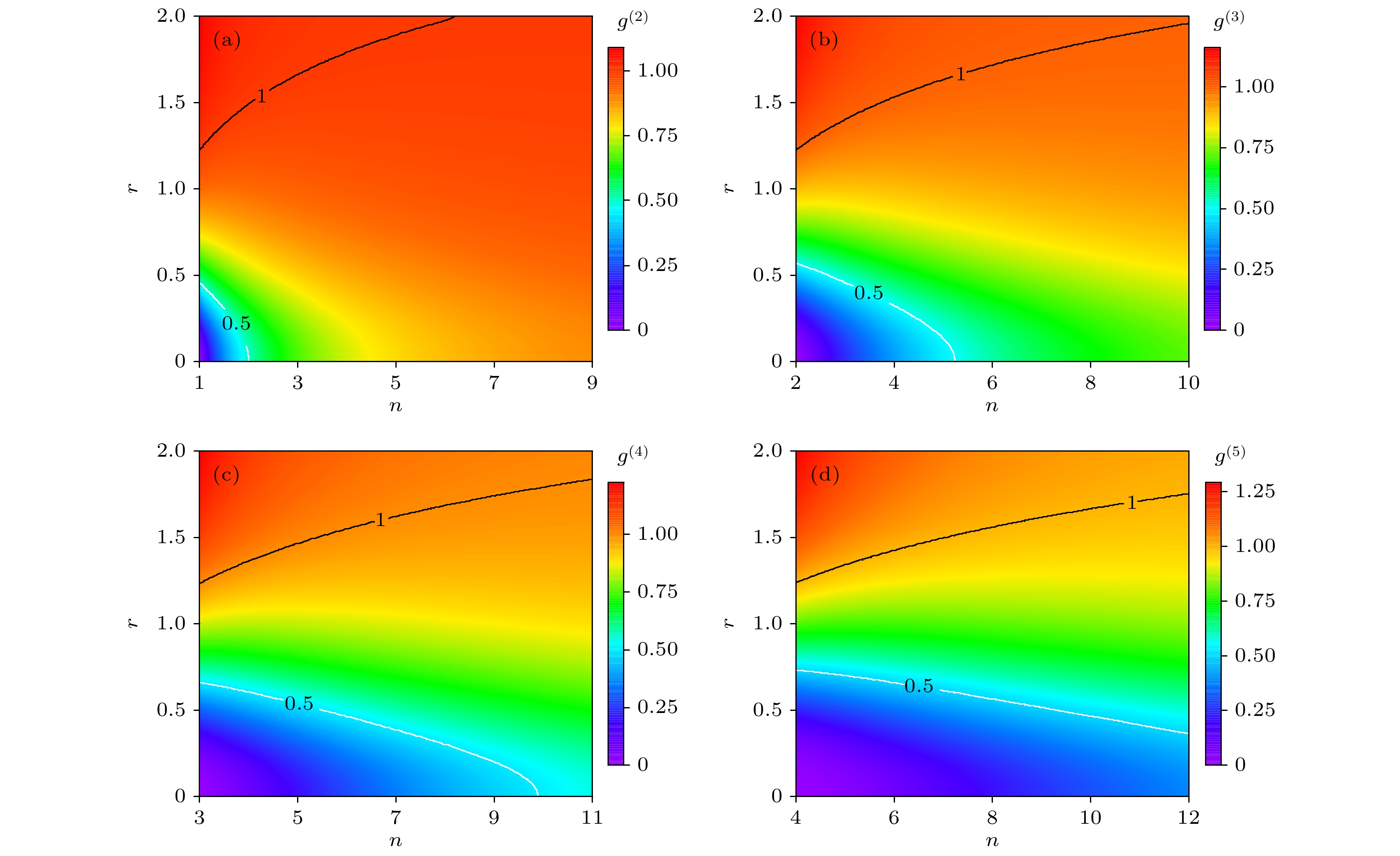
$ {g^{(n)}} $ 与压缩相位$ \theta $ 无关, 但其随着压缩参数$ r $ 和压缩光子数$ n $ 呈明显的变化. 图3为理想条件下相位无关压缩数态光场的二阶相干度(a)、三阶相干度(b)、四阶相干度(c)和五阶相干度(d)随压缩光子数$ n $ 和压缩参数$ r $ 的变化结果. 图中彩色渐变区域表示$ {g^{(n)}} $ 从反聚束区域到聚束区域的过渡(图示范围内$ {g^{({2})}} $ ∈[1.60×10–5, 1.09],$ {g^{({3})}} $ ∈[9.02×10–6, 1.16],$ {g^{({4})}} $ ∈[4.75×10–6, 1.22],$ {g^{({5})}} $ ∈[9.39×10–6, 1.30]). 当压缩参数$ r $ 较小(0—0.5)时, 少光子数区域有较强的反聚束效应, 随着光子数$ n $ 的增大, 光场的反聚束效应逐渐减小; 相反, 当压缩参数$ r $ 较大(1—2)时, 多光子数区域仅有很弱的反聚束效应, 且随着压缩参数$ r $ 的增大, 光场从反聚束效应逐渐过渡为聚束效应. 对比不同阶的相干性结果可以发现, 在压缩参数$ r $ 极小的情况下, 四阶相干度$ {g^{({4})}} $ 在光子数$ n $ 为9的情况下仍能保持较强的反聚束效应($ {g^{(n)}} $ <0.5), 但三阶相干度$ {g^{({3})}} $ 与二阶相干度$ {g^{({2})}} $ 分别仅在光子数$ n $ 为6和3的情况下就无法产生较强的反聚束效应. 随着压缩参数$ r $ 的增大, 四阶相干度$ {g^{({4})}} $ 相比于低阶相干度在光子数为11为情况下就可以产生明显的聚束效应($ {g^{(n)}} $ >1). 因此, 更高阶的相干性相较于低阶的相干性有变化更大的反聚束区域以及更强的聚束值.综合上述分析, 通过不同压缩参数
$ r $ 作用后产生的压缩热态光场相较于经典的热态光场拥有极强的超聚束特性. 同时, 通过不同压缩参数$ r $ 作用后产生的压缩数态光场能够出现反聚束效应, 也能出现聚束效应, 相比于单纯的数态光场有着更丰富的非经典特性和量子调控资源. 此外, 在固定范围的压缩参数和光子数条件下, 更高阶的相干性对光场的探测有更高的灵敏度和鲁棒性. -
考虑实验条件下, 系统的探测效率
$\eta $ 和实际的背景噪声$\gamma $ 会对压缩光场的高阶相干性$ {g^{(n)}} $ 的理想结果产生扰动影响. (1)式—(4)式建立了多级联HBT测量系统用于分析实验条件下压缩热态与压缩数态光场的高阶相干函数. 将(8)式和(12)式代入多级联HBT测量模型即可得到特定条件下光场高阶相干函数$ {g^{(n)}} $ 随不同参数的变化结果.由图2结果可知, 压缩热态光场的高阶相干性
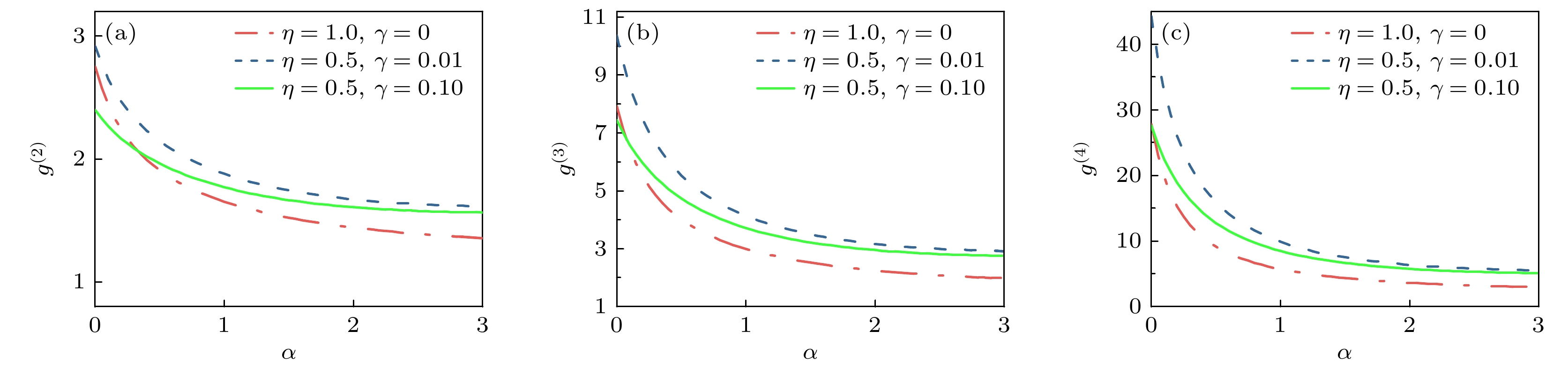
$ {g^{(n)}} $ 具有显著的超聚束效应. 图4为压缩参数$ r = 1 $ , 探测效率与背景噪声分别为红色点线($\eta = 1$ ,$\gamma = 0$ )、蓝色虚线($\eta= 0.5 $ ,$\gamma = 0.01$ )和绿色实线($\eta = 0.5$ ,$\gamma= 0.1 $ )的条件下, 压缩热态光场高阶相干性$ {g^{(n)}} $ 随平均光子数$ \alpha $ 的变化结果. 结果表明, 压缩热态光场高阶相干性$ {g^{(n)}} $ 随平均光子数$ \alpha $ 增大而减小, 当平均光子数$ \alpha $ 较小时, 高阶相干性探测会受到背景噪声的扰动; 而当平均光子数$ \alpha $ 较大时, 受限于单光子探测器死时间, 难以准确地获取压缩数态光场的全部信息, 导致测量结果偏离理想值. 进一步分析表明, 压缩热态光场在平均光子数$ \alpha $ 较小时出现显著的超聚束效应. 压缩参数$ r = 1$ 时, 各阶相干函数的峰值达$ {g^{({2})}} = 2.750$ ,$ {g^{({3})}} = 7.922$ ,$ {g^{({4})}}= 27.811 $ , 均大于单模热态光场的各阶相干度, 同时, 更高阶的相干度$ {g^{(n)}} $ 能够探测到更强的超聚束效应.图5为平均光子数
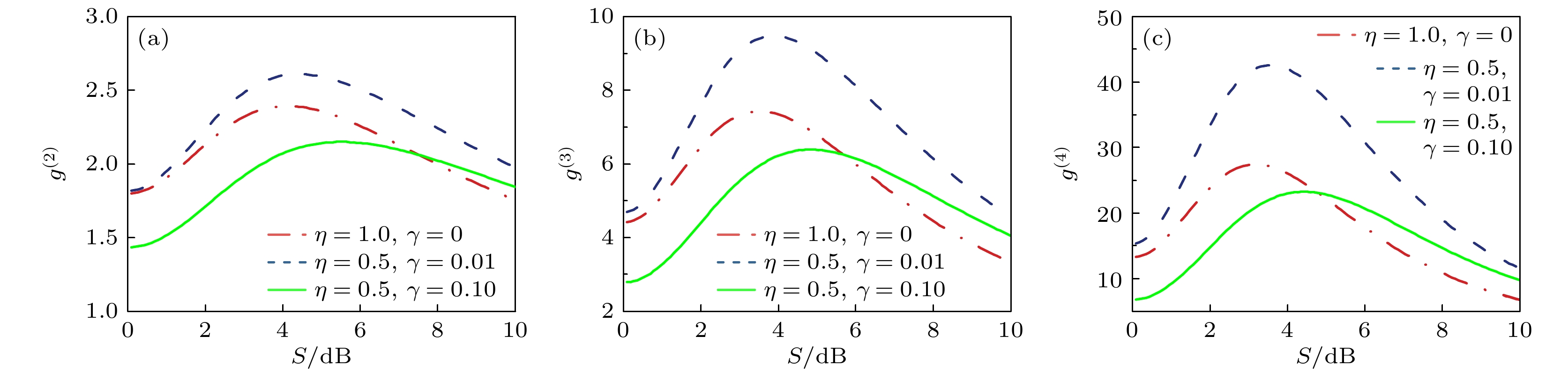
$ \alpha= 0.5 $ , 探测效率与背景噪声分别为红色点线($\eta = 1$ ,$\gamma = 0$ )、蓝色虚线($\eta = 0.5$ ,$\gamma = 0.01$ )、绿色实线($\eta = 0.5$ ,$\gamma = 0.1$ )的条件下, 压缩热态光场高阶光子关联$ {g^{(n)}} $ 随压缩度$S$ 的变化结果. 结果表明, 随着压缩度$S$ 的增大, 压缩热态光场高阶相干性$ {g^{(n)}} $ 先递增至极大值, 然后逐渐减小, 当平均光子数$ \alpha = 0.5$ 时, 通过调控压缩度$ S $ , 最大超聚束值为$ {g^{({4})}} = 42.60 $ . 在实验条件下, 考虑单光子探测器的探测效率与入射光场的衰减, 系统的总探测效率$\eta $ 在50%附近. 因此, 相比于理想条件(红色点线), 当背景噪声较小时 (蓝色虚线,$\gamma $ = 0.01), 聚束峰值显著增大; 当背景噪声稍大时(绿色实线,$\gamma = 0.1$ ), 聚束峰值略微减小, 但相对偏差较小. 进一步分析表明, 当压缩度分别为${S^{(2)}}= 5.47$ ,${S^{(3)}}= 4.86$ 和${S^{(4)}}= 4.43$ 时, 可以得到压缩热态光场高阶相干性超聚束效应的极大值$ {g^{({2})}} $ = 2.149,$ {g^{({3})}} $ = 6.389和$ {g^{({4})}} $ = 23.228, 相比于理想条件分别存在7.18%, 7.13%和5.48%的相对偏差. 因此, 更高阶的相干性相较于低阶相干性不仅对参数变化具有更高的灵敏度, 而且能够更精确地对光场统计特性进行测量, 对较高的背景噪声具有更强的鲁棒性. 此外, 随着测量噪声的增大, 探测系统的有效信噪比下降, 导致高阶相干函数的峰值出现右移现象, 其本质是测量噪声的引入提高了光场的平均光子数, 削弱了压缩热态的超聚束效应, 从而使得高阶相干函数峰值在更强压缩条件下才能显现.由图3可知, 压缩数态光场的高阶相干性
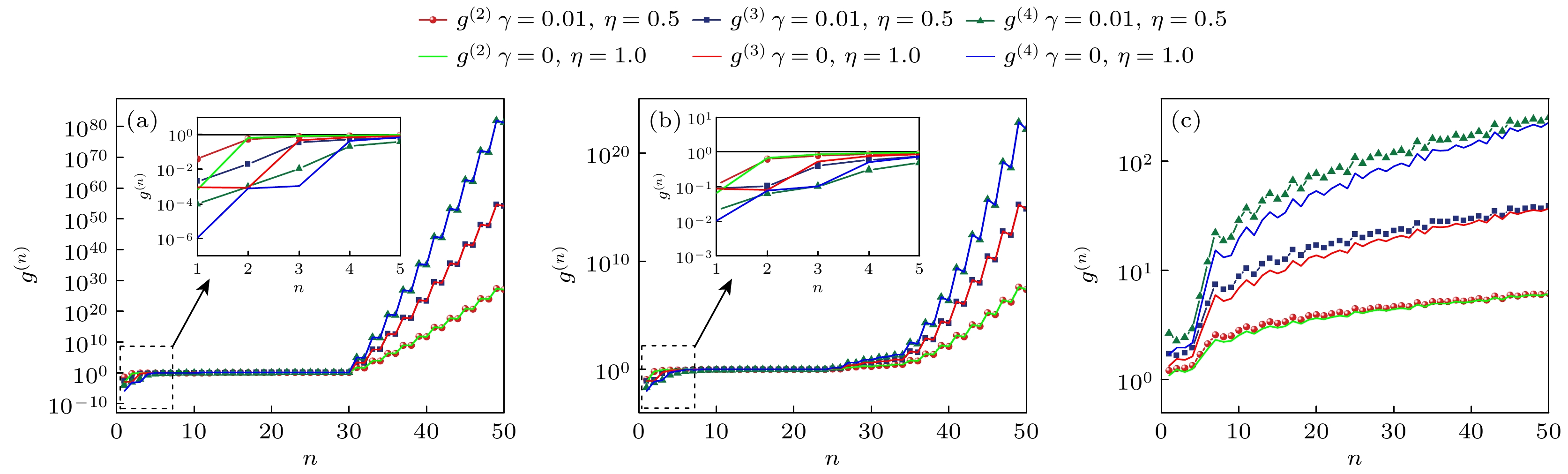
$ {g^{(n)}} $ 与光子数$ n $ 成正相关. 图6为当背景噪声$\gamma $ = 0.01, 探测效率$\eta $ = 0.5的实验条件以及背景噪声$\gamma $ = 0, 探测效率$\eta $ = 1的理想条件下, 压缩参数$ r $ 分别为0.01, 0.1和1时, 压缩数态高阶相干性$ {g^{(n)}} $ 随光子数$ n $ 的变化结果. 结果表明, 当压缩参数$ r $ 较小时[图5(a), (b)], 压缩少光子数($ n $ ∈[0, 5])产生的压缩数态光场具有明显的反聚束效应, 随着$ n $ 的增大, 光场从泊松光场逐渐演变为超聚束光场, 而且由于压缩数态光场只有全奇数或全偶数的光子数分布特性, 从而在超聚束区域产生独特的振荡特性, 压缩光子数$ n $ 为偶数的相干函数$ {g^{(n)}} $ 要略小于前一项光子数$ n $ 为奇数的结果. 当压缩参数$ r $ 较大时[图5(c)], 压缩数态光场始终存在超聚束效应, 且随着$ n $ 的增大, 超聚束效应也显著提高. 进一步分析理想条件与实验条件的偏差, 压缩数态光场在压缩少光子数$ n $ 时, 由于少光子数情况下背景噪声对信号光场影响增大, 因此对高阶相干性的影响也变大, 理想条件与实验条件下的结果偏差变大, 尤其是压缩单光子态时的情况. 如图5(a)所示, 当压缩参数$ r $ 为0.01时, 各阶相干性的相对误差为二阶5773.24%、三阶125.62%、四阶8767.23%; 当压缩参数$ r $ 为0.1时[图5(b)]各阶相干性的相对误差约为二阶70.29%、三阶1.99%、四阶102.79%; 当压缩参数r为1时(图5(c)), 各阶相干性的相对误差约为二阶11.20%、三阶28.33%、四阶57.02%, 因此在实际过程中, 需要严格控制背景噪声才能更精确地测量弱光压缩数态的高阶相干性. 在压缩较大光子数$ n $ 时, 当压缩参数$ r $ 取值较小[图5(a), (b)], 理想条件与实验条件的结果近乎一致, 原因是大光子数情况下, 背景噪声的影响降低, 得到与理想值接近的探测结果; 但当压缩参数$ r $ 取值较大时[图5(c)], 可以精细地观察到各阶相干性$ {g^{(n)}} $ 产生的不同偏差, 更高阶的相干性比低阶的相干性偏离程度更大, 意味着高阶相干性探测对光场特性测量具有更高的敏感度.实验条件下, 由于背景噪声
$\gamma $ 相对变化较小, 探测效率$\eta $ 的大小决定着能否精确地探测压缩光场的高阶相干性$ {g^{(n)}} $ . 图7为压缩参数$ r $ = 0.1, 压缩光子数分别为$ n $ = 1,$ n $ = 5和$ n $ = 15时, 压缩数态在不同背景噪声$\gamma $ = 0.01(绿色实线)、$\gamma $ = 0.1(绿色虚线)、$\gamma = 0.2$ (红色点线)情况下的高阶相干性$ {g^{(n)}} $ 随探测效率$\eta $ 的变化结果. 结果表明, 当探测效率$\eta $ 极小(趋近于0)时, 光场的各阶相干性$ {g^{(n)}} $ 趋近于1, 这是因为较小的探测效率导致信号光的有效光子数远小于背景噪声, 高阶相干性表征的结果趋于服从泊松分布的背景噪声. 随着探测效率$\eta $ 的增大, 背景噪声对信号光的扰动影响逐渐减小, 光场的各阶相干性$ {g^{(n)}} $ 趋近相同的测量结果. 压缩单光子态产生的压缩数态光场具有较强的反聚束效应, 如图7(a1)—(c1), 随着探测效率$\eta $ 的增大, 高阶相干性$ {g^{(n)}} $ 单调递减并趋近于定值, 其中四阶相干性$ {g^{({4})}} $ 的变化最剧烈, 反聚束效应最强. 当压缩光子数$ n $ = 5和$ n $ = 15时, 高阶相干性$ {g^{(n)}} $ 随着探测效率$\eta $ 的增大先减小至极小值, 接着逐渐增大, 如图7(a2)—(c2)和图7(a3)—(c3). 对比各阶相干性$ {g^{(n)}} $ , 更高阶的相干性相比于低阶相干性对光场参数有更敏感的响应. 进一步对比发现, 压缩光子数$ n $ = 15的各阶相干性$ {g^{(n)}} $ 在探测效率趋于1时, 不同大小的背景噪声条件下的结果更接近, 这是由于在相同探测效率$\eta $ 的情况下, 压缩更多光子数产生的压缩数态光场的信息量占比更高, 受背景噪声扰动的影响更小.数态光场表现出反聚束效应, 通过压缩算符作用后产生的相应压缩数态光场出现了部分聚束区域. 图8为背景噪声
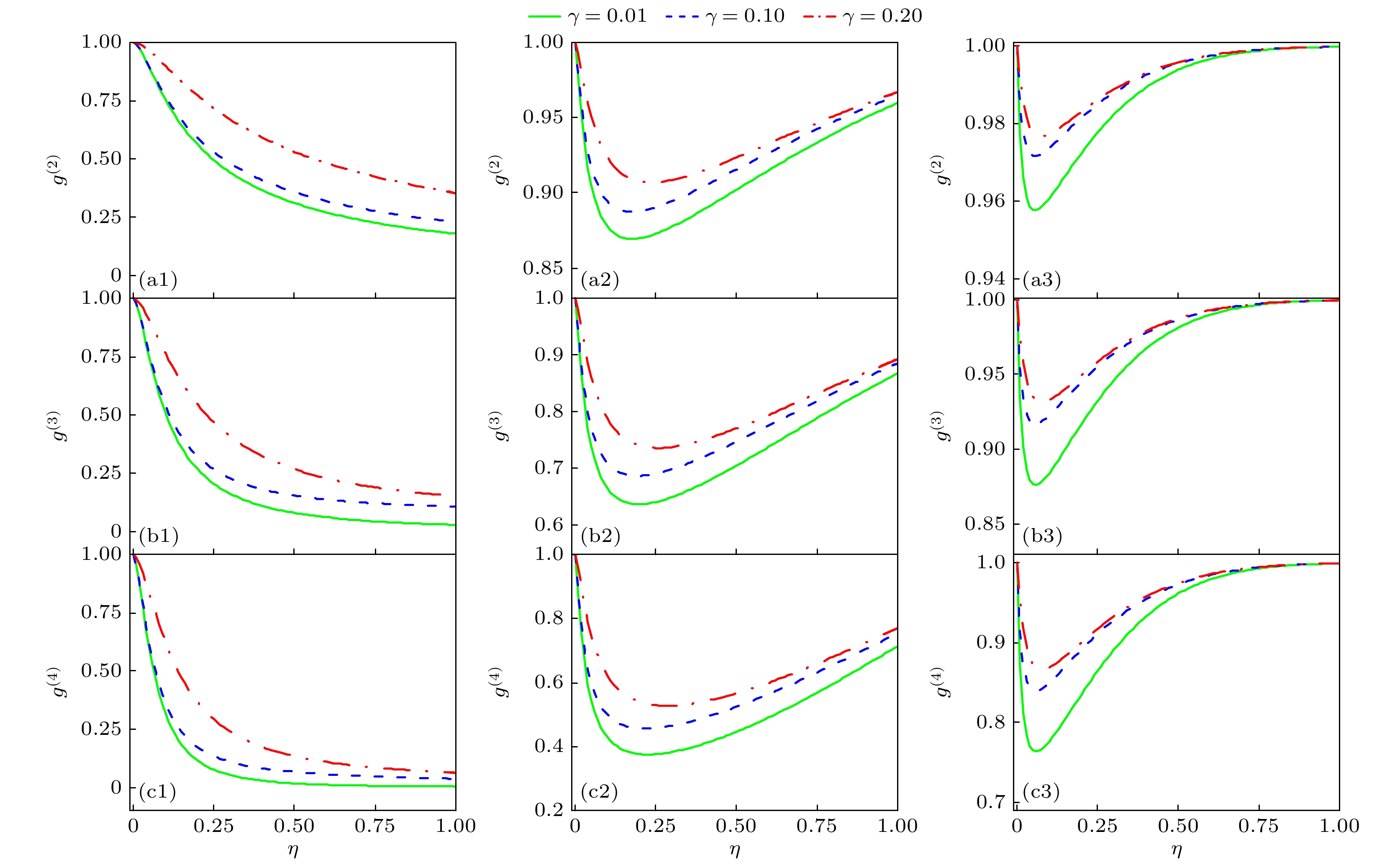
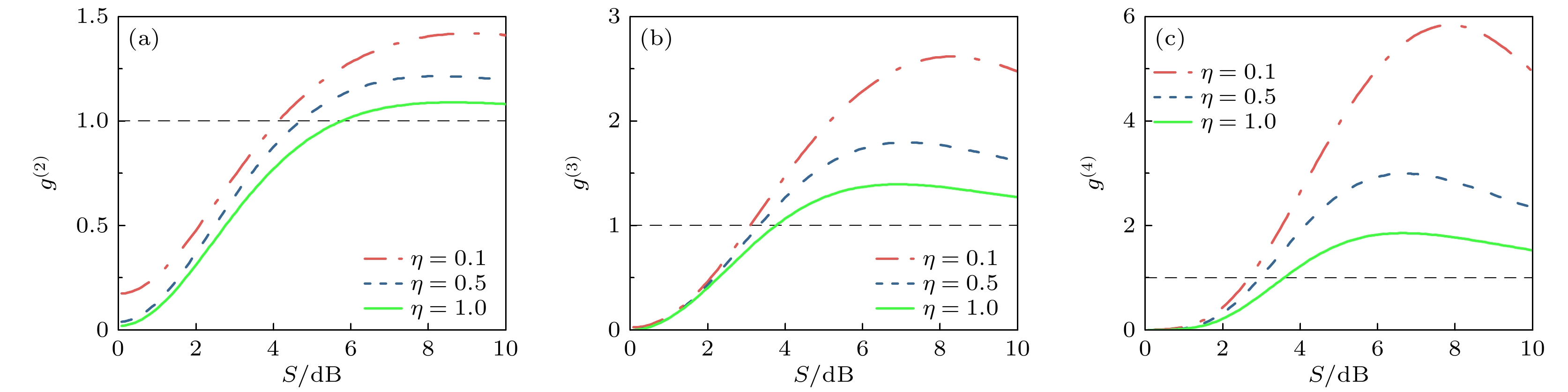
$\gamma $ = 0.01, 压缩光子数$ n $ = 1时, 压缩数态在不同探测效率$\eta $ = 0.1(红色点线)、$\eta $ = 0.5(蓝色虚线)、$\eta $ = 1(绿色实线)情况下的高阶相干性$ {g^{(n)}} $ 随压缩度$S$ /(dB)的变化结果, 图中黑色虚线表示各阶相干函数$ {g^{(n)}} $ 从反聚束到聚束效应的转变临界点. 结果表明, 当压缩度$S$ 较小时, 光场仍然保持单光子态的强反聚束特性. 随着压缩度$S$ 的增大, 各阶相干性$ {g^{(n)}} $ 均有显著的增大趋势, 同时产生聚束效应. 对比各阶相干性[图6(a)—(c)], 四阶相干性$ {g^{({4})}} $ 相比于三阶相干性$ {g^{({3})}} $ 和二阶相干性$ {g^{({2})}} $ 具有更大的产生聚束效应的压缩度$S$ 范围, 并能探测到更强的聚束效应. 进一步分析可知, 探测效率$\eta $ 越大, 在更大的压缩度$S$ 的情况下才能达到从反聚束到聚束效应的转变临界点. 此外, 四阶相干性$ {g^{({4})}} $ 在不同探测效率$\eta $ 的情况下, 会产生更显著的差异, 这意味着更高阶的相干性对压缩度$S$ 和探测效率$\eta $ 的交叉响应更敏感, 可以更精确地表征压缩数态光场的信息. -
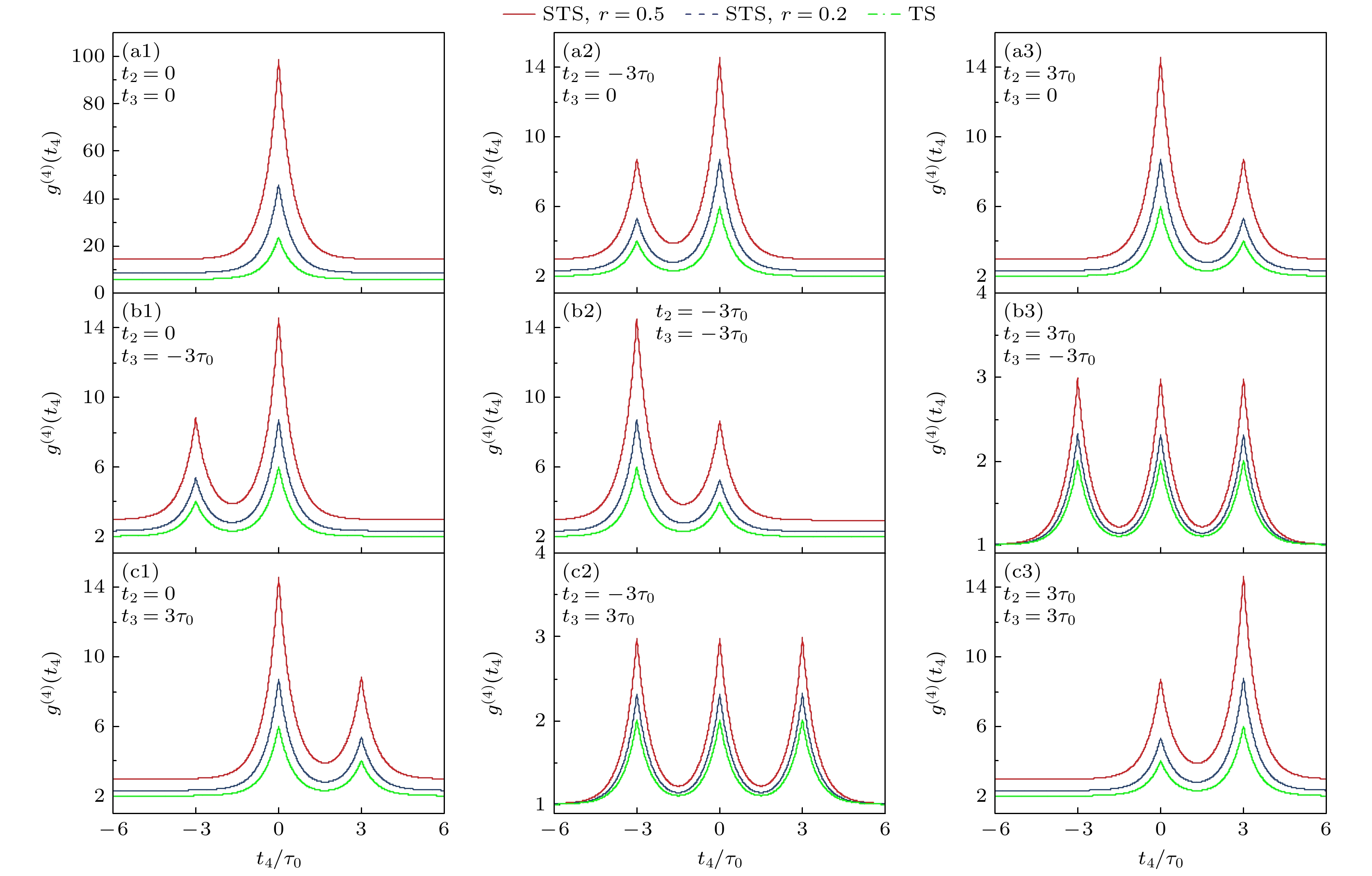
考虑了光场的高阶相干性与聚束特性, 通过(13)式—(16)式推导得出了全时延条件下压缩热态光场与经典热态光场的高阶相干性
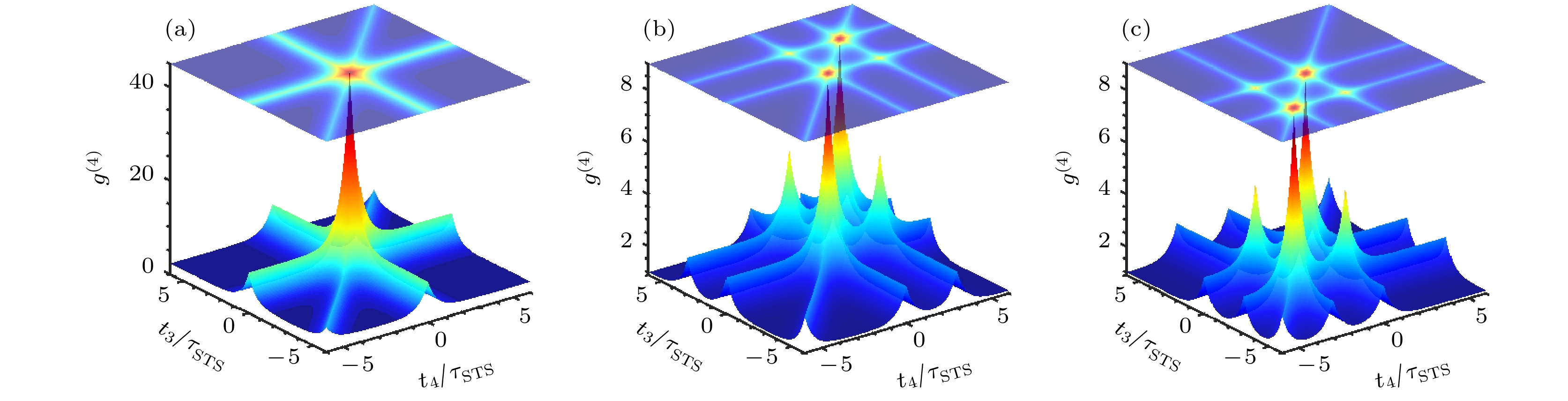
$ {g^{(n)}} $ . 图9为平均光子数$ \alpha $ = 1, 压缩参数$ r $ = 0.2时, 压缩热态光场全时延条件下的四阶相干性$ {g^{({4})}} $ 随延迟时间$ {t_2} $ ,$ {t_3} $ ,$ {t_4} $ 的变化结果, 图9(a)表示第1路与第2路光纤均不进行延迟的情况, 图9(b), (c)分别表示将第2路光纤延迟±3倍压缩热态光场相干时间$3 {\tau _{{\text{STS}}}} $ 的情况. 结果表明, 当所有延迟时间均为零时(图9(a)), 四阶相干性$ {g^{({4})}} $ 达到最大值45.94, 源于压缩操作增强了光子聚束特性, 相较于热态光场$ {g^{({4})}} $ =24产生了超聚束效应. 当三路光子同步时(图9(b), (c)), 四阶相干性$ {g^{({4})}} $ 达到8.73, 这反映了部分光子间的同步性仍能维持一定关联强度, 而非同步光子使整体关联下降, 但仍然高于热态光场在相同条件下的理论结果$ {g^{({4})}} $ = 4.如图10所示, 红色实线表示平均光子数
$ \alpha $ = 1, 压缩参数$ r $ = 0.5的压缩热态光场, 蓝色虚线表示平均光子数$ \alpha $ = 1, 压缩参数$ r $ = 0.2的压缩热态光场, 绿色点线表示无压缩的经典热态光场. 热态光场与压缩热态光场的相干时间在通常情况下是相同的. 两者都受限于原始热态光场的宽频谱带宽, 因此相干时间$ {\tau _{{\text{STS}}}} $ 和$ {\tau _{{\text{TS}}}} $ 没有显著差异. 结果表明, 压缩热态光场在相干时间范围附近全时延四阶相干性$ {g^{({4})}} $ 均显著高于经典热态光场. 另外, 可以发现当$ {t_1} $ ,$ {t_2} $ ,$ {t_3} $ 有两路延迟时间相等时, 例如图10(a2)中$ {t_2} = - 3 \tau_{\text{STS}} $ ,$ {t_1} = {t_3} = 0$ 时和图10(b1)中$ {t_3} = - 3\tau _{{\text{STS}}} $ ,$ {t_1} = {t_2} = 0$ 时, 相干函数图像具有相似的高阶关联对称性, 这种对称性表明压缩热态光场的高阶相干函数对延迟时间的变化具有周期性依赖, 理论曲线与低阶相干函数$ {g^{(1)}} $ 的平方和交叉项高度一致. 与四阶相干性的结果类似, 当所有延迟时间均为零时, 三阶相干性$ {g^{({3})}} $ 达到的最大值, 相较于热态光场$ {g^{({3})}} $ = 6产生了超聚束效应. 同时, 压缩热态光场全时延三阶相干性也显著高于经典热态光场, 具有类似的高阶关联对称性. -
基于多级联Hanbury Brown-Twiss单光子探测方案, 通过调控压缩参数
$ r $ , 压缩光子数$ n $ 和平均光子数$ \alpha $ , 研究并分析了理想情况下压缩热态光场的高阶光子超聚束特性和压缩数态光场的高阶光子反聚束特性. 当压缩参数$ r $ ∈[0, 1]时, 压缩热态的最大超聚束值可达$ {g^{({5})}} $ = 2.24 × 1014, 而压缩数态呈现出从反聚束到聚束效应的连续变化, 最小的反聚束值可达$ {g^{({5})}} $ = 9.39 × 10–6. 同时, 研究分析了实验条件下考虑背景噪声$\gamma $ 和探测效率$\eta $ 时, 压缩热态与压缩数态光场高阶光子相干性. 在平均光子数$ \alpha $ 较小时, 通过调控压缩度$S$ 可得到压缩热态光场显著的超聚束效应, 当$ \alpha $ = 0.5时, 压缩度分别为${S^{(2)}}$ = 5.47,${S^{(3)}}$ = 4.86和${S^{(4)}}$ = 4.43可得超聚束效应的极大值$ {g^{({2})}} $ = 2.149,$ {g^{({3})}} $ = 6.389和$ {g^{({4})}} $ = 23.228; 通过调控压缩光子数$ n $ 以及压缩度$S$ 可实现压缩数态光场高阶相干函数从反聚束效应到超聚束效应的大范围连续变化. 此外, 在环境噪声较大, 探测效率较低的情况下, 更高阶的相干性相比于低阶相干性对光场参数有更敏感的响应, 而且在多光子的压缩数态光场的条件下, 受背景噪声扰动的影响更小, 鲁棒性更高. 另外, 还研究了全时延条件下压缩热态光场高阶光子相干函数的变化特性, 压缩热态光场在相干时间$ {\tau _{{\text{STS}}}} $ 范围附近全时延高阶相干性$ {g^{(n)}} $ 均显著高于经典热态光场. 即使单路引入较大时延, 部分光子间的同步性仍能维持一定关联强度, 而非同步光子使整体相干性下降, 但仍然高于热态光场在相同条件下的理论结果. 本文对高阶相干性调控分析的理论工作, 未来实验上可通过构建光学参量放大系统与级联HBT单光子探测系统, 以实现对高阶相干函数的精确测量. 综上所述, 考虑环境噪声、探测效率与时间延迟, 通过调控平均光子数、压缩光子数与压缩参数, 可实现超聚束压缩热态光场的制备与高阶相干度大范围连续可调的压缩数态光场的制备, 助力于高效量子态的制备与调控以及高分辨量子成像.
超聚束压缩热态与压缩数态光场的高阶相干性
High-order coherence of super-bunching squeezed thermal states and squeezed number states of light fields
-
摘要: 光场的聚束和反聚束效应反映了光子的时空关联性, 是判别量子统计经典性与非经典性的关键指标, 在量子信息处理和精密测量中发挥着重要作用. 本文基于多级联Hanbury Brown-Twiss单光子探测方案研究了压缩热态与压缩数态光场全时延高阶相干函数$ {g^{(n)}} $的超聚束与反聚束效应. 分析了不同压缩参数$ r $、平均光子数$ \alpha $和压缩光子数$ n $条件下, 压缩热态与压缩数态光场的高阶相干性, 结果表明压缩热态光场具有显著的超聚束效应, 最大超聚束值为$ {g^{({5})}} $= 2.24 × 1014; 而压缩数态光场呈明显的反聚束特性, 最小反聚束值为$ {g^{({5})}} = $$ 9.39 \times 10^{-6}$. 并考虑实验条件下背景噪声$\gamma $和探测效率$\eta $的影响, 在探测效率较低、背景噪声较大的情况下, 平均光子数$ \alpha $较小的压缩热态光场仍可保持良好的超聚束特性, 当平均光子数$ \alpha= 0.5 $ 时, 通过调控压缩度$ S $, 最大超聚束值为$ {g^{({4})}}= 42.60 $. 另外, 通过调控压缩数态光场的压缩光子数$ n $和压缩度$ S $, 可实现高阶相干函数从反聚束到超聚束效应的连续大范围变化, 且其高阶相干度对环境噪声与探测效率有较强的鲁棒性. 进而研究了压缩热态光场在全时延条件下, 尤其是在相干时间范围内的高阶相干函数的变化特性, 其高阶相干度$ {g^{(n)}} $显著高于经典热态光场. 上述研究结果表明, 压缩热态光场的高阶光子超聚束特性, 及压缩数态光场的高阶相干度大范围连续可调性, 有助于高效量子态的制备调控与高分辨量子成像.Abstract:
The bunching and antibunching effects of light fields reflect the spatiotemporal correlation of photons and are key indicators for distinguishing classical and non-classical quantum statistics. They play a crucial role in quantum information processing and precise measurement. In this paper, we investigate the super-bunching and antibunching effects of the full-time-delay higher-order coherence function $ {g^{(n)}} $ for squeezed thermal states and squeezed number states based on a multi-cascaded Hanbury Brown–Twiss single-photon detection scheme. Under ideal conditions, the high-order coherence of squeezed thermal states and squeezed number states is analyzed by changing compression parameter $ r $, average photon number $ \alpha $, and squeezed photon number $ n $. The results indicate that when the compression parameter $ r \in [0, 1] $, the squeezed thermal state exhibits a significant super-bunching effect, with super-bunching values of each order being $ {g^{({2})}} = 9.98 \times 10^5$, $ {g^{({3})}} = 8.98 \times 10^6$, $ {g^{({4})}} = 8.96 \times 10^{12}$, $ {g^{({5})}} = 2.24 \times 10^{14}$. The squeezed number state exhibits a continuous transition from antibunching to bunching behavior, with coherence degrees of different orders being $ {g^{({2})}} \in [1.60 \times 10^{-5}, 1.09] $, $ {g^{({3})}} \in [9.02 \times 10^{-6}, 1.16] $, $ {g^{({4})}} \in [4.75 \times 10^{-6}, 1.22] $, and $ {g^{({5})}} \in [9.39 \times 10^{-6}, 1.30]) $. Simultaneously, this study analyzes the high-order photon coherence of squeezed thermal states and squeezed number states under experimental conditions, with background noise $\gamma $ and detection efficiency $\eta $ taken into account. When detection efficiency is relatively low and background noise is substantial, the higher-order coherence of squeezed thermal states with smaller average photon number $ \alpha $ is disturbed by background noise, but still maintains good super-bunching characteristics. However, when the average photon number $ \alpha $ becomes large, which is limited by the dead time of single-photon detector, it is challenging to accurately obtain all the information about the squeezed number state light field, leading measurement results to deviate from the ideal values. When the average photon number is $ \alpha = 0.5$, the super-bunching effects reach their maximum values of $ {g^{({2})}} = 2.149 $, $ {g^{({3})}} = 6.389 $和$ {g^{({4})}} = 23.228 $, corresponding to the squeezing degrees $ {S^{({2})}} = 5.47$, $ {S^{(3)}}= 4.86 $ and = 4.43, respectively. Furthermore, by adjusting the number of squeezed photons $ n $ and the squeezing degree of the squeezed number state light field, $S$, a continuous and wide-ranging change of high-order coherence function can be achieved, transforming from anti-bunching effect to super-bunching effect. Additionally, under the conditions of high environmental noise and low detection efficiency, higher-order coherence exhibits greater sensitivity to variations in optical field parameters than lower-order coherence. Furthermore, squeezed number states with multi-photon characteristics are less susceptible to disturbances from background noise, demonstrating stronger robustness. In addition, the variation characteristics of the high-order photon coherence function of the squeezed thermal state light field under the full time-delay conditions are investigated. The full time-delay high-order coherence $ {g^{(n)}} $ of the squeezed thermal state light field near the coherence time range $ {\tau _{{\text{STS}}}} $ is significantly higher than that of the classical thermal state light field. Even when a significant time delay is introduced into one of the optical paths, partial synchronization among photons can still maintain a certain correlation strength. Although unsynchronized photons lead to an overall reduction in coherence, the coherence is still higher than the theoretical predictions for thermal states under identical conditions. Based on the theoretical framework established in this work, future experiments may focus on adjusting the pump power, intracavity loss, and crystal temperature of optical parametric amplifiers to jointly control the squeezing degree and mean photon number, enabling stable generation of squeezed thermal states in different parameter regimes. Additionally, the precise measurement of higher-order coherence can be achieved using cascaded HBT detection systems with multiple inputs and high temporal resolution. In summary, by considering environmental noise, detection efficiency, and time delay, and by adjusting the average photon number, the number of squeezed photons, and the squeezing parameters, this method can prepare super-bunching squeezed thermal states and squeezed number states, whose higher-order coherence can be continuously adjusted over a wide range, thereby facilitating efficient quantum state preparation and manipulation, as well as high-resolution quantum imaging. -

-
图 2 相位无关压缩热态高阶相干函数
$ {g^{(n)}} $ 随光场平均光子数$ \alpha $ 和压缩参数$ r $ 变化的超聚束结果 (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ ; (d)$ {g^{(5)}} $ Figure 2. Super-bunching results of higher-order coherence function
$ {g^{(n)}} $ in phase-independent squeezed thermal state varying with mean photon number$ \alpha $ and squeezing parameter$ r $ : (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ ; (d)$ {g^{(5)}} $ .图 3 相位无关压缩数态高阶相干函数
$ {g^{(n)}} $ 随压缩光子数$ n $ 和压缩参数$ r $ 变化的结果 (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ ; (d)$ {g^{(5)}} $ Figure 3. Higher-order coherence function
$ {g^{(n)}} $ of phase-independent squeezed number state varying with photon number$ n $ before squeezing and squeezing parameter$ r $ : (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ ; (d)$ {g^{(5)}} $ .图 4 压缩参数
$ r $ = 1, 探测效率与背景噪声分别为($\eta $ = 1,$\gamma $ = 0), ($\eta $ = 0.5,$\gamma $ = 0.01)和($\eta $ = 0.5,$\gamma $ = 0.1)的情况下, 压缩热态光场高阶相干函数$ {g^{(n)}} $ 随平均光子数$ \alpha $ 的变化结果 (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ Figure 4. Higher-order coherence function
$ {g^{(n)}} $ of squeezed thermal state varying with mean photon number$ \alpha $ when squeezing parameter$ r $ = 1, under detection efficiency and background noise conditions of ($\eta $ = 1,$\gamma $ = 0), ($\eta $ = 0.5,$\gamma $ = 0.01), and ($\eta $ = 0.5,$\gamma $ = 0.1): (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ .图 5 平均光子数
$ \alpha $ = 0.5, 探测效率与背景噪声分别为($\eta $ = 1,$\gamma $ = 0), ($\eta $ = 0.5,$\gamma $ = 0.01)和($\eta $ = 0.5,$\gamma $ = 0.1)的情况下, 压缩热态光场高阶相干函数$ {g^{(n)}} $ 随压缩度$S$ 的变化结果 (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ Figure 5. Higher-order coherence function
$ {g^{(n)}} $ of squeezed thermal state varying with squeezing degree$S$ when mean photon number$ \alpha $ = 0.5, under detection efficiency and background noise conditions of ($\eta $ = 1,$\gamma $ = 0), ($\eta $ = 0.5,$\gamma $ = 0.01), and ($\eta $ = 0.5,$\gamma $ = 0.1): (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ .图 6 实验条件下(
$\eta $ = 0.5,$\gamma $ = 0.01)和理想条件下($\eta $ = 1,$\gamma $ = 0), 压缩参数 (a)$ r $ = 0.01, (b)$ r $ = 0.1和(c)$ r $ = 1时, 压缩数态高阶相干函数$ {g^{(n)}} $ 随压缩前数态光子数$ n $ 变化的结果Figure 6. Higher-order coherence function
$ {g^{(n)}} $ of squeezed number state varying with photon number$ n $ without squeezing under experimental conditions ($\eta $ = 0.5,$\gamma $ = 0.01) and ideal conditions ($\eta $ = 1,$\gamma $ = 0), with squeezing parameter (a)$ r $ = 0.01, (b)$ r $ = 0.1, and (c)$ r $ = 1.图 7 压缩参数
$ r $ = 0.1, 压缩光子数分别为 (a1)—(c1)$ n $ = 1, (a2)—(c2)$ n $ = 5和(a3)—(c3)$ n $ = 15时, 压缩数态在不同背景噪声$\gamma $ = 0.01, 0.1, 0.2的情况下的高阶相干函数$ {g^{(n)}} $ 随探测效率$\eta $ 的变化结果Figure 7. Higher-order coherence function
$ {g^{(n)}} $ of squeezed number state varying with detection efficiency$\eta $ at squeezing parameter$ r $ = 0.1, with squeezed photon number (a1)–(c1)$ n $ = 1, (a2)–(c2)$ n $ = 5, and (a3)–(c3)$ n $ = 15, under different background noises$\gamma $ = 0.01, 0.1, 0.2.图 8 背景噪声
$\gamma $ = 0.01, 压缩光子数$ n $ = 1时, 压缩数态在不同探测效率$\eta $ = 0.1, 0.5, 1情况下的高阶相干函数$ {g^{(n)}} $ 随压缩度$S$ 的变化结果 (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ Figure 8. Higher-order coherence function
$ {g^{(n)}} $ of squeezed number state varying with squeezing degree$S$ at background noise$\gamma $ = 0.01 and squeezed photon number$ n $ = 1, under different detection efficiencies$\eta $ = 0.1, 0.5, 1: (a)$ {g^{(2)}} $ ; (b)$ {g^{(3)}} $ ; (c)$ {g^{(4)}} $ .图 9 平均光子数
$ \alpha $ = 1, 压缩参数$ r $ = 0.2, 压缩热态光场全时延条件下的四阶相干性$ {g^{(4)}} $ 随延迟时间$ {t_3} $ ,$ {t_4} $ 的变化结果 (a)$ {t_1} $ =$ 0{\tau _{{\text{STS}}}} $ ;$ {t_2} $ =$ 0{\tau _{{\text{STS}}}} $ ; (b)$ {t_1} $ =$ 0{\tau _{{\text{STS}}}} $ ;$ {t_2} $ =$ 3{\tau _{{\text{STS}}}} $ ; (c)$ {t_1} $ =$ 0{\tau _{{\text{STS}}}} $ ;$ {t_2} $ =$ - 3{\tau _{{\text{STS}}}} $ Figure 9. Fourth-order degree of coherence
$ {g^{(4)}} $ of squeezed thermal state varying with delay times$ {t_3} $ ,$ {t_4} $ under full-delay conditions at mean photon number$ \alpha $ = 1 and squeezing parameter$ r $ = 0.2: (a)$ {t_1} $ =$ 0{\tau _{{\text{STS}}}} $ ;$ {t_2} $ =$ 0{\tau _{{\text{STS}}}} $ ; (b)$ {t_1} $ =$ 0{\tau _{{\text{STS}}}} $ ;$ {t_2} $ =$ 3{\tau _{{\text{STS}}}} $ ; (c)$ {t_1} $ =$ 0{\tau _{{\text{STS}}}} $ ;$ {t_2} $ =$ - 3{\tau _{{\text{STS}}}} $ . -
[1] 彭堃墀, 黄茂全, 刘晶, 廉毅敏, 张天才, 于辰, 谢常德, 郭光灿 1993 物理学报 42 1079 doi: 10.3321/j.issn:1000-3290.1993.07.008 Peng K C, Huang M Q, Liu J, Lian Y M, Zhang T C, Yu C, Xie C D, Guo G C 1993 Acta Phys. Sin. 42 1079 doi: 10.3321/j.issn:1000-3290.1993.07.008 [2] Breitenbach G, Schiller S, Mlynek J 1997 Nature 387 471 doi: 10.1038/387471a0 [3] 李庆回, 姚文秀, 李番, 田龙, 王雅君, 郑耀辉 2021 物理学报 70 154203 doi: 10.7498/aps.70.20210318 Li Q H, Yao W X, Li F, Tian L, Wang Y J, Zheng Y H 2021 Acta Phys. Sin. 70 154203 doi: 10.7498/aps.70.20210318 [4] Bachor H, Ralph T C 2004 A Guide to Experiments in Quantum Optics (Berlin: Wiley) p232 [5] Slusher R E, Hollberg L W, Yurke B, Mertz J C, Valley J F 1985 Phys. Rev. Lett. 55 2409 doi: 10.1103/PhysRevLett.55.2409 [6] Wu L A, Kimble H J, Hall J L, Wu H 1986 Phys. Rev. Lett. 57 2520 doi: 10.1103/PhysRevLett.57.2520 [7] Vollmer C E, Baune C, Samblowski A, Eberle T, Händchen V, Fiurášek J, Schnabel R 2014 Phys. Rev. Lett. 112 73602 doi: 10.1103/PhysRevLett.112.073602 [8] Kala V, Kopylov D, Marek P, Sharapova P 2025 Opt. Express 33 14000 doi: 10.1364/OE.550358 [9] Dorfman K, Liu S S, Lou Y B, Wei T X, Jing J T, Schlawin F, Mukamel S 2021 Proc. Natl. Acad. Sci. 118 e2105601118 doi: 10.1073/pnas.2105601118 [10] Chembo Y K 2016 Phys. Rev. A 93 33820 doi: 10.1103/PhysRevA.93.033820 [11] Kim S, Marino A M 2018 Opt. Express 26 33366 doi: 10.1364/OE.26.033366 [12] Silverstone J W, Bonneau D, Ohira K, Suzuki N, Yoshida H, Iizuka N, Ezaki M, Natarajan C M, Tanner M G, Hadfield R H 2014 Nat. Photonics 8 104 doi: 10.1038/nphoton.2013.339 [13] Arrazola J M, Bergholm V, Brádler K, Bromley T R, Collins M J, Dhand I, Fumagalli A, Gerrits T, Goussev A, Helt L G 2021 Nature 591 54 doi: 10.1038/s41586-021-03202-1 [14] Lu X, Li Q, Westly D A, Moille G, Singh A, Anant V, Srinivasan K 2019 Nat. Phys. 15 373 doi: 10.1038/s41567-018-0394-3 [15] Porto C, Rusca D, Cialdi S, Crespi A, Osellame R, Tamascelli D, Olivares S, Paris M G 2018 J. Opt. Soc. Am. B 35 1596 doi: 10.1364/JOSAB.35.001596 [16] Braunstein S L, Crouch D D 1991 Phys. Rev. A 43 330 doi: 10.1103/PhysRevA.43.330 [17] Fanizza M, Rosati M, Skotiniotis M, Calsamiglia J, Giovannetti V 2021 Quantum 5 608 doi: 10.22331/q-2021-12-23-608 [18] Deng X W, Hao S H, Tian C X, Su X L, Xie C D, Peng K C 2016 Appl. Phys. Lett. 108 081105 doi: 10.1063/1.4942464 [19] Yuen H P 2004 Quantum Squeezing (Vol. 27) (Berlin, Heidelberg: Springer Berlin Heidelberg) p227 [20] Lin S Q, Li W, Chen Z W, Shen J W, Ge B H, Pei Y Z 2016 Nat. Commun. 7 10287 doi: 10.1038/ncomms10287 [21] Lawrie B J, Lett P D, Marino A M, Pooser R C 2019 ACS Photonics 6 1307 doi: 10.1021/acsphotonics.9b00250 [22] Yang W H, Diao W T, Cai C X, Wu T, Wu K, Li Y, Li C, Duan C D, Leng H Y, Zi N K 2022 Chemosensors 11 18 doi: 10.3390/chemosensors11010018 [23] Zander J 2021 PhD Dissertation (Hamburg: Staats-und Universitätsbibliothek Hamburg Carl von Ossietzky [24] Zhang Y, Menotti M, Tan K, Vaidya V D, Mahler D H, Helt L G, Zatti L, Liscidini M, Morrison B, Vernon Z 2021 Nat. Commun. 12 2233 doi: 10.1038/s41467-021-22540-2 [25] Weedbrook C, Pirandola S, García-Patrón R, Cerf N J, Ralph T C, Shapiro J H, Lloyd S 2012 Rev. Mod. Phys. 84 621 doi: 10.1103/RevModPhys.84.621 [26] Dupays L, Chenu A 2021 Quantum 5 449 doi: 10.22331/q-2021-05-01-449 [27] Kim M S, de Oliveira F A M, Knight P L 1989 Phys. Rev. A 40 2494 doi: 10.1103/PhysRevA.40.2494 [28] Marian P, Marian T A 1993 Phys. Rev. A 47 4474 doi: 10.1103/PhysRevA.47.4474 [29] Rashid M, Tufarelli T, Bateman J, Vovrosh J, Hempston D, Kim M S, Ulbricht H 2016 Phys. Rev. Lett. 117 273601 doi: 10.1103/PhysRevLett.117.273601 [30] Albano L, Mundarain D F, Stephany J 2002 J. Opt. B: Quantum Semiclassical Opt. 4 352 doi: 10.1088/1464-4266/4/5/319 [31] Marian P 1991 Phys. Rev. A 44 3325 doi: 10.1103/PhysRevA.44.3325 [32] Liu R F, Fang A P, Zhou Y, Zhang P, Gao S Y, Li H R, Gao H, Li F L 2016 Phys. Rev. A 93 13822 doi: 10.1103/PhysRevA.93.013822 [33] Tan Q S, Liao J Q, Wang X, Nori F 2014 Phys. Rev. A 89 53822 doi: 10.1103/PhysRevA.89.053822 [34] Guo Y Q, Peng C S, Ji Y L, Li P, Guo Y Y, Guo X M 2018 Opt. Express 26 5991 doi: 10.1364/OE.26.005991 [35] Guo Y Q, Zhang H J, Guo X M, Zhang Y C, Zhang T C 2022 Opt. Express 30 8461 doi: 10.1364/OE.450204 [36] Guo Y Q, Li G, Zhang Y F, Zhang P F, Wang J M, Zhang T C 2012 Sci. China Phys. , Mech. Astron. 55 1523 doi: 10.1007/s11433-012-4847-x [37] Brown R H, Twiss R Q 1956 Nature 177 27 doi: 10.1038/177027a0 [38] 郭龑强, 王李静, 王宇, 房鑫, 赵彤, 郭晓敏 2020 物理学报 69 174204 doi: 10.7498/aps.69.20200325 Guo Y Q, Wang L J, Wang Y, Fang X, Zhao T, Guo X M Acta Phys. Sin. 2020 69 174204 doi: 10.7498/aps.69.20200325 [39] Liu Q, Luo K H, Chen X H, Wu L A 2010 Chin. Phys. B 19 94211 doi: 10.1088/1674-1056/19/9/094211 [40] Liu Y C, Kuang L M 2011 Phys. Rev. A 83 53808 doi: 10.1103/PhysRevA.83.053808 [41] Scully M O, Zubairy M S 1997 Quantum Optics (Cambridge: Cambridge University Press [42] 张浩杰, 郭龑强, 郭晓敏, 张健飞, 左冠华, 张玉驰, 张天才 2022 物理学报 71 194202 doi: 10.7498/aps.71.20220574 Zhang H J, Guo Y Q, Guo X M, Zhang J F, Zuo G H, Zhang Y C, Zhang T C 2022 Acta Phys. Sin. 71 194202 doi: 10.7498/aps.71.20220574 [43] Yu J, Qin Y, Qin J L, Wang H, Yan Z H, Jia X J, Peng K C 2020 Phys. Rev. Appl. 13 24037 doi: 10.1103/PhysRevApplied.13.024037 [44] Vignat C 2012 Stat. Probab. Lett. 82 67 doi: 10.1016/j.spl.2011.09.008 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: