高级搜索

高压下的色心磁共振和量子传感

downloadPDF

上一篇

下一篇

刘刚钦. 高压下的色心磁共振和量子传感[J]. 物理学报, 2025, 74(11): 117601-1. doi: 10.7498/aps.74.20250224
引用本文: 刘刚钦. 高压下的色心磁共振和量子传感[J]. 物理学报, 2025, 74(11): 117601-1. doi: 10.7498/aps.74.20250224
shu
Gangqin LIU. Magnetic resonance and quantum sensing with color centers under high pressures[J]. Acta Physica Sinica, 2025, 74(11): 117601-1. doi: 10.7498/aps.74.20250224
Citation: Gangqin LIU. Magnetic resonance and quantum sensing with color centers under high pressures[J]. Acta Physica Sinica, 2025, 74(11): 117601-1. doi: 10.7498/aps.74.20250224
shu

高压下的色心磁共振和量子传感

  • 1.

    中国科学院物理研究所, 北京凝聚态物理国家研究中心, 北京　100190

  • 2.

    中国科学院拓扑量子计算卓越创新中心, 北京　100190

    • 通讯作者: E-mail: gqliu@iphy.ac.cn.

  • 中图分类号: 76.70.Hb, 61.72.jn, 03.67.-a, 07.35.+k

Magnetic resonance and quantum sensing with color centers under high pressures

  • 1.

    Beijing National Laboratory for Condensed Matter Physics, Institute of Physics, Chinese Academy of Sciences, Beijing 100190, China

  • 2.

    CAS Center of Excellence in Topological Quantum Computation, Beijing 100190, China

    • Corresponding author: E-mail: gqliu@iphy.ac.cn.

  • MSC: 76.70.Hb, 61.72.jn, 03.67.-a, 07.35.+k

  • 摘要: 高压极端条件是实现和调控新奇物态的重要途径, 磁共振技术是材料微观磁结构和磁性表征的重要方法, 两者的融合为物质科学前沿研究提供了新的机遇. 然而, 传统磁共振技术受限于自旋极化度低、信号探测效率差等因素, 难以实现超高压极端条件下微米级小样品的原位测量. 近年来, 以金刚石氮空位中心为代表的色心量子传感迅速发展, 为高压极端条件下的磁共振和原位量子传感提供了全新解决方案. 本文总结了高压极端条件对金刚石氮空位中心自旋和光学性质的影响, 梳理了高压下色心磁共振的基本现象和规律. 同时, 以高压下微区磁成像、压强探测、超导迈斯纳效应测量等应用为例, 本文还介绍了高压下色心量子传感的近期研究进展.
    Abstract: High-pressure extreme conditions are crucial for realizing novel states and regulating material properties, while magnetic resonance technology is a widely used method to characterize microscopic magnetic structures and magnetic properties. The integration of these two fields offers new opportunities for cutting-edge research in condensed matter physics and materials science. However, conventional magnetic resonance is limited by several factors, such as low spin polarization and low signal detection efficiency, which makes in-situ measurement of micrometer-sized samples under ultra-high pressure a challenge. Recent advances in quantum sensing with color centers in solids, in particular, the development of quantum sensors based on nitrogen vacancy (NV) centers in diamond, provide an innovative solution for magnetic resonance and in-situ quantum sensing under high pressure. This article summarizes the effects of high-pressure conditions on the spin and optical properties, as well as on the magnetic resonance of diamond NV centers. In addition, this article reviews recent advances in high-pressure quantum sensing through applications such as magnetic imaging, pressure detection, and the study of the superconducting Meissner effect under high pressure.
  • 加载中

  • 图 1  高压下的金刚石色心量子传感. 左图为金刚石对顶砧的基本结构, 由两块特殊切割的金刚石和金属垫片构成, 垫片中心孔内装载样品并填充传压介质, 通过上下两片金刚石的挤压给样品施加高压. 右图为金刚石氮空位(nitrogen-vacancy, NV)中心的物理结构——由一个替代位氮原子和一个近邻空位构成. NV中心自旋状态可通过光学方法高效地极化、操控和读出, 可作为灵敏的纳米尺度量子传感器. 基于NV中心的量子传感完全兼容于金刚石对顶砧压机, 为高压极端条件下的磁共振和微区磁测量提供了全新的方案

    Figure 1.  Diamond NV center-based quantum sensing under high pressure. The figure on the left illustrates the basic structure of a diamond anvil cell, which consists of two specially cut diamonds and a metal seal. The sample is loaded into the central hole of the gasket, which is filled with a pressure-transmitting medium. High pressure is applied to the sample by compressing the upper and lower diamond anvils. The diagram on the right shows the physical structure of a nitrogen-vacancy (NV) center in diamond, which consists of a substituted nitrogen atom and an adjacent vacancy. The spin state of NV centers can be efficiently polarized, controlled and read out using optical methods, enabling sensitive quantum sensing at the nanoscale. NV-based quantum sensing is compatible with diamond anvil cells and provides a novel method to realize magnetic resonance and magnetic measurements under high pressure conditions.

    下载: 全尺寸图片 幻灯片

    图 2  金刚石NV中心量子传感工作原理　(a) 金刚石NV中心自旋能级结构和光学跃迁, 右侧为基态能级随外磁场的变化规律(塞曼效应); (b) 典型的光探磁共振(ODMR)谱线, 上图为零场ODMR谱线, 下图为外加24 G (1 G = 10–4 T)磁场的结果; 通过拟合共振频率, 可以得到NV中心所处位置的磁场信息

    Figure 2.  Working principle of diamond quantum sensing: (a) The energy level structure and the optical transitions of NV centers in diamond; the right diagram shows the ground states of an NV center under different external magnetic fields (Zeeman effect); (b) typical optically detected magnetic resonance (ODMR) spectra. Top: ODMR spectrum at zero-field. Bottom: ODMR spectrum under an external magnetic field of 24 G (1 G = 10–4 T). By fitting the resonance frequency of the ODMR spectra, we can determine the strength and orientation of the magnetic field.

    下载: 全尺寸图片 幻灯片

    图 3  高压极端条件对金刚石NV中心光学性质的影响　(a) 零声线(ZPL)和声子边带(PSB)的示意图[11]; (b) 金刚石对顶砧高压腔中引入NV中心的两种方法, 上图为在传压介质中放置包含NV中心的金刚石颗粒, 下图为在对顶砧砧面上制备NV中心[12]; (c)不同压强下金刚石NV中心的荧光光谱, 激发光源为532 nm激光, 该实验使用的NV中心来自微米金刚石颗粒[11]; (d) 金刚石NV中心ZPL随压强变化规律, 该实验使用了砧面上的NV中心, 结果显示静水压条件对于实现高压ODMR至关重要[12]

    Figure 3.  The influence of pressure on the optical properties of NV centers: (a) Schematic representation of the zero-phonon line (ZPL) and the phonon sideband (PSB) [11]; (b) two methods for placing NV centers in the DAC high-pressure chamber, the top diagram shows placement of diamond particles with NV centers in the pressure-transmitting medium, and the bottom diagram shows fabrication of shallow NV centers on the diamond culet [12]; (c) PL spectra of NV centers under different pressures, the experiment is performed with 532 nm laser excitation and NV centers in microdiamond [11]; (d) pressure dependence of the ZPL, the experiment is performed with shallow NV centers on the culet, the results emphasize the importance of the hydrostatic environment for ODMR at high pressure [12].

    下载: 全尺寸图片 幻灯片

    图 4  高压极端条件对金刚石NV中心自旋性质的影响　(a) 压强对NV中心基态能级的影响; (b) 沿(100)和(111)晶向切割的金刚石对顶砧砧面上NV中心的受力示意; (c) 不同压强下的NV中心零场ODMR谱线, 数据来自(111)切割的对顶砧砧面浅层NV中心[14]; (d), (e) 实验测量的NV中心零场劈裂值D随压强变化规律, 其中(d)图来自传压介质中的微米金刚石[11]; (e)图来自(100)切割的砧面浅层NV中心[12]; (f)图来自(111)切割的砧面浅层NV中心[11,14]

    Figure 4.  The influence of pressure on the spin properties of NV centers: (a) Ground states of NV centers with and without external pressure; (b) schematic representation of NV orientation and diamond cut direction; (c) ODMR spectra of NV centers under different pressures, the experiment is performed with shallow NV centers in (111) cut diamond [14]; (d), (e) pressure dependence of zero-field splitting, D; data are acquired with (d) NV centers in microdiamond [11], (e) shallow NV centers in (100) cut diamond [12], and (f) shallow NV centers in (111) cut diamond[11,14].

    下载: 全尺寸图片 幻灯片

    图 5  基于固态色心的量子传感工作压强和测磁灵敏度[14]

    Figure 5.  Working pressure and sensitivity of color center-based quantum sensing[14].

    下载: 全尺寸图片 幻灯片

    图 6  高压下金刚石中14N核磁共振[43]　(a)基于金刚石NV中心的高压磁共振示意图(左), 在激发态能级交叉点附近实现14N核自旋的动态极化(右); (b) 电子自旋-核自旋耦合系统的能级结构, 磁共振探测的频率用箭头标出; (c) 典型的金刚石内14N核磁共振谱线, 左侧数据NV中心处于$ |{m}_{{\mathrm{s}}}=0\rangle $态, 右侧数据NV中心处于$ |{m}_{{\mathrm{s}}}=-1\rangle $态; (d) 14N核自旋四极矩项Q和超精细耦合参数A//随压强变化规律; (e) NMR谱线线宽随压强依赖关系

    Figure 6.  NMR of 14N spin ensemble under high pressure[43]: (a) Schematic representation of high-pressure NMR enabled by NV centers(left), dynamical nuclear spin polarization of 14N nuclear spin at ESLAC(right); (b) energy levels of the coupled electron and nuclear spin system, with the transitions of the NMR measurements labeled; (c) typical NMR spectra of 14N spin ensemble under different pressures, NV electron spins in the $ |{m}_{{\mathrm{s}}}=0\rangle $ state(left), NV electron spins in the $ |{m}_{{\mathrm{s}}}=-1\rangle $ state(right); (d) absolute value of Q (red) and A// (blue) as a function of pressure; (e) pressure dependence of the width of 14N NMR spectra.

    下载: 全尺寸图片 幻灯片

    图 7  基于SiC和hBN中色心的高压量子传感　(a) 4H-SiC中的Si空位($ {{\mathrm{V}}}_{{\mathrm{S}}{\mathrm{i}}} $)色心(左)和双空位色心(右)物理结构[47]; (b), (c) 双空位色心PL5@SiC的ODMR谱线和对应零场劈裂值随压强变化规律[49]; (d) hBN中带负电的B空位$ {{\mathrm{V}}}_{{\mathrm{B}}}^{-} $物理结构; (e), (f) $ {{\mathrm{V}}}_{{\mathrm{B}}}^{-} $@hBN在不同压强下ODMR谱线和对应零场劈裂值随压强变化规律[50]

    Figure 7.  High-pressure quantum sensing with color centers in SiC and hBN: (a) The physical structure of Si vacancy and divacancy in 4H-SiC [47]; (b), (c) typical ODMR spectra of the PL5@SiC divacancy center and the pressure dependence of its zero-field splitting[49]; (d) the physical structure of B vacancy in hBN, $ {{\mathrm{V}}}_{{\mathrm{B}}}^{-} $; (e), (f) typical ODMR spectra of $ {{\mathrm{V}}}_{{\mathrm{B}}}^{-}@{\mathrm{h}}{\mathrm{B}}{\mathrm{N}} $ and the pressure dependence of its zero-field splitting[50].

    下载: 全尺寸图片 幻灯片

    图 8  兆巴高压下的Fe3O4颗粒磁成像和磁相变过程测量[14]　(a) 磁畴和近邻磁场随压强的演化示意图; (b), (c) 对顶砧选定位置(见图中标记)处的磁场$ {B}_{z}^{{\mathrm{m}}{\mathrm{a}}{\mathrm{g}}} $随压强变化规律; (d) ODMR线宽$ {\varGamma }^{{\mathrm{m}}{\mathrm{a}}{\mathrm{g}}} $随压强变化规律; (e) Fe3O4的相图, FM代表铁磁, FiM代表亚铁磁, PM代表顺磁; (f)—(j) 在压强为38.2, 45.5, 50.4, 58.4和65.0 GPa下的局部磁成像, 外加磁场约为240 G下对exp2中Fe3O4表面的磁场成像; 蓝色点划线标记了样品边界, 灰色点划线标记了磁畴边界

    Figure 8.  Magnetism evolution of magnetite to megabar pressures[14]: (a) Schematic diagram of the evolution of magnetic domains and their stray magnetic fields in magnetite with pressure; (b), (c) pressure dependence of the magnetite magnetic field $ {B}_{z}^{{\mathrm{m}}{\mathrm{a}}{\mathrm{g}}} $ at the selected positions; (d) pressure dependence of the linewidth broadening $ {\varGamma }^{{\mathrm{m}}{\mathrm{a}}{\mathrm{g}}} $; (e) the phase diagram of Fe3O4, FM stands for ferromagnetic, FiM stands for ferrimagnetic, and PM stands for paramagnetic; (f)–(j) magnetic field imaging of the surface of Fe3O4 in exp2 with an external magnetic field of ~240 G at pressures of 38.2, 45.5, 50.4, 58.4 and 65.0 GPa, respectively. The dashed blue line in (e) marks the Fe3O4 sample and dashed gray lines mark the magnetic domain wall.

    下载: 全尺寸图片 幻灯片

    图 9  高压下CeH9超导迈斯纳效应的实验测量[13]　(a) 测量抗磁现象的实验序列; (b) 样品及近邻区域的共聚焦荧光图; (c) 样品上蓝色标记位置在不同温度下的ODMR谱线, 该数据对应外加磁场为$ {H}_{{{z}}} $= 79 G, 且在零场降温后采集, 随着温度升高和靠近$ {T}_{{\mathrm{C}}} $, ODMR劈裂逐渐增加; (d) 局部磁场(左侧Y轴)和四电极法测量电阻(右侧Y轴)随温度变化, 零场降温后加场升温测试; (e) 在$ {H}_{{{z}}} $= 79 G磁场下, 降温过程中局部磁场和电阻随温度变温规律, 电阻在$ {T}_{{\mathrm{C}}}\approx $ 91 K时出现明显转变

    Figure 9.  Imaging the Meissner effect in CeH9 under high pressure[13]: (a) The experimental sequence for probing local diamagnetism; (b) confocal fluorescence image of the sample, ODMR spectroscopy is performed at the labeled points; (c) NV ODMR spectra collected at the blue spatial point in (b) on field heating at $ {H}_{{{z}}} $= 79 G (following zero-field cooling), the ODMR splitting increases as T is increased across $ {T}_{{\mathrm{C}}} $; (d) the local field, Bz (left y-axis) and the four-point resistance (right y-axis) as a function of temperature; (e) simultaneous measurements of four-point resistance (right y-axis) and the change in the local field, $ \delta {B}_{{{z}}} $ (left y-axis) on field cooling with $ {H}_{{{z}}} $= 79 G, the measured resistance identifies a clear transition at $ {T}_{{\mathrm{C}}}\approx $ 91 K.

    下载: 全尺寸图片 幻灯片

    图 10  高压下La3Ni2O7-δ和La2PrNi2O7超导迈斯纳效应的原位测量[40]　(a) La2PrNi2O7样品的共聚焦荧光扫描图, 传压介质为硅油; (b) 零场冷却到7 K后外加120 G磁场时的磁成像, 其中蓝色区域磁场小于外加磁场, 是典型的抗磁区域; (c) 典型位置的NV中心测得磁场随温度变温规律. 其中A0远离样品, 为测量参考点; A1在样品上, 低温区呈现出明显的抗磁现象; A2区在样品边沿, 低温下观测到了局部磁场增强, 在零场冷却加场升温(ZFC-FW)和场冷(FC)实验中观测到了相似现象, 外加磁场大小为120 G; (d) 不同样品和传压介质产生的超导抗磁信号对比, 外加磁场均为120 G

    Figure 10.  Probing the Meissner effect in pressurized bilayer nickelate La3Ni2O7-δ and La2PrNi2O7 [40]: (a) Fluorescence image of sample A (La2PrNi2O7 in silicon oil); (b) magnetic field imaging under an external magnetic field of HZ = 120 G after zero-field cooling of the sample to 7 K, the blue area shows clear diamagnetism; (c) ODMR splitting of three selected points under ZFC-FW and FC measurements, point A0 is far away from the sample and serves as a reference, point A1 is on the sample and local demagnetization is observed at low temperature, point A2 is located at the sample edge and a local enhancement of magnetic field is observed, similar phenomena are observed in the ZFC-FW and FC measurements, (d) comparison of the diamagnetism effect of the three samples during the ZFW-FW measurement, the external magnetic field is about 120 G.

    下载: 全尺寸图片 幻灯片
  • [1] Wang H, Tse J S, Tanaka K, Iitaka T, Ma Y M 2012 PNAS 109 6463 doi: 10.1073/pnas.1118168109
    [2] Drozdov A P, Eremets M I, Troyan I A, Ksenofontov V, Shylin S I 2015 Nature 525 73 doi: 10.1038/nature14964
    [3] Drozdov A P, Kong P P, Minkov V S, Besedin S P, Kuzovnikov M A, Mozaffari S, Balicas L, Balakirev F F, Graf D E, Prakapenka V B, Greenberg E, Knyazev D A, Tkacz M, Eremets M I 2019 Nature 569 528 doi: 10.1038/s41586-019-1201-8
    [4] Somayazulu M, Ahart M, Mishra A K, Geballe Z M, Baldini M, Meng Y, Struzhkin V V, Hemley R J 2019 Phys. Rev. Lett. 122 027001 doi: 10.1103/PhysRevLett.122.027001
    [5] Zhang L J, Wang Y C, Lv J, Ma Y M 2017 Nat. Rev. Mater. 2 17005 doi: 10.1038/natrevmats.2017.5
    [6] Ekimov E A, Sidorov V A, Bauer E D, Mel'nik N N, Curro N J, Thompson J D, Stishov S M 2004 Nature 428 542 doi: 10.1038/nature02449
    [7] Hirose K, Fei Y, Ma Y, Mao H K 1999 Nature 397 53 doi: 10.1038/16225
    [8] Hu Q Y, Kim D Y, Yang W G, Yang L X, Meng Y, Zhang L, Mao H K 2016 Nature 534 241 doi: 10.1038/nature18018
    [9] Meier T 2018 Annu. Rep. NMR Spectrosc. 93 1
    [10] Meier T, Trybel F, Khandarkhaeva S, Steinle-Neumann G, Chariton S, Fedotenko T, Petitgirard S, Hanfland M, Glazyrin K, Dubrovinskaia N, Dubrovinsky L 2019 Phys. Rev. X 9 031008
    [11] Dai J H, Shang Y X, Yu Y H, Xu Y, Yu H, Hong F, Yu X H, Pan X Y, Liu G Q 2022 Chin. Phys. Lett. 39 117601 doi: 10.1088/0256-307X/39/11/117601
    [12] Hilberer A, Toraille L, Dailledouze C, Adam M P, Hanlon L, Weck G, Schmidt M, Loubeyre P, Roch J F 2023 Phys. Rev. B 107 L220102 doi: 10.1103/PhysRevB.107.L220102
    [13] Bhattacharyya P, Chen W, Huang X, Chatterjee S, Huang B, Kobrin B, Lyu Y, Smart T J, Block M, Wang E, Wang Z, Wu W, Hsieh S, Ma H, Mandyam S, Chen B, Davis E, Geballe Z M, Zu C, Struzhkin V, Jeanloz R, Moore J E, Cui T, Galli G, Halperin B I, Laumann C R, Yao N Y 2024 Nature 627 73 doi: 10.1038/s41586-024-07026-7
    [14] Wang M Q, Wang Y, Liu Z X, Xu G Y, Yang B, Yu P, Sun H Y, Ye X Y, Zhou J W, Goncharov A F, Wang Y, Du J F 2024 Nat. Commun. 15 8843 doi: 10.1038/s41467-024-52272-y
    [15] Liu G Q, Feng X, Wang N, Li Q, Liu R B 2019 Nat. Commun. 10 1344 doi: 10.1038/s41467-019-09327-2
    [16] Fan J W, Guo S W, Lin C, Wang N, Liu G Q, Li Q, Liu R B 2024 Nano Lett. 24 14806 doi: 10.1021/acs.nanolett.4c04359
    [17] Fortman B, Mugica-Sanchez L, Tischler N, Selco C, Hang Y X, Holczer K, Takahashi C 2021 J Appl. Phys. 130 083901 doi: 10.1063/5.0055642
    [18] 刘刚钦 2022 物理学报 71 066101 doi: 10.7498/aps.71.20212072 Liu G Q 2022 Acta Phys. Sin. 71 066101 doi: 10.7498/aps.71.20212072
    [19] Rondin L, Tetienne J P, Hingant T, Roch J F, Maletinsky P, Jacques V 2014 Rep. Prog. Phys. 77 056503 doi: 10.1088/0034-4885/77/5/056503
    [20] Schirhagl R, Chang K, Loretz M, Degen C L 2014 Annu. Rev. Phys. Chem. 65 83 doi: 10.1146/annurev-physchem-040513-103659
    [21] Degen C L, Reinhard F, Cappellaro P 2017 Rev. Mod. Phys. 89 035002 doi: 10.1103/RevModPhys.89.035002
    [22] Casola F, Van Der Sar T, Yacoby A 2018 Nat. Rev. Mater. 3 17088 doi: 10.1038/natrevmats.2017.88
    [23] Liu G Q, Liu R B, Li Q 2022 Acc. Chem. Res. 56 95
    [24] 刘刚钦, 邢健, 潘新宇 2019 物理学报 68 120302 doi: 10.7498/aps.68.20190274 Liu G Q, Xing J, Pan X Y 2019 Acta Phys. Sin. 68 120302 doi: 10.7498/aps.68.20190274
    [25] 董杨, 杜博, 张少春, 陈向东, 孙方稳 2018 物理学报 67 160301 doi: 10.7498/aps.67.20180788 Dong Y, Du B, Zhang S C, Chen X D, Sun F W 2018 Acta Phys. Sin. 67 160301 doi: 10.7498/aps.67.20180788
    [26] 彭世杰, 刘颖, 马文超, 石发展, 杜江峰 2018 物理学报 67 167601 doi: 10.7498/aps.67.20181084 Peng S J, Liu Y, Ma W C, Shi F Z, Du J F 2018 Acta Phys. Sin. 67 167601 doi: 10.7498/aps.67.20181084
    [27] Aslam N, Zhou H Y, Urbach E K, Turner M J, Walsworth R L, Lukin M D, Park H 2023 Nat. Rev. Phys. 5 157 doi: 10.1038/s42254-023-00558-3
    [28] Wu Y, Weil T 2022 Adv. Sci. 9 2200059 doi: 10.1002/advs.202200059
    [29] Barry J F, Schloss J M, Bauch E, Turner M J, Hart C A, Pham L A, Walsworth R L 2020 Rev. Mod. Phys. 92 015004 doi: 10.1103/RevModPhys.92.015004
    [30] Lawson A W, Tang T Y 1950 Rev. Sci. Instrum. 21 815
    [31] Jayaraman A 1983 Rev. Mod. Phys. 55 65 doi: 10.1103/RevModPhys.55.65
    [32] Gruber A, Dräbenstedt A, Tietz C, Fleury L, Wrachtrup J, von Borczyskowski C 1997 Science 276 2012 doi: 10.1126/science.276.5321.2012
    [33] Doherty M W, Manson N B, Delaney P, Jelezko F, Wrachtrup J, Hollenberg L C L 2013 Phys. Rep. 528 1 doi: 10.1016/j.physrep.2013.02.001
    [34] Doherty M W, Struzhkin V V, Simpson D A, McGuinness L P, Meng Y F, Stacey A, Karle T J, Hemley R J, Manson N B, Hollenberg L C L, Prawer S 2014 Phys. Rev. Lett. 112 047601 doi: 10.1103/PhysRevLett.112.047601
    [35] Shang Y X, Hong F, Dai H J, Yu H, Lu Y N, Liu E K, Yu X H, Liu G Q, Pan X Y 2019 Chin. Phys. Lett. 36 086201 doi: 10.1088/0256-307X/36/8/086201
    [36] Yip K Y, Ho K O, Yu K Y, Chen Y, Zhang W, Kasahara S, Mizukami Y, Shibauchi T, Matsuda Y, Goh S K, Yang S 2019 Science 366 1355 doi: 10.1126/science.aaw4278
    [37] Shelton D P, Cabriales W, Salamat A 2024 Rev. Sci. Instrum. 95 083901 doi: 10.1063/5.0216877
    [38] Hsieh S, Bhattacharyya P, Zu C, Mittiga T, Smart T J, Machado F, Kobrin B, Höhn T O, Rui N Z, Kamrani M, Chatterjee S, Choi S, Zaletel M, Struzhkin V V, Moore J E, Levitas V I, Jeanloz R, Yao N Y 2019 Science 366 1349 doi: 10.1126/science.aaw4352
    [39] Lesik M, Plisson T, Toraille L, Renaud J, Occelli F, Schmidt M, Salord O, Delobbe A, Debuisschert T, Rondin L, Loubeyre P, Roch J F 2019 Science 366 1359 doi: 10.1126/science.aaw4329
    [40] Wen J Y, Xu Y, Wang G, He Z X, Chen Y, Wang N N, Lu T L, Ma X L, Jin F, Chen L C, Liu M, Fan J W, Liu X B, Pan X Y, Liu G Q, Cheng J G, Yu X H 2024 arXiv: 2410.10275 https://doi.org/10.48550/arXiv.2410.10275
    [41] Meijer J, Burchard B, Domhan M, Wittmann C, Gaebel T, Popa I, Jelezko F, Wrachtrup J 2005 Appl. Phys. Lett. 87 261909 doi: 10.1063/1.2103389
    [42] Lyapin S G, Ilichev I D, Novikov A P, Davydov V A, Agafonov V N 2018 Nanosystems: Physics, Chemistry, Mathematics 9 55
    [43] Shang Y X, Hong F, Dai J H, Lu Y N, Yu H, Yu Y H, Yu X H, Pan X Y, Liu G Q 2022 arXiv: 2203.10511 https://doi.org/10.48550/arXiv.2203.10511
    [44] Jacques V, Neumann P, Beck J, Markham M, Twitchen D, Meijer J, Kaiser F, Balasubramanian G, Jelezko F, Wrachtrup J 2009 Phys. Rev. Lett. 102 57403 doi: 10.1103/PhysRevLett.102.057403
    [45] London P, Scheuer J, Cai J M, Schwarz I, Retzker A, Plenio M B, Katagiri M, Teraji T, Koizumi S, Isoya J, Fischer R, McGuinness L P, Naydenov B, Jelezko F 2013 Phys. Rev. Lett. 111 067601 doi: 10.1103/PhysRevLett.111.067601
    [46] Liu G Q, Jiang Q Q, Chang Y C, Liu D Q, Li W X, Gu C Z, Po H C, Zhang W X, Zhao N, Pan X Y 2014 Nanoscale 6 10134 doi: 10.1039/C4NR02007C
    [47] Zhang G, Cheng Y, Chou J P, Gali A 2020 Appl. Phys. Rev. 7 031308 doi: 10.1063/5.0006075
    [48] Wang J F, Liu L, Liu X D, Li Q, Cui J M, Zhou D F, Zhou J Y, Wei Y, Xu H A, Xu W, Lin W X, Yan J W, He Z X, Liu Z H, Hao Z H, Li H O, Liu W, Xu J S, Gregoryanz E, Li C F 2023 Nat. Mater. 22 489 doi: 10.1038/s41563-023-01477-5
    [49] Liu L, Wang J F, Liu X D, Xu H A, Cui J M, Li Q, Zhou J Y, Lin W X, He Z X, Xu W, Wei Y, Liu Z H, Wang P, Hao Z H, Ding J F, Li H O, Liu W, Li H, You L X, Xu J S, Gregoryanz E, Li C F, Guo G C 2022 Nano Lett. 22 9943 doi: 10.1021/acs.nanolett.2c03378
    [50] He G H, Gong R T, Wang Z P, Liu Z W, Hong J, Zhang T X, Riofrio A L, Rehfuss Z, Chen M F, Yao C Y, Poirier T, Ye B T, Wang X, Ran S, Edgar J H, Zhang S X, Yao N Y, Zu C 2025 arXiv: 2501.03319
    [51] Zhong C, Wang Y P, Mai D, Ye C H, Li X D, Wang H, Dai R C, Wang Z P, Sun X Y, Zhang Z M 2024 Nano Lett. 24 4993
    [52] Mao H K 2024 Natl. Sci. Rev. 11 nwae004 doi: 10.1093/nsr/nwae004
    [53] Eremets M I 2024 Natl. Sci. Rev. 11 nwae047 doi: 10.1093/nsr/nwae047
    [54] Hamlin J J 2019 Nature 569 491 doi: 10.1038/d41586-019-01583-y
    [55] Sun H L, Huo M W, Hu X W, Li J Y, Liu Z J, Han Y F, Tang L Y, Mao Z Q, Yang P T, Wang B S, Cheng J G, Yao D X, Zhang G M, Wang M 2023 Nature 621 493 doi: 10.1038/s41586-023-06408-7
    [56] Wang N N, Wang G, Shen X L, Hou J, Luo J, Ma X P, Yang H X, Shi L F, Dou J, Feng J, Yang J, Shi Y Q, Ren Z A, Ma H M, Yang P T, Liu Z Y, Liu Y, Zhang H, Dong X L, Wang Y X, Jiang K, Hu J P, Nagasaki S, Kitagawa K, Calder S, Yan J Q, Sun J P, Wang B S, Zhou R, Uwatoko Y, Cheng J G 2024 Nature 634 579 doi: 10.1038/s41586-024-07996-8
    [57] Zhou Y Z, Guo J, Cai S, Sun H L, Li C Y, Zhao J Y, Wang P Y, Han J Y, Chen X T, Chen Y J, Wu Q, Ding Y, Xiang T, Mao H K, Sun L L 2025 Matter Radiat. Extremes 10 027801 doi: 10.1063/5.0247684
  • 加载中
图( 10)
计量
  • 文章访问数:  56
  • HTML全文浏览数:  56
  • PDF下载数:  4
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-24
  • 刊出日期:  2025-06-05

高压下的色心磁共振和量子传感

    通讯作者: E-mail: gqliu@iphy.ac.cn.
  • 1. 中国科学院物理研究所, 北京凝聚态物理国家研究中心, 北京　100190
  • 2. 中国科学院拓扑量子计算卓越创新中心, 北京　100190
  • 收稿日期:  2025-02-24

摘要: 高压极端条件是实现和调控新奇物态的重要途径, 磁共振技术是材料微观磁结构和磁性表征的重要方法, 两者的融合为物质科学前沿研究提供了新的机遇. 然而, 传统磁共振技术受限于自旋极化度低、信号探测效率差等因素, 难以实现超高压极端条件下微米级小样品的原位测量. 近年来, 以金刚石氮空位中心为代表的色心量子传感迅速发展, 为高压极端条件下的磁共振和原位量子传感提供了全新解决方案. 本文总结了高压极端条件对金刚石氮空位中心自旋和光学性质的影响, 梳理了高压下色心磁共振的基本现象和规律. 同时, 以高压下微区磁成像、压强探测、超导迈斯纳效应测量等应用为例, 本文还介绍了高压下色心量子传感的近期研究进展.

English Abstract

    全文HTML

    1.   引　言

    • 高压条件, 特别是基于金刚石对顶砧的超高压极端条件对于凝聚态物理、材料科学、地球与行星科学的基础研究至关重要. 在探索新奇物态方面, 高压条件可实现电子结构和物态调控, 例如H3S, LaH10等富氢材料在高压下可在近室温进入超导状态[1-4]. 在材料合成和性能优化方面, 高压极端条件可合成常压条件难以获得的超硬材料、含能材料等, 以及用于材料物性的优化[5,6]. 在地球与行星科学领域, 金刚石对顶砧和激光加热技术可在实验室模拟地球内部的高温高压状态[7,8], 为理解行星的内部结构和演化机制提供了独特的实验平台.

      然而, 在高压极端条件下进行物性测量是极为挑战的. 以表征物质微观磁性的磁共振技术为例, 尽管在物质科学基础研究中被广泛地使用, 其在高压极端条件下的应用就受到诸多限制. 一方面, 通常实验中可实现和维持高压条件的样品体积较小, 且压强越高体积越小. 例如, 100 GPa压强下样品腔体积仅为1 nL左右[9]; 而传统磁共振技术受限于其较低的自旋极化度等因素, 需要100 μL以上的样品体积才能获得足够的信噪比, 这导致传统的磁共振技术仅能在常压或较低压强下工作. 另一方面, 实现高压条件所需的核心部件, 如金刚石、金属垫片、传压介质等, 也对传感器的放置位置和方式带来了较强限制, 进一步加剧了高压下磁共振测量的难度. 值得一提的是, 通过特殊设计的楞次线圈(Lenz lenses), Meier等[10]实现了近100 GPa高压下的磁共振. 然而, 考虑到高压下物性表征的多样化需求, 特别是对微区磁性、压强、温度等物理量的灵敏测试需求, 亟需发展更加普适和适应更高压强的测量方案.

      近年, 以金刚石氮空位(nitrogen-vacancy, NV)中心为代表的色心量子传感为微区物性测量提供了全新解决方案. 色心结构广泛存在于金刚石、碳化硅、六方氮化硼等宽禁带材料中, 其缺陷能级在光学激发下辐射出荧光, 使得原本透明的材料表现出丰富的色彩, 因此它们被称为“色心”. 对于一些特殊的色心, 如金刚石NV中心、六方氮化硼中硼空位色心等, 它们的光学跃迁显著地依赖于自旋状态, 可通过光学方法实现自旋的高效极化和读出. 同时, 色心自旋状态对其所处环境极为敏感, 是天然的固态量子传感器, 可实现纳米尺度的磁、力、热等物理量的灵敏测量. 更重要的是, 结合金刚石自身优异的物理性质, 基于NV中心的量子传感可在兆巴(1 Mba = 100 GPa)高压[11-14]、上千开尔文 高温[15,16], 以及特斯拉级强磁场[17]等极端条件下 工作, 正在成为极端条件下微区物性测量的重要 工具[18].

      本文聚焦高压极端条件下的金刚石NV中心磁共振和量子传感. 我们将从NV中心量子传感和金刚石对顶砧高压技术的结合引入, 重点介绍高压极端条件对金刚石NV中心自身光学、自旋、核自旋超精细耦合等基本性质的影响; 随后, 我们以高压下微区磁测量和磁成像、压强测量、超导迈斯纳效应测量为例, 介绍高压下金刚石量子传感的近期应用进展. 本文也涉及碳化硅和六方氮化硼色心的高压调控结果. 关于金刚石氮空位中心量子传感的基础知识和应用见综述文献[19-29], 高压下的磁共振技术亦有专门的讨论[9].

    2.   金刚石对顶砧高压技术与自旋量子传感的结合

      2.1.   金刚石对顶砧简介

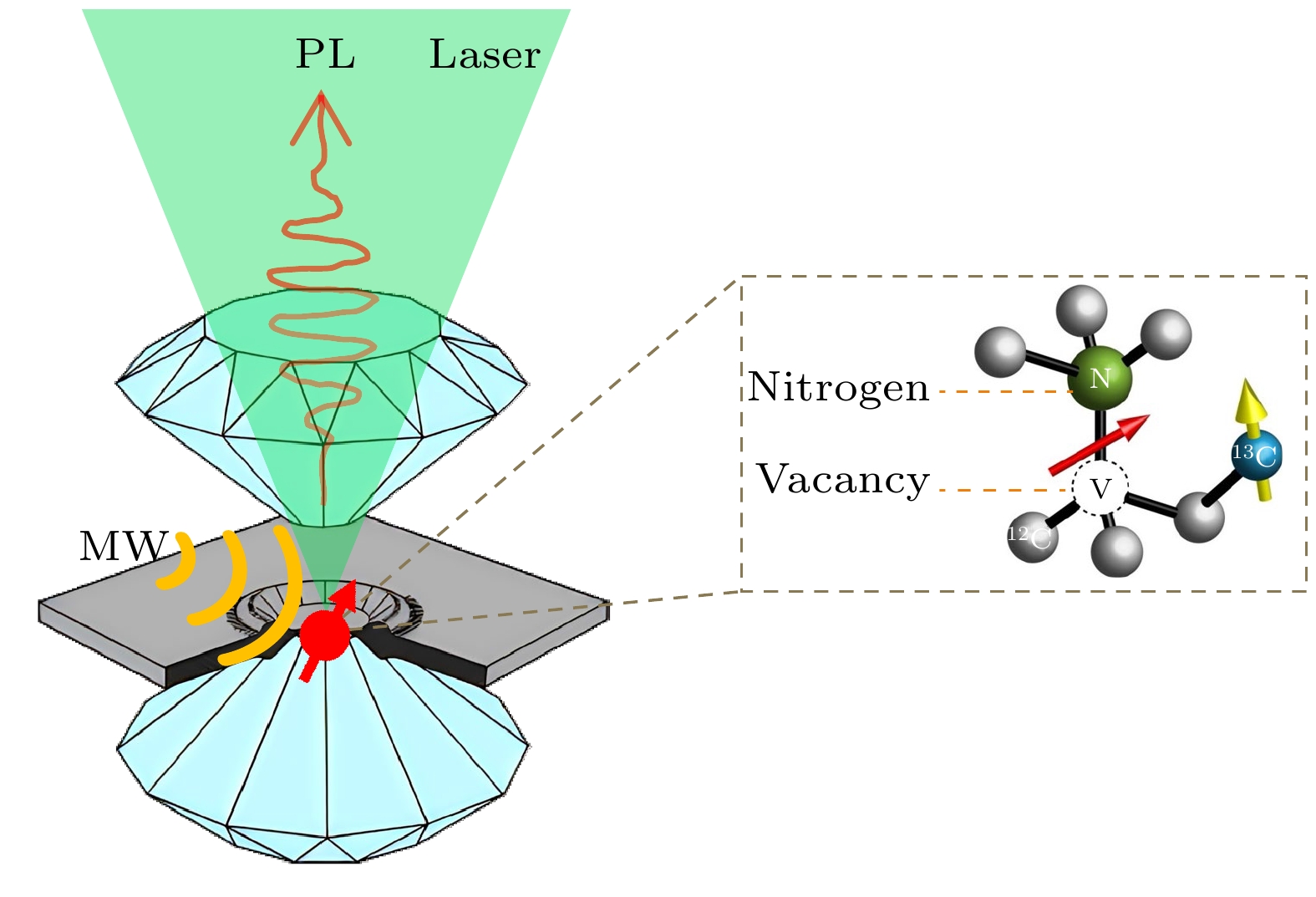
    • 金刚石对顶砧(diamond anvil cell, DAC)是实验室实现高压极端条件的核心装置. 如图1(a)所示, DAC由精密加工的金刚石、金属垫片、传压介质和机械加压系统等部件构成. 上下金刚石砧面和金属垫片中心的小孔构成了密闭的样品腔, 其内部填充传压介质和装载样品. 通过机械装置对金刚石施加压力, 可在样品位置实现超过兆巴高压的极端高压环境. 由于金刚石对可见光和X射线透明, 通过DAC窗口可以方便地开展X射线和光学测试.

      金刚石对顶砧技术的起源可追溯到1950年, Lawson等[30,31]提出透过金刚石可实现高压下的X射线衍射测量. 经过不断的改进, 金刚石对顶砧已成为高压研究的标志性工具. 20世纪80年代后, 随着激光加热、低温技术与同步辐射光源的发展, DAC实现了更宽温度范围(数千K)和更精准的物性测量. 在凝聚态物理和材料科学中, DAC被广泛应用于探索物质在极端条件下的相变行为, 如高压超导体的发现、金属氢的实验探索、地球内部矿物相变模拟等. DAC独特的高压调控能力为揭示材料性质、设计功能材料提供了不可替代的实验平台, 极大推动了高压物理、行星科学及材料科学等领域的发展.

      • 2.2.   金刚石NV中心量子传感

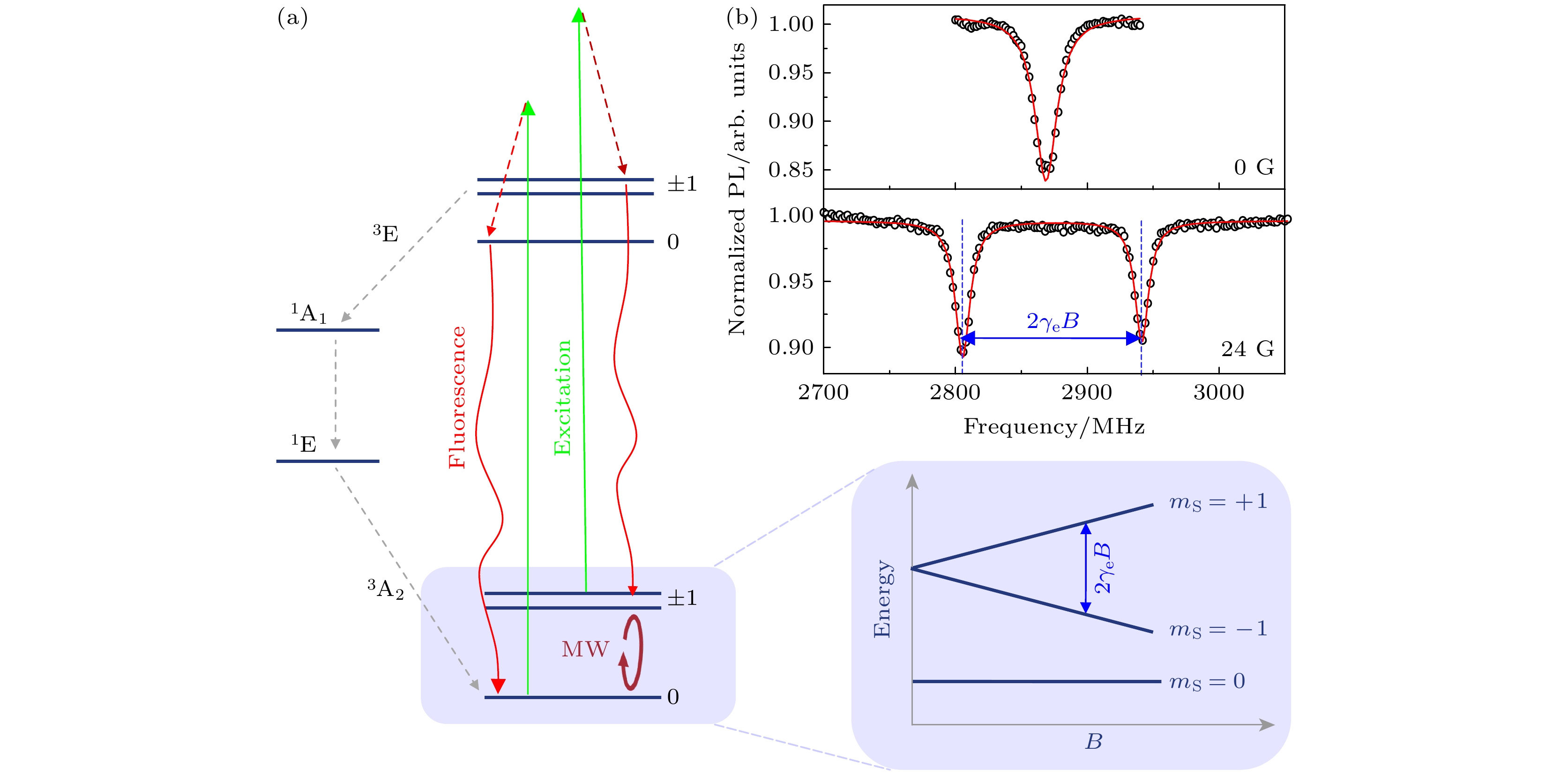
    • 1997年, Gruber等[32]用共聚焦显微成像分辨出了单个金刚石NV中心, 提出NV中心自旋可以作为量子比特的物理载体. 经过近30年的发展, 金刚石NV中心在量子计算、量子网络、量子传感等方向展现出极大的应用潜力, 这与NV中心独特的自旋和光学性质密切相关[33]. 如图2所示, 金刚石NV中心基态是自旋三重态($ S=1 $的电子自旋), 一般将量子比特或量子传感器的工作能级选定在基态$ {|m}_{{\mathrm{s}}}=0, \pm 1\rangle $上. 为了实现NV中心自旋状态的极化, 实验上通常会施加532 nm的激光脉冲. 在被激光激发后, $ {|m}_{{\mathrm{s}}}=0\rangle $的自旋状态会辐射荧光光子后返回基态; 而$ {|m}_{{\mathrm{s}}}=\pm 1\rangle $的自旋状态有更大概率通过自旋单态路径回到$ {|m}_{{\mathrm{s}}}=0\rangle $的状态. 仅需数微秒时间NV中心自旋就被极化到$ {m}_{{\mathrm{s}}}=0 $的状态. 该过程也提供了读出NV自旋状态的高效便捷机制——激光激发下, $ {|m}_{{\mathrm{s}}}=0\rangle $的状态发光较强, 为“亮态”; 而$ {|m}_{{\mathrm{s}}}=\pm 1\rangle $态因其经历的自旋单态跃迁过程在可见光区没有辐射, 对应的发光较弱, 为“暗态”. 于是, 通过测量NV中心的荧光强度就可以判断其所处的自旋状态.

      下面介绍金刚石NV中心量子传感的基本原理. 作为固体晶格中的一个缺陷自旋, NV中心自旋总在不断进动中, 其进动频率受到所处位置的晶格场、外加磁场和电场等因素的共同影响. 由于待测外场会影响NV中心进动频率, 而该频率可通过光探磁共振(optically detected magnetic resonance, ODMR)方法准确地测量出来[19,32]. 以磁场探测为例, 在室温常压下, NV中心基态$ {|m}_{{\mathrm{s}}}=0\rangle $和$ {|m}_{{\mathrm{s}}}=\pm 1\rangle $之间存在$ D=2.87 $GHz的零场劈裂. 在外加磁场$ \boldsymbol{B} $下, 其基态哈密顿量为: $ \boldsymbol{H}=hD{S}_{z}^{2}+ g{\mu }_{{\mathrm{B}}}\boldsymbol{B}\cdot \boldsymbol{S} $, 其中$ \boldsymbol{S}=({S}_{x}, {S}_{y}, {S}_{z}) $代表NV电子自旋算符, $ h $为普朗克常数, $ {\mu }_{{\mathrm{B}}} $为玻尔兹曼因子; 注意上述哈密顿量没有考虑电场、压强等参数耦合以及核自旋超精细相互作用. NV中心对外加磁场的响应体现在$ \boldsymbol{B}\cdot \boldsymbol{S} $一项上, 也就是塞曼效应(Zeeman effect). 在具体实验中, 一般通过记录NV中心荧光强度随微波频率的变化来获得光探磁共振谱线, 如图2(b)所示. 在零场时, $ {|m}_{{\mathrm{s}}}=\pm 1\rangle $对应的跃 迁频率简并, 只在2.87 GHz位置有一个共振谷; 若施加一个外磁场, $ {|m}_{{\mathrm{s}}}=+1\rangle $和$ |{m}_{{\mathrm{s}}}=-1\rangle $对应的跃迁频率出现了$ 2 g{\mu }_{{\mathrm{B}}}B $的差异, 反映在ODMR谱线的双峰劈裂特征上. 通过实验测量和分析ODMR谱共振峰位, 即可获得NV中心所处位置的磁场信息. 需要说明的是, 除了直接测量ODMR谱, 还可以通过脉冲调控, 磁场梯度等技术实现更丰富的自旋磁共振测量[19,29].

      • 2.3.   量子传感与金刚石对顶砧的结合

    • 通过上面讨论可知, 金刚石NV中心量子传感的实验实现需要激光激发、微波调控、荧光收集3个基本条件, 分别对应NV自旋量子态的极化、操控和读出3个环节. 考虑与金刚石对顶砧技术的结合: 激光激发和荧光探测均可通过透明的金刚石窗口实现, 如图1所示. 与常压下金刚石NV中心光探磁共振实验相比, 由于金刚石对顶砧自身的厚度和高折射率, 透过对顶砧进行NV中心的光学激发和探测效率显著降低. 为了缩短信号采集时间和提升信噪比, 高压下的金刚石NV中心量子调控实验均使用了集群NV中心. 微波调控方面, 可以通过对顶砧砧面上布置微波天线来施加, 一般使用铂或金等金属作为微波天线. 考虑到金属垫片一般为金属导电材质, 需要做好微波天线和垫片之间的绝缘.

      目前有两种方法可将NV中心引入金刚石对顶砧中. 其一是使用透明无色心的金刚石对顶砧, 然后将包含NV中心的金刚石(微米颗粒、纳米颗粒、以及块材金刚石)布置在传压介质中[11,34-37]. 该方法不需要提前处理金刚石对顶砧, 工艺相对简单; 由于金刚石颗粒完全包裹在传压介质中, 可实现相对较好的静水压条件, 同时能尽量靠近待测样品, 获得较强信号. 该方法的缺点是NV中心的分布和取向难以控制, 不利于实现待测物理量的空间成像. 另外, 在接近100 GPa的高压区间, 金刚石颗粒中的NV中心荧光大幅较低, ODMR谱线展宽和零场劈裂明显增加, 详见下文讨论.

      引入NV中心的另外一种方法是直接在金刚石砧面上进行离子注入和高温退火[12-14,38-40]. 离子注入可以在金刚石中引入空位及氮原子, 随后的高温退火(大于600 ℃)可以让晶格中的空位移动, 与氮原子结合形成稳定的NV中心结构[41]. 通过控制注入离子的能量和剂量, 可获得不同深度和密度的金刚石NV中心. 该方法引入的NV中心具有取向确定, 分布均匀等优势, 更适于进行砧面上物理场的空间成像. 需要说明的是, 金刚石对顶砧的切割方式会显著地影响其表面的NV中心的光学和自旋性质; 对于较高压强下的实验, 使用(111)切割的金刚石对顶砧可以实现较高的ODMR对比度及探测灵敏度, 详见下文讨论.

    3.   高压极端条件对色心自旋和光学性质的调控

    • 为了更好地理解和应用高压极端条件下的金刚石NV中心量子传感, 首先需要掌握高压条件对金刚石NV中心自身性质的调控规律. 本节将梳理常压至140 GPa区间(目前最高工作压强下)金刚石NV中心光学和自旋状态随压强变化规律, 对比分析高压下影响NV中心测磁灵敏度的主要因素. 进一步地, 结合动态核自旋极化技术, 还将展示高压下14N核磁共振实验结果, 讨论电子自旋-核自旋超精细相互作用随压强变化规律.

      • 3.1.   高压极端条件对NV中心光学性质的影响

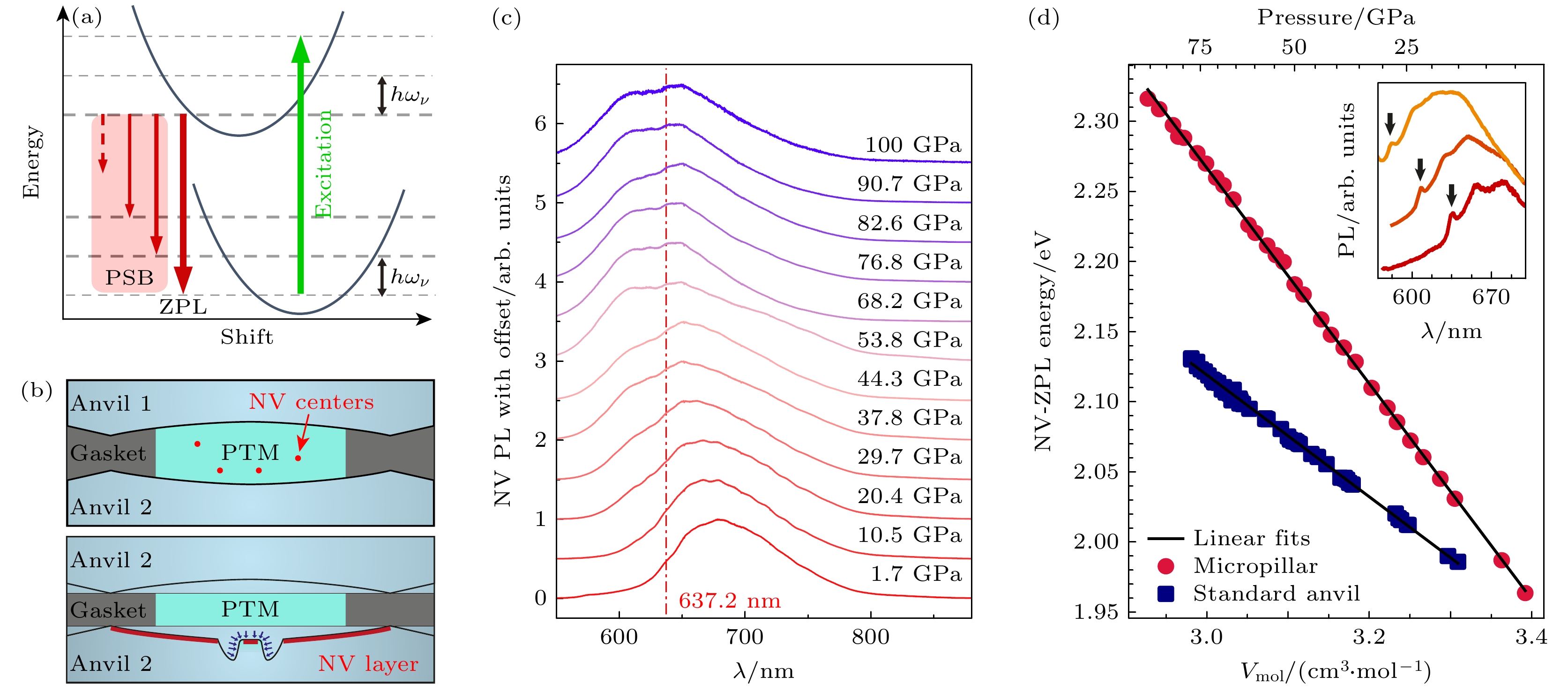
    • 2014年, Doherty等[34]首次报道了高压下金刚石NV中心光探磁共振实验结果, 该实验使用的NV中心来自CVD生长的单晶金刚石, 传压介质为NaCl和Ne. 在0—40 GPa范围内, 作者发现NV中心的零声子线(zero-phonon line, ZPL)随压强的增大而线性增大; 如果按照该斜率外推, 压强达到60 GPa时NV中心ZPL将达到2.3 eV, 实验所用的532 nm将不能激发NV中心. 如图3(a)所示, ZPL代表了NV中心激发态到基态的直接跃迁频率(无声子参与的辐射过程), ZPL的移动反映了压强对NV中心能级结构的影响. 随后, Lyapin等[42]在80 K低温测量了常压至51.7 GPa范围内的NV中心ZPL, 实验使用了He作为传压介质, 结果显示在高压区间NV中心ZPL随压强的变化趋缓, 而不是完全的线性规律.

      近年来, 金刚石NV中心的实验研究进入了兆巴区间. 通过将包含集群NV中心的微米金刚石装载在KBr传压介质中, Dai等[11]发现在接近140 GPa的高压下, 部分微米金刚石中NV中心仍然可以被532 nm激光所激发. 如图3(c)所示, 通过采集不同压强下的NV中心光致激发光谱, 观测到光谱随压强整体蓝移, 但移动速率在高压区明显减缓. 在另一个压强突破100 GPa的NV中心实验中, Hilberer 等[12]对比了静水压条件对NV光学性质的影响, 该实验使用的是对顶砧砧面注入产生的NV中. 如图3(b)所示, 为改善高压下NV中心所处位置的静水压条件, 他们利用聚焦离子束在DAC砧面上刻蚀了一个2 μm深的环形槽. 传压介质可以填充到这个槽中, 使得内部的金刚石NV中心获得更接近各向同性的压强. 图3(d)所示为在微结构内部和外部的NV中心ZPL随压强的变化规律. 可见, 处在更好静水压条件的NV中心可以工作到更高的压强; 另外, 加压方式也是影响NV中心ZPL随压强移动速率的重要因素. 需要注意的是, 该实验使用的金刚石砧面为(001)切割, 而金刚石切割方向也是影响NV中心工作压强的重要因素.

      • 3.2.   高压极端条件对NV中心自旋性质的影响

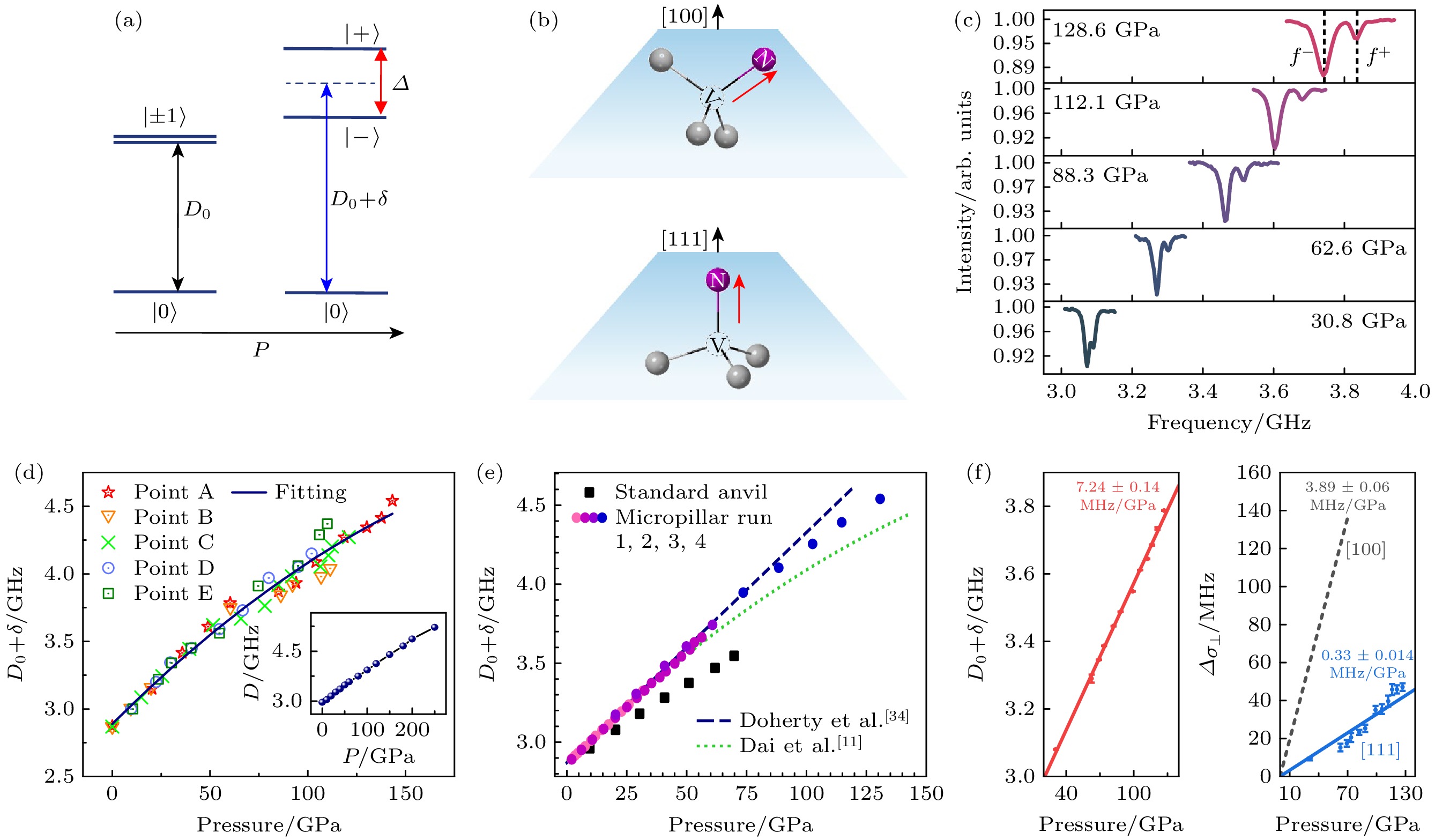
    • 接下来讨论压强对NV中心自旋能级的影响. 如图4(a), (b)所示, 考虑对顶砧高压环境下的单个金刚石NV中心, 压强将带来两方面的影响. 一方面, 各向同性的压力(理想的静水压条件), 或沿着NV中心量子化轴(金刚石[111]方向)施加的力, 会引起NV中心零场劈裂的移动, 实验表现为ODMR谱线中心频率的增大. 另一方面, 垂直于NV中心量子化轴的力, 会引起NV中心自旋状态的重组, 形成新的本征态, 实验表现为零场ODMR谱线的劈裂. 在实际的实验测量中, 通常激光光斑内有多个NV中心贡献荧光信号, 而不同NV中心所处位置的压强常常存在梯度, 且压强越高梯度越高[38], 这使得高压下的ODMR谱线出现压强梯度引起的额外展宽[11]. 图4(c)展示了不同压强下的金刚石NV中心零场ODMR[14], 随着压强的增大, 谱线中心峰位往高频移动, 谱线的劈裂逐渐增加, 共振谷的线宽也逐渐增大, 注意该实验使用了(111)切割砧面上的浅层NV中心.

      下面重点分析NV中心零场劈裂值$ D $随压强的变化规律. 对于包裹在KBr传压介质中的NV中心, 如图4(d)所示, 不同取向的NV中心零场劈裂随压强变化规律几乎一致, 可以用多项式公式来描述: $ D={D}_{0}+{A}_{1}P+{A}_{2}{P}^{2} $, 其中$ {D}_{0}=( $2.88±0.03) GHz, A1=(14.8±1.0) MHz/GPa, A2= (–27±7) kHz/GPa2 [11]. 对于对顶砧砧面上的浅层NV中心, 其零场劈裂的变化规律显著依赖于金刚石的切割方向: 对于(111)切割的金刚石, 实验给出NV中心零场劈裂随压强变化的斜率为(7.24±0.1) MHz/GPa [14]; 对于(001)切割的金刚石, 实验给出NV中心零场劈裂随压强变化斜率为(9.68±0.8) MHz/GPa[12]. 通过环形微槽填充传压介质来改善(001)切割砧面上NV中心压强环境后, $ D $值随压强变化斜率可增至(13.41±0.14) MHz/GPa, 接近包裹在传压介质中微米金刚石颗粒的实验结 果[12]. 值得一提的是, 金刚石NV中心零场劈裂随压强的变化规律提供了一种原位的、高空间分辨的(微米级)的压强标定方法.

      • 3.3.   高压极端条件对NV中心测磁灵敏度的影响

    • 下面主要分析高压条件对金刚石NV中心量子传感探测灵敏度的影响. 以磁场测量为例, 基于ODMR谱的磁场测量灵敏度估算公式为[19,29]

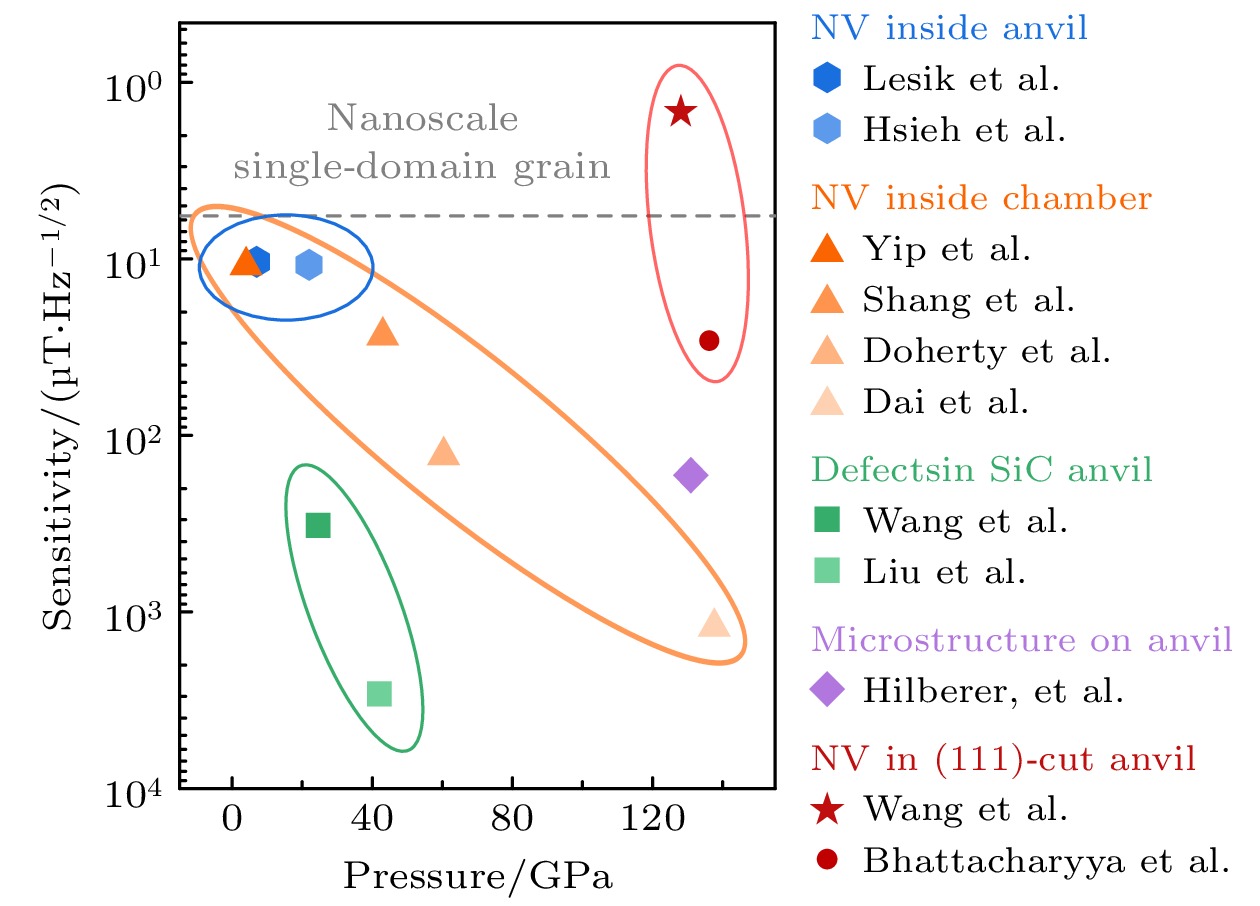
      其中$ g\approx 2.0 $为朗德因子, $ {\mu }_{{\mathrm{B}}} $为玻尔兹曼因子, $ h $ 为普朗克常数, 这三者均为常数; 与实验灵敏度直接相关的是实际探测到的荧光强度$ {L}_{0} $, ODMR谱线的线宽$ {{\Delta }}\nu $和对比度$ C $. 从量子精密测量灵敏度的角度来看, 高压极端条件赋予ODMR谱线的新特征主要是负面的. 首先, 非轴向压强带来的能级劈裂$ \varDelta $会降低NV中心在低场区间的测磁灵敏度, 只有在外加磁场较大(例如$ 2 g{\mu }_{{\mathrm{B}}}B\gg \varDelta $)时, NV自旋才能基本恢复塞曼效应的响应. 其次, 压强梯度会带来ODMR线宽增加$ {{\Delta }}\nu $和对比度$ C $的降低, 而两者都会降低NV中心量子传感的灵敏度. 第三, 金刚石压机结构的限制使得高压下荧光信号收集只能使用长工作距离和低数值孔径的物镜, 实际可收集的NV中心荧光强度$ {L}_{0} $相对于常压实验大幅降低. 另外, 上述效应会随着压强的进一步升高而愈发严重. 除了这些特征, 在一些实验中, 研究人员还观测到ODMR信号反转现象[12,13], 即共振频率不再是一个“谷”, 而是一个“峰”. 可见, 高压下金刚石NV中心的基本性质和调控规律还有很多值得深入研究的问题.

      总体来看, 在提升金刚石NV中心量子传感的工作压强的同时, 尽量减少或消除高压条件所带来的负面影响是金刚石量子传感的重要推进方向. 图5汇总了近期高压下金刚石NV中心量子传感的实验压强和测磁灵敏度[14](图中也包括SiC色心的高压实验结果). 可见, 通过将金刚石颗粒包裹在传压介质中, 利用相对较好的静水压环境可以实现高达140 GPa的ODMR测量, 但是压强梯度带来的线宽和荧光发光速率的降低使得对应实验的测磁灵敏度较低, 均在10 $ \text{μ}{\mathrm{T}}/\sqrt{{\mathrm{H}}{\mathrm{z}}} $以上, 且压强越高灵敏度越低. 对于(001)切割砧面上的金刚石NV中心, 目前实现的最高压强为130 GPa左右, 相应的灵敏度约为100 $ \text{μ}{\mathrm{T}}/\sqrt{{\mathrm{H}}{\mathrm{z}}} $ . 对于(111)切割砧面上的金刚石NV中心, 已实现的最高工作压强是近140 GPa, 同时其测磁灵敏度可达到$\text{μ}{\mathrm{T}}/\sqrt{{\mathrm{H}}{\mathrm{z}}} $量级. 该方案可以实现较好灵敏度的原因是高压下与金刚石(111)切割方向不匹配的NV中心不再发光(见图4(b) NV中心方向与金刚石切割方向示意图), 仅留下与加压方向取向一致的NV中心发光, 相应的ODMR谱线对比度大幅提升. 总体来看, 不断提升的工作压强和探测灵敏度为金刚石量子传感的应用奠定了坚实基础.

      • 3.4.   高压下的14N核磁共振

    • 相对于电子自旋, 核自旋的旋磁比弱3个数量级, 因此相同条件下核自旋具有更长的量子态相干时间; 同时, 对核自旋的操控也更加困难一些. 在金刚石中, 13C核自旋(自然丰度占比1.1%)和14N核自旋是最常见的核自旋. 借助光探磁共振技术, 可以实现NV中心近邻核自旋的相干操控, 为构筑高压下的量子传感提供了一个新的自由度. 本节讨论高压下NV中心14N核自旋的一种动态极化机制, 探索高压对核自旋超精细相互作用的影响[43].

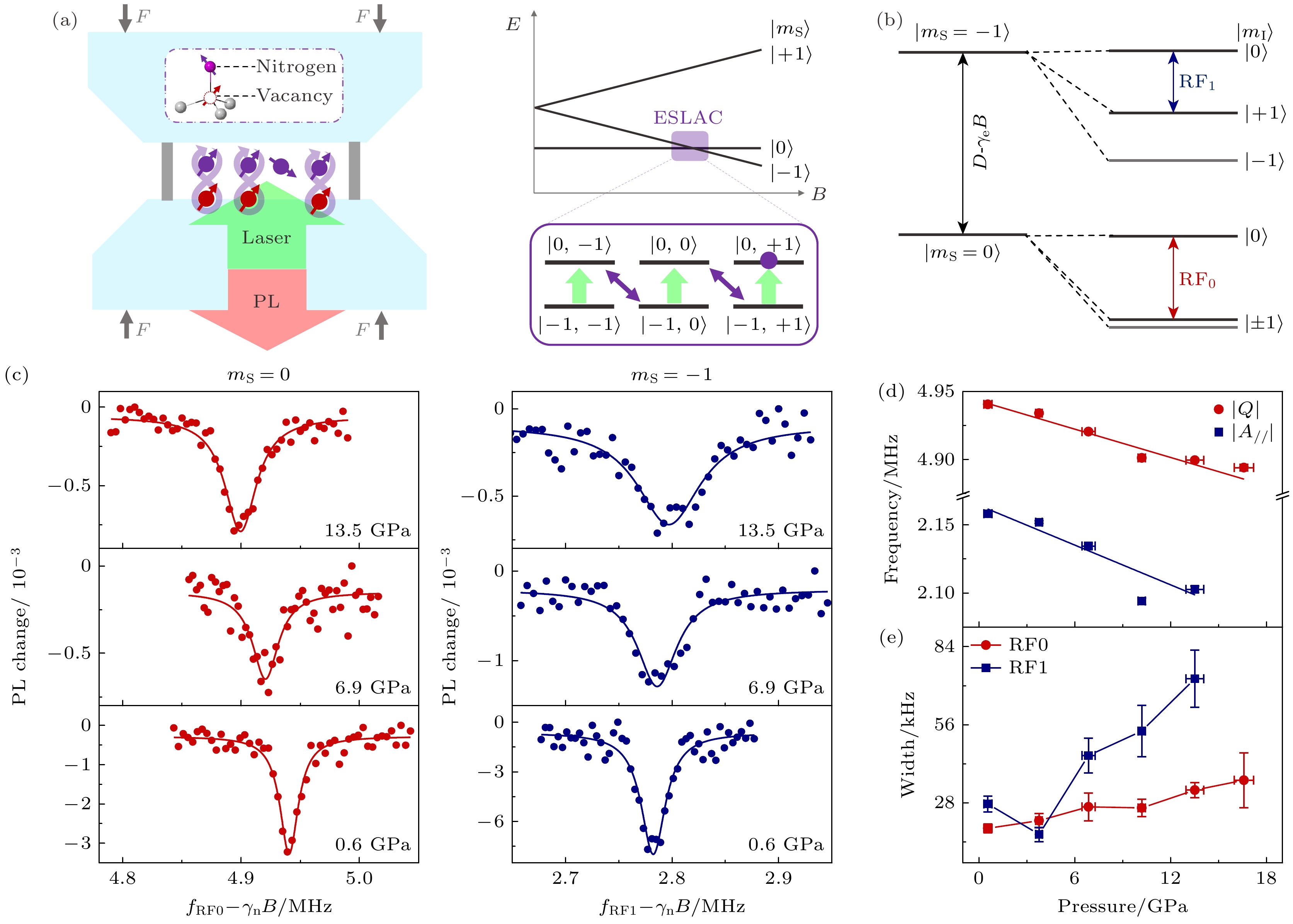
      在金刚石NV中心的激发态能级反交叉点(excited state level anti-crossing, ESLAC), 通过简单的光学脉冲即可实现高效的核自旋动态极化[44]. 操作之前, 处于热平衡态的14N核自旋几乎没有极化度, 3个状态上的布居数接近均等分布. 沿着NV轴方向施加约500 G (1 G=10–4 T)的磁场, 可将NV中心激发态能级移动到反交叉点附近, 此时NV中心激发态$ |{m}_{{\mathrm{s}}}=0\rangle $和$ |{m}_{{\mathrm{s}}}=-1\rangle $能级几乎重合, 使$ |0, -1\rangle \iff | -{\mathrm{1, 0}}\rangle $和$ |{\mathrm{0, 0}}\rangle \iff | -1, +1\rangle $(其中第1位代表电子自旋状态, 第2位代表核自旋状态, 下同)的跃迁较容易发生. 如果此时施加激光脉冲, 可将NV中心电子自旋和14N核自旋构成的复合系统直接极化到$ |0, +1\rangle $, 如图6(a)所示[43]. 该过程也提供了14N核自旋状态的光学读出方法. 另外, 除了基于ESLAC的极化方法, 还有一些其他方法可以实现NV中心近邻核自旋的动态极化, 感兴趣的读者可以通过相关文献进一步了解[45,46].

      对14N核自旋的操控需要施加与其频率共振的射频(radio-frequency, RF)脉冲. 图6(b)所示为电子自旋和核自旋的复合系统的能级结构. 由于NV中心电子自旋和14N核自旋的耦合较强, 电子自旋的状态将显著地影响核自旋的共振频率. 从极化获得的$ |0, +1\rangle $态出发, 仅需一个射频脉冲即可实现$ |0, +1\rangle\iff |{\mathrm{0, 0}}\rangle $的核自旋翻转, 我们将该操作记作RF0, 其频率为$ {f}_{{\mathrm{R}}{\mathrm{F}}0}=Q+{\gamma }_{n}B $, 其中$ Q $为核自旋的四极矩项, $ {\gamma }_{n}=0.3077 $ kHz/G是14N核的旋磁比. 我们也可以先施加一个微波π脉冲, 将复合系统制备到$ |-1, +1\rangle $再进行核自旋操控. 此时电子自旋处在$ |{m}_{{\mathrm{s}}}=-1\rangle $的状态, 14N核自旋在对应子空间的跃迁频率为$ {f}_{{\mathrm{R}}{\mathrm{F}}1}=Q+{A}_{/ /}+{\gamma }_{n}B $, 其中$ {A}_{/ /} $代表了电子自旋和核自旋的超精细相互作用. 注意表达式中$ Q $和$ {A}_{/ / } $与NV中心所处位置的压强和温度等参数有关[43].

      图6(c), (d)所示为高压下金刚石NV中心14N核自旋的核磁共振谱. 实验使用的是NV中心来自粒径约1 μm的微米金刚石, 传压介质为KBr, 外加磁场为460 G (1 G =10–4 T), 且沿着选定NV中心的量子化轴方向施加. 在较低的压强下, 14N核自旋的磁共振信号和常压结果类似, 对于NV中心在$ |{m}_{{\mathrm{s}}}=0\rangle $和$ |{m}_{{\mathrm{s}}}=-1\rangle $的两个状态, 核自旋的共振频率分别为4.96 MHz和2.16 MHz. 随着压强的增大, 核自旋磁共振谱线出现明显的左移现象, 对应的移动速率为$ {\mathrm{d}}Q/{\mathrm{d}}P=(3.5\pm 0.4) $ kHz/GPa和$ {\mathrm{d}}{A}_{/ /}/{\mathrm{d}}P=(4.9\pm 1.1) $ kHz/GPa. 核自旋的四极矩项与其所在位置的电场梯度有关, 而超精细相互作用同时受到偶极相互作用和费米接触作用(Fermi contact interaction)的影响. 两者的绝对值都随着压强的增大而减小, 推测是因为加压使得NV中心电子波函数一定程度远离了14N原子核. 除了中心频率的移动, 14N核自旋磁共振信号随压强增加还出现了明显的展宽, 如图6(e)所示, 这与电子自旋磁共振谱线的展宽原因相同, 都是集群NV中心所处位置的压强梯度引起的[43].

      在获得14N核自旋磁共振频率之后, 可以进一步实现高压下的核自旋量子态的相干操控和探索其自旋相干性质. 基于自由感应衰减(free induction decay, FID) 序列, 实验测得微米金刚石14N核自旋的退相位时间$ {T}_{\rm 2N}^{*} $= (70 ± 10) μs. 该值与实验获得的近30 kHz NMR谱线宽度基本吻合, 但与室温下高纯单晶中毫秒级的退相位时间相比明显偏短. 通过测量同样条件下的NV中心电子自旋弛豫时间$ {T}_{1{\mathrm{e}}} $= (354 ± 31) μs可知, 核自旋的相干性质受限于电子自旋的$ {T}_{1{\mathrm{e}}} $. 通过使用自旋环境更加纯净的金刚石单晶, 有望大幅提升核自旋的相干时间.

      总体来看, 高压条件增大了核自旋操控的技术难度, 改变了磁共振频率, 但工作原理和操控方法与常压条件并无不同. 沿着该方向, 后续亟需探索的问题是如何利用NV中心进行金刚石体外核自旋的极化和探测, 使得高压下的核磁共振适用于更普适的样品, 满足更多的测试需求[9].

      • 3.5.   碳化硅和六方氮化硼中色心的高压调控

    • 前文讨论集中在金刚石NV中心, 但所涉及的高压下色心自旋量子调控的物理原理和实验技术对于其他固态色心也有参考意义. 不同的材料体系和色心结构在实际应用中具备其特定的优势[47], 它们与高压技术的结合带来了更多的机会.

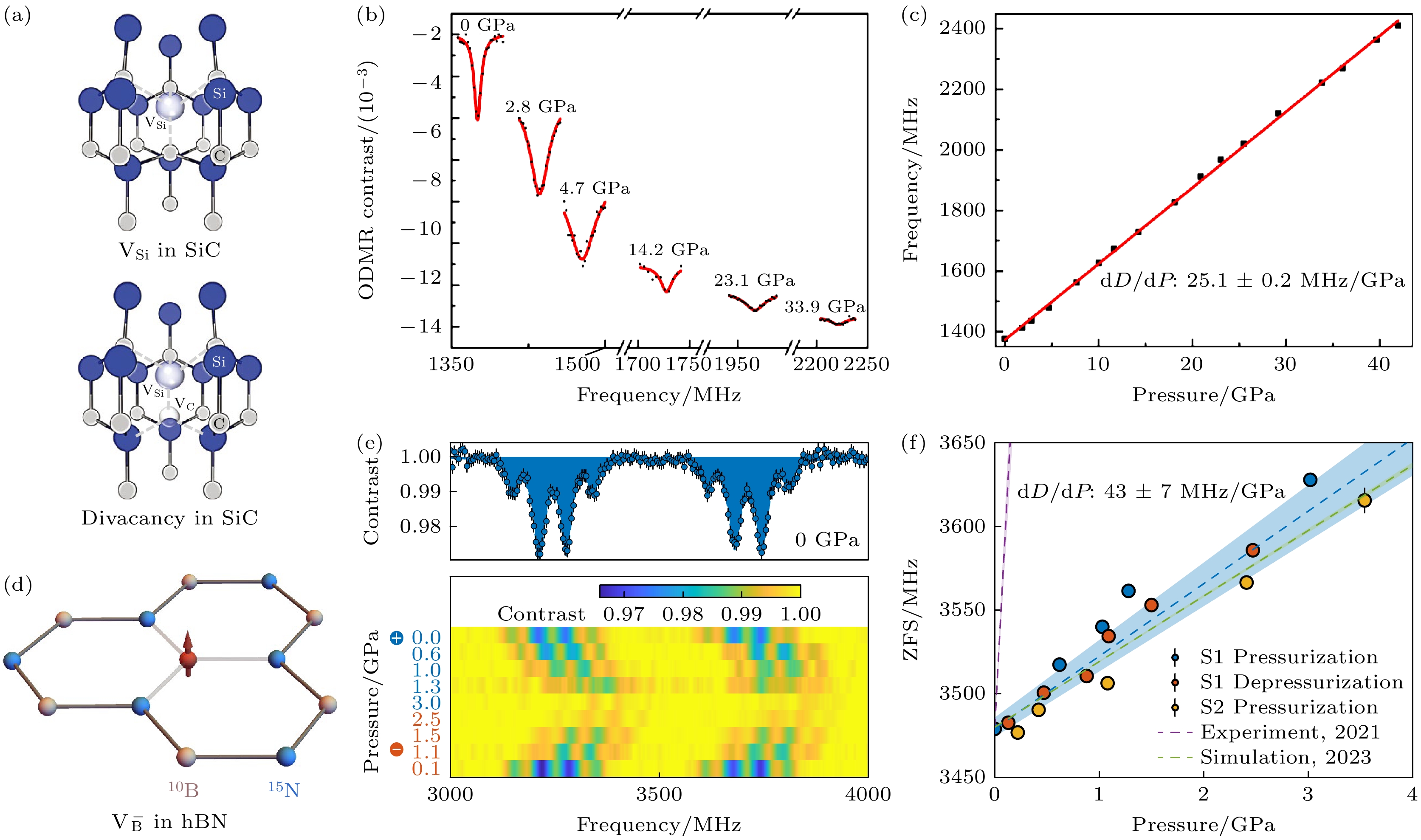
      碳化硅具备类似金刚石的物理性质, 也可以用于制备高压对顶砧, 但SiC在晶体尺寸、微加工难度、使用成本等方面优于金刚石. 2023年, Wang等[48]实现了4H-SiC中硅空位($ {{\mathrm{V}}}_{{\mathrm{S}}{\mathrm{i}}} $, 见图7(a))色心的高压调控. 该实验直接使用了SiC对顶砧砧面上的浅层色心. 在0—25 GPa的压强范围内, 加压引起的$ {{\mathrm{V}}}_{{\mathrm{S}}{\mathrm{i}}} $零场劈裂移动速率dD/dP为(0.31 ± 0.1) MHz/GPa, 该值仅为金刚石NV中心相应结果的1/50; 同期他们还研究了高压对SiC双空位(di-vacancy) 色心PL5和PL6的调控规律[49], 对应的dD/dP分别为(25.1 ± 0.2) MHz/GPa和(11.8 ± 0.3) MHz/GPa. 如图7所示, 这些实验都发现随着压强的增大, SiC中色心ODMR信号出现明显的线宽增大和对比度降低等现象, 这与金刚石NV中心高压下的实验现象类似.

      另一类备受关注的体系是六方氮化硼(hBN)中的色心. 由于hBN的二维层状结构特点, 易于转移, 可与二维材料、薄膜材料以及各种样品表面方便地结合. hBN中研究较多的色心结构是带负电的硼空位($ {{\mathrm{V}}}_{{\mathrm{B}}}^{-} $), 具有类似于金刚石NV中心的能级结构. 近期, He等[50]报道了高压下的hBN-$ {{\mathrm{V}}}_{{\mathrm{B}}}^{-} $色心高压调控结果. 如图7(e), (f)所示, 该色心零场劈裂随压强移动速率为(43 ± 0.3) MHz/GPa, 接近金刚石NV中心的3倍, 有望用于实现灵敏的原位压强测量.

    4.   高压下金刚石NV中心量子传感应用进展

    • 本节通过一些具体的应用案例介绍高压极端条件下金刚石量子传感实验研究进展. 由于具备微米级的空间分布率和极高的探测灵敏度, 特别是和金刚石对顶砧高压技术的完美兼容特点, 使得基于NV中心的量子传感在高压物性测量方面获得了越来越多的关注, 近期在高压下微区磁测量和磁成像, 超导迈斯纳效应测量等方面取得了系列突破.

      • 4.1.   高压下的磁测量和磁成像

    • 作为一个自旋缺陷, 金刚石NV中心是天然的磁传感器, 高压下的磁测量也是其受到最多关注的应用方向. 在原理验证阶段, 国际上多个研究组进行了压强调控的磁相变过程研究. 基于微米金刚石中的NV中心, Shang等[35]测量了铷铁硼(Nd2Fe14B)磁性颗粒的压强诱导磁相变过程. 常压下铷铁硼处于铁磁态, 随着压强的增大, 其磁性在6 GPa附近开始降低, 并在10 GPa以上完全进入顺磁状态. 基于DAC砧面上的浅层NV中心和宽场成像技术, Lesik等[39]测量了直径约5 μm的单质铁颗粒的近邻磁场分布, 实验获得了0—30 GPa范围内其磁性随压强的变化规律, 观测到压强带来的单质铁的$ \alpha \leftrightarrow \varepsilon $相变过程. Hsieh等[38]也用砧面浅层NV中心, 结合共聚焦显微成像技术, 研究了单质铁颗粒的压强调控相变过程, 实验给出相变临界压强为13.6 GPa; 在同一个工作中, 他们还表征了单质钆(Gd)的P-T相图, 展示了金刚石NV中心量子传感在磁噪音谱表征方面的独特优势. Shelton等[37]采用集群纳米金刚石中NV中心为传感器, 实验测量了11.4 μm的单质铁颗粒随压强的磁相变过程. Zhong等[51]测量了DAC内电流引起的磁场分布.

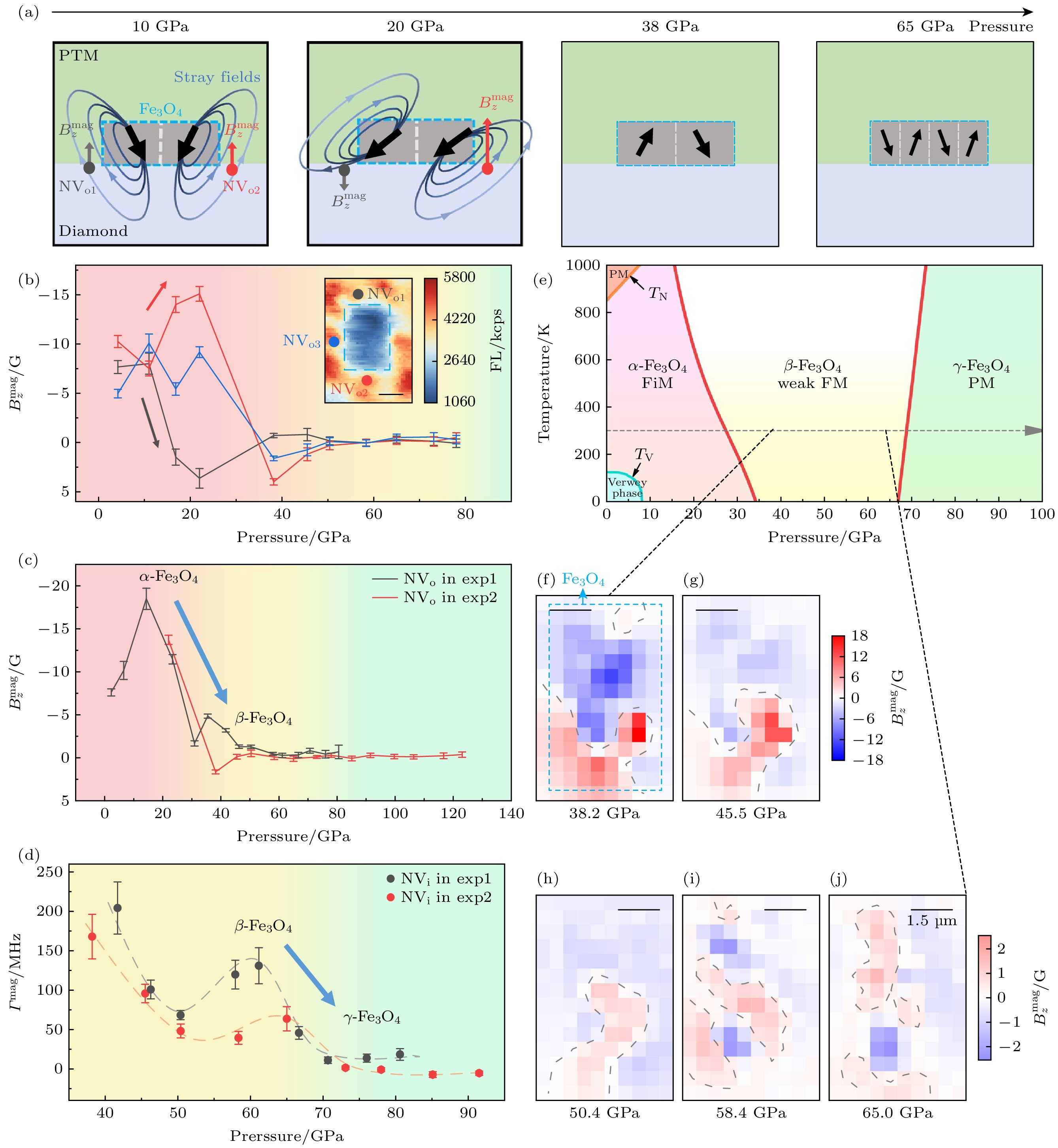
      近期, 金刚石NV中心高压磁测量进入了兆巴压强区间, 进一步拓展了该技术的应用范围. 基于(111)切割金刚石对顶砧面上的浅层NV中心, Wang等[14]在近130 GPa的压强下实现了约1 $ \text{μ}{\mathrm{T}}/\sqrt{{\mathrm{H}}{\mathrm{z}}} $的测磁灵敏度, 并基于该技术研究了磁铁矿颗粒(主要成分为Fe3O4)在兆巴高压下的磁性. 作为地壳中分布广泛且磁性稳定的矿物, 磁铁矿的磁性表征对古地磁学和地球磁场演化等问题具有重要意义, 而高压极端条件如何调控其磁性是一个关键环节. 该实验在室温进行, 粒径约 5 μm的Fe3O4颗粒被装载在金刚石对顶砧中, 实验使用的传压介质为KBr. 通过砧面上不同位置NV中心的逐点ODMR测量, 可在高压下直接获得样品内部磁畴分布情况, 如图8(f)—(j)所示.

      进一步地, 通过不同压强下的磁性测量, 实验观测到了随着压强的增大, 磁铁矿从亚铁磁性(α-Fe3O4)到弱铁磁性(β-Fe3O4), 最终到顺磁性(γ-Fe3O4)的磁性转变过程, 两次相变先后发生在近30 GPa和70 GPa. 通过样品外侧的近邻NV中心, 可以测量样品的整体磁性, 图8(c)所示为磁铁矿宏观磁性随压强演化规律. 对于样品正下方的NV中心, 由于受到样品产生的磁场梯度影响, 其ODMR谱线在低压区(α-Fe3O4)几乎没有对比度; 随着样品进入磁性较弱的β-Fe3O4相, 样品正下方的NV中心才给出一定对比度的ODMR谱, 同时谱线展现出较大的展宽. 随着压强的进一步增大, ODMR谱线展宽逐渐被抑制, 反映出样品磁性和局部磁场梯度的逐渐消失, 如图8(d)所示. 在更高的压强下(> 70 GPa), ODMR谱的劈裂和线宽都显示出样品不再具备宏观磁性. 这些结果澄清了关于β-Fe3O4低压强区间(< 40 GPa)磁性状态的争议, 同时排除了室温下从65 GPa—120 GPa压力范围内磁性恢复的可能性.

      • 4.2.   高压下氢化物超导迈斯纳效应测量

    • 高压极端条件在超导物性和超导机理研究中被广泛地使用. 压强可以改变晶体结构, 影响电子结构, 增强电子-声子耦合或电子关联效应, 从而提升超导临界温度TC. 其中一个备受关注的体系是高压下的富氢化合物: 2015年, Drozdov等[2]发现H3S在近150 GPa的高压下其超导转变温度可达203 K, 2019年又报道了LaH10样品在170 GPa高压下TC高达250 K, 已经接近室温[3,4]. 随后, 高压下的YH9, CeH6等更多氢化物超导体被陆续发现[52,53].

      为了验证超导现象, 需要零电阻和完全抗磁性(迈斯纳效应)两个独立的实验证据. 上文提到的高压下的超导体, 都有较明确的零电阻实验 现象, 而超导迈斯纳效应的实验证据却相对缺乏. 以实现近室温超导的LaH10体系为例[3], 在Nature期刊同期刊发的评述文章[54]写到“最后一个判据, 迈斯纳效应的观测, 目前尚未实现, 因为样品太小” (原文为: The final criterion — observation of the Meissner effect — is currently unattainable because the samples are too small). 在兆巴高压下, 典型的样品尺寸仅有数10 μm, 常用的交流磁化率方法由于探测灵敏度较低, 难以在超高压下获得可靠的实验信号. 基于SQUID的测量方法具有极高的测磁灵敏度, 但只能对压机整体进行测量, 导致金刚石对顶砧组件贡献的信号远大于高压腔内微小样品的信号. 这些技术挑战使得高压富氢体系的超导抗磁结果备受争议.

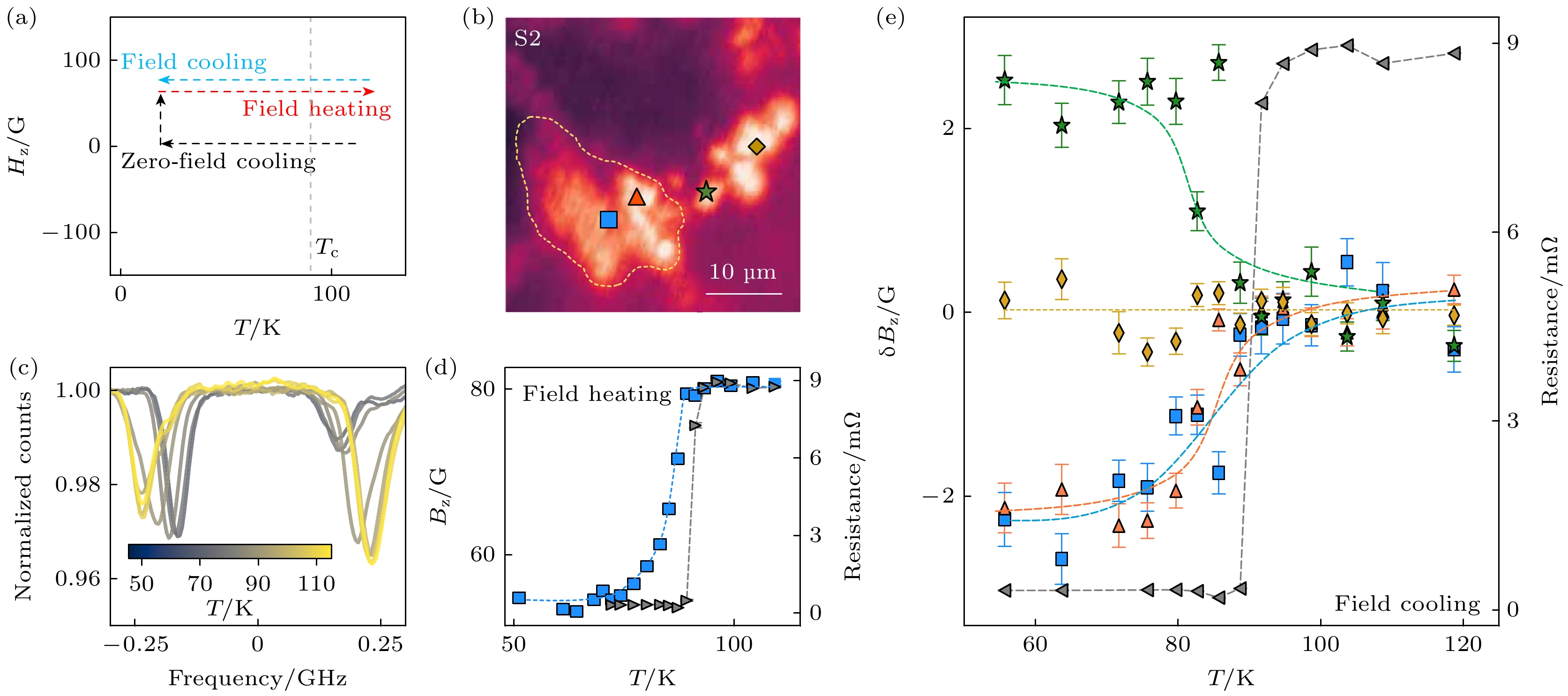
      基于金刚石NV中心的量子传感为高压下氢化物超导抗磁研究提供了重要的解决方案. 在原理验证阶段, 该技术被用于观测高压下MgB2 (7 GPa)和BaFe2(As0.59P0.41)2 (0—3 GPa)样品的超导抗磁现象测量[36,39]. 最近, Bhattacharyya等[13]报道了CeH9超导迈斯纳效应的直接观测结果. 实验使用了(111)切割金刚石砧面上的浅层NV中心作为高压极端条件下的原位传感器, NV中心的深度为50 nm. CeH9样品由氨硼烷(ammonia borane, NH3BH3)和铈单质(Ce, 纯度99.8%)在高压下激光加热合成, 对应的反应过程为$ {\mathrm{C}}{\mathrm{e}}+{{\mathrm{N}}{\mathrm{H}}}_{3}{{\mathrm{B}}{\mathrm{H}}}_{3}\to {{\mathrm{C}}{\mathrm{e}}{\mathrm{H}}}_{x}+c{\mathrm{B}}{\mathrm{N}} $. 图9(b)所示为其中一个样品的荧光扫描图, 白色虚线标记了高压腔内样品边界. 为表征样品的超导抗磁行为, 作者首先使用了零场冷-场热的测试序列, 如图9(a)所示. 在零场下将样品冷却到TC (约90 K)以下, 然后加上偏置磁场, 对空间上不同位置的NV中心进行ODMR测量以获得样品近邻区域的磁场分布. 图9(c)的ODMR谱线来自图9(b)中的蓝色标记点, 在TC以下温度, 该位置的磁场明显小于外加偏置场的大小; 随着温度的升高, NV中心感受到局部磁场逐渐增至和外加偏置场一样, 这说明测试位置的样品展现出了明显的抗磁行为. 同时, 通过对该样品进行电阻测量, 发现样品抗磁行为出现温度(71 K)低于电阻转变为零温度, 见图9(d)对比.

      为定量表征样品的抗磁行为, 可以定义参数$ s=\Delta {B}_{z}/\Delta {H}_{z} $, 即NV中心感受到的局部磁场和外加磁场的比值, $ s < 1 $说明存在抗磁现象. 实验测得的最小$ s $值为0.52, 显示出极强的抗磁性质. 进一步, 研究人员还进行了场冷过程的局部磁场测量, 见图9(e), 在样品内部观测到了相对弱一些的抗磁行为, 同时在样品边界上观测到局部磁场增加的现象, 这与场冷过程中超导样品将磁感线排除其体外的图像一致. 在场冷后去掉外磁场, 样品上部分位置表现出额外的剩余磁场, 推测是样品中存在磁通钉扎行为, 作者通过改变外场大小和进一步的变温过程证实了该图像[13].

      • 4.3.   高压下镍氧化物超导迈斯纳效应测量

    • 最近另一个备受关注的超导体系是Ruddlesden-Popper (R-P)系列的Lan+1NinO3n+1 (n = 1, 2, 3, ···, ∞)镍氧化物. 2023年, Sun等[55]报道La3Ni2O7单晶在14 GPa高压下出现TC约80 K的高温超导电性, 引起了国内外研究人员的广泛关注. 尽管该系列样品的超导状态不需要极端高压条件, 但相关样品存在化学组分不均匀、内顶角氧空位以及单层和三层R-P相共存等特点, 这使得该体系超导迈斯纳效应的实验测量较为挑战[56]. 例如, 基于交流磁化率测量方式, Zhou等[57]发现La3Ni2O7样品中超导体积占比不足1%.

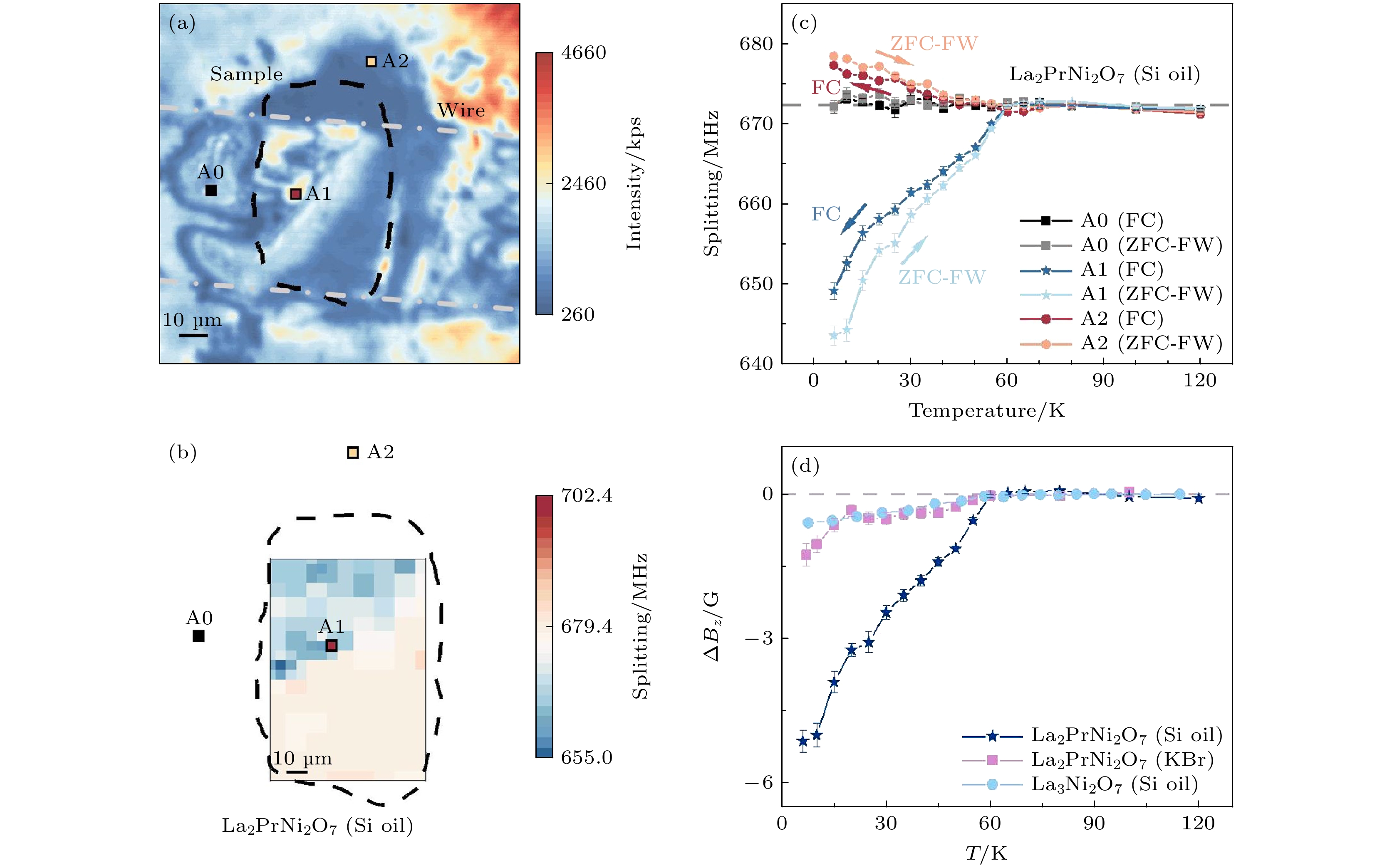
      近期, 通过采用离子半径较小的Pr部分替代La来抑制La3Ni2O7中其他R-P相交织共生问题, Wang等[56]成功制备了纯度较高的La2PrNi2O7多晶样品, 在近20 GPa的压强下观测到TC约60 K超导现象. 随后, Wen等[40]基于NV中心对该样品进行了高压下超导迈斯纳效应的直接测量. 实验使用了(111)切割金刚石对顶砧内的浅层NV中心, 两次实验分别使用了硅油和KBr为传压介质. 图10(a)展示了使用硅油作为传压介质时对顶砧内La2PrNi2O7样品的共聚焦荧光扫描图, 其 中黑色虚线描出了样品边界位置. 在对样品进行 零场降温后, 通过施加120 G的偏置磁场并对样品区域进行逐点ODMR测量, 发现样品上较大区域(图10(b)的蓝色区域)存在明显的抗磁行为, 即这些位置的NV中心感受到的局部磁场均小 于外加偏置场. 接下来, 通过监测样品上典型位 置的磁场随温度变温规律, 进一步确定了超导抗 磁现象. 如图10(c)所示, A1点位于样品上, 低温下出现典型的抗磁信号; A2点在样品边界, 在低温下表现出局部磁场增强; A0点在样品外, 低温下其局部磁场和外加偏置场一致. 随着温度的升高, 上述位置感受到的抗磁(或局部磁场增大)均逐渐 减小, 到60 K时所有位置都感受到一样的磁场. 另外, 在相同磁场下进行场冷实验, 这几个位置也观测到相应的局部磁场变化, 但抗磁幅度略有 减弱.

      研究团队对比了KBr和硅油两种传压介质对La2PrNi2O7样品抗磁信号的影响. 硅油在样品装载时及低压区为液态, 能提供更好的静水压环境. 作为固体传压介质, KBr提供的静水压条件相对差一些. 传压介质引起的压强条件区别也体现在了La2PrNi2O7样品的抗磁信号上. 一方面, KBr作为传压介质样品中出现抗磁的相对面积更小(有抗磁信号面积和所有测试面积之比). 另一方面, 在相同的偏置磁场(120 G)下, 比较两个样品中实验测得的最强抗磁信号, 硅油中的样品抗磁幅度是KBr中样品信号幅度2倍以上, 见图10(d)所示. 这些结果显示了静水压条件有利于实现镍氧化物超导抗磁现象.

      实验还研究了硅油中的La3Ni2O7样品的抗磁行为. 与前面的实验流程一致, 在近20 GPa的压强下, 通过对样品上不同位置进行零场冷-加场测试, 发现一些局部磁场减弱的信号. 结合场冷和场热数据, 实验进一步确定了信号来自样品超导抗磁行为. 值得说明的是, La3Ni2O7样品的抗磁信号较弱, 在120 G的偏置磁场下, 其抗磁信号带来的NV中心ODMR谱线变化, 与空间上不同位置压强梯度带来的ODMR变化相当. 为消除压强不均一对抗磁信号的影响, 实验还测量了零外磁场下的NV中心压强分布, 结合压强和磁场与NV中心的不同耦合关系, 将两者进行有效解耦, 给出了明确的超导抗磁信号[40].

    5.   结论和展望

    • 本文汇总了高压极端条件下, 特别是兆巴高压下金刚石NV中心光学和自旋性质, 讨论了高压下影响金刚石量子传感灵敏度的几个核心因素. 通过高压下磁铁矿的磁性测量, 氢化物CeH9、镍氧化物La3Ni2O7和La2PrNi2O7 超导迈斯纳效应测量这几个具体案例, 介绍了金刚石NV中心高压磁共振和量子传感的近期研究进展. 总体来看, 金刚石NV中心已可用于常压到140 GPa高压下的原位磁性表征, 空间分辨率接近1 μm, 高压下测磁灵敏度可达1 $ \text{μ}{\mathrm{T}}/\sqrt{{\mathrm{H}}{\mathrm{z}}} $, 这为高压极端条件下的原位磁测量, 特别是兆巴高压下超导迈斯纳效应测量提供了重要工具. 当然, 为实现近室温超导体如H2S, LaH10的原位表征, 尚需进一步提升金刚石NV中心的工作压强. 一方面, 可以采用基于(111)切割的金刚石对顶砧等方式, 让压强尽量保持与NV中心一样的对称性, 有望进一步提升其工作压强; 另一方面, 通过液态或气态传压介质来提供更好的静水压, 对于极端高压下的信号提取也是至关重要的.

      对于凝聚态物理、地球科学、材料科学等领域的前沿研究, 高压极端条件与极低温或高温, 以及强磁场等极端条件的联合将带来更丰富的调控手段. 金刚石NV中心ODMR的最高工作温度已接近1400 K[16], 最高工作磁场接近8 T[17] (均为单一指标). 同时, 除了作为磁传感器, 金刚石NV中心对所处位置的压强、温度、电场等物理量都有可 靠的响应, 可作为高压下多物理量联合测量传感 器[20]. 可见, 金刚石NV中心磁共振和量子传感技术的快速发展为综合极端条件下物性测量提供了新的机遇[22].

      最后, 值得一提的是, 本文主要以金刚石NV中心为讨论对象, 同时提及了高压极端条件对SiC和hBN中多种色心自旋的量子调控进展. 可见, 随着高压科学和色心量子传感的进一步发展和深度融合, 更加丰富和有趣的结果将会不断呈现, 让我们拭目以待.

    参考文献 (57)

目录

/

返回文章
返回