在生物磁共振实验中, 单个体素内的磁共振 信号来源于该体素内组织微环境中所有质子所 经历的物理和化学相互作用. 这些物理和化学效应包括质子的扩散、流动, 以及不同质子之间或不同组织微环境中质子之间的交换等. 根据质子/分子交换的机制, 可以将其粗略分为自由水中氢质 子与固态、半固态分子或受束缚水分子(如细胞 膜上的水分子)中氢质子的交换(通常定义为磁化转移(magnetic transfer))^[1,2]、自由水中氢质子与可移动的化合物中氢质子的交换带来的化学交换(chemical exchange)^[3,4], 以及通过扩散实现的不同组织微环境中水分子交换, 包括跨细胞膜交换(transcytolemmal water exchange)^[5,6].

质子/分子间的交换为磁共振测量提供了更丰富的对比度, 在生物医学领域被学者广泛研究. 磁化转移最早被Wolff和Balaban^[1]提出可作为一种新型的成像对比度, 磁化转移对髓鞘微结构的敏感性使其在研究白质疾病(如多发性硬化)方面得到应用^[7,8]. 基于化学交换的化学交换饱和转移磁共振成像(chemical exchange saturation transfer magnetic resonance imaging, CEST MRI)在2000年被Ward等^[4]提出, 可对组织中低浓度代谢物的 空间分布实现高灵敏度的定量. 其中, 在CEST基础上发展出来的酰胺质子转移(amide proton transfer, APT)成像由Zhou等^[9]于2003年提出, 后续被广泛应用. 目前, 相关技术已在临床中被应用到肿瘤的鉴别和分级^[10]、缺血性病变检测^[11,12]、骨关节炎进程监测^[13,14]等方面.

不同于上述对质子间转移和交换的测量, 在生物组织中还存在着由扩散驱动的不同组织微环境中的水分子跨膜运输, 早期研究揭示了水分子跨膜运输的两种形式: 单向净流动和稳态下双向交换, 它们在动力学上有所不同. 单向净流动通常是由渗透压差引起的, 发生在秒到分钟的时间尺度内, 例如水分子从低渗透压环境流向高渗透压环境^[15]. 然而, 稳态下的跨膜双向交换, 即水分子在膜两侧总量不变的情况下进行的双向流动, 在某些细胞中可以发生在毫秒到百毫秒内^[16]. 本文以下讨论将主要聚焦在稳态下的水分子跨膜交换.

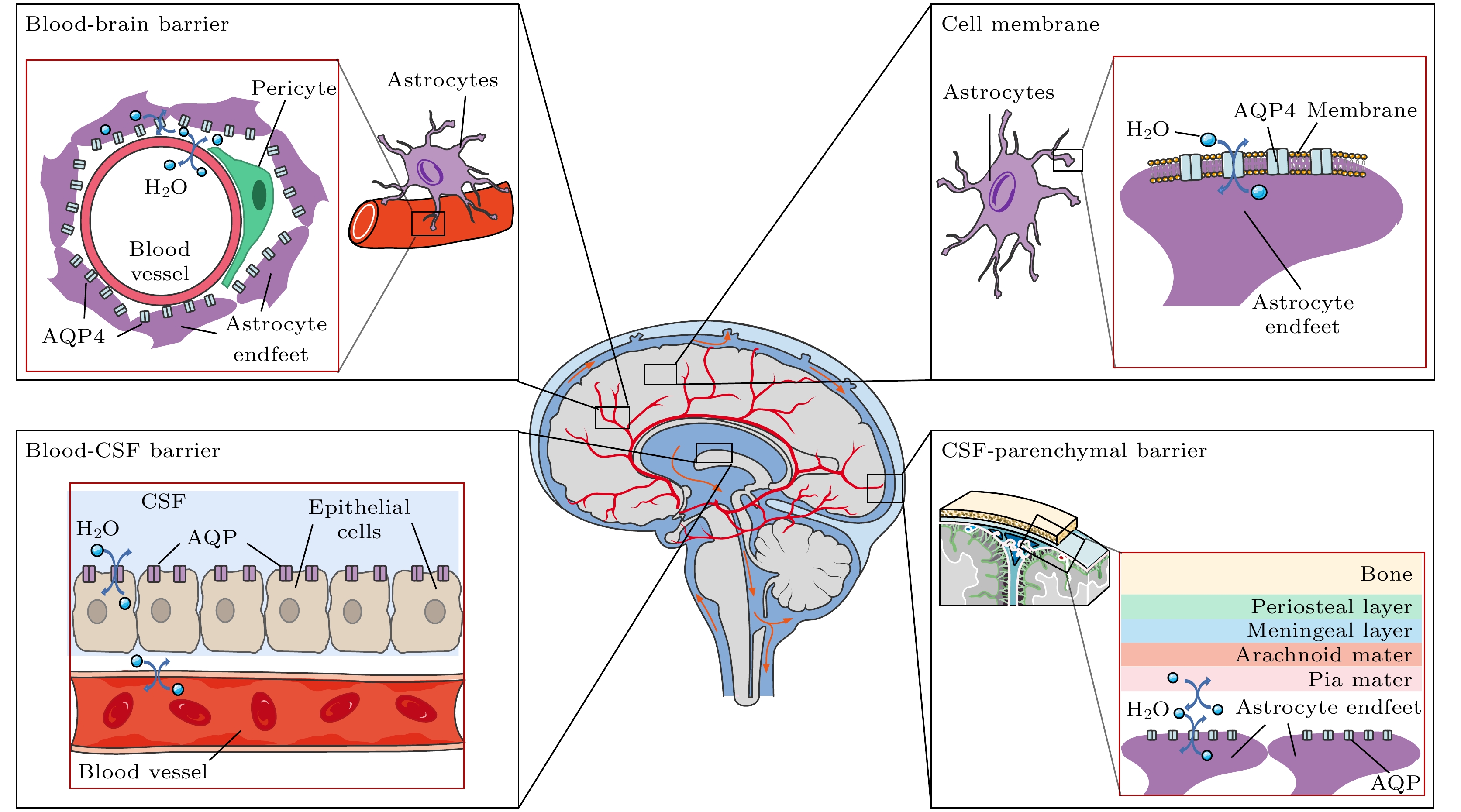
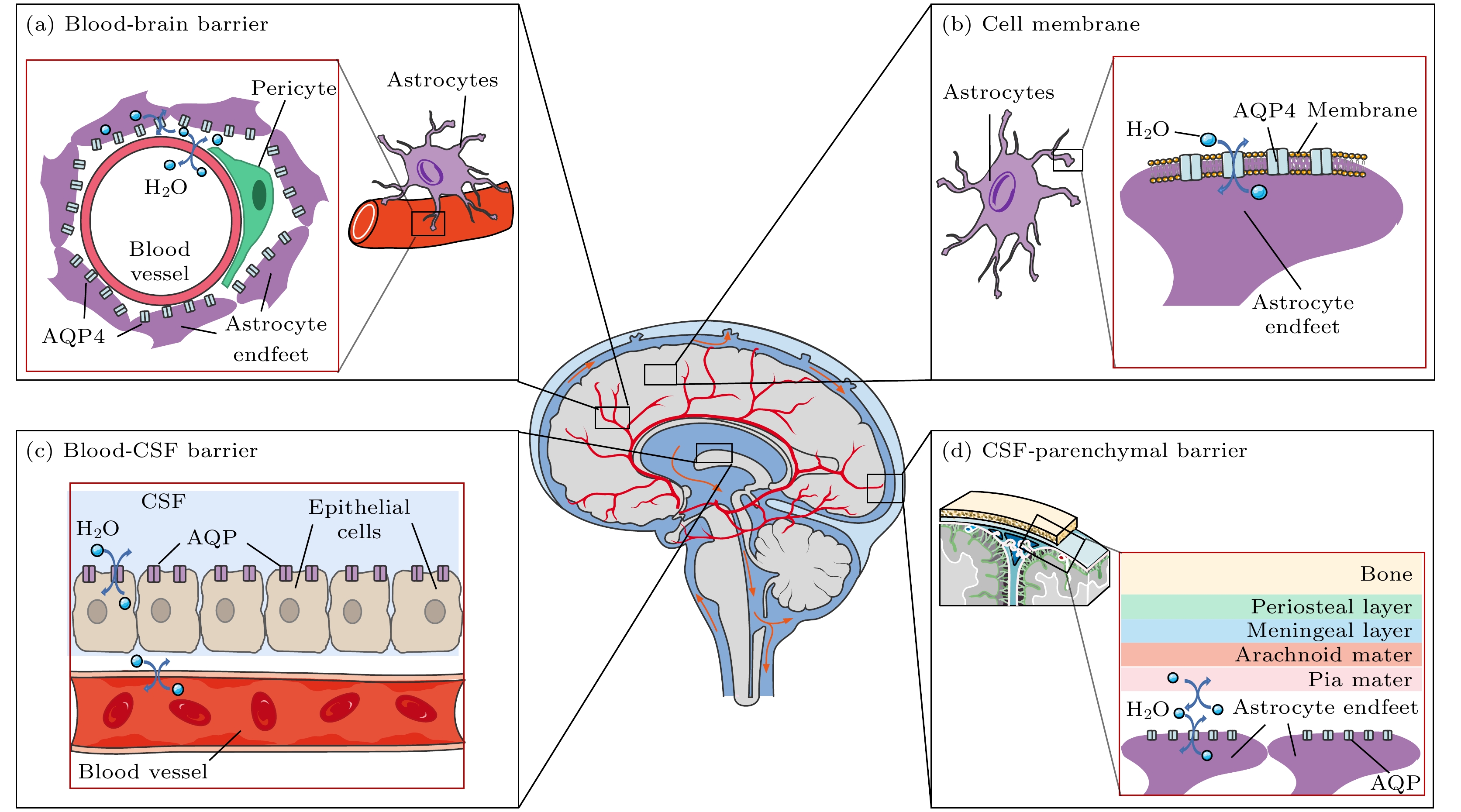
根据水分子所处组织微环境的结构不同和观察的空间尺度不同, 跨膜交换过程可以有非常多且不同的情形. 以颅内跨膜水交换为例, 大致包括: 1)水分子跨细胞膜交换^[17,18]; 2)水分子跨血脑屏障(blood-brain barrier, BBB)交换^[19]; 3)脉络丛中水分子跨血液-脑脊液屏障(blood-CSF barrier, BCSFB)交换^[20]; 4)水分子跨脑实质-蛛网膜下腔脑脊液屏障的交换(由星型胶质细胞尾足和软脑膜构成)^[21]. 脑组织中水分子跨膜过程概述如图1所示, 其中Arachnoid是蛛网膜; Astrocyte是星形胶质细胞; BBB(blood-brain barrier)表示血脑屏障, 由血管壁和星型胶质细胞尾足构成; Blood-CSF barrier是血液-脑脊液屏障, 由孔隙血管壁和室管膜细胞构成; Bone是骨; Cell membrane是细胞膜; CSF-parenchymal barrier是跨脑脊液-脑实质屏障; Endfeet是尾足; Blood vessel是血管; Epithelial cells是上皮细胞; Meningeal layer是脑膜层; Periosteal layer是骨膜层; Pericyte是周细胞; Pia mater是软脑膜.

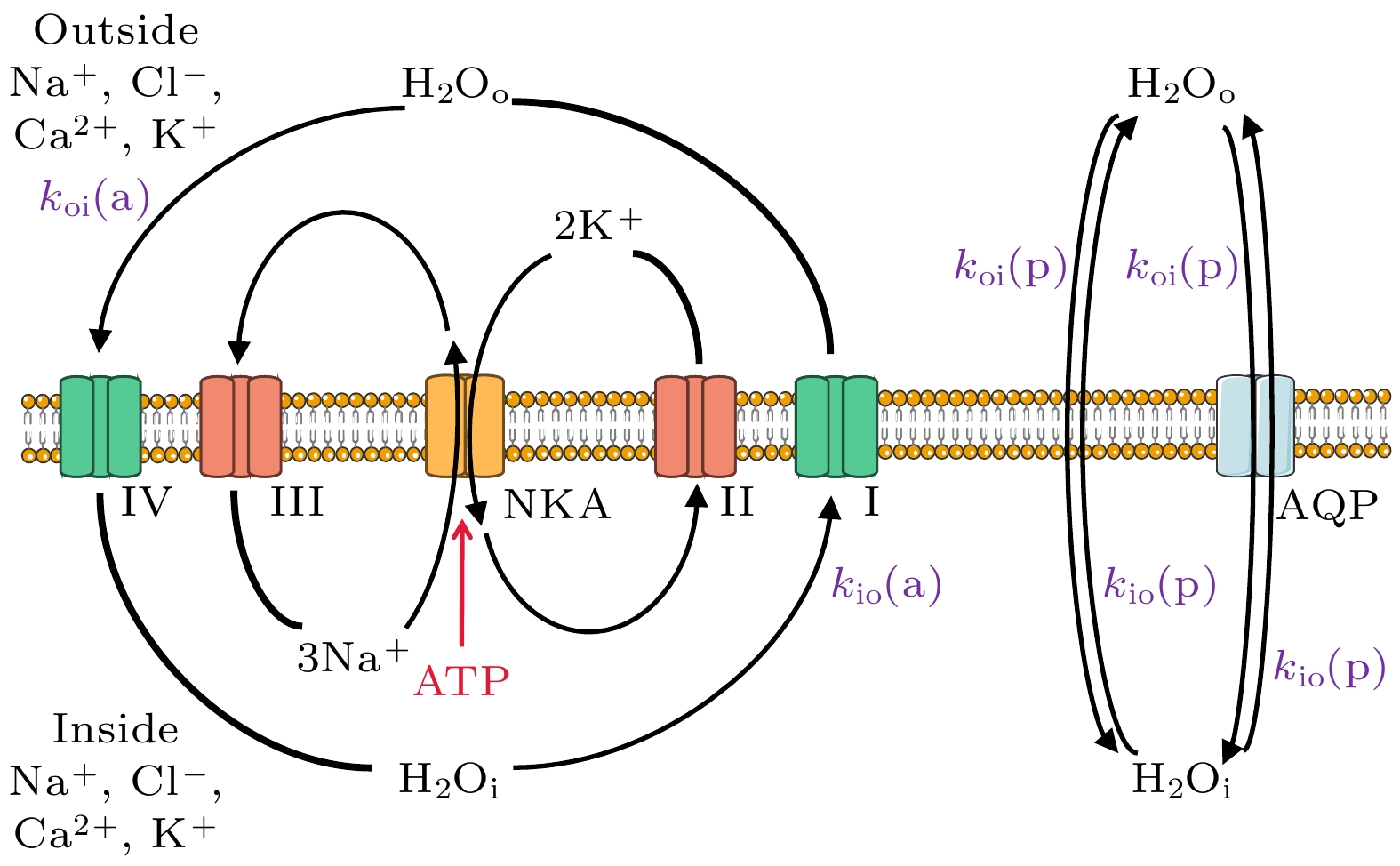
不同的水分子跨膜交换过程实现水分子交换的生物机制不同^[22]. 其中, 水分子跨细胞膜交换过程的生物学基础包括通过细胞膜磷脂双分子层进行扩散; 通过膜上的水通道蛋白进行被动运输^[17]; 由钠钾泵活性调控、水分子共运通道主导的“协同”运输^[23], 如图2所示. 在水分子跨BBB交换中, 相关研究表明其潜在机制之一是血液中的水分子通过内皮细胞上表达的系统转运蛋白(如NKCC1, GLUT1等)穿过内皮细胞^[24]. 在水分子跨BCSFB交换中, 脑室脉络丛中孔隙型毛细血管中的水分子会穿过内皮细胞, 并通过室管膜细胞上的协同转运蛋白(NKCC1)和AQP1进入和流出室管膜细胞最终到达脑室中^[20]. 在水分子跨脑实质-蛛网膜下腔脑脊液屏障交换中, 蛛网膜下腔中脑脊液里的水分子可通过星型胶质细胞尾足上的AQP4 (水通道蛋白4)与细胞内的水进行交换^[21].

近年来, 随着大脑类淋巴系统的发现, 以及越来越多的基础研究揭示了脑疾病中血脑屏障发 生破坏, 利用磁共振技术评估血脑屏障通透性以 及测量脑脊液与脑组织间水分子交换的研究受到了广泛关注. 特别地, 在水分子跨BBB交换上的磁共振测量上发展出了基于弛豫的方法^[25]、Wang等^[26,27]提出基于动脉自旋标记的方法, 以及最近Bai等^[28]提出的血管水过滤交换成像方法, Lin等^[29]提出的WEPCAST(water extraction with phase-contrast arterial spin tagging)方法. 更多关于水分子跨BBB交换的磁共振研究进展可参考Dickie等^[30]的综述报道. 在大脑液体循环系统中, 除水分子跨BBB的交换以外, 在脑实质中仍存在水分子跨单个细胞的细胞膜进行交换的过程. 该过程在维持正常细胞体积(如胶质细胞, 神经元), 评估肿瘤细胞代谢等方面有重要作用. 其中, 水分子跨细胞膜的交换速率/细胞内水分子停留时间被认为与肿瘤的侵袭性^[31,32]、治疗反应^[33,34]和脑水肿密切^[35]相关. 具体地, 如Chawla等^[34]发现平均细胞内水分子停留时间($ {\tau }_{{\mathrm{i}}} $)可作为头颈部鳞状细胞癌患者的预后标志物以预测患者的生存期. 因此, 定量化水分子跨细胞膜交换可能为与细胞膜通透性改变相关的疾病提供有用的生物标志物.

本文将重点针对水分子跨细胞膜交换的磁共振测量技术的研究进展进行介绍, 具体包括代表性技术的测量原理、数学/生物物理模型、不同技术的测量结果及验证, 旨在梳理该领域的发展历程, 讨论其在体应用的可行性和应用场景, 最后对该领域未来的发展进行展望.

经过数十年的发展, 磁共振领域目前在水分子跨细胞膜交换测量的技术大致以分为两类: 基于弛豫的方法和基于扩散的方法. 基于弛豫的方法通过加入对比剂, 改变某一组织微环境的纵向弛豫时间(T₁)或横向弛豫时间(T₂); 而基于扩散的方法是一种不依赖对比剂的测量技术, 其通过测量不同组织微环境中水分子的扩散率实现对水分子跨细胞膜交换速率的测量. 下文将分别对两大类方法的研究进展进行介绍.

考虑到目前关于水分子跨细胞膜运输过程的定量化参数仍未统一, 在介绍相关研究进展前, 本文先列出过往磁共振研究中表征水分子跨细胞膜运输速率的参数.

1)水分子交换速率常数$ k $, 并通过下标表示不同组分内水分子的速率常数, 如$ {k}_{{\mathrm{i}}{\mathrm{o}}} $表示细胞内水交换到细胞外空间的速率常数; $ {k}_{{\mathrm{o}}{\mathrm{i}}} $表示细胞外水交换到细胞内空间的速率常数. 其中, $ k={k}_{{\mathrm{i}}{\mathrm{o}}}+{k}_{{\mathrm{o}}{\mathrm{i}}} $, 在水分子稳态跨膜交换过程中, $ {k}_{{\mathrm{i}}{\mathrm{o}}}{f}_{{\mathrm{i}}}={k}_{{\mathrm{o}}{\mathrm{i}}}{f}_{{\mathrm{o}}} $, $ {f}_{{\mathrm{i}}} $和$ {f}_{{\mathrm{o}}} $分别为细胞内和细胞外水分子含量占比.

2)交换时间(exchange time) $ {\tau }_{{\mathrm{e}}{\mathrm{x}}} $, 其与k的关系为$ {\tau }_{{\mathrm{e}}{\mathrm{x}}}=1/k $. 有时论文也会报道细胞内水分子在细胞内的“停留时间” (residence time/lifetime) $ {\tau }_{{\mathrm{i}}} $, 以反映水分子跨细胞膜交换速率大小. 其与$ {\tau }_{{\mathrm{e}}{\mathrm{x}}} $的关系为$ {\tau }_{{\mathrm{e}}{\mathrm{x}}}={\tau }_{{\mathrm{i}}}{f}_{{\mathrm{o}}} $.

3)细胞膜通透性常数$ p $, 其为细胞膜的固有特性. 水分子稳态跨膜交换过程的模型如图3所示.

在20世纪70—80年代, 陆续涌现出基于弛豫磁共振方法的对离体细胞样本的水分子跨细胞膜运输速率测量的研究. 1972年, Conlon和Outhred^[36]通过向血液中加入Mn²⁺缩短血浆中的T₂弛豫时间, 使血液样本中存在双T₂弛豫时间的组分, 即血红细胞内较长的T₂组分和血浆中较短的T₂组分, 并用90°—180°脉冲序列进行信号采集, 拟合出加入Mn²⁺的血浆中的快弛豫组分的T₂和慢弛豫组分的T_2b. 由于拟合出的慢弛豫组分的弛豫时间$ {T}_{2{\mathrm{b}}} $会受到血红细胞内水“固有”的横向弛豫时间影响, 以及从血浆中进入到血红细胞内的水分子的T₂影响, 因此, 从一阶动力学角度出发, 可使用(1)式获取血红细胞内外水分子交换的交换时间$ {\tau }_{{\mathrm{e}}{\mathrm{x}}} $(文献[36]中将水分子表观交换时间记为$ {T}_{{\mathrm{a}}{\mathrm{e}}} $):

其中, $ {T}_{2{\mathrm{i}}} $为血红细胞内水分子“固有”的横向弛豫时间, 该参数通过对经过离心和沉淀的血红细胞单一样本测量得到. 基于该方法测量到的血液样本在37 ℃, 血细胞比容28%, 血浆水占比53%, 细胞外Mn²⁺在20 mmol/L左右或更大时, 血红细胞内外水交换时间在8 ms左右. 后续有学者延续该模型探究不同温度、渗透、病理状态下的血红细胞内外水分子交换时间^[37-39]. Conlon和Outhred^[36]提出的方法通过简单的公式实现对血红细胞内外水分子交换时间的测量. 然而, 该模型忽略了回流效应对交换时间测量的影响, 即细胞内水分子扩散/交换到细胞外后又扩散回到细胞内, 这种水分子的回流会导致观测到的弛豫行为更为复杂. 因此, 该公式需要在细胞外施加高浓度的Mn²⁺, 如此, 扩散到细胞外的水分子会迅速失去信号, 从而降低回流效应对交换时间估计的影响. 除了早期使用Mn²⁺作为对比剂的研究, 后续也有研究者使用稳定性更高、具有亲水性的钆对比剂, 通过主要影响T₁来测量水分子跨细胞的交换速率. 如, Gianolio等^[40]使用钆对比剂重新评估了血红细胞的水交换速率, 得到的细胞内水分子停留时间在20 ms左右, 比之前基于Mn²⁺得到的停留时间更长. Jia等^[41]使用钆对比剂测量不同细胞系的胶质瘤细胞的水分子跨细胞膜交换速率, 并探究了AQP4敲除和抑制下$ {k}_{{\mathrm{i}}{\mathrm{o}}} $如何受到影响, 以阐明胶质瘤细胞中水分子跨细胞交换过程的生理机制. 在该研究中, Jia等^[41]发现胶质瘤细胞中的$ {k}_{{\mathrm{i}}{\mathrm{o}}} $在10 s^–1左右, AQP4敲除和抑制后, $ {k}_{{\mathrm{i}}{\mathrm{o}}} $下降约50%. 除了使用对比剂的方法外, 还有使用其他方式改变细胞外组分弛豫时间的方法. Yang等^[42]在构建的三维立体细胞培养体模中, 通过灌注快速流动的液体改变细胞外组分的表观纵向弛豫时间以区分细胞内外组分. 在该研究中, Yang等^[42]发现星形胶质细胞和神经元的细胞内水分子停留时间分别在0.57 s和0.75 s左右.

在细胞悬液样本中, 由于细胞形态相对单一, 水分子所处的结构特征简单, 可以通过施加对比剂改变弛豫时间使其划分为细胞内、外两个组分. 然而, 在生物组织中, 由于组织结构更为复杂多样, 水分子的信号特征也更加复杂. 生物组织的磁共振研究中对水交换的关注可追溯到在生物组织中发现磁共振信号呈现多指数弛豫时间特征^[43-45]. 1972年, Belton等^[46]在青蛙肌肉组织中发现横向弛豫信号可以用三指数进行良好拟合, 并被解释为信号来自3个不同组分的水, 即肌原纤维和肌浆网中的水、细胞间隙中的水、强链接到蛋白质中的水. 此外, 作者发现随着温度改变, 3个组分的水分子体积占比发生改变. 作者推测该现象可能由不同组分间的水分子发生交换造成. 自此, 在生物组织中基于弛豫磁共振方法对水交换的研究拉开序幕.

不同于细胞悬液样本, 生物组织中的组分划分更为复杂, 因此需要更为完整的数学/生物物理模型描述水交换是如何影响磁共振的弛豫信号. 早在1958年, McConnell^[47]在Bloch方程的基础上考虑交换(化学交换)的影响, 给出双组分交换模型(two-site-exchange, 2SX), 并用在模型中给出一阶速率常数$ 1/\tau $, 用以描述交换信息. 1974年, Hazlewood等^[48]在大鼠腓肠肌上研究弛豫信号的多指数特征, 并用双组分交换模型去定量研究是否是结合水和自由水的交换引起组织中的多个弛豫时间分布. 此时, 在生物组织上基于2SX模型的交换研究多集中在质子交换, 如Sobol等^[49,50]在离体的小鼠后腿肌肉组织中测量出自由水和结合水的化学交换速率在30 s^–1左右.

然而, 不同于交换速率较快的化学交换, 在生物组织中, 水分子的交换更倾向于是一个更慢的、通过水分子扩散实现交换的过程. 基于2SX模型求由扩散驱动的水分子跨膜交换信息需要进一步的研究. 1984年, Herbst和Goldstein^[51]提出了2SX方程组的解析解, 将细胞内水分子停留时间、细胞内水分子含量占比和细胞外弛豫时间同双指数特征的弛豫信号联系起来, 给出测量水分子跨细胞膜交换速率, 而非化学交换速率的模型. 在2SX模型中, $ {T}_{2{\mathrm{a}}} $和$ {T}_{2{\mathrm{b}}} $分别代表信号双指数拟合中的横向弛豫时间不同的两个组分(并非细胞内和细胞外两个组分), $ {P}_{{\mathrm{a}}} $及$ {P}_{{\mathrm{b}}} $分别代表两个组分的水分子占比. 其中, $ {T}_{2{\mathrm{i}}} $为细胞内水分子的横向弛豫时间, $ {T}_{2{\mathrm{o}}} $表示细胞外空间水分子的横向弛豫时间, $ {P}_{{\mathrm{i}}} $及$ {P}_{{\mathrm{o}}} $分别代表两个组分的水分子占比, $ {\tau }_{{\mathrm{i}}} $及$ {\tau }_{{\mathrm{o}}} $分别为细胞内与细胞外水分子停留时间, 平衡状态下满足$ {P}_{{\mathrm{i}}}/{\tau }_{{\mathrm{i}}}={P}_{{\mathrm{o}}}/{\tau }_{{\mathrm{o}}} $.

值得注意的是, 在该研究中, 需要分离出血红细胞并测量细胞内的弛豫时间作为方程的已知量. 然而, 对于不可分离的测量系统, 如生物组织, 很难单独获取细胞内的水分子弛豫时间. 1989年, Mulkern等^[52]通过使用两次不同浓度的顺磁性对比剂, 分别得到两次浓度下的信号, 并拟合出各自的双组分弛豫速率. 随后, 在2SX的基础上, 推导出4个双组分弛豫速率与两个组分的水含量占比、两组分间的交换速率常数的表达式, 以此实现对水分子跨细胞膜交换速率的测量. 最后, Mulkern等^[52]在灌注的大鼠心脏的磁共振数据上进行了参数拟合和计算. 后续研究者在此模型的基础上开展了对离体神经组织中的水分子跨细胞膜交换测量. 如, Bai等^[23]在新生大鼠的脑切片上测量到$ {k}_{{\mathrm{i}}{\mathrm{o}}} $在2 s^–1左右, 并发现了神经组织中水分子跨细胞膜交换会受到钠钾泵活性的影响.

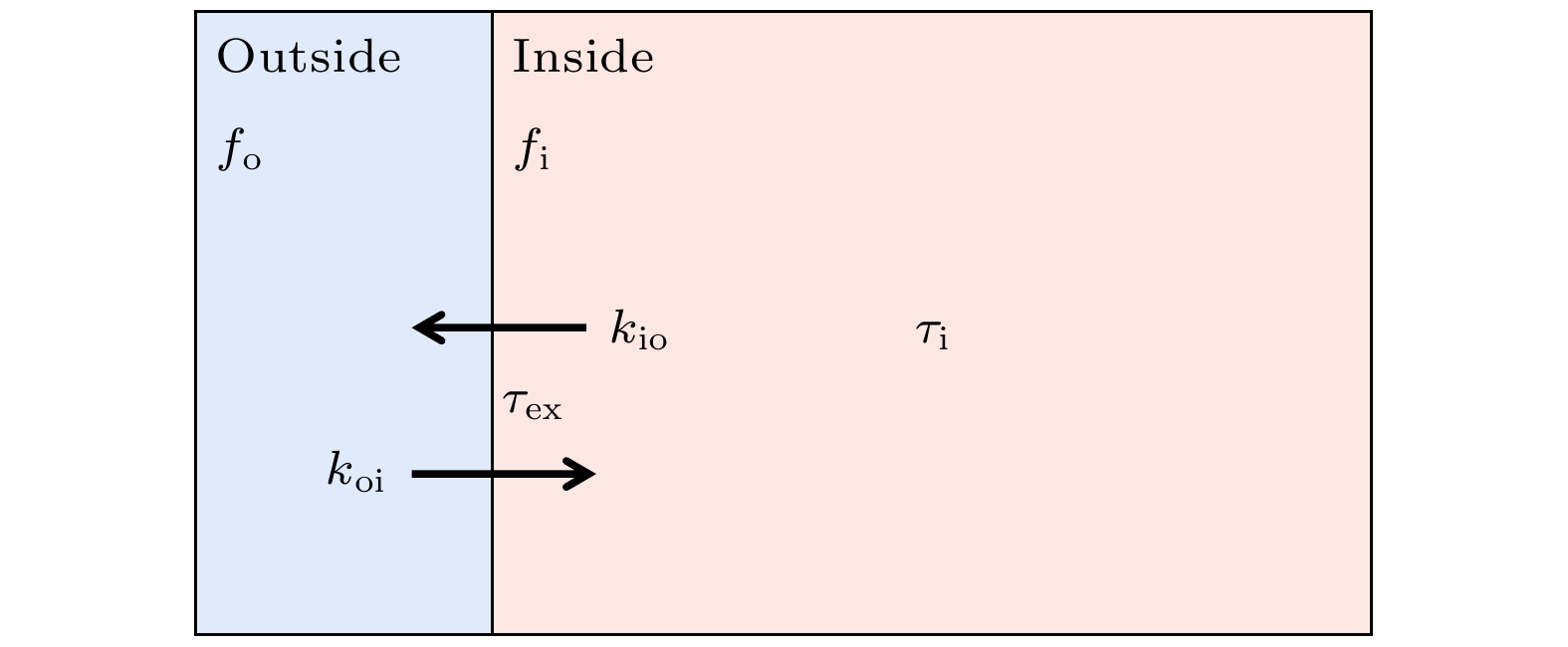
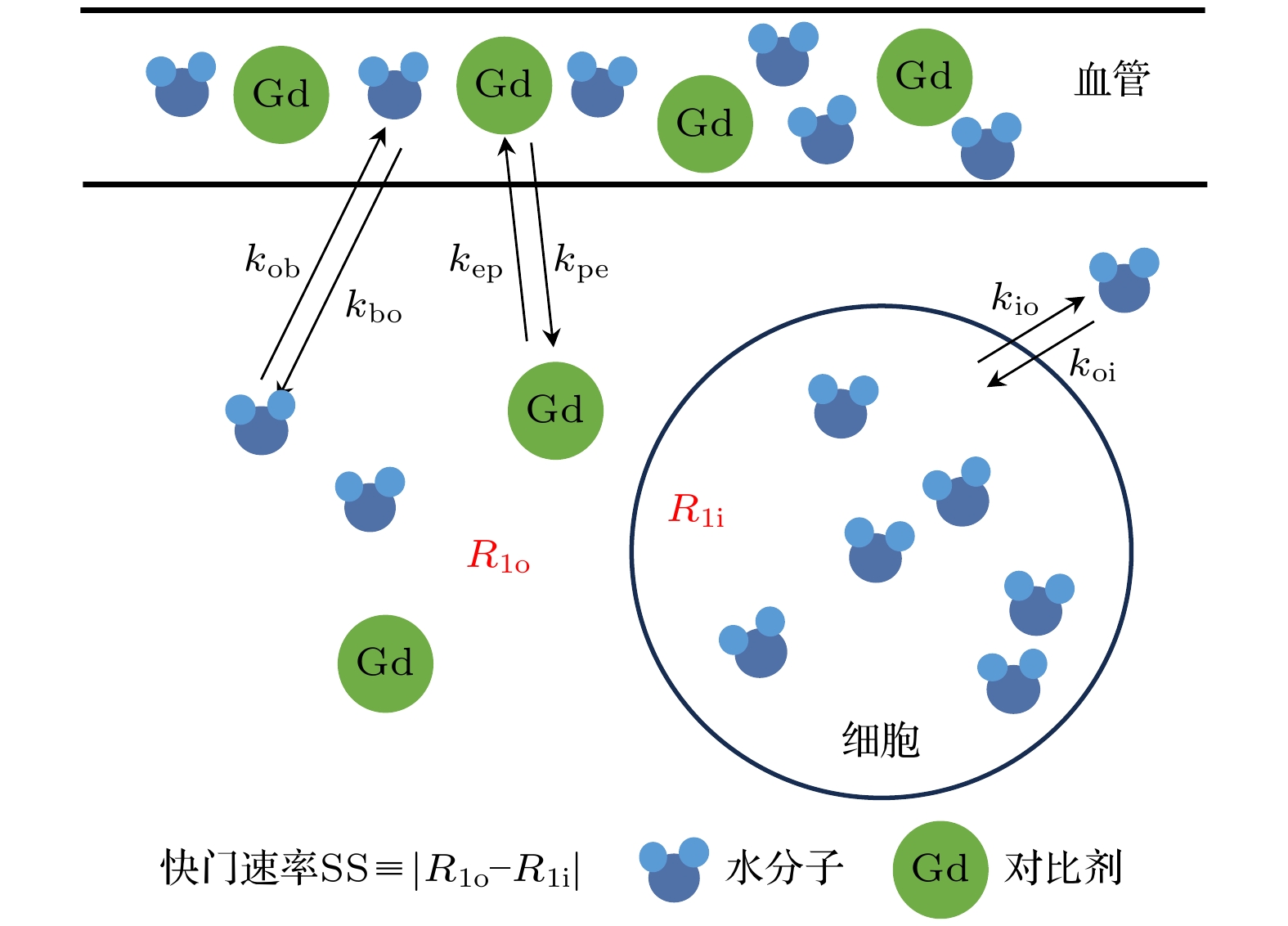
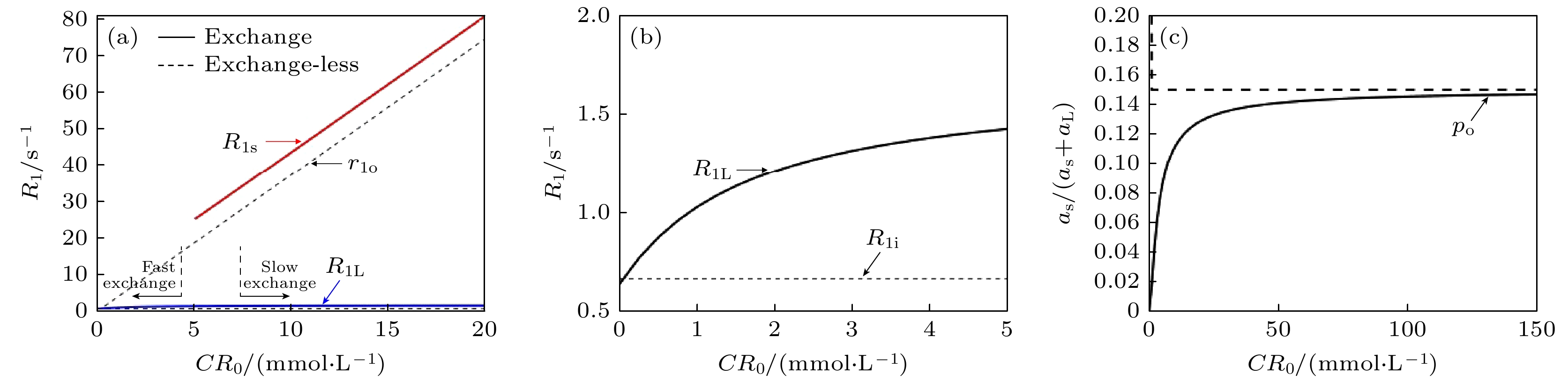
不同于离体生物组织测量, 在体测量中对比剂主要通过静脉注射, 血流灌注和血管渗透性使测量系统更为复杂. 1999年, Landis等^[25]提出快门速度(shutter-speed)的概念(见图4), 在体测量生物组织中的细胞内水分子流出速率$ {k}_{{\mathrm{i}}{\mathrm{o}}} $. 在这一理论框架中, 快门速度指细胞内外水分子纵向弛豫速率的差值($ \left|R{1}_{{\mathrm{i}}}-R{1}_{{\mathrm{o}}}\right| $), 其中, $ R{1}_{{\mathrm{i}}} $为细胞内水分子的纵向弛豫速率, $ R{1}_{{\mathrm{o}}} $表示细胞外(细胞间隙空间)水分子的纵向弛豫速率. 当$ {k}_{{\mathrm{i}}{\mathrm{o}}}+{k}_{{\mathrm{o}}{\mathrm{i}}} $远大于$ |R{1}_{{\mathrm{i}}}- R{1}_{{\mathrm{o}}}| $时, 系统被认为处于快速交换边界(fast-exchange-limit, FXL), 难以区分细胞内外的磁共振信号. 当控制细胞外对比剂浓度以改变$ R{1}_{o} $时, 即增大对比剂浓度提高$ R{1}_{{\mathrm{o}}} $可使$ {k}_{{\mathrm{i}}{\mathrm{o}}} $达到与$ \left|R{1}_{{\mathrm{i}}}-R{1}_{{\mathrm{o}}}\right| $接近的范围, 此时系统被认为处于慢交换区域(slow-exchange regime), 磁共振纵向弛豫信号呈现双指数特征. 其中, 纵向弛豫时间较大的组分的纵向弛豫速率$ {R}_{1{\mathrm{L}}} $和纵向弛豫时间较小的组分的纵向弛豫速率组分$ {R}_{1{\mathrm{s}}} $同细胞内水分子停留时间的关系, 以及快纵向弛豫组分的信号占比分数$ {a}_{{\mathrm{L}}} $和慢纵向弛豫组分的信号占比分数$ {a}_{{\mathrm{s}}} $分别为^[25]

其中, $ {r}_{1{\mathrm{o}}} $是加入对比剂后细胞间隙水分子的纵向弛豫速率, $ \left[{\mathrm{C}}{{\mathrm{R}}}_{{\mathrm{o}}}\right] $是对比剂浓度, $ {R}_{1{\mathrm{o}}0} $是在没有对比剂时细胞外水分子的纵向弛豫速率, $ {\tau }_{{\mathrm{i}}} $是细胞 内水分子停留时间, $ {p}_{{\mathrm{i}}} $是细胞内水分子含量占比. 关于$ {R}_{1{\mathrm{L}}} $, $ {R}_{1{\mathrm{S}}} $和$ {{a}_{{\mathrm{s}}}}/({{a}_{{\mathrm{s}}}+{a}_{{\mathrm{L}}}}) $随对比剂浓度的改变可参考图5.

Landis等^[25]利用提出的SSM理论框架对大鼠腿部肌肉进行在体测量, 得到的肌质组织中的细胞内水分子停留时间在1.1 s左右, 细胞外水分子体积分数为11%. 值得注意的是, 在该研究中Landis等^[25]采用静脉缓慢滴注的方式向大鼠体内注射对比剂, 以使细胞间隙的对比剂浓度逐渐达到稳态, 避免瞬时的血流动力学对信号的影响, 从而确保弛豫信号的改变由水分子跨细胞膜交换带来, 最终从弛豫信号中估计细胞内水分子停留时间. 然而, 该静脉缓慢滴注的方式很难在人体上进行, 除非大幅度增大对比剂的浓度, 否则需要更长的时间使组织中的对比剂浓度达到稳态(Landis等的研究中以0.01 mL/min的滴注速度需要约40 min达到稳态).

临床上, 通常采用静脉快速推注对比剂的方式进行磁共振增强扫描诊断肿瘤. 同期, 需静脉注射对比剂的动态增强磁共振(DCE-MRI)被广泛应用到肿瘤中, 以评估肿瘤中的灌注和血脑屏障通透性等^[53-56]. 然而, 此类研究使用的模型(如普朗克模型)通常假设对比剂浓度和测量的弛豫速率之间呈线性相关. 这一假设的前提是水分子跨细胞膜的交换速率非常快, 即对比剂在各个空间的分布是均匀的. 这一假设在血红细胞的水分子跨细胞膜交换($ {\tau }_{{\mathrm{i}}} \sim 10$ ms)中可以成立, 然而, 在其他水分子跨细胞膜交换中并不成立. 上述Landis等在1999年的研究也表明了水分子跨细胞膜的交换速率是“有限”的($ {\tau }_{{\mathrm{i}}} $~1 s). 2000年, Landis等^[57]在大鼠大腿肌肉和大鼠胶质瘤模型的在体对比剂推注实验中, 进一步验证了假设水分子跨细胞膜交换非常快的不合理性. 作者将原子发射光谱分析的血液中对比剂浓度和通过磁共振弛豫信号得到的对比剂浓度进行比对, 发现在水分子跨细胞膜交换非常快的假设下, 对比剂浓度低估近1/2. 因此, 在对比剂推注实验时, 对磁共振弛豫信号分析中考虑水分子跨细胞膜交换是有必要的^[58,59].

在对比剂快速推注的情景下, 组织中对比剂浓度随时间的变化会影响对水分子跨细胞膜交换速率的估计. 2003年, Yankeelov等^[60]将(8)式—(10)式和药代动力学理论结合, 以分析对比剂推注后不同时间点下的磁共振弛豫信号(DCE-MRI), 即$ {R}_{1{\mathrm{L}}} $, $ {R}_{1{\mathrm{S}}} $和$ {a}_{{\mathrm{s}}} $在对比剂通过采样区域时间段里是随着时间变化而变化的曲线:

其中, $ {R}_{10} $是在没有对比剂(CR)的情况下, 细胞外的纵向弛豫率常数, 即基线弛豫率常数, $ {R}_{1{\mathrm{i}}} $是在没有交换的情况下, 细胞外的纵向弛豫率常 数, $ {r}_{1{\mathrm{o}}} $是对比剂的弛豫率, $ \left[{\mathrm{C}}{{\mathrm{R}}}_{{\mathrm{o}}}\right] $是对比剂的浓度, $ {\tau }_{{\mathrm{i}}} $是细胞内水分子的平均寿命, $ {p}_{{\mathrm{o}}} $是细胞外水的比例, $ \left[{\mathrm{C}}{{\mathrm{R}}}_{{\mathrm{o}}}\right]\left(t\right) $是随时间变化的曲线. Yankeelov等^[53]则采用了Kety-Schmidt药代动力学公式描述从血浆中渗透到细胞间隙的对比剂浓度, 即

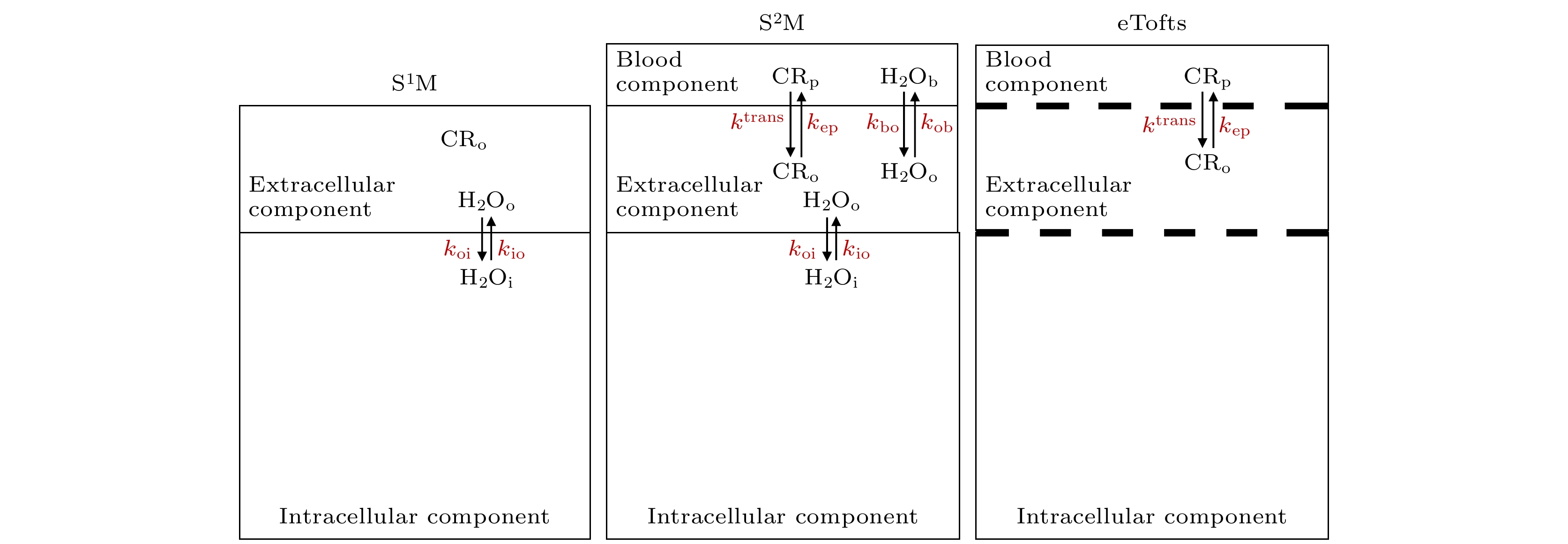
其中, L表示一级速率常数, 反映了对比剂从血浆向组织间隙的转移过程, $ L=E\cdot {F}_{{\mathrm{k}}}\left(1-h\right)/\left({f}_{{\mathrm{w}}}\cdot {p}_{{\mathrm{o}}}\right) $, $ E\cdot {F}_{{\mathrm{k}}} $为血浆中对比剂渗透比例和血流量的乘积, $ h $是血红细胞比容, $ {p}_{{\mathrm{o}}} $是细胞间隙水分子占比, $ {f}_{{\mathrm{w}}} $为系统中可被移动的溶质结合的水分子的体积占比, 常设置为0.8. 最后, 将(14)式代入(11)式—(13)式, 对磁共振弛豫信号进行分析. 在该研究中, 作者利用该分析模型在大鼠胶质瘤模型中, 得到细胞内水分子停留时间$ {\tau }_{{\mathrm{i}}} $, 细胞间隙水分子占比$ {p}_{{\mathrm{o}}} $, 细胞间隙对比剂弛豫速率$ {r}_{1{\mathrm{o}}} $, 细胞内水分子弛豫速率$ {R}_{1{\mathrm{i}}} $, 血浆中对比剂渗透比例和血流量的乘积$ E\cdot {F}_{{\mathrm{k}}} $.

然而, 值得注意的是在Yankeelov等^[53]给出的模型中, 即第1代快门速度模型(Shutter-speed model, SSM/S¹M), 忽略了对血管水含量占比的估计(假设为0), 因此它适用于血浆对比剂渗透速率较大的情况. 随后, Li等^[61]对模型进一步完善, 提出了第2代快门速度模型(S²M), 考虑了在血浆对比剂渗透速率较小的情况, 以更好地从D-MRI信号中估计血管壁通透性、细胞膜通透性、血管水占比、细胞水占比等信息. 该模型是一个包括了细胞内水、细胞间隙水和血管内水的三组分模型, 考虑了水分子跨细胞膜的交换和血管内外的水分子交换(参考图4). Li等^[61]对考虑了血管水的模型进行仿真实验, 得到对比剂推注后水分子跨血管交换的快门速度($ \left|R{1}_{{\mathrm{b}}}-R{1}_{{\mathrm{o}}}\right| $, $ R{1}_{{\mathrm{b}}} $为血管内水分子的弛豫速率, $ R{1}_{{\mathrm{o}}} $为细胞间隙水分子的弛豫速率)和水分子跨细胞膜交换的快门速度($ \left|R{1}_{{\mathrm{i}}}-R{1}_{{\mathrm{o}}}\right| $, $ R{1}_{{\mathrm{i}}} $为细胞内水分子的弛豫速率)随时间的变化曲线. 在不同血管内对比剂渗透速率($ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $)和不同时间下, 快门速度在变化, 因此水分子跨血管交换和跨细胞膜交换将处在不同的范围(快速交换范围或者慢速交换范围), 以此水分子跨血管交换和跨细胞膜交换对磁共振弛豫信号的“贡献”程度也不同. 该研究的仿真结果表明, 在血管内对比剂渗透速率($ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $)大于0.1 min^–1时, 第1代的SSM模型(S¹M), 即忽略水分子跨血管交换, 只考虑水分子跨细胞膜交换, 可以用来分析对比剂推注后的磁共振弛豫信号. 当$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $小于0.1 min^–1时, 可以采用第2代SSM模型(S²M)分析磁共振数据, 即同时考虑水分子跨血管和细胞膜的交换. Bai等^[62]在第2代SSM模型的基础上做了进一步的改进. 他们通过模拟发现当对比剂从血管中渗漏较少时, 对比剂对间质空间的横向弛豫时间改变较小. 例如, 脑组织中血脑屏障完整时, $ \left|R{1}_{{\mathrm{i}}}-R{1}_{{\mathrm{o}}}\right| $远小于k_io+k_oi, 此时第2代SSM模型对间质水摩尔分数占比(p_o)以及k_io估计不准. 因此, Bai等将第2代SSM模型细化为SSM_vas和SSM_full两个子模型. 前述的对比剂从血管中渗漏较少的情况适用于SSM_vas模型, 此时p_o被固定为0.2(脑组织中), k_io被固定为1000 s^–1, 即跨细胞膜水分子快速交换. 当对比剂从血管中渗出较多时, 此时满足$ \left|R{1}_{{\mathrm{i}}}-R{1}_{{\mathrm{o}}}\right| $大于k_io+k_oi的条件, 适用于SSM_full模型. 两个模型通过赤池信息准则进行自动适配以满足最佳拟合. Bai等使用这一改进模型发现了人脑多形性胶质母细胞瘤中$ {k}_{{\mathrm{i}}{\mathrm{o}}} $存在异质性. DCE-MRI不同模型的示意图见图6, 其中Blood component为血管组分; Extracellular component为细胞外组分; Intracellular component为细胞内组分.

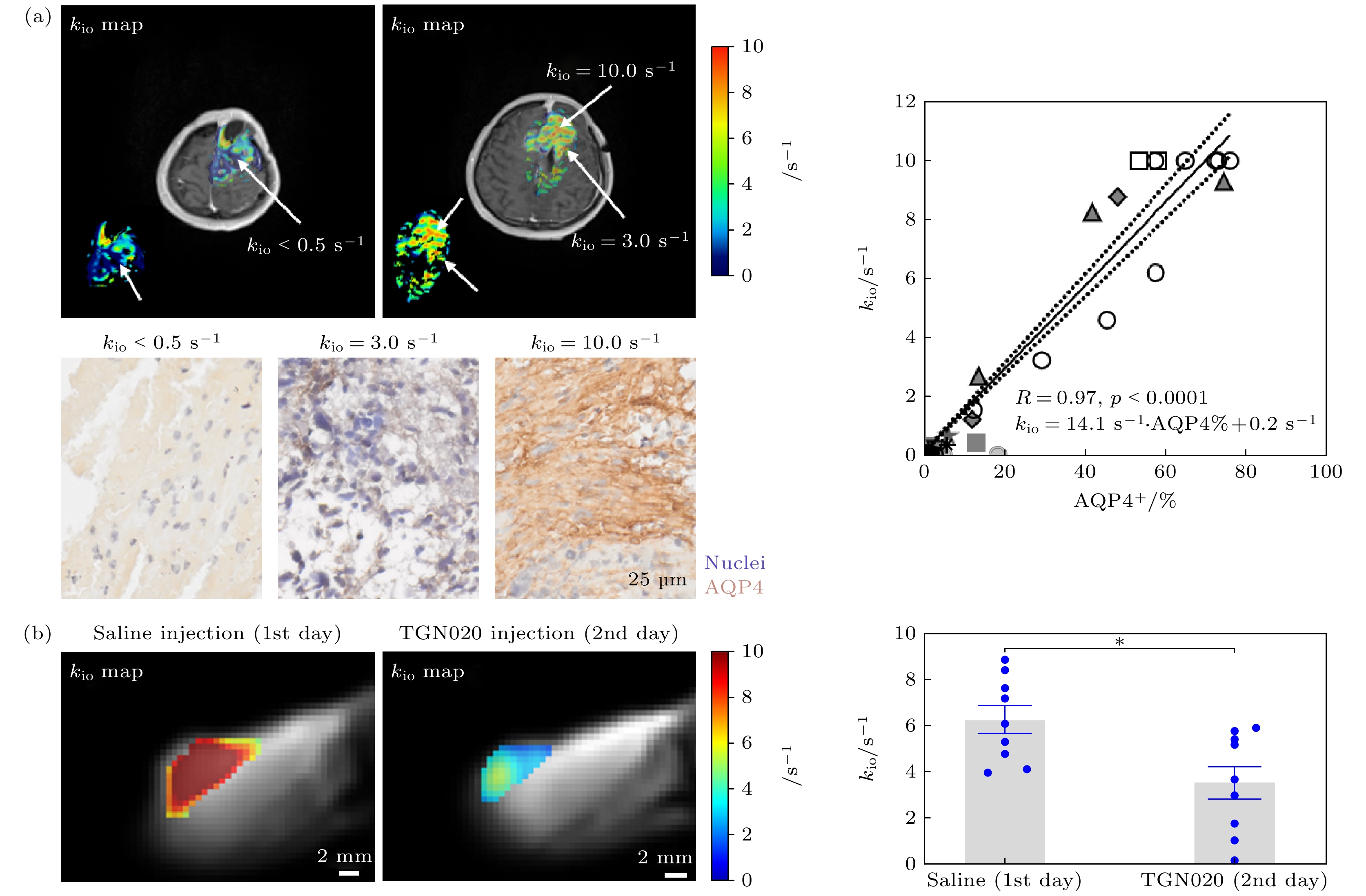
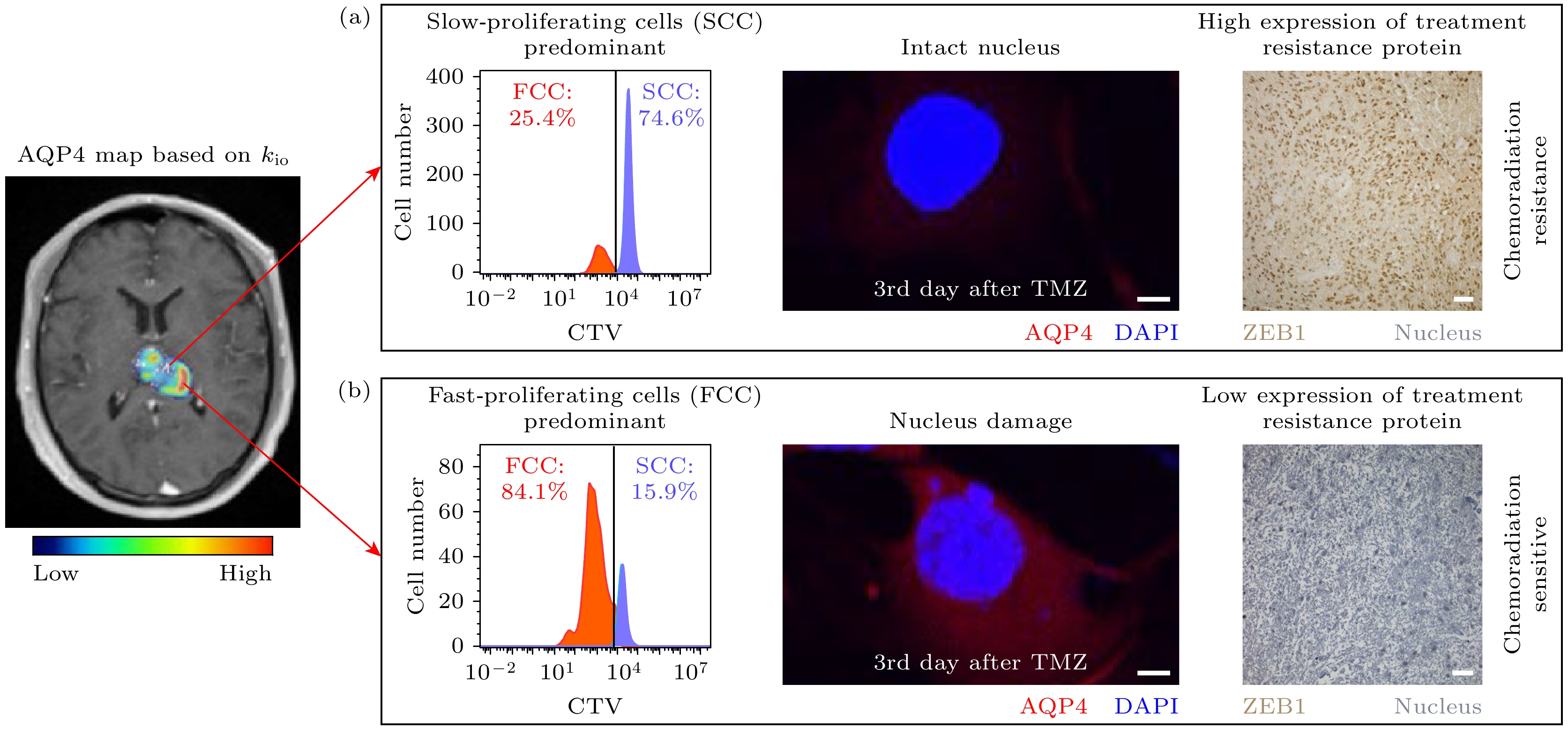
随后, 快门速度模型被应用到乳腺癌^[32,63,64]、前列腺癌^[65,66]、头颈部鳞状细胞癌^[33,67]等多种临床疾病中^[68]. 在乳腺癌上, 研究者发现在恶性浸润性导管癌, 快门速度模型能够揭示肿瘤内部的“热点”区域, 即肿瘤区域在参数上表现更强的空间异质性, 在“热点”区域有更强的血流灌注和血管壁渗透性, 然而在良性纤维腺瘤上未发现参数的空间异质性^[64]. 此外, 基于快门速度模型得到的影像参数更有助于分辨出恶性肿瘤和良性肿瘤, 尤其在$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $参数上. 与传统的药代动力学模型相比, 基于快门速度模型得到的$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $在恶性肿瘤上表现出更高的值, 但良性肿瘤上两种模型得到的$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $无明显差异. 这一发现有希望基于快门速度模型实现对恶性肿瘤与良性肿瘤更精确的区分^[63]. 类似地, 在前列腺癌上的相关研究表明, 基于快门速度模型得到的$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $可以更好地区分恶性和良性前列腺组织^[66]. 在头颈部鳞状细胞癌上, 快门速度模型相比于传统的药代动力学模型, 在超过75%的像素点上都表现出更好的拟合效果且残差更小, 且揭示了肿瘤不同区域的参数异质性, 如肿瘤外周的$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $较高, 而中心区域则表现为较低的$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $. 此外, 基于快门速度模型估计的肿瘤区域的细胞内水分子停留时间在211—364 ms^[33]. 上述的临床应用均表明在DCE-MRI数据分析中, 使用考虑水分子跨细胞膜交换过程的快门速度模型的必要性. 除了基于快门速度模型得到的$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $表现出的临床应用价值, 2022年, Jia等^[41]在胶质瘤上发现基于快门速度模型得到的细胞内水分子流出速率$ {k}_{{\mathrm{i}}{\mathrm{o}}} $是AQP4表达高敏感、高特异性的潜在影像标志物(图7), 并且发现AQP4表达水平与胶质瘤治疗抵抗存在直接相关, 如图8所示(Chemoradiation sensitive是放化疗敏感; Chemoradiation resistance是放化疗抵抗; FCC(fast-proliferating cells)是快增殖细胞; Nucleus是细胞核; SCC (slow-proliferating cells)是慢增殖细胞; Treatment resistance是治疗抵抗). 这表明在胶质瘤中有望通过$ {k}_{{\mathrm{i}}{\mathrm{o}}} $“映射”出肿瘤区域的AQP4表达水平分布图, 为胶质瘤的治疗评估等提供影像评估指标.

值得一提, 过往的研究通常认为水分子跨细胞膜交换过程是被动交换(通过磷脂双分子层扩散和通过水通道蛋白运输)在$ {k}_{{\mathrm{i}}{\mathrm{o}}} $测量值上起作用. 然而, 2011年Zhang等^[69]研究测量了不同氧合状态下酵母细胞的细胞膜通透性和细胞内水分子停留时间$ {\tau }_{{\mathrm{i}}} $, 结果发现其和细胞ATP密切相关, 特别是与离子通道转运膜蛋白(P-type H⁺-ATPase)的活性相关. 该研究暗示$ {k}_{{\mathrm{i}}{\mathrm{o}}} $的测量值可能同时受到水分子主动运输和被动运输的影响. 后续, Springer等^[23,70,71]发现$ {k}_{{\mathrm{i}}{\mathrm{o}}} $与脑组织中神经元放电活动相关, 并且受钠钾泵活动影响, 暗示$ {k}_{{\mathrm{i}}{\mathrm{o}}} $可能是细胞代谢活动检测的潜在影像标志物. 更多基于水跨膜交换表征代谢活动的研究进展可参考文献[72,73]. 这些研究提示, 不同细胞类型中水分子跨膜运输的主要分子途径可能不同.

基于扩散磁共振测量水分子跨细胞膜交换信息的研究可追溯到19世纪60年代. 经过近60年的研究, 该领域的主要测量技术在序列编码方式上可按照单扩散梯度编码序列(single diffusion encoding, SDE)^[74]和双扩散梯度编码序列(double diffusion encoding, DDE)^[75]划分. 在拟合水分子跨细胞膜交换速率的模型上, 大致可概括为基于双组分高斯扩散的Kärger模型, 考虑水分子扩散受限的Kärger模型, 以及一阶反应动力学模型(组分占比随时间变化). 下文将对其分别进行介绍.

1969年, Kärger^[76]从理论上推导出当系统中的水分子存在两个不同扩散率时, 其对脉冲梯度自旋回波信号的影响. 后续并给出分析两个扩散率不同的组分交换信息的Kärger模型^[77,78]. Kärger模型基于以下假设: 1)在扩散时间$ {t}_{{\mathrm{d}}} $下, 扩散长度远大于介质特征尺度($ \sqrt{D{t}_{{\mathrm{d}}}}\gg {l}_{{\mathrm{c}}} $, 其中D为扩散率, $ {t}_{{\mathrm{d}}} $为扩散时间, l_c为水分子遇到微观结构障碍的平均距离), 即扩散距离充分覆盖微观结构尺寸; 2)交换速率较慢, 水分子交换时间较长, 满足“屏障受限交换”的条件, 即$ \sqrt{D\tau }\gg {l}_{{\mathrm{c}}} $(其中$ \tau $为水分子交换时间), 使得介质可视为宏观均匀. 在Kärger模型中, 信号可表示为如下双指数形式^[79]:

其中, $ q=\sqrt{b/{t}_{{\mathrm{d}}}} $, b为扩散加权因子; 扩散时间$ {t}_{{\mathrm{d}}}=\Delta -\delta /3 $, $ {D}_{{{1, 2}}} $和$ {P}_{{{1, 2}}} $表达式如下:

其中, $ {\tau }_{{\mathrm{i}}\to {\mathrm{e}}} $和$ {\tau }_{{\mathrm{e}}\to {\mathrm{i}}} $为一个组分到另一个组分的交换时间, $ \rho $为组分s的信号占比. $ {D}_{{\mathrm{f}}} $和$ {D}_{{\mathrm{s}}} $分别是快组分和慢组分的水分子扩散率.

1976年, Andrasko^[80]同样对血红细胞的水分子跨细胞膜交换进行测量, 不同于1972年Conlon和Outhred^[36]的外源对比剂方法, Andrasko^[80]采用基于水分子扩散的磁共振方法, 根据 Kärger^[76–78]提出的两室交换模型使用脉冲梯度NMR方法在离体血红细胞上实现了非对比剂依赖地测量细胞内水分子流出速率. 通过测量不同扩散时间下的信号, 得到模型中的$ {D}_{1} $, 并假定细胞内外占比和血红细胞外水分子扩散率已知, 且细胞内水分子扩散受限, 即长扩散时间下细胞内水扩散率相比细胞外水分子扩散率可以忽略, 如此, (16)式可以简化为

其中, $ \tau $是交换时间, $ {D}_{{\mathrm{A}}} $是细胞外的水分子扩散率, $ {D}_{1} $测量得到的表观扩散系数, N是细胞内和细胞外水分子的比例, K是一个与梯度脉冲相关的实验常数. 基于该方法得到的人血红细胞内水分子交换时间在24 ℃ 为17 ms.

上述研究基于Kärger模型计算水分子交换时间时, 假定了细胞内、外水分子扩散率是已知常数, 且长扩散时间下细胞内水分子扩散率可以忽略, 即简化成(20)式. 然而, 同时期和后续的研究陆续表明细胞内水扩散率具有扩散时间依赖性. 例如, 1974年Neuman^[81]给出在均匀且无通透性的介质中, 基于自旋回波测量到的介质中水分子的表观扩散率是具有扩散时间依赖性的. 1978年, Tanner^[82]首次考虑了一组具有不同通透性的平行一维介质下, 基于自旋回波序列测量的表观扩散率是如何随着扩散时间、梯度强度的变化而改变, 并给出从测量到的表观扩散率反推介质几何参数(如平行介质的间距、介质的通透性)的理论模型. 后续, 1983年Tanner^[83]结合该理论模型, 利用脉冲梯度NMR对红细胞、酵母和虾等不同样本中的细胞内水扩散率进行了测量, 分析了在0.3—1.0 s的扩散时间范围内, 水分子扩散率和膜渗透性之间的关系. 以血红细胞为例, 结果表明真实的细胞内水分子扩散率(即细胞内水自由扩散, 不受细胞膜的影响下)是6.3×10^–6 cm²/s, 在长扩散时间(约大于100 ms)下, 受到细胞膜的影响细胞内水分子扩散率收敛到2.6×10^–6 cm²/s, 并在1978年的理论模型下, 计算得到细胞膜通透性为0.011 cm/s. Neuman^[81]和Tanner^[82]提出的理论模型和细胞悬液的实验均表明细胞内的水分子扩散率是具有扩散时间依赖性的.

后续有人对Kärger模型进行延伸, 即考虑细胞内水分子扩散率对扩散时间的依赖性, 而不是固定为常数. 其中包括1997年, Stanisz等^[84]考虑到神经纤维束中水分子扩散各向异性和细胞内水分子扩散受限, 对Kärger模型进行扩展, 提出一种解析模型用以描述基于PGSE测量的磁共振信号, 该模型可以给出不同组分的水分子扩散率、细胞膜通透性和表征细胞尺寸、占比的信息. 不同于Kärger模型中的双组分交换, 该研究提出的模型包括3个组分, 轴突、胶质细胞和细胞间隙空间, 且轴突膜和胶质细胞膜均具有通透性(三组分双交换系统). 该研究在离体牛视神经组织上利用该模型得到的轴突膜和胶质细胞膜通透性分别为0.0009 cm/s和0.0017 cm/s. 1998年, Pfeuffer等^[85]选择了胶质细胞悬液样本(双组分系统)研究了细胞内水分子扩散特征和细胞内外水分子跨膜交换过程. 该研究使用自旋回波和受激回波的NMR在胶质细胞样本中测量了扩散时间从5.3—2000 ms的信号(constant gradient, CG实验), 并根据CG实验获取细胞内水停留时间(~50 ms). 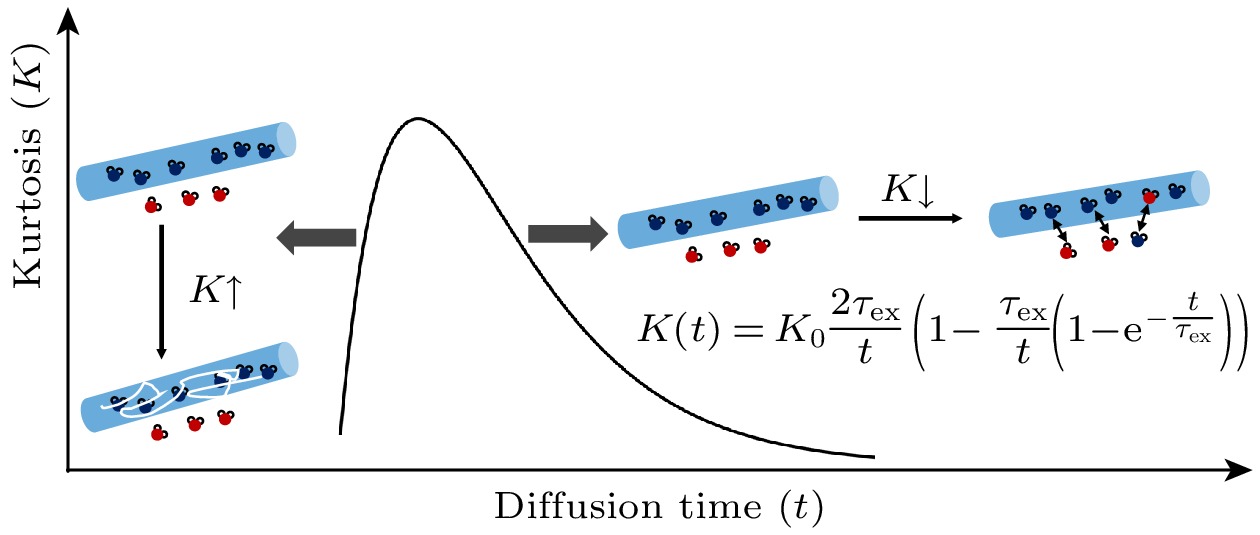在该研究中, 对细胞内水分子停留时间的估计仍然沿用1976年Andrasko^[80]使用的方法, 但不同的是作者使用$ {D}_{{\mathrm{a}}{\mathrm{p}}{\mathrm{p}}, {\mathrm{i}}{\mathrm{n}}{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}} $替换了Kärger模型中固定为常数的细胞内水分子扩散率$ {D}_{2} $, $ {D}_{{\mathrm{a}}{\mathrm{p}}{\mathrm{p}}, {\mathrm{i}}{\mathrm{n}}{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}} $是一个具有扩散时间依赖的表观扩散率, $ {D}_{{\mathrm{a}}{\mathrm{p}}{\mathrm{p}}, {\mathrm{i}}{\mathrm{n}}{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}} $可通过Tanner等^[86]给出的表征一个固定尺寸的介质里水分子扩散行为的磁共振信号公式对q值求导得到. Kärger模型的假设限制了其在一些场景下的应用, 如尺寸较大的细胞, 水分子跨膜交换速度很快, 或者扩散时间较短、高b值的实验等. 最近, Shi等^[87]探究了此类情况对Kärger模型估计的水分子跨膜交换的影响. 该研究的仿真结果表明, 在较大的细胞尺寸(>10 μm)、更大的梯度强度和更长的梯度持续时间的情况下, 会出现对水分子跨细胞膜交换速率的高估. 但在细胞尺寸较小时(<6 μm)中, 影响可以忽略不计.

2005年, Jensen等^[88]提出了用扩散峰度(kurtosis)描述生物组织中水分子的非高斯扩散行为. 在该项研究中, 作者除了给出从扩散磁共振信号中估计扩散峰度的模型, 并根据Kärger模型给出扩散峰度和水分子交换时间之间的理论关系, 如(21)式, 但文章并未进行相关实验:

其中, var(D)是扩散系数D的方差, 表示扩散系数在不同隔室中的变异程度, $ \bar{D} $是扩散系数的平均值, $ \alpha =t/\left({\tau }_{{\mathrm{a}}}{p}_{{\mathrm{b}}}\right)=t/\left({\tau }_{{\mathrm{b}}}{p}_{{\mathrm{a}}}\right) $, $ {\tau }_{{\mathrm{a}}} $和$ {\tau }_{{\mathrm{b}}} $是两个组分的水分子停留时间, $ {p}_{{\mathrm{a}}} $和$ {p}_{{\mathrm{b}}} $是两个组分水含量占比, 其中$ {p}_{{\mathrm{b}}}=1-{p}_{{\mathrm{a}}} $.

当$ t\ll {t}_{{\mathrm{m}}} $时, 扩散峰度K(t)接近于各室均为高斯扩散的理想状态下的值($ 3 {{\mathrm{v}}{\mathrm{a}}{\mathrm{r}}\left(D\right)}/{{\bar{D}}^{2}} $), 这表示在水交换影响较小的情况下, 扩散峰度主要由扩散系数的分布决定. 当$ t\gg {t}_{{\mathrm{m}}} $时, 即时间远大于水混合时间, 扩散峰度K(t)随时间t的延长而减小, 表现为1/t的形式, 此时是水交换对扩散峰度的下降起主要作用(图9). $ {t}_{{\mathrm{m}}}={\tau }_{{\mathrm{a}}}{p}_{{\mathrm{b}}}={\tau }_{{\mathrm{b}}}{p}_{{\mathrm{a}}} $是系统的水混合时间, 表示水在两个组分之间完全混合所需的时间. 2010年, Fieremans等^[89]通过仿真实验, 在一个由相同直径, 方向随机的圆柱体构成的系统里(模拟生物组织结构), 验证基于扩散峰度估计停留时间的可行性. 作者表明在膜通透性足够低的系统中, 且扩散时间较长时, 基于扩散峰度的模型可以良好地估计停留时间和膜通透性. 具体地, 膜通透性足够低的系统中, 细胞内水分子停留时间大于特征时间(characteristic time)(t_c是水分子扩散距离l_c的均方时间, 如此, 在扩散时间也较长的情况下, 系统的表观扩散率将不再随着扩散时间变化, 此时扩散峰度会随扩散时间下降, 利用该段的数据可对水分子停留时间进行良好估计. 然而, 在膜通透性过高的系统里, 该模型将会对停留时间低估(对通透性高估).

基于扩散峰度随扩散时间下降部分的曲线估计水分子停留时间((21)式)的方法后续也被用到不同胶质瘤小鼠模型和临床乳腺癌患者上^[90]. 其中, GL261和4T1肿瘤中估计的水分子停留时间是93 ms和68 ms; C57 BL/6和BALB/c肿瘤中估计的水分子停留时间是41 ms和30 ms. 在两种乳腺癌类型中估计的水分子停留时间为70 ms和106 ms^[90]. 2022年, Jelescu等^[91]提出NEXI (neurite exchange imaging)方法, 利用PGSE采集多b值多扩散时间的数据, 建立了表征灰质扩散信号的模型. 在该模型中, 作者纳入了各向异性的Kärger模型, 从扩散峰度随时间的变化曲线中拟合出水分子跨细胞膜的交换速率, 其在大鼠皮层和海马测量的细胞内水分子停留时间在15—60 ms. 随后, Uhl等将NEXI在健康被试中进行测试, 在全脑获取NEXI模型的参数, 包括水分子在细胞内停留时间、细胞内外水分子扩散率和细胞内水分子占比^[92]. 上述内容介绍了基于扩散峰度随扩散时间的变化曲线拟合水分子停留时间的相关研究. 需要注意的是, 该模型假设在该扩散时间下, 系统已达到“粗粒化”, 即系统的水分子表观扩散率不再随着扩散时间改变^[89]. 然而, 这一假设在真实实验中并不一定满足, 如先前在活体小鼠、人脑灰质、人脑白质上, 均报道过扩散率对扩散时间的依赖性(20—600 ms)^[93-95]. Uhl等^[92]的研究结果也同样展示了扩散率对扩散时间(20—49 ms)的依赖性, 即使很微弱. 水分子扩散率对扩散时间的依赖性也有可能是组织微结构的无序性(structural disorder)造成, 因此, 在此时模型的有效性可能有待研究.

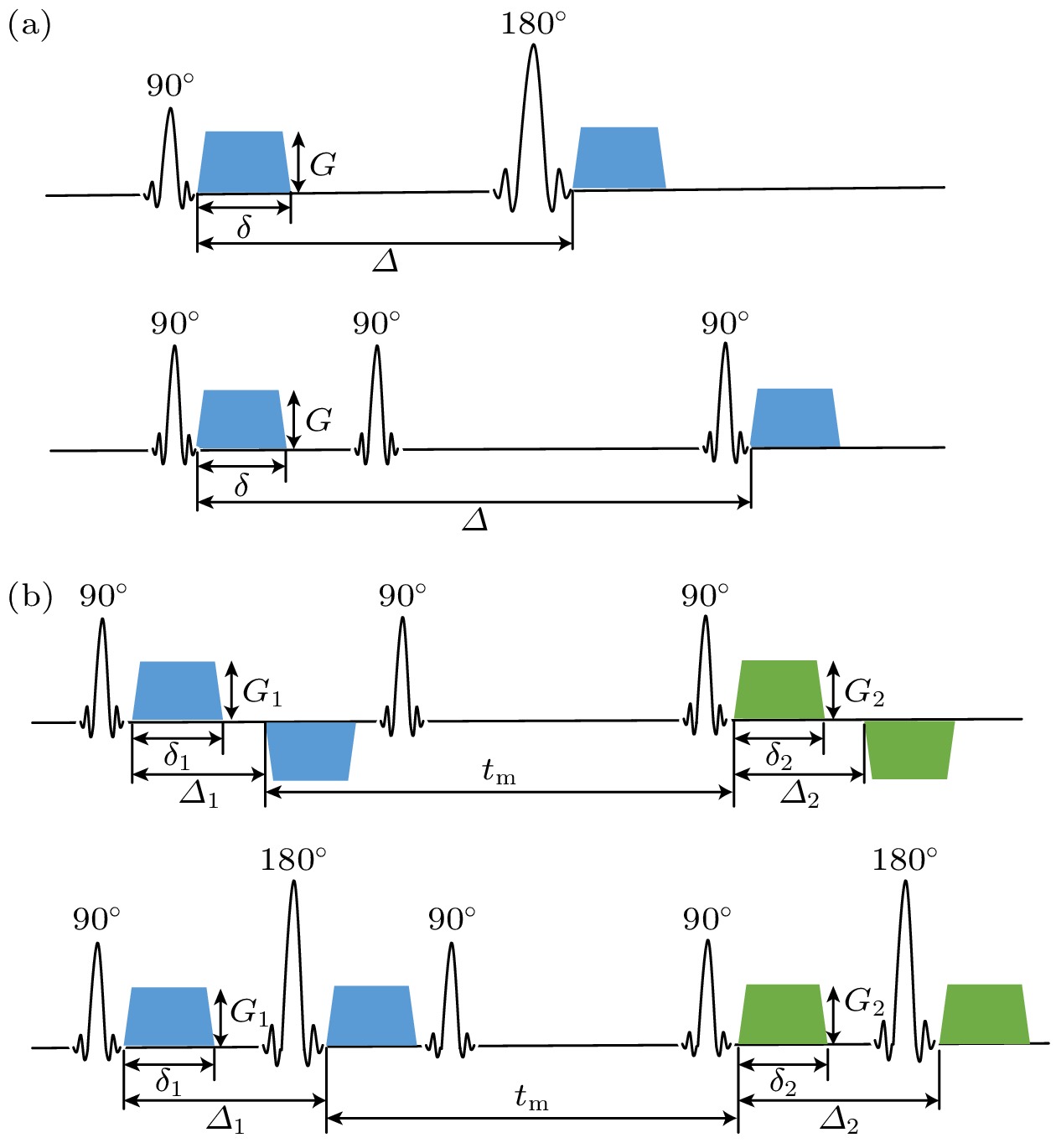
2004年, Callaghan和Furo^[96]提出了双扩散梯度编码交换谱技术(diffusion exchange spectroscopy, DEXSY)测量交换. 该技术使用两个被交换时间“隔开”的扩散梯度编码的序列, 用以测量多域液晶材料中水分子从一个域扩散/“交换”到另一个域的引起的整个系统扩散特征(用扩散率D表征)的变化. 该技术的序列图可参考图10所示, 在交换时间$ {t}_{{\mathrm{m}}} $内, 水分子从一个域扩散/“交换”到另一域, 通过测量不同扩散梯度强度、不同交换时间下的磁共振信号, 并利用二维拉普拉斯逆变换获取二维扩散谱. 在二维扩散谱中, 如果存在水分子从一个域扩散到另一域的情况, 则会出现偏离对角线的谱峰. 在该研究中, 作者通过分析不同交换时间下的非对角线上的谱峰偏离对角线的角度, 获取了多域液晶材料中域的尺寸信息.

DEXSY 最早应用在材料科学领域, 如, 利用DEXSY测量多层电解质膜对葡萄聚糖的通透性, 发现在测量时间设为200 ms时, 大约有1.5%的葡萄聚糖通过多层电解质膜^[97,98]. DEXSY虽然是一种不涉及生物物理模型建模的方法, 但它需要拉普拉斯逆变换获取水分子扩散特征, 因此在数学求解规程中存在不稳定性, 无法获取唯一解, 为了获取稳定的结果通常需要更多的数据点, 导致更长的扫描时间. 如DEXSY通常需要在单一交换时间下进行约1000次采集. 如果推算出水分子的交换速率, 需要使用一系列不同交换时间的数据点, 如此导致DEXSY数据采集时间更长, 限制了其在在体生物被试中的应用.

2018年, Cai等^[99]对DEXSY的采集点进行优化, 通过对第1个扩散加权模块(扩散加权因子b值为b₁)和第2个扩散加权模块(扩散加权因子b值为b₂)的信号再参数化, 实现对水分子扩散行为和交换行为带来的信号变化的区分. 即b_s = b₁+b₂下的信号为扩散的作用, b_d = b₂ – b₁下的信号为交换的作用. 作者使用4个数据点的情况下, 使用有限差分法计算b_s下的信号曲线曲率, 并给出通过曲率获取系统中组分体积占比的公式(注: 该组分占比是指不同时间下各组分的水分子动态占比). 最后, 基于双组分交换的假设, 利用一阶交换动力学模型, 对不同交换时间下的组分占比拟合, 获取系统的交换速率k. 在该研究中, 作者将其提出的采集方案和数据计算框架应用到一个由玻璃毛细管阵列组成的水模系统中, 对该水模进行成像, 计算了玻璃毛细管里的水和管外自由水之间的交换速率. 2019年, Williamson等^[100]在可保持数小时“活性”状态的离体小鼠脊髓, 以及经过多聚甲醛固定的小鼠脊髓上进行了DEXSY测量. 作者使用了梯度强度高达15.3 T/m的静态梯度场, 采用了自旋回波序列并结合能提高信噪比的CPMG(Carr-Purcell-Meiboom-Gill)回波链, 测量不同扩散时间下的信号衰减, 交换时间从0.2—300 ms变化, 发现利用Cai等^[99]提出的水分子交换速率的快速测量方法, 可得到脊髓组织中扩散受限的组分中的水分子同自由扩散的组分中的水分子交换速率为100 s^–1. 2020年, Breen-Norris等^[101]在酵母细胞悬液和在体的小鼠肿瘤模型上进行了单个交换时间(200 ms)下的DEXSY测量, 并定义了DEI指标(diffusion exchange index), 即二维扩散谱上偏离对角线的谱下体积和非对角线上谱下体积的比值, 用以反映水分子交换情况. 该研究首先通过仿真实验验证了DEI指标对细胞膜通透性的灵敏度, 在酵母细胞悬液和小鼠肿瘤模型上的DEI结果也初步表明了DEXSY技术在测量水分子跨膜交换速率的可行性, 然而该研究仍然缺乏对离体和在体实验结果的验证. 过往基于DEXSY的材料领域和生物领域的研究, 通过拉普拉斯逆变换得到二维扩散谱及水交换信息, 其背后的假设仍是水分子是高斯扩散, 但上述介绍中提到的生物系统中的水分子扩散是受限的. 非高斯扩散信号会导致二维扩散谱中受限扩散和交换产生的效应混淆. 2022年, Cai等^[102]通过仿真实验发现受限扩散会使二维扩散谱上的峰变宽且出现“假”的交换峰(偏离对角线的峰), 并提出REEDS-DE(restriction and exchange from equally-weighted double and single diffusion encoding)的采集方案, 旨在分开对受限扩散和交换的测量. 最后, Cai等^[102]在离体的新生小鼠脊髓上测量得到水分子交换速率k为75 s^–1. 此外, 人工智能技术的出现为磁共振采集方案的优化提供了新思路. 最近, Cheng等^[103]基于深度学习设计了一个物理模型引导的DEXSY加速网络(deep learning based sampling pattern optimization and parameter estimation, DL-SPOPE)以优化DEXSY降采样轨迹, 实现在指定采样时间的约束下获取可高准确度估计参数的采样轨迹. 该研究通过仿真实验和离体酵母细胞悬液的结果表明, 其提出的方法可以提供优化的降采样轨迹. 此外, 与其他采集轨迹和参数估计方法进行对比, 结果显示该网络在参数估计准确度和可重复性上均展现出较好的性能.

上述介绍的DEXSY相关研究从降低采集点的角度, 缩短了DEXSY在测量水交换信息上的扫描时间. 2006年, Ramadan等^[104,105]提出了一种名为扩散交换加权成像(DEWI)的数据简化和分析框架, 用于估计双室系统中的平均停留时间. 后来 该方法在临床扫描仪上用以对人脑进行研究. 与DEXSY方法相仿, DEWI基于DDE序列, 并采用两个相同的PGSE模块(即b₁ = b₂). Price等^[106]的研究表示, 在较长的交换时间下, DEWI测得的表观扩散系数(ADC)会有所增大, 这是由于长时间内交换效应的增强. 早在2009年, Åslund等^[107]提出了一种DEXSY的“简化”思路和测量技术, FEXSY(filter exchange spectroscopy)技术, 即通过固定第一个扩散加权强度降低采集点数量. FEXSY借鉴了Goldman-Shen实验以及Goldman等^[108,109]提出的双量子滤波/自旋扩散实验的思路, 即使用一个滤波块来“过滤”一部分信号, 实现不同组分信号的分离, 然后等待一段时间(定义为混合时间), 让不同组分“作用”(如不同组分的水分子交换), 恢复至平衡态再检测最终的信号. 在FEXSY中, 是根据不同组分的水分子扩散率不同, 将第1个扩散梯度的强度设置为固定值实现对系统中水分子扩散率较大组分的信号衰减. 在一定的交换时间下, 两组分的水分子交换引起信号的变化. 该研究中, 作者利用一阶动力学模型对细胞外水占比进行拟合((22)式), 得到水分子交换速率, 在酵母细胞悬液样本中测量出25 ℃ 下水分子跨细胞膜交换速率约为3.5 s^–1. 相比DEXSY技术, FEXSY通过固定了第一个扩散加权模块(过滤模块)的b值, 可以减少采样点并缩短扫描时间, 但该方法需要根据系统内不同组分的扩散率差异选择合适的过滤模块b值实现对某一组分信号的特异性的“过滤”. 如, 在细胞悬液样本中, 系统可以分为细胞内和细胞外水, 细胞外水呈现高斯扩散, 具有较高的扩散率($ {D}_{{\mathrm{e}}} $), 细胞内水呈现受限扩散, 扩散率为($ {D}_{{\mathrm{i}}} $). 在FEXSY中, 采集时需要包括满足$ b{D}_{{\mathrm{e}}}\ll 1 $的数据点以“捕获”细胞内外信号, 和$ 1/{D}_{{\mathrm{e}}} < b < 1/{D}_{{\mathrm{i}}} $的数据点以“捕获”细胞内信号, 确保信号对细胞外水占比随交换时间变化的敏感性最大化, 从而根据一阶动力学模型估计出交换速率k^[107]:

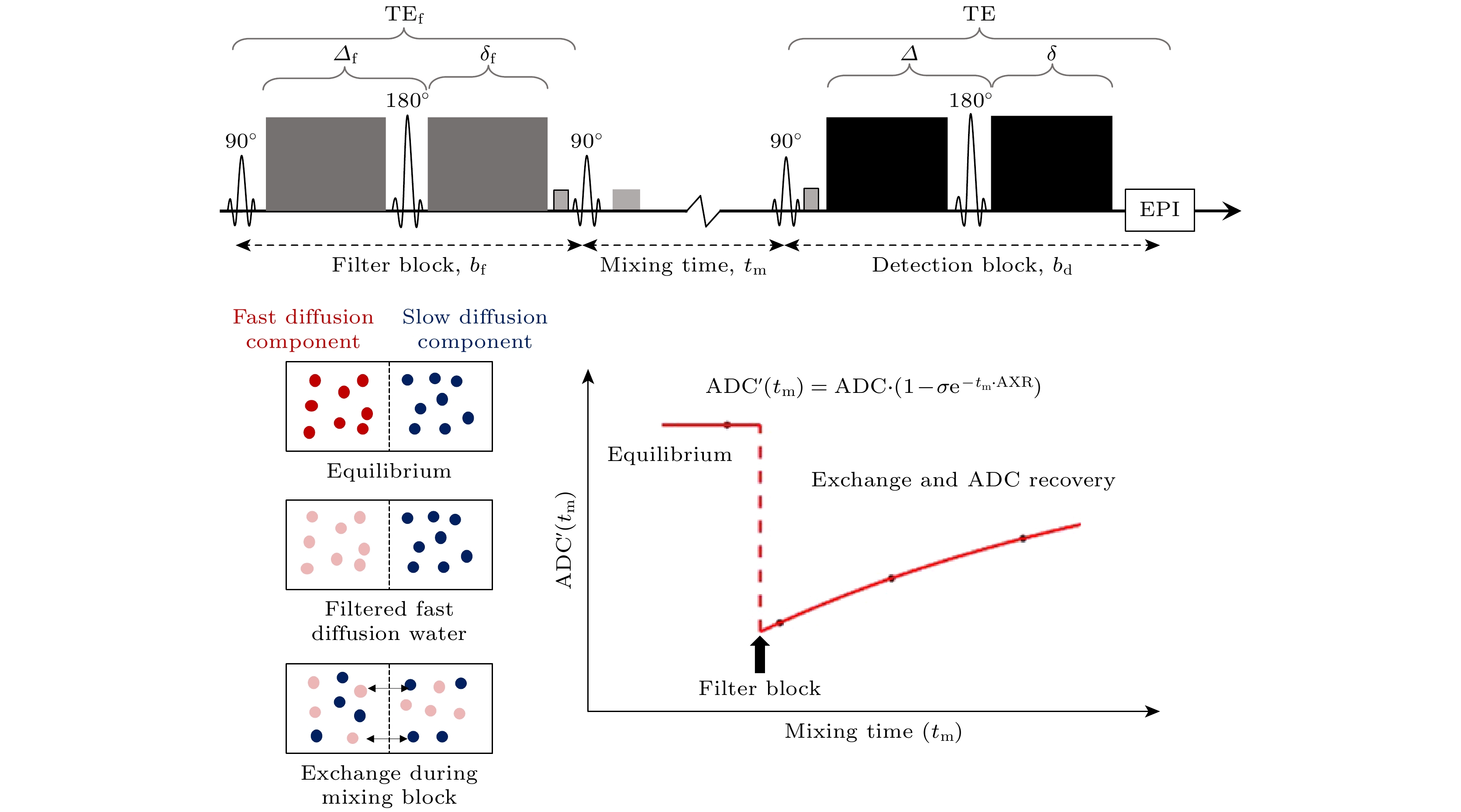
其中, $ {f}_{{\mathrm{e}}}\left({t}_{{\mathrm{m}}}\right) $是在混合时间$ {t}_{{\mathrm{m}}} $时的细胞外水分子的分数, $ {f}_{{\mathrm{e}}}^{{\mathrm{e}}{\mathrm{q}}} $是在平衡状态下细胞外水分子的分数, $ {f}_{{\mathrm{e}}}\left(0\right) $是初始时刻($ {t}_{{\mathrm{m}}}=0 $)细胞外水分子的分数, k是总交换速率常数, 包括从细胞内到细胞外的交换速率常数k_io和从细胞外到细胞内的交换速率常数k_oi.

2011年, Lasič等^[110]将成像模块引入FEXSY并提出过滤交换成像(filter exchange imaging, FEXI), 使其可以使用临床允许的扩散加权因子b值进行水分子交换速率的测量. 在FEXI中, 作者在b值较小时, 对FEXSY中使用的模型进行简化, 推导出(23)式, 引入水分子表观交换速率(apparent exchange rate, AXR)参数来反映水分子交换速率. FEXSY中在第2个扩散加权模块中仍然需要较多个不同b值数据实现对细胞外水分子占比的良好拟合, 但FEXI中可以仅使用两个b值对ADC计算, 进而对不同交换时间下的ADC拟合得到AXR. 作者利用FEXI在酵母细胞悬液样本中得到的AXR在1.7 s^–1左右:

其中, $ \sigma $定义为过滤系数, $ {\mathrm{A}}{\mathrm{D}}{{\mathrm{C}}}_{{\mathrm{e}}{\mathrm{q}}} $为平衡态时系统的表观扩散扩散率. 随后2013年, Nilsson等^[111]将FEXI方法应用到健康被试者和脑膜瘤患者中, 给出人脑AXR图, 测量出健康脑白质和灰质的AXR分别在1.1 s^–1和0.4 s^–1左右. 脑膜瘤患者的肿瘤实体部分则呈现出更高的AXR, 约为2.9 s^–1. FEXI序列示意图及其测量双组分系统中水分子跨膜交换的原理简图如图11所示, 其中Detection block为检测模块; Fast diffusion component为快扩散组分; Filter block为过滤模块; Mixing block为交换模块; Slow diffusion component为慢扩散组分.

自FEXI技术被提出, 其在肿瘤组织的水分子跨细胞膜交换速率测量上展现了一定的可行性, 如区分脑膜瘤实体和坏死区^[110]、不同的乳腺癌亚型^[112]. 然而, 由于正常脑组织中组织微环境更为复杂(细胞形态多样), 不同结构中的水分子扩散行为也更为复杂, 特异性“标记”某两个组分的水分子扩散信号, 实现对特定水分子跨膜交换过程的测量也更为困难. 2020年, Bai等^[28]根据IVIM, 即血管内外水分子表观速率相差1个数量级, 通过在FEXI的过滤模块中首先“过滤”血管内水信号, 实现对水分子跨血脑屏障通透性地测量. 相较于水分子跨血脑屏障交换, 在正常脑组织中由于细胞形态多样性, 细胞内外的水分子扩散行为也更为复杂, 特异性、有效地“标记”细胞内外的水分子扩散信号, 实现对水分子跨细胞膜交换过程的测量更为复杂. 例如, 2014年Sønderby等^[113]在离体猴脑白质中发现FEXI序列中扩散加权梯度方向和白质纤维主朝向夹角不同时, AXR也不同. 后续研究者在健康被试的脑白质上同样发现AXR的方向依赖性, 具体为扩散梯度方向垂直白质纤维主朝向时测量的AXR显著大于扩散梯度方向平行白质纤维主朝向时测量的AXR^[114,115]. 这些研究表明AXR结果会依赖于测量参数的选择, 然而, 不同实验参数下的AXR能否特异性表征某个水分子跨膜交换过程仍不明确. 此外, 在利用FEXI进行水分子跨细胞膜交换过程测量时, AXR是细胞膜通透性的间接表征, 会受细胞大小影响. 2021年Ludwig等^[116]通过仿真实验探究了细胞膜通透性, 细胞大小、朝向分布和实验参数对AXR估计的影响. 2022年, Khateri等^[117]通过仿真实验探究了除细胞膜通透性外, 不同组分由于形态特征不同带来的不同水分子扩散特征对AXR估计的影响.

此外, 在FEXI中根据ADC拟合AXR的模型中, 尚未考虑不同组分水分子弛豫的影响, 且其推导AXR的过程中使用的一阶动力学模型(更适用于化学反应动力学中关于化学底物反应速率问题), 可能不适用于生物组织中由扩散驱动的交换过程. 2024年, Ordinola等^[118]针对该问题, 提出一种更通用的水分子跨膜交换表达式, 以考虑水分子扩散、弛豫过程和几何形状的模型. 该模型从一维离散扩散谱方程出发推导了两个组分的水分子含量占比随时间的变化曲线, 以量化交换信息, 并在基于REXSY(relaxation exchange spectroscopy)序列的仿真数据上对模型进行评估. 在REXSY的仿真数据中, Ordinola等^[118]将其理论框架结果和Cai等^[99]的分析框架进行对比, 在水分子占比的曲线上表现出相似的趋势, 但仍存在数值差异.

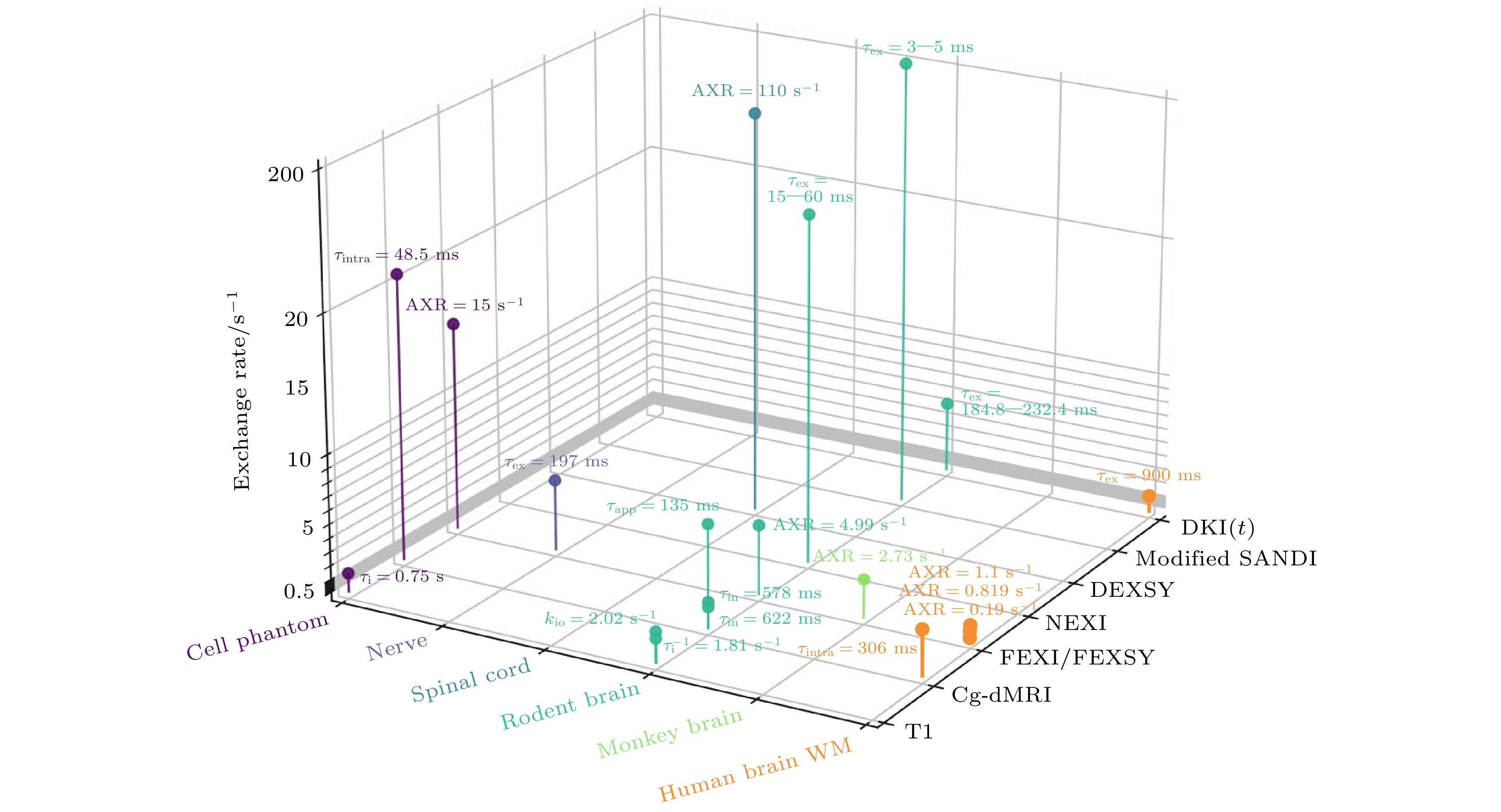
目前, 扩散磁共振领域存在着众多测量水分子跨膜交换的方法, 在同一测量样本上不同方法之间的横向比较有助于比较各种方法测量结果是否一致. Tian等^[119]通过仿真实验和细胞悬液实验评估了CG方法和FEXI方法在测量水分子跨细胞膜交换率常数方面的准确性和可行性. 结果表明没有噪声的情况下, 在k_io< 10 s^–1时CG方法能提供相对准确的参数估计, 但当k_io > 15 s^–1时, CG方法的估计值与真实值之间存在较大偏差. FEXI方法会高估k_io, 但在实际情况较低的SNR下能够提供更合理的参数估计, 即在k_io< 10 s^–1时, CG方法准确性更高, 但需要高SNR, FEXI方法则能在在体实验中的SNR范围下合理估计k_io. 2021年, Li等^[120]在离体小鼠脑组织上评估了FEXI和DKI(t)在测量水分子跨细胞膜运输速率上的一致性, 结果表明在胼胝体中, FEXI测量的AXR与DKI(t)测量的停留时间的倒数呈正相关, 表明两者在白质中对相同交换过程敏感. 然而, 在脑皮层中由于组织微结构的复杂性, 在现有的扩散时间范围下, 受限扩散和水分子交换对信号的影响“混杂”在一起, 基于DKI(t)的水分子交换速率测量受到组织微结构特征的影响, FEXI和DKI(t)的结果存在差异. 离体组织由于组织经过固定水分子的扩散行为会受到改变, 可能对水分子跨膜交换过程造成影响. 基于不同磁共振测量方法获取的不同生物样本的水分子跨膜交换速率或者交换时间如图12所示. 随后, Li等^[121]在健康被试上评估了FEXI和DKI(t)方法测量结果的一致性. 结果表明DKI(t)在较长扩散时间下(>100 ms), 其在脑白质上测量的水分子停留时间的倒数和基于FEXI得到的AXR存在显著相关. 然而, 在灰质上未发现两种方法的测量结果存在一致性.

上述在同一测量样本上的对比研究展示了不同方法可能对同一水分子跨膜过程敏感, 测量结果具有一定的一致性. 然而, 先前不同研究者的结果也显示了不同方法测量结果可能相差较大. 如测量大鼠脑组织中的水分子跨膜交换过程中, 基于NEXI方法得到的水分子停留时间在15—60 ms^[91], 基于改进的SANDI模型的测量结果为3—5 ms^[122], 基于弛豫方法得到的水分子交换速率常数为2 s^–1左右^[123]. 此外, 基于CG的方法, 在不同的扩散时间尺度下, 测量结果也相差较大. 扩散时间在55—395 ms时, 测量到的水分子停留时间为135 ms左右^[124], 扩散时间在23 ms—1.18 s时, 测量到的水分子停留时间为622 ms左右^[125]. 不同的实验条件, 如扩散时间范围, 不同扩散时间尺度下, 对不同的水分子跨膜交换过程敏感程度不同可能是测量结果存在差异的原因之一. 因此, 对不同技术的生理验证更有助于合理评估它们测量的灵敏度和特异性.

本文梳理了生物组织中水分子跨细胞膜交换的磁共振测量方法的发展历程, 主要包括基于弛豫时间和扩散率的两类测量方法. 在基于弛豫时间的测量方法中, 回顾了早期研究者在血红细胞悬液和离体生物组织样本上的测量方法, 以及近年来在体测量方面的进展, 重点介绍了从动态对比增强磁共振数据中估计水分子跨细胞膜交换速率的快门速度模型. 在基于扩散的测量方法中, 本文从不同序列编码方式的角度, 介绍了单扩散梯度编码模块和双扩散梯度编码模块在水分子跨细胞膜交换测量中的进展. 在单扩散梯度编码模块方法上, 重点梳理了不同生物物理模型的发展; 在双扩散梯度编码模块方法上, 介绍了采样方式不同的DEXSY和FEXSY方法, 以及FEXI的研究进展.

在基于弛豫的磁共振测量方法中, 临床可用的快门速度模型动态对比增强磁共振成像方法(SSM-DCE-MRI)能够在静脉注射对比剂的情况下, 通过造成细胞内外水分子的弛豫速率差异, 实现细胞内外信号的区分, 并在快门速度模型的理论框架下实现对在体组织中水分子跨细胞膜交换速率的测量. 目前, SSM-DCE-MRI已在乳腺癌、前列腺癌等疾病的研究中, 对良性和恶性肿瘤的区分显示出一定的应用价值^[63], 与传统的药代动力学模型相比, 该方法得到的$ {k}^{{\mathrm{t}}{\mathrm{r}}{\mathrm{a}}{\mathrm{n}}{\mathrm{s}}} $在恶性肿瘤上表现出更高的值, 且在恶性浸润性导管癌上表现出更强的空间异质性^[64], 这些研究表明该方法有助于更精确地区分恶性肿瘤与良性肿瘤. 此外, 最近的一项基于SSM-DCE-MRI的研究发现其测量的k_io是脑胶质瘤中AQP4表达高敏感、高特异性的潜在影像标志物, 且其评估的AQP4表达水平与胶质瘤治疗抵抗存在直接相关^[41]. 上述研究均显示出了SSM-DCE-MRI在测量肿瘤中的水分子跨细胞膜交换速率的可行性以及潜在临床价值.

然而, SSM-DCE-MRI仍具有一定的局限性: 1)在测量水分子跨细胞膜交换速率上, 要求有足够的对比剂通过血管壁渗透至细胞间隙, 这使其适用于血管通透性较大的肿瘤区域. 然而, 在血脑屏障完整的正常脑组织或血脑屏障轻微破坏的脑疾病中, 该方法则难以得到理想的拟合结果. 2) SSM-DCE-MRI在扫描流程和数据处理的繁杂程度可能限制其在临床上广泛应用的因素. 如在SSM-DCE-MRI的数据拟合中通常采用非线性最小二乘方法, 涉及大量迭代操作, 因而计算时间和算力成本较高. 近年来, 有研究通过深度神经网络优化了DCE-MRI基于经典药代动力学模型(如eTofts模型)的数据处理效率^[126,127]. 然而, 目前依然缺乏对SSM模型的参数估计优化. 在未来的研究中, 如何在待拟合参数更多的SSM模型中保持网络的可训练性和稳定性是该类研究的一个挑战.

基于扩散的水分子跨细胞膜交换速率的磁共振测量则不依赖外部对比剂, 而是利用水分子的扩散率作为对比度, 使其临床应用场景更为广泛. 如近年有研究使用单扩散梯度编码的序列, 结合机器学习的方法(随机森林回归)在多发性髓鞘硬化患者和髓鞘损伤的动物模型上实现了脑白质区域的水分子停留时间测量, 结果表明了发生脱髓鞘病变的区域的水分子停留时间更低, 即水分子跨轴突膜的交换速率增加^[128,129]. 此外, Lasič等^[112]在乳腺癌的在体研究中发现肿瘤组织的AXR值通常高于正常组织, 并且不同亚型的肿瘤组织的AXR值也有所不同, 如低级别浸润性导管癌的AXR值较低.

基于扩散的方法由于无需造影剂, 其临床适用范围更广, 而不仅仅局限于肿瘤. 然而, 该方法目前在序列编码和模型构建上仍有更多的发展空间. 如在单扩散梯度编码的磁共振测量技术中, 目前考虑水分子跨膜交换的模型大多建立在简化生物组织结构的基础上, 相关的简化假设可能影响对系统真实组织微结构特征和跨膜交换过程的测量. 因此, 在未来的研究中, 如何构建合理的理论模型, 以及针对不同模型的生理验证研究有助于找出更能真实表征水分子跨细胞膜交换过程的生物物理模型. 在双扩散梯度编码的磁共振测量技术中, 过滤交换谱/成像技术(FEXSY/FEXI)和DEXSY技术作为“无模型”的水分子跨细胞膜交换测量方法也存在一定的局限性(注: 此处“无模型”指的是它们使用较长的混合时间以使系统达到“粗粒化(coarse-graining)”, 因此未对组织微结构特征进行建模, 但其测量过程仍建立在双组分交换模型的基础上). 如在FEXSY/FEXI中, 通过将过滤模块中的b值设置在一定范围内, 以旨在衰减细胞外水分子信号, 实现细胞内外信号区分. 然而, 在生物组织中, 关于细胞内外水分子扩散率是否存在差异仍存在争议. 在DEXSY中, 虽然DEXSY不依赖细胞内外水分子扩散率的先验知识, 也无需特异性设计扩散编码强度以“标记”某一个组分的信号, 然而, 其测量到的扩散谱与生物组分(如细胞内外水分子)的扩散率之间的对应关系尚不明确. 因此, 在未来的研究中, 如何在信号采集端设计编码方式以提高对水分子跨细胞膜交换过程测量的灵敏性, 在参数拟合端构建合理的理论模型表征信号, 可能是未来研究的重要方向.

总之, 跨细胞膜水分子交换信息是表征细胞功能和状态的重要生物学指标, 已经在肿瘤增殖、神经元活动等多种生物医学场景中找到潜在应用价值. 基于弛豫和扩散的跨细胞膜水分子交换测量已经取得了很大进步, 但都有各自的局限性, 是磁共振领域的一个重要研究方向. 另一方面, 如何和人工智能深度融合, 借助人工智能解决磁共振测量中技术难题, 也是未来的一个发展方向.