高级搜索

高分辨率磁共振二维扩散成像技术综述

,  , 

downloadPDF

上一篇

下一篇

刘凡, 蒋渊丞, 郭华. 高分辨率磁共振二维扩散成像技术综述[J]. 物理学报, 2025, 74(11): 118703-1. doi: 10.7498/aps.74.20250235
引用本文: 刘凡, 蒋渊丞, 郭华. 高分辨率磁共振二维扩散成像技术综述[J]. 物理学报, 2025, 74(11): 118703-1. doi: 10.7498/aps.74.20250235
shu
Fan LIU, Yuancheng JIANG, Hua GUO. Review of high-resolution 2-dimensional diffusion magnetic resonance imaging techniques[J]. Acta Physica Sinica, 2025, 74(11): 118703-1. doi: 10.7498/aps.74.20250235
Citation: Fan LIU, Yuancheng JIANG, Hua GUO. Review of high-resolution 2-dimensional diffusion magnetic resonance imaging techniques[J]. Acta Physica Sinica, 2025, 74(11): 118703-1. doi: 10.7498/aps.74.20250235
shu

高分辨率磁共振二维扩散成像技术综述

  • 清华大学生物医学工程学院, 生物医学影像研究中心, 北京　100084

    • 作者简介: 刘凡. E-mail: liuf22@mails.tsinghua.edu.cn .
    通讯作者: E-mail: huaguo@mail.tsinghua.edu.cn.

  • 中图分类号: 87.61.-c

Review of high-resolution 2-dimensional diffusion magnetic resonance imaging techniques

  • Center for Biomedical Imaging Research, School of Biomedical Engineering, Tsinghua University, Beijing 100084, China

    • Corresponding author: E-mail: huaguo@mail.tsinghua.edu.cn.

  • MSC: 87.61.-c

  • 摘要: 磁共振扩散加权成像(DWI)在神经科学和临床疾病诊断中具有重要价值. 单次激发平面回波成像(ss-EPI)是DWI最常用的技术, 但受主磁场不均匀性和$\rm T_2/T_2^*$衰减的影响, 易出现几何变形、信噪比低等问题. 为解决这些问题, 研究者开发了更先进的高分辨率磁共振扩散成像技术. 本文对这些成像技术进行综述. 平面回波成像(EPI)方面, 本文介绍了读出分段EPI、交错采集EPI、点扩散函数编码EPI、EPTI等多次激发EPI DWI技术, 这些技术能够减小或消除几何变形、提高图像信噪比和分辨率. 此外, 多次激发EPI与多层同时激发技术(SMS)的结合能够缩短采集时间, 本文对此类技术进行简要介绍. 相较于EPI, 螺旋 (spiral)成像的信噪比和采样效率更高, 但对主磁场不均匀性更敏感. 在螺旋成像部分, 本文分别介绍了单次激发以及多次激发的spiral DWI成像, 以及二者与SMS技术的结合. 本文重点介绍了各类成像技术的原理、采集策略与重建方法. 最后, 本文阐述了高分辨率扩散成像的挑战和未来方向, 包括三维DWI、体部DWI、磁场探针、超强梯度磁共振系统以及超高场磁共振系统.
    Abstract: Diffusion-weighted magnetic resonance imaging (DWI) holds significant value in neuroscience and clinical disease diagnosis. The most commonly used single-shot echo-planar imaging (EPI) for DWI is affected by static magnetic field (B0) inhomogeneity and $\rm T_2/T_2^*$ decay, leading to geometric distortion, low signal-to-noise ratio (SNR), etc. To solve these problems, researchers have developed more advanced high-resolution diffusion MRI techniques. This article comprehensively reviews these imaging methods. In the context of echo-planar imaging (EPI), this review covers multi-shot EPI-based DWI techniques, including readout-segmented EPI (RS-EPI), interleaved EPI (iEPI), point spread function-encoded EPI (PSF-EPI), and echo-planar time-resolved imaging (EPTI). These methods effectively reduce or eliminate geometric distortions while improving SNR and spatial resolution. Additionally, the combination of multi-shot EPI with simultaneous multi-slice (SMS) acquisition can shorten scan time, which is also briefly discussed in this article. Compared with EPI, spiral imaging offers higher SNR and sampling efficiency but is more sensitive to B0 inhomogeneity. In the spiral imaging section, we review single-shot spiral DWI and multi-shot spiral DWI, as well as their integration with SMS techniques. This article emphasizes the concepts, acquisition strategies, and reconstruction methods of these imaging techniques. Finally, we discuss the challenges and future directions of high-resolution diffusion imaging, including 3D DWI, body DWI, magnetic field probes, ultra-high gradient systems, and ultra-high-field MRI systems.
  • 加载中

  • 图 1  ss-EPI DWI序列图

    Figure 1.  The pulse sequence diagram of ss-EPI DWI.

    下载: 全尺寸图片 幻灯片

    图 2  4次激发EPI DWI相位校正前(a)后(b)的对比

    Figure 2.  The comparison of 4-shot EPI diffusion-weighted images before (a) and after (b) motion-induced phase correction.

    下载: 全尺寸图片 幻灯片

    图 3  RS-EPI DWI的序列图和k空间轨迹

    Figure 3.  The pulse sequence diagram and k-space trajectory of RS-EPI DWI.

    下载: 全尺寸图片 幻灯片

    图 4  iEPI DWI的序列图和k空间轨迹

    Figure 4.  The pulse sequence diagram and k-space trajectory of iEPI DWI.

    下载: 全尺寸图片 幻灯片

    图 5  ss-EPI和不同激发次数的ms-EPI的对比

    Figure 5.  The comparison of ss-EPI and ms-EPI with different shot numbers.

    下载: 全尺寸图片 幻灯片

    图 6  变形CAIPI PSF-EPI的序列图和信号采集模式

    Figure 6.  The pulse sequence diagram and data sampling pattern of tilted CAIPI PSF-EPI.

    下载: 全尺寸图片 幻灯片

    图 7  iEPI, PSF-EPI和TSE在颅底成像的对比

    Figure 7.  The comparison of iEPI, PSF-EPI, and turbo spin-echo imaging in skull base.

    下载: 全尺寸图片 幻灯片

    图 8  ss-spiral DWI序列

    Figure 8.  The sequence diagram of ss-spiral DWI.

    下载: 全尺寸图片 幻灯片

    图 9  高倍降采的ss-spiral采集的亚毫米级高分辨率扩散成像结果, 层内分辨率为0.77 mm ×0.77 mm, 从上至下分别显示了6个具有代表性层面的b = 0图像、b = 1000 s/mm2的DWI图像、平均DWI和彩色FA图, 放大显示了小脑、脑桥、放射冠和颞叶等部位的精细结构

    Figure 9.  Results of submillimeter high-resolution diffusion imaging obtained from a ss-spiral acquisition with a high under-sampling rate. The in-plane resolution is 0.77 mm×0.77 mm, from top to bottom, the figure displays b= 0 images, DWI images with b = 1000 s/mm², mean DWI, and color FA maps for six representative slices. Enlarged views highlight fine structures in the cerebellum, pons, corona radiata, and temporal lobe.

    下载: 全尺寸图片 幻灯片

    图 10  ms-spiral DWI相位误差示意图. 施加扩散梯度会引起各次激发的相位不一致, 直接重建得到的图像会存在严重的混叠伪影

    Figure 10.  Schematic diagram of phase errors in ms-spiral DWI, applying diffusion gradients induces phase variations between shots, leading to severe aliasing artifacts in images reconstructed directly.

    下载: 全尺寸图片 幻灯片

    图 11  VDS, DDS, UDS轨迹的示意图, VDS的采样密度随螺旋半径增大而减小, DDS在k空间中心很高的采样密度, 在中心周围密度较低, UDS在整个k空间的采样密度保持一致

    Figure 11.  Schematic diagrams of VDS, DDS, and UDS trajectories, the sampling density of VDS decreases as the spiral radius increases, while DDS exhibits a very high sampling density at the center of k-space with lower density in the surrounding areas, UDS maintains a consistent sampling density throughout the entire k-space.

    下载: 全尺寸图片 幻灯片

    图 12  同时激发2个层面的6次激发螺旋扩散成像结果, 从上至下分别为b = 0图像、b = 800 s/mm2扩散图像、平均DWI图像和彩色FA图

    Figure 12.  Results of 6-shot spiral diffusion imaging with simultaneous excitation of two slices. From top to bottom: b = 0 images, b = 800 s/mm² diffusion images, mean DWI images, and color FA maps.

    下载: 全尺寸图片 幻灯片
  • [1] Basser P J, Mattiello J, LeBihan D 1994 Biophys. J. 66 259 doi: 10.1016/S0006-3495(94)80775-1
    [2] Mansfield P 1977 J. Phys. C: Solid State Phys. 10 L55 doi: 10.1088/0022-3719/10/3/004
    [3] Meyer C H, Hu B S, Nishimura D G, Macovski A 1992 Magn. Reson. Med. 28 202 doi: 10.1002/mrm.1910280204
    [4] Hennig J, Nauerth A, Friedburg H 1986 Magn. Reson. Med. 3 823 doi: 10.1002/mrm.1910030602
    [5] Pipe J G 1999 Magn. Reson. Med. 42 963 doi: 10.1002/(SICI)1522-2594(199911)42:5<963::AID-MRM17>3.0.CO;2-L
    [6] Holdsworth S J, O'Halloran R, Setsompop K 2019 NMR Biomed. 32 e4056 doi: 10.1002/nbm.4056
    [7] McNab J A, Polimeni J R, Wang R, Augustinack J C, Fujimoto K, Stevens A, Janssens T, Farivar R, Folkerth R D, Vanduffel W, Wald L L 2013 Neuroimage 69 87 doi: 10.1016/j.neuroimage.2012.11.065
    [8] Sodickson D K, Manning W J 1997 Magn. Reson. Med. 38 591 doi: 10.1002/mrm.1910380414
    [9] Pruessmann K P, Weiger M, Scheidegger M B, Boesiger P 1999 Magn. Reson. Med. 42 952 doi: 10.1002/(SICI)1522-2594(199911)42:5<952::AID-MRM16>3.0.CO;2-S
    [10] Griswold M A, Jakob P M, Heidemann R M, Nittka M, Jellus V, Wang J, Kiefer B, Haase A 2002 Magn. Reson. Med. 47 1202 doi: 10.1002/mrm.10171
    [11] Liu F, Wu L, Luo X, Li S, Wang Y, Zhong W, Feiweier T, Xu J, Shi D, Bao H 2025 J. Magn. Reson. Imaging
    [12] Uğurbil K, Xu J, Auerbach E J, Moeller S, Vu A T, Duarte-Carvajalino J M, Lenglet C, Wu X, Schmitter S, Van de Moortele P F, Strupp J, Sapiro G, De Martino F, Wang D, Harel N, Garwood M, Chen L, Feinberg D A, Smith S M, Miller K L, Sotiropoulos S N, Jbabdi S, Andersson J L R, Behrens T E J, Glasser M F, Van Essen D C, Yacoub E 2013 Neuroimage 80 80 doi: 10.1016/j.neuroimage.2013.05.012
    [13] Van Essen D C, Smith S M, Barch D M, Behrens T E J, Yacoub E, Ugurbil K 2013 Neuroimage 80 62 doi: 10.1016/j.neuroimage.2013.05.041
    [14] Holdsworth S J, Skare S, Newbould R D, Guzmann R, Blevins N H, Bammer R 2008 Eur. J. Radiol. 65 36 doi: 10.1016/j.ejrad.2007.09.016
    [15] Porter D A, Heidemann R M 2009 Magn. Reson. Med. 62 468 doi: 10.1002/mrm.22024
    [16] Robson M D, Anderson A W, Gore J C 1997 Magn. Reson. Med. 38 82 doi: 10.1002/mrm.1910380113
    [17] Butts K, Riederer S J, Ehman R L, Thompson R M, Jack C R 1994 Magn. Reson. Med. 31 67 doi: 10.1002/mrm.1910310111
    [18] Butts K, Pauly J, De Crespigny A, Moseley M 1997 Magn. Reson. Med. 38 741 doi: 10.1002/mrm.1910380510
    [19] Butts K, de Crespigny A, Pauly J M, Moseley M 1996 Magn. Reson. Med. 35 763 doi: 10.1002/mrm.1910350518
    [20] Zhang Z, Zhang B, Li M, Liang X, Chen X D, Liu R Y, Zhang X, Guo H 2017 J. Magn. Reson. Imaging 46 167 doi: 10.1002/jmri.25522
    [21] Jones D K 2010 Diffusion MRI (Oxford: Oxford University Press) pp187–188
    [22] Zeng H, Constable R T 2002 Magn. Reson. Med. 48 137 doi: 10.1002/mrm.10200
    [23] Robson M D, Gore J C, Constable R T 1997 Magn. Reson. Med. 38 733 doi: 10.1002/mrm.1910380509
    [24] In M H, Posnansky O, Speck O 2017 Neuroimage 148 20 doi: 10.1016/j.neuroimage.2017.01.008
    [25] Dong Z, Wang F, Reese T G, Manhard M K, Bilgic B, Wald L L, Guo H, Setsompop K 2019 Magn. Reson. Med. 81 377 doi: 10.1002/mrm.27413
    [26] Mansfield P 1984 Magn. Reson. Med. 1 370 doi: 10.1002/mrm.1910010308
    [27] Wang F Y X, Dong Z J, Reese T G, Bilgic B, Katherine Manhard M, Chen J, Polimeni J R, Wald L L, Setsompop K 2019 Magn. Reson. Med. 81 3599 doi: 10.1002/mrm.27673
    [28] Dong Z J, Wang F Y X, Reese T G, Bilgic B, Setsompop K 2020 Magn. Reson. Med. 84 2442 doi: 10.1002/mrm.28295
    [29] Dai E P, Lee P K, Dong Z J, Fu F, Setsompop K, McNab J A 2022 IEEE Trans. Med. Imaging 41 63 doi: 10.1109/TMI.2021.3104291
    [30] Dong Z J, Wang F, Wald L, Setsompop K 2022 Magn. Reson. Med. 88 164 doi: 10.1002/mrm.29198
    [31] Dong Z J, Reese T G, Lee H H, Huang S Y, Polimeni J R, Wald L L, Wang F 2025 Magn. Reson. Med. 93 1535 doi: 10.1002/mrm.30365
    [32] Lee Y, Wilm B J, Brunner D O, Gross S, Schmid T, Nagy Z, Pruessmann K P 2021 Magn. Reson. Med. 85 1924 doi: 10.1002/mrm.28554
    [33] Wilm B J, Barmet C, Gross S, Kasper L, Vannesjo S J, Haeberlin M, Dietrich B E, Brunner D O, Schmid T, Pruessmann K P 2017 Magn. Reson. Med. 77 83 doi: 10.1002/mrm.26493
    [34] Varela-Mattatall G, Dubovan P I, Santini T, Gilbert K M, Menon R S, Baron C A 2023 Magn. Reson. Med. 90 615 doi: 10.1002/mrm.29666
    [35] Wilm B J, Hennel F, Roesler M B, Weiger M, Pruessmann K P 2020 Magn. Reson. Med. 84 3117 doi: 10.1002/mrm.28346
    [36] Pruessmann K P, Weiger M, Börnert P, Boesiger P 2001 Magn. Reson. Med. 46 638 doi: 10.1002/mrm.1241
    [37] Heidemann R M, Griswold M A, Seiberlich N, Krüger G, Kannengiesser S A R, Kiefer B, Wiggins G, Wald L L, Jakob P M 2006 Magn. Reson. Med. 56 317 doi: 10.1002/mrm.20951
    [38] Liu C, Moseley M E, Bammer R 2005 Magn. Reson. Med. 54 1412 doi: 10.1002/mrm.20706
    [39] Liu C, Bammer R, Kim D-h, Moseley M E 2004 Magn. Reson. Med. 52 1388 doi: 10.1002/mrm.20288
    [40] Guo H, Ma X D, Zhang Z, Zhang B D, Yuan C, Huang F 2016 Magn. Reson. Med. 75 169 doi: 10.1002/mrm.25594
    [41] Li G Q, Ma X D, Li S S, Ye X Y, Börnert P, Zhou X J, Guo H 2023 Magn. Reson. Med. 90 133 doi: 10.1002/mrm.29633
    [42] Truong T K, Guidon A 2014 Magn. Reson. Med. 71 790 doi: 10.1002/mrm.24709
    [43] Hoge W S, Polimeni J R 2016 Magn. Reson. Med. 76 32 doi: 10.1002/mrm.25839
    [44] McKay J A, Moeller S, Zhang L, Auerbach E J, Nelson M T, Bolan P J 2019 Magn. Reson. Med. 81 2624 doi: 10.1002/mrm.27563
    [45] Larkman D J, Hajnal J V, Herlihy A H, Coutts G A, Young I R, Ehnholm G 2001 J. Magn. Reson. Imaging 13 313 doi: 10.1002/1522-2586(200102)13:2<313::AID-JMRI1045>3.0.CO;2-W
    [46] Setsompop K, Gagoski B A, Polimeni J R, Witzel T, Wedeen V J, Wald L L 2012 Magn. Reson. Med. 67 1210 doi: 10.1002/mrm.23097
    [47] Barth M, Breuer F, Koopmans P J, Norris D G, Poser B A 2016 Magn. Reson. Med. 75 63 doi: 10.1002/mrm.25897
    [48] Breuer F A, Blaimer M, Heidemann R M, Mueller M F, Griswold M A, Jakob P M 2005 Magn. Reson. Med. 53 684 doi: 10.1002/mrm.20401
    [49] Heidemann R M, Porter D A, Anwander A, Feiweier T, Heberlein K, Knösche T R, Turner R 2010 Magn. Reson. Med. 64 9 doi: 10.1002/mrm.22480
    [50] Frost R, Porter D A, Miller K L, Jezzard P 2012 Magn. Reson. Med. 68 441 doi: 10.1002/mrm.23242
    [51] Holdsworth S J, Skare S, Newbould R D, Bammer R 2009 Magn. Reson. Med. 62 1629 doi: 10.1002/mrm.22122
    [52] Bogner W, Pinker-Domenig K, Bickel H, Chmelik M, Weber M, Helbich T H, Trattnig S, Gruber S 2012 Radiology 263 64 doi: 10.1148/radiol.12111494
    [53] Bogner W, Pinker K, Zaric O, Baltzer P, Minarikova L, Porter D, Bago-Horvath Z, Dubsky P, Helbich T H, Trattnig S, Gruber S 2014 Radiology 274 74
    [54] Wisner D J, Rogers N, Deshpande V S, Newitt D N, Laub G A, Porter D A, Kornak J, Joe B N, Hylton N M 2014 J. Magn. Reson. Imaging 40 674 doi: 10.1002/jmri.24416
    [55] Tokoro H, Fujinaga Y, Ohya A, Ueda K, Shiobara A, Kitou Y, Ueda H, Kadoya M 2014 Eur. J. Radiol. 83 1728 doi: 10.1016/j.ejrad.2014.06.013
    [56] Foltz W D, Porter D A, Simeonov A, Aleong A, Jaffray D, Chung P, Han K, Ménard C 2015 Radiother. Oncol. 117 525 doi: 10.1016/j.radonc.2015.07.046
    [57] Thian Y L, Xie W, Porter D A, Weileng Ang B 2014 Acad. Radiol. 21 531 doi: 10.1016/j.acra.2014.01.005
    [58] Yeom K W, Holdsworth S J, Van A T, Iv M, Skare S, Lober R M, Bammer R 2013 Am. J. Roentgenol. 200 W437 doi: 10.2214/AJR.12.9854
    [59] Feinberg D A, Oshio K 1994 Magn. Reson. Med. 32 535 doi: 10.1002/mrm.1910320418
    [60] Jeong H K, Gore J C, Anderson A W 2013 Magn. Reson. Med. 69 793 doi: 10.1002/mrm.24320
    [61] Dai E P, Zhang Z, Ma X D, Dong Z J, Li X S, Xiong Y H, Yuan C, Guo H 2018 Magn. Reson. Med. 80 2024 doi: 10.1002/mrm.27190
    [62] Ma X D, Zhang Z, Dai E P, Guo H 2016 Neuroimage 138 88 doi: 10.1016/j.neuroimage.2016.05.079
    [63] Liu W T, Zhao X N, Ma Y J, Tang X, Gao J H 2016 Magn. Reson. Med. 75 280 doi: 10.1002/mrm.25586
    [64] Chen N K, Guidon A, Chang H C, Song A W 2013 Neuroimage 72 41 doi: 10.1016/j.neuroimage.2013.01.038
    [65] Guhaniyogi S, Chu M L, Chang H C, Song A W, Chen N K 2016 Magn. Reson. Med. 75 639 doi: 10.1002/mrm.25624
    [66] Herbst M, Zahneisen B, Knowles B, Zaitsev M, Ernst T 2015 Magn. Reson. Med. 74 1675 doi: 10.1002/mrm.25547
    [67] Zhang Z, Huang F, Ma X, Xie S, Guo H 2015 Neuroimage 105 552 doi: 10.1016/j.neuroimage.2014.10.022
    [68] Chu M L, Chang H C, Chung H W, Truong T K, Bashir M R, Chen N K 2015 Magn. Reson. Med. 74 1336 doi: 10.1002/mrm.25527
    [69] Hu Y, Levine E G, Tian Q, Moran C J, Wang X, Taviani V, Vasanawala S S, McNab J A, Daniel B A, Hargreaves B L 2019 Magn. Reson. Med. 81 1181 doi: 10.1002/mrm.27488
    [70] Mani M, Jacob M, Kelley D, Magnotta V 2017 Magn. Reson. Med. 78 494 doi: 10.1002/mrm.26382
    [71] Mani M, Aggarwal H K, Magnotta V, Jacob M 2020 Magn. Reson. Med. 83 2253 doi: 10.1002/mrm.28090
    [72] Liao C, Bilgic B, Tian Q, Stockmann J P, Cao X, Fan Q, Iyer S S, Wang F, Ngamsombat C, Lo W C, Manhard M K, Huang S Y, Wald L L, Setsompop K 2021 Magn. Reson. Med. 86 791 doi: 10.1002/mrm.28748
    [73] Jenkinson M, Beckmann C F, Behrens T E J, Woolrich M W, Smith S M 2012 Neuroimage 62 782 doi: 10.1016/j.neuroimage.2011.09.015
    [74] Andersson J L R, Skare S, Ashburner J 2003 Neuroimage 20 870 doi: 10.1016/S1053-8119(03)00336-7
    [75] Zahneisen B, Aksoy M, Maclaren J, Wuerslin C, Bammer R 2017 Neuroimage 153 97 doi: 10.1016/j.neuroimage.2017.03.052
    [76] Setsompop K, Fan Q, Stockmann J, Bilgic B, Huang S, Cauley S F, Nummenmaa A, Wang F, Rathi Y, Witzel T, Wald L L 2018 Magn. Reson. Med. 79 141 doi: 10.1002/mrm.26653
    [77] Liao C Y, Yarach U, Cao X Z, Iyer S S, Wang N, Kim T H, Tian Q Y, Bilgic B, Kerr A B, Setsompop K 2023 Neuroimage 275 120168 doi: 10.1016/j.neuroimage.2023.120168
    [78] Kim T H, Setsompop K, Haldar J P 2017 Magn. Reson. Med. 77 1021 doi: 10.1002/mrm.26182
    [79] Dong Y, Koolstra K, Li Z, Riedel M, van Osch M J P, Börnert P 2024 Magn. Reson. Med. 91 205 doi: 10.1002/mrm.29848
    [80] Dong Y, Atkinson D, Koolstra K, van Osch M J P, Börnert P 2025 Magn. Reson. Med. 93 1059 doi: 10.1002/mrm.30334
    [81] Bilgic B, Chatnuntawech I, Manhard M K, Tian Q, Liao C, Iyer S S, Cauley S F, Huang S Y, Polimeni J R, Wald L L, Setsompop K 2019 Magn. Reson. Med. 82 1343 doi: 10.1002/mrm.27813
    [82] Zhang H, Wang C Y, Chen W B, Wang F W, Yang Z D, Xu S, Wang H 2021 Neuroimage 244 118632 doi: 10.1016/j.neuroimage.2021.118632
    [83] Hu Y X, Xu Y Y, Tian Q Y, Chen F Y, Shi X W, Moran C J, Daniel B L, Hargreaves B A 2021 Magn. Reson. Med. 85 709 doi: 10.1002/mrm.28446
    [84] Chung J Y, In M H, Oh S H, Zaitsev M, Speck O, Cho Z H 2011 Magn. Reson. Mater. Phys. Biol. Med. 24 179 doi: 10.1007/s10334-011-0251-1
    [85] In M H, Posnansky O, Beall E B, Lowe M J, Speck O 2015 PLoS One 10 e0116320 doi: 10.1371/journal.pone.0116320
    [86] In M H, Speck O 2012 Magn. Reson. Mater. Phys. Biol. Med. 25 183 doi: 10.1007/s10334-011-0275-6
    [87] Oh S H, Chung J Y, In M H, Zaitsev M, Kim Y B, Speck O, Cho Z H 2012 Magn. Reson. Med. 68 1239 doi: 10.1002/mrm.23317
    [88] In M H, Cho S, Shu Y, Min H K, Bernstein M A, Speck O, Lee K H, Jo H J 2017 Neuroimage 158 26 doi: 10.1016/j.neuroimage.2017.06.069
    [89] Saritas E U, Cunningham C H, Lee J H, Han E T, Nishimura D G 2008 Magn. Reson. Med. 60 468 doi: 10.1002/mrm.21640
    [90] Wheeler-Kingshott C A M, Hickman S J, Parker G J M, Ciccarelli O, Symms M R, Miller D H, Barker G J 2002 Neuroimage 16 93 doi: 10.1006/nimg.2001.1022
    [91] Wheeler-Kingshott C A M, Parker G J M, Symms M R, Hickman S J, Tofts P S, Miller D H, Barker G J 2002 Magn. Reson. Med. 47 24 doi: 10.1002/mrm.10016
    [92] In M H, Tan E T, Trzasko J D, Shu Y, Kang D, Yarach U, Tao S, Gray E M, Huston Iii J, Bernstein M A 2020 J. Magn. Reson. Imaging 51 296 doi: 10.1002/jmri.26792
    [93] Hu Z X, Wang Y S, Dong Z J, Guo H 2019 Magn. Reson. Med. 82 251 doi: 10.1002/mrm.27717
    [94] Li S S, Wang Y S, Hu Z X, Guan L, Hai Y, Zhang H W, He L, Jiang W, Guo H 2021 Neuroimage 236 118043 doi: 10.1016/j.neuroimage.2021.118043
    [95] Hu Z X, Wang Y S, Zhang Z, Zhang J J, Zhang H M, Guo C J, Sun Y J, Guo H 2020 Neuroimage 221 117170 doi: 10.1016/j.neuroimage.2020.117170
    [96] Fair M J, Wang F, Dong Z J, Reese T G, Setsompop K 2020 Magn. Reson. Med. 83 2124 doi: 10.1002/mrm.28071
    [97] Fair M J, Liao C, Manhard M K, Setsompop K 2021 Magn. Reson. Med. 85 2417 doi: 10.1002/mrm.28579
    [98] Wang F, Dong Z J, Wald L L, Polimeni J R, Setsompop K 2021 Neuroimage 245 118641 doi: 10.1016/j.neuroimage.2021.118641
    [99] Dong Z J, Wang F, Chan K S, Reese T G, Bilgic B, Marques J P, Setsompop K 2021 Neuroimage 232 117897 doi: 10.1016/j.neuroimage.2021.117897
    [100] Wang F, Dong Z J, Reese T G, Rosen B, Wald L L, Setsompop K 2022 Neuroimage 250 118963 doi: 10.1016/j.neuroimage.2022.118963
    [101] Chang H C, Guhaniyogi S, Chen N K 2015 Magn. Reson. Med. 73 1872 doi: 10.1002/mrm.25318
    [102] Frost R, Jezzard P, Douaud G, Clare S, Porter D A, Miller K L 2015 Magn. Reson. Med. 74 136 doi: 10.1002/mrm.25391
    [103] Dai E P, Ma X D, Zhang Z, Yuan C, Guo H 2017 Magn. Reson. Med. 77 1593 doi: 10.1002/mrm.26249
    [104] Zahneisen B, Poser B A, Ernst T, Stenger V A 2014 Magn. Reson. Med. 71 2071 doi: 10.1002/mrm.24875
    [105] Blaimer M, Breuer F A, Mueller M, Seiberlich N, Ebel D, Heidemann R M, Griswold M A, Jakob P M 2006 Magn. Reson. Med. 56 1359 doi: 10.1002/mrm.21071
    [106] Herbst M, Deng W, Ernst T, Stenger V A 2017 Magn. Reson. Med. 78 1476 doi: 10.1002/mrm.26545
    [107] Dong Z J, Dai E P, Wang F Y, Zhang Z, Ma X D, Yuan C, Guo H 2018 Med. Phys. 45 3196 doi: 10.1002/mp.12974
    [108] Mani M, Jacob M, McKinnon G, Yang B, Rutt B, Kerr A, Magnotta V 2020 Magn. Reson. Med. 83 154 doi: 10.1002/mrm.27924
    [109] Dai E P, Mani M, McNab J A 2023 Magn. Reson. Med. 89 95 doi: 10.1002/mrm.29422
    [110] De Zanche N, Barmet C, Nordmeyer-Massner J A, Pruessmann K P 2008 Magn. Reson. Med. 60 176 doi: 10.1002/mrm.21624
    [111] Wilm B J, Nagy Z, Barmet C, Vannesjo S J, Kasper L, Haeberlin M, Gross S, Dietrich B E, Brunner D O, Schmid T, Pruessmann K P 2015 Magn. Reson. Med. 74 925 doi: 10.1002/mrm.25827
    [112] Kasper L, Engel M, Heinzle J, Mueller-Schrader M, Graedel N N, Reber J, Schmid T, Barmet C, Wilm B J, Stephan K E, Pruessmann K P 2022 Neuroimage 246 118738 doi: 10.1016/j.neuroimage.2021.118738
    [113] Fessler J A 2007 J. Magn. Reson. 188 191 doi: 10.1016/j.jmr.2007.06.012
    [114] Jackson J I, Meyer C H, Nishimura D G, Macovski A 1991 IEEE Trans. Med. Imaging 10 473 doi: 10.1109/42.97598
    [115] Pipe J G, Menon P 1999 Magn. Reson. Med. 41 179 doi: 10.1002/(SICI)1522-2594(199901)41:1<179::AID-MRM25>3.0.CO;2-V
    [116] Barnett A H, Magland J, Klinteberg L A 2019 SIAM J. Sci. Comput. 41 C479 doi: 10.1137/18M120885X
    [117] Lustig M, Pauly J M 2010 Magn. Reson. Med. 64 457 doi: 10.1002/mrm.22428
    [118] Hestenes M R, Stiefel E 1952 J. Res. Natl. Bur. Stand. 49 409 doi: 10.6028/jres.049.044
    [119] Qu P, Zhong K, Zhang B D, Wang J M, Shen G X 2005 Magn. Reson. Med. 54 1040 doi: 10.1002/mrm.20648
    [120] Samsonov A A, Kholmovski E G, Parker D L, Johnson C R 2004 Magn. Reson. Med. 52 1397 doi: 10.1002/mrm.20285
    [121] Zhang T, Pauly J M, Vasanawala S S, Lustig M 2013 Magn. Reson. Med. 69 571 doi: 10.1002/mrm.24267
    [122] Lustig M, Donoho D, Pauly J M 2007 Magn. Reson. Med. 58 1182 doi: 10.1002/mrm.21391
    [123] Murphy M, Alley M, Demmel J, Keutzer K, Vasanawala S, Lustig M 2012 IEEE Trans. Med. Imaging 31 1250 doi: 10.1109/TMI.2012.2188039
    [124] Moeller S, Pisharady P K, Ramanna S, Lenglet C, Wu X, Dowdle L, Yacoub E, Uğurbil K, Akçakaya M 2021 Neuroimage 226 117539 doi: 10.1016/j.neuroimage.2020.117539
    [125] Engel M, Mueller L, Döring A, Afzali M, Jones D K 2023 Magn. Reson. Med. 91 1323
    [126] Vannesjo S J, Graedel N N, Kasper L, Gross S, Busch J, Haeberlin M, Barmet C, Pruessmann K P 2016 Magn. Reson. Med. 76 45 doi: 10.1002/mrm.25841
    [127] Kim D H, Adalsteinsson E, Spielman D M 2003 Magn. Reson. Med. 50 214 doi: 10.1002/mrm.10493
    [128] Lin W, Börnert P, Huang F, Duensing G R, Reykowski A 2011 Magn. Reson. Med. 66 1067 doi: 10.1002/mrm.22900
    [129] Hu Z X, Ma X D, Truong T K, Song A W, Guo H 2017 Magn. Reson. Med. 78 172 doi: 10.1002/mrm.26361
    [130] Hu Z X, Zhang Z, Ma X D, Jing J, Guo H 2023 Med. Phys. 50 980 doi: 10.1002/mp.16146
    [131] Jiang Y C, Li G Q, Shao X, Guo H 2025 Magn. Reson. Med. 94 73 doi: 10.1002/mrm.30427
    [132] Frost R, Miller K L, Tijssen R H N, Porter D A, Jezzard P 2014 Magn. Reson. Med. 72 1565 doi: 10.1002/mrm.25062
    [133] Engström M, Skare S 2013 Magn. Reson. Med. 70 1507 doi: 10.1002/mrm.24594
    [134] Wu W, Poser B A, Douaud G, Frost R, In M-H, Speck O, Koopmans P J, Miller K L 2016 Neuroimage 143 1 doi: 10.1016/j.neuroimage.2016.08.054
    [135] Chen X, Wu W C, Chiew M 2024 Magn. Reson. Med. 91 2443 doi: 10.1002/mrm.30019
    [136] Li Z Y, Miller K L, Chen X, Chiew M, Wu W C 2025 IEEE Trans. Med. Imaging 44 632 doi: 10.1109/TMI.2024.3454994
    [137] Li Z Y, Miller K L, Andersson J L R, Zhang J Y, Liu S M, Guo H, Wu W C 2023 Magn. Reson. Med. 90 1484 doi: 10.1002/mrm.29741
    [138] Moeller S, Ramanna S, Lenglet C, Pisharady P K, Auerbach E J, Delabarre L, Wu X, Akcakaya M, Ugurbil K 2020 Magn. Reson. Med. 84 1747 doi: 10.1002/mrm.28231
    [139] Chang H C, Sundman M, Petit L, Guhaniyogi S, Chu M L, Petty C, Song A W, Chen N K 2015 Neuroimage 118 667 doi: 10.1016/j.neuroimage.2015.06.016
    [140] Dai E P, Wu Y, Wu W C, Guo R, Liu S M, Miller K L, Zhang Z, Guo H 2019 Magn. Reson. Med. 82 1012 doi: 10.1002/mrm.27793
    [141] Dai E P, Liu S M, Guo H 2021 Neuroimage 237 118099 doi: 10.1016/j.neuroimage.2021.118099
    [142] Zhang J Y, Liu S M, Dai E P, Ye X Y, Shi D W, Wu Y, Lu J, Guo H 2022 Magn. Reson. Med. 87 1546 doi: 10.1002/mrm.29047
    [143] Liu S M, Xiong Y H, Dai E P, Zhang J Y, Guo H 2021 Magn. Reson. Med. 86 2780 doi: 10.1002/mrm.28884
    [144] Liu S M, Zhang J Y, Shi D W, Guo H 2023 Magn. Reson. Med. 90 978 doi: 10.1002/mrm.29685
    [145] Holtrop J, Sutton B 2016 Journal of Medical Imaging 3 023501 doi: 10.1117/1.JMI.3.2.023501
    [146] Geng R, Zhang Y, Rice J, Muehler M R, Starekova J, Rutkowski D R, Uboha N V, Pirasteh A, Roldán-Alzate A, Guidon A, Hernando D 2023 Magn. Reson. Med. 89 908 doi: 10.1002/mrm.29531
    [147] Kara D, Liu Y, Chen S, Garrett T, Younis A, Sugawara M, Bolen M A, Bi X, Wazni O, Nakagawa H, Kwon D, Nguyen C 2025 Magn. Reson. Med. 93 673 doi: 10.1002/mrm.30308
    [148] Molendowska M, Palombo M, Foley K G, Narahari K, Fasano F, Jones D K, Alexander D C, Panagiotaki E, Tax C M W 2024 NMR Biomed. 37 e5229 doi: 10.1002/nbm.5229
    [149] Dong Y, Koolstra K, Riedel M, van Osch M J P, Börnert P 2021 Magn. Reson. Med. 86 3034 doi: 10.1002/mrm.28919
    [150] Dong Y, Riedel M, Koolstra K, van Osch M J P, Börnert P 2023 NMR Biomed. 36 e4822 doi: 10.1002/nbm.4822
    [151] Ramos‐Llordén G, Park D J, Kirsch J E, Scholz A, Keil B, Maffei C, Lee H H, Bilgic B, Edlow B L, Mekkaoui C, Yendiki A, Witzel T, Huang S Y 2024 Magn. Reson. Med. 91 541 doi: 10.1002/mrm.29873
    [152] Ma R, Akcakaya M, Moeller S, Auerbach E, Ugurbil K, Van de Moortele P F 2020 Neuroimage 216 116861 doi: 10.1016/j.neuroimage.2020.116861
    [153] Zhu A, Tarasek M, Hua Y, Fiveland E, Maier S E, Mazaheri Y, Fung M, Westin C F, Yeo D T, Szczepankiewicz F 2024 Magn. Reson. Med. 91 640 doi: 10.1002/mrm.29874
    [154] Feinberg D A, Beckett A J S, Vu A T, Stockmann J, Huber L, Ma S, Ahn S, Setsompop K, Cao X, Park S, Liu C, Wald L L, Polimeni J R, Mareyam A, Gruber B, Stirnberg R, Liao C, Yacoub E, Davids M, Bell P, Rummert E, Koehler M, Potthast A, Gonzalez-Insua I, Stocker S, Gunamony S, Dietz P 2023 Nat. Methods 20 2048 doi: 10.1038/s41592-023-02068-7
    [155] Huang S Y, Witzel T, Keil B, Scholz A, Davids M, Dietz P, Rummert E, Ramb R, Kirsch J E, Yendiki A, Fan Q, Tian Q, Ramos-Llordén G, Lee H-H, Nummenmaa A, Bilgic B, Setsompop K, Wang F, Avram A V, Komlosh M, Benjamini D, Magdoom K N, Pathak S, Schneider W, Novikov D S, Fieremans E, Tounekti S, Mekkaoui C, Augustinack J, Berger D, Shapson-Coe A, Lichtman J, Basser P J, Wald L L, Rosen B R 2021 Neuroimage 243 118530 doi: 10.1016/j.neuroimage.2021.118530
    [156] Foo T K, Tan E T, Vermilyea M E, Hua Y, Fiveland E W, Piel J E, Park K, Ricci J, Thompson P S, Graziani D 2020 Magn. Reson. Med. 83 2356 doi: 10.1002/mrm.28087
    [157] Setsompop K, Kimmlingen R, Eberlein E, Witzel T, Cohen-Adad J, McNab J A, Keil B, Tisdall M D, Hoecht P, Dietz P, Cauley S F, Tountcheva V, Matschl V, Lenz V H, Heberlein K, Potthast A, Thein H, Van Horn J, Toga A, Schmitt F, Lehne D, Rosen B R, Wedeen V, Wald L L 2013 Neuroimage 80 220 doi: 10.1016/j.neuroimage.2013.05.078
    [158] Fan Q, Witzel T, Nummenmaa A, Van Dijk K R A, Van Horn J D, Drews M K, Somerville L H, Sheridan M A, Santillana R M, Snyder J, Hedden T, Shaw E E, Hollinshead M O, Renvall V, Zanzonico R, Keil B, Cauley S, Polimeni J R, Tisdall D, Buckner R L, Wedeen V J, Wald L L, Toga A W, Rosen B R 2016 Neuroimage 124 1108 doi: 10.1016/j.neuroimage.2015.08.075
    [159] Dai E P, Zhu A, Yang G K, Quah K, Tan E T, Fiveland E, Foo T K, McNab J A 2023 Neuroimage 279 120328 doi: 10.1016/j.neuroimage.2023.120328
    [160] Pohmann R, Speck O, Scheffler K 2016 Magn. Reson. Med. 75 801 doi: 10.1002/mrm.25677
    [161] Wu X, Auerbach E J, Vu A T, Moeller S, Lenglet C, Schmitter S, Van de Moortele P F, Yacoub E, Uğurbil K 2018 Magn. Reson. Med. 80 1857 doi: 10.1002/mrm.27189
    [162] Shao X, Zhang Z, Ma X D, Liu F, Guo H, Ugurbil K, Wu X P 2025 Magn. Reson. Med. 93 1238 doi: 10.1002/mrm.30346
    [163] Koopmans P J, Boyacioğlu R, Barth M, Norris D G 2012 Neuroimage 62 1939 doi: 10.1016/j.neuroimage.2012.05.080
    [164] Wei Z D, Chen Q Y, Han S H, Zhang S H, Zhang N, Zhang L, Wang H N, He Q, Cao P, Zhang X L, Liang D, Liu X, Li Y, Zheng H R 2023 Quant. Imaging Med. Surg. 13 3222 doi: 10.21037/qims-22-945
    [165] Ma Y, Bruce I P, Yeh C H, Petrella J R, Song A W, Truong T-K 2023 Neuroimage 270 119993 doi: 10.1016/j.neuroimage.2023.119993
    [166] Feizollah S, Tardif C L 2023 Neuroimage 274 120159 doi: 10.1016/j.neuroimage.2023.120159
    [167] Qin Q 2012 Magn. Reson. Imaging 30 1134 doi: 10.1016/j.mri.2012.04.017
  • 加载中
图( 12)
计量
  • 文章访问数:  53
  • HTML全文浏览数:  53
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-06
  • 刊出日期:  2025-06-05

高分辨率磁共振二维扩散成像技术综述

    通讯作者: E-mail: huaguo@mail.tsinghua.edu.cn.
    作者简介: 刘凡. E-mail: liuf22@mails.tsinghua.edu.cn
  • 清华大学生物医学工程学院, 生物医学影像研究中心, 北京　100084
  • 收稿日期:  2025-02-06

摘要: 磁共振扩散加权成像(DWI)在神经科学和临床疾病诊断中具有重要价值. 单次激发平面回波成像(ss-EPI)是DWI最常用的技术, 但受主磁场不均匀性和$\rm T_2/T_2^*$衰减的影响, 易出现几何变形、信噪比低等问题. 为解决这些问题, 研究者开发了更先进的高分辨率磁共振扩散成像技术. 本文对这些成像技术进行综述. 平面回波成像(EPI)方面, 本文介绍了读出分段EPI、交错采集EPI、点扩散函数编码EPI、EPTI等多次激发EPI DWI技术, 这些技术能够减小或消除几何变形、提高图像信噪比和分辨率. 此外, 多次激发EPI与多层同时激发技术(SMS)的结合能够缩短采集时间, 本文对此类技术进行简要介绍. 相较于EPI, 螺旋 (spiral)成像的信噪比和采样效率更高, 但对主磁场不均匀性更敏感. 在螺旋成像部分, 本文分别介绍了单次激发以及多次激发的spiral DWI成像, 以及二者与SMS技术的结合. 本文重点介绍了各类成像技术的原理、采集策略与重建方法. 最后, 本文阐述了高分辨率扩散成像的挑战和未来方向, 包括三维DWI、体部DWI、磁场探针、超强梯度磁共振系统以及超高场磁共振系统.

English Abstract

    全文HTML

    1.   引　言

    • 扩散磁共振成像(diffusion magnetic resonance imaging, dMRI)通过测量水分子的随机热运动, 可以无创地探测生物组织的微观结构[1]. 磁共振扩散成像序列一般包括两个部分: 扩散准备模块和信号读出模块. 扩散准备模块施加连续的空间编码和解码梯度(也称为一对扩散编码梯度). 在扩散时间内, 具有位移的水分子空间解码不完全, 使得像素内失相位导致磁共振信号损失, 形成扩散对比度. 施加扩散准备模块后需要进行信号读出. 已有多种数据采集策略可用来读出信号, 且不同策略对应的图像重建方法不同, 例如平面回波成像(echo planer imaging, EPI)[2]、螺旋成像(spiral)[3]、快速自旋回波成像(fast spin echo, FSE或turbo spin echo, TSE)[4]、螺旋桨成像(periodically rotated overlapping parallel lines with enhanced reconstruction, PROPELLER)[5]等. 本文主要先介绍基于EPI的成像方法, 然后再介绍基于螺旋轨迹 (spiral) 的成像方法.

      最常用的 dMRI采集序列是单次激发平面回波成像(single shot echo planer imaging, ss-EPI)序列, 其通过一次激发信号, 在几十毫秒内完成整个k空间的信号的采集. 由于其成像速度快、对运动不敏感的成像特性, 该方法一直是扩散成像的主要采集策略. 然而, ss-EPI的长读出窗口会带来以下问题: 1)由于主磁场B0的不均匀性, 沿着带宽较低的相位编码 (PE) 方向产生较大的相位积累, 从而导致相位编码方向的图像变形; 2)回波时间TE较长, T2衰减显著, 信噪比较低, 此外, 扩散编码会进一步降低信噪比; 3)可采集信号的窗口有限, 同时远离k空间中心的数据$\rm T_2^* $衰减严重, 这都导致图像分辨率低, 有模糊伪影. 因此, ss-EPI在高分辨率高保真的扩散磁共振成像中的应用受到限制, 从而难以测量精细解剖结构中的扩散性质, 如灰白质交界和皮质内部[6,7].

      过去二十几年以来, 大量研究尝试提升扩散磁共振成像的空间分辨率、图像保真度和信噪比效率. 并行成像(parallel imaging, PI)技术[8–10]以加速因子$ R $对k空间进行降采, 通过加速k空间遍历来增大PE方向上的有效带宽, 同时利用多个并行通道之间的信号相关性恢复未采样的信号点, 实现更高的分辨率和保真度. 常见的重建算法包括基于图像域的线圈敏感度编码(sensitivity encoding, SENSE)[9]和基于k空间的泛化自校准部分并行采集(generalized auto-calibrating partially parallel acquisitions, GRAPPA)[10]. 当前, 基于并行成像的ss-EPI扩散加权磁共振成像(diffusion-weighted imaging, DWI)已广泛应用于临床诊断[11]和大规模神经科学研究, 例如人类连接组计划(human connectome project, HCP)[12,13]. 然而, 当加速因子$ R $较小时, 图像仍然受到几何变形和图像模糊的限制. 另一方面, 增大加速因子$ R $时, 信噪比以$ g\sqrt{R} $的倍数降低, 其中$ g $因子为与线圈灵敏度相关的参数[9]. 此外, 加速倍数还受到通道数目的限制, 加速因子$ R $过大时, 信号无法准确恢复, 图像中会出现混叠伪影. 在实践中, R通常设置为2或3用于扩散成像. 因此, EPI DWI仍然受到明显的失真影响, 特别是在高磁场强度或高空间分辨率下.

      为了改善以上问题, 近年来研究者们开发了基于多次激发平面回波(multi-shot EPI, ms-EPI)的高分辨率扩散成像技术. 其主要包括两类. 一类方法是, 每次激发只采集一小部分k空间, 从而增大相位编码方向的有效带宽, 有效抑制图像模糊和变形伪影. 此类多次激发平面回波技术包括读出分段EPI(readout-segmented EPI, RS-EPI)[14–16]、交错采集EPI(interleaved EPI, iEPI)[17–19]. 一般而言, 激发次数越多, 相位编码方向有效带宽越大, 图像变形和图像模糊伪影越小, 但依然无法完全消除图像变形[20], 并且代价是扫描时间随着激发次数成比例变长. 此外, 由于扩散编码期间组织的生理运动(如呼吸、血液和脑脊液搏动等)会导致每次激发的图像之间产生相位变化, 直接将多次激发采集的k空间数据合并成一个完整的k空间会造成严重伪影[21], 因此, 研究者们提出了不同方法对该相位变化进行校正. 另一类多次激发EPI成像技术在EPI读出信号前加入一个额外的相位梯度编码, 从信号解读来说, 相当于增加了一个额外的编码维度(形成一个三维 k空间), 能够实现完全无变形、无模糊、高保真度的DWI成像. 该技术称为点扩散函数编码的平面回波成像(point-spread-function encoded EPI, PSF-EPI)[22–25]. 还有一种方法是基于EPSI(echo planar spectrum imaging)编码[26]的平面回波时域解析成像方法(echo planer time-resolved imaging, EPTI)[27–31]. 此类技术的一大缺陷是采集时间过长, 因此近年来针对该类技术提出了一系列的降采和重建方案[25,27], 从而提高采集效率.

      除EPI以外, 螺旋成像也是一种高效的DWI图像采集方法. 最基本的螺旋成像采集序列是单次激发螺旋轨迹成像(single shot spiral, ss-spiral). ss-spiral从k空间中心开始向外周进行信号读出, 相较于EPI的采样效率和信噪比更高[32–35]. 然而, ss-spiral同样对B0不均匀性引起的偏共振敏感, 会造成图像模糊, 尤其是对于高分辨率成像时使用的长螺旋读出时间[33]. 并行成像虽可缓解此问题, 但如前所述, 其会降低图像信噪比, 并可能引入信号损失和混叠伪影[36,37].

      除了ss-spiral, 多次激发的螺旋轨迹成像(multi-shot spiral, ms-spiral)[38,39]也是一种常见的、基于螺旋成像的DWI成像方法. ms-spiral用于DWI采集时, 最关键的问题和ms-EPI类似, 就是不同激发之间图像会存在相位的变化. 如前所述, 这些相位变化由扩散梯度编码过程中的运动引起, 而如果不妥善解决这些相位, 最终的图像会出现明显的伪影. 为了解决这一问题, 有许多研究设计了独特的螺旋成像轨迹, 或是提出了专门的图像重建方法[40–42].

      本文将对近年来基于EPI和螺旋成像的高分辨率DWI成像技术进行简单的综述, 包括每个方法的概念、采集方案以及重建算法等.

    2.   ss-EPI DWI

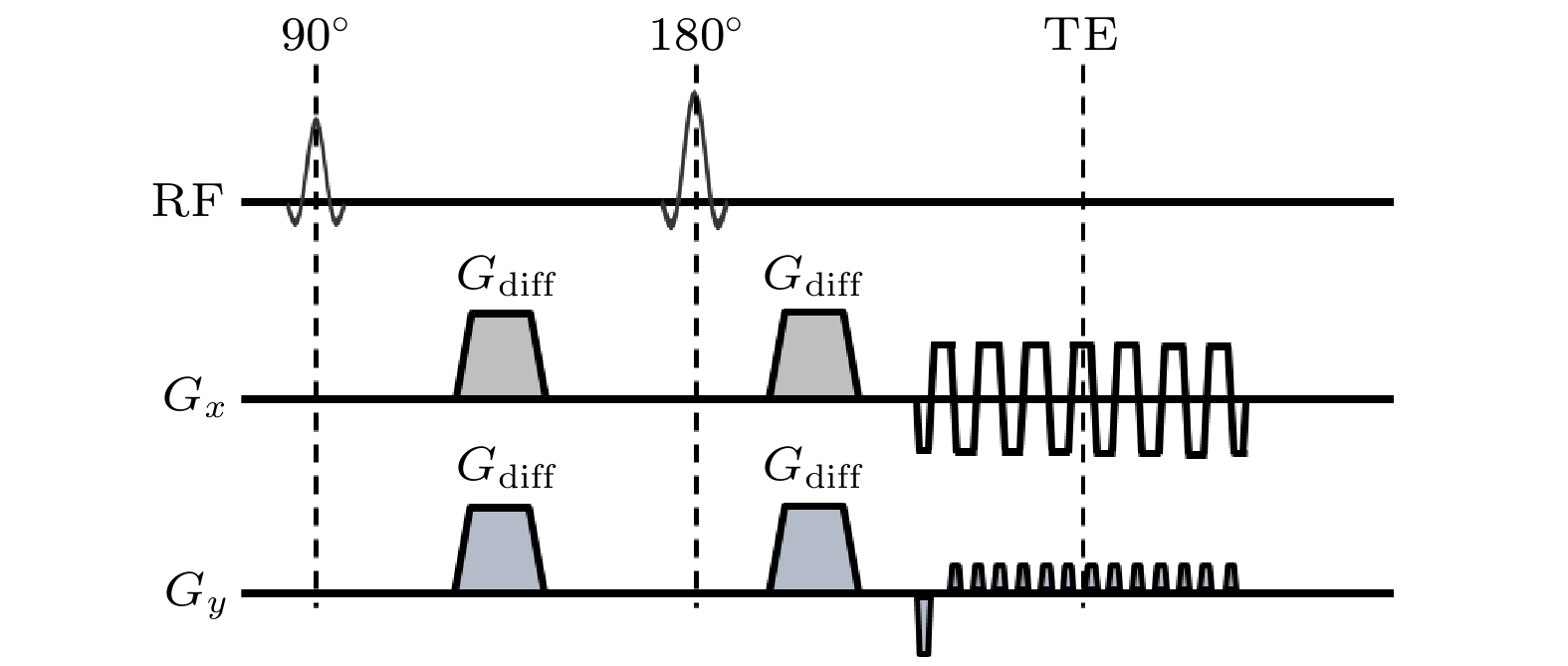
    • ss-EPI DWI序列时序如图1所示. 其通过一次激发采集整个k空间数据. 具体而言, 频率编码方向($ {k}_{x} $)使用极性快速交替的连续梯度$ {G}_{x} $, 完成正向和反向读出; 相位编码方向($ {k}_{y} $)使用离散的脉冲梯度($ {G}_{y} $), 每次读出前使k空间$ {k}_{y} $方向增大$ {{\Delta }}{k}_{y} $. 相邻回波之间的时间称为回波间隔(echo spacing, ESP), 其倒数称为相位编码方向的带宽.

      因奇数回波与偶数回波的读出方向相反, 在涡流、B0不均匀性及梯度延迟的影响下, 图像域的奇偶行间会产生相位差, 进而引发奈奎斯特伪影(Nyquist ghost). 通过采集不加相位编码的导航器提取该相位差, 能够校正奈奎斯特伪影. 针对奈奎斯特伪影校正, 研究者们还提出了双极性GRAPPA[43](dual polarity GRAPPA, DPG)、无参考方法(reference-less method)[44]等一系列更为鲁棒的技术.

      B0磁场不均匀性、T2衰减和$\rm T_2^* $衰减分别会造成图像变形、信噪比低以及图像模糊. 这些伪影可以通过增大EPI相位编码方向的带宽缓解. 一方面, 我们可以沿相位方向对k空间进行R倍的均匀降采(即$ {{\Delta }}{k}_{y} $增大R倍), 从而将有效带宽增大R倍. 降采带来的卷折伪影可以通过SENSE和GRAPPA等并行成像重建算法消除. 另一方面, 可以使用高性能梯度系统, 增大$ {G}_{x} $的切换率和最大幅值来缩小回波间隔. 为了改善这些伪影, 研究者们还开发了一系列更为先进的成像技术, 我们将在后文进行总结.

      除了以上缺陷, 二维ss-EPI成像技术还存在重复时间(TR)过长的问题(在高分辨率全脑成像中常常可以达到10 s以上). 在TR远大于T1的情况下, 由于纵向磁化矢量已经完全恢复, 延长TR不能提高信噪比, 因而采集的信噪比效率较低. 使用多层同时激发技术(simultaneous multi-slice imaging, SMS)[45–47], 又称为多带成像(multi-band imaging)能够在一定程度上解决该问题. SMS技术本质上是在层方向实现降采样与成像加速. 其通过将不同层的选层脉冲进行叠加, 获得复合的RF射频脉冲. 施加该脉冲可激发多个不同的层, 由此获得多层叠加在一起图像. 配合使用在层方向灵敏度存在足够区分度的接收线圈, 则可以在重建过程中将激发的多个层分离开来. Larkman等[45]最早在2001年成功利用线圈灵敏度在层方向的变化分离出多层图像, 从而显著缩短成像时间. 与并行成像技术不同, SMS技术在实现成像加速的同时, 因为增大了激发区域而提升了信号强度. 例如, 使用加速倍数为R的SMS成像进行加速时, RF脉冲激发了大约R倍数量的质子. 虽然成像TR和总采集时间均被缩短了R倍, 但在高分辨率的二维成像中, TR远大于组织的T1, 信号仍然能够得到充分的恢复. 因此, 仍然可以获得将近R倍的信号. 这使得SMS成像技术加速并不会像并行成像技术一样, 出现$ \sqrt{R} $倍的信噪比降低.

      SMS技术的一个重大进展是与梯度控制混叠技术(blipped-controlled aliasing in parallel imaging, blipped-CAIPI)的结合[46]. CAIPI技术(也被称作CAIPIRINHA, controlled aliasing in parallel imaging results in higher acceleration)[48]是通过基于RF脉冲的相位编码, 向同时激发的层引入相位编码方向的偏移, 增大混叠像素之间的距离, 便于将他们分离开来. Blipped-CAIPI技术是针对SMS EPI开发的. 在EPI读出阶段施加Gy三角波梯度的同时, 在层方向施加不同幅度和极性的Gz三角波梯度, 以此在同时激发的多个层中, 不同程度地引入平面内相位编码方向上的偏移, 实现类似于CAIPI技术的效果. 这使得可以在重建过程中更充分地利用线圈灵敏度信息, 分离混叠的多个层. 由blipped-CAIPI得到的混叠图像中, 不同层在相位编码方向的位置相互错开, 可以降低重建中的g因子, 即降低重建过程中的噪声放大倍数. 由于层间存在位移, 需要使用专门的slice-GRAPPA算法[46]将同时激发的层分开. 简单来说, 需要先采集预扫描校准数据, 该数据每次只激发一层. 然后对校准数据中的每一层拟合一个GRAPPA核, 将该GRAPPA核应用到混叠数据中, 估计出每一层的数据.

    3.   ms-EPI DWI的采集与重建

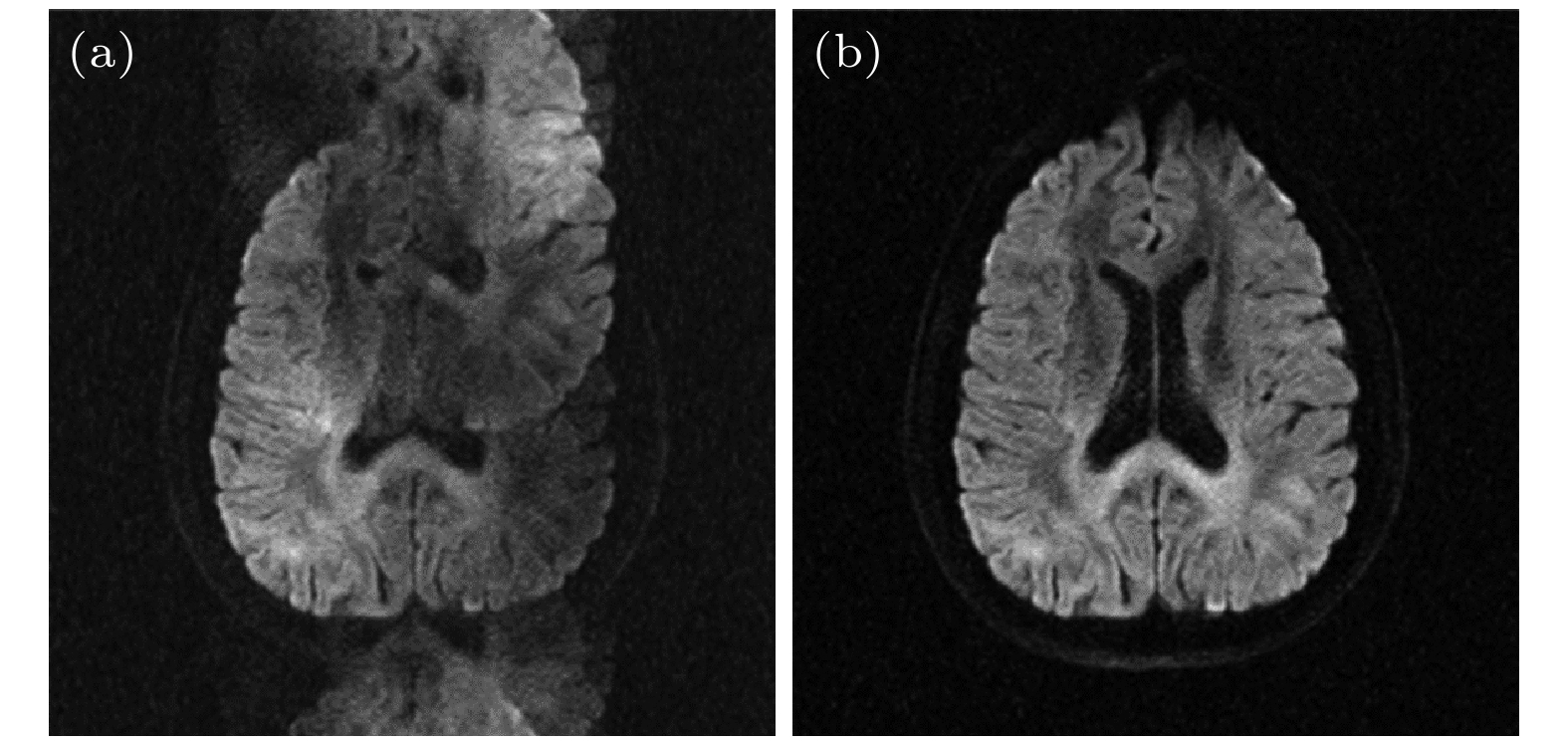
    • 由于并行成像加速倍数受到接收线圈通道数和信噪比的限制(通常最大为R = 3), 当成像的矩阵尺寸较大以及有效回波间隔较长时, ss-EPI仍受到图像变形和图像模糊的影响. ms-EPI技术能够提供高分辨率、低变形的扩散图像. ms-EPI扩散成像技术的主要挑战是不同激发之间的相位不一致. 其成因在于, 在施加强的扩散编码梯度时, 即使是受试者微小的生理运动(如心跳、呼吸、脑脊液搏动等), 也会在不同的激发之间产生剧烈的相位变化, 在最后的扩散加权图像中出现严重的混叠伪影(图2(a)). 因此重建过程中必须对该相位进行校正(图2(b)). 多次激发技术主要包括RS-EPI, iEPI, PSF-EPI以及EPTI.

      • 3.1.   RS-EPI

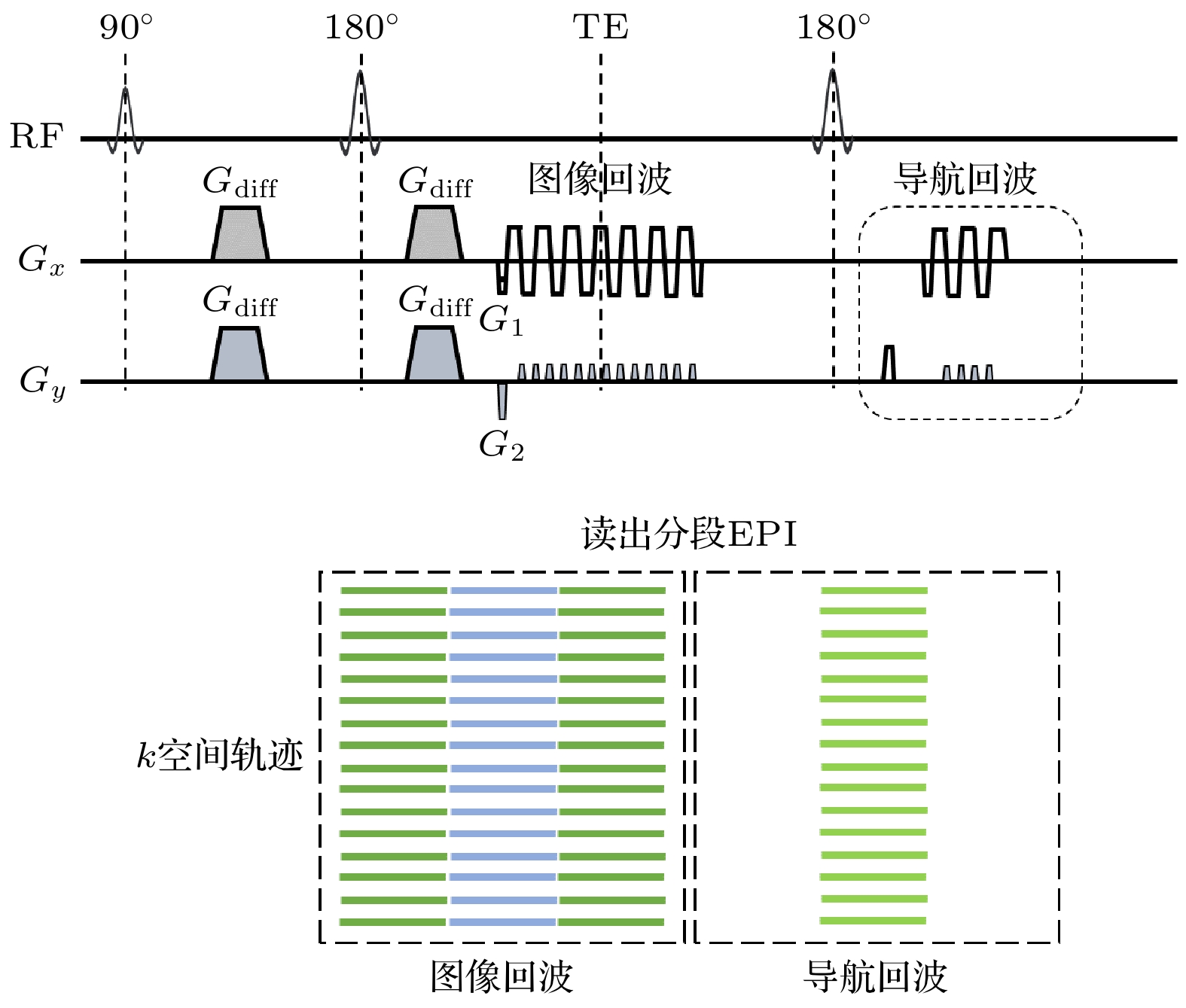
    • 如图3所示, RS-EPI的基本原理是, 将k空间沿着读出方向分成多个片段. 读出方向的G1在每次激发时变化以获取不同的k空间片段, 而沿着相位编码方向的G2保持恒定, 经过多次激发后采集到完整的k空间数据. 这样的采集方式能够增大相位编码方向的有效带宽, 从而减小图像变形和图像模糊.

      为了解决RS-EPI不同激发之间相位不一致的问题, 常用的方法是带导航回波(navigator echo)的相位校正方法. 其基本原理如图3上图所示. 在第1个180°重聚脉冲后, 采集图像回波(image echo), 用于填充扩散图像的k空间片段. 随后施加第2个180°重聚脉冲, 采集低分辨率的导航回波, 用于记录每次激发的相位信息. RS-EPI的特点是导航回波的变形水平总是和图像回波相同, 因此无需图像配准, 可直接在图像域减去导航回波的相位进行相位校正[15]. 同时, 导航回波图像的变形程度和信噪比不随激发次数的增加而改变, 这对于高分辨率扩散成像尤为重要.

      由于该方法需要额外采集导航回波数据, 会增加采集时间. 此外, RS-EPI形变抑制的增益受到片段宽度和最大梯度切换率的限制[14]. 这是因为在现代高梯度性能系统中, 会在读出梯度的爬升和下落期间采集EPI数据, 从而缩短整体采集时间. 而在RS-EPI中, 由于读出梯度的极性相较于ss-EPI和iEPI切换更为频繁, 读出窗口中最大梯度持续时间的占比更小, 读出效率更低. 因此, 虽然增加激发次数能够有效减小形变, 但是当使用中等分辨率时, 增加激发次数使得每个片段相对较窄, 数据基本都在读出梯度的上升沿和下降沿进行采集, 读出效率减小. 此时, 变形减小的收益不值得延长扫描时间. 当使用更高的分辨率时, RS-EPI的每个片段更宽, 更多的数据在读出梯度的平台期采集. 在这种情况下, 增加激发次数对减小变形的效果更为显著. 为了弥补降低的梯度使用效率并进一步较小变形, 研究者们还将GRAPPA集成到RS-EPI中[14,15,49–51]. 具体而言, 需要同时对图像回波和导航回波沿着相位编码方向降采, 然后使用GRAPPA解开混叠. 这种方法进一步增大了ky方向的有效带宽. 因其图像的高保真度, RS-EPI DWI已应用于临床诊断, 包括乳腺癌[52–54]、肝癌[55]、盆腔[56,57]和儿科神经病理[58]等.

      • 3.2.   iEPI

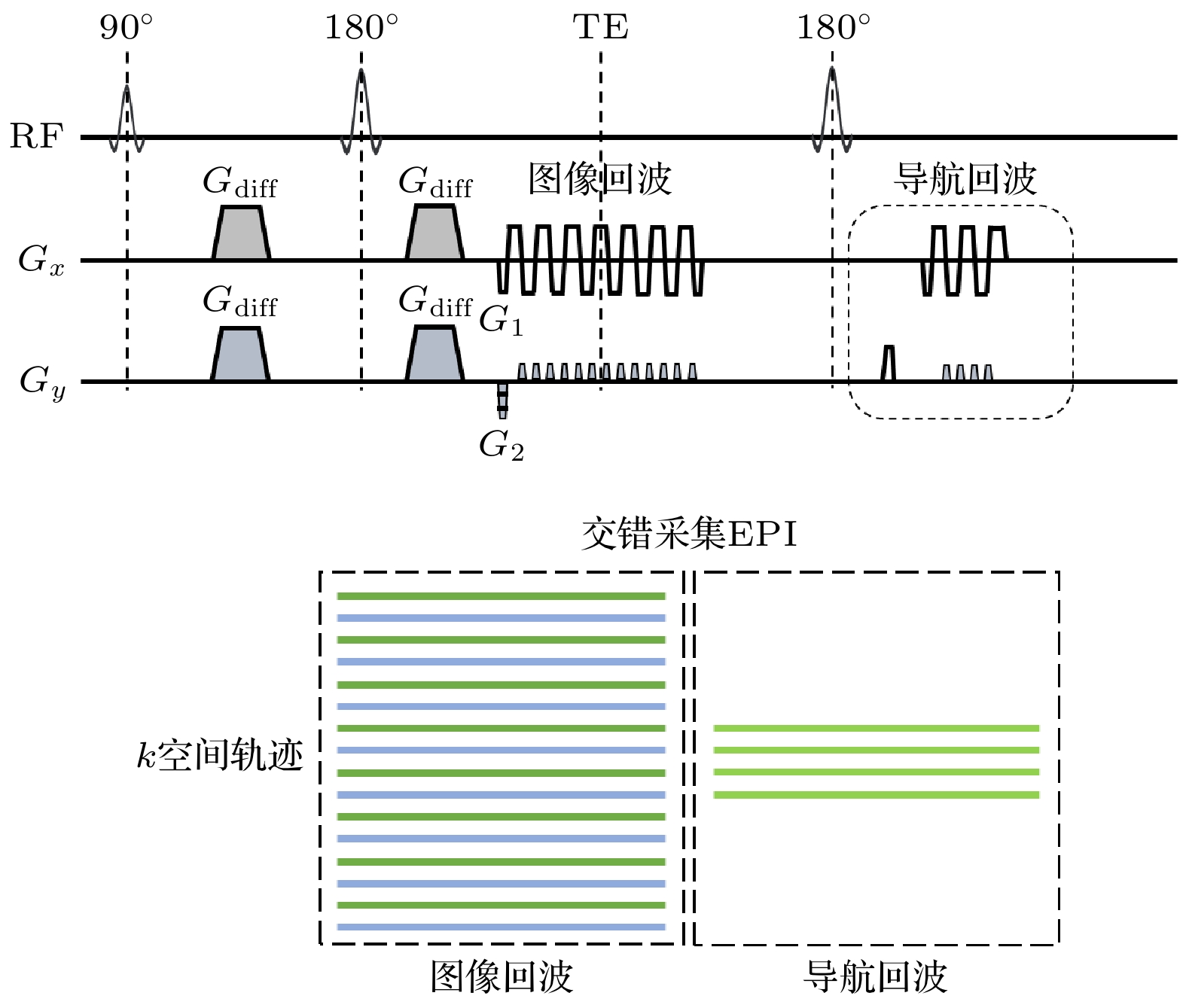
    • iEPI的k空间采样轨迹如图4下图所示, 其基本原理是通过沿着PE方向使用交错的EPI轨迹加速k空间的遍历, 或者是对一个k空间经过几次激发, 交错地完成采集, 从而减小有效回波间隔. 如图4上图所示, 每次激发G2变化以获得不同的k空间交错, 而G1保持不变. 和RS-EPI一样, iEPI通过施加第2个180°重聚脉冲采集低分辨率的导航回波, 用于相位校正. 为了避免由于各个分段之间的偏共振效应而导致的相位不连续性, 需要使用移位增量τ (1个EPI读出波瓣的持续时间除以分段因子)来移动每次激发的读出窗[59]. iEPI中激发间相位校正方法分为导航回波和计算导航.

      • 3.2.1.   基于导航回波的相位校正算法

    • iEPI可通过二维(2D)导航回波来校正生理运动引起的不同激发间的相位变化. IRIS技术[60]将采集的导航回波信号并入到SENSE模型中求解扩散图像. 由于有效带宽不同, 图像回波和导航回波之间可能存在变形差异, 因此需要进行图像配准或微调导航数据采样来准确地校正相位[60,61]. eGRAPPA将每次激发的相位当作一种编码信息, 通过导航回波训练k空间插值核系数, 从而恢复每次激发的k空间信号[62,63]. 相较于IRIS, eGRAPPA对导航回波的变形差异敏感度更低[61]. 基于导航回波的相位校正方法在图像回波和导航回波之间运动不同时可能会失败. 同时, iEPI扩散成像中导航回波的采集带宽往往低于成像回波, 因为两者会存在图像变形不一致的问题, 可能会影响后期相位校正算法的准确性. 此外, 这类方法需要额外施加一个180°重聚脉冲并采集回波数据, 这类方法会增加约1/3的采集时间. 对此, 研究者们开发了一系列基于计算导航的相位校正方法. 基于计算导航的方法又大致分为两大类, 分别是基于多路复用灵敏度编码和低秩约束的方法.

      • 3.2.2.   基于多路复用灵敏度编码的相位校正算法

    • Chen等[64]提出的多路复用灵敏度编码技术(multiplexed sensitivity-encoding, MUSE), 无需导航回波即可实现相位校正. MUSE算法的核心在于: 多次激发扩散成像采集时, 每一次激发采集的图像幅值相同, 但是相位不同; 通过并行成像的方法求出每次采集的相位, 就可以综合这些相位和所有的数据进行相位校正, 计算出扩散图像. 在MUSE算法中, 对于任意k空间采集轨迹得到的扩散图像可以被建模为

      其中, 向量$ \boldsymbol{d} $为采集的多通道扩散图像, 向量m为目标重建的扩散加权图像的幅值, 算子P为每次激发的不同相位, 算子S为线圈敏感度编码信息, 算子F为傅里叶变换, 算子G为笛卡尔坐标系采集到所使用的k空间轨迹, 算子R为从采集到的k空间数据格点化到笛卡尔坐标系, 算子V为逆傅里叶变换.

      在用iEPI序列采集多次激发扩散信号时, 非笛卡尔坐标系k空间重建的算子(G, R)可以简化为笛卡尔坐标系采集轨迹相关的算子, 进而将该MUSE模型简化为

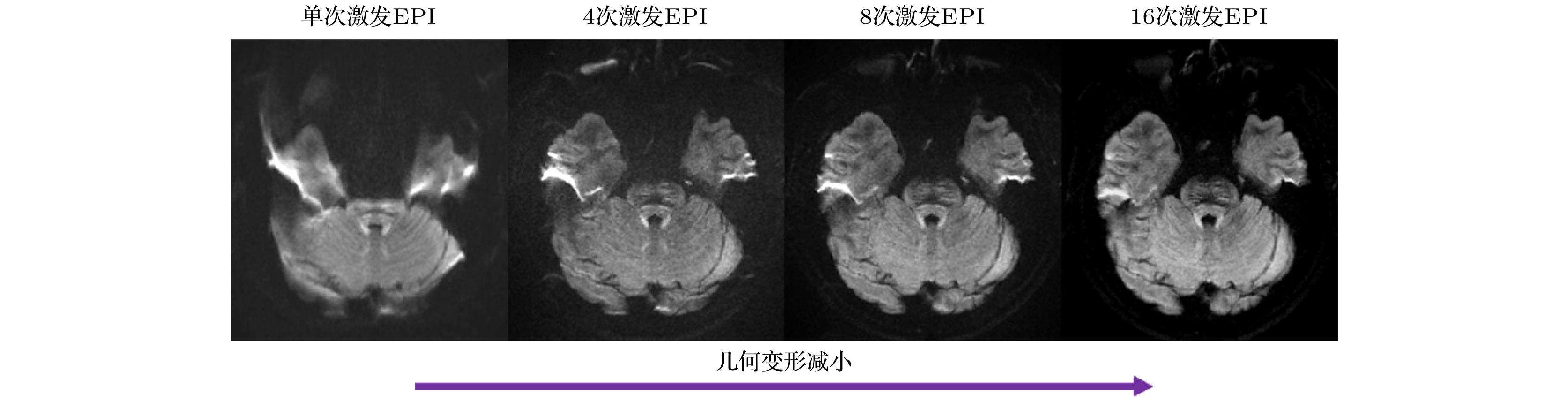
      其中, 算子Q代表iEPI序列交错采集时引入的额外的图像相位, 对于确定的序列与扫描参数, $ d $, Q, S都是已知的(S可以通过预扫描或者未施加扩散梯度的扫描中获取). 用传统并行成像算法求出导航相位P, 就能解出未知的扩散图像$ m $. MUSE算法需要进行多次的SENSE求解. 第1次是对于每一次激发单独求解(2)式, 使用传统SENSE算法求出第s次激发复数图像$ {i}_{s} $, 即对于(2)式进行求逆:

      其中, $ {N}_{{\mathrm{s}}{\mathrm{h}}{\mathrm{o}}{\mathrm{t}}} $为激发的次数. 传统的多次激发重建方法是直接平均所求得的所有$ {i}_{s} $. 与传统算法不同的是, MUSE利用传统SENSE求得$ {i}_{s} $之后, 将每一幅图$ {i}_{s} $的相位提出, 得到计算的相位$ {p}_{s} $, 将该相位作为已知信息, 用方程去求解(2)式中的扩散图像$ m $. 此时求解的方程数目是(3)式中的$ {N}_{{\mathrm{s}}{\mathrm{h}}{\mathrm{o}}{\mathrm{t}}} $倍, 原来由于降采造成的g因子引起的噪声和伪影将被抑制. 图5展示了ss-EPI, 4, 8, 16次激发EPI在颅底的扩散成像, 可见随着激发次数增多, 图像的几何变形变小(如颞叶处). 除了受试者微观运动带来的相位变化, 其宏观运动(例如头动、心跳)还会带来不同激发之间的像素不匹配, 从而造成图像模糊. 此外, 这类运动(如头的旋转)会改变扩散对比度, 进而造成扩散张量或者其他参数的错误估计. 针对不同激发之间的宏观运动, 研究者们对MUSE技术进行了进一步的修正[65,66]. 例如, AMUSE (augmented MUSE) [65]将SENSE重建的每个激发图像进行二维共配准, 保证像素对齐. 配准过程估计出的旋转矩阵和平移向量被集成到MUSE信号模型中. 该信号模型不仅包含了图像的运动, 还包含了b矩阵和扩散张量的运动, 保证了扩散加权的正确性. 实验表明, AMUSE能够降低激发间宏观运动带来的图像模糊并更加准确地估计扩散张量.

      MUSE的相位计算受到并行成像算法中通道数目的限制, 在8通道线圈中激发次数一般不超过4次, 否则可能会受到并行重建算法带来的噪声放大效应以及残余混叠伪影的干扰. 对此, 研究者们对MUSE技术进行改善, 提出了自反馈MUSE(self-feeding MUSE, SF-MUSE)[67]和凸集投影MUSE(projection onto convex sets MUSE, POCSMUSE)[68]. SF-MUSE[67]将MUSE重建的幅值图和初始SENSE导航求解的平滑相位图作为先验图像, 通过先验信息正则化SENSE提升图像质量. 接着再将正则化SENSE求得的相位图反馈至MUSE中, 迭代求解, 更加准确地估计相位和幅值. 结合MUSE和正则化SENSE的自反馈机制(self-feeding mechanism)使得在更多的激发次数下也能实现准确的相位估计. 此外, SF-MUSE重建框架中还引入了回顾式损坏数据监测和数据丢弃机制, 进一步抑制脑脊液(CSF)涌动带来的剧烈相位变化和信号缺失. 实验表明, SF-MUSE能够在8通道线圈的情况下稳健地重建出8次激发的图像. Chu 等[68]将MUSE推广至不规律采样和非笛卡尔采样的图像重建. 它将线圈灵敏度分布作为约束, 使用POCS逐步消除图像混叠. 对于不同激发之间相位变化剧烈的情况, 需要将SENSE求解的相位图作为迭代的约束. 针对通道数不足或激发次数较高时SENSE的病态问题, POCSMUSE对重建出的每个激发的相位图施加汉宁窗平滑约束. 集成线圈灵敏度分布、激发间相位变化以及汉宁窗平滑约束的POCSMUSE能用3个通道重建出4次激发的DWI图像. POCS-ICE[40]与POCSMUSE的原理类似, 但图像更新机制略有不同.

      • 3.2.3.   基于低秩约束的相位校正算法

    • 另一类iEPI的重建算法是基于相位的低秩假设. Hu等[69]假设运动引起的相位在空间维度上变化缓慢. 将一个块中的$ n $个像素作为单独的一列, 每一列来自不同的激发($ {N}_{s} $), 从而形成维度为$ n\times {N}_{s} $空间-激发矩阵$ {R}_{b}\left\{{\boldsymbol{m}}_{{\mathrm{1, 2}}, \cdots , {N}_{s}}\right\} $. 该矩阵可以分解为两个矩阵的乘积:

      其中, $ \boldsymbol{I} $的对角线元素为待求解的不带运动相位 的复数图像, $ \boldsymbol{\phi } $包含每次激发下每个像素的运动 相位. 如果运动引起的相位$ \theta $在空间变化上缓慢, 那么$ \boldsymbol{\phi } $应当是一个低秩矩阵. 由于$ \boldsymbol{I} $为满秩矩阵, 空间-激发矩阵$ {\boldsymbol{R}}_{b}\left\{{\boldsymbol{m}}_{{\mathrm{1, 2}}, \cdots , {N}_{s}}\right\} $也应当是一个低秩矩阵. 因此, 将前向模型和空间-激发局部低秩约束(shot–locally low-rank, Shot-LLR)结合起来重建DWI图像. 通过将秩约束替换为核范数约束, 使得优化问题转化为一个凸问题, 我们能够简化计算的复杂度:

      其中, $ {D}_{i} $为k空间降采样算子, $ {m}_{i} $为待重建的第i次激发图像, $ {y}_{i} $为采集的多通道k空间数据, $ F $为傅里叶变换算子, $ S $是多通道灵敏度图, $ \lambda $是正则化参数, $ \varOmega $是不重叠平铺整个图像的块集合.

      对于部分傅里叶采集的情况, 可以通过旋转共轭采集的k空间数据生成虚拟共轭激发(virtual conjugate shots, VCSs), 并将他们作为额外的激发次数集成到上述的求解问题中. 此时, 激发次数变为原来的2倍. 结果显示, Shot-LLR在8次激发的情况下重建出的图像相较于POCS-MUSE和POCS-ICE混叠伪影明显更小, 但仍存在局部的信号缺失. 进一步地, 将重建出来的各激发相位和平均后的幅值图作为POCS-ICE迭代的初值, 加快了POCS-ICE的收敛速度, 同时能够明显改善Shot-LLR中信号缺失的问题. 对于受呼吸和心跳影响, 运动更加剧烈的乳腺, Shot-LLR重建出的图像相较于POCS-ICE和POCSMUSE混叠伪影更少, 信噪比更高.

      值得注意的是, Shot-LLR方法是在图像域施加低秩约束. 类似地, 在k空间施加低秩约束也能校正运动引起的相位变化. 例如, Mani等[70]提出了“使用结构化低秩矩阵完成的多次激发灵敏度编码扩散数据恢复”技术(multi-shot sensitivity encoded diffusion data recovery using structured low rank matrix completion, MUSSELS). 该技术利用了不同激发之间的相消关系. 具体而言, 对于某个扩散编码方向的第p次激发和第q次激发, 有这样的相消关系: $ {m}_{p}(x){\phi }_{q}(x)-{m}_{q}(x){\phi }_{p}(x)=0 $, 其中$ {m}_{p}(x)=\rho (x){\phi }_{p}(x), {m}_{q}(x)=\rho (x){\phi }_{q}(x) $, $ \rho (x) $代表要求解的复数DWI图像, $ \phi (x) $代表叠加在它上面的运动引起的相位. 将该相消关系转换到k空间域, 可以得到: $ {M}_{p}(k)*{\varPhi }_{q}(k)-{M}_{q}(k)*{\varPhi }_{p}(k)= 0 $. 由于$ \phi (x) $在图像域是平滑的, 因此$ \varPhi (k) $在k空间域是$ \boldsymbol{r}\times \boldsymbol{r} $有限支撑的, k空间域的相消关系可以使用块-汉克尔矩阵(block-Hankel matrix)写为: $ \boldsymbol{H}({\boldsymbol{M}}_{p})\cdot {\boldsymbol{\varPhi }}_{q}-\boldsymbol{H}({\boldsymbol{M}}_{q})\cdot {\boldsymbol{\varPhi }}_{p}={\boldsymbol{0}} $. 其中, $ \boldsymbol{H}(\boldsymbol{M}) $的每一行为k空间中$ \boldsymbol{r}\times \boldsymbol{r} $滑动窗口内的值向量化, $ \boldsymbol{\varPhi } $为$ \boldsymbol{\varPhi }(\boldsymbol{k}) $展开后的向量. 因此$ \boldsymbol{H}(\boldsymbol{M})\cdot \boldsymbol{\varPhi } $为相消关系中的卷积操作. 将所有激发的块-汉克尔矩阵在列方向串联起来, 就能够得到块-汉克尔结构矩阵$ {\boldsymbol{H}}_{1}(\boldsymbol{M})=[\boldsymbol{H}({\boldsymbol{M}}_{1})\boldsymbol{H}({\boldsymbol{M}}_{2})\cdots \boldsymbol{H}({\boldsymbol{M}}_{{N}_{{\mathrm{s}}{\mathrm{h}}{\mathrm{o}}{\mathrm{t}}}})] $. 根据相消原理, $ {\boldsymbol{H}}_{1}(\boldsymbol{M}) $具有低秩性. 因此能对$ {\boldsymbol{H}}_{1}(\boldsymbol{M}) $施加核范数低秩约束来迭代优化出DWI图像, 而无需显式地求解$ \boldsymbol{\varPhi } $:

      其中, $ \boldsymbol{M} $是待求解图像的k空间, $ \boldsymbol{y} $是采集的多通道多次激发的k空间数据, $ F $和$ {F}^{-1} $分别是傅里叶变换和逆傅里叶变换算子, $ S $是多通道灵敏度图, $ D $是k空间降采样算子, $ \lambda $是正则化参数. 将各个激发的重建图像求平方和后, 就能得到最终的DWI重建图.

      在降采数据或信噪比低的数据中, 为了改善重建问题的条件数, 还能够在MUSSELS的基础上加上平滑正则. 根据傅里叶变换关系, 在k空间数据乘以$ -{\mathrm{j}}2{\mathrm{\pi }}{k}_{x} $和$ -{\mathrm{j}}2{\mathrm{\pi }}{k}_{y} $相当于对图像域求偏微分. 接着, 对求偏微分后的图像重新建立一个块-汉克尔结构矩阵. 同样, 该块-汉克尔结构矩阵是低秩的. 对该矩阵进行低秩约束, 就能够在解图像混叠的同时融入平滑正则.

      由于MUSSELS需要在每一次迭代中对巨大的块-汉克尔结构矩阵做奇异值分解, 造成计算速度较慢. 对此, 研究者们提出了迭代重加权最小二乘MUSSELS(iterative reweighted least squares formulation of MUSSELS, IRLS MUSSELS)[71], 减小了奇异值分解矩阵的计算复杂度并加快了收敛速度. 和Shot-LLR[69]类似, 针对部分傅里叶采集, 可以利用k空间的共轭对称性质, 将反转共轭的k空间数据的块-汉克尔矩阵串联在原来的结构矩阵中, 从而恢复没有采集的部分傅里叶数据. 带反转共轭的IRLS MUSSELS相较于带反转共轭的MUSSELS计算速度提升了约5倍.

      近年来, 研究者们提出了一系列新颖的iEPI采集技术和相应的重建算法, 这些重建算法都使用到了低秩约束. 例如, Liao等[72]提出了BUDA-EPI (multi-shot EPI with blip up- down acquisition)来获取无几何变形的扩散图像. 在BUDA-EPI中, 第1个激发的k空间轨迹朝ky正向遍历, 第2个激发的k空间朝ky负向遍历. 使用SENSE分别对两次激发的图像解混叠, 得到两幅几何变形方向不同的图像. 基于FSL软件中的TOPUP方法[73,74], 使用这两幅图片求得场图(field map). 将该场图引入带结构低秩约束的联合重建:

      其中, $ {m}_{i} $是待求解的无变形图像, $ {y}_{i} $是采集的多通道k空间数据, $ F $是傅里叶变换算子, $ S $是多通道灵敏度图, $ {D}_{i} $是k空间降采样算子, $ {E}_{i} $是估计的偏共振信息, $ \lambda $是正则化参数. 在这个前向模型中, 无形变的图像在x-ky混合空间根据场图的相位调制施加形变[75]. 该算法的精妙之处在于, 首先分别重建向上/向下跳变 (blip up/down) 的图像用于求解场图, 然后将该场图集成至模型中联合求解向上/向下跳变的图像, 同时使用向上/向下跳变两次激发间相位的低秩性约束, 重建出最终的DWI图像. 该方法相较于SENSE提高了重建的条件数, 重建图像的信噪比更高. 将该技术和gSlider[76]结合起来, 该团队实现了860 μm各向同性、无变形的DWI成像. 对于更高分辨率图像的采集, 偏共振在频率编码方向的相位积累会变多, 从而减小了两次激发的互补性, 进而影响重建的条件. 针对该问题, 使用动态B0匀场减小偏共振, 能够将DWI的分辨率推向600 μm各向同性. 介观尺度分辨率(如500 μm)采集回波链长度较长, 引入图像模糊的问题, Liao等[77]结合了circular-EPI轨迹和BUDA-EPI进行改善. 将BUDA-circular-EPI与gSlider集成在一起, 结合S-LORAKS[78]建立低秩约束重建图像, 能够获得高保真度、高信噪比、500 μm各向同性分辨率的DWI数据. 低秩约束的方法还应用到了水脂分离中. Dong等[79,80]开发了化学位移编码的ms-EPI成像技术, 对水图和脂肪图分别施加低秩约束, 能够同时实现可靠的水脂分离和激发间相位校正. 近年来, 研究者们还提出了一系列基于人工智能的ms-EPI DWI重建算法, 相较于传统算法, 可以实现更大降采倍数[81]、更高保真度[82]和更快的重建速度[83].

      • 3.3.   无变形无模糊的EPI

      3.3.1.   PSF-EPI

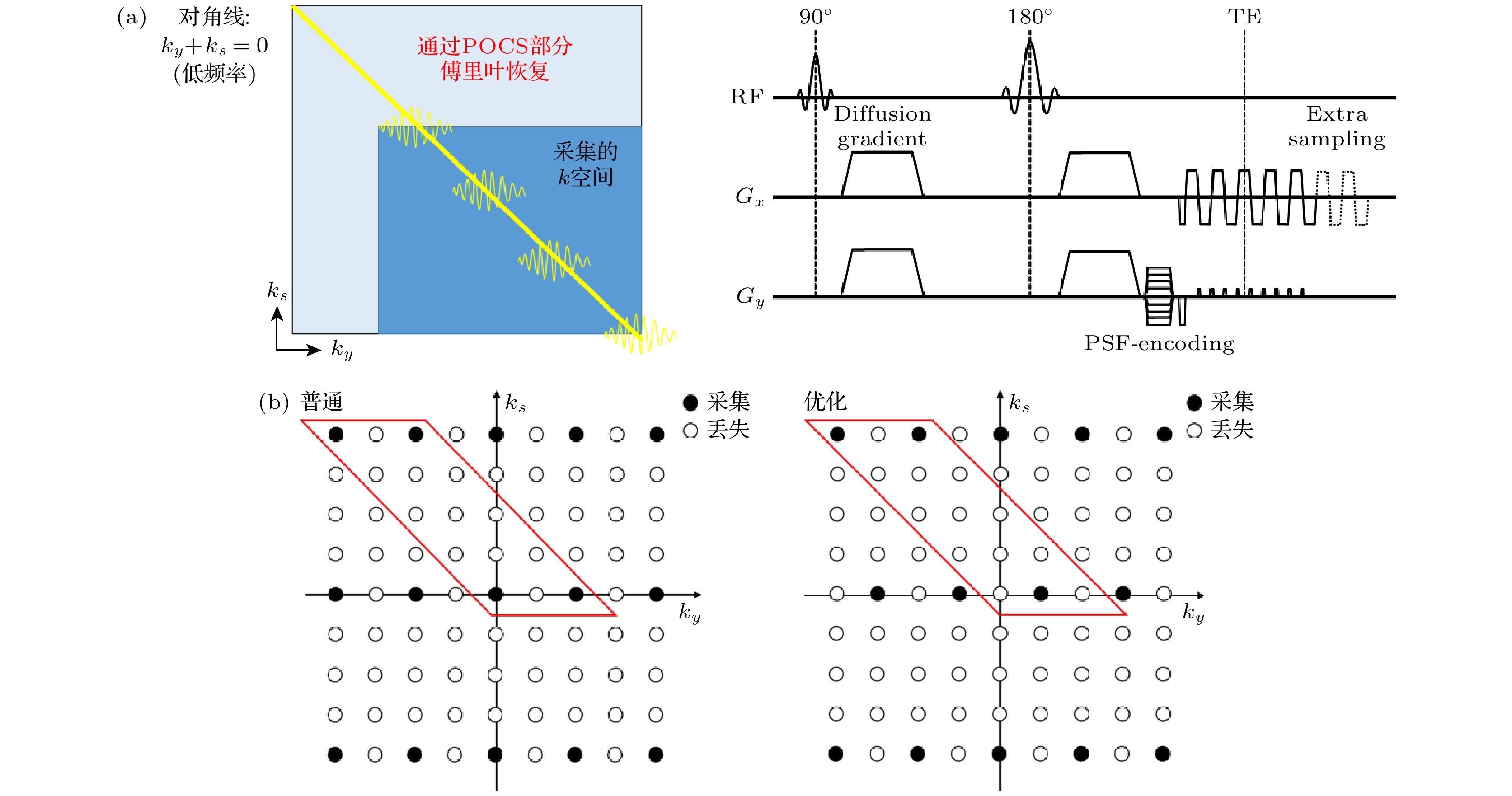
    • PSF-EPI最早由Robson等[23]提出. 相较于传统的EPI采集, PSF-EPI引入了一个额外的相位编码(也称作PSF编码, $ {k}_{s} $). 如图6(a)所示, 在每个EPI回波链之前沿相位编码方向施加一个随不同激发改变幅值的梯度, 即可得到不同的PSF编码. 经过多次激发后, 每一层图像能够得到由频率编码($ {k}_{x} $)、相位编码($ {k}_{y} $)和PSF编码组成的三维k空间. 其中, $ {k}_{s} $的范围和步长与$ {k}_{y} $相同. 对于每一个特定的$ {k}_{y} $, 由$ {k}_{x} $和$ {k}_{s} $组成的二维k空间数据中, 每个回波都具有相同的场不均匀性相位累积和$\rm T_2/T_2^*$衰减效应[84–87], 因此由该二维k空间数据得到的图像完全无变形及模糊伪影. 将所有$ {k}_{y} $位置得到的图像组合起来, 能够得到高信噪比、且物理意义上无形变无模糊的图像. 然而, 由于额外的PSF编码梯度, PSF-EPI的采集效率较低, 因此最初只作为校正扫描来对后续的EPI扫描进行回顾式变形校正[88].

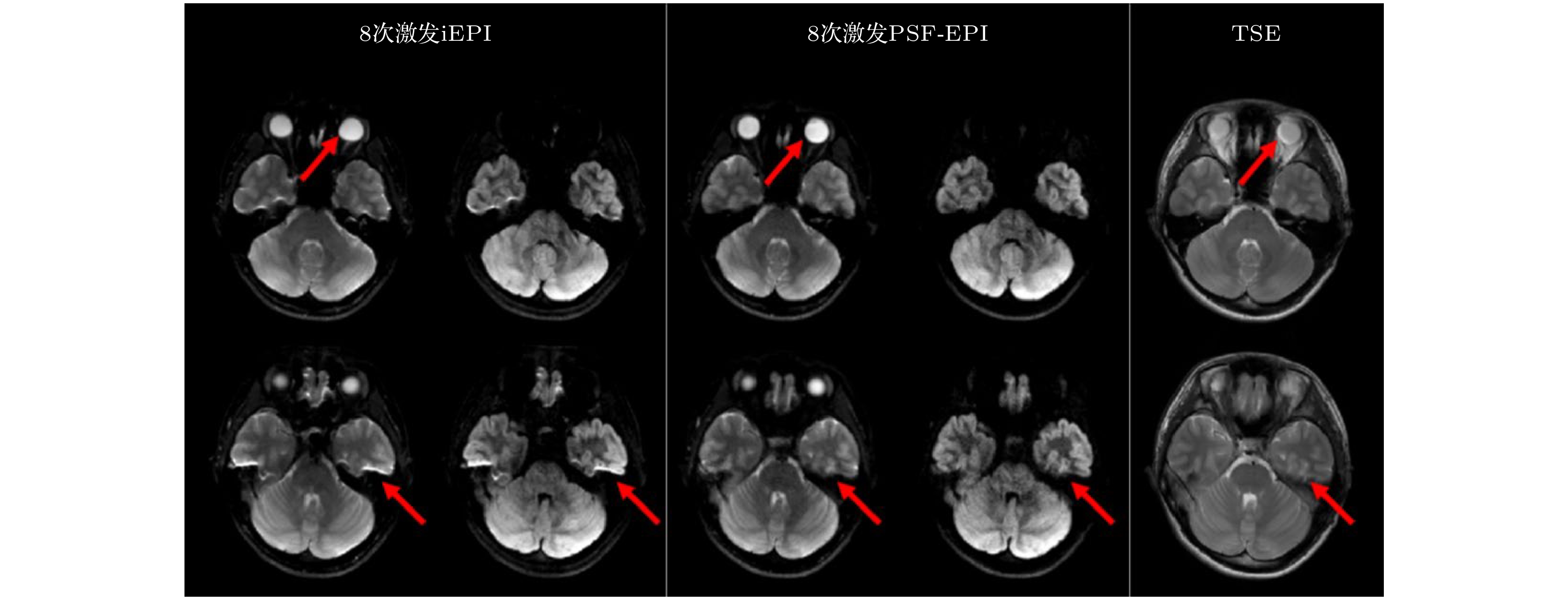
      使用小FOV[89–91]和并行成像[9,10]技术, 能够实现5—8倍加速, 但仍然不足以应用于临床[24]. Ho等[92]在高性能梯度上对PSF-EPI进行优化, 进一步降低了扫描时间. 为了进一步加速, 变形混叠控制技术(tilted controlled aliasing in volumetric parallel imaging, tilted CAIPI)[25]在相位编码方向(RPE)和PSF编码方向(RS)同时高倍降采. 相位编码方向降采降低了需要使用PSF编码的几何变形和模糊水平, 反过来实现了更快的PSF加速, 因此需要的EPI激发次数更少, 采集时间更短. Tilted CAIPI通过优化降采和重建充分利用相位和PSF编码信号的固有相关性. $ {k}_{y}\text{-}{k}_{s} $平面$ -45° $对角线上数据点的有效$ {G}_{y} $梯度编码相同, B0引起的相位积累和$\rm T_2^* $衰减不同. 因为邻近数据点的相位差异和$\rm T_2^* $衰减较小, 可以通过一个在倾斜的在多通道$ {k}_{x} \text{-}{k}_{s} $平面的紧凑核有效地捕捉这些效应, 通过GRAPPA式的插值方法恢复出未采样的数据点. 图7(b)中红色框代表一个PSF-PE GRAPPA重建的变形核(tilted kernel). 为了充分利用线圈灵敏度编码, 还使用了2D CAIPINHA的变形版本优化降采模式(图6(b)右), 称作tilted CAIPI. 为了训练PSF-PE GRAPPA的变形核权重, 需要额外采集一个校准(calibration)数据. 这个数据需要全采或通过PE-GRAPPA恢复到全采, 并且需要覆盖尽量大的k空间从而更加准确地估计核权重. 使用自导航的方法, 可以校正激发间的相位变化. 具体而言, 每一个PSF编码激发都包含了一部分二维低频信号($ {k}_{y}+{k}_{s}=0 $), 可以通过PE-GRAPPA估计每次激发的相位, 将该相位加到校准数据中作为额外信息训练PSF-PE GRAPPA核. 对所有缺失点完成插值后, 每次激发的运动相位直接通过之前估计的相位图被移除. 结合部分傅里叶技术, 该团队实现了20余倍加速, 所需要的激发次数降低至6—8次, 使得PSF-EPI可以运用于临床DTI研究. 图7展示了iEPI, PSF-EPI和快速自旋回波(TSE)成像在颅底的DWI成像. 观察到PSF-EPI能够消除几何变形, 而iEPI还有残余变形(眼球、颞叶). 利用PSF-EPI的多个回波移位图像, Hu等[93]实现了一套可靠的水脂分离技术. 此外, Li等[94]基于PSF-EPI实现了颈脊髓的水脂分离和高保真度DTI成像. 将PSF-EPI图像作为参考, Hu等[95]还开发了基于深度学习的ss-EPI变形校正技术.

      • 3.3.2.   EPTI

    • EPTI基于$ {k}_{y}\text{-}t $空间的采样策略[27]. 相位编码极性反转的ss-EPI, 多对比度EPI, 平面回波谱成像EPSI以及PSF-EPI在$ {k}_{y}\text{-}t $空间中的轨迹不同, 对应各自的图像变形、模糊、对比度、采集效率也均不相同. EPTI从平面回波谱成像EPSI发展出来, 其关键假设是能对$ {k}_{y}\text{-}t $空间高倍降采, 并利用时间维度和相位编码维度的相关性恢复丢失的数据点. 基于此假设, EPTI采用时-空混叠控制(spatio-temporal CAIPI)的采样轨迹, 通过多次激发高效地覆盖$ {k}_{y}\text{-}t $空间, 实现了快速、无变形、无模糊的多对比度成像. 最初版本的EPTI采用B0引导(B0-informed)的重建方法. 其假设与PSF-EPI中的类似, 每一条$ {k}_{y}\text{-}t $线(每次激发)相邻 数据点的差异是B0不均匀性引起的相位以及$\rm T_2^* $衰减. 该相位变化和$\rm T_2^* $衰减在相邻数据点之间是微小的, 因此可以将沿着时间维度的相位积累和$\rm T_2^* $衰减作为编码信息, 通过GRAPPA式的紧凑核插值出未采样的点. 完成$ {k}_{y}\text{-}t $空间重建后, 沿着相位编码和频率编码维度做傅里叶逆变换, 得到具有不同$\rm T_2/T_2^* $对比度的图像序列. 将EPTI采集集成到梯度回波自旋回波(GESE)序列中, 能够得到T2, $\rm T_2^* $, 质子密度(PD), B0和定量磁化率等定量图谱. 若集成到梯度回波(GE)序列中, 则能够降低TR, 实现快速的多对比度动态成像, 如动态$\rm T_2^* $成像、多回波BOLD fMRI和功能定量磁化率成像等.

      基于最初版本的EPTI及其重建框架, 研究者们进行了一系列进一步的技术开发. Fair等[96]针对剧烈宏观运动, 开发了带动态编码的PROPELLER EPTI(PEPTIDE), 提升了EPTI对运动的鲁棒性, 并证明了EPTI实现扩散-弛豫成像(diffusion-relaxometry imaging)的可行性[97]. Dong等[28]针对EPTI开发了子空间重建算法, 该算法使用低秩的子空间对时域信号演化进行建模, 显著减少了重建的未知数, 提升了EPTI重建的准确性. 基于此, 该团队还提出了变密度采样的时变CAIPI技术, 将EPTI扩展到了3D, 实现了72倍的降采样. Wang等[98]使用EPTI子空间重建在7 T实现了纯T2加权的SE-BOLD-fMRI. 基于3D EPTI, vFA-EPTI[99]能够快速采集全脑高分辨率的多回波多翻转角的梯度回波数据, 为髓鞘水成像的多隔室分析提供了丰富信息. 进一步地, Wang等[100]实现了1 min全脑1 mm各向同性的多参数定量成像(T2, T2, ${\mathrm{T}}_2^* $, PD, B1+). Dai等[29]提出了基于自导航笛卡尔EPTI(scEPTI)的扩散成像采集方案, 分析了EPTI扩散信号中不同的相位组成, 提出了一种方法合成全部相位匹配的导航器用于激发间的相位校正, 还利用时域维度幅值和相位的相关性来提升重建. Dong等[30]开发的ACE-EPTI针对扩散成像对EPTI序列采集进行了优化. 第1点是将每次激发的回波链开始时间和自旋回波时间对齐, 从而最大程度减小TE并使得回波链长度的设计更加灵活. 第2点在于优化了$ {k}_{y} $-$ t $编码的轨迹: 沿着时间维度进行相位编码互补的采集来控制混叠, 在k空间中心和早TE时更密集地采样从而提高信噪比和重建的准确性, 减小相邻时间点的$ {k}_{y} $变化来限制梯度blip的大小从而减小回波间隔和涡流, 每次激发采集的低频信号用于自导航的激发间相位校正. ACE-EPTI采集数据可以用子空间的方法重建:

      其中, $ c $是子空间基$ \phi $的系数图, $ S $是线圈灵敏度图, $ F $是傅里叶变换算子, $ {U}_{{\mathrm{s}}{\mathrm{h}}} $是第sh次激发的k-t空间降采样算子, $ {y}_{{\mathrm{s}}{\mathrm{h}}} $是第sh次采集的数据. $ R\left(c\right) $是施加在$ c $上的局部低秩约束, 利用空间上的低秩性提高重建的准确性和信噪比. $ {P}_{{\mathrm{s}}{\mathrm{h}}} $是第sh次激发沿着时间维度的相位演化算子, 包括背景相位、B0不均匀性引起的相位以及运动引起的相位. $ {P}_{{\mathrm{s}}{\mathrm{h}}} $的建模非常重要. 受涡流和梯度延迟会引起奇数和偶数回波之间的相位差. 通过满采的$ {k}_{y} $-$ t $空间数据能够提取该相位差并将其在$ {P}_{{\mathrm{s}}{\mathrm{h}}} $中作为背景相位予以校正. 接着使用子空间方法分别重建每次激发采集的低频信号, 将自旋回波时刻(第1个回波)的相位作为运动引起的相位, 将其加入$ {P}_{{\mathrm{s}}{\mathrm{h}}} $中. 由于场漂或涡流, B0图在不同的图像之间会不一样. 因此需要对其进行更新. 首先使用上一个图像的B0图进行初始重建, 估计出B0在时域上的改变. 然后用更新的B0图进行最后的重建. 基于以上方法, 该团队实现了3次激发的、自导航相位校正的、无变形无模糊的、亚毫米级平面内分辨率的扩散-弛豫成像. 进一步地, 该团队开发了Romer-EPTI(rotating-view motion-robust super-resolution EPTI)[31]. 该技术首先通过厚层采集减小TR和噪声, 然后绕着PE轴旋转选层-读出平面来编码和恢复高各向同性分辨率(旋转方向数目$ \geqslant \dfrac{{\mathrm{\pi }}}{2}\cdot \dfrac{{\mathrm{采}}{\mathrm{集}}{\mathrm{层}}{\mathrm{厚}}}{{\mathrm{目}}{\mathrm{标}}{\mathrm{层}}{\mathrm{厚}}} $). 这样的采集方式不仅对运动鲁棒, 还提升了信噪比效率. 通过超分辨率重建算法, 则能够从低分辨率图像中重建出高分辨率图像. 对于宏观运动, 将不同空间方向的低分辨率图像进行配准, 提取变换矩阵, 集成在超分辨率重建的前向模型中. 每一个低分辨率图像都由EPTI读出采集, 并利用ACE-EPTI[30]中的方法重建图像. 利用该技术, 该团队在3 T和7 T上实现了500 μm和485 μm各向同性的介观尺度扩散磁共振成像, 将人类在体DWI成像的分辨率推到前所未有的高度, 观察到了海马分层皮质折叠以及横跨内囊的灰质桥等精细结构.

      • 3.4.   与SMS技术相结合的ms-EPI DWI

    • 前文所提到的所有多次激发平面回波DWI 技术都能够和SMS结合起来, 从而有效地减小 TR和扫描时间, 提高信噪比效率. Chang等[101] 将MUSE技术扩展至多层同时激发. 首先使用SENSE算法从每一次激发中重建出无层内和层间混叠伪影的图像, 然后从中提取不同层、不同激发的运动相位, 再将该相位带回到信号模型中重建所有的层和不同激发的图像. Frost等[102]将基于blipped CAIPI的SMS技术[46]和读出分段EPI结合起来, 首先使用slice-GRAPPA[46]分开不同的层, 然后利用导航回波消除激发间的相位差, 在3 T和7 T上实现了DWI成像的加速. Dai等[103]结合blipped-CAIPI SMS技术, 带导航的iEPI以及3D k空间理论[104], 实现了一套加速的高分辨率DWI成像技术. 对于带blipped-CAIPI的SMS采集, 额外施加的梯度blip可以视作选层方向的相位编码梯度. 因此, blipped-CAPI SMS实际上是生成了一个降采的3D k空间, 因此可以通过2D GRAPPA[105]等算法恢复丢失的数据. 相位校正使用3D导航回波, 其采集也使用blipped-CAIPI SMS. DWI的重建过程主要分为两步, 首先利用从满采的b0数据中拟合的GRAPPA核恢复3D导航器的数据. 然后将成像数据的不同次激发分为不同的k空间, 利用3D导航器的数据训练权重, 插值恢复出全采的3D k空间数据, 以此同时解层混叠和校正激发间相位差. Herbst等[106]开发了SMS MUSE技术, 同样将blipped-CAIPI iEPI 采集到的数据视为3D k空间, 首先使用3D SENSE恢复满采的3D k空间, 并提取各激发的相位. 和MUSE一样, 将该相位加至信号前向模型中, 利用3D SENSE联合求解所有激发的图像. Dong等[107]开发了基于模型的SMS iEPI DWI重建算法, 将每次激发采集的数据视为高倍降采的3D k空间, 通过联合重建所有扩散方向的3D k空间, 直接估计出扩散张量. Mani等[108]将blipped-CAIPI SMS以及MUSSELS结合起来(SMS-MUSSELS). SMS-MUSSELS重建算法在前向模型中加入了不同层的blipped-CAIPI相位调制和及其信号加和, 并同时对不同层施加块汉克尔矩阵的低秩约束, 能够一步实现解层间混叠和每一次激发数据的恢复. Dai等[109]还开发了JULEP算法, 将MUSE和MUSSELS结合起来, 能够明显减小同时激发层数较大时, MUSE和MUSSELS出现的伪影.

    4.   ss-spiral DWI

    • 使用单次激发技术采集扩散磁共振图像有种种优点, 比如采集效率高、对受试者的运动不敏感等, 因此使用ss-spiral采集DWI图像也是目前的主流方法, 即使还没有应用到临床上. 在下文中将介绍几种基于ss-spiral DWI成像技术, 并介绍几种相应的重建方法.

      • 4.1.   2D ss-spiral DWI

      4.1.1.   2D ss-spiral DWI采集方法

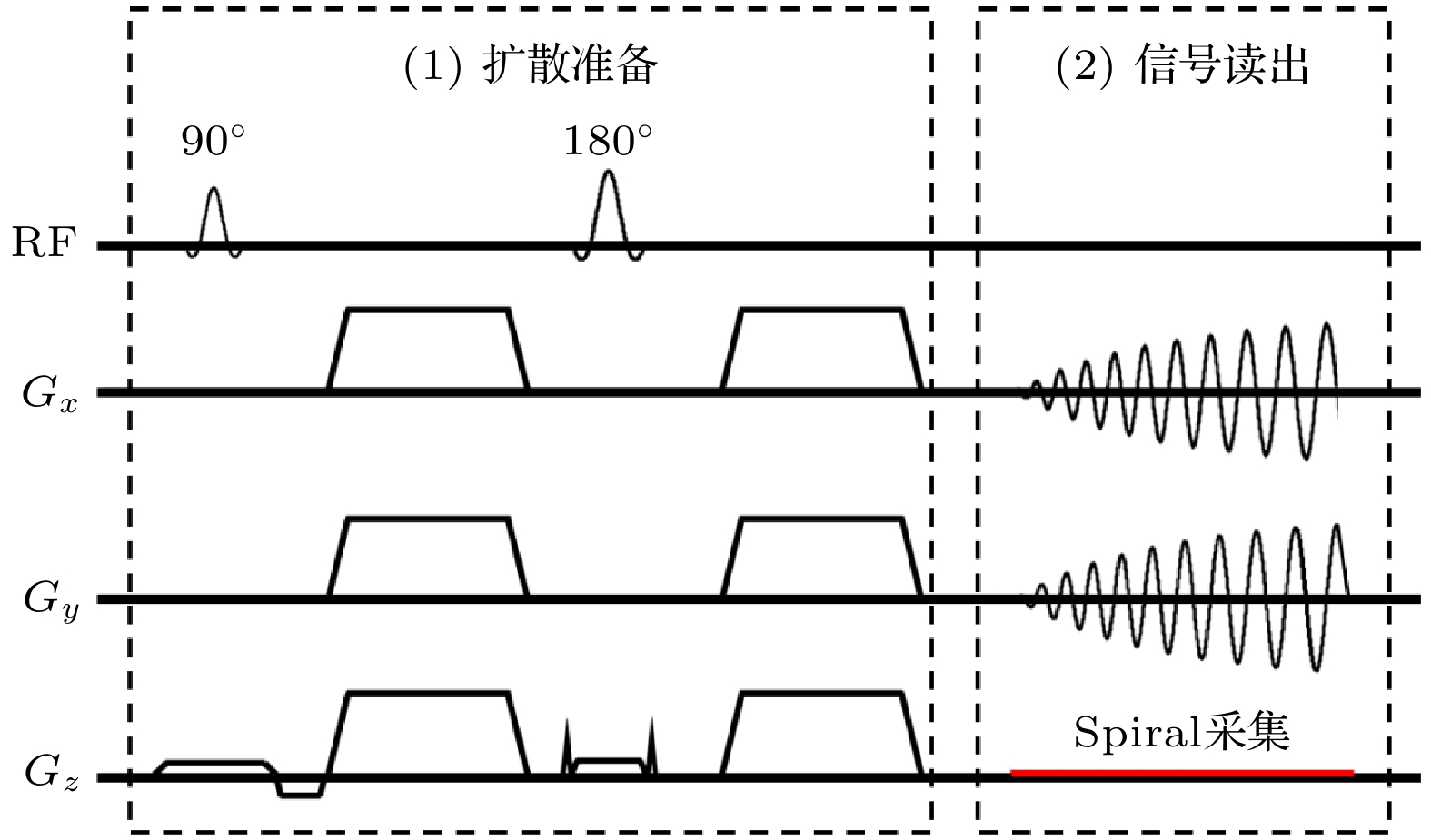
    • 最常见的spiral DWI成像为单次激发的采集, 使用一个简单的ss-spiral序列进行信号采集, 如图8所示, 序列中包含了扩散准备和螺旋读出部分, 和ss-EPI DWI非常接近. 如前所述, 螺旋成像对梯度系统不完美及B0场的偏共振效应非常敏感, 根据理论推导, 螺旋成像的一次读出越长, B0场不均匀性对其影响就越大, 所以一般认为, 螺旋成像的一次读出不能过长(≤40 ms), 这限制了螺旋成像可实现的空间分辨率. 为了在短读出的情况下提高空间分辨率, 一般可将ss-spiral采集技术与并行成像技术相结合, 即对k空间进行降采样, 并使用多通道的线圈敏感度信息来恢复最终的图像.

      近年来, 也有许多团队使用磁场探针对成像过程进行动态监测, 从而在采集时可以提升螺旋成像的读出长度[35,106,110–112]. 磁场探针是一种近年来出现的硬件设备, 其可以动态地监测主磁场、梯度场以及更高阶的场的信息, 从而让我们能够获得准确的螺旋轨迹信息. 2017年, Wilm等[33]在磁场探针的辅助下, 通过4倍的层内加速方式在常规梯度系统实现1.3 mm²的扩散成像, 螺旋采集的回波时间TE为34 ms, 明显短于相同成像参数下EPI采集的TE; 之后, Wilm等[35]在3.0T磁共振平台上采用超强梯度系统, 通过3倍的层内加速, 使用40.5 ms长的螺旋采样轨迹实现了0.68 mm2的亚毫米级高分辨率扩散成像, TE缩短至19 ms. 可以看到, ss-spiral采集的TE可以缩短, 在加入了磁场探针的辅助后, 读出也可以拉长, 这些都有助于实现高分辨率、高信噪比的DWI成像. 因此磁场探针对于螺旋成像有着非常大的帮助.

      • 4.1.2.   2D ss-spiral DWI重建方法

    • 在重建方面, 对于一般的螺旋采集数据, 最基础的重建方法为非均匀快速傅里叶变换(non-uniform fast Fourier transform, NUFFT)[113], 这一步可以将非笛卡尔采集的k空间数据变换到图像域. 一般而言, NUFFT的实现过程包括3个步骤, 密度补偿、数据网格化以及傅里叶变换. 螺旋读出在k空间不同位置的采样密度是不同的, 一般在中心附近会采集更多数据, 所以需要给不同的数据点加上不同的权重, 即使用一些函数对每个采样数据进行密度补偿. 密度补偿函数有多种类型[114,115]. 第2步网格化就是将做完密度补偿的k空间数据插值到笛卡尔网格上. 完成插值后, 最后使用常规的快速傅里叶变换(fast Fourier transform, FFT)就可完成NUFFT的全过程. NUFFT相对于FFT来说, 最大的问题是误差高、速度慢, 有许多工作致力于减小NUFFT的误差同时提升速度[116].

      对于没有降采样的ss-spiral数据来说, 直接使用NUFFT就可以获得重建后的图像. 但如前所述, ss-spiral的读出时间不能太长, 往往需要降采样来缩短螺旋读出长度, 并通过并行成像的方法来实现图像重建. 螺旋采集的并行成像技术主要可以分为两类: 基于图像域的CG-SENSE算法[36]以及基于k空间的非笛卡尔坐标的GRAPPA[37]和SPIRiT[117]等算法.

      首先介绍最经典也最为常用的基于图像域的CG-SENSE算法. CG-SENSE方法的基本观点是将图像重建转为一个优化问题. 具体而言, 磁共振的图像采集可以表示为如下模型:

      其中, $ \boldsymbol{E} $代表了图像采集编码矩阵, $ \boldsymbol{m} $表示向量化的采集获得k空间数据, $ v $表示原始图像. 重建的过程就是已知$ \boldsymbol{m} $和$ \boldsymbol{E} $, 求$ v $. 那么这显然就是一个凸优化问题. 具体而言, 矩阵$ \boldsymbol{E} $也可以具体表示为

      其中, $ {\boldsymbol{r}}_{\rho } $表示第$ \rho $个像素的坐标, $ {\boldsymbol{k}}_{\kappa } $表示k空间中的第$ \kappa $个数据点的坐标, $ {\boldsymbol{s}}_{\gamma } $表示第$ \gamma $个通道的灵敏度图. 如此定义$ \boldsymbol{E} $之后, 就可以定义$ \boldsymbol{m} $为一个$ {n}_{C}{n}_{K} $维度的向量, 其中$ {n}_{C} $是接收通道数, $ {n}_{K} $是k空间数据点数. $ \boldsymbol{v} $则可表示为一个$ {N}^{2} $维度的向量, 其中$ N $为图像矩阵的维度. 完成这些定义之后, 就可以使用共轭梯度(conjugate gradient, CG)算法[118]来优化(9)式得到重建结果. 这就是所谓的CG-SENSE算法.

      CG-SENSE算法的优点是其将图像重建建模为了一个优化问题, 问题描述简洁而直观, 同时其对k空间的采样轨迹没有要求, 适用于螺旋成像这种非笛卡尔采集的数据. 但从E的表达式中也不难发现, CG-SENSE的效果会严重依赖于灵敏度图的质量. 如果灵敏度图的质量不高或存在误差, 那么最终的重建结果质量也就会随之下降. 另外, 这是一个无约束的优化问题, 会存在陷入局部极值点之类的问题. 最后, 有研究表明CG-SENSE会存在一些数值不稳定的问题[119].

      针对上述问题, 也有一些CG-SENSE的改进算法被提出. 如为了解决CG-SENSE数值不稳定的问题, Samsonov等[120]提出了基于POCS的迭代SENSE算法POCSENSE, 该方法能有效地提升SENSE重建的数值稳定性, 但同样也增加了重建的用时. 近年来, Wilm等[33]就提出了扩展编码模型 (expanded encoding model), 该方法将B0场信息、梯度信息以及k空间编码信息共同加入(9)式的E矩阵中, 再进行CG迭代重建. 这样做的好处是可以将磁场探针获得的实时信息加入重建之中, 提升重建质量. 但如果没有磁场探针作为辅助, 该方法可能与传统的CG方法也没有太大区别.

      第2类主要的方法基于k空间的方法. 这一类方法通过校准数据来计算k空间的插值核, 然后用该核插值获得k空间缺失的数据, 完成重建. 最经典的k空间插值方法为GRAPPA, 但该方法依赖于笛卡尔采集的k空间, 无法直接用于螺旋成像. Heidemann等[37]因而提出了一种可用于螺旋成像的GRAPPA方法. 该方法首先将螺旋的采集点插值到若干条等间隔的k空间放射线上, 然后由于这些放射线之间的角度是一致的, 那么就可以用类似传统GRAPPA的方法进行插值以及最后的重建. 该方法的重建性能不错, 但是过程由于涉及插值过程, 可能比较繁琐, 并没有被广泛采用.

      另一种常用于螺旋成像的k空间方法是SPIRiT. SPIRiT会寻找一个k空间的插值内核 $ \boldsymbol{G} $使得

      然后就可以将重建过程写为如下优化问题:

      其中$ x $是恢复后的$ k $空间全采样笛卡尔数据, $ y $是采集得到的螺旋 k空间数据, $ \boldsymbol{D} $表示k空间降采样与插值矩阵, 可以将笛卡尔采集的数据点降采样并插值到螺旋轨迹上, $ {\mathrm{\lambda }} $是拉格朗日松弛系数. 通过求解上述的优化问题, 就可以得到恢复后的k空间数据, 再做一次傅里叶变换就可以得到图像. SPIRiT方法在高倍降采样的情况下有比CG-SENSE更好的效果, 但是其计算量较大, 重建速度较慢. 使用通道压缩方法[121]可以提升SPIRiT方法的速度.

      在上述两种方法的基础上, 压缩感知(compressed sensing, CS)方法[34,122]在近年来也常被运用以提升重建质量. 如Varela-Mattatall等[34]就在扩展编码模型的基础上加入了CS约束, 实现了高降采倍数、高信噪比的spiral DWI成像. CS约束也可以和SPIRiT方法结合, 即L1-SPIRiT[123]方法, 该方法相比于SPIRiT, 也有一些性能上的提升.

      综上所述, 基于ss-spiral的DWI重建方法有两大类: 第1类为CG-SENSE以及由其衍生的expanded encoding model等基于图像域的方法; 第2类为GRAPPA与SPIRiT等基于k空间插值的方法. CS方法也常被加入上述两类方法中用以提升重建质量.

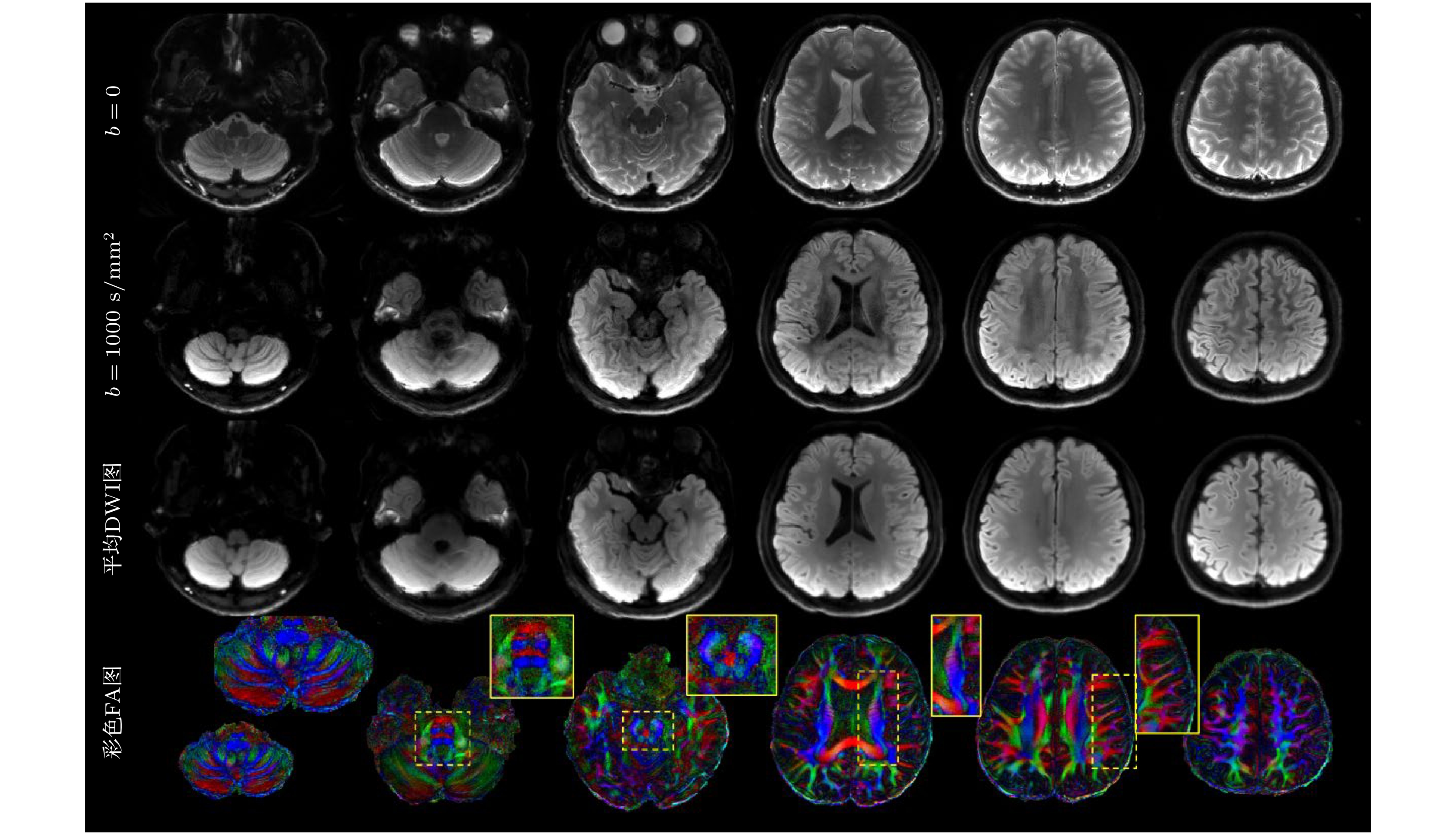
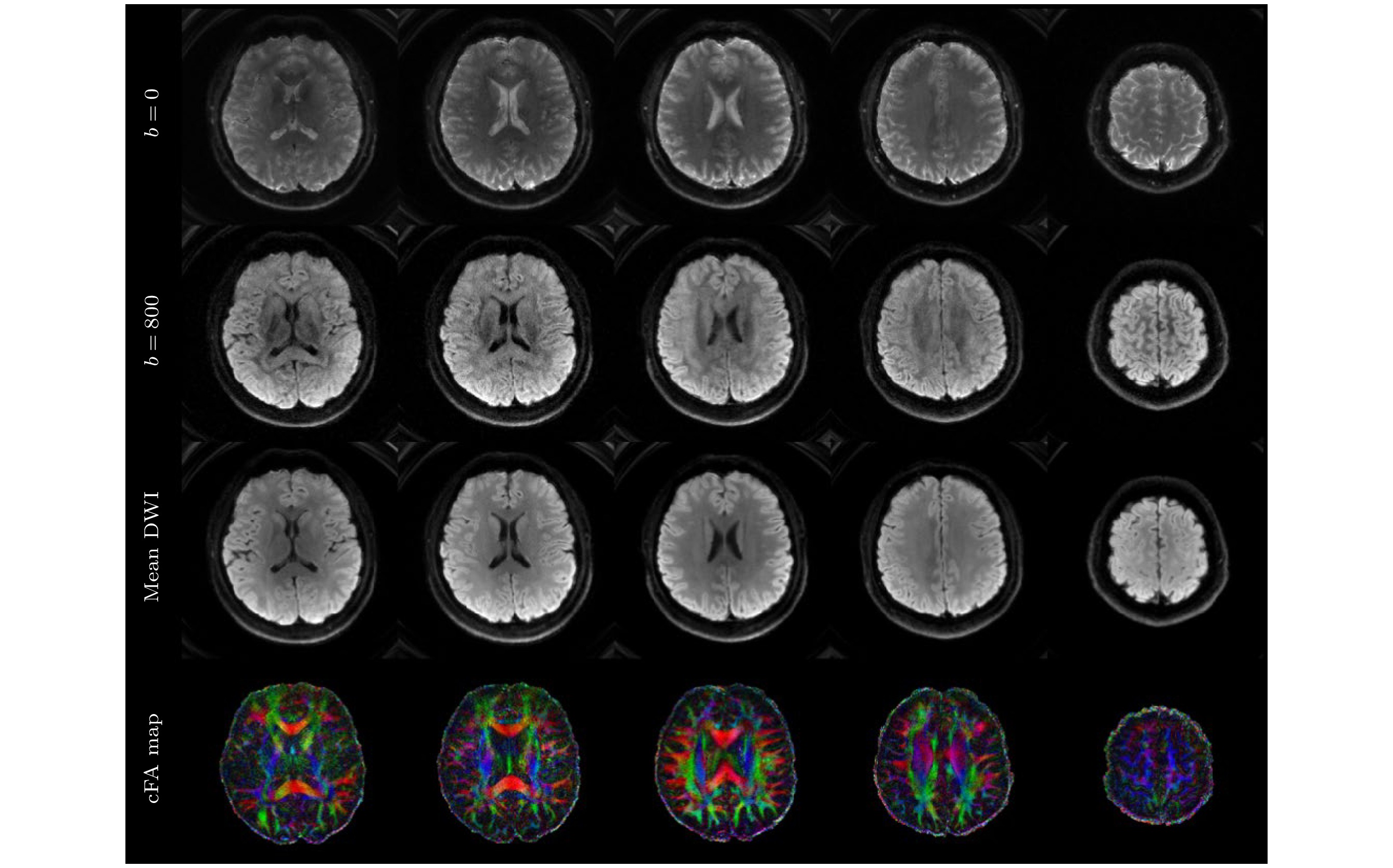
      在使用了上述的采集和重建方法之后, 我们就可以获得一些不错的DWI图像. 图9展示了使用ss-spiral采集得到的大脑DWI图像, 图像的分辨率为0.77 mm×0.77 mm×4 mm, 加速倍数为6, 使用了SPIRiT进行重建, 并使用了NORDIC[124]降噪. 图像的平均次数为18.

      • 4.2.   与SMS技术结合的2D ss-spiral DWI

    • 除了常规的2D采集, 近年来也有工作尝试将SMS技术与ss-spiral采集相结合, 实现多层同时激发的2D spiral DWI成像. 比如Herbst等[106]使用多层同时激发的RF脉冲进行激发, 并在螺旋读出中添加z方向的正弦波梯度实现CAIPI. 他们将该方法命名为wave-spiral采集, 并采集了分辨率为1.5 mm等体素的扩散图像. 在2023年, Engel等[125]也采用了类似的方法进行DWI图像采集, 他们在螺旋读出过程中加入了z方向的、变化的blip梯度, 实现了一种名为T-Hex spiral的采集手段. 他们证明了T-Hex spiral能提供比传统EPI采集更高的信噪比以及采集效率.

      在重建方面, 这些方法一般都会使用CG-SENSE进行重建. 这是因为z方向的梯度会让螺旋采集到的点散布在一个三维k空间中, 因此, 基于k空间的方法比如SPIRiT就需要使用三维的kernel来进行重建, 这会极大地提升SPIRiT算法的计算量. 而CG-SENSE算法可以轻易地将SMS采集信息加入到正向编码的过程中, 之后的求解逆问题过程也不会过分复杂.

      此外, 由于这些方法都在螺旋读出的同时加入了z方向的梯度来实现CAIPI, 所以就相当于引入了一个额外的梯度, 进一步增加了螺旋轨迹出现误差的概率. 为了解决这个轨迹误差, 研究者们往往需要使用GIRF[126]或者磁场探测等方法来实现轨迹的矫正.

    5.   ms-spiral DWI

    • 多次激发扩散成像技术的基本原理是将整个k空间分成多个部分, 在每次激发后仅对k空间的一部分数据进行采集, 经过多次激发后完成整个k空间的数据采集. 这种技术和降采样的ss-spiral成像一样, 都可以降低螺旋成像的读出长度以减少B0场不均匀和梯度场不完美对图像的影响; 同时它又可以做到对k空间进行全采样, 不会因为降采样影响图像的信噪比. 综上所述, 这是一种具有许多优点的技术. 下面就具体介绍几种ms-spiral成像的采集和重建方法.

      • 5.1.   2D ms-spiral DWI

    • 与ms-EPI DWI相同, 2D ms-spiral DWI成像的最关键问题是每次激发之间的相位变化问题.

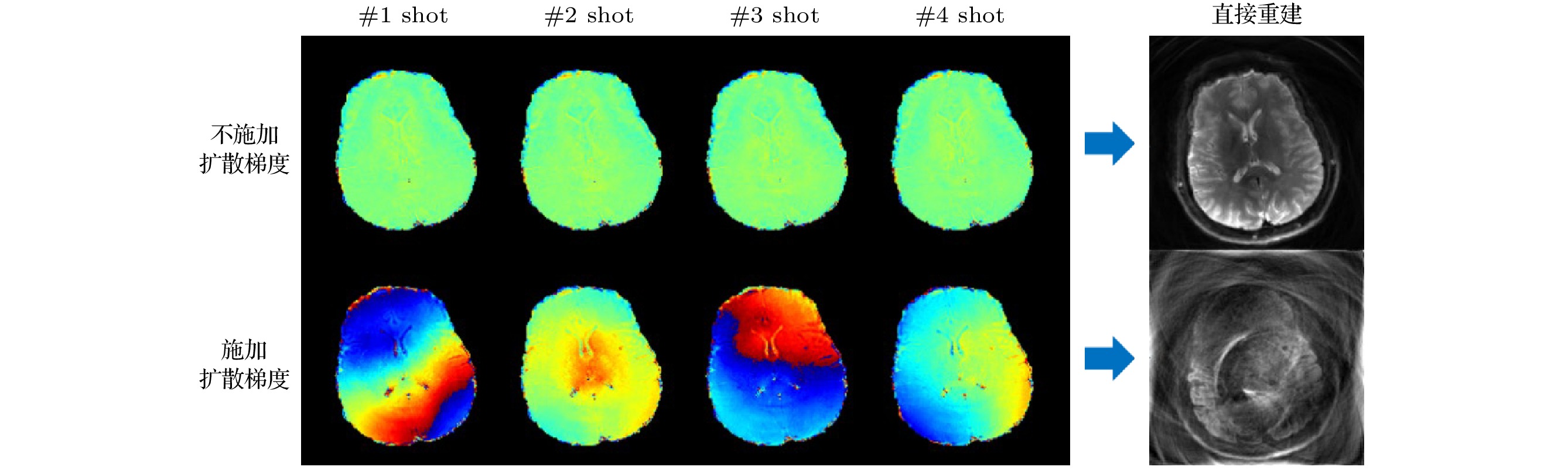
      对于单次激发扩散成像来说, 由于我们最终需要的图像是幅值图像, 所以运动造成的相位也不会对成像造成影响. 但是在多次激发成像中, 每次激发采集的数据都有不同的相位, 即各次激发之间存在相位变化. 如果将这些带有相位变化的数据直接拼合到一起, 最终的图像中就会出现明显的混叠伪影. 因此, 处理相位变化就是多次激发成像必须面对的问题. 如图10所示, 对于ms-spiral数据, 如果在采集中没有扩散梯度, 每个激发之间就几乎不会出现相位差别, 而假如使用了扩散梯度, 每个激发的相位均会存在明显差异. 此时如果将几个激发直接合并, 其结果会出现明显的错误.

      处理相位变化的方法就是获得导航数据来辅助最后的重建, 该导航数据会包含每次激发获得的相位信息, 我们可以用这个相位信息来对各次激发的相位进行矫正, 再将矫正后的k空间数据进行拼合并做一次反傅里叶变换, 就可以得到最终的重建DWI图像. 根据导航数据获得的方式不同, 可以将ms-spiral DWI成像方法分为3类: 带导航回波的成像、自导航的成像和计算导航成像. 接下来分别介绍每一种方法的采集与重建方法.

      • 5.1.1.   带导航回波的成像

    • 这种方法在EPI成像中较为常见. 一般的做法是在EPI采集完成后再施加一个180°的RF脉冲, 再采集一段导航数据. 而在螺旋成像中, 该方法并不常用, 几乎没有工作将该方法用于spiral DWI成像中, 因此不做过多介绍.

      • 5.1.2.   自导航的成像

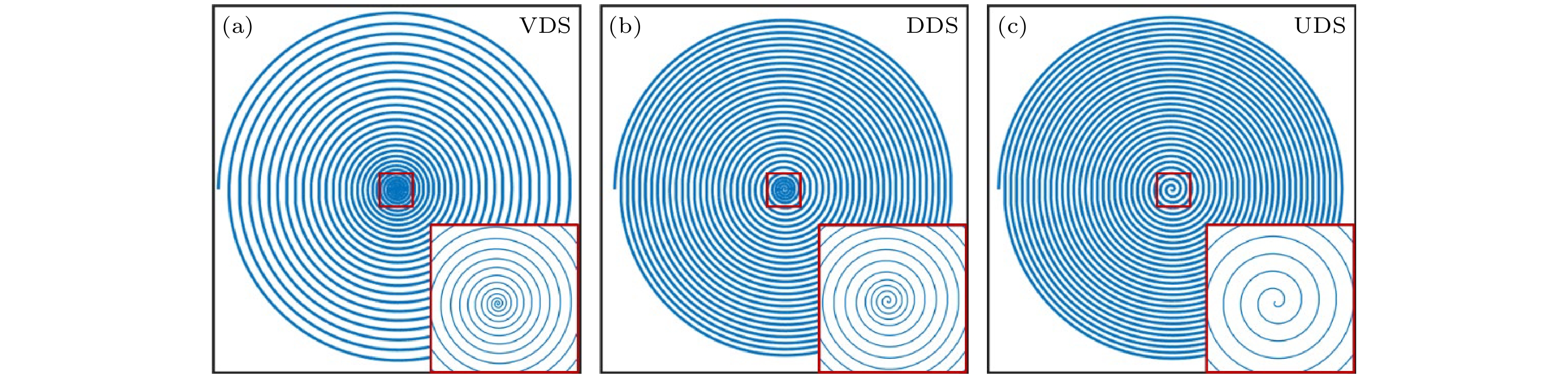
    • 这种方法需要特殊设计螺旋轨迹, 即让螺旋采集在k空间中心附近做到满采, 这样就可以用这个满采的k空间中心作为导航数据. 常见的这种螺旋轨迹有两类, 第1类为Kim等[127]提出的变密度螺旋采样轨迹(variable density spiral, VDS). VDS轨迹在k空间中心的密度最高, 离中心距离越远, 采集的密度也越低. 第2类轨迹为Lin等[128]提出的双密度螺旋采样轨迹(dual-density spiral, DDS). DDS采样轨迹在k空间中心满采, 在中心以外的地方密度降低. VDS和DDS轨迹都可以有效地让我们获得导航数据. 但这样的轨迹一般会比普通的均匀采样密度的螺旋轨迹(uniform density spiral, UDS)更长, 更容易受到B0场不均匀性的影响. 在相同的读出长度之下, 使用这些轨迹就会需要更多次的激发来填满k空间. VDS, DDS, 以及UDS的示意图如图11所示.

      如果使用VDS或者DDS进行采集, 这些数据的k空间中心相当于是全采样的, 因此我们可以首先拿出k空间中心的数据进行单独重建, 从而获得对应激发的相位信息. 在随后的重建中, 最简单的重建方法如下: 首先将该次激发的k空间数据通过NUFFT变换到图像域, 接着在图像域移除对应的相位, 接着将图像变换回k空间. 按照上述做法处理完每一次激发的数据后, 就可以将这些数据在k空间直接拼合, 然后做一个简单的NUFFT就可以得到最终的重建图像. 除了这种简单的重建 方法, 我们还可以这些相位信息加到CG-SENSE的前向模型中, 使用CG-SENSE对图像进行重建.

      • 5.1.3.   计算导航成像

    • 这一类方法使用普通的多次激发UDS轨迹填满k空间, 并通过并行成像方法还原每次激发的图像, 并从中提取相位信息作为导航数据. 这类方法的难点在于需要使用相对复杂的重建算法来解决各次激发之间相位不一致的问题. 与前两种相位校正方法相比, 这类方法无需采集额外的导航回波, 不会增加额外的扫描时间, 采集效率最高. 但是, 当激发的次数过高时, 这一类方法也会出现明显的问题: 并行成像方法很难很好地恢复每次激发的图像相位. 这就需要设计特殊的重建方法来提升图像质量.

      在重建中, 首先要通过每次激发的数据估计一个相位信息, 再将该相位信息用于重建. 该方法的经典代表为SENSE+CG方法[42]. SENSE+CG方法的步骤大致如下:

      1)使用 CG-SENSE方法重建出每一次激发的图像;

      2)获取每一幅图像的相位, 进行相位解卷绕与平滑;

      3)将每一次激发的相位信息加入(9)式的E矩阵中, CG迭代获得重建结果.

      这一方法简单直接, 可以有效地对ms-spiral DWI图像进行重建. 但该方法也存在两点直接的缺陷, 首先就是CG-SENSE本身具有的数值不稳定缺陷, 其次是当激发次数过高时, 每一次激发的降采样倍数都很高, 就难以获得一个很好的每次激发的相位图用以重建.

      针对上述两个问题, 研究人员提出了许多相应的方法[40,129,130]. 例如, 针对数值不稳定这一问题, Chu等[68]提出了POCSMUSE算法, 该方法与SENSE+CG的最大区别在于它使用了POCS作为迭代方法, 大幅提升了数值稳定性. 针对第二个问题加速倍数过高时相位信息可能存在误差这一问题, Guo等[40]提出了POCS-ICE算法, 在POCS迭代的过程中, 将每次激发的相位信息也进行更新, 这样就可以在很高激发次数的情况下也获得不错的效果.

      最后, 值得一提的是, 近年来有工作指出, 使用多次激发的UDS采集, 再使用计算导航的方法进行重建, 是一种信噪比最高、对B0场不均匀性相对最不敏感的ms-spiral DWI成像方法[41].

      • 5.2.   与SMS技术结合的2D ms-spiral DWI

    • 近年来, 也有一些工作将SMS技术和2D ms-spiral成像技术相结合, 实现2D SMS-ms-spiral成像. 下面对该技术进行简单介绍.

      在采集方面, 和SMS下的ss-spiral类似, SMS-ms-spiral也需要通过各种手段实现CAIPI成像, 以降低重建难度, 提升图像的信噪比. 常用的实现CAIPI方法为梯度编码, 即在螺旋读出的过程中施加z方向的梯度, Herbst等[106]就通过此方法实现了3层同时激发、激发次数为2的采集. 另一种CAIPI方法为RF脉冲编码, 该方法会修改每次激发的RF脉冲, 让每次激发的数据的k空间均带上不同的相位信息, 从而实现CAIPI. Jiang等[131]的工作就是通过这一方法实现了SMS-ms-spiral DWI采集.

      在重建方面, SMS-ms-spiral DWI成像会面临较大的挑战. 如前所述, 在多次激发的DWI成像中, 每次激发的数据都会带上不同的相位误差, 而SMS成像又会同时引入层方向的数据混叠. 这两个问题都需要在重建中进行解决. 目前的工作中, 一般都使用计算导航的方法来获得每次激发的相位误差信息, 并通过SENSE重建的方法来解决SMS混叠的问题. 具体来说, Herbst等[106]由于仅使用了两次激发, 所以他们首先使用3D SENSE重建每次激发的数据, 得到每次激发对应的相位信息, 并将该信息放入CG-SENSE的前向模型中, 再优化得到最终的图像结果. 该方法可以被认为是一个3D版本的SENSE+CG. 但该方法也存在明显的问题. 由于存在SMS加速, 每次激发的加速倍数都是层内激发次数乘上SMS加速倍数($ {R}_{{\mathrm{n}}{\mathrm{e}}{\mathrm{t}}}= {R}_{{\mathrm{i}}{\mathrm{n}}{\mathrm{p}}{\mathrm{l}}{\mathrm{a}}{\mathrm{n}}{\mathrm{e}}}\times {R}_{{\mathrm{S}}{\mathrm{M}}{\mathrm{S}}} $), 显然该加速倍数会随着层内或SMS加速倍数的增加而快速提升, 这就会让该方法在第1步无法获得高质量的相位误差信息, 最终的重建质量也会受到影响. 针对这一问题, Jiang等[131]提出了一种基于POCS的SMS-ms-spiral DWI重建方法, 该方法在每一次迭代中都会更新相位误差信息, 从而适用于单次激发加速倍数很高的场景. 图12所示为使用这种方法重建得到的同时激发两层, 一共使用6次激发的DWI图像, 可以看到图像具有很不错的图像质量.

    6.   挑战和展望

      6.1.   三维DWI

    • 本文讨论了2D采集以及结合了SMS的2D采集, 事实上, 为了进一步提升扩散磁共振成像的采集速度(信噪比效率), 可以使用3D采集技术. 相对2D DWI成像, 3D成像可以提供更高的图像分辨率、信噪比和更好的信噪比效率. 对于高级神经影像来说, 解剖结构像和功能成像都已有很好的3D成像方法, DWI成像的3D采集也势在必行. 近年来, 许多团队开发了3D EPI成像技术进行高分辨率DWI成像, 例如三维multislab[132–138], SMSlab[139–144]和gSlider[76]等. 相比之下, 只有非常少的团队尝试过使用三维螺旋进行扩散成像. Holtrop等[145]对三维spiral DWI的研究也是一个潜在的未来发展方向.

      • 6.2.   体部DWI

    • 当前, 高分辨率扩散磁共振大多应用在头部. 相较于头部DWI, 体部DWI存在更大挑战, 包括: 1)更低的信噪比; 2) B0场更加不均匀, 几何形变更加严重(如脊髓), 出现脂肪化学位移伪影的风险提高(如头颈、乳腺); 3) B1+场更加不均匀, 图像信号强度均一性更差; 4) T2和$\rm T_2^*$弛豫时间短, 图像分辨率受限; 5)运动伪影更加严重, 例如心脏、肝脏、胰腺、肾脏及膀胱等器官, 这一方面会使高b值图像出现信号丢失, 另一方面会导致多次采集的图像空间上发生错位, 造成图像模糊. 针对以上体部DWI的问题, 研究者们已经开发了一些前沿技术. 比如, 一些团队将运动补偿扩散梯度和ms-EPI结合起来, 减轻了心脏运动伪影, 在肝脏上实现了保真度更高的DWI成像[146]. 还有一些团队使用超强梯度系统和运动补偿, 实现了高信噪比的心脏DTI成像[147]. 在超强梯度系统中使用spiral DWI, 有团队实现了高信噪比高保真度的前列腺成像[148]. 另一些团队则关注体部DWI的压脂问题, 通过化学位移编码实现了更加鲁棒的压脂技术[79,80,149,150]. 围绕以上挑战做技术开发, 是扩散成像未来的一个研究方向.

      • 6.3.   磁场探针

    • 前文已经介绍了磁场探针对螺旋成像的巨大提升, 而事实上, 磁场探针也可以用于EPI的成像之中. EPI对梯度系统的不完美敏感, 造成奈奎斯特伪影. 虽然在临床系统上通过相位校正的方法能够解决该问题, 但是相位校正法没有考虑所有的梯度不完美. 此外, 梯度发热会使得这类校正失效. 扩散梯度引入的涡流场能够通过图像配准的方法校正, 但仿射变换不能反映真实的变形, 且配准对图像信噪比有要求. B0场漂也会引起图像变形和鬼影, 超过一阶的B0场漂只能在图像重建时进行校正, 因此需要场变化的信息. 已有研究表明, 使用磁场探针辅助EPI成像, 能够有效地提升图像质量, 同时减小图像伪影[111,151,152]. 未来, 结合磁场探针、超高场和超强梯度系统, 实现超高b值或超高分辨率扩散成像, 是神经影像的一个研究方向.

      • 6.4.   超强梯度磁共振系统

    • 通过提升梯度系统的最大幅值和切换率, 一方面能够减小EPI的读出间隔, 从而减小TE、图像模糊和几何变形、提高空间分辨率[153–155], 另一方面能够提高扩散编码效率, 从而实现超高b值成像[155–158]和短扩散时间成像[155,159]. 目前临床典型的全身梯度系统最大梯度幅值为40—80 mT/m, 最大梯度切换率为200 T/(m·s–1). 随着近年来梯度线圈和梯度功率放大器的发展, 越来越多的仅头梯度系统实现了性能突破. 例如, MAGNUS系统[156]能够达到200 mT/m及500 T/(m·s–1)性能, Connectome 2.0系统[155]能够达到500 mT/m及600 T/(m·s–1)的性能, Impulse系统[154]能够达到200 mT/m及900T/(m·s–1)的性能. 将在临床机器上开发的先进高分辨率成像技术迁移至超强梯度磁共振系统, 进一步提高空间分辨率, 有望观察到更加丰富的微观结构信息.

      • 6.5.   超高场磁共振系统

    • 由于本征信噪比与$ B_0^{1.65} $成正比[160], 因此超高场设备[154] (7 T)有望给扩散成像带来更高的分辨率. 目前在超高场上的扩散成像是一个研究热点, 但仍存在许多技术挑战. 第一, 超高场下更大的B1+不均匀性, 这使得颞叶和小脑处出现信号丢失. 使用并行发射技术(parallel transmission, pTx)[161,162]能够一定程度上解决该问题. 第二, 超高场中更剧烈的B0不均匀性会在EPI中导致更为严重的几何变形, 在螺旋成像中导致更加严重的图像模糊. 第三, 超高场T2和${\mathrm{T}}_2^* $弛豫时间短, 削弱图像分辨率. 通过设计新的采集策略在超高场中缩短TE和读出窗长度是一个潜在的研究方向. 第四, 比吸收率(specific absorption rate, SAR)在超高场中更高, 射频热效应更严重, 特别是压脂射频脉冲和多带射频脉冲. 利用pTx技术进行射频脉冲设计来降低SAR值[162,163], 是未来的一个研究方向. 最后, 近年推出的5 T全身磁共振系统[164], 为更高分辨率的体部DWI成像带来了希望. 在5 T磁共振中同时解决超高场和体部DWI的挑战, 也是一个潜在的研究方向.

    7.   总　结

    • 本文介绍了一系列的二维扩散磁共振成像方法, 并主要分为EPI和螺旋成像两部分进行了介绍. 在EPI部分, 重点介绍了RS-EPI, iEPI, PSF-EPI, EPTI等ms-EPI DWI技术, 还介绍了ms-EPI与SMS技术的结合. 相较于ss-EPI, ms-EPI能够显著提高扩散图像的保真度和信噪比. 其中, RS-EPI和iEPI技术已经应用于临床, 改善了临床诊断和疾病监测. 也有越来越多的研究使用这些高分辨率DWI成像技术在在体人脑中观察更加精细的解剖结构[31,165]. 在螺旋成像部分, 本文分别介绍了单次激发以及多次激发的spiral DWI成像, 以及二者与SMS技术的结合. 本文还对DWI技术的挑战和未来发展进行分析. 最后, 本文并没有对EPI和螺旋成像的优劣进行详细讨论, 但目前有一些文献关注了这一问题, 感兴趣的读者可以参阅文 献[166,167]报道的工作. 相信随着技术的发展, 高分辨率、高保真度、高信噪比以及高效率的扩散磁共振成像将成为临床诊断、监测以及神经科学研究中的重要工具, 也将为人类健康事业的发展做出更多贡献.

    参考文献 (167)

目录

/

返回文章
返回