首页
登录
注册
下载:
-
以超高剂量率(简称FLASH, 通常≥40 Gy/s)进行的放射治疗在显著提升对正常组织保护的同时, 可以保持较高的肿瘤控制概率, 这种现象被称为“FLASH效应”, 与之对应的超高剂量率放射治疗被称为“FLASH放射治疗”[1–3]. X射线FLASH(简称XFLASH)放射治疗具有深穿透和经济性好等特点, 但在临床前和临床应用中面临诸多剂量学难题, 实现束流的精确在线监测是其中关键挑战之一. 在常规放射治疗加速器中, 利用穿透电离室可实时监测和反馈束流的总剂量、剂量率、平整度、对称性等[4,5]. 在FLASH工况下, 由超高剂量率引起的电子-离子复合损失将使得穿透电离室的探测效率不稳定, 会随着剂量率和脉冲结构的改变出现显著变化, 难以对XFLASH束流进行准确的剂量测量与实时监测[6].
目前, 基于闪烁探测器、金刚石探测器、穿透电离室已开展部分FLASH束流监视技术探索. Vignati等[7]开发了薄片型硅探测器作为FLASH监视器. Levin等[8]基于平板型闪烁体作为探测器对FLASH加速器的束流进行监视, 探测器以20000 Hz帧率产生二维光束图像, 实现FLASH束流实时剂量监测与空间位置监测. 然而, 半导体和闪烁体会因辐照损伤造成类似电离室的饱和非线性响应[9]. 此外Marinelli等[10]改进了FlashDiamond探测器(TW60025), 实现了快速的信号传输并用于FLASH剂量监视, 但其探头较小, 不能提供束流在空间分布上的信息.
本研究使用低气压、窄间距电离室作为XFLASH放疗束流监视器. 基于Boag模型[11,12]可知, 降低电离室气压与电极间距均可有效抑制复合损失. 若使用低气压或窄间距电离室作为XFLASH束流监视器, 既可以避免传统穿透电离室由于复合损失引起的探测效率不稳定, 还可反映束流空间分布上的信息. 基于理论分析和数值模拟对低气压、窄间距电离室的电极间距和腔室气压等参数进行物理设计, 依据物理设计提供的数据进行工程设计, 研制了对应探测器并基于XFLASH加速器完成了详细的性能测试.
-
在临床应用中, 用于 FLASH 束流监视器的低气压或窄间距电离室面临着双重挑战. 一方面, 需要设定合适的气压、电场强度以及电极间距, 以确保电子-离子复合损失处于可接受的范围之内; 另一方面, 必须保证束流具有足够的穿透性, 避免在正常治疗距离处出现单脉冲剂量过低、剂量率不足的情况. 因此, 在研制探测器之前, 有必要开展细致的电子-离子复合损失计算以及束流损失模拟.
-
为了将电子-离子复合损失控制在可接受的范围, 研究了电离室气压、电极间距以及电压等3个关键因素与复合损失之间的联系, 用以精准确定电离室的气压、电极间距等关键参数.
从电离室的工作原理来看, 其工作过程可以清晰地划分为“辐射电离+电荷收集+采集分析”3个主要阶段. 在 FLASH 工况下, 电离室出现非线性响应问题的主要阶段集中在“电荷收集”环节. 为了有效解决这一问题, 一是通过降低辐射电离过程中产生的电荷量, 减轻电荷收集阶段的压力; 二是提升离子收集的性能, 优化电荷收集过程, 进而提高电荷收集的效率. 电离室的非线性响应与多种因素有关, 对应多种修正因子ks模型公式, 其中Boag模型[11,12]是较为细致的一种, 其ks的一阶近似表达式为
其中, Q0是腔内总电荷, A是腔气体因子, p是电子直接收集比例(未形成负离子); d是极间距离, e是元电荷, μ+和μ–是正负离子的迁移率, V是腔内体积, Uc是收集电压, α是正负电荷复合率常数. 理想情况下, 电荷收集效率应达到100%, 即ks = 1, 但实际上总会有部分电荷被复合抵消, 因此电离室追求的是(1)式的第2项(定义为复合比R)足够小. 临床上期望复合比R小于1%, 即边界工况为
又
其中正负离子迁移率基本与气压成反比、与电场成正比, 因此R可进一步近似表达为
其中,
$ {\mu }_{+0} $ 和$ {\mu }_{-0} $ 分别代表某特定气压和电场强度下特定气体的正负离子迁移率常数, P为气压.进一步地, 根据Thomson的研究表明[13], 在1013 hPa(标准大气压)以下时, 复合因子α与气压成正比. 同时, 也近似正比于电场E, 所以R进一步改写为
其中
$ {\alpha }_{0} $ 是某特定气压和电场强度下的离子复合系数, 是一个常数. Q0是密闭腔室内总电荷, 等于电荷密度ρ乘以体积V, 所以近似地, 电荷密度ρ正比于脉冲内剂量D和气压P, 因此
其中
$ {\rho }_{0} $ 是某特定脉冲内剂量和气压下产生的电荷密度, 是一个常数.若自由电子比例近似为一个常数, 将所有常数集中成一个常数k, 则有
其中
因此, 当剂量率D较大时, 为使R足够小, 需要尽量小的电极间距d、足够小的气压P、足够大的电极间电压Uc.
-
上述解析公式中运用了大量的近似处理, 为验证其准确性, 使用Numerical-ks-calculator程序[14]模拟分析了平板电离室电极间距、腔室气压、电离室高压等参数对复合损失修正因子Ks的影响. 该程序描述了电离室内电荷释放、输运及反应过程, 通过考虑载流子在电场中的形成、相互作用和运动, 计算电荷载流子密度的时间演化, 并输出电极的电荷收集效率, 以获得电子离子复合损失修正因子Ks. 程序的可调节输入参数为电离室电极间距、收集极直径、电离室极间电压、单位剂量产生的电荷量、电子离子迁移率等.
本研究中, 模型采用平板型电离室, 电极间距设置为1 mm, 电极直径为11 mm, 根据模拟条件设置不同的剂量与电离室极间电压, 根据气压调整单位剂量产生的电荷量、电子离子迁移率等.
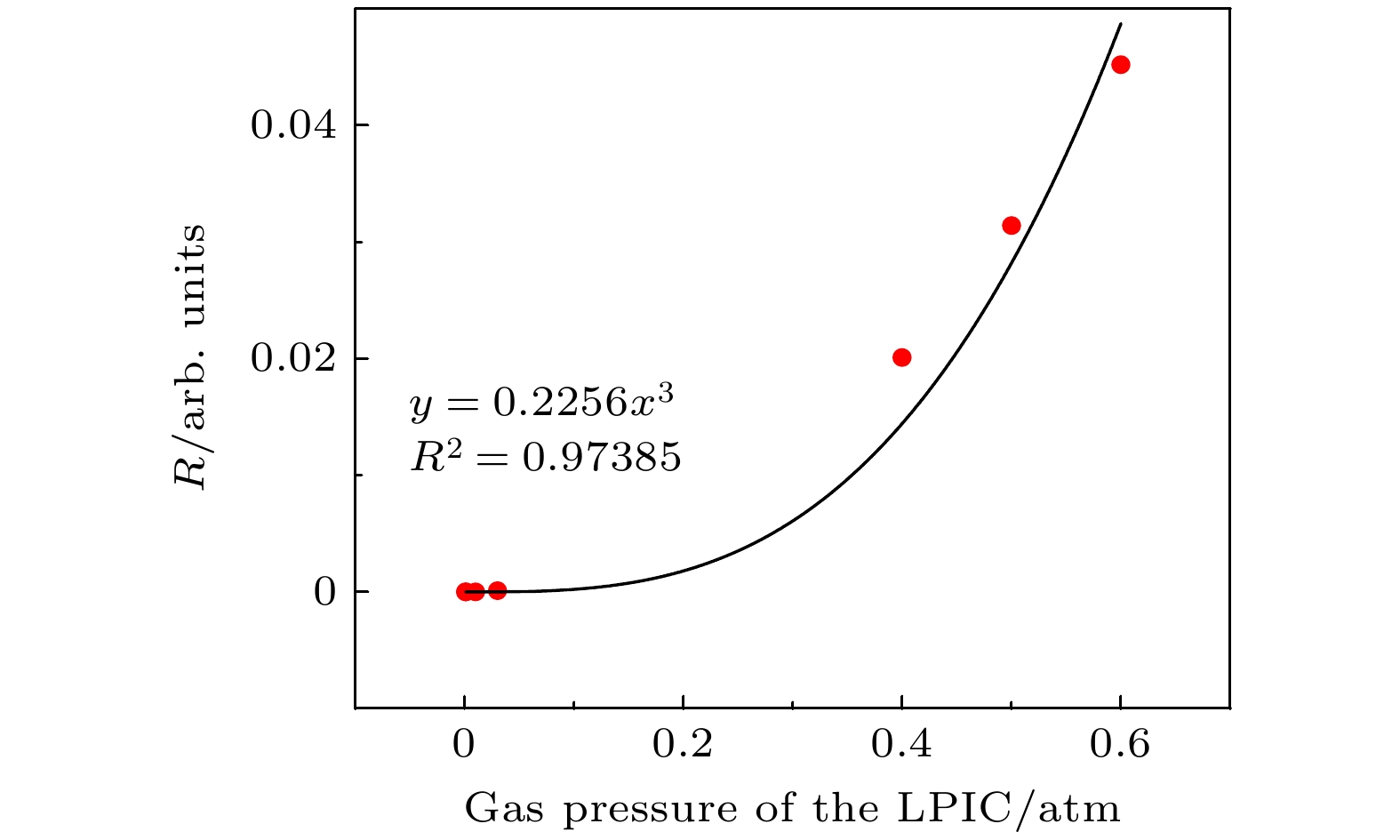
关于复合比R与气压P之间的关系验证, 模拟条件为单脉冲剂量1.1 Gy, 极间距0.1 mm, 电压–40 V工况下, 气压为0.0008—0.6 atm (1 atm =1.013×105 Pa)时, 复合比R与气压P的关系如图1所示. 通过对模拟数据的分析和处理, 得到复合比R与气压P拟合公式为
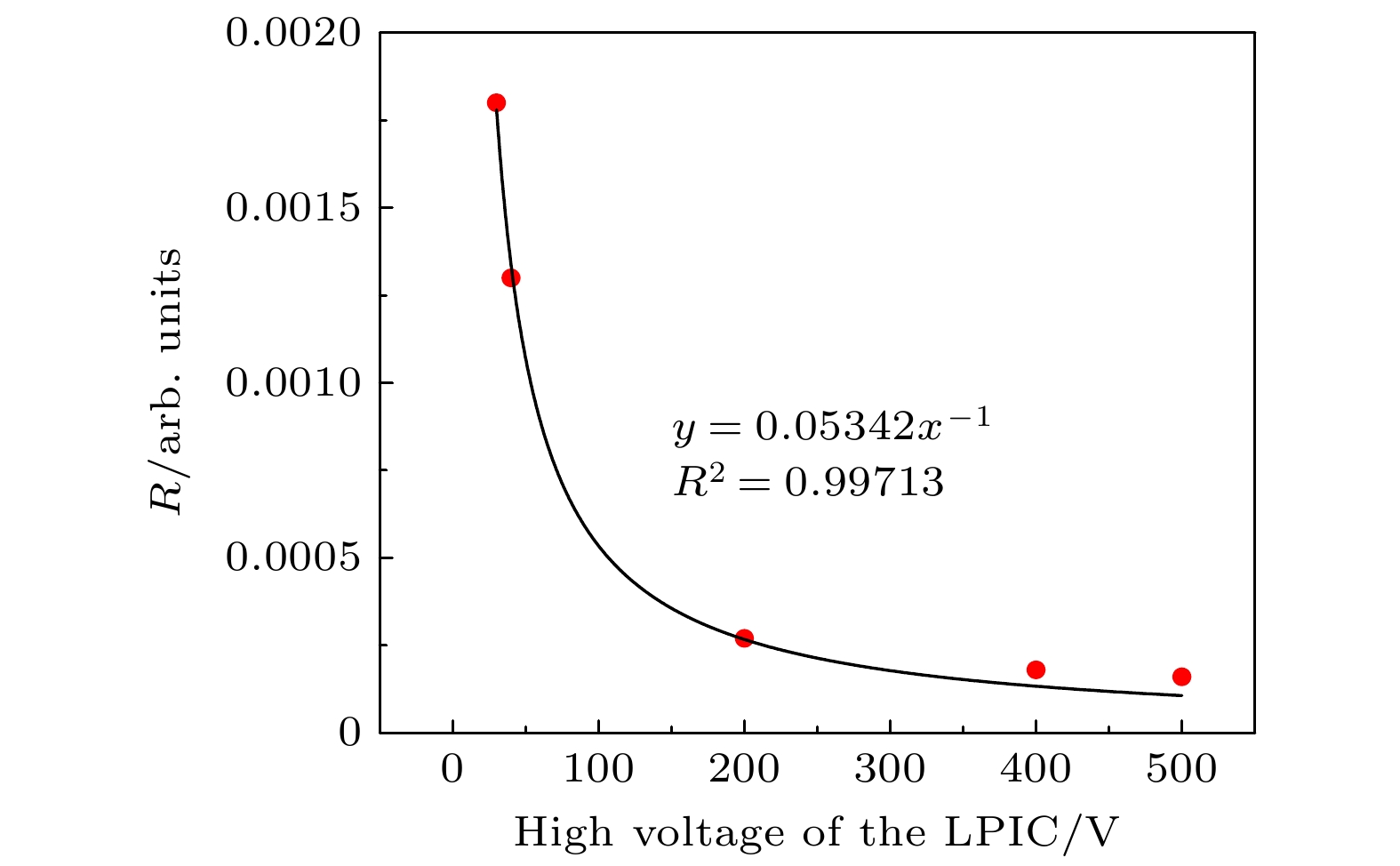
$R = 0.2256P^3 $ , 拟合决定系数$R^2 = 0.97385 $ .关于电压Uc对复合比R的影响, 设置单脉冲剂量为1.11 Gy, 极间距2 mm, 气压0.005 atm. 当电压从30 V变化至500 V时, 复合比R与电压Uc的关系如图2所示, 复合比R与气压P的拟合公式为
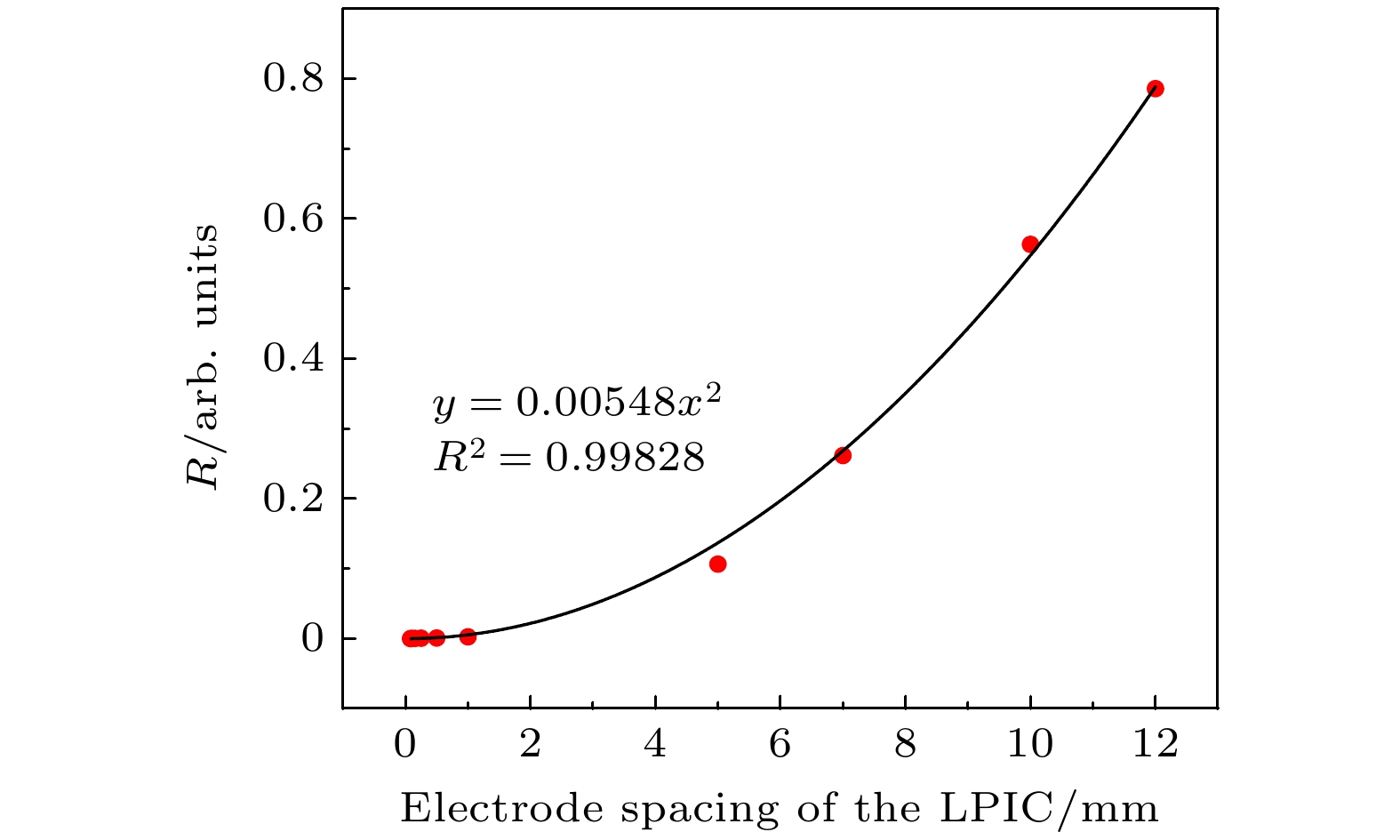
$R = 0.05342U_{\rm c}^{-1}$ , 拟合决定系数$R^2 = 0.99713 $ .为验证复合比R与极间距d之间的关系, 设置单脉冲剂量为82 Gy, 电压–400 V, 气压0.003 atm. 当极间距d从0.08 mm变化至12 mm时, 复合比R与间距d的关系如图3所示, 复合比R与间距d的拟合公式为R = 0.00548d 2, 拟合决定系数R2 = 0.99828.
以上模拟中, 复合比R与电极间距d、电离室高压Uc的拟合优于复合损失比R与腔室气压P的拟合, 原因可能是在2.1节的公式推导中, 与气压P相关的近似共有三次. 其中, 在推导(5)式时, 正负离子迁移率被近似正比于气压P; 推导(6)式时, 复合因子α根据经验公式被假设与气压P成正比; 推导(8)式时, 假设了电荷密度ρ正比于气压P. 因此, 这三次近似可能影响了(9)式的准确性. 经过与数值模拟的对比, 可以认为推导的关系式可以用于定性分析, 而电离室具体腔室气压和电极间距参数依然需要通过数值模拟确定.
-
模拟结果显示, 在电极间距0.1 mm, 单脉冲剂量1.1 Gy情况下, 电离室气压小于0.3 atm才能使得复合损失小于1%, 若电离室气压为标准大气压, 则要求电极间距小于0.1 mm. 若仅使用减小极间距的方式降低复合损失, 电极间距小于0.1 mm的要求不仅在工程上难以实现, 同时工作过程中任何微小的温度、震动、材料老化等影响都可以造成电极间空间的显著变化, 从而显著影响电离室收集电荷和剂量之间的关系(nC/Gy), 使得监视器的稳定性较差. 因此不宜通过单一调整极间距d来降低复合率.
此外, (9)式显示通过大幅度增大高压的方式也可以降低复合率, 但由于电压过高、电场过强时, 会产生碰撞电离, 使得离子、电子数目增大, 输出信号随着电压增大急剧上升. 此时, 输出信号与剂量的关系变得复杂且十分不稳定. 因此, 通过大幅提升电压来降低复合率这种方法的适用范围也十分有限.
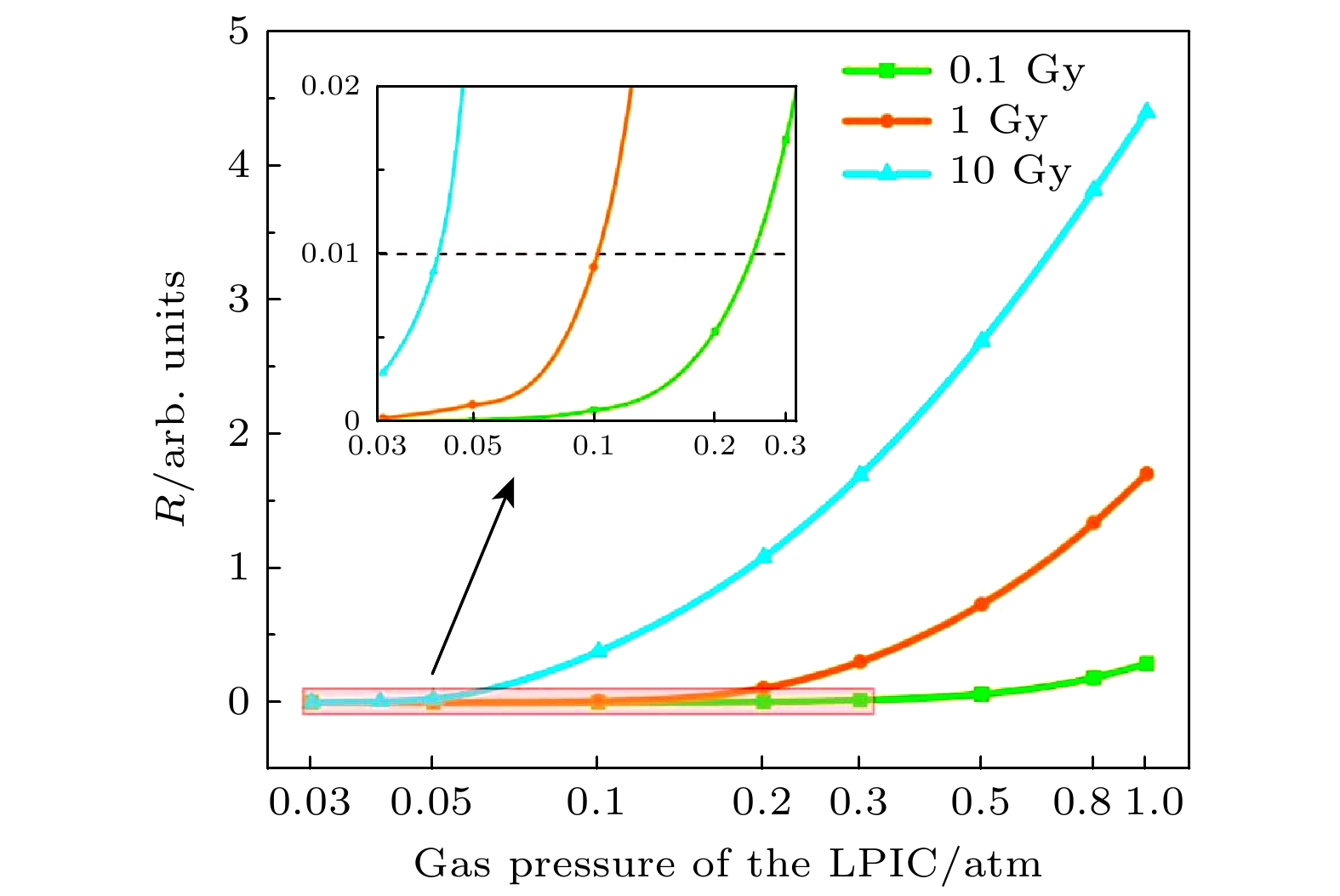
综上可知, 减小气压是减小电子离子复合比的最优方案, 具有很强的可行性. 根据XFLASH加速器工况及监视器所处位置的不同, 该监视器处的单脉冲剂量在0.1—10 Gy/pulse之间. 电极间距为1 mm时, 不同单脉冲剂量与气压的关系如图4所示. 为使复合比R小于0.01, 当单脉冲剂量分别为0.1, 1, 10 Gy时, LPIC腔室气压应分别小于0.2, 0.1, 0.04 atm.
-
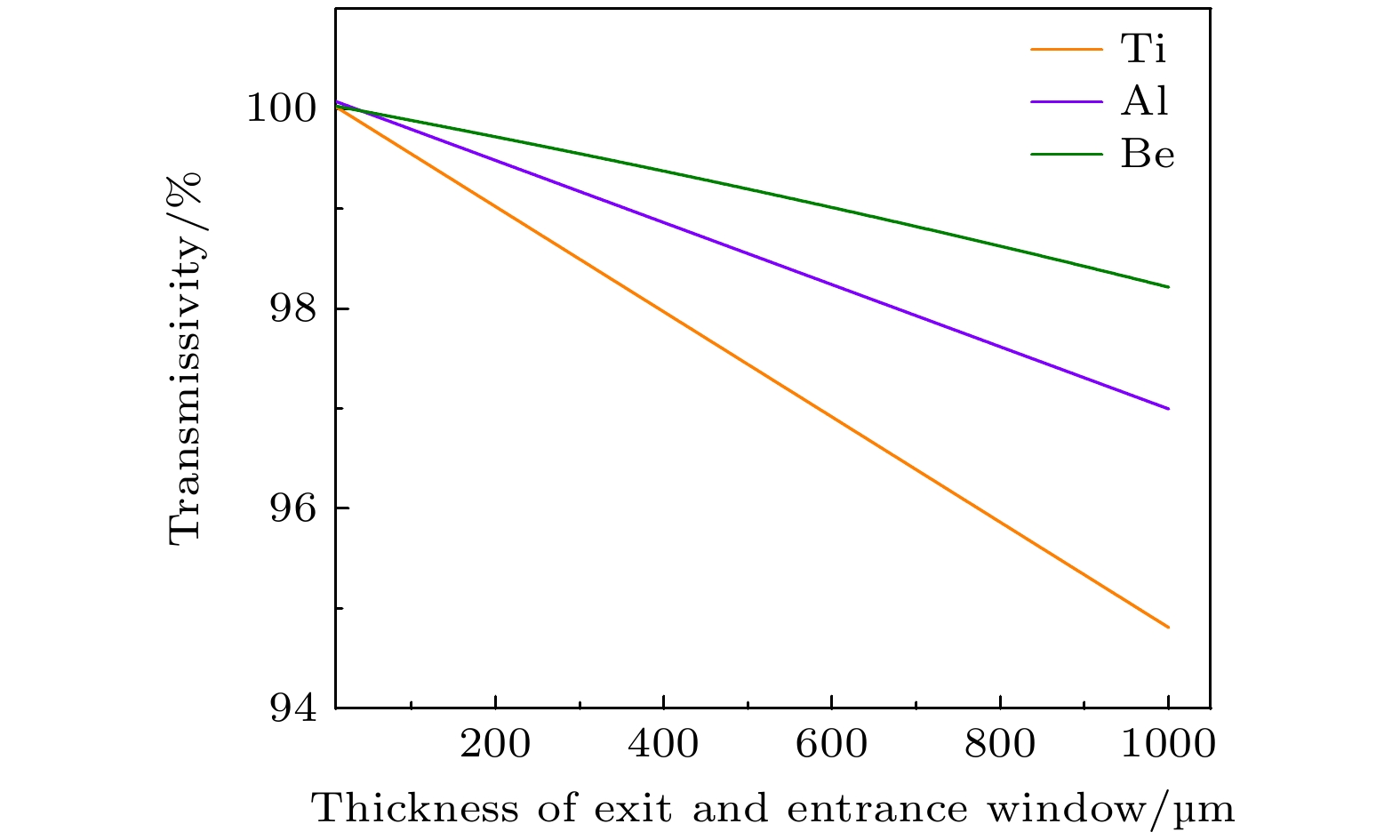
XFLASH放疗要求加速器提供超高剂量率束流. 电离室可能会阻挡并散射束流, 从而降低治疗过程中远端生物组织的吸收剂量率. 为了确保正常治疗距离处获得足够的剂量率, 针对低压电离室在XFLASH束条件下的穿透特性进行计算与优化. 利用MCNP模拟LPIC出射窗与入射窗材料、厚度对XFLASH射束穿透性的影响. 模拟中, 改变束窗的厚度和材料, 厚度范围为0—1000 μm, 材料为钛(Ti)、铝(Al)和铍(Be). 定义不同束窗与零厚度束窗导致的该剂量之比为透过率Tr. 如图5所示, 随着窗厚的增大, 透过率接近直线下降, 且Be好于Al, Al好于Ti, 说明高原子序数材料对射线的阻止本领较强. 总体上, 3种材料在0—1 mm的窗厚下均有较好的穿透性.
-
基于低压电离室的物理设计研制了原理样机, 并按照国家标准GB/T 15213—2016中关于剂量监测系统相关要求在XFLASH加速器上开展测试, 以验证其是否符合物理设计和满足临床需求. XFLASH加速器由中玖闪光医疗科技有限公司研制, 能稳定产生能量高达10 MeV高能电子束. 当高能电子束轰击钨靶时, 通过轫致辐射可以产生满足FLASH放疗需要的X射线. 在距离钨靶约100 cm处, 其平均剂量率可达80 Gy/s. 低气压电离室及XFLASH实验台如图6所示.
-
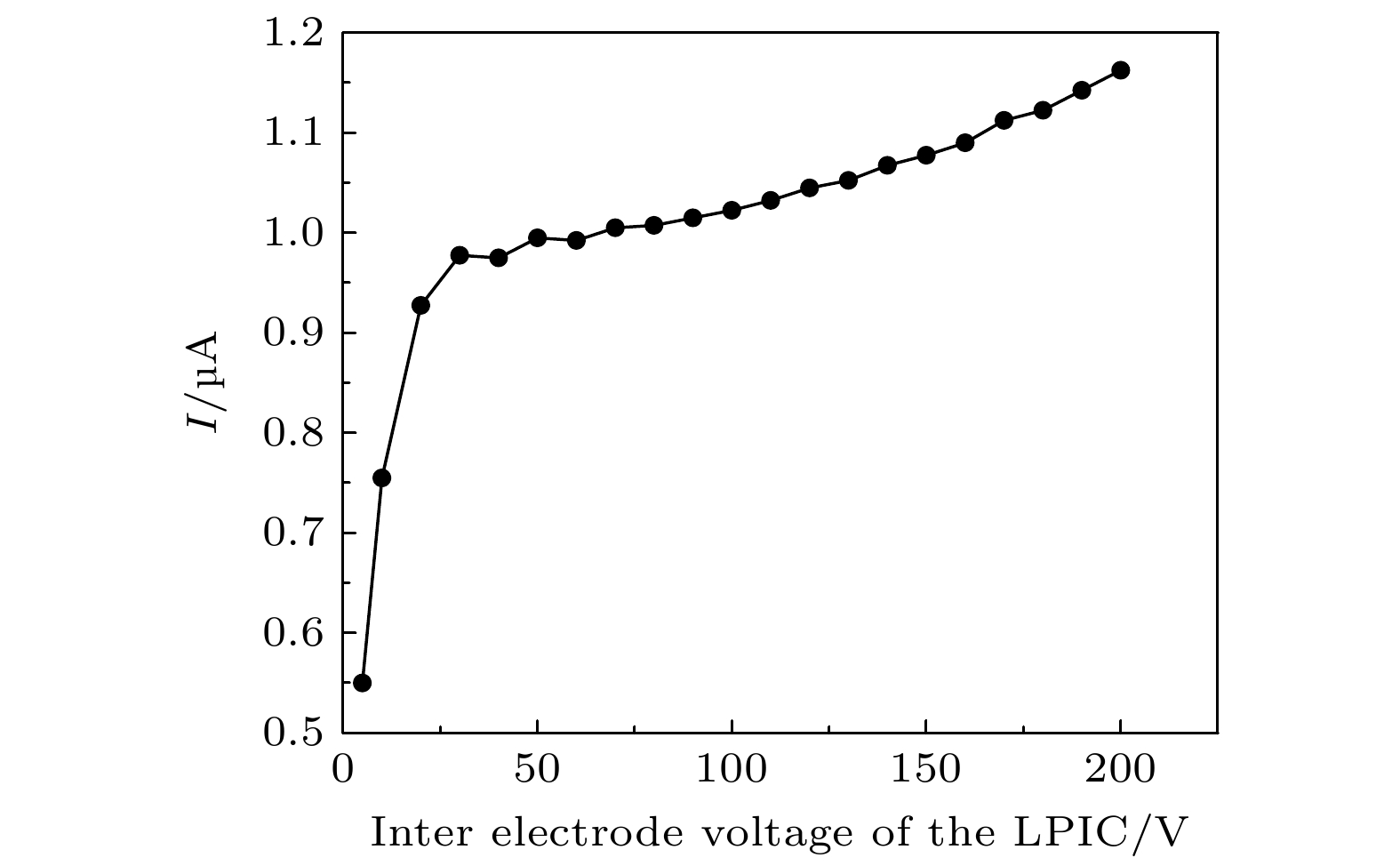
在XFLASH射束辐照下测量了低压电离室的特性曲线[15]. 加速器在固定工况下运行, 调节LPIC的极间电压从5—200 V, 测量监视器电流. 测量结果如图7所示. 坪特性曲线未展现明显的平台区域, 但仍然表现出信号随电压单调增大的趋势, 且当LPIC高压大于40 V时较为平坦. 当高压大于40 V时, 该坪曲线相对变化率均小于0.002 μA/V, 所用高压电源电压精度为0.2%, 因此在40—200 V范围内, 由电压稳定性引起信号电流相对波动最大值为0.069%, 远小于监视器总不确定度要求, 可忽略. 实际应用场景中, 若电离室电压具有良好稳定性, 则低气压电离室在相对剂量测量方面具有足够的可靠性.
-
依据国标GB/T 15213–2016中对医用X加速器剂量监视系统的相关要求, 对低压电离室进行剂量重复性测试. 剂量重复性由变异系数S表征, 如(11)式所示:
其中, Ri为剂量监测计数与剂量之比,
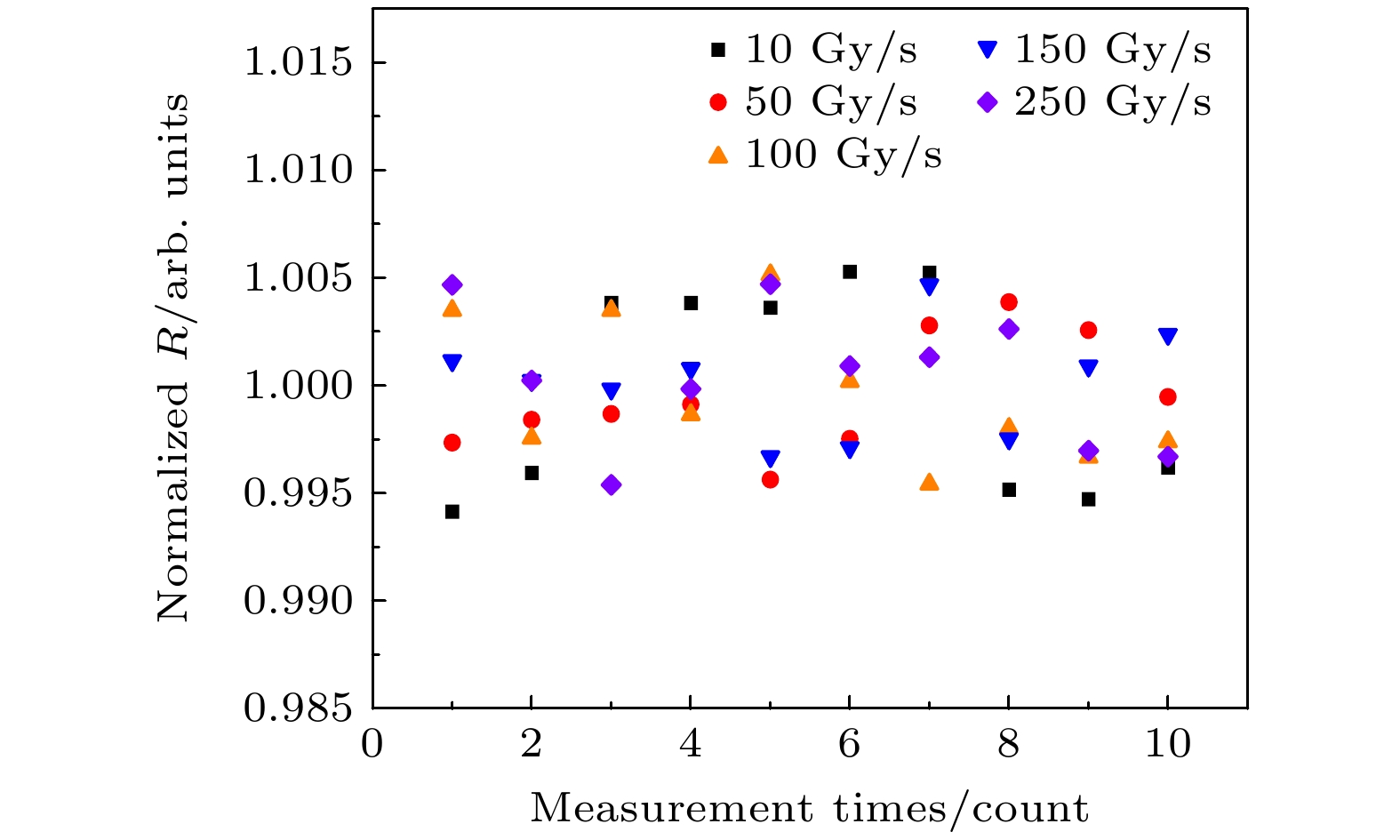
$ \bar{R} $ 为Ri的均值.按测试要求, FLASH 加速器以 10—250 Gy/s的剂量率发射相同数量的宏脉冲. LPIC测得值为其产生信号的电荷积分, 单位为MU. 使用TW60019作为剂量监视器. 测试结果如图8所示. 图8中10—250 Gy/s剂量率下变异系数S分别为0.49%, 0.27%, 0.33%, 0.25%, 0.32%, 均小于0.5%, 满足国标GB/T 15213-2016中对加速器剂量监视系统重复性的要求[16,17].
-
剂量线性主要研究监视器输出剂量(MU)与实际受照剂量率(Gy)之间的线性关系. 同理, 剂量率线性主要研究监视器输出剂量率(MU/s)与实际受照剂量率(Gy/s)之间的线性关系. 监视器的输出剂量率可通过监视器给出的跳数MU与曝光时间T1相除得到. 实际受照剂量率则由监视器位置的剂量测量值D来确认. 在实际实验中, 通过在监视器后方放置主动式剂量计测量剂量计处的剂量值D1, 继而通过之前测定的剂量转换关系
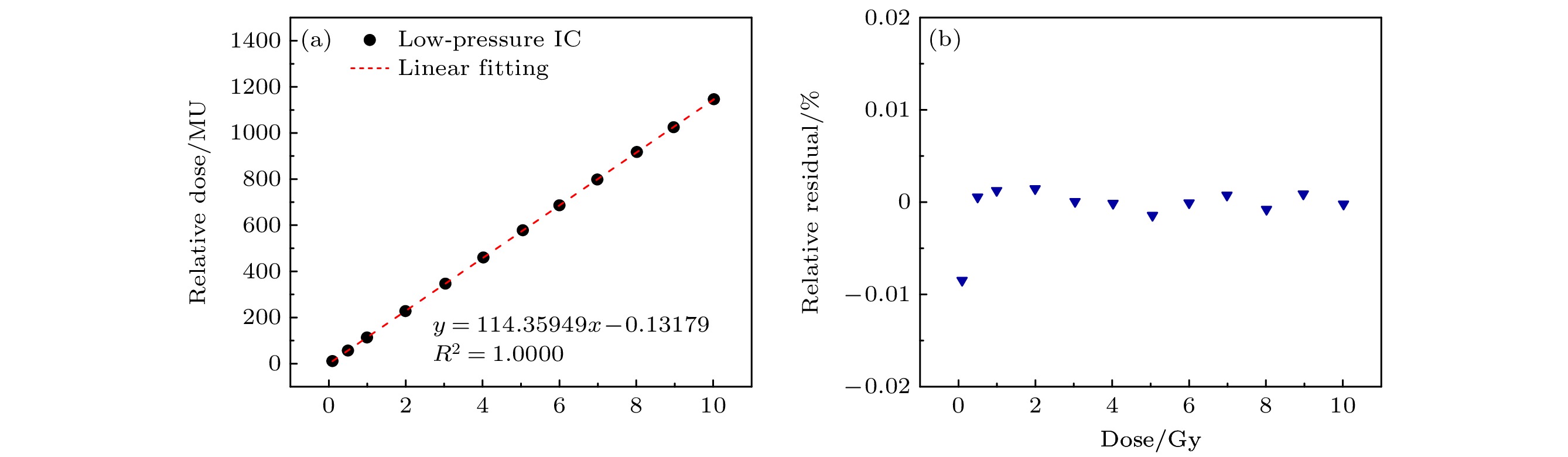
$ K=D/{D}_{1} $ 配合每次测量的D1值, 从而得到D值. 为全面获取剂量率线性情况, 使用两种方式改变剂量率: 调整宏脉冲重频和宏脉冲宽度. 通过拟合不低于5个测量点得到线性相关系数[18,19].将PTW60019金刚石剂量计探头安装在监视器后端次级准直器(3 cm×4 cm)后, SSD约50 cm, 水深3 cm. 剂量线性测量时, 固定脉宽与频率, 加速器出束不同剂量, 统计LPIC及PTW60019的测量结果. 实验结果如图9(a), (b)所示. 在所有测试条件下, 剂量与测量的脉冲计数之间具有高度线性关系, 决定系数(R2 > 0.999)证明剂量监视系统能够准确反映剂量.
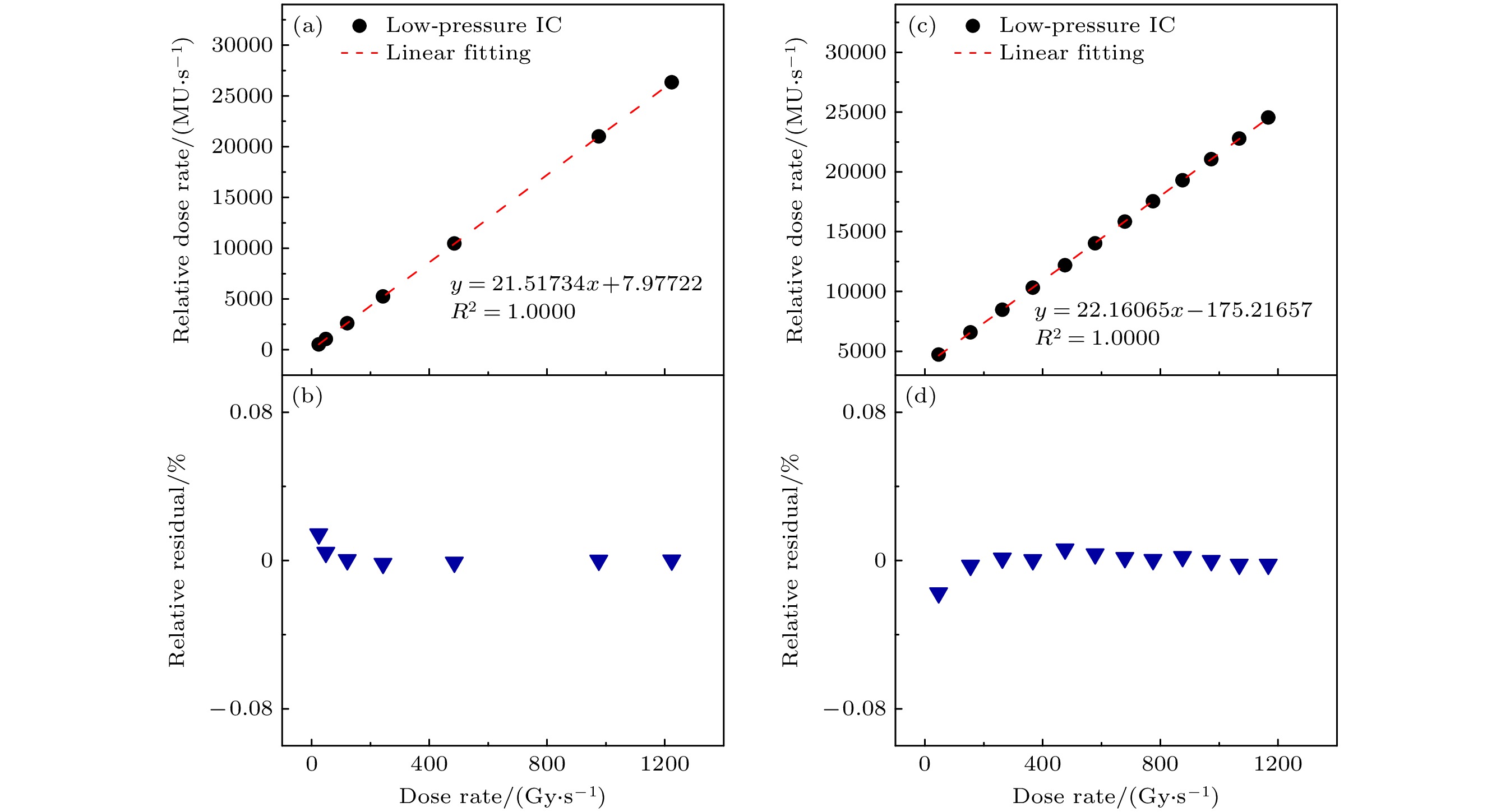
根据XFLASH加速器出束原理, 可以通过改变脉冲频率及脉冲宽度改变剂量率. 剂量率线性测量时, 分别在仅改变频率与仅改变脉宽的条件下测量. 测试时, 首先使XFLASH加速器固定宏脉冲宽度, 改变重频, 每次出束相同剂量, 统计LPIC与PTW60019的测量结果, 结果如图10(a), (b)所示. 其次, XFLASH加速器固定重频, 仅改变宏脉冲宽度, 统计LPIC与PTW60019的测量结果, 结果如图10(c), (d)所示. 由图10可知, LPIC在FLASH加速器常用频率及宏脉冲宽度范围内有良好的剂量率线性(R2 > 0.999), 最大相对残差小于0.02%, 远低于相关国家标准规定的±2%容许范围, 进一步验证了设备的可靠性, 满足临床应用需求.
综上所述, 低压电离室表现出优异的剂量线性及剂量率线性, 并完全符合剂量监测系统的相关国家标准. 这些研究结果表明其能够胜任XFLASH 束流的实时监测, 并具备在临床实践中推广应用的潜力[20,21].
-
本研究提出了一种用于 XFLASH 放射治疗束流监测的低压电离室, 深入开展了电离室腔室气压、电极间距等关键参数的物理设计. 基于设计研制了低压电离室工程样机, 利用XFLASH加速器进行了系统的性能测试, 并从剂量重复性、剂量线性以及剂量率线性等方面展开了深入的分析与评价. 研究结果表明, 低压电离室在剂量重复性、剂量线性和剂量率线性方面均展现出优良的性能, 能够精准且实时地实现对XFLASH束流参数的监测, 满足相关国家标准要求, 具备应用价值.
综上所述, 低气压电离室在超高剂量率辐照过程中能够在无显著饱和效应的情况下实现对束流的实时监测, 使其成为XFLASH放射治疗实时束流监测的有效工具, 为 XFLASH 放射治疗技术在临床应用中的进一步推广与发展提供坚实的技术支撑.
高能X射线FLASH放射治疗: 基于低气压电离室的束流监视器物理及性能
High-energy X-ray FLASH radiotherapy: Physics and performance study of beam monitoring based on low-pressure ionization chambers
-
摘要: 超高剂量率X射线(简称XFLASH)的剂量实时准确监测在XFLASH放射治疗临床前后都起着关键作用. 本文研究了一种用于XFLASH放射治疗剂量在线监测的低气压电离室(LPIC), 并将其作为XFLASH束流的监视器. 开展了电离室物理设计, 两个独立腔室分别放置高压极、收集极和保护极. 高压极与收集极电极间距为1 mm, 腔室气压约5 kPa. 实验分析了该监视器的坪曲线、剂量重复性、剂量线性等性能. 测试结果表明, 研制的低气压电离室表现出优异的剂量线性(R2 > 0.999)和剂量重复性(变异系数小于0.5%), 被证明是一种可靠的剂量监视器, 其性能满足国家标准对放射治疗剂量监视系统的要求.Abstract: This study solves the key challenge of real-time beam monitoring in ultra-high dose rate X-ray FLASH (XFLASH) radiotherapy, in which the traditional ionization chambers suffer serious electron-ion recombination losses at extreme dose rates (≥40 Gy/s). We propose a low-pressure ionization chamber (LPIC) as a novel beam monitor to achieve accurate dose measurement while maintaining beam penetration characteristics required for clinical applications. The LPIC is designed to have two independent chambers to accommodate high-voltage, collecting, and protecting electrodes. Key parameters include a 1-mm electrode gap and a reduced chamber pressure (~5 kPa) to mitigate recombination effects. Theoretical analysis based on the Boag model and numerical simulations (using the numerical-ks-calculator program) quantifies the dependence of recombination loss on pressure (P), electrode spacing (d ), and voltage (Uc). MCNP simulations evaluate X-ray transmission through chamber windows (Be, Al, Ti) with thickness up to 1000 μm. According to the national standards (GB/T15213-2016), a prototype LPIC is constructed and tested on a 10-MeV XFLASH accelerator (dose rate: 80 Gy/s) for plateau characteristics, dose repeatability, linearity, and dose-rate response. Theoretical analysis based on the Boag model reveals that the values of recombination ratio R scale with $P^3$, $d^2$, and $U_{\rm c}^{-1} $, which are validated by numerical simulations $(R = 0.2256P^3;\; R = 0.0534U_{\rm c}^{-1};\; R = 0.00548d^2) $. At 1.1 Gy/pulse, recombination losses are maintained below 1% at the optimal parameters: P < 0.3 atm for d = 0.1 mm or P < 0.04 atm for d = 1 mm. MCNP simulations show that X-ray transmission exceeds 90% for beryllium (Be), aluminum (Al), and titanium (Ti) windows with thickness ≤1000 μm. While 0.1-mm Be achieves the highest transmission (>99%), 1-mm Al (transmission ~95%) is selected as the optimal window material due to its clinical acceptability (<5% dose loss), cost-effectiveness, and easy fabrication. The prototype exhibits stable plateau characteristics (ΔI/I < 0.069% at Uc > 40V), exceptional dose repeatability (coefficient of variation <0.5% across 10–250 Gy/s), and linearity (R2 > 0.999 for dose and dose-rate measurements). These results confirm their compliance with the national standard (GB/T15213-2016) and are suitable for real-time XFLASH monitoring. The LPIC demonstrates robust suppression of recombination losses and reliable performance under XFLASH conditions. Its design, which is optimized via theoretical modeling and simulations, ensures high precision, which meets GB/T15213-2016 requirements, while preserving beam penetration. The use of 1-mm Al windows balances cost and function, making the LPIC a reliable clinical dose monitor. Future studies will focus on multi-channel LPIC arrays for two-dimensional beam profiling.
-
Key words:
- FLASH radiotherapy /
- low-pressure ionization chamber /
- beam monitor /
- performance testing .
-
-
图 3 复合损失比R与LPIC电极间距关系
Figure 3. Relationship between R and electrode spacing of the LPIC.
图 4 不同单脉冲剂量下复合损失比R与LPIC腔室气压之间的关系
Figure 4. The relationship between R and gas pressure of the LPIC under different single pulse doses.
图 5 LPIC窗厚与射束透射率关系
Figure 5. Relationship between transmissivity and the LPIC window thickness.
图 6 XFLASH加速器实验台及低气压电离室实物图
Figure 6. Physical image of the XFLASH accelerator experimental setup and LPIC.
图 8 重复性测量中归一到平均值的Ri
Figure 8. Normalized ratios of dose measurements using the LPIC to a reference.
-
[1] Diffenderfer E, Verginadis I, Michele M K, Shoniyozov K, Velalopoulou A, Goia D, Putt M, Hagan S, Avery S, Teo K, Zou W, Lin A, Swisher-McClure S, Koch C, Kennedy A, Minn A, Maity A, Busch T, Dong L, Koumenis C, Metz J, Cengel K 2020 Int. J. Radiat. Oncol. Biol. Phys. 106 440 doi: 10.1016/j.ijrobp.2019.10.049 [2] Sørensen B S, Sitarz M K, Ankjærgaard C, Johansen J, Andersen C E, Kanouta E, Overgaard C, Grau C, Poulsen P 2022 Radiother. Onco. 167 109 doi: 10.1016/j.radonc.2021.12.022 [3] Sørensen B S, Sitarz M K, Ankjærgaard C, Johansen Jacob Claus G, Andersen E, Kanouta E, Grau C, Poulsen P 2022 Radiother. Oncol. 175 178 doi: 10.1016/j.radonc.2022.05.014 [4] Böhlen T T, Germond J, Petersson K, Ozsahin E M, Herrera F G, Bailat C, Bochud F, Bourhis J, Moeckli R, Adrian G, Bailat C, Bochud F, Bourhis J, Moeckli R, Adrian G, 2023 Int. J. Radiat. Oncol. Biol. Phys. 117 1007 doi: 10.1016/j.ijrobp.2023.05.045 [5] Zhang Q X, Gerweck L E, Cascio E, Yang Q Y, Huang P G, Niemierko A, Bertolet A, Nesteruk K P, McNamara A, Schuemann J 2023 Phys. Med. Biol. 68 055010 doi: 10.1088/1361-6560/acb888 [6] Romano F, Bailat C, Ferretti C, Jorge P G, Lerch M L F, Darafsheh A 2022 Med. Phys. 49 4912 doi: 10.1002/mp.15649 [7] Vignati A, Giordanengo S, Federico F, Villarreal O A M, Milian F M, Mazza G, Shakarami Z, Cirio R, Monaco V, Sacchi R 2022 Front. Phys. 8 375 [8] Levin D, Friedman P, Ferretti C, Ristow N, Tecchio M, Litzenberg D, Bashkirov V, Schulte R 2024 Med. Phys. 51 2905 doi: 10.1002/mp.17018 [9] 艾自辉 2008 硕士学位论文 (绵阳: 中国工程物理研究院) Ai Z H 2008 M. S. Thesis (Mianyang: China Academy of Engineering Physics [10] Marinelli M, Martino F D, Sarto D D, Pensavalle J H, Felici G, Giunti L, Liso V D, Kranzer R, Verona C, Rinati G V 2023 Phys. Med. Biol. 68 175011 doi: 10.1088/1361-6560/acead0 [11] Boag J W, Hochhuser E, Balk O A 1996 Phys. Med. Biol. 41 885 doi: 10.1088/0031-9155/41/5/005 [12] Di Martino F, Giannelli M, Traino A C, Lazzeri M 2005 Med. Phys. 32 2204 doi: 10.1118/1.1940167 [13] Petersson K, Jaccard M, Germond J, Buchillier T, Bochud F, Bourhis J, Vozenin M, Bailat C 2017 Med. Phys. 44 1157 doi: 10.1002/mp.12111 [14] Gotz M, Karsch L, Pawelke J. Gotz M, Karsch L, Pawelke J 2017 Phys. Med. Biol. 62 8634 doi: 10.1088/1361-6560/aa8985 [15] Greening J R 1954 Br. J. Radiol. 27 163 doi: 10.1259/0007-1285-27-315-163 [16] Rathore R K S, Munshi P, Bhatia V K, Pandimani S 1988 Nucl. Eng. Des. 108 375 doi: 10.1016/0029-5493(88)90226-9 [17] Rinati G V, Felici G, Galante F, Gasparini A, Kranzer R, Mariani G, Pacitti M, Prestopino G, Schüller A, Vanreusel V, Verellen D, Verona C, Marinelli M 2022 Med. Phys. 49 5513 doi: 10.1002/mp.15782 [18] Schüler E, Acharya M, Montay-Gruel P, Loo B W, Vozenin M C, Maxim P G 2022 Med. Phys. 49 2082 doi: 10.1002/mp.15442 [19] Siddique S, Ruda H E, Chow J C L 2023 Cancers 15 3883 doi: 10.3390/cancers15153883 [20] Esplen N, Mendonca M S, Bazalova-Carter M 2020 Phys. Med. Biol. 65 23TR03 doi: 10.1088/1361-6560/abaa28 [21] Vanreusel, Gasparini A, Galante F, Mariani G, Pacitti M, Cociorb M, Giammanco A, Reniers B, Reulens N, Shonde T B, Vallet H, Vandenbroucke D, Peeters M, Leblans P, Ma B, Felici G, Verellen D, Nascimento L D F 2022 Phys. Medica. 103 127 doi: 10.1016/j.ejmp.2022.10.005 -
图( 10)
计量
- 文章访问数: 26
- HTML全文浏览数: 26
- PDF下载数: 2
- 施引文献: 0