量子密钥分发技术为远距离通信提供了理论上的信息安全保障, 允许通信双方在窃听者存在的情况下安全地交换密钥^[1]. 然而, 尽管量子密钥分发在理论研究和实验实现方面取得了显著进展, 实际应用中的安全性与理想模型所承诺的信息理论安全性之间仍存在显著差距^[2,3]. 特别在实际设备的实现中, 许多因素可能导致安全性下降, 尤其是设备与理想假设之间的差异.

对于量子密钥分发中的源端而言, 安全性漏洞主要来源于几个方面. 首先, 由于调制器精度的限制, 光源的状态制备可能存在缺陷^[4], 这会影响密钥分发的安全性. 其次, 调制器的侧信道或特洛伊木马攻击可能会导致信息泄露, 使得窃听者能够间接获取密钥信息^[5–9]. 此外, 调制器带宽的限制也可能引发不同脉冲之间的经典关联性, 这种关联性会破坏量子密钥分发的独立性假设, 进而影响系统的安全性^[10–17].

为了解决这些问题, 研究者们已经提出了一些针对关联光源的安全性证明方法^[16–19], 其中一种较为成熟的技术是基于参考技术的安全性分析, 被称为关联源量子密钥分发^[18]. 该方法能够有效处理源的关联性问题, 从而在一定程度上弥补了实验设备与理想模型之间的差异.

然而, 现有的关联源量子密钥分发协议^[18]在容忍关联性方面存在显著不足, 导致其在实际应用中表现出较低的密钥率、有限的性能以及较短的传输距离. 这些限制使得现有协议在大规模应用中的前景不容乐观. 针对这些问题, 本文提出了一种改进的关联源量子密钥分发协议, 摒弃了传统协议中基于损耗容忍的安全性分析框架^[4], 采用标准的BB84协议^[1]新的安全性分析.

在本研究中, 首先给出了改进协议的分析过程, 详细阐述了其在面对关联源时的安全性框架. 通过与传统协议在不同参数设置下的对比, 展示了新协议在性能上的显著提升, 特别是在密钥率和传输距离方面的改进. 本文结果表明, 改进后的协议在容忍源关联性方面表现更为优越, 能有效提高系统的整体性能, 使得关联源量子密钥分发技术向实际应用迈出了更为坚实的一步.

实际制备的态, 其非完美性质可以主要分为3部分^[18]. 其一是态制备不完美(state preparation flaw, SPF), 此外还有侧信道与关联性. 其中, 对于态制备不完美, 本文进行一个基础的假设, 即态制备不完美会使得BB84协议的4个态产生偏差, 即:

其中$ \left| {{j_{{\text{per}}}}} \right\rangle $(j = 0z, 1z, 0x, 1x)代表在Z基与X基下制备的bit为0, 1的态, δ表示态制备不完美的 大小.

对于侧信道与关联性, 首先考虑单独一个回合. 在存在侧信道与关联性的情况下, 可认为第k – 1回合的态能够影响第k回合的态. 则在第k – 1回合选择j_{k – 1}确定的情况下, 第k回合选择j_k制备的态$ \left| {{\varPsi _{{j_k}\left| {{j_{k - 1}}} \right.}}} \right\rangle $满足:

其中$ \big| {j_{_{{k_{{\text{per}}}}}}^ \bot } \big\rangle $表示未知维度与具体形式, 但是与$ \big| {j_{_{{k_{{\text{per}}}}}}^ \bot } \big\rangle $正交的态, 即侧信道态, ε表示侧信道与关联性的大小, $ \varepsilon \in \left[ {0, 1} \right] $, 其值越大表示关联性与侧信道越大.

为了分析协议的安全性, 将所有受到第k回合选择j_k的态全部写出, 这个态整体可以表示为

其中$ \big| {j'_{k_{\text{per}}}} \big\rangle $为不存在侧信道与关联性的完美态, 具体形式为

本协议仅需要表征态制备不完美参数δ, 关联范围ξ, 以及关联性与侧信道参数ε, 即可完成安全性分析.

进行关联源下的安全性分析, 实际上就是要分析这种情况下的相位误码. 不同于普通的BB84协议, 在存在侧信道与关联性的情况下, X基发送的态并不能直接用以估计相位误码, 因为真实的相位基的两个态在这种情况下并非与X基发送的态相同. 此时, 为了分析相位误码, 需要利用现有的测量值进行估计. 利用柯西-施瓦茨约束^[18], 可以在衡量X基发送态与真实相位基偏差的情况下, 估计真实的相位误码的值.

在开始安全性分析前, 首先介绍协议流程.

1)系统准备. 在执行QKD流程前, Alice预先表征态制备不完美参数δ, 关联范围ξ, 以及关联性与侧信道参数ε.

2)量子通信. 完成系统准备后, Alice和Bob双方进行QKD流程. 该协议在物理流程上与标准BB84类似. 在QKD流程的每一个回合, Alice与Bob双方分别执行:

① 态制备. 在每一回合, Alice以p_Z的选基概率选取Z基, 以余下的概率选取X基. 对于任意一个基, Alice以等概率选取比特0或1. Alice尝试按上述选择制备对应的4个BB84态, 形如(1)式—(4)式.

② 测量. Bob以另一个选基概率进行对应的测量. Bob记录本回合的基选择与测量结果∈{$\varnothing $, 0, 1}, 其中$ \varnothing$代表失败, 0与1代表测量到对应基下的比特值.

3)密钥筛选. Alice在公开信道上公布各轮的基选择, Bob在此基础上进一步公布该轮是否成功测量. 然后, 他们在成功测量的回合中都选Z基的部分生成密钥, 而都选X基的部分用于参数估计.

4)参数估计. Alice与Bob利用X基的比特误码率, 估计Z基下的相位误码率大小.

5)密钥生成. Alice和Bob进行经典后处理过程, 最终生成相同的安全密钥.

由纠缠等价协议, 真实的相位误码定义为Z基实际发送的态在其辅助粒子X基下测量得到的态. 简而言之, 相位误码发生的概率为

其中, $ p_{ax}^{{\text{vir}}} = \dfrac{{{p_{{{\text{Z}}_{\text{A}}}}}}}{2} \cdot \left[ {1 + {{\left( { - 1} \right)}^a} \left\langle {0{z_{{\text{per}}}}} \right|\left. {1{z_{{\text{per}}}}} \right\rangle } \right] $, $ {p_{{{\text{Z}}_{\text{B}}}}} $为Bob测量选Z基的概率, $ {\hat M_{ax}} $为在Eve攻击后, Bob在X基下的bit a对应的测量算符, $ \left| {\varPsi'_{ax}} \right\rangle $为真实的相位基, 其具体形式为

然而正如上文所述, 由于关联性, 实际发送的$ \left| {{\varPsi _{0 x}}} \right\rangle $, $ \left| {{\varPsi _{1 x}}} \right\rangle $, $ \left| {\varPsi'_{0 x}} \right\rangle $, $ \left| {\varPsi'_{1 x}} \right\rangle $并不相同.

为了利用实际测得的$ \big[ {\left| {{\varPsi _{ax}}} \right\rangle \left\langle {{\varPsi _{ax}}} \right|{{\hat M}_{bx}}} \big] $结果约束$ \big[ {\left| {{\varPsi _{ax}}} \right\rangle \left\langle {{\varPsi _{ax}}} \right|{{\hat M}_{bx}}} \big] $的大小, 需要衡量$ \left| {\left\langle {{{\varPsi _{ax}}}} \mathrel{\left | {\vphantom {{{\varPsi _{ax}}} {{\varPsi _{ax}}^\prime }}} \right. } {{{\varPsi _{ax}}^\prime }} \right\rangle } \right| $的大小, 以进行下一步分析. 首先, 由第3.1节的定义式可得

又因为协议没有对$ \left| {j'^{\bot}_{{k_{{\text{per}}}}}} \right\rangle $的具体形式做出假设, 则在对内积进行估计时, 需对$ \left| {a'^{\bot}_{k_{\text{per}}}} \right\rangle $与$ \left| {b'_{k_{\text{per}}}} \right\rangle $的内积进行最差的估计. 在这个思想下, 计算可得

由于本文对$ \left| {\varPsi _{ax}'} \right\rangle $的定义, 进一步计算可得

又由定义式, 可得$ \left| {\left\langle {{\varPsi _{0 x}}} \right|\left. {0 x_{{\text{per}}}'} \right\rangle } \right| = 1 - \varepsilon $, 则进一步放缩, 可得:

其中

同理, 可以计算$ \left| {\left\langle \left.{\varPsi _{1 x}'} \right| {{\varPsi _{1 x}}} \right\rangle } \right| \geqslant \varDelta $. Δ代表了真实相位基与发送的相位基的偏差. 有了这一区分度, 就可以利用柯西-施瓦茨约束^[18]对协议的相位误码率进行估计.

首先, 需要给出柯西-施瓦茨约束的具体形式, 其满足

其中

满足$ 0 < \hat M < 1 $.

记实际测到的两个相位误码事件的条件计数率为

则真实的相位误码可以由两个相位误码事件的计数率约束:

这就完成了对相位误码的分析, 进而完成了安全性分析.

完成对相位误码的分析, 由GLLP公式, 可以给出密钥率公式满足:

其中比特误码率$ {e_{\text{Z}}} $满足:

Z基计数率满足:

而相位误码率满足:

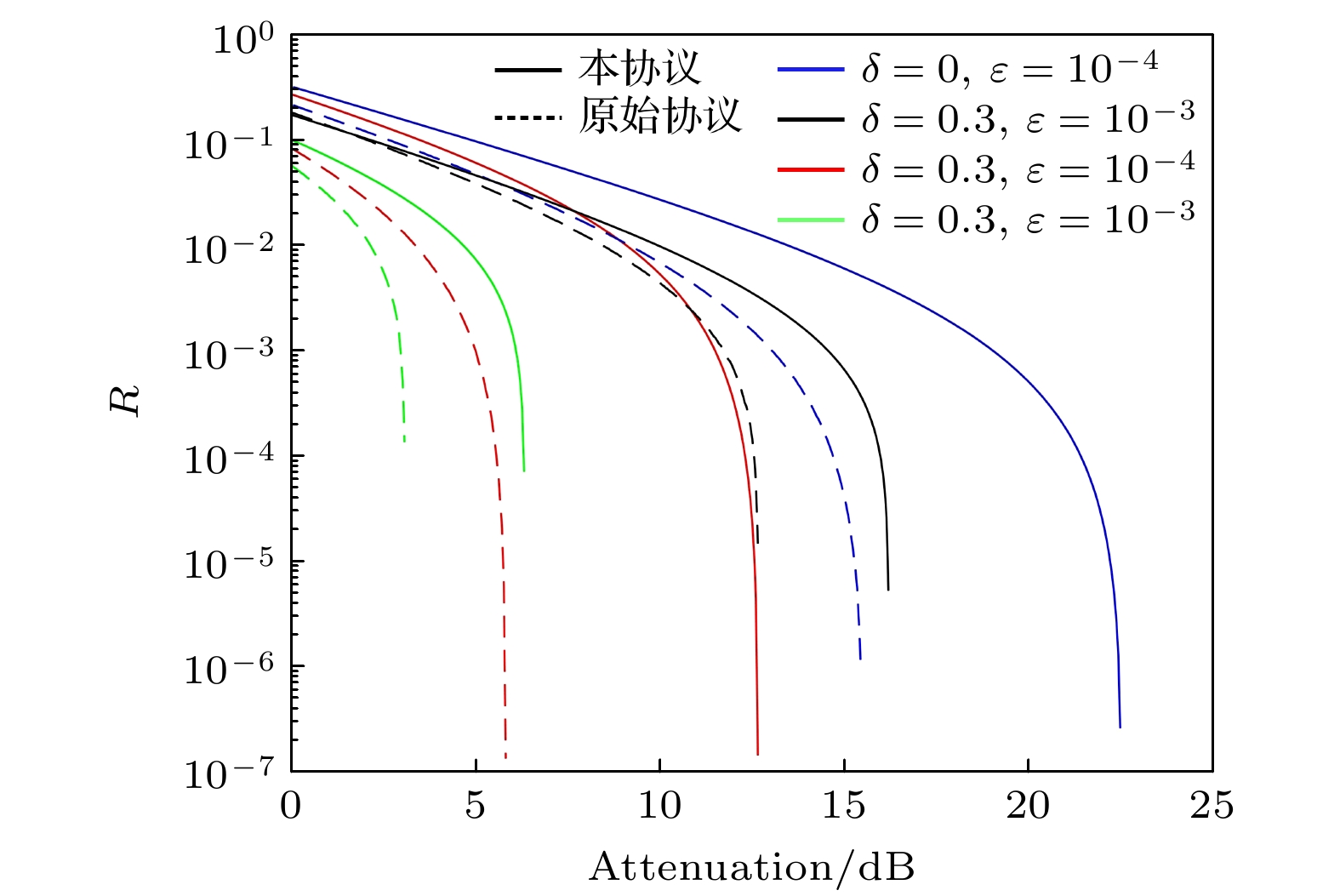
图1为本协议与现有的关联源量子密钥分发协议^[18]进行性能的对比. 其中探测器暗计数率P_d = 10^–7, 纠错效率f = 1.16, Alice与Bob选Z基的概率分别为2/3与1/2.

在仿真中, 态制备不完美参数δ = 0, 0.3, 侧信道与关联性参数$ \varepsilon = $10^–3, 10^–4, 分析4种情况下的密钥率. 可以看到, 在全部的情况中, 本文的改进协议都比现有的协议有更高的密钥率与极限距离. 同时, 关联性越大, 改进协议相较于现有协议的提升也越大; 在δ = 0的情况下, ε = 10^–3时, 0 dB处改进协议对于现有协议有3倍左右的密钥率提升, 且极限距离由6 dB提升至13 dB; ε = 10^–4时, 0 dB处改进协议对于现有协议有1.5倍左右的密钥率提升, 且极限距离由16 dB左右提升至22 dB. 但是, 改进的协议对于态制备不完美的容忍性要低于现有协议; 在ε = 10^–4的情况下, δ = 0时, 0 dB处改进协议对于现有协议有3倍左右的密钥率提升, 且极限距离由6 dB提升至13 dB; δ = 0.3时, 0 dB处改进协议对于现有协议有1.6倍左右的密钥率提升, 且极限距离由4 dB左右提升至6 dB左右.

仿真结果显示, 在各种关联性大小与态制备不完美的情况下, 改进的协议都有优于现有协议的密钥率表现. 且关联性大小越大, 改进协议的效果越好. 但是, 由于改进的协议放弃了现有协议以制备三态的损耗容忍协议^[4]为基础, 转而采用四态协议为基础, 其对态制备不完美的容忍能力略低于现有协议.

本文提出了一种改进的关联源量子密钥分发协议, 摒弃了传统基于损耗容忍的协议框架, 转而采用标准的BB84协议进行安全性分析. 通过分析和对比, 展示了改进协议在不同参数下的优势, 特别是在提高密钥率和延长传输距离方面. 具体来说, 我们的协议相比于现有协议, 在常规的态制备不完美大小下有1.5—3倍的密钥率提升以及2—6 dB的极限距离提升. 理论分析表明, 改进后的协议不仅能够有效应对源的关联性问题, 而且在实际应用中展现出更强的稳定性和更高的性能. 此外, 由于该协议在实现层面与BB84协议完全相同, 仅在参数估计步骤有所区别, 所以在引入诱骗态后, 该协议能在现有的BB84实验系统上运行.

未来的研究可以进一步探索该协议在不同实验条件下的表现, 结合更多的实验数据验证其实际可行性. 此外, 结合本文的想法, 进一步引入一些容忍态制备偏差类协议以进一步容忍态制备不完美也是此类协议的发展目标之一. 同时, 要将改进的协议与现有的量子通信网络和安全体系相结合. 随着量子密钥分发技术的不断发展, 改进后的协议将在量子通信和量子网络的实际部署中发挥重要作用, 推动量子信息技术的广泛应用和普及.