-
量子纠缠描述了两个以上粒子之间的特殊关联, 它作为量子信息领域的核心资源[1,2], 在量子计算与量子通信任务中发挥着重要的作用[3,4], 如量子密钥分发(QKD)[5,6]、量子传感与量子成像[7–9]、量子中继器[10]、量子隐形传态[11,12]等. 与传统通信技术相比, 量子通信技术使用量子比特(qubit)对信息进行编码, 基于量子态叠加原理和量子不可克隆定理, 量子信息网络在并行计算能力、安全性等方面具有显著优势, 其有望彻底改变未来的信息交换方式. 近年来, 随着光量子信息技术和量子光学器件的进步, 薄膜铌酸锂波导等光学器件推动了各种类型的量子网络的发展和完善, 例如点对点量子网络[13,14]、量子中继网络、全连接网络[15]. 其中全连接型量子通信网络的高度互联架构与其他类型的网络架构相比, 只需要极少的基础设施硬件即可实现多用户互联, 因此成为构建大规模城域网络的核心架构和重要支撑.
在全连接量子网络的研究中, 光子因其固有的低退相干特性、易操作易探测性以及与经典光通信基础设施的高度适配性, 成为量子信息传输与处理中信息的理想载体. 对于光量子系统, 可以使用包括偏振[16]、轨道角动量(OAM)[17], time-energy[18], time-bin在内的多种自由度(DOFs)进行编码, 使用不同自由度来实现纠缠[19]在量子信息处理中具备不同的优势. 对于易于生成和操纵的偏振纠缠态, 其经过合适偏振补偿后即可在远距离光纤中传输, 目前已被广泛应用于各类量子通信协议中[20–22]; 近年来, time-bin纠缠态凭借对于信道扰动的高鲁棒性及高维量子态的编码能力也得到了广泛关注[23,24]. 最近, Huang等[25]采用DWDM技术和基于集成周期性极化铌酸锂(PPLN)波导的time-bin纠缠源实现了一个多用户全连接量子网络. 然而, 使用单一自由度的纠缠态意味着每个量子比特只能携带有限的信息, 这个问题可以通过超纠缠网络的多自由度并行编码解决. 目前, 超纠缠态在量子计算、量子通信等领域得到了广泛的研究与应用[26–30], 利用光子多维度的超纠缠量子态可以实现更高维希尔伯特空间编码, 能够显著地增加量子信道容量. 得益于偏振自由度和time-bin自由度在远距离传输任务中表现出的优异性能, 这两个自由度的超纠缠被认为在量子信息应用中具有巨大的潜力.
在这里, 我们提出了一个超纠缠的量子网络, 使用偏振和time-bin DOFs进行编码, 利用高性能集成PPLN波导实现光子对的产生, 通过DWDM技术将三个偏振和time-bin的超纠缠态分配给三个终端用户, 形成全连接的网络拓扑结构. 通过实验证明, 偏振和time-bin纠缠的双光子可见度均高于94%, 这表明我们所构建的网络在这两个自由度具有高质量的纠缠, 经过100 km的传输后, 两种自由度的纠缠态保真度依旧在88%以上. 我们的方法为构建高信息容量、远距离通信的量子网络提供了新的解决方案.
-
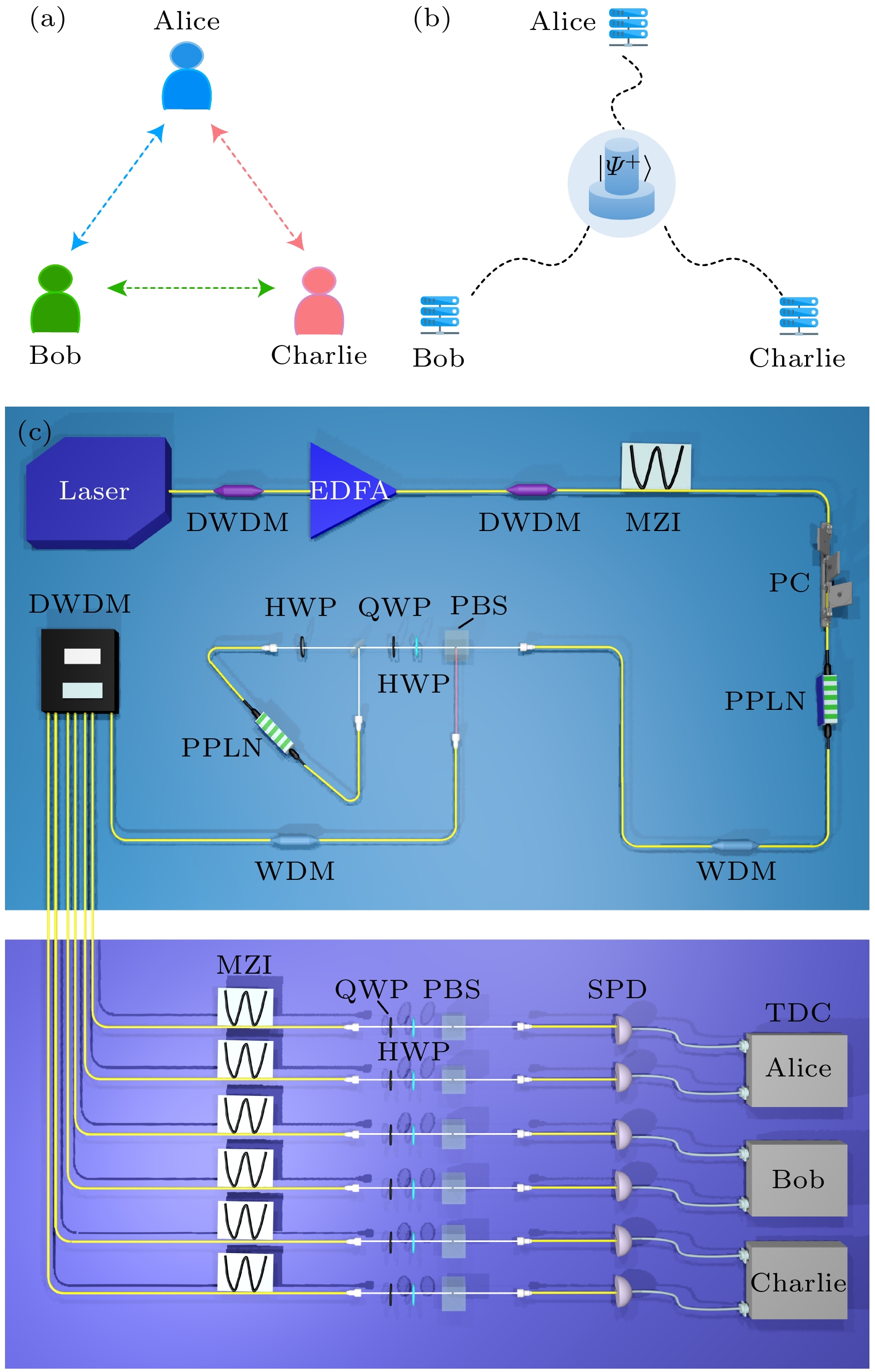
如图1(a)和图1(b)所示, 我们的网络架构分为物理层和网络通信层两个部分, 物理层由基于集成PPLN波导的偏振和time-bin DOFs sagnac型超纠缠源, 100-GHz的密集波分复用滤波器(DWDM), 用于纠缠分配的单模光纤以及超纠缠检测模块组成. 量子中心处理器制造出具备高质量超纠缠的纠缠光子对, 通过光纤分配给网络的用户, 形成了网络通信层. 在网络通信层, 每个用户节点都可以直接与网络中的其他用户进行通信.
实验设置如图1所示, 我们将重复频率60 MHz的宽带皮秒脉冲激光通过消光比为120 dB的国际电信联盟(ITU) 100 GHz DWDM, 选择32信道滤出我们需要的波长, 得到1551.74 nm的窄带激光, 通过掺铒光纤放大器放大后, 再次经过一个DWDM来抑制噪声. 接着将得到的皮秒脉冲激光送入1-GHz马赫-曾德干涉仪(MZI), 产生长臂时间模式和短臂时间模式分别为t1和t0的双脉冲, 将脉冲激光通过偏振控制器(PC)调整偏振到TM模式后入射到一个采用type-0型准相位匹配(e + e → e)的PPLNOI 波导中, TM模式的光经过波导进行倍频产生波长为775.9 nm的二次谐波, 使用1550/780 nm波分复用器(WDM)滤除多余的基频光, 倍频光经过双波长偏振分束器(DW-PBS)被送入一个由二向色镜、半波片、四分之一波片、双波长半波片、耦合器和一个PPLNOI 波导组成的Sagnac结构的偏振纠缠源, Sagnac结构具有相位自稳定的特点, 在纠缠源中产生偏振纠缠态的两个自发参量下转换(SPDC)过程发生在同一个波导内, 整体结构相对更稳定. 装置中的双波长半波片负责将水平偏振的光子转换为垂直偏振, 22.5°半波片则负责将倍频光的偏振调整为
$ \left| D \right\rangle = 1/\sqrt 2 \left( {\left| H \right\rangle + \left| V \right\rangle } \right) $ , SPDC过程产生的光子的双光子量子态表示为$|{\phi ^ + }\rangle = 1/\sqrt 2 ( |H{\rangle _s}|H{\rangle _i} + |V{\rangle _s}|V{\rangle _i} )$ , 考虑到两个时间上分离的脉冲经过SPDC过程生成的光子对具备time-bin纠缠的特征, Sagnac结构纠缠源中产生的量子态在偏振和time-bin DOF上存在超纠缠. 经过DW-PBS合束后耦合进单模光纤中, 分发至用户处.本文考虑实现3个用户之间的相互通信, 需要至少3个量子相关光子对. 我们选择6个标准的ITU信道中, 即信号光子从CH29到CH31, 闲置光子从CH33到CH35, 每个用户都配备两个1-GHz MZI, 一个偏振分析装置和两个单光子探测器, 探测器的探测效率为10%、暗计数水平为1000 Hz. 实验中的网络通信是点对点分别进行的.
-
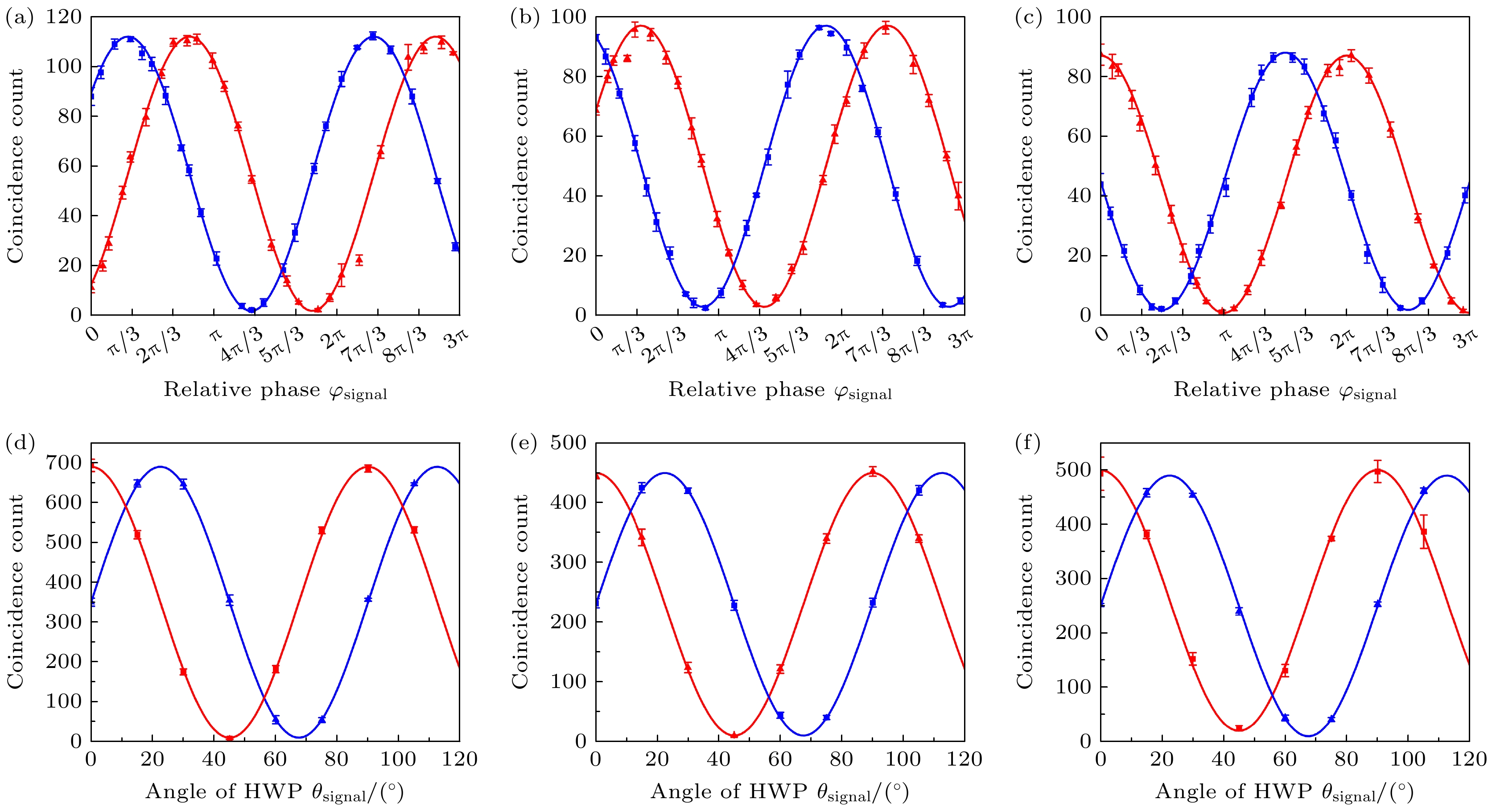
在量子通信任务中, 量子处理器能否为各个信道提供高质量的纠缠光子对是用户之间是否能够执行量子任务的关键, 所以我们需要对本文构建的全连接量子网络的性能进行表征. 我们首先通过测量 Franson-type 干涉对三个用户的time-bin纠缠质量进行了表征, Franson-type干涉仪由两个非平衡MZI组成, MZI的两臂的臂长差为1 ns, 两臂之间的相对相位通过对两个MZI内部的压电陶瓷施加电压进行改变, 在实验中, 我们将一个用户的MZI的相位分别设置为0和3π/2, 对另一个用户的干涉仪施加从0到7 V的外部电压进行相位扫描, 测得如图2(a), (b), (c)所示的Franson-type双光子干涉条纹, 获得平均干涉条纹对比度V, 由公式
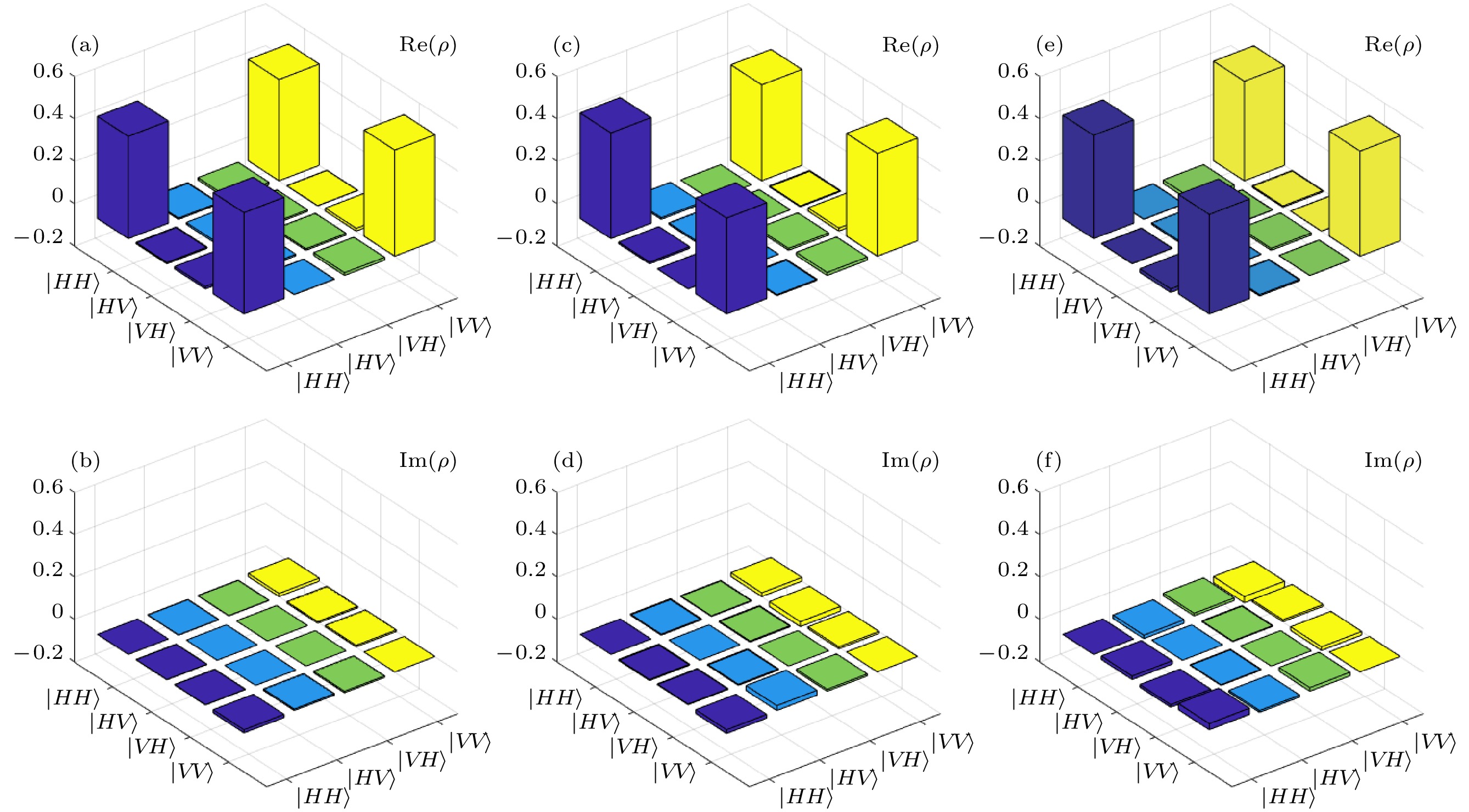
$V = \left( {{N_{{\text{max}}}} - {N_{{\text{min}}}}} \right)/\left( {{N_{{\text{max}}}} + {N_{{\text{min}}}}} \right)$ 求得, 分别为95.7%±0.5%, 95.4%±0.4%, 95.8%±0.5%, 超出违背CHSH不等式所需的经典局域界限71% [31,32], 证明在time-bin DOF下存在高质量纠缠.接下来我们利用偏振分束器、四分之一波片和半波片对网络的偏振纠缠质量进行分析. 首先利用标准的符合测量技术, 在两组非正交基矢量H/V和D/A的投影下进行了双光子干涉条纹的测量. 在两个相互通信的用户信道中, 将一个用户的偏振分析装置的半波片角度分别固定为0°和22.5°, 扫描另一用户的半波片角度, 记录在不同角度下的符合计数, 结果如图2(d), (e), (f)所示, 我们得到了三个用户共享的偏振纠缠态的典型双光子干涉条纹, 计算平均干涉条纹对比度, 分别为96.4%±0.7%, 96.2%±0.8%, 95.9%±0.4%, 并通过公式F = (3v+1)/4计算了相应量子态的保真度. 接着我们通过调节四分之一波片和半波片的角度, 对三对偏振量子态进行量子态层析, 并采用最大似然估计法重构量子态密度矩阵, 实验结果如图3所示, 我们计算得三个量子态的平均保真度
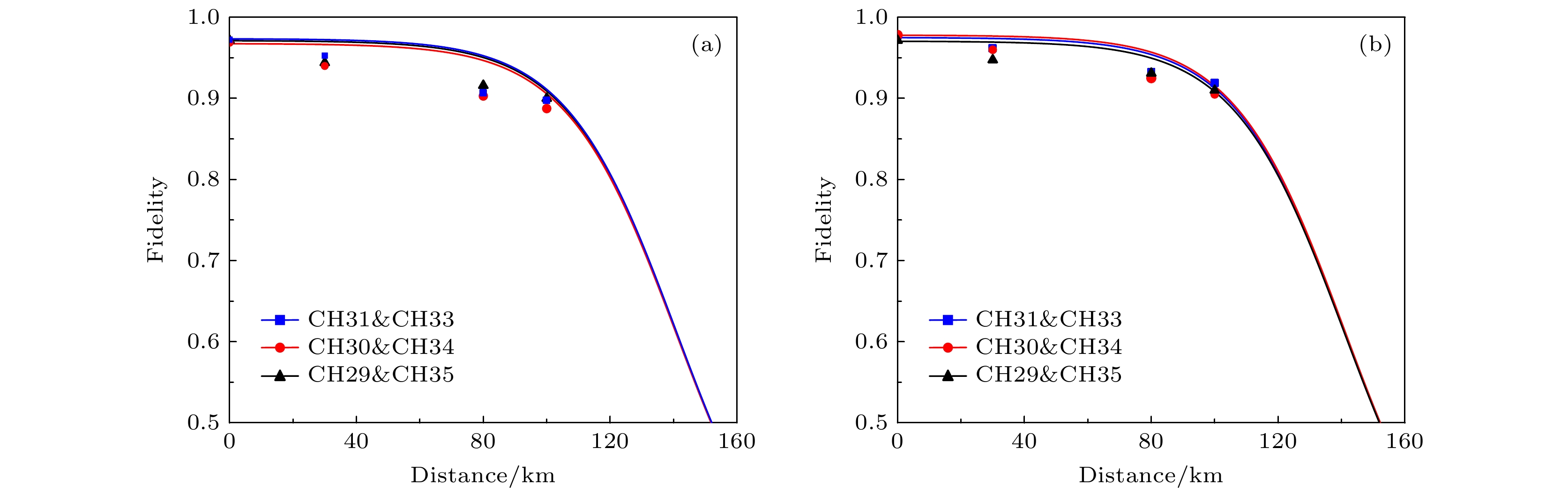
$F = \langle {\psi _{{\text{ideal}}}}|\rho |{\psi _{{\text{ideal}}}}\rangle $ =95.8%±1.1%. 由此我们证明了本文设计的全连接量子网络在偏振和time-bin DOFs上同时存在高质量的纠缠.本文构建超纠缠网络的目的是希望为量子通信任务提供一个新的平台, 而在真实的通信任务中, 受距离影响, 量子态在传播过程中会受到噪声、光纤衰减、散射、相位噪声等因素的影响, 导致量子态发生退相干或失真. 通过对远距离纠缠分发的保真度的测量, 我们可以了解并验证传输后量子态与原始态的相似性, 量化传输过程中的损耗情况. 在实验中, 我们使用可调衰减器和衰减系数为α = 0.2 dB/km的单模光纤进行了模拟100 km纠缠分发的桌上实验, 测量了各个信道0—100 km的量子态保真度, 结果如图4所示, 图中曲线为无噪声情况下纠缠保真度与传输距离的理论关系, 数据点则是我们测得的真实保真度, 可以看到, 在经过100 km传输后, 三个用户共享的超纠缠态的保真度仍保持在88%以上, 依旧超出了CHSH 贝尔不等式
$1/ \sqrt{2} $ 经典界限[31,32], 这说明量子态在长距离传输过程中保持了较高的质量和纠缠特性.在实际的量子通信网络构建中, 安全通信距离和安全成码率是非常重要的参数, 为满足安全通信的需要, 我们对本文提出的全连接网络在使用BBM92协议进行量子密钥分发时的安全成码率进行了数值模拟. 量子密钥分发的通信双方共同约定两组非正交基矢, 并对量子态进行编码, 接着随机采用不同的基矢对光子进行探测, 探测完成后, 通信双方通过经典信道分别公开制备和测量得到的信息, 对比后双方保留相同投影基下的测量结果, 这样就可以得到一个长度相同的原始密钥, 而与单向经典通信的量子密钥分发过程相比, 双向经典通信可以支持进行更远安全通信距离的量子密钥分发, 经过双向经典通信后, 我们的成码率可以表示为[33]
其中
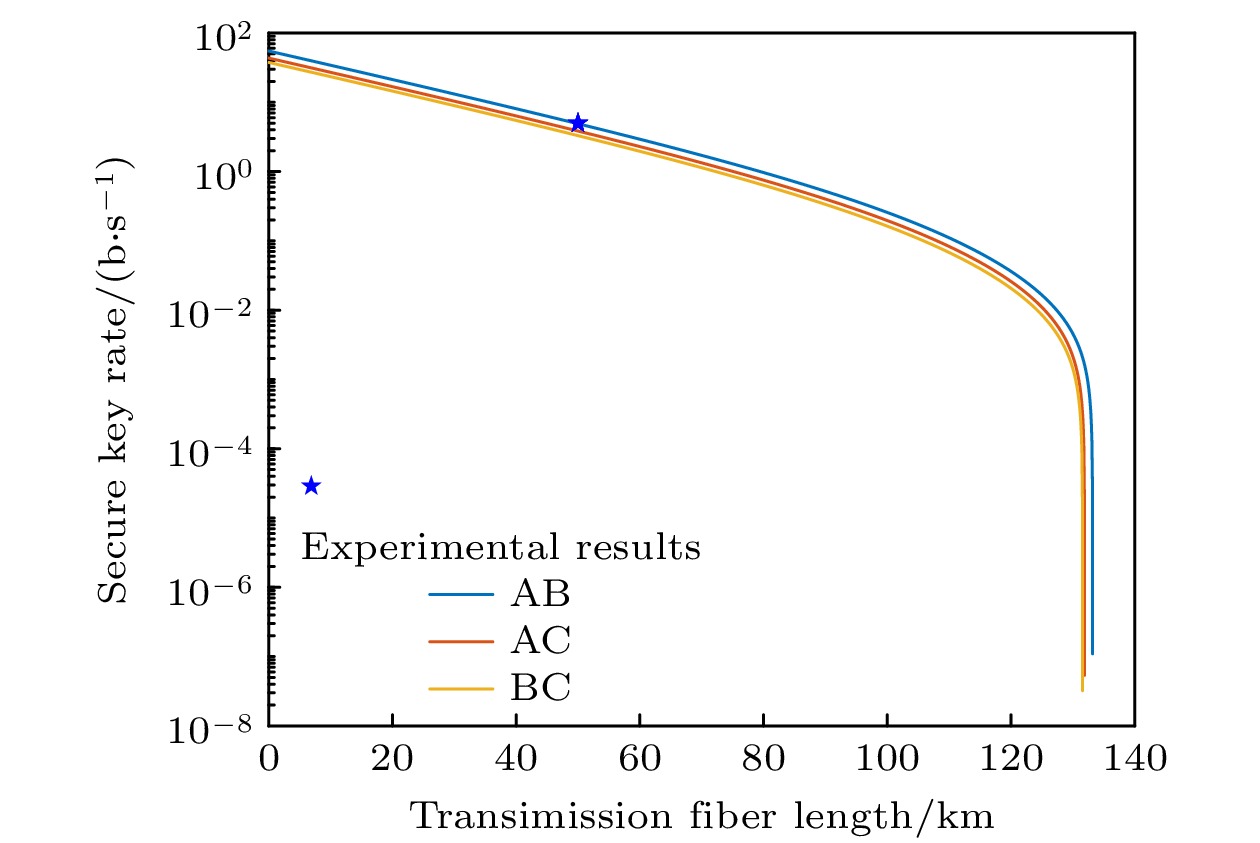
$Q$ 为原始密钥;${e_{\text{b}}}$ 和$ {e}_{\text{b}}^{ \prime } $ 表示比特误码率和经过随机配对后的比特误码率;$ {e}_{\text{p}}^{ \prime } $ 为相位误码率; f为纠错效率因子; 二元香农熵函数$H\left( x \right)$ 表示为[33]如图5所示, 通过(1)式, 将下转换的平均光子数控制为0.0015, 将纠错效率设置为f = 1.16, 计算了三个用户之间的安全成码率, 并测量了实验中网络系统的安全密钥率, 我们在50 km光纤距离得到了6 b/s的安全密钥速率, 验证了本文提出的超纠缠全连接网络中的各用户能够实现超过50 km的量子密钥分发, 同时, 我们可以使用更高重复频率的泵浦光来进行SPDC过程, 这样做可以有效提高网络中各个用户的安全成码率, 以支持更远距离的量子密钥分发.
-
我们基于PPLNOI波导, 利用DWDM技术和纠缠分发技术, 完成了一个偏振和time-bin自由度编码的三用户全连接量子网络. 在实验中, 使用脉冲激光通过Sagnac结构的纠缠源, 制备出三个同时在偏振和time-bin自由度上存在纠缠的光子对, 利用DWDM技术将它们复用到单模光纤中, 形成全连接的网络结构, 偏振和time-bin自由度下的双光子干涉对比度均大于95%, 同时经过100 km纠缠分发后, 两种纠缠态的保真度依旧大于88%, 证明了我们构建的网络具有高质量的超纠缠, 并可以应用于远距离光纤的传输与分发. 本文还计算了通过所构建的网络进行量子密钥分发时安全成码率和传输距离的关系, 实验证明, 使用本文所构建的网络可支持用户之间超过50 km的量子密钥分发. 我们的方法为构建大规模超纠缠量子网络提供了一个新的方案, 我们期望我们的方案可以为诸多量子信息任务, 例如超密集编码和量子隐形传态等应用提供一个高效的量子平台.
基于超纠缠的三用户全连接量子网络
A three-user fully connected quantum network based on hyperentanglement
-
摘要: 超纠缠作为一种多自由度上的高维量子纠缠现象, 在量子通信、量子计算和高维量子态操控中发挥着关键作用. 与单一自由度纠缠态不同, 超纠缠态在偏振、路径、轨道角动量等多个自由度上同时建立纠缠关系, 通过纠缠操控分发技术, 可以构建出高维量子信息网络. 基于此, 本文构建了一个超纠缠的全连接量子网络, 通过周期极化薄膜铌酸锂(PPLN)波导级联二次谐波产生和自发参量下转换过程实现偏振和time-bin自由度的超纠缠, 并使用密集波分复用(DWDM)技术, 将超纠缠态复用到单模光纤中传输给终端用户. 使用Franson-type干涉和双光子符合测量技术对纠缠态的质量进行表征, 同时对偏振纠缠态进行了量子态层析, 并利用纠缠分发技术在网络中实现长距离分发及量子密钥传输. 实验结果表明, 偏振纠缠和time-bin纠缠的双光子干涉对比度均大于95%, 并且在经过100 km纠缠分发后, 两种自由度的量子态保真度依旧高于88%, 证明了该网络具有高质量的超纠缠, 并且可以实现远距离的纠缠分发. 本文的方法为构建支持量子隐形传态、超密集编码等量子任务的大规模超纠缠的量子网络提供了一种新的方案.Abstract: Hyperentanglement, as a high-dimensional quantum entanglement phenomenon with multiple degrees of freedom, plays a critical role in quantum communication, quantum computing, and high-dimensional quantum state manipulation. Unlike entangled states in a single degree of freedom, hyperentangled states establish entanglement relationships simultaneously in multiple degrees of freedom, such as polarization, path, and orbital angular momentum. Through entanglement-based distribution techniques, high-dimensional quantum information networks can be constructed. On this basis, a fully connected quantum network with hyperentanglement is constructed in this work, and the polarization and time-bin degree-of-freedom hyperentanglement is realized through the process of second-harmonic generation and spontaneous parametric down-conversion in periodically poled lithium niobate (PPLN) waveguide cascades. The hyperentangled state is then multiplexed into a single-mode fiber by using dense wavelength division multiplexing (DWDM) technology for transmission to terminal users. The quality of the entangled states in the two degrees of freedom is characterized using Franson-type interference and photon-pair coincidence measurement techniques. Polarization entangled states are subjected to quantum state tomography, and entanglement distribution technology is employed to achieve long-distance distribution and quantum key transmission within the network. Experimental results show that the two-photon interference visibility of both polarization and time-bin entanglement is greater than 95%, demonstrating the high quality of the hyperentanglement in the network. After 100-km-entanglement distribution, the fidelity of the quantum states in both degrees of freedom remains above 88%, indicating the effectiveness of long-distance entanglement distribution in this network. Additionally, it is verified that this network supports the distribution of quantum keys over a distance of more than 50 km between users. These results confirm the feasibility of a fully connected quantum network with hyperentanglement and demonstrate the potential for constructing large-scale metropolitan networks by using hyperentanglement. As a higher-dimensional entanglement, hyperentangled states can significantly enhance the capacity and efficiency of quantum information processing. Although the quantum communication is still in its early stages of development, achieving stable storage and transmission of entangled states in large-scale metropolitan networks remains a great challenge. By utilizing the frequency conversion properties and high integration characteristics of the periodically poled lithium niobate waveguides, the three-user hyperentangled quantum network constructed in this work provides a new solution for developing the large-scale metropolitan networks with high-dimensional quantum information networks. It is expected to provide a new platform for quantum tasks such as superdense coding and quantum teleportation.
-
Key words:
- hyperentanglement /
- spontaneous parametric down-conversion /
- quantum network .
-

-
图 2 time-bin纠缠和偏振纠缠实验结果 (a) CH31&CH33 time-bin纠缠双光子干涉条纹; (b) CH30&CH34 time-bin纠缠双光子干涉条纹; (c) CH29&CH35 time-bin纠缠双光子干涉条纹; (d) CH31&CH33偏振纠缠双光子干涉条纹; (e) CH30&CH34偏振纠缠双光子干涉条纹; (f) CH29&CH35偏振纠缠双光子干涉条纹
Figure 2. Experimental results of time-bin entanglement and polarization entanglement: (a) Time-bin entangled biphoton interference fringes for CH31 & CH33; (b) time-bin entangled biphoton interference fringes for CH30 & CH34; (c) time-bin entangled biphoton interference fringes for CH29 & CH35; (d) polarization-entangled biphoton interference fringes for CH31 & CH33; (e) polarization-entangled biphoton interference fringes for CH30 & CH34; (f) polarization-entangled biphoton interference fringes for CH29 & CH35.
图 3 偏振纠缠态重构密度矩阵的实部和虚部 (a) CH31&CH33偏振纠缠态重构密度矩阵的实部; (b) CH31&CH33偏振纠缠态重构密度矩阵的虚部; (c) CH30&CH34偏振纠缠态重构密度矩阵的实部; (d) CH30&CH34偏振纠缠态重构密度矩阵的虚部; (e) CH29&CH35偏振纠缠态重构密度矩阵的实部; (f) CH29&CH35偏振纠缠态重构密度矩阵的虚部
Figure 3. Real and imaginary parts of the reconstructed density matrix for polarization-entangled states: (a) Real part of the reconstructed density matrix for CH31 & CH33 polarization-entangled states; (b) imaginary part of the reconstructed density matrix for CH31 & CH33 polarization-entangled states; (c) real part of the reconstructed density matrix for CH30 & CH34 polarization-entangled states; (d) imaginary part of the reconstructed density matrix for CH30 & CH34 polarization-entangled states; (e) real part of the reconstructed density matrix for CH29 & CH35 polarization-entangled states; (f) imaginary part of the reconstructed density matrix for CH29 & CH35 polarization-entangled states.
-
[1] Konrad T, de Melo F, Tiersch M, Kasztelan C, Aragão A, Buchleitner A 2008 Nat. Phys. 4 99 doi: 10.1038/nphys885 [2] Aspelmeyer M, Böhm H R, Gyatso T, Jennewein T, Kaltenbaek R, Lindenthal M, Molina-Terriza G, Poppe A, Resch K, Taraba M, Ursin R, Walther P, Zeilinger A 2003 Science 301 621 doi: 10.1126/science.1085593 [3] Maring N, Fyrillas A, Pont M, Ivanov E, Stepanov P, Margaria N, Hease W, Pishchagin A, Lemaître A, Sagnes I, Au T H, Boissier S, Bertasi E, Baert A, Valdivia M, Billard M, Acar O, Brieussel A, Mezher R, Wein S C, Salavrakos A, Sinnott P, Fioretto D A, Emeriau P E, Belabas N, Mansfield S, Senellart P, Senellart J, Somaschi N 2024 Nat. Photonics 18 603 doi: 10.1038/s41566-024-01403-4 [4] Gisin N, Thew R 2007 Nat. Photonics 1 165 doi: 10.1038/nphoton.2007.22 [5] Li W, Zhang L, Tan H, Lu Y, Liao S K, Huang J, Li H, Wang Z, Mao H K, Yan B, Li Q, Liu Y, Zhang Q, Peng C Z, You L, Xu F, Pan J W 2023 Nat. Photonics 17 416 doi: 10.1038/s41566-023-01166-4 [6] Zahidy M, Ribezzo D, De Lazzari C, Vagniluca I, Biagi N, Müller R, Occhipinti T, Oxenløwe L K, Galili M, Hayashi T, Cassioli D, Mecozzi A, Antonelli C, Zavatta A, Bacco D 2024 Nat. Commun. 15 1651 doi: 10.1038/s41467-024-45876-x [7] Ye J, Zoller P 2024 Phys. Rev. Lett. 132 190001 doi: 10.1103/PhysRevLett.132.190001 [8] Guo X, Breum C R, Borregaard J, Izumi S, Larsen M V, Gehring T, Christandl M, Neergaard-Nielsen J S, Andersen U L 2020 Nat. Phys. 16 281 doi: 10.1038/s41567-019-0743-x [9] Qiu X, Zhang D, Ma T, Lin F, Guo H, Zhang W, Chen L 2020 Adv. Quantum Technol. 3 2000073 doi: 10.1002/qute.202000073 [10] Azuma K, Economou S E, Elkouss D, Hilaire P, Jiang L, Lo H K, Tzitrin I 2023 Rev. Mod. Phys. 95 045006 doi: 10.1103/RevModPhys.95.045006 [11] Liu S, Lv Y, Wang X, Wang J, Lou Y, Jing J 2024 Phys. Rev. Lett. 132 100801 doi: 10.1103/PhysRevLett.132.100801 [12] Zhang Z, Sang Y 2023 Quantum Inf. Process. 22 201 doi: 10.1007/s11128-023-03950-1 [13] Peev M, Pacher C, Alléaume R, Barreiro C, Bouda J, Boxleitner W, Debuisschert T, Diamanti E, Dianati M, Dynes J F, Fasel S, Fossier S, Fürst M, Gautier J D, Gay O, Gisin N, Grangier P, Happe A, Hasani Y, Hentschel M, Hübel H, Humer G, Länger T, Legré M, Lieger R, Lodewyck J, Lorünser T, Lütkenhaus N, Marhold A, Matyus T, Maurhart O, Monat L, Nauerth S, Page J B, Poppe A, Querasser E, Ribordy G, Robyr S, Salvail L, Sharpe A W, Shields A J, Stucki D, Suda M, Tamas C, Themel T, Thew R T, Thoma Y, Treiber A, Trinkler P, Tualle-Brouri R, Vannel F, Walenta N, Weier H, Weinfurter H, Wimberger I, Yuan Z L, Zbinden H, Zeilinger A 2009 New J. Phys. 11 075001 doi: 10.1088/1367-2630/11/7/075001 [14] Sasaki M, Fujiwara M, Ishizuka H, Klaus W, Wakui K, Takeoka M, Miki S, Yamashita T, Wang Z, Tanaka A, Yoshino K, Nambu Y, Takahashi S, Tajima A, Tomita A, Domeki T, Hasegawa T, Sakai Y, Kobayashi H, Asai T, Shimizu K, Tokura T, Tsurumaru T, Matsui M, Honjo T, Tamaki K, Takesue H, Tokura Y, Dynes J F, Dixon A R, Sharpe A W, Yuan Z L, Shields A J, Uchikoga S, Legré M, Robyr S, Trinkler P, Monat L, Page J B, Ribordy G, Poppe A, Allacher A, Maurhart O, Länger T, Peev M, Zeilinger A 2011 Opt. Express 19 10387 doi: 10.1364/OE.19.010387 [15] Huang Y, Li Y, Qi Z, Yang Y, Zheng Y, Chen X 2023 Quantum Frontiers 2 4 doi: 10.1007/s44214-023-00030-4 [16] Jing X, Qian C, Weng C X, Li B H, Chen Z, Wang C Q, Tang J, Gu X W, Kong Y C, Chen T S, Yin H L, Jiang D, Niu B, Lu L L 2024 Sci. Adv. 10 eadp2877 doi: 10.1126/sciadv.adp2877 [17] Qi Z, Huang Y, Lu C, Ni F, Li Y, Zheng Y, Chen X 2023 Phys. Rev. Appl. 19 014045 doi: 10.1103/PhysRevApplied.19.014045 [18] Qi Z, Li Y, Huang Y, Feng J, Zheng Y, Chen X 2021 Light Sci. Appl. 10 183 doi: 10.1038/s41377-021-00634-2 [19] Wang X L, Cai X D, Su Z E, Chen M C, Wu D, Li L, Liu N L, Lu C Y, Pan J W 2015 Nature 518 516 doi: 10.1038/nature14246 [20] Wengerowsky S, Joshi S K, Steinlechner F, Hübel H, Ursin R 2018 Nature 564 225 doi: 10.1038/s41586-018-0766-y [21] Treiber A, Poppe A, Hentschel M, Ferrini D, Lorünser T, Querasser E, Matyus T, Hübel H, Zeilinger A 2009 New J. Phys. 11 045013 doi: 10.1088/1367-2630/11/4/045013 [22] Kaiser F, Issautier A, Ngah L A, Alibart O, Martin A, Tanzilli S 2013 Laser Phys. Lett. 10 045202 doi: 10.1088/1612-2011/10/4/045202 [23] Liu B X, Yang Y G, Xu G B, Jiang D H, Zhou Y H, Shi W M, Li D 2024 Physica A 639 129683 doi: 10.1016/j.physa.2024.129683 [24] Kim J H, Chae J W, Jeong Y C, Kim Y H 2022 APL Photonics 7 016106 doi: 10.1063/5.0073040 [25] Huang Y, Qi Z, Yang Y, Zhang Y, Li Y, Zheng Y, Chen X 2025 Laser Photonics Rev. 19 2301026 doi: 10.1002/lpor.202301026 [26] Xie Z, Zhong T, Shrestha S, Xu X, Liang J, Gong Y X, Bienfang J C, Restelli A, Shapiro J H, Wong F N C, Wei Wong C 2015 Nat. Phys. 9 536 [27] Luo M X, Li H R, Lai H, Wang X 2016 Sci. Rep. 6 25977 doi: 10.1038/srep25977 [28] Luo M X, Li H R, Lai H, Wang X 2016 Phys. Rev. A 93 012332 doi: 10.1103/PhysRevA.93.012332 [29] Erhard M, Krenn M, Zeilinger A 2020 Nat. Rev. Phys. 2 365 doi: 10.1038/s42254-020-0193-5 [30] Prabhu A V, Suri B, Chandrashekar C M 2021 Phys. Rev. A 103 052608 doi: 10.1103/PhysRevA.103.052608 [31] Clauser J F, Horne M A, Shimony A, Holt R A 1969 Phys. Rev. Lett. 23 880 doi: 10.1103/PhysRevLett.23.880 [32] Brunner N, Cavalcanti D, Pironio S, Scarani V, Wehner S 2014 Rev. Mod. Phys. 86 419 doi: 10.1103/RevModPhys.86.419 [33] Sun Q C, Mao Y L, Jiang Y F, Zhao Q, Chen S J, Zhang W, Zhang W J, Jiang X, Chen T Y, You L X, Li L, Huang Y D, Chen X F, Wang Z, Ma X, Zhang Q, Pan J W 2017 Phys. Rev. A 95 032306 doi: 10.1103/PhysRevA.95.032306 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: