高级搜索

氢键对聚丙烯复合材料分子结构与电荷输运特性的影响

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

李丽丽, 韩爽, 王玉龙, 刘统江, 李育哲, 高俊国. 氢键对聚丙烯复合材料分子结构与电荷输运特性的影响[J]. 物理学报, 2025, 74(12): 127702-1. doi: 10.7498/aps.74.20250277
引用本文: 李丽丽, 韩爽, 王玉龙, 刘统江, 李育哲, 高俊国. 氢键对聚丙烯复合材料分子结构与电荷输运特性的影响[J]. 物理学报, 2025, 74(12): 127702-1. doi: 10.7498/aps.74.20250277
shu
Lili LI, Shuang HAN, Yulong WANG, Tongjiang LIU, Yuzhe LI, Junguo GAO. Effects of hydrogen bond on molecular structure and charge transport characteristic of polypropylene composites[J]. Acta Physica Sinica, 2025, 74(12): 127702-1. doi: 10.7498/aps.74.20250277
Citation: Lili LI, Shuang HAN, Yulong WANG, Tongjiang LIU, Yuzhe LI, Junguo GAO. Effects of hydrogen bond on molecular structure and charge transport characteristic of polypropylene composites[J]. Acta Physica Sinica, 2025, 74(12): 127702-1. doi: 10.7498/aps.74.20250277
shu

氢键对聚丙烯复合材料分子结构与电荷输运特性的影响

  • 1.

    哈尔滨理工大学电气与电子工程学院, 工程电介质及其应用教育部重点实验室, 哈尔滨　150080

  • 2.

    四川省氢能源与多能互补微电网工程技术研究中心, 绵阳, 621000

    • 作者简介: 李丽丽: lily_li@hrbust.edu.cn .
    通讯作者: E-mail: wangyulong@hrbust.edu.cn.; 

  • 中图分类号: 77.84.Jd, 77.22.Jp, 63.20.dk, 47.11.Mn

Effects of hydrogen bond on molecular structure and charge transport characteristic of polypropylene composites

  • 1.

    Key Laboratory of Engineering Dielectrics and Its Application, Ministry of Education, College of Electrical and Electronic Engineering, Harbin University of Science and Technology, Harbin 150080, China

  • 2.

    Sichuan Provincial Engineering Research Center of Hydrogen Energy and Multi-energy Complementary Microgrid, Mianyang 62100, China

    • Corresponding author: E-mail: wangyulong@hrbust.edu.cn.; 

  • MSC: 77.84.Jd, 77.22.Jp, 63.20.dk, 47.11.Mn

  • 摘要: 模拟分子的结构和行为有助于更深刻地分析电荷输运特性变化的微观机理. 本研究采用分子动力学模拟方法, 深入探究氢键对马来酸(MA)接枝聚丙烯(PP)/聚偏二氟乙烯(PVDF)复合体系分子结构演变与电荷输运特性的调控机制, 并对其分子间相互作用能、自由体积、电子态密度、电荷差分密度以及陷阱能级进行仿真分析. 研究结果表明: 随着MA接枝量的增加, 氢键数量显著增多. 当MA质量分数为36.22%时, 氢键数量达到20的峰值, 分子间相互作用能增至极大值2171.63 kcal·mol–1, 自由体积分布达到极小值16.03%, 此时分子内部结构最为紧密. 当MA质量分数为52.97%时, 复合材料的带隙达到极小值3.13 eV, 陷阱能级深度亦达到极大值3.06 eV, 此时PP/PVDF复合材料在氢键形成的区域显示出更高的电子密度积累, 电子逸出概率显著地降低. 至此, 模拟结果证实了氢键的作用不仅改变了材料的分子结构, 还通过改变局部电荷分布状态直接影响电荷输运特性, 为设计功能性高分子复合电介质材料提供了理论依据.
    Abstract: Simulating molecular structures and dynamic behaviors presents critical insights into the microscopic mechanisms governing variations in charge transport properties. In this work, molecular dynamics (MD) simulations integrated with the Compass II force field and molecular modeling (including geometry optimization, annealing, and dynamic equilibration) are conducted to systematically analyze intermolecular interaction energy, free volume distribution, electronic density of states (DOS), charge differential density, and trap energy levels. aiming to unravel the regulatory role of hydrogen bonds in the structural evolution and charge transport dynamics of polypropylene (PP)/polyvinylidene fluoride (PVDF) composite systems. A quantitative framework is further established to correlate hydrogen bond density with key material performance metrics, such as free volume fraction, bandgap energy, and trap energy depth, thereby elucidating the hydrogen bond-mediated modulation of molecular architecture and charge transport behavior in PP/PVDF composites. Simulation results reveal a pronounced dependence of hydrogen bond formation on maleic acid (MA) grafting content. When the mass fraction of MA is 36.22%, the number of hydrogen bonds reaches a maximum value of 20, the intermolecular interaction energy increases to 2171.63 kcal·mol–1, and the free volume fraction reaches a minimum value of 16.03%. At this point, the internal structure of the molecule is most compact. When the mass fraction of MA increases to 52.97%, the band gap of the composite material reaches a minimum value of 3.13 eV, and the depth of the trap energy levels also reaches a maximum value of 3.06 eV. Spatial charge differential density analysis demonstrates that the enhanced electron density is localized near hydrogen-bonded region, thus suppressing electron escape probability by over 40% compared with the scenario in the non-bonded domains. All of the findings highlight a dual mechanism: hydrogen bonds not only reconfigure the molecular topology but also reshape the localized charge distribution, directly suppressing the carrier mobility and changing the charge transport pathways. These findings also establish a robust structure-property relationship, showing that hydrogen bond engineering serves as a pivotal strategy to tailor dielectric performance in polymer composites. By optimizing hydrogen bond density, the trade-off between structural compactness and electronic confinement can be strategically balanced, thus enabling the designing of PP-based dielectrics with low carbon footprints and superior insulating properties. This mechanistic understanding provides actionable guidelines for advancing high-performance insulating materials in energy storage systems, aerospace components, and next-generation electrical devices, where precise control over charge transport is paramount.
  • 加载中

  • 图 1  PP/PVDF复合材料空间结构　(a) PP; (b) PVDF; (c) PP-g-MA; (d) PP/PVDF

    Figure 1.  Spacial structure of PP/PVDF composites: (a) PP; (b) PVDF; (c) PP-g-MA; (d) PP/PVDF.

    下载: 全尺寸图片 幻灯片

    图 2  不同PP/PVDF复合材料分子结构模型　(a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#

    Figure 2.  Molecular structure models of different PP/PVDF composites: (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#.

    下载: 全尺寸图片 幻灯片

    图 3  2#复合材料的能量和温度随时间的变化　(a)能量随时间的变化; (b)温度随时间的变化

    Figure 3.  Time-dependent energy and temperature variation curves of composite 2# in the PP/PVDF system: (a) Energy variation curves over time; (b) temperature curve over time.

    下载: 全尺寸图片 幻灯片

    图 4  9#复合材料中氢键的位置

    Figure 4.  Spacial distribution of hydrogen bonds in composite 9#.

    下载: 全尺寸图片 幻灯片

    图 5  不同PP/PVDF复合材料的氢键数量变化趋势

    Figure 5.  Variation trend of hydrogen bond number of different PP/PVDF composites.

    下载: 全尺寸图片 幻灯片

    图 6  不同PP/PVDF复合材料自由体积模型　(a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#

    Figure 6.  Free volume models of different PP/PVDF composites: (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#

    下载: 全尺寸图片 幻灯片

    图 7  不同PP/PVDF复合材料的自由体积分布变化趋势

    Figure 7.  Variation trend of free volume distribution of different PP/PVDF composites.

    下载: 全尺寸图片 幻灯片

    图 8  不同PP/PVDF复合材料的态密度变化趋势

    Figure 8.  Variation trend of state density of different PP/PVDF composites.

    下载: 全尺寸图片 幻灯片

    图 9  不同PP/PVDF复合材料电荷差分密度　(a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#

    Figure 9.  Charge differential density of different PP/PVDF composites: (a) 1#; (b) 2#; (c) 3#; (d) 4#; (e) 5#; (f) 6#; (g) 7#; (h) 8#; (i) 9#.

    下载: 全尺寸图片 幻灯片

    图 10  不同PP/PVDF复合材料的陷阱能级变化趋势

    Figure 10.  Variation trend of trap energy levels of different PP/PVDF composites.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片

    表 1  Compass II力场势能和参数及单位

    Table 1.  Force field potential energy and parameters in COMPASS II.

    Epotential Function form Parameters and units
    Ebond $ {E_{{\text{bond}}}} = \displaystyle\sum\limits_{{\text{bonds}}} {{k_b}{{(r - {r_0})}^2} + k_b^{(3)}{{(r - {r_0})}^3} + k_b^{(4)}{{(r - {r_0})}^4}} $ kb/(kcal·mol–1·Å–2); r, r0/Å
    Eangle $ {E_{{\text{angle}}}} = \displaystyle\sum\limits_{{\text{angles}}} {{k_\theta }{{(\theta - {\theta _0})}^2} + k_\theta ^{(3)}{{(\theta - {\theta _0})}^3} + k_\theta ^{(4)}{{(\theta - {\theta _0})}^4}} $ kθ/(kcal·mol–1); θ, θ0/(°)
    Etorsion $ {E_{{\text{torsion}}}} = \displaystyle\sum\limits_{{\text{torsions}}} {{k_\varphi }(1 + \cos (n} \varphi - {\varphi _0})) $ kφ/(kcal·mol–1); φ, φ0/(°)
    Eout-of-plane $ {E_{{\text{out-of-plane}}}} = \displaystyle\sum\limits_{{\text{out-of-plane}}} {{k_\omega }{\omega ^2}} $ kω/(kcal·mol–1); ω/(°)
    Evdw $ {E_{{\text{vdW}}}} = \displaystyle\sum\limits_{i, j} {4\varepsilon \left[ {{{\left( {\frac{\sigma }{{{r_{ij}}}}} \right)}^{12}} - {{\left( {\frac{\sigma }{{{r_{ij}}}}} \right)}^6}} \right]} $ Ε/eV; σ/Å; rij/Å
    Eelectrostatic $ {E_{{\text{electrostatic}}}} = \displaystyle\sum\limits_{i, j} {\frac{{{q_i}{q_j}}}{{4\pi {\varepsilon _0}{r_{ij}}}}} $ qi, qj/e; rij/Å
    下载: 导出CSV

    表 2  不同PP/PVDF复合材料体系模型的编号及其质量分数

    Table 2.  Designation and mass fraction of different PP/PVDF composites models.

    试样编号
    PP-g-MA/%    		PVDF/%
    MAPP
    1#077.9422.26
    2#2.7475.5221.74
    3#5.3373.4121.26
    4#10.1369.5720.30
    5#14.5065.9419.56
    6#18.4762.8318.70
    7#22.0559.8418.11
    8#36.2248.5115.27
    9#52.9735.3411.69
    下载: 导出CSV

    表 3  NPT平衡后不同PP/PVDF复合材料能量和温度的波动范围

    Table 3.  Fluctuation range of energy and temperature of different PP/PVDF composites after NPT equilibrium.

    试样
    编号    		 平衡
    时间/ps    		 波动/%
    温度 Epotential Ekinetic Enon-bond Etotal
    1# 58.93 3.25 1.56 3.85 4.52 4.11
    2# 74.68 2.89 2.56 4.26 1.57 2.10
    3# 25.95 4.56 4.56 3.73 2.94 1.61
    4# 78.59 1.12 2.76 1.52 4.51 1.52
    5# 85.45 2.59 3.81 1.14 1.52 3.20
    6# 36.58 3.58 4.19 2.81 2.73 2.17
    7# 57.58 1.56 1.25 4.20 2.85 3.96
    8# 85.42 3.20 2.48 1.52 4.22 2.57
    9# 54.20 2.74 4.21 1.23 2.52 1.85
    下载: 导出CSV

    表 4  不同PP/PVDF复合材料的能量变化

    Table 4.  Energy evolution in different PP/PVDF composites.


    Enon-bond/(kcal·mol–1)
    Ediagonal/(kcal·mol–1)    		 Einteraction
    /(kcal·mol–1)    		 Etotal
    /(kcal·mol–1)
    Evdw Eelectrostatic Ebond Eangle Etorsion
    1# 84.65 853.99 214.04 371.93 –721.02 53.49 552.18
    2# 85.17 906.80 215.48 398.77 –728.18 63.88 601.15
    3# 86.71 977.26 217.09 412.65 –751.63 75.86 654.46
    4# 97.89 1083.01 218.45 448.12 –753.56 85.58 723.28
    5# 110.28 1205.79 242.31 453.70 –770.93 88.09 828.37
    6# 110.97 1332.96 264.16 536.79 –787.47 89.02 898.72
    7# 122.93 1462.88 268.80 547.69 –792.07 108.50 1002.49
    8# 132.42 2094.95 309.91 689.15 –858.76 127.05 1413.73
    9# 55.29 3377.36 402.88 1026.23 –1028.7 74.86 2171.63
    下载: 导出CSV
  • [1] Li H, Gadinski M R, Huang Y Q 2020 Energy Environ. Sci. 13 1279 doi: 10.1039/C9EE03603B
    [2] Tan D Q 2020 Adv. Funct. Mater. 30 1808567 doi: 10.1002/adfm.201808567
    [3] Pablo A R, Baltus C B, Sebastião V C, Sílvia H P 2024 Chem. Eng. Sci. 298 120319 doi: 10.1016/j.ces.2024.120319
    [4] 殷嘉鑫, 王强华 2024 物理学报 73 157401 doi: 10.7498/aps.73.20240807 Yin J X, Wang Q H 2024 Acta Phys. Sin. 73 157401 doi: 10.7498/aps.73.20240807
    [5] 罗兵, 李君洛, 王少杰, 胡世勋, 徐永生, 肖微, 徐刚毅, 何金良, 李琦 2024 中国电机工程学报 44 3371 doi: 10.13334/j.0258-8013.pcsee.230041 Luo B, Li J L, Wang S J, Hu S X, Xu Y S, Xiao W, Xu G Y, He J L, Li Q 2024 Proceedings of the CSEE 44 3371 doi: 10.13334/j.0258-8013.pcsee.230041
    [6] 樊林禛, 李琦, 袁浩, 黄上师, 何金良 2022 中国电机工程学报 45 4227 doi: 10.13334/j.0258-8013.pcsee.212510 Fan L Z, Li Q, Yuan H, Huang S S, He J L 2022 Proceedings of the CSEE 45 4227 doi: 10.13334/j.0258-8013.pcsee.212510
    [7] Ohuk L, Kim D, Kim H, Seong H L, Taehoon K, Kwon I, Keisuke S, Masayuki H, Jin H L, Dae H L, Kim M H, Masahiro K, Yu S G 2025 Compos. Sci. Technol. 259 110939 doi: 10.1016/j.compscitech.2024.110939
    [8] Hu S, Zhou Y, Yuan C, Wang W, Hu J 2020 High Voltage 5 249 doi: 10.1049/hve.2019.0159
    [9] 樊林禛, 郝国辉, 张雯嘉, 董新华, 屠幼萍, 胡世勋, 邵清, 郑重, 王伟, 袁浩, 李琦, 何金良 2023 中国电机工程学报 45 5251 doi: 10.13334/j.0258-8013.pcsee.220029 Fan L Z, Hao G H, Zhang W J, Dong X H, Tu Y P, Hu S X, Shao Q, Zheng Z, Wang W, Yuan H, Li Q, He J L 2023 Proceedings of the CSEE 45 5251 doi: 10.13334/j.0258-8013.pcsee.220029
    [10] 李琳, 王暄, 孙伟峰, 雷清泉 2013 物理学报 62 106201 doi: 10.7498/aps.62.106201 Li L, Wang X, Sun W F, Lei Q Q 2013 Acta Phys. Sin. 62 106201 doi: 10.7498/aps.62.106201
    [11] 李丽丽, 张晓虹, 王玉龙, 国家辉 2017 物理学报 66 087201 doi: 10.7498/aps.66.087201 Li L L, Zhang X H, Wang Y L, Guo J H 2017 Acta Phys. Sin. 66 087201 doi: 10.7498/aps.66.087201
    [12] Ulian G, Moro D, Valdrè G 2018 Micro Nano Lett. 13 4 doi: 10.1049/mnl.2017.0058
    [13] Duan X H, Wah H S, Martin G, John L, He J L 2020 High Voltage 5 397 doi: 10.1049/hve.2020.0081
    [14] Etcheverry M, Barbosa S E 2012 Materials 5 1084 doi: 10.3390/ma5061084
    [15] Kang J W, Choi K, John W H, Hu S L 1998 Polymer 39 7079 doi: 10.1016/S0032-3861(98)00071-8
    [16] 庞曦, 许天蕾, 刘鹏, 魏鼎欣, 谢宗良, 彭宗仁 2024 高电压技术 50 3 doi: 10.13336/j.1003-6520.hve.20230400 Pang X, Xu T L, Liu P, Wei D X, Xie Z L, Peng Z R 2024 High Voltage Engineering 50 3 doi: 10.13336/j.1003-6520.hve.20230400
    [17] 马超, 闵道敏, 李盛涛, 郑旭, 李西育, 闵超, 湛海涯 2017 物理学报 66 067701 doi: 10.7498/aps.66.067701 Ma C, Min D M, Li S T, Zheng X, Li X Y, Min C, Zhan H Y 2017 Acta Phys. Sin. 66 067701 doi: 10.7498/aps.66.067701
    [18] Boek E S, Coveney P V, Skipper N T 1995 Langmuir 11 46295 doi: 10.1021/la00012a008
    [19] Martínez, Mario J, Martínez L 2003 J. Comput. Chem. 24 819 doi: 10.1002/jcc.10216
    [20] 彭向阳, 姚驰, 余欣, 胡世勋, 范亚洲, 何金良 2023 高电压技术 49 4480 doi: 10.13336/j.1003-6520.hve.20231488 Peng X Y, Yao C, Yu X, Hu S X, Fan Y Z, He J L 2023 High Voltage Engineering 49 4480 doi: 10.13336/j.1003-6520.hve.20231488
    [21] 贾海鹏, 苏勋家, 侯根良, 曹小平, 毕松, 刘朝辉 2013 化工学报 64 1862 doi: 10.3969/j.issn.0438-1157.2013.05.049 Jia H P, Su X J, Hou G L, Cao X P, Bi S, Liu Z H 2013 J. Chem. Ind. Eng. 64 1862 doi: 10.3969/j.issn.0438-1157.2013.05.049
    [22] Ferraris G, Ivaldi G 1988 Acta Cryst 44 341 doi: 10.1107/S0108768188001648
    [23] 冯阳, 渠广昊, 李盛涛 2024 高电压技术 50 2363 doi: 10.13336/j.1003-6520.hve.20231508 Feng Y, Qu G H, Li S T 2024 High Voltage Engineering 50 2363 doi: 10.13336/j.1003-6520.hve.20231508
    [24] Ran Z Y, Luo Z, Li J L, Meng L, Liu Y H, Hu J, He J L, Li Q 2024 IEEE 5th International Conference on Dielectrics France, August 2–6, 2024, p1241
    [25] 樊金泽, 方展伯, 罗超杰, 张汇 2022 物理学报 71 127103 doi: 10.7498/aps.71.20220052 Fan J Z, Fang Z B, Luo C J, Zhang H 2022 Acta Phys. Sin. 71 127103 doi: 10.7498/aps.71.20220052
    [26] Li G C, Liu T Z, Gu Z L, Chen X L, Sun B B, Zhu Y W, Li S T, Wei Y H 2024 High Voltage 85 2397 doi: 10.1049/hve2.12497
    [27] 洪迪昆, 刘亮, 郭欣 2015 中国电机工程学报 35 6099 doi: 10.13334/j.0258-8013.pcsee.2015.23.017 Hong D K, Liu L, Guo X 2015 Proceedings of the CSEE 35 6099 doi: 10.13334/j.0258-8013.pcsee.2015.23.017
    [28] Li Q, Yao F Z, Liu Yang 2018 Annu. Rev. Mater. Res. 48 219 doi: 10.1146/annurev-matsci-070317-124435
    [29] Gabriel P, Jacob P T, Mikhail I, Wu Z G, John W L 2025 J. Chem. Phys. 162 054709 doi: 10.1063/5.0246100
    [30] 王进, 王军霞, 曾凡桂, 吴秀玲 2010 化学学报 68 1653 Wang J, Wang J X, Zeng F G, Wu X L 2010 Acta Chim Sinica 68 1653
    [31] 肖萌, 陈毓妍, 赵亦烁, 杜伯学 2024 高电压技术 50 2319 doi: 10.13336/j.1003-6520.hve.20232036 Xiao M, Chen Y Y, Zhao Y S, Du B X 2024 High Voltage Engineering 50 2319 doi: 10.13336/j.1003-6520.hve.20232036
    [32] Blaise P G, Le G C 2018 AIP Adv. 8 095228 doi: 10.1063/1.5047673
    [33] Li H, Ai D, Ren L, L 2019 Adv. Mater. 31 1900875 doi: 10.1002/adma.201900875
    [34] Zhou Y, Li Q, Dang B 2018 Adv. Mater. 30 1805672 doi: 10.1002/adma.201805672
    [35] 李盛涛, 谢东日, 闵道敏 2019 中国电机工程学报 39 6122 doi: 10.13334/j.0258-8013.pcsee.182401 Li S T, Xie D R, Min D M 2019 Proceedings of the CSEE 39 6122 doi: 10.13334/j.0258-8013.pcsee.182401
    [36] Wang J, David B A, Carlos A F, De L, Zhang D X, Alexander B, Aart W V, David S 2022 Composites Part A 159 16993 doi: 10.1016/j.compositesa.2022.106993
    [37] 国家辉 2014 硕士学位论文 (哈尔滨: 哈尔滨理工大学) Guo J H 2014 M. S. Thesis (Harbin: Harbin University of Science and Technology
  • 加载中
图( 11) 表( 4)
计量
  • 文章访问数:  177
  • HTML全文浏览数:  177
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-04
  • 刊出日期:  2025-06-20

氢键对聚丙烯复合材料分子结构与电荷输运特性的影响

    通讯作者: E-mail: wangyulong@hrbust.edu.cn.; 
    作者简介: 李丽丽: lily_li@hrbust.edu.cn
  • 1. 哈尔滨理工大学电气与电子工程学院, 工程电介质及其应用教育部重点实验室, 哈尔滨　150080
  • 2. 四川省氢能源与多能互补微电网工程技术研究中心, 绵阳, 621000
  • 收稿日期:  2025-03-04

摘要: 模拟分子的结构和行为有助于更深刻地分析电荷输运特性变化的微观机理. 本研究采用分子动力学模拟方法, 深入探究氢键对马来酸(MA)接枝聚丙烯(PP)/聚偏二氟乙烯(PVDF)复合体系分子结构演变与电荷输运特性的调控机制, 并对其分子间相互作用能、自由体积、电子态密度、电荷差分密度以及陷阱能级进行仿真分析. 研究结果表明: 随着MA接枝量的增加, 氢键数量显著增多. 当MA质量分数为36.22%时, 氢键数量达到20的峰值, 分子间相互作用能增至极大值2171.63 kcal·mol–1, 自由体积分布达到极小值16.03%, 此时分子内部结构最为紧密. 当MA质量分数为52.97%时, 复合材料的带隙达到极小值3.13 eV, 陷阱能级深度亦达到极大值3.06 eV, 此时PP/PVDF复合材料在氢键形成的区域显示出更高的电子密度积累, 电子逸出概率显著地降低. 至此, 模拟结果证实了氢键的作用不仅改变了材料的分子结构, 还通过改变局部电荷分布状态直接影响电荷输运特性, 为设计功能性高分子复合电介质材料提供了理论依据.

English Abstract

    全文HTML

    1.   引　言

    • 在“双碳”战略目标驱动下, 绝缘材料领域亟需突破传统热固性聚合物的环境约束, 开发兼具可回收性与低碳特性的新型电介质材料[1]. 传统交联聚乙烯(crosslinked polyethylene, XLPE)作为一种热固性聚合物难以回收利用, 因此开发绿色绝缘材料以减少环境污染显得尤为重要[2]. 聚丙烯(polypropylene, PP)逐渐代替XLPE成为新的绝缘材料, 开始广泛应用于能源、航空及电子电气领域.

      然而, 对于单一的PP材料而言, 由于其拉伸强度低、韧性不足以及空间电荷积聚问题严重[3], 难以满足高性能化和可持续发展的要求. 因此, 需要对PP进行改性处理, 开发功能化、可持续的PP复合材料成为当前材料科学的重要研究方向. 目前, 比较常用的改性方法是通过接枝和掺杂的方式[4]制备成复合材料. 罗兵等[5]通过将苯乙烯接枝到PP上, 制备了双向拉伸电介质薄膜, 使PP在120 ℃下的直流击穿场强得到提升, 能量密度从0.23 J/cm3提高到1.67 J/cm3, 展现出显著的温度稳定性. 樊林禛等[6]研究发现, 10%含量的苯乙烯接枝试样具有相对最优的热氧老化性能, 避免了纳米改性复合材料固有的无机纳米颗粒分散性问题.

      此外, 还可以通过掺杂其他高分子材料来实现电学性能调控. Ohuk等[7]研究发现, PP与聚偏二氟乙烯(polyvinylidene fluoride, PVDF)熔融共混形成的复合材料在25 ℃和110 ℃时的直流击穿强度值分别提高了110%和149%. Hu等[8]发现, 表面改性纳米颗粒对PP/MgO纳米复合材料内部引入了大量的深陷阱, 其中2.91%含量的复合材料的直流击穿强度最高, 约为27.4%. 樊林禛等[9]研究发现, 接枝St能够在PP试样内部增加深陷阱密度, 接枝试样的击穿强度在接枝率为3.38%时达到相对最优值, 其特征击穿强度较纯PP提升了约30.9%. 这些研究成果从分子结构设计、复合材料优化等角度为PP改性提供了重要理论支撑和实践依据. 然而, 尽管有大量文献对PP复合材料的微观结构以及电学性能进行了研究[10–12], 但氢键对PP复合材料的分子结构与电荷输运特性的影响研究至今未见报道.

      本文通过采用分子动力学模拟方法, 系统地探究不同数量的氢键对PP/PVDF复合材料中分子间的相互作用能、自由体积分布、HOMO-LUMO能级、电荷差分密度以及陷阱能级的影响规律, 揭示氢键对复合材料分子结构以及电荷输运特性的影响, 为开发兼具低碳特性与高性能的复合材料提供理论支撑.

    2.   模型构建

      2.1.   初始条件

    • 本研究采用多阶段分子模拟方法构建PP/PVDF复合材料的无定形模型, 首先对其进行分子建模、几何优化、退火、分子动力学平衡以及力学性能模拟. 力场选择基于Compass II (condensed-phase optimized molecular potentials for atomistic simulation studies II), 该力场通过实验数据与量子力学计算联合参数化, 可以精确地表征聚合物体系的非键相互作用与构象转变[13]. Compass II力场的总能量表示为多个能量项的组合, 包括键合项和非键合项, 其能量表达式如下[14]:

      式中 $ {E_{{\text{total}}}} $为总能量, 其等于键伸缩$ {E_{{\text{bond}}}} $、角弯曲$ {E_{{\text{angle}}}} $、二面角扭转$ {E_{{\text{torison}}}} $、平面外弯曲$ {E_{{\text{out-of-plane}}}} $、范德瓦耳斯能$ {E_{{\text{vdw}}}} $和静电作用能$ {E_{{\text{electrostatic}}}} $之和.

      Compass II力场势能和参数及单位如表1所列, 其中r是键长, ${r_0}$是平衡键长, ${k_b}$是二次项的力常数, $k_b^{(3)}$, $k_b^{(4)}$是三次和四次项系数, ${k_\theta }$是角度刚度常数, ${k_\varphi }$是控制扭转势能的常数, $ {k_\omega } $是平面外弯曲刚度常数, $\theta {\text{ }}$是键角, ${\theta _0}$是平衡键角, $\omega $描述了原子偏离平面的程度, ${r_{ij}}$是原子间距离, $\varepsilon $是深度, $\sigma $是距离参数, $ {q_i} $和${q_j}$分别是原子电荷, ${\varepsilon _0}$是真空介电常数.

      • 2.2.   PP/PVDF模型构建

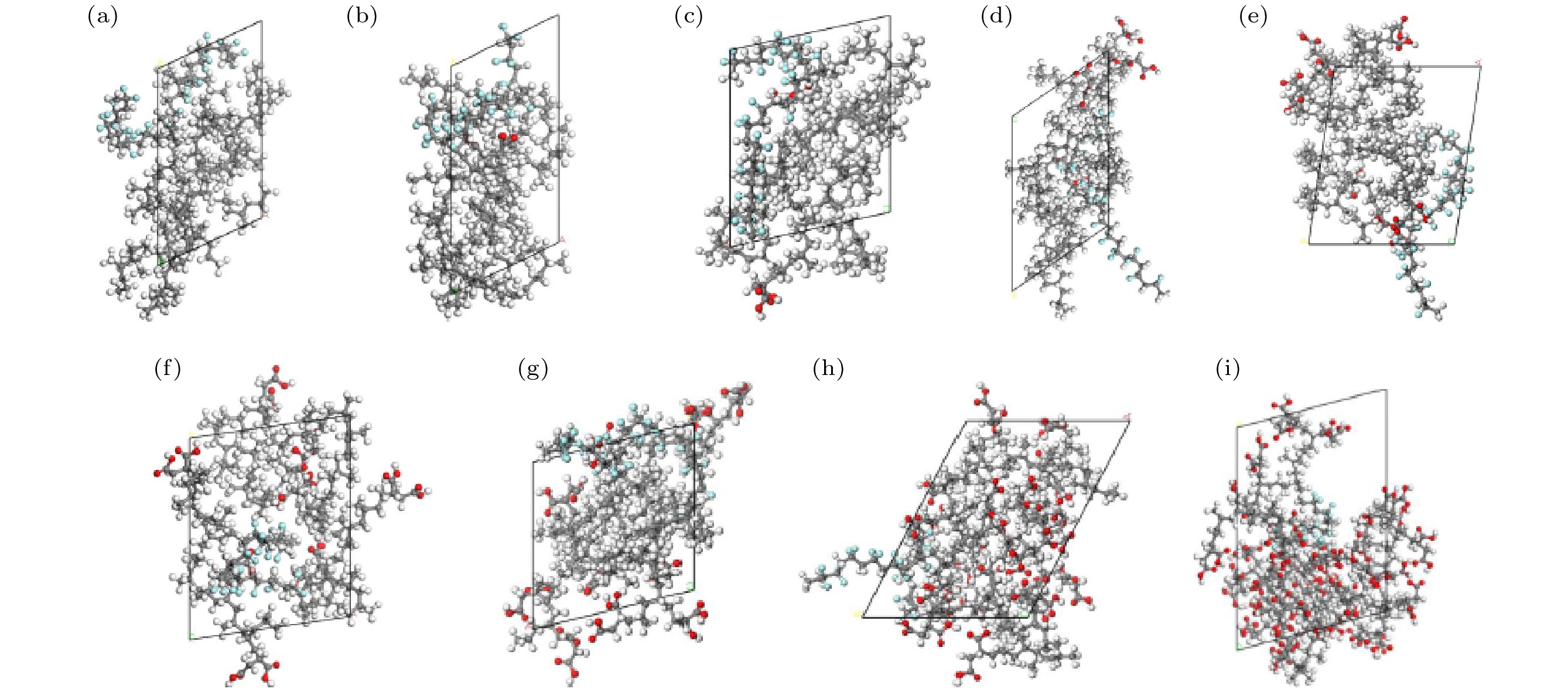
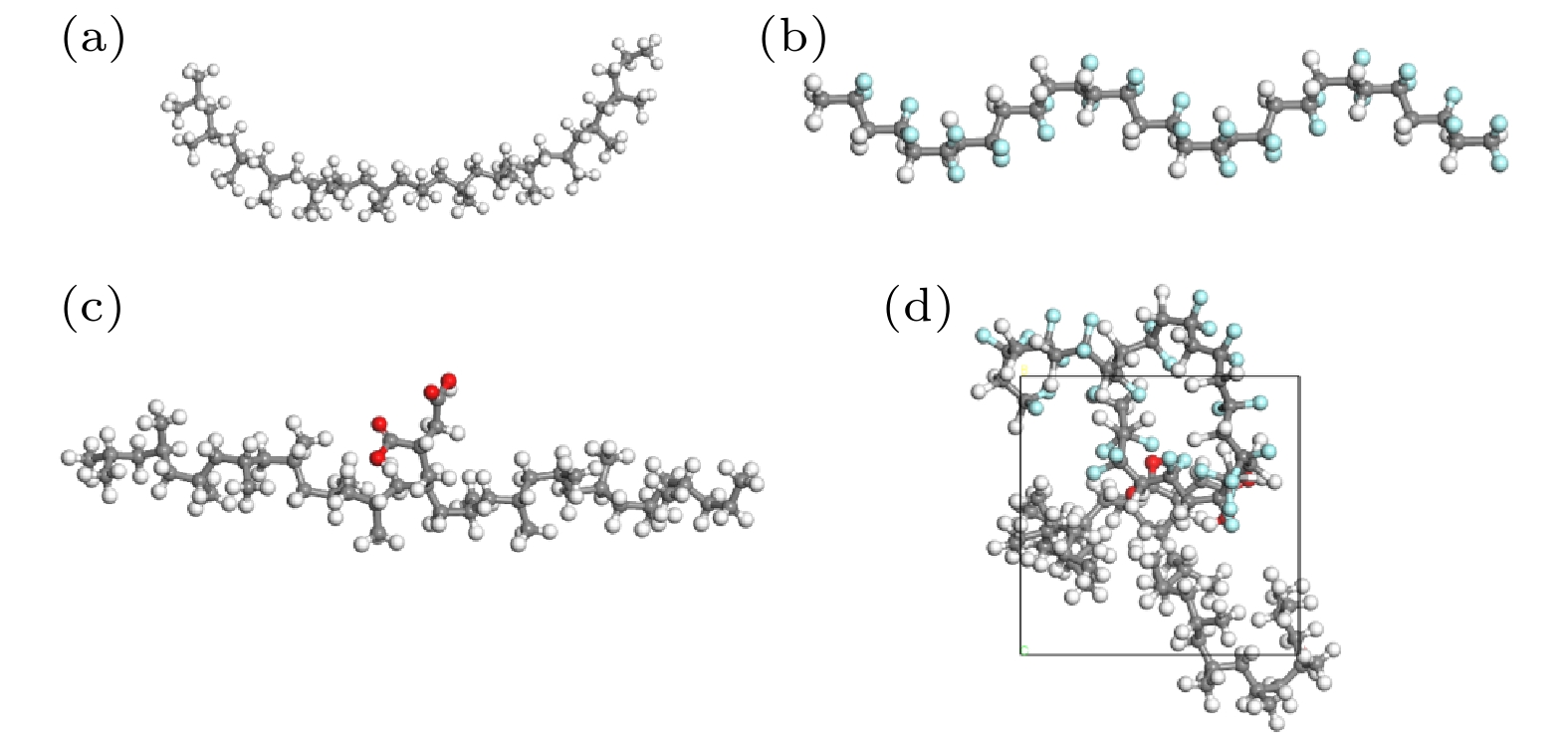
    • 研究发现, 聚合物在模拟过程中选取15个重复单元建立模型所得到的结果能够满足研究的精度要求[15]. 考虑实际情况, 本文构建了由15个重复单元组成的丙烯链作为PP模型, 以及相同长度的偏二氟乙烯链作为PVDF模型, 如图1(a)和图1(b)所示. 使用Build polymers建立PP和PVDF分子单链, 最后采用Amorphous Cell模块对4条PP分子链和1条PVDF分子链进行建模, 并进行以下设置: 温度为298.15 K, 压强为1.01×10–4 GPa, 最大迭代次数为1×104次. 对得到的分子结构分别进行结构优化、退火处理及分子动力学平衡过程[16]. 形成的晶胞如图2(a)所示, 其中白色为氢原子, 灰色为碳原子, 蓝色为氟原子, 黑色正方形为AC盒子, 晶胞类型为3D Triclinic.

      在PP和MA接枝的过程中, PP分子支链上的碳原子和MA碳-碳双键中的一个碳原子发生反应, PP支链上的碳原子碳氢键断裂, MA分子上的碳-碳双键断裂, 两者之间重新形成碳碳键[17], 得到如图1(c)所示的分子空间结构, 而PP/PVDF复合材料的分子空间结构如图1(d)所示.

      基于Boek等[18]的模型结构框架, 对PP/PVDF分子模型进行接枝处理. 首先, 对PP分子支链上的特定碳原子以及MA分子中碳-碳双键的活性碳原子进行标记, 分别指定为接枝反应位点与配对反应位点. 其次, 将PP与MA分子置于同一模拟体系内, 在NVT系综下进行分子动力学模拟, 通过热力学运动促使分子体系达到能量平衡状态, 为后续接枝反应提供动能基础. 再次, 以PP分子支链上标记的碳原子为中心, 设置动态反应半径初始值为5 Å, 采用动态反应半径机制, 通过梯度递增算法逐步扩展反应半径. 当MA标记碳原子与PP反应中心的间距进入当前反应半径范围内时, 触发接枝反应机制, 该过程包含PP碳原子的C—H单键断裂、MA的C=C双键解离以及两标记碳原子间共价键的建立. 当反应完成后, 再对PP反应位点进行氢原子补偿处理. 最后, 观察生成的分子结构中是否还存在碳-碳双键. 如果分子体系中仍然存在, 则采用自适应调整算法逐步增大反应半径参数, 循环迭代操作直至所有MA分子均完成接枝.

      通过上述过程得到PP分子链接枝的马来酸质量分数分别为0%, 2.74%, 5.33%, 10.13%, 14.50%, 18.47%, 22.05%, 36.22%, 52.97%的分子的微观结构, 并对其进行编号处理, 编号的含义如表2所列. 同时对其进行分子模型构建, 得到图2(b)—(i)所示的分子结构图. 其中红色为氧原子, 可以观察到MA分子已经成功接枝到PP分子链上.

      • 2.3.   分子动力学优化

    • 参考Martínez等[19]对材料结构优化、退火以及分子动力学平衡的优化参数设置, 首先对PP/PVDF复合材料进行结构优化. 在Forcite Tools模块中设置体系的能量收敛变化阈值为2.0×10–5 kcal·mol–1, 原子上施加的最大残余的阈值为1×10–3 kcal·mol–1·Å–1, 对晶体设置应力收敛标准为1×10–3 GPa, 每次迭代中原子位置变化阈值设置为1×10–5 Å. 在Compass II力场的作用下最大迭代次数为1×104步. 选择晶格常数优化, 使其允许晶胞参数在优化过程中变化, 让模型的结构和相变现象更加明显.

      接着对结构优化后的PP/PVDF复合材料模型进行退火处理. 在Forcite Tools模块中, 首先规定退火的起始温度为298.15 K, 为了达到PP/PVDF的熔点, 设置目标温度为500 K, 循环次数为五次, 时间步长为2×103步. 选择正则系综(NVT)后进行退火处理, 使材料的结构接近最低能量构型, 改善分子构型和晶体结构, 避免局部最小值, 提高优化效率.

      最后对退火后的分子模型进行分子动力学优化. 在Forcite Tools模块中使用Dynamics模块, 在Compass II力场作用下先选择正则系综(NVT)进行分子动力学模拟, 再在等温等压系统(NPT)下继续模拟. 其中, 静电作用和范德瓦耳斯作用采用Eward和Atom Based方法, 控温方法为Nose, 温度设置为298.15 K, 压强的控制采用Berendsen方法, 压强设置为1.01×10–4 GPa, 动力模拟时间为1×103 ps.

      • 2.4.   平衡状态分析

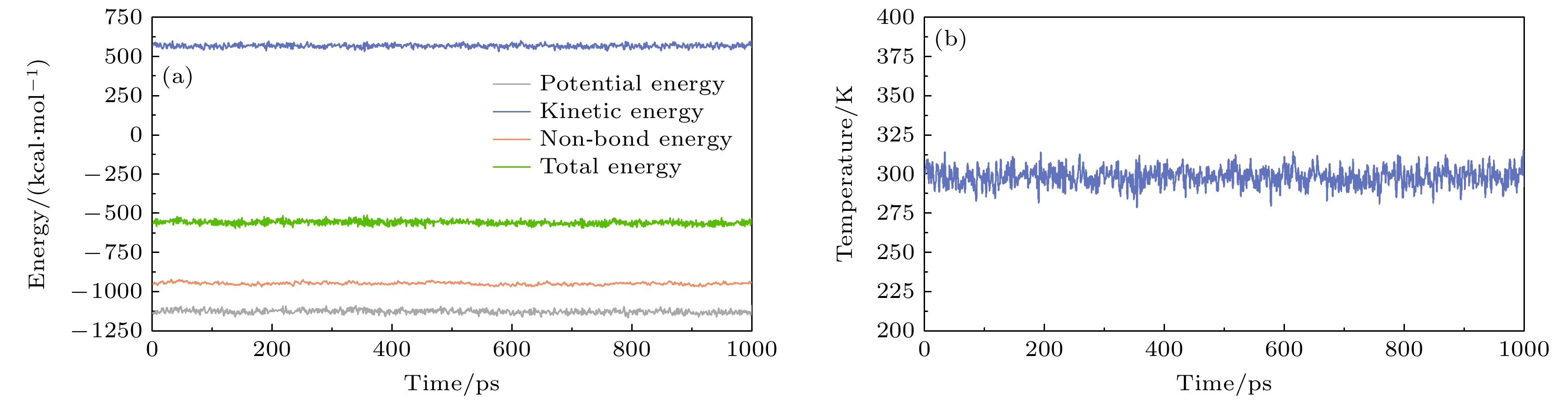
    • 在分子动力学优化过程中, 先后采用NVT系综和NPT系综对体系进行分子动力学平衡, 可以得到温度和能量的波动范围. 图3为2#复合材料在动力学模拟的0—1000 ps内能量和温度的变化曲线. 由图3可以看出, 波动起伏趋于稳定, 并且始终保持在恒定值附近, 说明体系已经达到热平衡. 体系的能量围绕恒定值发生缓慢波动(波动幅度不超过4.78%), 这符合Andersen热浴控温算法的理论预期[20], 表明此时PP/PVDF复合材料已经达到稳定状态. 通过上述方法, 分别统计了1#—9#复合材料的温度和各能量的波动幅度, 如表3所列. 从表3可以看出, 各复合材料的能量波动均小于5%. 根据贾海鹏等[21]对平衡状态的判断准则, 此时各体系都达到了能量最低状态, 说明分子动力学平衡满足系统条件, 完成了分子动力学平衡态的构建, 为后续的仿真分析提供了基础.

    3.   结果与讨论

      3.1.   氢键分析

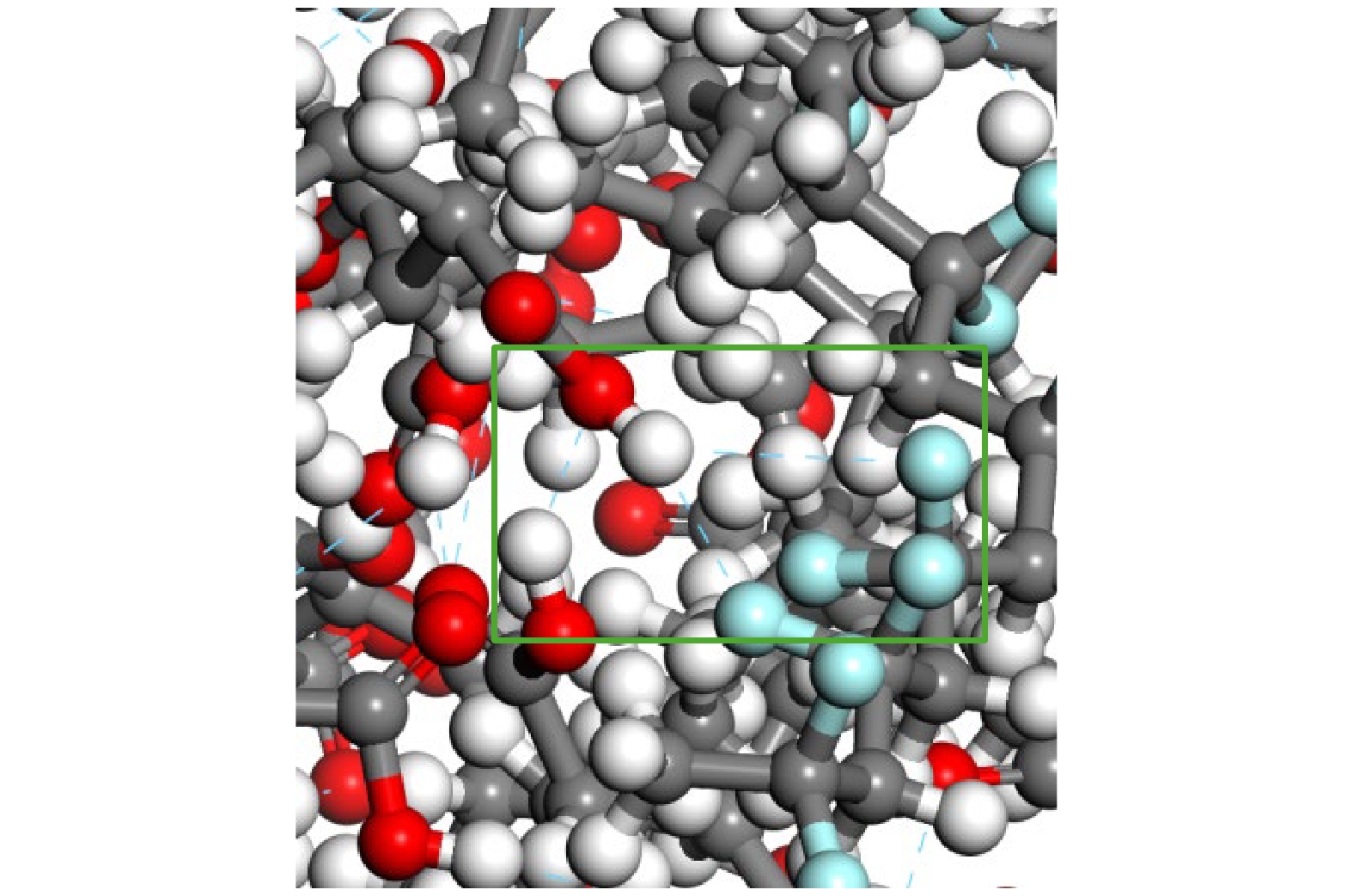
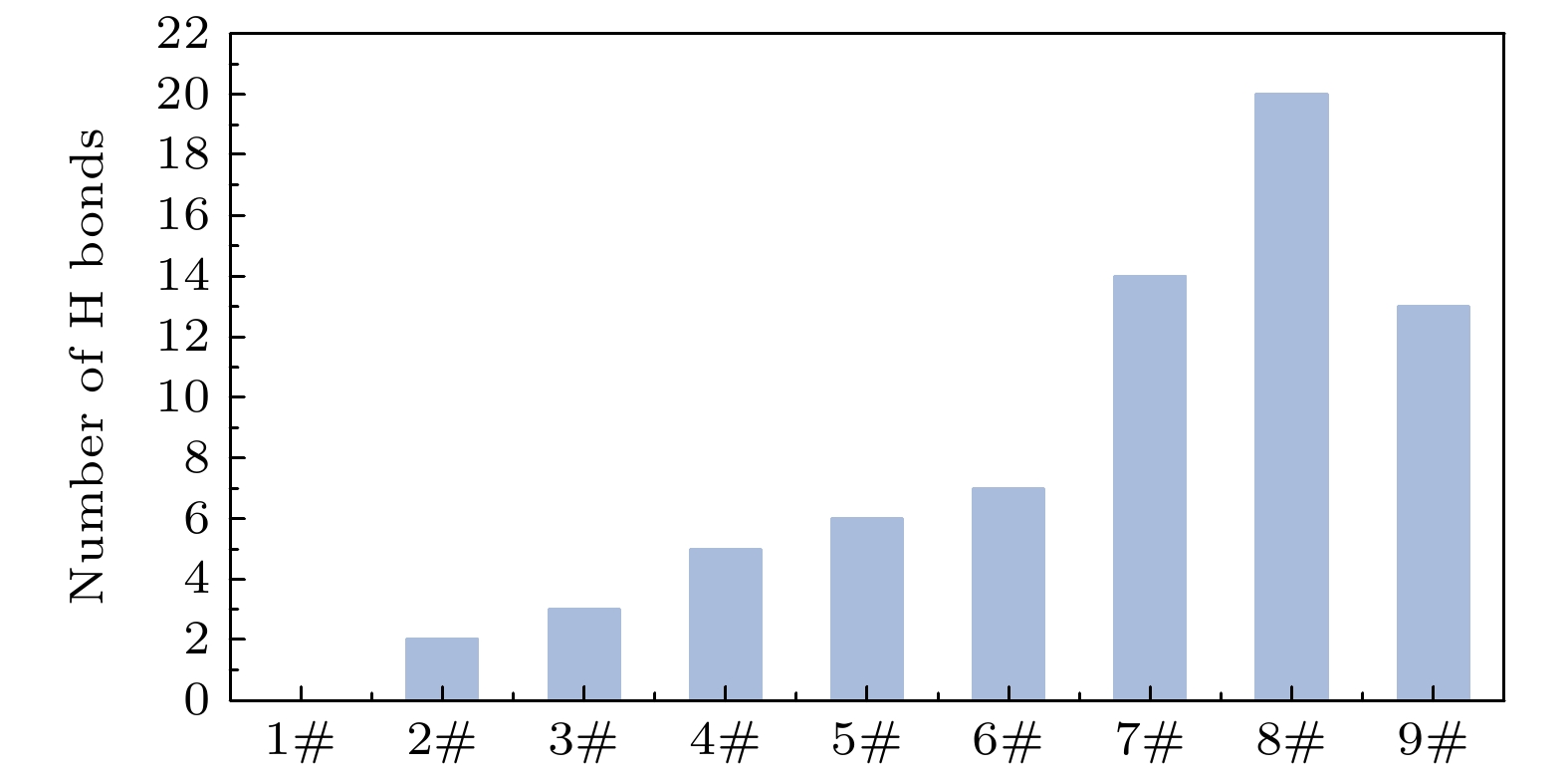
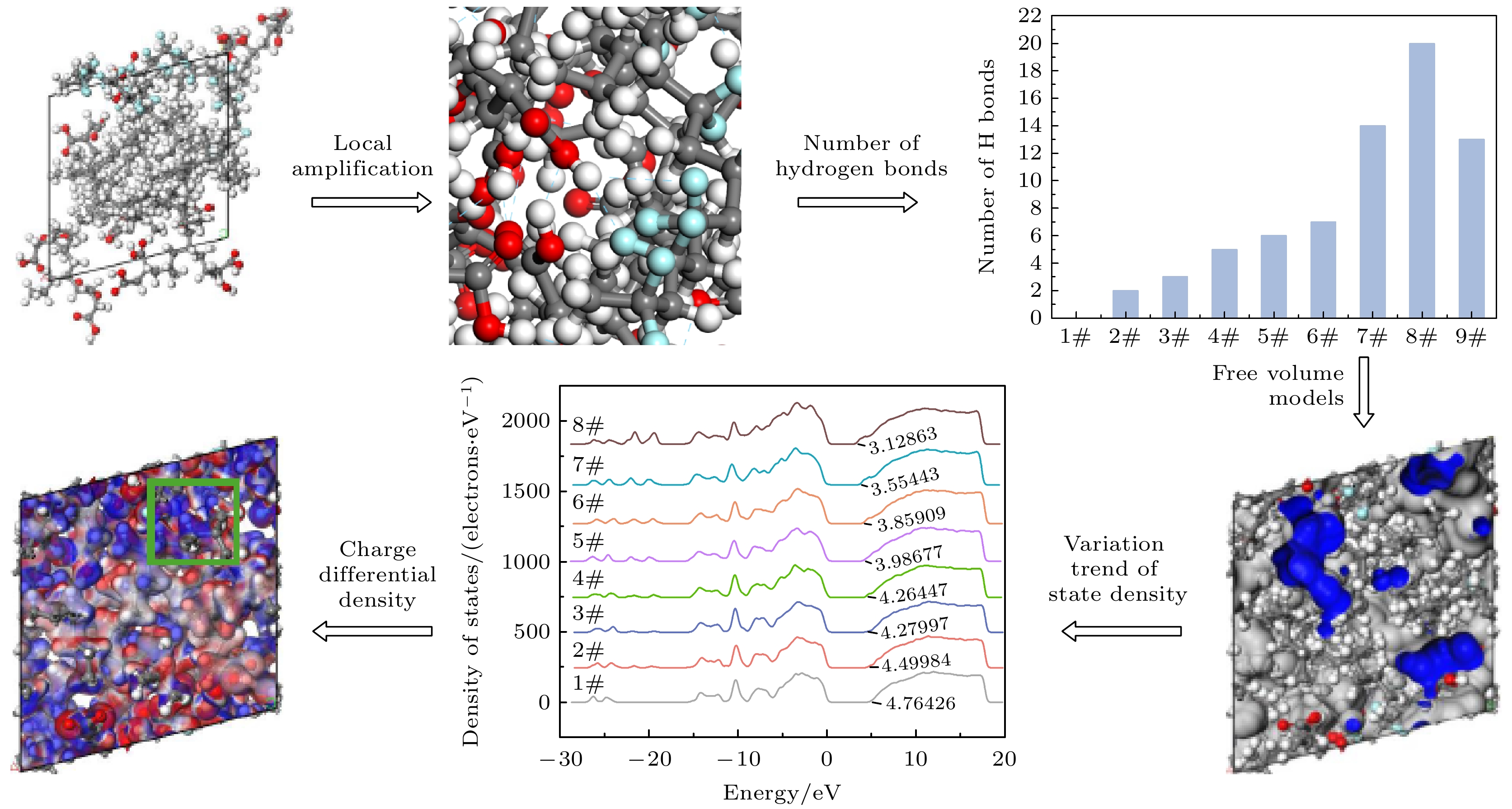
    • 基于Ferraris和Ivaldi[22]确立的氢键判据, 设定氢键键长≤3.5 Å, 键角≥135°. 在PP/PVDF复合材料分子结构中设定氢键形成的半径最大为3.5 Å, 形成的角度范围为135°—180°. 以9#为例, 通过仿真得到图4中氢键的位置图, 其中蓝色虚线表示PP/PVDF复合材料中形成的氢键. 由图4绿色方框中可以看出, 氟原子和氧原子与其周围的氢原子形成不同数量的氢键. 观察最终分子动力学平衡结构中PVDF上的氟原子和MA羟基上的氢原子形成氢键的过程, 记录氢键数量得到PP/PVDF复合材料在不同接枝率下的氢键数量关系如图5所示.

      通过图5可以看出: 随着MA质量分数的提高, 氢键数量从1#的0个逐渐增加到8#的20个. 这是由于分子中极性官能团数目增多, 使得与PVDF中氟原子形成氢键的氢原子数量增加. 在8#时达到极大值, 此时氢键的形成位点达到饱和. 但在9#处, 即MA质量分数达到52.97%时, 氢键数量降低到13个, 相比于8#时减小了35%. 分析产生上述规律的原因可能是由于以下几点.

      首先, 随着MA接枝含量的增加, MA分子中羧基的存在增强了空间位阻效应, 导致PP与PVDF分子间的堆积效应逐渐加剧, PP与PVDF分子间的距离变大, 这极大程度地限制了形成氢键的氟原子和氢原子间的相互靠近. 其次, 在PP与PVDF的体系中, 氟原子参与的氢键形成过程中出现氢原子过剩现象, 多个MA分子竞相争夺有限的氢键位点, 导致氢键位点达到过饱和状态. 最后, 由于原子间空间构型使C—F···H—O键角θ < 135°, 超出了临界范围, 因此无法形成有效氢键. 以上 分析说明, 随着MA质量分数的提高, 氢键的形 成位点增多, PVDF中氟原子和PP中氢原子形成氢键的概率增加. 然而, 当MA质量分数过高时, 空间位阻的作用效果增强, 氢键位点达到过饱和 状态, 反而导致PP/PVDF复合材料中氢键数量 减少.

      • 3.2.   能量分析

    • 由于氢键的作用, PP/PVDF复合材料中氟原子和氢原子之间产生新的键合, 导致分子间的作用能随之发生改变[23]. 因此对1#—9#试样进行相互作用能的模拟, 观察PVDF和PP的键合作用. 在Compass II力场下计算体系的势能, 得到PP/PVDF复合材料体系能量如表4所列.

      由表4数据分析可以得到以下规律: 首先, 分子间的范德瓦耳斯相互作用能从1#的84.65 kcal·mol–1增大到8#的132.42 kcal·mol–1. 这是由于氢键作用效果的增强, 导致PP与PVDF分子间的距离变小, 相互接触面积增多, 分子的色散能力变强. 但当MA接枝量达到9#时, 范德瓦耳斯相互作用能降低到55.29 kcal·mol–1减小了58.25%. 此时, 由于MA分子数过多, 阻碍了PP与PVDF分子间的有效接触, 使其接触面积减小, 导致分子间距离增大, 相互作用的效率降低, PP/PVDF复合材料体系变得更加不规则.

      其次, 静电相互作用能从1#的853.99 kcal·mol–1一直增加到9#的3377.36 kcal·mol–1. 这是由于静电作用能的强度与电荷量和分子间距离的平方成反比[24], 即使PP与PVDF因空间位阻的影响无法直接接触, 但它们仍能通过远距离发生静电作用.

      最后, 相互作用能从1#的53.49 kcal·mol–1增加到8#的127.05 kcal·mol–1后减小到9#的74.86 kcal·mol–1. 分析原因可能是: PVDF和PP分子链之间的相互作用能受到氢键作用效果、范德瓦耳斯相互作用能以及静电相互作用能共同影响. 尽管静电相互作用能显著地增加, 但其对总相互作用能的贡献仍弱于氢键与范德瓦耳斯作用, 无法抵消氢键和范德瓦耳斯相互作用能减弱所带来的负面影响, 因此相互作用能在9#时减小了41.08%.

      氢键数量的增加使PP/PVDF复合材料中出现了更多键合作用, 分子内部的范德瓦耳斯相互作用能、静电相互作用能、分子间相互作用能也随之增大. 因此各原子之间由于作用能的增加而彼此靠近, 复合材料的自由体积分布也会发生改变.

      • 3.3.   自由体积分布分析

    • 在氢键的作用下, PVDF中的氟原子和PP中的氢原子会相互靠近, 进而形成一种相对稳定的空间位置关系, 导致其结构和局部结构也会发生改变[25]. 为了更好地观察分析PP/PVDF复合材料的空间结构变化, 本文引入了自由体积参数来分析其变化规律. 自由体积反映了聚合物材料中分子链段的运动能力以及分子的空间结构状态. 自由体积的表达式如下[26]:

      式中, ${V_{\text{f}}}$为复合材料的自由体积, $ {V_{{\text{total}}}} $为复合材料的总体积, ${V_{{\text{occupied}}}}$为被原子或分子占据的空间体积. 自由体积越大, 分子链越容易产生移动和旋转, 分子的空间结构也就越疏松[27].

      PP/PVDF复合材料各编号下的自由体积如图6所示. 由图6可以观察到, 灰色部分为复合材料所占据的空间体积, 蓝色部分为复合材料的自由体积. 当氢键数量从1#增加到8#时, 蓝色部分所占据的空间逐渐减小, 此时分子结构更加紧密, PP/PVDF复合材料结构的自由体积减小. 但在MA质量分数达到52.97%时, MA侧链缠结形成局部团聚, 如图6(i)所示, 由于分子无序化程度增强, 自由体积增大, 蓝色部分占据空间变大, 使PP/PVDF复合材料的分子空间结构呈现先紧密后疏松的排布规律.

      为了更好地分析分子空间结构变化量及分子链段运动的自由空间, 通过计算自由体积分布来定量分析其变化规律[28]:

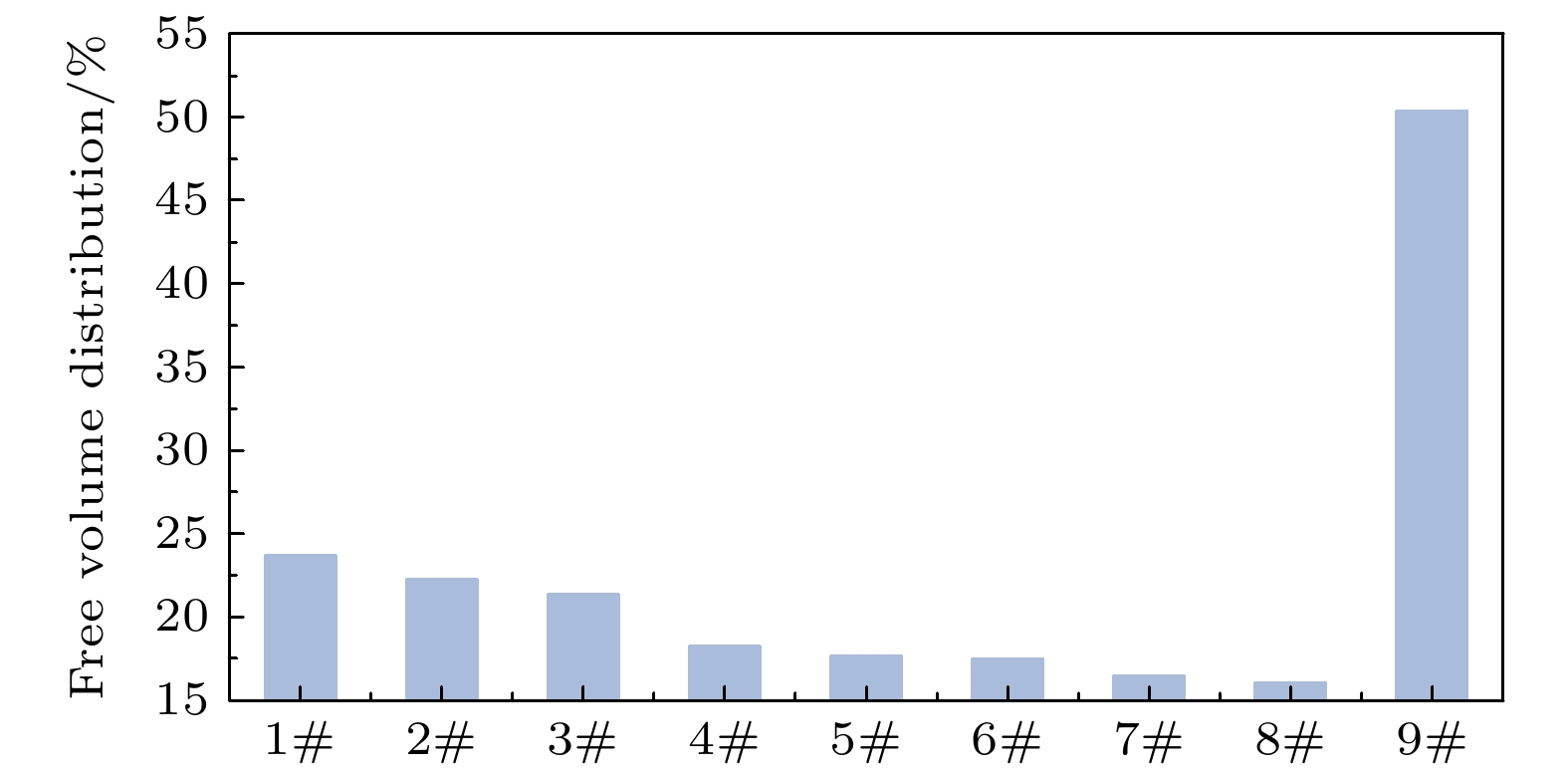
      式中, $ {f_{\text{v}}} $为材料的自由体积分布. 不同氢键数量下PP/PVDF复合材料的自由体积分布如图7所示. 从图7可以看出: 自由体积分布从1#的23.75%开始逐渐降低, 一直减小到8#的极小值16.03%, 减小了32.5%. 分析产生这种变化的原因是: 在PP/PVDF复合材料中, 氢键的作用使分子间产生新的键合. 随着PVDF中F原子与PP中H原子形成的氢键数量不断增多, 氢键的作用效果增强, 分子间距离不断减小, 分子的自由体积降低, PP/PVDF复合材料的空间结构逐渐变得紧密. 其次, 当MA质量分数超过36.22%时, 自由体积分布又增加到9#的50.64%. 这是由于空间位阻效应逐渐强于氢键对分子空间结构的作用, 导致分子链间距增大, 分子变得无序化, PP/PVDF复合材料的空间结构变得疏松.

      • 3.4.   HOMO-LUMO能级分析

    • 最高占据分子轨道(HOMO)与最低未占分子轨道(LUMO)的能级差(简称带隙)是分子电子结构的关键参数, 它反映了分子的电子跃迁难易程度、稳定性及反应活性[29]. 在聚合物和复合材料中, 氢键通过影响分子间的相互作用和体系中轨道的耦合方式, 使复合材料的电子态重新分布, 从而改变复合材料的HOMO-LUMO能级, 进而改变带隙[30].

      通过态密度在不同能量区间的分布, 可以观察到HOMO与LUMO能级结构的宽度、形状和位置. 态密度的计算公式如下[31]:

      式中, m为电子质量, E为电子所处能级的能量, h为普朗克常数. 随着空间结构中原子的排列和局部几何形状的变化, 原子间距也会变化, 进而影响PP/PVDF复合材料的电子相互作用, 从而影响HOMO-LUMO能级的形成及态密度的形态.

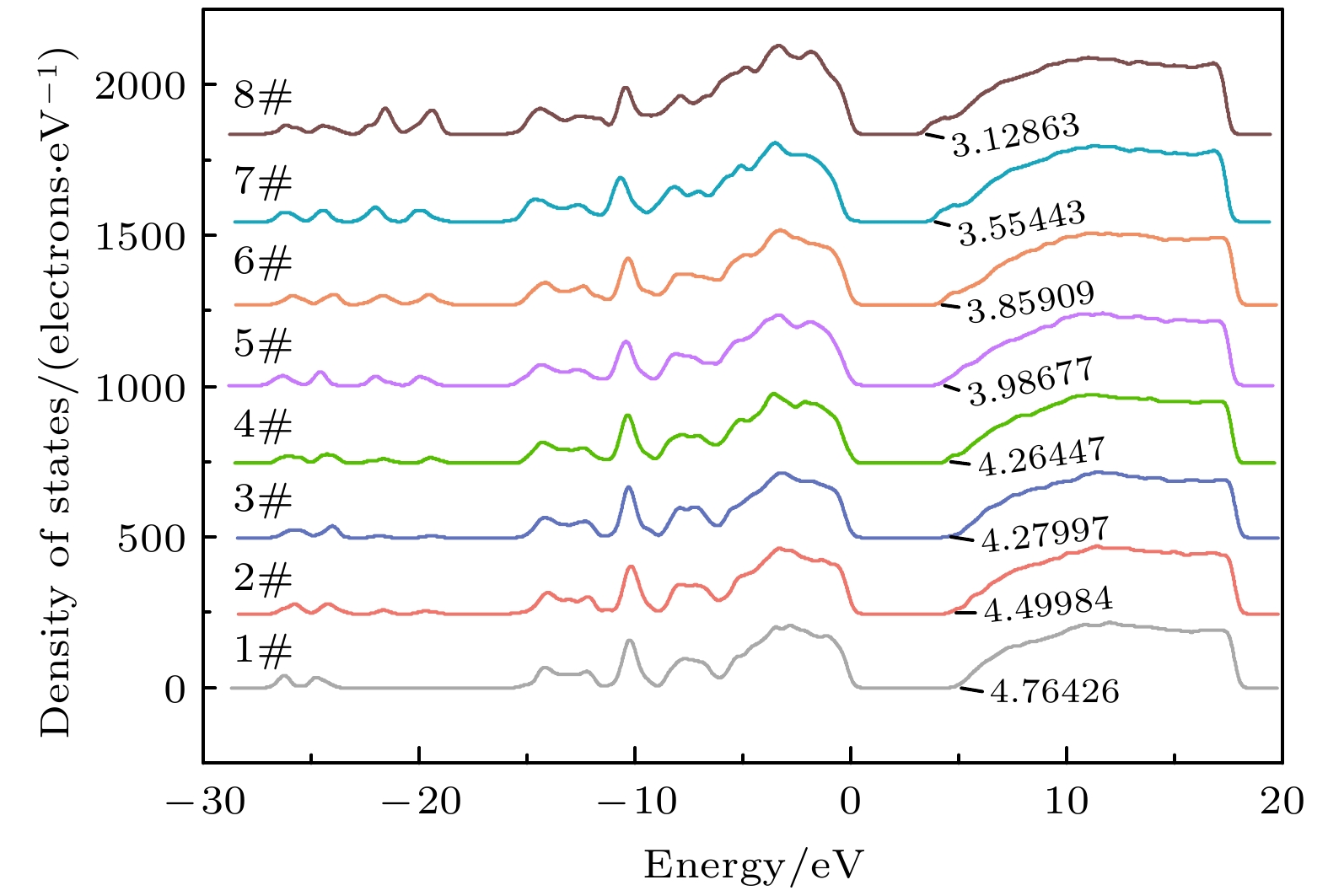
      参考Le等[32]对聚合物材料电子结构计算参数设置, 本文采用广义梯度近似下的Perdew-Burke-Ernzerhof泛函进行电子交换关联能的计算, 并将平面波基组的截断能设定为520 eV, 以确保能量收敛至1 meV/atom以内, 赝势选用投影缀加平面波. 通过仿真计算, 得到PP/PVDF复合材料的态密度(DOS)分布图如图8所示. 由于9#与1#—8#的变化规律相同, 因此只分析讨论1#—8#的模型数据. 从图8可以看出, 在0—5 eV的能量区间为PP/PVDF复合材料的带隙, 即带隙大小. 带隙从1#的4.76 eV开始逐渐减小, 一直减小到8#的3.13 eV, 减小了34.24%.

      分析原因可能是: 首先, 随着MA与PVDF之间形成的氢键数量增多, 更多的氢键使MA基团的π轨道与PP或PVDF的分子轨道发生重叠, 导致电子态的重新分布, 降低HOMO能级或提升LUMO能级的位置, 使态密度在0—5 eV区域的增强. 其次, 氢键的形成引起了分子间的电荷重组, 削弱了电子-空穴的激发能量, 从而降低体系的带隙, 使PP/PVDF复合材料的态密度图像的带隙逐渐减小.

      • 3.5.   电荷差分密度分析

    • 随着氢键数量的增加, 氢键的作用效果不断增强, 费米能级附近的态密度峰值逐渐增大, PP/PVDF复合材料带隙减小, 分子内部电荷差分密度也会发生变化[33]. 电荷差分密度指不同原子或分子之间的电荷分布差异, 反映了电子在不同区域的局部分布变化, 可以用来表示不同原子、分子或晶体位置之间的电荷差异. 电荷差分密度的计算公式为[34]

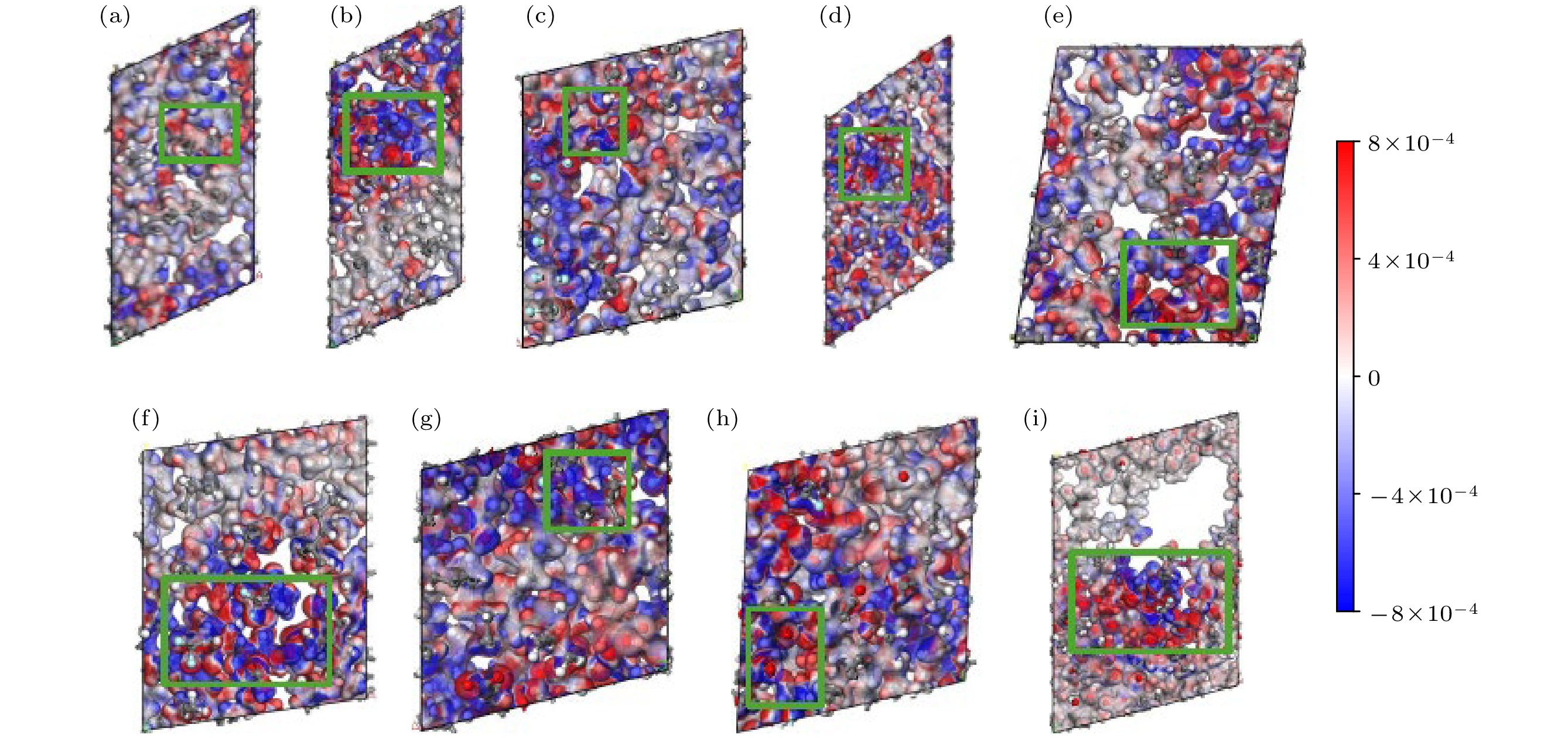
      式中, ${\rho _{{\text{AB}}}}$表示成键后体系的电荷密度, ${\rho _{\text{A}}}$和${\rho _{\text{B}}}$分别表示成键前原子A和原子B的电荷密度. 电荷差分密度可以用来研究PP/PVDF复合材料中氢键的相互作用. PVDF分子和PP形成的聚合物中, 通过电荷差分密度可以看出其分子间电荷密度分布的情况, 确定在氢键作用下的电子密度变化区域和程度.

      仿真得到PP/PVDF复合材料的电荷差分密度如图9所示. 由图9可以看出, 红色区域$\Delta \rho $>0表示电子积累, 蓝色区域$\Delta \rho $<0表示电子流失. 通过观察绿色方框区域可以看出, 氟原子周围呈现红色区域, 表示氟原子由于氢键的作用抢夺氢原子的电子, 原子周围呈现电负性. 而氢原子由于被夺得电子, 附近呈现蓝色区域, 使其周围电场为正电场. 分析原因可能是: 首先, 随着氢键数量的增加, PVDF中的氟原子与PP中的氢原子产生明显的电荷转移, 氟原子周围负电荷密度不断增加, 氢原子周围电荷密度不断减小. 体系中产生强的局部电场, 局部电子云发生重新分布, PVDF在形成氢键区域显示更高的电子密度积累. 其次, 氢键的形成会导致局部电子云的重新分布, 增强了材料局部区域的极性, 导致该区域的电子密度更高, 使氢键形成区域的电荷差分密度增大, 这些氢键作用区域的电子密度增加, 导致电荷的集中性不断增强, 局部电荷发生改变. 最后, 由于电子在氟原子周围集中形成“电荷岛”, 进而改变该区域的电荷差分密度. 但是在9#中, 由于空间位阻的影响, PP/PVDF复合材料中氢键数目减少, 导致自由体积分布增大, 分子结构变得疏松, 电荷差分密度减小.

      上述电荷分布重构所形成的局域高密度“电荷岛”不仅增强了界面区域的电子束缚效应, 同时诱导极性基团发生电荷重排, 形成具有高电子密度的区域结构. 此时产生的强局域电场具有双重效应: 一方面阻碍载流子有序迁移, 另一方面促进电荷在界面区域的聚集行为. 由于局域化电荷需克服更高能垒才能脱离束缚态, 因此载流子迁移路径的有效性受到显著抑制, 导致迁移率整体呈现下降趋势. 该现象与李盛涛等[35]在聚丙烯/氧化铝纳米复合材料中得出的结果具有一致性. 因此, 本研究结果进一步证实了空间电荷局域化对电荷输运的作用, 揭示了局域电场对电荷迁移路径的空间调控机制.

      • 3.6.   陷阱能级分析

    • 随着PP/PVDF复合材料中氢键数量的增加, 分子的空间电荷分布发生改变, 进而导致电荷陷阱能级发生变化. 陷阱能级反映了复合材料的局部能级状态、材料中局部分子间作用或极性基团对电子和空穴的捕获能力, 以及材料电学和光学行为的微观机制. 它描述了电子从材料的导带或空穴从价带被束缚在特定能级的现象, 体现了材料的局部结构特征和电场分布. 通过分子动力学与密度泛函理论相结合的方法, 计算了PP/PVDF复合材料体系内的电荷陷阱能级. 分子中电子的总能量${E_{\text{v}}}{\text{ }}[\rho ]{\text{ }}$为[36]

      式中, $\rho $为系统基态总电荷密度, $ {E_{\text{t}}}[\rho ] $为电子动能, $ {E_{\text{j}}}[\rho ] $为电子间库仑相互作用能, $ {E_{{\text{xc}}}}[\rho ] $为电子间交换关联能; $ {V_{{\text{ne}}}}(r)\rho (r){\mathrm{d}}r $为原子核库仑势. 根据国家辉[37]的仿真结果, 电介质陷阱深度即为聚合物分子导带底部的能量减去陷阱能级的能量:

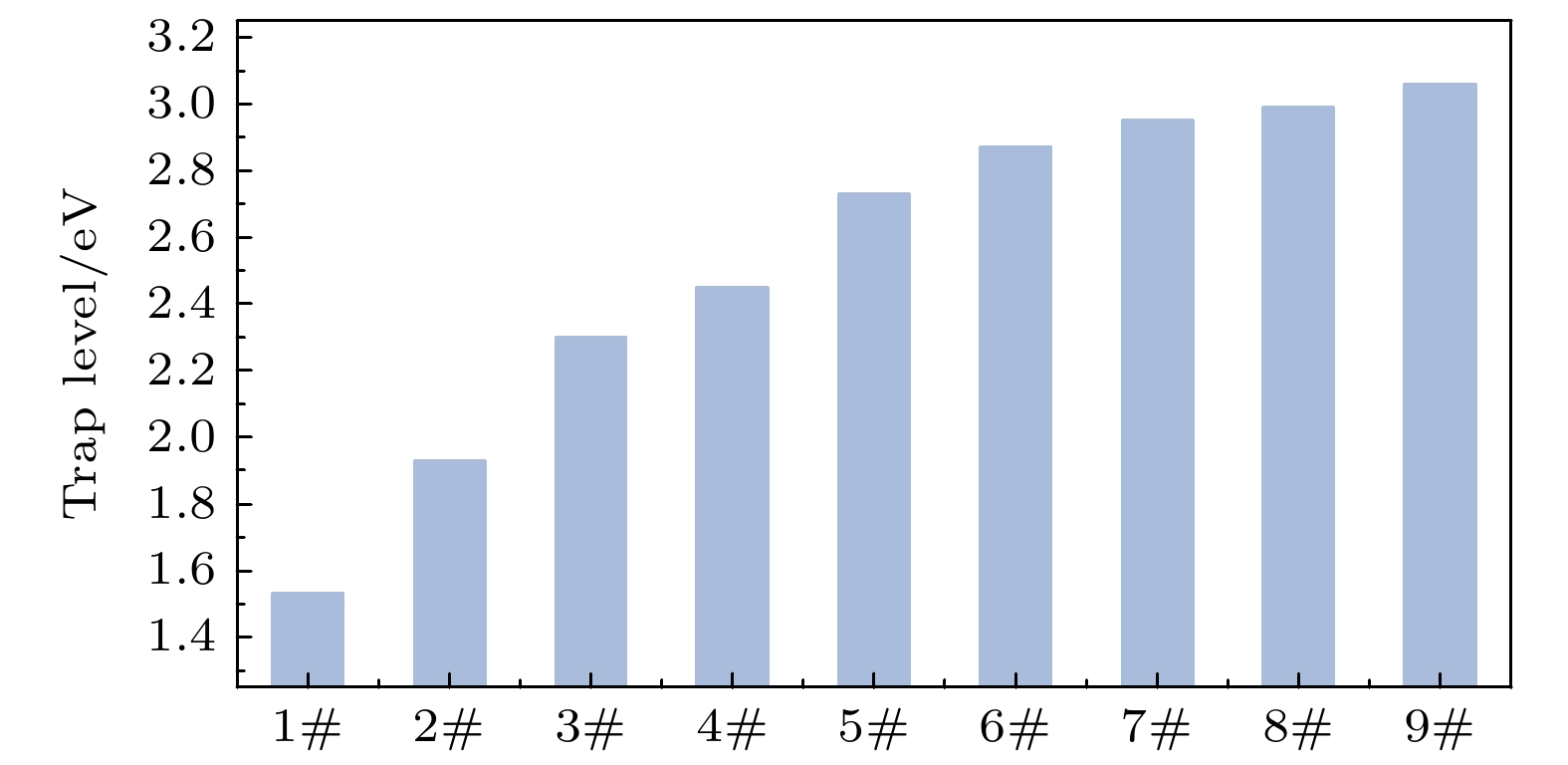
      式中, $ E(A) $为中性分子的平衡几何结构的总能量, $ E({A^ - }) $为中性分子在平衡几何结构情况下带一个负电荷的阴离子分子的总能量. 计算得到的PP/PVDF复合材料陷阱能级如图10所示.

      由图10可看出, 陷阱能级深度从1#的1.53 eV迅速增加到7#的2.95 eV, 增幅达92.81%. 分析原因可能是: 首先, 氢键的形成使PP/PVDF复合材料的自由体积减小, 导致分子链局部排列更加紧密或有序, 这种有序化产生了新的界面或缺陷, 成为电荷捕获中心, 加深了陷阱能级深度. 其次, 在PP/PVDF复合材料体系中, 由于氢键是一种较强的非共价相互作用, 它能够引起电子云的局部重排, 从而影响电子态的分布. 这种局部化效应会改变电子的运动性, 使得电子更容易被捕获到陷阱态中, 导致陷阱能级增加. 再次, 氢键通过局部电子重排影响HOMO能级与LUMO能级区域的电子密度, 使材料中的局部电子态变得更加密集, 陷阱能级更靠近能级差的中心. 局部电荷的重新排列使得电子更难以从这些陷阱中逃逸. 最后, 氢键增加了PVDF氟原子周围的电荷差异, 从而在PP/PVDF复合材料内部形成更多的陷阱态. 这些陷阱态降低了电子的迁移和捕获效率, 导致材料陷阱能级迅速增大.

      在7#—9#变化过程中, 陷阱能级深度从2.95 eV缓慢增加到3.06 eV, 增幅仅为3.73%. 这是由于随着体系中可以形成氢键的极性基团逐渐耗尽, 氢键数量趋于饱和, 此时新增的陷阱能级主要由原有氢键的动态重组(如断裂与再形成)贡献, 而非新键的生成, 导致增长速率下降. 另外, 当接枝率增加到一定程度后, 氢键数量接近饱和. 此时, PP/PVDF复合材料中的局部电场逐渐增强, 但陷阱形成的效率减弱, 材料内部的极性和局部缺陷趋于稳定, 陷阱态逐渐达到上限, 因此陷阱能级深度的增加量逐渐减小.

      从整体上看, PP/PVDF复合材料陷阱能级的增加, 使得复合材料对自由载流子的捕获能力增强, 显著延长自由载流子的捕获时间, 阻碍电荷的长程迁移过程, 进而导致载流子迁移率的整体下降. 这与彭向阳等[20]在硅烷接枝聚丙烯复合材料中得到的有关陷阱能级与电荷迁移率关系具有一致性, 揭示了陷阱能级与电荷输运的关系, 表明陷阱能级的调控是影响聚合物复合材料电荷输运特性的关键因素.

    4.   结　论

    • 通过对PP/PVDF复合材料进行分子动力学模拟, 探讨氢键对其自由体积和局部电荷分布的影响, 并从分子结构角度对电荷输运特性进行研究, 可以得到以下结论:

      1)氢键的分析表明, 当氢键的数量达到极大值20个时, 此时分子间的范德瓦耳斯相互作用能与分子间的相互作用能均达到最大值, 分别高达132.42 kcal·mol–1和127.05 kcal·mol–1, 表明PP/PVDF复合材料内氢键数量达到饱和状态.

      2)自由体积分布的分析表明, 当MA质量分数为36.22%时, PP/PVDF复合材料的自由体积分布达到极小值16.03%, 此时分子内部结构最为紧密. 但随着MA含量的增多, 由于空间位阻的影响, 分子间距离变大, 自由体积分布增大, 分子趋于无序化, 空间结构变得疏松.

      3)电荷输运特性的分析表明, 氢键的引入使PP/PVDF复合材料中原子之间的相互作用发生变化, 引起电子云的局部重排. 随着氢键数量的增加, 带隙达到极小值3.13 eV, 陷阱能级达到极大值3.06 eV. 此时, PVDF在形成氢键的区域显示出更高的电子密度积累, 使PP/PVDF复合材料对自由载流子的捕获能力增强, 显著延长自由载流子的捕获时间, 阻碍电荷的迁移, 导致载流子迁移率整体下降.

    参考文献 (37)

目录

/

返回文章
返回