-
随着人类社会的演进与发展, 城市规模持续扩张, 其空间结构与功能体系日趋复杂, 已成为承载人类文明演进的重要物理载体[1]. 我国城镇化率已超过65% (2024年统计数据), 随着城市化进程的加快, 城市内部的人口流动日益频繁, 如何科学有效地理解和预测人口流动特征和规律, 已成为城市规划和公共政策的重要议题[2,3]. 它不仅直接影响着城市的经济发展、资源配置及城市结构的优化[4-7], 同时也关乎城市居民的生活质量和社会稳定[8-12].
针对移动流量生成和预测的研究方法主要有基于统计物理和深度学习两类. 前者通过建立可解释的数学模型来描述人类移动规律, 其参数物理意义明确且具有小样本稳定性优势. 然而, 这类方法难以捕捉复杂的非线性时空依赖关系, 对突发事件的适应性较差[13]. 相比之下, 后者依托长短时记忆网络(LSTM), 图卷积网络(GCN)等深度学习框架, 通过自动提取时空特征实现预测精度突破, 在捕捉时空动态演化模式方面具有显著优势[14-17], 但其可解释性缺失与数据依赖性制约了在实际场景的应用[18].
在统计物理方法中, 引力模型和介入机会模型形成分野. Zipf[19]提出的引力模型将人口流动类比牛顿引力定律, 建立流量与人口正相关、与距离负相关的解析式, 广泛应用于交通规划[20,21]、空间经济[22,23]、传染病扩散[24]等场景. Stouffer[25]提出空间交互的介入机会模型, 认为距离和流动性并不直接相关, 决定人口流动的关键因素是介入机会的数量. 虽然介入机会模型从个体依序决策过程为构建新模型开启了新角度, 但在城市尺度应用中仍存在系统性偏差[26].
引力模型和介入机会模型都存在待估计参数, 这推动研究者从个体决策视角重构空间交互机制, 通过引入目的地选择的行为经济学假说, 摒弃了传统距离衰减函数, 构建出更具普适性的介入机会类模型, 如辐射模型[27]、人口权重机会模型[28]、机会优先选择模型[29]、统一机会模型[30]、目的地选择博弈模型[31]等. 作为该领域的里程碑, 辐射模型假设个体会选择最近且收益高于起点的目的地. 但其概率选择机制导致系统性预测偏差, 低估了长距离出行的比例. 而人口权重机会模型提出了一种新的目的地机会衰减机制, 并考虑了城市的有限尺寸效应, 克服了辐射模型不完全适用城市尺度的不足. 目的地选择博弈模型考虑了个人之间的空间相互作用所带来的拥挤效应, 并提供了一种推导引力模型的替代方法, 证明引力模型是该模型退化的平衡解决方案, 忽略了目的地的拥挤效应.
在过去半个世纪, 既有研究开展了大量模型对比实证[32-39]. 但方法论缺乏对模型多尺度的评价, 存在显著局限: 一是空间划分粗放, 主要研究跨城市与城市内部两个尺度上的模型效果; 二是分析维度单一, 通过计算全局精度指标与拟合概率分布曲线评估模型性能, 局限在模型的整体表现; 三是结论存在分歧, 尽管部分研究支持辐射模型在跨城市预测中的优势[40], 但另一些研究则指出引力模型在小尺度城市内部场景的适用性更佳[41-43], 这种粗粒度的评估范式未能系统揭示模型性能对空间、距离和人口尺度的敏感性机制, 难以适应现代都市圈多中心、高混合的功能格局.
为了分析不同模型在城市内部的使用范围和效果, 本文提出跨尺度比较方法, 基于城市结构的空间、距离、人口三个尺度, 选取了经典的引力模型、辐射模型、人口权重机会模型, 通过设计三组控制实验系统揭示模型性能的尺度依赖性, 分析模型在城市内部不同尺度下的性能和适用范围, 最后通过多因素方差分析(MANOVA)分解各变量对预测误差的贡献度. 这些研究对于城市内部流量的生成和预测有着重要的意义, 进而为改进模型提供数据支持.
-
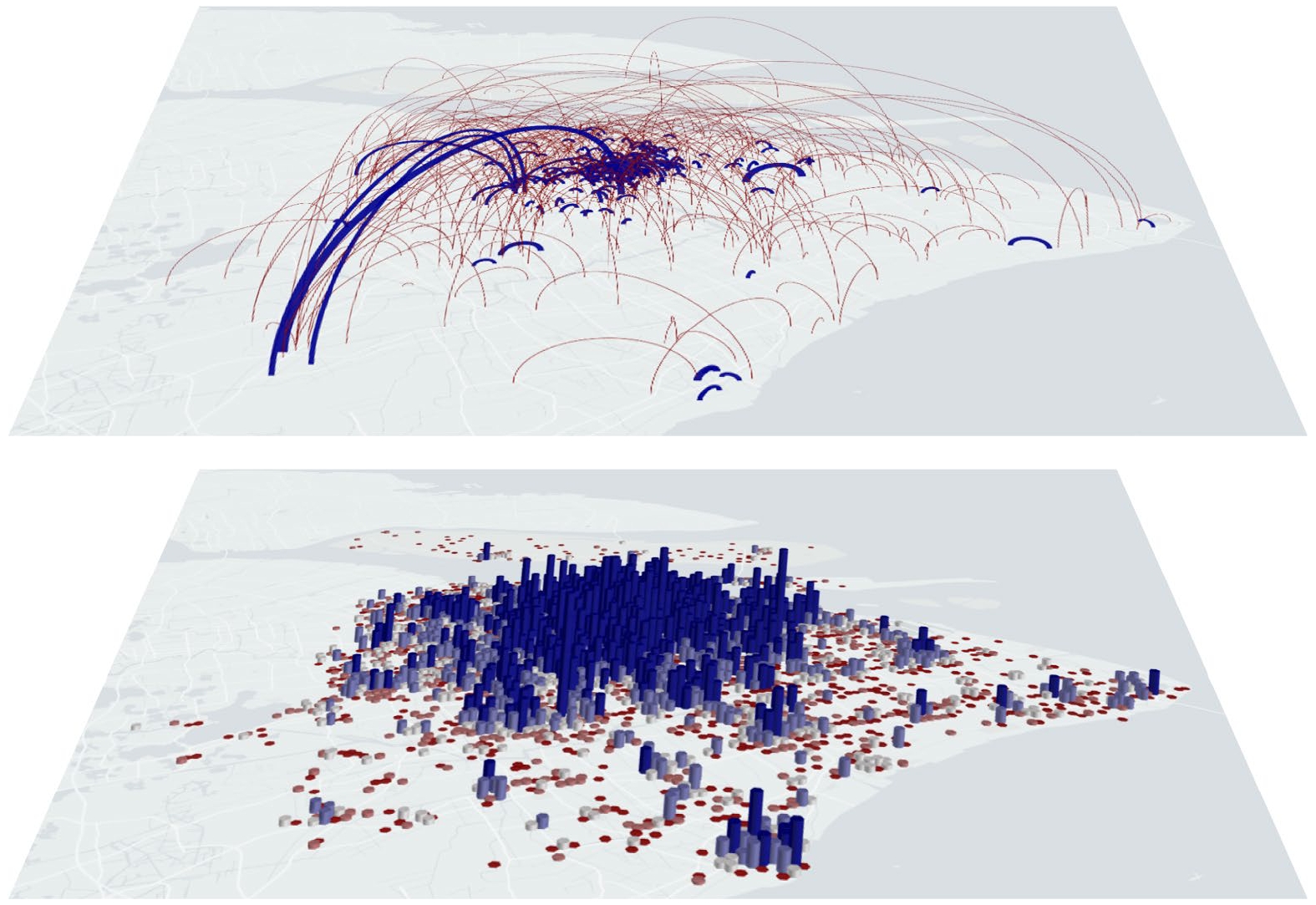
本研究采用中国某电信运营商提供的匿名化手机信令数据集, 采集时间窗口为2022年2月15—28日. 以上海市全域为研究范围, 基于GIS平台构建1 km × 1 km规则网格体系(WGS84坐标系), 通过两重过滤机制确保数据有效性: 1)空间过滤: 剔除持续无信号基站覆盖区域; 2)流量过滤: 排除流动量为0的网格单元. 最终形成包含6674个有效空间单元的研究样本集. 如图1所示, 基于样本集展示了上海市的人口及流量分布.
-
引力模型(gravity model, GM)源于经典的牛顿引力理论, 是运用最广泛的流量模型. GM模型认为两地之间的流量和地区人口数量成正比, 而与距离成反比, 最常用的GM模型可表示为
其中,
$ T_{ij} $ 是地点i到地点j的流量;$ m_i $ 和$ m_j $ 分别是两地的人口数量; 参数α是一个常数, 反映了模型的整体规模;$ \tau_1 $ 和$ \tau_2 $ 是与地区特性相关的指数;$ d_{ij} $ 是两地之间的距离; β则表示距离的影响程度.GM模型的优势在于简单性和易于理解, 使得研究者能够快速估算流量. 然而, 该模型也存在局限性, 例如未能充分考虑移动目的地选择过程中的其他社会经济因素. 因此, 研究者们相继提出了多种模型, 如介入机会模型等, 以更全面地捕捉人类行为及其流动模式.
-
辐射模型(radiation model, RM)是一种介入机会模型, 假设个体基于工作收益和通勤长度选择工作地点. 在Simini等[27]提出的基本模型中, 个体会综合评估确定性收益和随机性收益, 并优先选择离家最近且总期望收益超过居住地最佳工作机会的就业地点. 该模型将个体视为从居住地i发射并具有吸收阈值
$ z_{{X}}^{(i)} $ 的粒子X. 个体从居住地i出发, 被目的地j吸引的概率为其中,
$ s_{ij} $ 是以居住地i为圆心, 以$ d_{ij} $ 为半径的圆内的人口数, 不包含居住地和目的地的人口;$ P_{m_i}(z) $ 是经过$ m_i $ 次试验后, 从分布$ p(z) $ 中提取的最大值等于z的概率;$ P_{s_{ij}}( < z) $ 表示距离$ d_{ij} $ 之间的所有位置的吸收阈值都小于z,$ P_{m_j}( > z) $ 表示目的地j吸收阈值大于z.因此, (2)式可写为
从出发地i到目的地j的流量可以表示为
其中,
$ T_i $ 是出发地i的总出行流量. -
人口权重机会模型(population-weighted opportunities model, PWO): PWO模型在RM模型的基础上, 考虑了个体的选择会受到两地之间距离成本的影响. 假设目的地的吸引力与以目的地为中心、半径为
$ r_{ij} $ (起点i和终点j之间的距离)的圆形区域内人口$ S_{ij} $ 成反比, 并减去有限大小校正$ {1}/{M} $ , 目的地j对出发地i的相对吸引力为其中,
$ o_j $ 是目的地的总机会数; M是城市的总人口数;$ S_{ji} $ 是以居住地i为圆心, 以$ d_{ij} $ 为半径的圆内的人口数, 并且包含居住地和目的地的人口. 假设出发地到目的地的流量与$ A_j $ 成正比, 且$ o_j\propto m_j $ , 则从居住地i到目的地j的流量可以表示为 -
本文选择改进的Sørensen相似系数(common part of commuters, CPC)[44,45]来评估各模型的表现, 指标通过计算预测流量
$ y^{\mathrm{g}}\left(l_i, l_j\right) $ 和实际流量$ y^{\mathrm{r}}\left(l_i, l_j\right) $ 的相似性来衡量算法的效果, 相似度越高数值越接近1, 其计算公式为其中
$ y^{\mathrm{g}}\left(l_i, l_j\right) $ 为预测流量,$ y^{\mathrm{r}}\left(l_i, l_j\right) $ 为真实流量.变异系数(coefficient of variation, CV)用于衡量数据的离散程度(波动性), 计算公式为
其中, μ表示均值(mean), σ表示标准差(standard deviation).
相对变化幅度(Δ)量化不同尺度或条件下的指标差异, 其定义为
其中,
$ V_{\text{old}} $ 和$ V_{\text{new}} $ 分别表示初始值与变化后的值.$ \varDelta > 0 $ 表示增长幅度,$ \varDelta < 0 $ 表示下降幅度. -
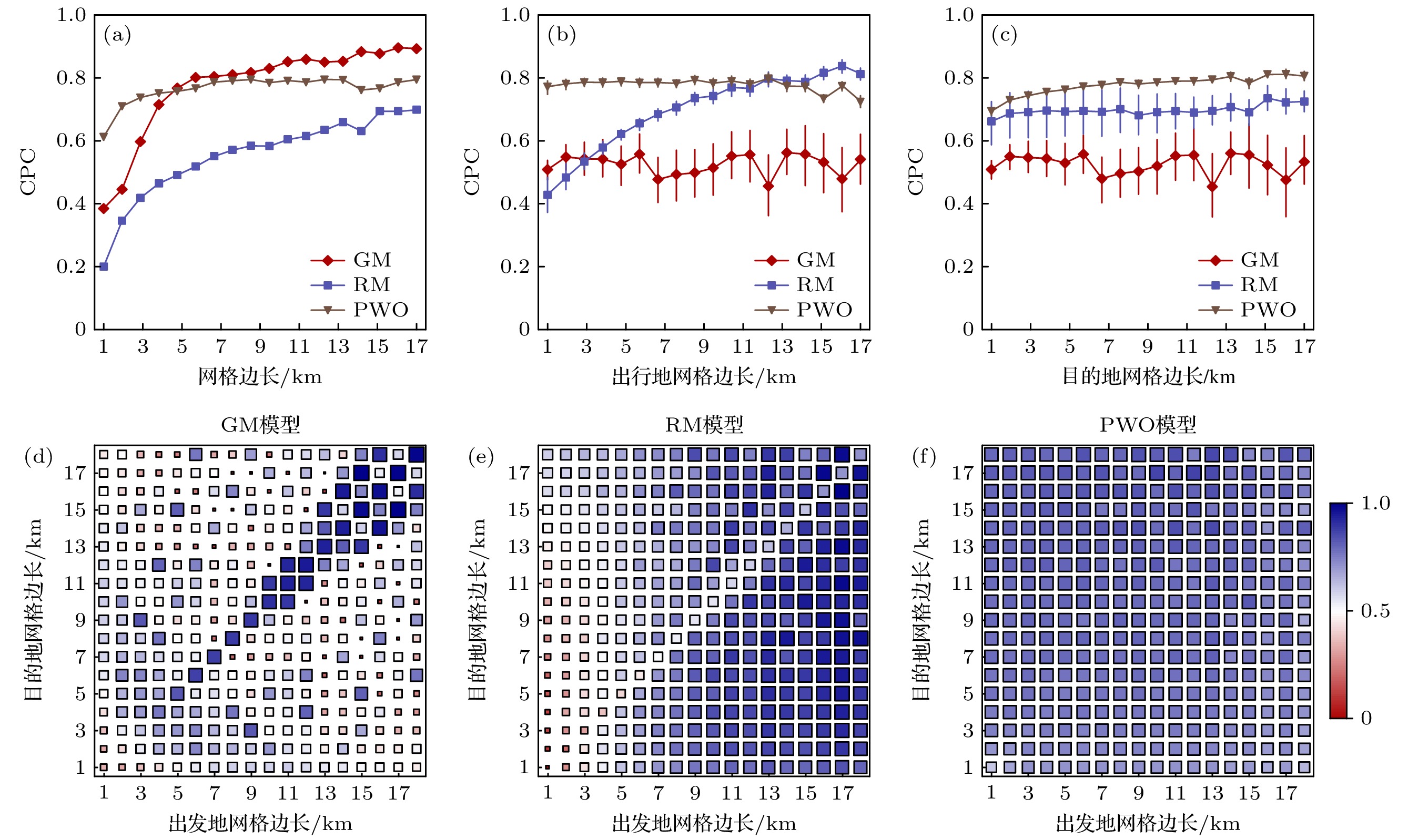
为系统评估出发地和目的地区域面积对模型性能的尺度影响, 本文构建多级网格划分框架: 基于上海市地理空间特征, 设置1 km × 1 km至18 km × 18 km的网格尺度范围(18 km为平均通勤距离的2倍), 计算CPC指标值, 对比分析GM模型、RM模型及PWO模型在不同空间尺度下的预测性能(图2).
当出发地与目的地网格尺度等比例扩展时(1—18 km), 三类模型呈现显著差异的尺度响应模式(图2(a)). 在小尺度范围(< 5 km), GM模型和RM模型的预测能力随尺度扩大而迅速提升, 其中GM模型在5 km尺度时, 其CPC值较1 km基准提升100% (0.32→0.64), RM模型提升135%(0.26→0.61); 而PWO模型表现出尺度不敏感性, 其CPC值仅从0.61微增至0.69 (Δ = 13%). 这种提升很大程度上和空间异质性相关, 在较小的网格空间尺度下, 网格属性结构差异更为显著, 传统模型在基于空间均质假设的前提下, 容易受到空间异质性的影响. PWO模型通过目的地人口权重机制, 有效缓解了细粒度划分导致的空间异质干扰. 不同模型受区域面积的影响程度也不一致, 当网格边长小于5 km时, GM模型效果低于PWO模型, 当网格边长超过5 km后, GM模型的表现逐渐超越PWO模型, 并且其预测能力随区域面积的进一步增大持续增强.
图2(b)和图2(c)揭示了单侧尺度变化的影响机制: GM模型与PWO模型具有尺度鲁棒性, CPC值分别在0.53 ± 0.04 (CV = 5.7%)和0.78 ± 0.01 (CV = 2.6%)区间波动. 与之形成鲜明对比, RM模型表现出空间不对称性——出发地尺度扩大使CPC值从0.42提升至0.78 (Δ = 85%), 而目的地尺度变化仅引起0.02 (CPC = 0.70)的微弱波动. 这表明RM模型“最近最佳机会”选择机制在小尺度出发地场景存在理论缺陷.
图2(d)—(f)的热力图进一步解析了双向尺度交互效应. GM模型对空间尺度差异最为敏感: 当出发地-目的地尺度差超过3 km时, 其CPC值下降40% (从0.75降至0.45), 这源于其理论框架的几何假设缺陷——将区域简化为点状质心, 忽视了面积差异引起的等效距离畸变(如18 km × 1 km矩形区域的质心偏移误差可达2.3 km). 反观PWO模型展现出优异的尺度兼容性, 验证了人口权重机制在平衡空间异质性方面的有效性. 值得注意的是, 既往研究多采用等尺度划分方法, 这导致对GM模型预测性能的高估误差达31% (以5 km × 5 km尺度为基准).
-
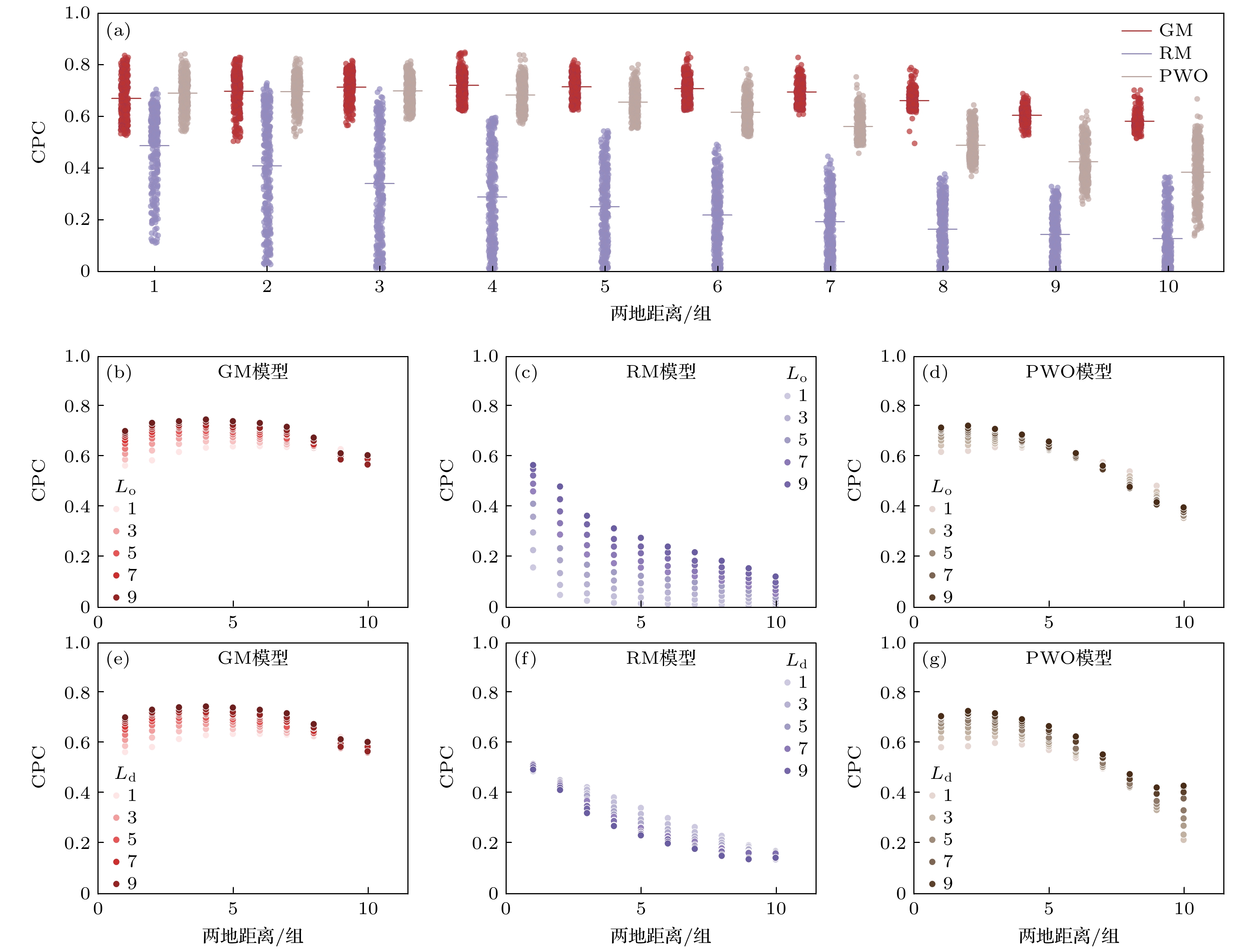
为了衡量出发地和目的地之间距离对模型性能的尺度影响, 本研究采用分位数分组法构建多尺度分析框架: 将出行距离按十分位数划分为10个区间, 通过CPC值评估三种模型在不同组别下的预测性能. 图3揭示了三类模型的距离敏感特性及其空间-距离尺度交互效应.
三类模型的CPC均值随距离增加呈下降趋势, 但衰减模式存在本质差异(图3(a)): GM模型表现出距离鲁棒性, 其CPC值从0.67平缓降至0.60, 衰减率仅10.4%; RM模型与PWO模型则呈现非线性衰减, RM模型CPC值剧降63% (0.49→0.18), 而PWO模型下降41% (0.68→0.40). 这种差异源于理论架构的本质区别——GM模型的距离衰减函数具有全局连续性, 而机会类模型的机会筛选机制在长距离场景存在选择偏误.
图3(b)—(d)揭示了空间尺度和距离尺度的交互效应, 分别展示了三种模型在不同区域面积下距离对模型效果的影响. 如图3(b)和图3(e)所示, GM模型随着距离尺度增加, 模型效果受空间尺度变化的影响降低, 当在大距离(组别9, 10)时, 基本不受区域面积变化的影响, 而在小距离(组别1, 2)时, 模型预测CPC差值接近0.2. RM模型出发地和目的地区域的空间尺度和距离尺度呈现相反的交互效应. 在相同距离上, 出发地面积越小, 模型效果越差, 而目的地面积越大, 模型效果越差. 当距离尺度组别
$ \leqslant $ 5时, PWO模型的效果随着出发地空间尺度增大而增强, 但是当距离尺度组别>5时, PWO模型的效果随着出发地空间尺度增大而削弱. -
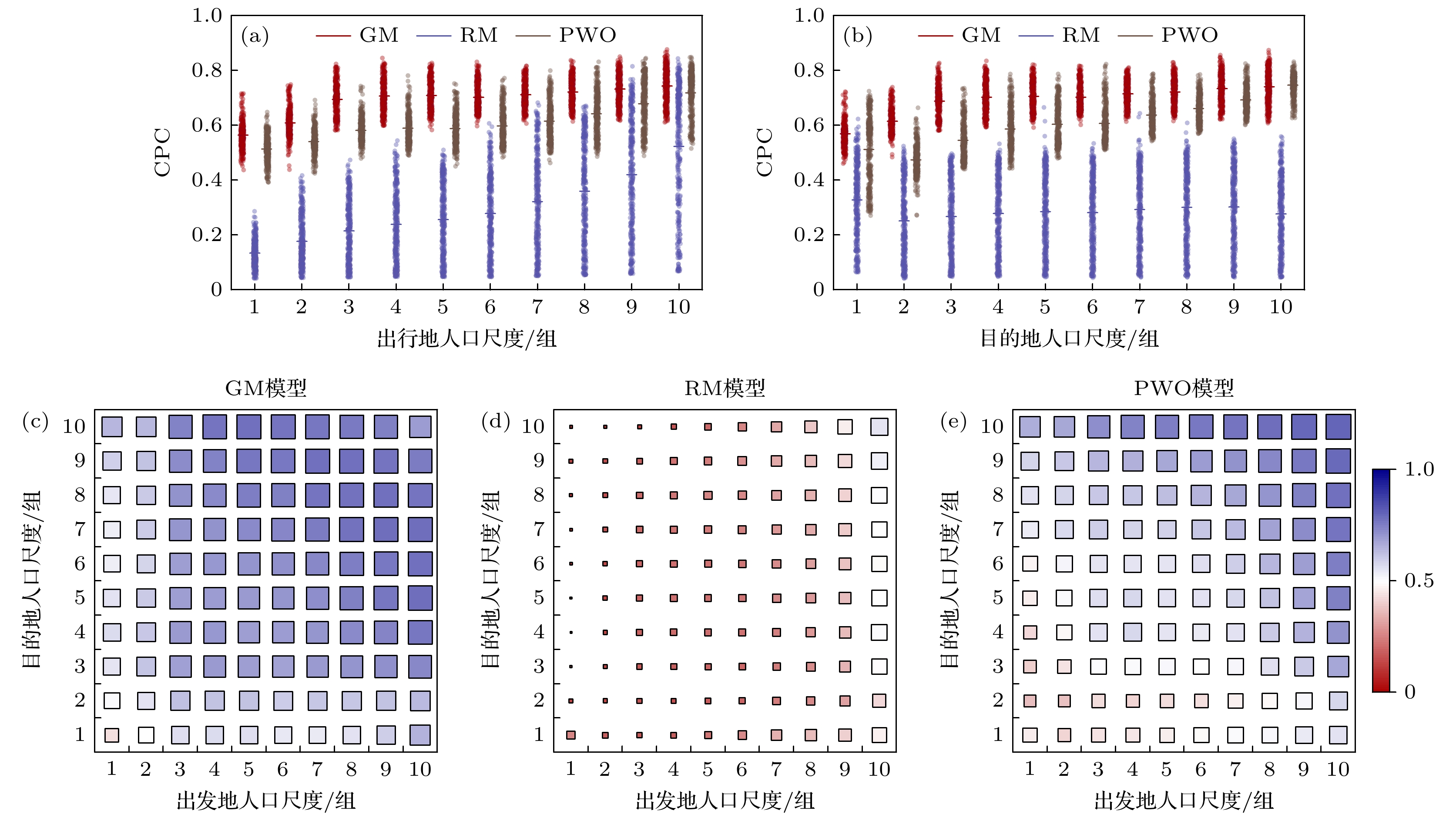
为了衡量出发地和目的地的人口密度对模型性能的影响, 本研究采用分位数分组法, 将出发地和目的地人口密度按照十分位数划分为10组, 求解三种模型在不同组别下的预测流量, 并计算CPC指标值.
相比于RM模型和PWO模型, GM模型在人口密度尺度上表现出更好的稳定性和预测效果. 如图4(a)和图4(b)所示, GM模型在各组的CPC指标值均在0.75附近, 在各组别CPC均值上均高于RM模型和PWO模型. 在图4(c)中也显示了GM模型在人口密度尺度下的稳定性, 在出发地和目的地人口密度尺度均大于3时, GM模型的效果几乎不受人口密度的影响.
介入机会模型(RM模型和PWO模型)受人口密度的影响较大, 在低人口密度情况下表现出明显的性能下降, 并且受到出发地和目的地人口密度的不对称影响. RM模型呈现强出发地密度依赖性, 在图4(a)中, RM模型的效果随着人口密度的增加而显著线性增加(最低组CPC值0.16, 最高组CPC值0.55); 但在图4(b)中, RM模型的效果并没有随着目的地人口密度的变化而变化, 结合3.1节中RM模型表现出受出发地格子尺度影响而不受目的地各自尺度影响的现象, 我们发现RM模型对出发地和目的地区域面积和人口密度尺度上表现出明显的不对称性, 模型效果受出发地的影响更大, 却基本不受目的地人口尺度的影响. 而PWO模型的效果随着出发地和目的地人口尺度的增大呈稳定线性增长趋势.
-
为了研究不同模型的适用场景及其对预测结果的影响, 本文基于多因素方差分析, 评估空间尺度(出发地面积、目的地面积)、距离尺度、人口尺度(出发地人口密度、目的地人口密度)三类五因子的主效应与交互作用. 本研究选取了出发地与目的地边长为1—18 km范围内的场景, 同时将人口密度和两地距离分为10组, 共生成225000个样本进行分析, 因变量为三种出行预测模型的CPC指标值.
分析结果表明, 五个因素对模型性能均具有显著影响(p < 0.001), 但各因素对三种模型的重要性和贡献存在显著差异(表1).
GM模型受人口密度主导. 对于GM模型, 人口密度对模型效果的影响最大, 其中出发地人口密度和目的地人口密度的F值分别为65161.60和61262.78. 此外出发地面积(F = 9010.36)和目的地面积(F = 10912.67)的主效应及其交互作用(F = 9073.67)同样显著. 尽管两地距离的效应在统计上显著(F = 688.56), 但相对作用远小于其他因素. 这表明GM模型更依赖人口密度和区域面积等核心特征.
RM模型呈现出发地驱动特征. 出发地面积对模型性能的影响最大, F值高达604629.24, 两地距离和出发地人口密度则紧随其后, F值分别为321208.57和179437.14. 相比之下, 目的地相关的因素对模型的影响较小, 目的地面积和目的地人口密度的F值分别为58721.23和1587.65. 表明RM模型对出发地的属性更为敏感, 而目的地属性对模型预测效果的影响相对较弱.
PWO模型表现出目的地敏感特性. 目的地面积和目的地人口密度的F值分别达到38511.97和127280.61, 显著高于出发地面积(F = 180.40)和出发地人口密度(F = 20934.69). 此外, PWO模型对两地距离的敏感性最强, F值最高, 为262932.37. 这一结果表明PWO模型更适用于以目的地吸引力为核心的场景分析, 同时受区域距离属性显著影响.
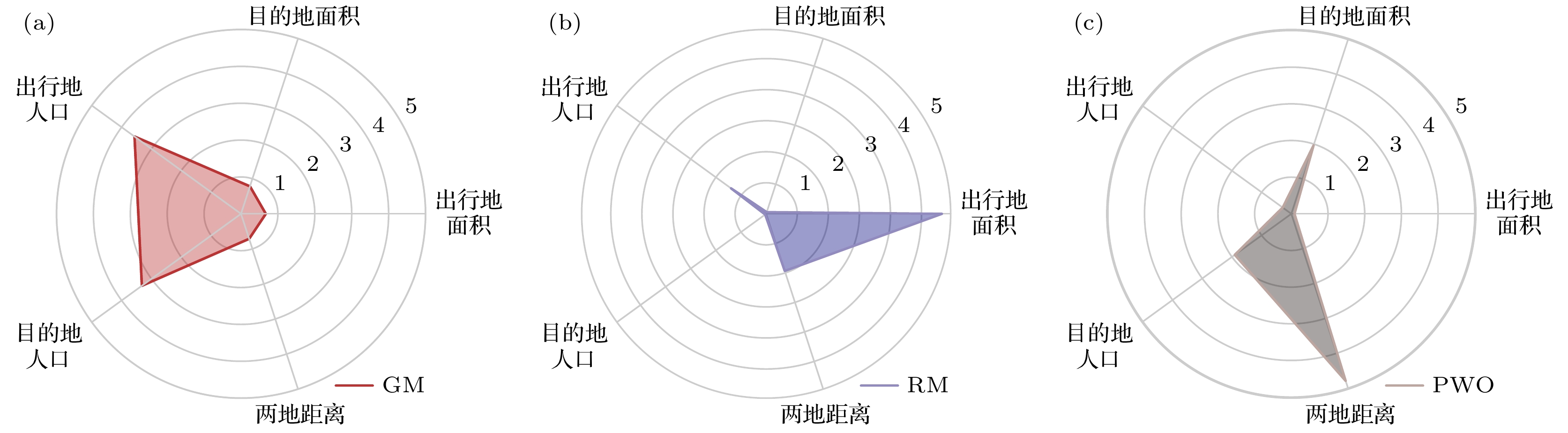
图5的雷达图展示了三类模型的驱动要素差异: GM模型形“双峰”特征(密度-面积主导), RM模型则展“三角”模式(出发地人口-出发地面积-距离), PWO模型“前倾”分布(距离主导). 不同模型在空间特征和人口属性上的敏感性不同, 适用场景也相应有所差异. GM模型受人口密度和区域面积的综合影响较大, 适合宏观范围的出行流动预测; RM模型对出发地和距离敏感性更高, 适合分析出发地驱动的短途流动特征; 而PWO模型对目的地属性和距离较为敏感, 更适用于研究目的地吸引力主导下的流动规律. 因此, 在实际应用中, 应根据具体的研究问题和场景选择合适的模型, 聚焦于主要影响因子和交互效应以优化预测效果.
-
本文通过跨尺度比较方法, 系统分析了GM模型、RM模型与人口权重机会模型(PWO)在城市移动流量预测中的性能差异及尺度依赖性. 研究结果表明, 三类模型在理论基础、驱动机制及适用场景上存在显著差异.
GM模型作为传统空间交互模型的代表, 基于牛顿引力定律, 将流量视为出发地与目的地人口规模的函数, 并与距离呈负相关关系. 该模型在小尺度下受空间异质性影响较大, 但在距离尺度较大的情景(>5 km)下表现出较强的鲁棒性, 适合远距、区域面积差异较小的场景. 然而, 其对空间异质性的敏感性需通过引入动态衰减参数进一步优化.
RM模型作为介入机会模型的经典变种, 强调目的地选择的“最近最佳机会”机制, 假设个体优先选择收益高于当前位置且距离最近的区域. 该模型在城市流量预测中因“最近机会”假设的局限性导致预测偏差, 但在出发地属性主导的短途流动分析(如通勤行为)中表现较好. 然而, RM模型对长距离预测存在系统性偏差, 未来需结合区域功能特征修正机会阈值, 以缓解小尺度偏差. 此外, RM模型对出发地人口密度高度敏感, 表明其在人口密集区域的适用性较强, 但在低密度区域的局限性较为明显.
PWO模型在RM模型基础上引入人口权重机制, 通过校正有限城市尺寸效应和目的地吸引力衰减, 提升了城市尺度的适应性. 该模型在目的地吸引力驱动的多中心城市(如商业区流量预测)中表现优异, 尤其是在小尺度场景(< 5 km)下展现出最优的兼容性. 然而, PWO模型在长距离预测中仍存在性能下降的问题, 未来可通过融合实时机会数据(如POI信息)进一步提升预测精度.
GM模型与介入机会模型各有优劣, 实际应用中需根据研究目标的核心驱动因素(人口、距离或目的地机会)选择模型(图6). 在跨尺度场景中, 根据实际情况选择模型进行预测, 比如远距离时选择GM模型, 近距离且两地面积较小时选择PWO模型. 未来研究可从构建混合模型、引入多源数据以及探索深度学习与传统模型的耦合框架等方向深入, 以在保持可解释性的同时提升非线性关系捕捉能力. 通过揭示模型的尺度敏感机制, 本研究为城市多场景流量预测提供了理论依据与方法支撑, 助力智慧城市规划和精细化治理.
城市移动流量模型的跨尺度比较方法
Cross-scale comparison methods for urban mobility models
-
摘要: 随着城市化进程的加速, 城市人口流动的精准预测成为城市规划与政策制定的重要基础. 然而, 现有移动模型在城市场景下的适应性尚不明确, 且缺乏系统性比较, 在不同尺度下的有效性尚不清晰. 本文提出一种城市移动流量模型的跨尺度比较方法, 系统分析了引力模型、辐射模型、人口权重机会模型在不同空间、距离和人口尺度下的表现. 基于上海移动数据的实证研究表明, 引力模型受距离影响较小, 但受人口密度和区域面积差异显著影响, 性能随人口规模上升而增强, 随面积差异增大而衰减(网格边长差值大于3 km时性能下降40%); 辐射模型对出发地属性敏感, 预测能力随出发地空间尺度和人口规模增加而增强, 小尺度场景存在系统性偏差; 人口权重机会模型通过人口权重机制在空间尺度上表现出优异的兼容性, 但随着距离增大效果下降, 并与人口规模正相关. 研究结果揭示了城市移动流量模型的适用场景和局限性, 为多场景下模型选择及优化提供了可操作的决策框架.Abstract: The acceleration of urbanization has rendered accurate prediction of intra-urban population mobility a fundamental requirement for urban planning and policy formulation. However, the adaptability and performance of existing mobility models on different spatial scales are still poorly understood, and there is a clear lack of a systematic evaluation framework that integrates spatial granularity, travel distance, and population heterogeneity. This study addresses these gaps by proposing a cross-scale comparative framework to evaluate three representative mobility models under varying urban conditions: the gravity model (GM), the radiation model (RM), and the population-weighted opportunities model (PWO). Using high-resolution mobile phone data from Shanghai, we construct three groups of controlled experiments to assess the performance of the model on spatial (grid size), distance, and population density scales. Furthermore, the multivariate analysis of variance (MANOVA) is further used to decompose the relative contributions of different spatial factors to prediction errors.The results indicate that there is distinct scale sensitivity between the models. Based on Newton’s principle of gravity, the GM exhibits high robustness over longer distances (>5 km), but its performance decreases under fine spatial granularity due to spatial heterogeneity. GM accuracy improves with population density but decreases significantly when regional area disparity exceeds a threshold, with prediction performance dropping by over 40% when grid size difference exceeds 3 km. The RM, based on the nearest-best-opportunity assumption, performs well for short-distance, origin-driven flows, such as commuting, but introduces systematic bias on a small scales. Its sensitivity to origin population density renders it more suitable for high-density urban cores. The PWO model enhances RM by combining destination population weights, demonstrating superior compatibility with spatial heterogeneity in dense and polycentric cities. Although it performs best in short distances (<5 km) PWO will fail as the driving distance increases.The MANOVA results demonstrate that GM is primarily influenced by population density and area scale, whereas RM and PWO exhibit greater sensitivity to distance and destination-related factors. On the basis of these findings, we propose a model selection strategy suitable for mobility drivers: GM is recommended for long-distance traffic prediction in spatially homogeneous regions, while PWO is recommended for short distance traffic prediction between densely populated small areas. RM serves as a complementary model when origin-driven flows dominate.This study not only elucidates the physical mechanisms behind the performance of scale-dependent model but also provides an actionable decision-making framework for model selection in different urban mobility scenarios. Future research will further improve predictive accuracy through the following methods: 1) developing hybrid models that integrate strengths of multiple frameworks; 2) incorporating multi-source spatial data (e.g. POIs land use); 3) coupling traditional models with deep learning approaches to enhance non-linear pattern recognition while maintaining interpretability.By revealing the scale sensitivity of mobility models, this work lays theoretical and methodological foundations for multi-scenario mobility prediction in smart city planning and fine-grained urban governance.
-
Key words:
- mobility flow /
- gravity model /
- radiation model /
- population-weighted opportunities model .
-

-
图 1 上海市人口及流量空间分布. 上图呈现了上海市人口流动的空间分布特征(基于抽样数据), 其中流量大小通过线条粗细和颜色深浅表示(流量越大, 线条越粗且颜色越偏蓝色); 下图展示了上海市各网格单元的人口规模分布情况, 其中网格内人口数量与柱状图高度呈正相关, 并通过颜色梯度表示(人口越多, 柱状图越高且颜色越偏蓝色; 人口越少, 柱状图越低且颜色越偏红色)
Figure 1. Spatial distribution of population and flow in Shanghai. The upper panel depicts the spatial pattern of population flow (based on sampled data), where the magnitude of flow is represented by both the thickness of the lines and the intensity of the color (greater flow is denoted by thicker lines with bluer tones). The lower panel illustrates the population distribution across grid cells in Shanghai, where the population size within each grid is represented by both the height of the bar and a color gradient (higher population corresponds to taller bars with bluer hues, while lower population is indicated by shorter bars with redder hues).
图 2 不同网格尺度下模型效果 (a)出发地和目的地网格尺度相等时模型预测效果; (b)出发地网格尺度对模型效果的影响; (c)目的地网格尺度对模型效果的影响; (d)—(f) GM模型、RM模型、PWO模型关于不同网格尺度下的效果热力图
Figure 2. The model performance at different grid scales: (a) The prediction performance of the model when the grid scales of the origin and destination are equal; (b) the impact of the grid scale of the origin on the model performance; (c) the impact of the grid scale of the destination on the model performance; (d)–(f) heatmaps of the performance of the gravity model, radiation model, and PWO model at different grid scales.
图 3 不同距离尺度下模型效果 (a)三种模型在不同距离尺度下的CPC值; (b)—(d)出发地空间尺度和距离尺度的交互效应, 出发地网格边长
$ L_o $ 越大, 颜色越深; (e)—(f)目的地空间尺度和距离尺度的交互效应, 目的地网格边长$ L_{\mathrm{d}} $ 越大, 颜色越深Figure 3. Model performance at different distance scales: (a) CPC values of the three models at different distance scales; (b)–(d) interaction effects between origin spatial scale and distance scale; (e)–(f) interaction effects between destination spatial scale and distance scale.
图 4 不同人口密度尺度下模型效果 (a)出发地人口密度对模型效果的影响; (b)目的地人口密度对模型效果的影响; (c)—(e) GM模型、RM模型、PWO模型关于不同人口密度尺度下的效果热力图
Figure 4. Model performance at different population density scales: (a) The impact of origin population density on model performance; (b) the impact of destination population on model performance; (c)–(e) heatmaps showing the performance of the gravity model, radiation model, and PWO model across different population scales.
表 1 不同模型多因素方差分析(ANOVA)结果
Table 1. Results of multi-factor ANOVA for different models.
因素 GM RM PWO F $ P_{\mathrm{R}} > F $ F $ P_{\mathrm{R}} > F $ F $ P_{\mathrm{R}} > F$ 出发地面积 9010 0 604629 0 180 0 目的地面积 10912 0 58721 0 38511 0 出发地面积∶的地面积 9073 0 5132 0 1117 0 出发地人口密度 65161 0 179437 0 20934 0 目的地人口密度 61262 0 1587 0 127280 0 两地距离 688 0 321208 0 262932 0 -
[1] Batty M 2008 Science 319 769 doi: 10.1126/science.1151419 [2] Andrienko G, Andrienko N, Boldrini C, Caldarelli G, Cintia P, Cresci S, Facchini A, Giannotti F, Gionis A, Guidotti R, Mathioudakis M, Muntean C I, Pappalardo L, Pedreschi D, Pournaras E, Pratesi F, Tesconi M, Trasarti R 2021 Int. J. Data. Sci. Anal. 11 311 doi: 10.1007/s41060-020-00207-3 [3] Barbosa H, Barthelemy M, Ghoshal G, James C R, Lenormand M, Louail T, Menezes R, Ramasco J J, Simini F, Tomasini M 2018 Phys. Rep. 734 1 doi: 10.1016/j.physrep.2018.01.001 [4] Xu Y, Belyi A, Bojic I, Ratti C 2018 Comput. Environ. Urban Syst. 72 51 doi: 10.1016/j.compenvurbsys.2018.04.001 [5] Guo Y T, Peeta S 2020 Travel Behav. Soc. 19 99 doi: 10.1016/j.tbs.2019.12.007 [6] Helbing D 2001 Rev. Mod. Phys. 73 1067 doi: 10.1103/RevModPhys.73.1067 [7] Toole J L, Colak S, Sturt B, Alexander L P, Evsukoff A, González M C 2015 Transp. Res. Part C Emerging Technol. 58 162 doi: 10.1016/j.trc.2015.04.022 [8] Voukelatou V, Gabrielli L, Miliou I, Cresci S, Sharma R, Tesconi M, Pappalardo L 2021 Int. J. Data. Sci. Anal. 11 279 doi: 10.1007/s41060-020-00224-2 [9] Louf R, Barthelemy M 2014 Sci. Rep. 4 5561 doi: 10.1038/srep05561 [10] Hufnagel L, Brockmann D, Geisel T 2004 Proc. Natl. Acad. Sci. 101 15124 doi: 10.1073/pnas.0308344101 [11] Xiong C F, Hu S H, Yang M F, Luo W Y, Zhang L 2020 Proc. Natl. Acad. Sci. 117 27087 doi: 10.1073/pnas.2010836117 [12] NaDai M D, Xu Y Y, Letouzé E, González M C, Lepri B 2020 Sci. Rep. 10 13871 doi: 10.1038/s41598-020-70808-2 [13] Simini F, Barlacchi G, Luca M, Pappalardo L 2021 Nat. Commun. 12 6576 doi: 10.1038/s41467-021-26752-4 [14] Yao X, Gao Y, Zhu D, Manley E, Wang J, Liu Y 2021 IEEE Trans. Intell. Transp. Syst. 22 7474 doi: 10.1109/TITS.2020.3003310 [15] Liu Z C, Miranda F, Xiong W T, Yang J Y, Wang Q, Silva C 2020 AAAI 34 808 doi: 10.1609/aaai.v34i01.5425 [16] Dai G N, Hu X Y, Ge Y M, Ning Z Q, Liu Y B 2021 Front. Comput. Sci. 15 152317 doi: 10.1007/s11704-020-9194-x [17] Tian C J, Zhu X N, Hu Z, Ma J 2020 Appl. Intell. 50 3057 doi: 10.1007/s10489-020-01698-0 [18] Luca M, Barlacchi G, Lepri B, Pappalardo L 2023 ACM Comput. Surv. 55 1 [19] Zipf G K 1946 Am. Sociol. Rev. 11 677 doi: 10.2307/2087063 [20] Goh S, Lee K, Park J S, Choi M Y 2012 Phys. Rev. E 86 26102 doi: 10.1103/PhysRevE.86.026102 [21] Krings G, Calabrese F, Ratti C, Blondel V D 2009 J. Stat. Mech: Theory Exp. 200 9 [22] Prieto Curiel R, Pappalardo L, Gabrielli L, Bishop S R 2018 PLoS One 1 3 [23] Wang Y X, Li X, Yao X, Li S, Liu Y 2022 Ann. Am. Assoc. Geogr. 112 1441 [24] Brockmann D, Helbing D 2013 Science 342 1337 doi: 10.1126/science.1245200 [25] Stouffer S A 1940 Am. Sociol. Rev. 5 845 doi: 10.2307/2084520 [26] Ortúzar J D D, Willumsen L G 2011 Modelling Transport (1st Ed.) (Hoboken: Wiley) pp207–208 [27] Simini F, González M C, Maritan A, Barabási A L 2012 Nature 484 96 doi: 10.1038/nature10856 [28] Yan X Y, Zhao C, Fan Y, Di Z R, Wang W X 2014 J. R. Soc. Interface 11 20140834 doi: 10.1098/rsif.2014.0834 [29] Liu E J, Yan X Y 2019 Physica A 526 121023 doi: 10.1016/j.physa.2019.04.259 [30] Liu E J, Yan X Y 2020 Sci. Rep. 10 4657 doi: 10.1038/s41598-020-61613-y [31] Yan X Y, Zhou T 2019 Sci. Rep. 9 9466 doi: 10.1038/s41598-019-46026-w [32] Lawson H C, Dearinger J A 1967 J. Highw. Div. 93 1 [33] Liang X, Zhao J C, Dong L, Xu K 2013 Sci. Rep. 3 2983 doi: 10.1038/srep02983 [34] Okabe A 1976 Reg. Sci. Urban Econ. 6 381 doi: 10.1016/0166-0462(76)90032-6 [35] Hong I, Jung W S, Jo H H 2019 PLoS One 1 4 [36] Kluge L, Schewe J 2021 Phys. Rev. E 104 54311 doi: 10.1103/PhysRevE.104.054311 [37] Piovani D, Arcaute E, Uchoa G, Wilson A, Batty M 2018 R. Soc. Open Sci. 5 171668 doi: 10.1098/rsos.171668 [38] Stefanouli M, Polyzos S 2017 Transp. Res. Procedia 24 65 doi: 10.1016/j.trpro.2017.05.069 [39] Yang Y X, Herrera C, Eagle N, González M C 2014 Sci. Rep. 4 5662 doi: 10.1038/srep05662 [40] Heydari S, Huang Z, Hiraoka T, De León Chávez A P, Ala-Nissila T, Leskelä L, Kivelä M, Saramäki J 2023 Travel Behav. Soc. 31 93 doi: 10.1016/j.tbs.2022.11.005 [41] Masucci A P, Serras J, Johansson A, Batty M 2013 Phys. Rev. E 88 22812 doi: 10.1103/PhysRevE.88.022812 [42] Palchykov V, Mitrović M, Jo H H, Saramäki J, Pan R K 2014 Sci. Rep. 4 6174 doi: 10.1038/srep06174 [43] Lenormand M, Bassolas A, Ramasco J J 2016 J. Transp. Geogr. 51 158 doi: 10.1016/j.jtrangeo.2015.12.008 [44] Lenormand M, Huet S, Gargiulo F, Deffuant G 2012 PLoS One 7 e45985 doi: 10.1371/journal.pone.0045985 [45] Gargiulo F, Lenormand M, Huet S, Baqueiro Espinosa O 2012 JASSS. 15 6 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: