高级搜索

石墨烯和二维超导体NbSe2层间拖拽效应

,  ,  ,  , 

downloadPDF

上一篇

下一篇

李渝豪, 朱丽君, 张弛, 李林, 曾长淦. 石墨烯和二维超导体NbSe2层间拖拽效应[J]. 物理学报, 2025, 74(14): 147302-1. doi: 10.7498/aps.74.20250361
引用本文: 李渝豪, 朱丽君, 张弛, 李林, 曾长淦. 石墨烯和二维超导体NbSe2层间拖拽效应[J]. 物理学报, 2025, 74(14): 147302-1. doi: 10.7498/aps.74.20250361
shu
Yuhao LI, Lijun ZHU, Chi ZHANG, Lin LI, Changgan ZENG. Interlayer drag effect between graphene and two-dimensional superconductor NbSe2[J]. Acta Physica Sinica, 2025, 74(14): 147302-1. doi: 10.7498/aps.74.20250361
Citation: Yuhao LI, Lijun ZHU, Chi ZHANG, Lin LI, Changgan ZENG. Interlayer drag effect between graphene and two-dimensional superconductor NbSe2[J]. Acta Physica Sinica, 2025, 74(14): 147302-1. doi: 10.7498/aps.74.20250361
shu

石墨烯和二维超导体NbSe2层间拖拽效应

  • 1.

    中国科学技术大学物理学院, 合肥　230026

  • 2.

    中国科学技术大学合肥微尺度物质科学国家研究中心, 合肥　230026

  • 3.

    合肥国家实验室, 合肥　230088

    • 作者简介: 李渝豪.E-mail: liiyuhao@mail.ustc.edu.cn .
    通讯作者: E-mail: lilin@ustc.edu.cn.;  E-mail: cgzeng@ustc.edu.cn.

  • 中图分类号: 73.22.-f, 74.81.-g, 72.80.Vp

Interlayer drag effect between graphene and two-dimensional superconductor NbSe2

  • 1.

    School of Physical Sciences, University of Science and Technology of China, Hefei 230026, China

  • 2.

    Hefei National Research Center for Physical Sciences at the Microscale, University of Science and Technology of China, Hefei 230026, China

  • 3.

    Hefei National Laboratory, Hefei 230088, China

    • Corresponding authors: E-mail:lilin@ustc.edu.cn.;  E-mail:cgzeng@ustc.edu.cn.

  • MSC: 73.22.-f, 74.81.-g, 72.80.Vp

  • 摘要: 由绝缘体间隔的两个导体间的层间拖拽效应是研究准粒子耦合和探索层间关联物态的重要途径, 而具有丰富可调物性的二维层状材料为研究拖拽效应提供了更多可能. 本文制备了石墨烯-氮化硼-二硒化铌这一电双层结构, 系统研究了二维半金属和二维超导体之间的拖拽效应. 当石墨烯作为驱动层, 二硒化铌作为被动层时, 可以在二硒化铌超导转变温度区间发现显著的拖拽响应, 表现出明显的超流拖拽特征; 而当二硒化铌处于正常金属态时, 拖拽信号消失. 磁场、栅压调制下的测试进一步表明, 拖拽响应与二硒化铌的超导转变直接相关, 且其符号不依赖石墨烯载流子类型. 更为重要的是, 通过对比不同器件发现, 这类超流拖拽响应仅出现在空气中解理的薄层二硒化铌中, 因此二硒化铌中超导的不均匀性是产生该效应的关键. 其机制可能源自非均匀超导体中量子涨落与二维半金属电荷密度波动之间的库仑耦合.
    Abstract: In an electronic double-layer system composed of two spatially adjacent but electrically insulated conductors, when current flows through one conductor (drive layer), its charge carriers transfer energy/momentum to the charge carriers in the other conductor (drag layer) through interlayer Coulomb coupling, thus generating a measurable voltage or current in the drag layer. This phenomenon is known as the interlayer drag effect. This effect provides a critical approach for studying quasiparticle interactions and investigating interlayer-correlated quantum states. Two-dimensional layered materials with highly tunable properties provide new opportunities for exploring the drag effect. In this study, we fabricate an electronic double-layer structure consisting of graphene and NbSe2 to systematically investigate the drag effect between a two-dimensional semimetal and a two-dimensional superconductor, wherein a thin hBN layer serves as the insulating spacer. When graphene acts as the drive layer and NbSe2 acts as the drag layer, a significant positive drag response is observed within the superconducting transition temperature range of NbSe2. In contrast, the drag signal vanishes when NbSe2 is in its normal metallic state. The measurements of magnetic field dependence reveal that the drag response disappears under high fields where the superconductivity of NbSe2 is suppressed, further confirming its direct correlation with the superconducting transition. The gate-voltage modulation experiments reveal that the drag response peaks when adjusting the Fermi level of graphene across the Dirac point. This is attributed to the reduced screening of interlayer interactions due to the ultra-low carrier concentration at this point. Notably, the sign of the supercurrent drag does not depend on the carrier type in graphene, ruling out the traditional momentum-transfer drag mechanism. Our results collectively demonstrate the realization of supercurrent drag effect, which has been attributed to Coulomb coupling between the quantum fluctuations of the superconducting phases in a superconductor and the charge densities in a normal conductor in previous study. Notably, by comparing different devices, it is found that this type of supercurrent drag responses occurs only in the thin NbSe2 layers cleaved in air. No significant signals are detected in thick NbSe2 layers or thin layers cleaved under the protection of argon. These results establish the importance of superconducting inhomogeneity in NbSe2 for generating supercurrent drag effect, indicating that drag measurements can also serve as a novel probe for investigating superconducting properties. Further investigation into the polarity and intensity of supercurrent drag signals may advance our understanding of inhomogeneous superconductivity, as well as interactions between normal carriers and Cooper pairs.
  • 加载中

  • 图 1  (a)石墨烯-NbSe2拖拽器件示意图; (b)石墨烯-NbSe2拖拽器件的光学显微图像, 单层石墨烯和双层NbSe2的轮廓分别用黑白虚线标示, 插图为转移前NbSe2层的光学显微图像

    Figure 1.  (a) Schematic diagram of graphene-NbSe2 drag device; (b) optical image of graphene-NbSe2 drag device, the outlines of monolayer graphene and NbSe2 flakes are marked with black and white dashed lines, respectively. Inset is the optical image of the NbSe2 layer before transfer.

    下载: 全尺寸图片 幻灯片

    图 2  (a)拖拽测试示意图; (b)器件#1中层间拖拽电阻(Rdrag)和NbSe2层内电阻($ {{R}}_{{\text{NbSe}}_{2}} $)随温度的变化曲线

    Figure 2.  (a) Schematic of the setup for drag measurements; (b) interlayer drag resistance (Rdrag) and intralayer resistance of NbSe2 ($ {{R}}_{{\text{NbSe}}_{2}} $) as functions of temperature for Device #1.

    下载: 全尺寸图片 幻灯片

    图 3  (a)器件#1中Rdrag和$ {{R}}_{{\text{NbSe}}_{2}} $随磁场强度的变化曲线, 测试温度为1.6 K; (b) Rdrag和(c) $ {{R}}_{{\text{NbSe}}_{2}} $随温度和磁场强度的变化

    Figure 3.  (a) Rdrag and $ {{R}}_{{\text{NbSe}}_{2}} $ as functions of magnetic field for Device #1, measured at 1.6 K; (b) Rdrag and (c) $ {{R}}_{{\text{NbSe}}_{2}} $ as functions of temperature and magnetic field.

    下载: 全尺寸图片 幻灯片

    图 4  (a)器件#1中Rdrag和石墨烯层内电阻Rgraphene随层间栅压的变化曲线, 测试温度为1.6 K; (b) Rdrag和(c) Rgraphene随温度和层间栅压的变化

    Figure 4.  (a) Rdrag and intralayer resistance of graphene (Rgraphene) as functions of interlayer gate voltage (Vint) for Device #1, measured at 1.6 K; (b) Rdrag and (c) Rgraphene as functions of temperature and Vint.

    下载: 全尺寸图片 幻灯片

    图 5  (a)器件#2中Rdrag和$ {{R}}_{{\text{NbSe}}_{2}} $随温度的变化曲线, 插图为该器件中所使用的NbSe2层的光学显微图像, 由薄层区域(~3层)和厚层区域(~5层)两部分构成; (b)拖拽耦合比r和$ {{R}}_{{\text{NbSe}}_{2}} $随温度的变化曲线

    Figure 5.  (a) Rdrag and $ {{R}}_{{\text{NbSe}}_{2}} $ as functions of temperature for Device #2, inset is optical image of the NbSe2 layer in this device, which is composed of a thin region I (~3 layers) and a thick region II (~5 layers); (b) passive-to-active ratio r (drag current/drive current) and $ {{R}}_{{\text{NbSe}}_{2}} $ as functions of temperature.

    下载: 全尺寸图片 幻灯片
  • [1] Narozhny B N, Levchenko A 2016 Rev. Mod. Phys. 88 025003 doi: 10.1103/RevModPhys.88.025003
    [2] Laroche D, Gervais G, Lilly M P, Reno J L 2014 Science 343 631 doi: 10.1126/science.1244152
    [3] Yamamoto M, Stopa M, Tokura Y, Hirayama Y, Tarucha S 2006 Science 313 204 doi: 10.1126/science.1126601
    [4] Eisenstein J P, MacDonald A H 2004 Nature 432 691 doi: 10.1038/nature03081
    [5] Tutuc E, Shayegan M, Huse D A 2004 Phys. Rev. Lett. 93 036802 doi: 10.1103/PhysRevLett.93.036802
    [6] Su J J, MacDonald A H 2008 Nat. Phys. 4 799 doi: 10.1038/nphys1055
    [7] Liu X, Watanabe K, Taniguchi T, Halperin B I, Kim P 2017 Nat. Phys. 13 746 doi: 10.1038/nphys4116
    [8] Li J I A, Taniguchi T, Watanabe K, Hone J, Dean C R 2017 Nat. Phys. 13 751 doi: 10.1038/nphys4140
    [9] Giaever I 1966 Phys. Rev. Lett. 16 460 doi: 10.1103/PhysRevLett.16.460
    [10] Duan J M, Yip S 1993 Phys. Rev. Lett. 70 3647 doi: 10.1103/PhysRevLett.70.3647
    [11] Shimshoni E 1995 Phys. Rev. B 51 9415 doi: 10.1103/PhysRevB.51.9415
    [12] Huang X, Bazàn G, Bernstein G H 1995 Phys. Rev. Lett. 74 4051 doi: 10.1103/PhysRevLett.74.4051
    [13] Giordano N, Monnier J D 1994 Phys. Rev. B 50 9363 doi: 10.1103/PhysRevB.50.9363
    [14] Kim S, Jo I, Nah J, Yao Z, Banerjee S K, Tutuc E 2011 Phys. Rev. B 83 161401 doi: 10.1103/PhysRevB.83.161401
    [15] Gorbachev R V, Geim A K, Katsnelson M I, Novoselov K S, Tudorovskiy T, Grigorieva I V, MacDonald A H, Morozov S V, Watanabe K, Taniguchi T, Ponomarenko L A 2012 Nat. Phys. 8 896 doi: 10.1038/nphys2441
    [16] Tao R, Li L, Xie H Y, Fan X D, Guo L H, Zhu L J, Yan Y D, Zhang Z Y, Zeng C G 2023 Nat. Phys. 19 372 doi: 10.1038/s41567-022-01902-7
    [17] Xi X X, Wang Z F, Zhao W W, Park J H, Law K T, Berger H, Forró L, Shan J, Mak K F 2016 Nat. Phys. 12 139 doi: 10.1038/nphys3538
    [18] Khestanova E, Birkbeck J, Zhu M, Cao Y, Yu G L, Ghazaryan D, Yin J, Berger H, Forró L, Taniguchi T, Watanabe K, Gorbachev R V, Mishchenko A, Geim A K, Grigorieva I V 2018 Nano Lett. 18 2623 doi: 10.1021/acs.nanolett.8b00443
    [19] Onishi S, Ugeda M M, Zhang Y, Chen Y, Ojeda-Aristizabal C, Ryu H, Mo S K, Hussain Z, Shen Z X, Crommie M F, Zettl A 2016 Phys. Status Solidi B 253 2396 doi: 10.1002/pssb.201600235
    [20] El-Bana M S, Wolverson D, Russo S, Balakrishnan G, Paul D M, Bending S J 2013 Supercond. Sci. Technol. 26 125020 doi: 10.1088/0953-2048/26/12/125020
    [21] Cao Y, Mishchenko A, Yu G L, Khestanova E, Rooney A P, Prestat E, Kretinin A V, Blake P, Shalom M B, Woods C, Chapman J, Balakrishnan G, Grigorieva I V, Novoselov K S, Piot B A, Potemski M, Watanabe K, Taniguchi T, Haigh S J, Geim A K, Gorbachev R V 2015 Nano Lett. 15 4914 doi: 10.1021/acs.nanolett.5b00648
    [22] Myers G E, Montet G L 1971 J. Phys. Chem. Solids 32 2645 doi: 10.1016/S0022-3697(71)80111-7
    [23] Chen Z, Swartz A G, Yoon H, Inoue H, Merz T A, Lu D, Xie Y, Yuan H, Hikita Y, Raghu S, Hwang H Y 2018 Nat. Commun. 9 4008 doi: 10.1038/s41467-018-06444-2
    [24] Bert J A, Kalisky B, Bell C, Kim M, Hikita Y, Hwang H Y, Moler K A 2011 Nat. Phys. 7 767 doi: 10.1038/nphys2079
  • 加载中
图( 5)
计量
  • 文章访问数:  20
  • HTML全文浏览数:  20
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-20
  • 刊出日期:  2025-07-20

石墨烯和二维超导体NbSe2层间拖拽效应

    通讯作者: E-mail: lilin@ustc.edu.cn.; 
    通讯作者: E-mail: cgzeng@ustc.edu.cn.
    作者简介: 李渝豪.E-mail: liiyuhao@mail.ustc.edu.cn
  • 1. 中国科学技术大学物理学院, 合肥　230026
  • 2. 中国科学技术大学合肥微尺度物质科学国家研究中心, 合肥　230026
  • 3. 合肥国家实验室, 合肥　230088
  • 收稿日期:  2025-03-20

摘要: 由绝缘体间隔的两个导体间的层间拖拽效应是研究准粒子耦合和探索层间关联物态的重要途径, 而具有丰富可调物性的二维层状材料为研究拖拽效应提供了更多可能. 本文制备了石墨烯-氮化硼-二硒化铌这一电双层结构, 系统研究了二维半金属和二维超导体之间的拖拽效应. 当石墨烯作为驱动层, 二硒化铌作为被动层时, 可以在二硒化铌超导转变温度区间发现显著的拖拽响应, 表现出明显的超流拖拽特征; 而当二硒化铌处于正常金属态时, 拖拽信号消失. 磁场、栅压调制下的测试进一步表明, 拖拽响应与二硒化铌的超导转变直接相关, 且其符号不依赖石墨烯载流子类型. 更为重要的是, 通过对比不同器件发现, 这类超流拖拽响应仅出现在空气中解理的薄层二硒化铌中, 因此二硒化铌中超导的不均匀性是产生该效应的关键. 其机制可能源自非均匀超导体中量子涨落与二维半金属电荷密度波动之间的库仑耦合.

English Abstract

    全文HTML

    1.   引　言

    • 对于两个空间邻近但彼此绝缘的导体组成的电双层结构, 当一个导体(驱动层)施加电流时, 其中载流子的动量/能量会通过层间耦合转移给另一个导体(被动层)中的载流子, 从而在被动层上产生可测量的电压(或电流), 这种现象被称作拖拽效应[1]. 拖拽效应主要源于层间库仑相互作用, 可以同时反映准粒子相互作用以及层内电子态特性, 也是发现新颖层间量子态的重要手段. 基于拖拽效应表征, 研究人员发现了多个层间和层内新奇物性, 例如量子线中的Luttinger液体[2]和Wigner晶体态[3], 层间隧穿增强[4]和间接激子超流态[5-8]等.

      早期理论研究表明, 如果将其中一层导体替换为超导体, 将会极大丰富拖拽效应的研究维度, 如探测超导序参量的涨落, 表征普通载流子与库珀对之间相互作用[9-11], 探索实现无耗散的超流拖拽效应[10]等等. 而相关实验研究主要集中在由绝缘氧化物薄膜隔开的金属和超导薄膜组成的电双层结构, 但实验结果间却存在显著差异. 在Ti/Au-AlOx体系中, 当Au薄膜作为驱动层时, 在被动层AlOₓ的超导转变温度区间观测到了负的拖拽信号; 而交换驱动层和被动层后拖拽信号消失[12]. 而在Sb-AlOx体系中, 当Sb作为驱动层时, 在AlOx超导转变温度区间表现出正的拖拽信号, 且交换驱动层和被动层后仍能在Sb层观测到信号[13]. 尽管这些研究初步揭示了超流拖拽效应的存在, 但是截然不同的实验表现使得在理论上理解相应微观机制变得困难. 一个可能的原因在于, 这类体系中较大的层间间距(>30 nm)和过高的载流子浓度使得拖拽信号本身非常微弱. 此外, 由于两层均缺乏可调控性, 进一步制约了系统的实验表征.

      二维材料的兴起为系统探究超流拖拽效应提供了更为理想的选择. 除了层内物性的高度可调性, 基于二维绝缘体薄片还可以大幅减少层间距至数纳米[7,8,14,15]. 如Tao等[16]构建了石墨烯和二维界面超导LaAlO3/SrTiO3(LAO/STO)组成的电双层结构. 在石墨烯层施加电流时, LAO/STO界面观测到由量子涨落诱导的巨幅超流拖拽效应, 最大拖拽耦合比r达0.3(r = Idrag/Idrive, 其中Idrag和Idrive分别为拖拽电流和驱动电流), 较传统金属薄膜体系提升两个数量级. 该效应被认为源于LAO/STO特殊的内禀不均匀性——局域超导相与金属相的共存, 使得超导体中量子涨落与石墨烯体系电荷密度波动发生相互作用, 从而产生超流拖拽效应[16]. 然而, 超导体的不均匀性是否是产生超流拖拽效应的必要条件? 超流拖拽信号的强度和符号由哪些因素决定? 这些问题仍需通过不同体系的对比实验进行验证和阐明. 而从应用角度, 系统探究导体和超导体间的拖拽效应, 将有望为在超导器件设计中规避或利用近邻元件间的相互作用提供参考.

      本研究选用具有较高超导转变温度且易解理的二维层状材料2H-NbSe2作为超导层, 构筑其与单层石墨烯的电双层结构, 两层之间利用六方 氮化硼(hBN)薄片作为绝缘层. 当在石墨烯层施加驱动电流时, 在NbSe2超导转变温区观测到正的超流拖拽信号, 该信号可被栅压和磁场显著调控. 对比实验表明, 超流拖拽效应仅在空气环境中解理的薄层NbSe2中出现, 而在厚层样品或氩气环境解理的薄层样品中完全消失, 表明超流拖拽效应的实现与器件制备过程中引入的超导不均匀性密切相关.

    2.   实验方法

    • 器件制备. 拖拽实验用器件基于垂直堆叠的石墨烯-NbSe2电双层结构, 利用hBN薄片作为中间绝缘层. 在制备方面, 首先采用机械解理法将NbSe2、单层石墨烯和hBN薄片剥离至Si/SiO2表面, 然后通过干法转移技术, 依次拾取hBN、单层石墨烯、hBN和NbSe2, 最终将该堆垛结构精确放置在Au预置电极表面(20 nm). 在获得高质量堆垛结构后, 采用电子束曝光结合反应离子刻蚀在石墨烯表面制备一维接触结构, 随后通过电子束蒸发沉积厚度为1/7/50 nm的Cr/Pd/Au电极, 最后使用银胶和金线将电极与测试系统样品台连接.

      低温输运测试. 层内和层间拖拽输运测试在低温强磁场平台上进行(牛津仪器). 使用Keithley 6220直流电源和2182A纳伏表分别施加电流和测量电压信号, 栅压信号则利用Keithley 2400源表施加. 对于拖拽效应测试, 为消除背景信号干扰, 采用双极模式以1 Hz频率交替切换电流极性. 通过对正负电流激励下测量的电压信号作差, 从而得出扣除背景后的电压信号. 在系统的测试之前, 要检查NbSe2和石墨烯之间的漏电流情况以避免其对于拖拽测试的影响. 实验使用Keithley 2400源表在NbSe2和石墨烯之间施加2 V电压, 并利用该仪表测量两层之间的漏电流. 当漏电流小于0.1 nA时, 认为漏电流可忽略不计.

    3.   结果与讨论

      3.1.   基本拖拽效应表征

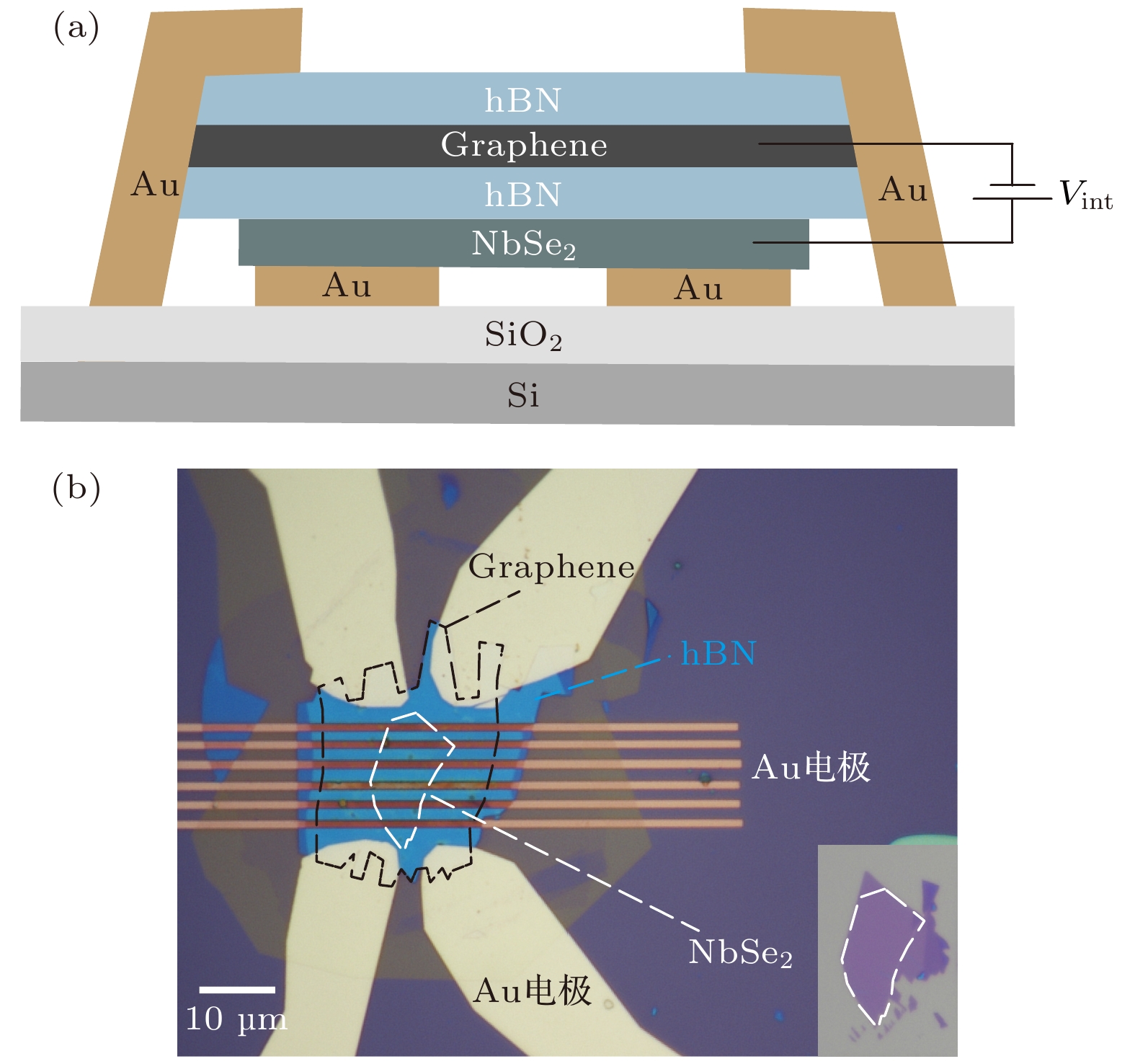
    • 图1(a)为本研究所用的石墨烯-NbSe2拖拽器件的示意图, 其中NbSe2在下层, 石墨烯在上层, 上中两层hBN分别充当器件的保护层和石墨烯与NbSe2之间的绝缘层. 通过施加层间栅压(Vint), 可以对石墨烯层的载流子浓度/极性进行调控. 图1(b)展示了器件#1的光学显微图像, 器件中所用中间hBN层(蓝色区域)厚度为15 nm, NbSe2层数为双层.

      图2(a)为拖拽测试的示意图. 实验中, 向石墨烯(主动层)施加驱动电流(Idrive = 2 μA), 在NbSe2(被动层)中测量由于层间相互作用导致的拖拽电压(Vdrag). 其中驱动电流值的选取要确保器件工作于线性I-V区间, 以排除热效应等的影响, 保证结果的准确性. 图2(b)展示了器件#1中层间Rdrag与NbSe2层内电阻($ {{R}}_{\text{NbSe}_2} $)随温度的变化曲线, 其中Rdrag = Vdrag/Idrive. 结果显示, 当温度高于4 K时, NbSe2处于正常金属态, 而相应的拖拽信号可忽略不计. 这是因为传统由动量转移主导的拖拽信号遵循与载流子浓度负相关的n–3/2关系[1], NbSe2载流子浓度高达1015 cm–2量级, 其强屏蔽效应显著抑制了拖拽效应. 互换驱动层和被动层, 当在NbSe2上施加驱动电流时, 石墨烯中也未能探测到拖拽信号. 当温度降至4 K时, NbSe2电阻开始明显降低, 表明其进入超导转变区间. 相应地, 在层间可以看到符号为正的拖拽信号, 其强度随着温度进一步降低而单调递增. 在最低测试温度1.6 K时, 拖拽信号达到最大值0.3 Ω. 值得说明的是, NbSe2的超导转变温度(Tc)明显低于块体样品(~7 K), 且超导转变温区也明显展宽. 即便是在最低测试温度的1.6 K, NbSe2也并未完全进入超导态. 这一方面是由于该器件中的NbSe2仅为两层, 而厚度降低本身会导致Tc的降低[17,18], 另一方面, NbSe2解理是在空气中进行, 使得超导电性被进一步抑制[19], 这会在后面进一步阐述.

      • 3.2.   磁场与层间栅压对拖拽效应的调制

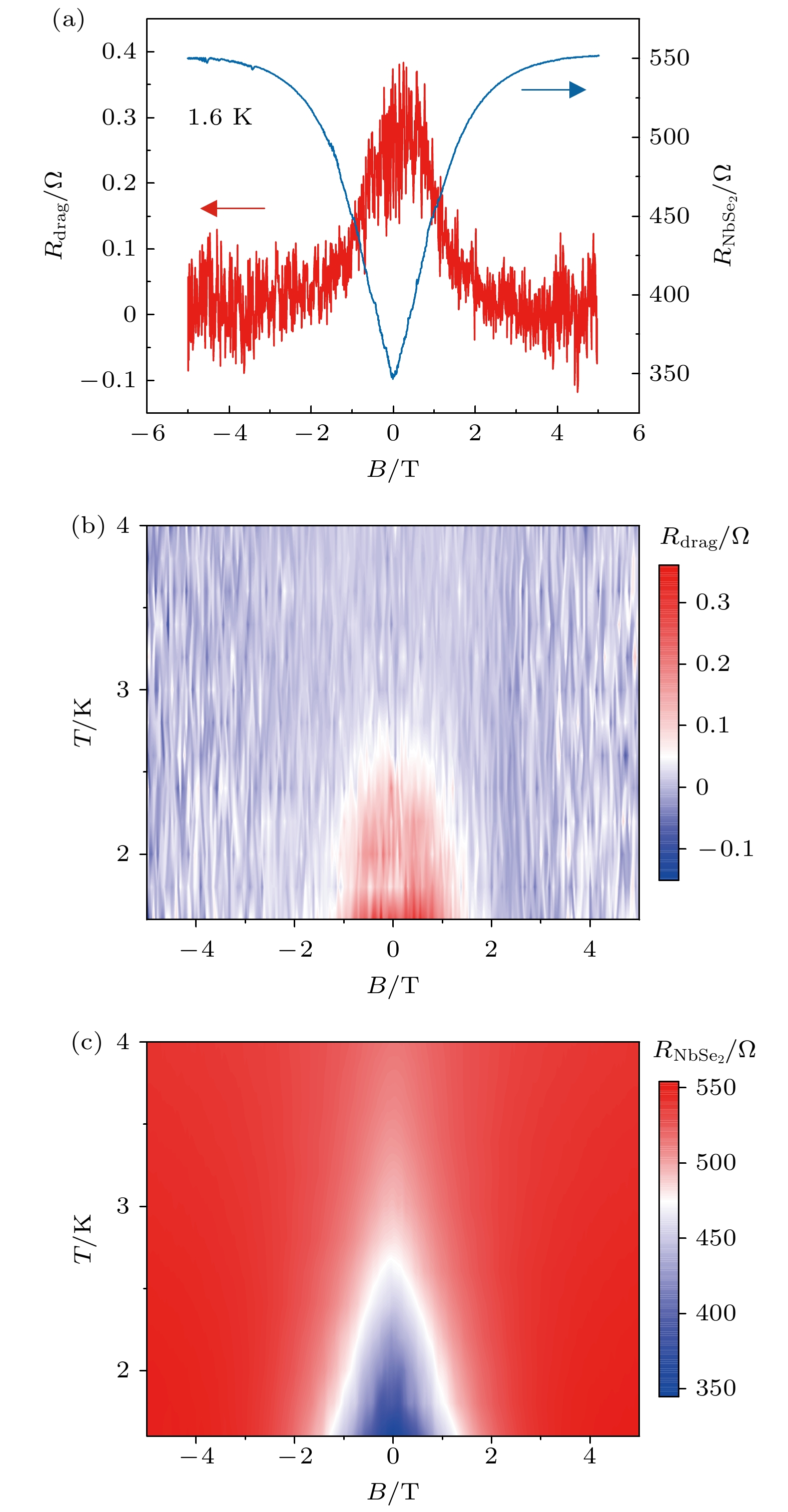
    • 由图2可知, 石墨烯-NbSe2器件中的拖拽响应的出现与NbSe2进入超导转变区间同步, 这与文献[12,13,16]报道的超流拖拽效应仅存在于超导转变区间的特征一致. 为了进一步探究拖拽响应和NbSe2超导特性的关联, 我们系统表征了拖拽信号在外加磁场下的演化行为. 如图3(a)所示, 当在1.6 K下施加垂直于NbSe2薄层方向的磁场时, 超导态逐渐被抑制, NbSe2层本身电阻随磁场强度增大显著增大. 相应地, 层间Rdrag持续下降, 在高磁场时趋于零, 对应NbSe2此时完全进入了正常金属态. 更进一步, 我们测量了更多温度下的磁场强度响应曲线. 图3(b)展示了Rdrag随温度和磁场强度的变化. 可以很明显地看到, 拖拽信号与NbSe2层内电阻一样(图3(c)), 均表现出穹顶状结构, 在测量的所有温度下, 非零的拖拽响应均严格限制在NbSe2的临界场范围内, 进一步佐证了本工作在该器件中观测到了显著的超流拖拽效应.

      在石墨烯-LAO/STO电双层结构的实验中, Tao等[16]观测到了符号为负的超流拖拽信号. 而当调节石墨烯费米面至狄拉克点(电荷中性点)时, 拖拽信号达到最大值. 这表明超流拖拽虽然不同于传统库仑拖拽, 但其强度依然受到载流子浓度的调制. 类似地, 在我们的器件中, 通过施加Vint可以有效调制石墨烯的层内输运, 进而用于验证其对于超流拖拽效应的可能调制. 图4(a)展示了1.6 K下石墨烯层内电阻(Rgraphene)和Rdrag随栅压的响应曲线. 石墨烯层内表现出典型的双极调控特性, 其狄拉克点位于Vint = –0.1 V处. 而相应地, Rdrag也在Vint = –0.1 V处达到最大值(0.4 Ω). 这可以归因于狄拉克点处载流子浓度最低, 导致对于层间相互作用的屏蔽效应显著减弱. 当栅压进一步增至Vint = ±2 V时, 石墨烯载流子浓度显著增大, 相应地Rdrag显著减小并趋于零. 更进一步地, 我们测量了更多温度下的层间栅压响应曲线. 图4(b), (c)分别展示了Rdrag和Rgraphene随温度和层间栅压的变化. 随着温度的升高, 石墨烯的狄拉克点位置基本保持不变. 而不同温度下拖拽信号也基本保持相对于Vint = –0.1 V对称分布的特征, 整体表现出穹顶状结构. 值得说明的是, 对于传统的基于动量转移的库仑拖拽, 拖拽电阻的极性应与载流子类型相关[1,14]. 但本实验中Rdrag则与石墨烯的载流子类型无关, 这排除了动量转移机制的可能性.

      • 3.3.   超流拖拽效应出现机制

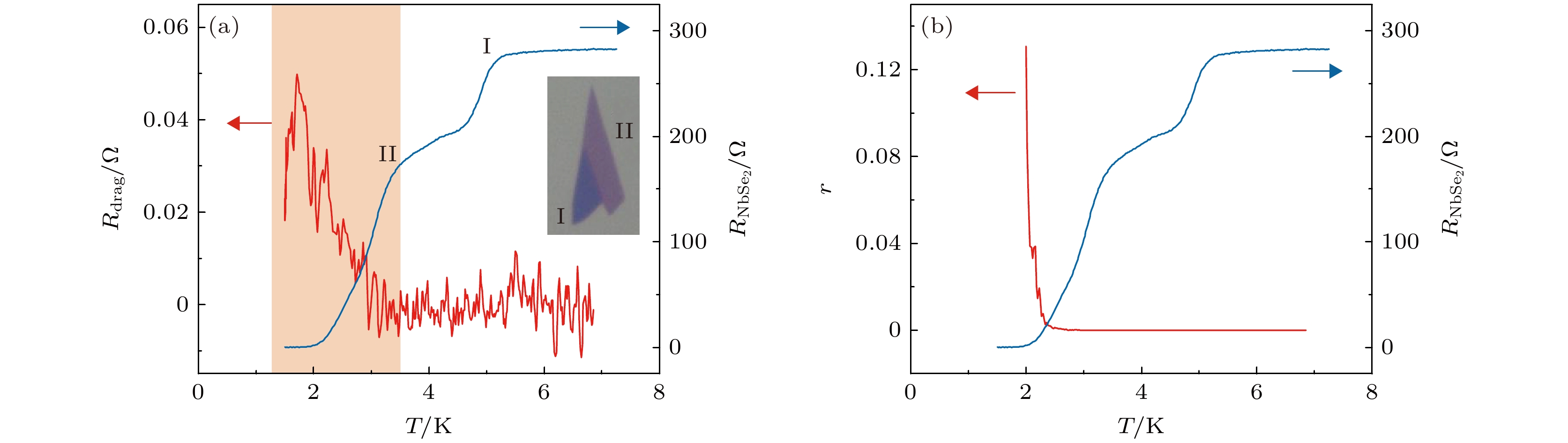
    • 由以上结果可知, 在石墨烯-NbSe2器件#1中观测到了与石墨烯-LAO/STO器件中类似的超流拖拽效应, 且拖拽信号其对于磁场和载流子浓度等的响应特性也均一致. 通过系统的对比我们发现, 当使用薄层NbSe2时, 获得可测量的拖拽信号的可能性显著增大. 为了更为直观地探究拖拽响应和NbSe2厚度的关联, 我们在器件#2中使用了阶梯状厚度分布的NbSe2薄片, 其中间hBN层厚度为13 nm. 如图5(a)插图所示, 通过原子力显微镜表征和光学衬度对比, 确认该NbSe2薄片包括了3层和5层两个厚度不同的区域. 图5(a)展示了Rdrag和$ {{R}}_{\text{NbSe}_2} $随温度的变化曲线. 随着温度降低, NbSe2层内电阻分别在5 K和3.5 K处出现两次显著的下降, 当温度低于2 K时, 电阻趋近于零. 基于NbSe2超导转变温度随厚度降低而降低这一特性推测[17,18], 5 K处对应于厚层区域的超导转变, 而3.5 K处则对应于薄层区域的超导转变. 相应地, 拖拽信号只在薄层NbSe2发生超导转变后开始出现. 值得注意的是, 随着温度从3.5 K进一步降低, Rdrag并不是单调增大, 而是先在1.7 K达到峰值(0.05 Ω), 然后随着温度进一步降低而减小. 此非单调性可通过Rdrag = Vdrag/Idrive = Idrag×$ {{R}}_{{\text{NbSe}}_{2}} $/Idrive定义解释, 其中Idrive和Idrag分别为石墨烯中施加的驱动电流和在超导层感应出的拖拽电流. 随温度降低, 拖拽电流Idrag持续增大, $ {{R}}_{{\text{NbSe}}_{2}} $则不断减小, 两者的竞争使得拖拽电阻Rdrag表现出非单调特性.

      图5的结果直观地展示了显著的拖拽信号仅在薄层NbSe2样品中出现. 由于器件#1和#2均是在空气中解理获得, 且文献[19]报道空气暴露会引发NbSe2降解, 导致出现转变温度下降和转变区间展宽, 甚至转变为绝缘态[20,21]. 这种超导电性被抑制被认为是与NbSe2发生光氧化反应生成氧化铌等产物有关[22]. 我们也据此推测我们器件中使用的NbSe2在解理和后续器件加工过程中, 超导电性由于这类非超导产物的出现而变得不均匀. 而这类不均匀性可能是出现超流拖拽效应的关键. 而在器件#2中, 厚层NbSe2无法探测到拖拽响应, 这可能与其不均匀性相对较弱有关. 为了进一步验证, 我们在氩气保护环境中解理了多个厚度≤3层的NbSe2薄片(NbSe2覆盖hBN保护层后取出), 然后进一步制备了石墨烯-NbSe2的拖拽器件, 结果在这类器件中均未探测到明显的拖拽信号. 这也进一步表明, 超导体的不均匀性应当是产生超流拖拽效应的必要条件.

      值得说明的是, 在石墨烯-LAO/STO体系中, 其观测到的超流拖拽效应被认为与LAO/STO体系内禀的非均匀超导特性密切相关[16]. LAO/STO二维界面在超导转变温度区间存在显著的超导相与金属相共存的现象, 使得体系表现出类似约瑟夫森结[23,24]. 理论分析表明, 石墨烯-LAO/STO体系中超流拖拽效应的出现, 源自这类非均匀超导体中量子涨落与石墨烯电荷涨落之间的相互作用[16]. 虽然这类相互作用还是由层间库仑相互作用主导, 但是其与超导特性密切相关. 基于此, 可认为石墨烯-NbSe2体系中观测到的超流拖拽信号, 以及此前基于超导金属体系的拖拽信号[12], 也应当是基于同样的机制, 即超导不均匀诱导的量子涨落. 区别在于LAO/STO是内禀的不均匀性, 而NbSe2和此前的超导金属体系, 则源自器件制备过程中引入的外禀不均匀性. 不均匀性的来源和强度等区别, 也可能是导致我们观测的超流拖拽信号的极性(正)与石墨烯-LAO/STO相反(负)的原因. 深入理解不均匀特性与超流拖拽效应的关联, 还需要后续进一步的理论探究.

      最后, 为了进一步量化分析, 参考之前的工作引入拖拽耦合比这一参数, 其定义为r = Idrag/Idrive = Rdrag/$ {{R}}_{{\text{NbSe}}_{2}} $, 该参数可以消除超导层内电阻对于拖拽信号的影响, 可以更为本征地反映层间拖拽效应的强度[16]. 图5(b)展示了器件#2中拖拽耦合比r随温度的变化曲线. 随着温度降低, r显著增大. 在可计算区间内其最大值可以达到0.13, 明显高于此前基于传统金属-超导金属体系的10–3. 此前层间栅压调制下的结果表明, 低载流子浓度会显著的增强拖拽响应. 石墨烯相对于Au等传统金属而言具有明显较低的载流子浓度, 这可能是石墨烯-NbSe2体系中拖拽耦合比得以提升的关键. 事实上, 石墨烯-LAO/STO体系与本实验相比, r值进一步增大(~0.3). 一个可能的原因是我们实验中使用的hBN绝缘层厚度(10—15 nm)相对于石墨烯-LAO/STO体系的LAO绝缘层(~2 nm)要更大, 从而减弱了层间库仑作用的强度. 此外, 作为超导层的NbSe2本身的正常态载流子浓度(1015 cm–2)也远高于LAO/STO界面(1013 cm–2), 进一步增强了层间屏蔽效应.

    4.   结　论

    • 本研究成功构筑了二维半金属石墨烯与二维超导体NbSe2组成的新型电双层结构. 通过系统地表征层内输运和层间拖拽输运, 在NbSe2超导转变区间观测到显著的超流拖拽效应. 利用二维体系物性高度可调的特点, 系统探究了磁场和栅压调制下拖拽信号的响应规律. 对比研究发现, 拖拽效应仅出现在空气中解理的薄层NbSe2中, 而在厚层或氩气保护下解理的薄层NbSe2中, 均未探测到明显的拖拽响应. 本文结果进一步证实了超导体的不均匀性是产生超流拖拽响应的必要条件, 而拖拽测试也因此有望成为研究超导特性的新型探针. 针对超流拖拽信号极性和强度等的进一步探究, 将为我们进一步理解非均匀超导, 阐明普通载流子和库珀对之间相互作用提供重要参考.

    参考文献 (24)

目录

/

返回文章
返回