高级搜索

Heusler合金Co2FeAlxSi1–x跨尺度结构有序度调控及其对磁致伸缩性能的影响

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

姚亮, 芦光辉, 杜杰, 刘永昌, 郗学奎, 王文洪. Heusler合金Co2FeAlxSi1–x跨尺度结构有序度调控及其对磁致伸缩性能的影响[J]. 物理学报, 2025, 74(14): 147303-1. doi: 10.7498/aps.74.20250358
引用本文: 姚亮, 芦光辉, 杜杰, 刘永昌, 郗学奎, 王文洪. Heusler合金Co2FeAlxSi1–x跨尺度结构有序度调控及其对磁致伸缩性能的影响[J]. 物理学报, 2025, 74(14): 147303-1. doi: 10.7498/aps.74.20250358
shu
Liang YAO, Guanghui LU, Jie DU, Yongchang LAU, Xuekui XI, Wenhong WANG. Control of cross-scale structural order of Heusler alloy Co2FeAlxSi1–x and its influence on magnetostrictive properties[J]. Acta Physica Sinica, 2025, 74(14): 147303-1. doi: 10.7498/aps.74.20250358
Citation: Liang YAO, Guanghui LU, Jie DU, Yongchang LAU, Xuekui XI, Wenhong WANG. Control of cross-scale structural order of Heusler alloy Co2FeAlxSi1–x and its influence on magnetostrictive properties[J]. Acta Physica Sinica, 2025, 74(14): 147303-1. doi: 10.7498/aps.74.20250358
shu

Heusler合金Co2FeAlxSi1–x跨尺度结构有序度调控及其对磁致伸缩性能的影响

  • 1.

    天津工业大学电子与信息工程学院, 天津　300387

  • 2.

    中国科学院物理研究所, 北京　100190

  • 3.

    中国科学院大学, 北京　100049

    • 作者简介: 姚亮.E-mail: leayao9@163.com .
    通讯作者: E-mail: xi@iphy.ac.cn.;  E-mail: wenhongwang@tiangong.edu.cn.

  • 中图分类号: 73.61.At, 64.60.Cn, 75.80.+q

Control of cross-scale structural order of Heusler alloy Co2FeAlxSi1–x and its influence on magnetostrictive properties

  • 1.

    School of Electronics and Information Engineering, Tiangong University, Tianjin 300387, China

  • 2.

    Institute of Physics, Chinses Academy of Sciences, Beijing 100190, China

  • 3.

    University of Chinese Academy of Sciences, Beijing 100049, China

    • Corresponding authors: E-mail: xi@iphy.ac.cn.;  E-mail: wenhongwang@tiangong.edu.cn.

  • MSC: 73.61.At, 64.60.Cn, 75.80.+q

  • 摘要: 本文通过实验系统研究了Heusler合金Co2FeAlxSi1–x (x = 0, 0.25, 0.5, 0.75, 1)体系中原子占位有序度与磁致伸缩的关联机制. 研究发现, Al掺杂可导致体系从高度有序的L21结构向B2无序结构转变, 并在x = 0.25—0.5时诱导L21/B2两相共存界面态的形成, 此时有序度计算结果显示SL21/SB2 = 0.5—0.9. 实验结果表明, 这种界面态的出现显著增强了饱和磁致伸缩系数并在过渡到B2结构后再次减小. 该结果定量揭示了原子的局部无序占位可通过降低立方对称性、引入局域晶格畸变并改变磁畴结构, 从而提升磁弹耦合的物理机制. 本研究报道了12种Co基Heusler合金的磁致伸缩系数, 其中Co2MnGa和Co2CrGa展现出优于其他Co基Heusler合金的潜力, 填补了该体系磁致伸缩性能参数的空白, 并验证了该多晶材料的线性正磁致伸缩特性; 提出了基于原子占位有序度调控的磁致伸缩性能优化策略, 为开发耐高温、高自旋极化率的磁致伸缩材料提供了新方向.
    Abstract: Co-based Heusler alloys have emerged as highly promising systems within the Heusler alloy family due to their high Curie temperatures and potential half-metallicity. Since the concept of half-metallic ferromagnets is proposed, these alloys have attracted significant attention because of their high spin polarization, excellent magnetic performance, and thermal stability. The existing studies predominantly focus on spin-transport properties, but systematic studies on their magnetostriction remain scarce. The electronic structure and magnetism of Co-based Heusler alloys are critically dependent on atomic-site ordering: their spin polarization, Curie temperature, and magnetocrystalline anisotropy are closely related to crystal structure, such as L21 and B2. A highly ordered L21 structure is essential for maintaining half-metallicity, as structural disorder can induce significant changes in electronic hybridization and exchange interactions, thereby significantly changing macroscopic magnetism. Additionally, ordering control is also expected to modulate magnetostriction by modifying lattice symmetry and local distortions. Notably, in Fe–Ga alloys, disorder engineering has been employed to induce local short-range order and lattice distortion, thereby enhancing magnetostriction, a mechanism that may similarly operate in Co-based systems. However, the higher lattice symmetry and stronger orbital hybridization in these alloys can lead to fundamentally distinct mechanisms, which needs to be validated experimentally. This study focuses on the Co2FeAlxSi1–x system to systematically probe the relationship between composition-driven structural evolution (i.e., L21 to B2 transition) and magnetostrictive performance through adjusting Al/Si ratio. The study aims to clarify the correlation between composition-induced structural evolution and magnetostrictive behavior, thereby revealing the regulatory role of atomic ordering in magnetoelastic coupling and providing theoretical insight for designing high-performance magnetostrictive materials.The correlation between atomic site ordering and magnetostriction in Heusler alloy Co2FeAlxSi1–x (x = 0, 0.25, 0.5, 0.75, 1) is systematically investigated in experiment. The results reveal that Al doping drives a structural transition from the highly ordered L21 phase to the disordered B2 phase, inducing a coexisting L21/B2 interface state at x = 0.25–0.5, with the calculated ordering parameters $S_{L2_1}/S_{B2} $ ranging from 0.5 to 0.9. The experimental data demonstrate that this interface state significantly enhances the saturation magnetostriction coefficient (λs), which subsequently decreases as it further transitions to the B2-dominated structure. These findings quantitatively clarify the physical mechanism by which local atomic disorder enhances magnetoelastic coupling through reducing cubic symmetry, localizing lattice distortion, and changing magnetic domain configuration. Furthermore, this study reports for the first time the magnetostriction coefficients of 12 Co-based Heusler alloys, among which Co2MnGa and Co2CrGa exhibit superior potential compared with other Co based Heusler alloys, filling the gap in magnetostriction performance parameters of this system. The linear positive magnetostriction behaviors of the polycrystalline materials are also validated. This study provides a strategy for optimizing magnetostriction performance through atomic site ordering control, and points out a new direction for the development of magnetostrictive materials with high-temperature stability and high spin polarization.
  • 加载中

  • 图 1  (a) Co2FeAlxSi1–x的晶体结构(L21结构和B2结构); (b) Co2FeAlxSi1–x样品的粉末XRD图谱; (c) Co2FeAlxSi1–x样品的晶格常数随Al含量x的变化关系

    Figure 1.  (a) Crystal structure of Co2FeAlxSi1–x (L21 structure and B2 structure); (b) powder XRD patterns of Co2FeAlxSi1–x; (b) variation of lattice constant with Al content x in Co2FeAlxSi1–x.

    下载: 全尺寸图片 幻灯片

    图 2  Co2FeAlxSi1–x样品退火1 d (a)和7 d (b)的粉末XRD图谱; (c)—(e)退火前后样品的有序度$S_{L2_1} $和SB2随Al含量x的变化关系 　　

    Figure 2.  (a), (b) Powder XRD patterns of Co2FeAlxSi1–x annealed for 1 day and 7 days; (c)–(e) variation of ordering degrees $S_{L2_1} $ and SB2 with Al content x before and after annealing.

    下载: 全尺寸图片 幻灯片

    图 3  (a) 3种不同有序态的磁致伸缩曲线; (b) Co2FeAlxSi1–x退火前后的磁致伸缩应变λs随Al含量x的变化关系

    Figure 3.  (a) Magnetostriction curves of three different ordered states; (b) variation of magnetostriction λs with Al content x in Co2FeAlxSi1–x before and after annealing.

    下载: 全尺寸图片 幻灯片

    图 4  (a) Co2FeAlxSi1–x的磁致伸缩应变λs随SL21的变化关系; (b) Co2FeAlxSi1–x的磁致伸缩应变λs随SL21/SB2的变化关系

    Figure 4.  (a) Variation of magnetostriction λs with SL21 and SB2 in Co2FeAlxSi1–x; (b) variation of magnetostriction λs with SL21/SB2 in Co2FeAlxSi1–x.

    下载: 全尺寸图片 幻灯片

    图 5  Co2FeAlxSi1–x的(a)M-H曲线与(b)磁致伸缩曲线

    Figure 5.  (a) M-H and (b) magnetostriction of Co2FeAlxSi1–x.

    下载: 全尺寸图片 幻灯片

    图 6  多晶材料转角磁致伸缩测量示意图

    Figure 6.  Schematic diagram of the rotational magnetostriction measurement for polycrystalline materials.

    下载: 全尺寸图片 幻灯片

    图 7  Co2FeAlxSi1–x的磁致伸缩应变λ随θ的变化关系

    Figure 7.  Variation of magnetostriction λ with θ in Co2FeAlxSi1–x.

    下载: 全尺寸图片 幻灯片

    表 1  部分Co基Heusler合金的晶格常数a, 居里温度Tc, 自旋极化率P [34–53]与磁致伸缩系数λs

    Table 1.  Lattice constant a, Curie temperature Tc, spin polarization P [34–53], and magnetostriction λs of selected co-based heusler alloys.

    成分a/ÅTc/KP/%λs/ppm
    Co2FeSi5.64511005722
    Co2FeAl5.72811705821
    Co2FeGa5.73710565924
    Co2VGa5.7923577513
    Co2CrAl5.887334628
    Co2CrGa5.7654956142
    Co2MnAl5.7496935914
    Co2MnGa5.7676945545
    Co2MnSi5.6549855618
    Co2MnGe5.7499055825
    Co2MnSn5.9848296020
    Co2MnSb5.943600508
    下载: 导出CSV
  • [1] Gupta R, Husain S, Kumar A, Brucas R, Rydberg A, Svedlindh P 2021 Adv. Opt. Mate. 9 2001987 doi: 10.1002/adom.202001987
    [2] Kimura T, Hashimoto N, Yamada S, Miyao M, Hamaya K 2012 NPG Asia Mater. 4 e13 doi: 10.1038/am.2012.24
    [3] Palmstrøm C J 2016 Prog. Cryst. Growth Ch. Mater. 62 371 doi: 10.1016/j.pcrysgrow.2016.04.020
    [4] Yamada S, Kato M, Ichikawa S, Yamada M, Naito T, Fujiwara Y, Hamaya K 2023 Adv. Electron. Mater. 9 2300045 doi: 10.1002/aelm.202300045
    [5] Bachaga T, Zhang J, Khitouni M, Sunol J J 2019 Int. J. Adv. Manuf. Technol. 103 2761 doi: 10.1007/s00170-019-03534-3
    [6] Planes A, Mañosa L, Moya X, Krenke T, Acet M, Wassermann E F 2007 J. Magn. Magn. Mater. 310 2767 doi: 10.1016/j.jmmm.2006.10.1041
    [7] de Groot R A, Mueller F M, Engen P G v, Buschow K H J 1983 Phys. Rev. Lett. 50 2024 doi: 10.1103/PhysRevLett.50.2024
    [8] Galanakis I, Mavropoulos P, Dederichs P H 2006 J. Phys. D: Appl. Phys. 39 765 doi: 10.1088/0022-3727/39/5/S01
    [9] Wang W H, Sukegawa H, Shan R, Mitani S, Inomata K 2009 Appl. Phys. Lett. 95 182502 doi: 10.1063/1.3258069
    [10] 杨艳敏, 李佳, 马洪然, 杨广, 毛秀娟, 李聪聪 2019 物理学报 68 046101 doi: 10.7498/aps.68.20181641 Yang Y M, Li J, Ma H R, Yang G, Mao X J, Li C C 2019 Acta Phys. Sin. 68 046101 doi: 10.7498/aps.68.20181641
    [11] Clark A E 1980 Ferromagnetic Materials (Vol. 1) (Amsterdam: North-Holland) p531
    [12] Clark A E, Restorff J B, Wun-Fogle M, Lograsso T A, Schlagel D L 2000 IEEE Trans. Magn. 36 3238 doi: 10.1109/20.908752
    [13] Lograsso T A, Ross A R, Schlagel D L, Clark A E, Wun-Fogle M 2003 J. Alloy. Compd. 350 95 doi: 10.1016/S0925-8388(02)00933-7
    [14] Guruswamy S, Srisukhumbowornchai N, Clark A E, Restorff J B, Wun-Fogle M 2000 Scr. Mater. 43 239 doi: 10.1016/S1359-6462(00)00397-3
    [15] Sakon T, Fujimoto N, Kanomata T, Adachi Y 2017 Metals 7 410 doi: 10.3390/met7100410
    [16] Ullakko K, Huang J K, Kantner C, O’Handley R C, Kokorin V V 1996 Appl. Phys. Lett. 69 1966 doi: 10.1063/1.117637
    [17] Sato M, Okazaki T, Furuya Y, Wuttig M 2003 Mater. Trans. 44 372 doi: 10.2320/matertrans.44.372
    [18] Zhang M, Brück E, Boer F R d, Wu G H 2005 J. Phys. D: Appl. Phys. 38 1361 doi: 10.1088/0022-3727/38/9/006
    [19] 代学芳, 孙晨光, 曲静萍, 李养贤, 朱伟, 陈京兰, 吴光恒 2009 物理学报 58 8602 doi: 10.3321/j.issn:1000-3290.2009.12.075 Dai X F, Sun C G, Qu J P, Li Y X, Zhu W, Chen J L, Wu G H 2009 Acta Phys. Sin. 58 8602 doi: 10.3321/j.issn:1000-3290.2009.12.075
    [20] Ravel B, Raphael M P, Harris V G, Huang Q 2002 Phys. Rev. B 65 184431 doi: 10.1103/PhysRevB.65.184431
    [21] Srivastava Y, Vajpai S K, Srivastava S 2017 J. Magn. Magn. Mater. 433 141 doi: 10.1016/j.jmmm.2017.02.060
    [22] 赵晶晶, 舒迪, 祁欣, 刘恩克, 朱伟, 冯琳, 王文洪, 吴光恒 2011 物理学报 60 107203 doi: 10.7498/aps.60.107203.2 Zhao J J, Shu D, Qi X, Liu E K, Zhu W, Feng L, Wang W H, Wu G H 2011 Acta Phys. Sin. 60 107203 doi: 10.7498/aps.60.107203.2
    [23] Chumak O, Nabiałek A, Baczewski L T, Seki T, Wang J, Takanashi K, Szymczak H 2025 arXiv: 2502.19102 [cond-mat. mtrl-sci]
    [24] Szwacki N G, Majewski J A 2016 J. Magn. Magn. Mater. 409 62 doi: 10.1016/j.jmmm.2016.02.031
    [25] 赵晶晶, 祁欣, 刘恩克, 朱伟, 钱金凤, 李贵江, 王文洪, 吴光恒 2011 物理学报 60 047108 doi: 10.7498/aps.60.047108 Zhao J J, Qi X, Liu E K, Zhu W, Qian J F, Li G J, Wang W H, Wu G H 2011 Acta Phys. Sin. 60 047108 doi: 10.7498/aps.60.047108
    [26] Balke B, Wurmehl S, Fecher G H, Felser C, Kübler J 2008 Sci. Technol. Adv. Mater. 9 014102 doi: 10.1088/1468-6996/9/1/014102
    [27] Titov A, Jiraskova Y, Zivotsky O, Bursik J, Janickovic D 2018 AIP Adv. 8 047206 doi: 10.1063/1.4993698
    [28] Bosu S, Sakuraba Y, Saito K, Wang H, Mitani S, Takanashi K 2010 Phys. Rev. B 81 054426 doi: 10.1103/PhysRevB.81.054426
    [29] Chopra H D, Wuttig M 2015 Nature 521 340 doi: 10.1038/nature14459
    [30] He Y K, Han Y J, Stamenov P, Kundys B, Coey J M D, Jiang C B, Xu H B 2018 Nature 556 E5 doi: 10.1038/nature25780
    [31] He Y K, Jiang C B, Coey J M D, Xu H B 2018 J. Magn. Magn. Mater. 466 351 doi: 10.1016/j.jmmm.2018.07.019
    [32] Clark A E, Wun-Fogle M 2002 Smart Structures and Materials 2002 Conference San Diego, Ca, Mar 18–21, 2000 p421
    [33] Ksenofontov V, Wójcik M, Wurmehl S, Schneider H, Balke B, Jakob G, Felser C 2010 J. Appl. Phys. 107 09B106 doi: 10.1063/1.3352572
    [34] Brown P J, Neumann K U, Webster P J, Ziebeck K R A 2000 J. Phys. -Condes. Matter 12 1827 doi: 10.1088/0953-8984/12/8/325
    [35] Buschow K H J, Vanengen P G 1981 J. Magn. Magn. Mater. 25 90 doi: 10.1016/0304-8853(81)90151-7
    [36] Buschow K H J, Vanengen P G, Jongebreur R 1983 J. Magn. Magn. Mater. 38 1 doi: 10.1016/0304-8853(83)90097-5
    [37] Guillemard C, Petit-Watelot S, Rojas-Sánchez J C, et al. 2019 Appl. Phy. Lett. 115 172401 doi: 10.1063/1.5121614
    [38] Kanomata T, Chieda Y, Endo K, et al. 2010 Phys. Rev. B 82 144415 doi: 10.1103/PhysRevB.82.144415
    [39] Karthik S V, Rajanikanth A, Takahashi Y K, Okhubo T, Hono K 2006 Appl. Phys. Lett. 89 3 doi: 10.1063/1.2245224
    [40] Kourov N I, Marchenkov V V, Perevozchikova Y A, Weber H W 2017 Phys. Solid State 59 898 doi: 10.1134/S1063783417050183
    [41] Kudryavtsev Y V, Uvarov N V, Iermolenko V N, Dubowik J 2010 J. Appl. Phys. 108 113708 doi: 10.1063/1.3511433
    [42] Nakatani T M, Gercsi Z, Rajanikanth A, Takahashi Y K, Hono K 2008 J. Phys. D: Appl. Phys. 41 225002 doi: 10.1088/0022-3727/41/22/225002
    [43] Nakatani T M, Rajanikanth A, Gercsi Z, Takahashi Y K, Inomata K, Hono K 2007 J. Appl. Phys. 102 8 doi: 10.1063/1.2767229
    [44] Paudel M R, Wolfe C S, Pathak A K, Dubenko I, Ali N, Osofsky M S, Prestigiacomo J C, Stadler S 2012 J. Appl. Phys. 111 023903 doi: 10.1063/1.3676264
    [45] Paudel M R, Wolfe C S, Patton H, Dubenko I, Ali N, Christodoulides J A, Stadler S 2009 J. Appl. Phys. 105 4 doi: 10.1063/1.3054291
    [46] Rajanikanth A, Takahashi Y K, Hono K 2007 J. Appl. Phys. 101 5 doi: 10.1063/1.2409775
    [47] Rajanikanth A, Takahashi Y K, Hono K 2008 J. Appl. Phys. 103 5 doi: 10.1063/1.2930867
    [48] Ritchie L, Xiao G, Ji Y, et al. 2003 Phys. Rev. B 68 104430 doi: 10.1103/PhysRevB.68.104430
    [49] Sakuraba Y, Nakata J, Oogane M, Ando Y, Kato H, Sakuma A, Miyazaki T, Kubota H 2006 Appl. Phys. Lett. 88 3 doi: 10.1063/1.2162867
    [50] Umetsu R Y, Kobayashi K, Fujita A, Kainuma R, Ishida K, Fukamichi K, Sakuma A 2008 Phys. Rev. B 77 104422 doi: 10.1103/PhysRevB.77.104422
    [51] Wurmehl S, Fecher G H, Ksenofontov V, Casper F, Stumm U, Felser C, Lin H J, Hwu Y 2006 J. Appl. Phys. 99 3 doi: 10.1063/1.2167330
    [52] Zhang M, Brück E, Boer F R d, Li Z Z, Wu G H 2004 J. Phys. D: Appl. Phys. 37 2049 doi: 10.1088/0022-3727/37/15/001
    [53] Zhang X Q, Xu H F, Lai B L, et al. 2018 Sci. Rep. 8 8074 doi: 10.1038/s41598-018-26285-9
  • 加载中
图( 7) 表( 1)
计量
  • 文章访问数:  25
  • HTML全文浏览数:  25
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-18
  • 刊出日期:  2025-07-20

Heusler合金Co2FeAlxSi1–x跨尺度结构有序度调控及其对磁致伸缩性能的影响

    通讯作者: E-mail: xi@iphy.ac.cn.; 
    通讯作者: E-mail: wenhongwang@tiangong.edu.cn.
    作者简介: 姚亮.E-mail: leayao9@163.com
  • 1. 天津工业大学电子与信息工程学院, 天津　300387
  • 2. 中国科学院物理研究所, 北京　100190
  • 3. 中国科学院大学, 北京　100049
  • 收稿日期:  2025-03-18

摘要: 本文通过实验系统研究了Heusler合金Co2FeAlxSi1–x (x = 0, 0.25, 0.5, 0.75, 1)体系中原子占位有序度与磁致伸缩的关联机制. 研究发现, Al掺杂可导致体系从高度有序的L21结构向B2无序结构转变, 并在x = 0.25—0.5时诱导L21/B2两相共存界面态的形成, 此时有序度计算结果显示SL21/SB2 = 0.5—0.9. 实验结果表明, 这种界面态的出现显著增强了饱和磁致伸缩系数并在过渡到B2结构后再次减小. 该结果定量揭示了原子的局部无序占位可通过降低立方对称性、引入局域晶格畸变并改变磁畴结构, 从而提升磁弹耦合的物理机制. 本研究报道了12种Co基Heusler合金的磁致伸缩系数, 其中Co2MnGa和Co2CrGa展现出优于其他Co基Heusler合金的潜力, 填补了该体系磁致伸缩性能参数的空白, 并验证了该多晶材料的线性正磁致伸缩特性; 提出了基于原子占位有序度调控的磁致伸缩性能优化策略, 为开发耐高温、高自旋极化率的磁致伸缩材料提供了新方向.

English Abstract

    全文HTML

    1.   引　言

    • 近年来, Heusler合金(化学式X2YZ)因其丰富的物理性质在自旋电子学器件[1–4]、形状记忆合金[5,6]等领域取得了卓著的研究成果. 其中, Co基Heusler合金因其高居里温度与潜在半金属性成为该家族中最具潜力的体系之一. 自1983年de Groot首次提出半金属铁磁体概念以来[7], 多种Co基Heusler合金(如Co2MnSi, Co2MnGe, Co2MnSn等)相继被理论预测或实验证实具有半金属性[8,9]. 此后Co基Heusler合金凭借其高自旋极化率、高居里温度和较强的磁性备受关注[10]. 然而, 当前研究多聚焦于其自旋输运特性, 对其磁致伸缩性能的系统探索仍处于起步阶段.

      磁致伸缩效应源于材料的磁弹耦合, 其本质是铁磁性材料中原子磁矩的有序排列与晶格形变之间的相互作用. 目前广泛应用的磁致伸缩材料主要有Tb-Dy-Fe合金与Fe-Ga合金. Tb-Dy-Fe合金有λs > 1000 ppm(1 ppm = 10–6)的巨磁致伸缩和低磁晶各向异性[11], 但是材料脆性大, 驱动磁场强而且稀土元素含量大, 在实际应用中受限. Clark等[12]在2000年首次发现Fe-Ga合金的磁致伸缩可达~200 ppm, 后有研究报道了Fe-Ga合金的磁致伸缩最大可达400 ppm[13], 而且具有良好的力学性能和较低的饱和磁场[14]. 值得注意的是, Heusler合金在磁致伸缩方向的研究长期集中于Ni2MnGa等基于马氏体相变的铁磁形状记忆合金材料[15,16], 后来Co2NiGa同样被发现为此类磁场驱动相变磁致伸缩材料[17–19], 其大应变源于磁场驱动马氏体孪晶的重排过程. 相比之下, Co基Heusler合金的立方对称性晶格与成分可调性为实现磁致伸缩性能优化提供了新思路——通过原子占位有序度调控, 可能在不依赖相变的条件下增强磁弹性响应.

      研究表明, Co基Heusler合金的复杂电子结构与磁性对原子占位有序度非常敏感, 其自旋极化率(P)和居里温度(Tc)都容易受晶体结构(如L21, B2, A2)的影响. 其中L21结构的高度有序是高自旋极化率的必要条件, 而无序结构会破坏半金属性导致自旋极化率降低, Ravel等[20]通过计算与实验发现了Co2MnSi中Co-Mn原子的无序占位严重降低了材料的自旋极化率. 另外, 原子占位也会影响d轨道电子的交换作用, 进而影响居里温度, Srivastava等[21]在Co2CrAl中用Fe取代Cr使晶体结构由A2无序转变为B2/A2混合结构并认为Fe原子占据空位增强了d-d交换作用进而导致了居里温度升高. 显然有序度可直接影响材料的电子结构与交换作用, 而这过程中也影响了磁性[22]与磁晶各向异性. 最近有研究发现, 通过对磁性Weyl半金属Co2MnGa薄膜在不同温度下进行退火来改变其有序度发现L21相的出现显著增强了立方磁晶各向异性[23]. 结合磁致伸缩效应的原理, 可以推测原子占位有序度对Co基Heusler合金的磁致伸缩性能也可能有相似的作用机制. 早在Fe-Ga合金中就有研究表明, 有序-无序机制可能是磁致伸缩性能增强的一个关键, 无序结构中的Ga原子沿特定晶体方向的局部短程有序导致晶格的四方畸变, 从而大幅度提升了Fe-Ga合金的磁致伸缩[13], 这揭示了无序工程在磁致伸缩材料设计中的潜力. 然而, Co基Heusler合金的高对称性晶格与强轨道杂化特性可能导致其响应机制显著不同, 亟待实验验证.

      Co2FeAlxSi1–x合金体系通过调整Al/Si比例能灵活调控系统有序度. 基于此, 本文以Co2FeAlxSi1–x合金为主要研究对象, 聚焦原子占位有序度与磁致伸缩性能两个要素. 通过掺杂Al原子替代Si位点, 调控Co2FeSi的原子占位有序度, 进而诱导结构转变, 来探究成分-结构-磁致伸缩性能的关联机制.

    2.   实验方法

    • Co2FeAlxSi1–x (x = 0, 0.25, 0.5, 0.75, 1)合金样品采用纯度大于99.9%的金属单质按照化学计量配比, 配比误差小于0.1%, 在氩气氛围保护下使用电弧炉均匀熔炼4次制备得到5种组分的多晶样品, 重量损失小于1%. 随后经过线切割得到磁致伸缩测量样品, 将不同样品分别真空密封在石英管内, 在873 K (600 ℃)下分别退火1 d和7 d, 随后自然冷却至室温. 采用Cu靶X射线粉末衍射仪(XRD)对退火前后的样品进行材料结构表征并计算晶格常数. 磁致伸缩测量采用标准电阻应变片法(应变片灵敏度系数k = 2.08 ± 0.01), 依托自搭建高精度磁致伸缩测量设备测量λ-H曲线和λ-θ曲线, 得到室温磁致伸缩结果. 采用振动样品磁强计(VSM, 磁场范围0—1.2 T)对磁致伸缩样品进行磁化曲线(M-H)测试, 以分析其磁化行为与有序度的关联性.

    3.   结果与讨论

      3.1.   Co2FeAlxSi1–x的晶体结构与有序度

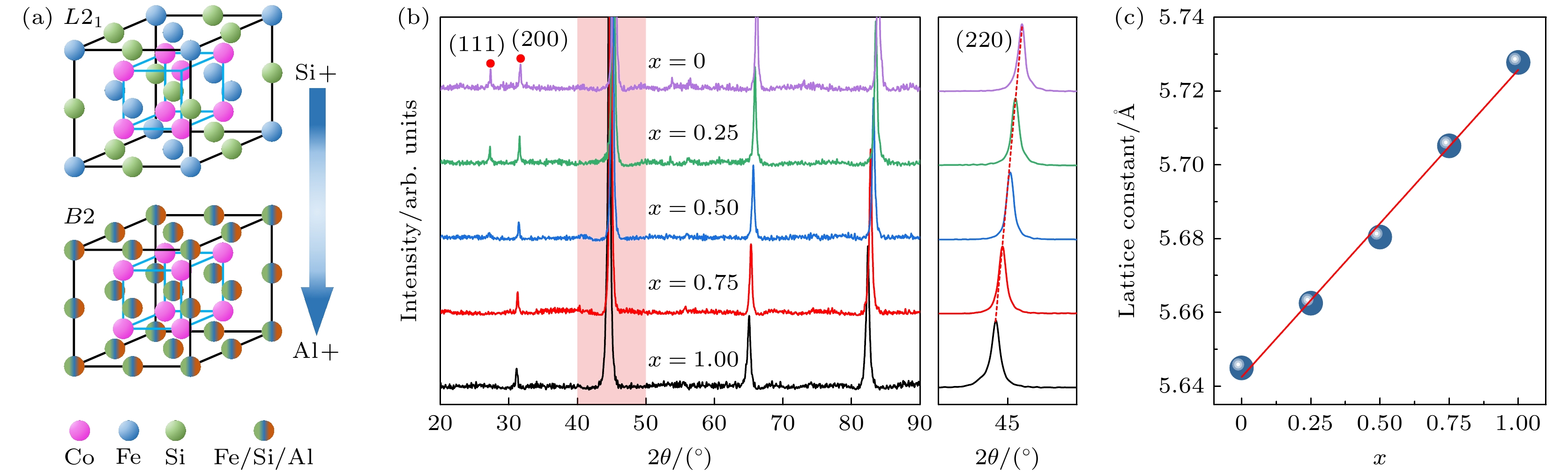
    • Full-Heusler合金是一种原子占位高度有序的三元金属间化合物, 其一般形式通常为X2YZ, 其中X, Y为过渡族金属, Z为主族元素, 理想情况下其晶体结构为L21结构, 各原子占据特定晶格位点形成长程有序结构, 后续实验证明了Co2FeAlxSi1–x的晶体结构为L21结构和B2结构, 如图1(a) 所示, L21结构可以看作由8个体心立方晶格堆叠而成, 其中4个Co原子分别占据体心位置, Fe原子和Si/Al原子在8个端点交替占位; B2结构为4个Co原子分别占据体心位置, 而Fe原子与(Si, Al)原子混乱占位.

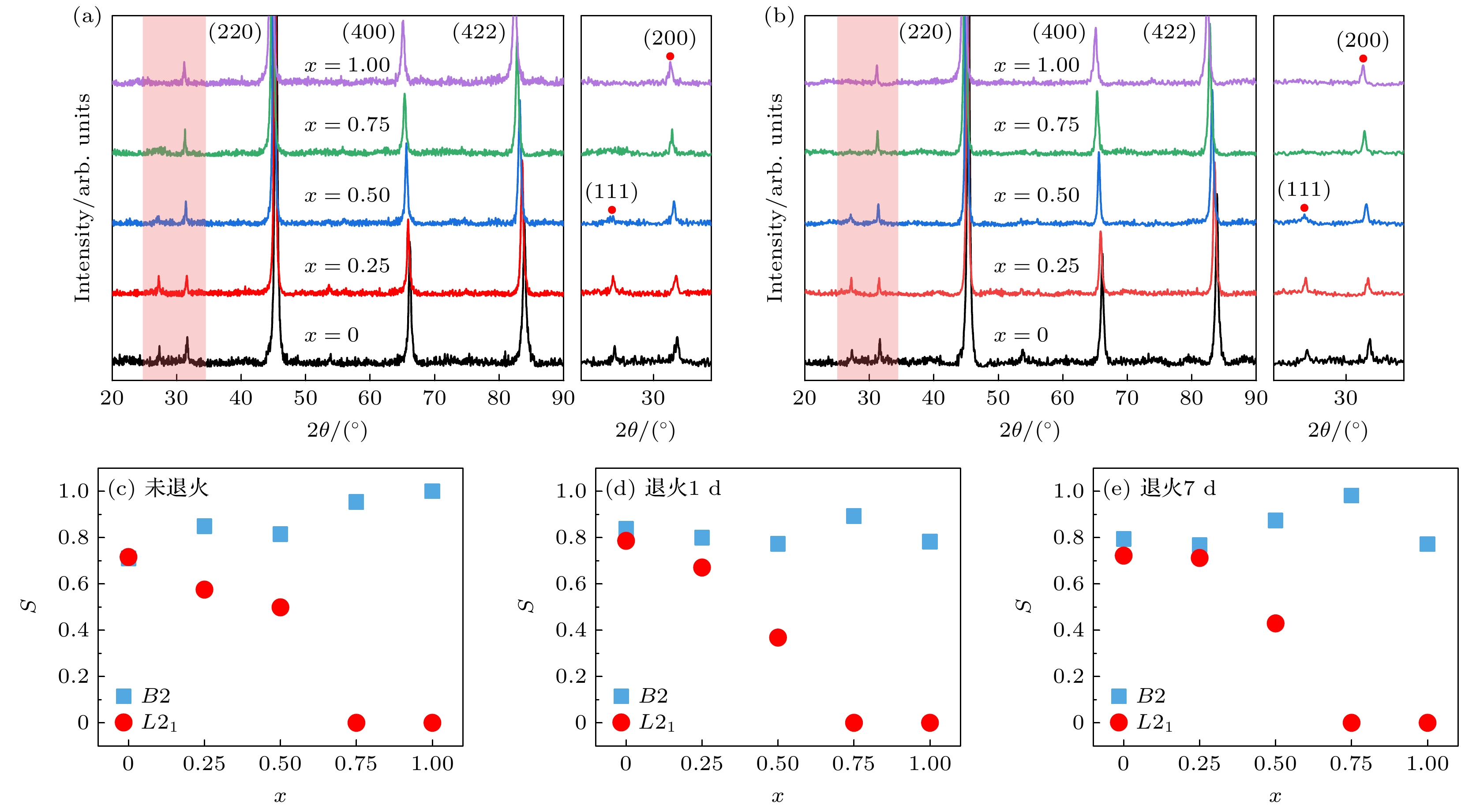
      根据X射线衍射可以确定材料的结构, 从Co2FeAlxSi1–x (x = 0, 0.25, 0.5, 0.75, 1)的粉末XRD结果(图1(b))可以看出, Al含量在0—0.5时, 除了几个主要衍射峰外, 在30°附近存在(111)和(200)两个超晶格峰, 而当Al含量在0.75—1时, 除几个主要衍射峰外, 在30°附近只存在(200)一个超晶格峰, 在高度有序的Heusler合金的XRD衍射峰中出现(111)和(200)则可以认定样品为L21结构, 如果只出现(200)则可以认定样品为B2结构. 因此在Co2FeAlxSi1–x体系中, 存在L21和B2两种结构, 在x ≤ 0.5时更容易形成L21高度有序结构, 而在x > 0.5时更容易形成B2有序结构, 也可以说富Si的条件有助于材料的有序化, 这是因为Si与过渡元素的p-d轨道杂化比Al更强, 稳定了L21结构[24,25]. 另外, 在XRD图谱中还可以清晰地看出随着Al含量的增大, (200)峰位明显向左偏移, 如图1(b)所示, 这直接证明了晶格常数的增大, 根据布拉格方程$n\lambda = 2 d\sin \theta $, 当晶格常数变化时, 晶面间距d会改变, 导致衍射角θ发生变化, 进而引起衍射峰的偏移. 在这里Al原子半径相对Si原子半径较大, 而且Al与过渡元素的p-d轨道杂化较弱, 因此随Al含量增大, 晶格常数增大, 晶面间距d也增大, 所以衍射角减小, 峰位向低角度偏移, 根据XRD结果可以估算得到晶格常数, 从图1(c)可以看出, 样品的晶格常数随Al含量的增大呈线性增大的趋势, 其中Co2FeSi (x = 0)的晶格常数为5.645 Å, Co2FeAl (x = 1)的晶格常数为5.728 Å, 这与已经报道的结果相近[26,27], x = 0.25, 0.5, 0.75时的晶格常数分别为5.662, 5.682, 5.705 Å.

      通常在实验中采用退火的手段来优化原子占位进而促进有序化, 将不同组分样品在873 K (600 ℃)的温度下分别退火. 图2(a), (b)分别为退火1 d和7 d的粉末XRD图谱, 右侧小图为红色阴影部分(111)和(200)的放大图. 可以看到在退火后依然存在明显的(111)和(200)超晶格峰, 所有样品仍然保持x ≤ 0.5时的L21结构和x > 0.5时的B2结构, 没有多余的杂相产生. 从(111)和(200)的放大图中可以观察到随Al含量增大, (111)超晶格峰强度减弱, 在x = 0.5时强度最弱, 在x = 0.75时(111)消失. XRD结果并不能明显表现出系统的有序程度, 有序度参数S可以直观表示出原子占位的有序程度. 进一步在25°—35°范围内精细化扫描(111)和(200)超晶格峰, 根据衍射峰相对强度, 可以通过以下两式来估算各个样品的原子占位有序度S:

      (1)式和(2)式可分别计算L21结构和B2结构的有序度参数S, I(111)和I(200)表示两个超晶格峰值强度, I(220)和I(400)表示两个主峰峰值强度, “exp”和“cal”分别表示XRD测量结果与理论有序度的计算结果, 理论值可通过模拟得到. 当S = 1时, 表示系统完全有序, 当S = 0时, 表示系统完全无序[28].

      图2(c)—(e)分别显示未退火, 退火1 d和退火7 d的有序度S随Al含量x的变化关系, 由计算结果可以直观地看出, x = 0—0.5时系统中主要为L21结构, 但随Al含量的增大, L21结构占比减小, B2结构占比增大, 表明此时系统处于L21结构和B2结构两相共存状态. x = 0时SL21最大, 在x = 0.7—0.8时, 最接近L21有序, 由于Si与Co, Fe的混合焓大于Al, 因此Si与这种过渡金属成键能力相对Al要更强, 强的键合力增强了原子占位稳定性, 因此随x的增大$S_{L2_1} $逐渐减小, 也就是说随着Al含量的增大, B2结构的占比是增大的. x = 0.25时$S_{L2_1} $为0.5—0.7, 到x = 0.5时$S_{L2_1}$减小至0.3—0.5. 在x = 0.75时已完全成为B2结构, 此时没有超晶格峰(111)出现, 计算结果与XRD测试结果完全相符. 另外, 整个体系中所有样品的SB2>0.7, 都维持着良好的B2结构, 值得注意的是, x = 1(Co2FeAl)样品在没有退火时(图2(c))SB2几乎达到了0.99, 呈现近乎理想的B2结构, 而退火1 d和7 d后(图2(d), (e))SB2较退火前有明显减小, 这可能是因为Al原子自身弱的成键能力和较大原子半径, 导致的不稳定加上退火时高温下的热扰动使得原子趋向混乱无序, 而自然冷却的条件使其更容易保持在了相对无序的状态, 这也可以解释在x ≥ 0.5时退火后的$S_{L2_1}$减小, 而x < 0.5时退火后$S_{L2_1}$增大的现象. 对于x = 0.25, 0.5, 0.75时, 系统的总能量随Al含量的增大而减小, 故$S_{L2_1} $减小. 另外, 可以观察到x = 0, 0.25, 0.5时, 退火后的$S_{L2_1}$相较于退火前增大, 而x = 0.75, 1时SB2较于退火前减小, 这一现象同样印证了上述观点.

      • 3.2.   Co2FeAlxSi1–x的有序度与磁致伸缩的关联性

    • 采用了自主搭建装置进一步测试了样品的磁致伸缩性能, 电阻应变片法可简单并精确测试材料的磁致伸缩系数(λs), 其基本过程为应变片随样品在施加不同磁场时产生不同大小的形变, 应变片上的电阻栅随之产生形变, 电阻栅形变后使其电阻发生变化, 测量其电阻变化即可得到样品本身的应变.

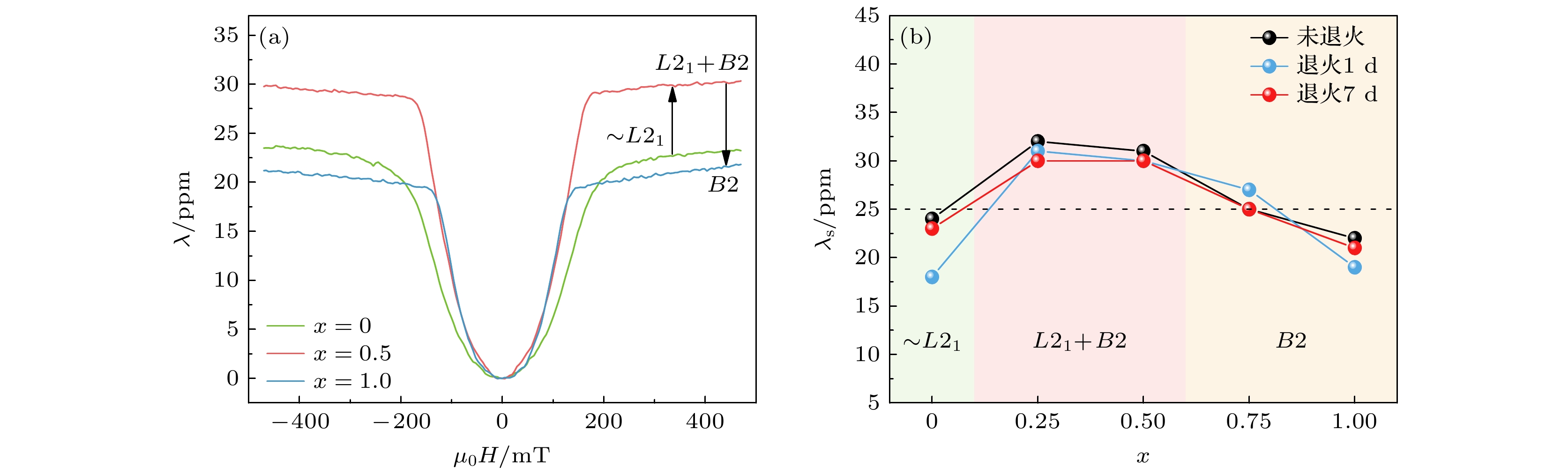
      经过磁致伸缩测量我们发现了Co2FeAlxSi1–x在不同有序结构下的磁致伸缩应变存在明显差异, 图3(a)分别为处于不同有序态下的3个已退火7 d样品的磁致伸缩曲线, 可以看到, 在L21+B2时λs明显增大. Co2FeAlxSi1–x所有样品退火前后的磁致伸缩测量结果如图3(b), 其中黑色、蓝色、红色曲线分别表示未退火样品、退火1 d和退火7 d样品的磁致伸缩应变随Al含量x的变化关系. 整体来看磁致伸缩应变λs随Al含量x的变化呈先增大后减小的趋势, λs从x = 0—0.25明显增大, x = 0.5时与x = 0.25时磁致伸缩值大小相近, 此时应变最大可达到30—32 ppm, 从0.5—1几乎呈线性减小的趋势. 值得注意的是, 正分的x = 0 (Co2FeSi)和x = 1(Co2FeAl)磁致伸缩应变始终是最小的(<25 ppm). 这些现象都说明了少量Al的引入是导致其磁致伸缩应变增大的根本原因, 过量的Al反而会导致磁致伸缩应变减小.

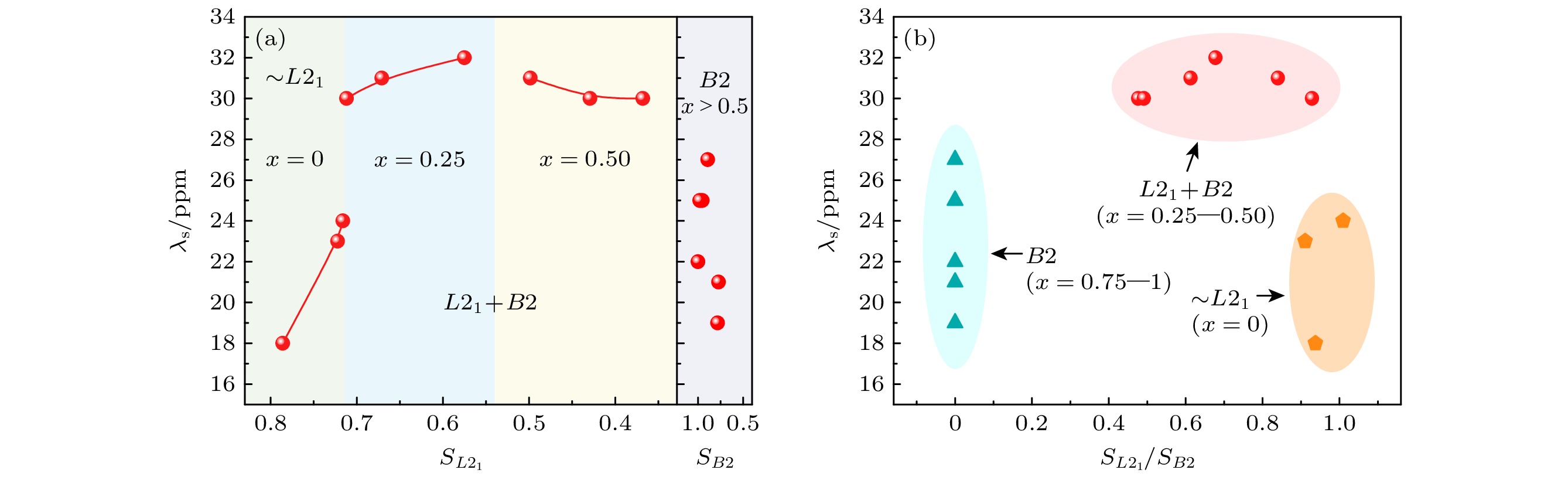
      将磁致伸缩测量结果与有序度计算结果进行综合分析, 因在x = 0—0.5时材料体系以L21结构为主导, 所以接下来将主要以L21结构进行分析. 图4(a)总结了x = 0—0.5的所有样品磁致伸缩应变λs随$S_{L2_1} $的变化关系, 其中绿色区域为Al含量为0时的磁致伸缩值, 蓝色区域为Al含量为0.25时的磁致伸缩值, 黄色区域为Al含量为0.5时的磁致伸缩值, 另外右侧小图为x = 0.75, 1时完全B2有序的结果. 不难看出λs随$S_{L2_1}$的减小呈现先增大, 再逐渐变缓, 然后减小的趋势, 其中在$S_{L2_1}$从0.8—0.7区间λs迅速增大, 随后在0.7—0.55区间内变缓, 在小于0.55后慢慢减小, 根据此变化趋势也可以推测出在$S_{L2_1}<0.4 $直到B2区域后λs会迅速减小. 由此可以得出: 1) 当材料为高度L21有序时各原子严格占位, 此时材料通常具有高自旋极化率和良好的磁性, 但磁致伸缩可能较低, 因为原子排列有序, 磁畴结构可能更规则, 磁矩的重新取向需要较高的能量, 导致晶格应变较小; 2) 当少量Al替代Si时, 结构从L21逐渐转向B2, Fe/(Si, Al)占位变得混乱导致$S_{L2_1} $降低, 此时处于L21和B2两相共存的界面态, 部分原子无序可能使原子间交换作用的强度不均匀, 降低晶体结构的对称性, 改变磁晶各向异性, 从而形成部分较大尺寸且方向随机的磁畴, 磁场下磁畴的旋转与移动更有助于增强磁弹耦合并产生较大的磁致伸缩应变; 3) 当更多Al掺入直至完全替代Si时, 材料完全转为B2结构, 此时原子无序程度更高, 原子占位过于混乱导致磁畴尺寸减小且方向过于随机, 此时磁晶各向异性更加弱, 磁畴之间的耦合作用减小, 使在宏观上无法形成一致的应变方向, 导致整体磁致伸缩减小.

      此前认为L21和B2两相共存的界面态会是磁致伸缩增大的主要原因, 因此也可以通过计算$S_{L2_1}/S_{B2} $作为参考来衡量不同有序态的占比对磁致伸缩的影响, $S_{L2_1}/S_{B2} $可以说明在界面态L21结构与B2结构的比例. 图4(b)为磁致伸缩值随$S_{L2_1}/S_{B2} $的值的变化关系, 其中绿色区域为完全B2结构, 此时$S_{L2_1}/S_{B2} $为0, 红色区域为两相共存的界面态, 橙色区域为接近完全L21结构. 可以看出红色区域的磁致伸缩值明显最大, 此时$S_{L2_1}/S_{B2} $的值为0.5—0.9, 这再次说明了以L21结构为主的少部分B2结构有助于提高整体的磁致伸缩性能.

      • 3.3.   Co2FeAlxSi1–x的M-H曲线与磁致伸缩性能分析

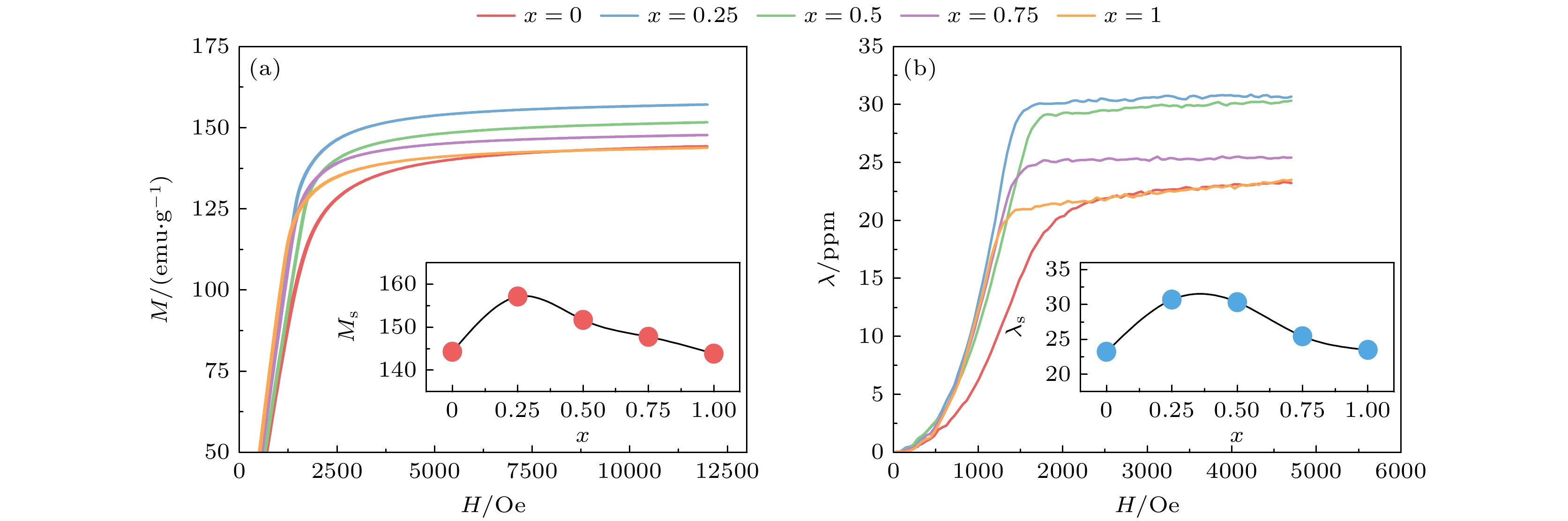
    • 通过VSM对Co2FeAlxSi1–x系列样品的磁化曲线(M-H)进行测试, 所有样品均为形状均匀的磁致伸缩测试专用样品. 实验结果表明(图5), M-H曲线中观测到的饱和磁场与对应样品的磁致伸缩曲线饱和磁场基本一致. 进一步分析发现, 与未掺杂的Co2FeSi(红色曲线)相比, Al元素的引入显著降低了样品的饱和磁场. 这是因为Al掺杂诱导的B2相内原子占位无序破坏了原本L21有序相的立方对称性, 从而显著削弱了磁晶各向异性能. 这种对称性破缺使材料磁矩在外加磁场中更易发生定向排列, 进而减少实现磁饱和所需的外加磁场强度.

      通过图5(a)的测试结果可以观察到, Co2FeAlxSi1–x合金的饱和磁化强度Ms随Al含量增大呈现先上升后下降的非单调变化规律. 当Al掺杂量较低时, Ms增大并在x = 0.25处达到峰值; 而随着Al含量进一步增大(x > 0.25), Ms开始线性下降, 直至Al完全替代Si的Co2FeAl (x = 1)降至最低值. 这是因为Al原子部分取代Si原子后, 材料中形成L21/B2两相共存结构. 界面区域的局部晶格畸变以及Al原子与Fe/Co的p-d轨道杂化效应协同增强了铁磁交换作用, 从而显著提升Ms. 随着Al含量增大, B2结构逐渐占据主导地位, Fe/Al原子的随机占位破坏了晶格的长程有序性从而导致交换作用弱化. 此外, Al原子的弱成键能力加剧了原子占位无序化, 最终在Co2FeAl中形成高度无序结构, 磁矩协同性大幅降低, 致使Ms减小. 值得注意的是, 对比图5(a), (b)的数据, Ms随Al含量的变化趋势与饱和磁致伸缩系数λs的变化规律高度相似, 表明磁化强度与磁致伸缩行为之间存在强关联性, 其物理本质源于晶格与磁矩的共同调控作用. 同时也证明了Al的引入诱导的原子占位无序界面产生的磁畴结构变化影响了磁致伸缩性能.

      • 3.4.   Co2FeAlxSi1–x的线性磁致伸缩

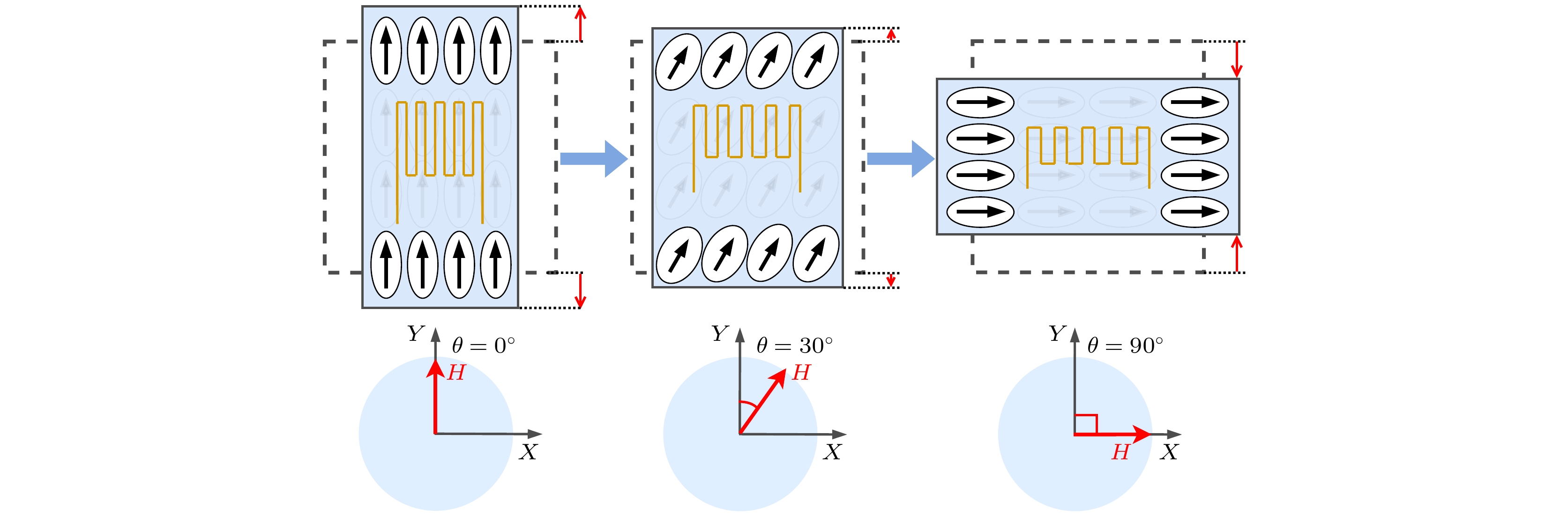
    • 一般铁磁性材料在磁场下表现为线性磁致伸缩, 样品在平行于磁场方向长度伸长时, 垂直磁场方向缩短, 总体积几乎保持不变[29–31]. 本文中Co2FeAlxSi1–x所有样品为电弧熔炼制备的立方晶系多晶材料, 由于多晶材料由大量随机取向的晶粒组成, 整体的磁致伸缩应变应该是各个晶粒应变的统计平均, 理论上各晶粒的各向异性应变会相互抵消, 导致宏观上各向同性. 因此认为, 如果多晶材料是各向同性的, 那么无论磁场方向如何旋转, 测量到的磁致伸缩应变应该与磁场方向无关, 即不随θ变化. 理论上来说, 立方晶系的Co2FeAlxSi1–x多晶材料也应属于体积守恒的线性磁致伸缩, 但是其不存在难易磁化轴上的角度依赖性, 因此可以说其磁致伸缩在不同角度的测量方向上存在分量, 如图6所示, 当磁场方向与测量方向相同时, 磁畴方向与测量方向平行, 此时磁致伸缩最大; 当磁场方向与测量方向呈30°时, 磁畴方向也与测量方向呈30°, 此时应变在测量方向上的分量减小; 当磁场方向与测量方向呈90°时, 磁畴方向也与测量方向垂直, 此时应变在测量方向上的分量为负值. 其线性磁致伸缩变化规律如下式[32]:

      其中, λs为平行于磁场方向的磁致伸缩大小, θ是磁场方向与应变测量方向的夹角, λθ为与磁场成θ角度时产生的应变分量. θ = 0°和θ =180°时为沿磁场方向的应变λθ = λs, θ = 90°时结果为垂直于磁场方向的应变λθ = –λs/2.

      由此将Co2FeAlxSi1–x (x = 0, 0.25, 0.5, 0.75, 1) 5个退火后的样品进行转角磁致伸缩测量来验证材料的体积守恒. 实验上固定应变片的位置, 以15°为间隔旋转磁场方向, 得到面内360°范围内的磁致伸缩应变数据, 并用(3)式进行拟合. 结果得出拟合曲线与实验数据比较吻合, 如图7所示, 结合这两组数据不难发现, 样品的λθ随磁场偏转角度θ呈周期性变化, 变化周期为180°, 这说明了多晶材料表现出与立方单晶类似的角度依赖性. 整体来看随着磁场偏转角度θ的增大, 应变λθ先从λs逐渐减小随后变为–λs/2再增大至λs, 当磁场方向与测量方向平行时, 也就是θ = 0°, ±180°, 达到曲线的峰值λs, 材料沿测试方向伸长, 此时应变最大; 开始偏转角度后, 应变为θ方向上的分量; 基于立方对称结构, 在θ达到约54.7°时应变为0, 随后偏转角度继续增大, 磁致伸缩应变由测量方向上的伸长转为缩短, 此时λθ为负值, 从图7可以看出, θ = ±90°时λθ位于波谷位置, 最终当磁场方向与测量方向成90°时缩短量最大, 应变大概为λs的一半, 这说明了材料的应变并没有宏观上的体积变化或者体积变化趋近于零, 充分证明了Co2FeAlxSi1–x在不同有序结构下的磁致伸缩应变均为体积守恒的线性磁致伸缩, 并且满足λtotal = 3λs/2.

      • 3.5.   部分Co基Heusler多晶合金的饱和磁致伸缩系数总结

    • 采用电弧熔炼的方法制备了Co2Fe-, Co2V-, Co2Cr-, Co2Mn-一共12种Co基Heusler合金的多晶并测量了它们的磁致伸缩值, 同时本文统计了这12种Co基Heusler合金的晶格常数, 居里温度与自旋极化率, 见表1. 根据表1数据可以看出, Co基Heusler合金的磁致伸缩普遍较小, 其中, Co2MnGa和Co2CrGa相对于其他Co基Heusler合金饱和磁致伸缩系数最高, 分别有45 ppm和42 ppm, 最低的Co2CrAl和Co2MnSb只有8 ppm, 可以说几乎没有应变产生. 理论上来说, 具有半金属性的Co基Heusler合金自旋极化率P接近100%, 但是由于实验上的原子占位无序或缺陷等影响, 实际测量得到的结果普遍在50%—60% [33]. 另外, 本文所研究的Co2FeSi 与Co2FeAl 的居里温度最高, 通过成分调控以及原子有序度调控机制有望发现耐高温、高自旋极化率的新型磁致伸缩材料.

    4.   结　论

    • 本研究通过原子占位有序度调控, 深入解析了Co2FeAlxSi1–x (x = 0, 0.25, 0.5, 0.75, 1)系列合金不同有序结构时其磁致伸缩性能的表现. Al掺杂通过削弱Si与过渡金属的强p-d轨道杂化, 驱动体系从L21有序向B2无序转变. 当x = 0.25—0.5时, L21/B2两相共存界面态通过局域晶格畸变改变磁畴各向异性, 使λs从18 ppm提高到31 ppm. 这一结果突破了传统Heusler合金依赖马氏体相变的磁致伸缩增强机制. 完全B2结构因原子占位过度混乱导致磁畴耦合减弱, λs回落至21 ppm, 证实了“适度无序”对性能优化的必要性. 转角磁致伸缩测量进一步验证了Co2FeAlxSi1–x多晶的各向同性的线性正磁致伸缩应变规律. 此外, 本研究还首次报道了12种Co基Heusler合金的磁致伸缩系数, 填补了该体系除居里温度、自旋极化率外的另一个重要参数的空白. 本研究从原子尺度揭示了无序工程对磁致伸缩性能的调控机制, 为高性能磁致伸缩材料的设计提供了新的理论与实验依据.

    参考文献 (53)

目录

/

返回文章
返回