高级搜索

基于现场可编程门阵列的高能效轻量化残差脉冲神经网络处理器实现

,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

侯悦, 项水英, 邹涛, 黄志权, 石尚轩, 郭星星, 张雅慧, 郑凌, 郝跃. 基于现场可编程门阵列的高能效轻量化残差脉冲神经网络处理器实现[J]. 物理学报, 2025, 74(14): 148701-1. doi: 10.7498/aps.74.20250390
引用本文: 侯悦, 项水英, 邹涛, 黄志权, 石尚轩, 郭星星, 张雅慧, 郑凌, 郝跃. 基于现场可编程门阵列的高能效轻量化残差脉冲神经网络处理器实现[J]. 物理学报, 2025, 74(14): 148701-1. doi: 10.7498/aps.74.20250390
shu
Yue HOU, Shuiying XIANG, Tao ZOU, Zhiquan HUANG, Shangxuan SHI, Xingxing GUO, Yahui ZHANG, Ling ZHENG, Yue HAO. Implementation of high-efficiency, lightweight residual spiking neural network processor based on field-programmable gate arrays[J]. Acta Physica Sinica, 2025, 74(14): 148701-1. doi: 10.7498/aps.74.20250390
Citation: Yue HOU, Shuiying XIANG, Tao ZOU, Zhiquan HUANG, Shangxuan SHI, Xingxing GUO, Yahui ZHANG, Ling ZHENG, Yue HAO. Implementation of high-efficiency, lightweight residual spiking neural network processor based on field-programmable gate arrays[J]. Acta Physica Sinica, 2025, 74(14): 148701-1. doi: 10.7498/aps.74.20250390
shu

基于现场可编程门阵列的高能效轻量化残差脉冲神经网络处理器实现

  • 1.

    西安电子科技大学, 空天地一体化综合业务网全国重点实验室, 西安　710071

  • 2.

    西安电子科技大学, 宽禁带半导体国家工程研究中心, 西安　710071

  • 3.

    西安邮电大学通信与信息工程学院, 西安　710121

    • 作者简介: 侯悦.E-mail: hy18834160096@163.com .
    通讯作者: E-mail: syxiang@xidian.edu.cn.; 

  • 中图分类号: 87.18.Sn, 07.05.Mh, 87.85.dq, 07.05.Pj

Implementation of high-efficiency, lightweight residual spiking neural network processor based on field-programmable gate arrays

  • 1.

    State Key Laboratory of Integrated Service Networks, Xidian University, Xi’an 710071, China

  • 2.

    State Key Discipline Laboratory of Wide Bandgap Semiconductor Technology, Xidian University, Xi’an 710071, China

  • 3.

    School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China

    • Corresponding author: E-mail: syxiang@xidian.edu.cn.; 

  • MSC: 87.18.Sn, 07.05.Mh, 87.85.dq, 07.05.Pj

  • 摘要: 随着脉冲神经网络(spiking neural network, SNN)在硬件部署优化方面的发展, 基于现场可编程门阵列(field-programmable gate array, FPGA)的SNN处理器因其高效性与灵活性成为研究热点. 然而, 现有方法依赖多时间步训练和可重配置计算架构, 增大了计算与存储压力, 降低了部署效率. 本文设计并实现了一种高能效、轻量化的残差SNN硬件加速器, 采用算法与硬件协同设计策略, 以优化SNN推理过程中的能效表现. 在算法上, 采用单时间步训练方法, 并引入分组卷积和批归一化(batch normalization, BN)层融合技术, 有效压缩网络规模至0.69M. 此外, 采用量化感知训练(quantization-aware training, QAT), 将网络参数精度限制为8 bit. 在硬件设计上, 本文通过层内资源复用提高FPGA资源利用率, 采用全流水层间架构提升计算吞吐率, 并利用块随机存取存储器(block random access memory, BRAM)存储网络参数和计算结果, 以提高存储效率. 实验表明, 该处理器在CIFAR-10数据集上分类准确率达到87.11%, 单张图片推理时间为3.98 ms, 能效为183.5 frames/(s·W), 较主流图形处理单元(graphics processing unit, GPU)平台能效提升至2倍以上, 与其他SNN处理器相比, 推理速度至少提升了4倍, 能效至少提升了5倍.
    Abstract: With the development of hardware-optimized deployment of spiking neural networks (SNNs), SNN processors based on field-programmable gate arrays (FPGAs) have become a research hotspot due to their efficiency and flexibility. However, existing methods rely on multi-timestep training and reconfigurable computing architectures, which increases computational and memory overhead, thus reducing deployment efficiency. This work presents an efficient and lightweight residual SNN accelerator that combines algorithm and hardware co-design to optimize inference energy efficiency. In terms of algorithm, we employ single-timesteps training, integrate grouped convolutions, and fuse batch normalization (BN) layers, thus compressing the network to only 0.69M parameters. Quantization-aware training (QAT) further constrains all parameters to 8-bit precision. In terms of hardware, the reuse of intra-layer resources maximizes FPGA utilization, a full pipeline cross-layer architecture improves throughput, and on-chip block RAM (BRAM) stores network parameters and intermediate results to improve memory efficiency. The experimental results show that the proposed processor achieves a classification accuracy of 87.11% on the CIFAR-10 dataset, with an inference time of 3.98 ms per image and an energy efficiency of 183.5 FPS/W. Compared with mainstream graphics processing unit (GPU) platforms, it achieves more than double the energy efficiency. Furthermore, compared with other SNN processors, it achieves at least a fourfold increase in inference speed and a fivefold improvement in energy efficiency.
  • 加载中

  • 图 1  ResNet-10脉冲神经网络结构

    Figure 1.  ResNet-10 spiking neural network structure.

    下载: 全尺寸图片 幻灯片

    图 2  标准卷积与分组卷积下ResNet-10各层参数量对比

    Figure 2.  Comparison of parameter counts for each layer of ResNet-10 under standard convolution and group convolution.

    下载: 全尺寸图片 幻灯片

    图 3  不同条件下测试准确率对比

    Figure 3.  Comparison of test accuracy under different conditions.

    下载: 全尺寸图片 幻灯片

    图 4  残差SNN处理器硬件总体架构图

    Figure 4.  Overall hardware architecture of the residual SNN processor.

    下载: 全尺寸图片 幻灯片

    图 5  卷积操作示意图

    Figure 5.  Schematic diagram of the convolution operation.

    下载: 全尺寸图片 幻灯片

    图 6  流水线设计　(a) 卷积数据处理流水线结构; (b)层间全流水架构

    Figure 6.  Pipeline design: (a) Convolution data processing pipeline structure; (b) fully pipelined inter-layer architecture.

    下载: 全尺寸图片 幻灯片

    表 1  残差SNN处理器资源利用率

    Table 1.  Resource utilization of residual SNN processors.

    名称消耗资源可用资源百分比/%
    LUTs13485942528031.71
    FF34172285056040.18
    BRAM674.5108062.45
    DSP3008427270.41
    下载: 导出CSV

    表 2  处理器和GPU平台在CIFAR-10数据集上的性能表现

    Table 2.  Performance of the processor and GPU platform on the CIFAR-10 dataset.

    硬件平台ZCU216 FPGAGeForce RTX 4060 Ti
    准确率/%88.1188.33
    功耗/W1.36951
    单张图片推理
    时间/ms    		3.980.243
    FPS2514115
    FPS/W183.580.7
    下载: 导出CSV

    表 3  在CIFAR-10数据集上与其他SNN处理器的性能比较

    Table 3.  Performance comparison with other SNN processors on the CIFAR-10 dataset.

    平台 E3NE[21] SCPU[22] SiBrain[23] Aliyev et al.[24] 本文
    FPGA型号 XCVU13 P Virtex-7 Virtex-7 XCVU13 P ZCU216
    频率/MHz 150 200 200 100 100
    SNN模型 AlexNet ResNet-11 CONVNet(VGG-11) VGG-9 ResNet-10
    模型深度 8 11 6(11) 9 10
    精度/bits 6 8 8(8) 4 8
    参数量/M — — 0.3(9.2) — 0.69
    LUTs/FFs 48k/50k 178k/127k 167k/136k(140k/122k) — 135k/342k
    准确率/% 80.6 90.60 82.93(90.25) 86.6 87.11
    功率/W 4.7 1.738 1.628(1.555) 0.73 1.369
    时延/ms 70 25.4 1.4(18.9) 59 3.98
    FPS 14.3 39.43 696(53) 16.95 251
    FPS/W 3.0 22.65 438.8(34.1) 23.21 183.5
    下载: 导出CSV
  • [1] Shelhamer E, Long J, Darrell T 2016 IEEE T. Pattern Anal. 39 640
    [2] Redmon J, Divvala S, Girshick R, Farhadi A 2016 Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Las Vegas, June 26–July 1, 2016 p779
    [3] 施岳, 欧攀, 郑明, 邰含旭, 王玉红, 段若楠, 吴坚 2024 物理学报 73 104202 doi: 10.7498/aps.73.20231902 Shi Y, Ou P, Zheng M, Tai H X, Wang Y H, Duan R N, Wu J 2024 Acta Phys. Sin. 73 104202 doi: 10.7498/aps.73.20231902
    [4] 应大卫, 张思慧, 邓书金, 武海斌 2023 物理学报 72 144201 doi: 10.7498/aps.72.20230449 Ying D W, Zhang S H, Deng S J, Wu H B 2023 Acta Phys. Sin. 72 144201 doi: 10.7498/aps.72.20230449
    [5] 曹自强, 赛斌, 吕欣 2020 物理学报 69 084203 doi: 10.7498/aps.69.20191721 Cao Z Q, Sai B, Lv X 2020 Acta Phys. Sin. 69 084203 doi: 10.7498/aps.69.20191721
    [6] Maass W 1997 Neural Networks 10 1659 doi: 10.1016/S0893-6080(97)00011-7
    [7] Nunes J D, Carvalho M, Carneiro D, Cardoso J S 2022 IEEE Access, 10 60738 doi: 10.1109/ACCESS.2022.3179968
    [8] 武长春, 周莆钧, 王俊杰, 李国, 胡绍刚, 于奇, 刘洋 2022 物理学报 71 148401 doi: 10.7498/aps.71.20220098 Wu C C, Zhou P J, Wang J J, Li G, Hu S G, Yu Q, Liu Y 2022 Acta Phys. Sin. 71 148401 doi: 10.7498/aps.71.20220098
    [9] Aliyev I, Svoboda K, Adegbija T, Fellous J M 2024 IEEE 17th International Symposium on Embedded Multicore/Many-core Systems-on-Chip (MCSoC) Kuala Lumpur, December 16-19, 2024 p413
    [10] Merolla P A, Arthur J V, Alvarez-Icaza R, Cassidy A S, Sawada J, Akopyan F, Jackson B L, Imam N, Guo C, Nakamura Y, Brezzo B, Vo I, Esser S K, Appuswamy R, Taba B, Amir A, Flickner M D, Risk W P, Manohar R, Modha D S 2014 Science 345 668 doi: 10.1126/science.1254642
    [11] Davies M, Srinivasa N, Lin T H, Chinya G, Cao Y, Choday S H, Dimou G, Joshi P, Imam N, Jain S, Liao Y, Lin C K, Lines A, Liu R, Mathaikutty D, McCoy S, Paul A, Tse J, Venkataramanan G, Weng Y H, Wild A, Yang Y, Wang H 2018 IEEE Micro 38 82 doi: 10.1109/MM.2018.112130359
    [12] 何磊, 王堃, 吴晨, 陶卓夫, 时霄, 苗斯元, 陆少强 2025 中国科学: 信息科学 55 796 doi: 10.1360/SSI-2024-0351 He L, Wang K, Wu C, Tao Z F, Shi X, Miao S Y, Lu S Q 2025 Sci. Sin. Inf. 55 796 doi: 10.1360/SSI-2024-0351
    [13] Gdaim S, Mtibaa A 2025 J. Real-Time Image Pr. 22 67 doi: 10.1007/s11554-025-01647-5
    [14] 严飞, 郑绪文, 孟川, 李楚, 刘银萍 2025 现代电子技术 48 151 Yan F, Zheng X W, Meng C, Li C, Liu Y P 2025 Modern Electron. Techn. 48 151
    [15] Liu Y J, Chen Y H, Ye W J, Gui Y 2022 IEEE T. Circuits I 69 2553
    [16] Ye W J, Chen Y H, Liu Y J 2022 IEEE T. Comput. Aid. D. 42 448
    [17] Panchapakesan S, Fang Z M, Li J 2022 ACM T. Reconfig. Techn. 15 48
    [18] Chen Q Y, Gao C, Fu Y X 2022 IEEE T. VLSI Syst. 30 1425 doi: 10.1109/TVLSI.2022.3196839
    [19] Wang S Q, Wang L, Deng Y, Yang Z J, Guo S S, Kang Z Y, Guo Y F, Xu W X 2020 J. Comput. Sci. Tech. 35 475 doi: 10.1007/s11390-020-9686-z
    [20] Biswal M R, Delwar T S, Siddique A, Behera P, Choi Y, Ryu J Y 2022 Sensors 22 8694 doi: 10.3390/s22228694
    [21] Gerlinghoff D, Wang Z, Gu X, Goh R S M, Luo T 2021 IEEE T. Parall. Distr. 33 3207
    [22] Chen Y H, Liu Y J, Ye W J, Chang C C 2023 IEEE T. Circuits II 70 3634
    [23] Chen Y H, Ye W J, Liu Y J, Zhou H H 2024 IEEE T. Circuits I 71 6482
    [24] Aliyev I, Lopez J, Adegbija T 2024 arXiv: 2411.15409[CS-Ar]
    [25] Stein R B, Hodgkin A L 1967 Proceedings of the Royal Society of London. Series B. Biological Sciences 167 64 doi: 10.1098/rspb.1967.0013
    [26] Eshraghian J K, Ward M, Neftci E O, Wang X, Lenz G, Dwivedi G 2023 Proc. IEEE 111 1016 doi: 10.1109/JPROC.2023.3308088
    [27] 刘浩, 柴洪峰, 孙权, 云昕, 李鑫 2023 中国工程科学 25 61 Liu H, Chai H F, Sun Q, Yun X, Li X 2023 Engineering 25 61
    [28] Krizhevsky A, Sutskever I, Hinton G E 2012 Adv. Neural Inf. Pro. Syst. 25 1097 doi: 10.1145/3065386
    [29] Huang G, Liu S, van der Maaten L, Weinberger K 2018 Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition Salt Lake City, US, June 18-22, 2018 p2752
    [30] Krizhevsky A, Hinton G https://www.cs.toronto.edu/~kriz/cifar.html [2025-3-22]
    [31] Ioffe S, Szegedy C 2015 arXiv: 1502.03167[CS-LG]
    [32] Zheng J W 2021 M. S. Thesis (Xi’an: Xidian University)(in Chinese)[郑俊伟 2021 硕士学位论文 (西安: 西安电子科技大学)]
    [33] Jacob B, Kligys S, Chen B, Tang M, Howard A, Adam H, Kalenichenko D 2018 Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Sale Lake City, June 18-22, 2018 p2704
    [34] Zhou S C, Wu Y X, Ni Z K, Zhou X Y, Wen H, Zou Y H 2016 arXiv: 1606.06160[cs. NE] https://doi.org/10.48550/arXiv.1606.06160
    [35] Liu Z, Cheng K T, Huang D, Xing E P, Shen Z 2022 Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition New Orleans, June 19-24, 2022 p4942
    [36] Chen Y H, Krishna T, Emer J S, Sze V 2016 IEEE J. Solid-St. Circ. 52 127
  • 加载中
图( 6) 表( 3)
计量
  • 文章访问数:  33
  • HTML全文浏览数:  33
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-26
  • 刊出日期:  2025-07-20

基于现场可编程门阵列的高能效轻量化残差脉冲神经网络处理器实现

    通讯作者: E-mail: syxiang@xidian.edu.cn.; 
    作者简介: 侯悦.E-mail: hy18834160096@163.com
  • 1. 西安电子科技大学, 空天地一体化综合业务网全国重点实验室, 西安　710071
  • 2. 西安电子科技大学, 宽禁带半导体国家工程研究中心, 西安　710071
  • 3. 西安邮电大学通信与信息工程学院, 西安　710121
  • 收稿日期:  2025-03-26

摘要: 随着脉冲神经网络(spiking neural network, SNN)在硬件部署优化方面的发展, 基于现场可编程门阵列(field-programmable gate array, FPGA)的SNN处理器因其高效性与灵活性成为研究热点. 然而, 现有方法依赖多时间步训练和可重配置计算架构, 增大了计算与存储压力, 降低了部署效率. 本文设计并实现了一种高能效、轻量化的残差SNN硬件加速器, 采用算法与硬件协同设计策略, 以优化SNN推理过程中的能效表现. 在算法上, 采用单时间步训练方法, 并引入分组卷积和批归一化(batch normalization, BN)层融合技术, 有效压缩网络规模至0.69M. 此外, 采用量化感知训练(quantization-aware training, QAT), 将网络参数精度限制为8 bit. 在硬件设计上, 本文通过层内资源复用提高FPGA资源利用率, 采用全流水层间架构提升计算吞吐率, 并利用块随机存取存储器(block random access memory, BRAM)存储网络参数和计算结果, 以提高存储效率. 实验表明, 该处理器在CIFAR-10数据集上分类准确率达到87.11%, 单张图片推理时间为3.98 ms, 能效为183.5 frames/(s·W), 较主流图形处理单元(graphics processing unit, GPU)平台能效提升至2倍以上, 与其他SNN处理器相比, 推理速度至少提升了4倍, 能效至少提升了5倍.

English Abstract

    全文HTML

    1.   引　言

    • 计算机科学技术与人工智能(artificial intelligence, AI)的飞速发展使得人工神经网络(artificial neural network, ANN)在图像处理、语音识别和目标跟踪等领域得到了广泛的应用[1–5]. 同时, 随着网络规模的不断扩大, 计算资源和能耗的需求迅速增加, 高昂的计算和存储成本成为了限制ANN发展的主要原因. 为了解决算力和存储能力的问题, 研究者们模仿生物神经系统工作机制, 提出了被誉为第3代神经网络的脉冲神经网络(spiking neural network, SNN)[6]. 与ANN相比, SNN的结构更接近人脑, 其采用脉冲序列完成各层之间信息的传递[7], 在计算效率和能效优化方面均得到巨大提升[8]. 此外, SNN的稀疏性使得神经元只在特定时间步激活, 网络也只在神经元激活时进行计算, 从而有效减少冗余计算, 降低硬件资源开销, 并显著提升能效[9].

      现场可编程门阵列(field-programmable gate array, FPGA)作为一种灵活且高效的硬件平台, 近年来逐步成为SNN加速的理想选择. 虽然与之对应的专用集成电路(application specific integrated circuit, ASIC)在性能和效率上可能会表现出更卓越的性能, 比如IBM的TrueNorth[10]和英特尔的Loihi[11]. 但是每一款ASIC芯片都是根据特定的需求和任务设计的, 一旦设计完成, 若需要修改就要重新设计芯片, 缺乏灵活性和适用性[12]. 而FPGA能够在保证高效计算的基础上体现出更高的灵活性和适用性[13], 设计人员可以根据任务和需求对硬件架构重新设计和编写, 以适应快速迭代的网络和算法更新, 提高加速器的性能[14]. 因此, 在需要灵活变更硬件架构的情况下, FPGA比ASIC更适合处理SNN的加速. 此外, SNN稀疏的特性, 使得大部分神经元在多数时刻保持静止, 只有少量神经元在特定时间点发放脉冲[9], FPGA可有效利用这种稀疏性, 在资源利用率与功耗方面展现出显著优势[15,16].

      近年来, 基于SNN的低功耗、事件驱动特性, 众多硬件架构被相继提出[17–20], 以实现更低的延迟和更高的能效. 2022年, Gerlinghoff等[21]提出了一种支持大规模SNN的端到端编译框架E3NE, 该框架采用多层次并行的全新编码方案, 有效提升了计算效率, 使硬件资源占用降低50%以上, 功耗减小20%, 并将推理延迟缩短了1个数量级; 2023年, Chen等[22]提出了一种高性能通用脉冲卷积处理单元(SCPU)及其硬件架构, 该处理器在CIFAR-10和CIFAR-100数据集上的识别率分别达到92.45%和68.55%, 前向推理帧率可达40 frames/s, 显著加速了深度SNN尤其是在残差块模型上的推理过程; 2024年, Chen等[23]进一步提出了SiBrain类脑计算硬件架构, 其核心包括用于脉冲卷积与池化计算的稀疏时空并行处理单元阵列, 以及负责脉冲全连接计算的全连接核心. 该架构实现了CIFAR-10数据集上90.25%的分类准确率, 能效高达83GSOPs/W; 同年, Aliyev等[24]首次提出直接编码混合推理架构, 其主要思想是通过密集核心直接处理输入层数据, 并利用稀疏核心进行事件驱动的脉冲卷积计算, 该方法在吞吐量和功耗方面相较现有方案均具备显著优势.

      尽管这些设计在提升SNN硬件加速器的性能方面取得了重要进展, 但仍存在一些局限性. 例如, 许多方案采用多时间步训练以提高网络精度, 这无形中增加了计算和存储开销. 此外, 大多数设计依赖可重配置计算架构, 并需要频繁访问片外存储器, 导致额外的时延和功耗. 为解决上述问题, 本文实现了一种轻量化的ResNet-10脉冲神经网络, 并采用单时间步训练方案以降低计算复杂度. 在网络中采取分组卷积、量化感知训练(quantization-aware training, QAT)、批归一化(batch normalization, BN)层融合等策略将模型参数量压缩到0.69M. 此外, 在FPGA平台上实现了基于该网络的处理器架构. 卷积计算单元采用层内资源复用策略, 以提高资源利用率, 层间则采用全流水架构以提高计算吞吐率. 网络参数和计算结果均存储于片上块随机存取存储器(block random access memory, BRAM). 最后, 本文所提出并实现的FPGA残差脉冲神经网络处理器在推理时间和能效方面均展现出卓越的性能.

    2.   网络设计与轻量化处理

    • SNN本质上具备稀疏性和事件驱动特性, 这种特性使其在神经形态处理器上能够实现高效计算. 然而, 在实际硬件部署中, SNN仍然面临诸多挑战. 一方面, 时间动态特性显著增加了计算复杂度; 另一方面, 存储膜电位的需求导致较高的内存占用, 进一步制约了系统的能效表现. 为了解决这些问题, 本文引入分组卷积、减少时间步、量化等关键技术, 对网络模型进行深度压缩, 以有效降低内存使用和计算开销. 这些方法不仅减少了数据计算和存储需求, 也提升了推理效率, 使深度SNN能够更高效地适配低功耗硬件平台.

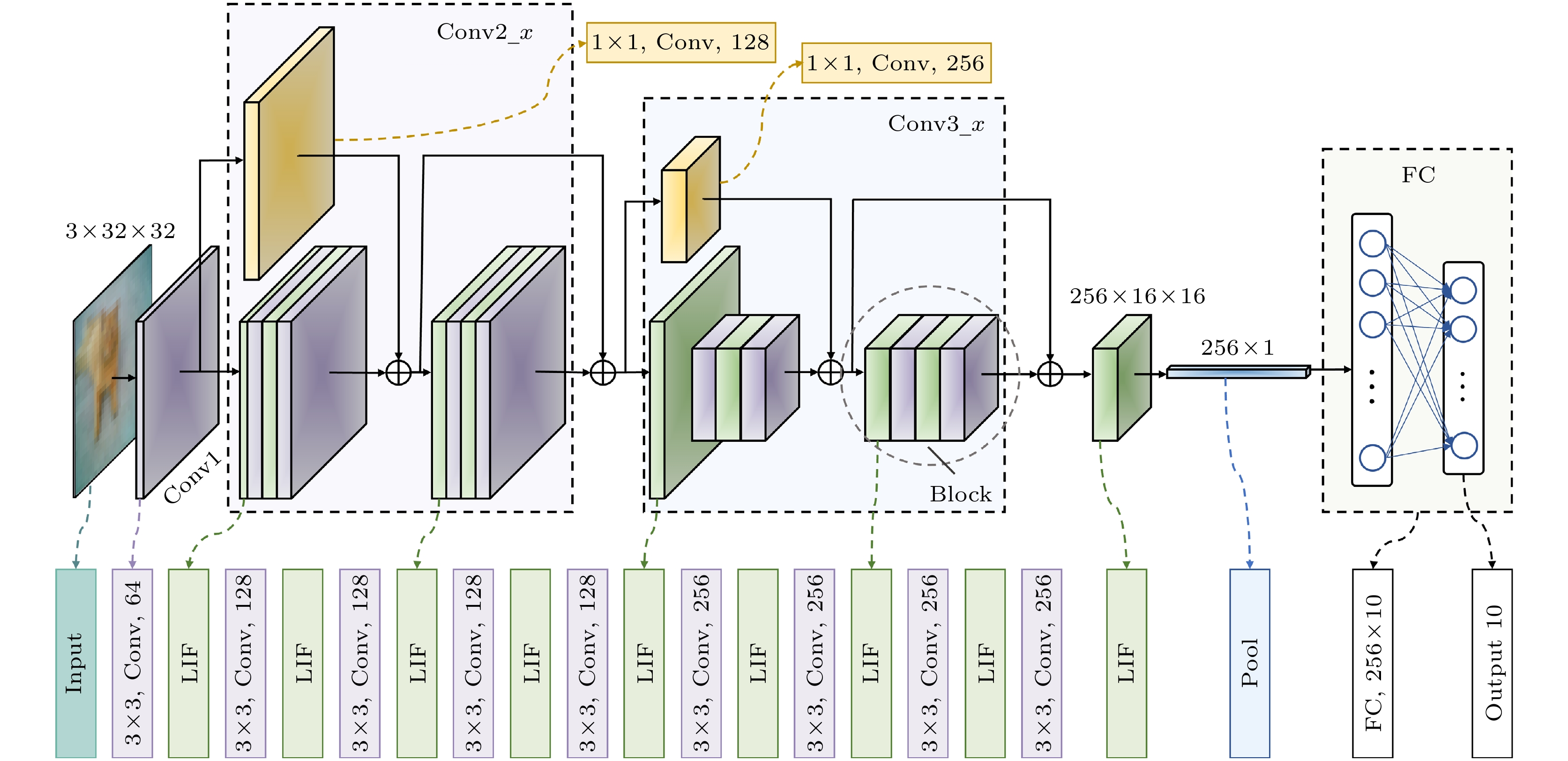
      本文所用网络模型为ResNet-18的变体, 为了压缩模型规模, 去掉了ResNet-18中64通道和512通道的部分, 仅保留10层可训练权重(不含残差连接shortcut), 即ResNet-10脉冲神经网络, 网络结构如图1所示. 其中Conv1为卷积编码层, 负责将输入转换为脉冲信号; Conv2_x和Conv3_x各含两个残差块(block), 作为特征提取模块, 主要由卷积层和激活层构成; 池化(pool)层位于全连接(fully connected, FC)层前, 将256张特征图压缩为256×1的向量.

      网络中的激活层采用LIF (leaky integrate-and-fire)神经元模型[25]. LIF神经元模型可以表示为[26]

      式中, ${I_{{\text{in}}}}$是输入的刺激电流, $U$是膜电压, $R$是膜电阻, $\tau $是电路的时间常数. 当多个前神经元对该神经元膜电位的加权和作用超过阈值的时候, 神经元被激发并向随后的连接发出一个脉冲信号${S_{{\text{out}}}}$:

      其中${U_{{\text{th}}}}$是膜电位的阈值.

      LIF神经元模型既保留了泄漏、积分和阈值发放等生物特性, 还极大地简化了计算模型, 其运算主要依赖加法与乘法操作, 便于在硬件上实现大规模神经元的部署, 尤其是需要低资源消耗和低功耗的移动设备、边缘计算设备等[27].

      • 2.1.   分组卷积策略

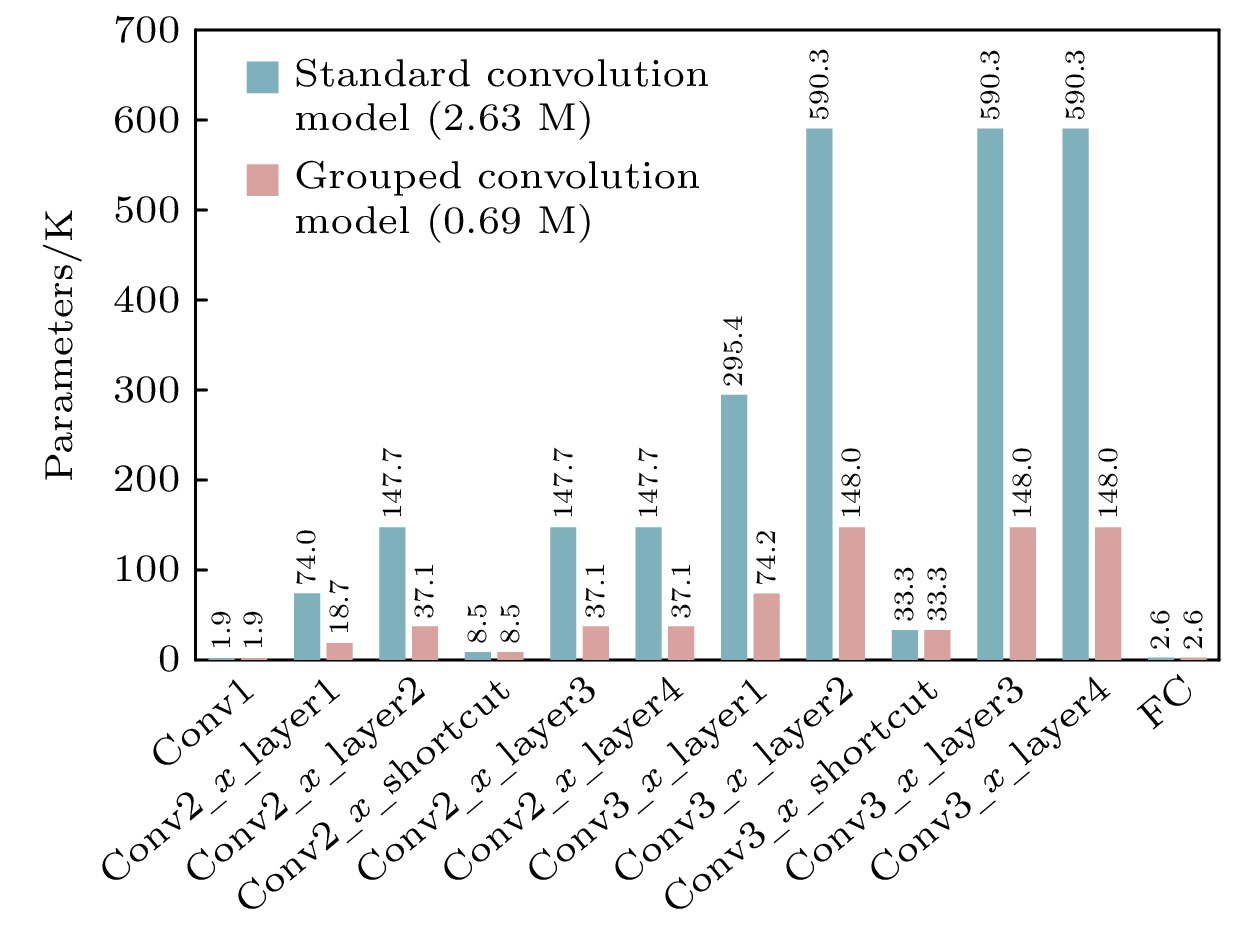
    • 分组卷积最早被用在AlexNet上切分网络, 解决内存有限问题[28]. 现在也被广泛用来减少模型的参数量, 提高计算效率并节省存储资源. 在分组卷积中, 输入和卷积核被分组, 每个卷积核都只与组内对应的特征图进行卷积操作. 假如输入特征图的通道为${C_{{\text{in}}}}$, 输出特征图的通道为${C_{{\text{out}}}}$, 输入数据的分组参数为$g$, 卷积核的大小为$k \times k$, 则每组输入特征图的数量为${C_{{\text{in}}}}/g$, 经过卷积计算输出特征图的数量为${C_{{\text{out}}}}/g$. 传统卷积参数量${P_{\text{c}}}$和分组卷积参数量${P_{\text{g}}}$分别可由(3)式和(4)式计算得出[29]:

      图2对比了一个时间步, 且$g = 4$条件下, 网络中分别采用标准卷积和分组卷积时各层的参数量. 结果表明, 引入分组卷积后, 模型参数量几乎可以降低为原来的1/4, 仅有0.69M.

      • 2.2.   时间步长选择

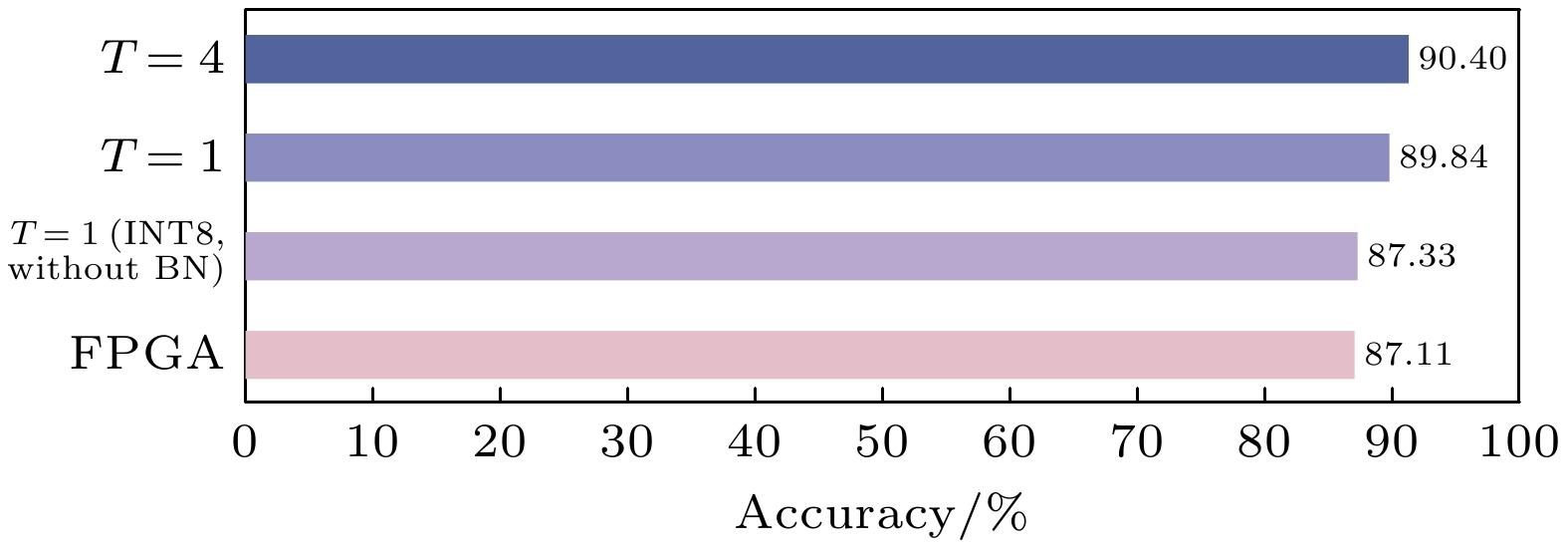
    • 作为SNN重要参数之一, 时间步长T的大小直接影响着网络性能. 较大的T值会增加网络的纵向深度, 提升信息表达能力, 但也显著增加计算开销; 而较小的T值虽然会降低模型复杂度和参数量, 但会带来准确率的下降. 图3比较了网络在CIFAR-10数据集[30]上不同条件下的测试准确率. 训练轮次为500轮时, T = 4的模型分类最大准确率为91.40%, T = 1的模型分类最大准确率为89.84%. 显然如果只考虑准确率, T = 4模型性能更好. 然而, 在硬件部署时, 快速推理速度与低功耗更为关键. 虽然T = 1模型在准确率上有所下降, 但其激活过程无需复杂计算和膜电位存储, 仅需将加权信号与阈值比较. 这不仅显著降低了硬件资源占用和计算时间, 还提升了部署效率. 综合考虑, 本文最终选择T = 1的模型.

      • 2.3.   BN层融合

    • 在神经网络中, 卷积层通常后接一个BN层, BN层通过标准化每层输入, 使激活函数的输入值集中在非线性函数的敏感区间内, 进而使梯度增大, 加速学习过程的收敛速度. 为了进一步压缩网络模型, 本文将BN层融合到了卷积层中.

      在训练过程中, 卷积操作可以表示为:

      其中, $ {x_i}(i = 1, 2, \cdots, n) $为第i个前神经元对当前神经元输入的信号, $ w_i\left(i=1,2,\cdots,n\right) $为第i个输入信号对应的权重, b表示神经元偏移量, y是该神经元的输出信号.

      BN层运算具体的算法见(6)式[31], 对于一个批次中的某样本, 假设BN层的输入为y, 则经过BN层后的输出为

      其中, $\mu $为该批次的均值, ${\sigma ^2}$为标准差, $\varepsilon $是为了避免除零错误引入的一个非常小的常数. $\gamma $和$\beta $是可变参数, 会在训练中和其他参数一样学习更新. 但是在推理过程中, 这4个数据是固定的, 可以通过线性计算将BN层融合到卷积层中, 上面的BN层计算公式可以变形为(7)式[32], 在推理时, 系数c和d都是常数:

      因此, 在网络推理时, 可以通过将卷积权重从原始值调整为c, 偏置从b调整为d, 从而实现卷积层与BN层的融合. 由于BN层的计算过程是线性的, 因此这一融合方式几乎不会影响模型精度. 此外, 去除BN层后, 不再需要执行开平方和除法等计算, 显著简化硬件设计, 减少计算和存储开销, 从而降低整体能耗.

      • 2.4.   参数量化

    • 对于量化, 本文采用QAT[33]方法将网络中浮点数转换为定点数, 通过在模型中插入伪量化节点以模拟量化误差的影响. 具体而言, 在前向传播过程中, 计算采用量化后的精度, 而在反向传播时, 梯度更新仍然使用浮点类型, 以减少量化对优化过程的影响. 量化操作在前向传播时遵循(8)式—(10)式[34], 而在反向传播时遵循(11)式[35]. 其中, $r$为浮点数, $q$为转换后的定点数, $S$为缩放因子, $k$为定点数的位宽. 参数的量化采用对称均匀量化, 需要求取最大绝对值, 即${r_{\max }}$:

      由于量化操作具有不连续性, 直接计算其梯度较为困难, 因此采用直通估计器(straight-through estimator, STE)进行近似梯度计算. STE通过忽略取整操作对梯度的影响, 使得梯度可以直接传递给未量化的变量, 从而使模型仍然能够通过梯度下降进行训练[35]. 这种方法有效降低了量化对模型优化的影响, 提高了量化网络的训练稳定性和最终精度.

      在本文实现中, 所有权重量化到 8 bit. 从图3可以看出, 在单时间步条件下, 融合BN层并以8 bit精度进行QAT微调100轮后, 模型测试准确率可达到87.33%. 与未进行BN层融合及量化的单时间步模型相比, 准确率降低2.51%. 在实际的应用中, 计算效率和能效相较于绝对的精度更加重要, 所以从综合性能出发, 本文在算法中选取时间步长T = 1、融合BN层, 并采用QAT将参数量化到8 bit的方案, 在保持较高精度的同时提升部署效率与硬件友好性.

    3.   处理器硬件系统的设计与实现

      3.1.   处理器整体框架设计

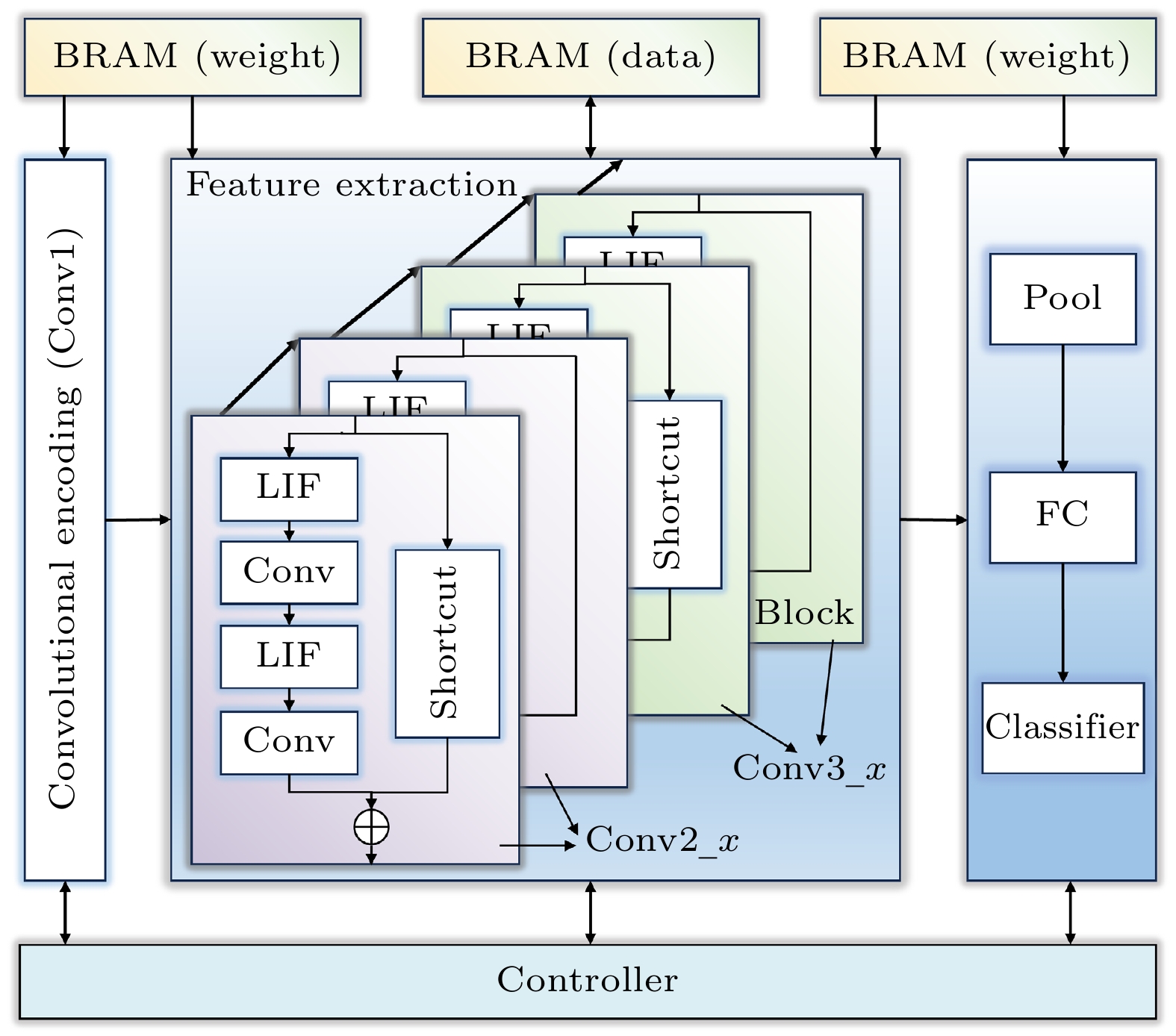
    • 本文设计的残差SNN处理器硬件架构见图4. 该架构核心部分为特征提取模块, 包括4个Block, 这4个Block并行运算以提高计算速度和处理效率. 每个Block内部包含两条分支计算路径, 一条分支路径执行两次激活和两次脉冲卷积操作, 另一条分支实现残差卷积或直接映射操作. 池化模块和全连接分类模块则负责接收来自特征提取部分输出的脉冲信号, 并对其进行处理, 最终生成分类结果. 在硬件设计中, 所有的网络参数和中间计算结果都存储在片上BRAM中, 确保数据的快速访问和存取, 避免外部存储器带来的访问时延. 整个系统的调度由控制器负责, 控制器通过精确的输入输出数据调度, 确保各个模块协同工作.

      • 3.2.   核心部分卷积模块设计

    • 在网络中, 卷积操作占据绝大部分计算和存储资源, 因此针对卷积的优化能够显著提升处理器效率. 本文借鉴Chen等[36]在Eyeriss芯片中的设计, 对卷积模块进行改进.

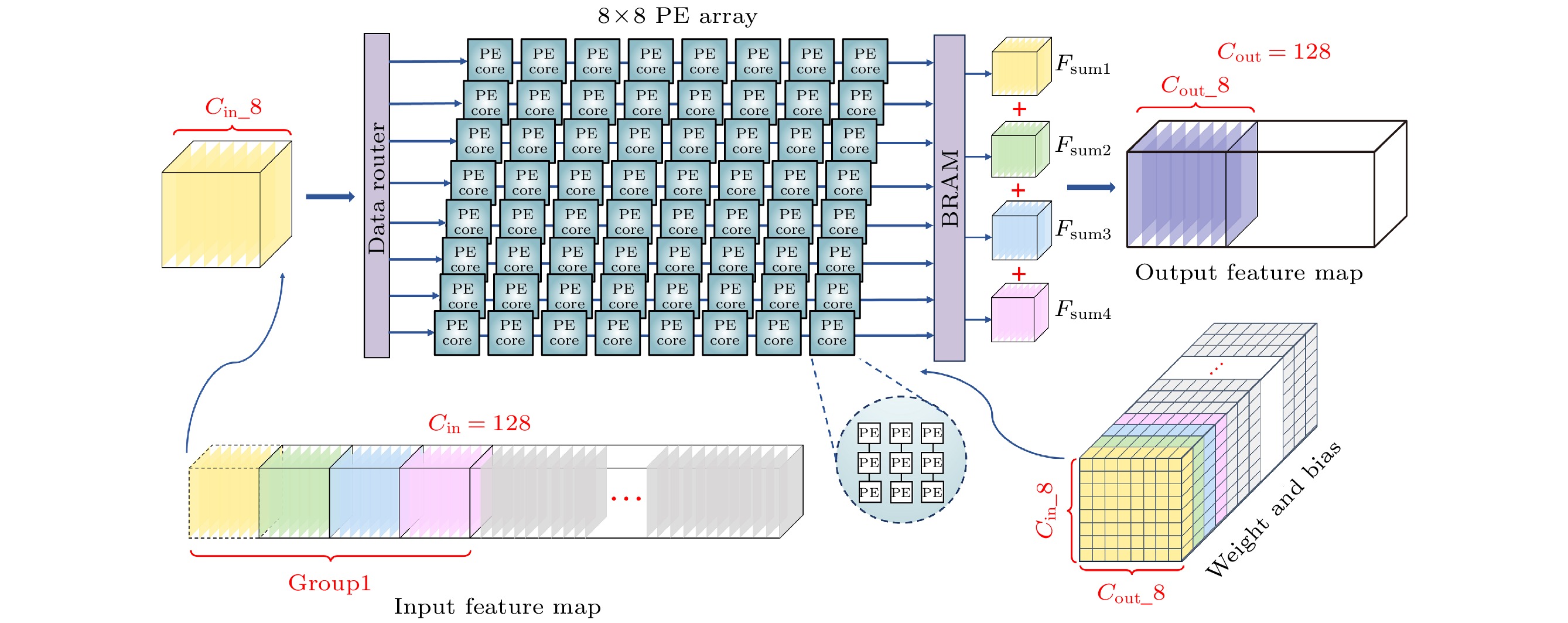
      图5为主路径中卷积操作的示意图. 每个计算单元(processing element, PE)可以完成一个乘加运算, 9个PE构成一个计算单元核心(processing element core, PE core), PE core在一个时钟完成一个3×3卷积核的操作. 卷积网络的主体计算单元阵列(processing element array, PE array)由64个PE core组成. 在PE array中, 权重和偏置事先从BRAM中加载进入网络, 权重加载成功后, 控制信号从存储特征图的BRAM中将图片读出, 并进行填充和滑动取值操作, 输入到PE Array中. 阵列中共有8个并行的输出通道, 每个输出通道又可以并行计算8个输入通道的值, 最后将8个输入通道得到的特征图相加得到输出特征图Fsum, 存入存放输出特征图的BRAM中. 因为输出通道共用输入通道的特征图, 所以特征图流入PE Array后对每一个输出通道进行广播.

      对于分组卷积的设计, 在图5中以128通道输入和128通道输出的卷积为例, 每个输出通道的结果取决于组内32个输入通道的特征图与对应卷积核的计算结果, 所以, 每8个输出通道的计算需要对PE array复用4次, 再将4次的结果(图5中的Fsum1-Fsum4)对应相加即可. 卷积过程中, 控制器负责切换输入特征图和卷积核参数. 权重和偏置按照PE array的物理排布存储于BRAM中, 每复用一次 PE array即切换一次; 输入特征图虽然也随PE array的工作节拍切换, 但在同一组输出特征图全部生成之前, 仅在组内循环使用, 不会重新从外部存储加载.

      由于网络采用全流水架构, 层间PE array结构并不通用. 编码层中, PE array大小为3×64, 因传递的信息为非脉冲信号, PE由数字信号处理器(digital signal processor, DSP)构成, 执行乘加运算. 主路径卷积中, PE array大小为8×8, 传递信息为脉冲信号, 无需DSP参与. 侧边残差卷积中, PE array大小为64×8, PE由DSP构成并执行乘加运算, 由于该部分卷积核大小为1×1, 所以每个PE core内仅包含一个PE.

      • 3.3.   流水线设计

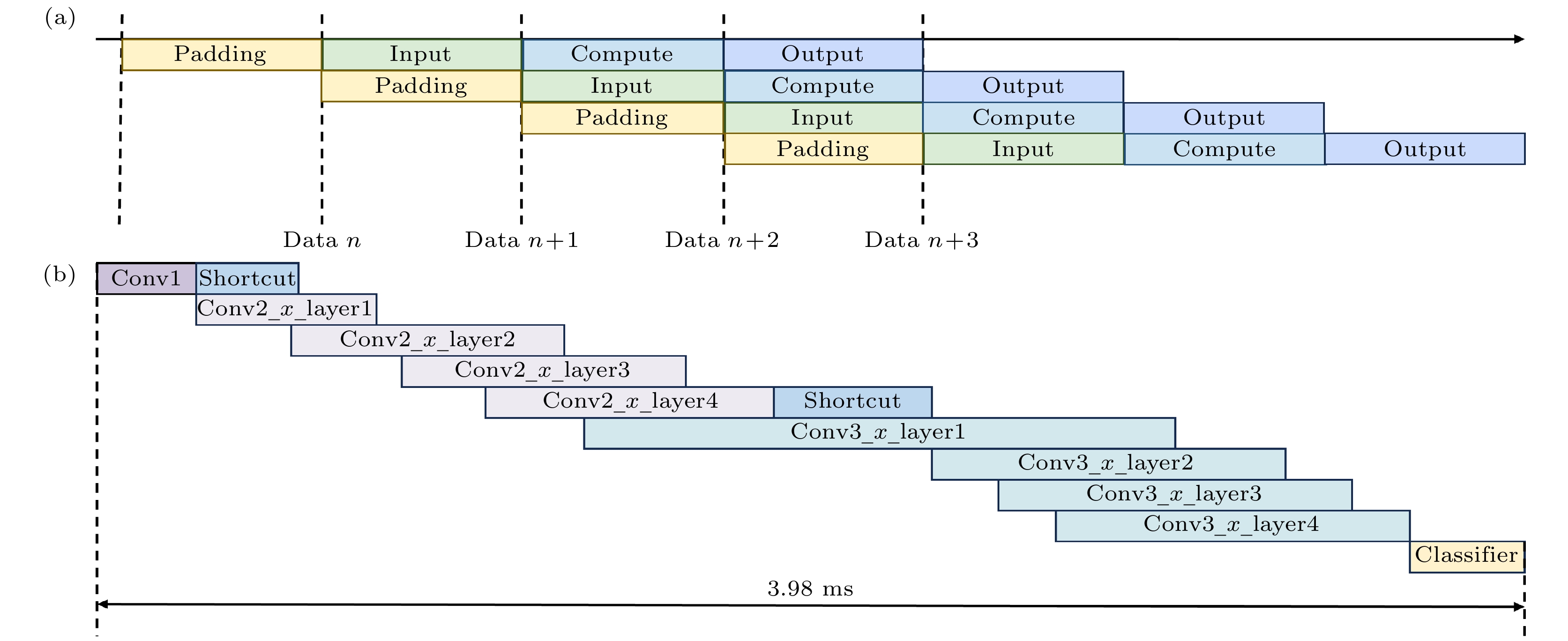
    • 卷积操作中数据处理包括填充(padding)、输入(input)、卷积计算(compute)和数据输出(output)4个独立的步骤, 彼此间互不干扰, 具备类似流水线的特性. 因此, 本文采用流水线优化卷积计算. 图6(a)为卷积操作数据处理中流水线结构的示意图, 可以看出, 流水线可以在不消耗太多资源的情况下减小时延, 提升系统吞吐量. 此外, 不仅卷积模块是流水线方式, 在其他部分设计中, 也参考了流水线的设计思想, 设计整体采用全流水层间架构, 如图6(b)所示. 全流水层间架构可以通过层间并行计算提高计算速度, 在该架构下, 单张图片推理时间仅为3.98 ms.

    4.   数据分析与讨论

    • 表1展示了处理器在FPGA上的资源消耗情况, 其中DSP和BRAM占比最高. 由于处理器采用了全片上存储策略, 因此BRAM占用比例较大. 同时, DSP资源的使用量直接影响着计算速率, 为了提高推理速度, 处理器也使用了较多的DSP资源.

      表2为本文在CIFAR-10数据集[30]上对处理器及GPU(GeForce RTX 4060 Ti)测试对比后的结果. 其中FPS表示处理器每秒可处理的图像帧数, 用来衡量其计算速度, FPS/W反映了处理器的能效, 即每消耗1 W功率可处理的图像帧数. 从中可以看出, 相比GPU, 处理器准确率下降0.22%. 这一差距主要源于训练时仅对权重和偏置进行量化, 而在FPGA推理时, 输入也经过量化处理, 导致最终准确率略有下降. 在FPGA上, 通过动态功耗和单张图片推理时间评估其性能; 在GPU上, 以10万张图片的推理时间计算单张推理时间, 并测得实时功耗, 从而计算其性能. 结果表明, FPGA处理单张图片的时间为GPU的16倍, 但能效提升超2倍. 可见, 即使资源有限, FPGA仍然实现较高能效, 展现出优越的计算资源利用率, 适用于边缘计算设备部署.

      表3对比了本文设计开发的残差SNN处理器与其他研究在CIFAR-10数据集上的图像识别性能. 表中数据均摘自各参考文献的原始结果, 或在文中提供的公开数据基础上进行统一计算与换算, 以确保公平可比.

      E3NE[21]是一个可以实现SNN推理的端到端FPGA加速框架, 其将高效编码和硬件并行化相结合, 在MNIST上可以实现99.1%的精度, 推理时间只需要0.294 ms. 但是网络较深时, 卷积层与池化层需在多个网络层间复用, 且参数存储在片外内存, 导致推理延迟增大, 进而降低能效. 在CIFAR-10任务中, E3NE采用8层浅层网络和6 bit量化, 虽然资源开销较小, 但识别精度受限. 相比之下, 本文处理器采用全流水层间架构, 使用8 bit定点量化和改进的ResNet-10网络, 在准确率上提升了6.51%的同时能效提升61倍. 尽管LUT和FF的使用量分别为E3NE的2.8倍和6.8倍, 但整体能效优势仍十分显著.

      SCPU[22]架构包含256个并行单元, 每个单元集成LIF脉冲神经元模块与两条计算路径, 分别支持标准脉冲卷积与残差脉冲卷积, 有效提升了并行计算能力. 该设计结合感知量化与卷积融合优化, 并跳过膜电位衰减和阈值判断, 进一步加快计算. 不过, 本文引入分组卷积与单时间步推理策略, 使模型更加轻量化, 在保证精度相当的同时, 实现了6倍的帧率提升与8倍的能效提升.

      SiBrain[23]架构则采用时空并行阵列, 在空间上支持多通道并行, 时间维度上可同步处理4个时间步, 显著降低推理延迟. 然而, 其权重存储依赖片外DDR, 增加了访问延迟. SiBrain在CIFAR-10数据集上测试了CONVNet与VGG-11两种模型, 其中CONVNet网络较浅, 能效表现较优但精度较本文低4.18%; 在VGG-11网络下, 虽然本文处理器精度略低, 但得益于单时间步推理策略, 以及全片上存储机制, 有效降低了图片处理时延, 使得推理帧率达到SiBrain的4倍, 能效提升超过5倍.

      Aliyev等[24]设计的处理器将网络划分为稀疏层与密集层, 依据负载需求灵活分配硬件资源. 其通过压缩脉冲序列(仅记录有效位“1”)以及设置时钟门控(仅为活跃区域提供时钟信号)、量化参数到4 bit、采用移位计算代替DSP等方法, 有效降低功耗至0.73 W. 然而, 该架构采用4 bit精度, 时间步长大于1, 存在精度和延迟上的限制. 相比之下, 本文处理器在保持更高精度的同时, 通过分组卷积降低参数规模并减少计算量, 实现了7.9倍的能效提升.

      可见, 本文处理器在确保准确率与其他研究相当的前提下, 通过采用全流水层间架构显著提升了运行效率, 在能效方面尤为突出. 此外, 本文设计完全映射于片上, 在无片外存储访问的情况下实现了卓越的性能, 不仅消除了E3NE等设计中可重配置计算架构所带来的额外功耗, 同时也大幅提升了数据吞吐量.

    5.   结　论

    • 本文设计并实现了一种高能效、轻量化的残差SNN硬件加速器, 采用算法与硬件协同设计的策略, 以优化SNN推理过程中的能效表现. 在算法层面, 本文实现了一种轻量化、适用于硬件部署的ResNet-10脉冲神经网络, 并采用单时间步长训练网络. 本文通过BN层融合、QAT量化和分组卷积方法, 使模型参数量压缩至0.69M. 在硬件设计上, 本文通过层内资源复用提高FPGA资源利用率, 采用全流水层间架构提升计算效率, 并利用BRAM存储网络参数和计算结果, 以减少片外存储访问. 最终, 本文在ZCU216 FPGA平台上完成了处理器的部署. 实验结果表明, 本文处理器与主流GPU平台相比, 能效提升超2倍; 与其他SNN处理器相比, 推理速度提升至少4倍, 能效提升至少5倍. 未来, 不仅可以进一步探索权重和特征图的稀疏性以压缩网络规模, 还可以进一步提升网络的全流水处理能力以缩短推理时延, 从而推动SNN硬件加速器在低功耗AI计算中的广泛应用.

    参考文献 (36)

目录

/

返回文章
返回